Open Access Article
Open Access ArticleDirect measurement of the viscosity of ternary aerosol mixtures†
Sunandan
Mahant
 a,
Emil Mark
Iversen
a,
Emil Mark
Iversen
 b,
Sabin
Kasparoglu
b,
Sabin
Kasparoglu
 a,
Merete
Bilde
a,
Merete
Bilde
 b and
Markus D.
Petters
b and
Markus D.
Petters
 *a
*a
aDepartment of Marine, Earth, and Atmospheric Science, North Carolina State University, Raleigh, North Carolina, USA. E-mail: mdpetter@ncsu.edu
bDepartment of Chemistry, Aarhus University, 8000 Aarhus C, Denmark
First published on 16th February 2023
Abstract
Secondary organic aerosols contribute a large fraction to atmospheric aerosols. The phase states of secondary organic aerosols influence heterogeneous and multiphase chemistry in the atmosphere and thus climate. In previous studies we have used the dual tandem differential mobility analyzer technique to characterize the temperature- and humidity-dependent viscosity and glass transition temperature of suspended particles. However, the technique requires high particle number concentrations, is a complex setup, is expensive, and measurements are time consuming. Here we demonstrate a new simplified and more cost-effective method to obtain similar data. The technique was used to measure the temperature where the viscosity is ∼107 Pa s for submicron particles composed of binary and ternary mixtures of the sucrose/tartaric acid/citric acid system. Sucrose, tartaric acid and citric acid are taken as proxies for viscous organic aerosol components in the atmosphere. A subset of data were compared to measurements with the dual-tandem differential mobility analyzer method. Results show good agreement between the two techniques. The same mixed chemical systems were modeled using an updated version of the parametric phase diagram model described in Kasparoglu et al. (2021, https://doi.org/10.5194/acp-21-1127-2021) as well as the predictions with the viscosity module of the Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients model (AIOMFAC-VISC). Results show that appropriately parameterized mixing rules are suitable to describe these mixtures. We anticipate that the new technique will accelerate discovery of aerosol phase transitions in aerosol research.
Environmental significanceAtmospheric particles have been shown to assume highly viscous or glassy phase states. Furthermore, prior research has shown that chemical reactions can be slowed or inhibited inside glassy particles. This, in turn, impacts the evolution and fate of particle borne pollutants in the atmosphere. The measurement of the viscosity of suspended submicron particles remains challenging. This work introduces a new method to measure viscous phase transitions. The technique is simpler, cheaper, and more powerful than previous methods. The method is applied to measure the viscosity for ternary mixtures and evaluate model predictions of the resulting phase diagram. We anticipate that this research will enable better characterization of amorphous phase transitions in ambient particles. |
1 Introduction
Atmospheric organic particles have been shown to exist in amorphous glassy or highly viscous phase states.1,2 Pure glassy organic compounds have been shown to nucleate ice at upper free tropospheric conditions.3 Glassy phase states also slow diffusion of molecules through the organic matrix compared to the liquid state.4 This may shield organic compounds from evaporation and chemical degradation and, in turn, lead to long-range transport of some harmful organic compounds.5 These findings motivated a decade of prior work seeking to improve the measurement of viscosity in particles and work to improve quantitative predictions of viscosity as a function of temperature, relative humidity, and chemical composition.Viscosity measurements of aerosol samples can be broadly categorized into online and offline methods. Offline methods collect the aerosol sample onto a substrate. Viscosity is then obtained by measurement of the mobility of insoluble beads embedded in the organic matrix,6 measurement of the restoration of shape in response to poking the sample with a needle,7 measurement of the fluorescence lifetime of molecular rotors embedded in the organic matrix,8 measurement of particle coalescence inside an optical trap or under an electron microscope,9,10 or measurement of particle roundness as a function of temperature.11 These offline techniques generally require the generation of several milligrams of material. Sample modification after collection via evaporation of semi-volatile compounds or uptake of moisture or reaction with atmospheric oxidants may occur. Viscosity at the nanoscale may diverge from those of bulk samples.12,13 Therefore, it is preferable to sample the aerosol directly from the source to probe viscosity while the particles are airborne without the need to separate the particles from their surrounding gas phase.
A few online methods for probing particle viscosity have been developed. These methods measure either the bounciness of particles entering an impactor,1 or the temperature or relative humidity at which particle agglomerates coalesce into spheres.14–17 Bounce factor measurements probe viscosity at ∼102 Pa s.18,19 In contrast, shape relaxation measurements probe viscosity at ∼107 Pa s. This corresponds to viscosities when particle diffusion predicted by the Stokes–Einstein equation slows to ∼6.6 × 10−20 m2 s−1 for 0.8 nm diffusing molecules.7 This viscosity typically occurs at temperatures ∼20–30 K warmer than the glass transition temperature for complex organic mixtures.20 For reference the diffusion coefficient implies an intraparticle mixing time of ∼9.6 hours for 300 nm particles and ∼5.8 min for 30 nm particles. Zhang et al.,16 Järvinen et al.,14 and Bell et al.17 measured the sintering of agglomerates formed by natural coagulation. These studies identified the change in agglomerate shape by measuring changes in particle density or changes in light depolarization. Rothfuss & Petters (2016)15 used the dual tandem differential mobility analyzer (DMA) method to synthesize dimer particles. Changes in shape were observed by measuring changes in particle mobility using a third DMA. Since the dimer particles are synthesized, the technique can in principle be applied to all sizes accessible with mobility analyzers as well as particle sources other than environmental chambers. In practice, however, the technique is limited by the need for high (>∼75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−3) size-selected particle number concentration when working with dimers of equal composition.21,22 Applications using the dual tandem DMA have thus been limited to particles generated by atomization15,23–25 and secondary organic aerosols generated from oxidation flow reactors.20,26,27 Measurements of ambient particle sources or particles generated inside an environmental chamber have not been possible. Online methods that work at low number concentration and with non-agglomerated particles are not yet available.
000 cm−3) size-selected particle number concentration when working with dimers of equal composition.21,22 Applications using the dual tandem DMA have thus been limited to particles generated by atomization15,23–25 and secondary organic aerosols generated from oxidation flow reactors.20,26,27 Measurements of ambient particle sources or particles generated inside an environmental chamber have not been possible. Online methods that work at low number concentration and with non-agglomerated particles are not yet available.
Predicting viscosity from chemical composition has generally followed established semi-empirical parameterizations. These parameterizations highlight the importance of mixing rules for glass transition, temperature dependence of viscosity, compound molecular weight, oxygen-to-carbon ratio, and functional group composition.12,23,25,28–32 Several studies have investigated the viscosity of mixed organic particles. These studies either discuss highly complex and not fully speciated mixtures such as secondary organic material12,28,29,33 or simple compositions with one or two solutes and the addition of particle phase water.10,23,24,31,34–37 Systematic studies testing mixing rules for more complex mimics with known composition are needed.
This work presents a new method that characterizes aerosol particle viscosity in the same order of magnitude as the shape relaxation technique, i.e., ∼107 Pa s. The method probes the restructuring of slightly aspherical particles due to temperature induced changes in viscosity. It uses a single DMA and a printed optical particle spectrometer, POPS.38 It is based on recent findings that demonstrated that the sintering of particle dimers can lead to an increase in light scattering intensity measured by the POPS.39 Here we show that the restructuring of slightly aspherical solid particles formed by rapid drying can also be detected in the POPS light scattering signal. The resulting technique provides measurements of viscosity at ∼107 Pa s. It allows for faster, simpler, and cheaper measurement of particle viscosity. Furthermore, it is not limited to the high particle number requirements of the dual tandem DMA. The new technique is applied to systematically characterize the temperature where binary or ternary mixtures comprising dry sucrose, citric acid, and tartaric acid restructure. It is shown that the results are comparable to those obtained from the dual tandem DMA method. The ternary system is modeled using a slightly modified version of an existing phase diagram model23 and the viscosity module of the web version of the Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients model, AIOMFAC-VISC.29
2 Methods
2.1 Measurement setup
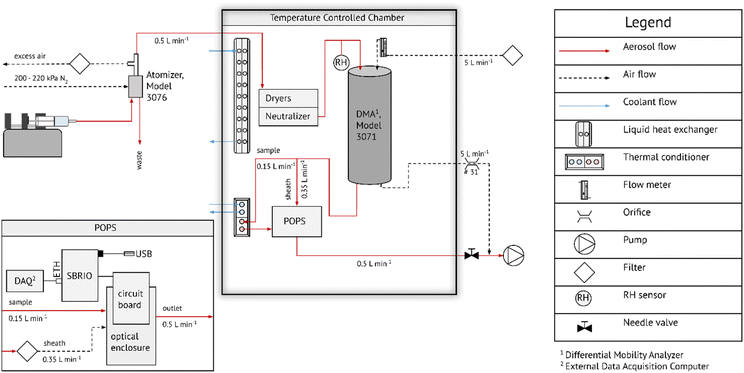
Fig. 1 shows a schematic of the experimental setup. A syringe infusion pump was used to feed liquid into a constant output atomizer (TSI 3076). Sample flow drawn from the atomizer was 0.5 L min−1. The sample flow was passed into an insulated box where the temperature was maintained at ∼8 °C using a liquid heat exchanger that was drawing cooling liquid from a chilled bath circulator. This temperature is referred to as the system temperature, Ts. The aerosol was dried using two silica gel columns followed by charge equilibration using a 210Po neutralizer. The sample relative humidity (RH) and temperature was measured using a Rotronic HC2 sensor. The sample flow RH was typically 1 < RH < 4% after drying. The particles passed through an electrostatic classifier, which consisted of a cylindrical DMA column (TSI 3071) operated at 5 L min−1 sheath flow. The sheath flow was drawn from N2 boiled off liquid N2 to ensure that the RH inside the DMA remained effectively zero. The monodisperse flow was split into sheath flow (0.35 L min−1) and sample flow (0.15 L min−1) using the modified flow setup of the POPS introduced in Kasparoglu et al. (2022).39 The sample flow is continuously measured from the pressure drop across a laminar flow element. Prior to entering the POPS, the sample flow was passed through a thermal conditioner (V = 28 cm−3), resulting in 11 s average residence time. The design of the thermal conditioner is described in detail in the ESI.† The temperature inside the thermal conditioner was ramped in a see-saw pattern at a rate of 2 K min−1. The lower and upper temperature of the ramp varied between experiments, but typically spanned >40 °C.The POPS is a lightweight optical particle spectrometer. Particles pass through a laser beam (405 nm), which in turn result in light scattering by the particle. The scattered light is measured by a photomultiplier tube. Each particle transit event is recorded in time and a pulse height is derived from the time trace. The pulse height is related to the particle size via Mie theory. In its standard configuration, the instrument is capable of measuring particles between 150 nm and 3000 nm at total particle number concentration <∼3000 cm−3. The version of the POPS used here is a prototype of the commercial version manufactured by Handix Scientific (1613 Prospect Park Way, Suite 100, Fort Collins, Colorado 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 USA). It is very close in design to the version described in Gao et al. (2016).38 Data acquisition is performed via single-board computer (sbRIO 9606, National Instruments, Austin, TX, USA), which extracts pulse height time traces produced from the photomultiplier tube. This data acquisition version registers zero counts once the count rate exceeds 10
525 USA). It is very close in design to the version described in Gao et al. (2016).38 Data acquisition is performed via single-board computer (sbRIO 9606, National Instruments, Austin, TX, USA), which extracts pulse height time traces produced from the photomultiplier tube. This data acquisition version registers zero counts once the count rate exceeds 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1. For reference, a count rate of 10
000 s−1. For reference, a count rate of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1 corresponds to 4000 cm−3 at a sample flow rate of 0.15 L min−1. To buffer against fluctuations in particle number concentration, mean particle concentrations were kept below 3000 cm−3 in all experiments. At those concentrations, the half-life due to coagulation is ∼200 h. Thus, coagulation between initial size selection and the POPS (<20 s) is negligible. Note that later commercial versions of the POPS use a Beaglebone computer with different software that only saturates the signal, but doesn't degrade it when the count rate becomes too high.39
000 s−1 corresponds to 4000 cm−3 at a sample flow rate of 0.15 L min−1. To buffer against fluctuations in particle number concentration, mean particle concentrations were kept below 3000 cm−3 in all experiments. At those concentrations, the half-life due to coagulation is ∼200 h. Thus, coagulation between initial size selection and the POPS (<20 s) is negligible. Note that later commercial versions of the POPS use a Beaglebone computer with different software that only saturates the signal, but doesn't degrade it when the count rate becomes too high.39
Single particle pulse height data are written in binary format to disk. These data can be post-processed and binned into pulse height histograms at a resolution up to 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535 bins, corresponding to the 16 bit resolution of the digitizer hardware. Alternatively, the data can be binned on the sbRIO and streamed to an external data acquisition computer using either serial or network communication. Here, the network interface was used. The typical bin resolution of the stream is 16 bins discretized in log space of digitizer units. It is possible to increase the bin resolution to 500 and adjust the range of digitizer units. Data were streamed to the external computer using 500 bins ranging between digitizer bins 100 and 10
535 bins, corresponding to the 16 bit resolution of the digitizer hardware. Alternatively, the data can be binned on the sbRIO and streamed to an external data acquisition computer using either serial or network communication. Here, the network interface was used. The typical bin resolution of the stream is 16 bins discretized in log space of digitizer units. It is possible to increase the bin resolution to 500 and adjust the range of digitizer units. Data were streamed to the external computer using 500 bins ranging between digitizer bins 100 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. This resolution was sufficient to resolve the particle phase change over a wide range of diameters (250–750 nm). Using the network data stream allowed for better integration with control software of the thermal conditioner and the DMA.
000. This resolution was sufficient to resolve the particle phase change over a wide range of diameters (250–750 nm). Using the network data stream allowed for better integration with control software of the thermal conditioner and the DMA.
Digitizer-PH time series were acquired at 1 Hz resolution. Fig. 2 shows two example count histograms of the digitizer-PH, one before and one after the phase change. Particles restructure upon heating, which results in a narrowing of the digitizer-PH distribution. In this example, the narrowing is evident only on the ascending branch of the PH histogram. This is due to interference by +2 charged particles and is explained in the results section. To quantify the narrowing, the first moment of the digitizer PH distribution at the leading edge of the histogram is calculated. Formally,
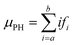 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535) so that the resulting μPH is independent of the selected bin resolution and comparable between different setups. Values for a and b were selected along the ascending branch of the digitizer-PH distribution via trial and error to maximize the change in μPH during the phase transition. However, the values were kept constant for experiments performed at the same DMA mobility diameter.
535) so that the resulting μPH is independent of the selected bin resolution and comparable between different setups. Values for a and b were selected along the ascending branch of the digitizer-PH distribution via trial and error to maximize the change in μPH during the phase transition. However, the values were kept constant for experiments performed at the same DMA mobility diameter.
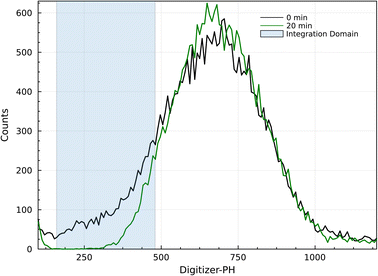 | ||
| Fig. 2 Example digitizer-PH frequency distributions before (black) and after (green) restructuring. The shaded area illustrates the integration domain in eqn (1). The evaluated μPH between 160 and 480 digitizer-PH is 375 and 440 before and after restructuring, respectively. | ||
The μPHversus thermal conditioner temperature forms a logistic curve that can be fit using a standard non-linear least squares algorithm to a model of the following functional form:
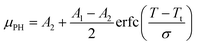 | (2) |
2.2 Determination of viscosity
Rothfus and Petters (2016)15 used electrical mobility measurements to trace the coalescence of bispherical dimer particles as a function of temperature. The resulting data from those experiments show a sigmoid relationship when plotting the mobility diameter of initially uncoalesced dimer particles versus temperature. This relationship is analogous to eqn (2). Rothfuss and Petters (2016) derived an approximate equation based on modified Frenkel sintering theory described in Pokluda et al. (1997)40 to relate the mobility measurements to viscosity at various points during the transition from uncoalesced to coalesced state: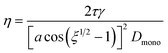 | (3) |
| Sucrose | Citric acid | Tartaric acid | |
|---|---|---|---|
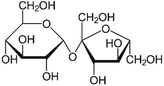
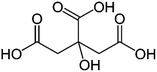
| a Molecular structures are taken from Wikimedia Commons. Sucrose and citric acid: public domain. Tartaric acid. b Rothfuss and Petters (2017).31 c Marsh et al. (2018).24 d Kasparoglu et al. (2021).23 e Assumed in this study to provide best agreement between measurement and model. | |||
| Structurea |
|
|
|
| Formula | C12H22O11 | C6H8O7 | C4H6O6 |
| AIOMFAC | 3 × CHO[ether], 8 × OH, 3 × CH2[alc], 5 × CH[alc], 1 × C | 3 × COOH, 1 × OH, 2 × CH2, 1 × C[alc] | 2 × COOH, 2 × OH, 2 × CH[alc] |
| T g,i [°C] | 68 ± 18b (72e) | 9 ± 5b (9e) | 15 ± 10b (10e) |
| k i [−] | 0.19c | 0.29d | 0.29e |
| D i [−] | 4.8d | 6.8d | 6.8e |
We hypothesize that measured changes in μPH are due to the restructuring/sintering of slightly aspherical particles. It is known,41,42 that particle asphericity is induced by rapid drying, followed by vitrification of the particle. We further postulate that Frenkel sintering theory can be applied to find the viscosity at Tt, assuming ξ = 2.5 (corresponding to midpoint of the geometry factor during dimer sintering), and Dmono = Dp/1.26, where Dp is the mobility diameter selected by the DMA in Fig. 1. The factor 1.26 is equal to the cube root of 2. Inclusion of this factor ensures that the assumed Dmono results in a sphere equivalent diameter of the restructured particle equals the nominal sphere equivalent selected dry diameter.
Our hypothesis is based on prior observations that have shown that Frenkel sintering theory can be applied to cases where sintering of dimers comprising spherules of different composition.25 A specific example involves the flow of a liquefying amorphous sucrose particles around solid probe sphere particles composed of sodium dodecyl sulfate. The inferred viscosity using the numerical model in that case is correct, even though the assumption of sintering of two spheres of equal composition underlying the theory is not satisfied.
The inferred viscosity value depends on the assumed surface tension. Uncertainty in surface tension has been shown to have a negligible effect on the retrieved viscosity relative to other experimental uncertainties.24 Here we assume γ = 0.084 J m−2 based on the value for dry sucrose.25 We thus estimate from the interpolation that the viscosity at Tt for Dp = 300 nm particles and τ = 11 s (time in the thermal conditioner) is 6.9 × 106 Pa s (ESI†).
2.3 Size dependent measurements
Measurements of transition temperature as a function of dry particle diameter were performed using pure sucrose particles. These measurements were performed using an earlier version of the experimental setup. The differences in setup between these experiments and mixture experiments are summarized as follows. First, the DMA used was a high-flow DMA column43 operated at 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 L min−1 sheath-to-sample flow ratio. The high-flow column was needed to select particles of up to 700 nm in diameter without the need to reduce the resolving power of the DMA. Second, the drier-DMA-POPS setup was not temperature controlled. Temperature control was unnecessary because the transition temperature of pure sucrose exceeded 80 °C. Third, the temperature in the thermal conditioner lagged the nominal setpoint temperature (discussed further below), which led to a redesign of the device used in subsequent experiments. This design is shown in Fig. S1 of the ESI† and eliminates the lag. Finally, 500 bin real-time streaming between the sbRIO and the external data acquisition system was not yet available. Therefore, the data use digitizer-PH distributions that were derived in post-processing from the single particle output stored on disk.
0.5 L min−1 sheath-to-sample flow ratio. The high-flow column was needed to select particles of up to 700 nm in diameter without the need to reduce the resolving power of the DMA. Second, the drier-DMA-POPS setup was not temperature controlled. Temperature control was unnecessary because the transition temperature of pure sucrose exceeded 80 °C. Third, the temperature in the thermal conditioner lagged the nominal setpoint temperature (discussed further below), which led to a redesign of the device used in subsequent experiments. This design is shown in Fig. S1 of the ESI† and eliminates the lag. Finally, 500 bin real-time streaming between the sbRIO and the external data acquisition system was not yet available. Therefore, the data use digitizer-PH distributions that were derived in post-processing from the single particle output stored on disk.
2.4 Sampling strategy
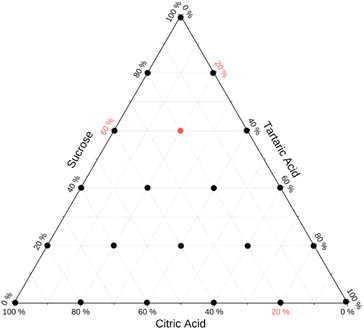
Internally mixed particles comprising varying weight fractions of sucrose, tartaric acid, and citric acid were analyzed. The weight fractions were selected based on a Latin hypercube sampling plan that ensures equidistant coverage over the entire parameter space. A total of 6 samples for each axis of binary mixtures was selected. This results in 21 mixtures to cover the full parameter space. Fig. 3 summarizes the weight fractions of these 21 mixtures on a ternary diagram.Mixed particles were generated by atomization from bulk solutions. Solutions were prepared by weighing the dry components followed by dissolution in HPLC grade water (Fisher Scientific). It was assumed that particles generated by atomizing these solutions reflect the weight fractions in the bulk solution. The atomizer was rinsed with HPLC grade water before switching to a new composition.
2.5 Mixture modelling
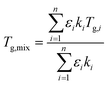 | (4) |
Viscosity as a function of temperature is obtained via the Angell scaled fragility23,44,45
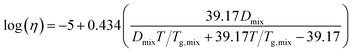 | (5) |
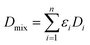 | (6) |
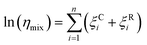 | (7) |
3 Results
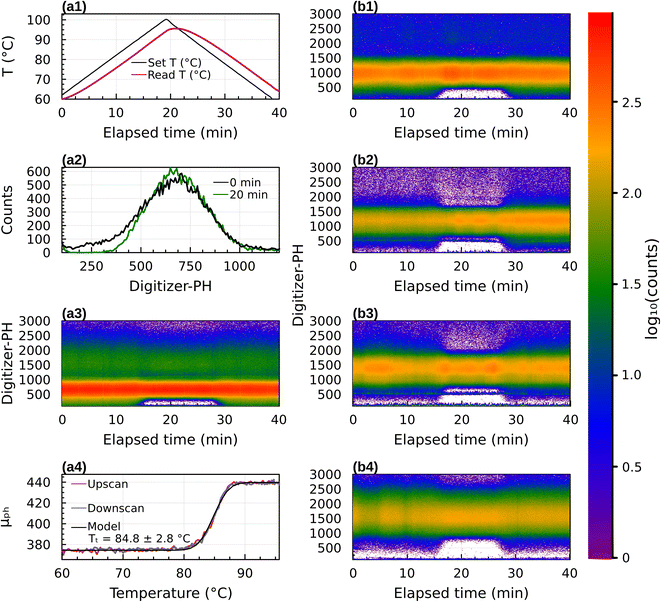
Results for 31 experiments are summarized in Table S1.† Date and start time are provided to allow readers to repeat the analysis with the raw data provided in the data archive. Fig. 4 shows data for pure sucrose. Panels (a1) to (a4) correspond to sucrose with Dp = 300 nm (diameter selected by the DMA). Panel (a1) illustrates temperature of the thermal conditioner during the 40 minute temperature scan from 60 °C to 100 °C and back to 60 °C. In these experiments (see Section 2.3) the temperature of the heated section lagged the setpoint, resulting in a slightly asymmetric and skewed temperature profile. Panel (a2) provides an example digitizer-PH histogram taken at 10 min and 20 min after the start of the scan. It is the same as shown in Fig. 2. The digitizer-PH is proportional to particle size.38,39 The peak in digitizer-PH histogram near 700 corresponds to +1 (300 nm) charged particles transmitted by the DMA. The difference at 10 and 20 min illustrates the optical signal that results from the phase transition. Panel (a3) is a false color representation of the digitizer-PH histogram during the 40 min temperature scan. The red and green color bands correspond to the +1 and +2 peaks. The mode diameter of the PH histogram remains constant throughout the temperature scan. However, at 15 min the PH distribution narrows and at 28 min the PH distribution broadens again. The narrowing and broadening occur for both the ascending and descending branch of the PH distribution, but it is obscured by the signal of the +2 charged particles on the descending branch. The narrowing can also be seen in the +2 band, although the signal is less strong. Panel (a4) shows the derived mean digitizer-PH calculated for bins between 160 and 480 versus temperature. The curve resolves the narrowing of the distribution, showing an ∼17% increase in μPH between 80 °C and 90 °C. The upscan and downscan of μPH are perfectly aligned. This demonstrates that the narrowing/broadening is due to temperature in the thermal conditioner. The lag of the temperature with the setpoint and asymmetry of the profile do not affect the result. (Nevertheless, the thermal conditioner was redesigned for the mixture experiments to eliminate the lag, cf. Fig. S1†). The fitted model indicates a transition temperature Tt = 84.8 ± 2.8 °C.Panels (b1) to (b4) are the same as (a3) but for sucrose with Dp = 350, 400, 450 and 500 nm, respectively. Multiply-charged particles are less dominant in these data, as the selected size is further away from the mode of the size distribution generated by the atomizer (which was not measured). These data confirm that the narrowing of digitizer-PH occurs both on the ascending and descending branch of the digitizer-PH distribution. Restructuring can be observed over a wide range of particle sizes.
Fig. 5a shows how the transition temperature for dry sucrose particles varies with the selected mobility diameter. The transition temperature increases with particle size. This is because larger particles need to be less viscous to flow over a given distance in the same time interval compared to smaller particles. Since the residence time in the thermal conditioner is fixed (11 s), the particles must be warmed further beyond the glass transition temperature to sufficiently lower the viscosity to induce restructuring.
 | ||
| Fig. 5 (a) Transition temperature for pure sucrose particles as a function of dry diameter. Error bars show the standard deviation of the logistic fit (eqn (2)). (b) Derived viscosity at the transition temperature based on particle diameter as described in Section 2.2 vs. the measured transition temperature. Symbol colors denote the particle dry diameter. Model lines correspond to D = 4.8. Line color corresponds to different Tg values. | ||
Fig. 5b shows the relationship between the transition temperature and derived viscosity (Section 2.2). For a constant Tg value, the temperature dependence of viscosity is given by eqn (5). Kasparoglu et al. (2021),23 show that D = 4.8 accurately describes the temperature dependence for dry sucrose, including data from multiple studies. Here, the data approximately follow the Tg = 71 °C isoline, except for particles <350 nm. The reason for the deviation is not entirely clear. Possible explanations are experimental uncertainty in viscosity determination or a true dependency of the glassification temperature for differently sized particles. Fig. 5a also shows the standard deviation of the logistic fit. Presumably, the midpoint of the transition is the most likely temperature where the transition occurs. Adding these error bars to Fig. 5b would indicate that the data follow the same isoline within experimental uncertainty. However, the full error bar is also likely an overestimate of the error, since the transition from shaped to spherical particle proceeds through a range of geometric shape factors ξ. Furthermore, viscosity depends on particle size via surface tension effects,12,13,49 even though the strongest dependency is expected for sub-50 nm sizes. Finally, the glass transition temperature is not a constant like the melting point, but depends on the thermodynamic trajectory during glass formation.50 Consequently, literature compilations of glass transition temperatures from multiple studies show a wide range of scatter.31 For sucrose this range is 68 ± 18 °C (Table 1). Thus a 2 °C difference in Tg for glasses formed during different experiments, possibly due to slightly different drying rates or a weak size dependence is not unreasonable. In fact, the general repeatability of measured transition temperature appears to be only within ∼4 °C. For example, a repeat of 300 nm sucrose with the setup shown in Fig. 1 yields a Tt that is 3.5 °C warmer than the one shown in Fig. 5 (see Table S1†).
A similar scatter around theoretical predictions will be shown below in Fig. 6. Based on this, we argue that Fig. 5 demonstrates that the μPH change is indicative of a phase transition. The phase transition corresponds to viscosity of ∼107 Pa s as proposed in Section 2.2. Measurements of Ttversus diameter can be used in principle to estimate the temperature dependence of viscosity, at least within a narrow range of ∼0.5 order of magnitude in viscosity. The accuracy of this approach, however, is limited by the weak dependence of viscosity on size and the experimental uncertainties outlined above.
 | ||
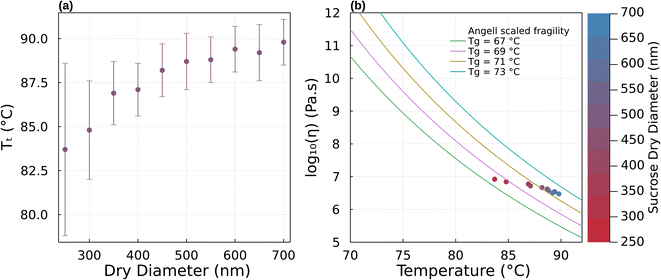
| Fig. 6 Transition temperature as a function of sucrose weight fraction for (a) sucrose/citric acid, (b) sucrose/tartaric acid, (c) citric acid/tartaric acid mixed particles. Blue symbols and standard deviation correspond to Tt ± σTt (Table S1†) from this study. Pink symbols are viscosity measurements reported in Fig. 5 of Marsh et al.24 measured using the dual tandem DMA method for ∼80 nm particles and correspond to 5 × 106 Pa s. The blue and red lines correspond to predictions of Tt by the phase diagram model and AIOMFAC-VISC model, respectively. The blue shading visualizes a ±5 °C uncertainty of the phase diagram model prediction. | ||
All subsequent data were obtained with the setup shown in Fig. 1. Fig. 6 summarizes transition temperatures obtained for binary particles of initial size 300 nm. The sucrose-citric acid mixtures are in excellent agreement with the measurements of Marsh et al. (2018)24 who investigated the same system characterizing the temperature where dimer particles prepared from 80 nm monomer particles coalesce. Coincidentally, the corresponding viscosity of the Marsh et al. (2018)24 data and the data here are similar in viscosity (5 × 106 Pa s vs. 6.9 × 106 Pa s). This is because the smaller particle size was compensated for by a shorter residence time in their study. This further confirms our hypothesis that the measurements derived via μPH correspond indeed to the viscosity posited in Section 2.2.
As in Marsh et al. (2018) the data indicate that the mixing rule given in eqn (4) is nonlinear. The parameteric phase diagram model, eqn (4)–(6) with parameters from Table 1, is self-consistent with the proposed viscosity probed by the measurement (Section 2.2). In contrast, predictions made with the AIOMFAC-VISC model significantly overestimate the transition temperature for all compositions.
Mixtures of sucrose and tartaric acid behave like sucrose and citric acid. This is unsurprising. The chemical structures of tartaric acid and citric acid are similar. The glass transition temperatures of tartaric and citric acid are also similar (Table 1). The agreement between the phase diagram model and data furthermore suggests that the fragility parameter D = 6.8 used for citric acid is also applicable for tartaric acid. Varying D between 4.7 and 9.1 would retain the agreement of the model and data within a ±5 °C uncertainty. Unlike sucrose–citric acid, predictions by the AIOMFAC-VISC model are in reasonable agreement with the data.
The Tt of citric acid and tartaric acid are almost identical. The Tt of the mixture is therefore expected to be independent of the relative weight fractions. Indeed, the transition temperature for particles that are mixtures of citric acid and tartaric acid show no strong trend with composition. Again, this is unsurprising due to the chemical similarity between the two compounds. However, the series might also be considered as a test of repeatability of the experiment. The combined data suggest that the transition temperature can be identified within a few °C.
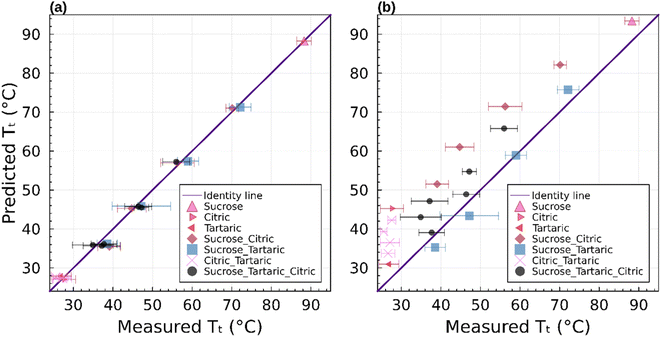
Fig. 7 summarizes the predicted and observed temperature for all 21 mixture experiments. Excellent agreement is obtained for the observed transition temperature and the transition temperature predicted by the parametric phase diagram model. From an experimental perspective, this indicates that ternary mixtures yield well-defined and plausible transition temperatures. From a theoretical perspective this indicates that eqn (4) is valid beyond its normal application to two component mixtures. Agreement between the observed transition temperature and predictions by AIOMFAC-VISC are less good.
4 Discussion
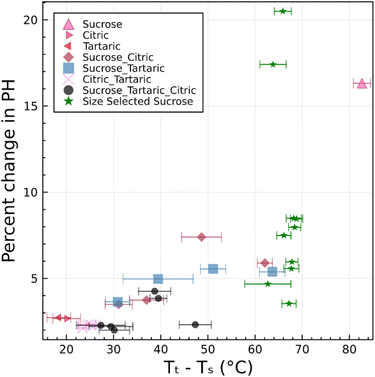
Fig. 5 and 6 clearly demonstrate that a single differential mobility analyzer coupled with a printed optical particle spectrometer can be used to detect the restructuring of amorphous particles upon heating. This corresponds to measurement of the temperature dependence of viscosity. Likewise, it should be possible to characterize humidity-dependent viscosity of particles. We expect that a phase transition can be observed upon cooling, which results in a temporary increase in RH. Although this is not explicitly demonstrated here, this method works well in the analogous dual tandem DMA method.15,23,25 Excellent agreement between results obtained using this new method and results obtained using the prior dual tandem DMA method is shown for heating experiments. Furthermore, excellent agreement is obtained between observed transition temperatures and predictions from theory that are constrained by bulk data. Combined, these results support the initial hypothesis that the narrowing of the pulse height distribution is due to restructuring of aspherical particles. This restructuring corresponds to a viscosity between 106 and 107 Pa s for particles in the 250–1000 nm range.The origin of particle asphericity is from rapid drying of the particles. This effect appears to be robust, as all 31 experiments showed restructuring. The restructuring is observed by a narrowing of the pulse-height distribution and is quantified by a change in pulse height along the leading edge of the pulse-height histogram (Fig. 4(a4)). The change in pulse height is larger for systems with higher glass transition temperature. Fig. 8 summarizes the percent change in pulse height as a function of the difference between the transition temperature and system temperature. The scattering of the data is significant. Furthermore, the observed change in pulse height is sensitive to the choice of the integral bounds a and b in eqn (1). Nevertheless, there is a consistent trend toward smaller changes in pulse height as the transition temperature approaches the system temperature. We estimate that ∼15 °C difference between the transition temperature and the system temperature is required to induce asphericity and to measure it with the setup described here. This is because restructuring could take place during transit through between the DMA and the POPS if the transition and system temperatures are too close. We have successfully operated the DMA-POPS system as cold as −15 °C (not shown here). Further cooling may be possible, but there is a danger of damage to the DMA due to differential thermal expansion of plastic and metal. With this constraint, viscous phase transitions can be observed for Tt > 0 °C.
We posit that asphericity induced by any process can be used to study phase transitions using the DMA-POPS system. As we have shown39 dimer coalescence can be observed with the POPS. In contrast to the results obtained here, the signal upon dimer coalescence is stronger. In those measurements, the mode of the pulse-height distribution increases, while here only a narrowing of the pulse-height distribution is observed. The observed narrowing is likely due to a subtle change in refractive index upon restructuring.51 Since the change in digitizer-PH is much larger during dimer coalescence, we expect that the coalescence of larger agglomerates can also be observed using this technique. The main constraint in relating the change in pulse height parameters to viscosity is the absence of information if multiple phases are present. Dry particles can separate into two or more phases.52 In such systems the observed transition will represent the restructuring of the less viscous phase only. It is unlikely that phase separation influenced the data shown in this work. Phase separation is expected to occur for chemically dissimilar species and generally occurs only for a subset of compositions in the phase space.53,54 If phase separation affects the data, discrepancies between the data and parametric phase diagram model are expected to be observed. For example, assuming that a 0.6/0.4 mixture of sucrose/citric acid phase separated, the resulting phase transition temperature would be expected to be that of pure citric acid. This would manifest as a discontinuity in Fig. 6a. Furthermore, it is not known how hydrated solid states will affect the measurement. Hydrated states can occur in some organic or inorganic particles even when drying the particle to low RH.55,56 It is likely that restructuring due to melting will still be observed. However, it is possible that heating will lead to further drying, which might also alias as a phase transition. Future studies using hydrated particles are needed to test this.
In the described technique, the residence time in the thermal conditioner is fixed (11 s). Particle evaporation may occur inside the thermal conditioner if the substance is volatile. Evaporation will shrink the particle and result in a decrease in particle size, and in turn a decrease in the digitizer-PH mode diameter. Thus, potential evaporation artifacts are readily identified in the data. Here no evaporation was observed for heating up to 20 °C above the observed phase transition. However, we note that dicarboxylic acids and secondary organic aerosol generated from oxidation flow reactors have shown evaporation just a few degrees warmer than the transition temperature.15,20,27 A related question is whether particles achieve equilibrium with respect to viscosity during transit in the thermal conditioner. Modelling studies with the KM-GAP model suggest that equilibration timescales for sucrose and citric acid are <11 s for the 106 Pa s phase transition, if the phase transition occurs at T > ∼ −25 °C.23 The ratio between equilibration time scale and transit time should be examined when probing phase transitions at colder temperature.
The binary and ternary compositions presented herein were selected to test whether the current theoretical framework to model viscosity, given by eqn (4)–(6), can be applied to dry multicomponent mixtures. The excellent agreement between this model and observations suggests that this is true. However, as pointed out previously,23 this agreement is predicated on tuned or known input parameters summarized in Table 1. In this instance, the parameters were mostly known from prior work with additional constraints from bulk measurements. Group contribution models such as AIOMFAC-VISC may estimate viscosity. However, as shown here, such estimates are currently less precise for the systems studied.
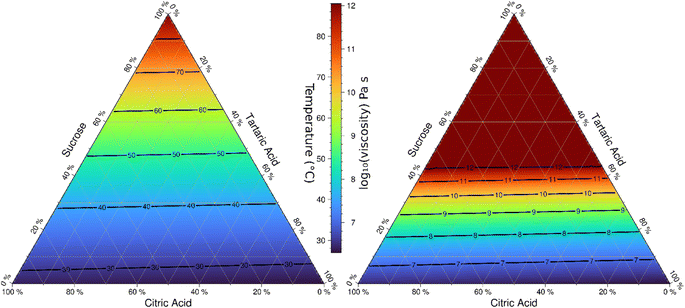
The phase diagram model is suitable to interpolate viscosity over the entire composition space. Fig. 9 shows the model-derived transition temperature corresponding to 6.9 × 106 Pa s for the ternary space as well as the predicted viscosity at 30 °C. This representation is similar to previous phase diagram models for sucrose/water and citric acid/water shown in Fig. 7 in Kasparoglu et al. (2021).23 The utility of such diagrams is to visualize and quantify the phase state and viscosity for a wide range of conditions. The almost symmetry in these ternary systems is due to the similarity of two of the molecules selected.
The new experimental technique presented here produces similar results as the previously used dual tandem DMA method. However, it is superior to the dual tandem DMA technique in several aspects. Only a single DMA, a thermal conditioner, and a POPS are needed. This simplifies the setup and is cheaper compared to the dual tandem DMA method, which requires three DMAs and at least two condensation particle counters, a coagulation chamber, multiple neutralizers, lead shielding to prevent spontaneous particle decharging, and an electrostatic precipitator.15,57 Furthermore, the dual tandem DMA setup requires very high number concentration of particles,21,22 necessitating working with broad DMA size cuts, multiple atomizers to generate particles, need to dry high sample flows, and frequent cleaning of the DMAs due to plugging. In contrast, the DMA-POPS method works with much lower particle concentrations e.g., 600 cm−3 that is used in this study. The time-requirement to obtain data is much shorter than that of the dual tandem DMA method. Application of the DMA-POPS will enable the systematic investigation of the phase transition for multi-component mixtures.
The sampling strategy (Fig. 3) and validation (Fig. 7a) can serve as a blueprint to extend studies to test model predictions for other multi-component mixtures. The mathematical solution for equidistant sample spacing in ternary space shown in Fig. 3 is straightforward. However, the generalized algorithmic generation of this sampling plan for n compounds is worth discussing. An important constraint is that dry weight fractions must sum to one. Thus, a Latin hypercube sampling plan involves generation of a grid of m points in the interval [0,1] in each of n−1 dimensions. Such plans are readily generated using optimization methods.58–60 This results in mn−1 hypothetical weight fraction compositions vectors w = {w1, w2…wn−1}. The weight fraction of the nth component is wn = 1 − ∑wi. Negative wn values are discarded. The algorithm yields the sampling plan shown in Fig. 2, assuming m = 6 (number of compositions along each binary axis) and n = 3 (number of solutes). In this case 21 out of 36 generated wn values are valid. This algorithm is readily scalable to higher dimensions and arbitrary sampling density. Optimal subsets of the Latin hypercube plan to limit the number of experiments can be generated.59 The efficacy of the model prediction for many-compound systems can then be systematically tested through evaluation plots shown in Fig. 7.
5 Conclusions
A new method to measure the temperature of the semi-solid phase transition is introduced. The technique measures the restructuring of aspherical particles formed during rapid drying. The observed restructuring corresponds to ∼107 Pa s. Only a single differential mobility analyzer, a thermal conditioner, and a printed particle optical spectrometer are needed. The technique is similar to, but simpler and cheaper than the previously used dual tandem differential mobility analyzer method.15 The temperature where viscosity is 6.9 × 106 Pa s is characterized for binary and ternary mixtures with up to three dry components. Internally mixed particles composed of sucrose, tartaric acid, and citric acid were characterized using a Latin hypercube sampling plan ensuring equidistant sampling in composition space. The experiments test the hypothesis whether mixing rules can be applied to multiple compositions. An updated version of the parametric phase diagram model described in Kasparoglu et al. (2021)23 was used to predict viscosity for each mixture. The model and data agree within measurement uncertainties. The phase diagram model provides a complete description of the amorphous ternary phase diagram of the sucrose/citric/tartaric acid system. Viscosity estimates by the functional group model AIOMFAC-VISC resolve the general trends with composition but are not in quantitative agreement with the data. The experimental setup and sampling methodology provide a blueprint to extend viscosity measurements to multicomponent mixtures.Data availability
Raw data underlying this manuscript are available via zenodo.61Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the U.S. National Science Foundation grant AGS-2037704. EMI and MB were supported by Independent Research Fund Denmark, Technology and Production Sciences (grant 0136-00345B). We also acknowledge support from Aarhus University Research Foundation (grant AUFF-E-2021-6-26).References
- A. Virtanen, J. Kannosto, H. Kuuluvainen, A. Arffman, J. Joutsensaari, E. Saukko, L. Hao, P. Yli-Pirilä, P. Tiitta, J. K. Holopainen, J. Keskinen, D. R. Worsnop, J. N. Smith and A. Laaksonen, Bounce behavior of freshly nucleated biogenic secondary organic aerosol particles, Atmos. Chem. Phys., 2011, 11, 8759–8766 CrossRef CAS.
- B. Zobrist, C. Marcolli, D. A. Pedernera and T. Koop, Do atmospheric aerosols form glasses?, Atmos. Chem. Phys., 2008, 8, 5221–5244 CrossRef CAS.
- B. J. Murray, T. W. Wilson, S. Dobbie, Z. Cui, S. M. R. K. Al-Jumur, O. Möhler, M. Schnaiter, R. Wagner, S. Benz, M. Niemand, H. Saathoff, V. Ebert, S. Wagner and B. Kärcher, Heterogeneous nucleation of ice particles on glassy aerosols under cirrus conditions, Nat. Geosci., 2010, 3, 233 CrossRef CAS.
- E. Abramson, D. Imre, J. Beránek, J. Wilson and A. Zelenyuk, Experimental determination of chemical diffusion within secondary organic aerosol particles, Phys. Chem. Chem. Phys., 2013, 15, 2983–2991 RSC.
- M. Shrivastava, S. Lou, A. Zelenyuk, R. C. Easter, R. A. Corley, B. D. Thrall, P. J. Rasch, J. D. Fast, S. L. Massey Simonich, H. Shen and S. Tao, Global long-range transport and lung cancer risk from polycyclic aromatic hydrocarbons shielded by coatings of organic aerosol, Proc. Natl. Acad. Sci., 2017, 114, 1246–1251 CrossRef CAS.
- L. Renbaum-Wolff, J. W. Grayson and A. K. Bertram, Technical Note: New methodology for measuring viscosities in small volumes characteristic of environmental chamber particle samples, Atmos. Chem. Phys., 2013, 13, 791–802 CrossRef CAS.
- L. Renbaum-Wolff, J. W. Grayson, A. P. Bateman, M. Kuwata, M. Sellier, B. J. Murray, J. E. Shilling, S. T. Martin and A. K. Bertram, Viscosity of α-pinene secondary organic material and implications for particle growth and reactivity, Proc. Natl. Acad. Sci., 2013, 110, 8014–8019 CrossRef CAS.
- N. A. Hosny, C. Fitzgerald, C. Tong, M. Kalberer, M. K. Kuimova and F. D. Pope, Fluorescent lifetime imaging of atmospheric aerosols: a direct probe of aerosol viscosity, Faraday Discuss., 2013, 165, 343–356 RSC.
- A. Pajunoja, J. Malila, L. Hao, J. Joutsensaari, K. E. J. Lehtinen and A. Virtanen, Estimating the Viscosity Range of SOA Particles Based on Their Coalescence Time, Aerosol Sci. Technol., 2014, 48, i–iv CrossRef CAS.
- R. M. Power, S. H. Simpson, J. P. Reid and A. J. Hudson, The transition from liquid to solid-like behaviour in ultrahigh viscosity aerosol particles, Chem. Sci., 2013, 4, 2597–2604 RSC.
- K. J. Kiland, K. L. Marroquin, N. R. Smith, S. Xu, S. A. Nizkorodov and A. K. Bertram, A New Hot-Stage Microscopy Technique for Measuring Temperature-Dependent Viscosities of Aerosol Particles and its Application to Farnesene Secondary Organic Aerosol, Atmos. Meas. Tech. Discuss, 2022, 2022, 1–25 Search PubMed.
- M. D. Petters and S. Kasparoglu, Predicting the influence of particle size on the glass transition temperature and viscosity of secondary organic material, Sci. Rep., 2020, 10, 15170 CrossRef CAS.
- S. S. Petters, Constraints on the Role of Laplace Pressure in Multiphase Reactions and Viscosity of Organic Aerosols, Geophys. Res. Lett., 2022, 49, e2022GL098959 CrossRef CAS.
- E. Järvinen, K. Ignatius, L. Nichman, T. B. Kristensen, C. Fuchs, C. R. Hoyle, N. Höppel, J. C. Corbin, J. Craven, J. Duplissy, S. Ehrhart, I. El Haddad, C. Frege, H. Gordon, T. Jokinen, P. Kallinger, J. Kirkby, A. Kiselev, K.-H. Naumann, T. Petäjä, T. Pinterich, A. S. H. Prevot, H. Saathoff, T. Schiebel, K. Sengupta, M. Simon, J. G. Slowik, J. Tröstl, A. Virtanen, P. Vochezer, S. Vogt, A. C. Wagner, R. Wagner, C. Williamson, P. M. Winkler, C. Yan, U. Baltensperger, N. M. Donahue, R. C. Flagan, M. Gallagher, A. Hansel, M. Kulmala, F. Stratmann, D. R. Worsnop, O. Möhler, T. Leisner and M. Schnaiter, Observation of viscosity transition in α-pinene secondary organic aerosol, Atmos. Chem. Phys., 2016, 16, 4423–4438 CrossRef.
- N. E. Rothfuss and M. D. Petters, Coalescence-based assessment of aerosol phase state using dimers prepared through a dual-differential mobility analyzer technique, Aerosol Sci. Technol., 2016, 50, 1294–1305 CrossRef CAS.
- Y. Zhang, M. S. Sanchez, C. Douet, Y. Wang, A. P. Bateman, Z. Gong, M. Kuwata, L. Renbaum-Wolff, B. B. Sato, P. F. Liu, A. K. Bertram, F. M. Geiger and S. T. Martin, Changing shapes and implied viscosities of suspended submicron particles, Atmos. Chem. Phys., 2015, 15, 7819–7829 CrossRef CAS.
- D. M. Bell, D. Imre, S. T. Martin and A. Zelenyuk, The properties and behavior of α-pinene secondary organic aerosol particles exposed to ammonia under dry conditions, Phys. Chem. Chem. Phys., 2017, 19, 6497–6507 RSC.
- A. P. Bateman, H. Belassein and S. T. Martin, Impactor Apparatus for the Study of Particle Rebound: Relative Humidity and Capillary Forces, Aerosol Sci. Technol., 2014, 48, 42–52 CrossRef CAS.
- J. H. Slade, A. P. Ault, A. T. Bui, J. C. Ditto, Z. Lei, A. L. Bondy, N. E. Olson, R. D. Cook, S. J. Desrochers, R. M. Harvey, M. H. Erickson, H. W. Wallace, S. L. Alvarez, J. H. Flynn, B. E. Boor, G. A. Petrucci, D. R. Gentner, R. J. Griffin and P. B. Shepson, Bouncier Particles at Night: Biogenic Secondary Organic Aerosol Chemistry and Sulfate Drive Diel Variations in the Aerosol Phase in a Mixed Forest, Environ. Sci. Technol., 2019, 53, 4977–4987 CrossRef CAS.
- S. Kasparoglu, R. Perkins, P. J. Ziemann, P. J. DeMott, S. M. Kreidenweis, Z. Finewax, B. L. Deming, M. P. DeVault and M. D. Petters, Experimental Determination of the Relationship Between Organic Aerosol Viscosity and Ice Nucleation at Upper Free Tropospheric Conditions, J. Geophys. Res.: Atmos., 2022, 127, e2021JD036296 CAS.
- M. D. Petters, A language to simplify computation of differential mobility analyzer response functions, Aerosol Sci. Technol., 2018, 52, 1437–1451 CrossRef CAS.
- N. E. Rothfuss, S. S. Petters, W. M. Champion, A. P. Grieshop and M. D. Petters, Characterization of a Dimer Preparation Method for Nanoscale Organic Aerosol, Aerosol Sci. Technol., 2019, 39, 998–1011 CrossRef.
- S. Kasparoglu, Y. Li, M. Shiraiwa and M. D. Petters, Toward closure between predicted and observed particle viscosity over a wide range of temperatures and relative humidity, Atmos. Chem. Phys., 2021, 21, 1127–1141 CrossRef CAS.
- A. Marsh, S. S. Petters, N. E. Rothfuss, G. Rovelli, Y. C. Song, J. P. Reid and M. D. Petters, Amorphous phase state diagrams and viscosity of ternary aqueous organic/organic and inorganic/organic mixtures, Phys. Chem. Chem. Phys., 2018, 20, 15086–15097 RSC.
- N. E. Rothfuss and M. D. Petters, Characterization of the temperature and humidity-dependent phase diagram of amorphous nanoscale organic aerosols, Phys. Chem. Chem. Phys., 2017, 19, 6532–6545 RSC.
- W. M. Champion, N. E. Rothfuss, M. D. Petters and A. P. Grieshop, Volatility and Viscosity Are Correlated in Terpene Secondary Organic Aerosol Formed in a Flow Reactor, Environ. Sci. Technol. Lett., 2019, 6, 513–519 CrossRef CAS.
- S. S. Petters, S. M. Kreidenweis, A. P. Grieshop, P. J. Ziemann and M. D. Petters, Temperature- and Humidity-Dependent Phase States of Secondary Organic Aerosols, Geophys. Res. Lett., 2019, 46, 1005–1013 CrossRef.
- W.-S. W. DeRieux, Y. Li, P. Lin, J. Laskin, A. Laskin, A. K. Bertram, S. A. Nizkorodov and M. Shiraiwa, Predicting the glass transition temperature and viscosity of secondary organic material using molecular composition, Atmos. Chem. Phys., 2018, 18, 6331–6351 CrossRef.
- N. R. Gervasi, D. O. Topping and A. Zuend, A predictive group-contribution model for the viscosity of aqueous organic aerosol, Atmos. Chem. Phys., 2020, 20, 2987–3008 CrossRef CAS.
- T. Koop, J. Bookhold, M. Shiraiwa and U. Pöschl, Glass transition and phase state of organic compounds: dependency on molecular properties and implications for secondary organic aerosols in the atmosphere, Phys. Chem. Chem. Phys., 2011, 13, 19238–19255 RSC.
- N. E. Rothfuss and M. D. Petters, Influence of Functional Groups on the Viscosity of Organic Aerosol, Environ. Sci. Technol., 2017, 51, 271–279 CrossRef CAS.
- M. Shiraiwa, Y. Li, A. P. Tsimpidi, V. A. Karydis, T. Berkemeier, S. N. Pandis, J. Lelieveld, T. Koop and U. Pöschl, Global distribution of particle phase state in atmospheric secondary organic aerosols, Nat. Commun., 2017, 8, 15002 CrossRef.
- J. Lilek and A. Zuend, A predictive viscosity model for aqueous electrolytes and mixed organic–inorganic aerosol phases, Atmos. Chem. Phys., 2022, 22, 3203–3233 CrossRef CAS.
- H. P. Dette, M. Qi, D. C. Schröder, A. Godt and T. Koop, Glass-Forming Properties of 3-Methylbutane-1,2,3-tricarboxylic Acid and Its Mixtures with Water and Pinonic Acid, J. Phys. Chem. A, 2014, 118, 7024–7033 CrossRef CAS.
- Y.-C. Song, J. Lilek, J. B. Lee, M. N. Chan, Z. Wu, A. Zuend and M. Song, Viscosity and phase state of aerosol particles consisting of sucrose mixed with inorganic salts, Atmos. Chem. Phys., 2021, 21, 10215–10228 CrossRef CAS.
- R. Jeong, J. Lilek, A. Zuend, R. Xu, M. N. Chan, D. Kim, H. G. Moon and M. Song, Viscosity and physical state of sucrose mixed with ammonium sulfate droplets, Atmos. Chem. Phys., 2022, 22, 8805–8817 CrossRef CAS.
- G. Rovelli, Y.-C. Song, A. M. Maclean, D. O. Topping, A. K. Bertram and J. P. Reid, Comparison of Approaches for Measuring and Predicting the Viscosity of Ternary Component Aerosol Particles, Anal. Chem., 2019, 91, 5074–5082 CrossRef CAS PubMed.
- R. S. Gao, H. Telg, R. J. McLaughlin, S. J. Ciciora, L. A. Watts, M. S. Richardson, J. P. Schwarz, A. E. Perring, T. D. Thornberry, A. W. Rollins, M. Z. Markovic, T. S. Bates, J. E. Johnson and D. W. Fahey, A light-weight, high-sensitivity particle spectrometer for PM2.5 aerosol measurements, Aerosol Sci. Technol., 2016, 50, 88–99 CrossRef CAS.
- S. Kasparoglu, M. M. Islam, N. Meskhidze and M. D. Petters, Characterization of a modified printed optical particle spectrometer for high-frequency and high-precision laboratory and field measurements, Atmos. Meas. Tech., 2022, 15, 5007–5018 CrossRef CAS.
- O. Pokluda, C. T. Bellehumeur and J. Vlachopoulos, Modification of Frenkel's model for sintering, AIChE J., 1997, 43, 3253–3256 CrossRef CAS.
- E. Mikhailov, S. Vlasenko, S. T. Martin, T. Koop and U. Pöschl, Amorphous and crystalline aerosol particles interacting with water vapor: conceptual framework and experimental evidence for restructuring, phase transitions and kinetic limitations, Atmos. Chem. Phys., 2009, 9, 9491–9522 CrossRef CAS.
- M. B. Altaf and M. A. Freedman, Effect of Drying Rate on Aerosol Particle Morphology, J. Phys. Chem. Lett., 2017, 8, 3613–3618 CrossRef CAS.
- L. A. Belfiore, Physical Properties of Macromolecules, John Wiley & Sons, Incorporated, Hoboken, United States, 2010 Search PubMed.
- C. A. Angell, Formation of Glasses from Liquids and Biopolymers, Science, 1995, 267, 1924 CrossRef CAS.
- C. A. Angell, Liquid Fragility and the Glass Transition in Water and Aqueous Solutions, Chem. Rev., 2002, 102, 2627–2650 CrossRef CAS.
- K. Kunal, C. G. Robertson, S. Pawlus, S. F. Hahn and A. P. Sokolov, Role of Chemical Structure in Fragility of Polymers: A Qualitative Picture, Macromolecules, 2008, 41, 7232–7238 CrossRef CAS.
- R. J. Speedy, Relations between a Liquid and Its Glasses, J. Phys. Chem. B, 1999, 103, 4060–4065 CrossRef CAS.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, Group-contribution estimation of activity coefficients in nonideal liquid mixtures, AIChE J., 1975, 21, 1086–1099 CrossRef CAS.
- Y. Cheng, H. Su, T. Koop, E. Mikhailov and U. Pöschl, Size dependence of phase transitions in aerosol nanoparticles, Nat. Commun., 2015, 6, 5923 CrossRef CAS.
- M. Giordano, M. Russo, P. Capoluongo, A. Cusano and L. Nicolais, The effect of cooling rate on the glass transition of an amorphous polymer, J. Non-Cryst. Solids, 2005, 351, 515–522 CrossRef CAS.
- M. R. McGrory, M. D. King and A. D. Ward, Using Mie Scattering to Determine the Wavelength-Dependent Refractive Index of Polystyrene Beads with Changing Temperature, J. Phys. Chem. A, 2020, 124, 9617–9625 CrossRef CAS.
- M. A. Freedman, Phase separation in organic aerosol, Chem. Soc. Rev., 2017, 46, 7694–7705 RSC.
- K. Gorkowski, N. M. Donahue and R. C. Sullivan, Aerosol Optical Tweezers Constrain the Morphology Evolution of Liquid-Liquid Phase-Separated Atmospheric Particles, Chem, 2020, 6, 204–220 CAS.
- M. Song, S. Ham, R. J. Andrews, Y. You and A. K. Bertram, Liquid–liquid phase separation in organic particles containing one and two organic species: importance of the average O:C, Atmos. Chem. Phys., 2018, 18, 12075–12084 CrossRef CAS.
- I. N. Tang, K. H. Fung, D. G. Imre and H. R. Munkelwitz, Phase Transformation and Metastability of Hygroscopic Microparticles, Aerosol Sci. Technol., 1995, 23, 443–453 CrossRef CAS.
- B. Rosati, A. Paul, E. M. Iversen, A. Massling and M. Bilde, Reconciling atmospheric water uptake by hydrate forming salts, Environ. Sci.: Processes Impacts, 2020, 22, 1759–1767 RSC.
- S. Kasparoglu, T. P. Wright and M. D. Petters, Open-hardware design and characterization of an electrostatic aerosol precipitator, HardwareX, 2022, 11, e00266 CrossRef.
- J. Eliáš and M. Vořechovský, Modification of the Audze–Eglājs criterion to achieve a uniform distribution of sampling points, Adv. Eng. Softw., 2016, 100, 82–96 CrossRef.
- M. Urquhart, E. Ljungskog and S. Sebben, Surrogate-based optimisation using adaptively scaled radial basis functions, Appl. Soft Comput., 2020, 88, 106050 CrossRef.
- S. Bates, J. Sienz and V. Toropov, Formulation of the Optimal Latin Hypercube Design of Experiments Using a Permutation Genetic Algorithm, in 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, American Institute of Aeronautics and Astronautics, Palm Springs, California, 2004 Search PubMed.
- S. Mahant, E. M. Iversen, S. Kasparoglu, M. Bilde and M. D. Petters, Dataset for “Direct Measurement of the Viscosity of Ternary Aerosol Mixtures”, Zenodo, 2023 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ea00160h |
| This journal is © The Royal Society of Chemistry 2023 |