Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reducing chemical complexity in representation of new-particle formation: evaluation of simplification approaches†
Tinja
Olenius
 *a,
Robert
Bergström
*a,
Robert
Bergström
 a,
Jakub
Kubečka
a,
Jakub
Kubečka
 b,
Nanna
Myllys
b,
Nanna
Myllys
 c and
Jonas
Elm
c and
Jonas
Elm
 b
b
aSwedish Meteorological and Hydrological Institute, SE-60176 Norrköping, Sweden. E-mail: tinja.olenius@alumni.helsinki.fi; Tel: +46 76 495 7787
bDepartment of Chemistry, Aarhus University, Langelandsgade 140, 8000 Aarhus C, Denmark
cDepartment of Chemistry, University of Helsinki, FI-00014 Helsinki, Finland
First published on 23rd January 2023
Abstract
Adequate representation of new-particle formation from vapors in aerosol microphysics and atmospheric transport models is essential for providing reliable predictions of ambient particle numbers and for interpretation of observations. Atmospheric particle formation processes involve multiple species, which complicates the derivation and implementation of data and parameterizations to describe the processes. Ideally, the representation of multi-compound mechanisms should be reduced, but remain accurate. Here, we evaluate common approaches to simplify the description of representative multi-compound acid–base chemistries by applying different theoretical molecular cluster data sets, focusing on simplifications (1) in formation rates that are used as input in aerosol process models and large-scale models, and (2) in cluster models that are applied to assess particle formation dynamics and survival to larger sizes. We test the following approaches: assuming non-interactive additive formation pathways, lumping of similar species, and application of quasi-unary approximations. We assess the possible biases of the simplifications for different types of chemistries and propose best practices for reducing the chemical complexity. We demonstrate that simplifications in formation rates are most often justifiable, but the choice of the preferred simplification method depends on the types of species and their similarity. Simplifications in cluster growth dynamics by quasi-unary approaches, on the other hand, are reasonable mainly for strong cluster formation involving very low-evaporating species and at excess concentration of the implicitly treated stabilizing compound.
Environmental significanceNew-particle formation is a major source of atmospheric aerosol particles, and thus an important factor affecting aerosol–cloud–climate processes. While model representation of particle formation mechanisms should preferably be concise and robust, the participation of multiple chemical species complicates the description. This work evaluates common approaches to simplify multi-compound chemistries, focusing on sulfuric acid–base systems. We provide assessments of reasonable simplifications for (1) incorporating formation rates in atmospheric models, and (2) detailed studies of new-particle formation and growth dynamics. This contributes to finding the best approaches for representing secondary particle sources, and mapping and reducing model uncertainties. |
1 Introduction
Formation of new aerosol particles from condensable vapors makes a major contribution to atmospheric aerosol numbers, and has significant—but uncertain—effects on aerosol–cloud–climate interactions, the global radiation budget, and air quality.1–3 The initial formation of nanometer-sized particles, occurring through clustering of gas-phase molecules to molecular clusters, is affected by multiple chemical compounds, including acid and base species and potentially also oxidized organic compounds.4,5 The clustering can proceed through multi-compound chemical mechanisms or parallel pathways,6,7 which need to be adequately represented in atmospheric aerosol models in order to capture the effects on particle concentrations.The main drivers of the initial particle formation process include mixtures of acid and base compounds.8–10 Specifically, sulfuric acid (H2SO4) is a central particle formation agent together with stabilizing base species, the most abundant of which is ammonia (NH3). In addition, atmospheric amines efficiently form molecular clusters with H2SO4.11 These include monoamines, i.e. mono-, di- and trimethylamine,12 of which dimethylamine has often been studied as a representative amine species,13 as well as diamines.14 Amines are typically more efficient clustering agents than NH3 but their atmospheric concentrations are generally much lower than that of NH3, although elevated close to the sources.15–17 Depending on the ambient conditions, these different base species can contribute to H2SO4-driven particle formation either alone or together.
The presence of multi-compound formation pathways increases the complexity of the description of the formation process in several ways. The functional form of the formation rate rapidly becomes very complex as the number of independent parameters increases, which complicates both the experimental and theoretical efforts to study the formation mechanisms, as well as their implementation in aerosol modeling. Experimental assessment of formation rates over a wide range of combinations of precursor vapors at different concentrations,18 as well as deriving robust parameterizations of the data, is laborious. Theoretical predictions of the properties of multi-compound molecular clusters of various compositions are likewise demanding. Such predictions are obtained by quantum chemical calculations,19 which require substantial computational resources when performed over large sets of cluster compositions. Simulations of molecular cluster population dynamics,20,21 generally applied together with quantum chemical input data to yield cluster concentrations and formation rates, also become more complex. A very large number of different molecular compositions can both increase the simulation time and make interpretation of results less straight-forward. Finally, implementation of formation rates in atmospheric models requires more sophisticated interfaces when multiple data sets are needed to determine the rates for different vapor species and their combinations. Overall, reducing chemical complexity in the representation of nanoparticle formation mechanisms by appropriate simplifications is highly desirable
(1) due to limitations in available experimental and theoretical data,
(2) for an optimized description of the process in large-scale models, and
(3) for robust interpretation of measurements by molecular cluster dynamics modeling.
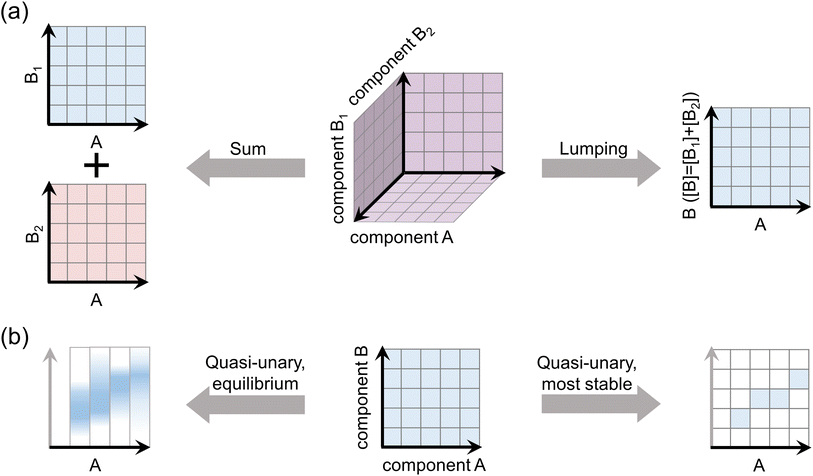
A common simplification that is routinely applied to account for several particle formation pathways is to assume that the formation rates J determined for different chemical systems are additive.3,22 For instance, if there exist data for particle formation from compounds A and B, and from A and C, the rates are summed to yield the total formation rate as Jtot = JAB + JAC. This corresponds to assuming that clustering pathways AB and AC do not interfere, meaning that compounds B and C compete to form clusters with A and/or do not form bonds with each other. While a simplified treatment is unavoidable when there exist no data for the three-component system ABC, potential errors arising from the sum approach have not been assessed for typical atmospheric clustering agents.
Another approach to reduce the number of compounds is to approximate chemically similar compounds as a lumped species. This has been assumed, for example, for amines.23 If the chemical properties of clusters in systems AB, AC, and ABC are very similar, it is justifiable to approximate the ABC system as AD, where D is a representative species with a concentration of [D] = [B] + [C]. However, in this case the sum approach may give distorted results, as it cannot generally be assumed that JAD([D] = [D]1 + [D]2) = JAD([D] = [D]1) + JAD([D] = [D]2). That is, the choice of simplification should depend on the properties of the chemical systems.
Multi-compound systems can also be reduced to quasi-unary systems by implicit treatment of compounds.24–28 This corresponds to assuming that one or more compounds do not need to be explicitly included, but only affect the cluster properties, most importantly the cluster evaporation rates which generally strongly depend on the molecular composition.29,30 This corresponds to representing, for example, all cluster compositions A3BX that consist of three molecules of compound A and any number of molecules of compound B, as a single cluster A3 with effective properties that are affected by the presence of B. Here, B is an enhancing species that cannot drive clustering on its own. This is justifiable, for instance, when the rate constants for collisions and evaporations of compound B are significantly higher than for A. The dynamic processes related to B thus occur in such short time scales that the cluster distribution is always instantaneously equilibrated with respect to B.25,26 Representative properties may also be a justifiable assumption when the clusters are likely to exist in specific, thermodynamically favorable compositions. For example, H2SO4–dimethylamine clusters have been observed to favor a close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio27,30 and have thus been approximated as a quasi-unary compound consisting of H2SO4–dimethylamine pairs.10,27
1 molar ratio27,30 and have thus been approximated as a quasi-unary compound consisting of H2SO4–dimethylamine pairs.10,27
In this work, we evaluate the approaches to simplify the representation of multi-compound new-particle formation. We test the validity of the typical simplifications by comparison against explicit simulations for atmospherically relevant H2SO4–base chemistries. The purpose is to answer the following questions:
(1) Can the simplified approaches be expected to represent the multi-compound systems with reasonable accuracy?
(2) How significant errors may the simplifications cause, in terms of the magnitude and direction of the possible errors?
(3) Does the applicability of the simplifications depend on the properties of the chemical system and/or the ambient conditions?
2 Validation of simplifications against explicit simulations
The simplification approaches, depicted in Fig. 1, are validated against explicit simulations of representative multi-compound chemical systems over a wide range of atmospheric conditions. We apply available sets of quantum chemical data for the thermodynamic properties of H2SO4–base clusters together with the cluster population dynamics model ACDC,31 as detailed below.2.1 Chemical systems and thermodynamic data sets
We focus on H2SO4–base chemistries where the primary bases of interest include ammonia (NH3) and dimethylamine (DMA). In order to ensure the generalizability of the results, we apply several quantum chemical data sets, as listed in Table 1. These are the most complete data sets available in terms of included cluster sizes and compositions, and they have been evaluated against laboratory measurements in previous works (see references in Table 1). These widely studied chemical systems represent weaker (NH3) and stronger (DMA) clustering agents that are also expected to interact and exhibit synergistic effects.32–34| Chemical system | Quantum chemical data sets | Cluster size range (max. numbers of H2SO4 and base molecules) | References |
|---|---|---|---|
| a For comparisons with H2SO4–NH3–DMA chemistry (Section 2.3.1), a smaller cluster set with up to 4 H2SO4 and 4 NH3 molecules is used for consistency. The 5 H2SO4, 5 NH3 set is used in the quasi-unary simulations (Section 2.3.2). b DLPNO_Besel is primarily applied for the H2SO4–NH3 chemistry in the quasi-unary simulations (Section 2.3.2) as it covers larger cluster sizes than other DLPNO-based data, which are used for the particle formation rate assessments (Section 2.3.1). | |||
| H2SO4–NH3, H2SO4–DMA, H2SO4–NH3–DMA | RICC2 | 4 H2SO4, 4 base, 5 H2SO4, 5 NH3a | Almeida et al. (2013)13 |
| Olenius et al. (2013)20 | |||
| Kürten et al. (2016)39 | |||
| DLPNO_Myllys | 4 H2SO4, 4 base | Myllys et al. (2019a)30 | |
| Myllys et al. (2019b)32 | |||
| DLPNO_Beselb | 6 H2SO4, 6 NH3 | Besel et al. (2020)40 | |
| DLPNO_Kubečka | 4 H2SO4, 4 base | Kubečka et al. (2022)37 | |
| H2SO4–GUA | DLPNO_Myllys | 4 H2SO4, 4 base | Myllys et al. (2018)35 |
| Myllys et al. (2019a)30 | |||
| H2SO4–base1–base2 with all combinations of NH3, MA, DMA, TMA, EDA | DLPNO_Kubečka | 4 H2SO4, 4 base | Kubečka et al. (2022)37 |
In addition, we perform tests with H2SO4–guanidine data. Guanidine, here referred to as GUA, is a very strong organobase that is able to form extremely low-evaporating clusters with H2SO4.30,35,36 Finally, we apply a set of multi-base data to simulate H2SO4–base1–base2 chemistries with different combinations of bases, including NH3, DMA, methylamine (MA), trimethylamine (TMA), and ethylenediamine (EDA).37 These amine species are observed in the ambient atmosphere, and cover weaker (MA) and stronger (DMA, TMA, EDA) clustering strengths.14,38 Further details of all data sets and simulation settings can be found in the ESI.†
2.2 Cluster dynamics simulations
Cluster concentrations and formation rates are simulated by the cluster population model ACDC,20,31 which generates and solves the time derivatives of all cluster concentrations Ci for a given set of cluster compositions i: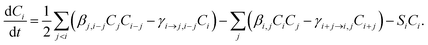 | (1) |
In eqn (1), the first sum includes all collisions that create composition i, and the corresponding reverse evaporations. The second sum includes collisions of cluster i with other clusters, and the reverse evaporations that produce composition i. βi,i is the rate constant for a collision between clusters i and j, and γi→j,i−j is the rate constant for evaporation of cluster i into products j and i − j. SiCi is a loss term corresponding to scavenging of clusters. Here, the collision constants are calculated using the kinetic gas theory, and the evaporation constants are obtained from the quantum chemical formation free energies.20 The loss rate constants correspond to scavenging by larger aerosol particles, characterized by the H2SO4 condensation sink CS as Si = CS × (dp,i/dp,H2SO4)−1.6, where dp,i and dp,H2SO4 are the diameters of cluster i and H2SO4, respectively.41 Ionic molecules are included when available (see ESI Section 1†) by adding collisions with ionizing species in eqn (1), corresponding to ionization and recombination processes.20
The solution to eqn (1) gives the cluster concentrations Ci, and the particle formation rate J is defined as
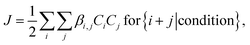 | (2) |
corresponding to the rate at which stable clusters grow beyond the simulated size range. In eqn (2), the summation goes over all collisions that lead to a stable collision product i + j according to the given stability criteria, denoted by {i + j | condition}20 (Table S1†). We focus on steady-state conditions, and perform simulations over sets of atmospherically relevant vapor concentrations, temperatures, and CS, from clean to highly polluted environments. As H2SO4 molecules tend to cluster with strong bases, we define the H2SO4 vapor concentration as the total concentration of H2SO4 monomers and H2SO4·base, where “base” refers to any base molecule. This is consistent with measurements, as the clustered molecules are expected to contribute to the H2SO4 signal.42
2.3 Simplified set-ups and comparison to explicit results
The test cases assess the effects of the sum assumption for particle formation mechanisms that involve interacting species that are either (1) different, or (2) very similar in terms of their clustering efficiency. This addresses the question of potential errors in total particle formation rates in aerosol microphysics and large-scale atmospheric models, which generally apply the sum approach. Furthermore, tests with the DLPNO_Kubečka data provide assessments on whether relatively similar bases are better represented by the sum or the lumping approach.
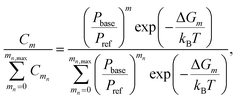 | (3) |
 | (4) |
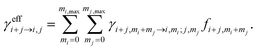 | (5) |
Second, a more simplified approach for a quasi-unary substance is applied by assuming that the base content of a given n-mer corresponds to the most stable composition. The substance is assumed to consist of H2SO4·base heterodimers, and cluster evaporation rates are set to those corresponding to the lowest total evaporation rate for a given n (ESI Section 2.2†). In this case, it is assumed that the base content can be represented by a single composition, which further simplifies the model treatment and interpretation of results.
The (H2SO4)n concentrations of the quasi-unary systems are compared to the total concentrations ∑(H2SO4)n·(base)m of the explicit systems for each n-mer. Here, the cluster concentrations are compared instead of formation rates as such one-compound model substances are typically applied to interpret observations of nanoparticle formation and growth27,44 and to assess cluster survival to larger sizes.45
3 Results and discussion
3.1 Simplifications in formation rates by assuming non-interacting or lumped species
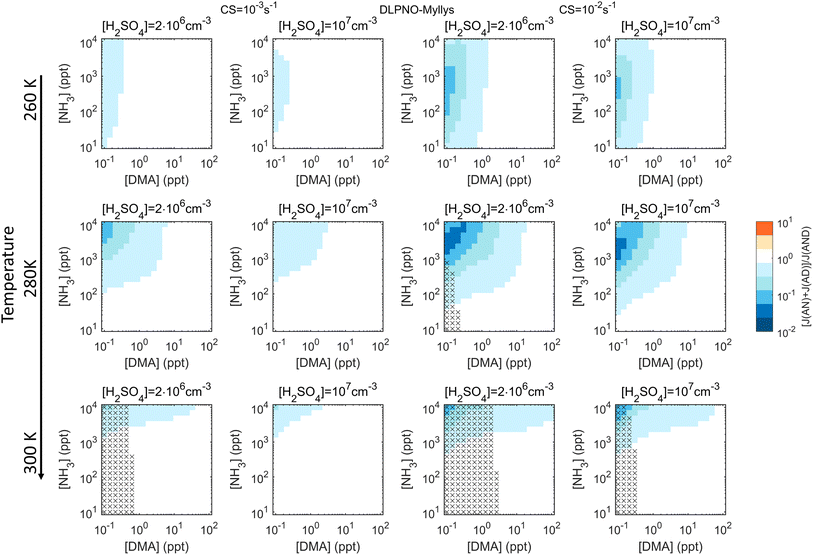
The ratio of the summed formation rates ∑J2-comp to the explicit three-component rate J3-comp for H2SO4–NH3–DMA at typical atmospheric base concentrations (Table 2) is shown in Fig. 2. The results are here shown only for the DLPNO_Myllys input data, as the RICC2 and DLPNO_Kubečka data give similar trends (see below). For such chemistry, the omission of base synergy can cause underprediction, but the errors are not very significant: the largest bias occurs at the combination of high [NH3] (mainly above ∼102–103 ppt) and low [DMA] (mainly below a few ppt) when the bases contribute together in an optimal way by enhanced initial cluster stabilization (DMA) and enhanced cluster growth (NH3). Under other conditions, [NH3] is not high enough for significant enhancement, and/or the formation process becomes dominated by the stronger base DMA. While the high [NH3]–low [DMA] conditions are common due to the different sources of the bases, the underprediction is typically clearly less than a factor of ∼10 at an average atmospheric scavenging sink of CS = 10−3 s−1. The bias increases with CS, and is here up to a factor of ∼30 under polluted conditions with CS = 10−2 s−1 at which efficient growth becomes more critical.| Base species | Clean and average environments (e.g. remote and marine sites) | Polluted environments (e.g. agricultural and urban sites, megacities) | References |
|---|---|---|---|
| NH3 | Tens of ppt to hundreds of ppt | ∼1 to ≳10 ppb | Nair and Yu (2020)46 |
| Croft et al. (2016)47 | |||
| Makkonen et al. (2014)48 | |||
| Xiao et al. (2021)9 | |||
| Amines (MA, DMA, TMA) | <1 ppt | ∼1 to ≳10 ppt | Yu and Luo (2014)38 |
| Yao et al. (2018)10 |
The corresponding results for the RICC2 and DLPNO_Kubečka data sets are given in the ESI.† While the absolute formation rates predicted by these data are mostly very different (Fig. S1†), the qualitative biases in the simplifications are consistent (Fig. S2 and S3†). The absolute biases are affected by the predicted quantitative cluster stabilities: lower stabilities (DLPNO_Kubečka) mostly result in more bias and higher stabilities (RICC2) in less bias, with DLPNO_Kubečka generally giving highest biases up to factors of ∼40–60. As effective cluster stabilities depend on vapor concentrations and temperature (i.e. molecular growth vs. evaporation), the conditions with largest biases may be somewhat shifted in the vapor concentration space or T space for the different data sets.
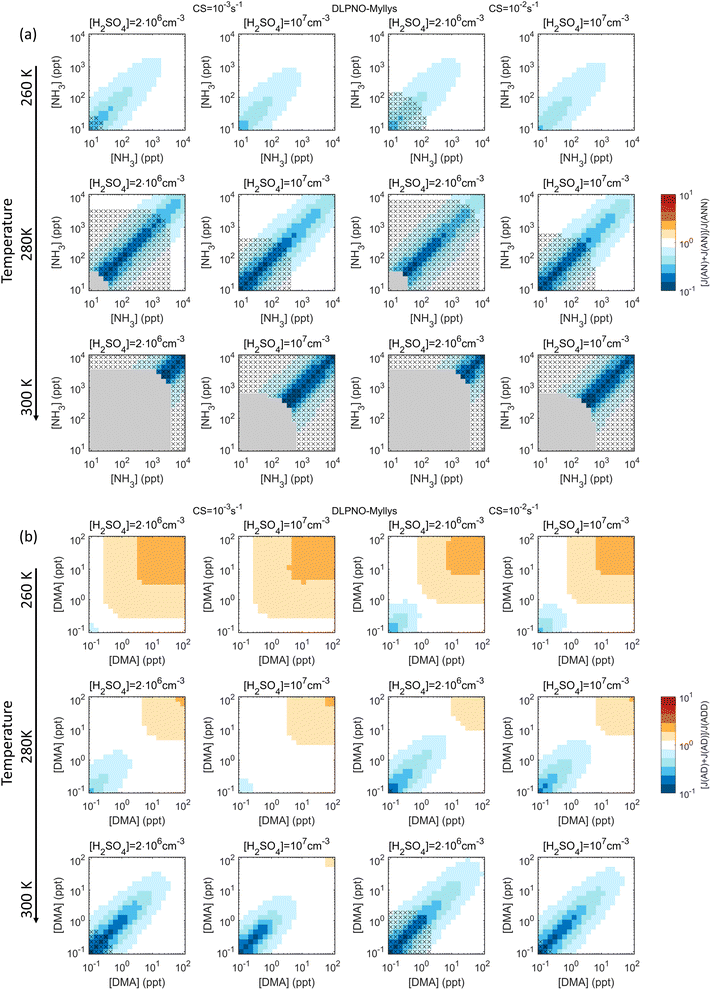
Fig. 3 shows ∑J2-comp/J3-comp for the synthetic test chemistries H2SO4–base1–base2, where the two bases have exactly the same properties. That is, clusters with equal amounts of H2SO4 and base are assumed to be similar regardless of whether they contain base1, base2, or both, and the cases are thus correctly represented by lumping. Here the largest effects occur around the diagonal [base1]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [base2] = 1
[base2] = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. For the weaker base represented by NH3, the sum approach leads to underprediction by factors of ≲5 (260 K) and ≲10 (280 K, 300 K). For the stronger base DMA, underprediction (up to factors of ≲10) and possibly overprediction (up to a factor of ∼2) occur at low and high [base], respectively. Base concentrations with the largest overprediction, however, correspond to very polluted environments. These trends are understood through the non-linear behavior of J as a function of vapor concentration, here [base]: at low [base], increase in [base] causes a stronger increase in J than at high [base] where the system eventually becomes saturated with respect to [base]. That is, as the slope of J decreases with increasing [base], the sum rates ∑J2-comp change from too low to too high. Under saturated conditions, the rate is double-counted by ∑J2-comp at base1 ≈ base2, as the explicit formation rate remains the same upon doubling of base concentration. These patterns are similar for RICC2 (Fig. S4†) and DLPNO_Kubečka (not shown; very similar to DLPNO_Myllys), with some shifts in the vapor concentration space due to the differences in predicted stabilities. For example, as RICC2 predicts higher stabilities, the underprediction is often less pronounced compared to the other data sets and also slight overprediction may occur, since J is less sensitive to [base] and saturates at lower [base].
1. For the weaker base represented by NH3, the sum approach leads to underprediction by factors of ≲5 (260 K) and ≲10 (280 K, 300 K). For the stronger base DMA, underprediction (up to factors of ≲10) and possibly overprediction (up to a factor of ∼2) occur at low and high [base], respectively. Base concentrations with the largest overprediction, however, correspond to very polluted environments. These trends are understood through the non-linear behavior of J as a function of vapor concentration, here [base]: at low [base], increase in [base] causes a stronger increase in J than at high [base] where the system eventually becomes saturated with respect to [base]. That is, as the slope of J decreases with increasing [base], the sum rates ∑J2-comp change from too low to too high. Under saturated conditions, the rate is double-counted by ∑J2-comp at base1 ≈ base2, as the explicit formation rate remains the same upon doubling of base concentration. These patterns are similar for RICC2 (Fig. S4†) and DLPNO_Kubečka (not shown; very similar to DLPNO_Myllys), with some shifts in the vapor concentration space due to the differences in predicted stabilities. For example, as RICC2 predicts higher stabilities, the underprediction is often less pronounced compared to the other data sets and also slight overprediction may occur, since J is less sensitive to [base] and saturates at lower [base].
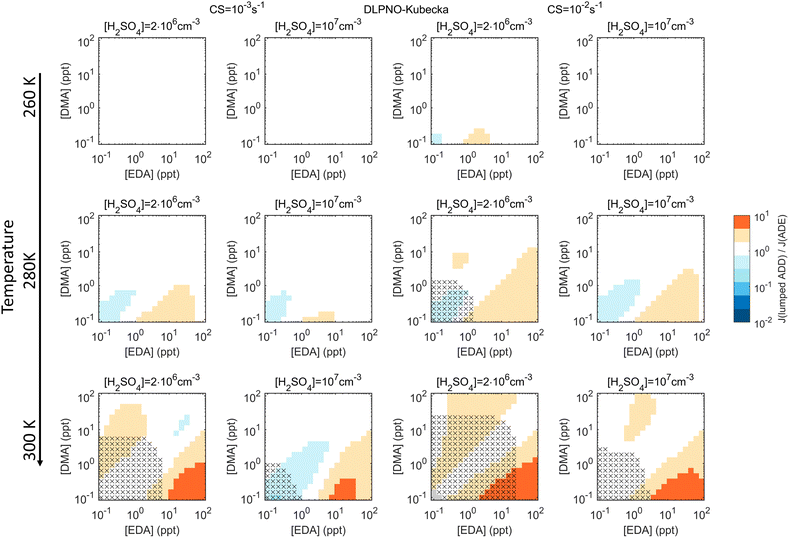
Assessments of lumping of different bases, conducted with the DLPNO_Kubečka multi-base data, suggest that DMA and EDA are similar enough to be better described by lumping than summing. Fig. 4 shows Jlumped/J3-comp, with Jlumped obtained assuming the properties of DMA and a total base concentration of [DMA] + [EDA] (see Fig. S6† for summing). Errors due to lumping are minor when [DMA] and [EDA] are of the same order, and become notable only at [DMA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [EDA] ≪ 1 when EDA is the dominating species.
[EDA] ≪ 1 when EDA is the dominating species.
However, here the lumping of TMA with DMA/EDA gives errors of similar order or higher than the sum approach (Fig. S7†). This is likely due to TMA being less efficient in cluster growth, as its three methyl groups cause steric hindrance. MA lies between NH3 and the other amines and thus cannot be lumped with any of these bases (e.g. Fig. S8†). Comparisons of lumping vs. summing for DLPNO_Kubečka are summarized in ESI Section 3†: for H2SO4–NH3–amine chemistries, trends in the biases of the sum approach are similar to those for H2SO4–NH3–DMA. For H2SO4–amine combinations, underprediction in summed J peaks when the amine concentrations are of the same order (except for MA for which biases peak at higher [MA]). For lumped J, patterns are less regular and wider ranges of conditions become biased—both low and high—when the species are not lumpable (e.g. Fig. S7†).
To find indicators for similarity, we compared the formation rates J2-comp of the isolated systems (ESI Section 3†). The differences in J2-comp generally follow the patterns of the error in the lumped rate Jlumped (e.g.Fig. 4); small differences (less than a factor of 10 between H2SO4–DMA and H2SO4–EDA) coincide with low errors in Jlumped. This suggests that the rates can be used as an indicator to assess similarity. In addition, a simple theoretical proxy based on acid·base heterodimer stability36 is in line with the comparisons (ESI Section 3†), and can thus serve as an additional measure.
The quantitative biases may be affected by the presence of ionic species. Ion effects are assessed using the RICC2 data set, which includes also charged clusters, assuming an average boundary layer ion production rate of 3 cm−3 s−1. For the H2SO4–NH3–DMA case, ions do not have notable effects on the bias at CS = 10−3 s−1 but significantly decrease the maximum biases at CS = 10−2 s−1, especially at T = 300 K (Fig. S2†). For the synthetic cases of identical bases, there are only minor effects for the strong base, but substantially less bias for the weaker base (Fig. S5†). This is due to J being less sensitive to vapor concentrations when the charge increases cluster stability. In general, ions are important for weaker clustering species and/or under conditions at which clusters are relatively less stable, such as low vapor concentrations and higher temperatures. Based on the RICC2 tests, ions can be expected to decrease the biases under such conditions.
To summarize, the commonly applied sum approach can be expected to give lower-limit assessments of the overall formation rate, here with the largest underprediction by factors of up to ∼10–100 (Table S2†) occurring at vapor level combinations at which all species are able to contribute (i.e. high and low concentrations for weak and strong clustering agents, respectively). The direction of the bias is consistent, as it follows from the omission of the total vapor concentration and similar behavior can thus be expected for other interacting chemistries. However, if model data and/or observations suggest very similar particle formation rates for stabilizing species with concentrations of the same magnitude, lumping is likely to involve less errors than summing of J.
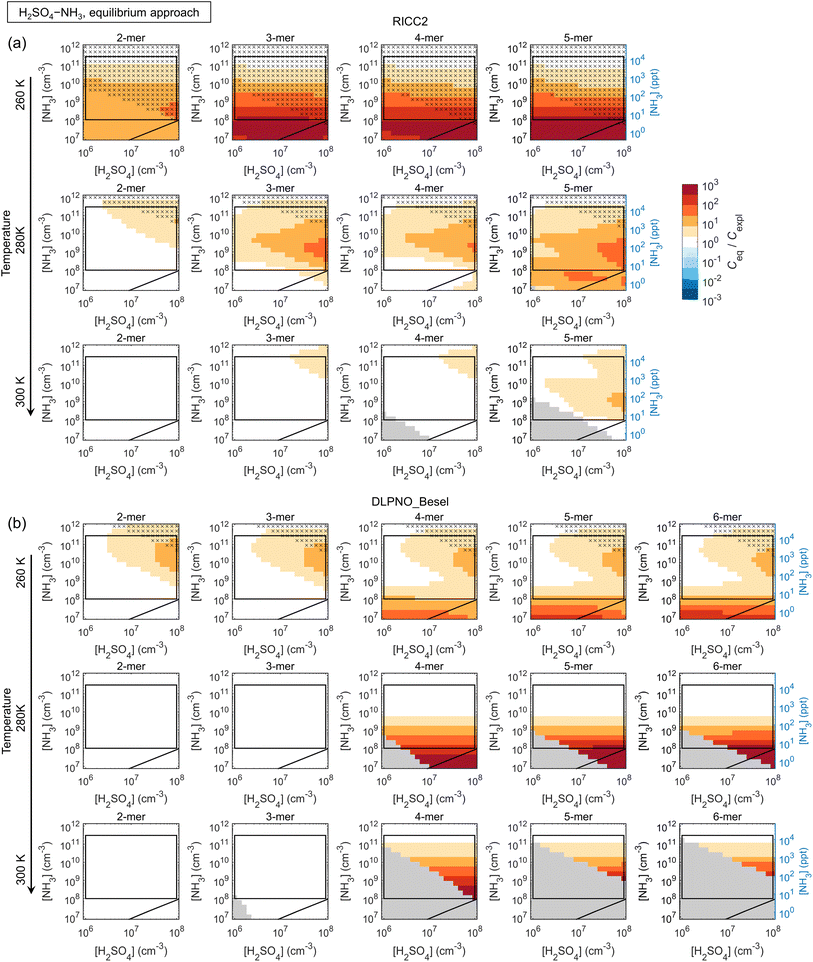
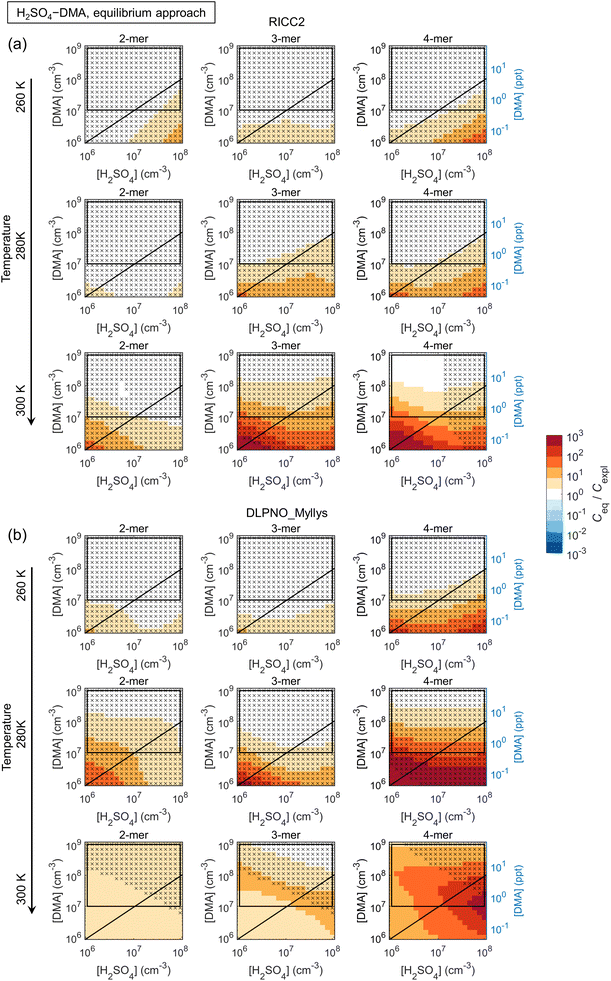
3.2 Simplifications in cluster dynamics by assuming quasi-unary chemical systems
The main conclusions can be summarized as follows: first, all data sets show a consistent tendency towards overprediction of n-mer concentrations by the equilibrium assumption by factors of up to ∼10–102 and even ≳103 especially at low [base]. The overprediction typically emerges and/or increases with increasing n and decreasing [base], although Ceq/Cexpl may also exhibit maxima along the base axis, likely linked to shifts in the most abundant compositions (i.e. shifts in the growth paths; Fig. S10†). The positive bias can be understood through base dynamics: the equilibrium approach assumes that cluster formation and growth are not limited by the availability of base vapor, which is not the case at low [base], leading to overpredicted Ceq.
Second, the comparison is often seemingly better for the more strongly clustering species H2SO4–DMA. However, this is not due to the clustering kinetics (most importantly the evaporation rates; eqn (5)) being well described by the effective equilibrium rate constants. Instead, the evaporation rates of the H2SO4–DMA clusters are often so low compared to vapor collision rates that their exact values do not have major effects. This was tested by re-running the equilibrium simulations with all clusters stabilized by 2 kcal mol−1, which decreases all evaporation rates by approximately two orders of magnitude. The conditions at which the n-mer concentrations Ceq,test of these test runs are within a factor of two from Ceq are marked in the figures with crosses, implying that the quantitative evaporation rates are not very important. Such cases include some of the low-temperature conditions for H2SO4–NH3, and most conditions for H2SO4–DMA. This type of condition can be experimentally identified based on high cluster concentrations: for the crossed areas, Cexpl ≳ 104–105 cm−3.
The figures can thus be interpreted as follows: under conditions with no bias and no crosses, the equilibrium assumption can be considered reasonable. Under conditions that have no bias but are marked with crosses, the quasi-unary approximation is reasonable but independent of the validity of the assumption, as well as of the exact rate constants. Under conditions with visible bias the clusters are not equilibrated with respect to base due to low [base] and/or evaporation effects, resulting in distorted predictions.
Also the weakly clustering H2SO4–NH3 case may show a good performance for the equilibrium assumption, but this depends strongly on the conditions, the cluster size (n-mer), and data set (i.e. the exact evaporation rates). For such chemistries, the assumption is thus more uncertain and unreliable. Overall, the effects of temperature on the quantitative Ceq/Cexpl vary somewhat with the species and data sets. Increasing temperature can facilitate equilibration by increasing evaporation rates and thus shortening evaporation time scales. On the other hand, increasing T may also introduce notable evaporation in a chemical system that has insignificant evaporation and thereby less bias at lower T. The quantitative Ceq/Cexpl ratios are also affected by the scavenging sink: here, we apply a reference sink of CS = 10−3 s−1, which is of the order of an average atmospheric sink or a wall loss sink in a clean chamber experiment.49 Test simulations with 10−4 s−1 and 10−2 s−1 show increasing overprediction with increasing CS (not shown). In general, scavenging effects become more significant at lower cluster concentrations which can occur, for example, at higher T, which may also contribute to the observed temperature trends.
The DLPNO_Kubečka data set that generally involves higher evaporation rates gives significantly more overprediction especially for the weaker clustering agents NH3 and MA, but the quasi-unary approach becomes less reliable also for DMA, as well as for EDA (not shown). Within DLPNO_Kubečka, TMA at low T gives the least bias for the quasi-unary assumption (Fig. S11†). Simulations with H2SO4–GUA (DLPNO_Myllys) are in line with these results: the guanidine-enhanced system with extremely low evaporation rates shows a good comparison even at high T (Fig. S12†).
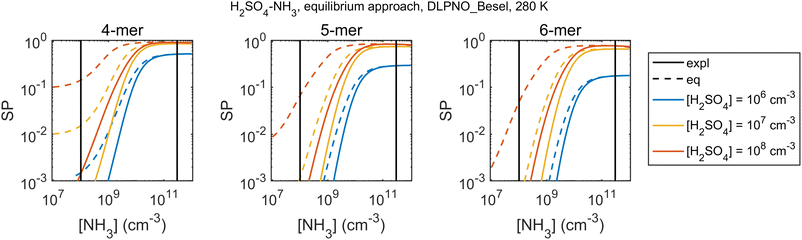
The bias and its size-dependence are directly linked to cluster survival probability assessments. Fig. 7 shows an example of a cluster survival parameter, here defined as the ratio SP = Cn/Cref where “ref” is a reference size smaller than n, for H2SO4–NH3 within DLPNO_Besel data. Here the survival parameter is overpredicted by the equilibrium approach, converging to the explicit results only at very high [NH3]. Quantitative survival estimates obtained by such a quasi-unary model should thus be interpreted with caution especially if NH3 is not in large excess.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [DMA] ≳ 1 when clustering becomes base-limited, and at higher T.
[DMA] ≳ 1 when clustering becomes base-limited, and at higher T.
Overall, while quasi-unary approximations are convenient for studying nanoparticle formation and growth dynamics, the results show that their applicability is limited to very strongly interacting, i.e. low-evaporating, species and/or low temperatures at excess base vapor. For weaker clustering agents such as H2SO4–NH3, which can be expected to be important on the global scale, the formation process is affected by multi-compound kinetics. Representing effective cluster properties through the distribution of base contents results in less bias than using a single composition, but the concentrations are often still significantly overpredicted. Vice versa, fitting a quasi-unary model to reproduce measurements cannot be expected to give rate constants that correspond to actual effective cluster properties. While the comparisons improve with increasing [base], the base concentrations at which the approximation becomes valid are often beyond typical atmospheric ranges, corresponding to very polluted environments. Application of quasi-unary approaches for such clustering agents generally leads to overprediction of nanoparticle concentrations, growth rates and survival probabilities. Overpredicted concentrations may also result in, for instance, overpredicted contribution of cluster coagulation to nanoparticle growth.
4 Conclusions
The evaluations for H2SO4–base chemistries indicate that some typical approaches to simplify multi-component particle formation can often be applied without sacrificing much accuracy, while others are reasonable only for specific, limited conditions. The trends in the biases are consistent and similar for different quantum chemical data sets. We tested simplifications for different parameters that are central in particle formation modeling: formation rates that are used in atmospheric aerosol models, and molecular cluster properties that are applied to assess cluster growth and survival, as summarized in Table 3.| Model parameter and simplification | Applicability for different types of compounds | |
|---|---|---|
| Formation rate | Different clustering properties | Similar clustering properties |
| a A checkmark implies that the simplification can in principle be applied without major errors, and a cross indicates that the simplification leads to distorted results and should not be applied. The applicability can depend on ambient conditions, as indicated in footnote b. b *Underprediction is expected at [base1] ≫ [base2], where base1 and base2 are weaker and stronger stabilizers, respectively, and [base2] is at the ppt or sub-ppt level. **Lumping is reasonable especially at similar concentrations of the compounds; for summing, underprediction is expected when the base concentrations are of the same order: [base1] ∼ [base2]. ***Applicable at low temperatures (here mainly ≲280 K) and excess concentration of the implicitly treated compound. | ||
| Summing of rates |
|
|
| Lumping of species |

|
|
The main results for formation rates J are as follows:
• For stabilizing compounds base1 and base2 with very different clustering efficiencies, the sum assumption J(H2SO4–base1–base2) ≈ J(H2SO4–base1) + J(H2SO4–base2) is biased towards underprediction for the combination of high [base1] and low [base2], where base1 and base2 are weaker and stronger stabilizers, respectively. The errors are minor especially for clean environments with low CS, but may increase to factors of up to ∼10–100 as CS increases to 10−3–10−2 s−1.
• As the clustering efficiencies of the species approach each other, the underprediction tendency shifts towards similar concentrations [base1] ∼ [base2].
• For very similar compounds, J is reasonably approximated by lumping the species through an effective vapor concentration [base] = [base1] + [base2]. The sum approach can result in errors of factors of up to ∼10–100 when [base1] and [base2] are of the same order. Under- and overprediction by the sum approach typically occur at lower and higher [base], respectively; the overprediction is minor and mainly occurs for strongly clustering species when J is saturated with respect to base.
• Similarity can be assessed based on formation rates, and additionally by a theoretical proxy involving the free energies of acid·base heterodimers. Minor differences in these indicators, here approximately by factors of ≲10, suggest similarity.
• A recent multi-base data set suggests that dimethylamine and ethylenediamine are similar enough to be lumped. The properties of trimethylamine are somewhat different compared to those of these two other amines, and lumping does not generally give better results than the sum approach.
• The presence of ions is expected to decrease the biases in the simplified formation rates. Charge enhances cluster binding, which reduces the differences in the relative stabilization efficiencies of different species.
Reducing H2SO4–base chemistries to quasi-unary H2SO4 systems for modeling molecular cluster concentrations is, in contrast, much more uncertain:
• The quasi-unary approaches are mainly applicable for strong stabilizing species with low-evaporating clusters at vapor concentrations that are high enough to not limit the cluster formation. Such a case is, for example, an efficiently clustering H2SO4–amine chemistry at [amine]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [H2SO4] > 1.
[H2SO4] > 1.
• Especially for weaker clustering species such as H2SO4–NH3 that are common particle formation agents on the global scale, and/or for warm conditions, cluster concentrations are overpredicted by up to 1–2 orders of magnitude, or even more, in the quasi-unary frameworks.
• The biases in cluster concentrations affect particle survival probability assessments, which can also be biased high, as the overprediction often emerges and/or increases with cluster size.
Simplifications in multi-compound chemistries are highly desirable for convenient representation, and the tests suggest that they can be possible especially for formation rates. The present results provide assessments of how and when to simplify and of the possible biases, thereby contributing to improved implementation of input data and understanding of model uncertainties.
Author contributions
Conceptualization, software (kinetic modeling), methodology: TO; formal analysis, investigation, visualization: RB and TO; resources (quantum chemical data and analysis): JK, NM, and JE; writing – original draft: TO; writing – review & editing: all authors.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
T. O. and R. B. acknowledge the Swedish Research Council VR (grant no. 2019-04853) and the Swedish Research Council for Sustainable Development FORMAS (grant no. 2019-01433) for financial support. J. K. and J. E. thank the Independent Research Fund Denmark (grant no. 9064-00001B). N. M. thanks the Academy of Finland for funding (grant no. 347775). We thank the CSC-IT Center for Science in Espoo, Finland, for providing computational resources.References
- V.-M. Kerminen, X. Chen, V. Vakkari, T. Petäjä, M. Kulmala and F. Bianchi, Atmospheric new particle formation and growth: review of field observations, Environ. Res. Lett., 2018, 13, 103003 CrossRef.
- S. Fuzzi, U. Baltensperger, K. Carslaw, S. Decesari, H. Denier van der Gon, M. C. Facchini, D. Fowler, I. Koren, B. Langford, U. Lohmann, E. Nemitz, S. Pandis, I. Riipinen, Y. Rudich, M. Schaap, J. G. Slowik, D. V. Spracklen, E. Vignati, M. Wild, M. Williams and S. Gilardoni, Particulate matter, air quality and climate: lessons learned and future needs, Atmos. Chem. Phys., 2015, 15, 8217–8299 CrossRef CAS.
- H. Gordon, J. Kirkby, U. Baltensperger, F. Bianchi, M. Breitenlechner, J. Curtius, A. Dias, J. Dommen, N. M. Donahue, E. M. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, C. Frege, C. Fuchs, A. Hansel, C. R. Hoyle, M. Kulmala, A. Kürten, K. Lehtipalo, V. Makhmutov, U. Molteni, M. P. Rissanen, Y. Stozkhov, J. Tröstl, G. Tsagkogeorgas, R. Wagner, C. Williamson, D. Wimmer, P. M. Winkler, C. Yan and K. S. Carslaw, Causes and importance of new particle formation in the present-day and preindustrial atmospheres, J. Geophys. Res.: Atmos., 2017, 122, 8739–8760 CrossRef.
- S.-H. Lee, H. Gordon, H. Yu, K. Lehtipalo, R. Haley, Y. Li and R. Zhang, New Particle Formation in the Atmosphere: From Molecular Clusters to Global Climate, J. Geophys. Res.: Atmos., 2019, 124, 7098–7146 CrossRef CAS.
- B. R. Bzdek and J. P. Reid, Perspective: Aerosol microphysics: From molecules to the chemical physics of aerosols, J. Chem. Phys., 2017, 147, 220901 CrossRef PubMed.
- K. Lehtipalo, C. Yan, L. Dada, F. Bianchi, M. Xiao, R. Wagner, D. Stolzenburg, L. R. Ahonen, A. Amorim, A. Baccarini, P. S. Bauer, B. Baumgartner, A. Bergen, A.-K. Bernhammer, M. Breitenlechner, S. Brilke, A. Buchholz, S. B. Mazon, D. Chen, X. Chen, A. Dias, J. Dommen, D. C. Draper, J. Duplissy, M. Ehn, H. Finkenzeller, L. Fischer, C. Frege, C. Fuchs, O. Garmash, H. Gordon, J. Hakala, X. He, L. Heikkinen, M. Heinritzi, J. C. Helm, V. Hofbauer, C. R. Hoyle, T. Jokinen, J. Kangasluoma, V.-M. Kerminen, C. Kim, J. Kirkby, J. Kontkanen, A. Kürten, M. J. Lawler, H. Mai, S. Mathot, R. L. Mauldin, U. Molteni, L. Nichman, W. Nie, T. Nieminen, A. Ojdanic, A. Onnela, M. Passananti, T. Petäjä, F. Piel, V. Pospisilova, L. L. J. Quéléver, M. P. Rissanen, C. Rose, N. Sarnela, S. Schallhart, S. Schuchmann, K. Sengupta, M. Simon, M. Sipilä, C. Tauber, A. Tomé, J. Tröstl, O. Väisänen, A. L. Vogel, R. Volkamer, A. C. Wagner, M. Wang, L. Weitz, D. Wimmer, P. Ye, A. Ylisirniö, Q. Zha, K. S. Carslaw, J. Curtius, N. M. Donahue, R. C. Flagan, A. Hansel, I. Riipinen, A. Virtanen, P. M. Winkler, U. Baltensperger, M. Kulmala and D. R. Worsnop, Multicomponent new particle formation from sulfuric acid, ammonia, and biogenic vapors, Sci. Adv., 2018, 4, eaau5363 CrossRef CAS PubMed.
- J. Elm, Unexpected Growth Coordinate in Large Clusters Consisting of Sulfuric Acid and C8H12O6 Tricarboxylic Acid, J. Phys. Chem. A, 2019, 123, 3170–3175 CrossRef CAS PubMed.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petäjä, M. Sipilä, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Järvinen, M. Äijälä, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkilä, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin, J. Duplissy, H. Vehkamäki, J. Bäck, A. Kortelainen, I. Riipinen, T. Kurtén, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. J. Lehtinen, A. Laaksonen, V.-M. Kerminen and D. R. Worsnop, Direct Observations of Atmospheric Aerosol Nucleation, Science, 2013, 339, 943–946 CrossRef CAS PubMed.
- M. Xiao, C. R. Hoyle, L. Dada, D. Stolzenburg, A. Kürten, M. Wang, H. Lamkaddam, O. Garmash, B. Mentler, U. Molteni, A. Baccarini, M. Simon, X.-C. He, K. Lehtipalo, L. R. Ahonen, R. Baalbaki, P. S. Bauer, L. Beck, D. Bell, F. Bianchi, S. Brilke, D. Chen, R. Chiu, A. Dias, J. Duplissy, H. Finkenzeller, H. Gordon, V. Hofbauer, C. Kim, T. K. Koenig, J. Lampilahti, C. P. Lee, Z. Li, H. Mai, V. Makhmutov, H. E. Manninen, R. Marten, S. Mathot, R. L. Mauldin, W. Nie, A. Onnela, E. Partoll, T. Petäjä, J. Pfeifer, V. Pospisilova, L. L. J. Quéléver, M. Rissanen, S. Schobesberger, S. Schuchmann, Y. Stozhkov, C. Tauber, Y. J. Tham, A. Tomé, M. Vazquez-Pufleau, A. C. Wagner, R. Wagner, Y. Wang, L. Weitz, D. Wimmer, Y. Wu, C. Yan, P. Ye, Q. Ye, Q. Zha, X. Zhou, A. Amorim, K. Carslaw, J. Curtius, A. Hansel, R. Volkamer, P. M. Winkler, R. C. Flagan, M. Kulmala, D. R. Worsnop, J. Kirkby, N. M. Donahue, U. Baltensperger, I. El Haddad and J. Dommen, The driving factors of new particle formation and growth in the polluted boundary layer, Atmos. Chem. Phys., 2021, 21, 14275–14291 CrossRef CAS.
- L. Yao, O. Garmash, F. Bianchi, J. Zheng, C. Yan, J. Kontkanen, H. Junninen, S. B. Mazon, M. Ehn, P. Paasonen, M. Sipilä, M. Wang, X. Wang, S. Xiao, H. Chen, Y. Lu, B. Zhang, D. Wang, Q. Fu, F. Geng, L. Li, H. Wang, L. Qiao, X. Yang, J. Chen, V.-M. Kerminen, T. Petäjä, D. R. Worsnop, M. Kulmala and L. Wang, Atmospheric new particle formation from sulfuric acid and amines in a Chinese megacity, Science, 2018, 361, 278–281 CrossRef CAS PubMed.
- W. A. Glasoe, K. Volz, B. Panta, N. Freshour, R. Bachman, D. R. Hanson, P. H. McMurry and C. Jen, Sulfuric acid nucleation: an experimental study of the effect of seven bases, J. Geophys. Res.: Atmos., 2015, 120, 1933–1950 CrossRef CAS.
- C. N. Jen, P. H. McMurry and D. R. Hanson, Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res.: Atmos., 2014, 119, 7502–7514 CrossRef CAS.
- J. Almeida, S. Schobesberger, A. Kürten, I. K. Ortega, O. Kupiainen-Määttä, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, N. M. Donahue, A. Downard, E. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, H. Henschel, T. Jokinen, H. Junninen, M. Kajos, J. Kangasluoma, H. Keskinen, A. Kupc, T. Kurtén, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, M. Leiminger, J. Leppä, V. Loukonen, V. Makhmutov, S. Mathot, M. J. McGrath, T. Nieminen, T. Olenius, A. Onnela, T. Petäjä, F. Riccobono, I. Riipinen, M. Rissanen, L. Rondo, T. Ruuskanen, F. D. Santos, N. Sarnela, S. Schallhart, R. Schnitzhofer, J. H. Seinfeld, M. Simon, M. Sipilä, Y. Stozhkov, F. Stratmann, A. Tomé, J. Tröstl, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Virtanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, C. Williamson, D. Wimmer, P. Ye, T. Yli-Juuti, K. S. Carslaw, M. Kulmala, J. Curtius, U. Baltensperger, D. R. Worsnop, H. Vehkamäki and J. Kirkby, Molecular understanding of sulphuric acid–amine particle nucleation in the atmosphere, Nature, 2013, 502, 359–363 CrossRef CAS PubMed.
- C. N. Jen, R. Bachman, J. Zhao, P. H. McMurry and D. R. Hanson, Diamine-sulfuric acid reactions are a potent source of new particle formation, Geophys. Res. Lett., 2016, 43, 867–873 CrossRef CAS.
- Y. You, V. P. Kanawade, J. A. de Gouw, A. B. Guenther, S. Madronich, M. R. Sierra-Hernández, M. Lawler, J. N. Smith, S. Takahama, G. Ruggeri, A. Koss, K. Olson, K. Baumann, R. J. Weber, A. Nenes, H. Guo, E. S. Edgerton, L. Porcelli, W. H. Brune, A. H. Goldstein and S.-H. Lee, Atmospheric amines and ammonia measured with a chemical ionization mass spectrometer (CIMS), Atmos. Chem. Phys., 2014, 14, 12181–12194 CrossRef.
- J. Zheng, Y. Ma, M. Chen, Q. Zhang, L. Wang, A. F. Khalizov, L. Yao, Z. Wang, X. Wang and L. Chen, Measurement of atmospheric amines and ammonia using the high resolution time-of-flight chemical ionization mass spectrometry, Atmos. Environ., 2015, 102, 249–259 CrossRef CAS.
- J. Mao, F. Yu, Y. Zhang, J. An, L. Wang, J. Zheng, L. Yao, G. Luo, W. Ma, Q. Yu, C. Huang, L. Li and L. Chen, High-resolution modeling of gaseous methylamines over a polluted region in China: source-dependent emissions and implications of spatial variations, Atmos. Chem. Phys., 2018, 18, 7933–7950 CrossRef CAS.
- L. Dada, K. Lehtipalo, J. Kontkanen, T. Nieminen, R. Baalbaki, L. Ahonen, J. Duplissy, C. Yan, B. Chu, T. Petäjä, K. Lehtinen, V.-M. Kerminen, M. Kulmala and J. Kangasluoma, Formation and growth of sub-3-nm aerosol particles in experimental chambers, Nat. Protoc., 2020, 15, 1013–1040 CrossRef CAS PubMed.
- J. Elm, J. Kubečka, V. Besel, M. J. Jääskeläinen, R. Halonen, T. Kurtén and H. Vehkamäki, Modeling the formation and growth of atmospheric molecular clusters: A review, J. Aerosol Sci., 2020, 149, 105621 CrossRef CAS.
- T. Olenius, O. Kupiainen-Määttä, I. K. Ortega, T. Kurtén and H. Vehkamäki, Free energy barrier in the growth of sulfuric acid–ammonia and sulfuric acid–dimethylamine clusters, J. Chem. Phys., 2013, 139, 084312 CrossRef CAS PubMed.
- J. Kontkanen, D. Stolzenburg, T. Olenius, C. Yan, L. Dada, L. Ahonen, M. Simon, K. Lehtipalo and I. Riipinen, What controls the observed size-dependency of the growth rates of sub-10 nm atmospheric particles?, Environ. Sci.: Atmos., 2022, 2, 449–468 CAS.
- E. M. Dunne, H. Gordon, A. Kürten, J. Almeida, J. Duplissy, C. Williamson, I. K. Ortega, K. J. Pringle, A. Adamov, U. Baltensperger, P. Barmet, F. Benduhn, F. Bianchi, M. Breitenlechner, A. Clarke, J. Curtius, J. Dommen, N. M. Donahue, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, T. Jokinen, J. Kangasluoma, J. Kirkby, M. Kulmala, A. Kupc, M. J. Lawler, K. Lehtipalo, V. Makhmutov, G. Mann, S. Mathot, J. Merikanto, P. Miettinen, A. Nenes, A. Onnela, A. Rap, C. L. S. Reddington, F. Riccobono, N. A. D. Richards, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Simon, M. Sipilä, J. N. Smith, Y. Stozkhov, A. Tomé, J. Tröstl, P. E. Wagner, D. Wimmer, P. M. Winkler, D. R. Worsnop and K. S. Carslaw, Global atmospheric particle formation from CERN CLOUD measurements, Science, 2016, 354, 1119–1124 CrossRef CAS PubMed.
- T. Bergman, A. Laaksonen, H. Korhonen, J. Malila, E. M. Dunne, T. Mielonen, K. E. J. Lehtinen, T. Kühn, A. Arola and H. Kokkola, Geographical and diurnal features of amine-enhanced boundary layer nucleation, J. Geophys. Res.: Atmos., 2015, 120, 9606–9624 CrossRef.
- F. Gelbard and J. H. Seinfeld, Simulation of multicomponent aerosol dynamics, J. Colloid Interface Sci., 1980, 78, 485–501 CrossRef CAS.
- H. Henschel, T. Kurtén and H. Vehkamäki, Computational Study on the Effect of Hydration on New Particle Formation in the Sulfuric Acid/Ammonia and Sulfuric Acid/Dimethylamine Systems, J. Phys. Chem. A, 2016, 120, 1886–1896 CrossRef CAS PubMed.
- F. Yu, A. B. Nadykto, J. Herb, G. Luo, K. M. Nazarenko and L. A. Uvarova, H2SO4–H2O–NH3 ternary ion-mediated nucleation (TIMN): kinetic-based model and comparison with CLOUD measurements, Atmos. Chem. Phys., 2018, 18, 17451–17474 CrossRef CAS.
- A. Kürten, T. Jokinen, M. Simon, M. Sipilä, N. Sarnela, H. Junninen, A. Adamov, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, N. M. Donahue, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, J. Hakala, A. Hansel, M. Heinritzi, M. Hutterli, J. Kangasluoma, J. Kirkby, A. Laaksonen, K. Lehtipalo, M. Leiminger, V. Makhmutov, S. Mathot, A. Onnela, T. Petäjä, A. P. Praplan, F. Riccobono, M. P. Rissanen, L. Rondo, S. Schobesberger, J. H. Seinfeld, G. Steiner, A. Tomé, J. Tröstl, P. M. Winkler, C. Williamson, D. Wimmer, P. Ye, U. Baltensperger, K. S. Carslaw, M. Kulmala, D. R. Worsnop and J. Curtius, Neutral molecular cluster formation of sulfuric acid–dimethylamine observed in real time under atmospheric conditions, Proc. Natl. Acad. Sci., 2014, 111, 15019–15024 CrossRef PubMed.
- J. S. Johnson and C. N. Jen, A sulfuric acid nucleation potential model for the atmosphere, Atmos. Chem. Phys., 2022, 22, 8287–8297 CrossRef CAS.
- I. K. Ortega, O. Kupiainen, T. Kurtén, T. Olenius, O. Wilkman, M. J. McGrath, V. Loukonen and H. Vehkamäki, From quantum chemical formation free energies to evaporation rates, Atmos. Chem. Phys., 2012, 12, 225–235 CrossRef CAS.
- N. Myllys, J. Kubečka, V. Besel, D. Alfaouri, T. Olenius, J. N. Smith and M. Passananti, Role of base strength, cluster structure and charge in sulfuric-acid-driven particle formation, Atmos. Chem. Phys., 2019, 19, 9753–9768 CrossRef CAS.
- T. Olenius, Atmospheric Cluster Dynamics Code: Software Repository, https://github.com/tolenius/ACDC, 2021 Search PubMed.
- N. Myllys, S. Chee, T. Olenius, M. Lawler and J. Smith, Molecular-Level Understanding of Synergistic Effects in Sulfuric Acid–Amine–Ammonia Mixed Clusters, J. Phys. Chem. A, 2019, 123, 2420–2425 CrossRef CAS PubMed.
- B. Temelso, E. F. Morrison, D. L. Speer, B. C. Cao, N. Appiah-Padi, G. Kim and G. C. Shields, Effect of Mixing Ammonia and Alkylamines on Sulfate Aerosol Formation, J. Phys. Chem. A, 2018, 122, 1612–1622 CrossRef CAS PubMed.
- H. Li, A. Ning, J. Zhong, H. Zhang, L. Liu, Y. Zhang, X. Zhang, X. C. Zeng and H. He, Influence of atmospheric conditions on sulfuric acid-dimethylamine-ammonia-based new particle formation, Chemosphere, 2020, 245, 125554 CrossRef CAS PubMed.
- N. Myllys, T. Ponkkonen, M. Passananti, J. Elm, H. Vehkamäki and T. Olenius, Guanidine: A Highly Efficient Stabilizer in Atmospheric New-Particle Formation, J. Phys. Chem. A, 2018, 122, 4717–4729 CrossRef CAS PubMed.
- S. Chee, K. Barsanti, J. N. Smith and N. Myllys, A predictive model for salt nanoparticle formation using heterodimer stability calculations, Atmos. Chem. Phys., 2021, 21, 11637–11654 CrossRef CAS.
- J. Kubečka, I. Neefjes, V. Besel, F. Qiao, H.-B. Xie and J. Elm, Atmospheric sulfuric acid–multi-base new particle formation revealed through quantum chemistry enhanced by machine learning, Environ. Sci. Technol. Search PubMed , under review.
- F. Yu and G. Luo, Modeling of gaseous methylamines in the global atmosphere: impacts of oxidation and aerosol uptake, Atmos. Chem. Phys., 2014, 14, 12455–12464 CrossRef.
- A. Kürten, F. Bianchi, J. Almeida, O. Kupiainen-Määttä, E. M. Dunne, J. Duplissy, C. Williamson, P. Barmet, M. Breitenlechner, J. Dommen, N. M. Donahue, R. C. Flagan, A. Franchin, H. Gordon, J. Hakala, A. Hansel, M. Heinritzi, L. Ickes, T. Jokinen, J. Kangasluoma, J. Kim, J. Kirkby, A. Kupc, K. Lehtipalo, M. Leiminger, V. Makhmutov, A. Onnela, I. K. Ortega, T. Petäjä, A. P. Praplan, F. Riccobono, M. P. Rissanen, L. Rondo, R. Schnitzhofer, S. Schobesberger, J. N. Smith, G. Steiner, Y. Stozhkov, A. Tomé, J. Tröstl, G. Tsagkogeorgas, P. E. Wagner, D. Wimmer, P. Ye, U. Baltensperger, K. Carslaw, M. Kulmala and J. Curtius, Experimental particle formation rates spanning tropospheric sulfuric acid and ammonia abundances, ion production rates, and temperatures, J. Geophys. Res.: Atmos., 2016, 121(12), 377–412 Search PubMed.
- V. Besel, J. Kubečka, T. Kurtén and H. Vehkamäki, Impact of Quantum Chemistry Parameter Choices and Cluster Distribution Model Settings on Modeled Atmospheric Particle Formation Rates, J. Phys. Chem. A, 2020, 124, 5931–5943 CrossRef CAS PubMed.
- K. E. J. Lehtinen, M. Dal Maso, M. Kulmala and V.-M. Kerminen, Estimating nucleation rates from apparent particle formation rates and vice versa: Revised formulation of the Kerminen–Kulmala equation, J. Aerosol Sci., 2007, 38, 988–994 CrossRef CAS.
- L. Rondo, S. Ehrhart, A. Kürten, A. Adamov, F. Bianchi, M. Breitenlechner, J. Duplissy, A. Franchin, J. Dommen, N. M. Donahue, E. M. Dunne, R. C. Flagan, J. Hakala, A. Hansel, H. Keskinen, J. Kim, T. Jokinen, K. Lehtipalo, M. Leiminger, A. Praplan, F. Riccobono, M. P. Rissanen, N. Sarnela, S. Schobesberger, M. Simon, M. Sipilä, J. N. Smith, A. Tomé, J. Tröstl, G. Tsagkogeorgas, P. Vaattovaara, P. M. Winkler, C. Williamson, D. Wimmer, U. Baltensperger, J. Kirkby, M. Kulmala, T. Petäjä, D. R. Worsnop and J. Curtius, Effect of dimethylamine on the gas phase sulfuric acid concentration measured by Chemical Ionization Mass Spectrometry, J. Geophys. Res.: Atmos., 2016, 121, 3036–3049 CrossRef CAS PubMed.
- A. Jaecker-Voirol, P. Mirabel and H. Reiss, Hydrates in supersaturated binary sulfuric acid–water vapor: A reexamination, J. Chem. Phys., 1987, 87, 4849–4852 CrossRef CAS.
- C. Li and P. H. McMurry, Errors in nanoparticle growth rates inferred from measurements in chemically reacting aerosol systems, Atmos. Chem. Phys., 2018, 18, 8979–8993 CrossRef.
- S. Tuovinen, R. Cai, V.-M. Kerminen, J. Jiang, C. Yan, M. Kulmala and J. Kontkanen, Survival probabilities of atmospheric particles: comparison based on theory, cluster population simulations, and observations in Beijing, Atmos. Chem. Phys., 2022, 22, 15071–15091 CrossRef CAS.
- A. A. Nair and F. Yu, Quantification of Atmospheric Ammonia Concentrations: A Review of Its Measurement and Modeling, Atmosphere, 2020, 11, 1092 CrossRef CAS.
- B. Croft, G. R. Wentworth, R. V. Martin, W. R. Leaitch, J. G. Murphy, B. N. Murphy, J. K. Kodros, J. P. D. Abbatt and J. R. Pierce, Contribution of Arctic seabird-colony ammonia to atmospheric particles and cloud-albedo radiative effect, Nat. Commun., 2016, 7, 13444 CrossRef CAS PubMed.
- U. Makkonen, A. Virkkula, H. Hellén, M. Hemmilä, J. Sund, M. Äijälä, M. Ehn, H. Junninen, P. Keronen, T. Petäjä, D. R. Worsnop, M. Kulmala and H. Hakola, Semi-continuous gas and inorganic aerosol measurements at a boreal forest site: seasonal and diurnal cycles of NH3, HONO and HNO3, Boreal Environ. Res., 2014, 19(suppl. B), 311–328 Search PubMed.
- A. Kürten, C. Williamson, J. Almeida, J. Kirkby and J. Curtius, On the derivation of particle nucleation rates from experimental formation rates, Atmos. Chem. Phys., 2015, 15, 4063–4075 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ea00174h |
| This journal is © The Royal Society of Chemistry 2023 |