Open Access Article
Open Access ArticleUsing spatiotemporal prediction models to quantify PM2.5 exposure due to daily movement†
Sakshi
Jain
a,
Albert A.
Presto
b and
Naomi
Zimmerman
 *a
*a
aDepartment of Mechanical Engineering, University of British Columbia, Vancouver, Canada. E-mail: nzimmerman@mech.ubc.ca; Fax: +1-604-822-2403; Tel: +1-604-822-9433
bDepartment of Mechanical Engineering, Carnegie Mellon University, Pittsburgh, USA
First published on 24th October 2023
Abstract
To date, epidemiological studies have generally not accounted for the spatiotemporal variations in PM2.5 concentration that populations experience. These studies typically infer exposure using home address and annually-averaged concentrations measured by a few centrally-located monitors. To quantify the impact of spatiotemporal variation on exposure estimates, this study uses land-use random forest models to estimate daily-average ambient PM2.5 concentrations in Allegheny County, USA. The data were collected using a network of 47 low-cost air quality sensors, and predictions were made for 50 × 50 m grids in Pittsburgh. Residential (PR) and commercial (PC) probability weighting values were assigned to each grid. The daily-average predictions were divided into “weekday” and “weekend” concentrations for each grid and averaged annually to estimate total annual exposure. Weighted stratified sampling was conducted using PR and PC values as probabilities, and weekdays and weekends as strata. Static models (population spends 24 hours per day in a fixed residential area) and dynamic models (estimates that account for time spent in residential and commercial areas) were created using these samples. The daily-average predicted concentrations across all grids ranged from 4–75 μg m−3 (μ = 12.0 μg m−3). Weekend concentrations were 10% higher than weekday concentrations, and commercial area concentrations were 9% higher than residential areas. These results support the hypotheses that exposure profiles vary due to movement between different areas and that exposure is underestimated when residents' mobility is ignored. Furthermore, exposure estimates may be affected due to the observed existence of temporal variations between weekdays and weekends. As low-cost sensor networks adoption grows, this work suggests that epidemiological exposure models can leverage these data to further refine exposure estimates and identify behaviors that may reduce exposure.
Environmental significanceThis study estimated the impact of spatiotemporal ambient PM2.5 variations on exposure using a low-cost air quality sensor (LCS) network in Pittsburgh, PA, USA. Exposure epidemiology typically relies on inferring exposure from residential address. We found that exposure estimates are consistently about 10% higher when the population spends more time in commercially-dense locations (dynamic model) vs. residentially-dense locations (static model) and that exposure was higher on weekends. This work demonstrates that LCS networks can be used to improve PM2.5 exposure estimates by informing concentration models that are more refined in space and time. Previous epidemiology research has shown that there is no PM2.5 concentration below which health effects are not observed, thus improvement in exposure estimates may improve or refine the existing knowledge on health impacts of low levels of PM2.5. |
1 Introduction
Exposure to particulate matter (PM2.5) is associated with several health problems, ranging from asthma to premature death.1,2 Short-term exposure to high PM2.5 concentrations can trigger cardiovascular-disease-related mortality and nonfatal events,3,4 while long-term exposure can lead to acute and chronic illnesses, including aggravated asthma, cardiovascular disease and lung cancer.1 As a result, a reduction of annual average PM2.5 concentrations by 10 μg m−3 has been associated with a 7.3% reduction in all-cause mortality in the US Medicare population.4To mitigate the public health effects of PM2.5, it is important to accurately estimate the population's exposure. The cumulative exposure of an individual is typically estimated by considering their exposure in three key contexts: (1) indoor environments, (2) during commuting, and (3) outdoor settings. To accurately gauge an individual's overall exposure, it is essential to account for a variety of factors specific to each context. Exposure assessments within indoor spaces are significantly affected by activities such as cooking and cleaning,5 and the building characteristics (e.g., presence of air filters, infiltration of ambient concentrations, windows open/closed).6 For commuting, factors such as the duration and mode of transportation (e.g., walking, driving, using public transit) play a dominant role in influencing the overall exposure levels.7 Ambient concentrations are inherently influenced by meteorological conditions (e.g., wind direction)8 and geography (e.g., elevation).9 These factors contribute to the complex interplay of exposure elements that need to be considered for a comprehensive estimation of an individual's exposure profile. However, there are challenges with properly assessing exposure considering these complex elements. Exposure is often inferred from PM2.5 concentrations taken via only a few centrally-located outdoor monitors.10–12 In contrast, previous studies have shown that small-scale spatial variations in PM2.5 exist.13,14 As such, peoples' movement exposes them to changing pollution concentrations, resulting in varying exposure profiles, which can impact a given person's consequent health.4,15 Additionally, exposure misclassification due to unaccounted human mobility can have effects on the epidemiological inferences derived and consequently, on relevant policies. Residence-only exposure profiles have been found to result in negative biases in the estimates,16–19 in essence, the relative risk is underestimated by ignoring mobility.
The effect of mobility on exposure levels has previously been assessed using wearable or portable personal monitors, which typically collect integrated filter samples for offline chemical analysis, and comparing the personal monitoring concentrations with ambient concentrations at home residences and applying correction factors. However, even though personal monitors are the most accurate method to estimate personal exposure, they have both logistic and cost constraints, such as recruiting an adequate number of individuals from representative populations to carry the monitors. Furthermore, the characteristics of participants (e.g., age, gender) may affect the accuracy of the correction factors used to infer personal exposure from ambient PM2.5.20 Personal monitors also suffer from measurement uncertainties, due to the low temporal resolution of the data (often 4–24 h).21 An alternate way of addressing the impacts of mobility and the discrepancy between personal exposure and at-residence concentrations is by including the spatial variability of the pollutant.15,22–24
Most exposure epidemiology studies are based on residential address;25 the daily movement of an individual (for work, recreation etc.) isn't typically accounted. Consequentially, the impact of spatial movement in a person's day is often not represented in epidemiology studies. There are some studies that have estimated movement-based exposure, using mobile phone data,16,17,26 activity-based data27 or agent-based models.18 However, their spatial resolution is coarse, ranging from 400 m16 up to 3 km.17,27
The lack of spatial resolution via ground measurements primarily exists because dense networks of regulatory monitoring stations aren't feasible due to their high initial capital investment and ongoing maintenance costs (USD 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–100
000–100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 per pollutant). To overcome the shortcomings associated with monitoring stations, lower-cost sensing technologies have increasingly been used as an alternative due to a combination of improved sensor technologies and researcher-developed methods for sensor calibration.28–32 Due to the low-cost and low power demands of low-cost sensors (LCS), they can be deployed to form a dense network, which can assist in capturing small-scale spatial variations. As such, although there are disadvantages associated with using low-cost sensors (sensitivities to environmental conditions28,33 and other pollutants,29,34 drifting of sensor readings35 that typically require calibration across the full range of meteorological conditions and pollutant concentrations), there are opportunities to use LCS to increase our understanding of air pollution exposure. By combining high spatial and temporal resolution surface maps of PM2.5 modelled from dense LCS networks,36 indoor–outdoor ratios in different micro-environments (home, commercial buildings, vehicles) and activity-based breathing rates, more accurate personal exposures can be estimated.37
000 per pollutant). To overcome the shortcomings associated with monitoring stations, lower-cost sensing technologies have increasingly been used as an alternative due to a combination of improved sensor technologies and researcher-developed methods for sensor calibration.28–32 Due to the low-cost and low power demands of low-cost sensors (LCS), they can be deployed to form a dense network, which can assist in capturing small-scale spatial variations. As such, although there are disadvantages associated with using low-cost sensors (sensitivities to environmental conditions28,33 and other pollutants,29,34 drifting of sensor readings35 that typically require calibration across the full range of meteorological conditions and pollutant concentrations), there are opportunities to use LCS to increase our understanding of air pollution exposure. By combining high spatial and temporal resolution surface maps of PM2.5 modelled from dense LCS networks,36 indoor–outdoor ratios in different micro-environments (home, commercial buildings, vehicles) and activity-based breathing rates, more accurate personal exposures can be estimated.37
In our previous work,36 we used data from a network of 47 low-cost PM2.5 sensors deployed between January–December 2017 in Allegheny County, Pennsylvania to develop land use regression models to predict daily PM2.5 concentrations at each 50 m × 50 m grid in Allegheny County in 2017 (see Sections S1 and S2 of the ESI† for more details on the data collection, days of data for each sensor, links to data repositories and the QA/QC protocols for the data from this prior study). In this work, we use these daily ambient PM2.5 predictions to compare the base case used in epidemiology (PM2.5 estimated at home addresses; static models) with an estimate where people spend time at both home and work/commercial locations (dynamic models). In this work, we use the term ‘exposure’ as a proxy for time-weighted ambient concentrations that the population experiences. As such, indoor concentrations are not considered for this work. Additionally, we have excluded exposure during commuting or transit; i.e., we are not replicating personal exposure. Instead, the term ‘movement’ implies that people aren't necessarily always located in the same place and may move from one land-use type to another. Overall, we aim to highlight the potential utility of the high spatiotemporal resolution ambient PM2.5 concentrations surface maps made possible by LCS networks on these exposure estimates.
2 Methods
2.1 PM2.5 measurements
As a part of Center for Air, Climate, and Energy Solutions (CACES) air quality monitoring network, a network of 47 Real-time Affordable Multi-Pollutant (RAMP) sensors (developed by SENSIT Technologies) was deployed in Allegheny County between January and December 2017; more details on sensor network and data used for this work can be found in Section S1 of ESI.† These sensors use a commercial light scattering sensor (either a Met-One Neighborhood Monitor or a PurpleAir PA-II) to collect 15 minute resolution PM2.5 data. Processing of this data to build land use regression concentration surface models is described in detail in Jain et al.36 and summarized here in Sections 2.1 and 2.2. In brief, the collected data were calibrated using the methods and calibration factors determined in Malings et al.35. This calibration was based on collocation with instrumentation meeting the US EPA Federal Equivalent Method standards for PM2.5. Mean absolute error ranged from 2.5–2.9 μg m−3 for 1 hour concentrations. Further calibration details are described in Section S2 of the ESI.† For this work, we identified 5 μg m−3 as the smallest concentration that can be reliably measured by the sensors (limit of detection, LOD). This was approximately 9% of the total data set across 47 sites and the 15 minute data below LOD was replaced with 3.53 μg m−3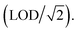 38,39 More information on LOD determination can be found in Section S3 of the ESI.†
38,39 More information on LOD determination can be found in Section S3 of the ESI.†
2.2 Land use regression modeling
The land use regression models for prediction modeling of daily average PM2.5 concentrations have been previously published in Jain et al.,36 with one primary change; for this work, we replaced the predicted concentrations from Jain et al.36 below the LOD with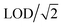 (in Jain et al.,36 concentrations below LOD were removed). We opted for this change to avoid the data set being skewed high.
(in Jain et al.,36 concentrations below LOD were removed). We opted for this change to avoid the data set being skewed high.
While full details are available in Jain et al.,36 briefly, to build the land use regression models the collected RAMP data was processed using signal decomposition (wavelet decomposition) into 4 separate signals:40 (1) regional concentrations, (2) persistent enhancements above the regional background (lasting >8 h), (3) long-lived (2–8 h) events and (4) short-lived (<2 h) events. The latter three signals were individually modeled using land-use random forests (LURF) and subsequently added together with the regional concentrations to re-create the total concentration and tested for validation using the leave-one location-out cross-validation (LOLOCV) technique.41,42 Various spatial and temporal variables were used as predictors in the model. The variables used in the final models can be found in Fig. 1 (blue box). Full details of all variables assessed are detailed in Jain et al.36 (see Table S2 in Section S4 in the ESI† for a summary). The value in brackets refers to the buffer sizes. Multiple buffer sizes represent different buffers used for different signals. Detailed information on the steps followed for prediction modeling for this work can be found in Section S5 of ESI.†
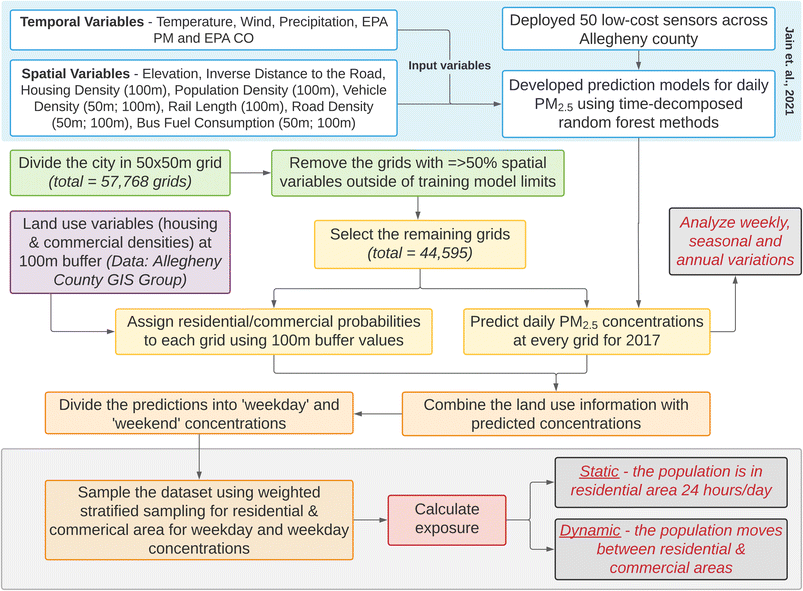 | ||
| Fig. 1 Flowchart of steps involved in this work. The blue box at the top represents the results from Jain et al.36 used for this work. The grey boxes are the outcomes. EPA CO and EPA PM in the blue box refer to daily measurements of CO and PM2.5 by the US EPA's Lawrenceville site in the city of Pittsburgh. | ||
The land use random forest model from Jain et al.36 was then applied to the City of Pittsburgh using a grid size of 50 × 50 m (total grids = 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768) to quantify the small-scale variations in PM2.5 concentrations. Grids where ≥50% of the spatial predictor variables exceeded the training model limits (both upper and lower limits from 47 training sites) were excluded from the assessment since random forests are incapable of extrapolation (remaining grids = 44
768) to quantify the small-scale variations in PM2.5 concentrations. Grids where ≥50% of the spatial predictor variables exceeded the training model limits (both upper and lower limits from 47 training sites) were excluded from the assessment since random forests are incapable of extrapolation (remaining grids = 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 595, 77% retained).
595, 77% retained).
Daily predictions were then consolidated at each grid in three ways: (1) annual average concentrations, (2) average winter (November–April) and average summer concentrations (May–October) and (3) average weekday and weekend concentrations. As such, daily predictions were separated seasonally (either summer or winter) or weekly (either weekday or weekend) and then averaged for each grid.
2.3 Land use: residential and commercial areas
Each 50 × 50 m grid in Pittsburgh was first assigned a residential and commercial density. This was done using the land cover area data set published by the Allegheny County GIS group43 that demarcates land cover into 14 types in the region (Section S6, ESI†). The residential density value was calculated as the total area that was demarcated as having land use type ‘residential’ (types 6, 7 and 8 in Section S6, ESI†) within a 100 m buffer of the centroid of each grid cell. The maximum residential value was 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 425 m2 (area = πr2; r = 100 m), i.e., when all the locations in the buffer area were categorized as ‘residential’; and the minimum value was 0 m2 when none of the locations in the buffer area were categorized as ‘residential’ (see map in Section S7, ESI†). Similarly, commercial density values were assigned using the same 100 m buffer process, except for areas demarcated by the Allegheny GIS Group as ‘commercial’ (type 10 in Section S6, ESI†). We chose 100 m as the buffer size for these calculations since the LURF model used for PM2.5 prediction determined that 100 m was the optimal buffer size for housing density (Fig. 1). These residential and commercial density values for each grid cell were then normalized on a scale from 0–1 and used as probability weights, PR and PC, respectively, for sampling (Section 2.4).
425 m2 (area = πr2; r = 100 m), i.e., when all the locations in the buffer area were categorized as ‘residential’; and the minimum value was 0 m2 when none of the locations in the buffer area were categorized as ‘residential’ (see map in Section S7, ESI†). Similarly, commercial density values were assigned using the same 100 m buffer process, except for areas demarcated by the Allegheny GIS Group as ‘commercial’ (type 10 in Section S6, ESI†). We chose 100 m as the buffer size for these calculations since the LURF model used for PM2.5 prediction determined that 100 m was the optimal buffer size for housing density (Fig. 1). These residential and commercial density values for each grid cell were then normalized on a scale from 0–1 and used as probability weights, PR and PC, respectively, for sampling (Section 2.4).
We chose to assess population exposure using this split between residential and commercial areas to acknowledge that a population spends time in both areas almost every day, but the exposure profiles might be different due to various factors (e.g., higher vehicle emissions in commercially-dense areas). The exposure estimate can be further improved by tracking individual people via personal notes or cellular network data. However due to lack of movement data, this is a recognized limitation of this work.
2.4 Sampling
For this work, we defined a sample as the average concentration (for the defined period) at a grid cell that is picked via weighted stratified sampling. To determine the minimum number of samples required to represent the population, the formula in eqn (1) was used:44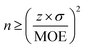 | (1) |
In eqn (1), z represents the desired confidence level (z = 1.96 at 95% CI) and σ is the standard deviation (annual average at each grid cell, 1.88 μg m−3). MOE, margin of error, is the acceptable tolerance level or sensitivity, set as the least count of PM2.5 measured by the RAMPs for this work (=0.01 μg m−3). With these inputs, the number of samples was determined to be approximately 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, as shown in eqn (2).
000, as shown in eqn (2).
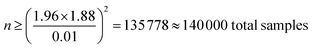 | (2) |
The daily predictions were then separated into ‘weekday’ and ‘weekend’ concentrations for each grid to acknowledge difference in human movement patterns during different days of the week and then averaged annually to estimate total annual exposure for different models (i.e., the weekend concentration of a sample is the average concentration over all 52 Saturdays and Sundays in 2017 at the selected grid cell. See Section S8 in the ESI† for more details).
Sampling was achieved using a weighted stratified sampling (with replacement) method, in which the population is divided into homogeneous strata (strata for this work: weekdays and weekends) and samples are selected from each stratum based on the assigned probability weights (Fig. 2). The probability weights PR and PC were used to calculate sampling fraction, such that, grids with higher probability weights were sampled more. For instance, between two grid cells with PR values as 0.1 and 0.2, the latter is twice as likely to be picked as a sample.
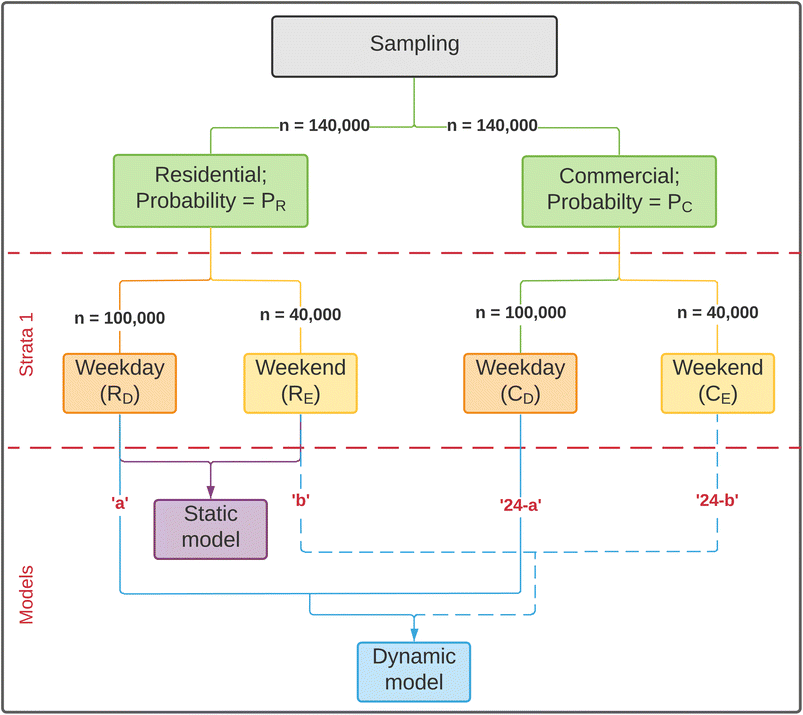 | ||
| Fig. 2 Flowchart for weighted stratified samples and resultant static and dynamic models. ‘a’ and ‘b’ represent the hours spent in the selected land-use type over weekdays or weekends. | ||
For each of the land use types (residential and commercial), a total of 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples were taken. The total number of samples were then divided into weekday and weekend concentrations based on population size of the strata (weekday size = 5 days, weekend size = 2 days). Therefore, 5/7 × 140
000 samples were taken. The total number of samples were then divided into weekday and weekend concentrations based on population size of the strata (weekday size = 5 days, weekend size = 2 days). Therefore, 5/7 × 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 = 100
000 = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples were taken of weekday concentrations and 2/7 × 140
000 samples were taken of weekday concentrations and 2/7 × 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 = 40
000 = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples were taken of weekend concentrations. The samples for residential and commercial areas were assessed for statistically significant differences using the Welch two sample t-test. The Welch two sample t-test was used since it doesn't assume that the two data sets have equal variances.
000 samples were taken of weekend concentrations. The samples for residential and commercial areas were assessed for statistically significant differences using the Welch two sample t-test. The Welch two sample t-test was used since it doesn't assume that the two data sets have equal variances.
2.5 Static and dynamic models
For this work, we used the term “exposure” as a proxy for time-weighted ambient concentrations, i.e., for the total ambient concentration of PM2.5 that the population experiences in different locations (eqn (3)).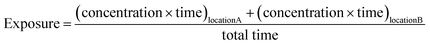 | (3) |
The ‘Static’ models assumes that residents spend 24 hours in a day in residential areas. ‘Dynamic’ models were defined as the models that account for movement between commercial and residential areas. These models were created using eqn (4) and (5) and were used to estimate difference in exposure to ambient PM2.5 due to daily movement.
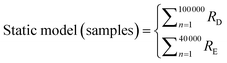 | (4) |
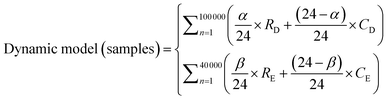 | (5) |
In eqn (4) and (5), R and C refer to sample concentrations taken for residential and commercial areas respectively. Subscripts D and E are the time periods, used for weekdays and weekends respectively (e.g., RD is the sampled concentration for the sample residential area over weekdays). α represents the number of hours spent in residential areas over weekdays, whereas β represents the number of hours spent in residential areas over weekends. As such, the individual exposure level will vary depending on the amount of time spent in each area.
For our analysis, α and β were estimated as 12 and 18 hours respectively for the Dynamic models, informed by data provided by US Bureau of Labor Statistics,45 to facilitate comparison with static models. The concentrations for static and dynamic models were assessed for statistically significant differences using the Welch two sample t-test. As mentioned previously, this test was chosen as it doesn't assume that the populations have equal variances.
The models (eqn (4) and (5)) are a fractional split and are not a true representation of time spent in residential or commercial areas (i.e., the model isn't informed by sub-daily movement; PM2.5 concentrations are modeled as daily averages). While the RAMP sensors have sub-daily measurement time resolution, PM2.5 concentrations were modeled as daily averages due to prediction modeling constraints (specifically a lack of sub-daily model inputs such as hourly traffic) and this is an identified limitation of this work.
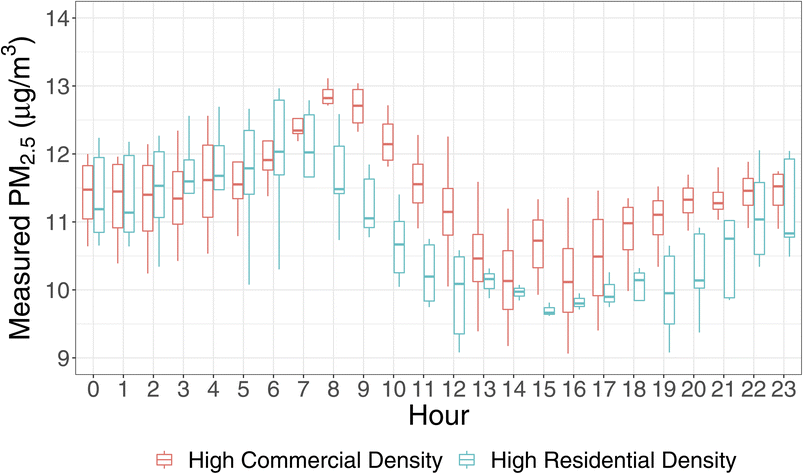
Nonetheless, we observed sub-daily variations at the 47 sites where low-cost sensors were deployed (Fig. 3). Although the nighttime concentrations were similar across the residential and commercial land use types, the sites with high commercial density (PC) were characterized by higher concentrations during daytime. As such, the static and dynamic models compared in this study are likely to have larger differences than reported here - this is because people are more likely to be in a commercial area at 2 PM (when the concentrations are higher in commercial areas) than 2 AM.
3 Results and discussion
3.1 Temporal variations
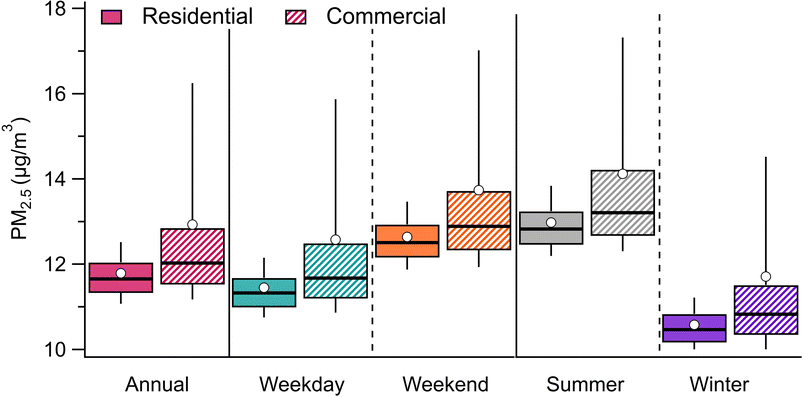
The daily average predicted concentrations across all grids ranged from 4 to 75 μg m−3, with an average of 12.0 μg m−3 [10th–90th percentiles: 6.6–18.6 μg m−3]. When averaged annually, concentrations varied between 10 and 30 μg m−3 across all grids, with an average of 12.2 μg m−3 [10th–90th percentiles: 11.1–13.8 μg m−3] (Fig. 4). These results illustrate the range of ambient concentrations to which residents were exposed. The annual average concentration at the US EPA's Lawrenceville site46 (AQS ID: 42-003-0008; Pittsburgh, PA) was reported to be 9.2 μg m−3. However, the RAMP collocated at the Lawrenceville site had an annual average measurement of 11.3 μg m−3, suggesting that RAMPs may be biased high, with an average difference of approximately 2 μg m−3.On average, summer (May–October) had higher concentrations than winter (November–April), with mean summer and winter concentrations of 13.4 and 11.0 μg m−3, respectively. Weekend (Saturday–Sunday) concentrations were 10% higher than weekday concentrations, with average concentrations of 11.9 and 13.1 μg m−3, respectively, across all grids. Fig. 5 shows the spatial variations in annual averages of predicted PM2.5 during weekdays (Monday–Friday) and weekends (Saturday–Sunday) and during summer (May–October) and winter (November–April) seasons.
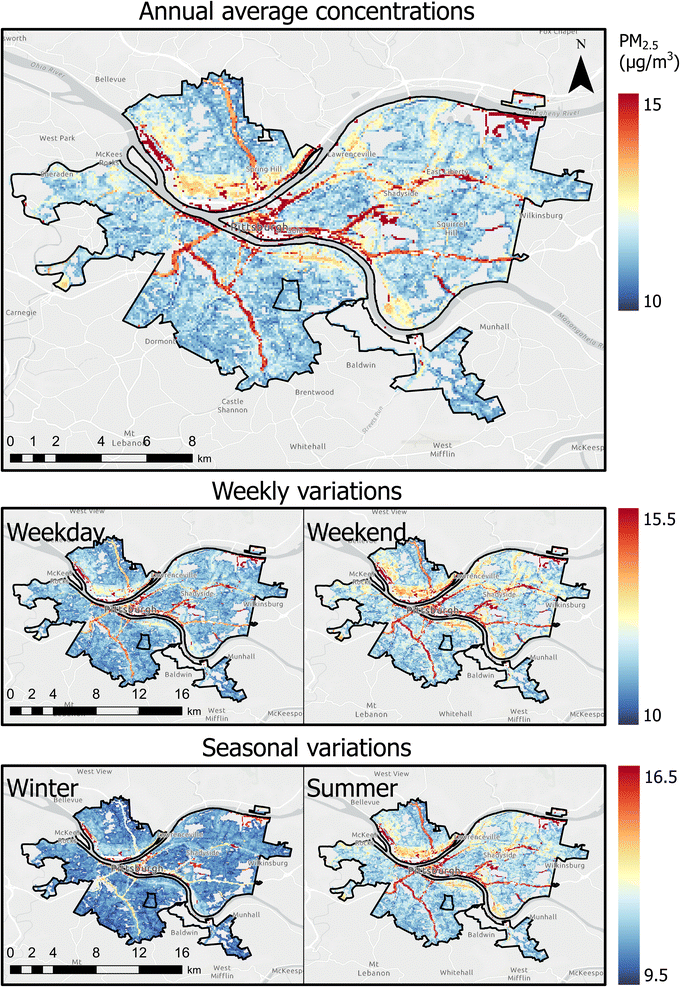 | ||
| Fig. 5 Spatial variations in annual averages of predicted PM2.5 during weekday (Monday–Friday) and weekends (Saturday–Sunday) and during summer (May–October) and winter (November–April) seasons. | ||
Overall, our results highlight important temporal variations in concentrations. Summer concentrations were 20% higher than winter concentrations, and weekend concentrations were 10% higher than weekday concentrations. These patterns are consistent with PM2.5 data obtained via a US EPA monitor in the City of Pittsburgh, which showed approximately 1.1 μg m−3 higher concentrations over weekends compared to weekdays.47 The higher weekend concentrations are likely due to increased traffic (especially trucks) in Allegheny County on weekends.48 While previous studies have examined daily variations in concentrations,16,18 our findings reinforce the existence of temporal variations and suggest the potential for improving short-term exposure through behavioral changes, such as choosing lower traffic roads for periods of active transportation (e.g., walking, cycling) when out on weekends.
3.2 Spatial variations
As introduced in Section 3.1, annual average concentrations across all grids varied between 10–30 μg m−3. This suggests that residents were exposed to a wide range of concentrations, which may be underestimated by relying on a single or limited number of stationary monitors.Upon visual inspection, highways and major roads were found to have higher predicted PM2.5 concentration (red lines in Fig. 5), which is a typical pattern that was expected since highways and major roadways experience elevated PM2.5 concentrations due to emissions from combustion, brake wear, tire wear, and resuspended dust.49 The figure also indicates downtown Pittsburgh had higher concentrations, which can be attributed to higher traffic densities and high restaurant density.50 These results are also comparable to black carbon spatial maps prepared in the Breathe Project.51 As such, along with details about personal movement between different areas (e.g., between different grid cells), the maps developed in Fig. 5 can be a useful tool in estimating the exposure of an individual.
By separating grid cells labeled as residential or commercial from the weighted stratified sampling, the commercial areas had 0.4 μg m−3 higher median values. The mean for commercial areas was 1.1 μg m−3 higher (sample standard deviations: σresidential: 0.7 μg m−3; σcommercial: 2.6 μg m−3) (Fig. 4) and the difference between averages were found to be statistically significant (p < 0.05). Additionally, the overall range of concentration that the modeled population was exposed to in commercial areas was noticeably higher, with the difference in 90th percentile concentrations up to 3.7 μg m−3 (30%).
Both measurement and modeling uncertainties pertain to this work. We estimated substantially higher normalized mean error (10–50% higher) for modeling by considering the range of outputs from the random forests, and therefore assumed uncertainties in modeling to have an overall higher effect. For uncertainties due to random forest modeling, we extracted the 5th and 95th percentile values, along with mean values, from the decision trees in the random forest model. This detailed uncertainty analysis can be found in the ESI, Section S9.† Broadly speaking, although absolute difference between static and dynamic models differed when uncertainties were taken into account, we found that average concentrations at commercial areas were always higher. As such, addressing the uncertainties reinforced our results that the average ambient PM2.5 concentration that the population was exposed to was always higher when the population stays in commercially-dense areas or moves between residential and commercial areas vs. when the population stays in residential areas only.
3.3 Static and dynamic models
We estimated exposure when the spatial mobility was ignored (static models) and compared it to estimated exposure when the spatial mobility was addressed (dynamic models). Static and dynamic models were based on time-weighted PM2.5 concentrations from different locations in the study area. Therefore, exposure estimates represent spatially averaged ambient concentrations, resulting in pseudo-mobility-based exposure.We used the annual average of the daily predicted concentrations for assessment of the static and dynamic models. The differences between the static and dynamic models were found to be statistically significant (p < 0.05), observed for 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples. The difference in concentration between different land-use types (residential and commercial) resulted in variations in exposure, i.e., this resulted in higher exposure across population for dynamic models compared to static models. In all instances, the dynamic model had higher average exposure compared to the static model, with an average difference up to 1.1 μg m−3, when population spends all their time in commercial areas (Fig. 6). To understand potential individual mobility effects, we also report the 10th and 90th percentile of differences between the static and dynamic models (10th percentile: 0.1; 90th percentile: 3.73 μg m−3), suggesting that for an individual, pollutant exposure differences may be as high as approximately 4 μg m−3.
000 samples. The difference in concentration between different land-use types (residential and commercial) resulted in variations in exposure, i.e., this resulted in higher exposure across population for dynamic models compared to static models. In all instances, the dynamic model had higher average exposure compared to the static model, with an average difference up to 1.1 μg m−3, when population spends all their time in commercial areas (Fig. 6). To understand potential individual mobility effects, we also report the 10th and 90th percentile of differences between the static and dynamic models (10th percentile: 0.1; 90th percentile: 3.73 μg m−3), suggesting that for an individual, pollutant exposure differences may be as high as approximately 4 μg m−3.
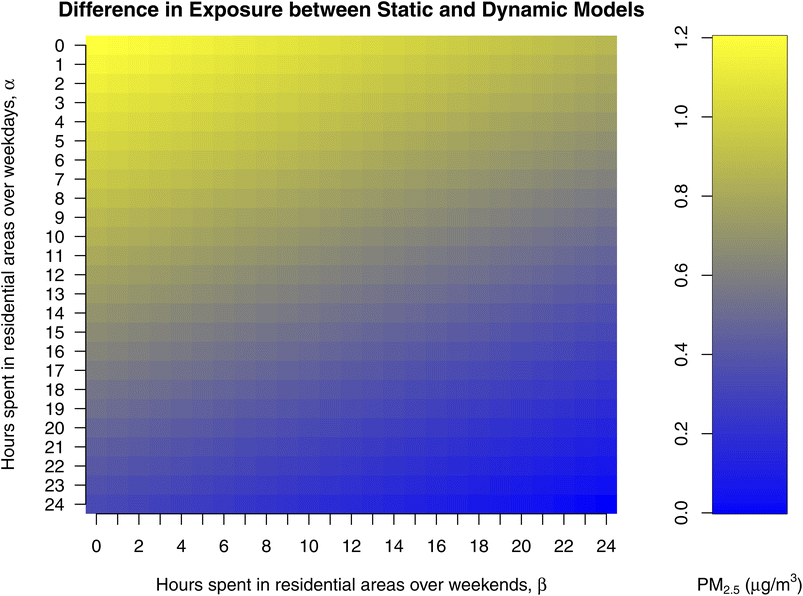 | ||
| Fig. 6 Scalar graph of difference in exposure between static and dynamic models informed by amount of time spent in residential area over weekdays and weekends separately, calculated using eqn (4) and (5). | ||
When assessed for α and β as 12 and 18 hours respectively in eqn (5), the mean exposure using the dynamic model was 0.5 μg m−3 higher compared to the static model and the difference between averages were found to be statistically significant (p < 0.05), (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) static = 11.8 μg m−3, s = 1.0 μg m−3;
static = 11.8 μg m−3, s = 1.0 μg m−3; ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) dynamic = 12.3 μg m−3, s = 1.3 μg m−3) (see Section S10, ESI†). The 90th percentile concentration for the dynamic model was 0.9 μg m−3 (7%) more than the static model. The mean difference (MD) and mean absolute error (MAE) were 0.5 μg m−3 and 0.7 μg m−3, respectively. The mean difference was higher over the weekdays (0.6 μg m−3) compared to weekends (0.3 μg m−3).
dynamic = 12.3 μg m−3, s = 1.3 μg m−3) (see Section S10, ESI†). The 90th percentile concentration for the dynamic model was 0.9 μg m−3 (7%) more than the static model. The mean difference (MD) and mean absolute error (MAE) were 0.5 μg m−3 and 0.7 μg m−3, respectively. The mean difference was higher over the weekdays (0.6 μg m−3) compared to weekends (0.3 μg m−3).
A few studies have previously calculated dynamic exposures and the impact of movement on exposure estimates. Nyhan et al.16 used mobile network data for mobility and estimated a difference between static and dynamic model of 0.02 μg m−3. Similarly, Lu18 used agent-based models and estimated a difference of 0.05 μg m−3. However, the above-mentioned research lacked fine spatial resolution (≤50 m) and is potentially one of the reasons behind smaller differences between the static and dynamic models than what was observed here (0.5 μg m−3, for the typical case we have considered). This may be due to our models capturing fine spatial scale variations in PM2.5 concentration. Our work also supports the importance of low-cost sensors to improve exposure estimates. This is in line the findings of Lu.18 However, our approach to is likely less intensive computationally when compared to agent-based models and as a result, may be more readily applied elsewhere. Additionally, none of the previous studies to our knowledge have separately analyzed weekday and weekend concentrations, which is an important outcome of our work and is recommended in future studies.
While this study excludes important aspects of true personal exposure (time indoors, exposure during commuting), the relative impact of higher concentrations in commercial areas is supported by other research on indoor/outdoor ratios used to convert ambient concentrations into indoor pollution estimates. For example, in Stamp et al.,52 indoor–outdoor ratios were determined hourly in London in several environments including an office building and apartments over a 6–9 month period. They found that the indoor–outdoor ratios were strongly influenced by building activity patterns with an average increase in the office indoor–outdoor ratio from 0.5 during non-operating hours to approximately 0.71 during operating hours. While this is only one study, it underscores that time spent in commercial zones (whether indoors or outdoors) is likely an important consideration for improving personal exposure estimates.
4 Conclusions
This work addresses some of the shortcomings associated with using static models (assuming that the population spends their whole time at home) to inform exposure for epidemiology studies. To do this, we leveraged data collected via a low-cost sensor network in Pittsburgh to estimate exposure to ambient concentrations across the city. The results of this work support the hypothesis that exposure estimates would be impacted by movement of an individual between different areas due to (1) spatial variations in PM2.5 concentrations, particularly in commercial areas, and (2) temporal variations such a weekend vs. weekday differences.Given our findings, a centrally-located monitoring station is not recommended for exposure assessment of the whole population as it could result in negative biases in health effect estimates, i.e., we may be underestimating exposure by using a few centrally-located monitors and residential address. Even though absolute PM2.5 concentration differences in this study were small, the resulting impact on health may still be substantial. This is supported by a recent report from the Health Effects Institute describing that even a 4.16 μg m−3 (one interquartile range in the study population long-term concentrations) increase in average annual PM2.5 concentration is associated with a 1.034 hazard ratio for total nonaccidental death [95% CI: 1.030–1.039].53 Furthermore, this same study concluded that there was no PM2.5 concentration below which no health effects were observed.53 This suggests that even small-scale reductions in PM2.5 concentration are beneficial and this warrants further research.
This study used low-cost sensor network data to create spatiotemporal pollutant concentration models and investigated the model's utility to identify hotspots and subsequent variations in exposure to ambient PM2.5 based on location and movement patterns. However, this work doesn't capture the unique movement of an individual and is one of the identified limitations. This would require movement data via cellular networks or personal notes, both of which were outside the scope for this work. Additionally, daily pollutant concentrations are approximated for sub-daily movement. This is due to a lack of time resolution in prediction model inputs, such as hourly average traffic volume, and is another identified limitation of this work. Going forward, if the appropriate sub-daily predictors become available, we recommend the development of hourly pollutant land use regression models, which could then be paired with agent-based models to simulate individual daily exposures. This work also assumes that indoor concentrations of PM2.5 are comparable to outdoor concentrations. To date, most epidemiology studies assume a static indoor–outdoor ratio;54 as such, the conclusions of this work may remain unchanged if indoor concentrations are introduced under this assumption. However, we recommend that this assumption should be routinely reassessed as more dynamic indoor–outdoor ratios (hourly or better) across many micro-environments are made available. Lastly, this work defines residential and commercial areas based on the residential and commercial densities via land cover information.43 The outcomes of this research may vary if alternative definitions are used for demarcating these areas. As such, different categorizations could potentially lead to varying results in the findings of this study. Going forward, it is likely that buildings and vehicles will become increasingly optimized using Internet of Things (IoT) devices as part of smart city infrastructure; such infrastructure will likely include air quality sensors. This IoT infrastructure could be used to refine indoor–outdoor ratios and activity patterns, which paired with ambient LCS networks, such as the one used here, could address many of these gaps.
Data availability
Calibrated 15 minute low-cost PM2.5 data is provided online at https://doi.org/10.5281/zenodo.8264657. Codes (in R language) required to recreate the results will be provided upon request.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work is part of the Center for Air, Climate, and Energy Solutions (CACES), which was supported by the U.S. Environmental Protection Agency (assistance agreement number RD83587301). This work was also partially funded by the U.S. EPA under assistance agreement RD83628601. It has not been formally reviewed by the U.S. EPA. The views expressed in this document are solely those of authors and do not necessarily reflect those of the Agency. The U.S. EPA does not endorse any products or commercial services mentioned in this publication. Funding for this study was also provided by the Heinz Endowment Fund (Grants E2375 and E3145), and the NSERC Discovery Grant Program (RGPIN-2018-04582). The authors also thank Prof. Michael Brauer for helpful conversations. This research was undertaken, in part, thanks to funding from the Canada Research Chairs Program. The authors would like to acknowledge that The University of British Columbia, where this work was conducted, is built on the traditional, ancestral and unceded territory of the Musqueam peoples. The sensor data used for this work was collected on the traditional, ancestral, and unceded territory of the Shawandasse Tula (Shawnee) and Osage peoples.References
- C. A. Pope III, Lung Cancer, Cardiopulmonary Mortality, and Long-term Exposure to Fine Particulate Air Pollution, J. Am. Med. Assoc., 2002, 287, 1132 CrossRef PubMed.
- M. Brauer, et al., Ambient Air Pollution Exposure Estimation for the Global Burden of Disease 2013, Environ. Sci. Technol., 2016, 50, 79–88 CrossRef CAS PubMed.
- R. D. Brook, S. Rajagopalan, C. A. Pope, J. R. Brook, A. Bhatnagar, A. V. Diez-Roux, F. Holguin, Y. Hong, R. V. Luepker, M. A. Mittleman, A. Peters, D. Siscovick, S. C. Smith, L. Whitsel and J. D. Kaufman, Particulate Matter Air Pollution and Cardiovascular Disease: An Update to the Scientific Statement From the American Heart Association, Circulation, 2010, 121, 2331–2378 CrossRef CAS PubMed.
- Q. Di, Y. Wang, A. Zanobetti, Y. Wang, P. Koutrakis, C. Choirat, F. Dominici and J. D. Schwartz, Air Pollution and Mortality in the Medicare Population, N. Engl. J. Med., 2017, 376, 2513–2522 CrossRef CAS PubMed.
- M. M. M. Abdel-Salam, Outdoor and indoor factors influencing particulate matter and carbon dioxide levels in naturally ventilated urban homes, J. Air Waste Manage. Assoc., 2021, 71, 60–69 CrossRef CAS PubMed.
- E. Majd, M. McCormack, M. Davis, F. Curriero, J. Berman, F. Connolly, P. Leaf, A. Rule, T. Green, D. Clemons-Erby, C. Gummerson and K. Koehler, Indoor air quality in inner-city schools and its associations with building characteristics and environmental factors, Environ. Res., 2019, 170, 83–91 CrossRef CAS PubMed.
- R. A. Chaney, H. D. Montgomery, J. H. King, N. R. Hendrickson, C. D. Sloan and J. D. Johnston, A Comparison of Perceived and Measured Commuter Air Pollution Exposures, J. Environ. Health, 2019, 82, 8–15 Search PubMed.
- N. Baldwin, O. Gilani, S. Raja, S. Batterman, R. Ganguly, P. Hopke, V. Berrocal, T. Robins and S. Hoogterp, Factors affecting pollutant concentrations in the near-road environment, Atmos. Environ., 2015, 115, 223–235 CrossRef CAS.
- X. Hu, L. A. Waller, A. Lyapustin, Y. Wang, M. Z. Al-Hamdan, W. L. Crosson, M. G. Estes, S. M. Estes, D. A. Quattrochi, S. J. Puttaswamy and Y. Liu, Estimating ground-level PM2.5 concentrations in the Southeastern United States using MAIAC AOD retrievals and a two-stage model, Remote Sens. Environ., 2014, 140, 220–232 CrossRef.
- J. Lepeule, F. Laden, D. Dockery and J. Schwartz, Chronic Exposure to Fine Particles and Mortality: An Extended Follow-up of the Harvard Six Cities Study from 1974 to 2009, Environ. Health Perspect., 2012, 120, 965–970 CrossRef PubMed.
- A. Zanobetti and J. Schwartz, The Effect of Fine and Coarse Particulate Air Pollution on Mortality: A National Analysis, Environ. Health Perspect., 2009, 117, 898–903 CrossRef PubMed.
- C. A. Garcia, P.-S. Yap, H.-Y. Park and B. L. Weller, Association of long-term PM2.5 exposure with mortality using different air pollution exposure models: impacts in rural and urban California, Int. J. Environ. Health Res., 2016, 26, 145–157 CrossRef CAS PubMed.
- M. Eeftens, et al., Development of Land Use Regression Models for PM 2.5 , PM 2.5 Absorbance, PM 10 and PM coarse in 20 European Study Areas; Results of the ESCAPE Project, Environ. Sci. Technol., 2012, 46, 11195–11205 CrossRef CAS PubMed.
- M. Wang, et al., Evaluation of Land Use Regression Models for NO2 and Particulate Matter in 20 European Study Areas: The ESCAPE Project, Environ. Sci. Technol., 2013, 47, 4357–4364 CrossRef CAS PubMed.
- M. Jerrett, R. T. Burnett, R. Ma, C. A. Pope, D. Krewski, K. B. Newbold, G. Thurston, Y. Shi, N. Finkelstein, E. E. Calle and M. J. Thun, Spatial Analysis of Air Pollution and Mortality in Los Angeles, Epidemiology, 2005, 16, 727–736 CrossRef PubMed.
- M. M. Nyhan, I. Kloog, R. Britter, C. Ratti and P. Koutrakis, Quantifying population exposure to air pollution using individual mobility patterns inferred from mobile phone data, J. Exposure Sci. Environ. Epidemiol., 2019, 29, 238–247 CrossRef CAS PubMed.
- X. Yu, C. Ivey, Z. Huang, S. Gurram, V. Sivaraman, H. Shen, N. Eluru, S. Hasan, L. Henneman, G. Shi, H. Zhang, H. Yu and J. Zheng, Quantifying the impact of daily mobility on errors in air pollution exposure estimation using mobile phone location data, Environ. Int., 2020, 141, 105772 CrossRef CAS PubMed.
- Y. Lu, Beyond air pollution at home: Assessment of personal exposure to PM2.5 using activity-based travel demand model and low-cost air sensor network data, Environ. Res., 2021, 201, 111549 CrossRef CAS PubMed.
- E. Setton, J. D. Marshall, M. Brauer, K. R. Lundquist, P. Hystad, P. Keller and D. Cloutier-Fisher, The impact of daily mobility on exposure to traffic-related air pollution and health effect estimates, J. Exposure Sci. Environ. Epidemiol., 2011, 21, 42–48 CrossRef PubMed.
- C. L. Avery, K. T. Mills, R. Williams, K. A. McGraw, C. Poole, R. L. Smith and E. A. Whitsel, Estimating Error in Using Ambient PM2.5 Concentrations as Proxies for Personal Exposures: A Review, Epidemiology, 2010, 21, 215–223 CrossRef PubMed.
- S.-C. C. Lung, N. Chen, J.-S. Hwang, S.-C. Hu, W.-C. V. Wang, T.-Y. J. Wen and C.-H. Liu, Panel study using novel sensing devices to assess associations of PM2.5 with heart rate variability and exposure sources, J. Exposure Sci. Environ. Epidemiol., 2020, 30, 937–948 CrossRef CAS PubMed.
- I. Kloog, B. Ridgway, P. Koutrakis, B. A. Coull and J. D. Schwartz, Long- and Short-Term Exposure to PM2.5 and Mortality: Using Novel Exposure Models, Epidemiology, 2013, 24, 555–561 CrossRef PubMed.
- y. Næss, P. Nafstad, G. Aamodt, B. Claussen and P. Rosland, Relation between Concentration of Air Pollution and Cause-Specific Mortality: Four-Year Exposures to Nitrogen Dioxide and Particulate Matter Pollutants in 470 Neighborhoods in Oslo, Norway, Am. J. Epidemiol., 2007, 165, 435–443 CrossRef PubMed.
- T. Li, Y. Guo, Y. Liu, J. Wang, Q. Wang, Z. Sun, M. Z. He and X. Shi, Estimating mortality burden attributable to short-term PM2.5 exposure: A national observational study in China, Environ. Int., 2019, 125, 245–251 CrossRef CAS PubMed.
- R. Friedrich and P. Bickel, Environmental External Costs of Transport, Springer, 2001 Search PubMed.
- B. Dewulf, T. Neutens, W. Lefebvre, G. Seynaeve, C. Vanpoucke, C. Beckx and N. Van de Weghe, Dynamic assessment of exposure to air pollution using mobile phone data, International Journal of Health Geographics, 2016, 15, 14 CrossRef PubMed.
- C. Beckx, L. Int Panis, T. Arentze, D. Janssens, R. Torfs, S. Broekx and G. Wets, A dynamic activity-based population modelling approach to evaluate exposure to air pollution: Methods and application to a Dutch urban area, Environ. Impact Assess. Rev., 2009, 29, 179–185 CrossRef.
- E. S. Cross, L. R. Williams, D. K. Lewis, G. R. Magoon, T. B. Onasch, M. L. Kaminsky, D. R. Worsnop and J. T. Jayne, Use of electrochemical sensors for measurement of air pollution: correcting interference response and validating measurements, Atmos. Meas. Tech., 2017, 10, 3575–3588 CrossRef CAS.
- N. Zimmerman, A. A. Presto, S. P. N. Kumar, J. Gu, A. Hauryliuk, E. S. Robinson, A. L. Robinson and R. Subramanian, A machine learning calibration model using random forests to improve sensor performance for lower-cost air quality monitoring, Atmos. Meas. Tech., 2018, 11, 291–313 CrossRef.
- E. G. Snyder, T. H. Watkins, P. A. Solomon, E. D. Thoma, R. W. Williams, G. S. W. Hagler, D. Shelow, D. A. Hindin, V. J. Kilaru and P. W. Preuss, The Changing Paradigm of Air Pollution Monitoring, Environ. Sci. Technol., 2013, 47, 11369–11377 CrossRef CAS PubMed.
- R. Piedrahita, Y. Xiang, N. Masson, J. Ortega, A. Collier, Y. Jiang, K. Li, R. P. Dick, Q. Lv, M. Hannigan and L. Shang, The next generation of low-cost personal air quality sensors for quantitative exposure monitoring, Atmos. Meas. Tech., 2014, 7, 3325–3336 CrossRef.
- J. Caubel, T. Cados and T. Kirchstetter, A New Black Carbon Sensor for Dense Air Quality Monitoring Networks, Sensors, 2018, 18, 738 CrossRef PubMed.
- P. deSouza, K. Barkjohn, A. Clements, J. Lee, R. Kahn, B. Crawford and P. Kinney, An analysis of degradation in low-cost particulate matter sensors, Environ. Sci.: Atmos., 2023, 3, 521–536 CAS.
- M. Mead, O. Popoola, G. Stewart, P. Landshoff, M. Calleja, M. Hayes, J. Baldovi, M. McLeod, T. Hodgson, J. Dicks, A. Lewis, J. Cohen, R. Baron, J. Saffell and R. Jones, The use of electrochemical sensors for monitoring urban air quality in low-cost, high-density networks, Atmos. Environ., 2013, 70, 186–203 CrossRef CAS.
- C. Malings, R. Tanzer, A. Hauryliuk, P. K. Saha, A. L. Robinson, A. A. Presto and R. Subramanian, Fine particle mass monitoring with low-cost sensors: Corrections and long-term performance evaluation, Aerosol Sci. Technol., 2020, 54, 160–174, DOI:10.1080/02786826.2019.1623863.
- S. Jain, A. A. Presto and N. Zimmerman, Spatial Modeling of Daily PM2.5, NO2, and CO Concentrations Measured by a Low-Cost Sensor Network: Comparison of Linear, Machine Learning, and Hybrid Land Use Models, Environ. Sci. Technol., 2021, 55, 8631–8641, DOI:10.1021/acs.est.1c02653.
- X. Du, Y. Wu, L. Fu, S. Wang, S. Zhang and J. Hao, Intake fraction of PM2.5 and NOX from vehicle emissions in Beijing based on personal exposure data, Atmos. Environ., 2012, 57, 233–243 CrossRef CAS.
- R. W. Hornung and L. D. Reed, Estimation of Average Concentration in the Presence of Nondetectable Values, Appl. Occup. Environ. Hyg., 1990, 5, 46–51 Search PubMed.
- M. A. Tekindal, B. D. Erdoğan and Y. Yavuz, Evaluating Left-Censored Data Through Substitution, Parametric, Semi-parametric, and Nonparametric Methods: A Simulation Study, Interdiscip. Sci.: Comput. Life Sci., 2017, 9, 153–172 Search PubMed.
- N. Zimmerman, H. Z. Li, A. Ellis, A. Hauryliuk, E. S. Robinson, P. Gu, R. U. Shah, Q. Ye, L. Snell, R. Subramanian, A. L. Robinson, J. S. Apte and A. A. Presto, Improving Correlations between Land Use and Air Pollutant Concentrations Using Wavelet Analysis: Insights from a Low-cost Sensor Network, Aerosol Air Qual. Res., 2020, 20, 314–328 Search PubMed.
- A. C. Just, R. O. Wright, J. Schwartz, B. A. Coull, A. A. Baccarelli, M. M. Tellez-Rojo, E. Moody, Y. Wang, A. Lyapustin and I. Kloog, Using High-Resolution Satellite Aerosol Optical Depth To Estimate Daily PM 2.5 Geographical Distribution in Mexico City, Environ. Sci. Technol., 2015, 49, 8576–8584 CrossRef CAS PubMed.
- G. L. Watson, D. Telesca, C. E. Reid, G. G. Pfister and M. Jerrett, Machine learning models accurately predict ozone exposure during wildfire events, Environ. Pollut., 2019, 254, 112792 CrossRef CAS PubMed.
- Allegheny County GIS Group, Allegheny County Land Cover Areas, 2015, https://services1.arcgis.com/vdNDkVykv9vEWFX4/arcgis/rest/services/Land_Cover/FeatureServer Search PubMed.
- L. W. Wayne, Simulation Modeling Using @RISK, Duxbury Press, 2000 Search PubMed.
- Bureau of Labor Statistics, American Time Use Survey — 2019 Results, 2020, issue: USDL-20-1275, https://www.bls.gov/news.release/pdf/atus.pdf Search PubMed.
- Allegheny County Health Department, Air Quality – Annual Data Summary. Criteria Pollutants and Selected Other Pollutants, 2017, https://www.alleghenycounty.us/uploadedFiles/Allegheny_Home/Health_Department/Resources/Data_and_Reporting/Air_Quality_Reports/2017-data-summary.pdf Search PubMed.
- United States Environmental Protection Agency, Air Data: Air Quality Data Collected at Outdoor Monitors across the US, 2023, https://www.epa.gov/outdoor-air-quality-data Search PubMed.
- Bureau of Planning and Research, Transportation Planning Division, 2017 Pennsylvania Traffic Data, 2017, https://gis.penndot.gov/BPR_PDF_FILES/Documents/Traffic/Traffic_Information/Annual_Report/2017/<?pdb_no 2017?>2017<?pdb END?>_Traffic_Information_Report.pdf Search PubMed.
- M. H. Askariyeh, M. Venugopal, H. Khreis, A. Birt and J. Zietsman, Near-Road Traffic-Related Air Pollution: Resuspended PM2.5 from Highways and Arterials, Int. J. Environ. Res. Public Health, 2020, 17, 2851 CrossRef CAS PubMed.
- R. Tanzer, C. Malings, A. Hauryliuk, R. Subramanian and A. A. Presto, Demonstration of a Low-Cost Multi-Pollutant Network to Quantify Intra-Urban Spatial Variations in Air Pollutant Source Impacts and to Evaluate Environmental Justice, Int. J. Environ. Res. Public Health, 2019, 16, 2523 CrossRef CAS PubMed.
- Breathe Collaborative, Pollution Map - Breathe Project, 2015, https://breatheproject.org/pollution-map/ Search PubMed.
- S. Stamp, E. Burman, L. Chatzidiakou, E. Cooper, Y. Wang and D. Mumovic, A critical evaluation of the dynamic nature of indoor-outdoor air quality ratios, Atmos. Environ., 2022, 273, 118955 CrossRef CAS.
- M. Brauer, et al., Mortality–Air Pollution Associations in Low Exposure Environments (MAPLE): Phase 2. Research Report (Health Effects Institute), 2022 Search PubMed.
- Environmental Protection Agency (EPA), Exposure Factors Handbook, 2011 edn, 2011 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: More information on the selection of prediction models and variables, spatial distribution at 100 m buffers for residential and commercial areas, effect of LOD on total amount of data, average daily concentrations and uncertainties in measurements and models. See DOI: https://doi.org/10.1039/d3ea00051f |
| This journal is © The Royal Society of Chemistry 2023 |