The driving effects of common atmospheric molecules for formation of clusters: the case of sulfuric acid, formic acid, hydrochloric acid, ammonia, and dimethylamine†
Received
13th June 2023
, Accepted 28th July 2023
First published on 31st July 2023
Abstract
One of the main sources of uncertainty for understanding global warming is understanding the formation of larger secondary aerosols. The beginning stages start with the formation of prenucleation complexes from precursor monomers of acids, bases, and organic molecules. The detailed interactions responsible for prenucleation and subsequent aerosol formation are difficult to decipher experimentally. We present a computational chemistry study of the interactions between three different acid molecules and two different bases. By combining a comprehensive search routine covering many thousands of configurations at the semiempirical level with high level quantum chemical calculations of approximately 1000 clusters for every possible combination of clusters containing a sulfuric acid molecule, a formic acid molecule, a hydrochloric acid molecule, an ammonia molecule, a dimethylamine molecule, and 0–3 water molecules, we have completed an exhaustive search of the DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy surface for this system. This first detailed study of HCl interacting with two other acids and two bases reveals the subtleties that exist in the formation of prenucleation complexes for this system. We find that nitric acid forms stronger interactions in dry clusters than hydrochloric acid does. Often as the clusters grow larger with hydration, the sequential energies of clusters containing hydrochloric acid become more favorable than those with nitric acid. The detailed geometries of each minimum free energy cluster are often more important than traditional acid or base strength, which makes a priori prediction of which atmospheric species will be most important for driving prenucleation growth quite difficult. The results presented in this paper add to the conclusions that hydrogen bond topology and the detailed structural interactions that are subtle interplays between enthalpy and entropy are as important as conventional ideas such as acid/base strength.
Environmental significance
Understanding how secondary aerosols form is extremely important as aerosols' impact on Earth's climate is one of the main sources of uncertainty for understanding global warming. The beginning stages for the formation of prenucleation complexes, that eventually lead to larger aerosols, cannot currently be investigated experimentally. We have determined the lowest Gibbs free energy clusters using robust computational chemistry methods, which allows for the prediction of the equilibrium concentrations of the sulfuric acid-formic acid-hydrochloric acid-ammonia-dimethylamine-water system. Comparisons to the sulfuric acid-formic acid-nitric acid-ammonia-dimethylamine-water system reveal that nitric acid drives dry nucleation better than hydrochloric acid, which is more stabilized by hydration. This indicates that different acids are able to stabilize prenucleation clusters at different stages of their growth.
|
1 Introduction
Atmospheric aerosols play a crucial role in Earth's climate. Their ability to scatter, absorb, and emit incoming solar radiation is believed to produce net cooling of the atmosphere, but current uncertainties match or exceed the expected cooling effects.1–4 The role of aerosols acting as cloud condensation nuclei (CCN) is of particular interest to better understand the climate. Secondary aerosol particles, which form in the gas phase, are estimated to account for at least half of all atmospheric new particle formation (NPF) by acting as centers for nucleation.5,6 Many studies have demonstrated the driving effect of sulfuric acid (SA) in forming prenucleation clusters, especially in the presence of other atmospheric acids and bases.7–74 Hydrochloric acid (HCl), on the other hand, has not been as well studied for its potential role in the formation of pre-nucleation clusters.75 It is estimated that 85% of the HCl in the atmosphere is produced from acid displacement of sea salt aerosols.76 The remaining atmospheric HCl enters as anthropogenic by-products of biomass burning,77 specifically coal,78 and chemical reactions driven by anthropogenic nitrogen oxide emissions.79 The oxidation of HCl into more reactive chlorine species could have a significant effect on atmospheric concentrations, especially at higher altitudes.80–82 The interactions of hydrochloric acid within acid–base clusters may provide important information on the outcomes and pathways of atmospheric chlorine species. Because the initial formation of neutral prenucleation clusters and their growth to small aerosols is experimentally and computationally difficult to assess, there is great uncertainty in the size and composition of acid–base clusters, leading researchers to explore a wide variety of different molecules.23,52,53,63–65,74 In addition to formation of prenucleation clusters, it is thought that organic acids play a role in stabilizing smaller clusters before evaporating.74 Most researchers have assumed that acids and bases will grow prenucleation clusters with equal number of acids and bases, as it is logical to assume that stabilization of the growing ensemble is accounted for in a complex containing the same number of strong acids and bases.23,52,53,63–65,74 However, no single experimental technique is able to analyse all of the aerosols that can be produced in the sub-nanometer to 10 nm size range,64 and as the atmosphere is filled with a tremendous number of different compounds, identifying the ones most important for nucleation is akin to finding a needle in a haystack.74 We have published several papers where we have examined weaker acids, as well as unequal numbers of acids and bases that form stable van der Waals complexes, and we have found that the detailed hydrogen bonding topology of particular clusters is often more important than traditional acid/base strength.55,66,68,73 In our previous paper, we explored the role of three acids, two bases, and 0–5 water molecules by computing all possible combinations of one sulfuric acid (SA), one formic acid (FA), one nitric acid (NA), one ammonia (A), one dimethylamine (DMA), and 0–5 waters (W).73 In the present work, we continue the exploration of atmospheric aerosols by examining all possible combinations of one SA, one FA, one HCl, one A, one DMA, and up to three waters. Swapping HCl for NA adds to the insights obtained from previous work.73
2 Methodology
Configurational sampling was employed to generate hundreds of thousands of possible combinations of SA, FA, HCl, A, DMA, and up to three W by using the genetic-algorithm-based protocol in the OGOLEM program,83,84 followed by semi-empirical geometry optimization of the initial configurations. This protocol uses an evolutionary algorithm to rearrange the initial configurations of generated clusters until convergence upon a final structure is reached. We used a pool size of 1000 and allowed for 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 global optimizations. These structures were then optimized using the GFN2-xTB semi-empirical method, resulting in a final pool of 1000 or slightly less for each simulation.85–87 To complete this study we simulated 56 systems containing HCl: HCl-W0–3, HCl-A-W0–3, HCl-DMA-W0–3, SA-FA-HCl-W0–3, SA-HCl-A-W0–3, SA-HCl-DMA-W0–3, FA-HCl-A-W0–3, FA-HCl-DMA-W0–3, HCl-A-DMA-W0–3, SA-FA-HCl-A-W0–3, SA-FA-HCl-DMA-W0–3, SA-HCl-A-DMA-W0–3, FA-HCl-A-DMA-W0–3, and SA-FA-HCl-A-DMA-W0–3 systems. Because of the uncertainties that arise from the use of low-level semi-empirical energies,55,88 we used a cut-off energy of 30 kcal mol−1 above the GFN2-xTB global minimum, thus keeping all structures with a possibility of becoming a minimum or close to one at a better level of theory. These extensive sets of GFN2-xTB structures were optimized at the DFT level of theory using the Gaussian 16 Rev. B01 program.89 The ωB97X-D functional90,91 was used with the 6-31++G** basis set92–94 to obtain a final set of DFT structures. The electronic energies of all structures that were within 8 kcal mol−1 of the ωB97X-D global minimum were then recalculated using the domain-based local pair natural orbital coupled cluster (DLPNO-CCSD(T)) method95–111 with singles, doubles, and semi-canonical perturbative triple excitations with three Dunning basis sets,112–115 cc-pVnZ (n = D, T, Q) using ORCA 5.0.1.111 The ωB97X-D frequencies were scaled by a factor of 0.971 to account for some anharmonicity,116,117 then used to estimate the thermodynamic corrections for H°, S°, and G° at a 1 atm standard state and temperatures of 216.65, 273.15, and 298.15 K using the THERMO.pl script118 from the National Institute of Science and Technology. The electronic energies from the three DLPNO-CCSD(T) calculations were used in a 4–5 inverse polynomial complete basis set extrapolation,119 and combined with the scaled DFT thermodynamic corrections to calculate the final Gibbs free energies. The entire methodology is depicted in Fig. 1. Structures that don't contain HCl were taken from our previous papers,66,73,88 and more explanation of our methodologies can be found in our recent review.74 Once all the G° values were calculated for the individual clusters, the ΔG° values of binding were calculated as follows:
000 global optimizations. These structures were then optimized using the GFN2-xTB semi-empirical method, resulting in a final pool of 1000 or slightly less for each simulation.85–87 To complete this study we simulated 56 systems containing HCl: HCl-W0–3, HCl-A-W0–3, HCl-DMA-W0–3, SA-FA-HCl-W0–3, SA-HCl-A-W0–3, SA-HCl-DMA-W0–3, FA-HCl-A-W0–3, FA-HCl-DMA-W0–3, HCl-A-DMA-W0–3, SA-FA-HCl-A-W0–3, SA-FA-HCl-DMA-W0–3, SA-HCl-A-DMA-W0–3, FA-HCl-A-DMA-W0–3, and SA-FA-HCl-A-DMA-W0–3 systems. Because of the uncertainties that arise from the use of low-level semi-empirical energies,55,88 we used a cut-off energy of 30 kcal mol−1 above the GFN2-xTB global minimum, thus keeping all structures with a possibility of becoming a minimum or close to one at a better level of theory. These extensive sets of GFN2-xTB structures were optimized at the DFT level of theory using the Gaussian 16 Rev. B01 program.89 The ωB97X-D functional90,91 was used with the 6-31++G** basis set92–94 to obtain a final set of DFT structures. The electronic energies of all structures that were within 8 kcal mol−1 of the ωB97X-D global minimum were then recalculated using the domain-based local pair natural orbital coupled cluster (DLPNO-CCSD(T)) method95–111 with singles, doubles, and semi-canonical perturbative triple excitations with three Dunning basis sets,112–115 cc-pVnZ (n = D, T, Q) using ORCA 5.0.1.111 The ωB97X-D frequencies were scaled by a factor of 0.971 to account for some anharmonicity,116,117 then used to estimate the thermodynamic corrections for H°, S°, and G° at a 1 atm standard state and temperatures of 216.65, 273.15, and 298.15 K using the THERMO.pl script118 from the National Institute of Science and Technology. The electronic energies from the three DLPNO-CCSD(T) calculations were used in a 4–5 inverse polynomial complete basis set extrapolation,119 and combined with the scaled DFT thermodynamic corrections to calculate the final Gibbs free energies. The entire methodology is depicted in Fig. 1. Structures that don't contain HCl were taken from our previous papers,66,73,88 and more explanation of our methodologies can be found in our recent review.74 Once all the G° values were calculated for the individual clusters, the ΔG° values of binding were calculated as follows:| |  | (1) |
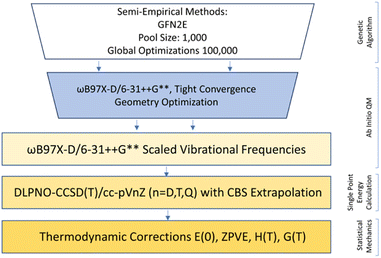 |
| | Fig. 1 Computational methodology employed to obtain the minimum free energy structures and ΔG° values. | |
In addition, the sequential binding energies for addition of a new molecule to an existing cluster were calculated as:
| | 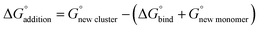 | (2) |
The sequential addition energies obtained from eqn (2) allow for computation of the equilibrium concentrations for every cluster, by assuming a closed system and using each 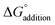 value along with estimates of initial concentrations of the monomers at a given temperature. For these simulations, the top of the troposphere is defined as 217 K while the bottom of the troposphere is 298 K, and estimates for the monomer concentrations are taken from the literature for 298 K, and reduced by a factor of 1000 at 217 K. We used a water concentration of 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere.120 Initial monomer concentrations from the literature22,120–128 at 298 K were reduced by three orders of magnitude at 217 K to compensate for the reduction of CCN-forming particles in the upper troposphere. This is a rough estimate based on the three orders of magnitude decrease in concentration of water, and we resort to this approximation since experimental concentrations of these monomers in the upper troposphere are difficult to measure. Combining these results with previous work allows for estimates of the most likely pathways for the formation of prenucleation complexes for these common acids and bases. The 56 HCl systems were combined with the relevant SA-FA-NA-A-DMA-W systems previously published73 to complete our analysis. Three caveats on our methodology are important to note.74 First, no search routine can ensure that all of the potential energy surface (PES) for these clusters has been exhaustively explored, so we may have missed the lowest Gibbs free energy structure. Second, in the funnel methodology (Fig. 1), we are computing the CCSD(T) electronic energies on the ωB97X-D geometries, which means we are making the electron correlation corrections on the DFT PES. Third, using the DLPNO routine and scaled harmonic frequencies leads to slightly more positive values. All three of these uncertainties will produce ΔG° values that are more positive than would be obtained if (a) a lower energy cluster is obtained, or if (b) the PES is improved so that it is closer to the CCSD(T) surface than the DFT surface, and if (c) anharmonic frequencies could be obtained instead of harmonic frequencies68 and CCSD(T) electronic energies could be computed directly instead of using the DLPNO routine.74
value along with estimates of initial concentrations of the monomers at a given temperature. For these simulations, the top of the troposphere is defined as 217 K while the bottom of the troposphere is 298 K, and estimates for the monomer concentrations are taken from the literature for 298 K, and reduced by a factor of 1000 at 217 K. We used a water concentration of 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere.120 Initial monomer concentrations from the literature22,120–128 at 298 K were reduced by three orders of magnitude at 217 K to compensate for the reduction of CCN-forming particles in the upper troposphere. This is a rough estimate based on the three orders of magnitude decrease in concentration of water, and we resort to this approximation since experimental concentrations of these monomers in the upper troposphere are difficult to measure. Combining these results with previous work allows for estimates of the most likely pathways for the formation of prenucleation complexes for these common acids and bases. The 56 HCl systems were combined with the relevant SA-FA-NA-A-DMA-W systems previously published73 to complete our analysis. Three caveats on our methodology are important to note.74 First, no search routine can ensure that all of the potential energy surface (PES) for these clusters has been exhaustively explored, so we may have missed the lowest Gibbs free energy structure. Second, in the funnel methodology (Fig. 1), we are computing the CCSD(T) electronic energies on the ωB97X-D geometries, which means we are making the electron correlation corrections on the DFT PES. Third, using the DLPNO routine and scaled harmonic frequencies leads to slightly more positive values. All three of these uncertainties will produce ΔG° values that are more positive than would be obtained if (a) a lower energy cluster is obtained, or if (b) the PES is improved so that it is closer to the CCSD(T) surface than the DFT surface, and if (c) anharmonic frequencies could be obtained instead of harmonic frequencies68 and CCSD(T) electronic energies could be computed directly instead of using the DLPNO routine.74
3 Results and discussion
3.1 HCl monomer and dimer systems
In the following discussion we briefly refer to the HCl monomer complexed with 1–3 waters and dimers of HCl, bound to one base, and their complexes with water, as most of these systems were previously reported and our results are consistent with published work. We have not included the two acid dimers with HCl (SA-HCl-W0–3 and FA-HCl-W0–3), as previous results indicate that these clusters would not likely be atmospherically relevant due to the lack of hydrogen bonding sites and bases for deprotonation.73 All our structures and energies for the monomer systems are included in the ESI (Fig. S1, S2 and Tables T1, T2†). Experiment and theory have demonstrated that it takes at least four water molecules to dissociate HCl in the gas-phase at low temperature,129 while DFT calculations predict that five water molecules are required at 298 K.130 Our data for the HCl-W0–3 system has very similar structures to these previous results (S1, T1).130 Of all possible dimers, only the HCl-DMA and HCl-A systems have not been previously discussed. A general finding comparing SA and HCl binding to the two bases is that the HCl-base dimers have energies significantly less negative than the SA-base dimers (S3, S4 and T3, T4), further affirming the significance of SA hydrogen bonding topology. Every HCl-DMA-W0–3 minima undergoes proton transfer from the acid to the base, and have ΔG° values roughly 10 kcal mol−1 (9.47–11.19 kcal mol−1 at 217 K and 8.96–11.27 kcal mol−1 at 298 K) more positive than the SA-DMA-W0–3 complexes (S4, T4), resulting from DMA's well known nucleating ability in the presence of SA.10 DMA and other amines have higher gas-phase basicities than ammonia,131 and this explains why studies of these small complexes have more negative Gibbs free energies of binding relative to ammonia.10,24,132–134 By contrast, HCl-A remains neutral in the dry state, but undergoes proton transfer when hydrated with one or more water molecules. The HCl-A-W0–3 clusters have ΔG° values that are about 10 kcal mol−1 (7.09–13.27 kcal mol−1 at 217 K and 6.87–12.75 kcal mol−1 at 298 K) more positive than the SA-A-Wn system (S3, T3). Regardless of atmospheric concentration, the role of acid strength is a far less influential contributor to more negative ΔG° values than hydrogen bonding topology.66 Both SA and HCl are strong acids in solution, but the slightly less strong SA forms dimers with more negative energies in the gas phase, demonstrating its role as a known driver of nucleation.
3.2 Trimers of one acid and two bases
Trimers of one acid and two bases have been shown to be less atmospherically relevant than other trimers,73 and this remains true for HCl-A-DMA (S5, T5). When SA is the acid, the ΔG° for the one acid-two base trimer is more negative than the HCl containing trimer. While HCl is a stronger acid than SA in the aqueous state, SA has unique bonding capabilities and can form more hydrogen bonds. SA-A-DMA has more negative energies of formation than HCl-A-DMA by roughly 11 kcal mol−1 (11.29 kcal mol−1 at 217 K and 10.95 kcal mol−1 at 298 K) (T5). Similarly, SA-A-DMA is more negative than NA-A-DMA by 9.92 kcal mol−1 at 217 K and 10.07 kcal mol−1 at 298 K. NA-A-DMA and HCl-A-DMA have similar energies, bond formations, and protonation patterns. In both clusters, the acid donates its proton to the DMA, and the three molecules form a ring with the A donating a hydrogen bond to the DMA and acid. The approximately one kcal mol−1 difference (1.37 kcal mol−1 at 217 K and 0.88 kcal mol−1 at 298 K) between HCl-A-DMA and NA-A-DMA is likely accounted for by the extra hydrogen bond in NA-A-DMA. NA-A-DMA-W0–3 has more hydrogen bonds than HCl-A-DMA-W0–3 in all states of hydration, yet HCl-A-DMA-W0–3 has more negative hydration energies than NA-A-DMA-W0–3 at all temperatures. While NA makes stronger dry pre-nucleation clusters in this system, HCl is more favorably hydrated. Additionally, the hydrogen bonds including chlorine are often longer than other interatomic distances between molecules. In HCl-A-DMA, the hydrogen bond from DMA to the chlorine ion is 1.82 Å and the London dispersion forces between the chlorine ion and the ammonium ion result in a N–H⋯Cl length of 2.50 Å. In the NA-A-DMA cluster, the NA-DMA hydrogen bond length is 1.54 Å and the NA-A hydrogen bond length is 2.05 Å. Shorter hydrogen bond lengths in the NA-A-DMA cluster contributes to its initial stabilization when compared to HCl-A-DMA. Even with its larger size, which increases the bond lengths within the clusters, the HCl cluster benefits more with the addition of waters, likely caused by the greater entropy associated with these structures. This is demonstrated by larger clusters containing HCl and will be further discussed in the respective sections. While these clusters are not predicted to be present in high atmospheric concentrations, they highlight the driving effects of different acids and further reinforce sulfuric acid's effectiveness when compared to other strong acids.
3.3 Trimers of two acids and one base
The larger clusters are less studied; therefore, we report all our findings in the next several sections. In the figures, hydrogen bonds are marked in blue, which have hydrogen-bonded distances of less than 2.20 Å and hydrogen bond angles between 140 and 180°. Red lines are used to denote van der Waals forces where the bond angle encompassing the hydrogen is less than 140° or the hydrogen-bond distance is greater than 2.20 Å. The formation energies of all dry trimers, tetramers, and pentamers are listed in Table 1. Hydrated two acid and one base clusters allow for observation and comparison of the driving effects of ammonia and dimethylamine. The two acid and one base structures containing HCl are displayed in Fig. 2 and have corresponding energetics in Table 2. The remaining two acid and one base trimers are in ESI Tables T6, T7 and Fig. S6, S7.† Formation of the SA-HCl-DMA cluster from its monomers has a ΔG° that is 10.54 kcal mol−1 more negative than that for formation of SA-HCl-A at 217 K, even though they both contain four hydrogen bonds and a proton transfer from the HCl to the base. This is because DMA is more favorable for pre-nucleation,10 especially in dry clusters. Upon hydration, the newly formed SA-HCl-A-W consists of a neutral HCl, a deprotonated SA, and the ammonium ion, which is the only instance of all the two acids and one base clusters where the HCl is not deprotonated (Fig. 2). In nearly every case, SA-HCl-A-W0–3 has more negative stepwise hydration energies than SA-HCl-DMA-W0–3 (Table 2). Cluster formation and growth is more favorable in the dry state with DMA, and more favorable when hydrated with ammonia, which is why SA-HCl-A-W0–3 has more negative stepwise hydration energies than SA-HCl-DMA-W0–3.135 When SA is replaced with FA, the ΔG° of the trimers becomes more positive by around 6–9 kcal mol−1 (6.01–6.50 kcal mol−1 at 217 K and 5.51–6.45 kcal mol−1 for replacing SA in SA-HCl-A-W0–3 and 7.96–9.76 kcal mol−1 at 217 K and 8.02–9.71 kcal mol−1 at 298 K for replacing SA in SA-HCl-DMA-W0–3) (Table 2). Both dry FA-HCl-A and FA-HCl-DMA have three hydrogen bonds, with the decrease in hydrogen bonds coming from the reduced bonding capabilities of FA compared to SA. We again note that DMA yields more stable clusters in the dry state,10 whereas upon hydration, ammonia enables more negative energies (Table 2). Ammonium has four hydrogen bonding sites, which allows the water molecules that are added to form more stable hydrogen bond geometries than are possible with the geometry of protonated DMA, which is restricted by only having two possible sites for hydrogen bonding. FA-HCl-A-W and FA-HCl-DMA-W both contain 3 hydrogen bonds, but FA-HCl-A-W has two hydrogen bonds and a van der Waals interaction contributed by A, whereas FA-HCl-DMA-W has only two hydrogen bonds coming from DMA (Fig. 2). The results of the trimers with HCl are energetically and structurally consistent with trimers from previous work.73 FA-NA-DMA and FA-HCl-DMA have ΔG° energies of formation within one kcal mol−1 (0.15 kcal mol−1 at 217 K and 0.83 kcal mol−1 at 298 K) (Table 1) and have very similar structures with the same number of hydrogen bonds (Fig. 2 and S7†). This further supports the idea that the acid identity is not always as significant in the energies of formation as hydrogen bonding topology.66 SA-HCl-DMA is 1.50 kcal mol−1 more positive than SA-NA-DMA at 217 K (Table 1). In SA-HCl-DMA, the hydrogen bond length from the chlorine ion to the hydrogen on DMA is 1.98 Å and the hydrogen bond lengths from the chlorine ion to the hydrogens on SA is 2.13 Å (Fig. 2). When HCl is replaced with NA, tighter bonds are formed between the monomers; the DMA-NA bond length is 1.85 Å and the SA-NA bond length is 1.52 Å (Fig. S7†). The bond length difference between the monomers in these two clusters will have a more stabilizing effect for SA-NA-DMA, which is likely why SA-NA-DMA is lower in energy than SA-HCl-DMA. The number and length of hydrogen bonds within two acid-one base trimers is more important to the energies of formation than the identity of the acid. Elm and co-workers have used ACDC to predict that SA-NA-Base clusters such as SA-NA-DMA show high cluster formation potential.136 Elm's group has used the same methodology to predict that only the SA-FA-DMA clusters are significantly enhanced relative to simulations that compare SA, methanesulfonic acid, ammonia and amine bases.137 Formation of the SA-FA-DMA complex has the lowest value of ΔG°, followed closely by the formation of the SA-NA-DMA cluster, and then the SA-HCl-DMA cluster (Table 1).
Table 1 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation of all dry trimers, tetramers, and pentamer in the systems sulfuric acid-formic acid-hydrochloric acid-ammonia-dimethylamine and sulfuric acid-formic acid-nitric acid-ammonia-dimethylaminea at atmospherically relevant temperatures and 1 atm pressure
| Cluster |
216.65 K |
273.15 K |
298.15 K |
|
Ref. 73.
|
| SA + FA + NA ⇌ SA-FA-NA |
−13.45 |
−9.50 |
−7.76 |
| SA + FA + HCl ⇌ SA-FA-HCl |
−8.18 |
−4.60 |
−3.02 |
| SA + FA + A ⇌ SA-FA-Aa |
−17.13 |
−13.39 |
−11.74 |
| SA + FA + DMA ⇌ SA-FA-DMAa |
−26.08 |
−22.19 |
−20.48 |
| SA + NA + A ⇌ SA-NA-Aa |
−15.74 |
−11.99 |
−10.40 |
| SA + NA + DMA ⇌ SA-NA-DMAa |
−25.19 |
−21.37 |
−19.69 |
| SA + HCl + A ⇌ SA-HCl-A |
−13.15 |
−9.52 |
−7.90 |
| SA + HCl + DMA ⇌ SA-HCl-DMA |
−23.69 |
−20.10 |
−18.50 |
| FA + NA + A ⇌ FA-NA-Aa |
−8.42 |
−5.25 |
−3.87 |
| FA + NA + DMA ⇌ FA-NA-DMAa |
−15.58 |
−11.46 |
−9.65 |
| FA + HCl + A ⇌ FA-HCl-A |
−6.65 |
−3.04 |
−1.45 |
| FA + HCl + DMA ⇌ FA-HCl-DMA |
−15.73 |
−12.09 |
−10.48 |
| SA + FA + NA + A ⇌ SA-FA-NA-Aa |
−24.77 |
−18.82 |
−16.28 |
| SA + FA + NA + DMA ⇌ SA-FA-NA-DMAa |
−33.41 |
−27.50 |
−24.90 |
| SA + FA + HCl + A ⇌ SA-FA-HCl-A |
−20.20 |
−14.83 |
−12.47 |
| SA + FA + HCl + DMA ⇌ SA-FA-HCl-DMA |
−28.92 |
−23.10 |
−20.59 |
| SA + FA + A + DMA ⇌ SA-FA-A-DMAa |
−30.63 |
−24.98 |
−22.49 |
| SA + NA + A + DMA ⇌ SA-NA-A-DMAa |
−33.31 |
−27.23 |
−24.55 |
| SA + HCl + A + DMA ⇌ SA-HCl-A-DMA |
−36.33 |
−30.87 |
−28.45 |
| FA + NA + A + DMA ⇌ FA-NA-A-DMAa |
−19.35 |
−13.94 |
−11.57 |
| FA + HCl + A + DMA ⇌ FA-HCl-A-DMA |
−17.85 |
−12.63 |
−10.32 |
| SA + FA + NA + A + DMA ⇌ SA-FA-NA-A-DMAa |
−39.56 |
−31.51 |
−28.00 |
| SA + FA + HCl + A + DMA ⇌ SA-FA-HCl-A-DMA |
−43.08 |
−35.34 |
−32.02 |
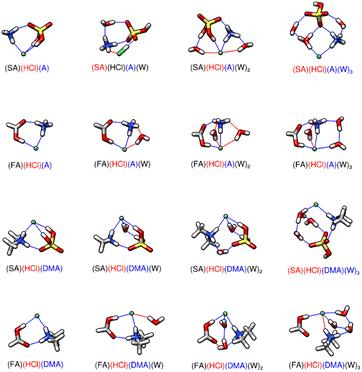 |
| | Fig. 2 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** minimum energy clusters for the sequential hydration of hydrochloric acid with one acid and one base. The molecule labels are colored according to charge as follows: blue = +1, black = 0, red = −1. Atoms are drawn in the following colors: hydrogen – white, carbon – grey, nitrogen – blue, oxygen – red, sulfur – yellow, chlorine – green. | |
Table 2 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation and sequential hydration of sulfuric acid-hydrochloric acid-ammonia, formic acid-hydrochloric acid-ammonia, sulfuric acid-hydrochloric acid-dimethylamine, and formic acid-hydrochloric acid-dimethylamine trimers at atmospherically relevant temperatures and 1 atm pressure
| Cluster |
216.65 K |
273.15 K |
298.15 K |
| SA + HCl + A ⇌ SA-HCl-A |
−13.15 |
−9.52 |
−7.90 |
| SA-HCl-A + W ⇌ SA-HCl-A-W |
−3.92 |
−2.50 |
−1.88 |
| SA-HCl-A-W + W ⇌ SA-HCl-A-W2 |
−3.54 |
−1.39 |
−0.45 |
| SA-HCl-A-W2 + W ⇌ SA-HCl-A-W3 |
−3.69 |
−2.06 |
−1.33 |
| FA + HCl + A ⇌ FA-HCl-A |
−6.65 |
−3.04 |
−1.45 |
| FA-HCl-A + W ⇌ FA-HCl-A-W |
−4.41 |
−2.80 |
−2.10 |
| FA-HCl-A-W + W ⇌ FA-HCl-A-W2 |
−3.53 |
−1.82 |
−1.17 |
| FA-HCl-A-W2 + W ⇌ FA-HCl-A-W3 |
−3.31 |
−1.70 |
−0.88 |
| SA + HCl + DMA ⇌ SA-HCl-DMA |
−23.69 |
−20.10 |
−18.50 |
| SA-HCl-DMA + W ⇌ SA-HCl-DMA-W |
−3.96 |
−1.97 |
−1.09 |
| SA-HCl-DMA-W + W ⇌ SA-HCl-DMA-W2 |
−2.75 |
−0.93 |
−0.13 |
| SA-HCl-DMA-W2 + W ⇌ SA-HCl-DMA-W3 |
−1.96 |
−0.24 |
0.52 |
| FA + HCl + DMA ⇌ FA-HCl-DMA |
−15.73 |
−12.09 |
−10.48 |
| FA-HCl-DMA + W ⇌ FA-HCl-DMA-W |
−2.68 |
−1.01 |
−0.28 |
| FA-HCl-DMA-W + W ⇌ FA-HCl-DMA-W2 |
−2.23 |
−0.16 |
0.75 |
| FA-HCl-DMA-W2 + W ⇌ FA-HCl-DMA-W3 |
−2.78 |
−1.08 |
−0.33 |
3.4 Tetramers of three acids and one base
Before discussing three acid and one base clusters, we note that we have calculated the lowest energy structures for SA-FA-NA, SA-FA-HCl, and their hydrates with one to three waters (Fig. S8, Table T8†). The cluster formation ΔG° values for SA-FA-NA are −13.45 kcal mol−1 at 217 K and −7.76 kcal mol−1 at 298 K, while those for SA-FA-HCl are about 5 kcal mol−1 (5.27 kcal mol−1 at 217 K and 4.74 kcal mol−1 at 298 K) more positive, likely caused by the fewer hydrogen bonding sites on HCl as compared to NA. The SA-FA-HCl-W hydrate is the most favorable, with a sequential hydration value of −4.22 kcal mol−1. As the three acid trimers still have relatively positive energies of formation and hydration compared to the two acid one base systems, the structures and energies of the three acid trimers are included only in the ESI.† The energies of formation and sequential hydration of the three acid and one base tetramer systems containing SA, FA, NA or HCl, and A or DMA are listed in Table 3. The corresponding minimum energy structures are shown in Fig. 3. The formation of the dry SA-FA-HCl-DMA cluster is 8.72–8.12 kcal mol−1 lower in free energy than forming the SA-FA-HCl-A cluster at all temperatures listed (Table 3). Interestingly, HCl remains neutral in dry SA-FA-HCl-A, with SA being deprotonated instead, which is unlike any of the hydrated three acid and one base clusters, where HCl is deprotonated (Fig. 3). Similar to the two acid and one base clusters, HCl remains protonated only when A is present in the dry cluster. Among the dry three acid and one base tetramers, SA-FA-NA-DMA has the most negative ΔG° with −33.41 kcal mol−1 at 217 K.73 The second most negative is SA-FA-HCl-DMA, which has a ΔG° of −28.92 kcal mol−1 at 217 K. The larger size of the chloride anion results in longer hydrogen bond distances with SA (1.88 Å) and FA (2.00 Å) while for the SA-FA-NA-DMA cluster, NA forms shorter and stronger hydrogen bonds with SA (1.58 & 1.85 Å). When examining the tetramers with A instead of DMA, the SA-FA-NA-A cluster is also more stable than the SA-FA-HCl-A cluster by 4.57 kcal mol−1 at 217 K (Table 3). In both clusters, SA undergoes a proton exchange with A, leaving the other acid, NA or HCl, neutral. SA-FA-NA-A forms five hydrogen bonds where SA-FA-HCl-A only forms four hydrogen bonds and a van der Waals interaction. When these clusters are hydrated, the sequential energies of hydration are more negative for the clusters containing HCl than those containing NA. For the clusters containing HCl, hydronium ions are present in the DMA clusters with two and three waters and in the ammonia cluster with three waters. The hydronium ions contribute three hydrogen bonds in all cases, providing additional stability to the hydrated clusters. The clusters containing NA instead of HCl do not contain any hydronium ions and have a smaller number of hydrogen bonds than the HCl clusters with hydronium ions. Regardless of the base present, NA forms more stable complexes than HCl in three acid and one base dry tetramers. However, hydration is more favorable for three acid and one base tetramers containing HCl. Thus, it may be that NA is more important for the first step of prenucleation and HCl is more important for growth and hydration of prenucleation clusters.
Table 3 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation and sequential hydration of sulfuric acid-formic acid-hydrochloric acid-dimethylamine, sulfuric acid-formic acid-hydrochloric acid-ammonia, sulfuric acid-formic acid-nitric acid-dimethylamine, and sulfuric acid-formic acid-nitric acid-ammonia tetramers at atmospherically relevant temperatures and 1 atm pressure
| Cluster |
216.65 K |
273.15 K |
298.15 K |
|
Ref. 73.
|
| SA + FA + NA + A ⇌ SA-FA-NA-Aa |
−24.77 |
−18.82 |
−16.28 |
| SA-FA-NA-A + W ⇌ SA-FA-NA-A-Wa |
−3.77 |
−2.38 |
−1.71 |
| SA-FA-NA-A-W + W ⇌ SA-FA-NA-A-W2a |
−2.81 |
−1.14 |
−0.40 |
| SA-FA-NA-A-W2 + W ⇌ SA-FA-NA-A-W3a |
−0.98 |
0.86 |
1.68 |
| SA + FA + HCl + A ⇌ SA-FA-HCl-A |
−20.20 |
−14.83 |
−12.47 |
| SA-FA-HCl-A + W ⇌ SA-FA-HCl-A-W |
−4.65 |
−2.48 |
−1.51 |
| SA-FA-HCl-A-W + W ⇌ SA-FA-HCl-A-W2 |
−2.88 |
−1.14 |
−0.38 |
| SA-FA-HCl-A-W2 + W ⇌ SA-FA-HCl-A-W3 |
−3.05 |
−1.03 |
−0.36 |
| SA + FA + NA + DMA ⇌ SA-FA-NA-DMAa |
−33.41 |
−27.50 |
−24.90 |
| SA-FA-NA-DMA + W ⇌ SA-FA-NA-DMA-Wa |
−2.39 |
−0.48 |
0.36 |
| SA-FA-NA-DMA-W + W ⇌ SA-FA-NA-DMA-W2a |
−1.81 |
−0.01 |
0.78 |
| SA-FA-NA-DMA-W2 + W ⇌ SA-FA-NA-DMA-W3a |
−0.87 |
0.82 |
1.57 |
| SA + FA + HCl + DMA ⇌ SA-FA-HCl-DMA |
−28.92 |
−23.10 |
−20.59 |
| SA-FA-HCl-DMA + W ⇌ SA-FA-HCl-DMA-W |
−4.93 |
−3.06 |
−2.17 |
| SA-FA-HCl-DMA-W + W ⇌ SA-FA-HCl-DMA-W2 |
−2.69 |
−0.85 |
−0.03 |
| SA-FA-HCl-DMA-W2 + W ⇌ SA-FA-HCl-DMA-W3 |
−2.04 |
−0.34 |
0.42 |
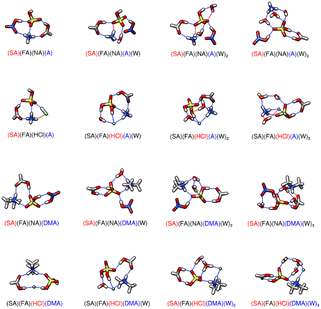 |
| | Fig. 3 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** minimum energy clusters for the sequential hydration of three acids with one base. The molecule labels are colored according to charge as follows: blue = +1, black = 0, red = −1. Atoms are drawn in the following colors: hydrogen – white, carbon – grey, nitrogen – blue, oxygen – red, sulfur – yellow, chlorine – green. | |
3.5 Tetramers of two acids and two bases
The two acid and two base tetramers are shown in Fig. 4, and the corresponding energies are listed in Table 4. It has been previously noted that a tetra-ionic cluster provides additional stability in the form of proton transfers,73 and that is also the case for the SA-HCl-A-DMA tetramer. The tetramer SA-HCl-A-DMA is 18.13–18.48 kcal mol−1 lower in ΔG° than FA-HCl-A-DMA at the temperatures listed. This energy difference is likely caused by SA-HCl-A-DMA being tetra-ionic while FA-HCl-A-DMA is di-ionic, with FA and A remaining neutral. SA-HCl-A-DMA has four hydrogen bonds, while FA-HCl-A-DMA has three hydrogen bonds. Both structures have a ring-like geometry with acids and bases opposite each other, which differs from the structures of di-ionic SA-FA-A-DMA and tetra-ionic SA-NA-A-DMA. SA-FA-A-DMA is 5.70 kcal mol−1 more positive in Gibbs free energy than SA-HCl-A-DMA at 217 K and SA-NA-A-DMA is 3.02 kcal mol−1 higher in ΔG°. SA-FA-A-DMA only has four hydrogen bonds and is a di-ionic cluster. When comparing FA-HCl-A-DMA and FA-NA-A-DMA in the dry state, the tetramer with NA has a lower ΔG° than the tetramer with HCl. This is different from the tetramers of SA-HCl-A-DMA and SA-NA-A-DMA, where the tetramer with HCl is more stable in the dry state. Both FA-HCl-A-DMA and FA-NA-A-DMA are di-ionic clusters with four hydrogen bonds. The 1.50 kcal mol−1 difference between the dry clusters at 217 K is likely a result of subtle hydrogen bond strength differences. When the tetramers are hydrated, their relative stabilities change due to the geometric stabilization of the added water molecule. As discussed by Bready et al.,73 SA-NA-A-DMA-W has a remarkably large first sequential hydration energy of −6.79 kcal mol−1 at 217 K and exhibits special stability. The tetra-ionic cluster is stabilized by the addition of the water molecule allowing for 7 hydrogen bonds. When SA-HCl-A-DMA is hydrated with one water, only 6 hydrogen bonds are formed for a first sequential hydration energy of −4.26 kcal mol−1 at 217 K. SA-HCl-A-DMA-W only has three hydrogen bonds that encompass SA whereas SA-NA-A-DMA-W utilizes 4 hydrogen bonding sites on SA. Upon hydration with one water, both SA-FA-A-DMA-W and FA-NA-A-DMA-W have 5 hydrogen bonds and FA-HCl-A-DMA-W has 3 hydrogen bonds. As the number of hydrogen bonds decrease in the hydrated tetramers, the stability of the clusters decreases as well. For the second and third sequential hydrations, SA-HCl-A-DMA-W2–3 have more negative sequential hydration values than SA-NA-A-DMA-W2–3, which is like the results in Section 3.3 where two acid-one base clusters with HCl have more negative hydration energies than when NA replaces HCl. These results support the statement that NA may be better for pre-nucleation cluster formation while HCl may be better for the growth and hydration of a prenucleation cluster.
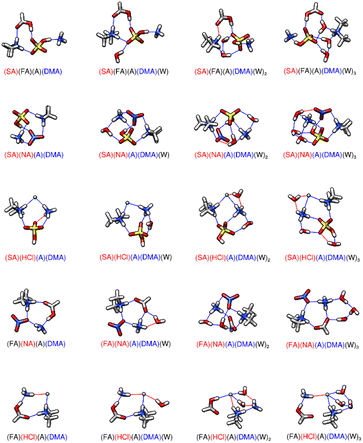 |
| | Fig. 4 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** minimum energy clusters for the sequential hydration of two acids with two bases. The molecule labels are colored according to charge as follows: blue = +1, black = 0, red = −1. Atoms are drawn in the following colors: hydrogen – white, carbon – grey, nitrogen – blue, oxygen – red, sulfur – yellow, chlorine – green. | |
Table 4 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation and sequential hydration of sulfuric acid-hydrochloric acid-ammonia-dimethylamine, formic acid-hydrochloric acid-ammonia-dimethylamine, sulfuric acid-formic acid-ammonia-dimethylamine, sulfuric acid-nitric acid-ammonia-dimethylamine, and formic acid-nitric acid-ammonia-dimethylamine tetramers at atmospherically relevant temperatures and 1 atm pressure
| Cluster |
216.65 K |
273.15 K |
298.15 K |
|
Ref. 73.
|
| SA + FA + A + DMA ⇌ SA-FA-A-DMAa |
−30.63 |
−24.98 |
−22.49 |
| SA-FA-A-DMA + W ⇌ SA-FA-A-DMA-Wa |
−2.25 |
−0.50 |
0.27 |
| SA-FA-A-DMA-W + W ⇌ SA-FA-A-DMA-W2a |
−1.07 |
1.10 |
1.99 |
| SA-FA-A-DMA-W2 + W ⇌ SA-FA-A-DMA-W3a |
−2.05 |
−0.48 |
0.28 |
| SA + NA + A + DMA ⇌ SA-NA-A-DMAa |
−33.31 |
−27.23 |
−24.55 |
| SA-NA-A-DMA + W ⇌ SA-NA-A-DMA-Wa |
−6.79 |
−4.84 |
−3.99 |
| SA-NA-A-DMA-W + W ⇌ SA-NA-A-DMA-W2a |
−1.60 |
0.48 |
1.40 |
| SA-NA-A-DMA-W2 + W ⇌ SA-NA-A-DMA-W3a |
−1.62 |
0.22 |
1.04 |
| SA + HCl + A + DMA ⇌ SA-HCl-A-DMA |
−36.33 |
−30.87 |
−28.45 |
| SA-HCl-A-DMA + W ⇌ SA-HCl-A-DMA-W |
−4.26 |
−2.45 |
−1.66 |
| SA-HCl-A-DMA-W + W ⇌ SA-HCl-A-DMA-W2 |
−3.18 |
−1.56 |
−0.84 |
| SA-HCl-A-DMA-W2 + W ⇌ SA-HCl-A-DMA-W3 |
−2.14 |
−0.36 |
0.42 |
| FA + NA + A + DMA ⇌ FA-NA-A-DMAa |
−19.35 |
−13.94 |
−11.57 |
| FA-NA-A-DMA + W ⇌ FA-NA-A-DMA-Wa |
−2.16 |
−0.32 |
0.50 |
| FA-NA-A-DMA-W + W ⇌ FA-NA-A-DMA-W2a |
−1.82 |
0.38 |
1.36 |
| FA-NA-A-DMA-W2 + W ⇌ FA-NA-A-DMA-W3a |
−2.73 |
−1.23 |
−0.66 |
| FA + HCl + A + DMA ⇌ FA-HCl-A-DMA |
−17.85 |
−12.63 |
−10.32 |
| FA-HCl-A-DMA + W ⇌ FA-HCl-A-DMA-W |
−2.50 |
−0.79 |
−0.04 |
| FA-HCl-A-DMA-W + W ⇌ FA-HCl-A-DMA-W2 |
−2.16 |
−0.10 |
0.81 |
| FA-HCl-A-DMA-W2 + W ⇌ FA-HCl-A-DMA-W3 |
−2.15 |
−0.74 |
-0.12 |
3.6 Pentamer of three acids and two bases
The system containing all three acids and both bases with zero to three waters is pictured in Fig. 5 with the respective energies listed in Table 5. In the dry state, SA-FA-HCl-A-DMA has 6 hydrogen bonds and an SA-FA dimer, noted for its strength and stability by Harold et al.66 SA-FA-HCl-A-DMA is 3.52 kcal mol−1 lower in Gibbs free energy than SA-FA-NA-A-DMA at 217 K (Table 5), possibly resulting in part from SA-FA-NA-A-DMA lacking the SA-FA dimer. Both pentamers are tetra-ionic with FA remaining neutral. Upon hydration with one water, SA-FA-HCl-A-DMA is slightly more stabilized than SA-FA-NA-A-DMA. This is likely due to SA-FA-HCl-A-DMA gaining two hydrogen bonds, whereas SA-FA-NA-A-DMA only gains one hydrogen bond and a van der Waals interaction. When the second water molecule is added, SA-FA-NA-A-DMA gains three hydrogen bonds and has a sequential hydration energy 1.22 kcal mol−1 lower than SA-FA-HCl-A-DMA at 217 K, which only gains two new hydrogen bonds. The third water destabilizes both clusters, as SA-FA-NA-A-DMA gains three weak London dispersion forces and SA-FA-HCl-A-DMA gains one hydrogen bond and one London dispersion forces, so that entropy is decreased more than enthalpy is increased. In all structures dry and hydrated, SA-FA-HCl-A-DMA-W0–3 has an SA-FA dimer within its geometry, likely helping stabilize it. The pentamer containing HCl has a more consistent geometry than SA-FA-NA-A-DMA-W0–3 throughout hydration and has more stabilizing first and third hydration energies than the NA pentamer and less stabilizing second hydration energies (Table 5). The large size of the chlorine ion leads to its Cl⋯H distances being longer as the system size increases, compared to a traditional hydrogen bond between NA and another monomer.
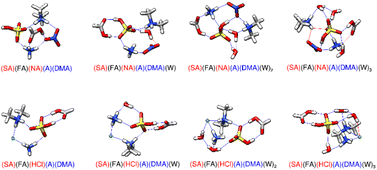 |
| | Fig. 5 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** minimum energy clusters for the sequential hydration of three acids with two bases. The molecule labels are colored according to charge as follows: blue = +1, black = 0, red = −1. Atoms are drawn in the following colors: hydrogen – white, carbon – grey, nitrogen – blue, oxygen – red, sulfur – yellow, chlorine – green. | |
Table 5 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation and sequential hydration of sulfuric acid-formic acid-hydrochloric acid-ammonia-dimethyl amine and sulfuric acid-formic acid-nitric acid-ammonia-dimethylamine pentamers at atmospherically relevant temperatures and 1 atm pressure
| Cluster |
216.65 K |
273.15 K |
298.15 K |
|
Ref. 73.
|
| SA + FA + NA + A + DMA ⇌ SA-FA-NA-A-DMAa |
−39.56 |
−31.53 |
−28.00 |
| SA-FA-NA-A-DMA + W ⇌ SA-FA-NA-A-DMA-Wa |
−4.13 |
3.09 |
4.03 |
| SA-FA-NA-A-DMA-W + W ⇌ SA-FA-NA-A-DMA-W2a |
−4.07 |
−1.54 |
−0.64 |
| SA-FA-NA-A-DMA-W2 + W ⇌ SA-FA-NA-A-DMA-W3a |
1.16 |
3.69 |
4.58 |
| SA + FA + HCl + A + DMA ⇌ SA-FA-HCl-A-DMA |
−43.08 |
−35.34 |
−32.02 |
| SA-FA-HCl-A-DMA + W ⇌ SA-FA-HCl-A-DMA-W |
−4.35 |
−2.67 |
−1.82 |
| SA-FA-HCl-A-DMA-W + W ⇌ SA-FA-HCl-A-DMA-W2 |
−2.85 |
−0.85 |
0.04 |
| SA-FA-HCl-A-DMA-W2 + W ⇌ SA-FA-HCl-A-DMA-W3 |
0.00 |
2.07 |
2.86 |
3.7 Equilibrium concentrations and pathways of formation
To calculate the equilibrium concentrations of the cluster, equilibrium constants were first calculated using the ΔG° values of the cluster at 217 K and 298 K. For both of these temperatures, a system of equations adapted from Odbadrakh et al.54 was used to calculate the equilibrium concentrations assuming a closed system of these three acids, two bases, and three waters. We note that the calculations account only for thermodynamics and do not account for the kinetics of the reaction. Therefore, the results of the calculations would likely change if additional kinetic atmospheric conditions like evaporation were included in the calculations. Initial starting concentrations of the monomers were 5 × 107 cm−3 for SA, 2 × 1011 cm−3 for FA, 1 × 109 cm−3 for HCl, 2 × 1011 cm−3 for A, and 2 × 109 cm3 for DMA at 298 K. These concentrations were chosen because they are atmospherically relevant over inland and urban areas.30,118–120,120–125 We chose a water concentration of 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere.120 Initial monomer concentrations from the literature22,120–128 at 298 K were reduced by three orders of magnitude at 217 K to compensate for the reduction of CCN-forming particles in the upper troposphere. This rough estimate is based on the three orders of magnitude decrease in water concentration, and we used this approximation since experimental concentrations of these monomers in the upper troposphere are difficult to measure. HCl is the product of the oxidation of reactive chlorine species from sea spray and biomass burning and can have concentrations largely affected by the proximity to a coast as well as the concentration of other atmospheric constituents.127,128 Ozone concentrations, gas phase ammonia concentrations, and atmospheric acidity all play a role in the relative concentration of HCl in different locations. HCl concentrations of 1 × 109 cm−3 have been reported in costal urban locations and mountain-top locations.123,126 To account for the decrease in monomer concentrations at the top of the troposphere, the initial concentrations of monomers have been decreased by three orders of magnitude to 5 × 104 cm−3 for SA, 2 × 108 cm−3 for FA, 1 × 106 cm−3 for HCl, 2 × 108 cm−3 for A, and 2 × 106 cm−3 for DMA at 217 K. The calculated equilibrium concentrations of atmospherically relevant clusters are shown in Table 6, where we have defined atmospherically relevant as equilibrium concentrations above one per cm−3. Atmospherically relevant dimers are comprised of mainly acid–base pairings and SA-FA. SA-DMA is the only dimer relevant at both 217 K and 298 K, likely a result of the role of SA and DMA as drivers of nucleation. The concentration of HCl-DMA is less than for FA-DMA and SA-DMA. HCl is not a known driver of nucleation and lacks the hydrogen bonding ability of SA and FA. Upon the addition of one and two waters to HCl-DMA, its concentration at 217 K and 298 K increases. The hydration of HCl-DMA provides an increase in hydrogen bonding sites and a more stable cluster. Two acid and one base clusters are the most atmospherically relevant of the trimers, particularly SA-HCl-DMA and SA-FA-DMA. SA and FA form a particularly strong complex, which has been previously studied by Harold et al.,66 and has a higher equilibrium concentration than most other dimers. When the magnitude of concentrations for all monomers is decreased by three orders, corresponding to the top of the troposphere at 217 K, clusters with an SA-FA complex have lower concentrations. This is a result of the driving force of SA and the importance of hydrogen bonding topology. The dry tetramer SA-HCl-A-DMA is barely atmospherically relevant at 217 K, but is not at 298 K. The pentamer is not atmospherically relevant at any temperature in our closed system simulation of these three acids, two bases, and three water molecules. To gain insight into prenucleation cluster growth, the ideal pathways of formation for the pentamer are derived from Table 6 by using an atmospherically relevant dimer cluster and then adding monomers sequentially until the pentamer is formed. These pathways are shown in Table 7. A high starting concentration of SA-DMA begins the optimal growth pathway and second-best pathway for the dry pentamer at 298 K and 217 K. Starting clusters with SA and DMA will result in good cluster growth because both are known drivers of pre-nucleation cluster formation. In the optimal pathway, HCl is added last at 217 K and is the first addition to the SA-DMA dimer at 298 K (Table 7). The only atmospherically relevant hydrated trimers are SA-FA-DMA-W1–2 and the optimal pathways of formation for SA-FA-DMA-W1 at 217 K and 298 K are shown in Table 8. When compared to the number of relevant hydrated clusters for the SA-FA-NA-A-DMA system, the SA-FA-HCl-A-DMA system is less atmospherically relevant. Clusters containing HCl often have more negative energies of hydration than clusters containing NA, but HCl clusters are less favourable for the first step in prenucleation than SA or NA. The low concentrations of this pentamer system may point to HCl being a poor driver of nucleation.
Table 6 Equilibrium concentrations of clusters that form at more than 1 cm−3 at 217 and 298 K. Initial concentrations of the monomers at 217 K were: SA = 5.00 × 104, FA = 2.00 × 108, HCl = 1.00 × 106, A = 2.00 × 108, DMA = 2.00 × 106. Initial concentrations of the monomers at 298 K were: SA = 5.00 × 107, FA = 2.00 × 1011, HCl = 1.00 × 109, A = 2.00 × 1011, DMA = 2.00 × 109. The water concentrations were 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere120
| Cluster |
216.65 K |
298.15 K |
| SA |
2.84 × 101 |
1.48 × 107 |
| FA |
2.00 × 108 |
1.99 × 1011 |
| HCl |
1.00 × 106 |
9.99 × 108 |
| A |
2.00 × 108 |
2.00 × 1011 |
| DMA |
1.95 × 106 |
1.98 × 109 |
| SA-FA |
3.77 × 10−2 |
1.03 × 103 |
| SA-A |
8.35 × 10−3 |
5.64 × 102 |
| SA-DMA |
2.42 × 104 |
1.14 × 107 |
| FA-A |
4.88 × 10−4 |
2.90 × 101 |
| FA-DMA |
6.05 × 10−1 |
5.00 × 102 |
| HCl-A |
2.26 × 10−4 |
3.37 |
| HCl-DMA |
4.39 × 10−3 |
4.24 |
| SA-FA-DMA |
1.96 × 103 |
9.87 × 103 |
| SA-HCl-DMA |
3.81 × 10−2 |
1.75 |
| SA-A-DMA |
2.41 × 10−3 |
1.05 |
| SA-HCl-A-DMA |
1.27 |
2.80 × 10−1 |
| SA-W1 |
2.39 × 101 |
1.50 × 107 |
| SA-W2 |
3.28 |
2.90 × 106 |
| SA-W3 |
7.19 × 10−2 |
1.45 × 105 |
| FA-W1 |
1.90 × 105 |
1.13 × 109 |
| FA-W2 |
1.06 × 103 |
1.99 × 107 |
| FA-W3 |
1.77 × 10−1 |
5.22 × 104 |
| HCl-W1 |
1.24 × 101 |
7.01 × 105 |
| HCl-W2 |
3.79 × 10−4 |
3.39 × 102 |
| A-W1 |
6.57 × 103 |
3.79 × 108 |
| A-W2 |
5.61 × 10−2 |
4.52 × 104 |
| A-W3 |
1.88 × 10−5 |
1.03 × 102 |
| DMA-W1 |
1.86 × 102 |
5.01 × 106 |
| DMA-W2 |
1.04 × 10−2 |
3.76 × 103 |
| SA-FA-W1 |
1.12 × 10−2 |
3.79 × 102 |
| SA-FA-W2 |
4.47 × 10−4 |
2.71 × 101 |
| SA-A-W1 |
6.27 × 10−4 |
8.20 × 101 |
| SA-A-W2 |
2.28 × 10−3 |
1.12 × 102 |
| SA-A-W3 |
8.32 × 10−5 |
1.21 × 101 |
| SA-DMA-W1 |
2.29 × 104 |
5.42 × 106 |
| SA-DMA-W2 |
7.10 × 102 |
3.06 × 105 |
| SA-DMA-W3 |
7.73 × 101 |
4.30 × 104 |
| FA-A-W1 |
2.63 × 10−3 |
4.56 × 101 |
| FA-DMA-W1 |
3.53 × 10−3 |
1.12 × 101 |
| HCl-DMA-W1 |
2.48 × 10−2 |
2.01 × 101 |
| HCl-DMA-W2 |
5.95 × 10−3 |
5.60 |
| HCl-DMA-W3 |
7.62 × 10−4 |
5.52 × 10−1 |
| SA-FA-DMA-W1 |
1.25 × 102 |
1.19 × 103 |
| SA-FA-DMA-W2 |
3.24 × 10−1 |
8.87 |
Table 7 Optimal pathways for growing the dry pentamer at 1 atm pressure according to equilibrium concentrations calculated using initial concentrations of [SA]0 = 5.00 × 107, [FA]0 = 2.00 × 1011, [HCl]0 = 1.00 × 109, [A]0 = 2.00 × 1011, and [DMA]0 = 2.00 × 109 at 298 K. Concentrations were decreased by 3 orders of magnitude for 217 K. The water concentrations were 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere120
|
|
216.65 K |
298.15 K |
| Optimal pathway |
SA + DMA ⇌ SA-DMA |
SA + DMA ⇌ SA-DMA |
| + FA ⇌ SA-FA-DMA |
+ HCl ⇌ SA-HCl-DMA |
| + A ⇌ SA-FA-A-DMA |
+ A ⇌ SA-HCl-A-DMA |
| + HCl ⇌ SA-FA-HCl-A-DMA |
+ FA ⇌ SA-FA-HCl-A-DMA |
| 2nd best pathway |
SA + DMA ⇌ SA-DMA |
SA + DMA ⇌ SA-DMA |
| + HCl ⇌ SA-HCl-DMA |
+ FA ⇌ SA-FA-DMA |
| + A ⇌ SA-HCl-A-DMA |
+ A ⇌ SA-FA-A-DMA |
| + FA ⇌ SA-FA-HCl-A-DMA |
+ HCl ⇌ SA-FA-HCl-A-DMA |
| 3rd best pathway |
SA + FA ⇌ SA-FA |
SA + FA ⇌ SA-FA |
| + DMA ⇌ SA-FA-DMA |
+ DMA ⇌ SA-FA-DMA |
| + A ⇌ SA-FA-A-DMA |
+ A ⇌ SA-FA-A-DMA |
| + HCl ⇌ SA-FA-HCl-A-DMA |
+ HCl ⇌ SA-FA-HCl-A-DMA |
Table 8 Optimal pathways for growing the SA-FA-DMA-W cluster at 1 atm pressure according to equilibrium concentrations calculated using initial concentrations of [SA]0 = 5.00 × 107, [FA]0 = 2.00 × 1011, [HCl]0 = 1.00 × 109, [A]0 = 2.00 × 1011, and [DMA]0 = 2.00 × 109 at 298 K. Concentrations were decreased by 3 orders of magnitude for 217 K. The water concentrations were 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere120
|
|
216.65 K |
298.15 K |
| Optimal pathway |
SA + DMA ⇌ SA-DMA |
SA + W ⇌ SA-W |
| + W ⇌ SA-DMA-W |
+ DMA ⇌ SA-DMA-W |
| + FA ⇌ SA-FA-DMA-W |
+ FA ⇌ SA-FA-DMA-W |
| 2nd best pathway |
SA + W ⇌ SA-W |
SA + DMA ⇌ SA-DMA |
| + DMA ⇌ SA-DMA-W |
+ W ⇌ SA-DMA-W |
| + FA ⇌ SA-FA-DMA-W |
+ FA ⇌ SA-FA-DMA-W |
| 3rd best pathway |
DMA + W ⇌ DMA-W |
DMA + W ⇌ DMA-W |
| + SA ⇌ SA-DMA-W |
+ SA ⇌ SA-DMA-W |
| + FA ⇌ SA-FA-DMA-W |
+ FA ⇌ SA-FA-DMA-W |
4 Conclusions
This is the fourth study on formation of prenucleation complexes of three different acid molecules and two different bases,73,136,137 and adds to the insights obtained from previous work. Accurate ΔG° values for the formation of every possible cluster that can be formed from a sulfuric acid molecule, a formic acid molecule, a hydrochloric acid molecule, an ammonia molecule, a dimethylamine molecule, and 0–3 water molecules were determined from a comprehensive search of the GFN2-xTB and ωB97X-D potential energy surfaces combined with DLPNO-CCSD(T)/CBS electronic energy calculations on the DFT geometries. This first detailed study of HCl interacting with two other acids and two bases reveals the subtleties in play when HCl is considered as a potential actor in the formation of prenucleation clusters. Because of the larger size of chlorine, many of the clusters that include HCl form longer distances between neighbouring molecules and have weaker interactions in the dry state. By comparison, nitric acid forms stronger interactions in small, dry, clusters than hydrochloric acid. However, as the clusters grow larger with hydration, the interactions with HCl often become stronger than those with HNO3. In many of the clusters explored in this paper, the SA-FA dimer stabilizes the overall clusters. Many subtleties are at play in the beginning stages of pre-nucleation and the importance of different factors changes with the system being investigated. Hydrogen bonding topology, acid/base strength, and complex structural interactions all play an important role in structure energetics and atmospheric relevance. Sometimes detailed hydrogen bonding topology is as important as conventional notions like acid/base strength, which makes a priori prediction of which atmospheric species will be most important for driving prenucleation growth quite difficult. Complexes with DMA and various acids form stronger dry complexes than does ammonia, yet the sequential hydration energies favor ammonia since the ammonium cation can form up to four hydrogen bonds while protonated DMA can only form two. For the three acid-one base systems, NA forms a stronger dry cluster than HCl, while stepwise hydration switches to favor the HCl clusters (Table 3). For the two acid-two base clusters containing SA, HCl is a stronger nucleator than NA. The first hydration favors the formation of the unusually strong SA-NA-A-DMA-W cluster, yet successive hydrations with a second and third water revert to the clusters with HCl (Table 4). While HCl forms a stronger two acid-two base system than NA when SA is the second acid, NA forms a stronger two acid-two base system when FA is the second acid (Table 1). As shown in Fig. 5 and Table 5, the SA-FA-HCl-A-DMA-W0–1 structures that are stabilized by the SA-FA dimer have more negative Gibbs free energies of formation than the comparable SA-FA-NA-A-DMA-W0–1 structures. Yet as an additional water is added, the stepwise hydration energies favor the structures with NA instead of HCl. Taken as a whole, the results presented in this paper add to the conclusions that hydrogen bond topology and the detailed structural interactions that are subtle interplays between enthalpy and entropy can be as important as conventional ideas such as acid/base strength.66 There is much future work that must be completed to gain a better understanding of the beginning stages of prenucleation.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Funding for this work was provided by grants CHE-16626238, CHE-1903871, and CHE-2018427 from the National Science Foundation (GCS), the Arnold and Mabel Beckman Foundation Beckman Scholar Award (CJB), and the Barry M. Goldwater Scholarship (CJB). High-performance computing resources were provided by the Research Corporation for Science Advancement (27446) and the MERCURY Consortium (https://www.mercuryconsortium.org).138,139 Molecular graphics and analyses performed with UCSF Chimera, developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco, with support from NIH P41-GM103311.
References
- K. A. Prather, C. D. Hatch and V. H. Grassian, Analysis of atmospheric aerosols, Annu. Rev. Anal. Chem., 2008, 1, 485–514 CrossRef CAS PubMed.
- M. O. Andreae and D. Rosenfeld, Aerosol-cloud-precipitation interactions. Part 1. The nature and sources of cloud-active aerosols, Earth-Sci. Rev., 2008, 89, 13–41 CrossRef.
-
IPCC, Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2021 Search PubMed.
- M. E. Gonzalez, A. F. Corral, E. Crosbie, H. Dadashazar, G. S. Diskin, E. L. Edwards, S. Kirschler, R. H. Moore, C. E. Robinson, J. S. Schlosser, M. Shook, C. Stahl, K. L. Thornhill, C. Voigt, E. Winstead, L. D. Ziemba and A. Sorooshian, Relationships between supermicrometer particle concentrations and cloud water sea salt and dust concentrations: analysis of MONARC and ACTIVATE data, Environ. Sci.: Atmos., 2022, 2, 738–752 CAS.
- J. Kontkanen, D. Stolzenburg, T. Olenius, C. Yan, L. Dada, L. Ahonen, M. Simon, K. Lehtipalo and I. Riipinen, What controls the observed size-dependency of the growth rates of sub-10 nm atmospheric particles?, Environ. Sci.: Atmos., 2022, 2, 449–468 CAS.
- A. A. Nair and F. Q. Yu, Quantification of Atmospheric Ammonia Concentrations: A Review of Its Measurement and Modeling, Atmosphere, 2020, 11, 1092 CrossRef CAS.
- J. N. Smith, K. F. Moore, P. H. McMurry and F. L. Eisele, Atmospheric measurements of sub-20 nm diameter particle chemical composition by thermal desorption chemical ionization mass spectrometry, Aerosol Sci. Technol., 2004, 38, 100–110 CrossRef CAS.
- M. Kulmala, H. Vehkamaki, T. Petaja, M. Dal Maso, A. Lauri, V. M. Kerminen, W. Birmili and P. H. McMurry, Formation and growth rates of ultrafine atmospheric particles: a review of observations, J. Aerosol Sci., 2004, 35, 143–176 CrossRef CAS.
- M. Kulmala, I. Riipinen, M. Sipila, H. E. Manninen, T. Petaja, H. Junninen, M. D. Maso, G. Mordas, A. Mirme, M. Vana, A. Hirsikko, L. Laakso, R. M. Harrison, I. Hanson, C. Leung, K. E. Lehtinen and V. M. Kerminen, Toward direct measurement of atmospheric nucleation, Science, 2007, 318, 89–92 CrossRef CAS PubMed.
- T. Kurtén, V. Loukonen, H. Vehkamäki and M. Kulmala, Amines are likely to enhance neutral and ion-induced sulfuric acid-water nucleation in the atmosphere more effectively than ammonia, Atmos. Chem. Phys., 2008, 8, 4095–4103 CrossRef.
- C. Kuang, P. H. McMurry, A. V. McCormick and F. L. Eisele, Dependence of nucleation rates on sulfuric acid vapor concentration in diverse atmospheric locations, J. Geophys. Res.: Atmos., 2008, 113, D10209 CrossRef.
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Evolution of organic aerosols in the atmosphere, Science, 2009, 326, 1525–1529 CrossRef CAS PubMed.
- J. N. Smith and G. J. Rathbone, Carboxylic acid characterization in nanoparticles by thermal desorption chemical ionization mass spectrometry, Int. J. Mass Spectrom., 2008, 274, 8–13 CrossRef CAS.
- J. N. Smith, K. C. Barsanti, H. R. Friedli, M. Ehn, M. Kulmala, D. R. Collins, J. H. Scheckman, B. J. Williams and P. H. McMurry, Observations of aminium salts in atmospheric nanoparticles and possible climatic implications, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6634–6639 CrossRef CAS PubMed.
- T. E. Morrell and G. C. Shields, Atmospheric implications for formation of clusters of ammonium and 1-10 water molecules, J. Phys. Chem. A, 2010, 114, 4266–4271 CrossRef CAS PubMed.
- J. Herb, A. B. Nadykto and F. Q. Yu, Large ternary hydrogen-bonded pre-nucleation clusters in the Earth's atmosphere, Chem. Phys. Lett., 2011, 518, 7–14 CrossRef CAS.
- J. Elm, M. Bilde and K. V. Mikkelsen, Assessment of Density Functional Theory in Predicting Structures and Free Energies of Reaction of Atmospheric Prenucleation Clusters, J. Chem. Theory Comput., 2012, 8, 2071–2077 CrossRef CAS PubMed.
- C. Kuang, M. Chen, J. Zhao, J. Smith, P. H. McMurry and J. Wang, Size and time-resolved growth rate measurements of 1 to 5 nm freshly formed atmospheric nuclei, Atmos. Chem. Phys., 2012, 12, 3573–3589 CrossRef CAS.
- P. M. Winkler, J. Ortega, T. Karl, L. Cappellin, H. R. Friedli, K. Barsanti, P. H. McMurry and J. N. Smith, Identification of the biogenic compounds responsible for size-dependent nanoparticle growth, Geophys. Res. Lett., 2012, 39, L20815 CrossRef.
- D. E. Husar, B. Temelso, A. L. Ashworth and G. C. Shields, Hydration of the bisulfate ion: atmospheric implications, J. Phys. Chem. A, 2012, 116, 5151–5163 CrossRef CAS PubMed.
- B. Temelso, T. E. Morrell, R. M. Shields, M. A. Allodi, E. K. Wood, K. N. Kirschner, T. C. Castonguay, K. A. Archer and G. C. Shields, Quantum mechanical study of sulfuric acid hydration: atmospheric implications, J. Phys. Chem. A, 2012, 116, 2209–2224 CrossRef CAS PubMed.
- B. Temelso, T. N. Phan and G. C. Shields, Computational study of the hydration of sulfuric acid dimers: implications for acid dissociation and aerosol formation, J. Phys. Chem. A, 2012, 116, 9745–9758 CrossRef CAS PubMed.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Nucleation and growth of nanoparticles in the atmosphere, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS PubMed.
- J. Almeida, S. Schobesberger, A. Kurten, I. K. Ortega, O. Kupiainen-Maatta, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, N. M. Donahue, A. Downard, E. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, H. Henschel, T. Jokinen, H. Junninen, M. Kajos, J. Kangasluoma, H. Keskinen, A. Kupc, T. Kurten, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, M. Leiminger, J. Leppa, V. Loukonen, V. Makhmutov, S. Mathot, M. J. McGrath, T. Nieminen, T. Olenius, A. Onnela, T. Petaja, F. Riccobono, I. Riipinen, M. Rissanen, L. Rondo, T. Ruuskanen, F. D. Santos, N. Sarnela, S. Schallhart, R. Schnitzhofer, J. H. Seinfeld, M. Simon, M. Sipila, Y. Stozhkov, F. Stratmann, A. Tome, J. Trostl, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Virtanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, C. Williamson, D. Wimmer, P. Ye, T. Yli-Juuti, K. S. Carslaw, M. Kulmala, J. Curtius, U. Baltensperger, D. R. Worsnop, H. Vehkamaki and J. Kirkby, Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere, Nature, 2013, 502, 359–363 CrossRef CAS PubMed.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petaja, M. Sipila, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Jarvinen, M. Aijala, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkila, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin III, J. Duplissy, H. Vehkamaki, J. Back, A. Kortelainen, I. Riipinen, T. Kurten, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. Lehtinen, A. Laaksonen, V. M. Kerminen and D. R. Worsnop, Direct observations of atmospheric aerosol nucleation, Science, 2013, 339, 943–946 CrossRef CAS PubMed.
- Y. Zhang, I. R. Turkmen, B. Wassermann, A. Erko and E. Ruhl, Structural motifs of pre-nucleation clusters, J. Chem. Phys., 2013, 139, 134506 CrossRef CAS PubMed.
- J. Elm, M. Bilde and K. V. Mikkelsen, Assessment of binding energies of atmospherically relevant clusters, Phys. Chem. Chem. Phys., 2013, 15, 16442–16445 RSC.
- J. Elm, M. Fard, M. Bilde and K. V. Mikkelsen, Interaction of glycine with common atmospheric nucleation precursors, J. Phys. Chem. A, 2013, 117, 12990–12997 CrossRef CAS PubMed.
- D. J. Bustos, B. Temelso and G. C. Shields, Hydration of the sulfuric acid-methylamine complex and implications for aerosol formation, J. Phys. Chem. A, 2014, 118, 7430–7441 CrossRef CAS PubMed.
- K. Lehtipalo, L. Rondo, J. Kontkanen, S. Schobesberger, T. Jokinen, N. Sarnela, A. Kurten, S. Ehrhart, A. Franchin, T. Nieminen, F. Riccobono, M. Sipila, T. Yli-Juuti, J. Duplissy, A. Adamov, L. Ahlm, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, A. J. Downard, E. M. Dunne, R. C. Flagan, R. Guida, J. Hakala, A. Hansel, W. Jud, J. Kangasluoma, V. M. Kerminen, H. Keskinen, J. Kim, J. Kirkby, A. Kupc, O. Kupiainen-Maatta, A. Laaksonen, M. J. Lawler, M. Leiminger, S. Mathot, T. Olenius, I. K. Ortega, A. Onnela, T. Petaja, A. Praplan, M. P. Rissanen, T. Ruuskanen, F. D. Santos, S. Schallhart, R. Schnitzhofer, M. Simon, J. N. Smith, J. Trostl, G. Tsagkogeorgas, A. Tome, P. Vaattovaara, H. Vehkamaki, A. E. Vrtala, P. E. Wagner, C. Williamson, D. Wimmer, P. M. Winkler, A. Virtanen, N. M. Donahue, K. S. Carslaw, U. Baltensperger, I. Riipinen, J. Curtius, D. R. Worsnop and M. Kulmala, The effect of acid-base clustering and ions on the growth of atmospheric nano-particles, Nat. Commun., 2016, 7, 11594 CrossRef CAS PubMed.
- J. Trostl, W. K. Chuang, H. Gordon, M. Heinritzi, C. Yan, U. Molteni, L. Ahlm, C. Frege, F. Bianchi, R. Wagner, M. Simon, K. Lehtipalo, C. Williamson, J. S. Craven, J. Duplissy, A. Adamov, J. Almeida, A. K. Bernhammer, M. Breitenlechner, S. Brilke, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, M. Gysel, A. Hansel, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, H. Keskinen, J. Kim, M. Krapf, A. Kurten, A. Laaksonen, M. Lawler, M. Leiminger, S. Mathot, O. Mohler, T. Nieminen, A. Onnela, T. Petaja, F. M. Piel, P. Miettinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Sipila, J. N. Smith, G. Steiner, A. Tome, A. Virtanen, A. C. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, K. S. Carslaw, J. Curtius, J. Dommen, J. Kirkby, M. Kulmala, I. Riipinen, D. R. Worsnop, N. M. Donahue and U. Baltensperger, The role of low-volatility organic compounds in initial particle growth in the atmosphere, Nature, 2016, 533, 527–531 CrossRef CAS PubMed.
- J. Elm, C. N. Jen, T. Kurten and H. Vehkamaki, Strong Hydrogen Bonded Molecular Interactions between Atmospheric Diamines and Sulfuric Acid, J. Phys. Chem. A, 2016, 120, 3693–3700 CrossRef CAS PubMed.
- F. Bianchi, J. Trostl, H. Junninen, C. Frege, S. Henne, C. R. Hoyle, U. Molteni, E. Herrmann, A. Adamov, N. Bukowiecki, X. Chen, J. Duplissy, M. Gysel, M. Hutterli, J. Kangasluoma, J. Kontkanen, A. Kurten, H. E. Manninen, S. Munch, O. Perakyla, T. Petaja, L. Rondo, C. Williamson, E. Weingartner, J. Curtius, D. R. Worsnop, M. Kulmala, J. Dommen and U. Baltensperger, New particle formation in the free troposphere: a question of chemistry and timing, Science, 2016, 352, 1109–1112 CrossRef CAS PubMed.
- H. Gordon, K. Sengupta, A. Rap, J. Duplissy, C. Frege, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Trostl, T. Nieminen, I. K. Ortega, R. Wagner, E. M. Dunne, A. Adamov, A. Amorim, A. K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. S. Craven, A. Dias, S. Ehrhart, L. Fischer, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, J. Kirkby, M. Krapf, A. Kurten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, S. A. Monks, A. Onnela, O. Perakyla, F. Piel, T. Petaja, A. P. Praplan, K. J. Pringle, N. A. Richards, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, S. Sharma, M. Sipila, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tome, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, J. Curtius and K. S. Carslaw, Reduced anthropogenic aerosol radiative forcing caused by biogenic new particle formation, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12053–12058 CrossRef CAS PubMed.
- J. Kirkby, J. Duplissy, K. Sengupta, C. Frege, H. Gordon, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Trostl, T. Nieminen, I. K. Ortega, R. Wagner, A. Adamov, A. Amorim, A. K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. Craven, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, M. Krapf, A. Kurten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, A. Onnela, O. Perakyla, F. Piel, T. Petaja, A. P. Praplan, K. Pringle, A. Rap, N. A. Richards, I. Riipinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, M. Sipila, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tome, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, K. S. Carslaw and J. Curtius, Ion-induced nucleation of pure biogenic particles, Nature, 2016, 533, 521–526 CrossRef CAS PubMed.
- J. Elm, Elucidating the Limiting Steps in Sulfuric Acid-Base New Particle Formation, J. Phys. Chem. A, 2017, 121, 8288–8295 CrossRef CAS PubMed.
- H.-B. Xie, J. Elm, R. Halonen, N. Myllys, T. Kurtén, M. Kulmala and H. Vehkamäki, The atmospheric fate of monoethanolamine: enhancing new particle formation of sulfuric acid as an important removal process, Environ. Sci. Technol., 2017, 51, 8422–8431 CrossRef CAS PubMed.
- H. H. Chen, S. Chee, M. J. Lawler, K. C. Barsanti, B. M. Wong and J. N. Smith, Size resolved chemical composition of nanoparticles from reactions of sulfuric acid with ammonia and dimethylamine, Aerosol Sci. Technol., 2018, 52, 1120–1133 CrossRef CAS.
- M. J. Lawler, M. P. Rissanen, M. Ehn, R. L. Mauldin, N. Sarnela, M. Sipila and J. N. Smith, Evidence for Diverse Biogeochemical Drivers of Boreal Forest New Particle Formation, Geophys. Res. Lett., 2018, 45, 2038–2046 CrossRef.
- L. Pichelstorfer, D. Stolzenburg, J. Ortega, T. Karl, H. Kokkola, A. Laakso, K. E. J. Lehtinen, J. N. Smith, P. H. McMurry and P. M. Winkler, Resolving nanoparticle growth mechanisms from size- and time-dependent growth rate analysis, Atmos. Chem. Phys., 2018, 18, 1307–1323 CrossRef CAS.
- N. Myllys, T. Ponkkonen, M. Passananti, J. Elm, H. Vehkamaki and T. Olenius, Guanidine: A Highly Efficient Stabilizer in Atmospheric New-Particle Formation, J. Phys. Chem. A, 2018, 122, 4717–4729 CrossRef CAS PubMed.
- S. E. Waller, Y. Yang, E. Castracane, E. E. Racow, J. J. Kreinbihl, K. A. Nickson and C. J. Johnson, The Interplay Between Hydrogen Bonding and Coulombic Forces in Determining the Structure of Sulfuric Acid-Amine Clusters, J. Phys. Chem. Lett., 2018, 9, 1216–1222 CrossRef CAS PubMed.
- Y. Yang, S. E. Waller, J. J. Kreinbihl and C. J. Johnson, Direct Link between Structure and Hydration in Ammonium and Aminium Bisulfate Clusters Implicated in Atmospheric New Particle Formation, J. Phys. Chem. Lett., 2018, 9, 5647–5652 CrossRef CAS PubMed.
- Y. Yang and C. J. Johnson, Hydration motifs of ammonium bisulfate clusters of relevance to atmospheric new particle formation, Faraday Discuss., 2019, 217, 47–66 RSC.
- F. Ma, H. B. Xie, J. Elm, J. Shen, J. Chen and H. Vehkamaki, Piperazine Enhancing Sulfuric Acid-Based New Particle Formation: Implications for the Atmospheric Fate of Piperazine, Environ. Sci. Technol., 2019, 53, 8785–8795 CrossRef CAS PubMed.
- J. Shen, H. B. Xie, J. Elm, F. Ma, J. Chen and H. Vehkamaki, Methanesulfonic Acid-driven New Particle Formation Enhanced by Monoethanolamine: A Computational Study, Environ. Sci. Technol., 2019, 53, 14387–14397 CrossRef PubMed.
- S. Chee, N. Myllys, K. C. Barsanti, B. M. Wong and J. N. Smith, An Experimental and Modeling Study of Nanoparticle Formation and Growth from Dimethylamine and Nitric Acid, J. Phys. Chem. A, 2019, 123, 5640–5648 CrossRef CAS PubMed.
- N. Myllys, S. Chee, T. Olenius, M. Lawler and J. Smith, Molecular-Level Understanding of Synergistic Effects in Sulfuric Acid-Amine-Ammonia Mixed Clusters, J. Phys. Chem. A, 2019, 123, 2420–2425 CrossRef CAS PubMed.
- N. Myllys, J. Kubecka, V. Besel, D. Alfaouri, T. Olenius, J. N. Smith and M. Passananti, Role of base strength, cluster structure and charge in sulfuric-acid-driven particle formation, Atmos. Chem. Phys., 2019, 19, 9753–9768 CrossRef CAS.
- N. Myllys, T. Ponkkonen, S. Chee and J. Smith, Enhancing Potential of Trimethylamine Oxide on Atmospheric Particle Formation, Atmosphere, 2019, 11, 35 CrossRef.
- M. Wang, W. Kong, R. Marten, X. C. He, D. Chen, J. Pfeifer, A. Heitto, J. Kontkanen, L. Dada, A. Kurten, T. Yli-Juuti, H. E. Manninen, S. Amanatidis, A. Amorim, R. Baalbaki, A. Baccarini, D. M. Bell, B. Bertozzi, S. Brakling, S. Brilke, L. C. Murillo, R. Chiu, B. Chu, L. P. De Menezes, J. Duplissy, H. Finkenzeller, L. G. Carracedo, M. Granzin, R. Guida, A. Hansel, V. Hofbauer, J. Krechmer, K. Lehtipalo, H. Lamkaddam, M. Lampimaki, C. P. Lee, V. Makhmutov, G. Marie, S. Mathot, R. L. Mauldin, B. Mentler, T. Muller, A. Onnela, E. Partoll, T. Petaja, M. Philippov, V. Pospisilova, A. Ranjithkumar, M. Rissanen, B. Rorup, W. Scholz, J. Shen, M. Simon, M. Sipila, G. Steiner, D. Stolzenburg, Y. J. Tham, A. Tome, A. C. Wagner, D. S. Wang, Y. Wang, S. K. Weber, P. M. Winkler, P. J. Wlasits, Y. Wu, M. Xiao, Q. Ye, M. Zauner-Wieczorek, X. Zhou, R. Volkamer, I. Riipinen, J. Dommen, J. Curtius, U. Baltensperger, M. Kulmala, D. R. Worsnop, J. Kirkby, J. H. Seinfeld, I. El-Haddad, R. C. Flagan and N. M. Donahue, Rapid growth of new atmospheric particles by nitric acid and ammonia condensation, Nature, 2020, 581, 184–189 CrossRef CAS PubMed.
- J. Elm, J. Kubecka, V. Besel, M. J. Jaaskelainen, R. Halonen, T. Kurten and H. Vehkamaki, Modeling the formation and growth of atmospheric molecular clusters: A review, J. Aerosol Sci., 2020, 149, 105621 CrossRef CAS.
- A. Leonardi, H. M. Ricker, A. G. Gale, B. T. Ball, T. T. Odbadrakh, G. C. Shields and J. G. Navea, Particle formation and surface processes on atmospheric aerosols: A review of applied quantum chemical calculations, Int. J. Quantum Chem., 2020, 120, e26350 CrossRef CAS.
- T. T. Odbadrakh, A. G. Gale, B. T. Ball, B. Temelso and G. C. Shields, Computation of Atmospheric Concentrations of Molecular Clusters from ab initio Thermochemistry, J. Visualized Exp., 2020, 158, e60964 Search PubMed.
- B. T. Ball, S. Vanovac, T. T. Odbadrakh and G. C. Shields, Monomers of Glycine and Serine Have a Limited Ability to Hydrate in the Atmosphere, J. Phys. Chem. A, 2021, 125, 8454–8467 CrossRef CAS PubMed.
- J. J. Kreinbihl, N. C. Frederiks and C. J. Johnson, Hydration motifs of ammonium bisulfate clusters show complex temperature dependence, J. Chem. Phys., 2021, 154, 014304 CrossRef CAS PubMed.
- J. Elm, Clusteromics I: Principles, Protocols, and Applications to Sulfuric Acid-Base Cluster Formation, ACS Omega, 2021, 6, 7804–7814 CrossRef CAS PubMed.
- J. Elm, Clusteromics II: Methanesulfonic Acid-Base Cluster Formation, ACS Omega, 2021, 6, 17035–17044 CrossRef CAS PubMed.
- H. B. Xie and J. Elm, Tri-Base Synergy in Sulfuric Acid-Base Clusters, Atmosphere, 2021, 12, 1260 CrossRef CAS.
- S. H. Jathar, C. D. Cappa, Y. He, J. R. Pierce, W. Chuang, K. R. Bilsback, J. H. Seinfeld, R. A. Zaveri and M. Shrivastava, A computationally efficient model to represent the chemistry, thermodynamics, and microphysics of secondary organic aerosols (simpleSOM): model development and application to α-pinene SOA, Environ. Sci.: Atmos., 2021, 1, 372–394 CAS.
- S. Chee, K. Barsanti, J. N. Smith and N. Myllys, A predictive model for salt nanoparticle formation using heterodimer stability calculations, Atmos. Chem. Phys., 2021, 21, 11637–11654 CrossRef CAS.
- N. Myllys, D. Myers, S. Chee and J. N. Smith, Molecular properties affecting the hydration of acid-base clusters, Phys. Chem. Chem. Phys., 2021, 23, 13106–13114 RSC.
- X. Zhang, S. Tan, X. Chen and S. Yin, Computational chemistry of cluster: Understanding the mechanism of atmospheric new particle formation at the molecular level, Chemosphere, 2022, 308, 136109 CrossRef CAS PubMed.
- J. N. Smith, D. C. Draper, S. Chee, M. Dam, H. Glicker, D. Myers, A. E. Thomas, M. J. Lawler and N. Myllys, Atmospheric clusters to nanoparticles: recent progress and challenges in closing the gap in chemical composition, J. Aerosol Sci., 2021, 153, 105733 CrossRef CAS.
- C. Li and R. Signorell, Understanding vapor nucleation on the molecular level: a review, J. Aerosol Sci., 2021, 153, 105676 CrossRef CAS.
- S. E. Harold, C. J. Bready, L. A. Juechter, L. A. Kurfman, S. Vanovac, V. R. Fowler, G. E. Mazaleski, T. T. Odbadrakh and G. C. Shields, Hydrogen-Bond Topology Is More Important Than Acid/Base Strength in Atmospheric Prenucleation Clusters, J. Phys. Chem. A, 2022, 126, 1718–1728 CrossRef CAS PubMed.
- R. J. Zhang, J. W. Shen, H. B. Xie, J. W. Chen and J. Elm, The role of organic acids in new particle formation from methanesulfonic acid and methylamine, Atmos. Chem. Phys., 2022, 22, 2639–2650 CrossRef CAS.
- C. J. Bready, S. Vanovac, T. T. Odbadrakh and G. C. Shields, Amino Acids Compete with Ammonia in Sulfuric Acid-Based Atmospheric Aerosol Prenucleation: The Case of Glycine and Serine, J. Phys. Chem. A, 2022, 126, 5195–5206 CrossRef CAS PubMed.
- A. Afzalifar, G. C. Shields, V. R. Fowler and R. H. A. Ras, Probing the Free Energy of Small Water Clusters: Revisiting Classical Nucleation Theory, J. Phys. Chem. Lett., 2022, 13, 8038–8046 CrossRef CAS PubMed.
- Y. Liu, H. B. Xie, F. Ma, J. Chen and J. Elm, Amine-Enhanced Methanesulfonic Acid-Driven Nucleation: Predictive Model and Cluster Formation Mechanism, Environ. Sci. Technol., 2022, 56, 7751–7760 CrossRef CAS PubMed.
- Z. Fu, H. B. Xie, J. Elm, Y. Liu, Z. Fu and J. Chen, Atmospheric Autoxidation of Organophosphate Esters, Environ. Sci. Technol., 2022, 56, 6944–6955 CrossRef CAS PubMed.
- J. Elm, Clusteromics III: Acid Synergy in Sulfuric Acid-Methanesulfonic Acid-Base Cluster Formation, ACS Omega, 2022, 7, 15206–15214 CrossRef CAS PubMed.
- C. J. Bready, V. R. Fowler, L. A. Juechter, L. A. Kurfman, G. E. Mazaleski and G. C. Shields, The driving effects of common atmospheric molecules for formation of prenucleation clusters: the case of sulfuric acid, formic acid, nitric acid, ammonia, and dimethyl amine, Environ. Sci.: Atmos., 2022, 2, 1469–1486 CAS.
- J. Elm, D. Ayoubi, M. Engsvang, A. B. Jensen, Y. Knattrup, J. Kubecka, C. J. Bready, V. R. Fowler, S. E. Harold, O. M. Longsworth and G. C. Shields, Quantum Chemical Modeling of Organic Enhanced Atmospheric Nucleation: A Critical Review, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2023, e1662 CrossRef.
- P. Sebastianelli, P. M. Cometto and R. G. Pereyra, Systematic Characterization of Gas Phase Binary Pre-Nucleation Complexes Containing H(2)SO(4) + X, [ X = NH(3), (CH(3))NH(2), (CH(3))(2)NH, (CH(3))(3)N, H(2)O, (CH(3))OH, (CH(3))(2)O, HF, CH(3)F, PH(3), (CH(3))PH(2), (CH(3))(2)PH, (CH(3))(3)P, H(2)S, (CH(3))SH, (CH(3))(2)S, HCl, (CH(3))Cl)]. A Computational Study, J. Phys. Chem. A, 2018, 122, 2116–2128 CrossRef CAS PubMed.
- X. Wang, D. J. Jacob, S. D. Eastham, M. P. Sulprizio, L. Zhu, Q. J. Chen, B. Alexander, T. Sherwen, M. J. Evans, B. H. Lee, J. D. Haskins, F. D. Lopez-Hilfiker, J. A. Thornton, G. L. Huey and H. Liao, The role of chlorine in global tropospheric chemistry, Atmos. Chem. Phys., 2019, 19, 3981–4003 CrossRef CAS.
- J. M. Lobert, W. C. Keene, J. A. Logan and R. Yevich, Global chlorine emissions from biomass burning: Reactive Chlorine Emissions Inventory, J. Geophys. Res.: Atmos., 1999, 104, 8373–8389 CrossRef CAS.
- A. McCulloch, M. L. Aucott, C. M. Benkovitz, T. E. Graedel, G. Kleiman, P. M. Midgley and Y. F. Li, Global emissions of hydrogen chloride and chloromethane from coal combustion, incineration and industrial activities: Reactive Chlorine Emissions Inventory, J. Geophys. Res.: Atmos., 1999, 104, 8391–8403 CrossRef CAS.
- S. T. Zhai, X. Wang, J. R. McConnell, L. Geng, J. Cole-Dai, M. Sigl, N. Chellman, T. Sherwen, R. Pound, K. Fujita, S. Hattori, J. M. Moch, L. Zhu, M. Evans, M. Legrand, P. F. Liu, D. Pasteris, Y. C. Chan, L. T. Murray and B. Alexander, Anthropogenic Impacts on Tropospheric Reactive Chlorine Since the Preindustrial, Geophys. Res. Lett., 2021, 48, e2021GL093808 CAS.
- B. J. Finlayson-Pitts, M. J. Ezell and J. N. Pitts, Formation of chemically active chlorine compounds by reactions of atmospheric NaCl particles with gaseous N2O5 and ClONO2, Nature, 1989, 337, 241–244 CrossRef CAS.
- M. G. Bryukov, B. Dellinger and V. D. Knyazev, Kinetics of the gas-phase reaction of OH with HCl, J. Phys. Chem. A, 2006, 110, 936–943 CrossRef CAS PubMed.
- M. S. Choi, X. Qiu, J. Zhang, S. Wang, X. Li, Y. Sun, J. Chen and Q. Ying, Study of Secondary Organic Aerosol Formation from Chlorine Radical-Initiated Oxidation of Volatile Organic Compounds in a Polluted Atmosphere Using a 3D Chemical Transport Model, Environ. Sci. Technol., 2020, 54, 13409–13418 CrossRef CAS PubMed.
- J. M. Dieterich and B. Hartke, OGOLEM: global cluster structure optimisation for arbitrary mixtures of flexible molecules. A multiscaling, object-oriented approach, Mol. Phys., 2010, 108, 279–291 CrossRef CAS.
- B. Hartke, Global optimization, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 879–887 CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB-An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Grimme, Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- L. A. Kurfman, T. T. Odbadrakh and G. C. Shields, Calculating Reliable Gibbs Free Energies for Formation of Gas-Phase Clusters that Are Critical for Atmospheric Chemistry: (H(2)SO(4))(3), J. Phys. Chem. A, 2021, 125, 3169–3176 CrossRef CAS PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01, Wallingford, CT, 2016 Search PubMed.
- J. D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- F. Neese, Prediction of molecular properties and molecular spectroscopy with density functional theory: From fundamental theory to exchange-coupling, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- F. Neese, A. Hansen and D. G. Liakos, Efficient and accurate approximations to the local coupled cluster singles doubles method using a truncated pair natural orbital basis, J. Chem. Phys., 2009, 131, 064103 CrossRef PubMed.
- F. Neese, F. Wennmohs and A. Hansen, Efficient and accurate local approximations to coupled-electron pair approaches: an attempt to revive the pair natural orbital method, J. Chem. Phys., 2009, 130, 114108 CrossRef PubMed.
- A. Hansen, D. G. Liakos and F. Neese, Efficient and accurate local single reference correlation methods for high-spin open-shell molecules using pair natural orbitals, J. Chem. Phys., 2011, 135, 214102 CrossRef PubMed.
- D. G. Liakos and F. Neese, Improved correlation energy extrapolation schemes based on local pair natural orbital methods, J. Phys. Chem. A, 2012, 116, 4801–4816 CrossRef CAS PubMed.
- F. Neese, The ORCA Program System, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- C. Riplinger and F. Neese, An efficient and near linear scaling pair natural orbital based local coupled cluster method, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, Natural triple excitations in local coupled cluster calculations with pair natural orbitals, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- D. G. Liakos and F. Neese, Is it possible to obtain coupled cluster quality energies at near density functional theory cost? Domain-based local pair natural orbital coupled cluster vs. modern density functional theory, J. Chem. Theory Comput., 2015, 11, 4054–4063 CrossRef CAS PubMed.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. Martin and F. Neese, Exploring the Accuracy Limits of Local Pair Natural Orbital Coupled-Cluster Theory, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, SparseMaps - A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- F. Pavosevic, C. Peng, P. Pinski, C. Riplinger, F. Neese and E. F. Valeev, SparseMaps-A systematic infrastructure for reduced scaling electronic structure methods. V. Linear scaling explicitly correlated coupled-cluster method with pair natural orbitals, J. Chem. Phys., 2017, 146, 174108 CrossRef PubMed.
- M. Sparta, M. Retegan, P. Pinski, C. Riplinger, U. Becker and F. Neese, Multilevel Approaches within the Local Pair Natural Orbital Framework, J. Chem. Theory Comput., 2017, 13, 3198–3207 CrossRef CAS PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, Communication: an improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)], J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- A. Altun, F. Neese and G. Bistoni, Extrapolation to the Limit of a Complete Pair Natural Orbital Space in Local Coupled-Cluster Calculations, J. Chem. Theory Comput., 2020, 16, 6142–6149 CrossRef CAS PubMed.
- D. G. Liakos, Y. Guo and F. Neese, Comprehensive Benchmark Results for the Domain Based Local Pair Natural Orbital Coupled Cluster Method (DLPNO-CCSD(T)) for Closed- and Open-Shell Systems, J. Phys. Chem. A, 2020, 124, 90–100 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- K. A. Peterson, D. E. Woon and T. H. Dunning, Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H+H2→H2+H reaction, J. Chem. Phys., 1994, 100, 7410–7415 CrossRef CAS.
- A. K. Wilson, T. van Mourik and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. VI. Sextuple zeta correlation consistent basis sets for boron through neon, J. Mol. Struct.: THEOCHEM, 1996, 388, 339–349 CrossRef CAS.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, Computational Thermochemistry: Scale Factor Databases and Scale Factors for Vibrational Frequencies Obtained from Electronic Model Chemistries, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
-
S. Kanchanakungwankul, J. L. Bao, J. Zheng, I. M. Alecu, B. J. Lynch and D. G. Truhlar, Database of frequency scale factors for electronic model chemistries-Version 5, 2021, https://comp.chem.umn.edu/freqscale/210722_Database_of_Freq_Scale_Factors_v5.pdf Search PubMed.
-
K. K. Irikura, THERMO.PL, NIST, 2002 Search PubMed.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
-
J. H. Seinfeld and S. N. Pandis, in Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, Wiley, Hoboken, NJ, 3rd edn, 2016 Search PubMed.
- S. Aloisio, P. E. Hintze and V. Vaida, The hydration of formic acid, J. Phys. Chem. A, 2002, 106, 363–370 CrossRef CAS.
- K. Acker, D. Moller, R. Auel, W. Wieprecht and D. Kalass, Concentrations of nitrous acid, nitric acid, nitrite and nitrate in the gas and aerosol phase at a site in the emission zone during ESCOMPTE 2001 experiment, Atmos. Res., 2005, 74, 507–524 CrossRef CAS.
- S. Preunkert, M. Legrand, B. Jourdain and I. Dombrowski-Etchevers, Acidic gases (HCOOH, CH3COOH, HNO3, HCl, and SO2) and related aerosol species at a high mountain Alpine site (4360 m elevation) in Europe, J. Geophys. Res.: Atmos., 2007, 112, D23S12 CrossRef.
- X. L. Ge, A. S. Wexler and S. L. Clegg, Atmospheric amines - Part II. Thermodynamic properties and gas/particle partitioning, Atmos. Environ., 2011, 45, 561–577 CrossRef CAS.
- X. L. Ge, A. S. Wexler and S. L. Clegg, Atmospheric amines - Part I. A review, Atmos. Environ., 2011, 45, 524–546 CrossRef CAS.
- S. N. Behera, R. Betha and R. Balasubramanian, Insights into Chemical Coupling among Acidic Gases, Ammonia and Secondary Inorganic Aerosols, Aerosol Air Qual. Res., 2013, 13, 1282–1296 CrossRef CAS.
- B. J. Su, T. Wang, G. H. Zhang, Y. Liang, C. Lv, Y. H. Hu, L. Li, Z. Zhou, X. M. Wang and X. H. Bi, A review of atmospheric aging of sea spray aerosols: potential factors affecting chloride depletion, Atmos. Environ., 2022, 290, 119365 CrossRef CAS.
- S. Solomon, K. Stone, P. Yu, D. M. Murphy, D. Kinnison, A. R. Ravishankara and P. Wang, Chlorine activation and enhanced ozone depletion induced by wildfire aerosol, Nature, 2023, 615, 259–264 CrossRef CAS PubMed.
- A. Gutberlet, G. Schwaab, O. Birer, M. Masia, A. Kaczmarek, H. Forbert, M. Havenith and D. Marx, Aggregation-induced dissociation of HCl(H2O)4 below 1 K: the smallest droplet of acid, Science, 2009, 324, 1545–1548 CrossRef CAS PubMed.
- A. Vargas-Caamal, J. L. Cabellos, F. Ortiz-Chi, H. S. Rzepa, A. Restrepo and G. Merino, How Many Water Molecules Does it Take to Dissociate HCl?, Chemistry, 2016, 22, 2812–2818 CrossRef CAS PubMed.
- E. P. L. Hunter and S. G. Lias, Evaluated Gas Phase Basicities and Proton Affinities of Molecules: An Update, J. Phys. Chem. Ref. Data, 1998, 27, 413–656 CrossRef CAS.
- F. Yu and G. Luo, Modeling of gaseous methylamines in the global atmosphere: impacts of oxidation and aerosol uptake, Atmos. Chem. Phys., 2014, 14, 12455–12464 CrossRef.
- A. B. Nadykto, J. Herb, F. Q. Yu and Y. S. Xu, Enhancement in the production of nucleating clusters due to dimethylamine and large uncertainties in the thermochemistry of amine-enhanced nucleation, Chem. Phys. Lett., 2014, 609, 42–49 CrossRef CAS.
- B. Temelso, E. F. Morrison, D. L. Speer, B. C. Cao, N. Appiah-Padi, G. Kim and G. C. Shields, Effect of Mixing Ammonia and Alkylamines on Sulfate Aerosol Formation, J. Phys. Chem. A, 2018, 122, 1612–1622 CrossRef CAS PubMed.
- J. W. DePalma, D. J. Doren and M. V. Johnston, Formation and growth of molecular clusters containing sulfuric acid, water, ammonia, and dimethylamine, J. Phys. Chem. A, 2014, 118, 5464–5473 CrossRef CAS PubMed.
- Y. Knattrup and J. Elm, Clusteromics IV: The Role of Nitric Acid in Atmospheric Cluster Formation, ACS Omega, 2022, 7, 31551–31560 CrossRef CAS PubMed.
- D. Ayoubi, Y. Knattrup and J. Elm, Clusteromics V.: Organic Enhanced Atmospheric Cluster Formation, ACS Omega, 2023, 8, 9621–9629 CrossRef CAS PubMed.
-
G. C. Shields, The Molecular Education and Research Consortium in Undergraduate Computational Chemistry (MERCURY): Twenty Years of Exceptional Success Supporting Undergraduate Research and Inclusive Excellence, Spur-Scholarship and Practice of Undergraduate Research, 2019, vol. 3, pp. 5–15 Search PubMed.
- G. C. Shields, Twenty years of exceptional success: The molecular education and research consortium in undergraduate computational chemistry (MERCURY), Int. J. Quantum Chem., 2020, 120, e26274 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Figures of minimum energy structures, sequential hydration tables, DFT and DLPNO-CCSD(T) energy tables, optimized structures, derivation of CBS extrapolation formula, and example calculations of stepwise energies. See DOI: https://doi.org/10.1039/d3ea00087g |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Conor J.
Bready
,
Conor J.
Bready
 and
George C.
Shields
and
George C.
Shields
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 global optimizations. These structures were then optimized using the GFN2-xTB semi-empirical method, resulting in a final pool of 1000 or slightly less for each simulation.85–87 To complete this study we simulated 56 systems containing HCl: HCl-W0–3, HCl-A-W0–3, HCl-DMA-W0–3, SA-FA-HCl-W0–3, SA-HCl-A-W0–3, SA-HCl-DMA-W0–3, FA-HCl-A-W0–3, FA-HCl-DMA-W0–3, HCl-A-DMA-W0–3, SA-FA-HCl-A-W0–3, SA-FA-HCl-DMA-W0–3, SA-HCl-A-DMA-W0–3, FA-HCl-A-DMA-W0–3, and SA-FA-HCl-A-DMA-W0–3 systems. Because of the uncertainties that arise from the use of low-level semi-empirical energies,55,88 we used a cut-off energy of 30 kcal mol−1 above the GFN2-xTB global minimum, thus keeping all structures with a possibility of becoming a minimum or close to one at a better level of theory. These extensive sets of GFN2-xTB structures were optimized at the DFT level of theory using the Gaussian 16 Rev. B01 program.89 The ωB97X-D functional90,91 was used with the 6-31++G** basis set92–94 to obtain a final set of DFT structures. The electronic energies of all structures that were within 8 kcal mol−1 of the ωB97X-D global minimum were then recalculated using the domain-based local pair natural orbital coupled cluster (DLPNO-CCSD(T)) method95–111 with singles, doubles, and semi-canonical perturbative triple excitations with three Dunning basis sets,112–115 cc-pVnZ (n = D, T, Q) using ORCA 5.0.1.111 The ωB97X-D frequencies were scaled by a factor of 0.971 to account for some anharmonicity,116,117 then used to estimate the thermodynamic corrections for H°, S°, and G° at a 1 atm standard state and temperatures of 216.65, 273.15, and 298.15 K using the THERMO.pl script118 from the National Institute of Science and Technology. The electronic energies from the three DLPNO-CCSD(T) calculations were used in a 4–5 inverse polynomial complete basis set extrapolation,119 and combined with the scaled DFT thermodynamic corrections to calculate the final Gibbs free energies. The entire methodology is depicted in Fig. 1. Structures that don't contain HCl were taken from our previous papers,66,73,88 and more explanation of our methodologies can be found in our recent review.74 Once all the G° values were calculated for the individual clusters, the ΔG° values of binding were calculated as follows:
000 global optimizations. These structures were then optimized using the GFN2-xTB semi-empirical method, resulting in a final pool of 1000 or slightly less for each simulation.85–87 To complete this study we simulated 56 systems containing HCl: HCl-W0–3, HCl-A-W0–3, HCl-DMA-W0–3, SA-FA-HCl-W0–3, SA-HCl-A-W0–3, SA-HCl-DMA-W0–3, FA-HCl-A-W0–3, FA-HCl-DMA-W0–3, HCl-A-DMA-W0–3, SA-FA-HCl-A-W0–3, SA-FA-HCl-DMA-W0–3, SA-HCl-A-DMA-W0–3, FA-HCl-A-DMA-W0–3, and SA-FA-HCl-A-DMA-W0–3 systems. Because of the uncertainties that arise from the use of low-level semi-empirical energies,55,88 we used a cut-off energy of 30 kcal mol−1 above the GFN2-xTB global minimum, thus keeping all structures with a possibility of becoming a minimum or close to one at a better level of theory. These extensive sets of GFN2-xTB structures were optimized at the DFT level of theory using the Gaussian 16 Rev. B01 program.89 The ωB97X-D functional90,91 was used with the 6-31++G** basis set92–94 to obtain a final set of DFT structures. The electronic energies of all structures that were within 8 kcal mol−1 of the ωB97X-D global minimum were then recalculated using the domain-based local pair natural orbital coupled cluster (DLPNO-CCSD(T)) method95–111 with singles, doubles, and semi-canonical perturbative triple excitations with three Dunning basis sets,112–115 cc-pVnZ (n = D, T, Q) using ORCA 5.0.1.111 The ωB97X-D frequencies were scaled by a factor of 0.971 to account for some anharmonicity,116,117 then used to estimate the thermodynamic corrections for H°, S°, and G° at a 1 atm standard state and temperatures of 216.65, 273.15, and 298.15 K using the THERMO.pl script118 from the National Institute of Science and Technology. The electronic energies from the three DLPNO-CCSD(T) calculations were used in a 4–5 inverse polynomial complete basis set extrapolation,119 and combined with the scaled DFT thermodynamic corrections to calculate the final Gibbs free energies. The entire methodology is depicted in Fig. 1. Structures that don't contain HCl were taken from our previous papers,66,73,88 and more explanation of our methodologies can be found in our recent review.74 Once all the G° values were calculated for the individual clusters, the ΔG° values of binding were calculated as follows:

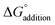 value along with estimates of initial concentrations of the monomers at a given temperature. For these simulations, the top of the troposphere is defined as 217 K while the bottom of the troposphere is 298 K, and estimates for the monomer concentrations are taken from the literature for 298 K, and reduced by a factor of 1000 at 217 K. We used a water concentration of 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere.120 Initial monomer concentrations from the literature22,120–128 at 298 K were reduced by three orders of magnitude at 217 K to compensate for the reduction of CCN-forming particles in the upper troposphere. This is a rough estimate based on the three orders of magnitude decrease in concentration of water, and we resort to this approximation since experimental concentrations of these monomers in the upper troposphere are difficult to measure. Combining these results with previous work allows for estimates of the most likely pathways for the formation of prenucleation complexes for these common acids and bases. The 56 HCl systems were combined with the relevant SA-FA-NA-A-DMA-W systems previously published73 to complete our analysis. Three caveats on our methodology are important to note.74 First, no search routine can ensure that all of the potential energy surface (PES) for these clusters has been exhaustively explored, so we may have missed the lowest Gibbs free energy structure. Second, in the funnel methodology (Fig. 1), we are computing the CCSD(T) electronic energies on the ωB97X-D geometries, which means we are making the electron correlation corrections on the DFT PES. Third, using the DLPNO routine and scaled harmonic frequencies leads to slightly more positive values. All three of these uncertainties will produce ΔG° values that are more positive than would be obtained if (a) a lower energy cluster is obtained, or if (b) the PES is improved so that it is closer to the CCSD(T) surface than the DFT surface, and if (c) anharmonic frequencies could be obtained instead of harmonic frequencies68 and CCSD(T) electronic energies could be computed directly instead of using the DLPNO routine.74
value along with estimates of initial concentrations of the monomers at a given temperature. For these simulations, the top of the troposphere is defined as 217 K while the bottom of the troposphere is 298 K, and estimates for the monomer concentrations are taken from the literature for 298 K, and reduced by a factor of 1000 at 217 K. We used a water concentration of 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere.120 Initial monomer concentrations from the literature22,120–128 at 298 K were reduced by three orders of magnitude at 217 K to compensate for the reduction of CCN-forming particles in the upper troposphere. This is a rough estimate based on the three orders of magnitude decrease in concentration of water, and we resort to this approximation since experimental concentrations of these monomers in the upper troposphere are difficult to measure. Combining these results with previous work allows for estimates of the most likely pathways for the formation of prenucleation complexes for these common acids and bases. The 56 HCl systems were combined with the relevant SA-FA-NA-A-DMA-W systems previously published73 to complete our analysis. Three caveats on our methodology are important to note.74 First, no search routine can ensure that all of the potential energy surface (PES) for these clusters has been exhaustively explored, so we may have missed the lowest Gibbs free energy structure. Second, in the funnel methodology (Fig. 1), we are computing the CCSD(T) electronic energies on the ωB97X-D geometries, which means we are making the electron correlation corrections on the DFT PES. Third, using the DLPNO routine and scaled harmonic frequencies leads to slightly more positive values. All three of these uncertainties will produce ΔG° values that are more positive than would be obtained if (a) a lower energy cluster is obtained, or if (b) the PES is improved so that it is closer to the CCSD(T) surface than the DFT surface, and if (c) anharmonic frequencies could be obtained instead of harmonic frequencies68 and CCSD(T) electronic energies could be computed directly instead of using the DLPNO routine.74



