Open Access Article
Open Access ArticleAsymmetric chloride-mediated electrochemical process for CO2 removal from oceanwater†
Seoni
Kim
 ac,
Michael P.
Nitzsche
ac,
Michael P.
Nitzsche
 ab,
Simon B.
Rufer
ab,
Simon B.
Rufer
 b,
Jack R.
Lake
b,
Kripa K.
Varanasi
b,
Jack R.
Lake
b,
Kripa K.
Varanasi
 *b and
T. Alan
Hatton
*b and
T. Alan
Hatton
 *a
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: tahatton@mit.edu
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: varanasi@mit.edu
cDepartment of Environmental Science and Engineering, Ewha Womans University, Seoul, 03760, Republic of Korea
First published on 13th February 2023
Abstract
In recent years, the ocean has come to be recognized as a global-scale reservoir for atmospheric CO2. The removal of CO2 from oceanwater is thus considered a compelling approach to reduce ambient CO2 concentrations, and potentially achieve net-negative emissions. As an effective means of oceanic CO2 capture, we report an asymmetric electrochemical system employing bismuth and silver electrodes that can capture and release chloride ions by faradaic reactions upon application of appropriate cell voltages. The difference in reaction stoichiometry between the two electrodes enables an electrochemical system architecture for a chloride-mediated electrochemical pH swing, which can be leveraged for effective removal of CO2 from oceanwater without costly bipolar membranes. With two silver–bismuth systems operating in tandem in a cyclic process, one acidifying the ocean water, and the other regenerating the electrodes through alkalization of the treated stream, CO2 can be continuously removed from simulated oceanwater with a relatively low energy consumption of 122 kJ mol−1, and high electron efficiency.
Broader contextIndustrial emissions of carbon dioxide are wreaking havoc on the environment as the continuing accumulation of CO2 in the atmosphere leads to rising temperatures and disruption of the global climate patterns. To mitigate this problem, in addition to reducing CO2 emissions from point sources, much attention has been given to negative emissions technologies to remove carbon dioxide directly from the ambient environment, where the very dilute levels of CO2 make removal challenging. The total amount of CO2 emissions partitioning into the oceans rivals that retained by the atmosphere, and thus effective means for its removal could augment the other negative emissions technologies to reduce the environmental burden imposed by this greenhouse gas. Approaches to removing CO2 from oceanwater rely on adjusting the water pH from about 8.1 to less than 7 to ensure that the speciation of dissolved inorganic carbon (DIC) from carbonates and bicarbonates is changed to molecular CO2 which can then be stripped off under vacuum. It is desirable that approaches be identified that do not require addition of chemicals, nor lead to parasitic reactions with the formation of undesirable compounds. For this reason, electrochemical systems have been considered as good options for pH swing in oceanwater since, because the reactions are driven by supplying electrons in a controllable manner, we can avoid chemical use and parasitic reactions. Current studies on CO2 removal from oceanwater have used bipolar membrane electrodialysis (BPMED), although the high cost of bipolar membranes might impede the commercialization of the process, and some of these architectures even present risks of toxic redox-couples leaking into the oceanwater. We propose a new approach based solely on electrochemical modulation of the pH to initially release the CO2 and then to alkalize the treated water before it is returned to the ocean. This approach (i) does not require expensive membranes or addition of chemicals, (ii) is easy to deploy, (iii) does not lead to formation of byproducts or secondary streams, and (iv) requires a lower energy input (122 kJ mol−1) than do other approaches, to the best of our knowledge. In addition, a preliminary technoeconomic analysis which suggests that this ocean capture system can be economically feasible. |
Introduction
Industrial emissions of carbon dioxide and other gases are wreaking havoc on the environment as the continuing accumulation of CO2 in the atmosphere leads to rising temperatures and disruption of the global climate patterns.1,2 While much attention has been focused on strategies for mitigation of the global CO2 release of almost 40 Gt per year through capture at point sources followed by geologic storage,3–8 more recently there has been a surge of interest in negative emissions technologies in which the offending gases (currently at an atmospheric concentration of ∼415 ppm9) are removed from the ambient environment itself through approaches such as direct air capture (DAC),10–15 bioenergy with carbon capture and sequestration (BECCS),16–18 and reforestation.19,20The focus on atmospheric accumulation has not yet been matched by a similar drive to reduce CO2 in oceans and other surface waters, which, since the dawn of the industrial era, have acted as large-scale carbon sinks, absorbing 30–40% of anthropogenic CO2 emissions.21,22 The resulting increased acidification of ocean waters has already led to destruction of coral reefs,23,24 and reduced carbonate ion concentrations harm shellfish and other marine life.25,26 Since the total amount of CO2 emissions partitioning into the oceans rivals that retained by the atmosphere, effective means for its removal could augment the other negative emissions technologies to reduce the environmental burden imposed by this greenhouse gas. The concentrations in oceanwater (on a volumetric basis) are much higher at 100 mg L−1 than that in the ambient air (0.77 mg L−1),27,28 and thus smaller volumes will need to be treated than in DAC, which could provide a processing advantage. Moreover, while direct air capture requires both capture of the CO2 by chemical complexation with a sorbent, and subsequent breaking of these bonds when the CO2 is recovered as a pure gas, only the latter step is needed for CO2 removal from surface waters, which avoids one of the steps usually required for CO2 mitigation from gaseous sources.29–31
Approaches to solving this challenging problem need to be identified that do not require addition of chemicals, nor lead to parasitic reactions with the formation of undesirable compounds. CO2 from the air dissolves in seawater as carbonic acid, which speciates as bicarbonate and carbonate ions by releasing protons according to the reactions32
| CO2 + H2O ⇄ H2CO3 ⇄ HCO3− + H+ | (1) |
| HCO3− ⇄ CO32− + H+ | (2) |
Since this equilibrium is based on the proton concentration, the dissolved inorganic carbon (DIC) can be converted back to molecular CO2 by simply lowering the pH of the ocean water; the CO2 can be removed as a pure gas by stripping under vacuum. The pH of the treated water can then be raised before it is returned to the ocean, which has the benefit of countering the acidification of the oceans, and fostering the further absorption of CO2 from the atmosphere. The discharge of the CO2-depleted water into the ocean after treatment imposes significant limitations in choosing a method of altering pH.29 For example, modulation of the pH through addition of acid or base raises concerns about residual chemicals affecting the marine ecosystem, as well as the added cost of chemical supplies. For this reason, electrochemical systems have been considered as good options for the pH swing of oceanwater due to their reversibility.29,33,34 Since the reactions are driven by supplying electrons in a controllable manner, we can avoid chemical use and parasitic reactions.31,35,36
To date, two approaches have been proposed for electrochemically driven CO2 removal from seawater: electro-deionization30,34 and electrodialysis.29,33,37–39 In the electro-deionization process, water splitting reactions generating hydrogen and oxygen gases occur at each electrode to modulate the pH, driving CO2 removal from the oceanwater.30,34 However, the high resistivity of the system and high overpotentials for the reactions lead to a high overall process energy consumption. In contrast, bipolar membrane electrodialysis (BPMED) provides a more energy-efficient means to dissociate water molecules.33,38 The water dissociation catalysts embedded in a bipolar membrane enable decomposition of water molecules into protons and hydroxide ions without generating gases,40 dramatically reducing the energy consumption to 242 kJ per mol of CO2 removed.37 The energy efficiency can be further improved by introducing a redox-couple in the electrolyte. By adopting the ferricyanide/ferrocyanide redox pair, Digdaya et al.29 demonstrated energy consumptions as low as 155 kJ mol−1. However, the high cost of bipolar membranes might impede the commercialization of the process, and these architectures present risks of toxic redox-couples leaking into the oceanwater.41
We describe here a new approach based solely on electrochemical modulation of the pH to initially release the CO2 and then to alkalize the treated water before it is returned to the ocean. This approach does not require expensive membranes or addition of chemicals, is easy to deploy, and does not lead to formation of byproducts or secondary streams. The CO2 removal modules can be installed on stationary platforms co-located with wind farms or solar islands in the seas, or on cargo ships plying the oceans; they can also be integrated with on-shore desalination processes to take advantage of the installed water-handling facilities. The captured CO2 can be injected directly from platforms into sub-surface geologic structures for long term sequestration, or used as a feedstock for fuels or for commodity and specialty chemicals production.
Concept
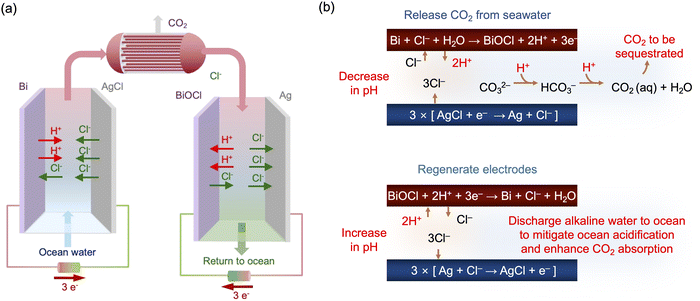
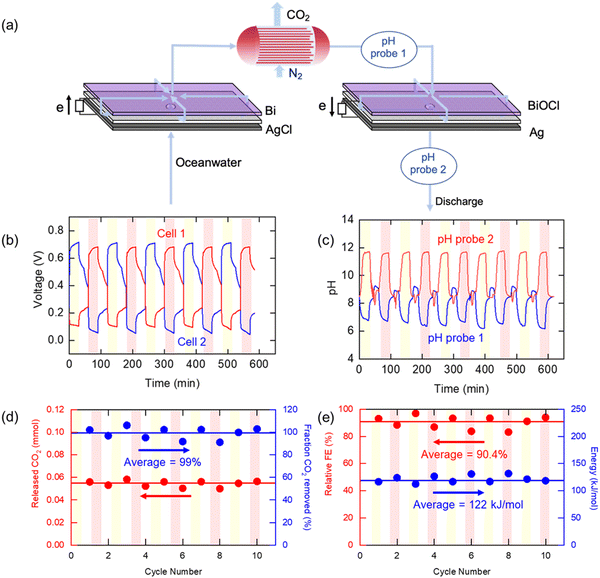
The pH of ocean water is currently at about 8.1, and most of the inorganic carbon exists in the form of bicarbonate and carbonate ions.39,42 As noted above, when the concentration of protons in water increases, the bicarbonate and carbonate ions re-speciate to molecular CO2, which can be then be stripped under vacuum. After the CO2 removal process is complete, the CO2-depleted stream can be re-alkalized before being returned to the ocean. The general principles of the process are illustrated schematically in Fig. 1(a), where two electrochemical cells work in tandem. In the first cell, protons are released by one electrode to modulate the pH of the feed stream, while the counter electrode releases chloride ions to ensure charge balance. In the second cell, the reverse reactions occur, with regeneration of the electrodes by storage of protons, recapture of chloride ions, and alkalization of the stream before it is returned to the ocean. In between these steps, molecular CO2 is stripped under vacuum in a hollow fiber membrane contactor. The cell pair is operated cyclically, with one cell operating until the active electrode is depleted of protons, and the other cell being regenerated as the active electrode is replenished. At the end of a cycle, i.e., when the active electrode is depleted, the flows to each cell are switched, and the polarity of the applied voltages reversed. For this approach, means for the storage and release of H+ through electrochemical reactions are required. Proton intercalation into metal oxides can be considered,43–45 but high concentrations of Na+ present in seawater interfere with H+ intercalation,46 making it difficult to use for a pH swing. Therefore, we adopted a method to change the pH that exploits chloride ions present in high concentration in ocean water as a mediator (Fig. 1(b)).A bismuth (Bi) electrode was used in which Bi reacts under an oxidizing potential to form bismuth oxychloride while releasing protons into the oceanwater feed according to the half reaction:47
| Bi + Cl− + H2O ⇄ BiOCl + 2H+ + 3e− E° = 0.16 V (vs. SHE) | (3) |
Silver chloride (AgCl) was selected as a counter electrode, because of its low overpotential, rapid kinetics, and high capacity for chloride ions. In ocean water, under reducing conditions, AgCl releases chloride ions without impacting the proton concentration, by the following half reaction:48
| AgCl + e− ⇄ Ag + Cl− E° = 0.23 V (vs. SHE) | (4) |
Based on the stoichiometry of the Bi reaction, two protons are released when three electrons are applied, decreasing the pH of the oceanwater to induce the speciation of the DIC toward molecular CO2; simultaneously, three chloride ions are released by the AgCl electrode, but one is lost to the formation of BiOCl. The overall reaction can be expressed as
| Bi + 3AgCl + H2O ⇄ BiOCl + 3Ag + 2Cl− + 2H+ ΔE° = 0.07 V | (5) |
From the positive cell potential for the overall reaction, the forward reaction should be spontaneous. Then, on reversal of these reactions, the CO2-depleted oceanwater can be re-alkalized, giving sufficient alkalinity to ocean water to reabsorb CO2, while regenerating the electrodes for the next cycle. This approach, which relies on a swing in chloride ion concentration between two different Cl− capture electrodes, bismuth and silver, to modulate the solution pH, is shown in this paper to have high faradaic efficiency under cyclic flow conditions, with a CO2 capture energy of 122 kJ mol−1.
Thermodynamic considerations
The desired pH target range for DIC speciation to be primarily toward molecular CO2 in solution can be assessed through equilibrium concentration calculations of the inorganic carbon species distribution. Here, we consider simulated seawater with a representative composition of 502.5 mM Na+, 500 mM Cl−, and varied concentrations of inorganic carbon species to ensure charge neutrality. The concentration of each inorganic carbon species can be calculated based on the acid dissociation constants Ka,1 and Ka,2, and on Henry's Law constant KH, defined as:49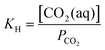 | (6) |
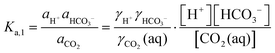 | (7) |
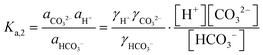 | (8) |
| [CO2(aq)] = KHPCO2 | (9) |
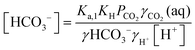 | (10) |
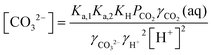 | (11) |
The initial concentration of aqueous CO2 is constant no matter the pH, and is determined by its partial pressure in the ambient air, PCO2. The concentrations of HCO3− and CO32−, on the other hand, are strongly affected by the proton concentration, and thus the total dissolved inorganic carbon (DIC) concentration is a function both PCO2 and [H+]:
| [DIC] = [CO2(aq)] + [HCO3−] + [CO3−] | (12) |
The activity coefficients for the charged species were calculated from the Debye–Hückel extension law:
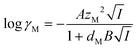 | (13) |
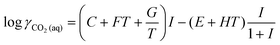 | (14) |
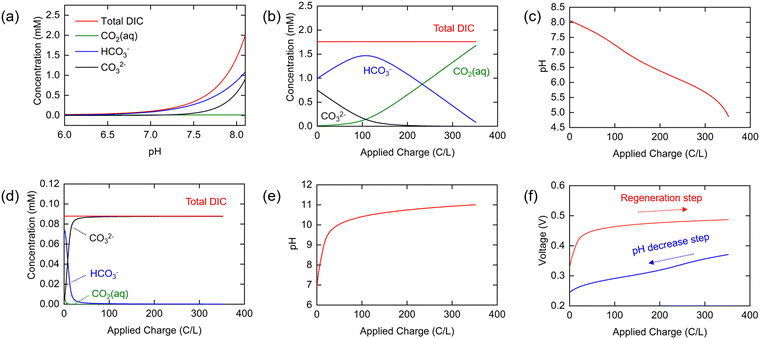
As shown in Fig. 2(a), the total DIC of the seawater in equilibrium with the ambient environment is at a concentration of 1.76 mM at pH 8.06, and the relative distributions of HCO3− and CO32− in this solution are 56% and 43%, respectively, under the ionic strength conditions used here. These values are significantly different from those calculated for ideal solution conditions with all activity coefficients set to unity (Fig. S1, ESI†), where the DIC concentration is larger at 2.5 mM, emphasizing the importance of incorporating the strong effect of ionic strength in thermodynamic analyses of CO2 speciation in seawater. It is clear that the total DIC solubility decreases sharply with decreasing pH, so that most of the DIC exists as molecular CO2 when the pH approaches neutral or slightly acidic conditions.
The equilibrium speciation calculated under different charging conditions can be used to estimate the energy requirement for electrochemical modulation of the proton concentration for CO2 desorption. Under constant current operation, the corresponding release rates of Cl− and H+ from the electrodes can be assumed to be constant. Given that net two moles of Cl− are released when three moles of electron flow in the electric circuit, the concentration of Cl− as a function of the applied charge Q can be written as
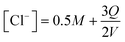 | (15) |
The aqueous feed solution is assumed to be in equilibrium with the ambient environment (containing 420 ppm of CO2), and thus the concentration of molecular CO2 is determined by Henry's Law, while [HCO3−] and [CO32−] are functions of the oceanwater pH, or [H+], as in eqn (10) and (11). Charge neutrality in the solution will then be satisfied through the balance equation
| [H+] + [Na+] = [Cl−] + [HCO3−] + 2[CO32−] + [OH−] | (16) |
Since [OH−] is a function of [H+], as determined by the water dissociation constant (Kw = 10−14),32 and the concentrations of the remaining ionic species are also functions of [H+], the overall concentration of dissolved inorganic species in the feed introduced to the electrochemical modules can be determined. This total DIC remains constant at [DIC]0 during charging, which impacts only the relative concentrations of the individual inorganic carbon species, which can be determined from
 | (17) |
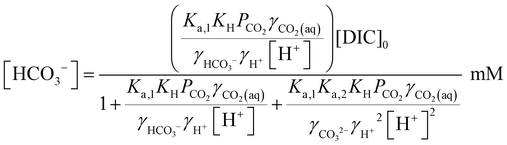 | (18) |
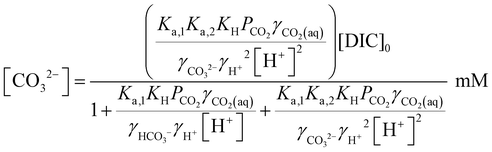 | (19) |
The changing distributions in the various components as charge transfer occurs are shown in Fig. 2(b). Of particular interest here is the concentration of molecular aqueous CO2 as a function of applied charge, as it is this quantity that will determine the conditions needed for effective stripping from the solution post-charging. Note that at low pH with a total [DIC]0 of about 1.8 mM, the fugacity, or effectively the partial pressure, is approximately 0.07 bar, and thus either a vacuum or a sweep gas must be used to strip the CO2 from the unsaturated solution. The pH is shown as a function of applied charge in Fig. 2(c). Initially, HCO3− and CO32− exist in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7 ratio, but the proportion of carbonate quickly decreases− with a lowering of the pH, to generate primarily HCO3−, which then decomposes to form molecular CO2 (or carbonic acid). Because proton release from the electrode is buffered by these combination reactions with HCO3− or CO32−, the relatively slow decrease in pH from 8.0 to about 6.0 is expected Fig. 2(c); when most of the HCO3− has been consumed, the pH drops rapidly, approaching 5.0.
0.7 ratio, but the proportion of carbonate quickly decreases− with a lowering of the pH, to generate primarily HCO3−, which then decomposes to form molecular CO2 (or carbonic acid). Because proton release from the electrode is buffered by these combination reactions with HCO3− or CO32−, the relatively slow decrease in pH from 8.0 to about 6.0 is expected Fig. 2(c); when most of the HCO3− has been consumed, the pH drops rapidly, approaching 5.0.
The reverse process is operative during the regeneration step, in which the concentration of Cl− increases linearly with applied charge, and [Na+] again remains constant (Fig. S2b, ESI†). The total DIC concentration is also constant, determined by the residual CO2 remaining in solution following the stripping step; we set it here as 5% of the initial DIC in oceanwater on the assumption that 95% of the DIC is removed by stripping (i.e., [DIC]0 = 0.1 mM for an initial oceanwater DIC of 2 mM). The calculated concentrations of individual inorganic carbon species during the regeneration step, determined from eqn (17)–(19) with [DIC]0 = 0.1 mM, are shown in Fig. 2(d), while the pH is shown in Fig. 2(e). It was assumed that the same total amount of charge was applied to the cell as in the first step to ensure complete regeneration of the electrodes. As the buffer capacity is low for the CO2-depleted oceanwater, the pH increases rapidly to 10 and ultimately reaches 11 by the end of the cycle. The proportion of CO32− in the DIC increases rapidly at the beginning of this process, reaching 99% when 64 C/L of charge is applied.
The electrochemical thermodynamic cycle can be constructed with the half-cell equilibrium potentials calculated according to the Nernst equation:
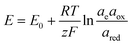 | (20) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), and ae, aox, and ared represent the activities of electrons, and oxidized and reduced species, respectively. If we assume that the activities of solids and electrons are unity, the electric potential established for the reactions at equilibrium can be expressed by the Nernst equation:
485 C mol−1), and ae, aox, and ared represent the activities of electrons, and oxidized and reduced species, respectively. If we assume that the activities of solids and electrons are unity, the electric potential established for the reactions at equilibrium can be expressed by the Nernst equation: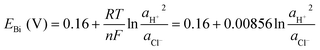 | (21) |
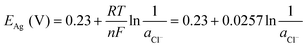 | (22) |
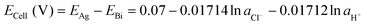 | (23) |
Since the equilibrium electrochemical potentials of the system are determined by the concentrations of H+ and Cl−, and these concentrations are dependent on the charge transferred, the equilibrium cell voltages for the pH decrease and electrode regeneration steps will also depend on the applied charge, as plotted in Fig. 2(f). In the absence of an overpotential, the voltage gap between the two steps was found to be significantly below 1 V, with an estimated thermodynamic minimum energy for the process given by
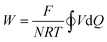 | (24) |
Electrode characterization
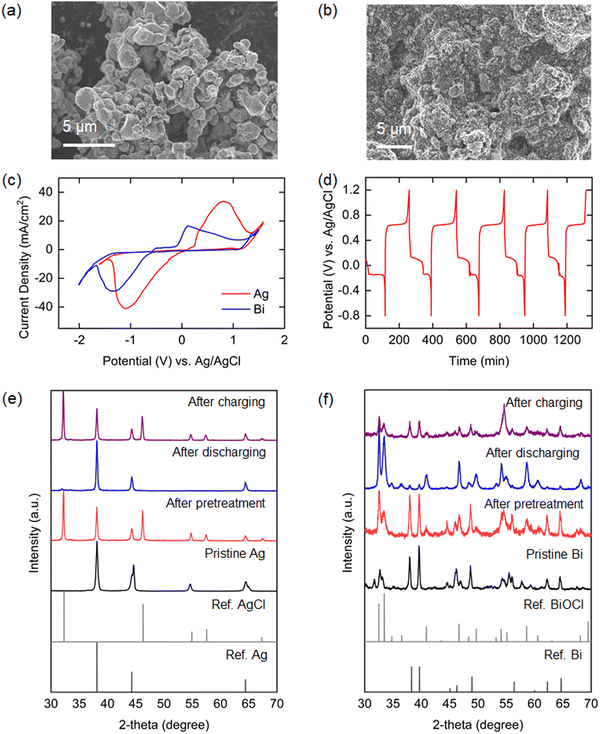
The material and electrochemical characteristics of the Ag and Bi electrodes employed in the electrochemical system will determine the efficacy of the process. The surface morphologies of the electrodes were observed by SEM. The Ag composite electrode with surface silver microparticles of 1–2 μm size is shown in Fig. 3(a), while Fig. 3(b) shows the surface structure of the Bi composite electrode prepared with sub-micrometer particle-sized bismuth powders obtained by ball-milling of large (hundreds of micrometers) pristine bismuth particles with conductive carbon (Fig. S2, ESI†). The electrochemical properties of the electrodes under simulated oceanwater conditions were investigated by cyclic voltammetry (CV) analysis. As shown in Fig. 3(c), both electrodes exhibited apparent reversible redox peaks in the solution that were well-matched with those of Ag/AgCl and Bi/BiOCl reactions. The onset potential difference for oxidation and reduction peaks was larger for Bi than for Ag, which might result in higher overpotential requirements. XRD analyses conducted before and after oxidation of the Bi and Ag electrodes in a simulated oceanwater yielded XRD patterns that show clearly that the crystalline structures of Bi and Ag converted to those of BiOCl and AgCl during oxidation (Fig. 3(e) and (f)).Static cell characterization
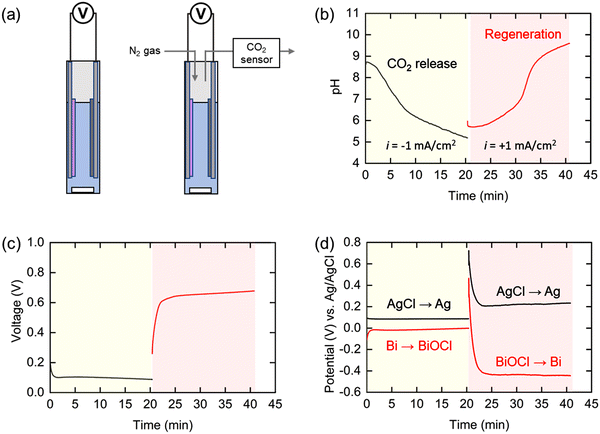
The pH swing system was first demonstrated in a static cell either in direct contact with ambient air, so that CO2 can transfer to and from the solution under alkalization and acidification conditions, respectively, or with release under a nitrogen sweep stream, as illustrated schematically in Fig. 4(a). The bismuth (Bi) and silver chloride (AgCl) electrodes were placed 1 cm apart in 9 mL simulated oceanwater, and the pH and electrochemical potentials of the individual electrodes were monitored throughout the operation. A current of −1 mA cm−2 was applied to the electrochemical cell until the total applied charge reached the amount theoretically required to remove 95% of the total DIC. At this point, +1 mA cm−2 of current was applied for the same length of time. When the negative current was applied, the pH decreased gently for a short time at the beginning of the operation, before dropping rapidly to a final value of 5.2 (Fig. 4(b)), indicating that the protons were successfully released into the electrochemical cell. This trend is consistent with that estimated by the thermodynamic analysis shown in Fig. 2(c). The initially slow increase in pH in the first half of the second step can be attributed to the residual CO2 in the solution acting as a buffer. After this residual CO2 was converted to bicarbonate, the pH rapidly increased to above 9 and another plateau appeared due to the conversion of the bicarbonate to carbonate. Measurements of the concentration of CO2 in a nitrogen sweep stream used to elute the evolved gas indicated that the diffusion of CO2 from the solution continued for up to 2 hours following completion of the first step (Fig. S3, ESI†).The cell voltage (i.e., difference in potentials between the two electrodes) plateaued at 0.1 V in the first step and between 0.6 and 0.7 V in the subsequent step (Fig. 4(c)), resulting in an average voltage gap of 0.55 V between the two steps. Given that the cell voltage of the BPMED in previous reports is usually above 1 V, this suggests that our proposed electrochemical system can be competitive energetically with the state-of-the-art process. The potential at each electrode was also monitored with a reference electrode during the operation (Fig. 4(d)). The electrochemical potential for the silver electrode was 0.1 V and 0.2 V (vs. Ag/AgCl) in the first and second steps, respectively, showing 0.1 V of potential difference between the two steps. On the other hand, the potential gap for the bismuth electrode was relatively large, 0.45 V calculated from the values of 0 V and −0.45 V (vs. Ag/AgCl) in the first and second steps, respectively. This indicates that the resistance due to the Bi/BiOCl reaction, which is significantly larger than that of the Ag/AgCl reaction, is the primary determinant of the energy consumption in this system. Given that the standard potential of Bi is −0.05 V (vs. Ag/AgCl), the reaction kinetics for the Bi to BiOCl oxidation is quite fast. On the other hand, the kinetics for the reduction reaction (BiOCl to Bi) is sluggish as water dissociation should be involved in the reaction mechanism to generate H+.
Continuous flow cyclic operation
For practical demonstration of the electrochemical Cl− swing proton modulation process, it will be necessary to implement these concepts in a continuous swing mode of operation. The ocean water entering the electrochemical modules needs to undergo three steps: (1) acidification to release CO2, (2) stripping of CO2 into a gaseous phase, and (3) re-alkalization to regenerate the electrodes for the next swing cycle. For these purposes, two cells were prepared with identical compositions (bismuth and silver) but in different oxidation states: Bi/AgCl for Cell 1 and BiOCl/Ag for Cell 2. As shown in Fig. 5(a), the oceanwater passed through the two cells consecutively with acidification of the oceanwater in Cell 1, and alkalization of the acidified water in Cell 2 once the CO2 had been stripped in a hollow fiber membrane contactor by a nitrogen sweep gas used to emulate vacuum degasification of the water in which the CO2 fugacity (partial pressure) is only ∼0.07 bar. The water was pumped to Cell 1 at a flow rate of 1.04 mL min−1, in which 99.3% of DIC could be removed from the oceanwater if the faradaic efficiency were to be 100%. CO2 removal was tracked by measuring the concentration of CO2 in the nitrogen sweep gas (5 mL min−1), and the pH of the CO2-depleted stream was monitored to evaluate the system performance. The water then entered Cell 2, in which the pH of the oceanwater increased by the reverse reactions of Cell 1. The pH of the effluent from Cell 2 was also monitored before discharge. After 30 min, the system was allowed to rest under the same flow conditions, with no current applied, before the operation mode was changed to the second step, in which the roles of the two cells were switched such that the oceanwater flowed in the opposite direction, sequentially passing through Cell 2 and then through Cell 1. The CO2 in the simulated oceanwater could be removed continuously by repeating these steps, discharging water with increased alkalinity.
Fig. 5(b) shows the measured voltage when the system operated under constant current conditions. A negative current (−1 mA cm−2) was applied for 30 minutes to Cell 1 to decrease pH in the ocean water, while a positive current (+1 mA cm−2) was applied for same amount of time to Cell 2 to increase the pH of CO2-depleted oceanwater. During the operation, the voltage of the charging cell was maintained at 0.7 V, while that of discharging cell was about 0.1 V. The voltage gap between two cells was 0.6 V on average, which is similar to the result shown for the static cell. Fig. 5(c) shows the pH profile during the operation. The pH of the effluent from the cells operating in the acidification mode decreased to 6, indicating that the ocean water was acidified, while in the regeneration cells the pH approached 12, as anticipated. The pH profiles were similar no matter which of the two cells was being used for acidification, and there was no observable decline in performance over ten cycles. When the acidified oceanwater passed through the membrane contactor, the CO2 was stripped out by the nitrogen sweep stream; there was a rapid increase in the measured CO2 concentration to 8000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm in the sweep stream when the current was applied to the electrochemical cells, as shown in Fig. S6 (ESI†), from which the average amount of CO2 removed per cycle of 0.0543 mmol, shown in Fig. 5(d), could be calculated, indicating that 87% of the DIC was removed from the oceanwater These calculations allowed for the fact that a small amount of CO2 (about 500 ppm) was released even during the rest period when no current was applied, which was subtracted from the concentration of CO2 released during the operation when estimate the amount of released CO2 in each step that could be attributed to pH modulation. Meanwhile, the pH measured in the re-alkalizing cell effluent reached about 10–11, which is consistent with the thermodynamic calculation (Fig. 2(e)). This value is much higher than the pH of the initial oceanwater, which was about 8, owing to the reduction in buffering capacity after most of the DIC was removed from solution. After discharge of the effluent into the ocean, the solution will be restored to pH ∼8, the typical pH of oceanwater, by absorbing CO2 from the atmosphere.
000 ppm in the sweep stream when the current was applied to the electrochemical cells, as shown in Fig. S6 (ESI†), from which the average amount of CO2 removed per cycle of 0.0543 mmol, shown in Fig. 5(d), could be calculated, indicating that 87% of the DIC was removed from the oceanwater These calculations allowed for the fact that a small amount of CO2 (about 500 ppm) was released even during the rest period when no current was applied, which was subtracted from the concentration of CO2 released during the operation when estimate the amount of released CO2 in each step that could be attributed to pH modulation. Meanwhile, the pH measured in the re-alkalizing cell effluent reached about 10–11, which is consistent with the thermodynamic calculation (Fig. 2(e)). This value is much higher than the pH of the initial oceanwater, which was about 8, owing to the reduction in buffering capacity after most of the DIC was removed from solution. After discharge of the effluent into the ocean, the solution will be restored to pH ∼8, the typical pH of oceanwater, by absorbing CO2 from the atmosphere.
Fig. 5(e) shows the relative faradaic efficiency (η) and the energy consumption during operation. Based on the stoichiometry of the electrochemical reactions, the theoretical maximum FE is 67%, as two protons are released for every 3 electrons applied to the system. Therefore, the relative η was defined as the η divided by the theoretical maximum η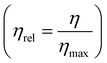 . During the 10-cycle operation, the average relative FE was 90.4%, and 122 kJ mol−1 of energy was expended, on average. Compared to previous studies that had electrochemical energy consumption of more than 155 kJ mol−1, our proposed system is energetically competitive at the applied current densities, with the caveat that these current densities are lower than those used in earlier studies; further development of this process may require increased current densities to reduce total electrode area needed.
. During the 10-cycle operation, the average relative FE was 90.4%, and 122 kJ mol−1 of energy was expended, on average. Compared to previous studies that had electrochemical energy consumption of more than 155 kJ mol−1, our proposed system is energetically competitive at the applied current densities, with the caveat that these current densities are lower than those used in earlier studies; further development of this process may require increased current densities to reduce total electrode area needed.
The contents of bismuth and silver in the effluent were measured by ICP-MS. No bismuth was detected in the effluent solution, but the content of silver was 0.255 mg L−1. Means for the amelioration of this slow loss of silver will need to be addressed through identification either of other electrode compositions, or of methods to prevent the dissolution of the silver electrode.
Additional tests were carried out using synthetic seawater with the same composition as seawater. As shown in Fig. S7 (ESI†), the amount of released CO2 decreased over the 4-cycle operation, dropping to 31% in the second cycle and further decreasing to 13% after four cycles relative to the first cycle. The reason for the rapid decrease is attributed to possible Mg(OH)2 formation on the electrode surface owing to the high local surface pH relative to that in the bulk flow. This pH difference is due to the establishment of a concentration boundary layer to balance the concentration-driven proton fluxes with the applied reducing current. With a lowered current density (+0.125 mA cm−2) in the regeneration step, the pH difference between the bulk and surface was reduced, and hence also the precipitation of fouling compounds such as Mg(OH)2, culminating in a 96% performance retention in the second cycle and 67% in the fourth. Strategies to enhance the overall stability of these electrochemical systems under more realistic conditions are clearly needed, and will be a focus of our future studies.
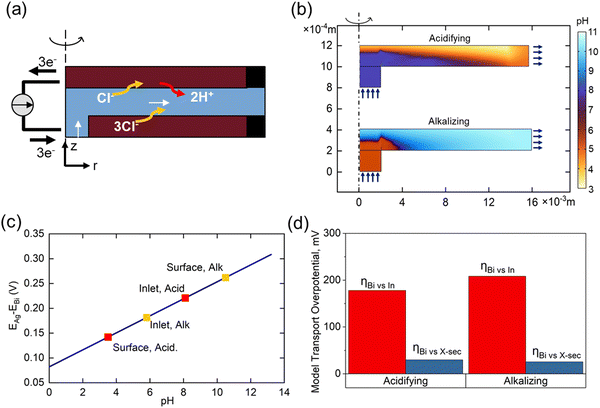
Transport modelling
The importance of transport phenomena on system performance was evaluated using a COMSOL Multiphysics model developed to determine ion distributions during flow cell operation. The simulated flow cell geometry was simplified to a 2D axisymmetric domain of an equal active surface area (6.25 cm2) and gap size (3 mm) as the experimental cell, and simulations were conducted under the same flow rate conditions (1 ccm). Physics were governed by coupling the time-dependent Nernst–Planck equations to a steady state flow profile. DIC interconversion was modelled pointwise by homogeneous rate laws.42 Electrodes were modelled as 2D electrode surfaces governed by Butler–Volmer kinetics, with externally applied potentials varied to elicit a steady state current density of 0.9 mA cm−2 (corresponding to an experimental 1 mA cm−2 with 90% faradaic efficiency). Electrolyte inlet compositions were selected to match simulated seawater (pH 8.1, 2 mM DIC) during acidification, and post-treatment water (pH 6, 0.1 mM DIC) during regeneration. Additional model parameters are detailed in the ESI.†Fig. 6(a) shows the COMSOL abstraction of the experimental flow cell, reduced to an equivalent 2D axisymmetric domain to minimize computational intensity while retaining essential transport characteristics. Fig. 6(b) illustrates the corresponding pH distributions during acidification and alkalization operations, with the r-coordinate compressed by a factor of 10 for clearer visualization. Due to the sluggish kinetics of conversion from HCO3− to CO2 relative to H+ diffusion timescales, a sharp reaction front can be observed during forward operation, dividing the channel into a highly acidic (pH ∼ 3.5) top region near the Bi electrode and a region of unaffected seawater near the Ag counter electrode. Prior to alkalization, 95% of DIC buffering capacity has been removed from the cell, resulting in a much smoother pH profile, with inhomogeneities primarily owing to recirculation effects near the inlet.
Fig. 6(c) illustrates the dependence of cell potential on pH experienced at the bismuth electrode, highlighting notable values in the system. Losses in performance due to variations in open circuit potential throughout the channel can be formulated as a concentration overpotential:
| ηk = |ΔΦeq([H]surf) − ΔΦeq([H]bulk)| | (25) |
Fig. 6(d) indicates the total measured overpotential experienced by the bismuth electrode in the real system relative to the inlet conditions, compared to average calculated concentration overpotentials relative to the inlet and channel cross section. Acidification calculations suggest that a significant portion of the Bi overpotential during this step might be due to an excess concentration of protons at the bismuth surface, whereas spatial variations in concentration likely only account for only a small portion of the re-alkalization overpotential. Mixing is therefore an important consideration in a real system, as improving the spatial uniformity of conversion of DIC to CO2 at a pH closer to 6 could improve energetics in the acidification step.
Overall performance of modules
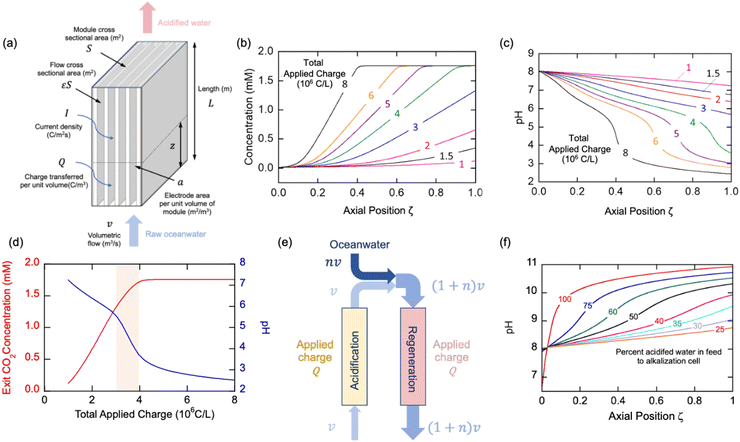
The thermodynamic model described earlier can be used to estimate the impact of current density and flow rates in the modules. Consider a module illustrated schematically in Fig. 7(a) of cross-sectional area S (m2) and length L (m), with flow channels occupying a fraction of this volume, the remainder being the electrode materials themselves. The volumetric rate at which seawater is treated is m3 s−1, while the current density is I (C m−2 s−1); the total electrode area per unit volume of module is given by (m2 m−3). The applied charge Q (C m−3) in the flowing seawater at point z in the module is obtained from the balance equation| vQ = IaεSz | (26) |
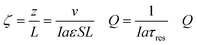 | (27) |
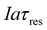 , which is the total charge accumulation per unit volume of treated water. The profiles in Fig. 7(b) and (c) showing the variation in molecular CO2 and pH, respectively, with position during the acidification process can be used to determine the residence times (and hence module size) required to attain a desired conversion of DIC to molecular CO2 for a given current density, or the current density required to treat a given amount of water in an existing module. Note that for some values of Iaτres full conversion of the DIC is attained fairly early in the unit, and the remainder of the module is not utilized effectively. An appropriate value for Iaτres can be obtained from the plot of the exit CO2 concentration vs. Iaτres as shown in Fig. 7(d) and will depend on the desired exit concentration. A total applied charge of between 3 and 4 × 106 C m−3 would be sufficient to convert the DIC in ocean water almost completely to molecular CO2 in the contactor.
, which is the total charge accumulation per unit volume of treated water. The profiles in Fig. 7(b) and (c) showing the variation in molecular CO2 and pH, respectively, with position during the acidification process can be used to determine the residence times (and hence module size) required to attain a desired conversion of DIC to molecular CO2 for a given current density, or the current density required to treat a given amount of water in an existing module. Note that for some values of Iaτres full conversion of the DIC is attained fairly early in the unit, and the remainder of the module is not utilized effectively. An appropriate value for Iaτres can be obtained from the plot of the exit CO2 concentration vs. Iaτres as shown in Fig. 7(d) and will depend on the desired exit concentration. A total applied charge of between 3 and 4 × 106 C m−3 would be sufficient to convert the DIC in ocean water almost completely to molecular CO2 in the contactor.
We can use a similar analysis to look at the regeneration modules, and explore scenarios for the reduction of the final pH in these modules. In many cases, it would be desirable to ensure that the pH did not reach levels of 9.5 or greater at which precipitates of, say, Mg(OH)2, form, which may foul the electrodes and reduce the overall efficiency of the process. A strategy to overcome this limitation would be to mix the decarbonated solution with fresh oceanwater as shown in Fig. 7(e) so that the residence time restrictions can be disentangled from the current density needs, and, moreover, the buffering capacity of the bicarbonate solution may limit the overall increase in pH. In Fig. 7(f) we illustrate the results from such a mixing of the acidified, decarbonated stream with fresh oceanwater in different proportions, which has the effect of increasing slightly the pH of the feed to the regeneration unit, but also decreases the required residence time in the unit for constant total charge transferred (i.e., constant Ia). With increasing addition of ocean water, the pH of the regeneration stream decreases, which is the desired effect. Since this increase in volumetric flow to the unit would be at the expense of added pumping costs, however. This simple model provides added insight into different operational strategies, but will need to be augmented with more detailed analyses that account for transport and other kinetic limitations within the cells, a topic for future studies.
Technoeconomic analysis and optimization
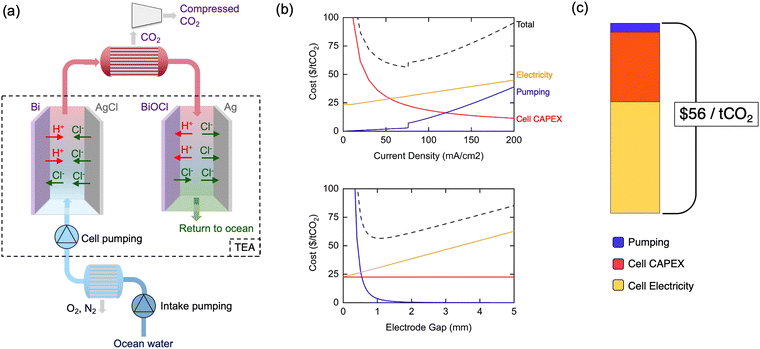
A detailed technoeconomic analysis (TEA) was performed to explore the economic viability and cost drivers of the asymmetric electrochemical pH-swing DOC approach when implemented at commercial scale. While a complete DOC system requires oceanwater intake, degasification, and compression systems,29,37 this analysis focuses on the systems specific to the electrochemical pH-swing approach developed herein. It is important to note that the asymmetric chlorine-mediated pH swing process is not expected to substantially change the operating requirements of the pre-filtration and subsequent degassing steps when compared to alternative methods of acidification (see ESI†). Thus, other analyses can provide estimates for the expected vacuum degassing, filtration, and auxiliary costs outside of the electrochemical system for a complete system involving the asymmetric cells.29,37,38For the electrochemical system, cost estimates for the cell stack capital expenditures (CAPEX), cell stack electricity costs, and pumping capital and operating costs are shown in Fig. 8(a). The CAPEX of the Bi/AgCl electrode cell stack at scale is estimated using alkaline water electrolyzer costs adjusted for our process specifics. Cell electricity costs are calculated using the experimental 122 kJ mol−1-CO2 as the base required energy and adding ohmic losses through the electrolyte which become relevant at high current densities and large cell gaps. Pumping investment and operating costs are calculated given the flow rate and pressure drop through the cells. Detailed calculations and assumptions can be found in ESI.†
The model cell stack operational current density and electrode gap are varied in the TEA as shown in Fig. 8(b), highlighting some key physical system design tradeoffs. At low current densities, large electrode areas are required and cause cell CAPEX costs to dominate. Beyond 76 mA cm−2, additional benefits from increasing current density are outweighed by increased ohmic losses through the oceanwater and increased pumping costs due to higher required flow velocities. Pumping costs dominate for slim electrode gaps, while ohmic losses drive costs at large electrode gaps, resulting in an optimum at 1.1 mm. The minimized system cost at these optimized parameters is $56 per tCO2 with cost components shown in Fig. 8(c).
The balancing act between the current density, gap width, and pumping costs is generalizable to all electrochemical DOC systems with flow between parallel electrodes, including electrodialysis systems. A notable effect of this interplay is the constraint of the current density to a value much lower than the >1 A cm−2 typically sought for large-scale industrial electrochemical plants.50–53 The inflexibly low conductivity of oceanwater and extremely high required oceanwater throughput are fundamental characteristics which elevate the relevance of electrolyte ohmic losses and limitations on the cell gap for current DOC systems compared to other large-scale electrochemical technologies. To the best of our knowledge, this effect has not been explored in previous technoeconomic or system analyses, which assume operation at higher current densities in excess of 100's of mA cm−2.
However, these physical tradeoffs reveal avenues for continued system cost reduction. Moving away from parallel-electrode architectures towards alternatives such as inter-digitated electrodes could decouple the opposing nature of electricity costs and pumping costs. With such a design, larger cell gaps which minimize pumping costs could be attained while keeping ohmic losses low and allowing higher current density operation. Though our base energy consumption of 122 kJ mol−1-CO2 is a record-low, it may still be substantially decreased towards the thermodynamic limit of 32 kJ mol−1-CO2. Finally, high cell stack CAPEX costs at low current densities motivate the development of electrodes which operate efficiently at higher current densities by mitigating the overpotentials shown in our transport modeling.
The $56 per tCO2 initial cost estimate of our asymmetric electrochemical pH-swing system is comparable to that of electrodialysis system costs under the same assumptions.29 The promising energetics of our process yield lower cell electricity costs, though our initial investment CAPEX estimates are slightly higher (see ESI† Note S3). However, our analysis does not account for replacements and O&M costs which we expect to be significantly lower for our system involving only two electrodes, no redox couples, and no membranes which typically require frequent replacement. The reduced part count and simplicity of our system is promising for its scalability.
Our electrochemical system cost estimates fall within commonly accepted targets of $100 per tCO2,54 but other system costs are critical to evaluate as well. Previous analyses indicate that intake filtration, pumping and gas separation costs may incur total process costs as high as $2000 per tCO2.29,37 At present, these costs dominate those associated with the electrochemical system and motivate further work in reducing degassing costs and pumping costs in addition to electrochemical improvements.
Conclusions
The chloride-mediated electrochemical pH swing system in this proof-of-concept study provides a new method to achieve negative emissions by removing CO2 from seawater without the use of expensive bipolar membranes or the need for specific anolytes and catholytes to drive the reactions in the electrode cells. In contrast to previously reported electrodialysis systems, the chloride-mediated electrochemical pH swing system is used to modulate the pH of oceanwater, and hence the speciation of the DIC, by reversible electrochemical reactions at the electrodes instead of by water dissociation in the bipolar membranes. These advances are possible through adoption of two different electrodes, bismuth and silver, that capture chloride ions. Continuous CO2 removal from simulated oceanwater was demonstrated by combining two silver–bismuth systems and showed robust behavior over 10 hours of operation. Removal of 87% of the DIC in the simulated oceanwater was observed, with 92% relative faradaic efficiency and 122 kJ mol−1 energy consumption. The bismuth electrode is inexpensive and can robustly modulate the pH of chloride-containing salt water regardless of the type and concentration of cations. On the other hand, although silver has the advantage of large capacity and low energy penalty, electrode dissolution will need to be overcome by modifying the silver particles or replacing silver with another material; this is to be the subject of future studies. Methods to overcome the fouling of electrodes during the regeneration step owing to local high surface pH conditions that promote the formation of precipitates such as Mg(OH)2 must be developed, and several engineering and electrochemical approaches are currently being considered to alleviate the fouling issues; one such method was discussed in which the degasified water was mixed with fresh ocean water before being fed to the regeneration cell to reduce the overall pH increase in the flow channel.For convenience, in the small demonstration unit a nitrogen sweep gas was used to emulate the drawing of a vacuum for disengagement of the CO2 (at a fugacity of ∼0.07 bar) from the acidified water, since the partial pressure of CO2 in the sweep stream will be on a par with the actual pressure of pure CO2 obtained under vacuum degasification at, say 0.01 bar. As with other published processes for CO2 removal from ocean waters, this low-pressure CO2 would need to be compressed either for use as a feedstock for production of chemicals, materials and fuels, or for sequestration in sub-surface geologic formations.
The techno-economic analysis shows that this ocean capture system can be economically feasible with costs ranging from $50–$100 per ton CO2 depending on the current applied and the gap between electrodes, and could be lowered to $56 per ton CO2 under optimized conditions. However, these calculations only considered the economic feasibility of the electrochemical system itself, and it is necessary to perform an integrated analysis, including other equipment such as intake systems, gas separations, and compression.
Experimental
Preparation of electrodes
The electrodes were prepared by mixing 80 wt% bismuth powder (Alpha Aesar), 10 wt% carbon black (Super P, Timcal), and 10 wt% polyvinylidene fluoride (PVDF, Sigma Aldrich) binder. Before the fabrication, the bismuth and carbon black were ball-milled together for 1 h to reduce particle size and increase the contact between bismuth and carbon powder. The mixture was dispersed in an organic solvent (N-methyl-2-pyrrolidone, NMP), and cast on a graphite sheet (200 μm of thickness) using the doctor blade method. The silver electrode was fabricated by mixing silver powder (Sigma Aldrich), carbon black (Super P, as conducting agent), and polytetrafluoroethylene (PTFE) binder (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by weight, respectively) in ethanol. The mixture was placed in a roll pressor and a sheet-type electrode was obtained with 200 μm of thickness. Both electrodes were dried in an oven overnight to remove the residual solvent.
1 by weight, respectively) in ethanol. The mixture was placed in a roll pressor and a sheet-type electrode was obtained with 200 μm of thickness. Both electrodes were dried in an oven overnight to remove the residual solvent.
Characterization of the electrodes
The surface morphology of the electrodes was characterized by field emission scanning electron microscopy (FE-SEM, Zeiss MERLIN). The crystalline structure was analyzed by X-ray diffraction (XRD, Rigaku) in a 2θ range of 10–80° with a ramping step of 5° min−1. Cyclic voltammetry (CV) analyses were carried out to determine the electrochemical properties of the electrodes in 0.5 M NaCl and 2.5 mM NaHCO3 solution in a three-electrode cell. A platinum wire was used as a counter electrode and a commercial Ag/AgCl (3 M KCl) was applied as a reference electrode. The CV scan was obtained by a potentiostat (PAR) with scan rates of 2 mV s−1.CO2 removal experiments
The flow-type CO2 removal cell was assembled with the silver chloride as a positive electrode and bismuth as a negative electrode. A pair of graphite sheets (∼200 μm of thickness) was used as current collectors to connect the electrodes to the potentiostat. The silver electrode was cut into a square shape (2.5 × 2.5 cm2) with a 3 mm hole located at the center to make a flow channel between the electrodes. The bismuth electrode was also cut into a square shape without any hole. For the flow channel, two nylon spacers (∼100 μm) and one filter paper (∼200 μm) were placed between the electrodes. For the test, a simulated oceanwater containing 0.5 M of NaCl and 2.5 mM of NaHCO3 was pumped into the cell at a flow rate of 1.04 mL min−1 with a peristaltic pump. Two pH micro electrodes (8220BNWP, thermo fisher) were connected to the flow channel to monitor the pH of the effluents from each cell, and the data were acquired with isoPods (eDAQ). A membrane contactor was used to promote the CO2 release from water into a flowing nitrogen sweep stream, which was used to emulate the drawing of a vacuum on the unit. A CO2 sensor (CO2 Meter) was connected right after the membrane contactor to measure the concentration of CO2 in the gas phase. The content of silver and bismuth in the effluent was analyzed with ion-coupled plasma-mass spectroscopy (ICP-MS, Agilent). For this measurement, the effluent and 5 M nitric acid solution were mixed in a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 volume ratio.
4 volume ratio.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported under ARPA-E Grant DE-AR0001409.References
- IPCC, IPCC special report on carbon dioxide capture and storage, Cambridge University Press, New York, 2005 Search PubMed.
- M. Bui, C. S. Adjiman, A. Bardow, E. J. Anthony, A. Boston, S. Brown, P. S. Fennell, S. Fuss, A. Galindo, L. A. Hackett, J. P. Hallett, H. J. Herzog, G. Jackson, J. Kemper, S. Krevor, G. C. Maitland, M. Matuszewski, I. S. Metcalfe, C. Petit, G. Puxty, J. Reimer, D. M. Reiner, E. S. Rubin, S. A. Scott, N. Shah, B. Smit, J. P. M. Trusler, P. Webley, J. Wilcox and N. Mac Dowell, Energy Environ. Sci., 2018, 11, 1062–1176 RSC.
- P. Folger, Science, 2009, 325, 1652–1654 CrossRef PubMed.
- M. Wang, A. Lawal, P. Stephenson, J. Sidders and C. Ramshaw, Chem. Eng. Res. Des., 2011, 89, 1609–1624 CrossRef CAS.
- M. C. Stern, F. Simeon, H. Herzog and T. A. Hatton, Energy Environ. Sci., 2013, 6, 2505–2517 RSC.
- N. Mac Dowell, P. S. Fennell, N. Shah and G. C. Maitland, Nat. Clim. Change, 2017, 7, 243–249 CrossRef CAS.
- Y. Wang, L. Zhao, A. Otto, M. Robinius and D. Stolten, Energy Procedia, 2017, 114, 650–665 CrossRef CAS.
- F. M. Orr, Science, 2009, 325, 1656–1658 CrossRef CAS PubMed.
- K. Hashimoto, Global Carbon Dioxide Recycling for Global Sustainable Development by Renewable Energy, Springer, Singapore, 2019, pp.5–17 Search PubMed.
- D. W. Keith, Science, 2009, 325, 1654–1655 CrossRef CAS PubMed.
- T. Gasser, C. Guivarch, K. Tachiiri, C. D. Jones and P. Ciais, Nat. Commun., 2015, 6, 7958 CrossRef CAS PubMed.
- J. Hansen, M. Sato, P. Kharecha, K. Von Schuckmann and D. J. Beerling, Earth Syst. Dyn., 2017, 8, 577–616 CrossRef.
- E. S. Sanz-Pérez, C. R. Murdock, S. A. Didas and C. W. Jones, Chem. Rev., 2016, 116, 11840–11876 CrossRef PubMed.
- D. W. Keith, G. Holmes, D. St. Angelo and K. Heidel, Joule, 2018, 2, 1573–1594 CrossRef CAS.
- S. Voskian and T. A. Hatton, Energy Environ. Sci., 2019, 12, 3530–3547 RSC.
- M. Obersteiner, C. Azar, S. Kossmeier, R. Mechler, K. Mollersten, S. Nilsson, P. REad, Y. Yamagata and J. Yan, IIASA Interim Rep., 2001, 1–23 Search PubMed.
- F. Creutzig, N. H. Ravindranath, G. Berndes, S. Bolwig, R. Bright, F. Cherubini, H. Chum, E. Corbera, M. Delucchi, A. Faaij, J. Fargione, H. Haberl, G. Heath, O. Lucon, R. Plevin, A. Popp, C. Robledo-Abad, S. Rose, P. Smith, A. Stromman, S. Suh and O. Masera, GCB Bioenergy, 2015, 7, 916–944 CrossRef CAS.
- C. Halliday and T. A. Hatton, Ind. Eng. Chem. Res., 2020, 59, 22582–22596 CrossRef CAS.
- B. Locatelli, C. P. Catterall, P. Imbach, C. Kumar, R. Lasco, E. Marín-Spiotta, B. Mercer, J. S. Powers, N. Schwartz and M. Uriarte, Restor. Ecol., 2015, 23, 337–343 CrossRef.
- J. Busch, J. Engelmann, S. C. Cook-Patton, B. W. Griscom, T. Kroeger, H. Possingham and P. Shyamsundar, Nat. Clim. Change, 2019, 9, 463–466 CrossRef CAS.
- P. Landschützer, N. Gruber and D. C. E. Bakker, Global Biogeochem. Cycles, 2016, 30, 1396–1417 CrossRef.
- N. Gruber, D. Clement, B. R. Carter, R. A. Feely, S. van Heuven, M. Hoppema, M. Ishii, R. M. Key, A. Kozyr, S. K. Lauvset, C. Lo Monaco, J. T. Mathis, A. Murata, A. Olsen, F. F. Perez, C. L. Sabine, T. Tanhua and R. Wanninkhof, Science, 2019, 363, 1193–1199 CrossRef CAS PubMed.
- S. C. Doney, V. J. Fabry, R. A. Feely and J. A. Kleypas, Annu. Rev. Mater. Sci., 2009, 1, 169–192 Search PubMed.
- C. D. Harvell, P. F. Sale, A. J. Edwards, K. Caldeira, N. Knowlton and C. M. Eakin, Science, 2007, 318, 1737–1743 CrossRef PubMed.
- A. D. Moy, W. R. Howard, S. G. Bray and T. W. Trull, Nat. Geosci., 2009, 2, 276–280 CrossRef CAS.
- F. Gazeau, C. Quiblier, J. M. Jansen, J. P. Gattuso, J. J. Middelburg and C. H. R. Heip, Geophys. Res. Lett., 2007, 34, 1–5 CrossRef.
- C. Content, Oceans and the Atmospheric Carbon Content, 2011 Search PubMed.
- F. J. Millero, Chem. Rev., 2007, 107, 308–341 CrossRef CAS PubMed.
- I. A. Digdaya, I. Sullivan, M. Lin, L. Han, W. H. Cheng, H. A. Atwater and C. Xiang, Nat. Commun., 2020, 11, 1–10 CrossRef PubMed.
- H. D. Willauer, F. DiMascio, D. R. Hardy and F. W. Williams, Energy Fuels, 2017, 31, 1723–1730 CrossRef CAS.
- R. Sharifian, R. M. Wagterveld, I. A. Digdaya, C. Xiang and D. A. Vermaas, Energy Environ. Sci., 2021, 14, 781–814 RSC.
- V. Snoeyink and D. Jenkins, Water Chemistry, John Wiley & Sons, New York, 1st edn, 1980 Search PubMed.
- M. D. Eisaman, J. L. B. Rivest, S. D. Karnitz, C. F. de Lannoy, A. Jose, R. W. DeVaul and K. Hannun, Int. J. Greenhouse Gas Control, 2018, 70, 254–261 CrossRef CAS.
- H. D. Willauer, F. Dimascio, D. R. Hardy and F. W. Williams, Ind. Eng. Chem. Res., 2014, 53, 12192–12200 CrossRef CAS.
- S. Jin, M. Wu, R. G. Gordon, M. J. Aziz and D. G. Kwabi, Energy Environ. Sci., 2020, 13, 3706–3722 RSC.
- K. M. Diederichsen, R. Sharifian, J. S. Kang, Y. Liu, S. Kim, B. M. Gallant, D. Vermaas and T. A. Hatton, Nat. Rev. Methods Primers, 2022, 2, 68 CrossRef CAS.
- M. D. Eisaman, K. Parajuly, A. Tuganov, C. Eldershaw, N. Chang and K. A. Littau, Energy Environ. Sci., 2012, 5, 7346–7352 RSC.
- C. F. de Lannoy, M. D. Eisaman, A. Jose, S. D. Karnitz, R. W. DeVaul, K. Hannun and J. L. B. Rivest, Int. J. Greenhouse Gas Control, 2018, 70, 243–253 CrossRef CAS.
- B. D. Patterson, F. Mo, A. Borgschulte, M. Hillestad, F. Joos, T. Kristiansen, S. Sunde and J. A. van Bokhoven, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 12212–12219 CrossRef CAS PubMed.
- R. Pärnamäe, S. Mareev, V. Nikonenko, S. Melnikov, N. Sheldeshov, V. Zabolotskii, H. V. M. Hamelers and M. Tedesco, J. Membr. Sci., 2021, 617, 118538 CrossRef.
- C. Du, J. R. Du, X. Zhao, F. Cheng, M. E. A. Ali and X. Feng, Ind. Eng. Chem. Res., 2021, 60, 3115–3129 CrossRef CAS.
- R. E. Zeebe and D. Wolf-Gladrow, CO2 in seawater: Equlibrium, kinetics, isotopes, Elsevier Science B.V., 1st edn, 2001 Search PubMed.
- M. Rahimi, G. Catalini, S. Hariharan, M. Wang, M. Puccini and T. A. Hatton, Cell Rep. Phys. Sci., 2020, 1, 100033 CrossRef.
- M. Rahimi, G. Catalini, M. Puccini and T. A. Hatton, RSC Adv., 2020, 10, 16832–16843 RSC.
- T. Kim, B. E. Logan and C. A. Gorski, Environ. Sci. Technol. Lett., 2017, 4, 49–53 CrossRef CAS.
- V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597–1614 RSC.
- D. H. Nam and K. S. Choi, J. Am. Chem. Soc., 2017, 139, 11055–11063 CrossRef CAS PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical methods: Fundamentals and applications, John Wiley & Sons, New York, 2nd edn, 2001 Search PubMed.
- P. Atkins and J. de Paula, Atkins’ physical chemistry, Oxford university press, Oxford, 10th edn, 2014 Search PubMed.
- S. Shiva Kumar and V. Himabindu, Mater. Sci. Energy Technol., 2019, 2, 442–454 Search PubMed.
- A. Villagra and P. Millet, Int. J. Hydrogen Energy, 2019, 44, 9708–9717 CrossRef CAS.
- J. B. Todd, JOM, 1981, 33, 42–45 CrossRef CAS.
- J. I. Otashu and M. Baldea, Comput. Chem. Eng., 2019, 121, 396–408 CrossRef CAS.
- Office of Fossil Energy and Carbon Management, Carbon Negative Shot, https://www.energy.gov/fecm/carbon-negative-shot, (accessed 24 October 2022).
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ee03804h |
| This journal is © The Royal Society of Chemistry 2023 |