Open Access Article
Open Access ArticleA survey of Earth-abundant metal oxides as oxygen evolution electrocatalysts in acidic media (pH < 1)†
Jiahao
Yu
 ab,
Stefano
Giancola
ab,
Stefano
Giancola
 a,
Bahareh
Khezri
a,
Bahareh
Khezri
 ab,
David
Nieto-Castro
ab,
David
Nieto-Castro
 a,
Jesús
Redondo
a,
Jesús
Redondo
 cd,
Frederik
Schiller
cd,
Frederik
Schiller
 ei,
Sara
Barja
ei,
Sara
Barja
 cef,
Maria Chiara
Spadaro
cef,
Maria Chiara
Spadaro
 g,
Jordi
Arbiol
g,
Jordi
Arbiol
 gh,
Felipe A.
Garcés-Pineda
gh,
Felipe A.
Garcés-Pineda
 *a and
José Ramón
Galán-Mascarós
*a and
José Ramón
Galán-Mascarós
 *ah
*ah
aInstitute of Chemical Research of Catalonia (ICIQ-CERCA), The Barcelona Institute of Science and Technology (BIST), Av. Països Catalans 16, 43007 Tarragona, Spain. E-mail: fgarces@iciq.es; jrgalan@iciq.es
bDepartament de Química Física i Inorgànica, Universitat Rovira i Virgili, Marcel. lí Domingo 1, 43007 Tarragona, Spain
cDepartment of Polymers and Advanced Materials, Centro de Física de Materiales, University of the Basque Country UPV/EHU, 20018 San Sebastián, Spain
dDepartment of Surface and Plasma Science, Faculty of Mathematics and Physics, Charles University, 18000, Prague 8, Czech Republic
eDonostia International Physics Center (DIPC), 20018 San Sebastian, Spain
fIKERBASQUE, Basque Foundation for Science, 48009 Bilbao, Spain
gCatalan Institute of Nanoscience and Nanotechnology (ICN2), CSIC and BIST, Campus UAB, Bellaterra, 08193 Barcelona, Catalonia, Spain
hICREA, Passeig Lluis Companys, 23, 08010 Barcelona, Spain
iCentro de Física de Materiales (CSIC-UPV-EHU) and Materials Physics Center (MPC), 20018 San Sebastián, Spain
First published on 2nd August 2023
Abstract
Electrolytic hydrogen appears as one of the most promising options to store renewable energy. In this water splitting process, the sluggish kinetics of the 4-electron oxygen evolution reaction (OER) with its high overpotentials have been widely regarded as the bottleneck to facilitate a fast, energy-efficient process. In alkaline media, numerous earth-abundant metal oxides are efficient OER catalysts, stabilized by the high concentration of hydroxide anions in the electrolyte. However, under acidic conditions, where the hydrogen evolution reaction (HER) is technologically preferred, only noble metal-based oxides (RuO2 and IrO2) are suitable OER catalysts, putting into question the scalability to wide-spread applications due to their scarcity and high cost. Most earth abundant metal oxides dissolve at high proton concentrations. A promising strategy to avoid this drawback consists of incorporating these catalysts into partially hydrophobic composite electrodes. Following this strategy, we have been able to conduct an extensive survey of the activity and stability of mono-, bi- and trimetallic earth-abundant transition metal oxides during the electrocatalytic OER under strongly acidic conditions. Our results confirm the general validity of the strategy by using a hydrophobic electrode to confer high stability to common metal oxides under these harsh conditions. Among all OER catalysts investigated, we found that simple manganese oxides appeared as the most active also exhibiting high, long-term stability. In particular, the stability of Mn2O3 oxide in the OER in acidic media was well confirmed by post-electrolysis characterization data.
Broader contextAcidic water electrolysis from electrolytes with high proton concentration has advantages in hydrogen production. However, only noble metals (typically iridium) are viable oxygen evolution (OER) catalysts to promote acidic water oxidation, limiting the techno-economic development of this technology. We are introducing a novel strategy to stabilize OER catalysts from earth abundant transition metals, by blending them into a partially hydrophobic electrode support. Under these conditions, we have investigated a variety of mono-, bi- and trimetallic oxides, to discover that Mn2O3 is the most active phase, reaching a competitive performance when compared with IrOx, with a remarkable performance stability for over 24 h. The implementation of an analogous approach towards real electrolyzers may open promising opportunities for the substitution of noble metals by economic, viable counterparts. |
Introduction
Electrolytic hydrogen from water splitting is in high demand to support the deployment of renewable energy as an energy storage medium, in the required transition from fossil fuels.1,2 One of the challenges in water electrolysis remains the oxidation catalysts for the anodic oxygen evolution reaction (OER). This 4-electron process is one of the main causes for the slow kinetics and high overpotentials.3 Competitive catalysts from earth abundant materials are required for a viable, large-scale deployment of water electrolysers.Numerous earth-abundant materials are able to work as OER electrocatalysts in alkaline media, reaching excellent performance, for instance the family of nickel–iron mixed oxides or (oxo) hydroxides.4–7 But alkaline technologies have several disadvantages, such as the need for corrosive media (hot, concentrated KOH solutions), and the relatively low current densities achieved, as limited by the OH− transport through the separator/anion-exchange membrane. Significantly higher current densities can be achieved under acidic conditions, thanks to the ultrafast proton transport through a proton exchange solid electrolyte (membrane) and the high proton concentration available for hydrogen generation (HER).8 However, only IrO2-based catalysts are efficient and stable under these conditions. At low pH, inexpensive metal oxides suffer serious dissolution and deactivation, particularly when working at high potentials/current densities.9–11
Several strategies have been proposed to stabilize earth-abundant metal oxides as OER electrocatalysts in acidic media.12–18 Crystalline nickel manganese antimonate on antimony-doped tin oxide (ATO) became stable at current densities of 10 mA cm−2 for 168 h in 1 M H2SO4, finely tuning the metal ratio.12 Co2MnO4 demonstrated robust performance (1500 h) at 200 mA cm−2 at pH 1 when supported on a Pt/Ti mesh.14 Although high overpotentials were needed, these reports are promising results towards earth-abundant OER catalysis under acidic conditions.
Recently,19 we demonstrated that the use of a hydrophobic binder in the anode composition is able to stabilize Co3O4, otherwise unstable under these conditions.20 A Co3O4/CPO (graphitic carbon + paraffin oil) composite sustained a current density of up to 100 mA cm−2 in a 1 M H2SO4 electrolyte. This very same electrode architecture cannot be scaled up to industrial applications, given the intrinsic long-term instability of carbon conducting supports under the OER. But our results confirm the validity of this approach to stabilize the active catalysts at low current densities. Taking advantage of this, here we report a wide screening of first row transition metal (Mn, Fe, Co, Ni and Zn) oxides with mono-, bi- and trimetallic equimolecular composition as OER catalysts in 1 M H2SO4. Interestingly, we found that even Mn-based oxides appear stabilized, while otherwise were characterized as highly unstable.21,22 Protected by the paraffin oil, Mn2O3 anodes showed the best performance in terms of lower overpotentials to reach 10 mA cm−2, with excellent stability (>24 h) when working in 1 M sulfuric acid solution without a sign of fatigue or deactivation. The incorporation of a second or third metal did not improve the activity of the Mn-based oxide. Conversely, the Mn doping was critical to improve the OER activity of some other oxides, such as FeOx, NiOx and FeNiOx, with >120 mV overpotential decrease at 10 mA cm−2 current density. Our results confirm the general stabilizing effect of a partially hydrophobic, conducting binder to allow earth-abundant transition metal oxides to sustain water oxidation in acidic environments.
Experimental
Synthesis
All reagents were commercially available and used as received. Mixed metal oxides were prepared by modified method available in the literature.23 The overall metal concentration of metal (Mn, Fe, Co, Ni and Zn) nitrates was fixed as 0.0125 M, and the corresponding amount of each metallic precursor was calculated in the equivalent ratio (Table S1, ESI†). They were dissolved in 50 mL distilled water with constant stirring. Then, glycine (25 mM) was added into the above solutions and stirred until clear solutions were obtained. Afterwards, the solutions were heated up to 210 °C until total solvent evaporation and glycine combustion. The resulting porous dark solids were collected and calcined at 1100 °C in a tubular oven for 1 h. The synthesis of Mn2O3 followed an analogous procedure, but the calcination step was carried out at 600 °C. For the synthesis of Mn3O4 as a pure phase, we followed a different procedure: Mn(NO3)2·4H2O (0.151 g) and benzimidazole (0.142 g) were dissolved into 15 mL DMF and then the homogeneous solution was transferred into a Teflon-lined stainless steel autoclave. The sealed autoclave was put into an oven and kept at 140 °C for 24 h. After cooling down to room temperature, the brown product was filtered out and washed with acetone, and then dried at 60 °C.The composite electrodes were prepared by 2 hour ball-milling at 20 s−1 of a mixture of paraffin oil (20 mg), graphite powder (80 mg) and oxides (40 mg), namely, MOx/GPO, MM′Ox/GPO or MM′M′′Ox/GPO (M, M′, M′′: Mn, Fe, Co, Ni, Zn). With Mn2O3 the added amount of was decreased to 10 and 20 mg, these electrodes were named as 10-Mn2O3/GPO and 20-Mn2O3/GPO, respectively.
To prepare the (Mn2O3 + graphite)/GC (glassy carbon) electrode, graphite powder (80 mg) and Mn2O3 (40 mg) were mixed by ball milling firstly. Then, 10 mg of above mixture, 25 μL Nafion 117 containing solution and 975 μL ethanol aqueous solution (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in volume) were sonicated for 30 min to obtain dispersed black ink. Finally, 7 μL ink was drop-cast on the GC electrode for comparison experiments.
1 in volume) were sonicated for 30 min to obtain dispersed black ink. Finally, 7 μL ink was drop-cast on the GC electrode for comparison experiments.
Electrochemistry
All electrochemical experiments were performed under ambient conditions using a Bio-Logic VMP3 multichannel potentiostat and implemented with a three-electrode configuration using 1 M H2SO4 (pH 0.1) as the electrolyte solution, carbon rod as the counter electrode, Ag/AgCl (3 M KCl) as the reference electrode and a pocket working electrode (0.07 cm2 surface area and 4 mm depth) filled with the GPO composites. The actual mass amounts of the MOx/GPO, MM′Ox/GPO and MM′M′′Ox/GPO composites in the electrode pocket were measured with an analytical weight balance and indicated in Table S1 (ESI†). Although it is difficult to estimate the actual active layer, an estimation is suggested that 1/8 of the total electrode pocket volume is used as the maximum limit in contact with the solution in order to determine the mass loading for comparison.17 All potentials were measured versus the Ag/AgCl electrode and converted to the RHE reference scale using ERHE = EAg/AgCl + 0.21 + 0.059 pH (V) while overpotentials η = ERHE – 1.23 V. Every LSV (linear sweep voltammetry) curve was recorded with a 1 mV s−1 scan rate for activity comparison after 10-CV (cyclic voltammetry) cycle activation. All current densities were calculated based on the geometrical surface area of the electrodes. The Ohmic drop was determined for all electrochemical data by using the automatic current interrupt (CI) software (Table S1, ESI†). The iR drop, experimentally determined using the CI technique, was corrected for all the electrodes. Tafel slopes were estimated from the LSV curves by plotting overpotential η vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j (j = current density). The potential vs. RHE to drive 1 mA cm−2 was used to define onset potential. Chronopotentiometry tests were carried out at fixed current density of 10 mA cm−2. For the electrochemical double-layer capacitance (EDLC) measurements, open circuit potentials (OCPs) vs. the Ag/AgCl were firstly recorded for 30 min to reach rather stable values. Then CV experiments were carried out with 50 mV s−1 scan rate. Combined with above CV measurements, the 100 mV potential windows centered at OCPs could be determined and cyclic voltammetry were then carried out under scanning rates of 20, 40, 60, 80 and 100 mV s−1. The current density differences between the minimum and maximum values at OCPs vs. the Ag/AgCl and the corresponding scanning rates were plotted to calculate the EDLC value (1/2 of the slope of current density–scan rate plots).24 Electrochemical impedance spectroscopy (EIS) was performed by means of a typical three-electrode cell in the frequency range from 200 kHz to 100 mHz with 6 points per decade under OCP after CV activation. CVs were collected between 50 and 200 mV s−1 and the surface concentration of redox active Mn centers was extracted from the slope of the linear relationship between the peak current of the reduction wave and the scan rate,25 according to the following equation:
j (j = current density). The potential vs. RHE to drive 1 mA cm−2 was used to define onset potential. Chronopotentiometry tests were carried out at fixed current density of 10 mA cm−2. For the electrochemical double-layer capacitance (EDLC) measurements, open circuit potentials (OCPs) vs. the Ag/AgCl were firstly recorded for 30 min to reach rather stable values. Then CV experiments were carried out with 50 mV s−1 scan rate. Combined with above CV measurements, the 100 mV potential windows centered at OCPs could be determined and cyclic voltammetry were then carried out under scanning rates of 20, 40, 60, 80 and 100 mV s−1. The current density differences between the minimum and maximum values at OCPs vs. the Ag/AgCl and the corresponding scanning rates were plotted to calculate the EDLC value (1/2 of the slope of current density–scan rate plots).24 Electrochemical impedance spectroscopy (EIS) was performed by means of a typical three-electrode cell in the frequency range from 200 kHz to 100 mHz with 6 points per decade under OCP after CV activation. CVs were collected between 50 and 200 mV s−1 and the surface concentration of redox active Mn centers was extracted from the slope of the linear relationship between the peak current of the reduction wave and the scan rate,25 according to the following equation: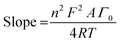 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1); A = electrode surface area (0.07 cm−2); Γ0 = surface concentration (mol cm−2); R = ideal gas constant (0.082 atm L K−1 mol−1); and T = temperature (293 K).
485 C mol−1); A = electrode surface area (0.07 cm−2); Γ0 = surface concentration (mol cm−2); R = ideal gas constant (0.082 atm L K−1 mol−1); and T = temperature (293 K).
The turnover frequency (TOF) per active site was calculated using the equation
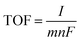 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), m is 4 for oxygen evolution.26
485 C mol−1), m is 4 for oxygen evolution.26
Faradaic efficiency
In order to evaluate the faradaic efficiency towards oxygen production, the chronopotentiometric experiment was carried out applying a fixed current (10 mA cm−2) while the oxygen concentration in the headspace was measured in situ by using an Ocean Optics NeoFOX sensing system equipped with an FOSPOR probe. The FOSPOR probe was calibrated with a two-point calibration, fixing 0% O2 under N2 flow and 20.9% O2 in air. The experiment was performed in a home-made H-type cell with a frit glass separating both compartments and a connection for the sensor to be inserted in the anodic gas headspace (∼2.5 mL) (Fig. S1, ESI†). The solution was completely deaerated by purging with N2 before starting the experiment, for at least 1 h. Then N2 flow was removed and a base line of 10 min was recorded before starting the chronoamperometry.The mols of O2 generated during the electrochemical experiment were calculated via the following equation, considering ideal gas behavior:
nO2,exp = % O2g·Ptotal·Vgas![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) space·R−1T−1/100 space·R−1T−1/100 | (3) |
| nO2,far = Qne−1F−1 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1).
485 C mol−1).
Then faradaic efficiency (in %), FE, is calculated as follows:
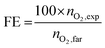 | (5) |
Physical characterization
Powder X-ray diffraction (PXRD) data were recorded with a Bruker D8 Advance Series equipped with a VANTEC-1 PSD3 detector. Elemental analyses were carried out on an Agilent (ICPMS7900) inductively coupled plasma spectrometer with a mass detector (ICP-MS) at the University of Valencia. X-ray photoelectron spectroscopy (XPS) was carried out holding the sample at room temperature and illuminating it with a monochromatized Al Kα source (hν = 1486.6 eV) from a microfocus setup (SPECS Focus 600). The excited photo-electrons were collected by a SPECS 150 hemispherical analyzer at emission and incidence angles of 40° and 60°, respectively. The powder electrodes were deposited on top of indium tape for the XPS measurements. High resolution transmission electron microscopy (HRTEM) and scanning transmission electron microscopy (STEM) investigations were performed on a field emission gun FEI Tecnai F20 microscope. High angle annular dark-field (HAADF) STEM was combined with electron energy loss spectroscopy (EELS) on a Tecnai microscope by using a GATAN QUANTUM energy filter in order to obtain compositional maps.Results and discussion
Metal oxide preparation
It has been well documented that catalyst preparation and processing may affect electrochemical performance.27–32 To minimize synthetic effects, all oxides for this survey were prepared by the very same combustion methodology.22 We prepared twenty five oxides in total with the following ratio among reagents: MOx (monometallic); MM′Ox (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio); and MM′M′′Ox (33
50 ratio); and MM′M′′Ox (33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 ratio).
33 ratio).
Although this method did not yield completely homogeneous materials for each composition, we chose it as a common method for all materials, to minimize performance differences originated from the use different synthetic preparation methods. The dominant crystalline phases in the products were identified by powder X-ray diffraction (PXRD) and assigned to Powder Diffraction File (PDF) cards (Fig. S2–26, ESI†). According to the structural data, most of the materials contained single crystalline phases (Table 1) with some exceptions. Metal composition was determined by energy-dispersive X-ray (EDX) spectra, and in good agreement with the reagent ratio (Fig. S7–S26 and Table S1, ESI†).
| Catalyst | Crystalline phases found |
|---|---|
| MnOx | Mn2O3, Mn3O4 |
| FeOx | Fe2O3 |
| CoOx | Co3O4 |
| NiOx | NiO |
| ZnOx | ZnO |
| MnFeOx | (Mn, Fe)2O3 |
| MnCoOx | (Co, Mn)3O4 |
| MnNiOx | Ni6MnO8 |
| MnZnOx | ZnMnO3, ZnMn3O4 |
| FeCoOx | (Co, Fe)2O3 |
| FeNiOx | NiFe2O4 |
| FeZnOx | ZnFe2O4, ZnO |
| CoNiOx | (Co, Ni)O |
| CoZnOx | ZnCo2O4, ZnO |
| NiZnOx | (Ni, Zn)O |
| MnFeCoOx | (Mn, Fe, Co)3O4 |
| MnFeNiOx | (Mn, Ni)Fe2O4, (Mn, Fe)Ni2O4 |
| MnFeZnOx | ZnMn3O4, (Fe, Zn)0.85O, MnFe2O4 |
| MnCoNiOx | Ni6MnO8, (Co, Ni)O |
| MnCoZnOx | (Mn, Zn)Co2O4 |
| MnNiZnOx | Ni6MnO8, (Ni, Zn)O |
| FeCoNiOx | (Co, Ni)Fe2O4 |
| FeCoZnOx | (Fe, Co)2O3, ZnO |
| FeNiZnOx | Fe3O4, (Ni, Zn)O |
| CoNiZnOx | CoNiO2, ZnCo2O4, ZnO |
The oxides were mixed with graphite (G) and paraffin oil (PO) in the desired ratio (see the Experimental section) to obtain homogeneous composites (MOx/GPO, MM′Ox/GPO and MM′M′′Ox/GPO) to be inserted into the pocket of a working electrode.
Comparative OER performance
We applied the same experimental protocol to collect the linear sweep voltammetry (LSV) for all of the oxide electrodes in 1 M H2SO4 electrolyte (Fig. 1). In the monometallic series, we observed that MnOx shows a pre-catalytic, reversible event that we assigned to a Mn3+/Mn4+ oxidation (Fig. 1a). MnOx/GPO offered the best voltage efficiency, reaching ≈50 mA cm−2 at 1.73 V although the pre-catalytic event does not allow the onset potential to be directly estimated. All other oxides showed onset potentials >1.55 V (vs. RHE) with current densities below 20 mA cm−2 at 1.73 V vs. RHE (Fig. 1b and Table 2), with decreasing activity as Co > Fe > Zn > Ni. The H2SO4 electrolyte used does not contain metallic impurities, precluding Fe uptake, well known to enhance the activity of NiOx phases.33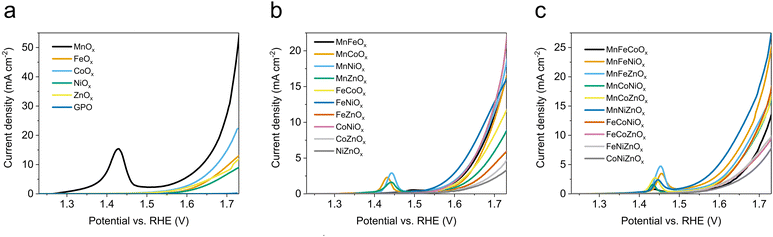 | ||
| Fig. 1 LSV curves in 1 M H2SO4 electrolyte (pH 0.1) with 1 mV s−1 scan rate of (a) MOx/GPO, (b) MM′Ox/GPO, (c) MM′M′′Ox/GPO. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h)
h)
| Electrode | η 10 (V) j = 10 mA cm−2 | j 500 (mA cm−2) η = 500 mV | η t=0.1 (V) |
η
t=2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h (V) h (V) |
|---|---|---|---|---|
| MnOx | 0.407 | 52 | 0.421 | 0.425 |
| FeOx | 0.473 | 14 | 0.544 | 0.536 |
| CoOx | 0.443 | 22 | 0.468 | 0.466 |
| NiOx | — | 9 | 0.596 | 0.604 |
| ZnOx | 0.486 | 12 | 0.582 | 0.591 |
| MnFeOx | 0.465 | 16 | 0.485 | 0.466 |
| MnCoOx | 0.467 | 16 | 0.496 | 0.495 |
| MnNiOx | 0.459 | 18 | 0.488 | 0.480 |
| MnZnOx | — | 9 | 0.546 | 0.488 |
| FeCoOx | 0.485 | 12 | 0.550 | 0.537 |
| FeNiOx | 0.448 | 16 | 0.537 | 0.548 |
| FeZnOx | — | 6 | 0.615 | 0.588 |
| CoNiOx | 0.454 | 23 | 0.496 | 0.488 |
| CoZnOx | — | 5 | 0.565 | 0.528 |
| NiZnOx | — | 3 | 0.617 | 0.588 |
| MnFeCoOx | 0.484 | 14 | 0.499 | 0.478 |
| MnFeNiOx | 0.437 | 25 | 0.467 | 0.462 |
| MnFeZnOx | 0.453 | 17 | 0.511 | 0.476 |
| MnCoNiOx | 0.462 | 16 | 0.502 | 0.477 |
| MnCoZnOx | 0.462 | 17 | 0.497 | 0.468 |
| MnNiZnOx | 0.417 | 27 | 0.472 | 0.470 |
| FeCoNiOx | 0.458 | 17 | 0.539 | 0.528 |
| FeCoZnOx | — | 9 | 0.537 | 0.518 |
| FeNiZnOx | — | 10 | 0.568 | 0.564 |
| CoNiZnOx | — | 8 | 0.558 | 0.533 |
| Mn2O3 | 0.328 | 124 | 0.358 | 0.365 |
| Mn3O4 | 0.282 | 74 | 0.438 | 0.432 |
In the bimetallic oxide series, the highest current density was found for the CoNiOx, reaching 23 mA cm−2 at 1.73 V vs. RHE (Fig. 1b), still far from the activity found in MnOx/GPO electrodes. Meanwhile, pre-catalytic oxidation peaks were found for all Mn-containing catalysts, in which MnFeOx, MnCox, MnNiOx showed quite similar activities. The rest of the series exhibited lower performance (Table 2). The FeNi oxide, which is regarded as most efficient OER electrocatalyst in alkaline media, appeared to offer the best performance before 1.7 V and then be overpassed by CoNi and MnNi oxides.7,34,35
The trimetallic series (Fig. 1c), follows the same trend with the appearance of a pre-catalytic event in Mn-containing oxides. In this case, the highest activity was found for MnNiZnOx, reaching 27 mA cm−2 at 1.73 V vs. RHE. No material exhibited an electrocatalytic OER performance matching that of MnOx/GPO electrodes.
Beyond activity, stability is a crucial feature required for OER electrocatalysts. To evaluate this, we used the benchmarking protocol proposed by Jaramillo et al.,6,36 comparing the evolution of overpotential during a 2 h chronopotentiometry at 10 mA cm−2. The results for the most active electrodes are shown in Fig. S27 (ESI†), with their benchmarking comparison with other electrocatalysts in recent literature (Fig. 2). We found good stability for all oxides examined in this survey, suggesting the validity of the approach: a hydrophobic binder/surface confers great stability to (almost) all metal oxides during the OER under extremely acidic conditions, opening an interesting strategy towards future applications. Some oxides (such as MnZnOx, CoZnOx) improved their activity during the tests. We selected MnOx/GPO as the best performing catalyst for further studies, to better define structure/performance correlations.
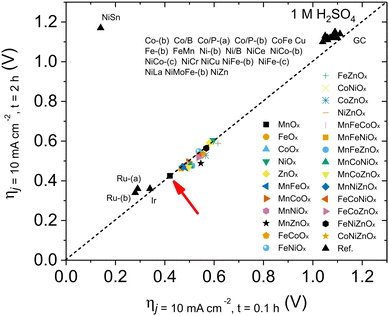 | ||
| Fig. 2 Benchmarking of the activity/stability features for OER electrocatalysts in acidic media following the protocol by Jaramillo et al.6 | ||
OER with Mn oxides in 1 M H2SO4
As described before (Table 1 and Fig. S2, ESI†), the MnOx obtained with our standardized synthetic method was indeed a mixture of two crystalline phases, Mn2O3 and Mn3O4. We prepared the Mn2O3 and Mn3O4 single phases to identify their actual OER catalytic activity. We used two different synthetic protocols to obtain pure phases of each. GPO electrodes were prepared and characterized following the same previous protocols.After 10-cycle CV activation (Fig. S28, ESI†), LSV data of Mn2O3/GPO and Mn3O4/GPO were measured and collected. The results indicated that Mn2O3/GPO offered better OER activity, reaching a current density of 124 mA cm−2 at 1.73 V (Fig. 3a). Interestingly, the Mn3O4/GPO electrodes offered instead analogous performance to the original MnOx/GPO electrodes. The electrochemical double-layer capacitance (EDLC) data, which are proportional to the electrochemically active area, were estimated at 29 and 10 mF cm−2 for Mn2O3/GPO and Mn3O4/GPO respectively (Fig. S29, ESI†). This larger EDLC may contribute to the higher electrochemical activity observed. However, this should not be the only significant effect, since other parameters point also towards a genuine better catalytic performance for Mn2O3/GPO.
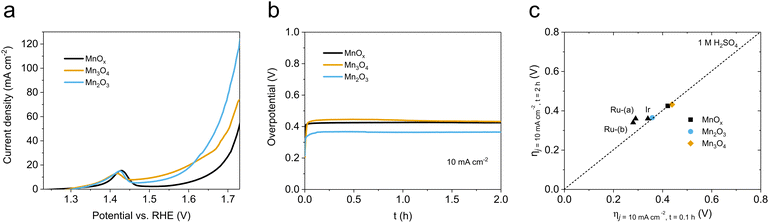 | ||
| Fig. 3 (a) electrocatalytic activity of MnOx/GPO, Mn3O4/GPO and Mn2O3/GPO; (b) stability tests of MnOx/GPO, Mn3O4/GPO and Mn2O3/GPO in chronopotentiometry measurements at 10 mA cm−2; (c) benchmarking of the activity/stability features between our Mn-based oxide and noble metal-based electrocatalysts according to the study of Jaramillo et al.6 | ||
The total density of active centers can be estimated from the Mn4+/Mn3+ quasi-reversible redox pair observed in the CV data (Fig. S30, ESI†). The measurements at different scan rates allowed us to estimate a 172 nmol cm−2 density for Mn2O3/GPO and 100 nmol cm−2 density for Mn3O4/GPO, respectively. Besides, a higher TOF value was found for Mn2O3/GPO (0.0013 s−1) compared to that of Mn3O4/GPO (0.00071 s−1) under a 500 mV overpotential. In addition to the larger density of active Mn3+/Mn4+ centers and turnover frequency per active site, the smaller Nyquist semicircle diameter in the electrochemical impedance spectroscopy (Fig. S31, ESI†) showed a faster charge transfer for Mn2O3/GPO with a lower Rct value of 10 Ω compared to 17 Ω of Mn3O4/GPO. This suggests a faster reaction mechanism also supported by the Tafel analysis: a distinct Tafel slope of 158 mV dec−1 was found for Mn2O3/GPO, much lower than the 287 mV dec−1 found for Mn3O4 (Fig. S32, ESI†). The Tafel slope is directly dependent on the kinetics of the rate-limiting step, and not on the total number of available active sites.37 MnOx/GPO electrodes showed a quite similar Tafel slope (157 mV dec−1) to that of Mn2O3/GPO, showing the dominant contribution of the Mn2O3 active phase. The previous benchmarking protocol applied to Mn2O3/GPO showed a stable, low overpotential of ≤365 mV, to maintain a comparable performance of noble metal (Fig. 3b and c). The long-term stability of this catalyst was also confirmed during a 24 h chronopotentiometry at 10 mA cm−2 (Fig. S33, ESI†). Besides, this excellent stability was much better than that of other Mn-based materials towards OER in acid (Table S2, ESI†). After the benchmarking experiment, we analyzed the electrolyte content to check for any Mn leaching (Table S3, ESI†). We found the presence of Mn just at the ppb level, accounting for a maximum leaching of ≈0.38% of the total. With these data, we can estimate a stability number38 of 130, and an activity-stability factor39 of 52. An estimated lifetime of 3914 h is comparable and competitive to that of noble metal-based catalysts under analogous conditions. This is a promising performance/stability matching for noble metal oxide catalysts under acidic conditions.
To confirm the critical role of the hydrophobic binder, we performed analogous experiments with Mn2O3 on glassy carbon electrodes (Mn2O3/GC), without the addition of paraffin oil. The electrochemistry of this electrode differed significantly from that observed for the related Mn2O3/GPO electrode. Lower currents were reached, below 1.5 mA cm−2 at a 500 mV overpotential (Fig. S34A, ESI†). Moreover, the Mn2O3/GC electrodes completely lost activity after just ∼15 minutes under a 2 mA cm−2 density (current (Fig. S34B, ESI†). This fast deactivation in the absence of the paraffin oil supports its active protective role in the GPO binder.19,21,22
Finally, we measured anodic oxygen evolution during chronopotentiometry experiments with Mn2O3/GPO electrodes at a constant current density of 10 mA cm−2 (Fig. S35, ESI†). >99% faradaic efficiency was obtained, confirming that the dominant catalysis process was the OER under these conditions.
Post-electrolysis Mn2O3/GPO characterization
We characterized the structural and chemical evolution of the Mn2O3/GPO electrodes after these 2 h electrolysis at 10 mA cm−2 in 1 M H2SO4, further confirming the stability of Mn2O3 as a genuine OER catalyst. The PXRD patterns confirm the presence and stability of the Mn2O3 phase as no significant change nor shift were found in the observed peaks (Fig. S36, ESI†). This suggests no evident structural changes are occurring in the bulk of the material Mn2O3.We also investigated the Mn2O3/GPO composite after 2 h electrolysis at 10 mA cm−2 by means of HRTEM (Fig. 4). The HRTEM images and STEM-EELS analyses also confirmed a high structural and chemical stability (Fig. S37–S41, ESI†). As we can observe in Fig. 4a, the NPs still have the orthorhombic Pbca α-Mn2O3 atomic structure (S.G.: 61) imaged along its [101] zone axis. The presence of crystalline graphite has been also evidenced with the 2H oriented structure along its [0001] zone axis. In Fig. 4b both top and side views are reported and highlighted in the frequency filtered map, in red and yellow respectively. In Fig. 4c the STEM-HAADF image and STEM-EELS analysis is reported observing that the elements are homogeneously distributed confirming the atomic ratio evaluated from the HRTEM analysis. The crystalline nature of the graphite is also evidenced as it has been possible to extrapolate its contribution from the amorphous C arising from the TEM grid support. For STEM-EELS the C K edge at 284 eV (blue for amorphous and orange for graphite), O K edge at 532 eV (green) and Mn L edge at 640 eV (red) have been used. On the right side of Fig. 4c the relative composition analysis of Mn and O is also reported, to evaluate the atomic ratio of the investigated NPs. By comparing the HRTEM and STEM-EELS analysis from all the investigated samples we can observe that neither crystallinity nor particle size are affected by the electrochemical process.
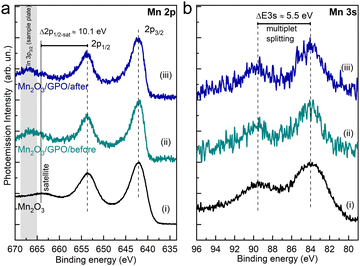
We employed X-ray photoemission spectroscopy to determine the surface chemical composition of the electrodes before and after the electrocatalytic process. Fig. 5a shows the Mn 2p core-level of the Mn2O3/GPO composite before (ii) and after (iii) the electrochemical test. The spectra of Mn2O3 without the binder (i) are provided for reference.
The two main emission peaks correspond to the 2p3/2 and 2p1/2 components arising from the spin–orbit splitting. The different possible oxidation states of a transition metal in an oxide contribute to the 2p core level line shape. In this considered Mn case, this involves Mn2+, Mn3+ and Mn4+ oxidation states, which challenges the unambiguous assignment of the oxide formed (Fig. S42, ESI†). Still, the absence of satellites peaks at about 6 eV higher binding energies from 2p1/2 and 2p3/2 components fairly allows us to exclude the MnO phase,40 while the observance of the Mn 2p1/2 satellite structure (ΔE2p1/2-sat ≈ 10.1 eV) supports the presence of the Mn2O3 phase41,42 identified by HRTEM analysis. Note that the apparent attenuation of the described satellite in the Mn2O3/GPO samples is related to the overlap with the In 3p3/2 photoemission peak from the In foil used as a sample plate (see the Experimental section).
Relevantly, we do not observe a variation of the Mn 2p line shape, nor energy shift in the binding energy of the 2p components, from the electrode after the OER compared to the as-synthesized electrode. In addition to the line shape of the Mn 2p spectra, analysis of the energy separation of the two peaks characteristics of the Mn 3s core-level has been used to identify the Mn oxidation state. Fig. 5b shows the Mn 3s spectra of the Mn2O3/GPO composite before (ii) and after (iii) the electrochemical test, as well as the Mn2O3 reference (i). The energy peak separation of the Mn 3s multiplet splitting ΔE3s ≈ 5.5 eV, constant across the three compounds, additionally supports the absence of significant changes in the oxidation state of the catalyst due to the electrochemical performance.41,42
These experiments showed the bulk and functional stability of Mn2O3/GPO electrodes during acidic OER electrocatalysis. Nevertheless, we cannot discard surface reconstruction occurring under operation conditions. This is a challenging task that will be worth investigating using appropriate techniques.43
Conclusions
In summary, we have carried out a survey of earth abundant transition metal oxides as oxygen evolution electrocatalysts under acidic conditions using a conductive and partially hydrophobic support to confer on them good stability. This reliable strategy has allowed us to compare their electrochemical performance despite their intrinsic instability towards dissolution or deactivation. Among all the oxides tested, Mn2O3-based anodes successfully passed the benchmarking protocol in acidic media and were able to deliver 10 mA cm−2 in 1 M sulfuric acid solution (pH < 0.1) at a low overpotential η < 365 mV. Besides, the critical role of Mn doping was also found to greatly improve the acidic OER performance. These comprehensive findings will be helpful in the challenge of stabilizing earth-abundant electrocatalysts for the acidic OER, and they confirm that the promising activity of Mn centers under these conditions, superior to all the other transition metals investigated. Efficient elemental doping and structural engineering could further improve the electrocatalytic performance of Mn2O3.Author contributions
J.R.G.M. and F.A.G.P. conceived the original concept and designed the project. J.Y. and F.A.G.P. coordinated the efforts of the research team. J.Y., F.A.G.P., B.K. and D.N.C. synthesized, processed and structurally characterized the materials and electrodes. J.Y. performed the electrochemical experiments and analyzed the data. J.Y. and S.G. quantified the oxygen evolution. J.R., F.S., and S.B. collected and analyzed the XPS data. M.C.S. and J. A. collected and analyzed the TEM data. J.Y., F.A.G.P., and J.R.G.M. co-wrote the manuscript with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful for the support from MCIN/AEI/10.13039/501100011033/ and “ERDF A way of making Europe” through projects RED2022-134508-T (CAT&SCALE), PID2021-124796OB-I00 and PID2020-116093RB-C43&C44 funded by MCIN/AEI/10.13039/501100011033; from the Generalitat de Catalunya (2021SGR1154 and 2021SGR00457), and from the Basque Government (IT-1591-22). S.B. acknowledges RYC-2017-21931 funded via MCIN/AEI/10.13039/501100011033 and by ESF Investing in your future and UPV/EHU project EHUrOPE19/01. ICIQ and ICN2 are supported by the Ministerio de Ciencia e Innovación through the Severo Ochoa Excellence Accreditations CEX2019-000925-S (MCIN/AEI) and CEX2021-001214-S; and by the CERCA Programme/Generalitat de Catalunya. J.Y. thanks the China Scholarship Council (CSC) for predoctoral fellowships (File No. 201806270234). J.R. acknowledges the Czech Science Foundation and funding from PIF outgoing project number 22-18079O. M.C.S. has received funding from the European Union's Horizon 2020 research and innovation programme under Marie Skodowska-Curie grant 754510 (PROBIST) and the Severo Ochoa programme. M.C.S. is also thankful for the funding from the postdoctoral fellowship Juan de la Cierva Incorporation from MICINN (JCI-2019) and the Severo Ochoa programme. This study is part of the Advanced Materials programme and was supported by MCIN with funding from the European Union NextGenerationEU (PRTR-C17.I1) and the Generalitat de Catalunya.References
- Z. W. She, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, 1–12 Search PubMed.
- S. G. Nnabuife, J. Ugbeh-Johnson, N. E. Okeke and C. Ogbonnaya, Carbon Capture Sci. Technol., 2022, 3, 100042 CrossRef CAS.
- Z. Chen, L. Guo, L. Pan, T. Yan, Z. He, Y. Li, C. Shi, Z. F. Huang, X. Zhang and J. J. Zou, Adv. Energy Mater., 2022, 12, 2103670 CrossRef CAS.
- H. Ding, H. Liu, W. Chu, C. Wu and Y. Xie, Chem. Rev., 2021, 121, 13174–13212 CrossRef CAS PubMed.
- J. Yu, G. Cheng and W. Luo, J. Mater. Chem. A, 2017, 5, 11229–11235 RSC.
- C. C. L. McCrory, S. Jung, I. M. Ferrer, S. M. Chatman, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2015, 137, 4347–4357 CrossRef CAS PubMed.
- M. Gong and H. Dai, Nano Res., 2015, 8, 23–39 CrossRef CAS.
- C. Spöri, J. T. H. Kwan, A. Bonakdarpour, D. P. Wilkinson and P. Strasser, Angew. Chem., Int. Ed., 2017, 56, 5994–6021 CrossRef PubMed.
- T. Reier, H. N. Nong, D. Teschner, R. Schlögl and P. Strasser, Adv. Energy Mater., 2017, 7, 1601275 CrossRef.
- Z. Lei, T. Wang, B. Zhao, W. Cai, Y. Liu, S. Jiao, Q. Li, R. Cao and M. Liu, Adv. Energy Mater., 2020, 10, 200478 Search PubMed.
- Y. Liu, X. Liang, H. Chen, R. Gao, L. Shi, L. Yang and X. Zou, Chinese J. Catal., 2021, 42, 1054–1077 CrossRef CAS.
- I. A. Moreno-Hernandez, C. A. Macfarland, C. G. Read, K. M. Papadantonakis, B. S. Brunschwig and N. S. Lewis, Energy Environ. Sci., 2017, 10, 2103–2108 RSC.
- M. Chatti, J. L. Gardiner, M. Fournier, B. Johannessen, T. Williams, T. R. Gengenbach, N. Pai, C. Nguyen, D. R. MacFarlane, R. K. Hocking and A. N. Simonov, Nat. Catal., 2019, 2, 457–465 CrossRef CAS.
- A. Li, S. Kong, C. Guo, H. Ooka, K. Adachi, D. Hashizume, Q. Jiang, H. Han, J. Xiao and R. Nakamura, Nat. Catal., 2022, 5, 109–118 CrossRef CAS.
- S. Pan, H. Li, D. Liu, R. Huang, X. Pan, D. Ren, J. Li, M. Shakouri, Q. Zhang, M. Wang, C. Wei, L. Mai, B. Zhang, Y. Zhao, Z. Wang, M. Graetzel and X. Zhang, Nat. Commun., 2022, 13, 2294 CrossRef CAS PubMed.
- J. Huang, H. Sheng, R. D. Ross, J. Han, X. Wang, B. Song and S. Jin, Nat. Commun., 2021, 12, 3036 CrossRef CAS PubMed.
- M. Blasco-Ahicart, J. Soriano-Lopez, J. J. Carbo, J. M. Poblet and J. R. Galan-Mascaros, Nat. Chem., 2018, 10, 24–30 CrossRef CAS PubMed.
- P. Y. Tang, L. J. Han, F. S. Hegner, P. Paciok, M. Biset-Peiró, H. C. Du, X. K. Wei, L. Jin, H. B. Xie, Q. Shi, T. Andreu, M. Lira-Cantú, M. Heggen, R. E. Dunin-Borkowski, N. López, J. R. Galán-Mascarós, J. R. Morante and J. Arbiol, Adv. Energy Mater., 2019, 9, 1901836 CrossRef.
- J. Yu, F. A. Garcés-Pineda, J. González-Cobos, M. Peña-Díaz, C. Rogero, S. Giménez, M. C. Spadaro, J. Arbiol, S. Barja and J. R. Galán-Mascarós, Nat. Commun., 2022, 13, 4341 CrossRef CAS PubMed.
- M. Etzi Coller Pascuzzi, M. van Velzen, J. P. Hofmann and E. J. M. Hensen, ChemCatChem, 2021, 13, 459–467 CrossRef CAS.
- L. Zhou, A. Shinde, J. H. Montoya, A. Singh, S. Gul, J. Yano, Y. Ye, E. J. Crumlin, M. H. Richter, J. K. Cooper, H. S. Stein, J. A. Haber, K. A. Persson and J. M. Gregoire, ACS Catal., 2018, 8, 10938–10948 CrossRef CAS.
- L. G. Bloor, P. I. Molina, M. D. Symes and L. Cronin, J. Am. Chem. Soc., 2014, 136, 3304–3311 CrossRef CAS PubMed.
- J. Y. C. Chen, J. T. Miller, J. B. Gerken and S. S. Stahl, Energy Environ. Sci., 2014, 7, 1382–1386 RSC.
- D. M. Morales and M. Risch, JPhys Energy, 2021, 3, 34013 CrossRef CAS.
- S. Pintado, S. Goberna-Ferrón, E. C. Escudero-Adán and J. R. Galán-Mascarós, J. Am. Chem. Soc., 2013, 135, 13270–13273 CrossRef CAS PubMed.
- J. Zhu, Y. Guo, F. Liu, H. Xu, L. Gong, W. Shi, D. Chen, P. Wang, Y. Yang, C. Zhang, J. Wu, J. Luo and S. Mu, Angew. Chem., Int. Ed., 2021, 60, 12328–12334 CrossRef CAS PubMed.
- D. Chen, R. Yu, D. Wu, H. Zhao, P. Wang, J. Zhu, P. Ji, Z. Pu, L. Chen, J. Yu and S. Mu, Nano Energy, 2022, 100, 107445 CrossRef CAS.
- Q. Ma and S. Mu, Interdiscip. Mater., 2023, 2, 53–90 CrossRef.
- A. Govind Rajan, J. M. P. Martirez and E. A. Carter, ACS Catal., 2020, 10, 11177–11234 CrossRef CAS.
- P. Wang and B. Wang, ACS Appl. Mater. Interfaces, 2021, 13, 59593–59617 CrossRef CAS PubMed.
- Q. Xu, J. Zhang, H. Zhang, L. Zhang, L. Chen, Y. Hu, H. Jiang and C. Li, Energy Environ. Sci., 2021, 14, 5228–5259 RSC.
- S. Li, Y. Gao, N. Li, L. Ge, X. Bu and P. Feng, Energy Environ. Sci., 2021, 14, 1897–1927 RSC.
- L. Trotochaud, S. L. Young, J. K. Ranney and S. W. Boettcher, J. Am. Chem. Soc., 2014, 136, 6744–6753 CrossRef CAS PubMed.
- F. Song and X. Hu, Nat. Commun., 2014, 5, 4477 CrossRef CAS PubMed.
- F. A. Garcés-Pineda, H. Chuong Nguyën, M. Blasco-Ahicart, M. García-Tecedor, M. de Fez Febré, P. Y. Tang, J. Arbiol, S. Giménez, J. R. Galán-Mascarós and N. López, ChemSusChem, 2021, 14, 1595–1601 CrossRef PubMed.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 13801 CrossRef PubMed.
- S. Geiger, O. Kasian, M. Ledendecker, E. Pizzutilo, A. M. Mingers, W. T. Fu, O. Diaz-Morales, Z. Li, T. Oellers, L. Fruchter, A. Ludwig, K. J. J. Mayrhofer, M. T. M. Koper and S. Cherevko, Nat. Catal., 2018, 1, 508–515 CrossRef CAS.
- Y. T. Kim, P. P. Lopes, S. A. Park, A. Y. Lee, J. Lim, H. Lee, S. Back, Y. Jung, N. Danilovic, V. Stamenkovic, J. Erlebacher, J. Snyder and N. M. Markovic, Nat. Commun., 2017, 8, 1449 CrossRef PubMed.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- M. A. Stranick, Surf. Sci. Spectra, 1999, 6, 39 CrossRef CAS.
- Y. Gorlin and T. F. Jaramillo, J. Am. Chem. Soc., 2010, 132, 13612–13614 CrossRef CAS PubMed.
- X. Luo, X. Tan, P. Ji, L. Chen, J. Yu and S. Mu, EnergyChem, 2022, 5, 100091 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ey00101f |
| This journal is © The Royal Society of Chemistry 2023 |