Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Deconvoluting kinetics and transport effects of ionic liquid layers on FeN4-based oxygen reduction catalysts†
Silvia
Favero
 a,
Ifan E. L.
Stephens
a,
Ifan E. L.
Stephens
 *b and
Maria-Magdalena
Titirici
*b and
Maria-Magdalena
Titirici
 *a
*a
aDepartment of Chemical Engineering, Imperial College London, South Kensington Campus, Exhibition Rd, London, SW7 2AZ, UK. E-mail: m.titirici@imperial.ac.uk
bDepartment of Materials, Imperial College London, White City Campus, 80 Wood Ln, London, W12 7TA, UK
First published on 15th July 2023
Abstract
The use of ionic liquid layers has been reported to improve both the activity and durability of several oxygen reduction catalysts. However, the development of this technology has been hindered by the lack of understanding of the mechanism behind this performance enhancement. In this work, we use a library of ionic liquids to modify a model FeN4 catalyst (iron phthalocyanine), to decouple the effects of ionic liquid layers on oxygen reduction kinetics and oxygen transport. Our results show that oxygen reduction activity at low overpotentials it determined by the ionic liquids’ influence on the *OH binding energy on the active sites, while oxygen solubility and diffusivity controls transport at high overpotentials. Finally, using nitrogen physisorption, we have demonstrated that the distribution of the ionic liquids on the catalyst is inhomogeneous, and depends on the nature of the ionic liquid used.
Broader contextHydrogen fuel cells are emerging as an effective technology for the production of green electricity. However, their widespread commercialization is hindered by the requirement of platinum to catalyse the sluggish oxygen reduction reaction, taking place at the cathode of fuel cells. Research has been therefore focusing on developing cheaper and more sustainable alternative catalysts. Among such catalysts, those based on iron, an in particular on an FeN4 active site, have shown promising performance, but are still behind platinum in terms of both activity and durability. More recently, a technique as emerged to improve the performance of oxygen reduction catalysts, based on the addition of a thin film of hydrophobic and oxygenophilic ionic liquids. |
1. Introduction
To mitigate global warming, green H2 and its utilization in fuel cells have been identified as key technologies. The biggest drawback of low temperature hydrogen fuel cells is the high content of platinum-group-metals (PGM), required to drive the sluggish oxygen reduction reaction (ORR). Despite recent efforts on decreasing platinum, at the present state 0.1 to 0.2 gPt kW−1 are still required,1 accounting for 40–50% of the overall cost of fuel cells for automotive applications.2At the same time, PGM-free ORR catalysts have been developed, with impressive recent advances in both stability and activity, with a particular attention to iron and nitrogen-doped carbons (Fe–N–C).3,4 Nevertheless, their performance is still far from the activity and durability targets set by the US department of energy and the European commission's fuel cell and hydrogen joint undertaking.5,6
Amongst different approaches to improve the performance of PGM-free oxygen reduction catalysts,7,8 implementing thin films of oxygenophilic ionic liquids (IL) holds particular promise.9–24 This technique, which was first reported for platinum-based catalysts,11 is also effective for some noble-metal-free catalysts.13,21,23,25 As we highlighted in a recent review, this technique holds a remarkable potential to improve activity, durability and even selectivity of oxygen reduction catalysts in a facile and inexpensive manner.26 However, progress in this direction is limited by the lack of understanding of the mechanism behind performance enhancement in presence of ionic liquid layers.
Most frequently, the high oxygen solubility in ionic liquids has been used to explain the improved kinetics of oxygen reduction.10–12,18,23 However, this explanation alone fails to rationalise all observed phenomena, in particular, the lack of a linear dependence of ORR kinetics on oxygen concentration.18 These complexities are compounded by the challenges in measuring O2 transport in ionic liquids, as a result of the relatively low solubility of oxygen, compared to more studied gases, such as CO2.27 Oxygen solubility results reported in different manuscripts27–34 display large variations, with a percentage error of up to 60% (Fig. S6a, ESI†).26 Moreover, to the best of our knowledge, results obtained with different experimental techniques have never been compared in a single study.27,31,32,35 Most studies neglect the difference between O2 concentration and thermodynamic activity, which is inappropriate for oxygenophilic ionic liquids. Since the field – thus far – has lacked a quantitative parametrization of O2 transport through ionic liquids, it has been unable to deconvolute the effects of O2 diffusivity and solubility that leads to the maximum ORR activity as a function of thickness of the ionic liquid layer.20,23,25,36,37
This has been explained by the combined effect of the high oxygen solubility in ionic liquids, responsible for the initial increase in activity, and the low oxygen diffusivity, which introduces transport limitations in IL layers.
On top of transport-related phenomena, the ionic liquid can also influence the kinetics of oxygen reduction, via modification of the thermodynamics activity of oxygen, or of the intrinsic activity of the catalyst, for example via electronic effects on the active site or changes to the binding energy of key intermediates. For example, the reduced water presence at the interface could cause a dehydration and consequent destabilization of the HO* intermediate, which should cause an activity increase for those catalyst on the weak HO* binding side of the Sabatier volcano.38,39 Hunag et al. showed that on Pt/C, the peak commonly attributed to the adsorption of oxygenated species moves to more positive potential in presence of the ionic liquid MTBD BETI37 indicating a destabilization of the HO* intermediate.38,39 However, there is no systematic study of the effect of ionic liquids on the binding energy of oxygenated intermediates and on the effect of this phenomenon on the activity of the catalyst.
Finally, an aspect that has been largely overlooked is the distribution of the ionic liquid on the catalyst support. The attempts at quantitatively correlating ORR activity to the properties of ionic liquids so far reported generally simplify the system, by assuming that ionic liquids form a thin homogeneous layer on the surface of the catalysts and that all the active sites are in contact with the ionic liquid.
In this work, we deconvolute and quantify the above-mentioned phenomena controlling O2 reduction on non-precious metal catalysts modified by ionic liquid thin films. We report for the first time, an experimental method to distinguish between the solubility and thermodynamics activity of oxygen in ionic liquids. Additionally, we compare experimental oxygen transport results obtained using different techniques, obtaining a reliable estimate of oxygen transport parameters in ionic liquids. By deriving equations from first principles, we quantify the effect of oxygen solubility, diffusivity and thickness of the ionic liquid layer on the overall rate of reaction. Our analysis offers a facile and novel way to predict the effect of ionic liquids on the oxygen transport and to forecast the ideal properties of ionic liquid layers. To account for the role of kinetics, we use voltametric analysis to monitor the effect of a library of ionic liquids on the *OH binding energy of Fe(II) phthalocyanine (FePC). Finally, using thermal analysis and nitrogen physisorption, we explore how the distribution of the ionic liquids on the surface depends on the nature of the ionic liquid itself.
2. Results and discussion
The effect of the ionic liquid layer on the kinetics of oxygen reduction
Pyrolyzed FeN4 catalysts are among the most active PGM-free catalysts reported so far, but they suffer from the existence of a wide variety of Fe species, and the difficulty of identifying and characterizing the active sites.40–44 Therefore, in this manuscript we decided to use iron(II) phthalocyanine (FePC) as a model FeN4 catalyst with well-defined active site. FePC was deposited on conductive graphene and modified with the addition of 5 selected ionic liquids (20 w%), shown in Fig. 1a (characterization of the pristine catalyst can be found in the ESI,† Section S11). The effect of the ionic liquids on the overall ORR performance of the catalyst was studied using a three-electrode cell, with a rotating disc working electrode (RDE). Linear sweep voltammograms were collected in oxygen saturated 0.1 M KOH and are shown in Fig. 1b. Clearly, the addition of the ionic liquid has a significant impact on both ORR kinetics at low current densities and oxygen transport at high current densities, effects that vary significantly with the chemical structure of the ionic liquid itself. | ||
| Fig. 1 (a) Structure and abbreviation of the ionic liquids used in this work. (B) Cathodic linear sweep voltammograms of the FePC/G catalyst, modified with the addition of 20 w% ionic liquids. Data were collected in oxygen saturated 0.1 M KOH, with a scan rate of 10 mV s−1 and rotational speed of 1200 rpm, at a temperature of 25 °C. The pristine catalyst loading was maintained constant at 0.14 mg cm−2 with an addition of 20 w% ionic liquid. Before recording the oxygen reduction activity, the catalyst was pre-conditioned with 5 cyclic voltammograms in nitrogen-saturated electrolyte, in a potential range of 0.1 V vs. RHE to 1.0 V vs. RHE. The ORR activity of the pristine catalyst is comparable to that reported in literature, as shown in Fig. S1e (ESI†). (c) Background-subtracted square wave voltammogram of FePC/G modified by the addition of ionic liquids, zoom-in on the high potential peak. Obtained in N2-saturated 0.1 M KOH, using a potential step of 4 mV, modulation amplitude of 20 mV and a frequency of 2 Hz, resulting in a scan-rate of 8 mV s−1, at a temperature of 25 °C. The pristine catalyst loading was maintained constant at 0.14 mg cm−2 with an addition of 20 w% ionic liquid. Before recording the square-wave voltammogram, the catalyst was pre-conditioned with 5 cyclic voltammograms in nitrogen-saturated electrolyte, in a potential range of 0.1 V vs. RHE to 1.0 V vs. RHE. After the CVs, SWV measurements were repeated 3 times in the same potential range and no change was observed between the scans. The second scan is shown here. (d) Potential for 0.1 mA cm−2 (in O2-saturated 0.1 M KOH), as a function of the position of the square-voltammetry peak in N2 saturated 0.1 M KOH. Data presented are the average of three independent measurements and the error represents the highest and lowest data measured. The position of the SWV peak was determined using a peak finding function on the original SWV data. For the y-axis, the onset potential would be the best descriptor of ORR kinetics, as it does not include transport effects. Since the onset potential is somewhat controversial to define, we present the potential at which we observe a current low enough to be deconvoluted from mass-transport effects, chosen as 0.1 mA cm−2. (e) Ex-situ XANES of FePC/G modified by the addition of 20 w% of the ionic liquids EIM NTF2 and BMIM PF6, at the Fe K edge. | ||
First of all, we focused our study on the effect of the selected ionic liquids in the kinetics region of the LSV. The mechanism of oxygen reduction on iron-based catalysts is still debated, even for the case of model molecules with defined structure, like iron phthalocyanine. Nevertheless, it is still possible to gain some insight by simply monitoring the position of the cyclic voltammetry (CV) peaks. In fact, the high potential CV peak of FePC is attributed to *OH desorption,45–47 and its position is therefore an experimental measurement of the *OH binding energy on the catalyst site. The scaling relationship existing between the binding energies of oxygenated intermediates on active sites causes a well-known volcano-type dependence of the ORR activity on the binding energy of any intermediate. A similar volcano can therefore be obtained relating the activity for oxygen reduction to the position of the high potential CV peak.46 This phenomenon allowed us to observe the effect of ionic liquid on the *OH binding energy and the effect on ORR kinetics, by monitoring the position of the high potential peak. Rather than cyclic voltammetry, we used square-wave voltammetry (SWV) to obtain a more accurate identification of the peak position, thanks to high rejection of capacitative current and better sensitivity to faradaic processes (as shown in Fig. S1b and c, ESI†).48Fig. 1c shows the background-subtracted SWV results (original data shown in Fig. S1c, ESI†). The difference in height and shape of the peaks can be attributed to a difference of distribution of the ionic liquids on the catalyst, causing a change in accessibility of the active site and a broader range of *OH desorption potentials. As it can be observed from Fig. 1c, the presence of ionic liquids has a visible effect on the position of the high-potential peak, suggesting an alteration of the *OH binding energy. In particular, all the ionic liquids except EIM NTF2 move the peak to less positive potentials, suggesting a strengthening of the *OH bond.
Fig. 1d shows ORR activity as a function of the position of the SWV peak. There is a good correlation between the catalyst performance and the peak position, suggesting that the effect on *OH binding energy dominates the change in ORR kinetics caused by the ionic liquids. In line with reports that the pristine catalyst (FePC) should lie on the strong-binding side of the Sabatier activity volcano,49 the ionic liquids that strengthen the *OH bond are found to decrease the ORR activity.45 This appears in contrast to reports that the same ionic liquid layers that are hereby detrimental for ORR kinetics, have a positive impact on platinum-based catalysts.15,37,50 This observation shows how the effect of ionic liquids depends not only the nature of the liquid itself, but also on that of the catalyst. Therefore, it is clear that the effect of ionic liquids on different active sites cannot be inferred from that of iron phthalocyanine. Nevertheless, we expect transition metal MN4 catalysts, which present a similar active site, to follow the trends shown here.
A possible explanation of the effect of ionic liquids on the *OH bond originates from their hydrophobic nature. The decrease in water concentration around the active sites could cause a dehydration of the *OH intermediate and its consequent destabilization.51,52 This could explain the weakening of the *OH bond reported after the addition of ionic liquid on Pt/C catalysts,15 but not strengthening observed on FePC. In this case, the change in *OH binding energy could be attributed to co-adsorption of the IL cation, similarly to what has been previously reported for electrolyte alkali cations, which have been shown to weaken *OH adsorption on platinum.53,54 In this case, the effect of the ionic liquid should be primarily controlled by the nature of the cation. However, the results seem to suggest that both the anion and the cation contribute to strengthening the *OH bond, with PF6 anion and pyrrolidinium cations offering the greatest effect. The experimental characterization of the potential-dependent interaction of ionic liquids with the active site and validation of their effects on key intermediates is extremely challenging and various effects are likely to contribute to the observed changes in kinetics.
Although we take the view that the effect on the *OH bond has a strong influence on ORR kinetics, we cannot exclude the possibility that other factors might play an important role. Even in the absence of liquid water and potential control, ex situ XANES data obtained at the Fe K-edge of FePC/G (Fig. 1e) show that the ionic liquids influence the propensity of the Fe towards oxidation, causing a slight shift in the whiteline and a modification of the pre-peak intensity. In particular, EIM NTF2 appears to decrease the oxidation state of Fe, while BMIM PF6 has the opposite effect. This could cause a change in affinity to *OH and *O and explain the observed weakening of *OH bond for EIM NTF2 and strengthening for BMIM PF6.
Finally, it cannot be excluded that the ionic liquids might block access to some active sites, thus decreasing catalyst utilization. However, this phenomenon alone would not explain the observed modification of the *OH bond.
Reliably determining oxygen transport data in ionic liquids
In the previous section we isolated the effect of ionic liquid layers on the kinetic of oxygen reduction and identified a descriptor (the *OH binding energy), to predict the effect of ionic liquids on the ORR kinetics. Now, we will move on to discuss the effect of ILs on oxygen transport, starting from the reliable determination of oxygen solubility in ionic liquids.Given the high variability in the oxygen transport data reported in the literature and the unavoidable sources of error associated with experimentally determining transport parameters, we decided to compare oxygen permeability results obtained using three of the most common techniques: gravimetric, volumetric and electrochemical. The first two are based on the incremental addition of oxygen, while monitoring the weight or pressure, respectively, while the electrochemical method relies on the 1-electron reaction of dissolved oxygen on a microelectrode. Details of the experimental procedure can be found in the method section, while an in-depth discussion of the advantages, sources of error of each technique and choice of fitting times can be found in the ESI,† Section S2 and S3.
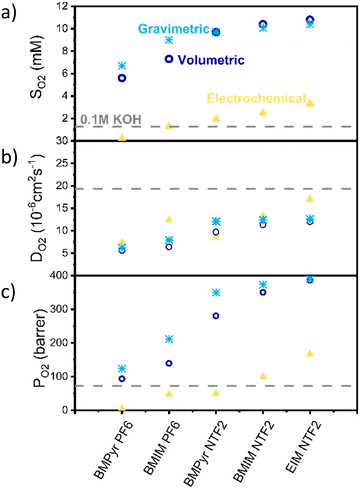
Fig. 2 shows the solubility (a), diffusivity (b) and permeability (c) results obtained with the different techniques. Solubility results obtained with all the methods show the same trend, with the anion having the biggest influence on oxygen solubility (with NTF2 > PF6). However, while the volumetric and gravimetric methods are in good agreement, the electrochemical method appears to consistently predict lower values.
Despite all the possible sources of inaccuracy, the significant difference observed between the electrochemical and other methods cannot be solely attributed to experimental errors. We instead propose that the electrochemical method calculates the thermodynamics activity of oxygen (aO2), rather than its solubility. Activity is a thermodynamics concept which represent the “effective concentration” of a species in a mixture and is related to the concentration of the species via the activity coefficient (γ) as shown in eqn (1).
| aO2 = γcO2 | (1) |
Hereby we proposed a novel technique to experimentally determine oxygen activity and solubility in ionic liquids. To the best of our knowledge, this is the first time that the thermodynamics activity of oxygen in ionic liquids has been experimentally determined. It is also the first time that results obtained with different techniques have been directly compared and it provides an explanation for the wide variety or reported data regarding oxygen solubility.
Regarding the diffusion coefficient (Fig. 2b), as expected the electrochemical method appears in better agreement with the other two.
Fig. 2c also shows a comparison between the permeability values calculated with these methods. Permeability here is defined as the product of oxygen solubility and diffusivity, divided by the oxygen pressure, is reported in barrer, and is a measure of the ability of the ionic liquid to transport oxygen. According to the results obtained via the electrochemical method, oxygen permeability in BMIm NTf2 and EIm NTf2 is higher than in the electrolyte, indicating that oxygen transport should be faster in these ionic liquids than in aqueous electrolyte.
It should also be noticed that, for the nature of the measurements, these could only be performed in degassed, water-free ionic liquids, while under operating conditions the ionic liquid would be saturated with water. While this is likely to affect both solubility and diffusivity of oxygen, the change has been shown to be below 10% for similarly hydrophobic ionic liquids and it is reasonable to expect that the observed trends would hold in presence of water.55,56
The effect of ionic liquid layers on oxygen transport
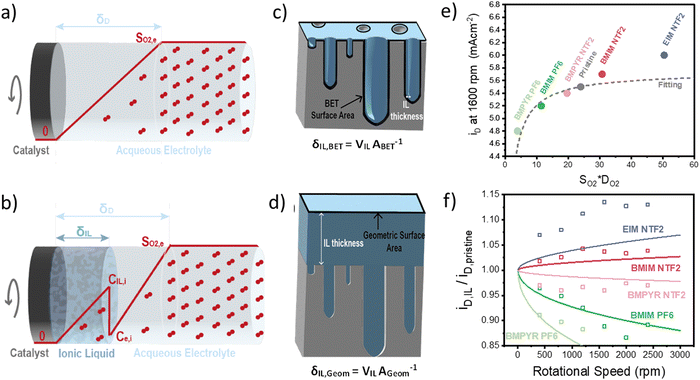
Once we obtained reliable experimental measurements for oxygen solubility, thermodynamic activity and diffusivity in ionic liquids, these results were used to predict the effect of ionic liquid layers on the transport of oxygen to the surface of the rotating-disk electrode.In the RDE configuration and transport-limited conditions, oxygen transport is controlled by diffusion through the so-called diffusion layer, as shown by the oxygen concentration profiles in Fig. 3a and b. In absence of the ionic liquid, oxygen concentration is zero at the catalyst surface and equal to oxygen solubility in the electrolyte at a distance equal to the diffusion thickness. When a thin film on ionic liquid is added on the surface of the catalyst, discontinuity in oxygen concentration is introduced at the ionic liquid/electrolyte interface. Assuming that the resistance to oxygen transfer across the interface is negligible, the catalyst surface is flat and the ionic liquid is a homogeneous film, oxygen transport can be calculated as shown in eqn (2) (see Sections S5 and S6, ESI†).
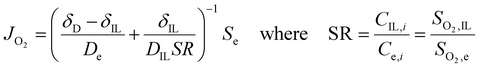 | (2) |
The results of this model, compared to the experimental diffusion-limited current at 1600 rpm, are shown in Fig. 3e. As expected, the transport-limited current increases with the permeability of oxygen in the ionic liquid but the dependence is not linear as oxygen transport is controlled by the layer with lowest oxygen permeability. This results in the current decreasing much faster for ionic liquid with permeability lower than the electrolyte, than it increases in the opposite case. The main conclusion is that oxygenophilic ionic liquid can be used to improve oxygen transport, but not as much as a linear correlation with oxygen permeability would predict.
Using eqn (2), we can also observe the effect of various parameters, such as the thickness of the ionic liquids or of the diffusion layer, on the current density. Fig. 3f shows the ratio of the diffusion-limited current in presence and absence of the ionic liquids, as a function of the rotational speed. The effect of the ionic liquid layer becomes more pronounced with higher rotational speeds. The model fits the experimental data reasonably well and the discrepancies might result from an inhomogeneous distribution of the ionic liquid on the catalyst, which is discussed in the following section.
So far, we have discussed the effect of oxygen transport in diffusion-limited conditions. When both the oxygen transport and reaction kinetics play a role, the effect of the ionic liquid is more complex. On one side, the ionic liquid affects the transport of oxygen as described above, while on the other side it changes the concentration of oxygen at the catalyst surface, influencing the rate of reaction. In this case, the total oxygen flux or oxygen reaction rate can be calculated according to eqn (3).
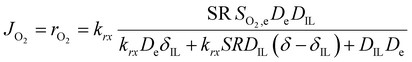 | (3) |
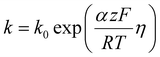 | (4) |
This equation highlights how the ionic liquids affect both the rate of reaction (through oxygen solubility) and the transport of oxygen (through oxygen permeability), with the relative effect depending on the applied potential. Given a library of ionic liquids with known oxygen transport properties, eqn (3) offers an analytical expression to determine which ionic liquid would provide the highest current at any overpotential. Clearly, the ideal ionic liquid should feature both high oxygen solubility and diffusivity. However, these two parameters cannot usually be independently tuned.29 Unless this limit is overcome, the optimal ionic liquid layer should maximize the oxygen solubility, while minimizing the thickness. The minimum thickness would be a monolayer of ionic liquid, which has been previously estimated to be of roughly of 1 nm.57–59 In this case, the diffusion layer (≈300–400 μm depending on the rotational rate) would be orders of magnitude larger than the thickness of the ionic liquid (≈1 nm) and the expression for the oxygen flux could be simplified as shown in eqn (5). This shows that for monolayers of ionic liquids, oxygen reduction would be insensitive to the diffusivity of oxygen in the ionic liquid and would only depend on the activity of oxygen in it. For example, for the selected catalyst, if a monolayer of ionic liquid with a solubility ratio of 2 is added, the current at 0.90 V vs. RHE is predicted to increase by 60%, from 1.53 mA cm−2 to 2.41 mA cm−2. Fig. S9 in the ESI,† shows the effect of a monolayer of ionic liquid on the oxygen reduction current as a function of applied potential and solubility ratio.
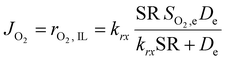 | (5) |
The distribution of ionic liquids on the catalyst support
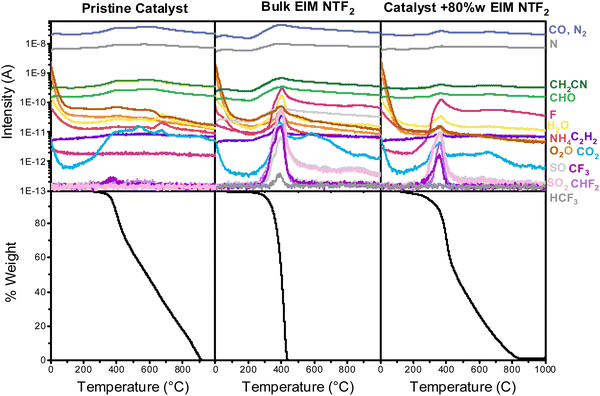
From the above analysis, it can be deduced that, for practical applications, the ideal ionic liquid layer for oxygen reduction should have high oxygen solubility, minimum thickness and homogeneous distribution. This observation leads to the necessity of understanding how ionic liquids distribute on the catalyst surface, which we will hereby achieve via thermal analysis and nitrogen physisorption.Differential scanning calorimetry (DSC) and thermogravimetric analysis coupled with mass spectroscopy (TG-MS) were used to confirm the interaction between the ionic liquid and the catalyst, exploiting the fact that the properties of an liquid confined into porous materials are different from those of liquid in the bulk.60 DSC measurements on bulk EIM NTF2 and on the EIM NTF2-modified catalyst show that the typical glass transition, crystallization and melting peaks present in the pure ionic liquid disappear upon impregnation on the porous catalysts (Section S7, ESI†). This confirms that EIM NTF2 has been successfully incorporated on the catalyst and that the ionic liquid remains in an unaffected liquid state up to −100 °C.
Fig. 4 shows the results of TG-MS. While the bulk ionic liquid starts to decompose at 222 °C, the onset decomposition temperature of the ionic liquid incorporated in the catalyst decreases to 200 °C (Section S7, ESI†).61,62 When comparing different ionic liquid loadings (Fig. S10, ESI†), it can also be noticed that at higher loading the onset decomposition temperature of the confined ionic liquid approaches that of the bulk, confirming that the thermal stability drop originates from interaction of the ionic liquid with the support.
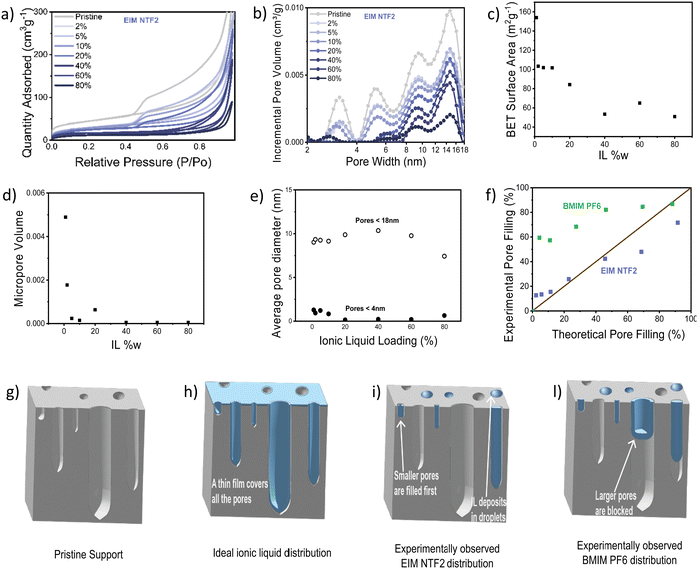
Nitrogen physisorption further allowed us to study IL distribution in the catalyst pores, with an incremental loading of 2 w% to 80 w%. Fig. 5a and b show the N2 sorption isotherm and pore diameter distribution of the catalyst modified with EIM NTF2. As expected, the impregnation with the ionic liquid leads to a decrease in both surface area and pore volume. The micropore volume decreases rapidly and is almost nil already at 10 w% ionic liquid loading (Fig. 5d), while the average pore diameter remains quite stable throughout the ionic liquid addition (Fig. 5e), suggesting that EIM NTF2 is completely filling up some pores (starting from the micropores), leaving others dry. In fact, if the ionic liquid were to distribute uniformly on the surface of the catalyst, one would expect a gradual broadening of the pore diameter distribution and a linear decrease in the average diameter. This indicates that the support–ion interactions are weaker than ion–ion interactions. The fact that the BET surface area initially decreases, but remains constant above 40 w% IL loading (Fig. 5c), also supports this hypothesis, as above this value the ionic liquid keeps filling up increasingly larger pores and depositing in the form of droplets, while leaving a significant proportion of the surface uncovered. Similar dependence of the BET surface area63 and electrochemical surface area20 on the ionic liquid loading have been already reported.
Since it has been reported that different anions can cause a different distribution of the ionic liquid on a support,57 we studied the effect of the other anion considered in this study (PF6), by looking at BMIM PF6. This ionic liquid showed a similar behavior to EIM NTF2, with a rapid decrease in micropore volume and constant average pore diameter (Fig. S12, ESI†). However, as it can be observed in Fig. 5f, for the case of BMIM PF6, the pore filling degree experimentally determined by nitrogen physisorption is much higher than the volume of ionic liquid that was added to the sample. This suggests that BMIM PF6 can sit at the entrance of some pores, blocking access to them without fully filling their volume.
The IL distribution deduced from this study are summarized in Fig. 5g–l. Rather than forming an ideal monolayer (Fig. 5h), our experiments suggest that EIM NTF2 distribute inhomogeneously, gradually fill up the some pores starting from the smallest (Fig. 5i) while BMIM PF6 offers a similar behavior while also blocking access to some pores (Fig. 5l).
3. Conclusion
In this work, the effects of ionic liquids on the transport of oxygen and kinetics of oxygen reduction were studied and deconvoluted.• To account for the effect of ionic liquids on kinetics, we correlated the voltametric peak for *OH adsorption to the kinetic activity. There is a strong correlation between the peak position and oxygen reduction activity. Ionic liquids were found to generally strengthen the bond, having a detrimental effect on the ORR kinetics of FePC. We hypothesize that the co-adsorption of the IL cations might cause the observed change in *OH bond.
• To address the lack of reproducibility in the reported values for oxygen transport in ionic liquids, we compared the results obtained with three common methods. We developed a facile method to experimentally distinguish oxygen solubility (via gravimetric and volumetric techniques) and the thermodynamic activity of oxygen in electrochemical conditions (via electrochemical methods).
• Having characterized oxygen permeability in the ionic liquids, we quantified the effect of ILs on the transport of oxygen. We derived an equation to allow the calculation of oxygen reduction current at a given potential, knowing the kinetics of oxygen reduction on the pristine catalyst and the transport properties of oxygen in the ionic liquids. This equation additionally allowed us to conclude that the highest ORR activity can be obtained by maximizing oxygen solubility in ILs, at the expenses of diffusivity, while using a homogeneous layer of ionic liquid with minimum thickness.
• Finally, using nitrogen physisorption, we were able to characterize the distribution of ionic liquids on the catalyst surface. EIM NTF2 was observed to deposit in clusters, gradually filling the pores, starting from the smallest. BMIM PF6 showed a similar behavior but was additionally found to sit at the entrance of some pores, blocking access to them. This highlights the potential of further improving solid catalysts with ionic liquid layers, by optimizing the synthesis method, to allow the formation of uniform layers.
We envisage that our findings are also applicable to other electrochemical reactions. In particular, the hydrophobic nature of these ionic liquids could be further beneficial for the reactions that compete with hydrogen evolution, such as CO2 reduction64,65 and N2 reduction.66 Additionally, oxygenophilic ionic liquids can also be used to significantly increase the concentration of carbon dioxide at the active site. In fact, the solubility of CO2 in ionic liquids is three orders of magnitude higher than in water.67,68 The method hereby proposed to experimentally distinguish between oxygen solubility and thermodynamic activity in ionic liquids could also be applied to carbon dioxide (and in principle to any other gas), to obtain a more reliable prediction of their performance, which could find application in CO2 capture and CO2 reduction. Of course, the effect of ionic liquids on the performance of CO2 reduction or N2 reduction catalysts would be complex and multifaceted, like it is for ORR. The application of ionic liquid layers to these reactions would require a separate optimization but this work offers a platform and systematic approach in this direction.
4. Materials and methods
Materials
Iron(II) phtalocyanine was purchased from Sigma-Aldrich and used as received. The ionic liquids 1-ethylimidazolium bis(trifluoromethylsulfonyl)imide (EIm NTf2), 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide (BMIm NTf2), 1-butyl-3-methylimidazolium hexafluorophosphate (BMIm PF6), 1-butyl-1-methylpyrrolidinium bis(trifluoromethylsulfonyl)imide (BMPyr NTf2), 1-butyl-1-methylpyrrolidinium hexafluorophosphate (BMPyr PF6) were purchased from IoLiTec and used as received. Thermally exfoliated graphene was used as received.Synthesis of ionic liquid-modified catalysts
Iron(II) phtalocyanine was selected as a model catalyst for all the electrochemical tests and graphene was chosen as a support thanks to its high conductivity.In the synthesis of a typical catalyst, FePc and graphene were grinded in a mortar in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio. The resulting powder was dispersed in a mixture of 30% IPA in water at a concentration of 4 mg mL−1. The of ionic liquid was added to the mixture and ultrasonicated for 10 minutes using a tip sonicator. Unless otherwise stated, 20 w% of the ionic liquid was added with respect to the pristine catalyst. The resulting solution was finally mixed for 48 hours to allow full contact between the catalyst and ionic liquid. The pristine catalyst was subject to the same treatment, to account for any modifications that might result from sonication and stirring.
1 mass ratio. The resulting powder was dispersed in a mixture of 30% IPA in water at a concentration of 4 mg mL−1. The of ionic liquid was added to the mixture and ultrasonicated for 10 minutes using a tip sonicator. Unless otherwise stated, 20 w% of the ionic liquid was added with respect to the pristine catalyst. The resulting solution was finally mixed for 48 hours to allow full contact between the catalyst and ionic liquid. The pristine catalyst was subject to the same treatment, to account for any modifications that might result from sonication and stirring.
The resulting solution was freeze dried, to obtain the catalyst powder, which is referred to as FePC/G + IL.
Electrochemical testing
Catalyst inks at a concentration of 2 mgFePC/G mL−1 were prepared by dispersing 2 mg of pristine catalyst in 1 mL of 30%IPA in water with 18 μL of Nafion, followed by 20 minutes of bath sonication and 10 minutes of probe ultrasonication.5 μL of the catalyst ink was spin-coated on a rotating disc electrode (3 mm radius, RDE, Metrohm, previously polished with a micropolish cloth and 0.05 μm alumina suspension), resulting in a loading of 0.14 mg cm−2 (based on the mass of the FePC/G catalyst). The electrode was left to dry for 2 hours before testing.
Electrochemical measurements were performed in a 3-electrode electrochemical cell, featuring a rotating disk working electrode, a graphite rod counter electrode and a Hg/HgO reference electrode. The reference electrode was calibrated regularly and all the potentials in this paper are reported vs. RHE. The ohmic drop was determined after every LSV experiment, by fitting the high frequency semicircle obtained from impedance spectroscopy. The ohmic drop was found to be 13 Ω ca. for all the samples tested. All the reported data have been iR corrected.
In a typical experiment, the electrolyte (0.1 M KOH, Suprapur®, Merch) was saturated with oxygen (399.9998% Ultrapure Plus, Air Products) and linear sweep voltammograms (LSV) were collected at a scan rate of 10 mV s−1 and rotational speed ranging from 400 to 2400 rpm. Cyclic voltammograms (CV) were collected in static, N2-saturated (399.99998% BIP® Plus, Air Products) 0.1 M KOH at a scan rate of 50 mV s−1. Finally, square-wave voltammograms (SWV) were collected under the same conditions, using a potential step of 4 mV, modulation amplitude of 20 mV and a frequency of 2 Hz, resulting in a scan-rate of 8 mV s−1.
Oxygen transport-gravimetric
Oxygen solubility with gravimetric measurements was determined using a gravimetric gas sorption analyser (Isochema IGA-002). This instruments features an ultrasensitive microbalance, with a capacity of 1 g, resolution of 0.1 μg and ±1 μg and allows the precise control of pressure, from submillibar to 20 bar. Experiments were typically performed at 1, 2 and 3 bar and all the absorption measurements in this work were performed in dynamic mode, in order to ensure an exhaustive control of the set-point pressure. The temperature was maintained at 25 °C and regulated by an external water bath.In a typical experiment, around 150 mg of the ionic liquid was loaded in the machine and degassed at 50 °C for 24 h under vacuum (10−7 bar). Temperature was therefore reduced to 25 °C and the weight was recorded. Oxygen was introduced, up to a set pressure, under constant temperature and the sample weight was monitored. A minimum equilibration time of 2 hours was utilized, and the samples were typically equilibrating in 3 to 4 hours. Desorption experiments were performed in a similar manner.
All the collected data were subsequently buoyancy-corrected. Firstly, an experiment was performed with the empty sample holder (SH), in order to determine the mass and volume of the sample holder (mSH,VSH). In absence of a sample, the mass read (mread,SH) is equal to the real mass of the sample holder (which does not change with pressure) and the buoyancy effect (which is proportional to the density of oxygen and the volume of the sample holder). Knowing how the gas density (ρ) changes with pressure (data obtained from NIST69), the volume of the sample holder is calculated. Similarly, from the solubility experiments, the mass of the sample holder and sample (mSH+Sample) can be calculated from the balance reading (mread) by subtracting the effect of buoyancy, knowing the volume of the sample holder and that of the sample (obtained from the calculated mass and the known density).
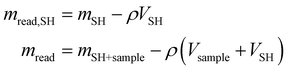 | (6) |
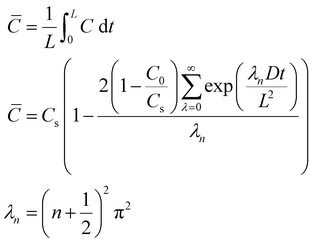 | (7) |
Oxygen transport – volumetric
A micromeritics 3 Flex proposity analyser was used to calculate oxygen transport parameters volumetrically. Using micromeritics VacPrep, 2 mL of ionic liquids were degassed at 10−6 bar, 50 °C for 24 hours. The samples were consequently transferred to the porosity analyser, using a check seal, to avoid contact with atmosphere.In a typical experiment, 2 mL of sample are used and the mass is accurately determined by weighting the sample before and after degassing. Oxygen is supplied at ambient temperature at a set-point pressure through a manifold, of known volume. Then the decrease in pressure in monitored, and from the steady-state value (Pmeas), the amount of gas absorbed is determined (Vads,stp), by the difference between the expected pressure and the observed one, according to eqn (8). To calculate the expected pressure, from the volume of amount of gas introduced in the same, it is necessary to know the free space, i.e. the space in the sample holder that is not occupied by the sample, accurately. The free space (Vfree) is calculated repeating the same experiment with argon as a absorptive gas, which is assumed not to be absorbed by ionic liquid, or only in negligible amounts. The free volume is therefore calculated starting from the known volume of gas introduced (Vclosed,stp), at standard temperature (Tst) and pressure (Pst) the temperature of the sample (Tsample), according to eqn (9).
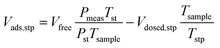 | (8) |
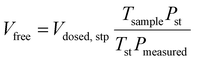 | (9) |
Oxygen transport – electrochemical chronoamperometry
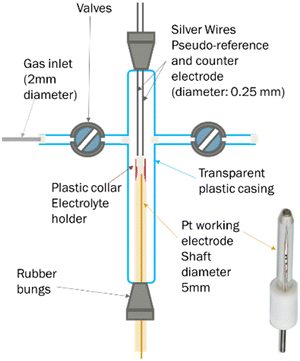
A less common approach to the determination of gas solubility in ionic liquids is electrochemical. For this, we used an in-house made T-cell (Fig. 6), following a structure previously reported.71 In brief, this consists of a platinum microelectrode (purchased from Metrohm, 10 μm nominal diameter) and two silver wires, acting as working, counter and pseudo-reference electrodes respectively. On top of the working electrode is a plastic collar, where the ionic liquid was inserted. The cell also featured two valve, which allows the connection to the gas inlet or vacuum pump.In a typical experiment, 100 μL of the ionic liquid are loaded in the plastic collar and degassed in the cell, at 50 °C for 24 hours. Afterwards, the cell is disconnected from the line and connected to oxygen at 1 bar. Cyclic voltammograms are periodically recorded to monitor the attainment of oxygen saturation in the ionic liquid. The potential is then stepped from a value at which the faradaic current is negligible, to one where oxygen reduction is mass transfer limited. The potentials to be applied were determined by observation of the cyclic voltammograms.
Time-dependent data are recorded for a minute, after which the potential is brought back to its original value and the oxygen is left to saturate for 15 minutes before repeating the experiment. The oxygen solubility (CO2) and diffusivity (DO2) was then calculated by fitting the time-dependent current to the Shoup–Szabo equation, shown below
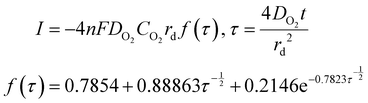 | (10) |
Data were fitted starting from 0.02 s and finishing at 1 s. Earlier data were discarded to minimize current contributions from non-faradaic charging, while was stopped at 1 s, because around this value, the resultant DO2 and CO2 were found to be independent of fitting time.
Thermal analysis
A thermal analysis Q200 DSC was used to determine phase transition temperatures. The samples were vacuum dried for 12 h at 80 °C before the experiments, to remove moisture. The samples were therefore cooled at −100 °C followed by a 10 minutes isotherm and finally the DSC thermograms were recorded from −100 °C to 500 °C at a heating rate of 10 °C min−1.A thermal analyzer (Netzsch TG 209 F1 Libra), coupled with a mass spectrometer (Netzsch QMS 403 D Aeolos) were used to study the thermal stability of the ionic liquids and catalysts. Once again, all the samples were vacuum dried for 12 h at 80 °C before the experiments. TGA thermogram were collected from 25 °C to 1000 °C, at a heating rate of 10 °C min−1, under a nitrogen flow of 40 mL min−1. At the same time, mass spectrometry data were collected, in a mass range of 2 u to 100 u. Around 15 mg of sample were used in each measurement. The low amount of sample was selected to avoid heat transfer limitations.
Porosity analysis
Nitrogen sorption isotherms were measured at 77 K using a Tristar sorption analyser from Micromeritics. Before the measurements, the samples were degassed at 453 K for 24 h in vacuum. The surface area was determined from the linearised BET equation, the micropore volume was obtained via the t-plot and the pore volume distribution was determined using the NLDFT model for carbon slit pores.X-ray absorption spectroscopy
The ex situ XAS measurements at the Fe K-edge, were performed in transmission mode at the beamline I20-EDE at Diamond light source. The catalysts were mixed with 50 w% cellulose and pressed to obtain pellets, that were consequently analysed ex situ. The XAS data were processed using the Athena program.Conflicts of interest
There are no conflicts to declare.References
- K. Jiao, et al., Designing the next generation of proton-exchange membrane fuel cells, Nature, 2021, 595, 361–369 CrossRef CAS PubMed.
- U. Martinez, et al., Progress in the Development of Fe-Based PGM-Free Electrocatalysts for the Oxygen Reduction Reaction, Adv. Mater., 2019, 31, 1–20 Search PubMed.
- M. Primbs, et al., Establishing reactivity descriptors for platinum group metal (PGM)-free Fe–N–C catalysts for PEM fuel cells, Energy Environ. Sci., 2020, 13, 2480–2500 RSC.
- M. Titirici, S. G. Baird, T. D. Sparks, S. Min Yang, A. Brandt-Talbot, O. Hosseinaei, D. P. Harper, R. M. Parker, S. Vignolini, L. A. Berglund, Y. Li, H.-L. Gao, L.-B. Mao and S.-H. Yu, The Sustainable Materials Roadmap, J. Phys. Mater., 2022, 5, 032001 CrossRef.
- Office of Energy Efficiency and Renewable Energy. Fuel Cell Technologies Office: Multi-Year Research, Development, and Demonstration Plan: 3.4 Fuel Cells. (2016) doi:Department of Energy.
- Fuel Cells and Hydrogen 2 Joint Undertaking (FCH JU). Addendum to the Multi-Annual Work Plan 2014-2020. (2018).
- K. Kumar, et al., Physical and Chemical Considerations for Improving Catalytic Activity and Stability of Non-Precious-Metal Oxygen Reduction Reaction Catalysts, ACS Catal., 2018, 8, 11264–11276 CrossRef CAS.
- J. Cui, Q. Chen, X. Li and S. Zhang, Recent advances in non-precious metal electrocatalysts for oxygen reduction in acidic media and PEMFCs: an activity, stability and mechanism study, Green Chem., 2021, 23, 6898–6925 RSC.
- T. Wang et al. , Enhancing the Catalysis of Oxygen Reduction Reaction via Tuning Interfacial Hydrogen Bonds, 2020, pp. 1–33 Search PubMed.
- J. Snyder, K. Livi and J. Erlebacher, Oxygen reduction reaction performance of [MTBD][beti]-encapsulated nanoporous NiPt alloy nanoparticles, Adv. Funct. Mater., 2013, 23, 5494–5501 CrossRef CAS.
- J. Snyder, T. Fujita, M. W. Chen and J. Erlebacher, Oxygen reduction in nanoporous metal-ionic liquid composite electrocatalysts, Nat. Mater., 2010, 9, 904–907 CrossRef CAS.
- H. Zhang, J. Liang, B. Xia, Y. Li and S. Du, Ionic liquid modified Pt/C electrocatalysts for cathode application in proton exchange membrane fuel cells, Front. Chem. Sci. Eng., 2019, 13, 695–701 CrossRef CAS.
- Z. Yu, et al., Interfacial engineering of heterogeneous molecular electrocatalysts using ionic liquids towards efficient hydrogen peroxide production, Chin. J. Catal., 2022, 43, 1238–1246 CrossRef CAS.
- A. Avid, et al., Revealing the role of ionic liquids in promoting fuel cell catalysts reactivity and durability, Nat. Commun., 2022, 13, 1–13 Search PubMed.
- G. R. Zhang, et al., Tuning the Electrocatalytic Performance of Ionic Liquid Modified Pt Catalysts for the Oxygen Reduction Reaction via Cationic Chain Engineering, ACS Catal., 2018, 8, 8244–8254 CrossRef CAS.
- Y. Li, et al., Modifying the Electrocatalyst-Ionomer Interface via Sulfonated Poly(ionic liquid) Block Copolymers to Enable High-Performance Polymer Electrolyte Fuel Cells, ACS Energy Lett., 2020, 5, 1726–1731 CrossRef CAS.
- M. Sobota, et al., Ligand effects in SCILL model systems: site-specific interactions with Pt and Pd nanoparticles, Adv. Mater., 2011, 23, 2617–2621 CrossRef CAS PubMed.
- E. Benn, H. Uvegi and J. Erlebacher, Characterization of Nanoporous Metal-Ionic Liquid Composites for the Electrochemical Oxygen Reduction Reaction, J. Electrochem. Soc., 2015, 162, H759–H766 CrossRef CAS.
- M. Wang, et al., Ionic Liquid-Modified Microporous ZnCoNC-Based Electrocatalysts for Polymer Electrolyte Fuel Cells, ACS Energy Lett., 2019, 4(9), 2104–2110 CrossRef CAS.
- G. R. Zhang, M. Munoz and B. J. M. Etzold, Boosting performance of low temperature fuel cell catalysts by subtle ionic liquid modification, ACS Appl. Mater. Interfaces, 2015, 7, 3562–3570 CrossRef CAS.
- M. Qiao, et al., Oxygenophilic ionic liquids promote the oxygen reduction reaction in Pt-free carbon electrocatalysts, Mater. Horiz., 2017, 4, 895–899 RSC.
- X. Yan, et al., Improving Oxygen Reduction Performance by Using Protic Poly(Ionic Liquid) as Proton Conductors, ACS Appl. Mater. Interfaces, 2019, 11, 6111–6117 CrossRef CAS PubMed.
- M. Wang, et al., Ionic Liquid-Modified Microporous ZnCoNC-Based Electrocatalysts for Polymer Electrolyte Fuel Cells, ACS Energy Lett., 2019, 4, 2104–2110 CrossRef CAS.
- S. Doblinger, J. Lee and D. S. Silvester, Effect of Ionic Liquid Structure on the Oxygen Reduction Reaction under Humidified Conditions, J. Phys. Chem. C, 2019, 123, 10727–10737 CrossRef CAS.
- I. Martinaiou, et al., Improved electrochemical performance of Fe–N–C catalysts through ionic liquid modification in alkaline media, J. Power Sources, 2018, 375, 222–232 CrossRef CAS.
- S. Favero, I. E. L. Stephens and M. M. Titirici, Engineering the Electrochemical Interface of Oxygen Reduction Electrocatalysts with Ionic Liquids: A Review, Adv. Energy Sustainable Res., 2021, 2, 2000062 CrossRef CAS.
- Z. Lei, C. Dai and B. Chen, Gas solubility in ionic liquids, Chem. Rev., 2014, 114, 1289–1326 CrossRef CAS PubMed.
- J. Kumełan, Á. P. S. Kamps, I. Urukova, D. Tuma and G. Maurer, Solubility of oxygen in the ionic liquid [bmim][PF6]: experimental and molecular simulation results, J. Chem. Thermodyn., 2005, 37, 595–602 CrossRef.
- G. Vanhoutte, S. D. Hojniak, F. Bardé, K. Binnemans and J. Fransaera, Fluorine-functionalized ionic liquids with high oxygen solubility, RSC Adv., 2018, 8, 4525–4530 RSC.
- J. L. Anthony, J. L. Anderson, E. J. Maginn and J. F. Brennecke, Anion Effects on Gas Solubility in Ionic Liquids, J. Phys. Chem. B, 2005, 109, 6366–6374 CrossRef CAS PubMed.
- T. Song, O. Morales-Collazo and J. F. Brennecke, Solubility and Diffusivity of Oxygen in Ionic Liquids, J. Chem. Eng. Data, 2019, 64, 4956–4967 CrossRef CAS.
- M. B. Shiflett and E. J. Maginn, The solubility of gases in ionic liquids, AIChE J., 2017, 63, 4722–4737 CrossRef CAS.
- A. R. Neale, et al., Effect of cation structure on the oxygen solubility and diffusivity in a range of bis{(trifluoromethyl)sulfonyl}imide anion based ionic liquids for lithium-air battery electrolytes, Phys. Chem. Chem. Phys., 2016, 18, 11251–11262 RSC.
- I. Bahadur, K. Osman, C. Coquelet, P. Naidoo and D. Ramjugernath, Solubilities of carbon dioxide and oxygen in the ionic liquids methyl trioctyl ammonium bis(trifluoromethylsulfonyl)imide, 1-butyl-3-methyl imidazolium bis(trifluoromethylsulfonyl)imide, and 1-butyl-3-methyl imidazolium methyl sulfate, J. Phys. Chem. B, 2015, 119, 1503–1514 CrossRef CAS PubMed.
- M. Inaba, et al., Benchmarking high surface area electrocatalysts in a gas diffusion electrode: measurement of oxygen reduction activities under realistic conditions, Energy Environ. Sci., 2018, 11, 988–994 RSC.
- M. George, et al., Effect of Ionic Liquid Modification on the ORR Performance and Degradation Mechanism of Trimetallic PtNiMo/C Catalysts, ACS Catal., 2019, 9, 8682–8692 CrossRef CAS PubMed.
- K. Huang, T. Song, O. Morales-Collazo, H. Jia and J. F. Brennecke, Enhancing Pt/C Catalysts for the Oxygen Reduction Reaction with Protic Ionic Liquids: The Effect of Anion Structure, J. Electrochem. Soc., 2017, 164, F1448–F1459 CrossRef CAS.
- H. S. Casalongue, et al., Direct observation of the oxygenated species during oxygen reduction on a platinum fuel cell cathode, Nat. Commun., 2013, 4, 1–23 Search PubMed.
- S. Favero, I. E. L. Stephens and M. M. Titirici, Engineering the Electrochemical Interface of Oxygen Reduction Electrocatalysts with Ionic Liquids: A Review, Adv. Energy Sustain. Res, 2021, 2, 2000062 CrossRef CAS.
- M. Shao, Electrocatalysis in Fuel Cells, 2013, pp. 271–338 Search PubMed.
- K. Holst-Olesen, L. Silvioli, J. Rossmeisl and M. Arenz, Enhanced Oxygen Reduction Reaction on Fe/N/C Catalyst in Acetate Buffer Electrolyte, ACS Catal., 2019, 9, 3082–3089 CrossRef CAS.
- Q. Jia, et al., Spectroscopic insights into the nature of active sites in iron–nitrogen–carbon electrocatalysts for oxygen reduction in acid, Nano Energy, 2016, 29, 65–82 CrossRef CAS.
- L. Ni, et al., Active Site Identification in FeNC Catalysts and Their Assignment to the Oxygen Reduction Reaction Pathway by In Situ 57 Fe Mössbauer Spectroscopy, Adv. Energy Sustainable Res., 2021, 2, 2000064 CrossRef CAS.
- S. Mitchell, et al., Automated Image Analysis for Single-Atom Detection in Catalytic Materials by Transmission Electron Microscopy, J. Am. Chem. Soc., 2022, 144, 8018–8029 CrossRef CAS PubMed.
- J. H. Zagal and M. T. M. Koper, Reactivity Descriptors for the Activity of Molecular MN4 Catalysts for the Oxygen Reduction Reaction, Angew. Chem., Int. Ed., 2016, 55, 14510–14521 CrossRef CAS PubMed.
- J. H. Zagal, Metallophthalocyanines as catalysts in electrochemical reactions, Coord. Chem. Rev., 1992, 119, 89–136 CrossRef CAS.
- K. D. Jensen, et al., Elucidation of the Oxygen Reduction Volcano in Alkaline Media using a Copper-Platinum(111) Alloy, Angew. Chemie, 2018, 130, 2850–2855 CrossRef.
- F. R. Simoes and M. G. Xavier, Electrochemical Sensors. Nanoscience and its Applications, Square Wave Voltammetry, 2017, ch. 6.2.4.3 Search PubMed.
- W. Yang, et al., Theory-Driven Design of Electrocatalysts for the Two-Electron Oxygen Reduction Reaction Based on Dispersed Metal Phthalocyanines, CCS Chem., 2021, 4, 228–236 Search PubMed.
- G. R. Zhang, M. Munoz and B. J. M. Etzold, Accelerating oxygen-reduction catalysts through preventing poisoning with non-reactive species by using hydrophobic ionic liquids, Angew. Chem., Int. Ed., 2016, 55, 2257–2261 CrossRef CAS PubMed.
- H. S. Casalongue, et al., Direct observation of the oxygenated species during oxygen reduction on a platinum fuel cell cathode, Nat. Commun., 2013, 4, 2817 CrossRef.
- Z. Da He, S. Hanselman, Y. X. Chen, M. T. M. Koper and F. Calle-Vallejo, Importance of Solvation for the Accurate Prediction of Oxygen Reduction Activities of Pt-Based Electrocatalysts, J. Phys. Chem. Lett., 2017, 8, 2243–2246 CrossRef CAS PubMed.
- X. Chen, I. T. McCrum, K. A. Schwarz, M. J. Janik and M. T. M. Koper, Co-adsorption of Cations as the Cause of the Apparent pH Dependence of Hydrogen Adsorption on a Stepped Platinum Single-Crystal Electrode, Angew. Chemie, 2017, 129, 15221–15225 CrossRef.
- K. Kodama, et al., Effect of the Side-Chain Structure of Perfluoro-Sulfonic Acid Ionomers on the Oxygen Reduction Reaction on the Surface of Pt, ACS Catal., 2018, 8, 694–700 CrossRef CAS.
- D. Fu, X. Sun, J. Pu and S. Zhao, Effect of Water Content on the Solubility of CO2 in the Ionic Liquid [bmim][PF6], J. Chem. Eng. Data, 2006, 51, 371–375 CrossRef CAS.
- X. Liao, et al., Solubility of CO2 in Ionic Liquids with Additional Water and Methanol: Modeling with PC-SAFT Equation of State, Ind. Eng. Chem. Res, 2022, 61, 14364–14373 CrossRef CAS.
- M. T. Heinze, et al., Solid-ionic liquid interfaces: pore filling revisited, Phys. Chem. Chem. Phys., 2014, 16, 24359–24372 RSC.
- A. K. Tripathi, Y. L. Verma and R. K. Singh, Thermal, electrical and structural studies on ionic liquid confined in ordered mesoporous MCM-41, J. Mater. Chem. A, 2015, 3, 23809–23820 RSC.
- D. N. Lapshin, M. Jorge, E. E. B. Campbell and L. Sarkisov, On competitive gas adsorption and absorption phenomena in thin films of ionic liquids, J. Mater. Chem. A, 2020, 8, 11781–11799 RSC.
- M. P. Singh, R. K. Singh and S. Chandra, Ionic liquids confined in porous matrices: physicochemical properties and applications, Prog. Mater. Sci., 2014, 64, 73–120 CrossRef CAS.
- M. Y. Keating, F. Gao and J. B. Ramsey, TGA-MS study of the decomposition of phosphorus-containing ionic liquids trihexyl(tetradecyl) phosphonium decanoate and trihexyltetradecylphosphonium bis[(trifluoromethyl)sulfonyl] amide, J. Therm. Anal. Calorim., 2011, 106, 207–211, DOI:10.1007/s10973-011-1528-3.
- C. Neise, C. Rautenberg, U. Bentrup and M. Beck, Stability studies of ionic liquid [EMIm][NTf2] under short term thermal exposure, RSC Adv., 2016, 6, 48462–48468 RSC.
- U. Kernchen, B. Etzold, W. Korth and A. Jess, Solid catalyst ionic liquid layer (SCILL) – A new concept to improve selectivity illustrated by hydrogenation of cyclooctadiene, Chem. Eng. Technol., 2007, 30, 985–994 CrossRef CAS.
- Z. Han, R. Kortlever, H.-Y. Chen, J. C. Peters and T. Agapie, CO2 Reduction Selective for C ≥ 2 Products on Polycrystalline Copper with N-Substituted Pyridinium Additives, ACS Cent. Sci., 2017, 3, 853–859 CrossRef CAS PubMed.
- D. Wakerley, et al., Bio-inspired hydrophobicity promotes CO2 reduction on a Cu surface, Nat. Mater., 2019, 18, 1222–1227 CrossRef CAS PubMed.
- N. Lazouski, et al., Proton Donors Induce a Differential Transport Effect for Selectivity toward Ammonia in Lithium-Mediated Nitrogen Reduction, ACS Catal., 2022, 12, 5197–5208 CrossRef CAS.
- K. Anderson, et al., Carbon dioxide uptake from natural gas by binary ionic liquid–water mixtures, Green Chem., 2015, 17, 4340–4354 RSC.
- A. Wilke, J. Yuan, M. Antonietti and J. Weber, Enhanced Carbon Dioxide Adsorption by a Mesoporous Poly(ionic liquid), ACS Macro Lett., 2012, 1, 1028–1031 CrossRef CAS PubMed.
- NIST Chemistry WebBook SRD 69. Isothermal Properties for Oxygen. https://webbook.nist.gov/cgi/fluid.cgi?T=25&PLow=0&PHigh=3&PInc=0.1&Applet=on&Digits=5&ID=C7782447&Action=Load&Type=IsoTherm&TUnit=C&PUnit=bar&DUnit=g%2Fml&HUnit=kJ%2Fmol&WUnit=m%2Fs&VisUnit=uPa*s&STUnit=N%2Fm&RefState=DEF (2021).
- M. Gonzalez-Miquel, J. Bedia, C. Abrusci, J. Palomar and F. Rodriguez, Anion effects on kinetics and thermodynamics of CO2 absorption in ionic liquids, J. Phys. Chem. B, 2013, 117, 3398–3406 CrossRef CAS PubMed.
- U. Schröder, et al., Water-induced accelerated ion diffusion: voltammetric studies in 1-methyl-3-[2,6-(S)-dimethylocten-2-yl]imidazolium tetrafluoroborate, 1-butyl-3-methylimidazolium tetrafluoroborate and hexafluorophosphate ionic liquids, New J. Chem., 2000, 24, 1009–1015 RSC.
- D. Zhang, T. Okajima, F. Matsumoto and T. Ohsaka, Electroreduction of Dioxygen in 1-n-Alkyl-3-methylimidazolium Tetrafluoroborate Room-Temperature Ionic Liquids, J. Electrochem. Soc., 2004, 151, D31 CrossRef CAS.
- Y. Wang, E. I. Rogers and R. G. Compton, The measurement of the diffusion coefficients of ferrocene and ferrocenium and their temperature dependence in acetonitrile using double potential step microdisk electrode chronoamperometry, J. Electroanal. Chem., 2010, 648, 15–19 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ey00166k |
| This journal is © The Royal Society of Chemistry 2023 |