Open Access Article
Open Access ArticleReal-time visualisation of ion exchange in molecularly confined spaces where electric double layers overlap
Ulrich
Ramach†
ab,
Jinhoon
Lee†
 c,
Florian
Altmann†
a,
Martin
Schussek
a,
Matteo
Olgiati
ab,
Joanna
Dziadkowiec
c,
Florian
Altmann†
a,
Martin
Schussek
a,
Matteo
Olgiati
ab,
Joanna
Dziadkowiec
 d,
Laura L. E.
Mears
d,
Laura L. E.
Mears
 a,
Alper T.
Celebi
a,
Dong Woog
Lee
a,
Alper T.
Celebi
a,
Dong Woog
Lee
 *c and
Markus
Valtiner
*c and
Markus
Valtiner
 *ab
*ab
aVienna University of Technology, Wiedner Hauptstrasse 8-10, Vienna, Austria. E-mail: markus.valtiner@tuwien.ac.at
bCEST (Centre for Electrochemical Surface Technology), Viktor-Kaplan-Strasse 2, Wiener Neustadt, Austria
cUlsan National Institute of Science & Technology, 50 UNIST-gil, Eonyang-eup, Ulju-gun, Ulsan, South Korea. E-mail: dongwoog.lee@unist.ac.kr
dNJORD Centre, Department of Physics, University of Oslo, Oslo 0371, Norway
First published on 29th March 2023
Abstract
Ion interactions with interfaces and transport in confined spaces, where electric double layers overlap, are essential in many areas, ranging from crevice corrosion to understanding and creating nano-fluidic devices at the sub 10 nm scale. Tracking the spatial and temporal evolution of ion exchange, as well as local surface potentials, in such extreme confinement situations is both experimentally and theoretically challenging. Here, we track in real-time the transport processes of ionic species (LiClO4) confined between a negatively charged mica surface and an electrochemically modulated gold surface using a high-speed in situ sensing Surface Forces Apparatus. With millisecond temporal and sub-micrometer spatial resolution we capture the force and distance equilibration of ions in the confinement of D ≈ 2–3 nm in an overlapping electric double layer (EDL) during ion exchange. Our data indicate that an equilibrated ion concentration front progresses with a velocity of 100–200 μm s−1 into a confined nano-slit. This is in the same order of magnitude and in agreement with continuum estimates from diffusive mass transport calculations. We also compare the ion structuring using high resolution imaging, molecular dynamics simulations, and calculations based on a continuum model for the EDL. With this data we can predict the amount of ion exchange, as well as the force between the two surfaces due to overlapping EDLs, and critically discuss experimental and theoretical limitations and possibilities.
1 Introduction
Charge regulation within molecularly confined gaps and pores, where electric double layers (EDLs) overlap, is of high importance for the control of many different processes, functions and conduction mechanisms in nature and technology. Examples are: chloride migration into nm-sized corroding cracks accelerates corrosion, leading to stress corrosion cracking of steel tubes within days;1 ionic conductance through charged sub 2 nm-thin channels of Nafion membranes determines the efficiency of electrochemical energy conversion devices such as fuel cells and electrolysers;2,3 in nano-fluidic systems flow is driven through channels with overlapping double layers.4 For instance, for ion-controlled devices (iontronics) confining walls with variable surface charge may be used to tune electrically-induced flows in extremely thin nano-fluidic devices, where the EDLs are highly overlapped.5 These devices may enable new applications in selective ion-filtration, lab-on-a-chip applications, and water purification to name just a few examples.Sub 10 nm confinement effects are also central for energy conversion devices (e.g. fuel cells, batteries and electrocatalysts), considering that nano-structured materials are being designed for increasing energy densities, active areas and efficiencies.7–9 However, nano-structuring can significantly alter charge/mass transport mechanisms.10,11 Ion-to-pore size ratios12,13 and ion–surface interactions under polarisation14–16 play a key role during nano-pore charging processes that occur in those devices. Also in nano-fluidics and in geological dissolution processes, fluid-filled nano-channel geometries substantially alter ion diffusion (concentration gradient driven) and ion migration (field gradient driven), by altering the apparent diffusion coefficient of ionic species.17–20 Theoretical considerations of hindrance factors for diffusivity in porous media21 date back to the seminal work of Renkin.22 He suggested a modification to the diffusion coefficient of a species as a function of the pore radius based on Faxen's law.23 Furthermore, charge exchange within porous metal electrodes can be well described by the transmission line model,24–27 which describes experimentally observed charging dynamics of microporous electrodes well. Generally, data at the microporous scale (pore diameters below 1 μm) suggest that spatial confinement slows down ion exchange processes, with non-linear dynamics. In microporous systems, the thickness of the electric double layer, where recharging occurs, is often considered insignificant in comparison to the total pore volume of a system, although surface conduction may play an important role as well.25 As such, altered diffusion and migration pathways are decisive for charging kinetics of microscale confined electric double layers. However, for nanoscale confinement well below 10 nm, the structure of overlapping electric double layers essentially controls the charge regulation and ion transport. For instance, experimental data on diffusion through carbon nanotubes showed unexpectedly fast transport species with high selectivity,28–30 when the distance of confining walls confining walls is in the range of the ionic diameter.
A molecularly-resolved visualisation of ion transport in sub nano-meter confinement, so far, has been reconstructed from simulation studies,31 indicating a decisive effect of ion–surface interactions.32,33 A direct experimental verification of theoretical approaches by experimental real-time visualisation of ion exchange in a single and idealised model pore at the nanoscale has not been achieved to date. However, experimental measurements of ion exchange processes in nano-cavities, where EDLs overlap, are essential to progress our understanding of charge regulation in nanoscale ion-controlled processes. In this direction, electrochemical potential shifts, applied to walls of a nano-confined (20–500 nm) slit in the interferometry-based Surface Forces Apparatus (SFA) technique, drive recurring changes both in slit separation and in the measured interaction forces.34,35 In an SFA experiment distance changes are analysed by measuring the wavelength shift of fringes of equal chromatic order (FECO) by white light interferometry in an optical cavity that forms the nano-confined slit geometry.36 Distance changes (ΔD) directly correlate with transient forces F = k ΔD, and thereby relate to the ongoing charge regulation inside an electrochemically modulated slit.37 Data indicated that charge regulation occurred in line with predictions of the transmission line model25–27 for slit geometries of 20 nm or larger.
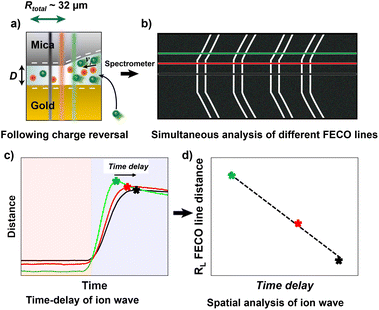
Here, we use a similar approach with a modified Surface Forces Apparatus, enabling simultaneous real-time force and distance sensing,38 to resolve the ion exchange kinetics in a molecularly confined slit. As shown in Fig. 1a, the slit is formed between two cross-cylindrical disks, with a well controlled gap distance (D) in the range of 2–3 nm. The setup schematic and principles of FECO analysis are shown in Fig. 1a–c. A charge reversal of the gold surface manipulates D between the two apposing surfaces, resulting in a change of D due to charge regulation. This change can be observed in real-time over an established confined area with diameter DL, as indicated in Fig. 1b. In detail, the contact area forms a circular slit pore with the FECO flattened (panel c), which can then be analysed line-by-line over the imaged wavelength spectrum using a multiple matrix approach6,39 (panel d), allowing for a radial/spatial resolution of gap distance changes during ion-exchange. This, if using a fast enough capture frequency (200 Hz in this work), allows for a time-resolved observation of gap size changes in 3D, during an active charge regulation (in a 70 mM LiClO4 electrolyte) as indicated in Fig. 1e and f.
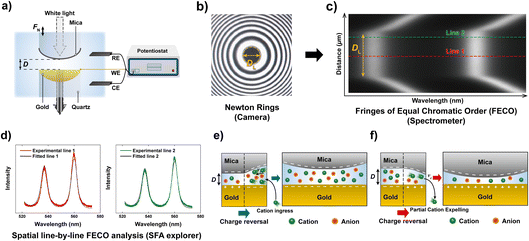 | ||
| Fig. 1 General schematic of the measured effect and measuring principle. (a) Schematic of the SFA measurement setup in an electrochemistry configuration. (b) Interference pattern (Newton's rings) using white light. The diameter of the contact (DL) is indicated. (c) Measured FECO of a contact with the diameter DL. Different lines are highlighted to exemplify the spatial analysis method used. (d) Analysis of different FECO lines. A slight shift of wavelength, which translates to a shift in distance, can be observed. The fitted lines were obtained using the SFA Explorer software.6 (e) Schematic of ion transport in a confined gap. The reversal of polarisation of the gold surface, from a positive to a negative potential, attracts the cations, resulting in a change in gap thickness. (f) Reversing the polarisation to positive potentials expels the cations, resulting in a decrease in gap thickness. | ||
We will also make comparisons of the ion distributions within the confinement obtained from atomic force microscopy (AFM), molecular dynamics (MD) simulations, and a continuum model combining the Poisson–Boltzmann (PB) equation for the diffuse layer with a capacitor model for the Stern layer at the surfaces. The latter allows the calculation of the force between the mica and gold surface due to overlapping EDLs, depending on the applied electric potential and gap distance D. The predictions are further compared with SFA force and distance data. This will allow us to show how comprehensively the combination of complementary techniques can be applied to understand the ion transport kinetics in a nano-confined slit pore.
2 Materials and methods
2.1 Materials
All reagents were of analytical grade and used as received without further purification. Chloroform (99.9%, Sigma Aldrich), HPLC-grade ethanol (VWR) and LiClO4 (Sigma Aldrich) were used as supplied. Water was purified with a Milli-Q System (Merck). High-purity gold and silver (99.99%, Goodfellow) were used for PVD/sputtering processes. Muscovite mica layers (optical grade V1, S&J Trading Company, USA) were manually cleaved to uniform thicknesses ranging from 4–5 μm.2.2 Surface Forces Apparatus (SFA)
2.3 High resolution AFM
Highly-resolved topographies of muscovite mica were obtained using a Cypher ES AFM (Asylum Research, Oxford Instruments), using high-frequency gold-coated arrow headed cantilevers (Arrow UHF-AuD, NanoWorld). The cantilevers were photo-thermally excited in amplitude modulation (amplitude 3–5 Å, tapping frequency ∼600 kHz). Mica was freshly cleaved before each measurement and its surface was imaged while exposed to solutions containing LiNO3 at 10 and 200 mM. The collected data were also re-processed by applying a low-pass filter that removes high-frequency noise (i.e. above 1/5 of the Nyquist frequency).2.4 Molecular dynamics simulations
MD simulations were carried out on a three-dimensional model consisting of a LiClO4 solution confined between a mica and a gold surface. The mica crystal structure (KAl2Si3AlO10(OH)2) was constructed using X-ray diffraction data,40 and the surface was comprised of 32 unit cells (8 × 4). For each tetrahedral sheet, aluminum atoms replace one of the four Si atoms. These isomorphic substitutions were applied regularly on the mica structure, and resulted in a negative surface charge. In accordance with Löwenstein's avoidance rule,41 the substitutions do not occur in neighbouring tetrahedra. The gold surface (6 atomic layers) was constructed using an FCC lattice with a lattice constant of 4.0783 Å. The dimensions of the simulation system in lateral directions are 4.2 nm and 3.6 nm, and the separation distance in the z-direction is 6.0 nm. This distance is large enough to obtain a bulk liquid density in the channel centre. The bulk water density was maintained at 997 kg m−3 for 298.15 K temperature. The bulk ionic concentration of LiClO4 was fixed at 500 mM. Such high concentrations are usually necessary in MD simulations for the sake of better statistics and reduced computational costs. To mimic an externally applied potential on a gold surface, partial electric charges were equally assigned on the gold atoms of the first three layers. In our simulations, mica has a constant surface charge density of −0.33 C m−2, while the gold surface charge density was defined as 0 and −0.06 C m−2. Electrical neutrality hereby was maintained by an excess of counterions.Atomic interactions were described using Lennard–Jones (LJ) and Coulomb potentials. We used general force fields such as the SPC/E model for water molecules,42 CLAYFF for the mica surface,43 the OPLS-AA model for perchloride,44 the Heinz model45 for gold, and the Joung and Cheatham model for lithium ions.46 The short range LJ and Coulomb potentials were truncated within a distance of 11 Å. The long-range electrostatic forces were handled using the particle–particle–particle–mesh (PPPM) method with a root mean accuracy of 10−5.47 The interactions between dissimilar atoms were calculated using the Lorentz–Berthelot mixing rule. Mica and gold slabs were constrained at their original positions, so that they show a rigid wall behavior, while all remaining atomic species were allowed to move freely. For water molecules, bond lengths and angles were kept rigid using the SHAKE algorithm.48
All simulations were performed using the Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).49 Periodic boundary conditions were applied in the lateral directions, while the domain was bound by channel walls in the z-direction. Electrostatic interactions in the reduced periodicity were computed using the slab modification method. In this method, the system is treated as periodic in the z-direction, inserting a large empty volume between atom slabs and removing dipole inter-slab interactions.50 Initial velocities of water molecules and ions were randomly assigned using the Gaussian distribution at 298.15 K. The Nose–Hoover thermostat was used to maintain a constant temperature in a microcanonical (NVT) ensemble. The Verlet algorithm was set to integrate Newton's equations of motion. Each simulation initially ran for 2 ns with a 0.5 fs time step for thermal equilibration, and then ran for an additional 10 ns for data collection. The statistical averaging was determined from five independent simulations, each one started from different initial conditions. For comparison with AFM images, we additionally performed MD simulations of a 200 mM LiNO3 solution on mica surfaces in the absence of a gold wall.
2.5 Numerical modelling
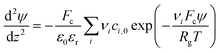 | (1) |
The Stern layer, where ions are in close vicinity to the surface (i.e. specifically adsorbed), can be modelled as a capacitor. Thus, the potential drop in this layer ψδ is given by51
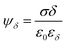 | (2) |
The non-linear ordinary differential equation is solved numerically on the z domain using the chebfun54 package in Matlab®.55 The concentration profile in the gap then follows from the potential distribution obtained from this Stern model
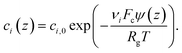 | (3) |
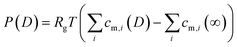 | (4) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) i|ψapp,gold over the gap distance D for a given potential ψapp,gold applied to the gold surface can be calculated with
i|ψapp,gold over the gap distance D for a given potential ψapp,gold applied to the gold surface can be calculated with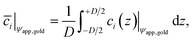 | (5) |
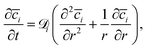 | (6) |
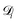 is the diffusion coefficient for species i in the confinement. For a bulk liquid, the diffusion coefficient of a spherical particle can be approximated using the Stokes–Einstein relation57
is the diffusion coefficient for species i in the confinement. For a bulk liquid, the diffusion coefficient of a spherical particle can be approximated using the Stokes–Einstein relation57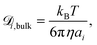 | (7) |
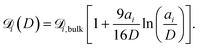 | (8) |
The ion transport equation, (eqn (6)), is solved numerically using a differentiation matrix approach.58 Due to radial symmetry ∂![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) i/∂r = 0 must apply at r = 0. The average concentration for the case of a positively charged gold surface is set as the initial condition for the ion concentrations at each point along the radial direction,
i/∂r = 0 must apply at r = 0. The average concentration for the case of a positively charged gold surface is set as the initial condition for the ion concentrations at each point along the radial direction, ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) i(t = 0, r) =
i(t = 0, r) = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) i|+0.3 V. At the edge between the confinement and the bulk (r = R), the average concentration for a negatively charged gold surface
i|+0.3 V. At the edge between the confinement and the bulk (r = R), the average concentration for a negatively charged gold surface ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) i|−0.3 V is imposed as a Dirichlet boundary condition throughout the simulation. This enables us to investigate the system response in terms of EDL equilibration due to diffusive ion transport directly after charge reversal from +0.3 V to −0.3 V: the rate of the equilibrated ion front into the confined volume (veq) can then be obtained by considering the time (teq) that is required for the ion concentration to reach the respective boundary condition
i|−0.3 V is imposed as a Dirichlet boundary condition throughout the simulation. This enables us to investigate the system response in terms of EDL equilibration due to diffusive ion transport directly after charge reversal from +0.3 V to −0.3 V: the rate of the equilibrated ion front into the confined volume (veq) can then be obtained by considering the time (teq) that is required for the ion concentration to reach the respective boundary condition ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) i|−0.3 V everywhere in the confinement, as follows
i|−0.3 V everywhere in the confinement, as follows
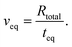 | (9) |
3 Results and discussion
For ion exchange experiments in nano-confinement we established a contact as seen in Fig. 1, with a typical radius Rtotal of about 30–40 μm defined in Fig. 3, between gold and mica in a solution with an ionic strength of 70 mM LiClO4, which corresponds to a Debye length (λD) of 1.15 nm. In this work we chose a perchlorate salt (LiClO4) as a model electrolyte for two reasons. Firstly, Li+ ions show a low affinity to the wall surfaces.59 This limits Stern layer effects, which we also confirm with high resolution imaging data using AFM and comparative MD simulations for mica. Secondly, perchlorate interacts only weakly with gold, limiting any specific interactions within the EDL.A constant force load was applied and recorded using a strain gauge, which creates a geometrically flat and round shaped slit pore, at a distance and hence electrolyte thicknesses of D of about 2–3 nm between mica and an electrochemically modulated gold surface. At this distance, the interaction between the two apposing surfaces is highly repulsive due to the overlap of the electric double layers of the gold and the highly-charged mica surface.
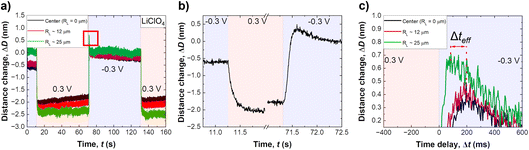
Fig. 2a shows a typical distance change versus time profile during application of a step potential, from −0.3 V to +0.3 V. As illustrated in the schematic in Fig. 3a and b, three lines are plotted, one at the centre of the contact (black), one at the edge (green) and one in the middle between these two (red). Data shows a negative distance change upon stepping from a negative to a positive applied potential, and vice versa for the reverse potential step. Both shape and distance changes are highly reproducible over a large number of repetitions and different samples. The distance step at the edge of an established slit is slightly larger, by about 5 Å, which likely relates to the lower pressure at the edge of a slit pore, and hence lower confining pressure (which is not entirely uniform over the established slit). As can be seen, the distance change appears during a time interval well below one second, highlighting the necessity for a high-speed measurement setup.
Fig. 2b shows a close up of the distance change during potential stepping. The distance change occurs within 250–300 ms, which is the time that is required to equilibrate the overlapping EDL to the new potential by exchanging charge with the bulk reservoir. Interestingly, the positive step and the negative step show different equilibration profiles of the distance with time. When stepping from negative to positive potential, a continuous exponential drop of the distance occurs, which is in line with an equilibrated drop of local potential and ion expulsion. However, when stepping from the positive to the negative potential regime, a distinctive overshoot of the distance at Δt = 100–200 ms occurs, which equilibrates within 1–2 seconds. Regardless, a clear trend of time delay between different FECO lines, at the pore opening and at the centre of the contact (RL = 0), can be observed. Fig. 2c shows a time delay for the equilibrated ion concentration front when it moves into the centre of the circular slit pore, which corresponds to a charge regulation front.
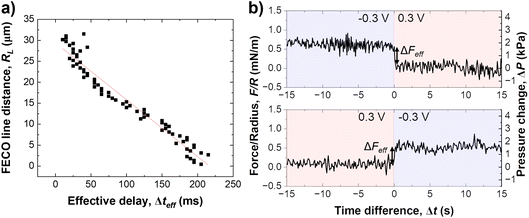
As schematically described in Fig. 3a–c, a local analysis of the distance change shows a clear delay for the EDL equilibration in the centre of the slit pore (cf. caption for details). We can track the time delay of the the equilibrated ion concentration front on any point of the curve. Here, we deliberately choose to track the overshoot maximum, which is within 15% of the fully equilibrated distance. As shown in Fig. 3d this should allow us to closely track the progression of the equilibrated ion concentration front. Fig. 4a shows that the tracked point of the charge migration wave transitions nearly linearly towards the centre (with an R2 = 0.94). The slope of this linear regression suggests a motion of the equilibrated front with a velocity of 186 ± 63 μm s−1 over independent experiments. The quite large error bar may relate to slightly different contact geometries over independent experiments as well as the higher signal-to-noise ratio of the high frame rate readout. This may be improved with higher sensitivity detectors in future work. However, the measured velocity of the equilibrated front is in good agreement with the ion speed of vion = 160 μm s−1 obtained from the numerical model. Further details on the numerical model will be discussed later.
Fig. 4b shows the force response during a potential change in both directions. Clearly, the change of the disjoining force, see Section 2.5, ΔF, which integrates over the entire contact geometry, occurs much more quickly compared to the observed charge regulation. This suggests that the electrostatic force is balanced quickly, while ion transport and equilibration of the EDL in the confined area proceeds on a longer time scale. The change in force per radius, ΔFeff is about 0.5 mN m−1 or 2 kPa, when the force is divided by the contact area. The force change is similar in both directions of the step potential switch, and is related to the charge regulation of the non-confined area of the gold electrode. It is expected, and consistent with previous work,34 that the recharging of the openly exposed gold (D ≥ 20 nm) results in an electrostatic force pulse.
However, the distance overshoot observed during recharging from positive to negative potentials in this nano-confined recharging experiment is not related to an electrostatic force due to the non-equilibrated double layer in the gap. Instead, these data suggest that charge regulation and potential change progress simultaneously into the confined zone between the two plates, i.e. the applied potential does not immediately apply to the confined area.
With an aim to understand the charge regulation mechanism, it is now interesting to further rationalise the ion distribution and charge regulation in the confined nano-slit using both MD simulations as well as a continuum based on the Stern model of the EDL (see methods for details). It appears necessary, (1) to understand the double layer structure of the confining surface, (2) to assess if the charge regulation of the gold surface influences the Stern layer structure of the EDL at the confining mica side, and (3) to compare experimental data to simulations of the overlapping EDL at varying potential, to correlate experimental and predicted distance changes at the applied potentials.
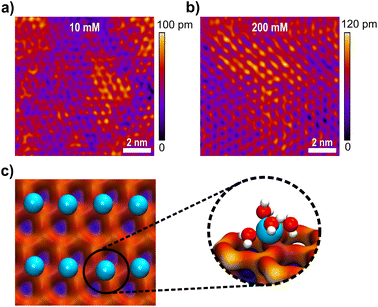
Fig. 5a and b show high resolution AFM images of the mica surface at low and high ionic strengths. Both images show a very clear resolution of the mica lattice, which compares well to the expected structure simulated by MD simulations in Fig. 5c. The data further show that Li+ ions adsorb to the mica surface with an increasing coverage from 10 mM to 200 mM solutions. The Li+ ions are clearly visible as round shaped structures that adsorb to the corners of the hexagonal mica lattice. However, even at 200 mM the lattice is not saturated with Li+ ions, suggesting that the mica charge is not fully screened within the inner double layer. AFM images further suggest that Li+ adsorbs on the surface at one of the tetrahedral oxygen sites of a hexagonal ring, presumably on top of a substitution site, where mica carries a localised negative charge. This adsorption position is also confirmed in MD simulations, shown in Fig. 5c. In MD simulations Li+ ions interact strongly with the oxygen atom of the hexagonal surface structure. Li+ ions retain 4 inner hydration shell waters, which is in line with the observed 4–5 waters that can be accommodated in the first hydration shell.60 At the surface the 5th position is saturated by the surface oxygen, suggesting a specific adsorption in the inner double layer, with a weak acceptor site.
The ion concentration profiles in Fig. 6a and b further show that Li+ ions exhibit a significant layering within the first 1–2 Å of the surface, characterising the Stern layer thickness, which is close to the vdW radius of lithium. MD simulations clearly indicate that the total amount of Li+ ions in the Stern layer, however, cannot compensate the full surface charge of mica. Within the MD cell about 5–10% of the total surface charge remains uncompensated at simulated bulk ionic strengths up to 500 mM. As such, we hypothesize at lower experimental concentrations, a significant amount of surface charge will be screened in the diffuse double layer. Similarly, AFM images show that the Li+ population in the inner double layer depends on the bulk concentration, showing higher Li+ adsorption at higher concentration. However, no charge compensation, as seen for freshly cleaved mica in vacuum,61 is visible even at 200 mM bulk concentration.
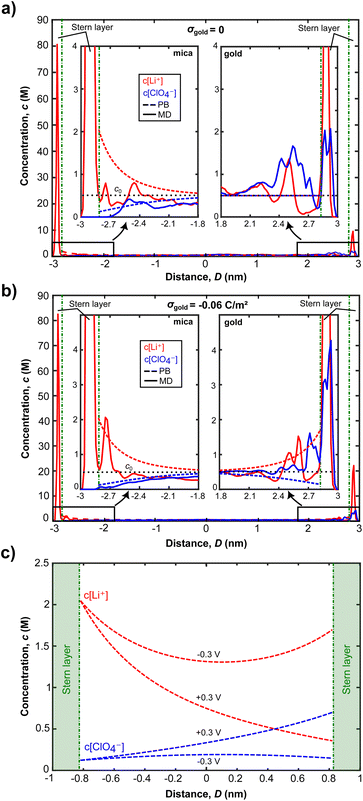
There is a similar picture for the ion distributions at the gold surface. The strongly structured inner EDL of gold also extends over a few Å, with the remaining charge screened in the diffuse double layer. Fig. 6a and b show that changing the gold potential controls the ion distribution near the gold surface, whereas it does not significantly influence the amount of Li+ ions adsorbed on mica. As the surface charge density of gold increases from 0 to −0.06 C m−2, the Li+ ion concentration of the first peaks stays the same for both surface charge values. At σ = −0.06 C m−2, we see that the second peak of the Li+ concentration at the mica surface corresponds to only one Li+ ion difference, compared to the case of σ = 0. The change in the second peak is therefore statistically not significant. Contrastingly, the Li+ concentration near the gold surface increases 2.2 times. Additionally, we see a significant layering of ClO4− ions near the gold for both neutral and negatively charged cases, but this is not the case for mica. This can be attributed to the strong repulsion forces induced by negatively charged mica, making ClO4− ions get closer to the gold surface and interact weakly with the gold atoms and adsorbed Li+ ions there. These results clearly indicate that the charge regulation occurs near the gold surface due to the exchange of ions when an electric potential is applied.
As seen in Fig. 6a and b, for D = 6 nm, ion concentrations from both MD simulations and the Stern model converge to the bulk ionic concentration within 1.5 nm from both surfaces. This indicates that the EDLs overlap for the experimentally established distance of D = 2 nm, which can further be observed from the Stern model predictions of ion concentrations in Fig. 6c: the number of co- and counter ions at the confinement midplane do not match their respective bulk concentration of 500 mM for both −0.3 and +0.3 V. As a result, a disjoining pressure, given in eqn (4), is established.
Fig. 6c further shows that the charge regulation for overlapping EDLs mainly occurs on the gold surface and is driven by the (diffusive) exchange of ions: more Li+ ions are present in the confinement for an applied potential of −0.3 V compared to the +0.3 V case. When the gold surface potential is stepped from −0.3 V to +0.3 V cations are expelled from the confinement to be replaced by anions, predominantly on the gold side. Contrastingly, the mica side is only weakly affected. Given the MD simulation data, and the experimental Debye length of 1.15 nm at the experimental concentration of 70 mM LiClO4, application of a Stern model to fit the ion exchange appears justified. A typical limit for application of continuum models is that the experimental distance is greater than the Debye length, which applies to the experimentally set and varying distances.
The PB equation does not capture the finite ion size and ion correlation effects62,63 and therefore fails to accurately predict concentration profiles obtained in MD simulations. By modelling the Stern layer as a capacitor,51 we include the finite vdW diameter of the counter ions in eqn (2). Therefore a more accurate description of ion distributions, close to the surface, and in the midplane, is obtained. With this model, the potential drop in the Stern layer is linear and provides a boundary condition for the PB equation that describes the diffuse part of the EDL. The ion concentrations obtained from this Stern model are then used to calculate the disjoining pressure given in eqn (4).
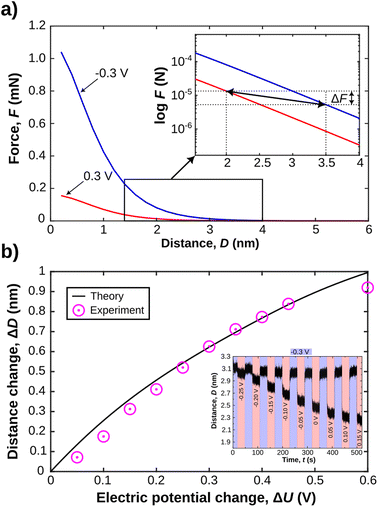
Fig. 7a shows force versus distance profiles for overlapping EDLs calculated with eqn (4). A number of aspects of the model parameter choices need to be clarified. (1) In the applied model, the Stern layer thickness is modelled with the vdW radius of 176 pm for the Li+ ions. This is in line with the inner double layer structure obtained in MD simulations, shown in Fig. 6, where it extends about 1–2 Å from the surface.
(2) The mica potential is modelled at a constant charge in the Stern layer, which results in a potential drop of 164 mV across this layer. This is consistent with the molecularly resolved understanding of the mica interface, that can be derived from high resolution AFM imaging. In addition, the observed structure compares well with MD simulations of the ions in the inner double layer, both under confinement and non-confinement conditions. As such, the confining mica side appears as a charged but mostly unaffected wall during experimentally enforced charge regulation.
(3) The choice of the model for the charge evolution within the inner double layer at the gold surface must be justified. As seen from MD simulations, most of the gold surface charge is screened by the inner EDL, while only a small fraction of the applied surface potential decays over the outer. Therefore, we selected the choice of the inner double layer charge based on the expected dependency of the potential drop over the outer double layer. We extracted the gold surface potential dependence on the applied electric potential from experimental data.53 This relationship is almost linear over applied potentials from −700 to 100 mV with respect to the potential of zero charge. For applied potentials between −300 and 300 mV the corresponding surface potentials are in the range of −22 and 17 mV.
(4) It should be noted that we estimate the total disjoining force only from the EDL repulsion, eqn (4), while vdW interactions as well as inner double layer forces are neglected. This is justified by the fact that we measure the charge regulation at distances where the latter two contributions are small, compared to the EDL repulsion for distances above 1–2 nm. This is in line with previous data from force versus distance analysis as a function of the applied potential.53,59,64–66
Finally, the experimentally well-characterised potential of zero charge for gold must be set for the modelling of the force distance profiles. In this work, we utilise a platinum pseudo reference electrode. Based on comparing the experimental pseudo reference with cyclic voltammetry during the course of an experiment, we can reference the electrode back to the SHE, using the experimentally observed gold oxidation peak. As such, our experimental zero is close to the SHE, with an estimated error of less than 50 mV. Hence, we expect the potential of zero charge at about 150–200 mV67 for a LiClO4 solution, with respect to the platinum pseudo reference.
With these assumptions clarified, we can now proceed to compare experimental and theoretical analysis of the charge regulation process. In the inset in Fig. 7a, a semi-log plot of the force versus distance profile shows the expected disjoining force for experimentally relevant gap thicknesses under constant applied potentials. As indicated we can utilise these force profiles to extract both the expected distance change, and the expected force change after charge regulation when equilibrium is again fully reestablished. In Fig. 7b we show the evolution of the expected distance change as a function of the applied potential change. We further compare this to experimentally obtained distance variations as a function of potential change. The inset in Fig. 7b shows an experimental data set, where the potential step is increased linearly by 50 mV, with a starting potential of −300 mV. The distance changes are then compared to the theoretically expected ones, based on the Stern model for the confinement and eqn (4) for the disjoining pressure due to overlapping EDLs. These data fit the expected theoretical trend very well. This is one central finding of this work. Indeed, a continuum-based Stern model – with inner and outer EDL – can explain equilibrium distances upon experimentally induced charge regulation very well, even at high confinement of the apposing EDLs of the confining walls. In addition, the predicted change in the disjoining force ΔF of the EDL, due to the distance and potential shift, when derived from the theoretically predicted force distance profile, is in the μN range. This is in good agreement with the experimentally observed force change, shown in Fig. 4b. Deviations are likely due to the simplified treatment neglecting vdW as well as inner double layer repulsion, which should mildly modify the simulated force profile at D ≥ 1–2 nm.51,68
We finally rationalise the experimentally measured velocity of the equilibrated ion concentration front of 186 μm s−1 by modelling the ion transport into the gap after the gold potential is switched. Here, Fick's law of diffusion for a radially symmetric cylindrical system, eqn (6), is used. The diffusion coefficient is modified with eqn (8) to account for hindrance effects in the nano-confinement. The averaged ion concentrations for the electric potentials before and after the switch, eqn (5), serve as the initial condition in the gap and boundary condition at the edge, respectively. Then, the velocity of the equilibrated ion concentration front into a cylindrical slit pore of radius Rtotal = 32 μm is obtained from the time it takes for the concentration to reach the imposed boundary condition everywhere in the system, eqn (9). This provides a velocity of 160 μm s−1 in close agreement with the experimental data and suggests that the charge regulation in the gap is mainly due to the diffusive transport of ions. Despite this good agreement, we want to cautiously emphasise that this is a very simplistic treatment, which will need further in depth study with models that approximate the experimental setting in more detail. Yet, it is still interesting to note that the experimental ion equilibration velocity appears to proceed at the time scale of a diffusive transport mechanism, even for strongly overlapping double layers.
4 Concluding remarks
In conclusion, an electrochemically modulated in situ sensing SFA, with a high speed sensor, is an effective tool to observe charge regulation in confined spaces. With an experimentally established slit-pore, ion concentration front can be traced in 3D inside nano-confined cylindrical slit pores, where electric double layers overlap. It should be noted that, in comparison to potential device architectures in nano-fluidics, the SFA varies both the surface charge as well as the distance during a recharging experiment, which complicates theoretical treatments of the system.We are able to accurately capture the force and distance changes as a function of the potential with a continuum model based on the Stern layer picture of the EDL. We justified the usage of the Stern model based on a molecularly resolved understanding of the inner double layer structure using MD simulations as well as AFM imaging. Simulation and imaging agree very well for the mica side. However, imaging on the gold side was, to date, not successful as a function of an applied potential. This is likely due to the smaller scale of the lattice constant of the gold surface. In addition, the template stripped gold, with its preferential (111) orientation is molecularly smooth but not perfectly single crystalline at the surface.
We could further experimentally extract for the first time the velocity of the EDL equilibration transitions into a cylindrical nano-confinement. For the LiClO4 solution between a mica and a gold surface the data suggests a velocity of about 186 μm s−1. It should be noted that this velocity is not directly related to the ion diffusion rate/coefficient. It is an equilibration time, which is the time it takes for fully equilibrating the confined ion distribution with respect to the boundary conditions of the confining walls. Nevertheless, the equilibration time offers an experimentally observable parameter that should allow us to determine diffusion coefficients, given a proper theoretical description of the dynamic charge regulation process in such highly overlapping EDLs. Interestingly, measured equilibration times can be approximated well by a simple diffusion model. Diffusion based modelling predicts a velocity of the equilibrated ion concentration front in the experimental range of around 160 μm s−1. This suggests that diffusion is the main mechanism for ion equilibration in an electrochemically modulated nano-pore.
This work further supports the concept that a continuum model, ideally coupled to atomistic modelling of the inner double layer, can well describe ion exchange in molecularly confined gaps down to thicknesses of just 1–2 nm. In our current model, we justify assumptions of the used Stern model with MD simulations as well as experimental visualisation of the inner double layer structure, at least for one side of the confined space. Further work may focus on directly coupling atomistic and continuum descriptions for the EDL and its dynamics.62 It will now be interesting to study this type of system, both experimentally and theoretically, towards the limits where the continuum description must fail (e.g. strongly adsorbing ions, crowding situations at high applied potentials, large ions).
Author contributions
JL & UR performed experiments and analysed data. MS, AC & FA conducted simulations. MO performed AFM experiments. JD performed preliminary SFA experiments. AC, LM, and JD supported conceptual development of the manuscript. DWL & MV conceptually developed this work and supervised the manuscript writing process. All authors contributed to the writing and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the European Research Council (ERC-StG 677663) as well as the Gesellschaft für Forschungsförderung Niederösterreich (Lsc19-26) as well as funding from the research promotion agency (FFG) of Austria via CEST GmbH (COMET Centre of Electrochemical and Surface Technology, 865864) as well as Ministry of Trade, Industry & Energy/Korea Institute of Energy Technology Evaluation and Planning (MOTIE/KETEP) (20214000000660) as well as National Research Foundation (NRF) of Korea (2022R1F1A1074416) and support by the 2023 Research Fund (1.230040.01) of Ulsan National Institute of Science and Technology (UNIST). JD acknowledges support from the Research Council of Norway, FRIPRO Grant 286733. FA acknowledges support from LAM Research GmbH (Villach, Austria) within a COMET project (FFG, 865864). We thank Hsiu-Wei Cheng and Valentina Wieser for their preliminary SFA experiments that informed the refinement of the optimal experimental parameters and theoretical interpretations.69 We thank Julian Pichler for his support with visualisation of MD simulations. All simulations were carried out using high performance computing facilities in Austria, hence we acknowledge the Vienna Scientific Cluster (VSC).Notes and references
- R. C. Newman, in Corrosion Mechanisms in Theory and Practice, CRC Press, Boca Raton, FL, USA, 2011, pp. 511–556 Search PubMed.
- L. M. Ostertag, X. Ling, K. F. Domke, S. H. Parekh and M. Valtiner, Phys. Chem. Chem. Phys., 2018, 20, 11722–11729 RSC.
- K. A. Mauritz and R. B. Moore, Chem. Rev., 2004, 104, 4535–4586 CrossRef CAS PubMed.
- Y. Xu, Adv. Mater., 2018, 30, 1702419 CrossRef PubMed.
- S. Z. Bisri, S. Shimizu, M. Nakano and Y. Iwasa, Adv. Mater., 2017, 29, 1607054 CrossRef PubMed.
- K. A. Schwenzfeier, A. Erbe, P. Bilotto, M. Lengauer, C. Merola, H.-W. Cheng, L. L. Mears and M. Valtiner, Rev. Sci. Instrum., 2019, 90, 043908 CrossRef PubMed.
- Y. Li, H. Cao and J. Yu, ACS Nano, 2018, 12, 4096–4104 CrossRef CAS PubMed.
- C. Pean, B. Daffos, B. Rotenberg, P. Levitz, M. Haefele, P.-L. Taberna, P. Simon and M. Salanne, J. Am. Chem. Soc., 2015, 137, 12627–12632 CrossRef CAS PubMed.
- Z. Ling, C. E. Ren, M.-Q. Zhao, J. Yang, J. M. Giammarco, J. Qiu, M. W. Barsoum and Y. Gogotsi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 16676–16681 CrossRef CAS PubMed.
- C. Galeano, J. C. Meier, V. Peinecke, H. Bongard, I. Katsounaros, A. A. Topalov, A. Lu, K. J. J. Mayrhofer and F. Schüth, J. Am. Chem. Soc., 2012, 134, 20457–20465 CrossRef CAS PubMed.
- H.-W. Cheng and M. Valtiner, Curr. Opin. Colloid Interface Sci., 2020, 47, 126–136 CrossRef CAS.
- C. Largeot, C. Portet, J. Chmiola, P.-L. Taberna, Y. Gogotsi and P. Simon, J. Am. Chem. Soc., 2008, 130, 2730–2731 CrossRef CAS PubMed.
- R. Lin, P. Huang, J. Segalini, C. Largeot, P.-L. Taberna, J. Chmiola, Y. Gogotsi and P. Simon, Electrochim. Acta, 2009, 54, 7025–7032 CrossRef CAS.
- S. Baldelli, Acc. Chem. Res., 2008, 41, 421–431 CrossRef CAS PubMed.
- N. Nishi, Y. Hirano, T. Motokawa and T. Kakiuchi, Phys. Chem. Chem. Phys., 2013, 15, 11615–11619 RSC.
- Y. Lauw, M. D. Horne, T. Rodopoulos, V. Lockett, B. Akgun, W. A. Hamilton and A. R. Nelson, Langmuir, 2012, 28, 7374–7381 CrossRef CAS PubMed.
- S. Das and S. Chakraborty, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 012501 CrossRef PubMed.
- C. Merola, H.-W. Cheng, K. Schwenzfeier, K. Kristiansen, Y.-J. Chen, H. A. Dobbs, J. N. Israelachvili and M. Valtiner, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 9541–9546 CrossRef CAS PubMed.
- K. Kristiansen, M. Valtiner, G. W. Greene, J. R. Boles and J. N. Israelachvili, Geochim. Cosmochim. Acta, 2011, 75, 6882–6892 CrossRef CAS.
- J. Dziadkowiec, B. Zareeipolgardani, D. K. Dysthe and A. Røyne, Sci. Rep., 2019, 9, 1–15 CrossRef CAS PubMed.
- P. Simonnin, B. Noetinger, C. Nieto-Draghi, V. Marry and B. Rotenberg, J. Chem. Theory Comput., 2017, 13, 2881–2889 CrossRef CAS PubMed.
- E. M. Renkin, J. Gen. Physiol., 1954, 38, 225 CAS.
- P. Dechadilok and W. M. Deen, Ind. Eng. Chem. Res., 2006, 45, 6953–6959 CrossRef CAS.
- J. Moškon and M. Gaberšček, J. Power Sources Adv., 2021, 7, 100047 CrossRef.
- M. Mirzadeh, F. Gibou and T. M. Squires, Phys. Rev. Lett., 2014, 113, 097701 CrossRef CAS PubMed.
- R. de Levie, Electrochim. Acta, 1963, 8, 751–780 CrossRef.
- P. M. Biesheuvel and M. Z. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031502 CrossRef CAS PubMed.
- S. F. Buchsbaum, M. L. Jue, A. M. Sawvel, C. Chen, E. R. Meshot, S. J. Park, M. Wood, K. J. Wu, C. L. Bilodeau, F. Aydin, T. A. Pham, E. Y. Lau and F. Fornasiero, Adv. Sci., 2021, 8, 2001802 CrossRef CAS PubMed.
- A. Esfandiar, B. Radha, F. Wang, Q. Yang, S. Hu, S. Garaj, R. Nair, A. Geim and K. Gopinadhan, Science, 2017, 358, 511–513 CrossRef CAS PubMed.
- A. Ghoufi, A. Szymczyk and P. Malfreyt, Sci. Rep., 2016, 6, 1–9 CrossRef PubMed.
- A. Gupta, P. J. Zuk and H. A. Stone, Phys. Rev. Lett., 2020, 125, 076001 CrossRef CAS PubMed.
- S. Kondrat, P. Wu, R. Qiao and A. A. Kornyshev, Nat. Mater., 2014, 13, 387 CrossRef CAS PubMed.
- S. Kondrat and A. Kornyshev, J. Phys. Chem. C, 2013, 117, 12399–12406 CrossRef CAS.
- R. Tivony, S. Safran, P. Pincus, G. Silbert and J. Klein, Nat. Commun., 2018, 9, 4203 CrossRef PubMed.
- R. Tivony, Y. Zhang and J. Klein, J. Phys. Chem. C, 2021, 125(6), 3616–3622 CrossRef CAS PubMed.
- J. Israelachvili, Y. Min, M. Akbulut, A. Alig, G. Carver, W. Greene, K. Kristiansen, E. Meyer, N. Pesika, K. Rosenberg and H. Zeng, Rep. Prog. Phys., 2010, 73, 036601 CrossRef.
- B. R. Shrestha, T. Baimpos, S. Raman and M. Valtiner, ACS Nano, 2014, 8, 5979–5987 CrossRef CAS PubMed.
- V. Wieser, P. Bilotto, U. Ramach, H. Yuan, K. Schwenzfeier, H.-W. Cheng and M. Valtiner, J. Vac. Sci. Technol., A, 2021, 39, 023201 CrossRef CAS.
- M. Schubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 4265–4274 CrossRef CAS PubMed.
- S. M. Richardson and J. W. Richardson, Am. Mineral., 1982, 67, 69–75 CAS.
- W. Loewenstein, Am. Mineral., 1954, 39, 92–96 CAS.
- H. J. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- R. T. Cygan, J.-J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266 CrossRef CAS.
- B. Doherty, X. Zhong, S. Gathiaka, B. Li and O. Acevedo, J. Chem. Theory Comput., 2017, 13, 6131–6145 CrossRef CAS PubMed.
- H. Heinz, R. A. Vaia, B. L. Farmer and R. R. Naik, J. Phys. Chem. C, 2008, 112, 17281–17290 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- S. J. Plimpton, R. Pollock and M. J. Stevens, SIAM Conference on Parallel Processing for Scientific Computing, 1997 Search PubMed.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- I.-C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 3rd edn, 2011 Search PubMed.
- W. R. Fawcett, Condens. Matter Phys., 2005, 8, 413 CrossRef.
- A. C. Hillier, S. Kim and A. J. Bard, J. Phys. Chem., 1996, 100, 18808–18817 CrossRef CAS.
- T. A. Driscoll, N. Hale and L. N. Trefethen, Chebfun Guide, Pafnuty Publications, 2014 Search PubMed.
- The MathWorks Inc., Matlab® Search PubMed.
- E. Cussler, Diffusion, Cambridge University Press, 3rd edn, 2007 Search PubMed.
- A. Einstein, Ann. Phys., 1905, 322, 549–560 CrossRef.
- L. N. Trefethen, Spectral Methods in MATLAB, Society for Industrial and Applied Mathematics, 2000 Search PubMed.
- T. Baimpos, B. R. Shrestha, S. Raman and M. Valtiner, Langmuir, 2014, 30, 4322–4332 CrossRef CAS PubMed.
- P. E. Mason, S. Ansell, G. W. Neilson and S. B. Rempe, J. Phys. Chem. B, 2015, 119, 2003–2009 CrossRef CAS PubMed.
- G. Franceschi, P. Kocán, A. Conti, S. Brandstetter, J. Balajka, I. Sokolović, M. Valtiner, F. Mittendorfer, M. Schmid, M. Setvín and U. Diebold, Nat. Commun., 2023, 14, 1–8 Search PubMed.
- R. Qiao and N. R. Aluru, J. Chem. Phys., 2003, 118, 4692–4701 CrossRef CAS.
- B. J. Kirby, Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices, Cambridge University Press, 2010 Search PubMed.
- M. Valtiner, X. Banquy, K. Kristiansen, G. W. Greene and J. N. Israelachvili, Langmuir, 2012, 28, 13080–13093 CrossRef CAS PubMed.
- R. Tivony and J. Klein, Faraday Discuss., 2017, 199, 261–277 RSC.
- J. Wang and A. J. Bard, J. Phys. Chem. B, 2001, 105, 5217–5222 CrossRef CAS.
- D. D. Bode Jr, T. N. Andersen and H. Eyring, J. Phys. Chem., 1967, 71, 792–797 CrossRef.
- A. J. Bard and L. R. Faulkner, et al. , Electrochem. Methods, 2001, 2, 580–632 Search PubMed.
- H.-W. Cheng, J. Dziadkowiec, V. Wieser, A. M. Imre and M. Valtiner, arXiv, 2021, preprint, DOI:10.48550/arXiv.2104.01157.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |