Unified quantum theory of electrochemical kinetics by coupled ion–electron transfer†
Received
25th May 2023
, Accepted 25th May 2023
First published on 31st May 2023
Abstract
A general theory of coupled ion–electron transfer (CIET) is presented, which unifies Marcus kinetics of electron transfer (ET) with Butler–Volmer kinetics of ion transfer (IT). In the limit of large reorganization energy, the theory predicts normal Marcus kinetics of “electron-coupled ion transfer” (ECIT). In the limit of large ion transfer energies, the theory predicts Butler–Volmer kinetics of “ion-coupled electron transfer” (ICET), where the charge transfer coefficient and exchange current are connected to microscopic properties of the electrode/electrolyte interface. In the ICET regime, the reductive and oxidative branches of Tafel’s law are predicted to hold over a wide range of overpotentials, bounded by the ion-transfer energies for oxidation and reduction, respectively. The probability distribution of transferring electron energies in CIET smoothly interpolates between a shifted Gaussian distribution for ECIT (as in the Gerischer–Marcus theory of ET) to an asymmetric, fat-tailed Meixner distribution centered at the Fermi level for ICET. The latter may help interpret asymmetric line shapes in x-ray photo-electron spectroscopy (XPS) and Auger electron spectroscopy (AES) for metal surfaces in terms of shake-up relaxation of the ionized atom and its image polaron by ICET. In the limit of large overpotentials, the theory predicts a transition to inverted Marcus ECIT, leading to a universal reaction-limited current for metal electrodes, dominated by barrierless quantum transitions. Uniformly valid, closed-form asymptotic approximations are derived that smoothly transition between the limiting rate expressions for ICET and ECIT for metal electrodes, using simple but accurate mathematical functions. The theory is applied to lithium intercalation in lithium iron phosphate (LFP) and found to provide a consistent description of the observed current dependence on overpotential, temperature and concentration. CIET theory thus provides a critical bridge between quantum electrochemistry and electrochemical engineering, which may find many other applications and extensions.
1 Introduction
Charge transfer at the electrode/electrolyte interface is the most fundamental aspect of electrochemical systems, but its understanding remains incomplete. By contrast, the bulk properties of electrodes and electrolytes are increasingly investigated and modeled at the molecular level. Their atomic structure and thermodynamic and transport properties can be measured by experiments and accurately predicted by ab initio quantum mechanical theories and simulations.1 For crystalline electrodes and electrolytes, quantum simulations of bulk properties have become so accurate that they are beginning to replace experimental measurements and guide the discovery of new materials.2 Progress is underway to better understand properties of disordered bulk liquid and solid electrolytes, as well as the molecular structure of electrode/electrolyte interfaces.3,4
Faradaic reaction rates at electrode/electrolyte interfaces, however, remain challenging to predict from first principles. This is partly due to the lack of a simple mathematical framework with which to describe both ion transfer (IT) and electron transfer (ET) processes based on quantum mechanics. Here, we develop such a theory for non-adiabatic charge transfer processes, which unifies Butler–Volmer kinetics of IT with Marcus kinetics of ET in a single quantum mechanical framework of coupled ion–electron transfer (CIET).
2 A brief history of electrochemical kinetics
2.1 Ion transfer theory
The standard model of charge transfer kinetics in electrochemistry5–8 and electrochemical engineering9,10 is the Butler–Volmer (BV) equation:11,12| |
I = I0(e−αn![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) − e(1−α)n − e(1−α)n![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) ) ) | (1) |
where I is the reduction current, I0 the exchange current, α the charge-transfer coefficient or symmetry factor, n the number of electrons transferred, and ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) = eη/kBT the dimensionless activation overpotential η, scaled to the thermal voltage, kBT/e. The BV equation has remained unchanged for over a century since the seminal work of Tafel,13,14 Butler,11,15–18 Bowden19 and Erdey-Gruz and Volmer12,20 on the reaction kinetics of electrolysis, motivated by Tafel's limiting law,13
= eη/kBT the dimensionless activation overpotential η, scaled to the thermal voltage, kBT/e. The BV equation has remained unchanged for over a century since the seminal work of Tafel,13,14 Butler,11,15–18 Bowden19 and Erdey-Gruz and Volmer12,20 on the reaction kinetics of electrolysis, motivated by Tafel's limiting law,13| |
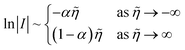 | (2) |
The BV equation has since been used to describe faradaic reaction kinetics in all fields of electroanalytical chemistry6,21 and electrochemical systems,9,10 including batteries, fuel cells, electrodeposition, corrosion, electrocatalysis, and iontronics (the topic of this Faraday Discussions meeting).
The BV equation is almost universally accepted by experimentalists as the model of electrochemical kinetics, although empirical modifications are often required to fit experimental data. For example, in order to reveal pure BV kinetics, it is usually necessary to correct for what are considered spurious “IR drops” associated with “film resistance”.9,10 The BV equation has also been extended in many other ways, e.g. to account for adsorption isotherms of reaction intermediates,7,8 Frumkin effects of double-layer charge,5,22,23 and non-equilibrium thermodynamics of phase transformations.24
Despite many successes in fitting experimental data, the BV equation is considered to be phenomenological, and it lacks a consistent theoretical framework with which to interpret fitted parameters or design improved electrode interfaces. It does not explicitly take into account the microscopic physics of charge transfer, such as charge solvation, ion coordination, double-layer structure, electrode band structure, electronic coupling and quantum tunneling between the acceptor and donor states at interfaces.25,26 As such, quantitative connections cannot be made between the BV parameters (I0, α) and material properties, such as dielectric constants, electrode crystal structure, electrolyte chemistry, etc., which could be validated experimentally or predicted by molecular simulations.
Textbook derivations of the BV equation are based on a simple picture of ion transfer (IT) biased by the local electric field,6–10 as sketched in Fig. 1. The reaction complex explores a landscape of excess chemical potential along a spatial reaction coordinate ξ between the reduced and oxidized states, while transferring n electrons. The chemical part of the activation barrier is assumed to remain constant and at fixed position,
as the reaction is biased by a constant local electric field,
E = −
ηf/(
ξR −
ξO), where
ηf is the formal overpotential, and
ξR −
ξO is the distance for ion transfer, often associated with the thickness of the Stern layer of solvation on the electrode.
27–29 Based on this picture of the reaction mechanism, a thermodynamically consistent derivation of the exchange current yields the formula,
| |
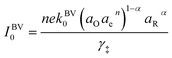 | (4) |
where
k0 is an attempt frequency,
γ‡ is the activity coefficient of the ion-transfer transition state, and
aO,
aR and
ae are the activities of the oxidized state, reduced state, and electrons, defined below.
24
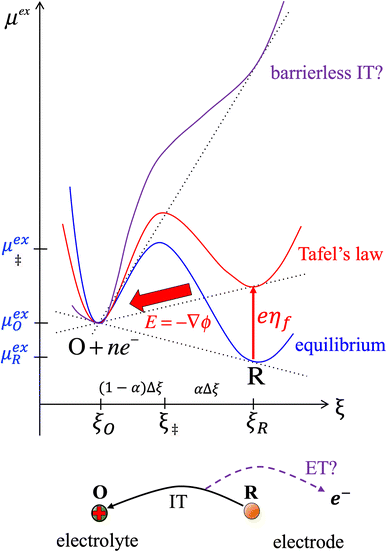 |
| | Fig. 1 Phenomenological theory of ion transfer (IT) to explain Butler–Volmer kinetics6–10 – and its limitations. The reaction complex is hypothesized to move along a classical charge-transfer reaction coordinate ξ (typically the position of an ion) between the reduced state R and the oxidized state O, as n electrons are transferred to the electrode (R → O + ne−), in a landscape of excess chemical potential μex.24 The chemical part of the activation barrier, μex‡, fixed at position ξ‡ = αξR + (1 − α)ξO, is assumed to be independent of formal overpotential ηf, which is postulated to create a constant electric field, E = −ηf/Δξ, driving the charge-transfer reaction over a distance, Δξ = ξR − ξO, set by the Stern layer thickness on the electrode. This construction leads to the BV equation (1) and Tafel's limiting law for moderate overpotentials, but the model breaks down at large overpotentials, e.g. as shown for (1 − α)neηf > (μex‡ − μexO)eq, when the activation barrier vanishes, and classical transition state theory no longer applies. The model also fails to explain exactly when and how electron transfer (ET) occurs, as the proposed reaction mechanism only accounts for ion transfer (IT). [Adapted from Bazant (2013).24] | |
Although the IT reaction mechanism in Fig. 1 is widely accepted as the justification for BV kinetics, it contains many theoretical inconsistencies. Although ηf is varied by changing the potential of electrons in the electrode, the model does not specify exactly when or how electron transfer occurs. Moreover, the activity of electrons is usually neglected by setting ae = 1, and the electrode band structure, which provides electrons over a range of different energies, is not considered at all. The derivation also only applies to moderate overpotentials, much smaller than the chemical energy barrier. As shown in Fig. 1, larger overpotentials would result in barrier-less ion transfer, which cannot be described by classical transition state theory. These limitations of ion transfer theory are well known, but usually overlooked when fitting the BV equation to experimental data. We shall see that the key to resolving these inconsistencies is a quantum mechanical treatment of electron transfer (ET).
2.2 Electron transfer theory
An electrochemical reaction, by definition, involves the transfer of at least one electron between two distinct chemical states. The oxidized state donates an electron, and the reduced state accepts it. In order to conserve charge, there must be ions present in either the reduced or oxidized states, or both. In pure ET reactions, the reactants remain unchanged, except that the oxidized state is reduced, and the reduced state oxidized, by the transferring electrons. Such reactions are common in chemistry and biology and are described by quantum mechanical ET theory.25,26,30–32
The modern theory of ET kinetics was pioneered by R. A. Marcus starting in 195630,33–36 and recognized by the 1992 Nobel Prize in Chemistry.37 Since quantum-mechanical ET is isoenergetic, Marcus postulated that ET must occur when fluctuations reorganize the solvent (or more generally, the molecular environment) so as to temporarily align the electron energy levels of the diabatic reduced and oxidized states38,39 and thus allow ET to occur “in the dark” without absorbing or emitting photons. Importantly, Marcus went beyond earlier models of non-adiabatic ET and solvent-reorganization developed by Weiss40 to predict a novel Gaussian dependence of the reaction rate on overpotential, by modeling the activation barrier for ET as the intersection of two parabolae describing solvent reorganization in the harmonic approximation.30,33,36,37 Marcus summarized his theoretical predictions for experimentalists at a Faraday Discussion in 1960,41 which he later recognized as a turning point in the field.37
It is not widely appreciated that the field of quantum electrochemistry predated Marcus by a quarter century. In 1931, R. W. Gurney published the seminal paper on “quantum mechanics of electrolysis” in which he modeled proton transfer and reduction at a metallic electrode as a process of quantum tunneling involving electrons sampled from the Fermi–Dirac distribution,42 similar to modern formulations in quantum electrochemistry.6,25,26 Gurney further assumed a linear dependence of the proton transfer energy with position, before and after “neutralization” by the electron, from which he was able to derive Tafel's law.42 Although the nature of the energy barrier and its dependence on overpotential were not yet clear, Gurney's theory was a radically “new line of attack” in electrochemistry at a time of apparently some lingering doubts about the atomic nature of matter, which he felt compelled to acknowledge in his conclusion: “In deriving these quantities [neutralization potentials] we have used the only available vocabulary – that of molecular spectroscopy. The existence of definite molecules is not, however, a necessary assumption.”42
In 1936, J. A. V. Butler adapted Gurney's model for specific adsorption of protons on a metal electrode and the linear approximation of the energy landscape for ion transfer (IT) to derive the BV equation.18 Although quantum aspects of ET were not fully taken into account, the visionary papers of Gurney and Butler were the first to propose a reaction mechanism coupling IT and ET, in the specific case of the Volmer step in the hydrogen evolution reaction in acidic solutions.43 Below, we shall see that the Gurney–Butler theory corresponds to the limit of infinitely fast ET and holds up to moderately large overpotentials in the Tafel regime.
Starting in the late 1950s, the modern quantum mechanical foundations of ET theory were laid by Hush,44–46 Levich, Dogonadze, Chizmadzhev and Kuznetsov26,27,36,47–50 and Marcus30,36,51,52 with later extensions by Calef and Wolynes,53,54 Schmickler and Santos,25,31 Nazmutdinov,32 Matyushov and Voth,55,56 and many others. These theories mostly assume adiabatic ET, where a single electron is shared between the reduced and oxidized states in a particular hybrid wavefunction, as the solvent fluctuates to facilitate its gradual transfer. In the opposite limit of non-adiabatic ET, where the electronic coupling is weak, solvent reorganization does not always lead to ET, and independent, rare events of quantum tunneling can occur in parallel between the reactant and all available diabatic electronic states.38,39
Despite its many successes, ET theory – by itself – fails to provide a consistent theoretical framework for faradaic reaction kinetics at electrodes. In particular, ET theory cannot explain the vast experimental literature supporting the BV equation and, especially, Tafel's limiting law, eqn (2). This is considered by many electrochemists to be a fatal flaw in our current understanding of quantum electrochemistry, still awaiting resolution:
“Tafel's law is one of the most tested and verified laws of nature. It is also one with the broadest applicability… The ability to replicate Tafel's law is the first requirement of any theory of electrode kinetics. It represents a filter that may be used to discard models of electron transfer which predict current–potential relationships that are not observed.” – J. O. Bockris, A. K. N. Reddy and M. E. Gamboa-Aldeco (p. 1510).7
Recent electrochemistry textbooks attempt to resolve this paradox by noting that Marcus theory predicts BV kinetics with α = 1/2 (for symmetric ET), if the overpotential is much smaller than the reorganization energy (usually on the order of 100 meV ≈ 4kBT),6,21,25 but this is only an asymptotic limit. The same is true of more sophisticated models of nonlinear solvation,55,56 related to asymmetric Marcus–Hush kinetics,57,58 which again rely on the limit of small overpotentials to justify Tafel's law with α ≠ 1/2.
The persistence of Tafel's law to much larger overpotentials, sometimes spanning many decades in current with overpotentials reaching the 1 V scale of chemical bond breaking, is fundamentally inconsistent with the curved Tafel plots predicted by all ET theories,6–8,62 as shown in Fig. 2, and cannot be explained by Taylor expansion of the quantum mechanical ET rate equations. Instead, curvature of the Tafel plot is an unavoidable consequence of the nonlinear shape of the free energy landscapes for solvent re-organization in the reduced and oxidized diabatic states, including the parabolic (“harmonic”) shapes introduced by Marcus:
“The quantum mechanical formulation of electrode reactions still possesses the Achilles' heel of earlier formulations; it is restricted to nonbond-breaking, seldom occurring outer-sphere reactions and involves the harmonic approximation for the energy variation, which is the main reason it cannot replicate Tafel's law.” (ibid., p. 1523).7
In contrast, the original Gurney–Butler model of electrolysis suggests that rate-limiting, bond-breaking classical IT is responsible for Tafel's law, but the role of quantum mechanical ET, the defining aspect of electrochemical reactions, still remains to be explained, nearly a century later.
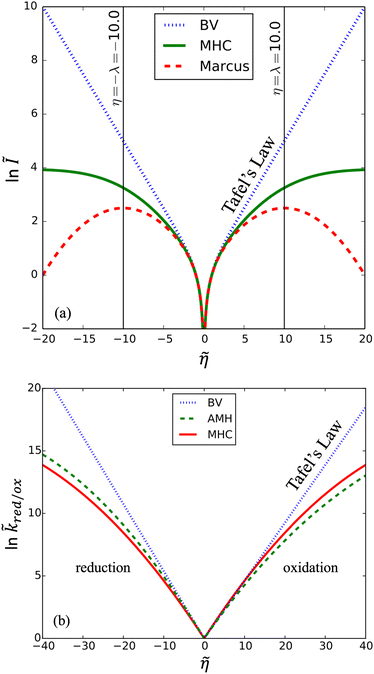 |
| | Fig. 2 Failure of quantum theories of electron transfer (ET) to predict Tafel's law as a limit of the Butler–Volmer equation (BV), eqn (1), the most widely used model of electrochemical kinetics.6,8,10,59 In countless experimental studies, reaction rates of oxidation and reduction, kox and kred, respectively, as well as the faradaic current I at an electrode, have exhibited persistent exponential dependence on overpotential, η, corresponding to a straight line “Tafel plot” of ln|I| vs. η over several decades of dimensionless current Ĩ = I/I0 (scaled to the exchange current, I0) and overpotential, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) (scaled to the thermal voltage, kBT/e) up to the scale of chemical bond breaking (|η| ∼ 1 eV). In contrast, all quantum mechanical models of ET predict curved Tafel plots, including (a) symmetric ET for localized electronic states (Marcus kinetics) or metallic electrodes (Marcus–Hush–Chidsey/MHC kinetics) and (b) asymmetric ET for metallic electrodes (asymmetric Marcus–Hush/AMH kinetics). At best, these models can asymptotically match the linear Tafel plot at low overpotentials, |η| ≪ λ, much smaller than the Marcus reorganization energy λ, which is typically at the scale of 100 meV ≈ 4kBT. [Adapted from (a) Zeng et al. (2014)60 and (b) Zeng et al. (2015).61] (scaled to the thermal voltage, kBT/e) up to the scale of chemical bond breaking (|η| ∼ 1 eV). In contrast, all quantum mechanical models of ET predict curved Tafel plots, including (a) symmetric ET for localized electronic states (Marcus kinetics) or metallic electrodes (Marcus–Hush–Chidsey/MHC kinetics) and (b) asymmetric ET for metallic electrodes (asymmetric Marcus–Hush/AMH kinetics). At best, these models can asymptotically match the linear Tafel plot at low overpotentials, |η| ≪ λ, much smaller than the Marcus reorganization energy λ, which is typically at the scale of 100 meV ≈ 4kBT. [Adapted from (a) Zeng et al. (2014)60 and (b) Zeng et al. (2015).61] | |
2.3 Toward a theory of coupled ion–electron transfer
Motivated by electrolysis and electrodeposition, new theories of faradaic reaction kinetics have emerged over the past 30 years in which ET is coupled with IT at the electrode/electrolyte interface.25,31,64 Soon after Marcus received the Nobel Prize, Cukier and Nocera introduced the theory of proton-coupled electron transfer (PCET),65,66 and Schmickler67,68 and Koper69,70 developed quantum mechanical theories of coupled adiabatic ET and bond-breaking IT reaction kinetics at metal electrodes, where interactions of the reactant with the solvent and with the metal depend on its separation from the interface. The literature has focused on situations, such as PCET71–78 or concerted proton–electron transfer (CPET),69,79–81 where both protons and electrons are treated quantum mechanically, assuming isolated reactants in a dilute solution at the electrode interface. These theories have also focused on predicting activation energies and exchange current trends, rather than the overpotential dependence of the reaction.
Much less attention has been paid to situations, such as ion intercalation, where the ions behave classically and experience strong interactions in concentrated solutions and solids, including phase transformations driven by large overpotentials. This requires re-formulating theories of charge transfer, including Butler–Volmer and Marcus kinetics, within a general framework of electrochemical nonequilibrium thermodynamics.24,82 In electrochemical engineering, ion intercalation has long been viewed as an exclusively IT process, described by BV kinetics9 and leading to capacitive charge storage, analogous to specific adsorption of ions on surfaces.83
In 2014, Peng Bai and the author suggested a different reaction mechanism, in which ion intercalation is a fast IT step, facilitated by a slow ET step between a metallic additive or coating and a poorly conducting host material.84 (Below, I suggest the term “electron-coupled ion transfer” (ECIT) to describe this reaction mechanism.) In the case of lithium iron phosphate (LFP), we provided experimental evidence that Li+ intercalation rates extracted from phase-separation dynamics obey Marcus–Hush–Chidsey (MHC) kinetics,85–87 based on the hypothesis that Li+ insertion into the crystal is facilitated by non-adiabatic ET from the metallic carbon coating to form a polaron by reducing a neighboring iron redox site (Fe3+/Fe2+),63 as shown in Fig. 3. This unorthodox picture of ET-limited intercalation was immediately met with skepticism. For example, it was shown that Tafel plots extracted from nonlinear impedance spectra for LFP could “perfectly obey the Butler–Volmer equation”,88 albeit only after fitting series resistances and neglecting known heterogeneities arising from phase separation.89–91 The importance of IT in LFP was also underscored by my earlier work on driven phase separation modeled by generalized BV kinetics,24,84,90–94 although the overpotential dependence had never been systematically explored.
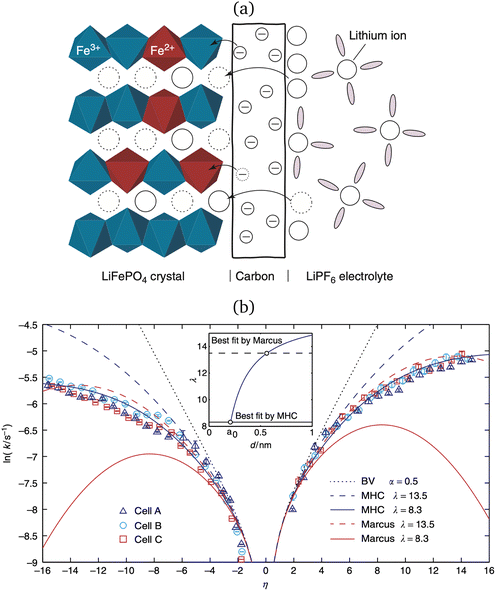 |
| | Fig. 3 Kinetics of lithium intercalation in lithium iron phosphate (LFP). (a) Reaction mechanism defined here as “electron-coupled ion transfer (ECIT)”, in which ion insertion is limited by electron transfer from the carbon coating to reduce a neighboring iron redox site and form a neutral polaron. (b) Evidence for Marcus kinetics in LFP from Tafel plots of the rate constant for reaction-limited nanoparticle phase transformations versus dimensionless overpotential (scaled to kBT/e = 26 mV), fitted to the Marcus–Hush–Chidsey (MHC) model. [Reproduced from Bai and Bazant (2014).63] | |
Perhaps another reason that quantum-mechanical ET theory was never applied in electrochemical engineering, until recently, was the lack of a simple rate expression to serve as an alternative to the BV equation. Also in 2014, Yi Zeng and I addressed this problem by publishing accurate closed-form approximations for both symmetric MHC kinetics60 and asymmetric Marcus–Hush (AMH) kinetics61 using matched asymptotic expansions of the Fermi integrals of the Marcus reaction rate in the limits of large and small reorganization energy. In contrast to various series expansions of the MHC rate,95,96 the matched asymptotic approximations are uniformly valid for all parameter values.60 This mathematical simplification enabled ET theory to be used for the first time in simulations of electrochemical systems, such as Li-ion battery cycling97–99 and electrodeposition.100–102 For battery simulations, Raymond Smith and I also adapted the generalized MHC formula to include ion-transfer effects in the prefactor,97 consistent with the ET-limited CIET rate equation presented below, but without any microscopic justification.
Recently, Dimitrios Fraggedakis and the author (building on contributions of Bai, Zeng, Smith, and other students and collaborators) developed the first mathematical theory of coupled ion–electron transfer (CIET), where electrons tunnel quantum mechanically in response to solvent reorganization, coupled with classical ion transfer based on nonequilibrium thermodynamics,103 based on the two-dimensional diabatic free energy landscape shown in Fig. 4(top). Under certain assumptions, shown below to correspond to ET rate limitation, our theory of the CIET rate for a metal electrode reduces to MHC kinetics with a concentration-dependent prefactor. This rate expression has been used in battery simulations,104 which were able to fit the raw chronoamperometry data of Bai63 better than BV kinetics, even with a fitted series resistance,103 as shown in Fig. 4(bottom). This limit of CIET theory was also able to accurately predict the concentration dependence of the lithium intercalation rate in LFP nanoparticles,105 as revealed by learning the model from a large dataset of operando X-ray images,106 which we revisit at the end of this paper using the general theory. The ET-limited theory has been adapted to successfully describe interphase formation in sodium electrodeposition from solid electrolytes.100 It has also been used to predict how electronic structure influences the stability of driven electrode interfaces, including intercalation and electrodeposition.101 Curved Tafel plots and morphological transitions seen in recent experiments on lithium electrodeposition could perhaps also be understood through the lens of CIET,107 although BV kinetics are more typically observed for electrodeposition and electrocatalysis at metal electrodes. In the original CIET paper, we noted several limits where the CIET barrier could be approximated by that of Butler–Volmer kinetics,103 but we stopped short of deriving a general theory that could unify BV and Marcus kinetics in a common formalism based on microscopic material properties. That is the focus of the present work.
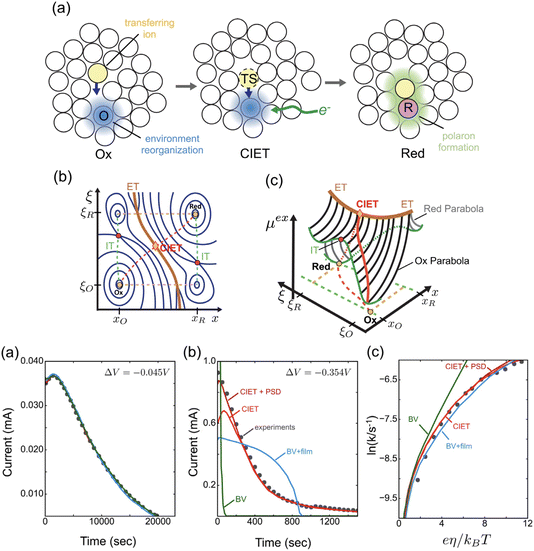 |
| | Fig. 4 (Top) (a) Schematic of coupled ion–electron transfer (CIET) with the two-dimensional landscape of excess chemical potential, shown as (b) a contour plot and (c) a surface plot, indicating the diabatic reduced and oxidized states for IT separated by the ET surface at the diabatic crossing, and the minimum energy barrier of the CIET transition state. (Bottom) Simulations of chronoamperometry using the ET-limited CIET (ECIT) model based on MHC kinetics for a single particle and a porous electrode with the measured particle size distribution (PSD), as well as the Butler–Volmer model with and without a fitted film resistance, compared to the raw experimental data of Bai and Bazant63 for (a) low voltage pulses, (b) high voltage pulses, and (c) the resulting Tafel plot. [Reproduced from Fraggedakis et al. (2021).103] | |
2.4 Outline
The paper is organized as follows. We begin by developing the general theory of nonadiabatic CIET kinetics in Section 3. We then consider three distinguished limits of the theory corresponding to normal Marcus kinetics for large reorganization energy (Section 4), quantum Butler–Volmer kinetics for large ion-transfer free energies (Section 5), and inverted Marcus kinetics at large overpotentials (Section 6) leading to a universal reaction-limited current for metal electrodes. We proceed to derive uniformly valid approximations for the CIET rate by asymptotic matching of these exact limiting cases in Section 7. Reflecting on these results in Section 8, we derive probability distributions of transferring electron energies from the CIET rate formula. In Section 9, we discuss possible corrections of the theory for adiabatic ET. In Section 10, we summarize our simple analytical approximations for the faradaic current by CIET at a metal electrode. Finally, in Section 11, we revisit the original motivation for CIET theory by re-analyzing experimental data for intercalation rates in LFP nanoparticles. We conclude in Section 12 with a brief outlook on the future of CIET theory.
3 General theory
From the perspective of nonequilibrium thermodynamics, each term in a general faradaic reaction (eqn (7) below) represents an ensemble of chemical species at a certain electrochemical potential (e.g. in the grand canonical ensemble at constant temperature and pressure). In my original work re-formulating Marcus kinetics in terms of non-equilibrium thermodynamics,24 I defined the activity and excess chemical potential of electrons as general concepts, but did not explicitly account for the quantum mechanical properties of electrodes. The theory was extended for integration over the electronic band structure with Smith104 and, importantly, in the first detailed treatment of CIET kinetics with Fraggedakis.103 These papers tacitly assumed non-adiabatic ET limited reactions and did not explicitly construct all of the thermodynamic variables in the original theory. Here, we fill in some details, clarify and relax various assumptions, and develop a more general theory of CIET kinetics, which leads to a similar MHC-like formula for the case of ET-limited reactions, while also predicting BV kinetics for the more common case of IT-limited reactions within the same unified quantum framework.
3.1 Nonequilibrium thermodynamics of charge transfer
3.1.1 Electrochemical potentials and overpotentials.
The theory begins with three definitions of the (diffusional) electrochemical potential μi of species i based on nonequilibrium thermodynamics:24| |
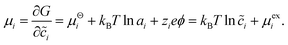 | (5) |
The first is the variational derivative of the free energy functional, G[{![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i(
i(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t)},{ϕi},T,P], the Gibbs free energy for an open system at temperature T and pressure P, with respect to the dimensionless concentration
,t)},{ϕi},T,P], the Gibbs free energy for an open system at temperature T and pressure P, with respect to the dimensionless concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i(
i(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) (scaled to a reference value crefi), which expresses the free energy required to create a particle of species i at position
,t) (scaled to a reference value crefi), which expresses the free energy required to create a particle of species i at position ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) and time t. The second definition separates departures from a reference state electrochemical potential, μΘi, into a short-range chemical contribution depending on the activity ai and a long-range electrostatic contribution for a species of charge zie in the potential of mean force ϕ. The third definition expresses the Boltzmann distribution of concentration,
and time t. The second definition separates departures from a reference state electrochemical potential, μΘi, into a short-range chemical contribution depending on the activity ai and a long-range electrostatic contribution for a species of charge zie in the potential of mean force ϕ. The third definition expresses the Boltzmann distribution of concentration, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i = exp((μi − μexi)/kBT), in the total “excess” chemical potential
i = exp((μi − μexi)/kBT), in the total “excess” chemical potential| |
μexi = μΘi + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi + zieϕ, γi + zieϕ, | (6) |
where γi = ai/![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i is the activity coefficient. For a set of reactants, μi denotes the sum of their electrochemical potentials, while ai and
i is the activity coefficient. For a set of reactants, μi denotes the sum of their electrochemical potentials, while ai and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i denote the product of their activities and dimensionless concentrations, respectively.
i denote the product of their activities and dimensionless concentrations, respectively.
For the general reduction reaction,
the activation overpotential, η, is equal to the free energy of reaction ΔG per charge transferred,| |
| eη = ΔG = μR − μO − μe. | (8) |
It is also convenient to define the formal overpotential, ηf, based on excess chemical potentials of the reduced and oxidized species,| |
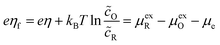 | (9) |
Note that in our compact notation for the reaction, eqn (7), the oxidized state O or the reduced state R may involve multiple chemical species, ∑jsjAj, in which case its concentration, activity and electrochemical potential are given by:24| |
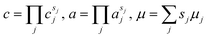 | (10) |
respectively. For example, in the case of the hydrogen evolution reaction in basic solutions,| |
| 2H2O + 2e− → H2 + 2OH− | (11) |
we have| |
| aO = aH2O2, μO = 2μH2O, aR = aH2aOH−2, μR = μH2 + 2μOH− | (12) |
where aH2O ≈ 1, aOH− = 1014−pH (M) and aH2 = PH2 (atm). In the case of lithium intercalation in iron phosphate,| |
| Li+ + e− → Li(int) = LiFePO4 − FePO4 | (13) |
we have aO = aLi+ and aR = aLi = aLiFePO4/aFePO4, where, for example, the latter could be described by a regular solution model.24,108 This example also illustrates our consistent use of diffusional electrochemical potentials in condensed systems,24 such as μLiint = μLiFePO4 − μFePO4, which expresses the free energy change to create an intercalated lithium ion, while removing a vacancy.
3.1.2 Faradaic current density.
The net reduction current density, the rate of electron consumption per active area of the electrode/electrolyte interface, can be expressed as the difference of forward (reduction) and backward (oxidation) current densities,| |
| J = e(kredcO − koxcR) | (14) |
where kred and kox are the reduction and oxidation rate constants, which depend on ηf and have units of velocity, if we use volumetric concentrations for a first order reaction. More generally, if the reaction has order ni in a reactant of concentration ci, then the units of k are velocity times concentration to the power ni − 1. For interfacial reactions, it is more convenient to define the mean area of a reacting site As and express the current density in terms of dimensionless concentrations, or mean coverages of the surface sites, as| |
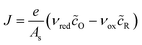 | (15) |
where| |
| νred/ox = kred/oxcrefO/RAs | (16) |
is the frequency of reduction or oxidation, whose inverse is the mean time between reaction events at a given surface site. The total current I is the integral of J over the interfacial area A, or simply I = JA for a uniform current density.
As we shall see below, it is natural to scale the CIET reaction frequency to an effective solvent polarization frequency, νs, for the environment of the donor/acceptor sites near the electrode/electrolyte interface, which sets the scale for ET rates. This frequency scale dominates CIET kinetics at very large overpotentials, which exceed (and effectively eliminate) all barriers to classical IT, leaving only quantum mechanical ET to limit the overall rate. With this insight, we define dimensionless current density as
| |
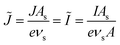 | (17) |
where the last equality assumes a uniform current density. This allows us to express our results in terms of dimensionless current carried by a pseudo-first-order redox reaction,where the dimensionless rate constants are given by| |
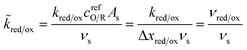 | (19) |
in terms of an effective interfacial thickness, Δxred/ox = (AscrefO/R)−1, which converts the solvent polarization frequency νs into a characteristic reaction velocity, Δxred/oxνs.
The interfacial coverages of the reduced and oxidized species at the electrode/electrolyte interface, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O and
O and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R, will generally be different than in the nearby bulk phases outside the double layer. Assuming each species has bulk activity ai,b and undergoes fast adsorption on a set of discrete sites at the interface, we arrive at a generalized Langmuir isotherm,24
R, will generally be different than in the nearby bulk phases outside the double layer. Assuming each species has bulk activity ai,b and undergoes fast adsorption on a set of discrete sites at the interface, we arrive at a generalized Langmuir isotherm,24
| |
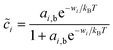 | (20) |
where wi is the work of surface adsorption (i = O, R). This general form includes the Temkin isotherm, commonly used in electrochemistry,7 if wi has a linear dependence on ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i due to lateral pair interactions, as the regular solution model.24 Fraggedakis et al.103 assumed wO = wR, but we will consider the general asymmetric case, wR ≠ wO. For liquids and solids, surface adsorption is usually fast compared to transport and reaction kinetics, but for high-temperature gas electrodes, surface adsorption can be rate-limiting in the overall electrochemical reaction.109,110
i due to lateral pair interactions, as the regular solution model.24 Fraggedakis et al.103 assumed wO = wR, but we will consider the general asymmetric case, wR ≠ wO. For liquids and solids, surface adsorption is usually fast compared to transport and reaction kinetics, but for high-temperature gas electrodes, surface adsorption can be rate-limiting in the overall electrochemical reaction.109,110
3.1.3 Activation barriers for charge transfer.
As noted above, radiationless ET is isoenergetic, facilitated by slow thermal fluctuations of the molecular environment that bring the reduced and oxidized states to the transition state. For a given electron energy ε, the reaction complex explores a landscape of excess chemical potential until it overcomes an activation barrier μex‡, determined by the reaction mechanism (below).24 The reduction and oxidation rate constants,| |
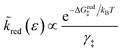 | (21) |
| |
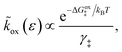 | (22) |
respectively, include activation barriers of excess free energy given by| |
| ΔGred‡ = μex‡ − μexO − μexe | (23) |
as well as a common activity coefficient of the transition state γ‡, which accounts for entropic effects on the transition state,24 such as excluded volume of ions and occupied energy levels of electrons. For consistency with the theory of reaction kinetics based on nonequilibrium thermodynamics,24 we only require that the free energy barriers are large compared to the thermal energy,so that barrier crossings are rare events at the scale of molecular vibrations, as in classical transition state theory.1,111,112
The transition state activity coefficient contributes an additional universal term, kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ‡, to the excess chemical potential of the transition state, μex‡. The excess free energy barriers, ΔGred‡ and ΔGox‡, generally depend on the excess free energy of reaction,
γ‡, to the excess chemical potential of the transition state, μex‡. The excess free energy barriers, ΔGred‡ and ΔGox‡, generally depend on the excess free energy of reaction,
| |
| ΔGex = μexR − μexO − μexe = eηf + μe − μexe | (26) |
so as to satisfy the de Donder relation:24| |
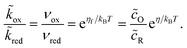 | (27) |
In principle, the relationship between ΔGred/ox‡ and ΔGex, as well as the transition state activity coefficient γ‡, can be derived from a microscopic model of the reaction mechanism, such as the phenomenological model of classical ion transfer used to derive the BV equation in Fig. 1. Since electrochemical reactions necessarily involve electrons, however, any realistic and predictive model must be based on quantum mechanics.
3.2 Quantum physics of electron transfer
3.2.1 Activity and excess chemical potential of electrons.
Electrons participating in the reduction reaction (7) are drawn from the Fermi sea of the electrode with electrochemical potential, μe = εF − eϕe, where εF is the Fermi level and ϕe is the local electrostatic potential. The probability of finding an electron at energy ε is given by the Fermi–Dirac distribution,| |
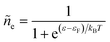 | (28) |
and the probability of finding a hole at the same energy is| |
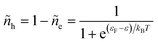 | (29) |
These dimensionless filling fractions for energy levels relate the number densities of electrons and holes (per unit of energy), ne(ε) = ñe(ε)ρe(ε) and nh(ε) = ñh(ε)ρe(ε), respectively, to the electronic density of states, ρe(ε), describing the band structure of the electrode.
Treating electrons in the same framework as ions using eqn (5), we write
| |
μe = μΘe + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ae − eϕe ae − eϕe | (30) |
and define μΘe = ε0F as the Fermi level of the electrode in a reference state in order to construct the electron activity,| |
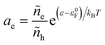 | (31) |
such that ae = 1 for ε = ε0F and ae > 1 for excited states with ε > ε0F. We can also define the excess chemical potential of electrons, μexe, via| |
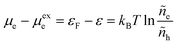 | (32) |
which allows us to express the excess free energy of reaction aswhere we use the definition of formal overpotential, eqn (9). In eqn (32), the ratio| |
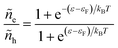 | (34) |
is an effective concentration for reactive electrons, which represents the creation of electron while removing a hole, consistent with the definition of diffusional electrochemical potential for ions. Equivalently, one could write the reduction reaction in a more familiar form aswhere e− = e − h in eqn (7) is the consistent representation of the reactive electron, when defining diffusional chemical potentials. The two approaches lead to the same formula for the nonadiabatic ET rate below, first proposed by Gurney42 based on eqn (35), but the equivalent formulation of eqn (7) allows us to consistently define the activity coefficient of the transition state, based on the general theory of non-equilibrium thermodynamics of charge transfer kinetics.24
3.2.2 Adiabatic versus nonadiabatic ET.
It is important to distinguish the two types of ET reactions, adiabatic and non-adiabatic, which may be coupled with IT.25,26 In adiabatic ET, a single electron is shared between strongly coupled reduced and oxidized states in a hybrid orbital, which slowly adjusts as the solvent reorganizes causing the electron probability density to shift its weight between the oxidized (acceptor) and reduced (donor) states. In cases where adiabatic ET is coupled with either classical IT67–70 or quantum-mechanical proton transfer,65,66 quantum computations can be performed to construct an energy landscape for specific reactants and solvents, and simple rate expressions can be derived based on a model Hamiltonian,25,31,32,55,56,113e.g. generalizing the Anderson–Newns model for chemisorption on metals.114 In this theoretical framework, the nature of the ET reaction is governed by the chemisorption function,25,31,32,113where HDA2 = |〈ψA|VDA|ψD〉|2 is the electronic coupling matrix element between the wavefunctions of the electron donor and acceptor, ψA and ψD, respectively, in the interaction potential, VDA. In models of adiabatic ET, chemisorption functions are usually defined separately for each band,31 but more generally all bands should be included in the total electronic density of states ρe(ε). In the wide-band approximation for metal electrodes25,31 (the most typical situation for faradaic reactions), the chemisorption function is evaluated at the Fermi level, Δe(εF). Adiabatic ET requires strong quantum coupling of the donor and acceptor states, which remains intact under thermal fluctuations, Δe ≫ kBT.
In non-adiabatic ET for Δe ≪ kBT, the reduced and oxidized quantum states are only weakly coupled and retain their separate “diabatic” chemical identities, until quantum tunneling of electrons from the band structure causes a transition between these states at some energy below the diabatic crossing.38 In this regime, the barrier profile between the diabatic states could in principle be calculated by constrained density functional theory.39 The non-adiabatic condition is usually satisfied for outer-sphere ET between well-separated donor and acceptor wavefunctions, as HDA2 decays exponentially with separation distance at the Angstrom scale. Following Levich, Dogonadze and Kuznetsov,26,27,30,36,48 the quantum tunneling rate can then be approximated as a constant
| |
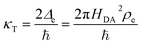 | (37) |
using first-order perturbation theory (Fermi's Golden Rule),25,31 where ℏ = h/2π and h = Planck's constant. Since the tunneling rate is smaller than the thermal quantum frequency, κT ≪ kBT/h, non-adiabatic electron transfer is a rare event at the scale of molecular vibrations. When non-adiabatic ET is coupled with ion transfer,103 therefore, it is possible to express the rate as an integral over the band structure of a generalized Marcus rate expression, accounting for both the positions of the ions and the reorganization of the solvent. As the environment fluctuates, the electronic coupling between the reduced and oxidized states remains weak and affects only the prefactor of the reaction rate via a constant tunneling probability.
3.2.3 Nonadiabatic CIET kinetics.
For non-adiabatic CIET at an electrode, we express the reduction and oxidation rate constants as| |
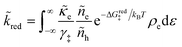 | (38) |
| |
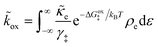 | (39) |
where ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e is the dimensionless ET coefficient, scaled to the solvent polarization frequency, νs. This formulation can describe weakly adiabatic ET, where
e is the dimensionless ET coefficient, scaled to the solvent polarization frequency, νs. This formulation can describe weakly adiabatic ET, where ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e is approximately independent of electron energy,25,31,52 but it is most accurate for non-adiabatic ET in the limit of weak coupling, described above. In that case, the electron transmission coefficient is independent of electron energy ε and approximately given by,
e is approximately independent of electron energy,25,31,52 but it is most accurate for non-adiabatic ET in the limit of weak coupling, described above. In that case, the electron transmission coefficient is independent of electron energy ε and approximately given by,| |
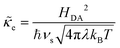 | (40) |
where λ is the solvent reorganization energy.25,26,31,32 More general expressions for ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e are available for weakly adiabatic ET with multiple crossings based on Landau–Zener theory.26,58,115 Note that
e are available for weakly adiabatic ET with multiple crossings based on Landau–Zener theory.26,58,115 Note that ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e → 1 for adiabatic ET.
e → 1 for adiabatic ET.
The present theory contains some significant clarifications and extensions compared to the original CIET theory of Fraggedakis et al.103 In the reduction rate, eqn (38), we have defined the dimensionless concentration of electrons as ñe/ñh, to be consistent with our definition of diffusional electrochemical potential of electrons, μexe, in eqn (32), as well as the dimensionless concentrations of the reduced and oxidized chemical species, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R and
R and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O, respectively, in the reduction current, eqn (14). The diffusional electrochemical potential enforces the Pauli exclusion principle for fermions by requiring that the creation of a particle always destroys a hole, as expressed by Fermi–Dirac statistics in eqn (32). Consistent with the way the reduction reaction is written, eqn (7), we do not include a hole in the reduced state. However, it is still necessary to integrate over the possible energies of electrons created by the oxidation reaction, eqn (39), since the activation barrier ΔGox‡ is electron energy dependent. We also choose the solvent polarization frequency νs as the natural frequency scale for CIET with non-adiabatic ET, in which case the CIET rate scales with the quantum tunneling frequency, κT.
O, respectively, in the reduction current, eqn (14). The diffusional electrochemical potential enforces the Pauli exclusion principle for fermions by requiring that the creation of a particle always destroys a hole, as expressed by Fermi–Dirac statistics in eqn (32). Consistent with the way the reduction reaction is written, eqn (7), we do not include a hole in the reduced state. However, it is still necessary to integrate over the possible energies of electrons created by the oxidation reaction, eqn (39), since the activation barrier ΔGox‡ is electron energy dependent. We also choose the solvent polarization frequency νs as the natural frequency scale for CIET with non-adiabatic ET, in which case the CIET rate scales with the quantum tunneling frequency, κT.
In general, the CIET free-energy barriers for oxidation and reduction, ΔGox‡(ξ,ΔGex) and ΔGred‡(ξ,ΔGex), respectively, depend on both the ion transfer coordinate, ξ, and the excess free energy of reaction, ΔGex(ηf,ε), which in turn depends on the formal overpotential, ηf, and the electron energy, ε, sampled from the band structure, according to eqn (33). In order to derive these relations, we must postulate a mechanistic model for the CIET transition state, which combines classical IT and quantum mechanical ET.
3.3 Transition state for coupled ion–electron transfer
3.3.1 Activity coefficient of the CIET transition state.
We begin by specifying the activity coefficient of the CIET transition state as the product of ionic and electronic terms:which express general entropic contributions that are assumed not to depend on the microscopic reaction coordinates introduced below. These contributions are rooted in the exclusion of certain states of the molecular reactants, including ions and neutral species, as well as the electrons. The IT term γIT‡ mainly reflects excluded volume constraints on ion transfer, which we assume do not depend on the IT reaction coordinate of the CIET transition state (ξ‡ below). For example, in cases of ion adsorption, intercalation or electrodeposition, we could set| |
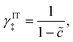 | (42) |
so that (γIT‡)−1 = 1 − ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) is equal to the probability of finding a vacancy among reactive ions with coverage
is equal to the probability of finding a vacancy among reactive ions with coverage ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) on the electrode/electrolyte interface.24 Other choices for γIT‡ might express volume exclusion among random loose packings of hard spheres, e.g. via the Carnahan–Starling equation of state.116
on the electrode/electrolyte interface.24 Other choices for γIT‡ might express volume exclusion among random loose packings of hard spheres, e.g. via the Carnahan–Starling equation of state.116
In contrast, there is only one choice for the ET term γET‡ to enforce the Pauli exclusion principle, which prohibits any two electrons from sharing the same quantum state. By analogy with eqn (42), we must set γET‡ to the inverse hole concentration,
| |
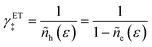 | (43) |
to reflect excluded energy constraints on electron transfer in the electrode. Consistent with the notion of diabatic states in ET theory,38 we assume that γET‡ does not depend on the solvent reorganization coordinate at the CIET transition state (q‡ below), because the band structure of the electrode remains unchanged by isoenergetic ET. Summarizing these general considerations, we express universal entropic contributions to the excess free energy of the CIET transition state as| |
μex,ent‡ = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ‡ = kBT γ‡ = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γIT‡ − kBT γIT‡ − kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ñh(ε) ñh(ε) | (44) |
for IT and ET, respectively. For a given model of γIT‡, there may be additional specific entropic contributions to the excess chemical potential landscape of the reaction mechanism, which could contribute to temperature dependence of the free energy barriers, ΔGred/ox‡, derived below, although it is always possible to redefine γIT‡ to incorporate all entropic contributions to the excess chemical potential of the transition state, μex‡, consistent with eqn (6).
Substituting eqn (44) and (40) into eqn (38) and (39), we arrive at more familiar expressions for non-adiabatic reduction and oxidation rates in quantum electrochemistry,25,26 first introduced by Gurney42 and developed in detail by Levich, Dogonadze and Chizmadzhev:26,27,36,48,50
| |
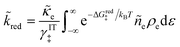 | (45) |
| |
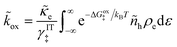 | (46) |
with an important new prefactor (γIT‡)−1 that accounts for the entropic barrier (e.g. from excluded volume) for IT at the transition state.24,103 The more standard appearance of ñe in the reduction rate and ñh in the oxidation rate corresponds to writing the net reduction reaction in the form of eqn (35), where an electron is replaced by a hole, when the faradaic reaction occurs. We have also made the standard approximation that the solvent polarization frequency, νs, and the electronic coupling, HDA2, are independent of the IT coordinate ξ, which should be a good approximation for outer-sphere non-adiabatic ET. As such, the electron transmission coefficient, ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e, has been factored out of the integrals above.
e, has been factored out of the integrals above.
3.3.2 Free energy barrier for nonadiabatic CIET.
We postulate that the reaction complex in eqn (7) explores a landscape of excess chemical potential μex driven by thermal noise.24 Following Fraggedakis et al.,103 we construct a two-dimensional landscape, μex(q,ξ), where ξ is again the IT reaction coordinate, and q is the ET reaction coordinate, which describes reorganization of the solvent (or more generally, the electronic environment), as shown in Fig. 5. Following Marcus,33,37 we postulate separate, overlapping landscapes for two diabatic quantum states,38 the initial state O + e− and the final state R of the reduction reaction, making harmonic approximations of parabolic dependencies on the reorganization coordinate,| |
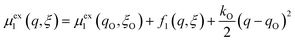 | (47) |
| |
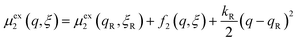 | (48) |
where μex1(q,ξ) = μexO(q,ξ) + μexe(q,ξ) and μex2(q,ξ) = μexR(q,ξ). The functions, f1(q,ξ) and f2(q,ξ), describe the excess free energy of IT – without ET – in the diabatic basis starting from local minima at the oxidized state, f1(qO,ξO) = 0, or the reduced state, f2(qR,ξR) = 0, respectively. The excess free energy of reaction, eqn (33), is given by,| |
| ΔGex = μex2(qR,ξR) − μex1(qO,ξO). | (49) |
The set of possible ET transition states corresponds to the intersection of the two diabatic IT surfaces,| |
| μexET(ξ) = μex1(q‡,ξ) = μex2(q‡,ξ). | (50) |
The most likely CIET transition state corresponds to the minimum of μexET(ξ), which is attained at the IT coordinate, ξ‡. At each IT coordinate ξ, ET can occur either non-adiabatically, by quantum tunneling at an excess chemical potential just below μexET(ξ), or adiabatically, through a shared electronic state in the diabatic basis.38 As long as the electron coupling is weak compared to the reorganization energy, HDA2 ≪ λ, both limits lead to similar rate expressions, except for the prefactor. As noted above, the prefactor in eqn (45) and (46) is for non-adiabatic ET.
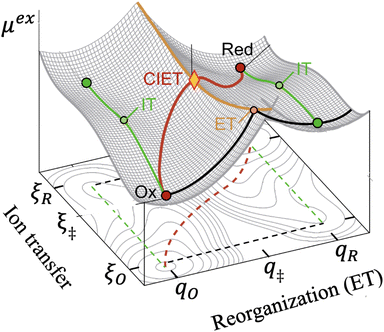 |
| | Fig. 5 Free energy landscape for coupled ion–electron transfer (CIET)103 between diabatic reduced (Red) and oxidized (Ox) states.38 The excess chemical potential of the reaction complex, μex(ξ,q), is a function of the ion-transfer coordinate ξ (typically the position of a reactive ion) and the Marcus solvent reorganization coordinate, q. The oxidized ground state at (ξO,qO) consists of the oxidized species and an electron in the electrode, and the reduced ground state at (ξR,qR) corresponds to the reduced species. The green paths indicate ion transfer (IT) without electron transfer (ET), while the black paths indicate ET without IT. The orange activation barrier surface is formed by the intersection of Marcus parabolae at q‡(ξ), where fast, iso-energetic ET is facilitated by slow IT. The lowest energy path in red corresponds to CIET over the saddle point at q‡(ξ‡). [Adapted from Fig. 4b of Sood et al. (2021)117 by Daniel Cogswell.] | |
To further simplify the problem, we make several assumptions, which can be relaxed in some cases (below). Following most of the quantum electrochemistry literature, we assume symmetric ET with kO = kR = k, which ensures the existence of a unique transition state from the intersection of pairs of Marcus parabolae with the same curvature. We also assume a separable free energy with f1(q,ξ) ≈ f1(qO,ξ) and f2(q,ξ) ≈ f2(qR,ξ), which implies that ion transfer occurs independently from solvent relaxation. These are both good approximations, whenever ET and IT are physically separated at the Angstrom scale of quantum tunneling. For example, the reduced state could consist of a polaron (separated ion–electron pair) in an ion-intercalation electrode.63,103 For electrodeposition or electrocatalysis at metal electrodes,31 these approximations break down when the transferring ion is itself reduced for inner-sphere, adiabatic CIET,118 but they may still hold for cases of outer-sphere or weakly adiabatic CIET.119
In principle, CIET theory can be extended (below) for the general case of asymmetric ET with kO ≠ kR, but this requires circumventing the mathematical fact that parabolae with different curvatures may not intersect to determine a well-defined transition state. The most common theoretical framework for asymmetric ET is based on asymmetric Marcus–Hush (AMH) theory.51,57,58,61,120 The AMH theory expands the solvent reorganization landscape μex(q,ξ) for small overpotentials and large reorganization energies to obtain the first cubic corrections to the Marcus parabolae in the variable q. These terms are straightforward to add to the general CIET free energy landscape, eqn (47) and (48), but complicate the analysis and lose validity at large overpotentials, where the diabatic states do not cross. Let us thus postpone the discussion of AMH theory in CIET and focus on symmetric ET, kO = kR = k, while allowing for strong asymmetry in IT.
In the general case of symmetric ET and separable IT, we can solve for the ET activation barrier, μexET(ξ), from the intersection of the Marcus parabolae, which occurs at the solvent reorganization coordinate,
| |
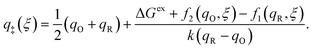 | (51) |
For small values of the driving force, |ΔGex| < λ, the barrier surface lies in the normal region, qO < q‡(ξ) < qR, as shown in Fig. 5. For large values of the driving force, |ΔGex| > λ, which are always possible for some range of electron energies, the barrier surface lies within the Marcus inverted region, where either q‡(ξ) < qO or q‡(ξ) > qR (not shown in the figure).
Substituting eqn (51) into eqn (47) and (48), we arrive at the ET activation barriers (at the diabatic crossings) for oxidation, eqn (24), and reduction, eqn (23), respectively:
| |
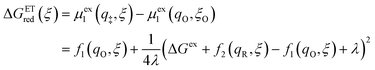 | (52) |
| |
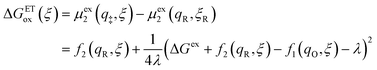 | (53) |
where we define the usual Marcus reorganization energy for ET,37| |
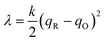 | (54) |
which arises from the general CIET theory, as a result of our assumptions of symmetric harmonic reorganization for ET and separable IT dependence in the free energy landscape. Under these approximations, the solvent polarization frequency can be expressed as 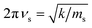 ,
,| |
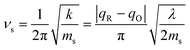 | (55) |
where ms is an effective mass for harmonic oscillations along the solvent reorganization coordinate, q.
For subsequent analysis, it is convenient to rewrite the CIET barriers as
| |
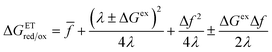 | (56) |
in terms of the combined variables,| |
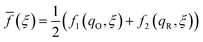 | (57) |
| |
| Δf(ξ) = f2(qR,ξ) − f1(qO,ξ) | (58) |
which correspond to the mean and difference of the IT barriers for reduction and oxidation, when ET occurs at a given IT coordinate ξ.
Fraggedakis et al.103 postulated that Δf(ξ‡) ≈ 0 at the CIET transition state, which leads to the original Marcus barriers for ET,
| |
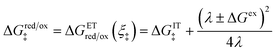 | (59) |
but with an extra term for an effective IT barrier, ΔGIT‡ = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (ξ‡), which contributes a common Arrhenius prefactor to kred and kox. However, no conditions were given to justify this postulate, and no formula was given for ΔGIT‡. Instead, the effective IT barrier was expressed empirically as ΔGIT‡ = αITΔEIT in terms of an overall ion transfer energy, ΔEIT, multiplied by a phenomenological IT coefficient, αIT ≈ 1/2, inspired by the Butler–Volmer equation.103 In this context, one might expect αIT to be a symmetry factor,
(ξ‡), which contributes a common Arrhenius prefactor to kred and kox. However, no conditions were given to justify this postulate, and no formula was given for ΔGIT‡. Instead, the effective IT barrier was expressed empirically as ΔGIT‡ = αITΔEIT in terms of an overall ion transfer energy, ΔEIT, multiplied by a phenomenological IT coefficient, αIT ≈ 1/2, inspired by the Butler–Volmer equation.103 In this context, one might expect αIT to be a symmetry factor,| |
| ξ‡ = αITξO + (1 − αIT)ξR | (60) |
reflecting the position of the effective IT barrier relative to that of the oxidized and reduced states.6,7 However, it would still be unclear whether the energy ΔEIT corresponds to reduction or oxidation, except in the symmetric case of equal IT energies with αIT = 1/2. Of course, rather than making arbitrary postulates about the transition state, it would be more satisfying and consistent to derive such quantities systematically from the general theory.
In principle, the CIET free energy landscape μex(q,ξ) could be predicted by ab initio molecular dynamics (AIMD) quantum mechanical calculations, e.g. using constrained density functional theory (CDFT) to compute the diabatic states,38,39,121–124 from which the most probable solvent reorganization coordinate, q‡(ξ), and barriers, ΔGox‡(ξ) and ΔGred‡(ξ), for CIET could be obtained numerically for each IT coordinate ξ and inserted into the integrals for the reduction and oxidation rates, kred and kox. In general, the excess free energy landscapes for IT in the oxidized and reduced diabatic states, f1(q,ξ) and f2(q,ξ), respectively, may depend on the ET solvent reorganization coordinate q, as well as the IT coordinate ξ.
In the following sections, we consider three asymptotic limits of CIET theory, which correspond to rate limitation by either IT or (normal or inverted) ET. These universal limiting cases generalize and unify Butler–Volmer and Marcus kinetics, respectively. We then proceed to derive a simple, uniformly valid formula for all parameter values by asymptotic matching of these limits.
4 Marcus kinetics of electron-coupled ion transfer (ECIT)
4.1 Symmetric normal electron transfer
Here, we show that the Marcus IT barrier, eqn (59), augmented by a certain IT barrier, eqn (62), can be derived from the general CIET theory in the limit where the ET step is rate limiting and the overpotential is small enough to remain in the normal region of Marcus kinetics. To be clear, nonadiabatic ET by quantum tunneling is still instantaneous and isoenergetic, but the prerequisite solvent reorganization is slow compared to IT, which may begin before ET but is rapidly completed after ET. We refer to this CIET reaction mechanism as “electron-coupled ion transfer” (ECIT).
In the regime of Normal ECIT, we require that both the effective IT free energy barrier, ΔGIT‡, and the magnitude of the formal overpotential, e|ηf| (converted to an energy by the electron charge e), are smaller than the reorganization energy:
| |
| λ ≫ ΔGIT‡,e|ηf|,kBT,Δe (Normal ECIT) | (61) |
where
λ ≫
kBT is required by
eqn (25) and
Δe ≪
kBT for nonadiabatic ET. In this regime of CIET theory, we shall see that the IT barrier can be expressed explicitly in terms of the diabatic free energy landscapes as
| |
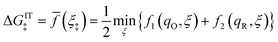 | (62) |
where
ξ =
ξ‡ is the IT coordinate of the transition state, which minimizes Δ
GIT‡. Given specific models for
f1(
q,
ξ) and
f2(
q,
ξ), such as the linear approximations introduced below, we can use
eqn (62) to determine
ξ‡ for a specific reaction.
For a given value of ξ‡, let us show that the CIET barriers, ΔGred/ox‡, indeed approach the Marcus form proposed by Fraggedakis et al., eqn (59), with ΔGIT‡ = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (ξ‡) given by eqn (62) in the asymptotic limit of Normal ECIT, eqn (61). Our goal is to prove that the first two terms in eqn (56) dominate in the asymptotic limit of eqn (61). We begin by stating the triangle inequality, |Δf| ≤ 2
(ξ‡) given by eqn (62) in the asymptotic limit of Normal ECIT, eqn (61). Our goal is to prove that the first two terms in eqn (56) dominate in the asymptotic limit of eqn (61). We begin by stating the triangle inequality, |Δf| ≤ 2![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , since f1, f2 ≥ 0, which helps us show that the third term in eqn (56) is asymptotically dominated by the first term:
, since f1, f2 ≥ 0, which helps us show that the third term in eqn (56) is asymptotically dominated by the first term:
| |
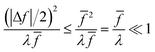 | (63) |
Bounding the fourth term, which directly couples the ET coordinate
q and the IT coordinate
ξ, is more subtle. By the same argument as in
eqn (63), the fourth term in
eqn (56) is also asymptotically dominated by the first term, but only in the limit of small driving force, |Δ
Gex|≪
λ, shown in
Fig. 6(a). Given the definition, Δ
Gex =
eηf +
εF −
ε, this condition is satisfied at small formal overpotentials,
e|
ηf|≪
λ, for the most probable electrons and holes participating in the reaction, which have energies near the Fermi surface in the assumed limit of small thermal energy,
eqn (25).
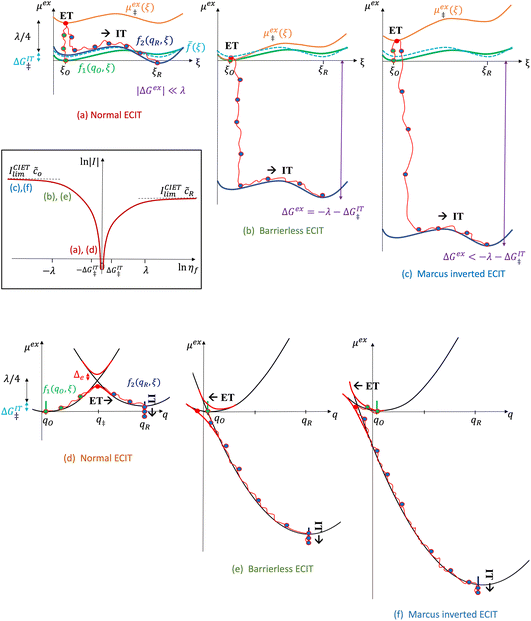 |
| | Fig. 6 Physics of ET-limited nonadiabatic CIET, or “electron-coupled ion transfer” (ECIT), at a metal electrode, where the Marcus reorganization energy λ is much larger than the ion transfer barrier, ΔGIT‡, thermal energy kBT and chemisorption function, Δe. The path of the reaction complex (red) is shown in the landscape of excess chemical potential μex(q,ξ) from Fig. 5 viewed along the IT coordinate ξ from the oxidized state ξO to the reduced state ξR in (a)–(c). The same paths are shown in (d)–(f) viewed along the ET reorganization coordinate q from qO to qR. The theory assumes that ET occurs close to the diabatic crossing, either by quantum tunneling or via adiabatic states with weak electronic coupling HDA ≪ λ (red curves in (d)). The oxidized state has IT energy f1(qO,ξ) (green), and the reduced state has IT energy f2(qR,ξ) (blue). The CIET barrier is μex‡(ξ) = μex(q‡,ξ) (orange). Three cases are depicted for the excess free energy of reaction, ΔGex = eηf + εF − ε, the sum of the formal overpotential ηf and the electron energy ε below the Fermi level εF. In (a) and (d), for unbiased ECIT with ΔGex = 0, the rate limiting process is ET with a large barrier λ/4 (for symmetric ET) in addition to the small IT barrier ΔGIT‡ ≈ ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (ξ) (light blue). In (b) and (e), electrons at ΔGex = −λ are able to make barrierless ET transitions, which dominate in the limit of large negative overpotentials, and facilitate IT at a constant rate. In (c) and (f), for ΔGex < −λ, the reaction complex enters the Marcus inverted region with a larger ET barrier and smaller contribution to the total current. (Inset) Tafel plot showing the scenarios (a)–(c)/(d)–(f) for reduction, where the Tafel slope is αET for the beginning of the negative reduction branch and 1 − αET for the positive oxidation branch. On both sides, the brief Tafel regime transitions to Marcus ECIT reaction limit current, when the overpotential exceeds the reorganization energy. (ξ) (light blue). In (b) and (e), electrons at ΔGex = −λ are able to make barrierless ET transitions, which dominate in the limit of large negative overpotentials, and facilitate IT at a constant rate. In (c) and (f), for ΔGex < −λ, the reaction complex enters the Marcus inverted region with a larger ET barrier and smaller contribution to the total current. (Inset) Tafel plot showing the scenarios (a)–(c)/(d)–(f) for reduction, where the Tafel slope is αET for the beginning of the negative reduction branch and 1 − αET for the positive oxidation branch. On both sides, the brief Tafel regime transitions to Marcus ECIT reaction limit current, when the overpotential exceeds the reorganization energy. | |
On the other hand, if the driving force is large enough to enter the Marcus inverted region, |ΔGex| ≫ λ, as shown in Fig. 6(c), then the approximation of Fraggedakis et al., eqn (59) and (62), breaks down, although in a subtle way. In this regime, the fourth term becomes asymptotically dominated by the second term:
| |
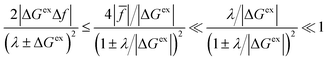 | (64) |
where we use
eqn (63) in the second step, which establishes the same approximation for almost all values of the parameters, seemingly even in the limit of large overpotentials. However, this is not correct, since the approximation always breaks down for electrons (or holes) whose energies are close to the point of barrierless ET, where ±Δ
Gex ≈ −
λ, shown in
Fig. 6(b). In this case, the second term in
eqn (56) vanishes, and, although the fourth term is still asymptotically bounded by the first term:
| |
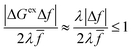 | (65) |
(where we use the triangle inequality again), it cannot be neglected. While only a small range of electron or hole energies can complete barrierless ET, it is well known that these contributions dominate in the Marcus inverted region for an electrode. Below, we shall describe the new regime of inverted ECIT. For now, we have shown that in the regime of Normal ECIT,
eqn (61), the integration over all electron energies
ε in
eqn (45) and
(46) can be performed using only the first two terms of
eqn (59) for the CIET barrier.
The resulting asymptotic rate expression for symmetric Normal ECIT is given by:
| |
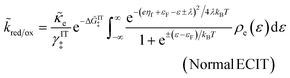 | (66) |
where we define Δ
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) IT‡
IT‡ = Δ
GIT‡/
kBT. The Normal ECIT rate formula is identical to the Marcus expression for pure, symmetric ET at an electrode
36,51,60,86,125 (
ρe = constant), except for an important new IT-dependent prefactor, which contains the activity coefficient
γIT and effective free energy barrier Δ
GIT‡ for IT. Recall that the current is given by
eqn (14) in terms of the
kred and
kox.
For an ideal metal electrode with a uniform density of electronic states (ρe = constant), we recover the ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f-dependence of MHC kinetics85 with an IT-dependent Arrhenius prefactor,
f-dependence of MHC kinetics85 with an IT-dependent Arrhenius prefactor,
| |
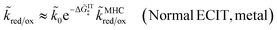 | (67) |
where we define the dimensionless characteristic rate constant,
| |
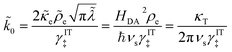 | (68) |
with dimensional form,
| |
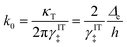 | (69) |
and where we adopt the uniformly valid approximation of Zeng
et al.60 for the integrals in
eqn (67) to define the dimensionless MHC rate,
| |
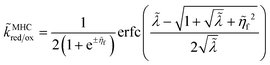 | (70) |
in terms of the dimensionless variables,
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f
f =
eηf/
kBT,
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
=
λ/
kBT, and
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) e
e =
ρekBT. Although various series expansions of the MHC integrals are available for different asymptotic limits of the parameters,
95,96 the closed-form approximation of
eqn (70) has the advantage of being simpler and uniformly valid for all values of
λ and
ηf. Compared to the MHC integral,
eqn (67), the maximum relative error of
eqn (70) is around 5%, while maintaining high accuracy for large and small
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
, as well as large formal overpotentials,
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f
f, since it was derived by asymptotic matching of exact results for these limiting cases.
60
The analytical approximation of the Normal ECIT rate for a metal electrode, eqn (67)–(70), is convenient for calculations of important quantities, such as the dimensionless exchange current,
| |
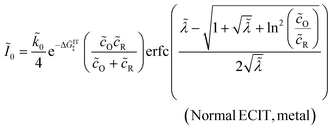 | (71) |
which is defined by the linear response,
Ĩ ∼
Ĩ0![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif)
, where
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif)
=
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f
f + ln(
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R
R/
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O
O) is a small total overpotential, |
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif)
| ≪ 1. In contrast to phenomenological BV theory,
eqn (4), the exchange current for ECIT does not have simple power-law dependence on the reactant concentrations,
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O
O and
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R
R. CIET kinetics is also non-separable, in the sense that the current cannot be expressed as a function of overpotential times a function of concentrations, in contrast to the separable form of the phenomenological BV equation,
eqn (1). Note that for the typical low-temperature regime,
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
≫ 1, the exchange current for symmetric ECIT has an Arrhenius temperature dependence,
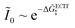
, with
| |
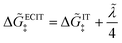 | (72) |
where the second term is the classical Marcus activation barrier for symmetric ET.
Eqn (66) is the main of Fraggedakis et al.,103 but here we clarify its range of validity, eqn (61), and provide an explicit formula for the effective IT barrier in eqn (62). The analytical approximation for normal ECIT at metal electrode, eqn (67)–(70), has already been widely used in modeling Li-ion batteries,98,99,104,105,126–128 metal electrodeposition100–102 and solid-oxide fuel cells,110 but without a clear understanding of its applicability and microscopic interpretation provided here. Since the (scaled) MHC rates tend to unity at large formal overpotentials,
| |
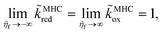 | (73) |
the Normal ECIT rate for a metal electrode also extrapolates to a constant,
| |
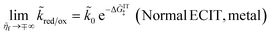 | (74) |
but it is important to recognize that this limit is not physically valid, since it exceeds the range of validity of Normal ECIT,
e|
ηf| ≪
λ. Even when ET is slow compared to IT, Δ
GIT‡ ≪
λ, a more general analysis of CIET theory is required to account for Inverted ECIT at large overpotentials, which leads to a somewhat different formula for the limiting reaction rate (below).
4.2 Asymmetric normal electron transfer
Although the vast majority of ET models are symmetric, as noted above, there has been growing interest in the asymmetric Marcus–Hush model,51,120 led by Compton et al.57,58,129–131 for faradaic reactions involving inner-sphere ET. The AMH model introduces cubic terms in the free-energy landscape, which approximate the different nonlinear solvation characteristics of the reduced and oxidized states.55,56 While the intersection of these diabatic surfaces is not always guaranteed at large overpotentials, the transition state always exists – by definition – for asymmetric Normal ECIT, by restriction to sufficiently small overpotentials.
For inner-sphere ET, the vibrational force constants are generally different for the reduced and oxidized states. In AMH theory,51,120 this asymmetry is controlled by a new dimensionless parameter, γ, which can be expressed in terms of the inner-sphere reorganization energy λi as
| |
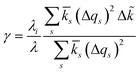 | (75) |
where we define the dimensionless difference
| |
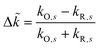 | (76) |
and the harmonic mean
| |
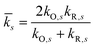 | (77) |
of the inner-shell force constants,
kR,s and
kO,s, of the reduced and oxidized states along the generalized solvent coordinate, Δ
qs, of the
sth phonon mode.
58 The sign of
γ determines whether the larger force constants are in the oxidized (
γ > 0) or reduced (
γ < 0) states, while
γ = 0 for the symmetric case.
For asymmetric Normal ECIT in the AMH approximation, the generalization of the quadratic CIET barrier, eqn (59), is a cubic function of ΔGex:
| |
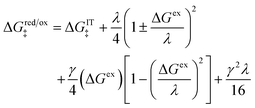 | (78) |
where the effective IT energy barrier is given by
| |
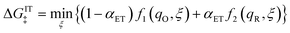 | (79) |
in terms of the ET symmetry factor
| |
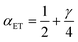 | (80) |
which is obtained by linearizing
eqn (78) in the limit |Δ
Gex| ≪
λ. A hallmark of CIET is that the weights for the IT energies of the reduced and oxidized states,
f1(
qO,
ξ) and
f2(
qR,
ξ), in the effective IT barrier Δ
GIT‡ are determined by the assumed symmetry of solvent reorganization controlling ET.
For a metal electrode, the rate integrals for asymmetric Normal ECIT can be approximately evaluated as
| |
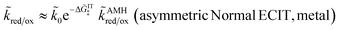 | (81) |
using the asymptotic approximation of Zeng
et al.61 for AMH kinetics:
| |
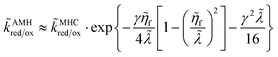 | (82) |
which reduces to MHC kinetics for
γ = 0.
Although nonlinear solvation effects in ET can break symmetry in the reduction and oxidation rates, they still cannot explain Tafel's law. The symmetry factor, αET, was derived by linearization for small values of ΔGex and does not hold at large formal overpotentials. In order to predict linear Tafel plots, one must consider CIET rate limitation by asymmetric IT.
5 Butler–Volmer kinetics of ion-coupled electron transfer (ICET)
Ion transfer tends to be asymmetric when coupled with nonadiabatic ET, since the compensating electron occupies different wavefunctions in the reduced and oxidized states, leading to differences in both the electrostatic energy and coordination chemistry of the ions. As such, we can generally characterize the IT barriers for reduction and oxidation with distinct free energy differences, βred and βox, respectively. Without loss of generality, we assume f1(q,ξ) ≤ βred and f2(q,ξ) ≤ βred in the CIET landscape of excess chemical potential, eqn (47) and (48). Assuming the coupled ET is characterized by a reorganization energy, λ, we now turn our attention to the opposite limit of IT rate limitation,| |
| βred/ox ≫ λ,e|ηf|,kBT,Δe (ICET) | (83) |
which we refer to as “ion-coupled electron transfer” (ICET), when ET occurs suddenly in response to slow IT, as shown in Fig. 7. (The term “ICET” was perhaps first used by Daniel Nocera in 2022, private communication.) Here we develop a detailed theory for the nonadiabatic case, but we argue below that similar results hold for adiabatic ICET. In contrast to ECIT, eqn (61), which corresponds to a regular limit of CIET theory, the ICET limit, eqn (83), is singular and must be treated with care.
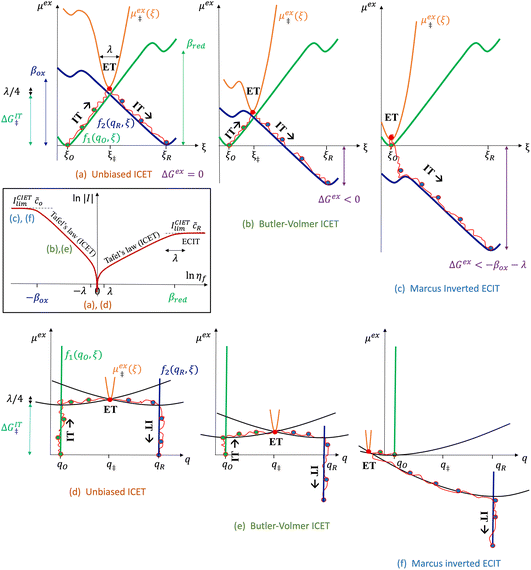 |
| | Fig. 7 Physics of IT-limited non-adiabatic CIET, or “ion-coupled electron transfer” (ICET), at a metal electrode, where the ion transfer barrier, ΔGIT‡, exceeds the reorganization energy λ, thermal energy kBT and chemisorption function, Δe. In this limit, the path of the reaction complex (red) is shown in the two dimensional landscape of excess chemical potential μex(q,ξ), shown in Fig. 5, viewed along the IT coordinate ξ from the oxidized state ξO to the reduced state ξR, in (a)–(c), and the dependence on the ET solvent reorganization coordinate q is shown for the same cases in (d)–(f). The oxidized state has IT energy f1(qO,ξ) (green), and the reduced state has IT energy f2(qR,ξ) (blue). The CIET barrier is μex‡(ξ) = μex(q‡,ξ) (orange). Three cases are depicted for the excess chemical potential applied between the reduced and oxidized states, ΔGex = eηf + εF − ε, which is the sum of the formal overpotential ηf and the electron energy ε below the Fermi level εF, sampled from the band structure of the electrode ρe(ε) according to the Fermi–Dirac distribution ñe(ε): in (a) and (d) for unbiased ICET with ΔGex = 0, the rate limiting process is IT with a large barrier βox (in the reduction direction) in addition to the small ET barrier λ/4 (light blue). In (b) and (e) for moderate overpotentials, ΔGex < 0, Butler–Volmer kinetics holds for ICET. In (c) and (f) at even larger driving force, ΔGex < −βox − λ, the reaction complex enters the Marcus inverted region of ECIT, as the ion sits at the oxidized state before ET triggers IT to complete the reaction. (Inset) Tafel plot showing the scenarios (a)–(c) for reduction, where the Tafel slope is αIT = βred/(βred + βox) for the negative reduction branch and 1 − αIT for the positive oxidation branch. On both sides, the straight-line Tafel regime transitions to a reaction limited current for Inverted ECIT, when the overpotential exceeds the ion-transfer energy. | |
As noted in the introduction, Butler18 was the first to consider what we call “ICET” in the singular limit of infinitely fast ET, λ → 0. In that case, as illustrated in Fig. 7, the parabolic ET contributions to the CIET activation barriers diverge in eqn (52) and (53) for all values of the IT coordinate ξ as λ → 0:
| |
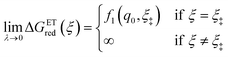 | (84) |
| |
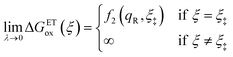 | (85) |
except at special values of
ξ =
ξ‡ where those terms identically vanish. These transition state values of the IT coordinate are determined implicitly by intersections of IT free energy landscapes for reduction and oxidation, shifted by the overpotential:
| |
| ΔGex + f2(qO,ξ‡) = f1(qR,ξ‡) | (86) |
Of course, we must assume (for now) that such intersections exist, which is expected up to moderately large overpotentials, −
βox < Δ
Gex <
βred, and guaranteed if
f1(
qO,
ξ) and
f2(
qR,
ξ) are also monotonic functions.
The general formula eqn (86) determines the transition state IT coordinate, ξ‡(ΔGex), for any intersecting f1(qO,ξ) and f2(qR,ξ) in the limit λ → 0, but we now introduce a critical approximation, which leads to BV kinetics for sufficiently small but finite λ. Following Gurney42 and Butler,18 it is convenient to assume linear dependence of the IT free energy landscapes,
| |
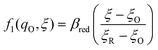 | (87) |
| |
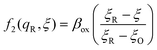 | (88) |
as sketched in
Fig. 8, but we make this approximation in the general quantum-mechanical framework of CIET theory,
eqn (47) and
(48). We assume asymmetric IT and symmetric IT with small but finite
λ, in the ICET regime,
eqn (83), for general situations as sketched in
Fig. 7. Note that
βred and
βox have units of energy, since we have rescaled the IT reaction coordinate
ξ by the total displacement, (
ξR −
ξO), from the oxidized state to the reduced state.
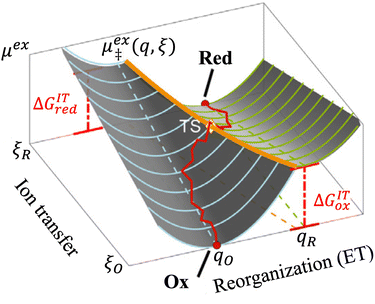 |
| | Fig. 8 Free energy landscape of IT-limited CIET, which we refer to as “ion-coupled electron transfer” (ICET), in the linear approximation of the ion-transfer coordinate ξ dependence of free energy of the diabatic reduced and oxidized states, eqn (87) and (88), respectively. For nonadiabatic ET, this approximation enables a quantum mechanical derivation of the Butler–Volmer equation, eqn (1), with the charge transfer coefficient (or symmetry factor), α, given by eqn (91) and the exchange current I0 given by eqn (101) and (102). The quantum BV equation based on nonadiabatic CIET theory is valid for IT rate limitation, eqn (83), where the IT free energies βred/ox are much larger than the reorganization energy λ, thermal energy kBT, formal overpotential e|ηf|, and electronic coupling |HDA|. [Adapted from Fig. 5a of Fraggedakis et al. (2021).103] | |
By minimizing the free energy barrier, we find that the transition state occurs at the following coordinates,
| |
| q‡ = αITqR + (1 − αIT)qO | (89) |
| |
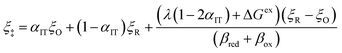 | (90) |
where the charge transfer coefficient (or symmetry factor) for IT takes the Gurney–Butler form,
7,18,42| |
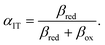 | (91) |
Using
eqn (33), the free energy barriers for ICET can then be expressed in terms of the formal overpotential,
ηf, and the electron energy relative to the Fermi level,
ε −
εF:
| |
| ΔGred‡ = αITΔGex + ΔGICET‡ | (92) |
| |
| ΔGox‡ = −(1 − αIT)ΔGex + ΔGICET‡ | (93) |
as well an overall activation energy for ICET controlling the reaction rate prefactor,
| |
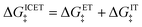 | (94) |
which is the sum of a contribution from ET
| |
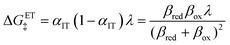 | (95) |
and another from IT
| |
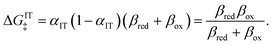 | (96) |
The ET part of the ICET activation energy,
eqn (95), is an asymmetric generalization of the Marcus barrier for symmetric ET, Δ
GET‡ =
λ/4 for
αIT = 1/2, which also arises in our result for the ECIT barrier above in
eqn (72). The IT part of the ICET activation energy,
eqn (96), is likewise an asymmetric generalization of the activation energy for symmetric ECIT,
eqn (62), since we have
| |
| ΔGIT‡ = (1 − αIT)f1(qO,ξ) + αITf2(qR,ξ) | (97) |
which does not depend on
ξ in the linear approximation. This expression also matches the expected IT barrier for asymmetric ET-limited CIET,
eqn (79), if we set
αET =
αIT =
α, which supports the physical picture that IT is the dominant source of asymmetry in CIET.
Substituting into eqn (45) and (46) and using eqn (33) and (14), we can derive rate expressions for ICET,
| |
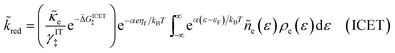 | (98) |
| |
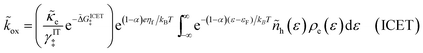 | (99) |
where Δ
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ICET‡
ICET‡ = Δ
GICET‡/
kBT. By converting from formal to total overpotential using
eqn (9), we finally arrive at the BV equation (for one electron transfer),
| |
ĨICET = ĨICET0(e−α![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) − e(1−α) − e(1−α)![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) ) ) | (100) |
with all parameters determined by the quantum theory of ICET. The charge transfer coefficient,
α =
αIT, is given by
eqn (91), as predicted by Gurney–Butler theory,
7,18,42 but CIET theory also provides a quantum-mechanical formula for the BV exchange current for ICET, given by
| |
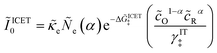 | (101) |
where we define a dimensionless prefactor
| |
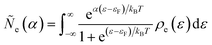 | (102) |
which can be interpreted as the relative number of electronic states participating in ET as a function of
α, the charge transfer coefficient for IT.
The quantum-mechanical BV exchange current density predicted by ICET theory, eqn (101) and (102), differs from that of phenomenological IT theory, eqn (4), in several fundamental ways. First, the activities aO and aR have been replaced by concentrations, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O and
O and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R, respectively. Second, the empirical lumped prefactor, nekBV0aen(1−α), has been replaced by the product of the electron transmission coefficient
R, respectively. Second, the empirical lumped prefactor, nekBV0aen(1−α), has been replaced by the product of the electron transmission coefficient ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e, the effective number of participating electronic states Ñe(α), and an Arrhenius prefactor, where the activation energy, ΔGICET‡, is expressed in terms of both the ET reorganization energy and the mean IT barrier.
e, the effective number of participating electronic states Ñe(α), and an Arrhenius prefactor, where the activation energy, ΔGICET‡, is expressed in terms of both the ET reorganization energy and the mean IT barrier.
The factor Ne(α) rescales the BV reaction rate according to the number of accessible electronic states near the Fermi level in the band structure of the electrode, ρe(ε). It is also a sensitive function of the charge-transfer coefficient, α, because asymmetry in the IT energy landscape increases the range of electron and hole energies that can contribute to the rate for a given formal overpotential. In the case of a metallic electrode with ρe = constant, this integral can be evaluated by residue calculus,
| |
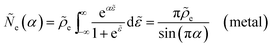 | (103) |
to complete a simple analytical formula for the reaction rate. For symmetric IT,
α = 1/2, a minimum of
Ñe = π
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) e
e is attained, while
Ñe → ∞ for highly asymmetric IT,
α → 0 or
α → 1, as the number of electrons diverges due to the nearly flat IT energy landscape of either the reduced or the oxidized state. It is important to recognize that
α → 0, 1 is a pathological limit of the ICET model using the Gurney–Butler linear approximation of the IT free energy landscapes, since the transition state
ξ‡ for many electron levels will lie far outside the physically meaningful range,
ξO ≤
ξ ≤
ξR.
CIET theory thus provides a rigorous, quantum-mechanical derivation of Butler–Volmer kinetics, including Tafel's limiting law, which clarifies its range of applicability and underlying physics (apparently for the first time). We see that the BV equation is valid for IT-limited CIET (or ICET) satisfying eqn (83), as long as the overpotential is not so large that Tafel's law breaks down. For a metal electrode, the quantum-mechanical ICET exchange current has the following dimensional form:
| |
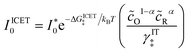 | (104) |
where
| |
| ΔGICET‡ = α(1 − α)(λ + βred + βox) | (105) |
and
| |
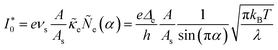 | (106) |
The importance of ET in quantum Butler–Volmer kinetics of ICET is underscored by the presence of the dimensionless Marcus reorganization energy,
, in both the exchange current prefactor,
, and the activation barrier, Δ
GICET‡.
6 Barrierless ECIT at the end of Tafel's law
“In spite of almost a century of confirming data, there is still a frontier in the study of Tafel's law. Is there an overpotential at which it will break down?” (ibid., p. 1511).7
CIET theory is finally able to answer to this question. As shown in Fig. 8, the phenomenological derivation of the BV equation clearly breaks down when the formal overpotential exceeds the chemical barriers for IT. In that case, the transition state can no longer be identified without considering coupled Marcus kinetics of ET. The general definition of these barriers is given in terms of the diabatic free energy surfaces by
| |
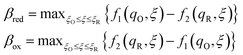 | (107) |
as shown in
Fig. 7. If the formal overpotential further exceeds the following bounds set by the reorganization energy,
| |
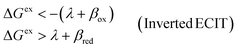 | (108) |
then barrierless transitions become possible, which will dominate the current as usual, according to Marcus theory for metal electrodes.
25,51 CIET theory thus predicts a universal transition from either Marcus kinetics of Normal ECIT or Butler–Volmer kinetics of ICET to a new regime of “Inverted ECIT” at large overpotentials, where Tafel's law breaks down. In the case of ICET at a metal electrode, a constant reaction-limited current is attained, dominated by barrierless transitions, which are always possible at large overpotentials for some electrons deep within the Fermi sea. The scale of this transition region is set by
λ for non-adiabatic CIET, but below we argue that the basic concept of a reaction-limited current beyond Tafel's law should still hold for adiabatic CIET with the scale set instead by
Δe.
The basic physics of Inverted ECIT are sketched in Fig. 7 for the case of a transition from ICET at low overpotentials to Inverted ECIT at large overpotentials. When the free energy of reaction leaves the ICET range, −βox < ΔGex < βred, the IT coordinate of the lowest-energy transition state becomes pinned at a value that attains one of the bounds in eqn (107). If the diabatic curves are monotonic across the IT range, ξO < ξ < ξR, then the IT coordinate of the Inverted ECIT transition state is pinned at its equilibrium value (in the absence of any overpotential):
| |
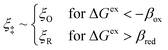 | (109) |
as the ions await ET to trigger the ECIT reaction. For sufficiently large excess free energies of reaction satisfying,
eqn (108), the diabatic IT curves,
f1(
qO,
ξ) and
f2(
qR,
ξ), no longer intersect, as shown in
Fig. 7(c), and the transition state arises in the Marcus inverted region for ET, shown in
Fig. 7(f).
Following our derivation of ECIT kinetics above, the corresponding activation barriers take the form,
| |
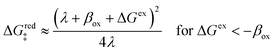 | (110) |
| |
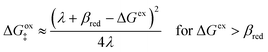 | (111) |
Compared to the original Marcus theory for ECIT,
eqn (59), the excess free energy of reaction, Δ
Gex, is now shifted by a certain IT free energy,
βred or
βox, generally given by
eqn (107). Although it may seem counter-intuitive, the reduction (or oxidation) rate for large negative (or positive) overpotentials is controlled by the opposite IT free energy for oxidation (or reduction), respectively, which sets the other side of the ECIT transition state, following ET and prior to IT.
For a metallic electrode (ρe = constant), the asymptotic activation barriers in eqn (110) and (112) imply that Tafel's law smoothly transitions to a reaction-limited current according to shifted Marcus ECIT curves, which are generally different for reduction
| |
Ĩ ∼ ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) 0 0![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O O![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) MHCred( MHCred(![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) , ,![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f + f + ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox) for ox) for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f < − f < −![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox ox | (112) |
and for oxidation
| |
Ĩ ∼ ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) 0 0![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R R![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) MHCox( MHCox(![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) , ,![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f − f − ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red) for red) for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f > f > ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red red | (113) |
based on different shifts of the MHC formula,
eqn (70). Since
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) MHCred/ox
MHCred/ox → 1 as |
ηf| → ∞, CIET theory thus predicts a universal limited reaction rate for metallic electrodes corresponding to barrierless ECIT,
| |
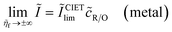 | (114) |
where the dimensionless limiting current in the standard state, (
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R/O
R/O = 1), is given by
ĨCIETlim =
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) 0
0, or, with units restored,
| |
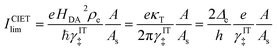 | (115) |
An important prediction of CIET theory for metal electrodes is that the universal limiting current is fully quantum mechanical with vanishing activation energy,
i.e. no Arrhenius dependence on temperature. As anticipated above, the universal CIET limiting current differs from the extrapolated limiting current of Normal ECIT,
eqn (74), by the absence of the IT activation energy barrier, Δ
GIT‡ → 0, which has been overcome by the applied overpotential. Instead, the CIET limiting current is set by the quantum tunneling current,
eκT, for barrierless transitions between the donor and acceptor states and scales with the number of reacting surface sites
A/
As and the inverse activity coefficient of the IT transition state, (
γIT‡)
−1, which is proportional to its excluded volume.
We expect that it would be difficult to unambiguously observe the CIET reaction-limited current for a given faradaic reaction experimentally. At such large overpotentials, exceeding all IT and ET barriers for the desired reaction, various side reactions would likely also be triggered, e.g. contributing to rapid growth of solid-electrolyte interphase (SEI) or bubble generation on the metal surface. Transport limitation leading to concentration polarization and ohmic drops from series resistances are also difficult to avoid, whenever large faradaic currents are achieved. The key to testing this prediction of CIET theory thus would be to find ways to slow down both IT and ET, for example with electrode compositions that suppress IT by enhancing ion crowding, γIT‡ ≫ 1, and resistive electrode coatings to limit ET.
7 Uniformly valid approximation for CIET kinetics
In the preceding three sections, we have derived general limiting expressions for the faradaic current by CIET, regardless of the details of the diabatic free energy landscape, in three asymptotic limits:
(1) Normal Marcus kinetics of ECIT for λ ≫ βred/ox,e|ηf|,kBT,Δe with a new IT-dependent prefactor,
(2) Butler–Volmer kinetics of ICET for βred/ox ≫ λ,e|ηf|,kBT,Δe with a new quantum-mechanical formula for the exchange current, and
(3) Inverted Marcus kinetics of ECIT for e|ηf| > βred/ox + λ in a new “post-Tafel” regime, shifted by the red/ox IT energies.
Our CIET theoretical framework thus unifies and justifies the famous limits of BV kinetics for IT and Marcus kinetics for nonadiabatic ET. More importantly, it can also provide uniformly valid rate expressions that interpolate between these limits, for any specific model of the diabatic free-energy landscapes, which leads to a rich set of new kinetic models for CIET. For accurate predictions, the diabatic states can be modeled by CDFT or other ab initio quantum calculations, but it can be even more useful (at least for experimentalists and engineers) to develop simple, uniformly valid analytical approximations for the CIET reaction rates by asymptotic matching of the results above. The resulting alternatives to (and extensions of) the BV equation can then be fitted to experiments to infer microscopic parameters and/or used in engineering simulations of electrochemical systems.
Asymptotic matching requires finding mathematical expressions that uphold known asymptotic limits and interpolate smoothly between them, while balancing accuracy (to be checked against the full model and/or experimental data) and elegance (analytical simplicity for modeling and simulation). Uniformly valid asymptotic approximations of pure ET kinetics are already available in both symmetric (MHC)61 and asymmetric (AMH)61 forms and were used above to model the corresponding ECIT limits of CIET kinetics. It is more challenging to develop such approximations for the general CIET theory, because the free energy landscape is two-dimensional and must be described with sufficiently simple approximations (e.g. low-order polynomials) to allow evaluation of the Fermi integrals. In order to do so and illustrate the overall form of a complete CIET theory, we shall make somewhat more restrictive assumptions, leaving open the possibility of deriving more accurate, general approximations in the future.
We consider the simplest possible approximation of the free energy landscape, which imposes strict constraints on the IT coordinate, ξO ≤ ξ ≤ ξR, in the model of ICET above, motivated by the transition to ECIT in eqn (109). We postulate that the diabatic free-energy surfaces are parabolic in the ET reorganization coordinate q and linear in the IT coordinate ξ,
| |
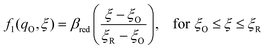 | (116) |
| |
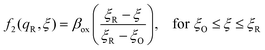 | (117) |
| |
| fi(q,ξ) = ∞, for ξ < ξR, ξ > ξO, i = 1, 2 | (118) |
while diverging outside the allowed range of IT coordinates. These truncated linear approximations of the diabatic free energy surfaces allow us to derive uniformly valid asymptotic approximations of the CIET rates for both symmetric and asymmetric IT.
7.1 Symmetric nonadiabatic CIET
For symmetric IT, where βred = βox = β, the free energy barriers in this model can be written compactly as| |
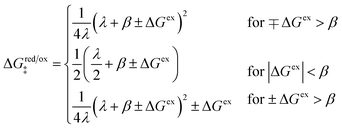 | (119) |
which satisfies the De Donder relation, eqn (27), in the form, | |
| ΔGred‡ − ΔGox‡ = ΔGex. | (120) |
These approximate barriers can be inserted into the Fermi integrals to obtain the CIET rates for a general electrode,| |
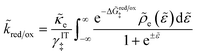 | (121) |
where ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = (ε − εF)/kBT. These uniformly valid approximations are nearly exact for the truncated linear models in eqn (116)–(118). They also reproduce the barriers derived above in the three asymptotic regimes of the general theory, while interpolating smoothly between them with continuously differentiable functions. After integration over the electron energies, the rate formulae in eqn (139) thus possess two continuous derivatives.
= (ε − εF)/kBT. These uniformly valid approximations are nearly exact for the truncated linear models in eqn (116)–(118). They also reproduce the barriers derived above in the three asymptotic regimes of the general theory, while interpolating smoothly between them with continuously differentiable functions. After integration over the electron energies, the rate formulae in eqn (139) thus possess two continuous derivatives.
In order to obtain a simple formula, we consider the typical case of a metal electrode, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) e = constant, and replace the Fermi–Dirac functions with Heaviside step functions,25,60
e = constant, and replace the Fermi–Dirac functions with Heaviside step functions,25,60
| |
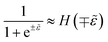 | (122) |
which is valid for low temperatures,
kBT ≪
λ,
β, as required for validity of transition state theory. We also neglect the high-energy Marcus tails for reverse bias (±Δ
Gex >
β) in
eqn (119), which introduces only exponentially small errors, slightly violating the De Donder relation,
eqn (120). This allows us to perform the integrals in
eqn (139) to obtain closed-form uniformly valid approximations for the symmetric CIET rate constants (
Fig. 9),
| |
 | (123) |
where we scale the rate constants to their universal limiting value
k0 in
eqn (69) and introduce an asymptotic matching factor,
M(
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f
f), which interpolates between the exact prefactors for large and small overpotentials derived above. This factor is required for mathematical accuracy in the asymptotic limits, but could be set to
M = 1 in most cases, given the crude physical accuracy of the truncated linear approximation of the diabatic free energy landscape,
eqn (118).
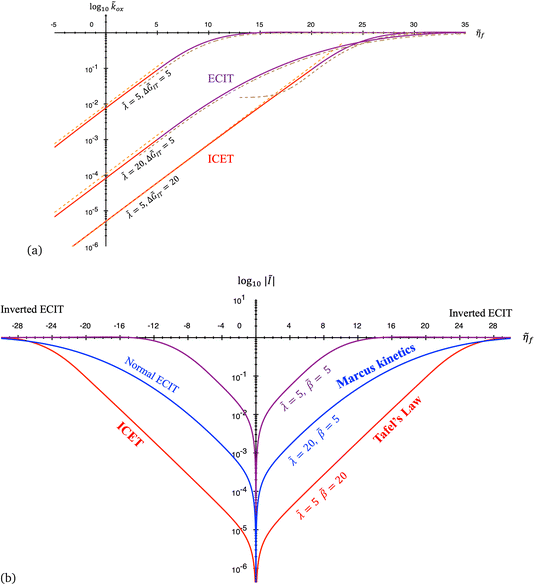 |
| | Fig. 9 Unification of Butler–Volmer and Marcus kinetics: uniformly valid approximation of symmetric nonadiabatic CIET kinetics at a metal electrode, eqn (123). (a) Linear–log plot of the dimensionless oxidation rate constant, ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ox, scaled to the universal limiting rate k0 in the standard state ( ox, scaled to the universal limiting rate k0 in the standard state (![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O = O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = 1), versus dimensionless formal overpotential, R = 1), versus dimensionless formal overpotential, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f, scaled to kBT/e, for three cases of reorganization energy, f, scaled to kBT/e, for three cases of reorganization energy, ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) , and ion transfer free energy, , and ion transfer free energy, ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) (scaled to kBT). Dashed curves show the asymptotic approximations for ICET for (scaled to kBT). Dashed curves show the asymptotic approximations for ICET for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f < f < ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) and for ECIT for and for ECIT for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f > f > ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) , which have been matched to obtain the uniformly valid approximations (solid curves). (b) Tafel plot of the absolute value of the CIET current, |Ĩ|, scaled to the limiting current, ek0, versus dimensionless formal overpotential for the cases in (a), assuming standard conditions for the reactants, , which have been matched to obtain the uniformly valid approximations (solid curves). (b) Tafel plot of the absolute value of the CIET current, |Ĩ|, scaled to the limiting current, ek0, versus dimensionless formal overpotential for the cases in (a), assuming standard conditions for the reactants, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O = O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = 1. For ICET over a wide range of formal overpotentials, kBT ≪ eηf ≪ β, the theory is able to exactly reproduce Tafel's law, eqn (2), and predict its breakdown, as explained in Fig. 7. R = 1. For ICET over a wide range of formal overpotentials, kBT ≪ eηf ≪ β, the theory is able to exactly reproduce Tafel's law, eqn (2), and predict its breakdown, as explained in Fig. 7. | |
If high mathematical accuracy is desired for this physical model, then the matching factor can be chosen to correct for small errors introduced in eqn (123) compared to the exact integral formula, eqn (139), resulting from the low-temperature approximation, eqn (122). At high formal overpotentials, |![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f| ≫ 1, the approximation of eqn (123) reaches a limiting rate given by
f| ≫ 1, the approximation of eqn (123) reaches a limiting rate given by
| |
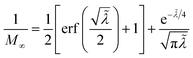 | (124) |
which slightly over-estimates the correct universal value,
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) red/ox
red/ox →
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) 0
0, but rapidly converges in the relevant low-temperature limit,
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
≫ 1. For example,
M−1∞ = 1.2 for
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
= 1, and
M−1∞ = 1.02 for
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
= 4. For small formal overpotentials, |
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f
f| ≪ 1, we must set
| |
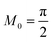 | (125) |
in order to recover the exact exchange current for ICET,
eqn (101). The transition from this value to the limiting value should occur for |
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f
f| >
![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif)
over a range set by
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
, so we could choose the matching function to be
| |
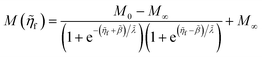 | (126) |
where we control the transition with Fermi–Dirac functions (
Fig. 10). The asymptotic matching prefactor factor,
M(
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f
f), introduces some curvature of the Tafel plot for ICET, even at low formal overpotentials, which physically corresponds to smoothing of the sharp minima in the truncated linear approximations of the diabatic free energy landscape.
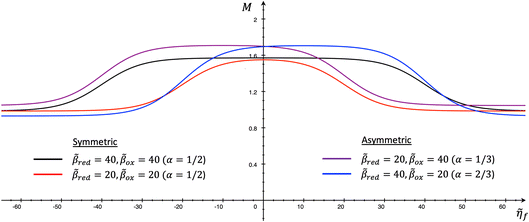 |
| | Fig. 10 Asymptotic matching function, M(![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f), plotted for the ICET regime with parameters shown for symmetric cases, eqn (124)–(126), and asymmetric cases, eqn (130)–(132) with f), plotted for the ICET regime with parameters shown for symmetric cases, eqn (124)–(126), and asymmetric cases, eqn (130)–(132) with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 5. = 5. | |
As shown in Fig. 11, this formula smoothly interpolates between BV kinetics of ICET and Marcus kinetics of ECIT. The theory is thus able to predict Tafel's law from quantum electrochemistry. Unlike previous ET or IT theories, CIET theory predicts Tafel's law in the limit of IT rate limitation (ICET) across a wide range of formal overpotentials, kBT ≪ |eηf| ≪ β, while also predicting its failure by transition to ET limitation (Inverted ECIT) at large overpotentials, |eηf| ≫ β.
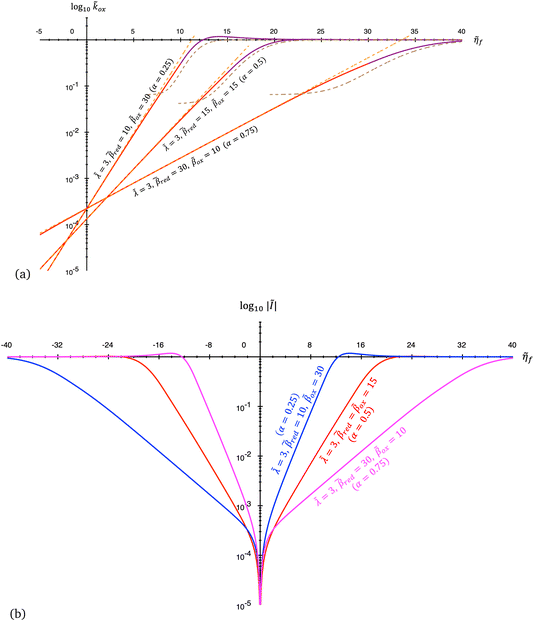 |
| | Fig. 11 Tafel's law and its breakdown at large overpotentials: uniformly valid approximation of asymmetric nonadiabatic ICET kinetics at a metal electrode, eqn (128) and (129). (a) Linear–log plot of the dimensionless oxidation rate constant, ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ox, ( ox, (![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O = O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = 1), versus dimensionless formal overpotential, R = 1), versus dimensionless formal overpotential, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f, for three cases of f, for three cases of ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) , , ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red and red and ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox. Dashed curves show the asymptotic approximations for ICET (− ox. Dashed curves show the asymptotic approximations for ICET (−![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox < ox < ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f < f < ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red) and for ECIT ( red) and for ECIT (![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f < − f < −![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox, ox, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f > f > ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red), which have been matched to obtain the uniformly valid approximations (solid curves). (b) Tafel plot of the absolute value of the dimensionless CIET current, |Ĩ|, versus red), which have been matched to obtain the uniformly valid approximations (solid curves). (b) Tafel plot of the absolute value of the dimensionless CIET current, |Ĩ|, versus ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f for the cases in (a), assuming f for the cases in (a), assuming ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O = O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = 1. R = 1. | |
7.2 Asymmetric nonadiabatic CIET
For asymmetric IT, where βred ≠ βox and thus α ≠ 1/2, we must find a simple approximation for the CIET barrier under the truncated linear approximations, eqn (116)–(118), which reproduces the BV equation and Tafel's law in the ICET regime of moderate overpotentials, while smoothly transitioning to the exact limiting current for barrierless ECIT at large overpotentials. As a generalization of the symmetric case, eqn (119), we propose the following approximations:| |
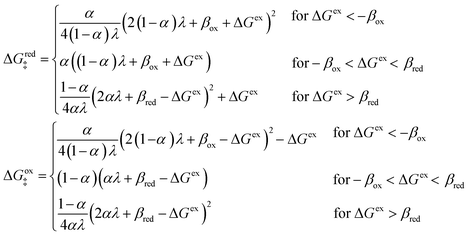 | (127) |
where below we shall again neglect the high-energy Marcus tails for reverse bias (ΔGex > βred for reduction and ΔGex < −βox for oxidation) with exponentially small errors, violating the De Donder relation, eqn (120). These approximations of the barriers are continuously differentiable, so the associated reaction rate constants will be continuously twice differentiable after performing the Fermi integrals. In order to achieve such smooth approximations, we have modified the curvature of the Marcus parabolae, by replacing λ with αλ/(1 − α), but this only affects the transition from the exact quantum Tafel's law to the barrierless ECIT limiting current. Moreover, this approximation effectively blurs the distinction between asymmetric ET and IT at large overpotentials, where we set α ≈ αIT ≈ αET for the general case of asymmetric CIET.
Again, we take the low temperature limit of the Fermi–Dirac distributions, eqn (122), and perform the rate integrals, eqn (139), now using the approximate barriers in eqn (127) to obtain closed-form uniformly valid approximations for the asymmetric CIET rate constants for reduction,
| |
 | (128) |
and for oxidation,
| |
 | (129) |
where we have multiplied the oxidation rate by
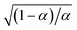
and the reduction rate by
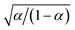
in order to approximate the correct limiting behavior at large overpotentials. In particular, the dimensionless rate constants now tend to a limiting value,
| |
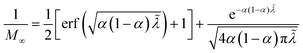 | (130) |
which approximates the barrierless ECIT rate,
kunired/ox →
k0, in the low temperature limit,
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
≫ 1. In order to recover the exact exchange current for ICET,
eqn (101), we must also set
| |
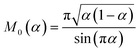 | (131) |
which reproduces
M0(1/2) = π/2 for the symmetric case. Since sin(π
α) ≈ 4
α(1 −
α) for 0 <
α < 1, the matching factor can be approximated as
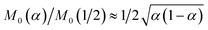
, which diverges in the limits of fully asymmetric charge transfer,
α → 0, 1, and thus should be included in the uniformly valid approximation. The transition to the limiting value should occur for
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f
f < −
![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox
ox for reduction and
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f
f >
![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red
red for oxidation over a range set by
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
. Once again controlling these transitions with Fermi–Dirac functions, we choose
| |
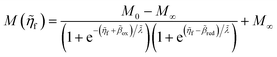 | (132) |
With these matching factors (
Fig. 10) included, the uniformly valid approximations,
eqn (128) and
(129), reproduce the exact asymptotic rates for large and small formal overpotentials and maintain small mathematical errors for all parameter values. Physically, these corrected approximations predict small curvatures of the Tafel plot in the ICET regime associated with smoothing the unphysically sharp minima of the diabatic free energy landscapes in the truncated linear approximations.
8 Distributions of electron energies in CIET
8.1 Gaussian statistics for symmetric ECIT
Following Gerischer,25,31,132 we can interpret the non-adiabatic Normal ECIT rate probabilistically,| |
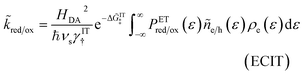 | (133) |
as an integral over the conditional probability of ET for each available electron or hole state in the electrode,| |
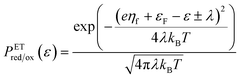 | (134) |
The same statistics, PETred/ox(ε), apply to the limit of Inverted ECIT, which corresponds to Δ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) IT‡ = 0 in eqn (133). From this perspective, the probability of nonadiabatic ET from/to state ε during reduction/oxidation has a normal Gaussian distribution with mean and variance,respectively, as shown in Fig. 12(b).
IT‡ = 0 in eqn (133). From this perspective, the probability of nonadiabatic ET from/to state ε during reduction/oxidation has a normal Gaussian distribution with mean and variance,respectively, as shown in Fig. 12(b).
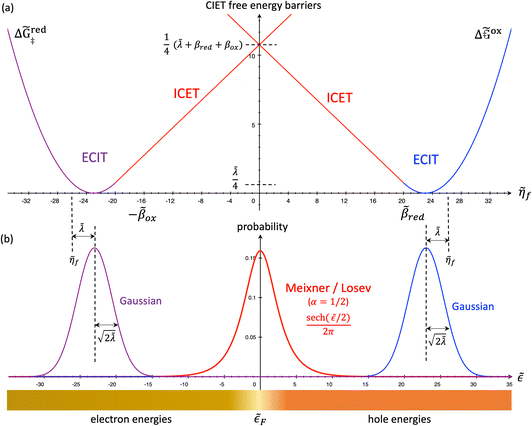 |
| | Fig. 12 Quantum statistics of transferring electron energies for symmetric ICET at a metal electrode. (a) Uniformly valid approximation of the CIET energy barriers for ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red = red = ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox = 20 and ox = 20 and ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 3, and (b) corresponding electron energy distributions for = 3, and (b) corresponding electron energy distributions for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f = −26, 0, 26. f = −26, 0, 26. | |
The Gaussian statistics of symmetric ECIT can also be derived directly from quantum mechanical transitions of displaced harmonic oscillators (DHO),133,134 which represent the quantum analog of classical transitions between the Marcus parabolae for the diabatic states for inner-sphere ET, where λ is a thermally averaged spring constant for the vibrations. At finite temperature, the most probable electron transition occurs at the electron resonance of the Fermi level, shifted by the reorganization energy, as in eqn (135). It is important to stress, however, that Gerischer's interpretation with Gaussian statistics only holds for the symmetric Normal ECIT limit of the general CIET theory.
8.2 Modified Gaussian statistics for Asymmetric ECIT
In our general theory of CIET, the transition to ECIT at large overpotentials can lead to modified Gaussian statistics in the asymmetric case, α ≠ 1/2. In particular, our uniformly valid approximation of the asymmetric CIET barriers preserves the Gaussian shape of the distribution of transferring electron energies but predicts different means,| |
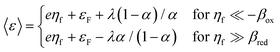 | (137) |
and variances,| |
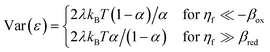 | (138) |
for the reduction and oxidation reactions, respectively. Examples of these rescaled Gaussian distributions for ECIT are shown in Fig. 13(a) and compared with the CIET barriers. In this model, the reorganization energy under extreme overpotentials has been rescaled as λ →λ(1 − α)/α for reduction and λ →λα/(1 − α) for oxidation, so that the local barriers for forward and backward ECIT smoothly transition from those of ICET and inherit the same asymmetry. This is a different way to model asymmetric ET compared to the AMH theory described above. Here, asymmetric solvent reorganization depends on over-potential, as a result of strong coupling with asymmetric IT.
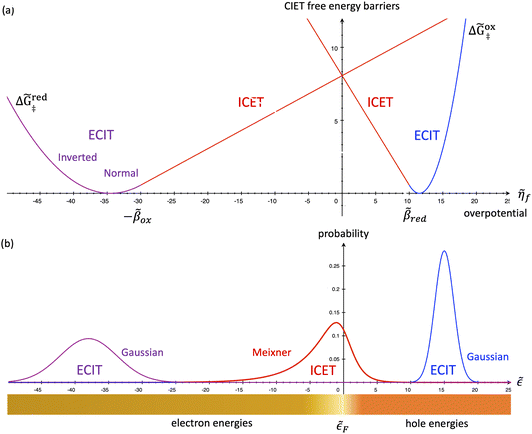 |
| | Fig. 13 Quantum statistics of transferring electron energies for asymmetric ICET at a metal electrode. (a) Uniformly valid approximation of the CIET free energy barriers for reduction and oxidation, eqn (127), for α = 0.25, ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red = 30, red = 30, ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox = 10, ox = 10, ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 3. Linear regions for ICET are shown in red, and quadratic regions for Normal and Inverted ECIT are shown in purple for reduction and blue for oxidation. (b) Probability distributions, PCIETred/ox( = 3. Linear regions for ICET are shown in red, and quadratic regions for Normal and Inverted ECIT are shown in purple for reduction and blue for oxidation. (b) Probability distributions, PCIETred/ox(![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ), for the dimensionless energy of the transferring electron or hole, ), for the dimensionless energy of the transferring electron or hole, ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = (ε − εF)/kBT. Over the full range of formal overpotentials for ICET, −βox < ηf < βred, the electrons or holes are sampled from a Meixner–Losev skewed hyperbolic secant distribution, eqn (141), which is peaked at the Fermi level with a fat tail in the direction of the flatter diabatic free energy landscape, e.g. for lower electron energies (or larger binding energies) if βox > βred or α < 1/2 as shown. For large formal overpotentials in the Normal and Inverted regimes of ECIT, the electrons or holes are sampled from Gerischer's shifted Gaussian distributions, eqn (134), with rescaled parameters, shown for = (ε − εF)/kBT. Over the full range of formal overpotentials for ICET, −βox < ηf < βred, the electrons or holes are sampled from a Meixner–Losev skewed hyperbolic secant distribution, eqn (141), which is peaked at the Fermi level with a fat tail in the direction of the flatter diabatic free energy landscape, e.g. for lower electron energies (or larger binding energies) if βox > βred or α < 1/2 as shown. For large formal overpotentials in the Normal and Inverted regimes of ECIT, the electrons or holes are sampled from Gerischer's shifted Gaussian distributions, eqn (134), with rescaled parameters, shown for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f = − 45, 15. f = − 45, 15. | |
8.3 General statistics of electron energies in CIET
Whenever IT is significantly coupled to ET, the quantum statistics of transferring electron energies are non-Gaussian. This can be seen by rewriting the CIET rate constants for a metal electrode, eqn (139), as| |
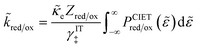 | (139) |
where we define the probability PCIETred/ox(![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ) that an electron or hole with dimensionless energy
) that an electron or hole with dimensionless energy ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = (ε − εF)/kBT participates in the CIET reduction or oxidation reaction, respectively:
= (ε − εF)/kBT participates in the CIET reduction or oxidation reaction, respectively:| |
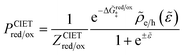 | (140) |
which is normalized by ZCIETred/ox. For example, the uniformly valid approximations above correspond to different choices of the barriers, eqn (119) and (127), for symmetric or asymmetric IT, respectively, which smoothly transition between statistics of ICET and ECIT as |![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f| passes through
f| passes through ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red/ox. It appears that the general CIET distributions have not been studied before in probability and statistics, and their mathematical properties await systematic characterization.
red/ox. It appears that the general CIET distributions have not been studied before in probability and statistics, and their mathematical properties await systematic characterization.
8.4 Meixner statistics of electron energies for ICET
In the symmetric ICET regime for a metal electrode, the conditional probability of ET is an exponential random variable, whose density multiplies the Fermi–Dirac distribution to obtain a Meixner distribution135 of electron energies:| |
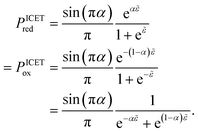 | (141) |
The normalization factor is given by| |
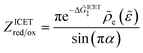 | (142) |
where Δ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ICET‡ is given by eqn (155). In contrast to ECIT, the Fermi level (
ICET‡ is given by eqn (155). In contrast to ECIT, the Fermi level (![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = 0) is always close to the most probable energy for electrons or holes involved in reduction or oxidation by ICET at a metal electrode, respectively, regardless of the overpotential or reorganization energy. For the symmetric ICET (α = 1/2), the electron energy (for reduction) or hole energy (for oxidation) are sampled from the hyperbolic secant distribution
= 0) is always close to the most probable energy for electrons or holes involved in reduction or oxidation by ICET at a metal electrode, respectively, regardless of the overpotential or reorganization energy. For the symmetric ICET (α = 1/2), the electron energy (for reduction) or hole energy (for oxidation) are sampled from the hyperbolic secant distribution| |
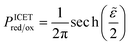 | (143) |
which has mean and variance,respectively, and excess kurtosis, 2. The latter indicates that the distribution is leptokurtotic, meaning that it has fat tails and a more sharply peaked central region compared to a normal (or Gaussian) distribution.
The limiting electron energy distributions are shown in Fig. 12 for symmetric ICET and in Fig. 13 for asymmetric ICET. For symmetric ICET, eqn (145), the participating electrons and holes lie within a few kBT of the Fermi level, but for asymmetric ICET, eqn (141), the distribution of transferring electron energies is strongly skewed with a fat tail to favor either electrons far below the Fermi level for α → 0 or holes far above the Fermi level for α → 1. As noted above, these are singular limits associated with diverging faradaic reaction rates, as the number of participating electrons Ñe diverges for α → 0, 1.
It would be interesting to develop quantum mechanical models for the non-Gaussian statistics of electron energies participating in nonadiabatic CIET, generalizing the DHO model for Marcus kinetics of nonadiabatic ET.133,134 The most natural quantum model would involve “displaced linear oscillators”, where the IT coordinate is described, for example, by the truncated linear wells of eqn (118). One could also assume bilinear wells of the form,
| |
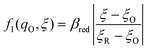 | (146) |
| |
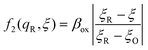 | (147) |
or other, more realistic models of the diabatic states with smoothed parabolic minima in the IT coordinate, in addition to the harmonic approximation for the solvent reorganization coordinate
q in
eqn (47) and
(48). In the ICET limit, we expect that such quantum models would yield Meixner statistics of electron transfer,
eqn (141), from first-order perturbation theory in the semi-classical limit, while also providing a fully quantum mechanical derivation of the Butler–Volmer equation.
8.5 CIET effects in photo-electron spectroscopy
The ICET distribution of electron energies, eqn (141), is an example of a generalized hyperbolic secant distribution136 from the Meixner family of stochastic processes.135,137,138 These distributions have received relatively little attention in statistics,139 although they are used to describe non-Gaussian fluctuations of stock prices in financial mathematics.140 In physics, skewed hyperbolic secant distributions have been proposed to fit asymmetric peaks in X-ray photoelectron spectroscopy (XPS) by Losev,141,142 but without any physical justification. The electron energy distribution for ICET appears to be the first case of Meixner–Losev statistics derived from a physical model.
Asymmetric line shapes are commonly observed in both XPS143,144 and Auger electron spectroscopy (AES)145,146 of metal surfaces, and they are fitted to either cascades of symmetric line shapes or various skewed functions.141,147,148 In XPS of simple metals, asymmetric line shapes are usually fitted to the skewed Lorentzian shape of Doniach and Šunjić149 (with power-law tails) and attributed to many-body interactions between conduction electrons and the final-state core hole.144,150,151 For chemically-oxidized metal surfaces, similar asymmetric line shapes are also observed if the oxide film has a wide band of conducting states near the Fermi level to accept shake-up electrons, while more symmetric line shapes are observed for insulating oxide films.143,152 Interestingly, the Losev line shape141,142 (with exponential tails) has also been shown to fit XPS line shapes for conducting oxide and sulphide films on metal surfaces.153
The final state of core-electron photo-emission is an ionized atom (with a core hole), which feels a strong Coulomb attraction to the metal surface, as it draws in electrons (and repels holes) in the conduction band near the Fermi level to form a meta-stable ion-image polaron pair near the surface. This shake-up process of polaron formation can be viewed as a CIET reaction, where ionized atom transfer into the surface is coupled with electron transfer from the bulk conduction band to a nearby, weakly-coupled orbital. The binding energy of the transferring electron (relative to the Fermi energy) is subtracted from the emitted photo-electron energy, resulting in a larger apparent binding energy for the original core electron.
CIET theory provides a simple alternative explanation for the observed trends in XPS line shapes on metal surfaces. For insulating surface films, the ET step is rate limiting and leads to the Gerischer–Marcus Gaussian line shape of ECIT. For conducting surface films, the IT step is rate limiting and leads to the Meixner–Losev line shape of ICET. In that case, the relative ease of reduction, βred < βox, (resulting from the core hole) explains the skew of the distribution to larger binding energies, α < 1/2, as shown in Fig. 13(b).
Stronger signatures of CIET should be apparent in AES, where ionic relaxation is known to play an important role in spectra with asymmetric line shapes.145,146 Auger electron photo-emission creates a doubly-ionized atom (with core and valence holes), which can attract two conduction electrons to form a divalent polaron by CIET. Given the larger ion transfer energies for divalent ions, the AES shake-up process is even more likely influenced by ICET, which again skews the line shape to larger binding energies.
9 Adiabatic ICET and electrocatalysis
The mathematical theory of CIET developed here is strictly valid only for nonadiabatic ET with weak electronic coupling, Δe ≪ kBT, but we expect some of its key predictions to be universally valid, even in the opposite limit of strong coupling, Δe ≫ kBT, where ET is adiabatic, involving electrons that are shared in hybrid orbitals between the diabatic states. In the weakly adiabatic regime, where the electronic coupling is much smaller than the reorganization energy, kBT < Δe ≪ λ, the level splitting partly lowers the ET free energy barriers, ΔGred/oxET, compared to the non-adiabatic CIET theory, as shown in Fig. 6(c)–(e), although the prefactor changes and becomes roughly independent of the electronic coupling.25,31,154 As such, we expect similar functional forms for the limits of ECIT and ICET kinetics, but with a modified prefactor that could in principle be derived from quantum calculations. In the strongly adiabatic regime, typical of electrocatalysis, the electronic coupling may become comparable to or exceed the reorganization energy, Δe > λ, effectively eliminating the Marcus ET barrier, and a modified approach becomes necessary.
Schmickler67 first proposed a unified quantum theory of adiabatic ET coupled with IT across the double layer at an electrode/electrolyte interface, based on a model Hamiltonian with electronic and solvent contributions, H = He + Hsol, each of which depend on the distance ξ of the ionic reactant from the electrode surface. The electronic part of the Hamiltonian He(ξ) is adapted from the Anderson–Newns model for chemisorption on metal surfaces for the case of one electronic state on the reactant exchanging electrons with the electrode, where the coupling matrix elements depend on ξ. The solvent Hamiltonian Hsol(ξ) describes quantum harmonic oscillators for inner-sphere and outer-sphere modes perturbed by a linear interaction of the reactant and each solvent mode, where the coupling constants again depend on position ξ. For a particular choice of the dominant solvent mode, q, the model predicts a two-dimensional (q,ξ) energy landscape, which allows the activation barrier to be calculated, either by a simple analytical model or a more realistic quantum computation. However, the model does not account for the applied overpotential, so it is mainly used to predict trends in the exchange current prefactor with microscopic properties, e.g. explaining why silver electrodeposition is so fast, despite its large solvation energy (as a result of close approach of the solvated ion facilitating ET).118
Building on ideas of Savéant,155,156 Koper and Voth extended Schmickler's adiabatic ET/IT model to account for bond-breaking electron transfer (BBET) between the reactant and the electrode, influenced by the overpotential.69 Similar to the earliest models of Gurney42 and Butler,18 they used Morse potentials in ξ for the bond-breaking interactions coupling the reactant electron to the electrode. They also postulated that the energy of the anti-bonding orbital was equal to the inner-sphere reorganization energy plus the experimental overpotential, εa = λ + η, for small overpotentials |η| ≪ λ. In this limit, the curved Tafel plot (characteristic of all ET theories) could be linearized to derive the charge transfer coefficient α as the degree of electron occupation of the anti-bonding orbital at the transition state,69 similar to Hush's original interpretation of α for adiabatic outer-sphere ET reactions.45 As noted in the Introduction, however, such ET theories are not able to explain the persistence of BV kinetics at higher potentials leading to Tafel's law.
In summary, since adiabatic ET models must take into account the molecular details of the electrode/electrolyte interface, they struggle to predict the charge transfer coefficient, let alone the full overpotential dependence of the reaction rate:
“The potential-energy surface will change when the electrode potential is varied; consequently the energy of activation will change too. These changes will depend on the structure of the double layer, so we cannot predict the transfer coefficient α unless we have a detailed model for the distribution of potential in the double layer.” – Schmickler and Santos (2010).25
From the perspective of CIET theory, it would indeed seem difficult to make any general predictions about the form of the reaction rate for strongly adiabatic ECIT, where Δe > λ ≫ βred/ox, since the electronic coupling overwhelms all other barriers and invalidates any use of transition state theory, but this is not the most common situation.
It is more typical for the IT free energies to be the largest in the system, βred/ox > Δe,λ,kBT, since they include energies of solvation-shell shedding and chemical-bond breaking and thus often exceed 1 eV. Chemisorption functions for ET, by contrast, are usually much smaller, with the ET rate transitioning from non-adiabatic to weakly adiabatic around Δe ≈ 1 meV and to strongly adiabatic for electrocatalysis around Δe ≈ 150 meV,154 which may exceed λ in some cases. Most systems are thus in the regime of ICET, already noted above in eqn (83), where the effect of adiabaticity is relatively small and only becomes important close to the transition state.
As shown in Fig. 14, whenever the linear approximations of the ξ-dependence of the diabatic free energy landscapes are valid, we expect BV kinetics to hold for adiabatic ICET, until a reaction-limited current is reached. Even for strongly adiabatic ICET with βred/ox ≫ Δe > λ, the same functional form of the ICET rate should hold, since the kinetics are dominated by slow classical IT in the diabatic states, except within Δe of the transition state, where the reduced and oxidized states create hybrid orbitals along the ξ axis to lower the effective barrier for fast adiabatic ET, as shown in Fig. 14(a) and (b). In contrast, for weakly adiabatic ICET (Fig. 7) or ECIT (Fig. 6), the red/ox hybridization occurs preferentially along the solvent reorganization coordinate, q, blurring the intersection of the Marcus parabolae. As long as the IT barriers are large, however, the main effect of adiabaticity is to lower the ICET activation barrier by Δe:
| |
| ΔGICET‡ ≈ α(1 − α)(λ + βred + βox) − Δe | (148) |
where
Δe is constant in the wide band approximation for a metal electrode. The adiabatic correction in
eqn (148) is valid as long as the overall barrier exceeds the thermal energy
in order to justify the use of classical transition state theory in the CIET derivation. We may expect a similar lowering of the IT barrier by
Δe to hold for weakly adiabatic ECIT,
eqn (72), as long as the corrected barrier is larger than the thermal energy.
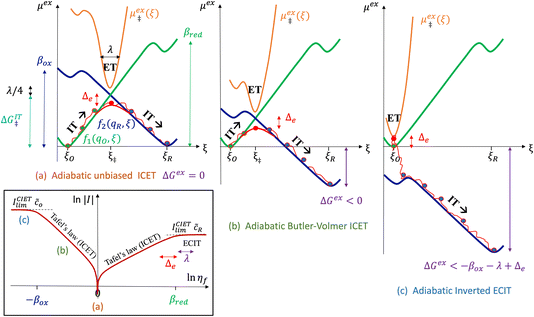 |
| | Fig. 14 Physics of strongly adiabatic ion-coupled electron transfer (ICET), where the chemisorption function (or electronic coupling) is larger than the reorganization energy and thermal energy, Δe > λ,kBT, but smaller than the ion-transfer free energies, Δe ≪ βred/ox. In normal adiabatic ICET (a) and (b), the transferring electron remains in one of the diabatic states during IT until thermal fluctuations along the coordinate ξ activate the reduced and oxidized states to within Δe of the Gurney–Volmer diabatic crossing, yielding Butler–Volmer kinetics of ICET. (In contrast, for weakly adiabatic ICET (Fig. 7) or ECIT (Fig. 6), the orbitals mainly hybridize along the reorganization coordinate q, as in adiabatic ET theory.) During adiabatic ICET, Tafel's law may hold over a wide range of formal overpotentials, where the linear approximations of the ξ-dependence of the IT diabatic states holds, as shown in (b). At large formal overpotentials, ηf < −βox − λ + Δe for reduction or ηf > βred + λ − Δe for oxidation, there is a transition to adiabatic Inverted ECIT shown in (c), which, for a metal electrode, leads to the universal limiting current dominated by barrierless transitions below the Fermi level. | |
As with nonadiabatic CIET, whenever barrierless transitions become energetically favorable, they will also dominate the response of a metallic electrode for adiabatic ICET. At large formal overpotentials, ηf < −βox − λ + Δe for reduction or ηf > βred + λ − Δe for oxidation, we thus also expect a transition from adiabatic ICET to Inverted ECIT shown in Fig. 14(c). For a metal electrode, this again leads to the universal limiting current. In the transition regime, the ICET barrier, eqn (148), vanishes over a range of formal overpotentials e|Δηf| ≈ Δe + λ, in order to first overcome the remaining IT barrier reduced by adiabaticity and as well as the reorganization energy required to achieve the dominant barrierless transition.
Recent progress in quantum electrochemistry has opened the possibility that ab initio calculations may soon be able to test these predictions and further develop the theory of adiabatic CIET to enable evaluation of its parameters from first principles. Chan and Nørskov proposed a simple approximation to convert from constant charge to constant potential for the electrode, by dividing the free energy along the reaction path into a chemical part and an electrostatic part, given by  , where the charge ΔQ can be obtained by density functional theory (DFT) and ΔV is the electrode potential relative to computational vacuum (on the other side of the electrolyte).157,158 Although this approach neglects the polarization of interfacial dipoles and various details of the electric double layers, it provides a means to compute the free energy landscape of adiabatic CIET as a function of electrode potential. In a “computational tour de force”,31 Kronberg and Laasonen recently used DFT-based constrained MD simulations to calculate the adiabatic free energy barrier versus applied potential for hydrogen evolution on a platinum electrode, the Volmer reaction on Pt(111), albeit with relatively large values compared to experiments.159 Over some range of electrode potentials at different surface coverages, the free energy barriers vary almost linearly with formal overpotential, which would be consistent with BV kinetics of ICET, and there are also quadratic terms, perhaps similar to those arising in the more general CIET theory.
, where the charge ΔQ can be obtained by density functional theory (DFT) and ΔV is the electrode potential relative to computational vacuum (on the other side of the electrolyte).157,158 Although this approach neglects the polarization of interfacial dipoles and various details of the electric double layers, it provides a means to compute the free energy landscape of adiabatic CIET as a function of electrode potential. In a “computational tour de force”,31 Kronberg and Laasonen recently used DFT-based constrained MD simulations to calculate the adiabatic free energy barrier versus applied potential for hydrogen evolution on a platinum electrode, the Volmer reaction on Pt(111), albeit with relatively large values compared to experiments.159 Over some range of electrode potentials at different surface coverages, the free energy barriers vary almost linearly with formal overpotential, which would be consistent with BV kinetics of ICET, and there are also quadratic terms, perhaps similar to those arising in the more general CIET theory.
10 Summary of CIET kinetics for metal electrodes
In this section, we summarize the key predictions of CIET theory for faradaic reaction rates at metal electrodes in wide-band approximation (ρe ≈ constant), which is the most relevant limit for electrochemical engineering. Based on our analysis, we propose to replace phenomenological BV kinetics, eqn (1)–(4), with one of the following approximations, which correspond to different ordering of the three characteristic energies in the model, βred,βox,λ > kBT. The theory was developed for non-adiabatic CIET, Δe ≪ kBT, but corrections for weakly adiabatic CIET are possible if the electronic coupling Δe is much smaller than at least one of three energies governing CIET (βred, βox and λ).
10.1 Butler–Volmer kinetics of ICET
Ion-coupled electron transfer (ICET) at a metal electrode, illustrated in Fig. 7, is the most important limit of the general CIET theory, since the free energies of ion transfer are larger than the other energies in the model for most faradaic reactions:| |
| βred/ox ≫ λ,e|ηf|,Δe,kBT (ICET) | (150) |
In the ICET regime, for formal overpotentials in the range,| |
−(![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox + ox + ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ) ≪ ) ≪ ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f ≪ f ≪ ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red + red + ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) , , | (151) |
the uniformly valid approximation of the CIET current at a metal electrode has the asymptotic form of the BV equation,| |
I = IICET0M(![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f)(e−α f)(e−α![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) − e(1−α) − e(1−α)![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) ) ) | (152) |
multiplied by the matching function, M(![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f), given by eqn (130)–(132), which imparts slight curvature to the Tafel plot controlled by λ. In most cases, one can set
f), given by eqn (130)–(132), which imparts slight curvature to the Tafel plot controlled by λ. In most cases, one can set 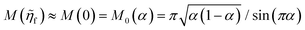 to recover the pure BV equation, which is exact in the limit of negligible reorganization energy, λ/βox/red → 0.
to recover the pure BV equation, which is exact in the limit of negligible reorganization energy, λ/βox/red → 0.
The charge-transfer coefficient is given by
| |
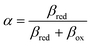 | (153) |
The parameters
βred and
βox are IT free energies, which generally depend on temperature. In contrast, the Marcus reorganization energy
λ has negligible temperature dependence. These are important predictions of CIET theory that can be tested experimentally.
The ICET exchange current (including the matching function) is given by
| |
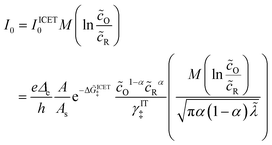 | (154) |
The ICET activation energy is
| |
| ΔGICET‡ = α(1 − α)(βred + βox + λ) − Δe | (155) |
| |
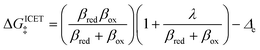 | (156) |
where we have added the simple correction for adiabatic ICET introduced above, which lowers the ICET barrier by
Δe and thus amplifies the reaction rate. Using
eqn (131) and
(132), the factor in parentheses in
eqn (154) can be replaced by
| |
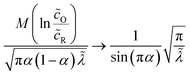 | (157) |
in the ICET limit,
λ/
βox/red → 0, consistent with
eqn (106).
10.2 Marcus kinetics of normal ECIT
As shown in Fig. 6, for rate-limiting Normal ECIT at large reorganization energies,| |
| λ ≫ βred/ox,|eηf|,Δe,kBT (Normal ECIT) | (158) |
over the range of formal overpotentials,the Faradaic current at a metal electrode can be approximated as| |
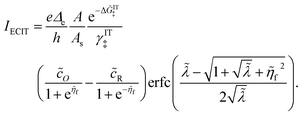 | (160) |
The IT energy barrier is generally defined as the mean of the diabatic IT free energies,| |
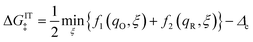 | (161) |
where the first term reduces to 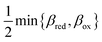 for the truncated linear approximation, eqn (118), and
for the truncated linear approximation, eqn (118), and 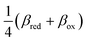 for the uniformly valid approximation of CIET kinetics, and the second term is a weakly adiabatic correction.
for the uniformly valid approximation of CIET kinetics, and the second term is a weakly adiabatic correction.
The exchange current is given by
| |
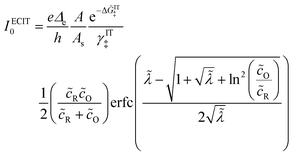 | (162) |
Note that we have set
M = 1 for the asymptotic limit,
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
≫
![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red/ox
red/ox, corresponding to ECIT. Considering the low-temperature expansion of
IECIT0, the total activation barrier at low overpotentials is given by
eqn (72), which is the symmetric case of
eqn (155) for
α = 1/2.
10.3 Reaction-limited current for inverted ECIT
In the limit of large overpotentials,| |
| e|ηf| ≫ βred/ox,λ,Δe,kBT (Inverted ECIT) | (163) |
a metal electrode will exhibit a constant reaction-limited current given by| |
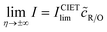 | (164) |
where| |
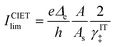 | (165) |
is the quantum-mechanical limiting current corresponding to barrierless nonadiabatic ECIT in the limit of weak electronic coupling, using Fermi's golden rule. Further developments in the theory of adiabatic CIET will be required to refine the prediction of the limiting current for more general situations, especially for electrocatalysis. However, we expect our theoretical framework of CIET to correctly predict the conditions for the breakdown of either MHC kinetics of Normal ECIT or BV kinetics of ICET, including Tafel's law, when the reaction passes to the Inverted ECIT regime.
10.4 Uniformly valid approximation for CIET
Whenever an experimental system is able to reach large overpotentials and probe the transition to reaction-limited current, we propose using the uniformly valid approximation of CIET kinetics, eqn (128)–(132). This may be the simplest possible analytical approximation that exactly reproduces all of the preceding limiting cases and smoothly transitions between them. It is strictly valid for nonadiabatic CIET with small electronic coupling, Δe ≪ kBT ≪ λ,βred/ox, but may also hold with barriers reduced by Δe for weakly adiabatic CIET, kBT < Δe ≪ λ,βred/ox and perhaps even strongly adiabatic ICET, kBT < λ < Δe ≪ βred/ox, as long as the classical IT barriers are large and dominate the reaction rate.
11 Application to lithium iron phosphate
In this section, we briefly illustrate the application of CIET theory to our motivating problem of lithium ion intercalation in LFP. For the reduction of a monovalent ion such as Li+ by intercalation into a solid electrode, we let ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R =
R = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) be the dimensionless intercalated ion concentration (or filling fraction) in the solid and
be the dimensionless intercalated ion concentration (or filling fraction) in the solid and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O =
O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) + be the dimensionless adsorbed surface concentration (or surface coverage) given by the adsorption isotherm, eqn (20). As noted above, the key requirement for ion intercalation is that the CIET transition state excludes one solid site, or equivalently, involves one vacancy, γIT‡ = (1 −
+ be the dimensionless adsorbed surface concentration (or surface coverage) given by the adsorption isotherm, eqn (20). As noted above, the key requirement for ion intercalation is that the CIET transition state excludes one solid site, or equivalently, involves one vacancy, γIT‡ = (1 − ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) )−1. From this theoretical perspective, we revisit the existing data for the rate dependence on overpotential, temperature and solid concentration.
)−1. From this theoretical perspective, we revisit the existing data for the rate dependence on overpotential, temperature and solid concentration.
11.1 Overpotential and temperature dependence
First, we consider the limiting case of Normal ECIT. As described in the introduction, CIET theory was born out of the hypothesis that ET from a metal coating (or surface contact) could limit the rate of ion intercalation in a poorly conducting solid electrode, such as LFP.63 By interpreting the non-monotonic chronoamperometry data for LFP porous electrodes (Fig. 4) using a statistical model of reaction-limited phase transformations,160 Bai and Bazant63 constructed Tafel plots (Fig. 3) for the rate constants for LFP intercalation versus overpotential (averaging over the microscopic concentration dependence) and found excellent agreement with MHC kinetics of ET (using the original integral form87 just before the analytical approximation of Zeng et al.60 became available). As shown in Fig. 3(b) and 15(a), the Tafel data over a wide range of overpotentials and three different temperatures was shown to fit the MHC equation with a single value of the reorganization energy, λ = 214 ± 1 meV (![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 8.3 at room temperature) and independently fitted prefactors for each branch of Tafel data, shown in Fig. 15(b). The small uncertainty (0.5%) in the fitted reorganization energy indicates that the overpotential dependence of ECIT for a metal surface, eqn (160), captures the shape of these Tafel curves very well. As noted by the authors, the fact that all of the Tafel curvatures can be accurately fitted (with 0.5% uncertainty) by a single, temperature-independent reorganization energy provides strong support for the hypothesis of ET limitation in these experiments. In contrast, any fitted series resistances, which are routinely invoked to curve Tafel plots with BV kinetics,88 must be temperature dependent, if they are to represent either ionic or electronic transport processes.
= 8.3 at room temperature) and independently fitted prefactors for each branch of Tafel data, shown in Fig. 15(b). The small uncertainty (0.5%) in the fitted reorganization energy indicates that the overpotential dependence of ECIT for a metal surface, eqn (160), captures the shape of these Tafel curves very well. As noted by the authors, the fact that all of the Tafel curvatures can be accurately fitted (with 0.5% uncertainty) by a single, temperature-independent reorganization energy provides strong support for the hypothesis of ET limitation in these experiments. In contrast, any fitted series resistances, which are routinely invoked to curve Tafel plots with BV kinetics,88 must be temperature dependent, if they are to represent either ionic or electronic transport processes.
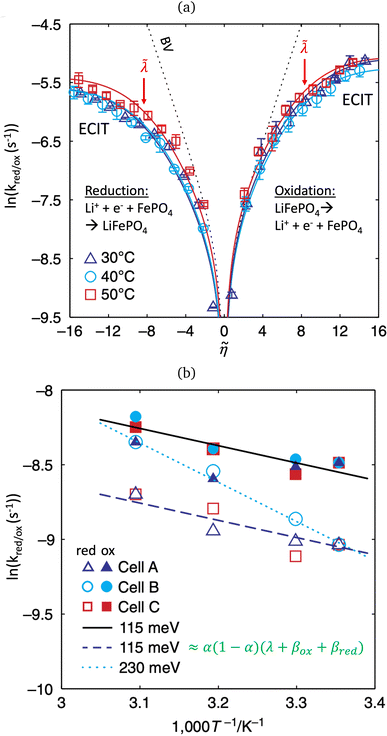 |
| | Fig. 15 Quantitative evidence for LFP intercalation by ECIT. (a) Tafel plots of rate constants, kred/ox, measured at different temperatures from the population dynamics of phase separation (assuming reaction limitation) and fitted to the MHC equation for ECIT (solid lines) with a single value of the reorganization energy, λ = 214 ± 1 meV and independently fitted prefactors for each Tafel branch. (b) Arrhenius plots of kred/ox revealing activation energies consistent with the prediction of nonadiabatic CIET theory at low overpotentials. [Adapted from Bai and Bazant (2014).63] | |
Further support for the ECIT hypothesis comes from the temperature dependence, shown in Fig. 15(b). Bai and Bazant63 noted that the observed activation barriers for LFP intercalation in the range 115–230 meV were much larger than the Marcus prediction, λ/4 = 53.5 meV for MHC kinetics. CIET theory is now able to attribute this discrepancy to the additional barrier ΔGIT‡ for ion transfer.103 In the truncated linear approximation, the general formula for the IT barrier in ECIT, eqn (161), implies βmin = min{βred ,βox} = 2ΔGIT‡ = 123–353 meV, where we assume weak electronic coupling (Δe ≪ λ,βred/ox) for nonadiabatic ECIT. The best fitting activation energy barrier (115 meV) corresponds to an ion transfer energy, βmin = 123 meV, which is indeed much smaller than the reorganization energy, λ = 214 meV, obtained from the Tafel data, consistent with the hypothesis of ECIT. Even the highest activation energy (230 meV) would imply βmin ≈ λ, so we conclude that LFP intercalation kinetics in the original experiments63 were consistent with CIET under at least partial ET limitation, λ ≥ βred/ox.
Despite this consistent theoretical interpretation, the experimental data in Fig. 15 deviates from symmetric ECIT kinetics, eqn (67), since the rate constant for oxidation (Li+ extraction) is somewhat larger than that of reduction (Li+ insertion) by roughly a factor of e0.5 = 1.65. There could be several reasons for the small, observed asymmetry. The diabatic free energy landscapes, eqn (47) and (48), could have different force constants, kO and kR, approximated by the generalized AMH model of asymmetric ECIT, eqn (82). Alternatively, we could assume symmetric ET, kO = kR = k, and shift the formal overpotential by Δ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) = Δln(
= Δln(![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) +/
+/![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ) ≈ 1, which would imply a larger surface coverage
) ≈ 1, which would imply a larger surface coverage![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) + by a factor of e ≈ 2.7 for oxidation versus reduction, assuming the slowest dynamics occurs for
+ by a factor of e ≈ 2.7 for oxidation versus reduction, assuming the slowest dynamics occurs for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) → 1 (since concentrations were not measured). Both models would slightly distort the excellent fit of the Tafel plots with MHC kinetics.
→ 1 (since concentrations were not measured). Both models would slightly distort the excellent fit of the Tafel plots with MHC kinetics.
Next, we consider the ICET limit of the theory. Although the Tafel data in Fig. 15 is well fitted by MHC kinetics of ECIT, another study of LFP intercalation kinetics by Heubner, Schneider and Michaelis88 based on nonlinear impedance spectroscopy found good agreement with nearly symmetric BV kinetics (α = 0.55) up to 200 meV overpotentials, after subtracting various series resistances and neglecting any concentration heterogeneity from phase separation.88 These experiments could also be consistent with CIET theory in the ICET regime, if βox > βred ≫ 200 meV ≫ λ, provided that the nonlinear current pulses are large enough to suppress phase separation by driven auto-inhibitory reactions.82,105,106 Unfortunately, temperature dependence was not measured, so we cannot perform this consistency check. Using eqn (155), we can at least estimate a consistent lower bound on the non-adiabatic ICET activation barrier, ΔGICET‡ ≫ (200 meV)/2 + λ/4, which could fall in the range of activation energies from Fig. 15(b) assuming a small reorganization energy, λ ≪ 200 meV, theoretically consistent with the ICET hypothesis. It is possible to have two different LFP electrodes exhibit different regimes of CIET kinetics, e.g. if the carbon coating and surface roughness are different, and we shall see that both ICET and ECIT lead to similar solid concentration dependence.
Regardless whether ET or IT is rate limiting, further evidence in favor of the general CIET theory is provided by the values of the inferred parameters, λ and βred/ox, which are quantitatively consistent with microscopic theories of charge transfer. In support of the ECIT hypothesis, the original paper noted that the fitted reorganization energy, λ = 214 meV, is identical to the Marcus outer-sphere value calculated from the dielectric properties and crystal structure of LFP,63 according to the reaction mechanism in Fig. 3(a). Here, we also infer the IT free energies, βmin = 123–353 meV for ECIT or βmin > 200 meV for ICIT, which are comparable to ab initio calculations of the diffusion barriers for Li+/e− polaron hopping in the bulk LFP (200–300 meV)161,162 as well as the (adiabatic) oxidation barriers to extract Li+ from charge-stabilized surface sites (150–200 meV).163 The fact that surface modification of LFP by sulfur or nitrogen anions lowers the calculated energy barriers for IT, while also exhibiting faster charge-transfer kinetics in experiments,163 also supports the hypothesis that CIET is rate limiting.
11.2 Solid concentration dependence
A major challenge in studying reaction kinetics in LFP is its strong tendency to separate into stable phases of high and low lithium ion concentration,24,90,106 which makes it impossible to know the active area and surface concentration profile in order to interpret electrochemical measurements quantitatively. Experiments are further confounded by reaction heterogeneities associated with fast and slow regions on the surface,106e.g. due to variations in surface coatings of active materials. These effects can only be unraveled by direct imaging of the local surface concentration under driven reactions and learning optimal models to fit the data.
Recently, H. Zhao et al. overcame this challenge by learning the physics of heterogeneous intercalation kinetics in LFP nanoparticles directly from a massive dataset from in operando scanning tunneling X-ray microscopy (STXM) images,105 building on the earlier experiments of Lim et al.106 Using inverse learning methods (PDE-constrained optimization, Markov-chain Monte Carlo and Bayesian inference), the unknown constitutive relations were obtained from the STXM data for a general modeling framework based on electrochemical nonequilibrium thermodynamics,24 which had previously been applied to LFP nanoparticles using classical models for reaction kinetics and phase separation dynamics.84,93,94,102 The learned model was able to reproduce over 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pixels of X-ray image data from 63 nanoparticles, each cycled through complete reduction (Li+ insertion) and oxidation (Li+ extraction), with only 7% global error across all pixels. Since the intercalation kinetics of carbon-coated LFP nanoparticles are famously fast along the b-axis of the LFP crystal exposed by the active (010) facet of the platelets,165,166 the experiments were limited to small overpotentials, on the order of several kBT/e. As such, the inverse learning process could not discern the overpotential dependence (assumed to be Butler–Volmer), but it was able to accurately extract the concentration dependence. Nanoscale spatial heterogeneities in the reaction rate constant were also learned from the STXM images and correlated with variations in carbon coating thickness, thereby enabling precise measurement of the underlying intercalation reaction kinetics.
000 pixels of X-ray image data from 63 nanoparticles, each cycled through complete reduction (Li+ insertion) and oxidation (Li+ extraction), with only 7% global error across all pixels. Since the intercalation kinetics of carbon-coated LFP nanoparticles are famously fast along the b-axis of the LFP crystal exposed by the active (010) facet of the platelets,165,166 the experiments were limited to small overpotentials, on the order of several kBT/e. As such, the inverse learning process could not discern the overpotential dependence (assumed to be Butler–Volmer), but it was able to accurately extract the concentration dependence. Nanoscale spatial heterogeneities in the reaction rate constant were also learned from the STXM images and correlated with variations in carbon coating thickness, thereby enabling precise measurement of the underlying intercalation reaction kinetics.
The concentration dependence of the exchange current learned from the X-ray data is shown in Fig. 16 and compared to theoretical predictions. In a striking validation of the theory, the CIET exchange current versus concentration predicts the learned asymmetric profile to within the experimental error for all of the parameters estimated from the electrochemical data above. The ECIT limit, eqn (162), which provides the best fit of the Tafel plots in Fig. 15, also fits the exchange current very well for most choices of concentrations, as illustrated by the values ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) + = 0.3 and
+ = 0.3 and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) → 1 for the slowest reduction reaction dominating the transient response. The ICET formula, eqn (154), almost perfectly fits the learned kinetics at high concentration using the same value of α = 0.4 inferred above from electrochemical data, while symmetic ICET with α = 0.5 provides an even better overall fit. Overall, the analysis supports the picture of lithium intercalation in carbon-coated LFP as a process limited by comparable barriers for ET and IT.
→ 1 for the slowest reduction reaction dominating the transient response. The ICET formula, eqn (154), almost perfectly fits the learned kinetics at high concentration using the same value of α = 0.4 inferred above from electrochemical data, while symmetic ICET with α = 0.5 provides an even better overall fit. Overall, the analysis supports the picture of lithium intercalation in carbon-coated LFP as a process limited by comparable barriers for ET and IT.
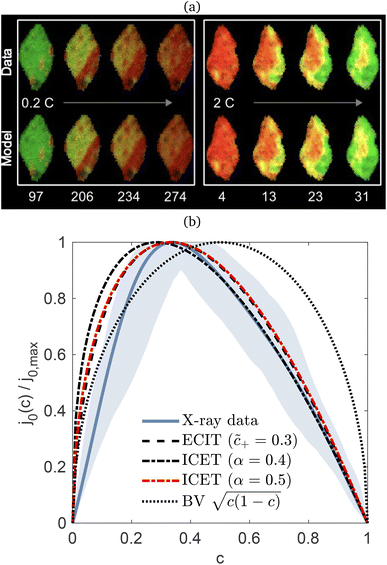 |
| | Fig. 16 Learning heterogeneous reaction kinetics of CIET from operando scanning tunneling X-ray microscopy (STXM)106 by solving inverse problems for the best model that fits all pixels of the X-ray image data.105 (a) Experimental images (top row) of LFP platelet nanoparticles undergoing driven phase transformations at different currents (0.2C and 2C with times shown below in minutes), compared with the learned model simulations with BV reaction kinetics (bottom row). (b) The normalized exchange current density profile learned from the X-ray images is shown as the solid blue curve with shaded blue range of uncertainty versus inserted lithium filling fraction, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = c, and compared with the theoretical predictions for ECIT, eqn (162), and ICET, eqn (154), using parameters that are also consistent with the Tafel data in Fig. 15. For comparison, the standard BV model with R = c, and compared with the theoretical predictions for ECIT, eqn (162), and ICET, eqn (154), using parameters that are also consistent with the Tafel data in Fig. 15. For comparison, the standard BV model with 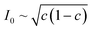 widely used in Li-ion battery simulations9,10,164 is not consistent with the experimental data. [Figure courtesy of Hongbo Zhao, adapted from Zhao et al. (2023).105] widely used in Li-ion battery simulations9,10,164 is not consistent with the experimental data. [Figure courtesy of Hongbo Zhao, adapted from Zhao et al. (2023).105] | |
An important general prediction of our CIET theory of ion intercalation kinetics is that the exchange current is proportional to the ion vacancy concentration in the electrode, Ĩ0 ∝ (1 − ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ). This linear trend is seen in both ECIT and ICET formulae, in excellent agreement with the X-ray data in Fig. 16. This prediction holds regardless of whether ET or IT is rate-limiting because it comes from the universal activity coefficient of the IT transition state for intercalation, which must capture the exclusion of one site,24, (γIT‡)−1 = 1 −
). This linear trend is seen in both ECIT and ICET formulae, in excellent agreement with the X-ray data in Fig. 16. This prediction holds regardless of whether ET or IT is rate-limiting because it comes from the universal activity coefficient of the IT transition state for intercalation, which must capture the exclusion of one site,24, (γIT‡)−1 = 1 − ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . In contrast, the standard empirical model of intercalation kinetics, used in popular porous electrode theory models and battery simulation software, postulates
. In contrast, the standard empirical model of intercalation kinetics, used in popular porous electrode theory models and battery simulation software, postulates 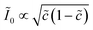 , which scales with the square root of the vacancy concentration.9,164 This model is inconsistent with the X-ray data, as well as the fundamental theory of CIET.
, which scales with the square root of the vacancy concentration.9,164 This model is inconsistent with the X-ray data, as well as the fundamental theory of CIET.
12 Conclusion and outlook
In summary, we have developed a theoretical framework of coupled ion–electron transfer (CIET) integrating the quantum physics of electron transfer (ET) with the non-equilibrium thermodynamics of ion transfer (IT). The theory can be applied to arbitrary diabatic free energy landscapes for the donor and acceptor states, but its scaling is controlled by six characteristic energies: the excess free energy of reaction, ΔGex, the thermal energy, kBT, the donor–acceptor electronic coupling, HDA, the Marcus reorganization energy of ET, λ, and the free energies of IT, βox and βred, in the donor and acceptor states, prior to oxidation and reduction, respectively.
Although CIET theory can be applied to chemical reactions in isolated molecules or bulk materials, our focus has been on faradaic reactions at electrode/electrolyte interfaces, where the reaction rate is controlled by the applied (formal) overpotential ηf. The thermodynamic driving force felt by electrons of energy ε relative to the Fermi level εF is given by ΔGex = eηf + εF − ε. For semiconductor electrodes, there are additional energy scales having to do with the band structure, but in the usual case of metal electrodes, we make the wide-band approximation and replace HDA with the chemisorption function, Δe. The physics of CIET are set by the relative magnitudes of the six characteristic energies, eηf, kBT, Δe, λ, βred and βox. The theory assumes thermally activated transitions (kBT ≪ λ,βred,ηox) and nonadiabatic ET (Δe ≪ kBT), but does not constrain the other parameters. For weakly adiabatic CIET (Δe ≪ λ,βred,βox), activation energies are effectively lowered by Δe.
For metal electrodes, we considered three asymptotic limits leading to simple rate expressions (summarized in Section 10), each corresponding to a distinct reaction mechanism. First, we showed that the original CIET theory103 tacitly assumed ET-limited reactions at small overpotentials (ηf,βred,βox ≪ λ), leading to normal Marcus kinetics of electron-coupled ion transfer (Normal ECIT). Second, we considered IT-limited reactions (λ ≪ βred, βox) and derived the Butler–Volmer (BV) equation as the fundamental rate expression for ion-coupled electron transfer (ICET). This appears to be the first quantum mechanical derivation of BV kinetics, which reproduces Tafel's limiting law over a wide range of overpotentials (−βox ≪ eηf ≪ βred). The ICET formula also connects the phenomenological BV parameters, α and I0, to microscopic properties of the electrode/electrolyte interface, which can be measured experimentally or predicted by quantum computation. The theory also predicts that the transferring electron energy in ICET is selected from a fat-tailed Meixner (skewed hyperbolic secant) distribution, rather than the Gaussian distribution of ECIT from Gerischer–Marcus theory. These electron energy distributions may find applications in describing asymmetric XPS and AES line shapes. Third, we predicted a universal transition to inverted Marcus kinetics of ECIT (Inverted ECIT) for large overpotentials (ηf ≪ − βox or ηf ≫ βred). For a metal electrode, the possibility of barrierless transitions during Inverted ECIT leads to a quantum-mechanical reaction-limited current with vanishing activation energy. Finally, we derived uniformly valid asymptotic approximations that smoothly interpolate between these three regimes, which are useful for intermediate cases where λ ≈ βred ≈ βox.
One such intermediate case appears to be lithium intercalation in lithium iron phosphate (LFP), a popular cathode material for Li-ion batteries. We revisited the original data revealing ET rate limitation in LFP (λ ≈ 215 meV)63 and concluded that there was indeed a somewhat smaller barrier for IT in those experiments (βmin ≈ 123 meV). If the kinetics lie closer to ICET than ECIT, however, due to different interfacial properties, this could help explain a subsequent study consistent with Butler–Volmer kinetics up to moderate overpotentials.88 The key to this analysis, which could be replicated in other studies, was to seek consistency between theoretical predictions of both overpotential dependence (Tafel plots) and temperature dependence (Arrhenius plots) of the CIET rate. It was also compelling to confirm that the parameters are consistent with barriers predicted by Marcus theory, as well as quantum calculations.
Since it is difficult to isolate faradaic currents at large overpotentials without causing side reactions or transport limitation, it is important to test other predictions of the model. Besides temperature dependence, the model makes falsifiable predictions about concentration dependence, in particular, that the intercalation rate vanishes linearly with vacancy concentration in the solid at high filling fractions. For LFP, the predicted concentration profiles of both ICET and ECIT exchange currents are in excellent agreement with X-ray image-based learning of reaction kinetics,105 lending further support to the hypothesis of CIET rate limitation for ion intercalation.
The new theory may find applications to other faradaic reactions in electrochemical engineering, such as electrodeposition and electrocatalysis. Since LFP is an electrical insulator exhibiting polaronic conduction of ion–electron pairs, it makes sense that ET from a metallic surface contact could contribute to CIET rate limitation. The situation is similar to metal electrodeposition from a ceramic solid electrolyte, which was recently shown by Williams et al. to be consistent with CIET theory100 (in the ECIT limit) for sodium plating from NaSICON solid electrolyte in solid-state Na-ion batteries.167 In contrast, most other Li-ion battery active materials, such as graphite anodes and transition metal oxide cathodes, are themselves metallic, and thus not as likely to exhibit ET rate limitation. Future studies of intercalation kinetics in these materials should also consider BV kinetics of ICET and test the predicted dependence on temperature, concentrations, and interfacial properties. The general features of limiting current and linear dependence on vacancy concentration may be quite robust, which may explain why ECIT theory helps explain the onset of lithium plating upon lattice saturation in graphite.98,168 A recent study of lithium electrodeposition from liquid electrolytes by Boyle et al. also showed evidence of ET limitation via curved Tafel plots measured with microelectrodes,107 but the data may be more consistent with ICET, which should explain the observed electrolyte dependence of the activation barrier better than my earlier theory based on ET limitation.24
Electrocatalysis normally involves strong electronic coupling leading to adiabatic ET, but we noted here that CIET theory may still apply if Δe ≪ βred/ox,λ. In a recent study of Bayesian model selection from experimental Tafel data for CO2 reduction to CO on gold surfaces in aqueous electrolytes, out of many models, the best fit was found by MHC kinetics of ECIT.169 Electrolysis of water and other electrocatalytic reactions also provide some of the clearest examples of Tafel's law,62 which can now be explained by adiabatic or nonadiabatic ICET theory in the limit of large IT free energies. Williams et al. recently generalized nonadiabatic ECIT theory for protons tunneling between quantized energy levels in response to slow ET, a reaction mechanism we would call "electron-coupled proton transfer" (ECPT).110 The theory accounts for electrostatic surface potentials and adsorbed proton dipole moments on mixed proton–electron conductor surfaces, such as Ni/galadonium-doped ceria, and predicts ECPT reaction rates of water electrolysis and hydrogen evolution in solid-oxide fuel cells (SOFC).110
Our theory also provides a useful framework for multiscale computation, to connect atomistic properties of electrode/electrolyte interfaces to faradaic reaction kinetics in electrochemical systems. Constrained density functional theory (CDFT),39 which has already been used to predict ET kinetics using Marcus theory, would be the ideal method to calculate ab initio diabatic energy surfaces38 for use in CIET theory. The advantage of the theory is its simplicity, in identifying a few key parameters and providing a convenient formula, e.g. for use in coarse-grained engineering models.104
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work builds on over a decade of research on ET/CIET kinetics in batteries with key contributions by Dimitrios Fraggedakis, Peng Bai, Yi Zeng, Nicholas Williams, Raymond Smith, Michael McEldrew, Yamini Krishnan, and Hongbo Zhao primarily funded by Toyota Research Institute via the D3BATT Center for Data-Driven Design of Rechargeable Batteries. The recent advances sprang from a collaboration funded by Shell with Yirui Zhang, Shakul Pathak, Armando Neto, Cristina Grosu and Yang Shao-Horn, who also provided useful comments on the manuscript. The author thanks Shakul for proofreading the equations, as well as Gisela Scott and the editors accommodating some revisions after the conference.
Notes and references
-
E. Kaxiras, Atomic and electronic structure of solids, 2003 Search PubMed.
- A. Urban, D.-H. Seo and G. Ceder, npj Comput. Mater., 2016, 2, 16002 CrossRef CAS.
- D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell Jr, B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940–7995 CrossRef CAS PubMed.
- L. Scalfi, M. Salanne and B. Rotenberg, Annu. Rev. Phys. Chem., 2021, 72, 189–212 CrossRef CAS PubMed.
- V. G. Levich and C. W. Tobias, J. Electrochem. Soc., 1963, 110, 251C CrossRef.
-
A. J. Bard and L. R. Faulkner, Electrochemical Methods, J. Wiley & Sons, Inc., New York, NY, 2001 Search PubMed.
-
J. O. Bockris, A. K. N. Reddy and M. E. Gamboa-Aldeco, Modern electrochemistry 2B: electrodics in chemistry, engineering, biology and environmental science, Springer Science & Business Media, 1998, vol. 2 Search PubMed.
-
J. O. Bockris, B. E. Conway and R. E. White, Modern aspects of electrochemistry, Springer Science & Business Media, 1992, vol. 22 Search PubMed.
-
J. Newman and N. P. Balsara, Electrochemical systems, John Wiley & Sons, 2021 Search PubMed.
-
T. F. Fuller and J. N. Harb, Electrochemical engineering, John Wiley & Sons, 2018 Search PubMed.
- J. A. V. Butler, Trans. Faraday Soc., 1932, 28, 379–382 RSC.
- T. Erdey-Grúz and M. Volmer, Z. Phys. Chem., 1931, 157A, 165 CrossRef.
- J. Tafel, Z. Phys. Chem., 1905, 50, 641–712 CrossRef CAS.
- G. Burstein, Corros. Sci., 2005, 47, 2858–2870 CrossRef CAS.
- J. A. V. Butler, Trans. Faraday Soc., 1924, 19, 659–665 RSC.
- J. A. V. Butler, Trans. Faraday Soc., 1924, 19, 729–733 RSC.
- J. A. V. Butler, Trans. Faraday Soc., 1924, 19, 734–739 RSC.
- J. A. V. Butler, Proc. R. Soc. London, Ser. A, 1936, 157, 423–433 CAS.
- F. P. Bowden, Proc. R. Soc. London, Ser. A, 1929, 125, 446–462 CAS.
- T. Erdey-Grúz and M. Volmer, Z. Phys. Chem., 1930, 150, 203–213 CrossRef.
-
R. G. Compton and C. E. Banks, Understanding voltammetry, World Scientific, 2018 Search PubMed.
- A. Frumkin, Z. Phys. Chem., 1933, 164A, 121–133 CrossRef.
- P. Biesheuvel, M. Van Soestbergen and M. Z. Bazant, Electrochim. Acta, 2009, 54, 4857–4871 CrossRef CAS.
- M. Z. Bazant, Acc. Chem. Res., 2013, 46, 1144–1160 CrossRef CAS PubMed.
-
W. Schmickler and E. Santos, Interfacial electrochemistry, Springer Science & Business Media, 2010 Search PubMed.
-
A. M. Kuznetsov and J. Ulstrup, Electron Transfer in Chemistry and Biology: An Introduction to the Theory, Wiley, 1999 Search PubMed.
- V. Levich and R. Dogonadze, Dokl. Akad. Nauk SSSR, 1959, 124, 123–126 CAS.
- M. Z. Bazant, K. T. Chu and B. J. Bayly, SIAM J. Appl. Math., 2005, 65, 1463–1484 CrossRef CAS.
- P. Biesheuvel, M. van Soestbergen and M. Bazant, Electrochim. Acta, 2009, 54, 4857–4871 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- E. Santos and W. Schmickler, Chem. Rev., 2022, 122, 10581–10598 CrossRef CAS PubMed.
- R. R. Nazmutdinov, M. D. Bronshtein, T. T. Zinkicheva and D. V. Glukhov, Int. J. Quantum Chem., 2016, 116, 189–201 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. Marcus, J. Chem. Phys., 1957, 26, 867–871 CrossRef CAS.
- R. Marcus, J. Chem. Phys., 1957, 26, 872–877 CrossRef CAS.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- T. Van Voorhis, T. Kowalczyk, B. Kaduk, L.-P. Wang, C.-L. Cheng and Q. Wu, Annu. Rev. Phys. Chem., 2010, 61, 149–170 CrossRef CAS PubMed.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321–370 CrossRef CAS PubMed.
- J. Weiss, Proc. R. Soc. London, Ser. A, 1954, 222, 128–141 CAS.
- R. A. Marcus, Discuss. Faraday Soc., 1960, 29, 21–31 RSC.
- R. W. Gurney, Proc. R. Soc. London, Ser. A, 1931, 134, 137–154 Search PubMed.
- M. Chatenet, B. G. Pollet, D. R. Dekel, F. Dionigi, J. Deseure, P. Millet, R. D. Braatz, M. Z. Bazant, M. Eikerling and I. Staffell,
et al.
, Chem. Soc. Rev., 2022, 51, 4583–4762 RSC.
- N. S. Hush, Ber. Bunsenges. Phys. Chem., 1957, 61, 734–738 CAS.
- N. S. Hush, J. Chem. Phys., 1958, 28, 962–972 CrossRef CAS.
- N. S. Hush, Trans. Faraday Soc., 1961, 57, 557–580 RSC.
-
V. G. Levich, in Advances in Electrochemistry and Electrochemical Engineering, ed. P. Delahay and C. W. Tobias, Interscience, New York, 1966, vol. 4, pp. 249–371 Search PubMed.
- R. R. Dogonadze and Y. A. Chizmadzhev, Dokl. Akad. Nauk SSSR, 1962, 145, 848–851 Search PubMed.
- R. R. Dogonadze, A. M. Kuznetsov and A. A. Chernenko, Russ. Chem. Rev., 1965, 34, 759–775 CrossRef.
- R. Dogonadze, A. Kuznetsov and M. Vorotyntsev, J. Electroanal. Chem. Interfacial Electrochem., 1970, 25, A17–A19 CrossRef.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679 CrossRef CAS.
- R. Marcus, J. Chem. Soc., Faraday Trans., 1996, 92, 3905–3908 RSC.
- D. F. Calef and P. G. Wolynes, J. Phys. Chem., 1983, 87, 3387–3400 CrossRef CAS.
- D. F. Calef and P. G. Wolynes, J. Chem. Phys., 1983, 78, 470–482 CrossRef CAS.
- D. V. Matyushov and G. A. Voth, J. Chem. Phys., 2000, 113, 5413–5424 CrossRef CAS.
- D. V. Matyushov, J. Chem. Phys., 2009, 130, 234704 CrossRef PubMed.
- E. Laborda, M. C. Henstridge and R. G. Compton, J. Electroanal. Chem., 2012, 667, 48–53 CrossRef CAS.
- E. Laborda, M. C. Henstridge, C. Batchelor-McAuley and R. G. Compton, Chem. Soc. Rev., 2013, 42, 4894–4905 RSC.
-
J. Newman and K. E. Thomas-Alyea, Electrochemical Systems, John Wiley and Sons, Hoboken, New Jersey, 3rd edn, 2004 Search PubMed.
- Y. Zeng, R. B. Smith, P. Bai and M. Z. Bazant, J. Electroanal. Chem., 2014, 735, 77–83 CrossRef CAS.
- Y. Zeng, P. Bai, R. B. Smith and M. Z. Bazant, J. Electroanal. Chem., 2015, 748, 52–57 CrossRef CAS.
- S. U. Khan and J. O. Bockris, J. Phys. Chem., 1983, 87, 2599–2603 CrossRef CAS.
- P. Bai and M. Z. Bazant, Nat. Commun., 2014, 5, 3585 CrossRef PubMed.
- J. M. Savéant, J. Am. Chem. Soc., 2008, 130, 4732–4741 CrossRef PubMed.
- R. Cukier, J. Phys. Chem., 1994, 98, 2377–2381 CrossRef CAS.
- R. I. Cukier and D. G. Nocera, Annu. Rev. Phys. Chem., 1998, 49, 337–369 CrossRef CAS PubMed.
- W. Schmickler, Chem. Phys. Lett., 1995, 237, 152–160 CrossRef CAS.
- W. Schmickler, Electrochim. Acta, 1996, 41, 2329–2338 CrossRef CAS.
- M. T. Koper and G. A. Voth, Chem. Phys. Lett., 1998, 282, 100–106 CrossRef CAS.
- C. Hartnig and M. T. Koper, J. Am. Chem. Soc., 2003, 125, 9840–9845 CrossRef CAS PubMed.
- S. Hammes-Schiffer, Acc. Chem. Res., 2001, 34, 273–281 CrossRef CAS PubMed.
- M. H. V. Huynh and T. J. Meyer, Chem. Rev., 2007, 107, 5004–5064 CrossRef CAS PubMed.
- E. Santos, K. Pötting and W. Schmickler, Faraday Discuss., 2009, 140, 209–218 RSC.
- E. Santos, A. Lundin, K. Pötting, P. Quaino and W. Schmickler, Phys. Rev. B, 2009, 79, 1–10 CrossRef.
- S. Y. Reece and D. G. Nocera, Annu. Rev. Biochem., 2009, 78, 673–699 CrossRef CAS PubMed.
- S. Hammes-Schiffer and A. V. Soudackov, J. Phys. Chem. B, 2008, 112, 14108–14123 CrossRef CAS PubMed.
- S. Horvath, L. E. Fernandez, A. V. Soudackov and S. Hammes-Schiffer, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15663–15668 CrossRef CAS PubMed.
- M. M. Melander, J. Electrochem. Soc., 2020, 167, 116518 CrossRef CAS.
- J.-M. Savéant, Annu. Rev. Anal. Chem., 2014, 7, 537–560 CrossRef PubMed.
- S. Hammes-Schiffer, Acc. Chem. Res., 2018, 51, 1975–1983 CrossRef CAS PubMed.
- G. A. Parada, Z. K. Goldsmith, S. Kolmar, B. P. Rimgard, B. Q. Mercado, L. Hammarström, S. Hammes-Schiffer and J. M. Mayer, Science, 2019, 364, 471–475 CrossRef CAS PubMed.
- M. Z. Bazant, Faraday Discuss., 2017, 199, 423–463 RSC.
- K. Singh, H. Bouwmeester, L. de Smet, M. Bazant and P. Biesheuvel, Phys. Rev. Appl., 2018, 9, 064036 CrossRef CAS.
- P. Bai, D. A. Cogswell and M. Z. Bazant, Nano Lett., 2011, 11, 4890–4896 CrossRef CAS PubMed.
- M. C. Henstridge, C. Batchelor-McAuley, R. Gusmão and R. G. Compton, Chem. Phys. Lett., 2011, 517, 108–112 CrossRef CAS.
- R. Kurchin and V. Viswanathan, J. Chem. Phys., 2020, 153, 134706 CrossRef CAS PubMed.
- C. E. Chidsey, Science, 1991, 251, 919–922 CrossRef CAS PubMed.
- C. Heubner, M. Schneider and A. Michaelis, J. Power Sources, 2015, 288, 115–120 CrossRef CAS.
- W. Dreyer, J. Jamnik, C. Guhlke, R. Huth, J. Moškon and M. Gaberšček, Nat. Mater., 2010, 9, 448–453 CrossRef CAS PubMed.
- T. R. Ferguson and M. Z. Bazant, Electrochim. Acta, 2014, 146, 89–97 CrossRef CAS.
- L. Li, Y.-c. K. Chen-Wiegart, J. Wang, P. Gao, Q. Ding, Y.-S. Yu, F. Wang, J. Cabana, J. Wang and S. Jin, Nat. Commun., 2015, 6, 6883 CrossRef CAS PubMed.
- G. K. Singh, G. Ceder and M. Z. Bazant, Electrochim. Acta, 2008, 53, 7599–7613 CrossRef CAS.
- D. A. Cogswell and M. Z. Bazant, ACS Nano, 2012, 6, 2215–2225 CrossRef CAS PubMed.
- D. A. Cogswell and M. Z. Bazant, Nano Lett., 2013, 13, 3036–3041 CrossRef CAS PubMed.
- B. Mamedov, J. Math. Chem., 2013, 51, 2699–2703 CrossRef CAS.
- K. B. Oldham and J. C. Myland, J. Electroanal. Chem., 2011, 655, 65–72 CrossRef CAS.
- R. B. Smith, E. Khoo and M. Z. Bazant, J. Phys. Chem. C, 2017, 121, 12505–12523 CrossRef CAS.
- T. Gao, Y. Han, D. Fraggedakis, S. Das, T. Zhou, C.-N. Yeh, S. Xu, W. C. Chueh, J. Li and M. Z. Bazant, Joule, 2021, 5, 393–414 CrossRef CAS.
- D. Zhuang and M. Z. Bazant, J. Electrochem. Soc., 2022, 169, 100536 CrossRef CAS.
- N. J. Williams, E. Quérel, I. D. Seymour, S. J. Skinner and A. Aguadero, Chem. Mater., 2023, 35, 863–869 CrossRef CAS PubMed.
- D. Fraggedakis and M. Z. Bazant, J. Chem. Phys., 2020, 152, 184703 CrossRef CAS PubMed.
- D. A. Cogswell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 011301(R) CrossRef PubMed.
- D. Fraggedakis, M. McEldrew, R. B. Smith, Y. Krishnan, Y. Zhang, P. Bai, W. C. Chueh, Y. Shao-Horn and M. Z. Bazant, Electrochim. Acta, 2021, 367, 137432 CrossRef CAS.
- R. B. Smith and M. Z. Bazant, J. Electrochem. Soc., 2017, 164, E3291–E3310 CrossRef CAS.
- H. Zhao, H. D. Deng, A. E. Cohen, J. Lim, Y. Li, D. Fraggedakis, B. Jiang, B. D. Storey, W. C. Chueh, R. D. Braatz and M. Z. Bazant, Nature, 2023 Search PubMed , in press.
- J. Lim, Y. Li, D. H. Alsem, H. So, S. C. Lee, P. Bai, D. A. Cogswell, X. Liu, N. Jin, Y.-s. Yu, N. J. Salmon, D. A. Shapiro, M. Z. Bazant, T. Tyliszczak and W. C. Chueh, Science, 2016, 353, 566–571 CrossRef CAS PubMed.
- D. T. Boyle, X. Kong, A. Pei, P. E. Rudnicki, F. Shi, W. Huang, Z. Bao, J. Qin and Y. Cui, ACS Energy Lett., 2020, 5, 701–709 CrossRef CAS.
- G. K. Singh, G. Ceder and M. Z. Bazant, Electrochim. Acta, 2008, 53, 7599–7613 CrossRef CAS.
- Y. Fu, S. Poizeau, A. Bertei, C. Qi, A. Mohanram, J. Pietras and M. Z. Bazant, Electrochim. Acta, 2015, 159, 71–80 CrossRef CAS.
- N. J. Williams, R. E. Warburton, I. D. Seymour, A. E. Cohen, M. Z. Bazant and S. J. Skinner, J. Chem. Phys., 2023, 158, 244107 CrossRef CAS PubMed.
- G. H. Vineyard, J. Phys. Chem. Solids, 1957, 3, 121–127 CrossRef CAS.
-
N. G. Van Kampen, Stochastic processes in physics and chemistry, Elsevier, 1992, vol. 1 Search PubMed.
- W. Schmickler, J. Electroanal. Chem., 1986, 204, 31–43 CrossRef CAS.
- J. Muscat and D. Newns, Prog. Surf. Sci., 1978, 9, 1–43 CrossRef CAS.
- S. W. Feldberg and N. Sutin, Chem. Phys., 2006, 324, 216–225 CrossRef CAS.
- M. Z. Bazant, M. S. Kilic, B. D. Storey and A. Ajdari, Adv. Colloid Interface Sci., 2009, 152, 48–88 CrossRef CAS PubMed.
- A. Sood, A. D. Poletayev, D. A. Cogswell, P. M. Csernica, J. T. Mefford, D. Fraggedakis, M. F. Toney, A. M. Lindenberg, M. Z. Bazant and W. C. Chueh, Nat. Rev. Mater., 2021, 6, 847–867 CrossRef CAS.
- L. M. Pinto, E. Spohr, P. Quaino, E. Santos and W. Schmickler, Angew. Chem., Int. Ed., 2013, 52, 7883–7885 CrossRef CAS PubMed.
- P. Quaino, N. Luque, R. Nazmutdinov, E. Santos and W. Schmickler, Angew. Chem., Int. Ed., 2012, 51, 12997–13000 CrossRef CAS PubMed.
- N. S. Hush, J. Electroanal. Chem., 1999, 460, 5–29 CrossRef CAS.
- Q. Wu and T. Van Voorhis, J. Chem. Phys., 2006, 125, 164105 CrossRef PubMed.
- M. Melander, E. Jónsson, J. J. Mortensen, T. Vegge and J. M. García Lastra, J. Chem. Theory Comput., 2016, 12, 5367–5378 CrossRef CAS PubMed.
- N. Holmberg and K. Laasonen, J. Chem. Theory Comput., 2017, 13, 587–601 CrossRef CAS PubMed.
- A. Hashemi, P. Peljo and K. Laasonen, J. Phys. Chem. C, 2023, 127, 3398–3407 CrossRef CAS PubMed.
- M. C. Henstridge, E. Laborda, N. V. Rees and R. G. Compton, Electrochim. Acta, 2012, 84, 12–20 CrossRef CAS.
- M. D. Berliner, D. A. Cogswell, M. Z. Bazant and R. D. Braatz, J. Electrochem. Soc., 2021, 168, 090504 CrossRef CAS.
- G. Galuppini, M. D. Berliner, D. A. Cogswell, D. Zhuang, M. Z. Bazant and R. D. Braatz, J. Power Sources, 2023, 573, 233009 CrossRef CAS.
- G. Galuppini, M. D. Berliner, H. Lian, D. Zhuang, M. Z. Bazant and R. D. Braatz, J. Power Sources, 2023, 580, 233272 CrossRef CAS.
- M. C. Henstridge, E. Laborda, Y. Wang, D. Suwatchara, N. Rees, Á. Molina, F. Martinez-Ortiz and R. G. Compton, J. Electroanal. Chem., 2012, 672, 45–52 CrossRef CAS.
- E. E. Tanner, L. Xiong, E. O. Barnes and R. G. Compton, J. Electroanal. Chem., 2014, 727, 59–68 CrossRef CAS.
- E. E. L. Tanner, E. O. Barnes, C. B. Tickell, P. Goodrich, C. Hardacre and R. G. Compton, J. Phys. Chem. C, 2015, 119, 7360–7370 CrossRef CAS.
- H. Gerischer, Z. Phys. Chem., 1960, 26, 223–247 CrossRef CAS.
- J. Jortner, J. Chem. Phys., 1976, 64, 4860–4867 CrossRef CAS.
-
A. Nitzan, Chemical dynamics in condensed phases: relaxation, transfer and reactions in condensed molecular systems, Oxford University Press, 2006 Search PubMed.
- J. Meixner, Journal of the London Mathematical Society, 1934, 1, 6–13 CrossRef.
- D. C. Vaughan, Commun. Stat. Theory Methods, 2002, 31, 219–238 CrossRef.
- C. Lai, Math. Chron., 1977, 6, 6–20 Search PubMed.
- B. Grigelionis, Lithuanian Mathematical Journal, 1999, 39, 33–41 CrossRef.
- P. Ding, Am. Stat., 2014, 68, 32–35 CrossRef.
-
M. J. Fischer, Generalized hyperbolic secant distributions: with applications to finance, Springer Science & Business Media, 2013 Search PubMed.
- A. Losev, Surf. Interface Anal., 1989, 14, 845–849 CrossRef CAS.
- A. Losev, Appl. Spectrosc., 1994, 48, 1289–1290 CrossRef CAS.
- D. J. Morgan, Surf. Interface Anal., 2023, 1–5 CAS.
-
G. Wertheim and P. Citrin, in Photoemission in solids I: general principles, M. Cardona and L. Ley, Springer Berlin, Heidelberg, 2005, pp. 197–236 Search PubMed.
- D. E. Ramaker, Crit. Rev. Solid State Mater. Sci., 1991, 17, 211–276 CrossRef CAS.
- H. Madden, Surf. Sci., 1983, 126, 80–100 CrossRef CAS.
- B. Moeini, M. R. Linford, N. Fairley, A. Barlow, P. Cumpson, D. Morgan, V. Fernandez and J. Baltrusaitis, Surf. Interface Anal., 2022, 54, 67–77 CrossRef CAS.
- M. Schmid, H.-P. Steinrück and J. M. Gottfried, Surf. Interface Anal., 2014, 46, 505–511 CrossRef CAS.
- S. Doniach and M. Šunjić, J. Phys. C: Solid State Phys., 1970, 3, 285 CrossRef CAS.
- P. H. Citrin and T. D. Thomas, J. Chem. Phys., 1972, 57, 4446–4461 CrossRef CAS.
- S. Hüfner and G. Werthaim, Phys. Rev. B: Solid State, 1975, 11, 678 CrossRef.
- M. J. Acres, H. Hussain, M. S. Walczak, M. Nikiel, C. Sewell, C. Rafols i Belles, E. A. Ahmad, A. S. Walton, C. A. Muryn, N. M. Harrison and R. Lindsay, Surf. Interface Anal., 202, 52, 507–512 CrossRef.
- A. Galtayries and J. Grimblot, J. Electron Spectrosc. Relat. Phenom., 1999, 98, 267–275 CrossRef.
- W. Schmickler and J. Mohr, J. Chem. Phys., 2002, 117, 2867–2872 CrossRef CAS.
- J. M. Savéant, Acc. Chem. Res., 1993, 26, 455–461 CrossRef.
- J. M. Saveant, J. Am. Chem. Soc., 1987, 109, 6788–6795 CrossRef CAS.
- K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2015, 6, 2663–2668 CrossRef CAS PubMed.
- K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2016, 7, 1686–1690 CrossRef CAS PubMed.
- R. Kronberg and K. Laasonen, ACS Catal., 2021, 11, 8062–8078 CrossRef CAS.
- P. Bai and G. Tian, Electrochim. Acta, 2013, 89, 644–651 CrossRef CAS.
- T. Maxisch, F. Zhou and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104301 CrossRef.
- G. K. P. Dathar, D. Sheppard, K. J. Stevenson and G. Henkelman, Chem. Mater., 2011, 23, 4032–4037 CrossRef CAS.
- K.-S. Park, P. Xiao, S.-Y. Kim, A. Dylla, Y.-M. Choi, G. Henkelman, K. J. Stevenson and J. B. Goodenough, Chem. Mater., 2012, 24, 3212–3218 CrossRef CAS.
- M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533 CrossRef CAS.
- R. Malik, F. Zhou and G. Ceder, Nat. Mater., 2011, 10, 587–590 CrossRef CAS PubMed.
- R. Malik, D. Burch, M. Bazant and G. Ceder, Nano Lett., 2010, 10, 4123–4127 CrossRef CAS PubMed.
- E. Quérel, N. J. Williams, I. D. Seymour, S. J. Skinner and A. Aguadero, Chem. Mater., 2023, 35, 853–862 CrossRef PubMed.
-
H. Lian and M. Z. Bazant, chemRxiv, 2023, preprint Search PubMed.
-
S. M. Brown, M. Orella, Y. W. Hsiao, Y. Román-Leshkov, Y. Surendranath, M. Z. Bazant and F. Brushett, chemRxiv, 2020, preprint, DOI:10.26434/chemrxiv.13244906.v1.
Footnote |
| † This is an extended version of the paper presented at the meeting. |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) − e(1−α)n
− e(1−α)n![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) )
)![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) = eη/kBT the dimensionless activation overpotential η, scaled to the thermal voltage, kBT/e. The BV equation has remained unchanged for over a century since the seminal work of Tafel,13,14 Butler,11,15–18 Bowden19 and Erdey-Gruz and Volmer12,20 on the reaction kinetics of electrolysis, motivated by Tafel's limiting law,13
= eη/kBT the dimensionless activation overpotential η, scaled to the thermal voltage, kBT/e. The BV equation has remained unchanged for over a century since the seminal work of Tafel,13,14 Butler,11,15–18 Bowden19 and Erdey-Gruz and Volmer12,20 on the reaction kinetics of electrolysis, motivated by Tafel's limiting law,13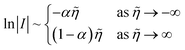
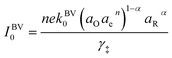


![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) (scaled to the thermal voltage, kBT/e) up to the scale of chemical bond breaking (|η| ∼ 1 eV). In contrast, all quantum mechanical models of ET predict curved Tafel plots, including (a) symmetric ET for localized electronic states (Marcus kinetics) or metallic electrodes (Marcus–Hush–Chidsey/MHC kinetics) and (b) asymmetric ET for metallic electrodes (asymmetric Marcus–Hush/AMH kinetics). At best, these models can asymptotically match the linear Tafel plot at low overpotentials, |η| ≪ λ, much smaller than the Marcus reorganization energy λ, which is typically at the scale of 100 meV ≈ 4kBT. [Adapted from (a) Zeng et al. (2014)60 and (b) Zeng et al. (2015).61]
(scaled to the thermal voltage, kBT/e) up to the scale of chemical bond breaking (|η| ∼ 1 eV). In contrast, all quantum mechanical models of ET predict curved Tafel plots, including (a) symmetric ET for localized electronic states (Marcus kinetics) or metallic electrodes (Marcus–Hush–Chidsey/MHC kinetics) and (b) asymmetric ET for metallic electrodes (asymmetric Marcus–Hush/AMH kinetics). At best, these models can asymptotically match the linear Tafel plot at low overpotentials, |η| ≪ λ, much smaller than the Marcus reorganization energy λ, which is typically at the scale of 100 meV ≈ 4kBT. [Adapted from (a) Zeng et al. (2014)60 and (b) Zeng et al. (2015).61]

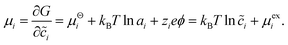
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i(
i(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t)},{ϕi},T,P], the Gibbs free energy for an open system at temperature T and pressure P, with respect to the dimensionless concentration
,t)},{ϕi},T,P], the Gibbs free energy for an open system at temperature T and pressure P, with respect to the dimensionless concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i(
i(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) (scaled to a reference value crefi), which expresses the free energy required to create a particle of species i at position
,t) (scaled to a reference value crefi), which expresses the free energy required to create a particle of species i at position ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) and time t. The second definition separates departures from a reference state electrochemical potential, μΘi, into a short-range chemical contribution depending on the activity ai and a long-range electrostatic contribution for a species of charge zie in the potential of mean force ϕ. The third definition expresses the Boltzmann distribution of concentration,
and time t. The second definition separates departures from a reference state electrochemical potential, μΘi, into a short-range chemical contribution depending on the activity ai and a long-range electrostatic contribution for a species of charge zie in the potential of mean force ϕ. The third definition expresses the Boltzmann distribution of concentration, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i = exp((μi − μexi)/kBT), in the total “excess” chemical potential
i = exp((μi − μexi)/kBT), in the total “excess” chemical potential![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi + zieϕ,
γi + zieϕ,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i is the activity coefficient. For a set of reactants, μi denotes the sum of their electrochemical potentials, while ai and
i is the activity coefficient. For a set of reactants, μi denotes the sum of their electrochemical potentials, while ai and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i denote the product of their activities and dimensionless concentrations, respectively.
i denote the product of their activities and dimensionless concentrations, respectively.
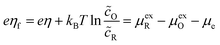
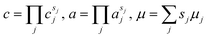
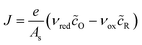
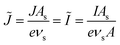
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) red
red![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O −
O − ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ox
ox![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R
R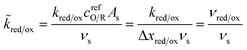
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O and
O and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R, will generally be different than in the nearby bulk phases outside the double layer. Assuming each species has bulk activity ai,b and undergoes fast adsorption on a set of discrete sites at the interface, we arrive at a generalized Langmuir isotherm,24
R, will generally be different than in the nearby bulk phases outside the double layer. Assuming each species has bulk activity ai,b and undergoes fast adsorption on a set of discrete sites at the interface, we arrive at a generalized Langmuir isotherm,24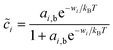
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i due to lateral pair interactions, as the regular solution model.24 Fraggedakis et al.103 assumed wO = wR, but we will consider the general asymmetric case, wR ≠ wO. For liquids and solids, surface adsorption is usually fast compared to transport and reaction kinetics, but for high-temperature gas electrodes, surface adsorption can be rate-limiting in the overall electrochemical reaction.109,110
i due to lateral pair interactions, as the regular solution model.24 Fraggedakis et al.103 assumed wO = wR, but we will consider the general asymmetric case, wR ≠ wO. For liquids and solids, surface adsorption is usually fast compared to transport and reaction kinetics, but for high-temperature gas electrodes, surface adsorption can be rate-limiting in the overall electrochemical reaction.109,110
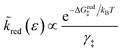
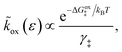
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ‡, to the excess chemical potential of the transition state, μex‡. The excess free energy barriers, ΔGred‡ and ΔGox‡, generally depend on the excess free energy of reaction,
γ‡, to the excess chemical potential of the transition state, μex‡. The excess free energy barriers, ΔGred‡ and ΔGox‡, generally depend on the excess free energy of reaction,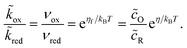
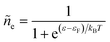
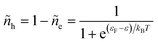
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ae − eϕe
ae − eϕe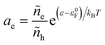
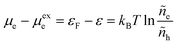
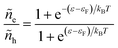
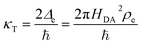
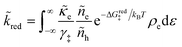
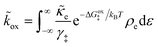
![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e is the dimensionless ET coefficient, scaled to the solvent polarization frequency, νs. This formulation can describe weakly adiabatic ET, where
e is the dimensionless ET coefficient, scaled to the solvent polarization frequency, νs. This formulation can describe weakly adiabatic ET, where ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e is approximately independent of electron energy,25,31,52 but it is most accurate for non-adiabatic ET in the limit of weak coupling, described above. In that case, the electron transmission coefficient is independent of electron energy ε and approximately given by,
e is approximately independent of electron energy,25,31,52 but it is most accurate for non-adiabatic ET in the limit of weak coupling, described above. In that case, the electron transmission coefficient is independent of electron energy ε and approximately given by,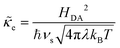
![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e are available for weakly adiabatic ET with multiple crossings based on Landau–Zener theory.26,58,115 Note that
e are available for weakly adiabatic ET with multiple crossings based on Landau–Zener theory.26,58,115 Note that ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e → 1 for adiabatic ET.
e → 1 for adiabatic ET.
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R and
R and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O, respectively, in the reduction current, eqn (14). The diffusional electrochemical potential enforces the Pauli exclusion principle for fermions by requiring that the creation of a particle always destroys a hole, as expressed by Fermi–Dirac statistics in eqn (32). Consistent with the way the reduction reaction is written, eqn (7), we do not include a hole in the reduced state. However, it is still necessary to integrate over the possible energies of electrons created by the oxidation reaction, eqn (39), since the activation barrier ΔGox‡ is electron energy dependent. We also choose the solvent polarization frequency νs as the natural frequency scale for CIET with non-adiabatic ET, in which case the CIET rate scales with the quantum tunneling frequency, κT.
O, respectively, in the reduction current, eqn (14). The diffusional electrochemical potential enforces the Pauli exclusion principle for fermions by requiring that the creation of a particle always destroys a hole, as expressed by Fermi–Dirac statistics in eqn (32). Consistent with the way the reduction reaction is written, eqn (7), we do not include a hole in the reduced state. However, it is still necessary to integrate over the possible energies of electrons created by the oxidation reaction, eqn (39), since the activation barrier ΔGox‡ is electron energy dependent. We also choose the solvent polarization frequency νs as the natural frequency scale for CIET with non-adiabatic ET, in which case the CIET rate scales with the quantum tunneling frequency, κT.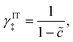
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) is equal to the probability of finding a vacancy among reactive ions with coverage
is equal to the probability of finding a vacancy among reactive ions with coverage ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) on the electrode/electrolyte interface.24 Other choices for γIT‡ might express volume exclusion among random loose packings of hard spheres, e.g. via the Carnahan–Starling equation of state.116
on the electrode/electrolyte interface.24 Other choices for γIT‡ might express volume exclusion among random loose packings of hard spheres, e.g. via the Carnahan–Starling equation of state.116
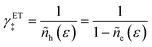
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ‡ = kBT
γ‡ = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γIT‡ − kBT
γIT‡ − kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ñh(ε)
ñh(ε)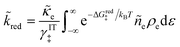
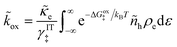
![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e, has been factored out of the integrals above.
e, has been factored out of the integrals above.
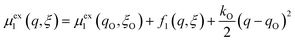
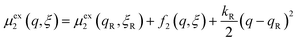

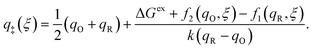
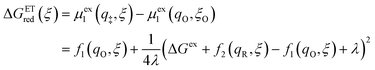
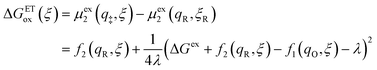
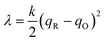
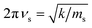 ,
,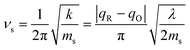
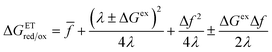
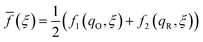
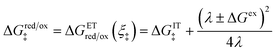
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (ξ‡), which contributes a common Arrhenius prefactor to kred and kox. However, no conditions were given to justify this postulate, and no formula was given for ΔGIT‡. Instead, the effective IT barrier was expressed empirically as ΔGIT‡ = αITΔEIT in terms of an overall ion transfer energy, ΔEIT, multiplied by a phenomenological IT coefficient, αIT ≈ 1/2, inspired by the Butler–Volmer equation.103 In this context, one might expect αIT to be a symmetry factor,
(ξ‡), which contributes a common Arrhenius prefactor to kred and kox. However, no conditions were given to justify this postulate, and no formula was given for ΔGIT‡. Instead, the effective IT barrier was expressed empirically as ΔGIT‡ = αITΔEIT in terms of an overall ion transfer energy, ΔEIT, multiplied by a phenomenological IT coefficient, αIT ≈ 1/2, inspired by the Butler–Volmer equation.103 In this context, one might expect αIT to be a symmetry factor,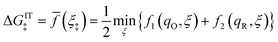
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (ξ‡) given by eqn (62) in the asymptotic limit of Normal ECIT, eqn (61). Our goal is to prove that the first two terms in eqn (56) dominate in the asymptotic limit of eqn (61). We begin by stating the triangle inequality, |Δf| ≤ 2
(ξ‡) given by eqn (62) in the asymptotic limit of Normal ECIT, eqn (61). Our goal is to prove that the first two terms in eqn (56) dominate in the asymptotic limit of eqn (61). We begin by stating the triangle inequality, |Δf| ≤ 2![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , since f1, f2 ≥ 0, which helps us show that the third term in eqn (56) is asymptotically dominated by the first term:
, since f1, f2 ≥ 0, which helps us show that the third term in eqn (56) is asymptotically dominated by the first term: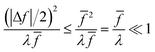

![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (ξ) (light blue). In (b) and (e), electrons at ΔGex = −λ are able to make barrierless ET transitions, which dominate in the limit of large negative overpotentials, and facilitate IT at a constant rate. In (c) and (f), for ΔGex < −λ, the reaction complex enters the Marcus inverted region with a larger ET barrier and smaller contribution to the total current. (Inset) Tafel plot showing the scenarios (a)–(c)/(d)–(f) for reduction, where the Tafel slope is αET for the beginning of the negative reduction branch and 1 − αET for the positive oxidation branch. On both sides, the brief Tafel regime transitions to Marcus ECIT reaction limit current, when the overpotential exceeds the reorganization energy.
(ξ) (light blue). In (b) and (e), electrons at ΔGex = −λ are able to make barrierless ET transitions, which dominate in the limit of large negative overpotentials, and facilitate IT at a constant rate. In (c) and (f), for ΔGex < −λ, the reaction complex enters the Marcus inverted region with a larger ET barrier and smaller contribution to the total current. (Inset) Tafel plot showing the scenarios (a)–(c)/(d)–(f) for reduction, where the Tafel slope is αET for the beginning of the negative reduction branch and 1 − αET for the positive oxidation branch. On both sides, the brief Tafel regime transitions to Marcus ECIT reaction limit current, when the overpotential exceeds the reorganization energy.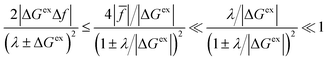
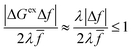
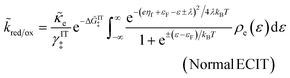
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) IT‡ = ΔGIT‡/kBT. The Normal ECIT rate formula is identical to the Marcus expression for pure, symmetric ET at an electrode36,51,60,86,125 (ρe = constant), except for an important new IT-dependent prefactor, which contains the activity coefficient γIT and effective free energy barrier ΔGIT‡ for IT. Recall that the current is given by eqn (14) in terms of the kred and kox.
IT‡ = ΔGIT‡/kBT. The Normal ECIT rate formula is identical to the Marcus expression for pure, symmetric ET at an electrode36,51,60,86,125 (ρe = constant), except for an important new IT-dependent prefactor, which contains the activity coefficient γIT and effective free energy barrier ΔGIT‡ for IT. Recall that the current is given by eqn (14) in terms of the kred and kox.
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f-dependence of MHC kinetics85 with an IT-dependent Arrhenius prefactor,
f-dependence of MHC kinetics85 with an IT-dependent Arrhenius prefactor,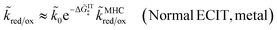
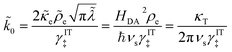
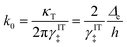
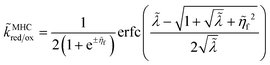
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f = eηf/kBT,
f = eηf/kBT, ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = λ/kBT, and
= λ/kBT, and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) e = ρekBT. Although various series expansions of the MHC integrals are available for different asymptotic limits of the parameters,95,96 the closed-form approximation of eqn (70) has the advantage of being simpler and uniformly valid for all values of λ and ηf. Compared to the MHC integral, eqn (67), the maximum relative error of eqn (70) is around 5%, while maintaining high accuracy for large and small
e = ρekBT. Although various series expansions of the MHC integrals are available for different asymptotic limits of the parameters,95,96 the closed-form approximation of eqn (70) has the advantage of being simpler and uniformly valid for all values of λ and ηf. Compared to the MHC integral, eqn (67), the maximum relative error of eqn (70) is around 5%, while maintaining high accuracy for large and small ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) , as well as large formal overpotentials,
, as well as large formal overpotentials, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f, since it was derived by asymptotic matching of exact results for these limiting cases.60
f, since it was derived by asymptotic matching of exact results for these limiting cases.60

![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) , where
, where ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) =
= ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f + ln(
f + ln(![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R/
R/![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O) is a small total overpotential, |
O) is a small total overpotential, |![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) | ≪ 1. In contrast to phenomenological BV theory, eqn (4), the exchange current for ECIT does not have simple power-law dependence on the reactant concentrations,
| ≪ 1. In contrast to phenomenological BV theory, eqn (4), the exchange current for ECIT does not have simple power-law dependence on the reactant concentrations, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O and
O and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R. CIET kinetics is also non-separable, in the sense that the current cannot be expressed as a function of overpotential times a function of concentrations, in contrast to the separable form of the phenomenological BV equation, eqn (1). Note that for the typical low-temperature regime,
R. CIET kinetics is also non-separable, in the sense that the current cannot be expressed as a function of overpotential times a function of concentrations, in contrast to the separable form of the phenomenological BV equation, eqn (1). Note that for the typical low-temperature regime, ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ≫ 1, the exchange current for symmetric ECIT has an Arrhenius temperature dependence,
≫ 1, the exchange current for symmetric ECIT has an Arrhenius temperature dependence, 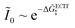 , with
, with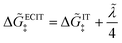
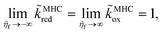
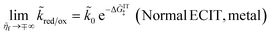
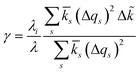
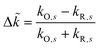
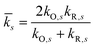
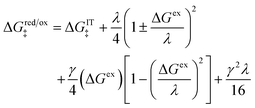
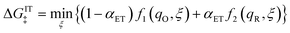
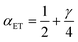
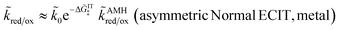
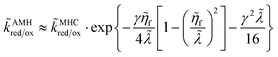

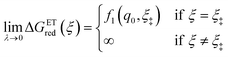
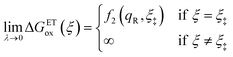
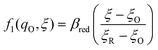
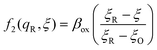

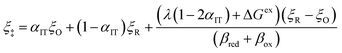
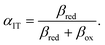
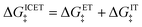
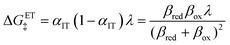
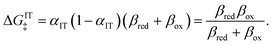
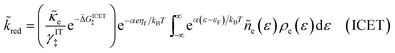
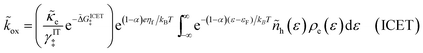
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ICET‡ = ΔGICET‡/kBT. By converting from formal to total overpotential using eqn (9), we finally arrive at the BV equation (for one electron transfer),
ICET‡ = ΔGICET‡/kBT. By converting from formal to total overpotential using eqn (9), we finally arrive at the BV equation (for one electron transfer),![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) − e(1−α)
− e(1−α)![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) )
)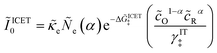
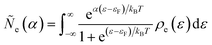
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O and
O and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R, respectively. Second, the empirical lumped prefactor, nekBV0aen(1−α), has been replaced by the product of the electron transmission coefficient
R, respectively. Second, the empirical lumped prefactor, nekBV0aen(1−α), has been replaced by the product of the electron transmission coefficient ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) e, the effective number of participating electronic states Ñe(α), and an Arrhenius prefactor, where the activation energy, ΔGICET‡, is expressed in terms of both the ET reorganization energy and the mean IT barrier.
e, the effective number of participating electronic states Ñe(α), and an Arrhenius prefactor, where the activation energy, ΔGICET‡, is expressed in terms of both the ET reorganization energy and the mean IT barrier.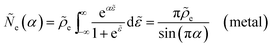
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) e is attained, while Ñe → ∞ for highly asymmetric IT, α → 0 or α → 1, as the number of electrons diverges due to the nearly flat IT energy landscape of either the reduced or the oxidized state. It is important to recognize that α → 0, 1 is a pathological limit of the ICET model using the Gurney–Butler linear approximation of the IT free energy landscapes, since the transition state ξ‡ for many electron levels will lie far outside the physically meaningful range, ξO ≤ ξ ≤ ξR.
e is attained, while Ñe → ∞ for highly asymmetric IT, α → 0 or α → 1, as the number of electrons diverges due to the nearly flat IT energy landscape of either the reduced or the oxidized state. It is important to recognize that α → 0, 1 is a pathological limit of the ICET model using the Gurney–Butler linear approximation of the IT free energy landscapes, since the transition state ξ‡ for many electron levels will lie far outside the physically meaningful range, ξO ≤ ξ ≤ ξR.
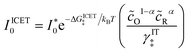
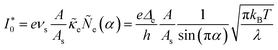
 , in both the exchange current prefactor,
, in both the exchange current prefactor,  , and the activation barrier, ΔGICET‡.
, and the activation barrier, ΔGICET‡.
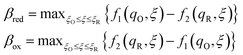
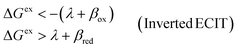
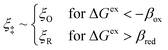
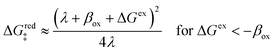
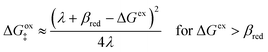
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) 0
0![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O
O![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) MHCred(
MHCred(![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ,
,![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f +
f + ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox) for
ox) for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f < −
f < −![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox
ox![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) 0
0![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R
R![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) MHCox(
MHCox(![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ,
,![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f −
f − ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red) for
red) for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f >
f > ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red
red![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) MHCred/ox → 1 as |ηf| → ∞, CIET theory thus predicts a universal limited reaction rate for metallic electrodes corresponding to barrierless ECIT,
MHCred/ox → 1 as |ηf| → ∞, CIET theory thus predicts a universal limited reaction rate for metallic electrodes corresponding to barrierless ECIT,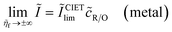
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R/O = 1), is given by ĨCIETlim =
R/O = 1), is given by ĨCIETlim = ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) 0, or, with units restored,
0, or, with units restored,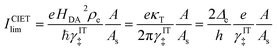
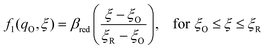
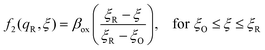
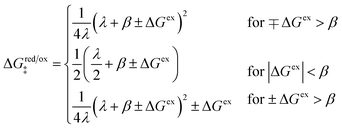
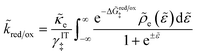
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = (ε − εF)/kBT. These uniformly valid approximations are nearly exact for the truncated linear models in eqn (116)–(118). They also reproduce the barriers derived above in the three asymptotic regimes of the general theory, while interpolating smoothly between them with continuously differentiable functions. After integration over the electron energies, the rate formulae in eqn (139) thus possess two continuous derivatives.
= (ε − εF)/kBT. These uniformly valid approximations are nearly exact for the truncated linear models in eqn (116)–(118). They also reproduce the barriers derived above in the three asymptotic regimes of the general theory, while interpolating smoothly between them with continuously differentiable functions. After integration over the electron energies, the rate formulae in eqn (139) thus possess two continuous derivatives.
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) e = constant, and replace the Fermi–Dirac functions with Heaviside step functions,25,60
e = constant, and replace the Fermi–Dirac functions with Heaviside step functions,25,60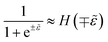

![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f), which interpolates between the exact prefactors for large and small overpotentials derived above. This factor is required for mathematical accuracy in the asymptotic limits, but could be set to M = 1 in most cases, given the crude physical accuracy of the truncated linear approximation of the diabatic free energy landscape, eqn (118).
f), which interpolates between the exact prefactors for large and small overpotentials derived above. This factor is required for mathematical accuracy in the asymptotic limits, but could be set to M = 1 in most cases, given the crude physical accuracy of the truncated linear approximation of the diabatic free energy landscape, eqn (118).

![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ox, scaled to the universal limiting rate k0 in the standard state (
ox, scaled to the universal limiting rate k0 in the standard state (![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O =
O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = 1), versus dimensionless formal overpotential,
R = 1), versus dimensionless formal overpotential, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f, scaled to kBT/e, for three cases of reorganization energy,
f, scaled to kBT/e, for three cases of reorganization energy, ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) , and ion transfer free energy,
, and ion transfer free energy, ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) (scaled to kBT). Dashed curves show the asymptotic approximations for ICET for
(scaled to kBT). Dashed curves show the asymptotic approximations for ICET for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f <
f < ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) and for ECIT for
and for ECIT for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f >
f > ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) , which have been matched to obtain the uniformly valid approximations (solid curves). (b) Tafel plot of the absolute value of the CIET current, |Ĩ|, scaled to the limiting current, ek0, versus dimensionless formal overpotential for the cases in (a), assuming standard conditions for the reactants,
, which have been matched to obtain the uniformly valid approximations (solid curves). (b) Tafel plot of the absolute value of the CIET current, |Ĩ|, scaled to the limiting current, ek0, versus dimensionless formal overpotential for the cases in (a), assuming standard conditions for the reactants, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O =
O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = 1. For ICET over a wide range of formal overpotentials, kBT ≪ eηf ≪ β, the theory is able to exactly reproduce Tafel's law, eqn (2), and predict its breakdown, as explained in Fig. 7.
R = 1. For ICET over a wide range of formal overpotentials, kBT ≪ eηf ≪ β, the theory is able to exactly reproduce Tafel's law, eqn (2), and predict its breakdown, as explained in Fig. 7.![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f| ≫ 1, the approximation of eqn (123) reaches a limiting rate given by
f| ≫ 1, the approximation of eqn (123) reaches a limiting rate given by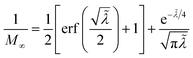
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) red/ox →
red/ox → ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) 0, but rapidly converges in the relevant low-temperature limit,
0, but rapidly converges in the relevant low-temperature limit, ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ≫ 1. For example, M−1∞ = 1.2 for
≫ 1. For example, M−1∞ = 1.2 for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 1, and M−1∞ = 1.02 for
= 1, and M−1∞ = 1.02 for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 4. For small formal overpotentials, |
= 4. For small formal overpotentials, |![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f| ≪ 1, we must set
f| ≪ 1, we must set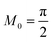
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f| >
f| > ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) over a range set by
over a range set by ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) , so we could choose the matching function to be
, so we could choose the matching function to be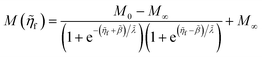
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f), introduces some curvature of the Tafel plot for ICET, even at low formal overpotentials, which physically corresponds to smoothing of the sharp minima in the truncated linear approximations of the diabatic free energy landscape.
f), introduces some curvature of the Tafel plot for ICET, even at low formal overpotentials, which physically corresponds to smoothing of the sharp minima in the truncated linear approximations of the diabatic free energy landscape.

![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f), plotted for the ICET regime with parameters shown for symmetric cases, eqn (124)–(126), and asymmetric cases, eqn (130)–(132) with
f), plotted for the ICET regime with parameters shown for symmetric cases, eqn (124)–(126), and asymmetric cases, eqn (130)–(132) with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 5.
= 5.
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ox, (
ox, (![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O =
O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = 1), versus dimensionless formal overpotential,
R = 1), versus dimensionless formal overpotential, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f, for three cases of
f, for three cases of ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ,
, ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red and
red and ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox. Dashed curves show the asymptotic approximations for ICET (−
ox. Dashed curves show the asymptotic approximations for ICET (−![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox <
ox < ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f <
f < ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red) and for ECIT (
red) and for ECIT (![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f < −
f < −![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox,
ox, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f >
f > ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red), which have been matched to obtain the uniformly valid approximations (solid curves). (b) Tafel plot of the absolute value of the dimensionless CIET current, |Ĩ|, versus
red), which have been matched to obtain the uniformly valid approximations (solid curves). (b) Tafel plot of the absolute value of the dimensionless CIET current, |Ĩ|, versus ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f for the cases in (a), assuming
f for the cases in (a), assuming ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O =
O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = 1.
R = 1.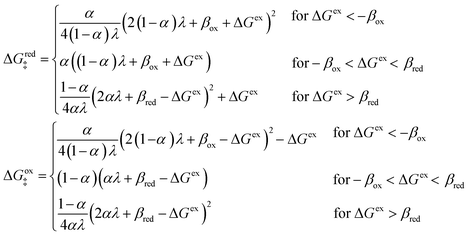


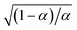 and the reduction rate by
and the reduction rate by 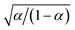 in order to approximate the correct limiting behavior at large overpotentials. In particular, the dimensionless rate constants now tend to a limiting value,
in order to approximate the correct limiting behavior at large overpotentials. In particular, the dimensionless rate constants now tend to a limiting value,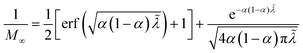
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ≫ 1. In order to recover the exact exchange current for ICET, eqn (101), we must also set
≫ 1. In order to recover the exact exchange current for ICET, eqn (101), we must also set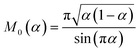
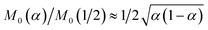 , which diverges in the limits of fully asymmetric charge transfer, α → 0, 1, and thus should be included in the uniformly valid approximation. The transition to the limiting value should occur for
, which diverges in the limits of fully asymmetric charge transfer, α → 0, 1, and thus should be included in the uniformly valid approximation. The transition to the limiting value should occur for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f < −
f < −![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox for reduction and
ox for reduction and ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f >
f > ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red for oxidation over a range set by
red for oxidation over a range set by ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) . Once again controlling these transitions with Fermi–Dirac functions, we choose
. Once again controlling these transitions with Fermi–Dirac functions, we choose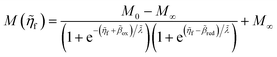
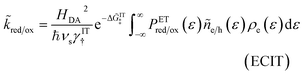
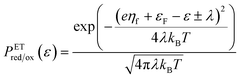
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) IT‡ = 0 in eqn (133). From this perspective, the probability of nonadiabatic ET from/to state ε during reduction/oxidation has a normal Gaussian distribution with mean and variance,
IT‡ = 0 in eqn (133). From this perspective, the probability of nonadiabatic ET from/to state ε during reduction/oxidation has a normal Gaussian distribution with mean and variance,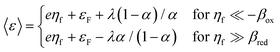
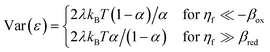

![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red = 30,
red = 30, ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox = 10,
ox = 10, ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 3. Linear regions for ICET are shown in red, and quadratic regions for Normal and Inverted ECIT are shown in purple for reduction and blue for oxidation. (b) Probability distributions, PCIETred/ox(
= 3. Linear regions for ICET are shown in red, and quadratic regions for Normal and Inverted ECIT are shown in purple for reduction and blue for oxidation. (b) Probability distributions, PCIETred/ox(![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ), for the dimensionless energy of the transferring electron or hole,
), for the dimensionless energy of the transferring electron or hole, ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = (ε − εF)/kBT. Over the full range of formal overpotentials for ICET, −βox < ηf < βred, the electrons or holes are sampled from a Meixner–Losev skewed hyperbolic secant distribution, eqn (141), which is peaked at the Fermi level with a fat tail in the direction of the flatter diabatic free energy landscape, e.g. for lower electron energies (or larger binding energies) if βox > βred or α < 1/2 as shown. For large formal overpotentials in the Normal and Inverted regimes of ECIT, the electrons or holes are sampled from Gerischer's shifted Gaussian distributions, eqn (134), with rescaled parameters, shown for
= (ε − εF)/kBT. Over the full range of formal overpotentials for ICET, −βox < ηf < βred, the electrons or holes are sampled from a Meixner–Losev skewed hyperbolic secant distribution, eqn (141), which is peaked at the Fermi level with a fat tail in the direction of the flatter diabatic free energy landscape, e.g. for lower electron energies (or larger binding energies) if βox > βred or α < 1/2 as shown. For large formal overpotentials in the Normal and Inverted regimes of ECIT, the electrons or holes are sampled from Gerischer's shifted Gaussian distributions, eqn (134), with rescaled parameters, shown for ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f = − 45, 15.
f = − 45, 15.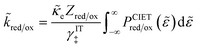
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ) that an electron or hole with dimensionless energy
) that an electron or hole with dimensionless energy ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = (ε − εF)/kBT participates in the CIET reduction or oxidation reaction, respectively:
= (ε − εF)/kBT participates in the CIET reduction or oxidation reaction, respectively: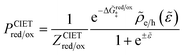
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f| passes through
f| passes through ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red/ox. It appears that the general CIET distributions have not been studied before in probability and statistics, and their mathematical properties await systematic characterization.
red/ox. It appears that the general CIET distributions have not been studied before in probability and statistics, and their mathematical properties await systematic characterization.
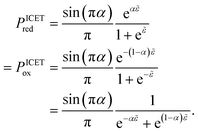
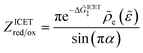
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ICET‡ is given by eqn (155). In contrast to ECIT, the Fermi level (
ICET‡ is given by eqn (155). In contrast to ECIT, the Fermi level (![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = 0) is always close to the most probable energy for electrons or holes involved in reduction or oxidation by ICET at a metal electrode, respectively, regardless of the overpotential or reorganization energy. For the symmetric ICET (α = 1/2), the electron energy (for reduction) or hole energy (for oxidation) are sampled from the hyperbolic secant distribution
= 0) is always close to the most probable energy for electrons or holes involved in reduction or oxidation by ICET at a metal electrode, respectively, regardless of the overpotential or reorganization energy. For the symmetric ICET (α = 1/2), the electron energy (for reduction) or hole energy (for oxidation) are sampled from the hyperbolic secant distribution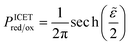
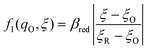
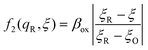

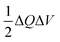 , where the charge ΔQ can be obtained by density functional theory (DFT) and ΔV is the electrode potential relative to computational vacuum (on the other side of the electrolyte).157,158 Although this approach neglects the polarization of interfacial dipoles and various details of the electric double layers, it provides a means to compute the free energy landscape of adiabatic CIET as a function of electrode potential. In a “computational tour de force”,31 Kronberg and Laasonen recently used DFT-based constrained MD simulations to calculate the adiabatic free energy barrier versus applied potential for hydrogen evolution on a platinum electrode, the Volmer reaction on Pt(111), albeit with relatively large values compared to experiments.159 Over some range of electrode potentials at different surface coverages, the free energy barriers vary almost linearly with formal overpotential, which would be consistent with BV kinetics of ICET, and there are also quadratic terms, perhaps similar to those arising in the more general CIET theory.
, where the charge ΔQ can be obtained by density functional theory (DFT) and ΔV is the electrode potential relative to computational vacuum (on the other side of the electrolyte).157,158 Although this approach neglects the polarization of interfacial dipoles and various details of the electric double layers, it provides a means to compute the free energy landscape of adiabatic CIET as a function of electrode potential. In a “computational tour de force”,31 Kronberg and Laasonen recently used DFT-based constrained MD simulations to calculate the adiabatic free energy barrier versus applied potential for hydrogen evolution on a platinum electrode, the Volmer reaction on Pt(111), albeit with relatively large values compared to experiments.159 Over some range of electrode potentials at different surface coverages, the free energy barriers vary almost linearly with formal overpotential, which would be consistent with BV kinetics of ICET, and there are also quadratic terms, perhaps similar to those arising in the more general CIET theory.![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) ox +
ox + ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ) ≪
) ≪ ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f ≪
f ≪ ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red +
red + ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ,
,![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f)(e−α
f)(e−α![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) − e(1−α)
− e(1−α)![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) )
)![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) f), given by eqn (130)–(132), which imparts slight curvature to the Tafel plot controlled by λ. In most cases, one can set
f), given by eqn (130)–(132), which imparts slight curvature to the Tafel plot controlled by λ. In most cases, one can set 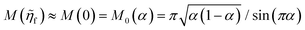 to recover the pure BV equation, which is exact in the limit of negligible reorganization energy, λ/βox/red → 0.
to recover the pure BV equation, which is exact in the limit of negligible reorganization energy, λ/βox/red → 0.
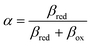

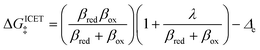
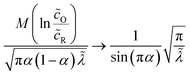
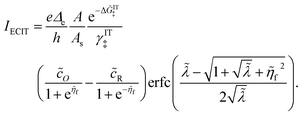
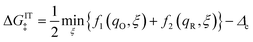
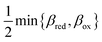 for the truncated linear approximation, eqn (118), and
for the truncated linear approximation, eqn (118), and 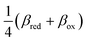 for the uniformly valid approximation of CIET kinetics, and the second term is a weakly adiabatic correction.
for the uniformly valid approximation of CIET kinetics, and the second term is a weakly adiabatic correction.

![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ≫
≫ ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) red/ox, corresponding to ECIT. Considering the low-temperature expansion of IECIT0, the total activation barrier at low overpotentials is given by eqn (72), which is the symmetric case of eqn (155) for α = 1/2.
red/ox, corresponding to ECIT. Considering the low-temperature expansion of IECIT0, the total activation barrier at low overpotentials is given by eqn (72), which is the symmetric case of eqn (155) for α = 1/2.
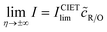
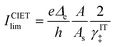
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R =
R = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) be the dimensionless intercalated ion concentration (or filling fraction) in the solid and
be the dimensionless intercalated ion concentration (or filling fraction) in the solid and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O =
O = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) + be the dimensionless adsorbed surface concentration (or surface coverage) given by the adsorption isotherm, eqn (20). As noted above, the key requirement for ion intercalation is that the CIET transition state excludes one solid site, or equivalently, involves one vacancy, γIT‡ = (1 −
+ be the dimensionless adsorbed surface concentration (or surface coverage) given by the adsorption isotherm, eqn (20). As noted above, the key requirement for ion intercalation is that the CIET transition state excludes one solid site, or equivalently, involves one vacancy, γIT‡ = (1 − ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) )−1. From this theoretical perspective, we revisit the existing data for the rate dependence on overpotential, temperature and solid concentration.
)−1. From this theoretical perspective, we revisit the existing data for the rate dependence on overpotential, temperature and solid concentration.
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 8.3 at room temperature) and independently fitted prefactors for each branch of Tafel data, shown in Fig. 15(b). The small uncertainty (0.5%) in the fitted reorganization energy indicates that the overpotential dependence of ECIT for a metal surface, eqn (160), captures the shape of these Tafel curves very well. As noted by the authors, the fact that all of the Tafel curvatures can be accurately fitted (with 0.5% uncertainty) by a single, temperature-independent reorganization energy provides strong support for the hypothesis of ET limitation in these experiments. In contrast, any fitted series resistances, which are routinely invoked to curve Tafel plots with BV kinetics,88 must be temperature dependent, if they are to represent either ionic or electronic transport processes.
= 8.3 at room temperature) and independently fitted prefactors for each branch of Tafel data, shown in Fig. 15(b). The small uncertainty (0.5%) in the fitted reorganization energy indicates that the overpotential dependence of ECIT for a metal surface, eqn (160), captures the shape of these Tafel curves very well. As noted by the authors, the fact that all of the Tafel curvatures can be accurately fitted (with 0.5% uncertainty) by a single, temperature-independent reorganization energy provides strong support for the hypothesis of ET limitation in these experiments. In contrast, any fitted series resistances, which are routinely invoked to curve Tafel plots with BV kinetics,88 must be temperature dependent, if they are to represent either ionic or electronic transport processes.

![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) = Δln(
= Δln(![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) +/
+/![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ) ≈ 1, which would imply a larger surface coverage
) ≈ 1, which would imply a larger surface coverage![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) + by a factor of e ≈ 2.7 for oxidation versus reduction, assuming the slowest dynamics occurs for
+ by a factor of e ≈ 2.7 for oxidation versus reduction, assuming the slowest dynamics occurs for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) → 1 (since concentrations were not measured). Both models would slightly distort the excellent fit of the Tafel plots with MHC kinetics.
→ 1 (since concentrations were not measured). Both models would slightly distort the excellent fit of the Tafel plots with MHC kinetics.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pixels of X-ray image data from 63 nanoparticles, each cycled through complete reduction (Li+ insertion) and oxidation (Li+ extraction), with only 7% global error across all pixels. Since the intercalation kinetics of carbon-coated LFP nanoparticles are famously fast along the b-axis of the LFP crystal exposed by the active (010) facet of the platelets,165,166 the experiments were limited to small overpotentials, on the order of several kBT/e. As such, the inverse learning process could not discern the overpotential dependence (assumed to be Butler–Volmer), but it was able to accurately extract the concentration dependence. Nanoscale spatial heterogeneities in the reaction rate constant were also learned from the STXM images and correlated with variations in carbon coating thickness, thereby enabling precise measurement of the underlying intercalation reaction kinetics.
000 pixels of X-ray image data from 63 nanoparticles, each cycled through complete reduction (Li+ insertion) and oxidation (Li+ extraction), with only 7% global error across all pixels. Since the intercalation kinetics of carbon-coated LFP nanoparticles are famously fast along the b-axis of the LFP crystal exposed by the active (010) facet of the platelets,165,166 the experiments were limited to small overpotentials, on the order of several kBT/e. As such, the inverse learning process could not discern the overpotential dependence (assumed to be Butler–Volmer), but it was able to accurately extract the concentration dependence. Nanoscale spatial heterogeneities in the reaction rate constant were also learned from the STXM images and correlated with variations in carbon coating thickness, thereby enabling precise measurement of the underlying intercalation reaction kinetics.![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) + = 0.3 and
+ = 0.3 and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) → 1 for the slowest reduction reaction dominating the transient response. The ICET formula, eqn (154), almost perfectly fits the learned kinetics at high concentration using the same value of α = 0.4 inferred above from electrochemical data, while symmetic ICET with α = 0.5 provides an even better overall fit. Overall, the analysis supports the picture of lithium intercalation in carbon-coated LFP as a process limited by comparable barriers for ET and IT.
→ 1 for the slowest reduction reaction dominating the transient response. The ICET formula, eqn (154), almost perfectly fits the learned kinetics at high concentration using the same value of α = 0.4 inferred above from electrochemical data, while symmetic ICET with α = 0.5 provides an even better overall fit. Overall, the analysis supports the picture of lithium intercalation in carbon-coated LFP as a process limited by comparable barriers for ET and IT.
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) R = c, and compared with the theoretical predictions for ECIT, eqn (162), and ICET, eqn (154), using parameters that are also consistent with the Tafel data in Fig. 15. For comparison, the standard BV model with
R = c, and compared with the theoretical predictions for ECIT, eqn (162), and ICET, eqn (154), using parameters that are also consistent with the Tafel data in Fig. 15. For comparison, the standard BV model with  widely used in Li-ion battery simulations9,10,164 is not consistent with the experimental data. [Figure courtesy of Hongbo Zhao, adapted from Zhao et al. (2023).105]
widely used in Li-ion battery simulations9,10,164 is not consistent with the experimental data. [Figure courtesy of Hongbo Zhao, adapted from Zhao et al. (2023).105]![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ). This linear trend is seen in both ECIT and ICET formulae, in excellent agreement with the X-ray data in Fig. 16. This prediction holds regardless of whether ET or IT is rate-limiting because it comes from the universal activity coefficient of the IT transition state for intercalation, which must capture the exclusion of one site,24, (γIT‡)−1 = 1 −
). This linear trend is seen in both ECIT and ICET formulae, in excellent agreement with the X-ray data in Fig. 16. This prediction holds regardless of whether ET or IT is rate-limiting because it comes from the universal activity coefficient of the IT transition state for intercalation, which must capture the exclusion of one site,24, (γIT‡)−1 = 1 − ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . In contrast, the standard empirical model of intercalation kinetics, used in popular porous electrode theory models and battery simulation software, postulates
. In contrast, the standard empirical model of intercalation kinetics, used in popular porous electrode theory models and battery simulation software, postulates 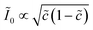 , which scales with the square root of the vacancy concentration.9,164 This model is inconsistent with the X-ray data, as well as the fundamental theory of CIET.
, which scales with the square root of the vacancy concentration.9,164 This model is inconsistent with the X-ray data, as well as the fundamental theory of CIET.
