Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Insights into the reaction network and kinetics of xylose conversion over combined Lewis/Brønsted acid catalysts in a flow microreactor†
Wenze
Guo
 ab,
Herman Carolus
Bruining
a,
Hero Jan
Heeres
ab,
Herman Carolus
Bruining
a,
Hero Jan
Heeres
 a and
Jun
Yue
a and
Jun
Yue
 *a
*a
aDepartment of Chemical Engineering, Engineering and Technology Institute Groningen, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: yue.jun@rug.nl
bState Key Laboratory of Chemical Engineering, Department of Chemical Engineering, East China University of Science and Technology, Shanghai 200237, PR China
First published on 4th April 2023
Abstract
The catalytic effect of Lewis acid on xylose conversion to furfural has been widely reported, while the underlying reaction network and kinetics are not fully elucidated. This work presents experimental and kinetic modelling studies on xylose conversion to furfural, using AlCl3/HCl as combined Lewis/Brønsted acid catalysts in monophasic water or a biphasic water–methyl isobutyl ketone system in a flow microreactor. The reaction network and kinetics were developed, where Al(OH)2+ was identified as the catalytically active species for isomerization between xylose, lyxose and xylulose, while both Al(OH)2+ and H+ catalyze the sugar dehydration to furfural and side reactions leading to humins (e.g., sugar condensation and furfural degradation). The promoting effect of AlCl3 is attributed to not only the tandem catalysis through xylulose, but also the parallel Al(OH)2+-catalyzed sugar dehydration. Within the studied range (120 to 180 °C, 0.05–0.4 M HCl, 0.04–0.12 M AlCl3), the furfural selectivity relied mainly on the concentration ratio of HCl to AlCl3 rather than their individual concentrations or the temperature. The volcano-like evolution of the maximum furfural yield with increasing HCl/AlCl3 ratio is related to (i) the lower reaction orders in Al(OH)2+ for reactions forming furfural than for side reactions; and (ii) a gradual shift of the dominant reaction pathway from the Al(OH)2+-catalyzed one towards H+-catalyzed one. An optimized furfural yield up to 90% was achieved with 40 mM AlCl3 and 100 mM HCl at 160 °C from 1 M xylose in a continuous slug flow microreactor. The catalytic aqueous phase could be recycled and reused four times without performance loss.
1. Introduction
Worldwide industrial and economic development has led to a steady depletion of fossil reserves and significant CO2 emission. To alleviate these environmental issues, significant research attention has been given to utilizing lignocellulosic biomass, which is composed mainly of cellulose, hemicellulose and lignin, as a green and sustainable alternative feedstock for the production of fuels, materials and chemicals.1,2 In a biomass valorization network, one representative pathway is the conversion of lignocellulosic carbohydrates to bio-based furanic platform chemicals.3,4 One such carbohydrate is xylose, the most abundant pentose in the hemicellulose fraction (25–35% on a dry basis).5 Dehydration of xylose produces furfural, a versatile building block for the production of a spectrum of biofuels, biobased polymers and chemicals.6 For example, the hydrogenation of furfural produces furfuryl alcohol as the monomer of furan resins,7 2-methylfuran and 2-methyltetrahydrofuran as potential liquid transportation fuel additives,2,8,9 and tetrahydrofuran as a widely used industrial specialty solvent.10 Moreover, furfural can be transformed via a series of aldol condensation and dehydration/hydrogenation reactions to liquid alkanes that serve as gasoline, diesel or aviation fuel.11Typically, furfural is produced by xylose dehydration in water under the catalysis of homogeneous Brønsted acids such as HCl, H2SO4 and H3PO4, which involves the dehydration of xylose to furfural and a series of undesirable side reactions leading to humins, such as xylose condensation and furfural degradation.12 Furfural production from biomass has a long history of over 100 years (dating back to 1921 by the Quaker Oats Company13) and currently is still conducted in energy-intensive processes using high-pressure steam to supply heat and strip out furfural in batch or continuous reactors over homogeneous acid catalysts, which gives limited furfural yields of only ca. 50% due to the severe carbon loss to humins.14 Heterogeneous catalysis is usually preferred due to the ease of catalyst separation and reuse, and solid acid catalysts have received significant attention for the synthesis of furanics from C5/C6 sugars.14–18 However, issues still need to be addressed such as the poor hydrothermal stability of solid acid catalysts, long reaction time (>1 h), and need for frequent regeneration due to the humin deposition.14,15 Consequently, a green and efficient homogeneous catalytic system and process is still attractive for (scaled-up) furfural production.
One typical strategy to improve the furfural yield is suppressing the furfural degradation by its in situ extraction from the aqueous reaction media using an organic phase (i.e., biphasic solvent system). It is well known that batch reactors for reactions in biphasic systems usually suffer from poor flow pattern control and mixing when scaled up, and as such the low heat/mass transfer efficiency therein tends to limit the xylose conversion and furfural yield. Recently, continuous flow processing in microreactors has been used as a promising tool for fast kinetic studies and an efficient production platform for the synthesis of furanics such as 5-hydroxymethylfurfural (HMF) or 5-chloromethylfurfural (CMF) from C6 sugars in monophasic or biphasic solvent systems,18–26 due to advantages such as the superior heat/mass transfer rates, precise process control and ease of productivity increase.27,28 Comparatively, there have been fewer reports about the application of microreactors for furfural synthesis. We have recently reported the use of a slug flow microreactor for xylose conversion over an HCl catalyst in a water (with 10 wt% NaCl addition)–methyl isobutyl ketone biphasic system, where a promising furfural yield up to 93% was achieved at 180 °C and 4 min.29 The furfural extraction rate was estimated to be two orders of magnitude higher than the rate of furfural formation or degradation, rendering the reaction under kinetic control.
Besides furfural degradation, which can be mitigated by efficient extraction, xylose condensation is the other cause of the carbon loss to humins. Therefore, another strategy to boost the furfural yield is to regulate the xylose reaction network to reduce its condensation. Our recent work demonstrated the use of chloride ions to improve the xylose reaction kinetics by promoting the xylose dehydration and suppressing its condensation.29 Beyond the high furfural yield (93% from 1 M xylose), the addition of 10 wt% NaCl in the aqueous phase somewhat increased the viscosity and imposed additional operation difficulty for the microreactor system. Therefore, in this work we have explored another possibility to improve the xylose conversion chemistry. It has been reported that xylulose, an isomer of xylose, gives by far higher kinetic rates and furfural yields compared with xylose.30 In the past years, several mineral Lewis acids such as Cr(III), Fe(III) and Al(III) have been reported to be active for xylose isomerization to xylulose in water.30–33 This opens the opportunity for a concept of tandem catalysis where xylose is isomerized in situ to xylulose (over a Lewis acid) followed by xylulose dehydration to furfural (over a Brønsted acid) in high yields. Among others, Cr(III) is toxic and carcinogenic, and Fe(III) is highly active for the side reactions leading to humins,31 while Al(III) (e.g. AlCl3) is cheap with low toxicity. Yang et al.32 reported a furfural yield of 75% from xylose in a NaCl–water/tetrahydrofuran biphasic system using AlCl3 as the catalyst at 140 °C in a microwave-heated batch reactor. Yang et al.33 reported a furfural yield of up to 87.8% from xylan using Al2(SO4)3 as the catalyst under microwave conditions, and the hexa-coordinated Al(OH)2+ species were suggested to be the active sites for xylose–xylulose isomerization via ESI-MS spectrometry. However, in both cases, Al(III) was used solely without the addition of an external Brønsted acid, which might deviate from the optimal scenario for tandem acid catalysis. It is known that Al(III) hydrolyzes rapidly in water to form various species such as [Al(H2O)6]3+, [Al(OH)(H2O)5]2+ and [Al(OH)2(H2O)4]+, etc., depending on the pH value, initial Al(III) concentration and temperature. Considering that Lewis and Brønsted acids catalyze different reactions, and the amount of Lewis acidic Al species is regulated by Brønsted acidity via a hydrolysis equilibrium (eqn (S1)–(S4)†), it is important to investigate the interaction between the two acid types and the relevant effects on the sub-reactions within the xylose conversion network. Mittal et al.34 briefly reported furfural synthesis from hemicellulose (present in untreated poplar wood) over a combination of 33 mM HCl and 8 mM AlCl3 in a monophasic dioxane/water (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) solvent system, where a promising furfural yield of 91% was obtained at 200 °C in 5 min. Lopes et al.31 investigated the catalytic effect of CrCl3, FeCl3 and AlCl3 combined with formic acid as the catalyst for xylose conversion in monophasic water, and the best result was found with AlCl3, giving a furfural yield of ca. 70% at 130 °C. An empirical kinetic model was developed; however, it lacks insights into the catalytically active Al species and their amount variation with Brønsted acidity, which limits the model's use for other conditions. In general, despite the promising furfural yields over the AlCl3 catalyst as reported in the literature, deep knowledge is still required on aspects such as (i) the xylose conversion network and the role of Lewis and Brønsted acids therein; (ii) the catalytically active Al species responsible for the sub-reactions within the xylose conversion network; (iii) the interaction between the Lewis acid (AlCl3) and Brønsted acid (HCl), and their regulating effects on xylose conversion; and (iv) a comprehensive kinetic model with the quantitative incorporation of catalytically active Al species under varying reaction conditions. Such a model has not been reported so far, but is of great importance for a proper process design and optimization for efficient furfural production from xylose via synergetic Lewis/Brønsted acid catalysis, and thus is one of the aims in this work.
1) solvent system, where a promising furfural yield of 91% was obtained at 200 °C in 5 min. Lopes et al.31 investigated the catalytic effect of CrCl3, FeCl3 and AlCl3 combined with formic acid as the catalyst for xylose conversion in monophasic water, and the best result was found with AlCl3, giving a furfural yield of ca. 70% at 130 °C. An empirical kinetic model was developed; however, it lacks insights into the catalytically active Al species and their amount variation with Brønsted acidity, which limits the model's use for other conditions. In general, despite the promising furfural yields over the AlCl3 catalyst as reported in the literature, deep knowledge is still required on aspects such as (i) the xylose conversion network and the role of Lewis and Brønsted acids therein; (ii) the catalytically active Al species responsible for the sub-reactions within the xylose conversion network; (iii) the interaction between the Lewis acid (AlCl3) and Brønsted acid (HCl), and their regulating effects on xylose conversion; and (iv) a comprehensive kinetic model with the quantitative incorporation of catalytically active Al species under varying reaction conditions. Such a model has not been reported so far, but is of great importance for a proper process design and optimization for efficient furfural production from xylose via synergetic Lewis/Brønsted acid catalysis, and thus is one of the aims in this work.
Herein, experiments on xylose (as well as lyxose, xylulose and furfural) using AlCl3 or (and) HCl as the catalyst were firstly performed in monophasic water in a flow microreactor to study the kinetics under varying conditions (temperature of 120 to 180 °C, HCl concentration of 0.05 to 0.4 M, AlCl3 concentration of 0.04 to 0.12 M, and each substrate concentration of 0.01 to 0.5 M). Based on the reaction results, the xylose conversion network was developed and the role of Lewis and Brønsted acids therein was elucidated. Advanced mass spectroscopy on model reactants was performed to identify the catalytically active Al species and study its variation with varying AlCl3/HCl ratios. The amounts of active Al species were quantified according to the hydrolysis equilibrium of AlCl3 and incorporated into the kinetic model, which consists of a separate Brønsted acid-catalyzed part and a Lewis acid-catalyzed part. Kinetic parameters for the conversion of individual sugars and furfural over Al species or H+ were estimated by fitting the model to the experimental data. Furthermore, xylose conversion using the combined AlCl3/HCl catalyst was performed in a water–methyl isobutyl ketone (MIBK; inexpensive, low toxicity and high furfural partition capacity) biphasic system in a slug flow microreactor, where the results were shown to be well described by the kinetic model with the incorporation of furfural extraction between the phases. Process optimization for the furfural yield was conducted based on the kinetic model. Moreover, the recyclability and reusability of the homogeneous catalyst were also demonstrated, and a performance comparison with literature work was made to highlight the potential of the present process using microreactors for the efficient furfural synthesis from xylose.
2. Methods
2.1 Materials
D-Xylose (99 wt%), D-lyxose (99 wt%), aluminum chloride hexahydrate (99 wt%), and hydrochloric acid (37 wt%) were all purchased from Sigma-Aldrich Co., Ltd. MIBK (99 wt%) was purchased from Acros Organics Co., Ltd. D-Xylulose was purchased from Carbosynth, UK. All chemicals were of chemical grade and used as received without any further treatment. Milli-Q water was used to prepare solutions throughout all the experiments. Perfluoroalkoxy alkane (PFA) tubing (inner diameter: 1.65 mm) was supplied by the Swagelok company and used as capillary microreactors.2.2 Experimental setup and procedure
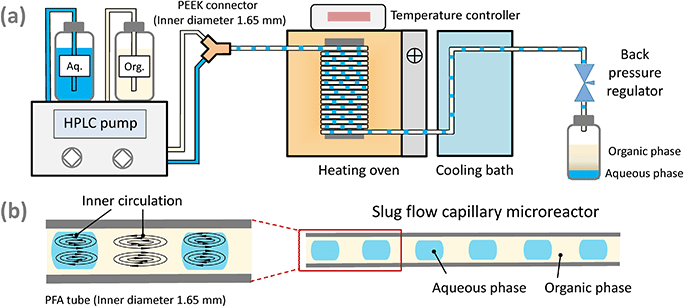
Experiments on the conversion of sugars or furfural using HCl and (or) AlCl3 as the catalyst were conducted in the microreactor in monophasic water or biphasic water–MIBK solvent systems. Monophasic experiments were performed to study the xylose conversion network and the role of HCl and AlCl3 under a wide range of conditions, including a temperature range from 120 to 180 °C, initial concentration of substrates (xylose, xylulose, lyxose and furfural) between 0.01 and 0.5 M, HCl concentration of 0.05 to 0.4 M, and AlCl3 concentration of 0.04 to 0.12 M (cf. more details in Table S1†). Biphasic experiments were performed under some representative conditions mentioned above in a slug flow microreactor, with an initial organic to aqueous volumetric flow ratio (O/A) of 1 to 4 (fed at 20 °C).Fig. 1a shows the slug flow microreactor setup used for xylose conversion to furfural. The setup and procedure are similar to that reported in our previous work.19,20,29 Typically, the aqueous feed contained sugars or furfural as well as HCl and (or) AlCl3 catalyst, and the organic feed was MIBK. Both phases were fed to the microreactor using a binary HPLC pump unit (Agilent 1200 Series). A uniform slug flow was generated in the downstream PFA capillary microreactor by mixing two phases in a polyether ether ketone (PEEK) Y-connector (inner diameter: 1.65 mm; Fig. 1b). The hydrophobic nature of the PFA microreactor renders MIBK as the continuous phase, and the aqueous reaction phase as droplets which are not in direct contact with the microreactor to avoid humin deposition on the wall causing blockage.19,20,29 The microreactor was coiled around an aluminum block in an oven maintained at a certain temperature. The reaction was quenched by a water bath (ca. 20 °C) at the microreactor exit. The pressure in the microreactor was maintained at ca. 10 bar by a back-pressure regulator at the end of the microreactor to maintain the reactor content in the liquid state. Product samples were collected after the system reached steady state (i.e., after ca. 4 times the residence time in the microreactor). The length of the microreactor (L), i.e., the section inside the oven, is typically 3.3 m. For experiments aimed at investigating the mass transfer limitation, microreactors of 1.2 m and 16.9 m length were also used. The residence time (τ) in the microreactor was varied by adjusting the flow rates (details about the calculation of τ and the actual flow rates have been previously reported19). The collected aqueous and organic phases were filtered through a polytetrafluoroethylene (PTFE, 0.45 μm) filter, and subsequently analyzed by high performance liquid chromatography (HPLC) and gas chromatography (GC), respectively.
Monophasic kinetic experiments were performed in the same setup as above with the organic-phase flow being stopped. Before each run, the microreactor was flushed with water to remove any possibly remained humins.
The above monophasic and biphasic experiments under representative conditions were conducted at least twice, the results of which are reproducible within a 5% standard deviation.
2.3 Analysis and characterization
The composition of the aqueous phase was analyzed by an Agilent 1200 HPLC, equipped with an Agilent 1200 pump, a refractive index detector, a standard ultraviolet detector as well as a Bio-Rad organic acid column (Aminex HPX-87H). A diluted aqueous H2SO4 solution (5 mM, 0.55 mL min−1) was used as the eluent, and the temperature of the column was maintained at 60 °C. A difficulty in the analysis is in the quantification of xylulose and lyxose due to their similar retention times on the HPLC chromatogram leading to severe overlapping30,31 (12.9 min for xylulose and 13.1 min for lyxose in this work; cf. Fig. S1a†), which may be the reason that some earlier studies have not reported lyxose as a xylose isomerization product.32,33 In this work, this issue was addressed using a Gaussian deconvolution method for data treatment,31 where the peak areas of xylulose and lyxose were obtained by deconvoluting their overlapped curve (Fig. S1b; the details are discussed in section S2 in the ESI†). The organic phase was analyzed by TraceGC Ultra GC, equipped with a flame ionization detector and a fused silica column (Stabilwax-DA). The concentrations of the components in the aqueous and organic samples were determined from the calibration curves obtained using the standard solutions with known compounds and concentrations.Electro-spray ionization mass spectra (ESI-MS) were recorded on an Orbitrap XL mass spectrometer (Thermo Fisher Scientific) with ESI ionization in the positive mode. Solution samples of xylose, lyxose, xylulose and furfural containing AlCl3 and HCl were measured in the range of m/z 100–600 in positive mode. The data acquisition and analyses were performed on Xcalibur software.
2.4 Definitions and calculations
The conversion of substrate i (Xi) and the yield of product j (Yj) are defined by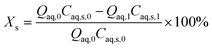 | (1) |
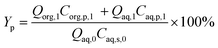 | (2) |
| Qaq,1 = Qaq,0γaq | (3) |
| Qorg,1 = Qorg,0γorg | (4) |
The carbon balance is defined by
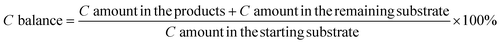 | (5) |
The carbon balance is based on the quantified known products by HPLC and GC (xylose, xylulose, lyxose and furfural). It does not account for the non-identified soluble/insoluble byproducts.
The amount of aluminum species and H+ in water under varying temperatures and initial concentrations of AlCl3 and HCl is calculated according to the hydrolysis equilibrium of AlCl3 in water. The calculation procedure and the results under some representative conditions are provided in sections S4, S8 and Table S5 of the ESI.†
3. Results and discussion
3.1 Furfural synthesis from xylose using HCl or combined HCl/AlCl3 as the catalyst in a biphasic slug flow microreactor
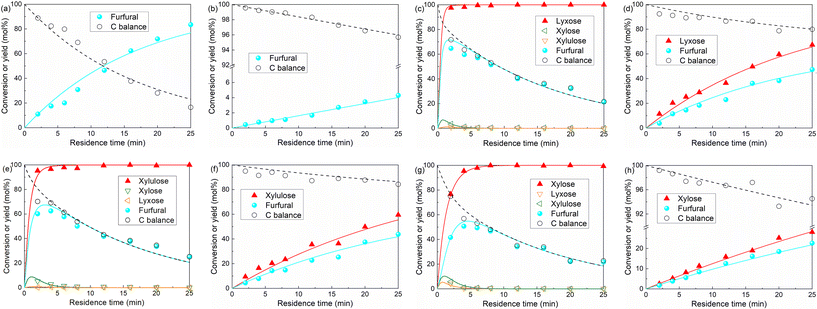
We first demonstrated xylose conversion using HCl with or without the addition of AlCl3 as the catalyst at 160 °C in the water/MIBK biphasic system in slug flow microreactors. In a typical run over the individual HCl (200 mM) catalyst, the furfural yield increased gradually to a maximum of 79% at 25 min with a xylose conversion of 97%. In the meantime, the carbon balance decreased gradually to less than 80%, due to the carbon loss to humins via xylose condensation and furfural degradation (Fig. 2a). After the addition of 40 mM AlCl3, xylulose and lyxose appeared as the respect isomerization and epimerization products of xylose, the yields of which showed clear maxima at an early stage of the reaction, indicating that these are intermediate products which were fast prone to further chemistry (Fig. 2b). Moreover, a far higher xylose conversion rate, as well as a higher furfural yield, were observed in comparison with the case catalyzed by solely HCl (Fig. 2a). The furfural yield reached 86% at 16 min and then stayed stable with a prolonged residence time to 25 min. The improved carbon balance, which remained over 85%, suggests a reduced overall humin formation (Fig. 2b). A similar promoting effect of AlCl3 was also observed with the addition of 80 mM AlCl3 and 120 mM AlCl3, and no distinct differences in the xylose conversion and product yields were observed among these different AlCl3 loadings under the current reaction conditions (Fig. 2b–d). Besides AlCl3, other Lewis acids such as CrCl3 and FeCl3 have also been reported to improve the furfural yield, and most researchers attributed this to the tandem catalysis comprising xylose isomerization to xylulose followed by xylulose dehydration to furfural in higher yields.30–33 To compare the reaction performance of xylose with its isomers, benchmark experiments with xylulose and lyxose as the substrate were performed under otherwise the same conditions (160 °C, 200 mM HCl) (Fig. S2†). Indeed, a higher conversion rate was observed for xylulose and lyxose (Fig. S2a†). However, despite the higher furfural yield obtained from xylulose, the maximum furfural yield is only ca. 82%, which is lower than that (ca. 86%) in the present work using combined HCl/AlCl3 as the catalyst, not to mention the lower maximum furfural yield (ca. 74%) given by lyxose, the other isomer of xylose (Fig. S2b†). Therefore, we believe that the tandem catalysis via xylulose at least should not be the only reason for the promoting effect of Lewis acid AlCl3. To reveal more fine details for a deeper process understanding and optimization, clear insights into the xylose reaction network, the role of HCl and AlCl3 therein, and the reaction kinetics are of great importance and will be addressed hereafter (vide infra).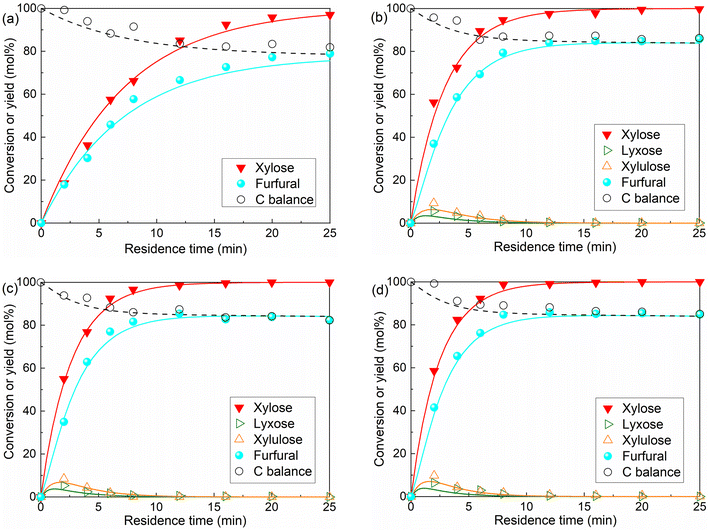 | ||
| Fig. 2 Furfural synthesis from xylose in a biphasic slug flow microreactor over (a) 200 mM HCl, (b) 200 mM HCl and 40 mM AlCl3, (c) 200 mM HCl and 80 mM AlCl3, and (d) 200 mM HCl and 120 mM AlCl3. Reaction conditions: 160 °C, 0.1 M xylose, L = 3.3 m, O/A = 4. Symbols denote the experimental data and lines are the model values (the same in Fig. 3, 7–9 and 14 shown hereafter). | ||
3.2 Xylose conversion network and the role of Lewis and Brønsted acids: monophasic experiments with sugars or furfural using AlCl3 or HCl as the catalyst in the microreactor
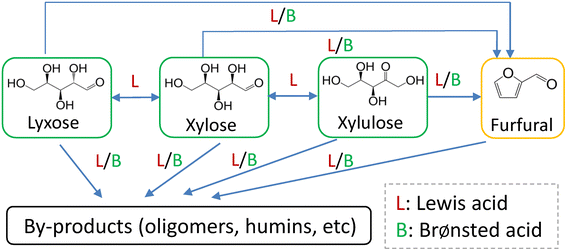
Since AlCl3 hydrolyzes in water to form various aluminum species and H+ (cf. eqn (S1)–(S6)†), the catalytic effect of AlCl3 may be related to all of them. To understand the role of Lewis acid (Al species from AlCl3) and Brønsted acid (H+) catalysts in the reaction (e.g., glucose conversion), some researchers conducted comparative reactions over individual AlCl3 or HCl while maintaining the pH for both cases identical at room temperature.35 However, this might not be precise as the hydrolysis equilibrium of AlCl3 in water is a strong function of temperature (eqn (S6)†), and thus the actual H+ concentration in AlCl3 solution at the reaction temperature differs significantly from that at room temperature. For example, the H+ concentration in 40 mM AlCl3 solution was calculated to increase from 0.39 mM at 20 °C to 19 mM at 160 °C (Table S5†). Therefore, to understand the xylose conversion network and precisely distinguish the impact of Lewis and Brønsted acids, herein monophasic experiments with xylose and its reaction intermediates (furfural, lyxose and xylulose) were comparatively investigated under the catalysis of either AlCl3 (40 mM) or HCl (21.1 mM) with equal Brønsted acidity (19.0 mM H+) at 160 °C.3.3 Insights into the catalytically active Al species for the sub-reactions within the xylose conversion network
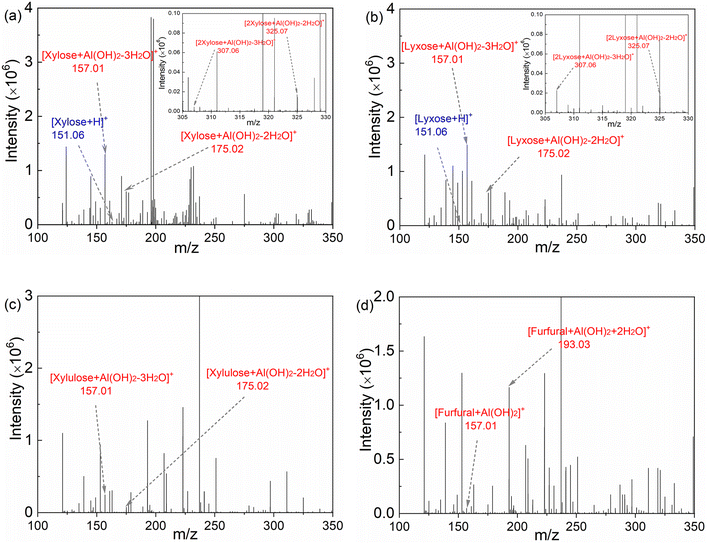
In order to establish a comprehensive kinetic model that incorporates the interaction between Lewis and Brønsted acids and the corresponding impact on the xylose conversion under varying reaction conditions, it is important to determine the catalytically active Al species for the sub-reactions within the xylose conversion network. Lewis acidic metal ions such as Cr3+, Fe3+ and Al3+ have been reported to catalyze the xylose conversion to furfural.30–33 However, it is difficult to identify their catalytically active species, due to the presence of a number of metal species that are in equilibrium with each other in water. For instance, AlCl3 rapidly hydrolyzes in water to form various species such as [Al(H2O)6]3+, [Al(OH)(H2O)5]2+, [Al(OH)2(H2O)4]+ and [Al(OH)4]−, the amount of which depends on the initial AlCl3 concentration, Brønsted acidity and temperature (cf. section S4 in the ESI†).40 Yang et al.33 observed xylose-coordinated Al(OH)2+ compounds in ESI-MS spectroscopy and suggested Al(OH)2+ as the active sites for xylose–xylulose isomerization using Al2(SO4)3 as the catalyst in water. However, the coordination of Al species with other intermediates (lyxose, xylulose and furfural) within the xylose conversion network was not studied in their work and thus it lacks a comprehensive overview of the active Al species for different sub-reactions.To gain insights into the active Al species for all the sub-reactions, herein aqueous AlCl3/HCl solutions (40 mM AlCl3 and 200 mM HCl) containing xylose, lyxose, xylulose or furfural were prepared and characterized by ESI-MS spectroscopy (Fig. 5). Peaks of [C5sugar + Al(OH)2–2H2O]+, [C5sugar + Al(OH)2–3H2O]+, [2C5sugar + Al(OH)2–2H2O]+ and [2C5sugar + Al(OH)2–3H2O]+ fragments (at m/z = 175.02, 157.01, 325.07 and 307.06, respectively) are present in the ESI-MS spectra of both the xylose and lyxose solutions (Fig. 5a and b). The spectrum of the xylulose solution also shows peaks at m/z = 157.01 and 175.02, corresponding to [xylulose + Al(OH)2–3H2O]+ and [xylulose + Al(OH)2–2H2O]+, respectively (Fig. 5c). Peaks from furfural-coordinated Al(OH)2+ compounds such as [furfural + Al(OH)2]+ and [furfural + Al(OH)2 + 2H2O]+ were also observed in the spectra of furfural solution at m/z = 157.01 and 193.03, respectively (Fig. 5d). The above-mentioned coordination compounds of [Al(OH)2]+ with xylose, lyxose, xylulose and furfural indicate that [Al(OH)2]+ is the main species that coordinates with xylose and its intermediates during the xylose conversion. Moreover, peaks corresponding to [Al + (xylose)n]3+, [Al(OH) + (xylose)n]2+ or [Al(OH)3 + xylose + nH]n+ species were not detected in the ESI-MS spectra of all samples. Therefore, [Al(OH)2]+ is believed to be the catalytically active Al species for the sub-reactions within the xylose reaction network.
An increase in the intensity of the peaks from xylose-coordinated Al(OH)2+ compounds was observed with increasing AlCl3 loading (Fig. S3†), indicating that the amount of Al(OH)2+ as the catalytically active sites is a function of the relative Lewis/Brønsted acidity of the solution (cf. eqn (S1)–(S5)†). To provide more quantitative insights into the amounts of H+ and Al(OH)2+ for kinetic studies, their concentrations under varying temperatures and initial concentrations of AlCl3 and HCl were calculated and shown in Fig. 6. Generally, the increase of temperature and AlCl3 concentration promotes the hydrolysis of AlCl3 towards producing more H+ and Al(OH)2+ (Fig. 6a and b; the slight decrease of H+ concentration from 120 to 140 °C is caused by the volume increase of water at higher temperatures), while the increase of HCl concentration largely suppresses the formation of Al(OH)2+ (Fig. 6b). Such an interaction between AlCl3 and HCl clearly indicates the importance of optimizing the relative Lewis/Brønsted acidity for the maximized furfural yields.
 | ||
| Fig. 6 Concentration of Al(OH)2+ and H+ in water as a function of (a) temperature and (b) HCl concentration at different AlCl3 concentrations. Conditions: 160 °C, 40 mM AlCl3, 100 mM HCl (unless otherwise stated); concentrations are estimated according to eqn (S5)–(S8).† | ||
3.4 Kinetic behavior of the conversion of xylose, lyxose, xylulose and furfural in the microreactor
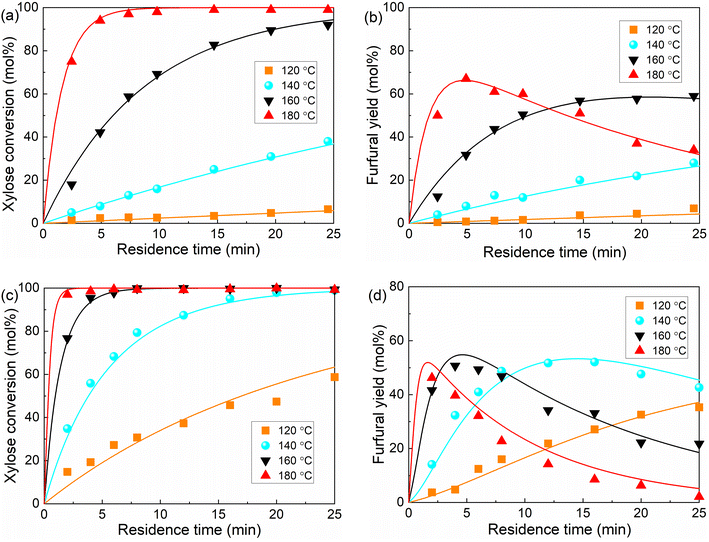
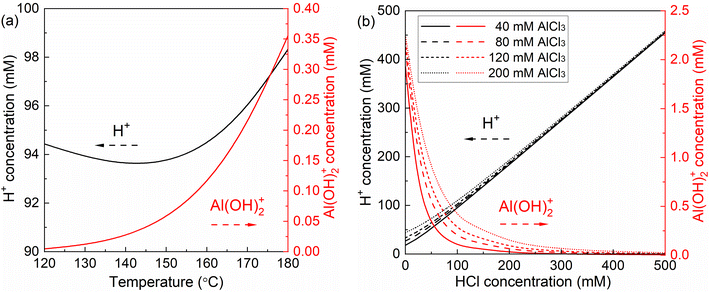
To acquire kinetic insights into xylose conversion over AlCl3/HCl in water, monophasic experiments were conducted in microreactors regarding the effect of the reaction temperature and concentrations of substrate and catalyst (individual HCl, AlCl3 or their combination) on the conversion of xylose, lyxose, xylulose and furfural in water. Moreover, biphasic experiments with varying O/A ratios and temperatures were also performed in microreactors to study the effect of the biphasic operation on the xylose conversion.For the HCl-catalyzed reactions of xylose, lyxose, xylulose and furfural in water, a higher HCl concentration significantly promoted their consumption rate, whereas a minor effect was observed on the maximum furfural yields from the sugars (Fig. S9†), which suggests similar reaction orders in H+ concentration among the HCl-catalyzed sub-reactions. For the AlCl3-catalyzed reactions, a very slight increase in sugar (xylose, lyxose and xylulose) conversion and a decrease in furfural yield were observed at higher AlCl3 concentrations within the studied range (40–120 mM; Fig. S10–S13†), indicating an overall smaller reaction order in Al(OH)2+ for the desirable reaction forming furfural than for side reactions involving furfural within the AlCl3-catalyzed sugar conversion network. Moreover, it was noticed that the actual concentration of the produced Al(OH)2+ did not differ much between these different initial AlCl3 concentrations without the external HCl addition (being 1.93, 2.10 and 2.18 mM for 40, 80 and 120 mM AlCl3, respectively; cf. Fig. 6b, entries 3, 5 and 6 of Table S5†), which explains the performance similarity in the sugar conversion among these varying AlCl3 concentrations.
As revealed in Fig. 6b, a relatively larger difference in the amount of Al(OH)2+ between different initial AlCl3 concentrations can be realized with a proper addition of HCl (20–200 mM). Thus, AlCl3 was used in combination with HCl (100 mM) to better study the effect of Al(OH)2+ concentration as well as the synergy between Lewis and Brønsted acids on the xylose conversion. It was observed that although the xylose conversion over combined AlCl3/HCl is slower than in the AlCl3-only case, it is still much faster compared with the HCl-only case, and increased monotonically with increasing AlCl3 concentration (Fig. 8a). Considering the much smaller amount of Al(OH)2+ (in the AlCl3-catalyzed case) than that of H+ (in the HCl-catalyzed case), the faster xylose conversion in the former case indicates a significantly higher activity of Al(OH)2+ than H+. The higher concentration of AlCl3 (and thus Al(OH)2+) promoted both the formation and consumption of the intermediate sugars, leading to their higher yields in the beginning but lower yields at later stage of the reaction (Fig. S16b and c†), which suggests lower reaction orders in Al(OH)2+ for the xylose isomerization reactions than for the further conversion of these isomers (to furfural or humins). Moreover, a relatively lower maximum furfural yield was obtained over AlCl3 (40 mM) than over HCl (100 mM), due to the more severe side reaction over Al(OH)2+ leading to humins (Fig. 8b). Comparatively, the combined AlCl3/HCl catalyst gave higher furfural yields than both AlCl3 and HCl (Fig. 8b), though the furfural yield decreased with increasing AlCl3 (or Al(OH)2+) concentration within the studied range (40–200 mM). This trend is in line with the xylose conversion over an AlCl3-only catalyst of different amounts (Fig. S10d†). Thus, side reactions are believed to be of a higher reaction order in Al(OH)2+ than reactions forming furfural within the studied AlCl3 concentration range.
 | ||
| Fig. 8 Effect of the AlCl3/HCl molar ratio on (a) xylose conversion and (b) furfural yields in water in the microreactor. Reaction conditions: 160 °C, 0.1 M xylose. The yields of lyxose and xylulose are given in Fig. S16.† | ||
For both HCl-catalyzed and AlCl3-catalyzed cases, the reaction of xylose, lyxose, xylulose or furfural at different substrate concentrations shows a similar conversion of sugars (as well as the corresponding furfural yield) and conversion of furfural with the catalyst concentration (Fig. S14–S16†), which is indicative of an overall first-order reaction order with respect to the substrate (especially regarding the furfural formation) for both catalysts.
3.5 Kinetic modelling studies
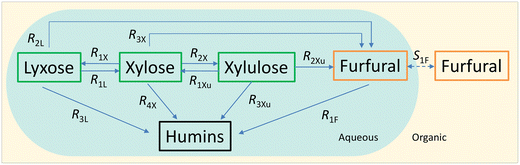
The experimental studies in section 3.4 have shown a different temperature-dependency of xylose conversion over AlCl3 and HCl, a different activity of AlCl3 and HCl, as well as a positive effect of their combination for xylose conversion to furfural. For a comprehensive process understanding and optimization, a kinetic model that quantitatively captures the role of both Lewis and Brønsted acids (Al(OH)2+ and H+) in xylose conversion and incorporates the furfural extraction between the phases is addressed herein.In this section, the kinetic model for reactions in monophasic (water) and biphasic (water/MIBK) systems was established based on a simplified overview of the revealed xylose conversion network (cf.Fig. 4 and 10). In Fig. 10, R1X, R2X, R3X and R4X represent the reaction rates for xylose conversion to lyxose, xylulose, furfural and humins, respectively; R1L, R2L and R3L are the reaction rates for lyxose conversion to xylose, furfural and humins, respectively; R1Xu, R2Xu and R3Xu denote the reaction rates for xylulose conversion to xylose, furfural and humins, respectively; R1F is the reaction rate for furfural degradation; and S1F is the transfer rate of furfural from water to MIBK phase.
In the present monophasic microreactor system, it has been proved that the axial diffusion is negligible (characterized by the sufficiently large Bodenstein numbers of xylose and furfural of the order of ca. 106–107), and the parabolic velocity profile within the laminar flow can be compensated by the fast radial diffusion (characterized by the Fourier numbers of xylose and furfural being (much) larger than 1) to afford an approximate plug flow behaviour.29,41 Therefore, here a simplified plug flow model was adopted for kinetic modelling.
Based on the reaction network in Fig. 10, the mole balance of different substances in water in microreactor can be expressed as
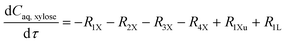 | (6) |
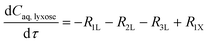 | (7) |
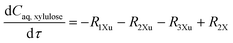 | (8) |
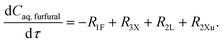 | (9) |
In the present work, experimental studies regarding the effect of substrate concentration show that the sugar conversions (and the corresponding furfural yield) and the furfural conversion over either AlCl3 or HCl are independent of the substrate concentrations (Fig. S14 and S15†). Therefore, a first-order dependence on the reactant is assumed for all H+-catalyzed and Al(OH)2+-catalyzed sub-reactions. According to the role of Lewis and Brønsted acids in the xylose conversion network (Fig. 4), the rates of the sub-reactions (Rij; i = 1, 2, 3 or 4; j = X, L, Xu or F, representing xylose, lyxose, xylulose or furfural, respectively, the same hereafter) can be divided into two groups: the ones catalyzed by only Lewis acids and the other ones catalyzed by both Lewis and Brønsted acids.
For reactions catalyzed by only Lewis acids (i.e., R1X, R2X, R1L and R1Xu; Fig. 4 and 10), the reaction rates are defined as
| RiX = kappL,iXCaq,xylose | (10) |
| RiL = kappL,iLCaq,lyxose | (11) |
| RiXu = kappL,iXuCaq,xylulose | (12) |
| RiX = (kappL,iX + kappB,iX)Caq,xylose | (13) |
| RiL = (kappL,iL + kappB,iL)Caq,lyxose | (14) |
| RiXu = (kappL,iXu + kappB,iXu)Caq,xylulose | (15) |
| RiF = (kappL,iF + kappB,iF)Caq,furfural | (16) |
In the above eqn (10)–(16), kappL,iX and kappB,iX (i = 1, 2, 3 or 4; j = X, L, Xu or F) are the apparent reaction rate constants for the sub-reactions catalyzed by a Lewis acid Al(OH)2+ and Brønsted acid H+, respectively (cf. the more detailed definition in Table S6†). Considering the reversible epimerization between xylose and lyxose, and the isomerization between xylose and xylulose, there are kappL,1L = kappL,1X/K1X and kappL,1Xu = kappL,2X/K2X, where K1X and K2X are the corresponding equilibrium constants. The values of K1X and K2X under different temperatures are calculated from the kinetic parameters reported in the literature42 and provided in Table S7.†
At the start of the reactions, the temperature of the reactant can be quickly raised from the initial room temperature (ca. 20 °C) to the final reaction temperature (T) within seconds due to the excellent heat transfer efficiency in the current microreactor setup;19 as such this heating-up stage is reasonably neglected for kinetic modelling in this work. After heating-up, the density of the aqueous phase decreased so that its volumetric flow rate at the reaction temperature T (Qaq) differed from its initial value at ca. 20 °C (Qaq,0), and is corrected as
| Qaq = Qaq,0αmono,aq | (17) |
| αmono,aq = 0.921 + 0.062e0.007T | (18) |
Considering the phase volume change, the conversion and yield in the model are calculated as
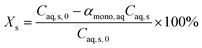 | (19) |
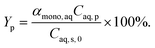 | (20) |
In summary, the developed kinetic model for xylose conversion in monophasic water in microreactors comprises a set of nonlinear ordinary differential equations (ODE) for the mole balances of sugars and furfural (eqn (6)–(9)), together with equations to describe the reaction rates (eqn (10)–(16)) and phase volume change (eqn (17) and (18)). The apparent reaction rate constants (kappL,ij and kappB,ij) were then determined by simultaneously processing the experimental data in Matlab R2010a (MathWorks) using the lsqnonlin nonlinear least-squares fitting function, based on a Trust-region-reflexive algorithm to perform a local minimization of the errors between the model values and experimental data (i.e., in terms of the reactant conversion and product yields).
Considering the phase volume change, for a given set of initial concentrations of AlCl3 and HCl at 20 °C (CAlCl3, 0 and CHCl,0), there are CAlCl3 = CAlCl3, 0/αmono,aq and CHCl = CHCl,0/αmono,aq at the reaction temperature, which are needed for the estimation of CAl(OH)2+ and CH+ (cf. section S4 and Table S5†). For a first-order reaction with respect to the catalyst, the corresponding apparent reaction rate constant should be linearly dependent on the catalyst concentration. Such a linear relationship was clearly observed between kappB,ij and CH+ for all H+-catalyzed sub-reactions (at 160 °C; Fig. S17a†), indicating a first-order for H+ concentration. Thus, it is reasonable to describe kappB,ij as
| kappB,ij = kB,ijCH+ | (21) |
Comparatively, a non-linear relationship was observed between kappL,ij and CAl(OH)2+ (e.g., at 160 °C; not shown for brevity). Therefore, for Al(OH)2+-catalyzed sub-reactions a power law approach was applied with the reaction order in Al(OH)2+ as the unknown, and then kappL,ij was described as
| kappL,ij = kL,ijCAl(OH)2+nL,ij | (22) |
In eqn (21) and (22), kB,ij and kL,ij are the intrinsic reaction rate constants for H+- and Al(OH)2+-catalyzed sub-reactions, respectively. nL,ij represents the reaction order in Al(OH)2+. Eqn (22) can be rearranged as
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kappL,ij = nL,ij kappL,ij = nL,ij![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CAl(OH)2+ + ln CAl(OH)2+ + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kL,ij kL,ij | (23) |
A linear relationship between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kappL,ij and lnCAl(OH)2+ was obtained (Fig. S17b†), and after a linear regression, the corresponding reaction orders nL,ij and intrinsic reaction rate constants kL,ij were determined from the slopes and intercepts, respectively.
kappL,ij and lnCAl(OH)2+ was obtained (Fig. S17b†), and after a linear regression, the corresponding reaction orders nL,ij and intrinsic reaction rate constants kL,ij were determined from the slopes and intercepts, respectively.
The temperature dependency of the intrinsic reaction rate constants (kB,ij or kL,ij) is described according to the Arrhenius equation as
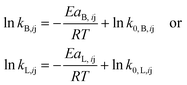 | (24) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kB,ij or ln
kB,ij or ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kL,ij) versus the inverse reaction temperature (1/T) and fitting according to the Arrhenius expression (eqn (24)). The best estimations of the intrinsic kinetic parameters and their standard deviations are given in Table 1. Generally, the H+-catalyzed reactions have higher activation energies compared with the Al(OH)2+-catalyzed ones, in line with the observed higher activity of Al(OH)2+ than H+ (Fig. 8). For H+-catalyzed reactions, the activation energies for the desired sugar dehydration reaction producing furfural (EaB,3X, EaB,2L and EaB,2Xu), and for the side reactions of sugar condensation to humins (EaB,4X, EaB,3L and EaB,3Xu), are both higher than that for furfural degradation to humins. Similar results were also found in Al(OH)2+-catalyzed reactions, where activation energies for sugar condensation to humins (EaL,4X, EaL,3L, EaL,3Xu) are even higher than that for sugar dehydration to furfural (EaL,3X, EaL,2L, EaL,2Xu). This suggests that the formation of both furfural and humins from the sugars is promoted at higher temperatures, corroborating the importance of temperature analysis for maximized furfural yields (vide infra). Moreover, the reaction orders in Al(OH)2+ (nL,ij) are smaller than 1, consistent with the higher activity of Al(OH)2+ than H+ at a low amount, which was also revealed by the by far higher kappL,ij than kappB,ij at the same catalyst concentration within the studied range (Fig. S18a and b†). The reaction orders in Al(OH)2+ (nL,ij) for sugar dehydration to furfural (nL,3X, nL,2L, nL,2Xu) are also smaller than those for sugar condensation (nL,4X, nL,3L, nL,3Xu) and furfural degradation to humins (nL,1F), implying that humin formation from furfural and sugars is more enhanced at higher concentrations of Al(OH)2+ compared with furfural formation. This is consistent with the lower furfural yields over sole AlCl3 than that catalyzed by combined AlCl3/HCl (Fig. 8b); as such, the selection of acid concentration and a proper AlCl3/HCl ratio is of importance in the process optimization (vide infra).
kL,ij) versus the inverse reaction temperature (1/T) and fitting according to the Arrhenius expression (eqn (24)). The best estimations of the intrinsic kinetic parameters and their standard deviations are given in Table 1. Generally, the H+-catalyzed reactions have higher activation energies compared with the Al(OH)2+-catalyzed ones, in line with the observed higher activity of Al(OH)2+ than H+ (Fig. 8). For H+-catalyzed reactions, the activation energies for the desired sugar dehydration reaction producing furfural (EaB,3X, EaB,2L and EaB,2Xu), and for the side reactions of sugar condensation to humins (EaB,4X, EaB,3L and EaB,3Xu), are both higher than that for furfural degradation to humins. Similar results were also found in Al(OH)2+-catalyzed reactions, where activation energies for sugar condensation to humins (EaL,4X, EaL,3L, EaL,3Xu) are even higher than that for sugar dehydration to furfural (EaL,3X, EaL,2L, EaL,2Xu). This suggests that the formation of both furfural and humins from the sugars is promoted at higher temperatures, corroborating the importance of temperature analysis for maximized furfural yields (vide infra). Moreover, the reaction orders in Al(OH)2+ (nL,ij) are smaller than 1, consistent with the higher activity of Al(OH)2+ than H+ at a low amount, which was also revealed by the by far higher kappL,ij than kappB,ij at the same catalyst concentration within the studied range (Fig. S18a and b†). The reaction orders in Al(OH)2+ (nL,ij) for sugar dehydration to furfural (nL,3X, nL,2L, nL,2Xu) are also smaller than those for sugar condensation (nL,4X, nL,3L, nL,3Xu) and furfural degradation to humins (nL,1F), implying that humin formation from furfural and sugars is more enhanced at higher concentrations of Al(OH)2+ compared with furfural formation. This is consistent with the lower furfural yields over sole AlCl3 than that catalyzed by combined AlCl3/HCl (Fig. 8b); as such, the selection of acid concentration and a proper AlCl3/HCl ratio is of importance in the process optimization (vide infra).
| ij | Reaction | H+ | [Al(OH)2]+ | |||
|---|---|---|---|---|---|---|
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k0,B,ij k0,B,ij![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
Ea B,ij (kJ mol−1) | lnk0,L,ij![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
Ea L,ij (kJ mol−1) |
n
L,ij![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
||
| a Corresponding reversible reactions (R1L and R1Xu) were modeled using equilibrium constants calculated from the literature42 (cf. Table S6†). b Units of k0 expressed in L mol−1 min−1. c Units of k0 expressed in LnL, ij mol−nL, ij min−1. | ||||||
| 1X | Xylose to lyxosea | — | — | 26.4 ± 3.3 | 94.7 ± 11.4 | 0.28 ± 0.02 |
| 2X | Xylose to xylulosea | — | — | 27.2 ± 1.7 | 97.3 ± 6.0 | 0.26 ± 0.02 |
| 3X | Xylose to furfural | 38.1 ± 1.0 | 139.7 ± 4.4 | 15.0 ± 0.7 | 58.7 ± 2.4 | 0.25 ± 0.04 |
| 4X | Xylose to humins | 34.6 ± 4.4 | 131.9 ± 6.3 | 31.5 ± 2.5 | 99.7 ± 8.7 | 0.95 ± 0.04 |
| 2L | Lyxose to furfural | 45.2 ± 2.7 | 162.8 ± 18.2 | 24.8 ± 0.5 | 82.3 ± 1.8 | 0.19 ± 0.04 |
| 3L | Lyxose to humins | 46.9 ± 2.4 | 171.1 ± 8.6 | 33.0 ± 0.7 | 99.4 ± 2.4 | 0.99 ± 0.03 |
| 2Xu | Xylulose to furfural | 26.4 ± 0.0 | 94.2 ± 0.0 | 25.5 ± 2.4 | 88.7 ± 8.3 | 0.21 ± 0.03 |
| 3Xu | Xylulose to humins | 23.2 ± 2.7 | 86.7 ± 8.9 | 32.4 ± 1.1 | 101.5 ± 3.7 | 0.98 ± 0.03 |
| 1F | Furfural to humins | 21.2 ± 1.1 | 85.4 ± 5.1 | 8.1 ± 1.1 | 26.7 ± 4.0 | 0.56 ± 0.02 |
| Qaq,1 = Qaq,0αbi,aq | (25) |
| Qorg,1 = Qorg,0αbi,org | (26) |
| αbi = u + vewT | (27) |
It is assumed that the organic solvent MIBK is non-reactive and served only as an extraction medium;20 then the mole balance in both phases (Caq,furfural and Corg,furfural) is described by
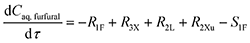 | (28) |
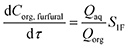 | (29) |
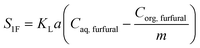 | (30) |
| m = a − bT | (31) |
In the current biphasic experiments in slug flow microreactors, the mass transfer limitation has been both theoretically estimated and experimentally proved to be absent (cf. section S11 and Fig. S21†); therefore the furfural concentrations in both phases can be also assumed to reach equilibrium immediately, as expressed by
| Corg,furfural = mCaq,furfural | (32) |
By combining with eqn (29) and (32), eqn (28) is simplified to
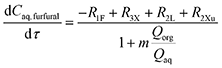 | (33) |
For given concentrations of HCl and AlCl3 at 20 °C (i.e., CAlCl3,0 and CHCl,0), their concentrations at the reaction temperature in the biphasic system are corrected as CAlCl3 = CAlCl3,0/αbi,aq and CHCl = CHCl,0/αbi,aq, which are used for the estimation of CAl(OH)2+ and CH+ (cf. section S4 and Table S5†).
The model equations in the current biphasic system are represented by eqn (6)–(8) and (33) for the aqueous phase concentration and eqn (32) for the organic phase concentration. Based on the estimated kinetic constants (Table 1), the m values (eqn (31)) and the phase volume change (eqn (25)–(27)), the component concentration during the reaction was modelled. Then, substrate conversion (Xs) and product yield (Yp) in the biphasic system in microreactor are calculated by
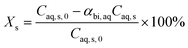 | (34) |
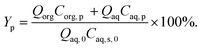 | (35) |
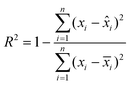 | (36) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) i is the predicted value by the kinetic model,
i is the predicted value by the kinetic model, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) i denotes the mean of the experimental data, and n indicates the number of experimental data.
i denotes the mean of the experimental data, and n indicates the number of experimental data.
For monophasic experiments, the developed kinetic model precisely predicts the evolution of the conversions or yields of all the components during the reaction in microreactors (Fig. 3, 7, 8, S4–S13†), and a good fit between the experimental data and model values was obtained for all components, as reflected in the corresponding R2 being close to 1 (Fig. S22a†). In the biphasic system, though the experimental data thereof were not used for kinetic parameter estimation, still a good prediction of the evolution trend of the components (Fig. 2 and 9) as well as a good agreement between the experimental data and model predictions (Fig. S22b†) was achieved, supporting the validity of the current kinetic model.
3.6 Model implication and process optimization
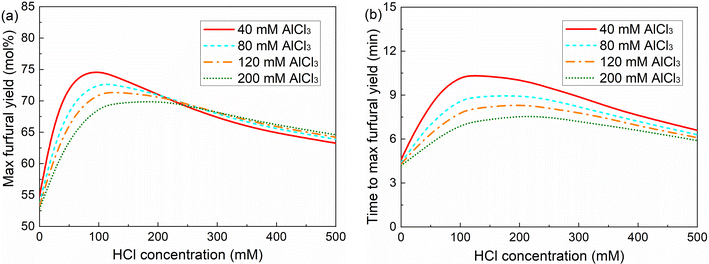
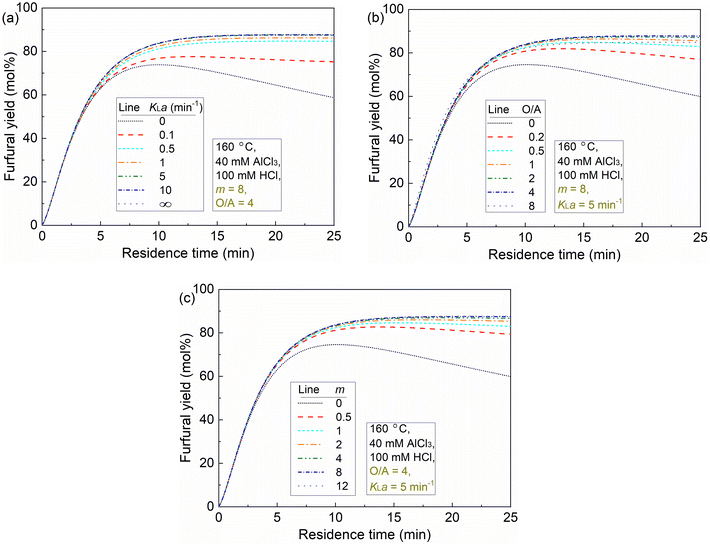
Generally, at a low HCl addition (0–20 mM), a minor difference in the maximum furfural yield was found between varying AlCl3 concentrations within the studied range (Fig. 11), as also reflected in the experimental results of xylose conversion over 40, 80 and 120 mM AlCl3 (Fig. S10†), which is because of the similar amount of Al(OH)2+ and H+ therein (Fig. 6b). At a moderate HCl addition (e.g., 20–200 mM), where a relatively large difference in the amount of Al(OH)2+ and H+ was realized, a higher AlCl3 addition leads to a lower maximum furfural yield, due to the higher reaction orders in Al(OH)2+ for reactions leading to humins than that for reactions producing furfural (Table 1). At a high HCl concentration over 200 mM, the difference in the maximum furfural yield among different AlCl3 additions becomes minor again (a slightly lower furfural yield at lower AlCl3 loading), as the hydrolysis of AlCl3 is highly suppressed by high Brønsted acidity leading to a small amount of Al(OH)2+ generated, and as such xylose conversion tends to be catalyzed mainly by H+. This is also consistent with the experimental findings that a minor difference in xylose conversion and furfural yield was observed for different AlCl3 additions in combination with 200 mM HCl (Fig. 2). Moreover, a generally higher AlCl3 concentration promotes the overall reaction rate (less time is required to reach the maximum furfural yield; Fig. 11b). Regardless of the AlCl3 addition, with increasing HCl addition the overall reaction rate firstly decreases as the prevalent Al(OH)2+-catalyzed reactions are gradually suppressed, and then increases when H+-catalyzed reactions are promoted and turn prevalent. Above all, the cooperativity between the AlCl3 and HCl is dependent on the relative amount of the catalytically active Al(OH)2+ and H+ therein, which affords different activity and selectivity for xylose conversion to furfural. Generally, the implications here are also well consistent with the experimental results reported in the literature on the C5/C6 sugar conversion to furfural or HMF over combined Lewis/Brønsted acid catalysts (e.g., CrCl3/HCl) in water.30,31,43,44 Towards a maximized furfural yield and acceptable reaction rate, here 40 mM AlCl3 and 100 mM HCl was selected as the optimized combination of Lewis and Brønsted acidity within the studied concentration range.
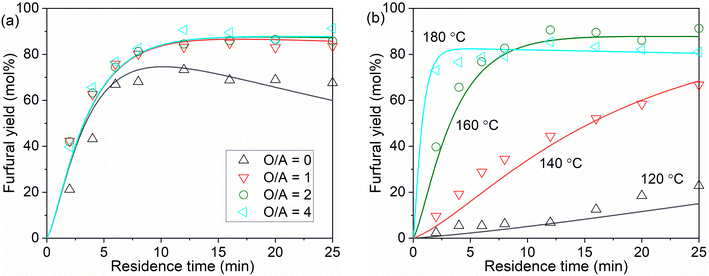
Generally, at a sufficient O/A of 4 and m of 8 (the partition coefficient of furfural in water/MIBK at 160 °C; eqn (31)), the furfural yield increases rapidly with the increase of KLa (i.e., decrease of mass transfer resistance), and levels off after KLa reaches 0.5 min−1 (Fig. 12a). The plateau at KLa above 5 min−1 is due to the by far higher rate of furfural extraction than furfural degradation, indicating an absence of the mass transfer limitation. In principle, increases of both O/A and m lead to a higher driving force and capacity for furfural extraction. Under a high KLa of 5 min−1 and a high m (e.g. m = 8), the furfural yield increases fast with increasing O/A and reaches a plateau even at a low O/A ratio (e.g., O/A = 0.5; Fig. 12b). Notably, a too high O/A ratio such as 8 might decrease the furfural yield due to the large phase volume change causing the AlCl3/HCl concentration (ratio) to deviate from the optimal value (Fig. 12b and Table S5, entries 11–15†). Similarly, the analysis of m combined with high KLa (5 min−1) and O/A (4) indicates that furfural yield increases with increasing m and quickly levels off even at a relatively low m of 2 (Fig. 12c). The analysis of O/A and m suggests their complementary relationship and similar promoting effect on the driving force and capacity for furfural extraction.
In our biphasic experiments in slug flow microreactors (L = 3.3 m), the KLa value is estimated to be sufficiently high (e.g., being 2.5–8.9 min−1 for an O/A of 4, and should be even higher for lower O/A ratios given the higher interfacial area therein; cf. section S11). Considering also the high partition coefficient (m) of furfural in the water–MIBK system (being ca. 7–8 at 120–180 °C; cf. eqn (31)), our case is exactly the one shown in Fig. 12b, where the furfural yield should increase fast with the increase of O/A and reach a plateau even at a relatively low O/A level. This is correctly reflected in our experimental results regarding the effect of O/A ratios (Fig. 9), where the furfural yield was largely promoted even at a low O/A ratio of 1 while further increasing the O/A ratio only led to a slight further increase in the furfural yield. Considering also the cost of the organic solvent and its downstream separation, an initial O/A ratio of 4 was selected as the optimal for furfural synthesis.
In the presence of combined AlCl3 and HCl as the catalyst, a higher reaction temperature not only promotes the kinetics, but also tends to shift the hydrolysis equilibrium of AlCl3 in water towards generating more H+ and Al(OH)2+ (Fig. 6). In the biphasic system, the increase of temperature leads to lower furfural partition in the MIBK phase (Fig. S19†) and thus less capacity and a lower driving force for furfural extraction. Moreover, the temperature also regulates the liquid density and partial miscibility between the water and MIBK, leading to the volume change of the two phases (Table S2†) and furthermore the concentration change of the reactants and catalysts. Taking into account all the abovementioned effects of temperature, the furfural yield from xylose conversion in the monophasic and biphasic systems at varying reaction temperatures is modeled under the optimized conditions (40 mM AlCl3, 100 mM HCl, O/A = 4), as shown in Fig. 13.
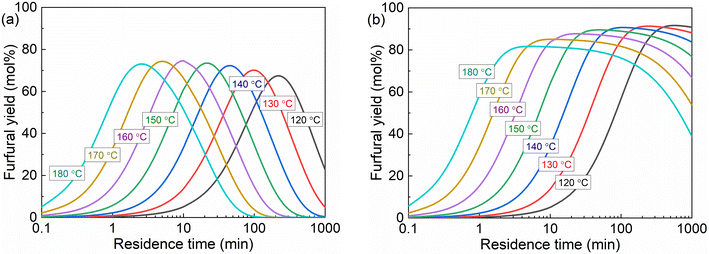 | ||
| Fig. 13 Furfural yields from xylose at varying temperatures in the (a) monophasic water and (b) biphasic water–MIBK system. Conditions: 0.5 M xylose, 40 mM AlCl3, 100 mM HCl, O/A = 4 (fed at 20 °C). | ||
In monophasic water, the maximum furfural yields are generally similar for temperatures between 120 and 160 °C, and gradually decrease at higher temperatures than 160 °C (Fig. 13a). In the biphasic system, a more distinct decreasing trend of furfural yields with increasing reaction temperature is found (Fig. 13b). This evolution trend of furfural yields with temperature is apparently different from that catalyzed by individual H+ or Al(OH)2+ in water, where a higher temperature leads to higher furfural yields (Fig. S23–S26†). In the current water–MIBK biphasic system, the partition coefficient of furfural (ca. 7–8) and the actual O/A ratios (ca. 5–6) at 120–180 °C have been revealed to be sufficient (Fig. 12b) and thus should have a very limited effect on furfural yields with varying temperatures. Therefore, the decreased furfural yields at higher temperatures should be a result of the decreased aqueous phase volume and significantly increased concentration of Al(OH)2+ and H+ in water (Table S5†), leading to somewhat of a deviation of the Al(OH)2+/H+ concentration ratio from the optimal value. Generally, considering also the longer residence time to reach the maximum furfural yield at lower temperatures, 160 °C was selected as the optimized temperature for xylose conversion in the biphasic system.
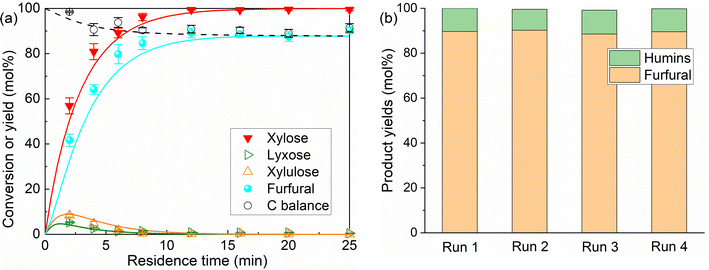
3.7 Optimized furfural synthesis in microreactors, catalyst recyclability and performance comparison with literature works
Based on the experimental results and model implications, favorable process conditions such as 160 °C, 40 mM AlCl3, 100 mM HCl and O/A = 4 were adapted in combination with a high xylose concentration (i.e., 1 M) to optimize the furfural (space–time) yields in slug flow microreactors. A highest furfural yield of up to 90% was achieved within a short residence time of 12 min at an almost full xylose conversion (Fig. 14a). The majority of furfural (e.g., over 98% at 20 °C with O/A = 4) being extracted into the organic MIBK phase with a complete xylose conversion also largely facilitates the recycling of the catalytic aqueous phase by a simple phase separation (via decantation) followed by filtering out the small amount of humins. The recycled aqueous phase was then reused to prepare the fresh xylose feedstock for the following reaction runs. As shown in Fig. 14b, no distinct performance loss was observed after four consecutive 8-hour runs, corroborating the stability and sustainability of the present process. Additionally, the MIBK phase is also recyclable as it is feasible to separate furfural (boiling point: 162 °C at 101.3 kPa, and 90 °C at 8.7 kPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45) from MIBK (boiling point: 117 °C at 101.3 kPa, and 25 °C at 2.66 kPa
45) from MIBK (boiling point: 117 °C at 101.3 kPa, and 25 °C at 2.66 kPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45) by vacuum distillation at relatively lower temperatures (<80 °C) to avoid the thermal degradation of furfural which usually occurs at temperatures over 100 °C.46
45) by vacuum distillation at relatively lower temperatures (<80 °C) to avoid the thermal degradation of furfural which usually occurs at temperatures over 100 °C.46
The performance of the current catalytic and microreactor system was compared with the representative literature using homogeneous or heterogeneous catalysts for furfural synthesis from xylose in water–organic biphasic systems in batch or flow reactors. Generally, in this work a much higher furfural yield (e.g., Yfurfural = 90%) and space–time yield (e.g., STYfurfural = 11.64 mol min−1 m−3) were achieved from 1 M (15 wt%) xylose feedstock, compared with the literature using a batch reactor (Yfurfural = 42–80%; STYfurfural = 0.03–7.5 mol min−1 m−3) (cf. details in Table S8†). The lower STYfurfural in the literature is attributed to a lower substrate concentration, large reactor volume, and particularly the batch operation mode with an extended reaction time and limited furfural yields. In contrast, literature works related to the continuous flow reaction mode usually give a better STYfurfural. For example, Papaioannou et al.47 conducted xylose conversion to furfural using H2SO4 as a catalyst in a water–toluene biphasic system in a slug flow millireactor (inner diameter: 4.1 mm). Despite the limited furfural yield (ca. 56%), still a good STYfurfural was obtained (19.89 mol min−1 m−3) thanks to a small reactor volume and a short residence time (2.5 min). In our previous work,41 xylose conversion was performed over HCl/NaCl in a slug flow microreactor, where a meritorious furfural yield (93%) and STYfurfural of 35.96 mol min−1 m−3 were achieved from 1 M xylose. However, it was found that the addition of 10 wt% NaCl (used as a promotor) in water largely increased the viscosity and thus the operation difficulty for the microreactor system. As such, the present catalytic system in this work holds its unique merits in addition to desirable furfural (space–time) yields (e.g., mild operation requirements for the microreactor setup with only a low concentration of AlCl3 as an additional catalyst component). Besides water, non-aqueous solvents have also been reported to be effective for xylose conversion, such as ionic liquids, polar aprotic solvents like DMSO, and deep eutectic solvents.48–50 However, though good yields were obtained (over 60%), these systems are still in the early stage of lab-scale research and gave a relatively low STYfurfural due to a long reaction time and batch reaction mode, not to mention the high cost and difficulty in downstream furfural separation. Therefore, this work using water as a cheap and green solvent, and AlCl3/HCl as a low-cost, recyclable and low-toxicity catalyst, with the high furfural (space–time) yield achieved in a slug flow microreactor, represents a promising approach for efficient furfural synthesis.
4. Conclusion
Furfural production from lignocellulose-derived carbohydrates such as xylose represents an important reaction with a long history in bio-refineries. Experimental findings have been reported regarding the promoting effect of a Lewis acid (in combination with a Brønsted acid) on xylose conversion to furfural. In order to acquire deep insights into the reaction network and kinetics for better process understanding and optimization, we performed systematic experimental and kinetic modelling studies on xylose conversion, using AlCl3/HCl as a combined Lewis/Brønsted acid catalyst in both monophasic water and biphasic water–MIBK systems, over a broad range of reaction conditions such as a temperature window of 120 to 180 °C, HCl concentrations of 0.05 to 0.4 M, AlCl3 concentrations of 0.04 to 0.12 M, and initial substrate (xylose, lyxose, xylulose and furfural) concentrations of 0.01 to 0.5 M. Microreactors were used as both a platform for the fast monophasic kinetic experiments, and a process intensification tool for the efficient furfural synthesis in the biphasic system (under slug flow pattern). After optimization, a furfural yield up to 90% from 1 M xylose was achieved over 40 mM AlCl3 and 100 mM HCl at 160 °C and 12 min.Based on the experimental results, an extensive reaction network was revealed covering a series of parallel and tandem reactions of isomerization, dehydration and degradation from xylose. The regulatory role of the Lewis and Brønsted acids therein was interpreted as that only Lewis acid catalyzes the isomerization and epimerization between xylose, lyxose and xylulose, while both the Lewis and Brønsted acids are active for sugar dehydration to furfural and side reactions leading to humins such as sugar condensation and furfural degradation. Particularly, the promoting effect of Lewis acid on xylose conversion to furfural is attributed to not only the tandem catalysis via xylulose, but also the parallel direct Lewis acid-catalyzed sugar dehydration. Through ESI-MS spectroscopy characterization, Al(OH)2+ was identified as the active Al species that coordinates with xylose, furfural and intermediate sugars (lyxose and xylulose) in water, thus behaving as Lewis acid sites responsible for the sub-reactions within the xylose conversion network. The amount of Al(OH)2+ and H+ in water was determined via the hydrolysis equilibrium of AlCl3 given a certain temperature and initial concentration of AlCl3 and HCl, and used for the development of the kinetic model from the results of the monophasic experiments. The model can also predict well the results of biphasic experiments after the incorporation of furfural extraction between the two phases, with the consideration of phase volume change as a function of temperature and phase partial miscibility. The rates of all sub-reactions behave with a first-order dependency on the substrates and H+, while their reaction orders in Al(OH)2+ were estimated to fall in the range 0.19–0.99. Experimental results and model predictions revealed a volcano-like dependency of the achievable maximum furfural yields (in monophasic water) on the relative molar ratios of HCl to AlCl3 (and furthermore, the molar ratio of Al(OH)2+ to H+), whereas varying the concentration of HCl or AlCl3 as a sole catalyst is not effective for improving furfural yields. This evolution trend of furfural yields with the increase of HCl/AlCl3 molar ratio is related to (i) the lower reaction orders in Al(OH)2+ for the reactions producing furfural than that for side reactions; and (ii) a gradual shift of the dominant reaction from Al(OH)2+-catalyzed pathways towards H+-catalyzed ones.
Model prediction assuming Al(OH)2+ or H+ as the sole catalyst shows higher furfural yields with temperature increase within the studied range for both Al(OH)2+- and H+-catalyzed reactions due to the higher activation energy for furfural formation reactions than that for furfural degradation. However, in the AlCl3-involved reactions (containing both Al(OH)2+ and H+) the experiments and model implication show similar (for monophasic experiments) or lower (for biphasic experiments) furfural yields with the increase of temperature. This is due to the more promoted hydrolysis of AlCl3 and significant phase volume change (particularly for the biphasic system with larger partial phase miscibility) at higher temperatures, leading to a deviation of the Al(OH)2+/H+ molar ratio from the optimal value and thus lower furfural yields. In the present slug flow microreactor, the furfural extraction rate was estimated to be two orders of magnitude higher than the rate of furfural degradation, rendering the reaction under kinetic control, which has also been experimentally proved with varying microreactor lengths. An analysis of humin sources (i.e., xylose condensation or furfural degradation) indicates that the former side reaction is largely suppressed by the improved chemistry from properly combined AlCl3/HCl, and the latter is almost completely prevented in the biphasic system by the efficient furfural extraction and high furfural partition into MIBK. As a result, the furfural (space–time) yield in this work is rather promising compared with the literature. High furfural partition into the organic phase also allowed a simple downstream phase separation and recycling of the catalytic aqueous phase, which was used for four consecutive 8-hour runs without distinct performance loss.
Generally, this work revealed useful insights for understanding the complicated reaction network and kinetics of xylose conversion over combined Lewis/Brønsted acids, and demonstrated an efficient and sustainable process for furfural synthesis using slug flow microreactors as a production platform.
Conflicts of interest
The authors declare that there is no conflict of interest.Acknowledgements
Part of the present research was financially supported by the University of Groningen (start-up package in the area of green chemistry and technology). The China Scholarship Council is gratefully acknowledged for financial support (grant number 201606740069 for Wenze Guo). Wenze Guo gratefully acknowledges Dr Jozef G. M. Winkelman for the insightful discussions on kinetic modelling details.References
- A. Corma, S. Iborra and A. Velty, Chem. Rev., 2007, 107, 2411–2502 CrossRef CAS PubMed.
- G. W. Huber, S. Iborra and A. Corma, Chem. Rev., 2006, 106, 4044–4098 CrossRef CAS PubMed.
- R.-J. van Putten, J. C. van der Waal, E. de Jong, C. B. Rasrendra, H. J. Heeres and J. G. de Vries, Chem. Rev., 2013, 113, 1499–1597 CrossRef CAS PubMed.
- L. T. Mika, E. Cséfalvay and Á. Németh, Chem. Rev., 2018, 118, 505–613 CrossRef CAS PubMed.
- P. Mäki-Arvela, T. Salmi, B. Holmbom, S. Willför and D. Y. Murzin, Chem. Rev., 2011, 111, 5638–5666 CrossRef PubMed.
- R. Mariscal, P. Maireles-Torres, M. Ojeda, I. Sádaba and M. López Granados, Energy Environ. Sci., 2016, 9, 1144–1189 RSC.
- J. A. Brydson, in Plastics Materials (Seventh Edition), ed. J. A. Brydson, Butterworth-Heinemann, Oxford, 1999, pp. 810–813 Search PubMed.
- F. Dong, Y. Zhu, G. Ding, J. Cui, X. Li and Y. Li, ChemSusChem, 2015, 8, 1534–1537 CrossRef CAS PubMed.
- J. Kijeński, P. Winiarek, T. Paryjczak, A. Lewicki and A. Mikołajska, Appl. Catal., A, 2002, 233, 171–182 CrossRef.
- D. F. Aycock, Org. Process Res. Dev., 2007, 11, 156–159 CrossRef CAS.
- G. W. Huber, J. N. Chheda, C. J. Barrett and J. A. Dumesic, Science, 2005, 308, 1446 CrossRef CAS PubMed.
- B. Danon, G. Marcotullio and W. de Jong, Green Chem., 2014, 16, 39–54 RSC.
- H. J. Brownlee and C. S. Miner, Ind. Eng. Chem., 1948, 40, 201–204 CrossRef CAS.
- R. Karinen, K. Vilonen and M. Niemelä, ChemSusChem, 2011, 4, 1002–1016 CrossRef CAS PubMed.
- J. S. Kruger, V. Nikolakis and D. G. Vlachos, Curr. Opin. Chem. Eng., 2012, 1, 312–320 CrossRef CAS.
- R. Weingarten, G. A. Tompsett, W. C. Conner and G. W. Huber, J. Catal., 2011, 279, 174–182 CrossRef CAS.
- W. Guo, E. J. M. Hensen, W. Qi, H. J. Heeres and J. Yue, ACS Sustainable Chem. Eng., 2022, 10, 10157–10168 CrossRef CAS.
- W. Guo, T. Kortenbach, W. Qi, E. Hensen, H. Jan Heeres and J. Yue, Appl. Catal., B, 2022, 301, 120800 CrossRef CAS.
- W. Guo, H. J. Heeres and J. Yue, Chem. Eng. J., 2020, 381, 122754 CrossRef CAS.
- W. Guo, Z. Zhang, J. Hacking, H. J. Heeres and J. Yue, Chem. Eng. J., 2021, 409, 128182 CrossRef CAS.
- R. M. Abdilla-Santes, W. Guo, P. C. A. Bruijnincx, J. Yue, P. J. Deuss and H. J. Heeres, ChemSusChem, 2019, 12, 4304–4312 CrossRef CAS PubMed.
- M. Brasholz, K. von Kanel, C. H. Hornung, S. Saubern and J. Tsanaktsidis, Green Chem., 2011, 13, 1114–1117 RSC.
- T. M. Kohl, B. Bizet, P. Kevan, C. Sellwood, J. Tsanaktsidis and C. H. Hornung, React. Chem. Eng., 2017, 2, 541–549 RSC.
- T. Shimanouchi, Y. Kataoka, T. Tanifuji, Y. Kimura, S. Fujioka and K. Terasaka, AIChE J., 2016, 62, 2135–2143 CrossRef CAS.
- Y. Muranaka, H. Nakagawa, R. Masaki, T. Maki and K. Mae, Ind. Eng. Chem. Res., 2017, 56, 10998–11005 CrossRef CAS.
- P. Desir, B. Saha and D. G. Vlachos, Energy Environ. Sci., 2019, 12, 2463–2475 RSC.
- J. A. Bennett, Z. S. Campbell and M. Abolhasani, Curr. Opin. Chem. Eng., 2019, 26, 9–19 CrossRef.
- J.-i. Yoshida, H. Kim and A. Nagaki, ChemSusChem, 2011, 4, 331–340 CrossRef CAS PubMed.
- W. Guo, H. C. Bruining, H. J. Heeres and J. Yue, AIChE J., 2022, 68, e17606 CAS.
- V. Choudhary, S. I. Sandler and D. G. Vlachos, ACS Catal., 2012, 2, 2022–2028 CrossRef CAS.
- M. Lopes, K. Dussan and J. J. Leahy, Chem. Eng. J., 2017, 323, 278–286 CrossRef CAS.
- Y. Yang, C.-W. Hu and M. M. Abu-Omar, ChemSusChem, 2012, 5, 405–410 CrossRef CAS PubMed.
- T. Yang, Y.-H. Zhou, S.-Z. Zhu, H. Pan and Y.-B. Huang, ChemSusChem, 2017, 10, 4066–4079 CrossRef CAS PubMed.
- A. Mittal, H. M. Pilath and D. K. Johnson, Energy Fuels, 2020, 34, 3284–3293 CrossRef CAS.
- J. Tang, L. Zhu, X. Fu, J. Dai, X. Guo and C. Hu, ACS Catal., 2017, 7, 256–266 CrossRef CAS.
- R. Noma, K. Nakajima, K. Kamata, M. Kitano, S. Hayashi and M. Hara, J. Phys. Chem. C, 2015, 119, 17117–17125 CrossRef CAS.
- K. Nakajima, R. Noma, M. Kitano and M. Hara, J. Mol. Catal. A: Chem., 2014, 388, 100–105 CrossRef.
- K. Nakajima, Y. Baba, R. Noma, M. Kitano, J. N. Kondo, S. Hayashi and M. Hara, J. Am. Chem. Soc., 2011, 133, 4224–4227 CrossRef CAS PubMed.
- K. Nakajima, R. Noma, M. Kitano and M. Hara, J. Phys. Chem. C, 2013, 117, 16028–16033 CrossRef CAS.
- W. L. Bourcier, K. G. Knauss and K. J. Jackson, Geochim. Cosmochim. Acta, 1993, 57, 747–762 CrossRef CAS.
- W. Guo, Doctoral dissertation, University of Groningen, 2021. DOI:10.33612/diss.178033475.
- I. Delidovich, M. S. Gyngazova, N. Sánchez-Bastardo, J. P. Wohland, C. Hoppe and P. Drabo, Green Chem., 2018, 20, 724–734 RSC.
- T. D. Swift, H. Nguyen, A. Anderko, V. Nikolakis and D. G. Vlachos, Green Chem., 2015, 17, 4725–4735 RSC.
- V. Choudhary, A. B. Pinar, S. I. Sandler, D. G. Vlachos and R. F. Lobo, ACS Catal., 2011, 1, 1724–1728 CrossRef CAS.
- NIST Chemistry Webbook., https://webbook.nist.gov/chemistry/fluid/.
- J. N. Chheda, Y. Román-Leshkov and J. A. Dumesic, Green Chem., 2007, 9, 342–350 RSC.
- M. Papaioannou, R. J. T. Kleijwegt, J. van der Schaaf and M. F. Neira d'Angelo, Ind. Eng. Chem. Res., 2019, 58, 16106–16115 CrossRef CAS.
- E. Lam, E. Majid, A. C. W. Leung, J. H. Chong, K. A. Mahmoud and J. H. T. Luong, ChemSusChem, 2011, 4, 535–541 CrossRef CAS PubMed.
- S. Peleteiro, S. Rivas, J. L. Alonso, V. Santos and J. C. Parajó, Bioresour. Technol., 2016, 202, 181–191 CrossRef CAS PubMed.
- E. S. Morais, M. G. Freire, C. S. R. Freire, J. A. P. Coutinho and A. J. D. Silvestre, ChemSusChem, 2020, 13, 784–790 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3gc00153a |
| This journal is © The Royal Society of Chemistry 2023 |