Open Access Article
Open Access ArticleA new multidisciplinary non-destructive protocol for the analysis of stony meteorites: gamma spectroscopy, neutron and muon techniques supported by Raman microscopy and SEM-EDS
Riccardo
Rossini
 abcd,
Daniela
Di Martino
abcd,
Daniela
Di Martino
 *ab,
Toluwalase
Agoro
*ab,
Toluwalase
Agoro
 d,
Matteo
Cataldo
abd,
Giuseppe
Gorini
ab,
Adrian D.
Hillier
d,
Matthias
Laubenstein
d,
Matteo
Cataldo
abd,
Giuseppe
Gorini
ab,
Adrian D.
Hillier
d,
Matthias
Laubenstein
 e,
Giulia
Marcucci
e,
Giulia
Marcucci
 abd,
Maya
Musa
abd,
Maya
Musa
 af,
Maria Pia
Riccardi
gh,
Antonella
Scherillo
d and
Massimiliano
Clemenza
ab
af,
Maria Pia
Riccardi
gh,
Antonella
Scherillo
d and
Massimiliano
Clemenza
ab
aDepartment of Physics G. Occhialini, University of Milano-Bicocca, Milan, Italy. E-mail: daniela.dimartino@unimib.it
bMilano-Bicocca Division, INFN, Milan, Italy
cDepartment of Physics, University of Pavia, Pavia Division, INFN, Pavia, Italy
dISIS Neutron and Muon Source, STFC, Didcot, UK
eLaboratori Nazionali del Gran Sasso (LNGS), INFN, Assergi - L'Aquila, Italy
fDepartment of Earth and Environmental Sciences (DISAT), University of Milano-Bicocca, Milan, Italy
gDepartment of Earth and Environmental Sciences, University of Pavia, Pavia, Italy
hArvedi Laboratory, CISRiC, University of Pavia, Pavia, Italy
First published on 21st November 2022
Abstract
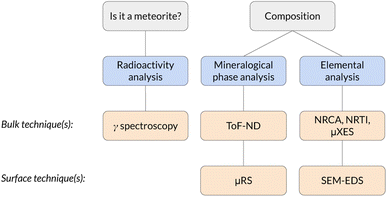
The physical and chemical characterisation of meteorites is of paramount importance in the study of the formation of the Solar System. In this work we show the feasibility of a complete set of non-destructive measurements to perform such a characterisation using a stony meteorite as a mock-up sample. The identification of the sample as a meteorite was performed by means of gamma ray spectrometry, which identified the presence of cosmogenic 26Al. Time-of-Flight Neutron Diffraction (ToF-ND) enabled the mineralogical phase quantification and the analysis of the presence of strains and substitutions in each mineral. Neutron Resonance Capture Analysis (NRCA), Neutron Resonance Transmission Imaging (NRTI) and Muonic Atom X-Ray Spectroscopy (MAXRS) allowed a study of the presence and the space distribution of certain elements. Furthermore, micro-Raman Spectroscopy (μRS) and Scanning Electron Microscopy with Energy-Dispersive X-ray Spectroscopy (SEM-EDS) were also considered in order to validate the protocol.
1 Introduction
The non-destructive characterisation of valuable samples like meteorites is of paramount importance in terms of sample conservation and measurement repeatability. Meteorites are a heterogeneous class of samples which are typically classified by means of average destructive quantification and petrological observation. The latter ones, despite being technically non-destructive, require the extraction of a thin section, which is a destructive procedure. In general, the dominant physical characterisation techniques used to analyse meteorites make use of probes with a small depth of penetration in materials (<1 mm), such as X rays and electrons. We refer to them as surface techniques. The aim of this study is to make use of physical characterisation techniques based on radiation with a long average range in materials (centimeters) to study the volume of the sample instead of its surface. Examples of such radiation are neutrons, muons and gamma rays. These bulk techniques enable to study also the internal part of the sample without causing major damage to the specimen. Meteorites are important for their scientific-cultural meaning, but their characterisation could also entail relevant implications on the knowledge on the cosmogenesis and the formation of the Solar System.In this framework, a completely non-destructive protocol is presented, which makes use of bulk techniques to characterise the elemental, mineral and radio-isotopic composition of the sample.1,2 Passive techniques, such as the collection of the radiation emitted by the sample, were also considered (in particular the collection of gamma rays, which is a bulk technique).
The first important procedure to carry out is to determine whether or not a received sample is a meteorite. On this purpose, gamma ray spectrometry is used to look for the presence of certain radionuclides which are formed by nuclear reactions involving primary cosmic rays and which have half-life smaller than the time of existence of the Earth atmosphere (around 109 years).3 The presence of such nuclides confirms the fact that the sample spent long periods of time outside the Earth atmosphere and therefore it may prove its meteoric origin. The main cosmogenic radionuclides with these characteristics, ordered by decreasing half-life, are:126Al (t1/2 = 7.6 × 105 years), 60Co (t1/2 = 5.27 years), 22Na (t1/2 = 2.6 years), 54Mn (t1/2 = 312 days), 46Sc (t1/2 = 84 days) and 48V (t1/2 = 16 days). If the sample fall is recent (for instance, a time less than 5τ of 22Na has passed, about 10 years, where t1/2 = τ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) one could perform standard gamma ray spectrometry. Otherwise, high-sensitivity and low-background gamma ray spectrometry is needed, as the long half-life of 26Al (the only one left in this latter case) implies it has a small activity. This is also required whenever the sample is just too small to have an acceptable activity for standard gamma ray spectrometry.
2) one could perform standard gamma ray spectrometry. Otherwise, high-sensitivity and low-background gamma ray spectrometry is needed, as the long half-life of 26Al (the only one left in this latter case) implies it has a small activity. This is also required whenever the sample is just too small to have an acceptable activity for standard gamma ray spectrometry.
It is then important to characterise the mineral and elemental composition of the sample. The former analysis is carried out by exploiting the Time-of-Flight (ToF) technique to perform Neutron Diffraction (ND) from a pulsed thermal-epithermal neutron beam. ToF-ND enables mineralogical phase characterisation and quantification in the bulk of the sample, due to the long range of neutrons in most materials, with respect to other particles.
A qualitative bulk elemental characterisation is made possible thanks to the analysis of the absorbed neutron spectrum during the exposition of the sample into a thermal-epithermal pulsed neutron beam. Neutron Resonance Capture Analysis (NRCA)4 consists in the study of the captured neutron spectrum by timing the gamma rays promptly emitted after each beam spill. This technique returns a bulk information on the whole analysed area. On the other hand, Neutron Resonance Transmission Imaging (NRTI)5,6 consists in the acquisition of a space-resolved Time-of-Flight neutron spectrum in transmission by means of a neutron beam monitor. As a consequence, NRTI allows elemental mapping. Therefore, NRCA and NRTI spectra are complementary and they return consistent information. Furthermore, in the case of NRTI, information is space-resolved, whereas in NRCA it is averaged on all the part of the sample crossed by the neutron beam. Neutron techniques were applied to meteorites a few times.7,8 A combined ToF-ND and neutron-capture imaging protocol has already been applied to chondrites, particularly to the Chelyabinsk meteorite.9
Muonic atom X-ray Emission Spectroscopy (μXES), a novel technique for elemental characterization, is also exploited. μXES is a method based on the detection of high energy X-rays emitted by the sample after negative muon irradiation. This irradiation causes the formation of muonic atoms, whose characteristic X-ray emission allows the elemental characterisation of the sample. The shape of the muon energy loss curve dE/dx (the Bragg peak) enables such measurements at different depth into the material, by tuning the muon beam momentum.10–14 Even though the sensitivity to trace elements is still not optimised, this technique enables the non-destructive quantification of major elements in the bulk of a sample, and it is therefore a unique quantitative probe of the internal elemental composition of a sample.
It has been decided to introduce two consolidated surface techniques, such as Raman spectroscopy and Scanning Electron Microscopy, in order to validate the protocol. Furthermore, these methods allowed a more complete overview on the sample, enabling space-resolved mapping measurements. These techniques should be applied on a thin section (R003, see next section), which is typically available for many meteorites as it is used for petrological observation. Micro-Raman Spectroscopy (μRS) is used to identify the main mineral phases present in the sample in a space-sensitive way, even though the technique is basically qualitative. By Scanning Electron Microscopy in BackScattered Electrons (BSE-SEM) imaging it is possible to characterise the morphology of a surface by mapping the local average atomic number Z in greyscale. In this way, it is possible to identify different structures in order to study their elemental composition with the EDS microprobe. The space-sensitive quantitative elemental characterisation in this protocol is performed on the thin section R003 by means of Energy Dispersive X-ray Spectroscopy (EDS), consisting in the collection of the X-ray spectrum emitted while Scanning Electron Microscopy (SEM) is running.
The whole protocol, schematised in Fig. 1, has been tested for the first time on a supposed meteorite coming from a private collection. This is the first time a completely non-destructive bulk and surface analysis protocol is applied to a meteorite.
2 Materials and methods
2.1 Samples
The analysis protocol has been applied on an supposed meteorite, coming from the Middle East desert, which has belonged to a private collection for more than 20 years. During this period, the sample was cut into 2 massive pieces in order to extract a standard petrological (thickness 30 μm) thin section for transmitted light observations, which was used to identify the sample as a chondrite, a class of stony meteorites.15These samples, which are shown in Fig. 2, have the following features:
 | ||
| Fig. 2 The three samples from the same meteorite studied in this work: R001 and R002 are bulk samples, whereas R003 is a standard petrological thin section. | ||
• Sample R001 is a 12.61(36) g tip of the chondrite, with size 22.23 × 33.11 × 13.17 mm3;
• Sample R002 is a 14.65(14) g central slice of the chondrite, with size 26.95 × 35.97 × 6.41 mm3;
• Sample R003 is a standard petrological thin section (30 μm thick) obtained from sample R002.
The average density, measured on samples R001 and R002, is (2.1 ± 0.1) g cm−3. From the thin section analysis we identified the presence of aluminium in cracks and fissures, a clear evidence of the fact that the thin section polishing was made with alumina. As it was not possible to quantify aluminium, which is a key element in this sample, from the thin section. As a consequence, one of the two surfaces of sample R002 has been polished in order to perform EDS on it. The polishing was carried out with SiC with grain size 18 μm and 15 μm and with diamond paste with grains of 3–6 μm, 1–3 μm and finally 0.25 μm.
2.2 Low-background gamma ray spectrometry
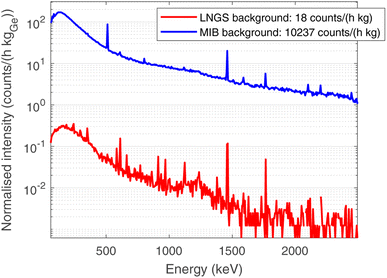
In order to optimise the bulk characterisation of the radioisotopes present in the sample, a low-background High-Purity Germanium detector (HPGe) was used, located at the STELLA (SubTErranean Low Level Assay) laboratory16 within the subterranean Laboratori Nazionali del Gran Sasso (LNGS) underneath the Gran Sasso mountain, at a depth of 3800 mwe (meters of water equivalent). In particular, it is a p-type coaxial low-background HPGe detector from ORTEC (the relative efficiency at the 1332.52 keV peak of 60Co is 84%, the energy resolution 1.9 keV).Fig. 3 shows the comparison between the gamma ray background at the STELLA facility at LNGS (lower curve) and the one measured at sea level in the radioactivity laboratory of the University of Milano-Bicocca (MIB, upper curve). Both spectra are normalised to count rate and detector mass, which is approximately proportional to the efficiency. The gamma ray background at LNGS is about two or three orders of magnitude lower than the one at MIB. The huge difference between these spectra results from the great depth of LNGS under the Gran Sasso mountain, but also from the choice of low-radioactivity materials in the construction of the detector and the LNGS facility itself.
In order to obtain the activity of 26Al, the Monte Carlo (MC) simulation code Arby, based on the CERN software package Geant4,17 was used to calculate the Full Energy Peak (FEP) efficiency of the 26Al emission, taking into account the sample geometry and composition, the detector geometry and the absorption of radiation by the detector dead layers and the sample itself. As the MC is carried out by simulating single-isotope decays, considering all electromagnetic, strong and weak processes which may occur, it returns the value of efficiency weighed by the branching ratio of the selected peak (εBR). The sample composition used in the MC simulation is the same obtained by means of the EDS campaign described in the previous section. The FEP efficiencies are used to obtain the activity from the count rate of each peak, which is calculated by Gauss-fitting.
2.3 Time-of-flight neutron diffraction (ToF-ND)
The INES diffractometer at the ISIS Neutron and Muon Source in Didcot (UK) has been used.18 It is endowed with a completely motorised and programmable sample holder (x–y–z–ω) and 9 neutron detection banks, featured with 16 3He detectors each. In addition, it also hosts the instrumentation for the neutron resonance measurements, as described in the next section.The 50 Hz pulsed neutron beam is produced by the spallation of 800 MeV protons (supplied by a synchrotron having total current 210 μA) against a tungsten target. As slow neutrons are required for Tof-ND and many other applications, a water-based moderator is used to thermalise the neutron beam, obtaining a quasi-Maxwell distribution with kT = 25 meV, corresponding to room temperature.
For each investigated spot, 9 histograms were acquired, one for each detection bank, and standard Rietveld refinement procedure has been applied to extract the required information. In order to perform these analyses, the GSAS software has been used.19 In particular, the analysis was divided into two parts:
• Phase analysis, a multi-spectral refinement on all banks excluding the one at smallest 2θ angle (forward scattering) with the objective of identifying and quantifying the phases present in the sample;
• Peak shape analysis, a refinement on the highest-2θ bank only (back scattering) in order to extract information about the peak shape and the crystal structure. The reason for the choice of this spectrum for this task relies both on its optimal spectral resolution and the minimised sensitivity to the thickness of the sample, provided it is approximately below 1 cm, as in this case. These considerations are made particularly for the INES geometry and might not hold in general.18
ToF-ND measurements were applied on two 2 × 2 cm2 regions for each sample, in order to verify the uniform distribution of mineral phases in the whole sample. The neutron beam of irradiation for each spot corresponds to an integrated proton current of 1500 μAh on the spallation target, totalling around 8 h 30 min of measurement for each of the 4 regions.
2.4 Neutron resonance capture analysis (NRCA) and neutron resonance transmission imaging (NRTI)
The neutron-based qualitative elemental characterisation is carried out while performing ToF-ND at INES. In particular, NRCA is performed by means of three time-resolved YAP detectors positioned below the INES detection banks, outside the neutron beam. Typically, the three spectra are consistent with each other and they are merged. As the resulting spectrum is relative to the whole inspected area, it does not allow elemental mapping. The low-ToF region of the spectrum, around 30 μs after the beam spill, is saturated by the noise and therefore it does not contain crucial information. On the other hand, NRTI is made possible at INES by a n-GEM (neutron Gas Electron Multiplier) detector20 in transmission with respect to the beam. The resulting information can be visualised by means of bi-dimensional maps, but the space resolution is limited by the current space resolution of n-GEM detectors (around 0.75 mm). In this case, as the n-GEM detector has a good neutron/gamma discrimination, all the ToF interval between two beam spills (25 ms) is usable, even the first 30 μs. In principle, the quantification of some elements may be possible, but further simulation and calibration on the INES setup is needed and it is scheduled to be carried out in the next years.2.5 Muonic atom X-ray emission spectroscopy (μXES)
The μXES measurement is performed at the RIKEN facility at the ISIS Neutron and Muon Source, UK. The technique consists of two sets of measurements at different momentum of the non-collimated negative muon beam: one at 20 MeV per c and one at 40 MeV per c. In this work, this technique was applied only to sample R001. The sample was wrapped in an aluminium foil, to facilitate the positioning on the sample holder, and placed 10 cm after the beam exit, with two HPGe detectors positioned 15 cm from the meteorite. Aluminium is also a reference for the depth selection during the measurements, since it acts as an interface between the interior and the exterior of the sample.The analysis procedure consists in peak identification and quantification of the related count rate by Gauss-fitting for each peak and each value of beam momentum. At this point, each peak is weighed according to the efficiency curve of the detection system in that configuration, obtained by MC simulation on the Arby interface for Geant4.17
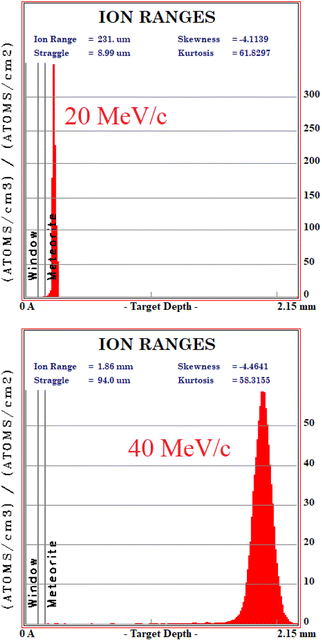
In order to understand at which depth is released the energy of the muon beam at the various values of the beam momentum, MC simulation on SRIM21 are also carried out, taking into account a 3% momentum spread. Both values of momentum were simulated (10 k events each) obtaining the Bragg curve 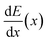 . The depth interval in which most energy is released corresponds to the area analysed by the technique, since most muonic atoms are formed in that depth interval. The results, reported in Fig. 4, show that in the 20 MeV per c run the measurement is sensitive to the aluminium foil and the surface of the sample (few μm), whereas the bulk of the sample (∼1.5 mm) is being investigated in the 40 MeV per c run.
. The depth interval in which most energy is released corresponds to the area analysed by the technique, since most muonic atoms are formed in that depth interval. The results, reported in Fig. 4, show that in the 20 MeV per c run the measurement is sensitive to the aluminium foil and the surface of the sample (few μm), whereas the bulk of the sample (∼1.5 mm) is being investigated in the 40 MeV per c run.
2.6 Micro-Raman spectroscopy (μRS)
A Renishaw in-via reflex μ-spectrometer coupled in confocality with a Leica optical microscope has been used. It is endowed with two laser sources: a 632.8 nm, 25 mW He–Ne laser and a 514.5 nm, 100 mW solid state laser. The detection system consists in a Charged Coupled Device (CCD) and two different motorised diffraction gratings with 1800 lines per mm and 3200 lines per mm. The microscope is featured with 3 long working distance objectives, 5 × (0.12 numerical aperture – NA), 50 × (0.75 NA), 100 × (0.75 NA), and 2 short working distance objectives, 20 × (0.40 NA), 50 × (0.50 NA). Further details on the experimental setup are available in ref. 22.2.7 Scanning electron microscopy in backscattered electrons (BSE-SEM) with energy dispersive X-ray spectroscopy (EDS)
The instrument used for this purpose is a Tescan FE-SEM Mira 3XMU-series equipped with an EDAX spectrometer based on an Apollo XL Silicon Drift Detector (SDD). The instrument has been set to work at 15.8 mm working distance with a 20 kV accelerating voltage and 12 mA beam current. The relative elemental quantification is calculated from the EDS spectrum by the ZAF method. This technique is based on the comparison of the area under Kα emission peaks with standards, correcting the effect given by average atomic number (Z), self-absorption (A), and fluorescence excitation (F) on the X-ray emission. Details on the EDS measurements can be found in ref. 22.3 Results and discussion
3.1 Low-background gamma ray spectrometry results
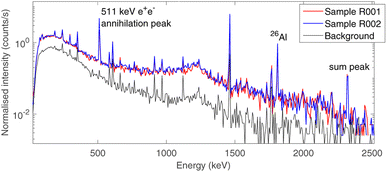
The choice of using low-background gamma ray spectrometry in an underground laboratory as LNGS was made due to the expected age of the sample, as described in Section 2.2.Aluminium-26 is a β+ emitter,23 which decays on a 1808 keV excited state of 26Mg as a main decay channel (Branching ratio BR 82%).24 This state promptly de-excites to the ground state of 26Mg by emitting a single 1808 keV gamma ray. As a consequence, the presence of 26Al is marked by the 1808 keV gamma peak, the 511 keV e+e− annihilation peak and the 2319 keV sum peak, as the excited state of 26Mg has a negligible half-life (4.76·10−13 s). The time-normalised gamma spectra of background and of the two bulk samples (R001 and R002) are shown in Fig. 5. The background acquisition lasted 30 days, whereas the measurements of the samples lasted 16 days each. All other peaks correspond to primordial radioactivity normally present in Earth rocks too (40K, 232Th chain, 238U chain).25
The activity of 26Al was estimated from both the 1808 keV and the 2319 keV peak, as the probability of random 511 keV and 1808 keV coincidences can be neglected due to the low activity of the sample.
The resulting values for the specific activity of 26Al are reported in Table 1 (efficiencies are simulated as specified in Section 2.2). These values are t-Student confident with each other and their weighted value returns an estimation for the specific activity of 26Al in the whole sample:
| A = (0.92 ± 0.06) Bq kg−1 |
| Sample | Mass (g) | Isotope | Peak (keV) | Counts/h | Activity (mBq) | Specific activity (Bq kg−1) |
|---|---|---|---|---|---|---|
| R001 | 12.61(36) | 26Al | 1808 | 0.90 ± 0.05 | 12.2 ± 1.4 | 0.97 ± 0.09 |
| R001 | 12.61(36) | 26Al | 2319 | 0.22 ± 0.02 | 12.2 ± 1.8 | 0.97 ± 0.17 |
| R002 | 14.65(14) | 26Al | 1808 | 0.97 ± 0.05 | 12.6 ± 1.4 | 0.86 ± 0.10 |
| R002 | 14.65(14) | 26Al | 2319 | 0.21 ± 0.02 | 12.6 ± 1.9 | 0.86 ± 0.14 |
A rough estimation of the amount of 26Al in Earth rocks can be given by the concentration of this isotope in ground-level dust,26i.e. 0.07 ± 0.03 particles per m3. Calculating the concentration of 26Al in our samples we get (9.5 ± 0.8)·1014 particles per m3, and the difference between these values is around 13 standard deviations (calculated by t-Student test). As a consequence, this value is not consistent with the typical amount of 26Al contained in Earth rocks27 and one can conclude that the sample is a meteorite. The slight difference in the values of A for the two samples, which can be observed in Table 1, is also present in the quantification of all the measurable fossil radioisotopes in the samples, which is reported in a previous work.28 However, the uncertainty introduced by MC systematics makes these values consistent with each other.
3.2 ToF-ND results
In this section, the analysis of one spot in sample R002 is presented, as the four diffractograms are consistent with each other.The fitted spectrum of bank 6 (2θ = 73.1°) coming from the multi-spectral fit for phase analysis is depicted in Fig. 6. The main mineral phases identified in this sample are forsterite (olivine, Mg2SiO4), enstatite (pyroxene, Mg2(Si2O6) and magnetite (cubic Fe3O4). Furthermore, troilite (FeS) and kamacite (Fe–Ni alloy with Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni ratio around 95
Ni ratio around 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, originating from Ni substitutions) have also been found. As the sample was contained in an aluminium holder during the measurements, Al has also been added in the refinement, but it was subtracted from the mineral phase quantification. The quantitative results of phase analysis are reported in Table 2, where each phase is reported in % wt over the total crystalline component.
5, originating from Ni substitutions) have also been found. As the sample was contained in an aluminium holder during the measurements, Al has also been added in the refinement, but it was subtracted from the mineral phase quantification. The quantitative results of phase analysis are reported in Table 2, where each phase is reported in % wt over the total crystalline component.
| Phase | % wt over crystalline component |
|---|---|
| Forsterite | 56.0 ± 0.5 |
| Enstatite | 30.2 ± 0.5 |
| Magnetite | 5.89 ± 0.14 |
| Troilite | 6.1 ± 0.3 |
| Kamacite | 0.80 ± 0.03 |
In peak shape analysis only the three major phases were added and the cells were refined in order to extract cell parameters a, b and c, which are presented in Table 3. In particular, the value of a for forsterite resulted to be (4.7703 ± 0.0002) Å, which lies in between the nominal values for forsterite Mg2SiO4 (4.7540 Å) and fayalite Fe2SiO4 (4.8211 Å). As these two phases share the same lattice structure, the Vegard law29,30 can be applied, which assumes that the value of the cell parameter grows linearly from the forsterite to the fayalite value as the ratio of Fe substitutions increases. This procedure is depicted in Fig. 7. In this way, it was possible to estimate the amount of Fe substitutions as (24.3 ± 0.3)%.
| Phase | a (Å) | b (Å) | c (Å) |
|---|---|---|---|
| Forsterite | 4.7703 ± 0.0002 | 10.2323 ± 0.0006 | 5.9967 ± 0.0003 |
| Enstatite | 18.2515 ± 0.0017 | 8.8631 ± 0.0009 | 5.1970 ± 0.0005 |
| Magnetite | 8.3994 ± 0.0005 | 8.3994 ± 0.0005 | 8.3994 ± 0.0005 |
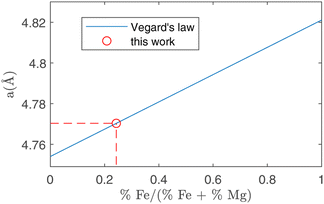 | ||
| Fig. 7 Running of the a crystal cell parameter as a function of the relative amount of Fe substitutions. The two extremes in this plot are forsterite (without Fe, abscissa = 0) and fayalite (without Mg, abscissa = 1). Using the value for a obtained in forsterite with ToF-ND (circle, see Table 3) it is possible to estimate the amount of Fe substitutions using the Vegard law (solid line). | ||
It is typically possible to estimate the amount of Ni in kamacite with a similar procedure. However, it was not possible in this case due to the negligible amount of kamacite, which did not allow this quantification. As a consequence, we manually set a 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ratio between Fe and Ni, later confirmed by EDS measurements as reported in Section 3.6. Nevertheless, the described procedure of kamacite calibration by means of the Vegard's law may be interesting in the study of iron meteorites, where the major phases are typically kamacite and taenite.7
5 ratio between Fe and Ni, later confirmed by EDS measurements as reported in Section 3.6. Nevertheless, the described procedure of kamacite calibration by means of the Vegard's law may be interesting in the study of iron meteorites, where the major phases are typically kamacite and taenite.7
It is also possible to study the texture and strains in the crystals, on a few specific neutron beamlines.31 Indeed, the lattice alterations can give information about the extreme conditions withstood by the sample during its formation and its fall in the atmosphere.
3.3 NRCA and NRTI results
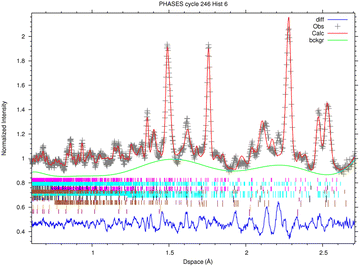
The NRCA measurements were carried out together with the ToF-ND data acquisition. The interesting 40–160 μs region in time-of-flight of the NRCA spectrum is presented in Fig. 8 together with the peak identification performed with the ENDF/B-VIII.0 database of neutron-capture cross sections.32 No other relevant structures were visible in the full 30–1000 μs time-of-flight NRCA spectrum. It was obtained by merging the four sampled spectra as they were all consistent with each other. The region of interest is below 3 keV, i.e. over 30 μs, in order to avoid the gamma ray background promptly generated during spallation and moderation. This technique allowed to identify the presence of Fe, Mn and Co. The fact that Mn and Co peaks are larger than the Fe one is not due to energy resolution, but it is a direct consequence of the shape of the resonance in the cross section around the peak energy. | ||
| Fig. 8 The 40–160 keV zoom of the NRCA spectrum on sample R002 with peak identification by means of the ENDF/B-VIII.0 database, accessed through the KAERI website.32 In the inset the full NRCA spectrum is displayed, with the same axes. | ||
Regarding NRTI, the analysis on the sole sample R002 is here presented, as no difference has been identified between R001 and R002. Furthermore, having sample R002 constant thickness, no further corrections are needed, which should be applied to sample R001 as it has a more complex geometry. The main results of NRTI applied to sample R002 are reported in Fig. 9. The total transmission coefficient, calculated on the integrated spectrum, shows that the sample has a uniform neutron absorption within the space resolution of the detector in use (750 μm). The neutron transmission spectrum is also presented in the same figure with peak attribution. It is important to notice that the NRTI spectrum in the (40–160) μs range is complementary to the NRCA spectrum in the same range, as one would expect. This technique allows the identification of Fe, Mn and Co, enabling the investigation of all the neutron energy range as the n-GEM discriminated gamma rays from neutrons. As a consequence it makes possible the study of the time-of-flight spectrum from 0 to 30 μs too, which was excluded by NRCA.
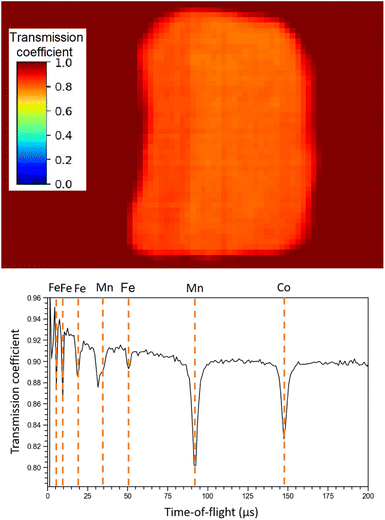 | ||
| Fig. 9 NRTI integrated transmission coefficient on sample R002 (up), showing the uniformity of the sample, and NRTI spectrum on R002 (down) with peak identification by means of the ENDF/B-VIII.0 database, accessed through the KAERI website.32 | ||
Unlike the ToF-ND and neutron-capture analysis of the Chelyabinsk meteorite,9 whose inhomogeneities made it interesting to perform Neutron Tomography (NT), in this case the sample proved to be homogeneous at mm scale inspected by NRTI. We therefore decided not to further analyse these data.
3.4 μXES results
The four main elements have been quantified in the bulk on the 40 MeV per c run data, i.e. investigating around 1–2 mm under the surface (as one can derive from Fig. 4). The % wt of the main elements are: O (30.6 ± 0.9)%, Si (23.6 ± 0.1)%, Mg (23.2 ± 0.1)% and Fe (22.6 ± 0.1)%. These elements are the main constituents of the mineral phases observed by ToF-ND, as a consequence these two techniques return consistent results. In Section 3.6 these results are discussed and compared to the results of EDS.3.5 μRS results
The μ-Raman mapping spectroscopy confirms the predominance of forsterite and enstatite on the thin section, which can be considered representative of the whole sample. This is because many portions of the thin section were analysed, returning consistent results. The μRS spectra of these two phases, obtained on sample R003, are reported in Fig. 10 with the band attribution.33 In addition, traces of diopside (pyroxene, CaMg(Si2O6)), hematite (iron oxide) and quartz (tectosilicate, SiO2) were identified, along with traces of laser-induced anhydrite.34 In particular, the Raman signal is visible only in chondrules, whereas the inter-chondrular matrix appears almost completely Raman-inactive. Fig. 14 shows an overview on the chondrules cross-mapped with μRS and EDS: two chondrules have been studied with both techniques (A and B), whereas two different chondrules were used as mock-ups to understand the main mineral phases (chondrule C, studied with μRS) and the difference in the composition of glass and forsterite (chondrule D, studied with EDS). Detailed results from μRS and EDS mapping can be found in a previous work.22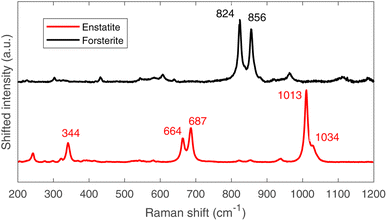 | ||
| Fig. 10 Raman spectra of forsterite (up, black) and enstatite (down, red), with peak identification.33 | ||
It is crucial to make use of μRS for phase identification as the identification of phases can be cumbersome in ToF-ND and therefore μRS may lead in the ToF-ND data analysis.
3.6 BSE-SEM and EDS results
It has been decided to study with these techniques the same structures in sample R003 investigated with μRS, but other Raman-inactive portions have also been analysed, like the intra-chondrular glass and the metallic relics. For example, the study of chondrule D (see Fig. 14) allowed to identify the richness of the intra-chondrular glass in certain elements such as Si, O, Ca, Na & Al, whereas the surrounding forsterite contains Mg, O & Si above all. The BSE-SEM and EDS mapping measurements are extensively presented in a previous work.22The EDS elemental composition, obtained by repeating the EDS measurement on 20 spots identified as made of forsterite or enstatite (10 spots each) by μRS, is reported in standard box plots in Fig. 11. It is important to observe the different amount of Si, O and Mg, the three main constituents of these two minerals. Furthermore, one can observe the presence of Fe substitutions in both minerals. The amount of substitutions in forsterite can be estimated as Fe/(Fe + Mg) = (23 ± 5)%, which is t-Student consistent (t = 0.29) with the estimation that can be obtained with the ToF-ND applying the Vegard law (24.3 ± 0.3)%. The amount of Fe substitutions in enstatite has not been calculated due to the big relative uncertainty on the amount of Fe.
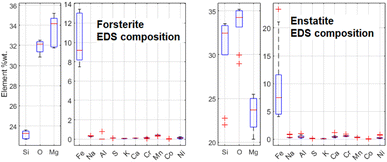 | ||
| Fig. 11 Comparison between the elemental composition of forsterite and enstatite crystals, obtained by means of 10 EDS measurements for each mineral. | ||
Some Fe-based relics have been studied too. This part of the probing resulted in the identification of two classes of metallic structures: a Fe–Ni alloy and a Fe–S mineral. An example of the aspect of these relics at BSE-SEM can be seen in Fig. 12. All these relics were surrounded by an iron-based oxidised material. The elemental quantification of these two classes of iron-based structures is reported in Fig. 13. This analysis is consistent with ToF-ND in identifying relevant quantities of magnetite (iron oxide) together with iron compounds with sulfur (troilite) and nickel (kamacite). Those latter phases can be considered Raman-inactive, which is the reason why the inter-chondrular matrix is totally black when observed by μRS. The Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni ratio in the left box in Fig. 12 has been used in defining the kamacite atomic composition for the ToF-ND data analysis.
Ni ratio in the left box in Fig. 12 has been used in defining the kamacite atomic composition for the ToF-ND data analysis.
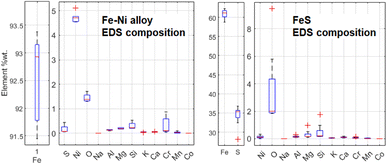 | ||
| Fig. 13 Comparison between elemental composition of Fe–Ni and Fe–S structures, obtained by means of 5 EDS measurements for Fe–Ni and 8 ones for Fe–S. | ||
 | ||
| Fig. 14 Combined μRS and SEM-EDS mapping study on four chondrules on the thin section R003. Further details can be found in a previous work.22 | ||
In order to have a complete elemental composition on the sample avoiding the overestimation of aluminium due to the thin section treatment method, repeated wide-range EDS measurements were carried out on the polished surface of sample R002. In particular, 100 s EDS measurements were carried out on 5 × 6 mm non-intersecting areas in standard SEM conditions, returning the composition reported in Table 4. The results on the first four phases (normalised totalling 100%) are all consistent within 3σ with the values obtained by μXES (evaluation made with the t-Student test).
| Element | % wt | Element | % wt |
|---|---|---|---|
| O | 28.1 ± 0.6 | Ni | 1.44 ± 0.11 |
| Si | 23.0 ± 0.4 | Na | 0.51 ± 0.04 |
| Fe | 22.5 ± 0.7 | Cr | 0.46 ± 0.04 |
| Mg | 18.7 ± 0.3 | Mn | 0.29 ± 0.05 |
| Al | 1.66 ± 0.08 | K | 0.145 ± 0.016 |
| Ca | 1.65 ± 0.05 | P | 0.04 ± 0.02 |
| S | 1.5 ± 0.3 | Co |
A great effort is being made in trying to make these NRCA and NRTI quantitative techniques and μXES more sensitive to low-concentration elements. This would be useful in order to skip the use of a statistically-relevant EDS campaign for elemental quantification. In fact, EDS still requires a polished surface, obtained with a destructive procedure, which can also alter the microstructure of the sample.
4 Conclusions
In conclusion, this multidisciplinary protocol enables the characterisation of the sample in a non-destructive way. In particular, gamma ray spectrometry allows to identify the sample as a meteorite by searching for the presence of cosmogenic radionuclides. If the sample fall is recent (less than about ten years), standard gamma ray spectrometry can be performed, whereas in case of an older fall, low-background gamma ray spectrometry is required. In this case, the presence of 26Al is a marker of the meteoric origin of the studied sample.It is of crucial importance to notice that the overlapping of surface and bulk techniques is not only a cross-check, because they all return significant information which help the interpretation of other data and contribute to the characterisation of the sample.
In fact, ToF-ND enables the user to perform mineral phase quantification and lattice analysis, provided a hint on the present phases which can be given by a few μRS measurements. We also gave an estimation for the amount of Fe substitutions is forsterite which proved to be consistent with the EDS elemental quantification. However, a thorough mapping of the sample surfaces by means of μRS can yield a precise mineral phase spatial distribution, which can not be obtained with ToF-ND. In some minor phases such as kamacite, the amount of Ni substitutions had to be extracted from a SEM-EDS campaign.
Finally, NRCA and NRTI return a marker of the presence of certain elements (in this case Co, Fe, Mn) while μXES quantifies the weight ratio among the main elements in the sample (O, Si, Mg, Fe). However, a consolidated technique such as SEM-EDS is still required for a trusted, complete and quantitative elemental characterisation, even though it requires a thin section or a polished surface.
Above all, this analysis protocol would enable to insert a meteoric sample into the standard meteorite classification framework without any destructive measurement. This sample proved to be a good mock-up for testing this protocol, whereas more tests are expected to be applied on catalogued meteorites from various classes. Furthermore, research and development is being carried out in order to be able to extract quantitative information on the elemental composition from NRCA and NRTI at INES.
Author contributions
D. D., G. G., M. M., M. P. R. A. S. and M. Cl. conceived the idea of a new methodology for the characterisation of meteorite samples based on a completely non-destructive protocol. M. M. and R. R. performed Raman experiments and data analysis. M. P. R. and R. R. carried out SEM measurements and data analysis. M. Cl., M. L. and R. R. carried out gamma ray measurements, performed MC simulation and analysed data. A. S. carried out neutron measurements, whereas data analysis was carried out by R. R. and A. S. (ToF-ND and NRCA) and G. M. and A. S. (NRTI). A. H., T. A. and M. Ca. carried out muon experiments and data analysis. All authors gave contributions in the results discussion. R. R. wrote the manuscript in consultation with all authors. All authors have read and approved the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported within the CNR-STFC Agreement 2021–2027, in particular regarding the activity at the ISIS Neutron and Muon Source. The neutron measurements were carried out at ISIS within the experiment number RB 2000255. The INFN – Laboratori Nazionali del Gran Sasso (Italy) and the Gulf Institute of Gemology (Oman) are thankfully acknowledged for the analytical support.References
- R. Hutchinson, Meteorites: a Petrologic, Chemical and Isotopic Synthesis, 1st edn, 2004 Search PubMed.
- W. Van Schmus and J. Wood, Geochim. Cosmochim. Acta, 1967, 31, 747–765 CrossRef CAS.
- V. Alexeev, M. Laubenstein, P. Povinec and G. Ustinova, Adv. Space Res., 2015, 56, 766–771 CrossRef CAS.
- H. Postma and P. Schillebeeckx, Encyclopedia of Analytical Chemistry, 2009 Search PubMed.
- G. Festa, E. Perelli Cippo and D. Di Martino, et al. , J. Anal. At. Spectrom., 2015, 30, 745–750 RSC.
- A. Fedrigo, D. Raspino, F. Grazzi and A. Scherillo, J. Anal. At. Spectrom., 2019, 34, 2420–2427 RSC.
- F. Grazzi, A. Scherillo, V. Moggi Cecchi, M. Morelli, G. Pratesi and S. Caporali, Minerals, 2018, 8, 19 CrossRef.
- K. Podurets and S. Kichanov, et al. , Crystallogr. Rep., 2021, 66, 254–266 CrossRef CAS.
- S. Kichanov, D. Kozlenko and A. Kirillov, et al. , SN Appl. Sci., 2019, 1, 1563 CrossRef CAS.
- A.D. Hillier, D. McK Paul and K. Ishida, Microchem. J., 2016, 125, 203–207 CrossRef CAS.
- M. Cataldo, M. Clemenza, K. Ishida and A. Hillier, Appl. Sci., 2022, 12, 4237 CrossRef CAS.
- M. Clemenza, M. Bonesini and M. Carpinelli, et al. , J. Radioanal. Nucl. Chem., 2019, 322, 1357–1363 CrossRef CAS.
- M. Clemenza, G. Baldazzi and G. Ballerini, et al. , Nucl. Instrum. Methods Phys. Res., Sect. A, 2019, 936, 27–28 CrossRef CAS.
- S. D'Amico and V. Venuti, Handbook of Cultural Heritage Analysis, 1st edn, 2022 Search PubMed.
- M. Grady, G. Pratesi, V. Moggi Cecchi, Atlas of Meteorites, 2014 Search PubMed.
- M. Laubenstein, Int. J. Mod. Phys. A, 2017, 32, 1743002 CrossRef CAS.
- A. S. Agostinelli, J. Allison and K. Amako, et al. , Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 506, 250–303 CrossRef.
- S. Imberti and W. Kockelmann, et al. , Meas. Sci. Technol., 2008, 19, 34003–34010 CrossRef.
- A. Larson and R. Von Dreele, Los Alamos National Laboratory Report LAUR, 2004, pp. 86–748 Search PubMed.
- F. Sauli, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 805, 2–24 CrossRef CAS.
- J. Ziegler, M. Ziegler and J. Biersack, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS.
- M. Musa, R. Rossini, D. Di Martino, M. Riccardi, M. Clemenza and G. Gorini, Materials, 2021, 14, 7585 CrossRef CAS PubMed.
- J. Parrington and H. Knox, et al. , Nuclides and Isotopes: Chart of the Nuclides, 1996 Search PubMed.
- C. M. Lederer, J. M. Hollander and I. Perlman, Table of Isotopes, 6th edn, 1967 Search PubMed.
- M. Eisenbud and T. Gesell, Environmental Radioactivity from Natural, Industrial and Military Sources, 4th edn, 1997 Search PubMed.
- M. Auer, D. Wagenbach and E. Wild, et al. , Earth Planet. Sci. Lett., 2009, 287, 453–462 CrossRef CAS.
- R. Middleton and J. Klein, Philos. Trans. R. Soc. London, Ser., 1987, 323, 121–143 CrossRef CAS.
- R. Rossini, M. Clemenza and D. Di Martinoet al., Low-background Gamma Spectroscopy and Neutron Diffraction in the Study of Stony Meteorites, submitted to Applied Radiation and Isotopes, 2022 Search PubMed.
- L. Vegard, Z. Phys., 1921, 5, 17–26 CrossRef CAS.
- R. Cattaneo, C. Chiaramonte Trerè and L. Mordeglia, et al. , J. Anal. At. Spectrom., 2011, 26, 1024 RSC.
- S. Nagler and A. Stoica, et al. , J. Anal. Methods Chem., 2019, 6164058 Search PubMed.
- Evaluated Nuclear Data File ENDF/B-VIII.0, https://atom.kaeri.re.kr/nuchart/, last accessed on 23rd of November, 2022 Search PubMed.
- H.-J. Schubnel and M. Pinetet al., in Utilité de la microsonde Raman pour l’identification non-destructive des gemmes, ed. A. F. de Gemmologie, 1st edn, 1992 Search PubMed.
- R. Fogel, Meteorit. Planet. Sci., 1997, 32, 577–591 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |