Open Access Article
Open Access ArticleA silica-related matrix effect on NanoSIMS Li isotopic analysis of glasses and its online calibration
Rui-Ying
Li
 ,
Jialong
Hao
,
Jialong
Hao
 ,
Wei
Yang
,
Wei
Yang
 *,
Heng-Ci
Tian
,
Sen
Hu
and
Yangting
Lin
*,
Heng-Ci
Tian
,
Sen
Hu
and
Yangting
Lin
Key Laboratory of Earth and Planetary Physics, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, P. R. China. E-mail: yangw@mail.iggcas.ac.cn
First published on 30th August 2023
Abstract
Accurate Li isotope analysis of silicate glasses using secondary ion mass spectrometry (SIMS) is challenging due to the matrix effect, which causes instrumental mass fractionation (IMF). The characteristics of the matrix effect vary for each element, necessitating empirical correction methods. Here, we present Li isotopic measurements on a set of silicate glasses spanning a broad compositional range from ultramafic to highly siliceous using a Cameca NanoSIMS 50L. A radio-frequency (RF)-O primary beam with an intensity of 1 nA was rastered over a 5 × 5 μm2 area on the sample, and the secondary ions 6Li, 7Li and 30Si were simultaneously detected. We observed a significant matrix effect on δ7Li in the silicate glasses, which yielded an IMF of up to 19‰, exceeding the analytical precision of <2.5‰ (1SD). The IMF is strongly correlated with the chemical compositions of the silicate glasses. To correct the matrix effect, we employed various correction schemes, including univariate and multivariable compositions. All results consistently indicated that silica exerted a dominant influence on the IMF. We then propose a straightforward “online” method to correct this silica-related matrix effect by utilizing simultaneously measured 30Si signals. This strategy improves the accuracy of the Li isotope measurements to within 3‰ and can be widely applied to anhydrous subalkaline magmatic glasses with compositions ranging from ultramafic to highly siliceous.
1. Introduction
Lithium is the lightest metal element with two stable isotopes – 6Li (7.52%) and 7Li (92.48%). The large mass difference (16%) between its isotopes results in considerable variations of Li isotopes in geological processes, making Li isotopes a geochemical tracer with broad applications. Due to the strong fluid mobility of Li, its isotopes are powerful tracers for the processes of mantle convection and crust/mantle recycling,1–4 as well as planetary weathering.5–9 Owing to the rapid diffusivity of Li and associated isotopic fractionations on meter-to-micrometer scales, Li isotopes have been employed as high-resolution geo-speedometers to reveal the history of magmatic exhalation10–14 and fluid–rock interactions.15 In addition, Li has also provided valuable information regarding Big Bang nucleosynthesis and the subsequent cosmic and stellar evolution.16–23The secondary ion mass spectrometry (SIMS) technique is widely used for Li isotope measurements and offers the advantage of efficiently assessing spatial correlations between concentration and isotopes at the micrometer scale.4,10,12,16–18,24–32 However, SIMS analysis is significantly affected by the matrix effect, leading to instrumental mass fractionation (IMF) that is critically dependent on the chemical compositions and/or structure of the analyte.4,24–26,28–31,33–43 Moreover, the characteristics of the matrix effect generally differ depending on the element, making the correction complex. In the case of Li measurement, previous studies have observed composition-dependent bias in minerals and silicate glasses.24–26,29–31,39 For Li concentration analysis, a Si-related matrix effect on silicates25,29 and an (Fe + Mn)-related matrix effect on tourmaline30 have been noted. Regarding Li isotope analysis, a Mg/(Mg + Fe)-related matrix effect on olivine24,31 and an (Fe + Mn)-related matrix effect on garnet39 were reported. Although SIMS energy filtering can be used to reduce the matrix effect, it could result in a signal loss for the desired secondary ions and unwanted effects for other simultaneously measured elements.26,29 A commonly used method to correct the matrix effect is to calibrate the unknown samples against matrix-matched reference materials with known concentrations and isotopic compositions.24,25,31,33,34,36–41,44–47 However, the reference materials may not always match the unknowns in composition. Therefore, it is necessary to develop a calibration strategy for the matrix effect on Li isotope analysis that can be applied to a wide range of samples.
This study aims to quantify the matrix effect on Li isotope analysis of silicate glasses and establish correction schemes applicable to glasses with a compositional range from komatiite to rhyolite. A NanoSIMS was used due to its high spatial resolution and multi-collection mode to measure Li isotopes with other elements.32,35,36,40,41,43,47–58
2. Samples and analytical procedures
2.1 Sample preparation
Five MPI-DING glasses spanning a wide range from ultramafic to highly siliceous composition were chosen for analysis, including GOR128-G (komatiite), ML3B-G (basalt), StHs6/80-G (andesite), T1-G (diorite) and ATHO-G (rhyolite). These samples were prepared by fusing natural rock powders.59 Detailed chemical compositions of these MPI-DING samples have been published by Jochum (2006).60 Preferred values for Li concentrations and Li isotopes are in range of 4.5–28.6 ppm and 2.1–17.1‰, respectively.60 Their compositions are summarized in Table 1. Fragments of the standard samples were cast in a tin–bismuth alloy mount and well-polished to expose the interior of the crystals. The sample mount was washed by ultrasonic cleaning in ethanol and coated with high-purity gold prior to analysis.| Compositions | GOR128-G | ML3B-G | T1-G | StHs6/80-G | ATHO-G |
|---|---|---|---|---|---|
| Komatiite | Basalt | Diorite | Andesite | Rhyolite | |
| a The chemical and Li isotopic compositions with uncertainties (1SD) of the glass standards are from Jochum (2006).60 Li isotopes are given relative to the reference material L-SVEC. b NBO/T: the ratio of non-bridging oxygen atoms per tetrahedrally coordinated cations, calculated as NBO/T = 2 (XMgO + XCaO + XFeO + XMnO + XNa2O + XK2O − XAl2O3)/(XSiO2 + 2XAl2O3) following the reference,61 and X is the mole fraction of the corresponding elements. c MAM: the mean atomic mass. | |||||
| SiO2a (wt%) | 46.1 ± 0.4 | 51.4 ± 0.6 | 58.6 ± 0.4 | 63.7 ± 0.5 | 75.6 ± 0.7 |
| MgOa (wt%) | 26.00 ± 0.30 | 6.59 ± 0.08 | 3.75 ± 0.04 | 1.97 ± 0.04 | 0.103 ± 0.01 |
| Al2O3a (wt%) | 9.9 ± 0.2 | 13.6 ± 0.2 | 17.1 ± 0.2 | 17.8 ± 0.2 | 12.2 ± 0.2 |
| FeOta (wt%) | 9.81 ± 0.12 | 10.90 ± 0.10 | 6.44 ± 0.06 | 4.37 ± 0.07 | 3.27 ± 0.10 |
| CaOa (wt%) | 6.2 ± 0.1 | 10.5 ± 0.1 | 7.1 ± 0.09 | 5.3 ± 0.1 | 1.7 ± 0.03 |
| TiO2a (wt%) | 0.29 ± 0.01 | 2.13 ± 0.09 | 0.76 ± 0.02 | 0.70 ± 0.02 | 0.26 ± 0.02 |
| K2Oa (wt%) | 0.04 ± 0.01 | 0.39 ± 0.09 | 1.96 ± 0.02 | 1.29 ± 0.02 | 2.64 ± 0.02 |
| Na2Oa (wt%) | 0.57 ± 0.03 | 2.40 ± 0.06 | 3.13 ± 0.09 | 4.44 ± 0.14 | 3.75 ± 0.31 |
| P2O5a (wt%) | 0.03 ± 0.01 | 0.23 ± 0.023 | 0.17 ± 0.03 | 0.16 ± 0.02 | 0.03 ± 0.004 |
| MnOa (wt%) | 0.18 ± 0.01 | 0.17 ± 0.01 | 0.13 ± 0.01 | 0.08 ± 0.004 | 0.11 ± 0.01 |
| K2O + Na2O (wt%) | 0.61 | 2.79 | 5.09 | 5.73 | 6.39 |
| H2Oa (wt%) | 0.026 | 0.015 | 0.026 | 0.025 | 0.014 |
| CO2a (ppm) | 4.4 | 4.7 | 6.3 | 4.4 | 3.7 |
| Lia (ppm) | 10.4 ± 1.7 | 4.5 ± 0.4 | 19.9 ± 0.9 | 20.7 ± 2.3 | 28.6 ± 1.8 |
| 7Li/6Litrue | 12.0336 | 12.0236 | 12.0213 | 12.0228 | 12.0363 |
| δ 7Lia (‰) | 14.4 ± 0.4 | 4.4 ± 0.4 | 2.1 ± 0.4 | 3.6 ± 0.4 | 17.1 ± 0.4 |
| NBO/Tb | 1.88 | 0.84 | 0.38 | 0.19 | 0.07 |
| MAM c | 22.0 | 22.9 | 22.2 | 21.6 | 21.5 |
2.2 Analytical conditions
We performed Li analyses using the Cameca NanoSIMS 50L instrument at the Institute of Geology and Geophysics, Chinese Academy of Sciences (IGGCAS) in Beijing. A radio-frequency (RF)-plasma source was applied to generate an 16O− primary beam with an impact energy of 16 keV and an intensity of 1 nA. A mass resolution (M/ΔM measured at a 10% peak height) of ∼5000 was set to separate any possible interference (e.g., 6LiH+) from the peaks of interest. Positive 6Li, 7Li and 30Si ions were simultaneously detected using electron multipliers (EMs) with 44 ns dead-time correction. Each analytical spot was pre-sputtering by 10 × 10 μm2 for ∼60 s to remove the coating and implant 16O− into the samples to stabilize the yield of the secondary ions. Afterward, the secondary ions were acquired from the central raster of 5 × 5 μm2. Each analysis consisted of 50 blocks of 20 cycles, with 64 × 64 pixels for a single cycle and a default counting time of 132 μs for each pixel. Then, the analytical sequences were set in the chained analysis mode of the NanoSIMS for the standard samples. The secondary ion beam centering at the entrance silt proceeded automatically after the pre-sputter. The total analysis time was approximately 10–11 min with a counting time of 9 min. The whole experiment was conducted in 3 sessions over three days, with each standard sample measured 25 times repeatedly. To eliminate the impact of potential sensitivity degradation of EMs, each EM was monitored and corrected using the pulse height distribution (PHD) curve every 12 hours.Then, the Li isotope and IMF values were expressed in per mil deviations as follows:
| δ7Limeasured = [(7Li/6Limeasured)/(7Li/6Li L-SVEC) − 1] × 1000 | (1) |
| IMF = [(7Li/6Limeasured)/(7Li/6Litrue) − 1)] × 1000 | (2) |
| δ7Licalibrated = δ7Limeasured − IMF | (3) |
| Analytical sessions | Samples | 7Li rate (cps) | RSDa (%) | 30Si rate (cps) | RSDa (%) | 7Li/6Limeasured | δ 7Limeasured (‰) | SDb (‰) | IMF (‰) | n |
|---|---|---|---|---|---|---|---|---|---|---|
| a RSD represents the relative standard deviation of 7Li and 30Si counting rates for repeated analysis of samples in a single session. b SD represents the standard deviation of δ7Limeasured values for repeated analysis of samples in a single session. | ||||||||||
| Session 1 | ATHO-G | 2.96 × 104 | 1.03 | 4.36 × 105 | 0.89 | 12.5279 | 42.3 | 1.2 | 24.8 | 5 |
| GOR128-G | 1.14 × 104 | 1.61 | 1.72 × 105 | 0.83 | 12.7226 | 58.5 | 1.9 | 43.5 | 5 | |
| StHs6/80-G | 2.38 × 104 | 0.80 | 2.93 × 105 | 0.35 | 12.4925 | 39.4 | 1.4 | 35.7 | 5 | |
| T1-G | 2.48 × 104 | 0.40 | 2.49 × 105 | 1.09 | 12.5147 | 41.2 | 1.2 | 39.0 | 5 | |
| ML3B-G | 5.76 × 103 | 0.41 | 2.03 × 105 | 0.47 | 12.5711 | 45.9 | 1.9 | 41.3 | 5 | |
| Session 2 | ATHO-G | 2.65 × 104 | 1.89 | 4.15 × 105 | 0.87 | 12.6163 | 49.7 | 2.3 | 32.0 | 10 |
| GOR128-G | 1.09 × 104 | 2.58 | 1.66 × 105 | 1.37 | 12.7577 | 61.4 | 1.7 | 46.4 | 10 | |
| StHs6/80-G | 2.28 × 104 | 0.77 | 2.85 × 105 | 0.61 | 12.4675 | 37.3 | 2.3 | 33.3 | 10 | |
| T1-G | 2.41 × 104 | 1.33 | 2.44 × 105 | 0.78 | 12.5149 | 41.2 | 1.9 | 39.1 | 10 | |
| ML3B-G | 5.27 × 103 | 1.45 | 1.94 × 105 | 0.54 | 12.6098 | 49.1 | 2.5 | 44.5 | 10 | |
| Session 3 | ATHO-G | 2.98 × 104 | 1.40 | 4.35 × 105 | 0.63 | 12.4690 | 37.4 | 1.8 | 20.0 | 10 |
| GOR128-G | 1.06 × 104 | 4.26 | 1.64 × 105 | 1.58 | 12.6305 | 50.9 | 2.3 | 35.9 | 10 | |
| StHs6/80-G | 2.46 × 104 | 1.06 | 2.92 × 105 | 0.69 | 12.3844 | 30.4 | 1.4 | 26.7 | 10 | |
| T1-G | 2.51 × 104 | 2.35 | 2.45 × 105 | 0.89 | 12.4722 | 37.7 | 1.9 | 35.5 | 10 | |
| ML3B-G | 5.66 × 103 | 1.82 | 1.96 × 105 | 0.74 | 12.5294 | 42.5 | 2.1 | 37.9 | 10 | |
3. Results
3.1 Li yields and IMF
ATHO-G, with the highest Li concentration of 28.6 ± 1.8 ppm among these samples (Table 1), shows a 7Li counting rate ranging from 2.65 × 104 to 2.98 × 104 counts per second (cps) in three analytical sessions (Table 2). For each session, the relative standard deviation (RSD) of its 7Li counting rate ranges between 1.03% and 1.89% (Table 2). The average 7Li+ yield of ATHO-G can be calculated to be approximately 1001 ± 65 cps nA−1 ppm−1. The measured δ7Li value of ATHO-G varies from 37.4‰ to 49.7‰ in the three sessions (Table 2). Accordingly, the IMF of ATHO-G ranges from 20.0‰ to 32.0‰ (Table 2).StHs6/80-G has a Li abundance of 20.7 ± 2.3 ppm (Table 1). It gains a 7Li counting rate of 2.28 × 104–2.46 × 104 cps with RSD values of 0.77–1.06% (Table 2) and a 7Li+ yield of 1147 ± 43 cps nA−1 ppm−1. The measured δ7Li value is 30.4–39.4‰, with the IMF calculated to be 26.7–35.7‰ (Table 2).
The Li concentration of T1-G is 19.9 ± 0.9 ppm (Table 1). T1-G yields 7Li counting rates of 2.41 × 104–2.51 × 104 with RSD values of 0.40–2.35% (Table 2). The average yield of 7Li+ is 1239 ± 24 cps nA−1 ppm−1 for T1-G. The measured δ7Li value is 37.7–41.2‰ (Table 2). As a result, the IMF is calculated to be 35.5–39.1‰ (Table 2).
GOR128-G has 10.4 ± 1.7 ppm Li (Table 1), and a range of 7Li counting rates of 1.06 × 104–1.14 × 104 (Table 2). The relative variation of 7Li counting rates for GOR128-G is 1.61–4.26%, which is higher than that of other samples in each session (Table 2). Its average yield of 7Li+ is calculated to be 1055 ± 41 cps nA−1 ppm−1. The measured δ7Li value of GOR128-G is 50.9–61.4‰ with an IMF of 35.9–46.4‰ (Table 2).
ML3B-G has the lowest Li abundance of 4.5 ± 0.4 ppm in this study (Table 1). It gains 7Li counting rates of 5.27 × 103–5.76 × 103 cps with RSD values of 0.41–1.82% (Table 2). The yield of 7Li+ for ML3B-G is 1236 ± 58 cpsn A−1 ppm−1. And the measured δ7Li value is 42.4–49.1‰, with the IMF varying from 37.9‰ to 44.5‰ (Table 2).
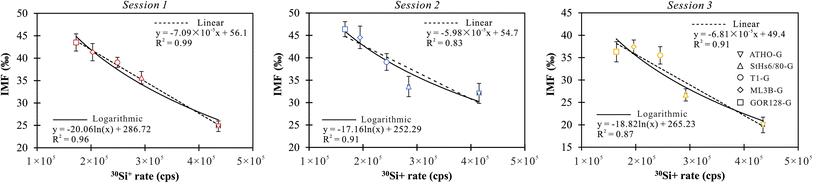
In summary, the 7Li counting rate is correlated with the Li abundance of the sample, while the RSD values of the counting rate mirror the instrumental steady-state and the uncertainty of the samples. The yield of Li ions and IMF values vary from sample to sample. The difference in IMF among various types of silicate glasses could reach 19‰ in a single session, resulting from the matrix effect on Li isotope analysis of silicate glasses (Table 2). A systematic 7Li/6Li ratio variation was observed for the same samples in different analytical sessions (Table 2). Comparisons of these sessions show variable IMF for a given sample (up to 12‰, Table 2), suggesting that the IMF is quite sensitive to slight shifts in the instrumental conditions.
3.2 Analytical precision
The analytical precision of the 7Li/6Li ratio determination is evaluated in terms of internal (within-spot analysis, SE) and external (spot-to-spot analysis, SD) precision. The internal precision of the 7Li/6Li ratio for each analytical point ranges from 0.9‰ to 2.1‰ (1SE), following the Poisson theoretical error determined qualitatively from counting statistics of 7Li and 6Li. Typically, it decreases with increasing Li concentration in the analyzed phase. The external precision of 7Li/6Li ratios over repeated analysis ranges from 1.2‰ to 2.5‰ (1SD) in a single analytical session (Table 2).Previous in situ Li isotope analytical methods established by SIMS and laser ablation-multiple collector-inductively coupled plasma-mass spectrometry (LA-MC-ICP-MS) have yielded a general reproducibility within 1–3‰ (1SD) (Table 3). Given the low abundance of Li in most of the samples, primary beam intensities with tens of nA were applied in the raster sizes of tens to hundreds of micrometers (Table 3). It is notable that the spatial resolution of Li isotope measurements in this study is ∼5 μm, significantly better than that in previous studies with comparable analytical reproducibility.
| Instruments | Analytical model | Primary beam intensity (nA) | Raster size (μm) | Precision (‰) | Ref. |
|---|---|---|---|---|---|
| a The precision is reported as 1SD for δ7Li. b The precision is reported as 1SE for δ7Li. c The beam size of the corresponding primary beam. The raster size in other studies represents the size of analytical area. | |||||
| NanoSIMS | Multi-collection | 1 | 5 | 1.2–2.5a | This study |
| SIMS | Multi-collection | 15 | 20 | 1a | 4 |
| SIMS | Magnetic peak switching | 30 | 30 | 1.5b | 12 |
| SIMS | Magnetic peak switching | 40 | 30 | 0.6a | 13 |
| SIMS | Magnetic peak switching | 50 | 25 | 0.5–2.8a | 17 |
| SIMS | Magnetic peak switching | 10 | 5c | 1–2a | 18 |
| SIMS | Magnetic peak switching | 15–30 | 30–50 | 0.7–1a | 24 |
| SIMS | Magnetic peak switching | 20 | 25 | 0.2–1a | 26 |
| SIMS | Multi-collection | 3–17 | 20 | 0.3–1.8b | 39 |
| SIMS | Magnetic peak switching | 20 | 12 | 0.5–1a | 62 |
| SIMS | Magnetic peak switching | 10–20 | 25 | 2a | 63 |
| SIMS | Magnetic peak switching | 14–30 | 5–20 | 2–5a | 64 |
| LA-MC-ICPMS | Multi-collection | n. d. | 125–150 | 0.5a | 65 |
| SIMS | Magnetic peak switching | 14–30 | 20–30 | 1a | 66 |
| LA-MC-ICPMS | Multi-collection | n. d. | 65–120 | <1a | 67 |
| SIMS | Magnetic peak switching | 28 | 20–30 | 1a | 68 |
| SIMS | Magnetic peak switching | 1–5 | 10–20 | 0.5–2.5a | 69 |
| LA-MC-ICPMS | Multi-collection | n. d. | 26 | 1a | 70 |
4. Discussion
The results from this study show that the relative IMF among silicate glasses can differ by up to 19‰ in a single session, far beyond the current analytical precision of <2.5‰ (1SD) (Table 2). These data presented by silicate glasses offer productive examples to investigate the matrix effect caused by variable chemical composition. Here, we evaluate several composition-dependent correction schemes for calibrating the IMF of Li isotope analysis in silicate glasses.4.1 Effects of non-bridging oxygen on IMF
Li ions in silicate glasses are coordinated with non-bridging oxygen (NBO). Studies on alkali-silicate glasses proposed that the insertion of Li and other alkali cations increases NBO sites and influences the glass properties (e.g., electrical conductivity).71–74 Thus, it is necessary to explore the effect of NBO on Li isotope-IMF variation. We estimated NBO/T following the method of Seetharaman (2013),61 with Na, K, Ca, Fe, Mg and Mn assumed to be network modifiers (NBO) and Si and Al to be network formers (T) (Table 1). The positive correlations between NBO/T and IMF are observed (Fig. 1). A best-fit empirical equation in the logarithmic form of IMF = a × ln(NBO/T) + c could be gained, with regression coefficient (R2) values ranging from 0.81 to 0.94 for different sessions (Fig. 1). Using the logarithmic fit as a correction scheme, 73% of the δ7Li values are reproduced within ±3‰ of their reference values. Such observations suggest that the IMF correction scheme based on NBO/T could be useful. However, the NBO/T values are estimated using the chemical compositions of the silicate glasses. In other words, different chemistry induces variation in the properties of silicate glasses, which in turn have an impact on the IMF of Li.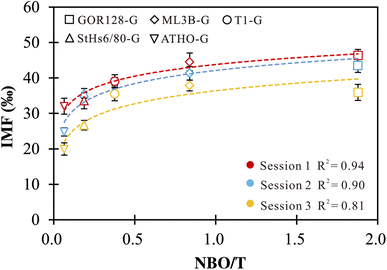 | ||
| Fig. 1 IMF values as a function of NBO/T of silicate glasses. The vertical error bars are the external precision of the measurements. | ||
4.2 Effects of mean atomic mass on IMF
The effect of mean atomic mass (MAM) on IMF has been previously proposed in the investigations of O isotopes of samples.33,34,37,38,42 Eiler et al. (1997)34 and Hervig et al. (1992)38 revealed considerable correlations between the O-isotope IMF and the MAM for both minerals and silicate glasses, while no robust connection was observed in other studies.33,37,42 In this study, positive correlations between the Li-isotope IMF and the MAM of the investigated silicate glasses are observed, but they are not sufficiently robust (Fig. 2). The MAM is an integrated parameter that fundamentally depends on compositions. The correlations between the MAM and IMF cannot isolate the influence caused by the changes in chemical compositions. In this regard, using an IMF-correction scheme based on the MAM does not offer a significant advantage.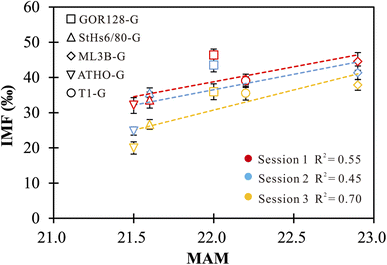 | ||
| Fig. 2 The correlations between IMF and MAM of silicate glasses. The vertical error bars represent the external precision of the measurements. | ||
4.3 Effects of chemical compositions on IMF
The chemical compositions of the investigated silicate glasses vary from ultramafic to highly siliceous covering a broad range of compositions. Both single and combined component effects on IMF variations are considered below.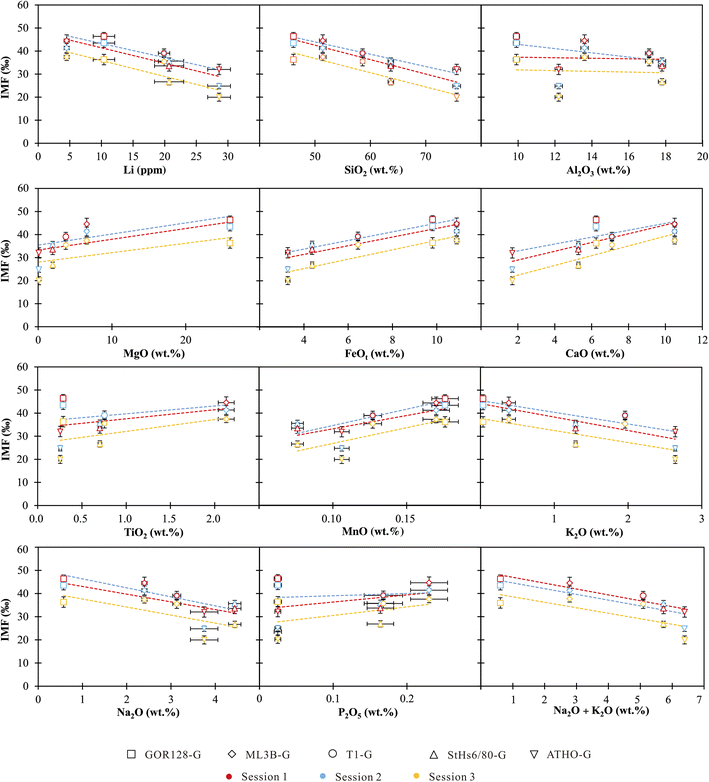 | ||
| Fig. 3 IMF as a function of single chemical compositions in silicate glasses. The vertical bars are the external precisions of the measurements, and the horizontal bars represent the precisions of the reference values from Jochum et al. (2006).60 | ||
Accordingly, we used the observed correlations between IMF and a single component to establish a correction scheme. Using Origin software (2021), the IMF correction scheme could be acquired through best-fit linear regressions in the form of IMF = diXi + c, where di is the empirical coefficient, Xi is the content of major and trace element i, and c is a constant. It shows robust correlations between IMF and Li, SiO2 and FeOt with relatively high R2 values of >0.7 (Table 4). Under the SiO2 correction scheme, 80% of the δ7Licalibrated values of the sample are reproduced within ±3‰ (Fig. 4) of their reference values. If using the Li content to correct IMF, 60% of the δ7Li values are estimated to range within ±3‰ (Fig. 4). When FeOt correction is applied, 73% of the δ7Li values in samples are reproduced within ±3‰ (Fig. 4). It seems that, then, the SiO2 content is most suitable to calibrate the Li isotope-IMF in silicate glasses.
| R 2 for sessions | Li | SiO2 | Al2O3 | MgO | FeOt | CaO | TiO2 | MnO | K2O | Na2O | P2O5 | K2O + Na2O |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Session 1 | 0.74 | 0.95 | 0.01 | 0.45 | 0.72 | 0.68 | 0.17 | 0.45 | 0.74 | 0.45 | 0.15 | 0.90 |
| Session 2 | 0.82 | 0.91 | 0.23 | 0.63 | 0.95 | 0.56 | 0.16 | 0.89 | 0.73 | 0.81 | 0.02 | 0.65 |
| Session 3 | 0.74 | 0.87 | 0.01 | 0.32 | 0.80 | 0.79 | 0.27 | 0.59 | 0.55 | 0.46 | 0.21 | 0.55 |
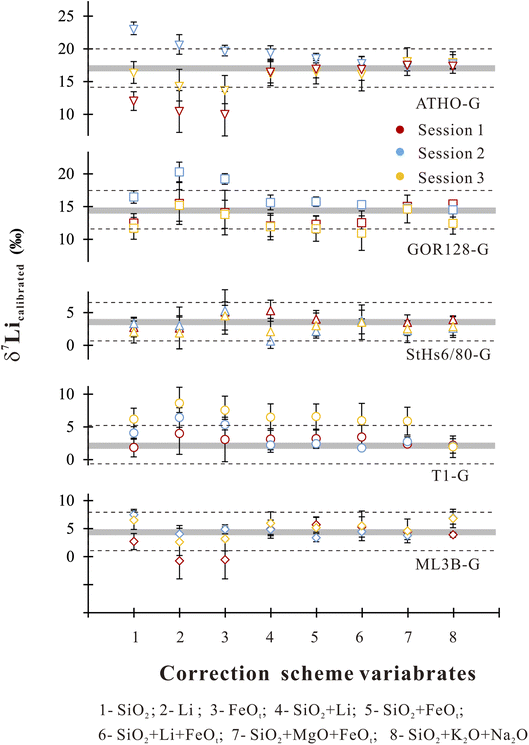 | ||
| Fig. 4 δ 7Li values estimated by using different correction schemes. The grey bands represent reference values for different samples.60 The dashed line circled the range of reproducibility within ±3 ‰ of the preferred values. The vertical bars represent the corresponding root-mean-square error for different correction schemes. | ||
| Analytical sessions | Parameters | |||
|---|---|---|---|---|
| IMF = dSiO2XSiO2 + dLiXLi + c | d SiO2 | d Li | c | R 2 |
| Session 1 | −0.82 | 0.19 | 82.14 | 0.91 |
| Session 2 | −0.44 | −0.14 | 67.52 | 0.87 |
| Session 3 | −0.56 | −0.08 | 65.40 | 0.74 |
| Analytical sessions | Parameters | |||
|---|---|---|---|---|
| IMF = dSiO2XSiO2 + dFeOtXFeOt + c | d SiO2 | d FeOt | c | R 2 |
| Session 1 | −0.93 | −1.01 | 98.91 | 0.94 |
| Session 2 | −0.23 | 1.18 | 44.82 | 0.94 |
| Session 3 | −0.49 | 0.59 | 56.21 | 0.81 |
| Analytical sessions | Parameters | ||||
|---|---|---|---|---|---|
| IMF = dSiO2XSiO2 + dFeOtXFeOt + dLiXLi + c | d SiO2 | d FeOt | d Li | c | R 2 |
| Session 1 | −0.90 | −1.35 | −0.15 | 102.50 | 0.89 |
| Session 2 | −0.24 | 2.47 | 0.49 | 27.93 | 0.99 |
| Session 3 | −0.53 | 1.15 | 0.24 | 50.55 | 0.65 |
| Analytical sessions | Parameters | ||||
|---|---|---|---|---|---|
| IMF = dSiO2XSiO2 + dFeOtXFeOt + dMgOXMgO + c | d SiO2 | d FeOt | d MgO | c | R 2 |
| Session 1 | −1.06 | −0.97 | −0.24 | 108.06 | 0.99 |
| Session 2 | −0.07 | 1.36 | 0.13 | 32.92 | 0.94 |
| Session 3 | −0.82 | 0.10 | −0.31 | 81.28 | 0.77 |
| Analytical sessions | Parameters | ||||
|---|---|---|---|---|---|
| IMF = dSiO2XSiO2 + dNa2OXNa2O + dK2OXK2O + c | d SiO2 | d Na2O | d K2O | c | R 2 |
| Session 1 | −0.97 | 1.88 | 1.66 | 86.66 | 0.99 |
| Session 2 | −0.41 | −1.50 | 0.61 | 66.70 | 0.87 |
| Session 3 | −1.19 | 0.96 | 5.05 | 92.61 | 0.86 |
It should be emphasized that the aforementioned multivariate correction methods cannot be implemented without taking SiO2 into account. This indicates that the SiO2 content has the greatest impact on the Li isotope matrix effect for silicate glasses, at least for the investigated samples. The silica-related matrix effect for silicate glasses has been previously observed to affect Li, Be, B, Mg, Ca and Al abundance,25,29,75 and O isotope analysis.33,37,46 The matrix effect on Li analysis has been previously noted as a function of voltage offset on low- and high-silica samples.26,29 A mechanism for such a silica-related matrix effect may be that significant changes in Li-ion energy distribution take place as a result of the silicon-induced enhancement of ionization.75
4.4 Online matrix effect correction
To assess the efficacy of the online-calibration strategies, four silicate glasses (e.g., ATHO-G, StHs6/80-G, ML3B-G and GOR128-G) were employed to obtain the calibrated equations and to correct the IMF of T1-G, which was treated as the unknown target. The calibration proceeded using both linear and logarithmic regression equations. Using Origin software (2021), the calibrated IMF values for T1-G in each session were estimated based on the 30Si+ signals and displayed as averages within the 95% confidence intervals (CIs). The results showed that the uncertainties of the predicted IMF range from 0.6‰–3.7‰ (1SD) for the linear regression calibration and 2.2‰–2.8‰ (1SD) for the logarithmic regression (Table 6). The accuracy of the online calibration method is estimated using the absolute difference between the IMF values measured from the analytical data and corrected using the calibration equation, denoted as ΔIMF = |IMFmeasured − IMFcorrected|. The results show that ΔIMF values vary from 0.7‰ to 3.5‰ in linear regression calibration and 0.4‰ to 4.4‰ in logarithmic regression (Table 6). The linear regression is slightly better than the logarithmic regression to calibrate Li isotope-IMF for silicate glasses.
| Analytical sessions | IMFcorrected in linear regression (‰) | Uncertainty (95% CI, ‰) | ΔIMF (‰) | IMFcorrected in logarithmic regression (‰) | Uncertainty (95% CI, ‰) | ΔIMF (‰) |
|---|---|---|---|---|---|---|
| Session 1 | 38.3 | ±0.6 | 0.7 | 37.2 | ±2.2 | 1.8 |
| Session 2 | 40.6 | ±3.7 | 1.6 | 39.5 | ±2.8 | 0.4 |
| Session 3 | 32.0 | ±3.3 | 3.5 | 31.1 | ±2.8 | 4.4 |
With the aim to directly compare the accuracy of the online method with the offline method under the aforementioned analytical procedure, the first comparison is made based on the data of sessions 1–3. The efficacy of the online method has been discussed in the above section, with ATHO-G, StHs6/80-G, ML3B-G and GOR128-G employed to obtain the calibrated equations and to correct the IMF of T1-G. Using the online method, the δ7Li of T1-G could be reproduced within 0.8–3.5‰ of its preferred value (Table 7). Then, we conduct the offline correction procedure. The best-fit curve in linear regression between the SiO2 contents and IMF of the ATHO-G, StHs6/80-G, ML3B-G and GOR128-G is estimated to predict the IMF of T1-G. It shows that the δ7Li of T1-G could be reproduced within 0.3–4.7‰ of the reference value (Table 7), which is equivalent to the online method.
| Session | Primary beam current | 7Li yield (cps nA−1 ppm−1) | 30Si yield (cps nA−1 wt%) | IMFmeasured (‰) | Online (Si counting rate-correction) | Offline (SiO2-correction) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IMFcorrected (‰) | Uncertainty (‰) | δ 7Licalibrated (‰) | Δ (‰) | IMFcorrected (‰) | Uncertainty (‰) | δ 7Licalibrated (‰) | Δ (‰) | |||||
| a Δ = |δ7Licalibrated – δ7Litrue|. | ||||||||||||
| 1 | 1 nA | 1244 | 4245 | 39.0 | 38.3 | 0.6 | 2.9 | 0.8 | 36.8 | 2.5 | 4.4 | 2.3 |
| 2 | 1 nA | 1213 | 4158 | 39.1 | 40.6 | 3.7 | 0.6 | 1.5 | 39.5 | 2.7 | 1.8 | 0.3 |
| 3 | 1 nA | 1260 | 4183 | 35.5 | 32.0 | 3.3 | 5.6 | 3.5 | 30.9 | 2.8 | 6.8 | 4.7 |
| 4 | 1 nA | 1230 | 3367 | 8.5 | 10.7 | 0.9 | 0.1 | 2.2 | 10.1 | 0.01 | 0.5 | 1.6 |
| 5 | 100 pA | 1110 | 4103 | 42.0 | 41.6 | 5.4 | 2.6 | 0.5 | 39.5 | 11.1 | 4.7 | 2.6 |
Given that the accuracy of the online method is highly dependent on the absolute 30Si+ intensities, it can vary considerably when the instrumental settings change. To assess the reliability of the online method, we applied different EMs for Si secondary ion detection and primary beam current individually in other independent analyses. In session 4, we used different EMs to collect Si secondary ions while maintaining other experimental conditions consistent with sessions 1–3 (Table 7). The samples ATHO-G, GOR128-G and ML3B-G were measured to calibrate the IMF of T1-G by using both online and offline methods. The results show that the δ7Li of T1-G could be reproduced within ± 1.6‰ using the offline method (Table 7). The online method could reproduce the δ7Li of T1-G within ± 2.2‰ of its reference values, even with a 20% reduction in the 30Si+ intensities (Table 7).
Furthermore, we applied various primary beam intensities to analyze Li isotopes. In consideration of the effective counting rate of 6Li+ ions and optimum EM capacity for 30Li+ ions, we decreased the beam current down to 100 pA in session 5 (Table 7). Samples ATHO-G, StHs6/80-G and KL2-G were used to calibrate the IMF of T1-G. KL2-G is a basaltic MPI-DING silicate glass, which has a SiO2 content of 50.3 ± 0.3 wt% and Li concentrations of 5.1 ± 0.5 ppm.60 Despite a considerable shift in the primary beam, the yield of 7Li and 30Si ions remained the same as those in sessions 1–3 (Table 7). In this scenario, the δ7Li of T1-G could be reproduced within ± 0.5‰ by using the online method and within ± 2.6‰ by using the offline method (Table 7).
In summary, the online-calibration strategy has equivalent reproductivity to the offline method, even when there is a significant change in the Si secondary ion counts. Compared with the offline method, the online method offers time-saving advantages for analyzing Li isotopes of silicate glasses with various compositions. It is also noteworthy that our method has two drawbacks. Although MPI-DING glasses cover a wide range of compositions, from ultramafic to highly siliceous, they do not encompass all natural glasses. As a result, our method is only applicable to anhydrous subalkaline magmatic glasses that fall within the range of MPI-DING glasses. Additionally, the calibration method is entirely empirical. Therefore, further research is necessary to explore the connection between element-specific parameters and ionization models.
5. Conclusions
In this study, we conducted Li isotope analysis on MPI-DING silicate glasses by using a NanoSIMS. The secondary ions, including 6Li+, 7Li+ and 30Si+, were detected simultaneously. The IMF exhibited variations up to 19‰ between mafic and rhyolite glasses, indicating a significant matrix effect on Li isotopic analysis in silicate glasses. Several correction models show that the IMF is strongly dependent on the chemical compositions of these silicate glasses, especially the SiO2 contents. We found that empirical correlations between the 30Si+ counting rate and IMF are useful as an IMF-correction scheme. A straightforward “online” method for the IMF calibration was then proposed taking advantage of simultaneously detected 6Li+, 7Li+ and 30Si+ signals. By applying this calibrated strategy, the IMF and δ7Li of samples can be reproduced within ±3‰ of the reference values. This method can be widely applied to anhydrous subalkaline magmatic glasses from compositional ultramafic to highly siliceous.Author contributions
Conceptualization: R.-Y. L., J. H., W. Y., and H.-C. T. Methodology: R.-Y. L. and J. H. Investigation: R.-Y. L. and J. H. Resources: W. Y., S. H., and Y. L. Writing – original draft: R.-Y. L., and W. Y. Writing – review & editing: all authors, Supervision: W. Y. Funding acquisition: R.-Y. L., W. Y., and J. H.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Axel Schmitt and two anonymous reviewers for their constructive comments and suggestions. This study was funded by the National Natural Science Foundation of China (No. 42103032, No. 42241103 and No. 42173036).References
- S. Agostini, J. G. Ryan, S. Tonarini and F. Innocenti, Earth Planet. Sci. Lett., 2008, 272, 139–147 CrossRef CAS.
- T. Elliott, A. Jeffcoate and C. Bouman, Earth Planet. Sci. Lett., 2004, 220, 231–245 CrossRef CAS.
- F. S. Genske, S. P. Turner, C. Beier, M.-F. Chu, S. Tonarini, N. J. Pearson and K. M. Haase, Chem. Geol., 2014, 373, 27–36 CrossRef CAS.
- K. Kobayashi, R. Tanaka, T. Moriguti, K. Shimizu and E. Nakamura, Chem. Geol., 2004, 212, 143–161 CrossRef CAS.
- A. G. Fairen, E. Losa-Adams, C. Gil-Lozano, L. Gago-Duport, E. R. Uceda, S. W. Squyres, J. A. Rodriguez, A. F. Davila and C. P. McKay, Geochem., Geophys., Geosyst., 2015, 16, 1172–1197 CrossRef CAS PubMed.
- S. Misra and P. N. Froelich, Science, 2012, 335, 818–823 CrossRef CAS PubMed.
- P. Négrel and R. Millot, Chem. Geol., 2019, 523, 121–132 CrossRef.
- F. Tong, Y. Xiao, H. Sun, Y. Wang, H. Wan, L.-F. Gou, Y. Gong, F. Huang, D.-Y. Li and Z. Hou, Sci. Total Environ., 2021, 785 Search PubMed.
- P. A. P. von Strandmann, S. A. Kasemann and J. B. Wimpenny, Elements: An International Magazine of Mineralogy, Geochemistry, and Petrology, 2020, vol. 16, pp. 253–258 Search PubMed.
- L. A. Coogan, S. A. Kasemann and S. Chakraborty, Earth Planet. Sci. Lett., 2005, 240, 415–424 CrossRef CAS.
- K. Gallagher and T. Elliott, Earth Planet. Sci. Lett., 2009, 278, 286–296 CrossRef CAS.
- A. Jeffcoate, T. Elliott, S. Kasemann, D. Ionov, K. Cooper and R. Brooker, Geochim. Cosmochim. Acta, 2007, 71, 202–218 CrossRef CAS.
- I. J. Parkinson, S. J. Hammond, R. H. James and N. W. Rogers, Earth Planet. Sci. Lett., 2007, 257, 609–621 CrossRef CAS.
- A. E. Rubin, K. M. Cooper, C. B. Till, A. J. Kent, F. Costa, M. Bose, D. Gravley, C. Deering and J. Cole, Science, 2017, 356, 1154–1156 CrossRef CAS PubMed.
- A. Beinlich, T. John, J. C. Vrijmoed, M. Tominaga, T. Magna and Y. Y. Podladchikov, Nat. Geosci., 2020, 13, 307–311 CrossRef CAS.
- P. Beck, J. Barrat, M. Chaussidon, P. Gillet and M. Bohn, Geochim. Cosmochim. Acta, 2004, 68, 2925–2933 CrossRef CAS.
- P. Beck, M. Chaussidon, J.-A. Barrat, P. Gillet and M. Bohn, Geochim. Cosmochim. Acta, 2006, 70, 4813–4825 CrossRef CAS.
- M.-C. Liu, M. Chaussidon and N. Matsuda, Geochim. Cosmochim. Acta, 2023, 341, 150–163 CrossRef CAS.
- T. Magna, U. Wiechert and A. N. Halliday, Earth Planet. Sci. Lett., 2006, 243, 336–353 CrossRef CAS.
- T. Magna, A. Deutsch, K. Mezger, R. Skála, H. M. Seitz, J. Mizera, Z. Řanda and L. Adolph, Geochim. Cosmochim. Acta, 2011, 75, 2137–2158 CrossRef CAS.
- H.-M. Seitz, G. P. Brey, S. Weyer, S. Durali, U. Ott, C. Münker and K. Mezger, Earth Planet. Sci. Lett., 2006, 245, 6–18 CrossRef CAS.
- H.-M. Seitz, J. Zipfel, G. P. Brey and U. Ott, Earth Planet. Sci. Lett., 2012, 329, 51–59 CrossRef.
- C. Shearer, G. Layne and J. Papike, Geochim. Cosmochim. Acta, 1994, 58, 5349–5362 CrossRef CAS.
- D. R. Bell, R. L. Hervig, P. R. Buseck and S. Aulbach, Chem. Geol., 2009, 258, 5–16 CrossRef CAS.
- J. C. M. De Hoog and Edinburgh Ion Microprobe Facility, Geostand. Geoanal. Res., 2018, 42, 513–522 CrossRef CAS.
- S. A. Kasemann, A. B. Jeffcoate and T. Elliott, Anal. Chem., 2005, 77, 5251–5257 CrossRef CAS PubMed.
- T. Ludwig, H. Marschall, P. P. von Strandmann, B. Shabaga, M. Fayek and F. Hawthorne, Mineral. Mag., 2011, 75, 2485–2494 CrossRef CAS.
- M. A. Marks, R. L. Rudnick, T. Ludwig, H. Marschall, T. Zack, R. Halama, W. F. McDonough, D. Rost, T. Wenzel and E. P. Vicenzi, Geostand. Geoanal. Res., 2008, 32, 295–310 CrossRef CAS.
- L. Ottolini, P. Bottazzi and R. Vannucci, Anal. Chem., 1993, 65, 1960–1968 CrossRef CAS.
- L. Ottolini and F. C. Hawthorne, Eur. J. Mineral., 1999, 11, 679–690 CrossRef CAS.
- B. X. Su, X. Y. Gu, E. Deloule, H. F. Zhang, Q. L. Li, X. H. Li, N. Vigier, Y. J. Tang, G. Q. Tang and Y. Liu, Geostand. Geoanal. Res., 2015, 39, 357–369 CrossRef CAS.
- M. Tang, R. L. Rudnick, W. F. McDonough, M. Bose and Y. Goreva, Earth Planet. Sci. Lett., 2017, 474, 110–119 CrossRef CAS.
- E. Dubinina, A. Borisov, M. Wiedenbeck and A. Rocholl, Chem. Geol., 2021, 578, 120322 CrossRef CAS.
- J. M. Eiler, C. M. Graham and J. W. Valley, Chem. Geol., 1997, 138, 221–244 CrossRef CAS.
- J. Hao, W. Yang, Y. Luo, S. Hu, Q.-Z. Yin and Y. Lin, J. Anal. At. Spectrom., 2016, 31, 2399–2409 RSC.
- J. Hao, S. Hu, R. Li, J. Ji, H. He, Y. Lin and W. Yang, Atomic Spectroscopy, 2022 Search PubMed.
- M. Hartley, T. Thordarson, C. Taylor and J. Fitton, Chem. Geol., 2012, 334, 312–323 CrossRef CAS.
- R. L. Hervig, P. Williams, R. M. Thomas, S. N. Schauer and I. M. Steele, Int. J. Mass Spectrom. Ion Processes, 1992, 120, 45–63 CrossRef CAS.
- W. F. Hoover, S. C. Penniston-Dorland, L. P. Baumgartner, A. S. Bouvier, D. Baker, B. Dragovic and A. Gion, Geostand. Geoanal. Res., 2021, 45, 477–499 CrossRef CAS.
- S. Hu, Y. Lin, J. Zhang, J. Hao, W. Yang and L. Deng, J. Anal. At. Spectrom., 2015, 30, 967–978 RSC.
- R.-Y. Li, J. Hao, S. Hu, W.-F. Zhang, X.-P. Xia, Y. Lin and W. Yanga, At. Spectrosc., 2022, 43, 77–83 CAS.
- D. Vielzeuf, M. Champenois, J. W. Valley, F. Brunet and J. L. Devidal, Chem. Geol., 2005, 223, 208–226 CrossRef CAS.
- W. Yang, S. Hu, J. Zhang, J. Hao and Y. Lin, Sci. China: Earth Sci., 2015, 58, 1758–1767 CrossRef CAS.
- V. R. Deline, W. Katz, C. A. Evans Jr. and P. Williams, Appl. Phys. Lett., 1978, 33, 832–835 CrossRef CAS.
- E. H. Hauri, A. M. Shaw, J. Wang, J. E. Dixon, P. L. King and C. Mandeville, Chem. Geol., 2006, 235, 352–365 CrossRef CAS.
- R. Ickert, J. Hiess, I. Williams, P. Holden, T. Ireland, P. Lanc, N. Schram, J. Foster and S. Clement, Chem. Geol., 2008, 257, 114–128 CrossRef CAS.
- J. Zhang, Y. Lin, W. Yang, W. Shen, J. Hao, S. Hu and M. Cao, J. Anal. At. Spectrom., 2014, 29, 1934–1943 RSC.
- J. Hao, W. Yang, W. Huang, Y. Xu, Y. Lin and H. Changela, Surf. Interface Anal., 2020, 52, 234–239 CrossRef CAS.
- J. Hao, W. Yang, S. Hu, r. Li, J. Ji, C. Hitesh and Y. Lin, J. Anal. At. Spectrom., 2021, 36, 1625–1633 RSC.
- H. He, J. Ji, Y. Zhang, S. Hu, Y. Lin, H. Hui, J. Hao, R.-Y. Li, W. Yang, H.-C. Tian, C. Zhang, M. Anand, R. Tartese, L. Gu, J.-H. Li, D. Zhang, Q. Mao, L.-H. Jia, X.-G. Li, Y. Chen, L. Zhang, H. Ni, S. Wu, H. Wang, Q. Li, H. He, X.-H. Li and F.-Y. Wu, Nat. Geosci., 2023, 16, 294–300 CrossRef CAS.
- P. Hoppe, S. Cohen and A. Meibom, Geostand. Geoanal. Res., 2013, 37, 111–154 CrossRef CAS.
- S. Hu, Y. Lin, W. Yang, W.-R. Z. Wang, J. Zhang, J. Hao and W. Xing, Sci. China: Earth Sci., 2016, 59, 2155–2164 CrossRef CAS.
- S. Hu, H. He, J. Ji, Y. Lin, H. Hui, M. Anand, R. Tartèse, Y. Yan, J. Hao, R. Li, L. Gu, Q. Guo, H. He and Z. Ouyang, Nature, 2021, 600, 49–53 CrossRef CAS PubMed.
- J. Ji, H. He, S. Hu, Y. Lin, H. Hui, J. Hao, R. Li, W. Yang, Y. Yan, H. Tian, C. Zhang, M. Anand, R. Tartèse, L. Gu, J. Li, D. Zhang, Q. Mao, L. Jia, Y. Chen, S. Wu, H. Wang, H. He, X. Li and F. Wu, Earth Planet. Sci. Lett., 2022, 591, 117636 CrossRef CAS.
- W. Yang, Y.-T. Lin, J.-C. Zhang, J.-L. Hao, W.-J. Shen and S. Hu, J. Anal. At. Spectrom., 2012, 27, 479–487 RSC.
- W. Yang, Y. Lin, J. Hao, J. Zhang, S. Hu and H. Ni, Contrib. Mineral. Petrol., 2016, 171, 28 CrossRef.
- J. Zhang, Y. Lin, W. Yang, J. Hao and S. Hu, Int. J. Mass Spectrom., 2016, 406, 48–54 CrossRef CAS.
- J. Zhang, Y. Lin, J. Yan, J. Li and W. Yang, Anal. Methods, 2017, 9, 6653–6661 RSC.
- K. P. Jochum, D. B. Dingwell, A. Rocholl, B. Stoll, A. W. Hofmann, S. Becker, A. Besmehn, D. Bessette, H.-J. Dietze, P. Dulski, J. Erzinger, E. Hellebrand, P. Hoppe, I. Horn, K. Janssens, G. A. Jenner, M. Klein, W. F. McDonough, M. Maetz, K. Mezger, C. Müker, I. K. Nikogosian, C. Pickhardt, I. Raczek, D. Rhede, H. M. Seufert, S. G. Simakin, A. V. Sobolev, B. Spettel, S. Straub, L. Vincze, A. Wallianos, G. Weckwerth, S. Weyer, D. Wolf and M. Zimmer, Geostand. Newsl., 2000, 24, 87–133 CrossRef CAS.
- K. P. Jochum, B. Stoll, K. Herwig, M. Willbold, A. W. Hofmann, M. Amini, S. Aarburg, W. Abouchami, E. Hellebrand and B. Mocek, Geochem., Geophys., Geosyst., 2006, 7, 1–44 CrossRef.
- S. Seetharaman, Treatise on Process Metallurgy Volume 1: Process Fundamentals, Newnes, 2013 Search PubMed.
- J. Cabato, R. Altherr, T. Ludwig and H.-P. Meyer, Contrib. Mineral. Petrol., 2013, 165, 1135–1154 CrossRef CAS.
- S. Decitre, E. Deloule, L. Reisberg, R. James, P. Agrinier and C. Mével, Geochem., Geophys., Geosyst., 2002, 3, 1–20 CrossRef.
- Y. Y. Gao, X. H. Li, W. L. Griffin, Y. J. Tang, N. J. Pearson, Y. Liu, M. F. Chu, Q. L. Li, G. Q. Tang and S. Y. O'Reilly, Sci. Rep., 2015, 5, 16878 CrossRef CAS PubMed.
- P. J. le Roux, J. Anal. At. Spectrom., 2010, 25, 1033–1038 RSC.
- X.-H. Li, Q.-L. Li, Y. Liu and G.-Q. Tang, J. Anal. At. Spectrom., 2011, 26, 352–358 RSC.
- J. Lin, Y. Liu, Z. Hu, W. Chen, L. Zhang and H. Chen, Geostand. Geoanal. Res., 2019, 43, 277–289 CrossRef CAS.
- L. Nasdala, F. Corfu, J. W. Valley, M. J. Spicuzza, F. Y. Wu, Q. L. Li, Y. H. Yang, C. Fisher, C. Münker and A. K. Kennedy, Geostand. Geoanal. Res., 2016, 40, 457–475 CrossRef CAS.
- F. Richter, M. Chaussidon, E. B. Watson, R. Mendybaev and V. Homolova, Geochim. Cosmochim. Acta, 2017, 219, 124–142 CrossRef CAS.
- L. K. Steinmann, M. Oeser, I. Horn, H.-M. Seitz and S. Weyer, J. Anal. At. Spectrom., 2019, 34, 1447–1458 RSC.
- K. Baral, A. Li and W. Y. Ching, J. Phys. Chem. A, 2017, 121, 7697–7708 CrossRef CAS PubMed.
- O. Gedeon, J. Zemek and K. Jurek, J. Non-Cryst. Solids, 2008, 354, 1169–1171 CrossRef CAS.
- C. McLaren, W. Heffner, R. Tessarollo, R. Raj and H. Jain, Appl. Phys. Lett., 2015, 107, 184101 CrossRef.
- Y. H. Rim, M. Kim, C. G. Baek and Y. S. Yang, J. Alloys Compd., 2020, 827 Search PubMed.
- N. Shimizu, Int. J. Mass Spectrom. Ion Processes, 1986, 69, 325–338 CrossRef CAS.
- L.-G. Wu, Q.-L. Li, Y. Liu, G.-Q. Tang, K. Lu, X.-X. Ling and X.-H. Li, J. Anal. At. Spectrom., 2020, 35, 1607–1613 RSC.
- J. Y. Xu, Q. L. Li, G. Q. Tang, K. Lu, Y. Liu, L. J. Feng and J. C. Melgarejo, Anal. Chem., 2022, 94, 7944–7951 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |