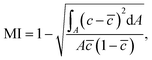On-demand microfluidic mixing by actuating integrated magnetic microwalls

Abstract

Various types of passive and active micromixers have been successfully developed to address the problem of mixing in microfluidic devices. However, many applications do not need fluids to be mixed at all times, or indeed require mixing to be turned on and off at will. Achieving such on-demand mixing is not feasible for passive mixers, particularly when the flow rate cannot be used as a control parameter. On the other hand, active mixers are usually not designed to be able to turn mixing off completely, and they often have complicated fabrication processes and special operation requirements, limiting the range of applications. In this work, we demonstrate an on-demand micromixer based on the actuation of magnetic microwalls. These are made by replica micromoulding and can be easily integrated within commercial microfluidic devices, such as the ibidi® 3-in-1 μ-Slide. Using a simple magnet, the microwalls can be actuated between a fully upright ‘on’ state, which turns on mixing by creating a meandering path in the main channel, and a fully collapsed ‘off’ state, which completely turns off mixing by opening up the channel leaving it unobstructed. Besides the increase in path length when the microwalls are activated, inertia effects also play a significant role for mixing due to the tight bends in the meandering flow path. We quantify the mixing effect using coloured fluids of different viscosities and at different flow rates, and we show that the microwalls can effectively enhance mixing across a wide range of operational conditions.

---

1. Introduction

Due to the small dimensions and low flow rates, mixing is intrinsically difficult to achieve in a microfluidic environment, while being a critical factor for many applications.^1–3 Examples are Point-of-Care antibody tests and high throughput generation of nanoparticles, for which waiting for mixing-by-diffusion can take too long to be truly useful in real-life applications. Many innovative solutions have therefore been developed to enhance microfluidic mixing, from static, structure-based micromixers, such as the herringbone mixers, to active ones that require power input, such as acoustic and electrostatic mixers. A more detailed survey of different types of micromixers can be found in the literature.^1,3,4

Despite these developments, the adoption of many of the solutions into commercial products has been slow. One reason is that the fabrication and/or actuation of the active micromixers are usually complicated,^5,6 and the processes involved may not be easily translated into mass production and/or established workflows.^7,8 On the other hand, static micromixers such as the herringbone⁹ and inertial effect mixers¹⁰ are now commercially available. However, the mixing effect of those types of devices cannot be turned off. Thus, the possibility of having the mixing and/or inertial effects activated on-demand can broaden the range of applications for these devices (see more in section 4).

In this paper, we describe the fabrication and actuation of magnetic microwalls for fluid mixing in microfluidic channels. The microwalls are made by replica micromolding in a hot-embossing setup, using a mixture of magnetic particles and a thermoplastic elastomer (TPE), and with a glass mould fabricated beforehand in a femtosecond-laser-assisted-etching (FLAE) process. Using a simple magnet, the microwalls can be actuated between a fully upright state, which creates a meandering path in the existing channel, and a fully collapsed state, which opens up the channel unobstructed. We have shown that the microwalls can be easily integrated in existing microfluidic devices, such as the ibidi® 3in1 μ-Slide commercial chip. The mixing effect of the microwalls has been quantified using fluids of different viscosities and at different flow rates, and we have shown that the microwalls can effectively enhance mixing across a wide range of these operational conditions. We also found that, besides the increase in path length when the microwalls are activated, inertia effects also play a significant role for mixing due to the tight bends in the meandering flow path.

2. Materials and methods

2.1. Fabrication of the microwall mixer and the magnetic actuation

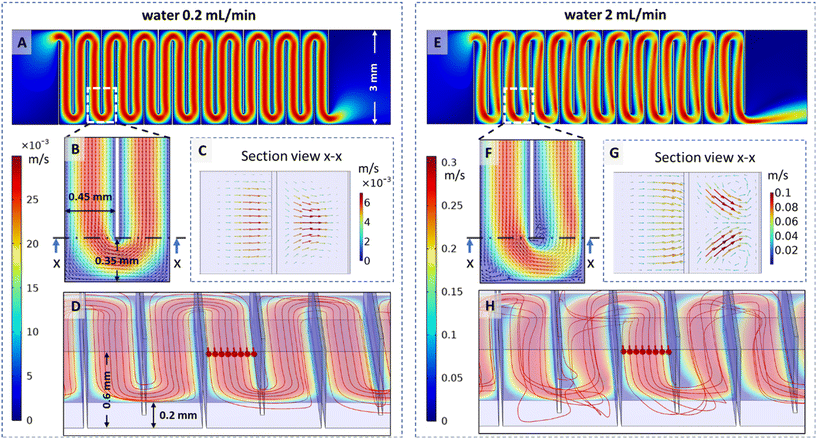
The magnetic microwalls are made in a moulding process using hot-embossing. A detailed description of the fabrication steps can be found in the ESI† I; briefly, the process is as shown in Fig. 1(A). First a mould is made of fused silica with an in-house femtosecond-laser-assisted-etching (FLAE) process.¹¹ Then, the surface of the fused silica is treated with trichloro(1H,1H,2H,2H-perfluorooctyl)silane to reduce adhesion with the microwalls during demoulding in a later step. A mixture of iron powder and a thermoplastic elastomer poly(styrene-block-isobutylene-block-styrene), or “magnetic SIBS”, is pressed into the mould using a hot-embossing setup (Specac), forming the microwalls. Thereafter, the hot-embossing process is performed once again using a sheet of polystyrene against the mould, so the elastic microwalls are thermally fused with the hard polystyrene substrate. The two-step moulding process also ensures that the base of the microwalls is flush with the rigid polystyrene surface, which is critical for the leak-free integration with the microfluidic channel. After demoulding carefully with the help of isopropyl alcohol, and drying afterwards, the substrate of the microwalls is finally bonded with a ‘3in1’ μ-Slide from ibidi® microfluidic chip using double sided tape (Tesa 4965 Original). This final step is performed under microscopic view to ensure that the microwalls are properly aligned with the channel. Since our substrate is made of polystyrene and is completely flat, the sealing effect is comparable to commercial products, and we have not observed any leakage in all our experiments.

Fig. 1 Fabrication and actuation of the magnetic microwall mixer. (A) The fabrication process: i. femtosecond laser patterning; ii. etching in 45% potassium hydroxide solution; iii. rinsed and dried mould; iv. surface treatment with trichloro(1H,1H,2H,2H-perfluorooctyl)silane; v and vi. first hot-embossing with magnetic SIBS – poly(styrene-block-isobutylene-block-styrene) pre-mixed with magnetic particles; vii. second hot-embossing step with polystyrene; viii and ix. demoulded microwalls and bounded with a microfluidic channel. (B) The microwall mixer integrated in an ibidi® 3in1 μ-Slide. The assembled channel is 3 mm wide, 0.6 mm high and 25 mm long. (C) Exposed microwalls at their initial resting position without magnetic actuation, which is 45 degrees to the surface; pictured without the μ-Slide. The microwalls are 600 μm-high, 2.65 mm-wide and 30 μm-thick and fabricated with a 350 μm alternating shift in the width direction, with 450 μm distance between each microwall in the direction of the channel. (D) The experimental setup showing one coloured and one clear stream pumped into the side inlets, and a 15 mm cubic neodymium magnet connected to a servo motor that is placed 4 mm beneath the μ-Slide for actuation. The insert shows the meandering path created by the microwalls. (E and F) The microwalls in the ‘on’ and ‘off’ state, respectively; the inserts on the bottom left show the corresponding magnet orientation. (G and H) Snapshots from a movie showing top-view of 2 mL min⁻¹ water flow when the microwalls are in the ‘on’ and ‘off’ state, respectively. The pictures are partially enhanced to show the microwalls. The movie showing the actuation of the microwalls can be found in the ESI.† All scale bars in this figure are 2 mm.

When not actuated, the microwalls are oriented at an inclined angle determined by the mould (Fig. 1(C)). When a magnetic field is applied perpendicular to the substrate, a magnetic torque is generated and the microwalls move to an upright orientation, see Fig. 1(E), and they force fluids to follow a serpentine path through the channel as shown in the insert in Fig. 1(D), thereby inducing fluid mixing (Fig. 1(G), more details in section 3.1). The actuation mechanism is similar to the actuation of magnetic artificial cilia,¹² which has been described in detail both experimentally^13–15 and numerically.¹⁶ Here we used a 15 mm cubic permanent magnet with a surface magnetic flux density of 390 mT and placed 4 mm below the microfluidic chip to actuate the microwalls, as shown in Fig. 1(D). Such actuation can also be achieved using electromagnets (see ESI† II for a home-made electromagnetic setup for turning ‘on’ the microwalls). When the poles of the magnet are aligned horizontally, the microwalls collapse onto the bottom substrate, and the channel opens unobstructed, as shown in Fig. 1(F) and (H).

2.2. Quantification of mixing

We performed quantification of mixing based on images. During an experiment, two streams of the same base fluid, one with dye (brilliant black) and one without, were injected into the two side inlets of the μ-Slide at the same flow rate (the middle inlet blocked), see Fig. 1(D). To investigate mixing with different viscosities, water (1 mPa s) and 87 ± 1 wt% glycerol in water (220 ± 40 mPa s, which will be simply referred to as glycerol) were used as base fluids for different sets of experiments. The flow rate of the inlet fluids was controlled by a double-syringe pump. The microwalls were then changed between the upright (‘on’) configuration and the collapsed (‘off’) configuration, see Fig. 1(G and H). Videos were captured with a microscope at the position downstream of the microwalls for later analyses.

The degree of mixing was quantified based on the evaluation of the intensity of segregation (IoS).¹⁷ A detailed description of the implementation of this quantification method can be found in the ESI III.† In short, for every set of experiment (water or glycerol as base fluid), a calibration measurement in a channel without microwalls was first performed, and the image of a clearly separated double stream was used to determine the intensity values of the dyed and undyed streams. The IoS method we adopted in this paper maps the grey value of each point to a concentration value, and the mixing index (MI) was then calculated by:

where A is the area of interest, c is the local concentration (from each pixel) and c̄ is the mean concentration (50%). MI = 1 for perfect mixing and MI = 0 when mixing is completely absent.

Note that this method of quantifying mixing has its limitations. First, it uses 2D images, so the information is based on the combined intensity throughout the depth of view, and it cannot be used to examine flow structures in 3D and their effect on mixing. Secondly, the mapping from the grey value to the concentration is calibrated by 0%, 50% (fully mixed) and 100% fluids (mapping curves can be seen in the ESI† III), and there are unavoidably inaccuracies in the mapping. However, since the width of the channel (3 mm) is much larger than the height (0.6 mm), the 2D images can reasonably represent the quality of mixing in the double flow (side-by-side) configuration of our experiments. And since the difference in MI when the microwall mixer is turned ‘on’ and ‘off’ is quite large (see results section 3.1), the errors from the concentration estimation becomes less significant due to the high signal-to-error ratio.

3. Results and discussion

3.1. Mixing in water and in glycerol

Fig. 2(A) shows the mixing results in water (1 mPa s) at different flow rates. At time 0, when the mixer is turned on, there is a clear increase in the mixing index, except at very low flow rates (0.1 mL min⁻¹), for which it takes a longer period for the mixed fluid to fully pass through the observation area. We can use Péclet number Pe = Lv/D to characterize the relative effect of convection and diffusion on the mixing, where L is the characteristic length, v is the flow velocity, and D is the diffusion constant. In practice, Pe can be used to estimate the length of the channel that is needed to achieve full mixing by diffusion, measured in the number of widths.¹⁸ If we consider the channel width and the microwall distance as L in the two states ‘on’ and ‘off’ respectively, and the average flow speed as v, the two states result in the same Pe when applying the same flow rate, since L and v are inversely proportional. Hence, for laminar flow, the improvement in mixing by activating the microwalls can largely be attributed to the increase in the ratio between the length and the width of the flow path, which is roughly equal to nw_m/d when the microwalls are on, with n being the number of microwalls,²²w_m the width of the walls (2.65 mm) and d the distance between the walls (0.45 mm), and nd/w_c when the microwalls are off, where w_c is the width of the channel (3 mm). The increase in the length/width ratio when switching from the off to the on state is therefore w_mw_c/d², or approximately 40 times in this case.

Fig. 2 The effect of microwalls actuation on mixing, measured at various flow rates and with different media. (A) Variation of the mixing index over time in water at different flow rates. The mixer was turned on at time 0 for all flow rates. Note that due to lower flow rate, such as for 0.1 mL min⁻¹, it takes more time for the flow to pass through the observation area to show the mixing effect. (B) Demonstration of the reversibility and reproducibility of mixing by repeatedly turning the mixer on and off, while keeping the flow rate of water at 1 mL min⁻¹ and 10 mL min⁻¹, respectively. (C) Change of mixing index over time in 87 wt% glycerol at different flow rates. The insert shows the change of mixing index at 0.1 mL min⁻¹ flow rate over longer time. The initial increase is caused by temporary agitation of the fluid when the microwalls change their configuration. The result of 0.4 mL min⁻¹ shows similar trend in a shorter timescale. (D and E) Snapshots showing the flow when the mixer is ‘on’ for water and glycerol, respectively. The dashed line boxes indicate the fixed area for measuring the mixing index.

The mixing effect is also reversible and reproducible. For 1 mL min⁻¹ and 10 mL min⁻¹ of water, Fig. 2(B) shows that the microwalls can be reliably turn on and off, and the mixing indices can be switched between two distinctive levels. The mixing effect is stronger at 10 mL min⁻¹ than at 1 mL min⁻¹, judged by the higher mixing index achieved. The increase in the mixing index at higher flow rate is rather counterintuitive because there is less time for the fluid to mix in the meandering channels. It is possible, however, that the increase in mixing index is a result of inertial effects, which will be discussed in more detail in section 3.2.

Fig. 2(C) shows the mixing results in 87 ± 1 wt% glycerol in water (with viscosity 220 ± 40 mPa s). It can be seen that the mixer can induce mixing when it is turned on at time 0, but the resulting mixing indices are lower than those with water at the same flow rates, by comparison with Fig. 2(A). The lower indices are the result of the higher Péclet number due to the higher viscosity, meaning that the two fluids will take longer to mix with the same flow condition. At relatively low flow rates, the increase in mixing index is temporary, as shown in the insert of Fig. 2(C) for 0.1 mL min⁻¹, but also seen at higher flow rates to a lower degree (see ESI† movies). This temporary increase in mixing index is caused by the agitation of the fluids in the volume occupied by the mixer when it changed its configuration from off to on. In principle, one can also make use of this effect and continuously agitate the fluid to mix high viscosity fluids, for example by using a continuously rotating magnet.^13,14 However, for some applications, a static on/off configuration might be desirable in order to simplify the mechanical design and reduce vibration. In the scope of this work, we aim at quantifying the mixing effect only in static configurations for a better comparison between different viscosities.

It can be also inferred from Fig. 2(C) that at relatively high flow rates of glycerol, e.g. 4 mL min⁻¹, higher mixing indices are achieved when the mixer is turned on, and the effect does not diminish afterwards, unlike for lower flow rates. This effect is caused by the uncontrolled flow pattern as a result of the deformation of the microwalls, as shown in the enhanced bottom left part of Fig. 2(E). The deformation results from the high fluid pressures at high flow rates when such a highly viscous medium is used. For comparison, Fig. 2(D) shows that the microwalls are not deformed at the same flow rate (4 mL min⁻¹) in water. The deformation of the microwalls creates openings between the ceiling of the channel and the top of the microwalls, where random streams of high and low concentration fluids can pass through without restrictions. The resulting flow pattern is composed of a large number of horizontal streamlines as shown on the right side of Fig. 2(E), most likely close to the ceiling of the channel. This is different from the streamline pattern that results from of the two fluids passing through a regular meandering channel, where all streamlines start from the opening of the last microwall, as shown in Fig. 2(D). The mixing indices at higher flow rates in glycerol are therefore less representative of the level of mixing, which is also a limitation of our chosen method for quantifying mixing, as discussed in section 2.2. However, for completeness, we keep these results in Fig. 2(C).

Note that having the microwalls in the ‘on’ state will increase the hydrodynamic resistance and hence the pressure drop across the channel. By making a simplifying assumption of a Poiseuille flow in the meandering channel, we can estimate a pressure drop of about 240 times larger for the ‘on’ state compared to the ‘off’ state. For example, for water flow at 1 mL min⁻¹, the pressure drop in the ‘on’ state across the microwalls is about 850 Pa, compared to about 3.5 Pa when they are in the ‘off’ state. The detailed calculation can be found in the ESI.†

3.2. Inertial effects in the microwall mixer

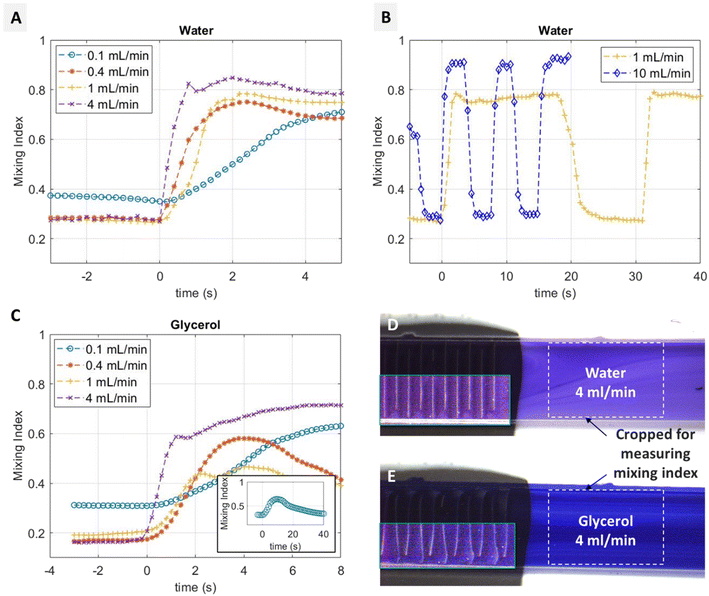
As mentioned earlier in section 3.1 and shown in Fig. 2(A), the mixing index increases at higher flow rates of water. This is rather counterintuitive, as one would expect that due to faster flow, the two streams have less time to mix by diffusion, which should result in less mixing. However, as will be discussed below and as shown in Fig. 3, at higher flow rates the inertial effects start to play a significant role, resulting in local vortices and Dean flow at the tight bends at the alternating ends of each microwall. These inertial effects disrupt the laminar flow patterns and introduce advective mixing, enhancing the overall mixing effect.

Fig. 3 3D simulations showing the inertial effects with the microwall mixer turned on. The two groups show the results when 0.2 mL min⁻¹ and 2 mL min⁻¹ water flows are applied, respectively. (A and B and E and F) Top view of the flow structures at the middle planes (0.3 mm) of the channels (0.6 mm-high) when the mixer is on. (C and G) Cross-sectional view in the flow direction showing the in-plane flow rotation just before and after the bend. (D and H) 3D streamlines showing the effect of in-plane rotations of the fluid in the bends at different flow rates; the streamlines pass through the arrow points, which are 0.2 mm above the bottom, and evenly spaced. The bigger colour bars indicate flow speed in the two groups except for C and G, which have separate colour bars. All colour bars are in m s⁻¹. The simulation was performed using COMSOL® Multiphysics.

Fig. 3 shows simulation results of the flow patterns in water, obtained using COMSOL Multiphysics®. The detailed simulation setup can be found in ESI† IV. The microwalls are implemented as static divisions in the channel in the ‘on’ position. Because the coloured and clear streams in the experiments have the same viscosity, and we are only investigating the flow pattern, the fluid is considered homogenous in the simulation. Fig. 3(A–D) show the laminar flow pattern with water at 0.2 mL min⁻¹ in the meandering channel as well as around the bends. In contrast, Fig. 3(E–H) shows that at 2 mL min⁻¹, inertial effects become significant, which can be seen from the vortices and dean flow patterns in Fig. 3(F–H). Such effects are the key working mechanism for inertial micromixers, such as the spiral channel mixers.^10,19,20 The effect can be characterized by a Dean number κ = δ^0.5Re, with δ being the ratio of the channel hydrodynamic radius to the radius of curvature, and Re is the Reynolds number. With our channel geometry and the applied flow rate, δ^0.5 is close to 1, and Re is approximately 10 for 0.2 mL min⁻¹ and 100 for 2 mL min⁻¹ water flows, resulting in a κ value of about 10 and 100 for 0.2 mL min⁻¹ and 2 mL min⁻¹, respectively. The relation between Re, κ and the observed enhancement of mixing is consistent with the literature, where similar relations were discovered using static channels with various types of geometries.²¹

The possibility to introduce inertial effects on-demand could also benefit other applications besides mixing,²⁰ such as cell sorting²² and separation of particles.²³ Specific dynamic structures tailored to those applications can be designed, and their manufacturability and actuation need to be taken into account early on. Certain aspects, such as mould geometry, filling, ease of demoulding and magnetic field strength and orientation can pose practical limitations to the configurations that can be realized, which might require further development of fabrication techniques as well as magnetic control methods.

4. Conclusion and outlook

In this study, we have fabricated magnetic microwalls using a micromoulding process and integrated them in a commercially available microfluidic channel (ibidi® 3in1 μ-Slide). The microwalls can be actuated on-demand with a permanent magnet to create a serpentine path in the channel. When two streams of fluids are pumped through the channel, actuating the microwalls results in an increase in the flow path length and introduces inertial effects above a moderate level of flow rate (∼1 mL min⁻¹ for water), which are both beneficial for fluid mixing.

We have experimentally quantified the effects of the microwalls on mixing in different fluids (water and 87 wt% glycerol) by pumping coloured and clear streams of the same base fluids side by side into the channel and calculating the mixing indices of the unmixed and mixed fluids from the videos taken during the experiments. The results clearly show a substantial enhancement of mixing when the microwalls are turned on, and the effect is both reversible and reproducible. The experiments also show that higher flow rates result in better mixing for water, due to inertial effects around the tight bends created by the microwalls. Results of numerical simulations performed using COMSOL® Multiphysics indeed show a significant change in flow patterns due to inertial effects when increasing the flow rate from 0.2 mL min⁻¹ to 2 mL min⁻¹.

The ability to induce mixing easily and reversibly in a microfluidic channel expand the opportunities for interesting applications. Multi-stream co-flowing channels, such as the μ-Slide used in this work, are often used in studies of chemotaxis, cancer metastasis and general cell migration.^24,25 In such setups, the spatial–temporal gradient is controlled by tuning the flow rates of the fluids with different concentration of the substances in question, so the gradient cannot be changed independently from the flow rate. With our approach, one can change the gradient without changing the flow rate in the same device, simply by turning on and off the microwalls, with the possibility of creating a wide range of combinations of both static and dynamic conditions for the mentioned biochemical studies. Many biological analysis and processes are significantly influenced by the level and duration of mixing of different components, such as PCR, antibody tests and flow cytometry, and our approach can also be used to switch between configurations with different levels of mixing in the same setup.

The possibility to activate inertial effects on-demand with the microwalls in a channel is another interesting aspect of our approach. Inertial effects can be used for flow focusing, cell sorting, and cell enrichment.^20,21 Being able to activate these applications on-demand can be useful, but it could be even more advantageous to be able to tune the inertial effects by changing the configuration of the microwalls, so the effect can be tuned to tailor-fit to the change of the application requirements and conditions, such as cell size and shape, flow rate and fluid viscosity. Due to the flexibility of the FLAE/molding process, other shapes and curvatures can also be made (see ESI†), which could bring a wider range of control and flexibility to the applications of inertial microfluidics. Of course, further detailed investigations of the microwall geometry and arrangement, as well as the resulting flow structures need to be carried out for specific applications.

We have shown that the microwall mixers can be made by replica moulding and can be easily integrated with commercially available chips, and they can be actuated simply by a magnet. This means that there is a relatively low threshold for mass production and adoption of such devices in various laboratory settings. We also hope that our findings can inspire new developments and new applications in areas yet unforeseen.

Author contributions

SB designed and conducted the experiments, collected data and wrote the original document. IFP and TW assisted in designing and conducting experiments, performing simulations and edited the manuscript. JdT supervised the research, edited the manuscript and provided financial support. YW conceptualized the idea, designed and supervised the research, conducted experiments, analyzed the results and wrote the manuscript.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The research leading to these results has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program under grant agreement no. 833214.

References

1. N. T. Nguyen and Z. Wu, Micromixers—a review, J. Micromech. Microeng., 2004, 15(2), R1–R16.
2. G. Seok Jeong, S. Chung, C. B. Kim and S. H. Lee, Applications of micromixing technology, Analyst, 2010, 135(3), 460–473.
3. G. Cai, L. Xue, H. Zhang and J. Lin, A Review on Micromixers, Micromachines, 2017, 8(9), 274.
4. E. S. Shanko, Y. van de Burgt, P. D. Anderson and J. M. J. den Toonder, Microfluidic Magnetic Mixing at Low Reynolds Numbers and in Stagnant Fluids, Micromachines, 2019, 10(11), 731.
5. G. G. Yaralioglu, I. O. Wygant, T. C. Marentis and B. T. Khuri-Yakub, Ultrasonic Mixing in Microfluidic Channels Using Integrated Transducers, Anal. Chem., 2004, 76(13), 3694–3698.
6. J. den Toonder, F. Bos, D. Broer, L. Filippini, M. Gillies and J. de Goede, et al., Artificial cilia for active micro-fluidic mixing, Lab Chip, 2008, 8(4), 533–541.
7. J. Deval, P. Tabeling and C. M. Ho, A dielectrophoretic chaotic mixer, in Technical Digest MEMS 2002 IEEE International Conference Fifteenth IEEE International Conference on Micro Electro Mechanical Systems (Cat No02CH37266), 2002, pp. 36–39.
8. S. Yu, T. J. Jeon and S. M. Kim, Active micromixer using electrokinetic effects in the micro/nanochannel junction, Chem. Eng. J., 2012, 197, 289–294.
9. A. D. Stroock, S. K. W. Dertinger, A. Ajdari, I. Mezic, H. A. Stone and G. M. Whitesides, Chaotic mixer for microchannels, Science, 2002, 295(5555), 647–651.
10. A. P. Sudarsan and V. M. Ugaz, Fluid mixing in planar spiral microchannels, Lab Chip, 2006, 6(1), 74–82.
11. Y. Bellouard, A. Said, M. Dugan and P. Bado, Fabrication of high-aspect ratio, micro-fluidic channels and tunnels using femtosecond laser pulses and chemical etching, Opt. Express, 2004, 12(10), 2120–2129.
12. T. u. Islam, Y. Wang, I. Aggarwal, Z. Cui, H. E. Amirabadi and H. Garg, et al., Microscopic artificial cilia – a review, Lab Chip, 2022, 22(9), 1650–1679.
13. J. Hussong, N. Schorr, J. Belardi, O. Prucker, J. Rühe and J. Westerweel, Experimental investigation of the flow induced by artificial cilia, Lab Chip, 2011, 11(12), 2017–2022.
14. Y. Wang, Y. Gao, H. M. Wyss, P. D. Anderson and J. M. J. den Toonder, Artificial cilia fabricated using magnetic fiber drawing generate substantial fluid flow, Microfluid. Nanofluid., 2015, 18(2), 167–174.
15. S. Zhang, Y. Wang, R. Lavrijsen, P. R. Onck and J. M. den Toonder, Versatile microfluidic flow generated by moulded magnetic artificial cilia, Sens. Actuators, B, 2018, 263, 614–624.
16. S. N. Khaderi, C. Craus, J. Hussong, N. Schorr, J. Belardi and J. Westerweel, et al., Magnetically-actuated artificial cilia for microfluidic propulsion, Lab Chip, 2011, 11(12), 2002–2010.
17. P. V. Danckwerts, The definition and measurement of some characteristics of mixtures, Appl. Sci. Res., Sect. A, 1952, 3(4), 279–296.
18. T. M. Squires and S. R. Quake, Microfluidics: Fluid physics at the nanoliter scale, Rev. Mod. Phys., 2005, 77(3), 977–1026.
19. R. H. Liu, M. A. Stremler, K. V. Sharp, M. G. Olsen, J. G. Santiago and R. J. Adrian, et al., Passive mixing in a three-dimensional serpentine microchannel, J. Microelectromech. Syst., 2000, 9(2), 190–197.
20. D. D. Carlo, Inertial microfluidics, Lab Chip, 2009, 9(21), 3038–3046.
21. J. Zhang, S. Yan, D. Yuan, G. Alici, N. T. Nguyen and M. E. Warkiani, et al., Fundamentals and applications of inertial microfluidics: a review, Lab Chip, 2016, 16(1), 10–34.
22. E. Ozkumur, A. M. Shah, J. C. Ciciliano, B. L. Emmink, D. T. Miyamoto and E. Brachtel, et al., Inertial focusing for tumor antigen-dependent and -independent sorting of rare circulating tumor cells, Sci. Transl. Med., 2013, 5(179), 179ra47.
23. D. Di Carlo, D. Irimia, R. G. Tompkins and M. Toner, Continuous inertial focusing, ordering, and separation of particles in microchannels, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(48), 18892–18897.
24. B. Meier, A. Zielinski, C. Weber, D. Arcizet, S. Youssef and T. Franosch, et al., Chemotactic cell trapping in controlled alternating gradient fields, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(28), 11417–11422.
25. M. Ruzycka, M. R. Cimpan, I. Rios-Mondragon and I. P. Grudzinski, Microfluidics for studying metastatic patterns of lung cancer, J. Nanobiotechnol., 2019, 17(1), 71.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc01168a

---