Open Access Article
Open Access ArticleA low-cost, label-free microfluidic scanning flow cytometer for high-accuracy quantification of size and refractive index of particles†
Riccardo
Reale
 *a,
Giovanna
Peruzzi
*a,
Giovanna
Peruzzi
 a,
Maryamsadat
Ghoreishi
a,
Maryamsadat
Ghoreishi
 a,
Helena
Stabile
a,
Helena
Stabile
 b,
Giancarlo
Ruocco
b,
Giancarlo
Ruocco
 a and
Marco
Leonetti
a and
Marco
Leonetti
 ac
ac
aCenter for Life Nano- & Neuro-Science, Italian Institute of Technology, Rome, Italy. E-mail: riccardo.reale@iit.it
bDepartment of Molecular Medicine, Sapienza University of Rome, Rome, Italy
cSoft and Living Matter Laboratory, Institute of Nanotechnology, Consiglio Nazionale delle Ricerche, 00185 Rome, Italy
First published on 10th March 2023
Abstract
Flow cytometers and fluorescence activated cells sorters (FCM/FACS) represent the gold standard for high-throughput single-cell analysis, but their usefulness for label-free applications is limited by the unreliability of forward and side scatter measurements. Scanning flow cytometers represent an appealing alternative, as they exploit measurements of the angle-resolved scattered light to provide accurate and quantitative estimates of cellular properties, but the requirements of current setups are unsuitable for integration with other lab-on-chip technologies or for point-of-care applications. Here we present the first microfluidic scanning flow cytometer (μSFC), able to achieve accurate angle-resolved scattering measurements within a standard polydimethylsiloxane microfluidic chip. The system exploits a low cost linearly variable optical density (OD) filter to reduce the dynamic range of the signal and to increase its signal-to-noise ratio. We present a performance comparison between the μSFC and commercial machines for the label free characterization of polymeric beads with different diameters and refractive indices. In contrast to FCM and FACS, the μSFC yields size estimates linearly correlated with nominal particle sizes (R2 = 0.99) and quantitative estimates of particle refractive indices. The feasibility of using the μSFC for the characterization of biological samples is demonstrated by analyzing a population of monocytes identified based on the morphology of a peripheral blood mononuclear cells sample, which yields values in agreement with the literature. The proposed μSFC combines low setup requirements with high performance, and has great potential for integration within other lab-on-chip systems for multi-parametric cell analysis and for next-generation point-of-care diagnostic applications.
Introduction
High-throughput biological analysis at the single-cell level is a key tool for several research fields, including immunology, molecular biology, bacteriology, cancer biology, and infectious disease monitoring, as it enables the assessment of variability and heterogeneity of cellular properties within a biological population.1 In recent years, distributions and variabilities of cellular properties (e.g. size, shape, refractive index, deformability) within a population have become increasingly relevant for basic research and diagnostic applications.2–5 For example, the dimensional characterization of monocytes (a type of leukocytes commonly known for their role in inflammatory processes6) has recently been proposed as a label-free indicator for point-of-care diagnostic applications. In particular, variations in the mean or width of the size distribution of a monocyte population have been highlighted as potential diagnostic tools for early-stages of sepsis7–10 and COVID-19 infections.11–15Flow cytometers (FCM) and fluorescence activated cells sorters (FACS) currently represent the gold standard for high-throughput single cell-analysis, as they can routinely analyze several thousand cells per second.1,16 These systems use excitation lasers to stimulate the cells and collection apparatuses (usually a mix of photomultiplier tubes and photodiodes) to measure scattered and fluorescent light. Measured FCM/FACS signals include the forward scattered light (FSC), i.e. the total light scattered at low angle (usually up to 20°, with variation depending on the manufacturer17,18), the side scattered light (SSC), i.e. the light scattered at ∼90°, and several fluorescence channels.19 While scattered light correlates with intrinsic cell properties, fluorescence signals are generated by labels previously attached to cells with an immune-specific process, requiring extensive manipulation of the sample and not suitable for point-of care (POC) diagnostic applications.20–22 Even though FSC is commonly used to discriminate cells based on their size,16,19,23 FSC is not proportional to either particle's diameter, cross-sectional area, or volume, due to the marked dependency that the low-angle scattering has with respect to the angular integration range and to its dependency on cell refractive index, among other factors.19,24,25 Moreover, FSC is highly dependent on the optical components used in the system, which may vary greatly among manufacturers. As a result, FSC measurements don't provide quantitative information on cell size and, in the best-case scenario, can be used as a relative size estimate within the same experiment.19 Similarly, SSC is commonly used to acquire qualitative information on cell granularity and on its internal complexity, but it fails to provide any quantitative information on intrinsic cell properties.1,19,24
Scanning flow cytometry (SFC) is an alternative high-throughput label-free approach for quantitative single-cell analysis, based on the angle-resolved measurement of scattered light.26,27 Thanks to its design, an SFC system can measure light scattered by particles as a function of the scattering angle, while they flow through the measurement region. The output of an SFC measurement is the scattering profile over an angular range, which can be used to extract quantitative information on particle intrinsic properties. SFC is particularly appealing for diagnostic applications, as it can reliably provide quantitative estimates of cell size and refractive index, as well estimates of cell shape and bacterial morphology.28–30 Nevertheless, available SFC systems require highly specialized components (e.g. custom flow cells, rotating detectors, motorized iris diaphragms, or numerous photomultiplier tubes) which makes them unsuitable for integration with other lab-on-chip technologies or for point-of-care (POC) applications.31–33
Here, we describe a simple, low-cost microfluidic scanning flow cytometry (μSFC) system for the high-throughput measurement of size and refractive index of single cells. The proposed system uses a single photoreceiver to perform an SFC measurement within a standard polydimethylsiloxane (PDMS) microchip exploiting a linearly variable optical density (OD) filter to reduce the dynamic range of the signal and to increase its signal-to-noise ratio (SNR). The variable filter consists of a glass slide coated with metal with variable density, and is commercially available or can be easily manufactured. The μSFC estimates the time-of-flight (ToF) of particles in the channel to compensate for flow-induced velocity variations and significantly reduce size and refractive index estimates dispersion without the need for an additional laser or detector. First, we demonstrate the superior performance of the μSFC with respect to label-free FCM/FACS for size and refractive index measurement on polymeric beads, and successively we show the applicability of the proposed approach to the analysis of a biological target (a monocytes population). The minimal setup requirements and high performance of the μSFC make it well suited for compact, POC diagnostic applications, as well as readily integrated into other lab-on-a-chip systems (e.g. in microfluidic impedance cytometers34,35) for multi-parametric cellular analysis or integrated real-time applications.36
Working principle
Angle-resolved scattering measurements
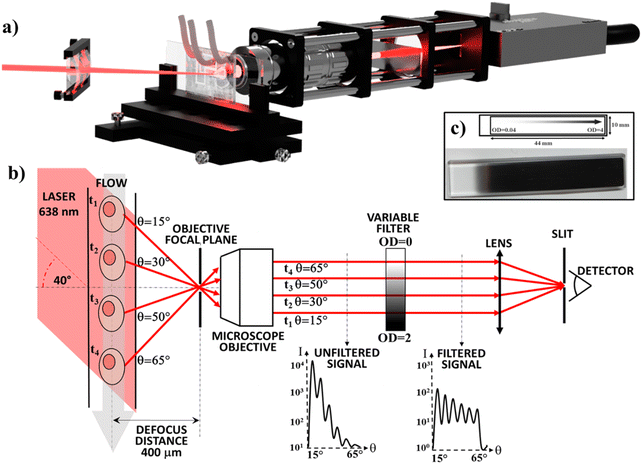
The μSFC can collect the angle-resolved scattered light using a single photoreceiver and is based on the setup previously described by Loken et al.27 A laser beam is focused by a cylindrical lens onto the microchannel where particles flow (Fig. 1). A microscope objective collects the light scattered by particles, which is focused onto the photoreceiver sensor by a lens. The microchannel lies on an out-of-focus plane located at a 400 μm distance with respect to the objective focal plane, resulting in each scattering angle being mapped into a spatial position in the back-focal plane of the objective, and allowing to select collected scattering angles using a slit placed on the lens focal plane (which creates its virtual image on the objective focal plane). In this configuration, a different subset of scattering angles is collected at each position along particle trajectories. As a result, different scattering angles will reach the detector at different times. The angular resolution is a function of the out-of-focus distance and of the slit width. When all other setup parameters are held constant, increasing the defocus distance will increase the angular resolution and decrease the signal intensity. The 400 μm defocus distance is the result of an experimental optimization between these two parameters. The angular range, i.e. the smallest and biggest angles that can be collected, depends on the objective numerical aperture. By placing the excitation laser beam at an angle with respect to the microchannel, it is possible to shift the center of the measured angular range.If a standard microfluidic chip is used instead of a high-spec flow cytometry flow cell,32 the signal-to-noise ratio (SNR) of the measurement is significantly reduced. In particular, the lack of a reliable and easy to implement 3D flow-focusing approach limits the flow-focusing to 2D. Thus, the channel size along the third dimension (usually the channel height) must be small (e.g. <40 μm) to minimize dispersion (e.g. to ensure similar laser excitation). As a result, interfaces are closer to particles and interfere more with the measurement. Manufacturing problems of the PDMS chip (e.g. impurities, air bubbles or curing inhomogeneity) can also lead to signal degradation and increased noise. Additionally, it's usually difficult to measure the angle-resolved scattered light over an angular range >40° with a single photoreceiver, as the signal has a dynamic range larger than the photoreceiver's.
In the μSFC, we included a linearly variable OD filter in the back-focal plane (see Fig. 1-b) of the objective to reduce the dynamic range and increase the SNR. The filter has a transmittance that depends logarithmically on its linear coordinate, and can filter spatially separated light with different OD. As a result, it can be used to selectively filter the high-intensity light scattered at low-angle more than the low-intensity light scattered at high-angle. A signal filtered this way has several key advantages compared to an unfiltered signal: (i) the dynamic range of the signal is significantly reduced, resulting in less stringent hardware requirements for the photodetector; (ii) particle angular oscillations frequencies in the power spectrum are easier to identify thanks to a higher separation from the lower frequency components; (iii) the event start/end timepoints can be clearly identified, enabling an accurate estimate of particles ToF.
Particle size estimation
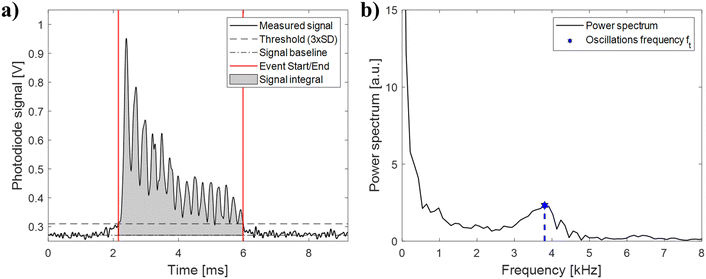
During analysis, the signal is segmented into individual events, each containing the signal string of one particle. As shown in Fig. 2, each event exhibits the oscillations predicted by the theoretical Mie scattering model.37 The angular oscillations frequency (fθ), i.e. the number of oscillations of the scattering profile over a defined angular window, is an intrinsic particle scattering property which yields information on particle size.38–40 In the proposed configuration, we can't directly measure fθ, because measurements are performed in the time domain and not in the angular domain. As a result, we can only measure ft, i.e. the time-domain frequency of the oscillations. While fθ doesn't depend on any measurement-specific parameters, ft depends on particle velocities resulting from the parabolic flow distribution. For example, if two particles with equal angular oscillations frequency are travelling at different velocities, the faster particle will appear to have higher oscillations frequency in the time-domain due to its higher velocity. It is possible to convert the time-domain frequency (ft) into the angular oscillations frequency (fθ) by normalizing with the event time-of-flight (ToF) according to: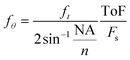 | (1) |
Particle refractive index estimation
Even though it's possible to quantitatively estimate particle refractive index from angle-resolved scattering data by solving the inverse light-scattering problem,41 it's a time- and computation-intensive procedure which is not well suited for real-time or POC applications, where computational power might be limited. We propose a faster method to extract estimates of particle refractive indices with lower computational cost. It assumes that the integral of the signal, i.e. total amount of light scattered in the observed angular range, depends only on particle size and refractive index mismatch between particle and carrier fluid (just like an ideal spherical particle scattering according to the Mie model,37cf. Fig. S2 of the ESI†). If the refractive index of the carrier fluid and the angular range measured are known, and if the particle size is determined using fθ, the signal integral becomes dependent only on the particle refractive index. Nevertheless, potential ToF differences between particles induced by the fluid can artificially increase the dispersion of the measurement (e.g. the integral of slower particles will appear higher because they spend more time in the measurement region). It's therefore best to normalize the signal integral by particle ToF, which is equivalent to computing the mean of the signal over the observed angular range. This normalization is enabled by the high SNR of the system, which allows estimating particle ToF. Refractive indices can then be mapped in a look-up table as a function of particle diameter and signal mean over the angular range of interest.Particle measurement range
The proposed system has been initially developed and calibrated for the analysis of particles with size similar to monocytes (i.e. 9–20 μm). This measurement range includes many other relevant biological targets, including fibroblasts, epithelial cells, hepatic cells, mesenchymal stem cells, and glioblastomas, among others. Nevertheless, the measurement range can be adjusted to analyze biological targets outside of this range. Two parameters are mostly responsible for the definition of the measurement range: i) the laser wavelength and ii) the laser spot width. i) Just like in FCM/FACS systems, the wavelength of the excitation laser is a key parameter defining the lower detection limit, and shorter wavelength lasers are required to detect smaller events reliably. By adopting a laser with a shorter wavelength (e.g. 488 nm) or a multi-laser configuration, the lower detection limit can be reduced. ii) The excitation beam is focused by a cylindrical lens into a strip in the center of the channel. The laser strip should be wide enough to excite the whole target cell, but at the same time, the wider the strip, the higher the background noise. Therefore, a thinner laser spot is required in order to characterize smaller particles (it can be achieved either using a cylindrical lens with shorter focal length, or with a cylindrical telescope to expand the laser beam before the final focusing lens).Materials and methods
Microfluidic chip
The μSFC was designed to be as simple as possible, to maximize integrability with other systems. The microfluidic chip is made of PDMS, and is fabricated with standard soft-lithography procedures using an SU-8 mold, and successively bonded to a glass microscopy slide after cleaning and plasma exposure.42 The microfluidic channels are formed by a sample channel and by two lateral sheath flow channels, which are designed to have the same hydraulic resistance and to focus the sample in the middle of the channel. The inlet and outlet holes lie on a different line with respect to the measurement region to avoid interactions between the incoming laser beam and the tubing coming out of the chip. The measurement region consists of a straight channel 120 μm wide and 25 μm high, and particles were focused within ±15 μm from the centre of the channel (cf. Fig. S3 of the ESI†).Optical setup
A 638 nm laser with a 200 mW output is used as the light source (Oxxius), which is focused onto the measurement region by a cylindrical lens (75 mm focal length), forming a strip 60 μm wide. The incoming beam lies on the same plane formed by the microchannel and objective, and forms a 40° angle with the microchannel. The chip is mounted on a xyz-stage with micrometric regulation, which is used to align the setup and to accurately move the channel to the desired out-of-focus distance (400 μm). Light scattered by particles is collected using a 50× infinity corrected long working-distance microscope objective with a 0.55 numerical aperture (Edmund Optics) resulting in a measurement over the 15–65° angular range. A rectangular, continuously variable, metallic optical density filter (0.075 OD-units per mm, Thorlabs, Fig. 1) is placed in the back-focal plane of the objective. The collected light is focused with a lens (75 mm focal length) onto a 10 μm slit placed in front of a variable gain photoreceiver (OE-200-SI, Femto), operated at a nominal gain of 108 V/W and a bandwidth of 200 kHz.Sample preparation
Beads with different diameters and refractive indexes in the range of common biological applications43,44 were purchased from different vendors, as described in Table 1. Refractive indices provided by vendors were independently verified using the approach previously described by Bolognesi et al.45 Healthy donors' peripheral blood mononuclear cells (PBMCs) were isolated by Lymphoprep (Nycomed) gradient centrifugation. The sample was composed by lymphocytes, monocytes, and debris, as verified by FCM (cf. Fig. S4 of the ESI†). During μSFC analysis, the lymphocytes were below the lower detection limit and only monocytes could be observed. Each particle population is dispersed in a 1× PBS buffer (n = 1.335) at a concentration of approximately 106 particles per ml, and the same buffer is used as sheath flow. For μSFC analysis, samples are loaded in glass Hamilton syringes (1 ml for the main flow and 10 ml for sheath flows) and pumped using syringe pumps (Harvard Instruments) at a flow rate of 10 μl min−1, with a 30 μl min−1 sheath flow, leading to a nominal throughput of ∼150 particles per second.| Material | Vendor | Mean size [μm] | Size CV | Refr. index |
|---|---|---|---|---|
| PS: polystyrene; PMMA: polymethylmethacrylate; SiO2: silica. | ||||
| PS | Spherotech, Inc. | 8.91 | <10% | 1.59 |
| PS | Polysciences, Inc. | 10 | <8% | 1.59 |
| PS | Polysciences, Inc. | 15.7 | <9% | 1.59 |
| PMMA | Microparticles, GmbH | 10.16 | <5% | 1.48 |
| SiO2 | Microparticles, GmbH | 9.98 | <5% | 1.42 |
FCM/FACS data acquisition
Flow cytometry measurements were performed using a flow cytometer BD LSRFortessa (Becton Dickinson, BD Biosciences, USA) equipped with a 488 nm Solid Sapphire 488/50 laser and a cell sorter BD FACSARIAIII (Becton Dickinson, BD Biosciences, USA) equipped with a 488 nm Solid Sapphire 488/20. Samples were pumped with a flow rate of 30 μl min−1, resulting in a nominal throughput of ∼150 particles per second. FSC and SSC measurements were acquired using FACSDiva software (BD Biosciences, version 6.1.3).μSFC data acquisition and analysis
Photoreceiver signals are continuously acquired for 1 minute at 500 kHz using a PCI express data acquisition card (PCIe-6321, National Instruments) and successively analyzed offline using a custom Matlab script. Before analysis, the acquired signal is filtered with a low-pass filter with 20 kHz cut-off frequency to remove high frequency noise. Successively, the signal is segmented into signal events containing single events using a peak-finding procedure. Data are selected and gated using the bivariate distribution fθvs. average intensity (cf. Fig. S5 of the ESI†). Coincidences, i.e. the simultaneous presence of 2 or more particles in the measurement region, yield signals with higher intensities which are discarded by thresholding. Coincidences were on average ∼13% of total events measured, but could potentially be recovered by using a more sophisticated signal analysis (e.g. a Bayesian approach46) to increase system throughput. The start/end points of each event are determined as the first and last time-points where the signal crosses a threshold (3 standard deviations of the baseline noise). A fast-Fourier transform (FFT) is used to compute the frequency power spectrum, and peak-finding is used to find the angular oscillations frequency peak. Single-shell theoretical Mie scattering profiles are computed using Matlab MieScat package.47Results
Performance comparison of μSFC and FCM/FACS for size estimation
Polymeric beads with different sizes and refractive indices were used to perform a direct performance comparison between μSFC and FCM/FACS for particle size estimation. Angle-resolved signals representative of each particle population measured with μSFC after de-noising can be found in Fig. S6 of the ESI.† Samples of polystyrene (PS, n = 1.59) beads with different diameters (9, 10, and 15 μm) were used to assess the effects of size, whereas beads with same diameter (10 μm) made of silica (SiO2, n = 1.42) or poly-methyl-methacrylate (PMMA, n = 1.48) were used to assess the effects of refractive indices (see Table 1). Each sample was measured and analyzed individually using μSFC and FCM. Results are shown in Fig. 3-a as bivariate distributions of angular oscillations frequency fθversus average signal intensity for the μSFC, and in Fig. 3-b as FSC versus SSC for the FCM. Both the measured FSC and fθ monotonously increase with increasing diameter of PS particles, (FSC equal to 5.1 ± 0.1 × 104, 6.9 ± 0.2 × 104, 12.6 ± 0.3 × 104 and fθ equal to 0.28 ± 0.01, 0.31 ± 0.01, 0.55 ± 0.02 for 9, 10, and 15 μm beads, respectively) showing that both systems yield consistent results for particle with the same refractive index. Nevertheless, when comparing measurements of beads with the same size made of different materials (10 μm PS, PMMA, and SiO2 beads), FCM measurements are heavily affected by particles refractive indices (FSC equal to 6.9 ± 0.2 × 104, 10.7 ± 0.4 × 104, 12.2 ± 1.9 × 104, respectively), whereas μSFC aren't (fθ equal to 0.31 ± 0.01, 0.31 ± 0.01, 0.33 ± 0.01, respectively). Additionally, FSC measurement errors depend on particles refractive indices, with larger standard deviations for lower refraction indices. This leads to coefficient of variations (CV) for FSC measurement outside manufacturer's range for SiO2 particles (CV = 16%). These results indicate that the proposed μSFC significantly outperforms FCM for particle size estimation, and confirm that extra care should be used when analyzing FSC data for size estimation, as both mean values and standard deviations are heavily affected by particles refractive indices. The performance difference is further demonstrated if a linear regression is used to correlate measurements with nominal diameters of the beads populations, assessing the ability of each system to provide quantitative size estimates. As shown in Fig. 3-c and d, the best fit for μSFC data achieves an R2 = 0.99, versus an R2 = 0.40 for FCM data (fit coefficients can be found in Table 2 – μSFC fit results). It is also worth noting that while FSC depends on several vendor-dependent parameters making difficult inter-machine comparisons, fθ is machine invariant, and can be compared with the theoretical Mie scattering model. As shown in Fig. 3-c, the fit of experimental μSFC data with the theoretical model yields an R2 = 0.88. Small discrepancies between data and model predictions may origin from errors in the event length estimation, which may result in the angular range actually measured being different from the nominal. Similar results are obtained if a FACS machine is used for the analysis (Fig. S7 of the ESI†). In particular, FACS performs better than FCM on PMMA beads, but still fails to correctly characterize SiO2 beads, resulting in an R2 = 0.54.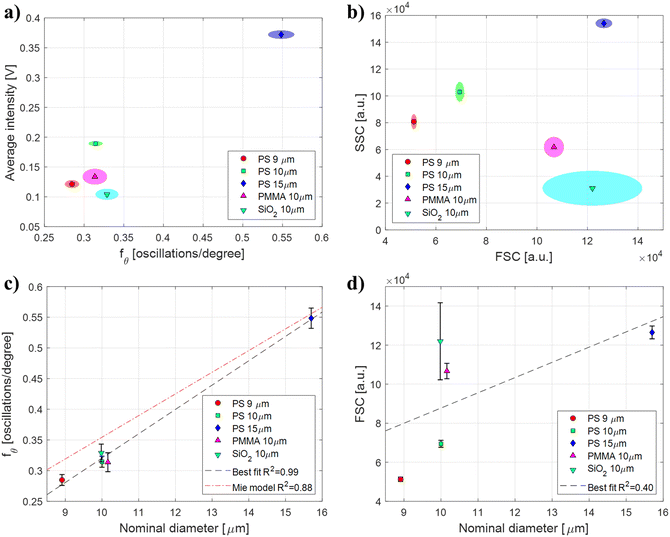 | ||
| Fig. 3 μSFC and FCM performance comparison. Polymeric beads with different sizes and refractive indices (Table 1) are used to compare the performance of μSFC and FCM for size estimation. a and b) Data are shown as bivariate distributions (>200 events each) of (a) angular oscillations frequency fθversus normalized integral for the μSFC, and (b) FSC versus SSC for the FCM. Markers represent distribution means, and shaded ellipses represent areas within one standard deviation of the mean. c and d) Linear regression of (c) angular oscillations frequency fθ and (d) FSC with nominal beads diameter. Markers represent distribution means and error bars represent one standard deviation. Black dashed line indicate the best-fit linear regression (R2 = 0.99 for the μSFC and R2 = 0.40 for the FCM). The red dotted line in (c) represents the regression with the theoretical Mie model (R2 = 0.88). Fit coefficients are reported in Table 2. | ||
| FIT TYPE | d = fθP0 + P1 | R 2 | |
|---|---|---|---|
| P 0 | P 1 | ||
| Best fit | 25.0 | 1.9 | 0.99 |
| Mie model | 28.3 | −0.034 | 0.88 |
Monocytes measurement
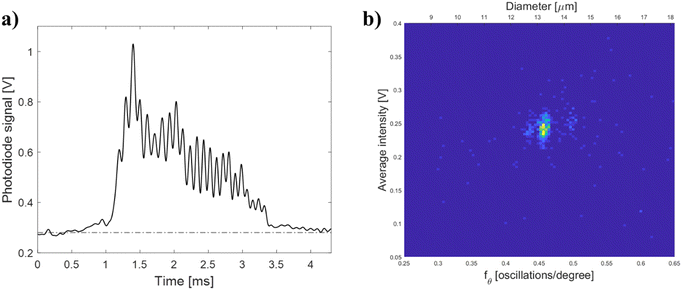
A monocyte population within a PBMC sample was analyzed with the μSFC to demonstrate the feasibility of the proposed system to perform biological measurements (lymphocytes were below current lower detection limit of ∼9 μm). An angle-resolved measurement representative of signals of the monocyte population is shown in Fig. 4-a. The signal has angular oscillations similar to the ones observed for polymeric beads which can be used to extract size estimates. The signal analysis previously described is used to obtain the bivariate distribution of angular frequency fθversus average signal intensity, as shown in Fig. 4-b. In particular, the monocyte population has an fθ = 0.46 ± 0.04, which correspond to a cell diameter d = 13.1 ± 1.1 μm using the theoretical model, or d = 13.6 ± 1.00 μm using the beads best-fit regression. Both size estimates are within the range of healthy monocytes.48,49 Similarly, the monocyte population has an average signal intensity equal to 0.24 ± 0.03 V, which using the look-up table calibrated with beads (cf. Fig. S2-b of the ESI†), yields a refractive index ∼1.54.Conclusions
We presented the first microfluidic scanning flow cytometer (μSFC), demonstrating its potential to characterize polymeric beads and a monocyte population. The low-cost μSFC achieves better performance than gold-standard FCM/FACS machines for particle size estimation and label-free analysis. Thanks to its simplicity, the system can be easily integrated within other lab-on-chip system and other point-of-care diagnostic applications. Future generation microchips will be potentially fabricated in materials with higher optical quality and feasible for mass production (e.g. glass or PMMA). Future work will also include the development of a machine learning approach for automated data analysis.50,51Ethical approval
Healthy donors' peripheral blood mononuclear cells (PBMCs) were collected and used from healthy volunteers after informed consent, in accordance with Italian laws and Research Ethics Committee guidelines at the Policlinico Umberto I Hospital (RIF.CE: 5192).Author contributions
Conceptualization: R. Reale, G. Ruocco, and M. Leonetti. Funding acquisition: G. Ruocco, and M. Leonetti. Investigation: R. Reale, G. Peruzzi, and M. Ghoreishi. Resources: H. Stabile. Original draft: R. Reale. Review & editing: R. Reale, G. Peruzzi, M. Ghoreishi, H. Stabile, G. Ruocco, and M. Leonetti.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Project LOCALSCENT, Grant PROT. A0375-2020-36549, Call POR-FESR “Gruppi di Ricerca 2020”. The research leading to these results has also been supported by European Research Council Synergy Grant ASTRA (no. 855923).References
- K. M. McKinnon, Curr. Protoc. Immunol., 2018, 120, 5.1.1 CrossRef PubMed.
- N. Komin and A. Skupin, Curr. Opin. Syst. Biol., 2017, 3, 154–160 CrossRef.
- R. Avraham, N. Haseley, D. Brown, C. Penaranda, H. B. Jijon, J. J. Trombetta, R. Satija, A. K. Shalek, R. J. Xavier, A. Regev and D. T. Hung, Cell, 2015, 162, 1309 CrossRef CAS PubMed.
- S. J. Altschuler and L. F. Wu, Cell, 2010, 141, 559 CrossRef CAS PubMed.
- Y. Jo, J. Jung, J. W. Lee, D. Shin, H. Park, K. T. Nam, J. H. Park and Y. Park, Sci. Rep., 2014, 4, 1–6 Search PubMed.
- C. Shi and E. G. Pamer, Nat. Rev. Immunol., 2011, 11, 762–774 CrossRef CAS PubMed.
- L. Agnello, A. Iacona, B. L. Sasso, C. Scazzone, M. Pantuso, R. V. Giglio, C. M. Gambino, A. M. Ciaccio, G. Bivona, M. Vidali and M. Ciaccio, Clin. Chem. Lab. Med., 2021, 59, 1600–1605 CrossRef CAS PubMed.
- E. D. Crouser, J. E. Parrillo, G. S. Martin, D. T. Huang, P. Hausfater, I. Grigorov, D. Careaga, T. Osborn, M. Hasan and L. Tejidor, J. Intensive Care, 2020, 8, 1–10 CrossRef PubMed.
- P. Hausfater, N. Robert Boter, C. Morales Indiano, M. Cancella de Abreu, A. M. Marin, J. Pernet, D. Quesada, I. Castro, D. Careaga, M. Arock, L. Tejidor and L. Velly, Crit. Care, 2021, 25, 227–239 CrossRef PubMed.
- L. Agnello, B. L. Sasso, M. Vidali, C. Scazzone, C. M. Gambino, R. V. Giglio, A. M. Ciaccio, G. Bivona and M. Ciaccio, Int. J. Lab. Hematol., 2021, 43, O183–O185 Search PubMed.
- D. Zhang, R. Guo, L. Lei, H. Liu, Y. Wang, Y. Wang, H. Qian, T. Dai, T. Zhang, Y. Lai, J. Wang, Z. Liu, T. Chen, A. He, M. O'Dwyer and J. Hu, J. Leukocyte Biol., 2021, 109, 13 CrossRef CAS PubMed.
- M. Cusinato, L. Hadcocks, S. Yona, T. Planche and D. Macallan, Int. J. Lab. Hematol., 2022, 1029–1039 CrossRef PubMed.
- G. Lippi, F. Sanchis-Gomar and B. M. Henry, Int. J. Lab. Hematol., 2021, 43, O161–O163 Search PubMed.
- M. Lorubbio, D. Tacconi, G. Iannelli, M. Feri, R. Scala, S. Montemerani, M. Mandò and A. Ognibene, Clin. Biochem., 2022, 103, 29–31 CrossRef CAS PubMed.
- L. Alsuwaidi, S. A. Heialy, N. Shaikh, F. A. Najjar, R. Seliem, A. Han and M. Hachim, BMC Infect. Dis., 2022, 22, 1–10 CrossRef PubMed.
- C. B. Black, T. D. Duensing, L. S. Trinkle and R. T. Dunlay, Assay Drug Dev. Technol., 2011, 9, 13 CrossRef CAS PubMed.
- X. Mao, A. A. Nawaz, S. C. S. Lin, M. I. Lapsley, Y. Zhao, J. P. McCoy, W. S. El-Deiry and T. J. Huang, Biomicrofluidics, 2012, 6, 024113 CrossRef PubMed.
- Optics & Detection - Flow Cytometry Guide|Bio-Rad, https://www.bio-rad-antibodies.com/flow-cytometry-optics-detection.html, (accessed 30 November 2022).
- H. M. Shapiro, Practical Flow Cytometry, Wiley, 2003 Search PubMed.
- E. C. Jensen, Anat. Rec., 2012, 295, 2031–2036 CrossRef CAS PubMed.
- Y. Suzuki, K. Kobayashi, Y. Wakisaka, D. Deng, S. Tanaka, C. J. Huang, C. Lei, C. W. Sun, H. Liu, Y. Fujiwaki, S. Lee, A. Isozaki, Y. Kasai, T. Hayakawa, S. Sakuma, F. Arai, K. Koizumi, H. Tezuka, M. Inaba, K. Hiraki, T. Ito, M. Hase, S. Matsusaka, K. Shiba, K. Suga, M. Nishikawa, M. Jona, Y. Yatomi, Y. Yalikun, Y. Tanaka, T. Sugimura, N. Nitta, K. Goda and Y. Ozeki, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 15842–15848 CrossRef CAS PubMed.
- M. Herbig, K. Tessmer, M. Nötzel, A. A. Nawaz, T. Santos-Ferreira, O. Borsch, S. J. Gasparini, J. Guck and M. Ader, Sci. Rep., 2022, 12, 1–17 CrossRef PubMed.
- A. D. Stern, A. H. Rahman and M. R. Birtwistle, Cytometry, Part A, 2017, 91, 14–24 CrossRef CAS PubMed.
- H. M. Shapiro, Methods Mol. Biol., 2018, 1678, 1–10 CrossRef CAS PubMed.
- C. Becker, J. Parker, M. Hechinger and R. Leif, in ISAC XXI Congress, San Diego, CA, USA, 2002 Search PubMed.
- V. P. Maltsev, Rev. Sci. Instrum., 1999, 71, 243 CrossRef.
- M. R. Loken, R. G. Sweet and L. A. Herzenberg, J. Histochem. Cytochem., 1976, 24, 284–291 CrossRef CAS PubMed.
- A. I. Konokhova, A. A. Gelash, M. A. Yurkin, A. V. Chernyshev and V. P. Maltsev, Cytometry, Part A, 2013, 83, 568–575 CrossRef PubMed.
- I. V. Kolesnikova, S. V. Potapov, M. A. Yurkin, A. G. Hoekstra, V. P. Maltsev and K. A. Semyanov, J. Quant. Spectrosc. Radiat. Transfer, 2006, 102, 37–45 CrossRef CAS.
- A. L. Litvinenko, V. M. Nekrasov, D. I. Strokotov, A. E. Moskalensky, A. V. Chernyshev, A. N. Shilova, A. A. Karpenko and V. P. Maltsev, Anal. Methods, 2021, 13, 3233–3241 RSC.
- D. Chen, X. Liu, J. Han, M. Jiang, Z. Wang and J. Qi, Sensors, 2019, 19, 2243 CrossRef CAS PubMed.
- E. S. Yastrebova, A. L. Litvinenko, D. I. Strokotov, R. S. Vladimirov, K. V. Gilev, V. M. Nekrasov, A. A. Karpenko and V. P. Maltsev, J. Opt., 2021, 23, 105606 CrossRef CAS.
- M. Geiser, S. Bolay, F. Truffer and D. Roßkamp, Opt. Express, 2007, 15, 2683–2690 CrossRef PubMed.
- T. Sun and H. Morgan, Microfluid. Nanofluid., 2010, 8, 423–443 CrossRef CAS.
- C. Petchakup, H. Li and H. W. Hou, Micromachines, 2017, 8, 87 CrossRef.
- J. McGrath, R. Reale, C. Honrado, P. Bisegna, N. Swami and F. Caselli, in 23nd International Conference on Miniaturized Systems for Chemistry and Life Sciences (MicroTAS 2019), 2019 Search PubMed.
- G. Mie, Ann. Phys., 1908, 330, 377–445 CrossRef.
- A. V. Romanov and M. A. Yurkin, Opt. Laser Technol., 2022, 151, 108047 CrossRef.
- Y. Luo, J. Huang and A. Adibi, Opt. Lett., 2007, 32, 1171–1173 CrossRef PubMed.
- K. A. Semyanov, P. A. Tarasov, A. E. Zharinov, A. V. Chernyshev, A. G. Hoekstra and V. P. Maltsev, Appl. Opt., 2004, 43, 5110–5115 CrossRef PubMed.
- V. P. Maltsev and V. N. Lopatin, Appl. Opt., 1997, 36, 6102 CrossRef CAS PubMed.
- J. Friend and L. Yeo, Biomicrofluidics, 2010, 4, 026502 CrossRef PubMed.
- P. Y. Liu, L. K. Chin, W. Ser, H. F. Chen, C. M. Hsieh, C. H. Lee, K. B. Sung, T. C. Ayi, P. H. Yap, B. Liedberg, K. Wang, T. Bourouina and Y. Leprince-Wang, Lab Chip, 2016, 16, 634–644 RSC.
- Q. Zhang, L. Zhong, P. Tang, Y. Yuan, S. Liu, J. Tian and X. Lu, Sci. Rep., 2017, 7, 1–10 CrossRef PubMed.
- G. Bolognesi, S. Bianchi, R. di Leonardo, H. Mushfique, J. Leach, H. Yin, M. Padgett and J. Cooper, Opt. Express, 2011, 19, 19245–19254 CrossRef CAS PubMed.
- F. Caselli, A. de Ninno, R. Reale, L. Businaro and P. Bisegna, IEEE Trans. Biomed. Eng., 2021, 68, 340–349 Search PubMed.
- MatScat-File Exchange-MATLAB Central, https://it.mathworks.com/matlabcentral/fileexchange/36831-matscat, (accessed 5 December 2022).
- J. Prinyakupt and C. Pluempitiwiriyawej, J. Geophys. Res. Planets, 2015, 14, 63 Search PubMed.
- K. Semyanov, A. Zharinov, P. Tarasov, M. Yurkin, I. Skribunov, D. van Bockstaele and V. Maltsev, Optics of Biological Particles, 2007, pp. 269–280 Search PubMed.
- F. Caselli, A. de Ninno, R. Reale, L. Businaro and P. Bisegna, in MicroTAS 2020 - 24th International Conference on Miniaturized Systems for Chemistry and Life Sciences, 2020 Search PubMed.
- C. Honrado, J. S. McGrath, R. Reale, P. Bisegna, N. S. Swami and F. Caselli, Anal. Bioanal. Chem., 2020, 412, 3835–3845 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc01179d |
| This journal is © The Royal Society of Chemistry 2023 |