Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A unified understanding of magnetorheological elastomers for rapid and extreme stiffness tuning†
Edward J.
Barron III
 ab,
Ella T.
Williams
a,
Ravi
Tutika
ab,
Nathan
Lazarus
c and
Michael D.
Bartlett
ab,
Ella T.
Williams
a,
Ravi
Tutika
ab,
Nathan
Lazarus
c and
Michael D.
Bartlett
 *ab
*ab
aMechanical Engineering, Soft Materials and Structures Lab, Virginia Tech, Blacksburg, VA 24061, USA. E-mail: mbartlett@vt.edu
bMacromolecules Innovation Institute, Virginia Tech, Blacksburg, VA 24061, USA
cElectrical and Computer Engineering Department, University of Delaware, Newark, DE 19716, USA
First published on 2nd October 2023
Abstract
Magnetorheological elastomers (MREs), which adapt their mechanical properties in response to a magnetic field, can enable changes in stiffness and shape for applications ranging from vibration isolators to shape morphing robots and soft adaptive grippers. Here, a unified design approach is introduced to create MRE materials for extreme stiffness tuning, up to 70×, with rapid (∼20 ms) and reversible shape change. This guides the creation of a hybrid MRE composite architecture that incorporates a combination of magnetic particles and magnetic fluids into elastomers. The role of both solid and fluid inclusions on magnetorheological response is systematically investigated and a predictive model is developed that captures the stiffness tuning response of MREs across diverse material microstructures and compositions. This general understanding enables MRE materials with programmable response and greatly enhanced stiffness tuning and rapid response times compared to many MRE, granular jamming, and phase change approaches. This insight is utilized to optimize composites for a soft adaptive gripper which grasps and releases objects of diverse geometries.
1 Introduction
Adaptive materials which change their stiffness and shape in response to engineering stimuli have emerged as important components for emerging applications such as reconfigurable and adaptive robots and machines.1–10 One essential feature of these materials is the ability to rapidly undergo extreme changes in stiffness to enable multifunctional components. Stiffness tuning can be accomplished at the material level by utilizing mechanisms such as phase change,11–13 granular jamming,14–16 or magnetic material response.17,18 The stiffness tuning capability of a material is typically an experimentally measured quantity for several performance parameters including the magnitude of stiffness, the stiffness tuning ratio, and the response time.19 For example, materials utilizing low melting point alloys and polymers have demonstrated large changes in stiffness by taking advantage of their solid–liquid phase transition in response to heat.4,11,13,20 Granular media rapidly responds to negative pressure with a transition between a fluid-like granular state, where particles freely move past each other, to a jammed state, where the jammed particles form a solid-like mechanical response.14–16,21 Magnetically active materials such as magnetorheological elastomers (MREs) have some of the fastest response times among stiffness tuning materials (<0.01 s),22,23 however, the stiffness change of traditional MRE systems (∼10×) is typically lower than that of other stiffness tuning materials.22,24 Improvement of the stiffness tuning effect of MREs offers the possibility to create adaptive materials with both rapid response and extreme stiffness tuning that enable the next generation of adaptive machines.Magnetic elastomer composites have traditionally been created by incorporating magnetic particles into soft elastomers such as silicones or polyurethanes,25 to provide a combination of soft mechanical response and magnetic functionality for applications including stretchable and adaptive electronics and sensing,26–31 automotive components,32–34 and soft robotic grippers.35–39 A key feature that has lead to substantial research of MREs is their magnetorheological effect, which leads to magnetic field-driven tunable stiffness,17,18 variable energy dissipation and damping,40,41 and shape-memory effects.42 To improve the stiffness tuning effect (often called the MR effect or MR ratio) of these materials, MREs have been created with varied parameters such as elastomer matrix material,43–50 magnetic particle size,28,43,48,51 shape,52–54 and volume fraction,44,55–57 and recently through the introduction of magnetic fluids as functional content.29,42,58 Magnetorheological fluids, which are magnetic fluids that rapidly change viscosity and yield stress when subjected to a magnetic field,59,60 have recently been used as inclusions for MREs. These fluid inclusions are incorporated as millimeter-scale droplets into elastomers through 3D printing or by micro-dispersing magnetorheological fluid droplets through mixing, and provide unique opportunities to achieve large stiffness tuning with highly deformable and adaptive properties.29,42,58,61 However, how stiffness tuning and response in these diverse MREs depends on material composition and microstructure is not well understood, which limits performance and programming of desired properties.
Here we determine a predictive model for the understanding and enhancement of MRE properties to optimize magnetic elastomers with rapid material response and extreme stiffness tuning. The model is validated through MREs with diverse material architectures, which includes traditional rigid particle composites (RCs), state-of-the-art magnetorheological fluid composites (FCs), and a new form of hybrid composite (HC) MRE which contains both rigid particles and magnetorheological fluids as discrete domains (Fig. 1a–c). We systematically investigate the effects of material structure and zero-field mechanical response on the MR effect of MREs, and find that our model unifies the stiffness tuning effect for each of the three investigated microstructures under a single predictive equation (Fig. 1d). This quantitative understanding of the relationship between zero-field modulus and MR effect allows for the optimization of MRE performance, which we show through the creation of MRE materials with unprecedented changes in stiffness (70×) (Fig. 1e) and rapid magnetic response times of ∼20 ms (Fig. S1†) (Movie S1†). The magnetorheological response of these materials gives rise to a rapidly reversible shape-locking and stiffness tuning effect (Fig. 1f), which we utilize through our multi-phase HC MRE (Fig. 1g) to create adaptive grippers for controlled manipulation of diverse objects.
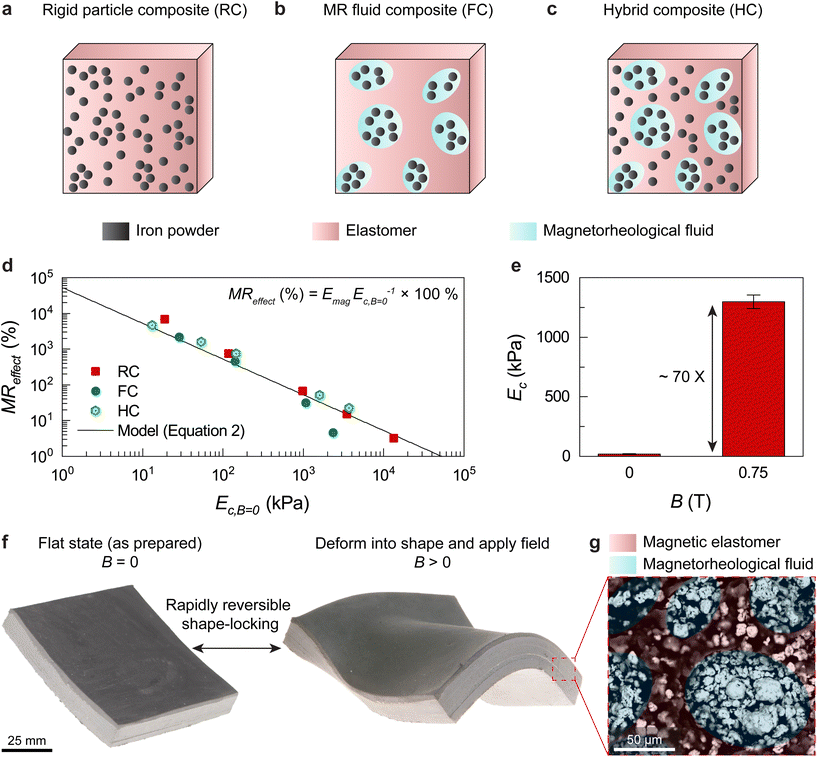 | ||
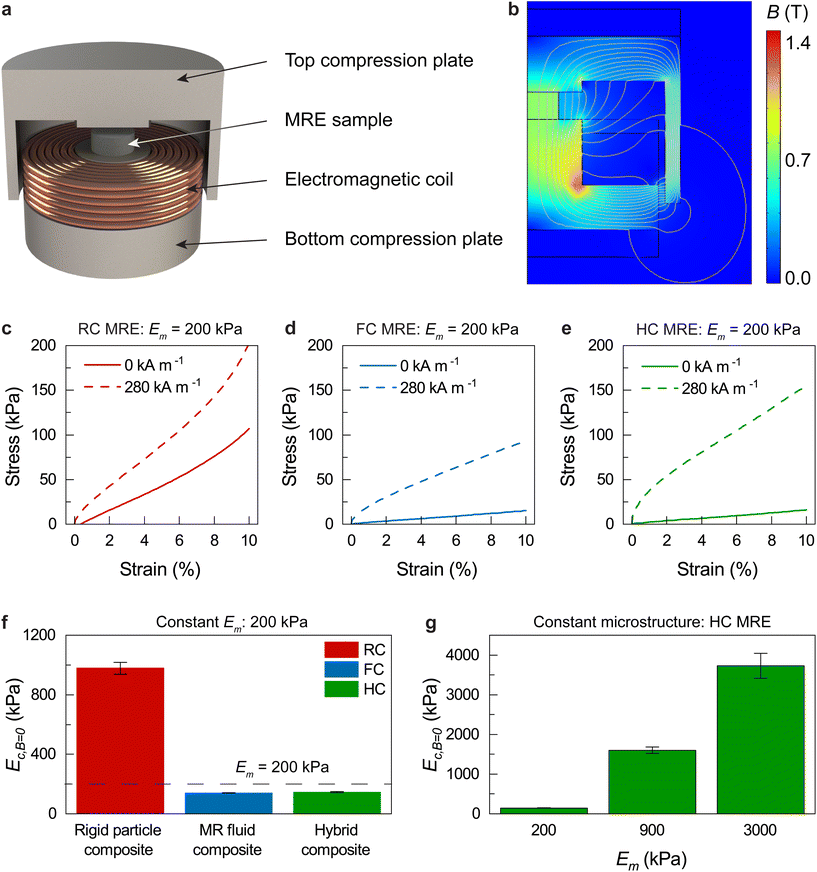
| Fig. 1 Material structure and properties. (a) Schematics of rigid particle composite (RC), (b) magnetorheological fluid composite (FC), and (c) hybid composite (HC) material architectures. (d) Effect of zero-field modulus on the relative MR effect of the materials tested in this work (Emag = 530 kPa for eqn (2)). (e) Change in stiffness of an RC MRE with no field applied and with a magnetic flux density of 0.75 T. (f) Image of a hybrid composite magnetorheological elastomer utilizing magnetorheological stiffness tuning to realize a shape memory effect. (g) SEM image of hybrid composite MRE. The image is artificially colored red for the magnetic elastomer phase and blue for the MR fluid phase. An unaltered image can be found in Fig. S2.† | ||
2 Results and discussion
2.1 Predicting MRE stiffness tuning
To predict the stiffness tuning of magnetically active composite materials, we consider a material effect from the composite zero-field modulus (Ec,B=0) and a magnetic contribution (Emag). When subjected to a magnetic field, we assume that the material and magnetic forces are additive (i.e. a parallel arrangement of springs) which yields a composite modulus, Ec, such that Ec = Ec,B=0 + Emag. We then normalize this equation by Ec,B=0 to understand how the tunability of the magnetic composite depends upon both the material contribution and the effective magnetic contribution: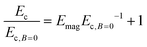 | (1) |
Eqn (1) gives an analytical expression for the MR enhancement factor 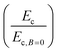 , which is the ratio between the composite modulus under a magnetic field (i.e. activated) and the zero-field modulus of the composite (i.e. unactivated), where large values indicate high stiffness tunability. When the MR enhancement factor approaches a value of 1, the composite modulus does not increase when subjected to a magnetic field, which occurs as Emag ≪ Ec,B=0. This provides a lower, physical limit to rigidity tuning when magnetic interactions are low or when the initial composite modulus is high. Eqn (1) provides a clear design paradigm where maximum rigidity tuning is achieved when magnetic interactions are increased or when initial composite modulus is lowered. From a materials design perspective, this requires an approach to achieve significant magnetic material loading to increase the magnetic effect, while still maintaining a soft composite response. Through this general guidance, we will show how composite microstructure and composition can be used to achieve high degrees of stiffness tuning and programmable composite modulus.
, which is the ratio between the composite modulus under a magnetic field (i.e. activated) and the zero-field modulus of the composite (i.e. unactivated), where large values indicate high stiffness tunability. When the MR enhancement factor approaches a value of 1, the composite modulus does not increase when subjected to a magnetic field, which occurs as Emag ≪ Ec,B=0. This provides a lower, physical limit to rigidity tuning when magnetic interactions are low or when the initial composite modulus is high. Eqn (1) provides a clear design paradigm where maximum rigidity tuning is achieved when magnetic interactions are increased or when initial composite modulus is lowered. From a materials design perspective, this requires an approach to achieve significant magnetic material loading to increase the magnetic effect, while still maintaining a soft composite response. Through this general guidance, we will show how composite microstructure and composition can be used to achieve high degrees of stiffness tuning and programmable composite modulus.
We can also rearrange this relationship to predict a parameter that is commonly used to quantify stiffness tuning for MREs: the MR effect (MReffect), or the relative change in modulus of the sample. By utilizing the relationship between parallel springs and solving for MReffect, the MR effect can be modeled as a function of Ec,B=0 and Emag:
| MReffect = EmagEc,B=0−1 × 100% | (2) |
These simple yet robust relationships provide an accurate fit to the data acquired in this work across RC, FC, and HC composite architectures over several orders of magnitude in zero-field modulus of the composites, where Emag is used as a fitting parameter (Fig. 1d). We consider Ec,B=0 a primary factor in determining the magnetorheological response, as previous work has shown that stiffness tuning becomes limited as the zero-field modulus of the composite increases.62 This is consistent with our results and prediction, where MReffect ∝ Ec,B=0–1, demonstrating that as Ec,B=0 increases MReffect decreases.
We note that eqn (1) and (2) are not simply the equations for the MR effect, which is typically an experimentally measured quantity relating the modulus of the material under a magnetic field (Ec) relative to the same material without a magnetic field (Ec,B=0), i.e.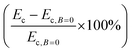 . Eqn (1) and (2) instead give insight into the stiffness tuning contributions from the inherent stiffness of the composite material (Ec,B=0) and the effective stiffness imparted to the material through an applied magnetic field (Emag).
. Eqn (1) and (2) instead give insight into the stiffness tuning contributions from the inherent stiffness of the composite material (Ec,B=0) and the effective stiffness imparted to the material through an applied magnetic field (Emag).
2.2 MRE composition
To determine the effect of microstructure on the magnetorheological response, as guided by eqn (1) and (2), we fabricate MREs of three different material architectures and mechanically quantify their stiffness tuning properties. RC MREs are fabricated with a volume fraction of 25% iron powder within the elastomer matrix. This volume fraction was chosen as it allowed for a low enough viscosity to be easily processed into testing geometries, while also imparting a significant magnetic response. FC MREs incorporate an iron based MRF that contains a volume fraction of 35% iron powder in a propylene glycol carrier fluid that is immiscible with the silicone matrix and processed to be contained as discrete microdroplets within the elastomer. The volume fraction of MRF in the FC MREs is 50%, leading to a total iron powder volume fraction of 17.5%. Above an MRF volume fraction of 50% large-scale phase separation occurred and evenly dispersing the MRF as microdroplets was a challenge. This volume fraction of MRF is higher than that reported in previous work for FC MREs which showed MRF volume fractions of 30–40%.42,61 HC MREs are fabricated with a volume fraction of 50% MRF, as well as 15% iron powder located in the elastomer matrix for a total iron particle volume fraction of 25%, which is equivalent to the volume fraction of magnetic content in the RC MREs. Scanning electron microscopy of the RC, FC, and HC material architectures can be found in Fig. S3 and S4.† In addition to investigating microstructure, the elastic modulus of the silicone matrix (Em) is varied to study the effect of zero-field modulus on the stiffness tuning capabilities for each of the MRE material architectures. Em is controlled by changing the crosslinking density of the silicone matrix, or by creating blends of two silicone elastomers with different matrix moduli (details in the Experimental section).2.3 MRE characterization
The MR effect of the magnetic elastomer composites is measured through a custom magnetorheological compression fixture (Fig. 2a). The MRE testing fixture consists of a copper electromagnetic coil integrated with a 1020 steel bottom compression plate and an outer steel housing (top compression plate). Compression tests are run on each material using the electromagnet with average magnetic field strengths of H = 0–280 kA m−1. Finite element analysis (FEA) is used to determine the average magnetic flux density through the samples (Fig. 2b), which is determined to be up to 0.75 T for the RC and HC MREs and up to 0.58 T for the FC MREs (Fig. S5†). The difference in flux density arises from the difference in magnetic content between the material architectures.Representative compression curves for RC, FC and HC MREs with constant Em = 200 kPa are shown in Fig. 2c–e respectively, with the solid lines representing the zero-field mechanical response and the dashed lines indicating the mechanical response with an applied field of 280 kA m−1. For the same matrix modulus, RC MREs demonstrate a more rigid zero-field mechanical response than the FC and HC MREs. This is attributed to the incorporation of MRF in both the FC and HC MREs, which mechanically cloaks the rigid character of the solid particle inclusions and creates a softer composite mechanical response. The RC MRE also shows a substantially smaller change in mechanical properties under the influence of a 280 kA m−1 field. From our understanding introduced in Fig. 1d we attribute this to the larger zero-field modulus of the RC MREs. Thus, to program the magnitude of the magnetorheological stiffness effect, it becomes necessary to control the zero-field modulus of the composite (Ec,B=0).
Control over Ec,B=0 is demonstrated through two material design strategies: the microstructure of the MREs can be changed to either increase or decrease the modulus of the composite by utilizing rigid particle or MRF inclusions, or Em can be varied through changes in elastomer crosslinking which has a strong influence on the composite modulus. These two design strategies allow for diversity of fabrication in the event that an application is limited by either the choice of elastomer or the magnetic inclusions. Fig. 2f shows the change in zero-field modulus with respect to each of the material architectures with a constant Em of 200 kPa. The compressive moduli are determined from the linear portion of the of the stress versus strain curves (details in Experimental). The addition of solid filler increases the zero-field modulus of the composite, while the addition of the MRF decreases the modulus of the composite. Fig. 2g shows the alternative method of controlling the zero-field modulus for a constant material architecture of HC MRE by varying the elastomer modulus, Em. Controlling the zero-field modulus of the composite by either of these two methods has a strong influence on the magnetorheological effect.
2.4 Active magnetorheological properties
For MREs to be utilized for active property tuning, it is essential to understand how the MRE material properties relate to the active stiffness tuning response. We determine that the zero-field modulus, Ec,B=0, is the controlling factor in determining the stiffness tuning capabilities of MREs. Fig. 3a shows the range of achievable modulus of MREs as a function of zero-field modulus. The lowest point on each bar represents the lowest achievable modulus (Ec,B=0) of the sample, while the highest point of each bar is the modulus under an applied field of H = 280 kA m−1. The softest MREs in this work were fabricated with Ec,B=0 on the order of 10 kPa, and demonstrate changes of stiffness of up to 70× their zero-field modulus. As the zero-field modulus is increased up to 13 MPa the relative tunability of the composite modulus decreases to only ∼3%. This decrease in mechanical tunability with respect to Ec,B=0 is a fundamental trade-off in these material systems that is attributed to stiffer material resisting the distortion of the composite by the magnetic inclusions,62,63 creating a large effect of Ec,B=0 relative to Emag.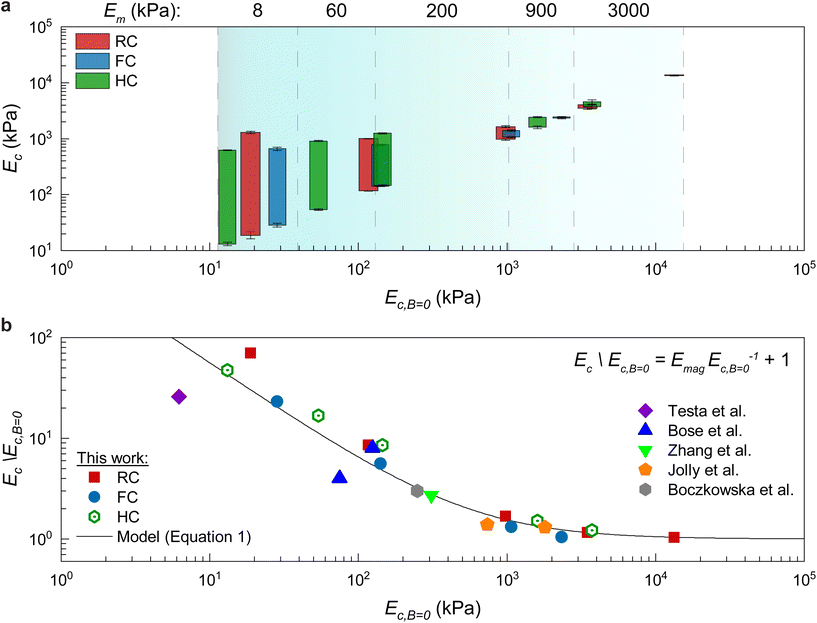 | ||
| Fig. 3 Magnetorheological stiffness tuning. (a) Range of achievable moduli of MREs as a function of their zero-field modulus. The bottom of the floating bars indicate the zero-field modulus of the sample, while the top of the bars correspond to the measured modulus with an applied field of 280 kA m−1. (b) Maximum measured magnetorheological enhancement ratio as a function of zero-field modulus for the materials tested in this work as well as literature data (Emag = 530 kPa for eqn (1)).17,24,42,56,57 | ||
Fig. 3b shows the maximum measured MR enhancement factor as a function of Ec,B=0 for the materials tested in this work as well as literature data.17,24,42,56,57 Here, we focus only on the maximum achievable stiffness tuning effect to understand the factors governing the creation of extreme stiffness tuning MREs. We find that eqn (1) accurately predicts the stiffness tuning effect of not only the MREs in this work, but of those reported in previous research as well by fitting the data to a single value of Emag. The data is fit with a value of Emag = 530 kPa, which remains accurate across the wide range of Ec,B=0, is independent of the investigated microstructures, and fits a wide variety of iron particle volume fractions ranging from 17–30%, and MRF volume fractions from 40–50%. The MR enhancement factor is shown to approach a value of 1, indicating a negligible change in modulus as Ec,B=0 is increased above 1 MPa, which quantifies the fundamental tradeoff between MRE active properties and their zero-field modulus. This is consistent with the prediction that when Emag ≪ Ec,B=0 the MR enhancement factor approaches 1. This finding is an essential result for the optimization of MREs, in that it provides evidence that the maximum magnetic contribution to the modulus is not drastically changed by any of the three material structures. Emag is instead likely primarily a factor of the magnetic properties of the inclusions, where iron is most commonly chosen because of its high permeability, high saturation, and low remnant magnetization.50,64
For materials with the same magnetic inclusions, the ability to tune Emag, even across relatively large changes in volume fraction, does not have as great of an effect on the maximum stiffness tuning effect as Ec,B=0. By understanding that zero-field modulus is a dominant factor in determining the stiffness tunability of these material systems, we can now program the MR effect through their zero-field response by utilizing either Em or material structure as discussed in Fig. 2f and g.
MREs have long been known to have rapid response times, however the stiffness tunability has been lacking when compared to other active material systems.22 By creating MREs with a sufficiently low zero-field modulus, we can produce materials with extreme stiffness tuning effects (MReffect = 7000%) that are greater than many granular jamming and low melting point systems,3,11,13,21 while showing faster response times on the order of ∼20 ms. The results of this work produce a clear design framework for MREs of diverse structures that allows for the optimization of MRE materials with extreme stiffness tuning capabilities and rapid response, overcoming trade-offs in MRE and phase change based stiffness tuning materials.
2.5 Adaptive MRE gripper
The magnetorheological response of the HC MREs leads to a shape-locking effect with a rapid material response to a magnetic field. Here we show a soft adaptive gripper capable of rapidly gripping and releasing delicate and rigid objects with diverse geometries (Fig. 4 and Movie S2†). The gripper consists of an HC MRE (Em = 200 kPa) membrane which becomes rigid and locked into shape through a magnetic field, integrated with an inflated air pocket which allows for rapid reversibility to drop the object upon reduction of the field. The MRE gripper is adhered to the center of the electromagnet (Fig. 4a), where the magnetic field is controlled electronically.The gripper is able to passively conform around delicate objects without damage, and then grasp upon the application of an applied magnetic field, which increases the stiffness of the MRE membrane and locks in the conformed shape. Fig. 4b demonstrates the grasping of a tomato, where (i) the gripper begins to approach the object, (ii) the gripper conforms around the object and the magnetic field is applied, (iii) the gripper is retracted while grasping the object, and (iv) after holding the object for 10 seconds at its original position, the magnetic field is turned off and the object rapidly drops from the gripper in less than 0.07 s. The adaptive gripper is also able to adapt to objects of complex geometry, which is shown through the grasping of a lego brick (Fig. 4c), objects of small cross-sectional area such as a marker (Fig. 4d), and complex, multipart shapes such as a cluster of grapes (Fig. 4e). This HC MRE composite gripper is enabling for areas such as robotic manipulation and manufacturing which may require diverse grasping capabilities.
3 Conclusion
A unified MRE stiffness tuning model is demonstrated which accurately predicts the stiffness tuning effect of diverse MRE architectures. As a result of this model, the fundamental tradeoff between MR effect and zero field modulus is quantified, and materials above Ec,B=0 = 1 MPa are shown to have a drastically reduced MR enhancement factor approaching 1. This fundamental understanding of MRE active properties is utilized to create MREs with unprecedented MR effects of up to 7000% that can respond on the order of 20 ms. The large mechanical adaptability and rapid response of the MREs shown in this work are expected to have applicability towards stiffness tuning elements for applications in robotics, transportation, and active technologies such as human–machine interfaces. Further, the improved understanding of the microstructure and magnetorheological response of soft composites is expected to have impacts on the development of active and programmable material systems for future advancements in functionality.4 Experimental section
4.1 Silicone elastomer fabrication and mechanical property control
The silicone elastomers in this work utilize Sylgard 184 poly(dimethylsiloxane) (PDMS) silicone elastomer (Dow Silicones) which is a two part silicone elastomer, Ecoflex 00-30 (Smooth-On) which is a two-part platinum-catalyzed silicone elastomer, or a combination of the two silicone elastomers to vary Em. The elastomers are prepared prior to the introduction of magnetic content. The silicone matrix with Em = 8 kPa is made utilizing PDMS. The PDMS is mixed with a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of base to curing agent in a dual asymmetric centrifugal (DAC) mixer under vacuum (FlackTek) at 1800 rpm for 100 s. For the silicone with Em = 60 kPa, the PDMS is mixed with a 45
1 ratio of base to curing agent in a dual asymmetric centrifugal (DAC) mixer under vacuum (FlackTek) at 1800 rpm for 100 s. For the silicone with Em = 60 kPa, the PDMS is mixed with a 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of base to curing agent at 1800 rpm for 100 s under vacuum. The silicone matrix with Em = 200 kPa is made utilizing Ecoflex 00-30. Ecoflex is mixed with equal parts by weight of part A and part B. The uncured elastomer is mixed for 270 s at 2000 rpm under a vacuum. The silicone matrix with Em = 900 kPa is made utilizing a combination of PDMS and Ecoflex 00-30. Ecoflex is mixed with equal parts by weight of part A and part B for 270 s at 2000 rpm under a vacuum. PDMS is mixed with a 10
1 ratio of base to curing agent at 1800 rpm for 100 s under vacuum. The silicone matrix with Em = 200 kPa is made utilizing Ecoflex 00-30. Ecoflex is mixed with equal parts by weight of part A and part B. The uncured elastomer is mixed for 270 s at 2000 rpm under a vacuum. The silicone matrix with Em = 900 kPa is made utilizing a combination of PDMS and Ecoflex 00-30. Ecoflex is mixed with equal parts by weight of part A and part B for 270 s at 2000 rpm under a vacuum. PDMS is mixed with a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of base to curing agent at 1800 rpm for 100 s. The two uncured elastomers are combined in a 1 to 1 ratio by weight. The mixture is then mixed for 270 s at 2000 rpm under a vacuum. The silicone matrix with Em = 3000 kPa is made utilizing PDMS. The PDMS is mixed with a 10
1 ratio of base to curing agent at 1800 rpm for 100 s. The two uncured elastomers are combined in a 1 to 1 ratio by weight. The mixture is then mixed for 270 s at 2000 rpm under a vacuum. The silicone matrix with Em = 3000 kPa is made utilizing PDMS. The PDMS is mixed with a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of base to curing agent at 1800 rpm for 100 s under vacuum. Further information about the composition of these silicones can be found in Table S1.†
1 ratio of base to curing agent at 1800 rpm for 100 s under vacuum. Further information about the composition of these silicones can be found in Table S1.†
4.2 Composite fabrication
RC MREs are fabricated with iron powder (mean particle diameter: 5 μm, US Research Nanomaterials) with a particle volume fraction of Ωcomposite = 25%. A 35% volume fraction of iron powder in propylene glycol is used to create the MRF used for both the FC and HC MREs (ΩMRF = 35%). FC MREs are fabricated with an MRF volume fraction of Ψ = 50%. The HC MRE consists of an MRF volume fraction Ψ = 50% and a magnetic elastomer phase with Ωmatrix = 15%. The total iron powder volume fraction for FC and HC MREs can be determined by Ωcomposite,FC = ΨΩMRF and Ωcomposite,HC = ΨΩMRF + (1 − Ψ)Ωmatrix, giving values of Ωcomposite,FC = 17.5% and Ωcomposite,HC = 25% respectively. Further information about the composition of these materials can be found in Table S2.†RC MREs are fabricated by adding the 25% by volume iron powder to the uncured silicone elastomer and then mixing at 800 rpm for 120 s under vacuum in a FlackTek SpeedMixer. The molded samples were then cured in a convection oven for at least 12 hours at 40 °C.
FC MREs are fabricated by adding the magneteorhelogical fluid to the uncured elastomer in a 50% mixture by volume. The composite is then mixed for 120 s at 800 rpm under vacuum in the SpeedMixer. The samples are cured by convection oven for at least 12 hours at 40 °C.
HC MREs are fabricated by adding 15% iron powder by volume to the uncured elastomer. Hexanes are added in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 proportion to the uncured elastomer by weight to reduce the viscosity for ease-of-processing. The composite is then mixed for 120 s at 800 rpm at atmospheric pressure in the SpeedMixer. The magnetorheological fluid is then added to the mixture in a 1
4 proportion to the uncured elastomer by weight to reduce the viscosity for ease-of-processing. The composite is then mixed for 120 s at 800 rpm at atmospheric pressure in the SpeedMixer. The magnetorheological fluid is then added to the mixture in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of MRF to elastomer and iron powder by volume. The mixture is then hand mixed. The material is poured into molds, placed under vacuum to remove residual hexanes, then cured for at least 12 hours in a convection oven at 40 °C.
1 ratio of MRF to elastomer and iron powder by volume. The mixture is then hand mixed. The material is poured into molds, placed under vacuum to remove residual hexanes, then cured for at least 12 hours in a convection oven at 40 °C.
4.3 Magnetorheological testing fixture
A two part magnetic compression testing fixture was machined out of 1020 steel. The bottom half of the fixture is a compression plate, and the top half is a steel housing to increase the magnetic flux density through the material. 500 turns of 18 AWG copper of wire are integrated with the bottom compression plate to provide the magnetic field. Currents of 0–7 A are supplied to the electromagnet resulting in average magnetic field strengths of H = 0–280 kA m−1.4.4 Magnetorheological compression tests
Compression samples were cured in 28.6 mm diameter, 12.5 mm deep molds. Samples are tested via a multi-step process with the MRE loaded in the magnetic compression testing fixture. Because the test fixture itself is subject to a force when a magnetic field is applied to the system, a series of reference tests are used to determine what proportion of the measured load was applied as a stress to the sample. First, reference data is taken by measuring the load exerted by the magnetic field on the sample at several static displacements and all applied currents. A power law curve is fit to the reference data for each sample to model the load exerted by the magnetic field during sample testing. Compression tests with three loading and unloading cycles are then carried out on the sample with currents from 0–7 A applied to the electromagnet. The load from the power law model is then subtracted from the compression test load data to determine the material response to the magnetic field. Tests were performed at a rate of 12 mm min−1 and the compressive modulus was calculated by determining the slope of a linear fit of the stress versus strain data from 2.5–7.5% strain.4.5 Adaptive gripper fabrication
The gripper is made from an HC MRE (Em = 200 kPa) cast into a 30 mL high form crucible. The uncured composite is placed under vacuum to remove residual hexanes. The material is then poured into the crucible and then checked for air inclusions. Then, the bulk of the material is poured out leaving a thin coating (similarly to a slipcasting process). The crucible is then immediately set upside down on the glass plate, which allows the excess material to flow down onto the plate creating a sealed bottom. The mold is then placed in a 40 °C oven and allowed to fully cure for at least 45 min.Author contributions
E. J. B., E. T. W., N. L., and M. D. B. designed research; E. J. B., E. T. W., and R. T. performed research; E. J. B., E. T. W., N. L., and M. D. B. analyzed data; E. J. B., E. T. W., N. L., and M. D. B. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support from the Office of Naval Research Young Investigator Program (YIP) (N000142112699) and by the Army Research Laboratory under cooperative agreement number W911NF-20-2-0039. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. This work was performed in part at the Nanoscale Characterization and Fabrication Laboratory, which is supported by the Virginia Tech National Center for Earth and Environmental Nanotechnology Infrastructure (NanoEarth), a member of the National Nanotechnology Coordinated Infrastructure (NNCI), supported by NSF (ECCS 1542100 and ECCS 2025151).References
- A. Mohammadi Nasab, S. Sharifi, S. Chen, Y. Jiao and W. Shan, Adv. Intell. Syst., 2021, 3, 2000166 CrossRef.
- M. A. Karimi, V. Alizadehyazdi, B.-P. Busque, H. M. Jaeger and M. Spenko, 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft), 2020, pp. 291–296.
- Y. Jiang, D. Chen, C. Liu and J. Li, Soft Rob., 2019, 6, 118–132 CrossRef PubMed.
- D. Hwang, E. J. Barron III, A. T. Haque and M. D. Bartlett, Sci. Rob., 2022, 7, eabg2171 CrossRef PubMed.
- J. W. Boley, W. M. Van Rees, C. Lissandrello, M. N. Horenstein, R. L. Truby, A. Kotikian, J. A. Lewis and L. Mahadevan, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 20856–20862 CrossRef CAS.
- A. L. Evenchik, A. Q. Kane, E. Oh and R. L. Truby, Annu. Rev. Mater. Res., 2023, 53, 225–251 CrossRef.
- T. Amadeo, D. Van Lewen, T. Janke, T. Ranzani, A. Devaiah, U. Upadhyay and S. Russo, Front. Robot. AI, 2022, 8, 731010 CrossRef PubMed.
- Y. Kim, H. Yuk, R. Zhao, S. A. Chester and X. Zhao, Nature, 2018, 558, 274–279 CrossRef CAS PubMed.
- Z. Xu, R. Hensleigh, N. J. Gerard, H. Cui, M. Oudich, W. Chen, Y. Jing and X. R. Zheng, Addit. Manuf., 2021, 47, 102321 CAS.
- L. T. Gaeta, K. J. McDonald, L. Kinnicutt, M. Le, S. Wilkinson-Flicker, Y. Jiang, T. Atakuru, E. Samur and T. Ranzani, Soft Matter, 2023, 19, 2623–2636 RSC.
- H. Dong and G. M. Walker, Smart Mater. Struct., 2012, 21, 042001 CrossRef.
- T. L. Buckner, M. C. Yuen, S. Y. Kim and R. Kramer-Bottiglio, Adv. Funct. Mater., 2019, 29, 1903368 CrossRef CAS.
- B. E. Schubert and D. Floreano, RSC Adv., 2013, 3, 24671–24679 RSC.
- I. De Falco, G. Gerboni, M. Cianchetti and A. Menciassi, J. Visualized Exp., 2015, 105, e53118 Search PubMed.
- A. Jiang, T. Ranzani, G. Gerboni, L. Lekstutyte, K. Althoefer, P. Dasgupta and T. Nanayakkara, Soft Rob., 2014, 1, 192–201 CrossRef.
- V. Wall, R. Deimel and O. Brock, 2015 IEEE International Conference on Robotics and Automation (ICRA), 2015, pp. 252–257.
- M. R. Jolly, J. D. Carlson, B. C. Muñoz and T. A. Bullions, J. Intell. Mater. Syst. Struct., 1996, 7, 613–622 CrossRef CAS.
- M. Moreno, J. Gonzalez-Rico, M. Lopez-Donaire, A. Arias and D. Garcia-Gonzalez, Composites, Part B, 2021, 224, 109148 CrossRef CAS.
- L. Wang, Y. Yang, Y. Chen, C. Majidi, F. Iida, E. Askounis and Q. Pei, Mater. Today, 2018, 21, 563–576 CrossRef CAS.
- W. Shan, T. Lu and C. Majidi, Smart Mater. Struct., 2013, 22, 085005 CrossRef CAS.
- C. B. Haverkamp, D. Hwang, C. Lee and M. D. Bartlett, Soft Matter, 2021, 17, 1731–1737 RSC.
- M. Manti, V. Cacucciolo and M. Cianchetti, IEEE Rob. Autom. Mag., 2016, 23, 93–106 Search PubMed.
- J. M. Ginder, M. E. Nichols, L. D. Elie and S. M. Clark, Smart structures and materials 2000: smart structures and integrated systems, 2000, pp. 418–425 Search PubMed.
- H. Böse, T. Gerlach and J. Ehrlich, J. Intell. Mater. Syst. Struct., 2021, 32, 1550–1564 CrossRef.
- A. K. Bastola and M. Hossain, Composites, Part B, 2020, 200, 108348 CrossRef CAS.
- V. Ramachandran, M. D. Bartlett, J. Wissman and C. Majidi, Extreme Mech. Lett., 2016, 9, 282–290 CrossRef.
- N. Lazarus, C. D. Meyer, S. S. Bedair, G. A. Slipher and I. M. Kierzewski, ACS Appl. Mater. Interfaces, 2015, 7, 10080–10084 CrossRef CAS.
- L. Cestarollo, S. Smolenski and A. El-Ghazaly, ACS Appl. Mater. Interfaces, 2022, 14, 19002–19011 CrossRef CAS.
- E. J. Barron III, R. S. Peterson, N. Lazarus and M. D. Bartlett, ACS Appl. Mater. Interfaces, 2020, 12, 50909–50917 CrossRef.
- K. Hong, M. Choe, S. Kim, H.-M. Lee, B.-J. Kim and S. Park, Polymers, 2021, 13, 2407 CrossRef CAS PubMed.
- M. Ralphs, W. Kong, R. Y. Wang and K. Rykaczewski, Adv. Mater. Interfaces, 2019, 6, 1801857 CrossRef.
- J. M. Ginder, M. E. Nichols, L. D. Elie and J. L. Tardiff, Smart Structures and Materials 1999: Smart Materials Technologies, 1999, pp. 131–138 Search PubMed.
- X.-M. Dong, Y. Miao, C.-R. Liao and W.-M. Chen, Trans. Nonferrous Met. Soc. China, 2009, 19, s611–s615 CrossRef CAS.
- J. M. Ginder, W. F. Schlotter and M. E. Nichols, Smart structures and materials 2001: damping and isolation, 2001, pp. 103–110 Search PubMed.
- J. Bernat, P. Gajewski, R. Kapela, A. Marcinkowska and P. Superczyńska, Sensors, 2022, 22, 2757 CrossRef.
- D.-S. Choi, T.-H. Kim, S.-H. Lee, C. Pang, J. W. Bae and S.-Y. Kim, ACS Appl. Mater. Interfaces, 2020, 12, 44147–44155 CrossRef CAS.
- Y. Tsugami, T. Barbié, K. Tadakuma and T. Nishida, 2017 11th Asian control conference (ASCC), 2017, pp. 778–783.
- J. A. Carpenter, T. B. Eberle, S. Schuerle, A. Rafsanjani and A. R. Studart, Adv. Intell. Syst., 2021, 3, 2000283 CrossRef.
- A. B. Croll, N. Hosseini and M. D. Bartlett, Adv. Mater. Technol., 2019, 4, 1900193 CrossRef.
- P. Zając, J. Kaleta, D. Lewandowski and A. Gasperowicz, Smart Mater. Struct., 2010, 19, 045014 CrossRef.
- S. R. Khimi and K. L. Pickering, Composites, Part B, 2015, 83, 175–183 CrossRef CAS.
- P. Testa, R. W. Style, J. Cui, C. Donnelly, E. Borisova, P. M. Derlet, E. R. Dufresne and L. J. Heyderman, Adv. Mater., 2019, 31, 1900561 CrossRef PubMed.
- R. K. Shuib, K. L. Pickering and B. R. Mace, J. Appl. Polym. Sci., 2015, 132, 41506 CrossRef.
- B. Dyniewicz, J. M. Bajkowski and C. I. Bajer, Mech. Syst. Signal Process., 2015, 60, 695–705 CrossRef.
- I. Bica, E. Anitas and L. Averis, J. Ind. Eng. Chem., 2015, 28, 86–90 CrossRef CAS.
- M. Yu, S. Qi, J. Fu, P. Yang and M. Zhu, Smart Mater. Struct., 2015, 24, 045009 CrossRef.
- T. Komatsuzaki and Y. Iwata, Shock Vib., 2015, 2015, 676508 Search PubMed.
- Y. Wang, X. Zhang, J. Oh and K. Chung, Smart Mater. Struct., 2015, 24, 095006 CrossRef.
- X. Qiao, X. Lu, X. Gong, T. Yang, K. Sun and X. Chen, Polym. Test., 2015, 47, 51–58 CrossRef CAS.
- S. S. Kang, K. Choi, J.-D. Nam and H. J. Choi, Materials, 2020, 13, 4597 CrossRef CAS PubMed.
- M. Yu, P. Yang, J. Fu, S. Liu and S. Qi, Smart Mater. Struct., 2016, 25, 085046 CrossRef.
- Y. Tong, X. Dong and M. Qi, Smart Mater. Struct., 2017, 26, 025023 CrossRef.
- A. Dobroserdova, M. Schümann, D. Borin, E. Novak, S. Odenbach and S. Kantorovich, Soft Matter, 2022, 18, 496–506 RSC.
- J. Silva, C. Gouveia, G. Dinis, A. Pinto and A. Pereira, Composites, Part B, 2022, 243, 110125 CrossRef CAS.
- Y. Zhou, S. Jerrams, A. Betts, G. Farrell and L. Chen, Mater. Des., 2015, 67, 398–404 CrossRef CAS.
- J. Zhang, Y. Qiao, M. Zhang and P. Zhai, Smart Mater. Struct., 2022, 31, 095010 CrossRef.
- A. Boczkowska, S. F. Awietjan and R. Wroblewski, Smart Mater. Struct., 2007, 16, 1924 CrossRef CAS.
- A. Bastola, V. Hoang and L. Li, Mater. Des., 2017, 114, 391–397 CrossRef CAS.
- M. Ashtiani, S. Hashemabadi and A. Ghaffari, J. Magn. Magn. Mater., 2015, 374, 716–730 CrossRef CAS.
- G. Bossis, S. Lacis, A. Meunier and O. Volkova, J. Magn. Magn. Mater., 2002, 252, 224–228 CrossRef CAS.
- P. Testa, B. Chappuis, S. Kistler, R. W. Style, L. J. Heyderman and E. R. Dufresne, Soft Matter, 2020, 16, 5806–5811 RSC.
- A. Boczkowska and S. Awietjan, WIT Trans. Eng. Sci., 2011, 72, 263–274 CAS.
- Z. Varga, G. Filipcsei and M. Zrínyi, Polymer, 2006, 47, 227–233 CrossRef CAS.
- Y. Li, J. Li, W. Li and H. Du, Smart Mater. Struct., 2014, 23, 123001 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lp00109a |
| This journal is © The Royal Society of Chemistry 2023 |