Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural effects of incorporating Cu+ and Cu2+ ions into silicate bioactive glasses using molecular dynamics simulations
M.
Soorani
 *,
E.
Mele
*,
E.
Mele
 and
J. K.
Christie
and
J. K.
Christie

Department of Materials, Loughborough University, Loughborough, LE11 3TU, UK. E-mail: M.Soorani@lboro.ac.uk
First published on 17th March 2023
Abstract
Copper oxide containing bioactive glasses have drawn attention because of their unique properties as biomaterials for targeted tissue engineering applications. This is due to their ability to act as stimulants for new tissue formation. In the present manuscript, we aim to study the structure and properties of copper incorporated bioactive glass 45S5 using molecular dynamic simulations using newly parameterized interaction potentials for Cu+–O and Cu2+–O oxides. The role of copper oxides in 45S5 glasses was elucidated by studying a series of glasses with compositions 46.1 mol% SiO2, 26.9 mol% CaO, 24.4 mol% Na2O, and 2.6 mol% P2O5 in which CuO (10, 15, and 20 mol%) was progressively substituted for Na2O. The local environment of Cu+ and Cu2+ ions within the glasses was explored and the ratio was calculated theoretically. The findings indicate that both Cu+ ions with a three-fold coordination and Cu2+ ions coordinated by six oxygen atoms participate in the silica network as network modifiers. The impact of Cu+ and Cu2+ ions on the overall glass network connectivity was likely to be small. The ratio of Cu+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cutotal has been found to increase with an increase in the content of CuO in the structure of the studied glasses. In the computational study of the glasses, the network connectivity was used to predict their bioactivity. From our study, it was concluded that incorporating Cu+ and Cu2+ ions in the structure of 45S5 glasses favours the bioactivity of these glasses.
Cutotal has been found to increase with an increase in the content of CuO in the structure of the studied glasses. In the computational study of the glasses, the network connectivity was used to predict their bioactivity. From our study, it was concluded that incorporating Cu+ and Cu2+ ions in the structure of 45S5 glasses favours the bioactivity of these glasses.
1. Introduction
Copper (Cu) as a trace mineral has been investigated for its therapeutic potential in the human body since it is a necessary micro-nutrient in maintaining body haemostasis.1,2 The amount of copper in humans depends on the gender, weight, and age.3 An individual with a body weight of 70 kg has about 110 mg of copper.4 Half of this amount is found in the bones and muscles while the rest is taken up by the skin, bone marrow, liver and brain.5 Copper exists in its reduced (Cu+ or cuprous) state inside cells.6 This makes it a suitable cofactor in different biological processes such as energy metabolism and anti-oxidant activity. Trace metals like this are referred to as biologically active. Free copper ions are harmful and toxic to the cells and because of this reason, the uptake, distribution and haemostasis of copper are highly regulated.7 Copper also plays an important role in the strength of skin, blood vessels, epithelial cells, and connective tissue, and participates in a wide variety of catalytic functions and molecular interactions throughout the body.8 Copper and its compounds have mostly been studied for their efficacy against pathogenic bacteria, microbes, viruses, and deadly fungal species.9,10 Copper is an essential element in maintaining the production of hemoglobin, myeline, and melanin as well as in regulating the function of the thyroid gland and it acts as an antioxidant and neutralizes free radical damage.8 Gene expression is also affected by copper-dependent enzymes.11Copper at a low dose (in a range up to 8.66 mg kg−1) is counted as an essential nutrient for the body.12,13 An excess amount of this element, beyond the range of human tolerance, would be toxic to the biological tissue and even lethal at doses between 50 and 54.4 mg kg−1 due to the production of free radicals that cause toxicity and inflammatory effects.13,14
The invention of bioactive glass (BG) paved the way for modern biomaterial-oriented regenerative medicine.15 From a tissue engineering point of view, BGs are excellent candidates in biological tissue regeneration and reconstruction as their physicochemical, mechanical, and biological features are comparable to those of biological tissue.16,17 Moreover, as potent materials they can be drawn into different forms such as powder, fibers, and 3D porous scaffolds which enhance the regeneration process of both hard and soft tissues.1 Cu-doped bioactive glasses (BGs) have also been studied for their applications in the synthesis of scaffolds in tissue engineering.13 Cu-containing silicate-based glasses can be beneficial both in hard tissue and soft tissue engineering as they are anti microorganisms, and they can prevent infection. They are also capable of promoting cell differentiation. Silicate-based bioactive glasses (SiBGs) are amorphous materials which are highly reactive under physiological conditions.18,19 SiBGs can bond with both soft tissue and bone.20 Silicate-based glasses with a wide range of formulations are characterized by a network structure of SiO4 polyhedra with some orthophosphate (PO4) substitution.21 The bioactivity of the glasses depends on the amount of network formers' oxide in glass formulations.22 The amount of bridging oxygens (BOs) in each SiO4 tetrahedron determines the bonding environment of network formers, and the overall network connectivity (NC) of the glass. In general, higher bioactivity is associated with a lower NC which favours the release of soluble silica fragments to the solution.23 To impart a particular property to SiBGs, various amounts of alkali and alkali-earth cations such as CaO and Na2O can be incorporated in the silicate network.24 These cations are known as network modifiers that can break some of the Si–O–Si bonds, leading to the formation of non-bridging oxygen atoms (NBOs),24,25 and depolymerizing the silicate network.23 The coordination environment, the structural arrangement, and stability of network modifier cations are crucial for the migration mechanism of these ions within the glass structure.26,27 These key structural factors will subsequently determine the dissolution rate of the SiBGs.23 The behaviour of different cations and anions was considered in Dietzel's structural model which was an extension to the approach of Zachariasen. Depending on the elements' respective charges, Dietzel was able to define the connection between the size and polarisability of the constituent ions by characterising elements based on Zachariasen's method. He introduced a scheme where the elements in the glass are classified based on their field strength (FS).28 Based on his definition of field strength, the elements in the glass can be network formers, glass modifiers, or intermediates. He described the field strength as the interacting force between the ionic charge (Z) and the ionic radius between the oxide ions (a)(Z/a−2 (Å−2)). In his proposed model, the tendency for glass formation increases with increasing field strength.29
Copper oxides can be present in glass in both Cu+ and Cu2+ oxidation states during thermal treatments,30 but Cu2+ is the more common oxidation state.31 However, exactly how Cu incorporates into the BG matrix at the atomic level is still poorly understood. The oxidation state and the introduction of an excessive amount of Cu into BG structures directly impact their performance in terms of bioactivity.32,33 In addition, the different oxidation states of Cu regulate various biological effects. For instance, Cu+ ions show considerably more antibacterial effects than Cu2+ ions under laboratory conditions.1,6,34,35 It is also reported that Cu+ ions show high antimicrobial potency which is achieved at very low surface concentrations of copper (∼5%).36 Toxicity and killing pathogens by copper-containing materials occur through rapid membrane damage upon the entry of copper ions into cells and degradation of DNA.37 Both Cu+ and Cu2+ oxidation states play an important role in homeostasis in human cells, but it is Cu+ that is transported by the major uptake pathway.38 It has been found that no adverse effects on glass bioactivity are caused by the incorporation of Cu into the BG network.39,40 Toxicological effects of Cu-containing BGs on murine cell macrophages have been studied and it was found that it would not cause toxic effects at low concentrations (in the range of up to 0.98 μg mL−1 or 2.5 mol%).41
Previous studies typically claim that Cu2+ ions are responsible species for the antipathogenic effect, and the importance of Cu+ ions was underestimated.42–58 Sometimes, the oxidation state of copper is not investigated44,51 or not investigated with appropriate techniques.
Several analytical techniques can be used to identify the ratio of the oxidation state of different species in solids, including X-ray photoelectron spectroscopy (XPS),59 electron energy loss spectroscopy (EELS),60 X-ray absorption spectroscopy (XAS),61 Raman spectroscopy,62 and ultraviolet/visible/infrared (UV/vis/IR) spectroscopy.63 XPS and EELS are perhaps the most widely used tools in materials characterization.64 The physicochemical properties of the BGs, including the oxidation state of Cu, depend on the selected synthesis method of glasses.65 Melt-quenching,66 the sol–gel method,67 and ion-exchange39 are effective methods for the production of Cu-containing BGs. It is expected that the two principal oxidation states of Cu exist in the samples synthesized using either the sol–gel method or the melting method, where thermal treatments above 500 °C are applied as reported by Mekki et al.30
More research must therefore be carried out in order to understand the effective use of Cu-containing BGs, because there are no substantial details about the fundamental underlying mechanism of bioactivity due to the lack of information about their atomistic structure such as the coordination environment, the NBO of e.g. network modifier cations and NC of the glasses. The relevant structural information to the glass bioactivity can be well understood and tailored using modern computational techniques such as molecular dynamics (MD) simulations, which in turn unveil other relevant effects.23,68 MD methods are powerful tools in materials sciences to study amorphous materials and glasses with multiple atomic species,69 and can be used as a complement to conventional experiments.70 Besides the experimental effort, the bioactivity of glasses and the degradation rate can be understood using MD simulations.71 The split network models or NBO and NC can be used to predict the glass bioactivity using MD simulations as effective tools to study glasses. To represent the polarisability of the oxide ions, a shell-model is incorporated into the model.72 The shell-model is crucial to represent the medium-range structure properly and hence the bioactivity.73 However, computer modeling of glasses has its own limitations as the time and special scales are largely different between the computer world and the laboratory-based experiments. For example, a much slower cooling rate is needed for the generation of a glass such as 1000 K s−1 in the real world, whereas ultrafast cooling rates are used in MD simulation due to the computation time, typically less than a microsecond.74 Moreover, the new algorithms should be developed to improve computational methods in better representing laboratory glasses.75
The method and the condition of glass preparation incorporating Cu ions in the glass structure determines the ratio of Cu+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu2+ ions in the glass.76 In particular, the occurrence of both Cu+ and Cu2+ in the glass depends on a set of temperature, duration and chemical factors in the melt.77 For example, using CuCl or CuO salts to incorporate Cu ions into the silicate-based glass via a melt-quenching method under a nitrogen atmosphere, most ions (around 80–90%) are Cu+ ions in the glass.30,78 The ratio of Cu2+
Cu2+ ions in the glass.76 In particular, the occurrence of both Cu+ and Cu2+ in the glass depends on a set of temperature, duration and chemical factors in the melt.77 For example, using CuCl or CuO salts to incorporate Cu ions into the silicate-based glass via a melt-quenching method under a nitrogen atmosphere, most ions (around 80–90%) are Cu+ ions in the glass.30,78 The ratio of Cu2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cutotal in Cu-containing phosphate-based glasses was studied by Mugoni et al.,79 and their results were included in the modelling approach by Broglia et al.,80 as we discuss later in the Results section.
Cutotal in Cu-containing phosphate-based glasses was studied by Mugoni et al.,79 and their results were included in the modelling approach by Broglia et al.,80 as we discuss later in the Results section.
We believe that the importance of different oxidation states of Cu in BGs has been underestimated, where the presence of cations in multiple oxidation states can promote different structural changes.81 The main focus of this paper is to investigate the influence of Cu substitution with both oxidation states in silicate-based glasses at the atomistic scale through the development of a polarisable force field.72 To the best of our knowledge, this is the first time that the effect of Cu+ and Cu2+ ions simultaneously in the BGs is studied via classical MD simulations. We used classical MD to simulate several compositions of copper-containing silicate-based bioactive glasses. Following development and validation of interatomic potentials for Cu+–O and Cu2+–O, we describe the local environment of the copper atoms, in terms of the pairwise radial distribution function (RDF),82 coordination number,23 field strength,28 network connectivity83 and bond length. The effect of copper incorporation on the bioactivity of silicate-based glasses is discussed and concluded.
2. Development of interatomic potentials for Cu+–O and Cu2+–O
Due to the lack of accurate parameters that describe the Cu+–O and Cu2+–O interactions simultaneously, an accurate interatomic potential was developed to take into account the inclusion of both oxidation states of copper ions in the glass structure. In our classical MD simulations, the interatomic interactions are described by the Born model of solids using full-charge pair potentials. In addition to the electrostatic interactions between ions, the short-range interactions are modelled using the Buckingham potential: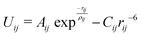 | (1) |
| Uij = D[1 − exp(−b(rij−r0))]2−D | (2) |
Cu+–O and Cu2+–O interatomic Buckingham potential parameters were derived using already existing potentials developed for silicate-based glasses. The existing potential parameters are listed in Table 1. The initial crystallographic data were collected from the Inorganic Crystal Structure Data file (ICSD) as a part of the Chemical Data Service at Daresbury.86 Two crystal structures, AlCuO2 and KCuO, were selected to reproduce the potential interaction parameters between Cu+–O interactions. Na2CuSi3O8 and CaCuO2 crystal structures were used for empirical fitting of Cu2+–O interactions.86 The transferability and reliability of the potentials were improved through a multi-structure empirical fitting.87,88 The General Utility Lattice Program (GULP) was used for energy minimisation.89,90 It is crucial to use accurate potentials in order to reproduce experimental data so that the studied structures can be predicted using those potentials when there is no experimental data available. In Table 2 the lattice parameters of the crystalline structures to which the potential was fitted are given. In this system, the accuracy was determined by averaging all unit cell parameters to less than 3% of error between the experimental data and the optimised lattice structure (Table 3). The optimised potential parameters for Cu+–O and Cu2+–O interactions were used for the subsequent MD simulations.
| Pairs | Å (eV) | ρ (Å) | C (eV Å6) |
|---|---|---|---|
| Na–Os | 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465.3453 465.3453 |
0.193931 | 0.0 |
| K–Os | 1000.30 | 0.36198 | 10.5690 |
| Si–Os | 1283.910 | 0.320520 | 10.66158 |
| Os–Os | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 764 764 |
0.149 | 27.88 |
| Ca–Os | 2152.3566 | 0.309227 | 0.09944 |
| P–Os | 1020.00 | 0.343220 | 0.03 |
| Triplets | (k3b) (eV rad−2) | θ (deg) |
|---|---|---|
| Os–Si–Os | 2.097 | 109.47 |
| Os–P–Os | 3.3588 | 109.47 |
| Os–Cu2+–Os | 4.933 | 90.0 |
| Core–shell | Core (e) | Shell (e) | k cs (eV Å−2) |
|---|---|---|---|
| Oc–Os | +0.8482 | −2.8482 | 74.92 |
| Pairs | Buckingham | ||
|---|---|---|---|
| Å (eV) | ρ (Å) | C (eV Å6) | |
| Cu+–Os | 608.5000 | 0.275 | 0.0 |
| Cu2+–Os | 3939.302102 | 0.285709 | 0.0 |
| Pair | Morse | ||
|---|---|---|---|
| D (eV) | β (Å−1) | r 0 (Å) | |
| Cu2+–Os | −0.10922 | 1.359548 | 3.273 |
| Materials | Parameters | Calc. | Exp. | Diff. (%) |
|---|---|---|---|---|
| K4Cu4O4 | a, b | 9.505 Å | 9.35 Å | 1.66 |
| c | 5.524 Å | 5.44 Å | 1.56 | |
| α, β | 90.0° | |||
| γ | 90° | |||
| AlCuO2 | a, b | 2.867 Å | 2.920 Å | 1.85 |
| c | 16.981 Å | 16.517 Å | −2.73 | |
| α, β | 90.0° | |||
| γ | 120° | |||
| CaCuO2 | a, b | 3.856 Å | 3.935 Å | 2.06 |
| c | 3.181 Å | 3.254 Å | 2.31 | |
| α, β, γ | 90.0° | |||
| Na8Cu4Si12O32 | a | 7.932 Å | 7.834 Å | 1.24 |
| b | 10.329 Å | 10.232 Å | −0.93 | |
| c | 9.601 Å | 9.783 Å | 1.90 | |
| α, γ | 90.0° | |||
| β | 105.6° | 108.9° | 2.31 |
3. Simulation details
The DLPOLY code93 was used to perform classical MD simulations of different copper-containing silicate-based glass compositions. The precise compositions and densities are given in Table 4. In the current study, the compositions were based on the structure of 45S5 BGs with compositions of 46.1 mol% SiO2, 26.9 mol% CaO, 24.4 mol% Na2O, and 2.6 mol% P2O5 with the Na2O being gradually substituted by CuO until 20 mol%. The compositions all share the same O/Si ratio, and hence network connectivity. By considering both the oxidation states of Cu, the ratio of Cu+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu2+ was included in the simulation in order to obtain an accurate simulation of the glass structure, as observed experimentally.30 The percentage of the ratio derived from experimental X-ray photoelectron spectroscopy30 performed by Mekki et al. on silicate-based compositions was used as the starting point to partition the ratio between Cu+ and Cu2+ ions. They reported amounts of Cu+ = 89% and Cu2+ = 10.3% in those glass samples.30 Since the ratio of Cu2+
Cu2+ was included in the simulation in order to obtain an accurate simulation of the glass structure, as observed experimentally.30 The percentage of the ratio derived from experimental X-ray photoelectron spectroscopy30 performed by Mekki et al. on silicate-based compositions was used as the starting point to partition the ratio between Cu+ and Cu2+ ions. They reported amounts of Cu+ = 89% and Cu2+ = 10.3% in those glass samples.30 Since the ratio of Cu2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cutotal is undetectable for compositions with less than 14 mol% Cu2O,30 the composition with 10 mol% of CuO was not simulated in the second batch. The overall charge neutrality of the entire system was maintained by correcting the number of oxygen ions.80
Cutotal is undetectable for compositions with less than 14 mol% Cu2O,30 the composition with 10 mol% of CuO was not simulated in the second batch. The overall charge neutrality of the entire system was maintained by correcting the number of oxygen ions.80
| Sample ID | SiO2 | Na2O | CaO | Cu+ (mol%) | Cu2+ | P2O5 | Density (g cm−3) |
|---|---|---|---|---|---|---|---|
| 1CuBG10 | 46.1 | 14.4 | 26.9 | 10.0 | 0.00 | 2.6 | 3.2069 |
| 1CuBG15 | 46.1 | 9.4 | 26.9 | 15.0 | 0.00 | 2.6 | 3.2420 |
| 1CuBG20 | 46.1 | 4.4 | 26.9 | 20.0 | 0.00 | 2.6 | 3.2771 |
| 2CuBG15 | 46.1 | 9.4 | 26.9 | 13.5 | 1.5 | 2.6 | 3.2420 |
| 2CuBG20 | 46.1 | 4.4 | 26.9 | 18.4 | 1.6 | 2.6 | 3.2771 |
To calculate an accurate ratio of Cu+ and Cu2+ ions in each sample, part of the Cu+ ions were changed into Cu2+ ions manually until an equilibrated system was obtained. In fact, the ratio of Cu+/Cu2+ ions was determined by finding a system in which energy is minimised. Because of this reason, the total ratio of Cu+ and Cu2+ ions varies in each glass composition, depending on the mol% of other ions in the system.
For all these compositions, the initial configuration was set up by placing 2000 atoms independently and randomly into a cubic periodic simulation box with a constant size subject only to the constraint that no two atoms were closer than about 80–90% of their expected interatomic separation. This gives the appropriate density for the compositions and prevents unphysical starting configurations. The densities of the studied compositions were obtained theoretically using a global model for calculating the glass density at room temperature published by Fluegel,94 and the numbers of atoms are given in Table 5.
| Sample ID | O | Si | Na | Ca | Cu+/Cu++ | P |
|---|---|---|---|---|---|---|
| 1.5pt1CuBG10 | 1102 | 325 | 188 | 190 | 156/0 | 36 |
| 1CuBG15 | 1102 | 325 | 132 | 190 | 212/0 | 36 |
| 1CuBG20 | 1102 | 325 | 62 | 190 | 282/0 | 36 |
| 2CuBG15 | 1108 | 327 | 134 | 191 | 190/11 | 36 |
| 2CuBG20 | 1108 | 327 | 62 | 191 | 256/14 | 36 |
Following an instantaneous relaxation at zero temperature, each model was cooled in a series of runs in NVT ensembles for 50 ps, decreasing the temperature in the following order at a cooling rate of 4 K ps−1: 2000 K, 1500 K, 1000 K, 650 K, and 300 K, ensuring that the system reached thermal equilibrium for each of the temperatures. The timestep was 0.2 fs, where the cut-offs for short-range potentials and electrostatic interactions were 8 Å and 12 Å, respectively. The Ewald summation method was applied to evaluate the electrostatic force in the system. All data are taken from averages of three independent simulations for each composition. The cooling rates for the classical MD are significantly higher than the ones used in typical experimental rates.95 This is because a short time scale is used in computer simulation that makes it impossible to simulate the quenching of the system with small cooling rates,96 but nonetheless the structure is known to be converged even at these cooling rates.97,98
4. Results
In the current study, the structures of the Cu-containing silica glasses are characterised, while the comparisons between Cu+ and Cu2+ were carried out to elucidate the differences. The effect of Cu+ and Cu2+ in substitution with Na ions on the structure of 45S5 bioglasses will also be discussed for the first time to the best of our knowledge.Fig. 1 shows the partial pair-correlation function g(r) as a function of bond length r for Cu+–O interactions in 1CuSiBG10, 1CuSiBG15, and 1CuSiBG20 compositions. The bond lengths are determined as the first peak of g(r) and coordination numbers are calculated using the information from g(r). As can be seen (Fig. 1), the Cu+–O bond length is about 1.71 Å for all compositions with just different intensities. The cut-off of 2.1 Å was used to calculate the coordination of Cu+–O interactions in 1CuSiBG15&20. The Cu+–O interaction exhibits short bond lengths (Fig. 1) in 2CuSiBG15 and 2CuSiBG20 compositions, at about 1.68 Å.
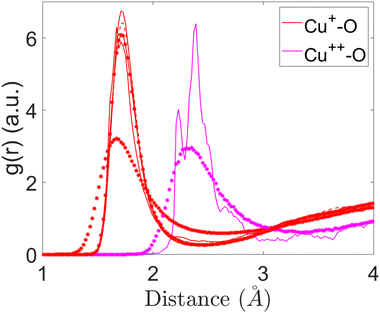 | ||
| Fig. 1 Partial pair-correlation functions of Cu+–O and Cu2+–O interactions for the studied compositions. | ||
Fig. 1 also illustrates the comparison of Cu2+–O interactions between 2CuSiBG15 and 2CuSiBG20 compositions. The Cu2+–O average bond distance is longer than that of Cu+–O in all compositions, but with a different pattern of bonding. The Cu2+–O interaction exhibits a bond length of 2.33 Å and the peak is broader in the 2CuSiBG20 composition. Whereas, the oxygen neighbours of Cu2+ are found at two different distances of 2.33 Å and 2.39 Å in the composition with a lower concentration of Cu (15 mol%). Table 6 presents the mean of bond length and coordination numbers for each Cu oxide.
| Sample ID | Oxide | Bond length (Å) | CN | ||
|---|---|---|---|---|---|
| Total | BO | NBO | |||
| 1CuSiBG10 | Cu+ | 1.71 | 3.0 | 0.2 | 2.8 |
| 1CuSiBG15 | Cu+ | 1.71 | 2.9 | 0.1 | 2.8 |
| 1CuSiBG20 | Cu+ | 1.71 | 2.8 | 0.1 | 2.7 |
| 2CuSiBG15 | Cu+ | 1.67 | 3.0 | 0.1 | 2.9 |
| 2CuSiBG20 | Cu+ | 1.69 | 3.0 | 0.4 | 2.6 |
| 2CuSiBG15 | Cu2+ | 2.23–2.39 | 6.1 | 1.6 | 4.5 |
| 2CuSiBG20 | Cu2+ | 2.31 | 6.0 | 0.8 | 5.2 |
We identified another short-intermediate range structure in the glass due to the presence of Cu2+ ions which promotes the binding of Cu2+ ions to the glass network formers by relatively covalent bonds. This may produce P–O⋯Cu2+ or Si–O⋯Cu2+ bonds.80 We computed this for Cu2+ ions present in the studied compositions here. The results are presented in Table 7. From the results it can be seen that Si–O⋯Cu and P–O⋯Cu distances are approximately 3.19–3.73 Å.
| Sample ID | Si–O⋯Cu2+ (Å) | P–O⋯Cu2+ (Å) |
|---|---|---|
| 2CuSiBG15 | 3.73 ± 0.14 | 3.19 ± 0.19 |
| 2CuSiBG20 | 3.53 ± 0.14 | 3.47 ± 0.19 |
4.1. Cation coordination numbers
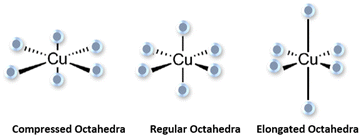
The coordination numbers of both Cu+ and Cu2+ cations were analysed and presented in Table 6. It was found that the CNs of Cu+ and Cu2+ ions change as a function of the oxidation state. The average CNs of Cu+–O and Cu2+–O were calculated to be 3.04 ± 0.27 and 6.05 ± 0.07, respectively. The CNs in Cu+ are lower than those in Cu2+ ions with a higher oxidation state, which has profound effects on bioactivity. The bond length also increases as the CN increases for the Cu2+ ions. As can be seen, the Cu+–O and Cu2+–O CNs do not differ drastically with the changing composition.Typical oxygen arrangements around Cu+ are shown in Fig. 2. Cu+ ions could be found coordinated by two and three oxygen atoms in the arrangement of linear and trigonal geometries, respectively. In all studied compositions, the geometry of Cu+–O is mainly trigonal with three oxygen atoms at a distance of about 1.68–1.71 Å. The coordination environment of Cu2+ ions are shown in molecular geometries as shown in Fig. 3 and as can be seen Cu2+ ions are surrounded by six oxygen atoms. The results show a complex with regular octahedral geometries (Fig. 3(a)) where the oxygen atoms are at the same distance from the Cu2+ central atom. A distorted octahedral geometry (Fig. 3(b)) has been observed for Cu2+ in composition with a lower Cu concentration where the oxygen atoms are surrounding the central atoms at two different distances based on the results from the pair-correlation function.
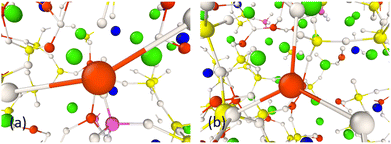 | ||
| Fig. 2 Snapshot of (a) linear and (b) trigonal structures of Cu+ ions in 1CuSiBG compositions. The colours are P (magneta), O (white), Ca (green), Na (navy), and Cu+ (red). | ||
4.2. Distribution of NBO
The percentage of NBO atoms in the first coordination shell of the cations in the studied compositions is shown in Fig. 4 and 5. This shows that in 1CuSiBGs10,15,20 compositions Cu+ has more NBO in its first coordination shell than Ca and Na ions. Also the percentage of NBO increases with an increase in the mol% of Cu2O in the glass as substituted with Na2O. The percentage of NBO provided by Ca is approximately similar in all compositions, and that for Na decreases. Table 8 shows the calculated field strength28 of cations based on their bond lengths in the 2CuSiBGs20 composition where both Cu+ and Cu2+ ions are present. From Table 8, Na has the smallest field strength (0.18) and Ca and Cu2+ show similar field strengths. It can be seen in Fig. 5, where the percentage distributions of NBO in the first coordination shell of Cu2 and Ca are about 85% which can explain the similarity of the these two ions' field strength. Thus, the three Ca, Na, and Cu+ cations fall into network modifier classes. From Fig. 5, increasing the mol% of Cu2O during substitution with Na2O decreases the percentage of NBO provided by Cu+ ions in the 2CuSiBG20 composition.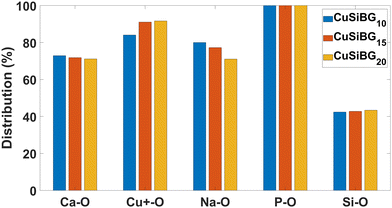 | ||
| Fig. 4 The percentage of NBO in the first coordination shell of all atoms in 1CuSiBGs10 1CuSiBGs15, and 1CuSiBGs20 compositions. | ||
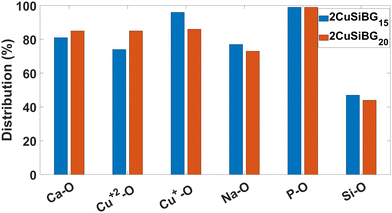 | ||
| Fig. 5 The percentage of NBO in the first coordination shell of all atoms in 2CuSiBGs15 and 2CuSiBGs20 compositions. | ||
| Ion | Interatomic distance (Å) | Field strength (Z/a2) (e Å−2) |
|---|---|---|
| Na+ | 2.34 | 0.18 |
| Cu+ | 1.69 | 0.35 |
| Cu2+ | 2.33 | 0.36 |
| Ca2+ | 2.33 | 0.36 |
| Si4+ | 1.61 | 1.54 |
| P5+ | 1.53 | 2.13 |
The bioactivity of the implemented glasses is controlled by the network connectivity of the glass as the key parameter.99 The network connectivity is defined as the average number of BO atoms per silicon atom.91 As can be seen from Fig. 4 and 5, the NBO atoms provided by Si–O interactions are similar in all studied compositions. It seems the substitution of Na for Cu+ and Cu2+ does not change the network connectivity, nor would we expect this, as the O/Si ratio is constant across all of our studied compositions.
5. Discussion
The present paper focusses on Cu-containing silicate-based glasses for use in tissue engineering. Previously, the addition of Cu+ ions into the basic BG composition has been only studied experimentally to investigate their effect on biological tissues.100 To the best of our knowledge, this is the first time that the effect of Cu+ and Cu2+ ions simultaneously in BGs is studied via classical MD simulations. The aim of the project is to describe precisely the effect of Cu ions in the structure of silicate-based BGs to understand the effects on the bioactivity. Based on the published studies, the Cu ions can occur in the glass in both Cu+ and Cu2+ oxidation states using conventional melting methods.30It was found by our study that Cu+ ions can be linear two-coordinated geometry and/or trigonal coordinated geometry within silicate-based BG (Fig. 2). Our findings show excellent agreement with the study conducted recently by Galante et al.,101 The Cu+–O bond shows a complicated bonding nature with both ionic and covalent characteristics.102 The charge transfer takes place from the Cu 4s shell to the 2p shell of O. The Cu 3d shells also interact with the 2p shell of O, but the net contribution is negligible. This is because the bonding and anti-bonding components cancel each other.103 The interaction between Cu and O was found to be predominantly covalent and the intermolecular O–O interaction is dominated by Coulomb repulsion. A linear structure can also be formed and this is due to the strong hybridisation of the O 2p shell with Cu 3d, forming bonding and anti-bonding linear combinations.104 From the results, it is clearly observable that linear coordinated Cu+ can be found in the system that contains a higher [Cu+/Cutotal] ratio, as we observe.
Our results (Fig. 3) show that Cu2+ exhibits octahedral geometries surrounded by six oxygen ions. Fig. 6 illustrates two prototypical Jahn–Teller distortions of an octahedral Cu2+ complex, compressed and elongated. The two distorted octahedral complexes are theoretically possible, but in practice elongated complexes are more common by far84 and no study has reported Jahn–Teller compressions for Cu2+. Also no noticeable linear structure can be seen in both 2Cu20SiBG and 2Cu15SiBG systems, where both Cu+ and Cu2+ were included. The electron distribution and the arrangement of atoms within the Cu2+ complexes are strongly affected by Jahn–Teller distortions.
The ratio between the ions is dependent on the glass composition. From the results, the coordination environment for Cu+ is predominantly 3 and that for Cu2+ is 6. In 1992, Kamiya et al. studied copper-containing alumino-silicate based glasses with a CuO concentration of 20 wt% and reported a coordination number of 2 for Cu+ and 4 for Cu2+.76 Later on in 2012, Silvestri et al. conducted a similar study using the X-ray Absoption Spectroscopy (XAS) technique and confirmed the results in Kamiya's study.105 Another study was performed recently in 2019 by Grund et al.106 to investigate the Cu+ and Cu2+ coordination environments in mixed alkali-lime-silicate glasses using X-ray and UV-Vis-NIR absorption spectroscopy. It was concluded that Cu+ is coordinated by two oxygen ions, whereas Cu2+ has a coordination of six oxygen ions.76,105,106 However, according to Grund et al., it is unlikely that all Cu+ ions are coordinated in a linear way with oxygen ions in amorphous materials such as glasses. Therefore, it is likely that Cu+–O coordination with a coordination number of three, as we observed, also occurs, which was neglected in these studies. The findings from our study using the MD method proves that Cu+ can be coordinated by two and three oxygen ions within the glass systems.
For both Cu+ and Cu2+, previous experiments have reported a broad range of bond lengths, with which our results are consistent. Previous studies reported a distance of 1.79–2.32 Å for Cu+–O in crystalline Cu2O.101,105,107–112 It was found that the distance between Cu+–O interactions is slightly shorter in crystalline systems than in glassy systems. In the present study, it was found that the Cu+–O interaction with a distance in the range of 1.68–1.71 Å is slightly shorter than all the mentioned investigations of Cu in glass. Three oxygen atoms at 1.71 Å gives rise to trigonally coordinated Cu+ atoms in 1CuSiBG10,15,20 compositions, whereas the primary shorter Cu+–O bond length is associated with a similar coordination in 2CuSiBG15,20 compositions. Cu2+ atoms were found to be coordinated by six oxygen atoms in an octahedral environment with the distance ranging between 2.23 Å and 2.39 Å. When an octahedral complex is distorted towards an elongated octahedron, two longer axial bonds and four equatorial shorter bonds are expected in the complex.84 The two axial Cu2+–O interactions of 2.1–2.9 Å have been reported as the most common bond length.113 A bond length of 2.4 Å has also been reported for axial interactions.84 The axial interaction in the range of 2.4–2.9 Å is considered as weaker, secondary, and predominantly electrostatic in nature.84 In addition, any interaction longer than 2.8 Å is considered as a van der Waals interaction only.84 In 2019, another study reported a bond length in the range of 1.89–1.91 Å for the equatorial Cu2+–O interactions in the glass compositions.106 In the same study the bond distances ranging from 2.20 to 2.24 Å have been reported for the Cu2+–O axial interactions. In the present study a sharp peak around 2.32 Å for Cu2+–O interactions in the 2Cu15SiBG composition can be associated with an axial bond length. Thus, in silicate-based BGs, Cu2+–O distances are shorter than those interactions in crystalline systems. However, it was also shown by the Mössbauer spectroscopy method that the coordination number and bond length of copper ions in silicate-based glasses depends on the composition.114
From the results presented in Fig. 4 and 5, it can be seen that the amount of Si-NBO bonding in the glass structure is within the range from 42 to 44% in all compositions. From this, it is assumed that the glass network connectivity remains unchanged by adding Cu+ and Cu2+ ions into the glass. The polarizability, mobility due to charges on ions, field strength, and concentration of ions within the BG structures are the key factors in determining the location and distribution of cations in the glass network. The size of ions are less important when the ions are replaced with the ones with similar ionic radii. However, the charge differences between the cations determine their distributions in the glass structure.115
When a melt of Cu2+ salt is used for implanting Cu into the glass, the Cu2+ ions initially are predominantly incorporated into glass. Then, the ions are reduced partially into their Cu+ state due to the singly charged vacancies of alkali ions in the glass network.116 It is likely that by increasing the concentration of divalent Cu salt, fewer Cu2+ ions will tend to be located near lone electron pairs of NBO atoms. From our results, the Cu2+ ions are assumed to form four short ionic bonds and two long polarized covalent bonds. In this case, the equatorial Cu2+–O bond length turns out to be similar to that of Cu+–O (2.23 Å).106 Based on the results (Table 6) for the 2Cu15SiBG composition, about two (1.6) of the six oxygen atoms around Cu2+ can be BO and the rest form NBO. Cu2+ ions with a higher charge than Cu+ in the glass network promoted the formation of a short-intermediate range structure (Table 7) and produced relatively covalent P–O–Cu2+ bonds, leading to more BO arrangements in the glass.117 It also causes a reduction of optimum sites for Cu+, reducing the number of NBO for this ion.
Our study indicates that Cu+ and Cu2+ bond-lengths and coordination numbers vary in different glass systems. However, the bioactivity of silicate-based glasses in terms of Si-NBO bonding in the glass network will remain unchanged following the inclusion of Cu in its both form of oxidation states, Cu+ and Cu2+. Apart from the network connectivity of the glass, the field strength of modifier cations can also influence on the bioactivity and dissolution behaviour of the glass.118 For example, Ca and Na ions have different effects on physical and chemical durability due to having different field strengths and bonding to the network structure. Calcium ions with higher field strength can bond to the glass network and increase the mechanical strength and durability of silicate-based glasses.118 It was found in the present study that Ca and Cu+ as well as Cu2+ show a similar field strength and the NBO percentage distribution decreases upon increasing the Cu2+ ions in the glass. We would not expect substantial changes in the bioactivity after the incorporation of copper, regardless of the oxidation state. A study conducted by Bejarano et al. also evidenced experimentally that by incorporating Cu2+ ions with substitution by CaO, the glass dissolution and the ion release became more difficult and due to a more stabilized glass structure.119 The fundamental mechanism behind this can be explained from our results. However, they have also not mentioned the presence of Cu+ ions in the glass due to the lack of information about the atomistic structure of Cu-incorporated BGs. When there is more than one modifier in the glass system, they compete for NBO with higher field strength cations within them.120
6. Conclusions
We have conducted classical molecular dynamics simulations of various copper-containing silicate glasses to characterize the Cu+ and Cu2+ ions' local environment within the bioactive silicate-based glasses and to understand the influence of both oxides on the structure and bioactivity of the glasses. Optimised potential parameters of Cu+–O and Cu2+–O interactions were developed and applied for subsequent molecular dynamics simulations.It was found that the structural effect of the addition of Cu2+ ions to silicate-based glasses can be investigated using MD models in the presence of Cu+ ions simultaneously in a certain ratio. We have found that the Cu+–O bond length with a planar geometry and coordination number of three is shorter than the Cu2+–O interactions' elongated octahedral geometry. The incorporated copper oxides in the structure of silicate-based glasses are expected to act as network modifiers. However, some Cu2+ ions bond to non-bridging oxygen atoms. The effect on the bioactivity of Cu incorporation is likely to be small.
Data availability
Data for this paper, including input files for DLPOLY, and analysis codes used to generate the results from the output, are available at https://doi.org/10.17028/rd.lboro.22294123.v1.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was funded by Loughborough University as part of the EPSRC/MRC Centre for Doctoral Training in Regenerative Medicine (grant no. EP/L015072/1). The authors acknowledge funding received from the UK Research and Innovation (UKRI) that supported the publication of this study.References
- G. Borkow, Curr. Chem. Biol., 2015, 8, 89–102 CrossRef PubMed.
- M. Bost, S. Houdart, M. Oberli, E. Kalonji, J.-F. Huneau and I. Margaritis, J. Trace Elem. Med. Biol., 2016, 35, 107–115 CrossRef CAS PubMed.
- G. Lockitch, A. C. Halstead, L. Wadsworth, G. Quigley, L. Reston and B. Jacobson, Clin. Chem., 1988, 34, 1625–1628 CrossRef CAS.
- R. S. Gibson, Principles of nutritional assessment, Oxford University Press, Oxford, 2005 Search PubMed.
- M. Angelova, S. Asenova, V. Nedkova and R. Koleva-Kolarova, Trakia J. Sci., 2011, 9, 88–98 Search PubMed.
- M. Solioz, Mycobact. Dis., 2016, 6(2), 1–4 Search PubMed.
- H. Tapiero, D. M. Townsend and K. D. Tew, Biomed. Pharmacother., 2003, 57, 386–398 CrossRef CAS PubMed.
- J. Osredkar, J. Clin. Toxicol., 2011, S:3, DOI:10.4172/2161-0495.s3-001.
- G. Borkow and J. Gabbay, Curr. Chem. Biol., 2009, 3, 272–278 CAS.
- C. Li, Y. Li and C. Ding, Int. J. Mol. Sci., 2019, 20, 175 CrossRef PubMed.
- R. Uauy, M. Olivares and M. Gonzalez, Am. J. Clin. Nutr., 1998, 67, 952S959S CrossRef PubMed.
- W. Feng, F. Ye, W. Xue, Z. Zhou and Y. J. Kang, Mol. Pharmacol., 2008, 75, 174–182 CrossRef PubMed.
- S. Kargozar, M. Mozafari, S. Ghodrat, E. Fiume and F. Baino, Mater. Sci. Eng., C, 2020, 111741 Search PubMed.
- A. P. Ingle, N. Duran and M. Rai, Appl. Microbiol. Biotechnol., 2013, 98, 1001–1009 CrossRef PubMed.
- F. Baino, I. Potestio and C. Vitale-Brovarone, Materials, 2018, 11, 1524 CrossRef PubMed.
- S. Kargozar, S. Hamzehlou and F. Baino, Materials, 2017, 10, 1429 CrossRef PubMed.
- F. Baino, S. Hamzehlou and S. Kargozar, J. Funct. Biomater., 2018, 9, 25 CrossRef PubMed.
- M. Fábián, Z. Kovács, J. L. Lábár, A. Sulyok, Z. E. Horváth, I. Székács and V. Kovács Kis, J. Mater. Sci., 2019, 55, 2303–2320 CrossRef.
- J. R. Jones, Acta Biomater., 2013, 9, 4457–4486 CrossRef CAS PubMed.
- N. Al-Harbi, H. Mohammed, Y. Al-Hadeethi, A. S. Bakry, A. Umar, M. A. Hussein, M. A. Abbassy, K. G. Vaidya, G. Al Berakdar, E. M. Mkawi and M. Nune, Pharmaceuticals, 2021, 14, 75 CrossRef CAS PubMed.
- I. Elgayar, A. E. Aliev, A. R. Boccaccini and R. G. Hill, J. Non-Cryst. Solids, 2005, 351, 173–183 CrossRef CAS.
- S. Kaya, M. Cresswell and A. R. Boccaccini, Mater. Sci. Eng., C, 2018, 83, 99–107 CrossRef CAS PubMed.
- A. Tilocca, Phys. Rev. B, 2007, 76, 224202 CrossRef.
- J. Sułowska, I. Wacławska and M. Szumera, J. Therm. Anal. Calorim., 2012, 109, 705–710 CrossRef.
- H. Scholze, Glass nature, structure, and properties, New York Berlin Heidelberg London Paris Tokyo Hong Kong Barcelona Springer, 1991 Search PubMed.
- C. Karlsson, E. Zanghellini, J. Swenson, B. Roling, D. T. Bowron and L. Börjesson, Phys. Rev. B, 2005, 72, 064206 CrossRef.
- H. Lammert and A. Heuer, Phys. Rev. B, 2004, 70, 024204 CrossRef.
- S. J. Watts, R. G. Hill, M. D. ODonnell and R. V. Law, J. Non-Cryst. Solids, 2010, 356, 517–524 CrossRef CAS.
- K. Stanton, PhD thesis, University of Limerick, 2000.
- A. Mekki, D. Holland and C. F. McConville, J. Non-Cryst. Solids, 1997, 215, 271–282 CrossRef CAS.
- W. Grochala and Z. Mazej, Philos. Trans. R. Soc., A, 2015, 373, 20140179 CrossRef PubMed.
- E. Metwalli, J. Non-Cryst. Solids, 2003, 317, 221–230 CrossRef CAS.
- J. Sułowska, I. Wacławska and M. Szumera, J. Therm. Anal. Calorim., 2012, 109, 705–710 CrossRef.
- S. Mathews, R. Kumar and M. Solioz, Appl. Environ. Microbiol., 2015, 81, 6399–6403 CrossRef CAS PubMed.
- M. Hans, A. Erbe, S. Mathews, Y. Chen, M. Solioz and F. Mücklich, Langmuir, 2013, 29, 16160–16166 CrossRef CAS PubMed.
- T. M. Gross, J. Lahiri, A. Golas, J. Luo, F. Verrier, J. L. Kurzejewski, D. E. Baker, J. Wang, P. F. Novak and M. J. Snyder, Nat. Commun., 2019, 10, 1979 CrossRef PubMed.
- C. E. Santo, E. W. Lam, C. G. Elowsky, D. Quaranta, D. W. Domaille, C. J. Chang and G. Grass, Appl. Environ. Microbiol., 2010, 77, 794–802 CrossRef PubMed.
- J. H. Kaplan and E. B. Maryon, Biophys. J., 2016, 110, 7–13 CrossRef CAS PubMed.
- M. Miola and E. Verné, Materials, 2016, 9, 405 CrossRef PubMed.
- M. Mozafari, S. Banijamali, F. Baino, S. Kargozar and R. G. Hill, Acta Biomater., 2019, 91, 35–47 CrossRef CAS PubMed.
- G. Kaur, N. Sriranganathan, S. G. Waldrop, P. Sharma and B. N. Chudasama, Biomed. Mater., 2017, 12, 045020 CrossRef PubMed.
- E. A. Abou Neel, I. Ahmed, J. Pratten, S. N. Nazhat and J. C. Knowles, Biomaterials, 2005, 26, 2247–2254 CrossRef CAS PubMed; A. Bonici, G. Lusvardi, G. Malavasi, L. Menabue and A. Piva, J. Eur. Ceram. Soc., 2012, 32, 2777–2783 CrossRef.
- V. Aina, G. Cerrato, G. Martra, G. Malavasi, G. Lusvardi and L. Menabue, Appl. Surf. Sci., 2013, 283, 240–248 CrossRef CAS.
- E. Wers and L. Bunetel, Bioceram. Dev. Appl., 2013, S:1, DOI:10.4172/2090-5025.s1-013.
- C. Wu, Y. Zhou, M. Xu, P. Han, L. Chen, J. Chang and Y. Xiao, Biomaterials, 2013, 34, 422–433 CrossRef CAS PubMed.
- H. Palza, B. Escobar, J. Bejarano, D. Bravo, M. Diaz-Dosque and J. Perez, Mater. Sci. Eng., C, 2013, 33, 3795–3801 CrossRef CAS PubMed.
- J. Bejarano, P. Caviedes and H. Palza, Biomed. Mater., 2015, 10, 025001 CrossRef PubMed.
- Y. Lin, W. Xiao, B. S. Bal and M. N. Rahaman, Mater. Sci. Eng., C, 2016, 67, 440–452 CrossRef CAS PubMed.
- H. Wang, S. Zhao, W. Xiao, J. Xue, Y. Shen, J. Zhou, W. Huang, M. N. Rahaman, C. Zhang and D. Wang, Mater. Sci. Eng., C, 2016, 58, 194–203 CrossRef CAS PubMed.
- A. Bari, N. Bloise, S. Fiorilli, G. Novajra, M. Vallet-Regí, G. Bruni, A. Torres-Pardo, J. M. González-Calbet, L. Visai and C. Vitale-Brovarone, Acta Biomater., 2017, 55, 493–504 CrossRef CAS PubMed; K. Zheng, X. Dai, M. Lu, N. Hüser, N. Taccardi and A. R. Boccaccini, Colloids Surf., B, 2017, 150, 159–167 CrossRef PubMed.
- R. Koohkan, T. Hooshmand, D. Mohebbi-Kalhori, M. Tahriri and M. T. Marefati, ACS Biomater. Sci. Eng., 2018, 4, 1797–1811 CAS.
- M. Miola, A. Cochis, A. Kumar, C. Arciola, L. Rimondini and E. Verné, Materials, 2018, 11, 961 CrossRef PubMed.
- B. A. E. Ben-Arfa, S. Neto, M. Salvado, R. C. Pullar and J. M. F. Ferreira, Acta Biomater., 2019, 87, 1742–7061 CrossRef PubMed.
- S. Mokhtari and A. W. Wren, Biomed. Glasses, 2019, 5, 13–33 Search PubMed.
- S. Kapoor, D. Brazete, I. C. Pereira, G. Bhatia, M. Kaur, L. F. Santos, D. Banerjee, A. Goel and J. M. F. Ferreira, J. Non-Cryst. Solids, 2019, 506, 98–108 CrossRef CAS.
- R. Lin, C. Deng, X. Li, Y. Liu, M. Zhang, C. Qin, Q. Yao, L. Wang and C. Wu, Theranostics, 2019, 9, 6300–6313 CrossRef CAS PubMed.
- S. Akhtach, Z. Tabia, K. El Mabrouk, M. Bricha and R. Belkhou, Ceram. Int., 2021, 47, 424–433 CrossRef CAS.
- J. Jiménez-Holguín, S. Sánchez-Salcedo, M. Vallet-Regí and A. J. Salinas, Microporous Mesoporous Mater., 2020, 308, 110454 CrossRef PubMed.
- F. Zhang, P. Wang, J. Koberstein, S. Khalid and S.-W. Chan, Surf. Sci., 2004, 563, 74–82 CrossRef CAS.
- L. A. J. Garvie and P. R. Buseck, J. Phys. Chem. Solids, 1999, 60, 1943–1947 CrossRef CAS.
- A. M. Shahin, F. Grandjean, G. J. Long and T. P. Schuman, Chem. Mater., 2004, 17, 315–321 CrossRef.
- T. Taniguchi, T. Watanabe, N. Sugiyama, A. K. Subramani, H. Wagata, N. Matsushita and M. Yoshimura, J. Phys. Chem. C, 2009, 113, 19789–19793 CrossRef CAS.
- A. S. Karakoti, S. Singh, A. Kumar, M. Malinska, S. V. N. T. Kuchibhatla, K. Wozniak, W. T. Self and S. Seal, J. Am. Chem. Soc., 2009, 131, 14144–14145 CrossRef CAS PubMed.
- C. M. Sims, R. A. Maier, A. C. Johnston-Peck, J. M. Gorham, V. A. Hackley and B. C. Nelson, Nanotechnology, 2018, 30, 085703 CrossRef PubMed.
- S. Kargozar, S. Ramakrishna and M. Mozafari, Curr. Opin. Biomed. Eng., 2019, 10, 181–190 CrossRef.
- S. Kapoor, D. Brazete, I. C. Pereira, G. Bhatia, M. Kaur, L. F. Santos, D. Banerjee, A. Goel and J. M. F. Ferreira, J. Non-Cryst. Solids, 2019, 506, 98–108 CrossRef CAS.
- R. Koohkan, T. Hooshmand, M. Tahriri and D. Mohebbi-Kalhori, Ceram. Int., 2018, 44, 2390–2399 CrossRef CAS.
- J. Du and L. R. Corrales, Phys. Rev. B, 2005, 72, 092201 CrossRef.
- M. Montazerian, E. D. Zanotto and J. C. Mauro, Int. Mater. Rev., 2019, 65, 297–321 CrossRef.
- J. Meller, Molecular Dynamics, John Wiley & Sons., 2001 Search PubMed.
- R. G. Hill and D. S. Brauer, J. Non-Cryst. Solids, 2011, 357(24), 3884–3887 CrossRef CAS.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef.
- A. Tilocca, J. Chem. Phys., 2008, 129, 084504 CrossRef PubMed.
- J. Ding, Y. Q. Cheng and E. Ma, Acta Mater., 2014, 69, 343–354 CrossRef CAS.
- J. Ding and E. Ma, npj Comput. Mater., 2017, 3(9), 1–12 CAS.
- K. Kamiya, T. Yoko and S. Sakka, J. Non-Cryst. Solids, 1986, 80, 405–411 CrossRef CAS.
- F. Gonella, A. Quaranta, S. Padovani, C. Sada, F. DAcapito, C. Maurizio, G. Battaglin and E. Cattaruzza, Appl. Phys. A: Mater. Sci. Process., 2005, 81, 1065–1071 CrossRef CAS.
- S. Sakka, K. Kamiya and K. Kato, J. Non-Cryst. Solids, 1982, 52, 77–90 CrossRef CAS.
- C. Mugoni, H. Jain, M. Montorsi, M. Montecchi, A. Kovalskiy and C. Siligardi, J. Non-Cryst. Solids, 2016, 447, 91–97 CrossRef CAS.
- G. Broglia, C. Mugoni, J. Du, C. Siligardi and M. Montorsi, J. Non-Cryst. Solids, 2014, 403, 53–61 CrossRef CAS.
- D. W. Davies, K. T. Butler, O. Isayev and A. Walsh, Faraday Discuss., 2018, 211, 553–568 RSC.
- Democritus: The Radial Distribution Function, https://people.bath.ac.uk/chsscp/teach/md.bho/Theory/rdf.html, (accessed 4 August 2022).
- G. Kaur, Clinical applications of biomaterials: state-of-the-art progress, trends, and novel approaches, Springer, Cham, Switzerland, 2017 Search PubMed.
- M. A. Halcrow, Chem. Soc. Rev., 2013, 42, 1784–1795 RSC.
- N. N. Eremin, L. I. Leonyuk and V. S. Urusov, J. Solid State Chem., 2001, 158, 162–168 CrossRef CAS.
- D. A. Fletcher, R. F. McMeeking and D. Parkin, J. Chem. Inf. Comput. Sci., 1996, 36, 746–749 CrossRef CAS.
- C. Randall, Rev. Mineral. Geochem., 2001, 42, 1–35 CrossRef.
- P. Tiwary, A. van de Walle and N. Grønbech-Jensen, Phys. Rev. B, 2009, 80, 174302 CrossRef.
- S. T. Bromley, S. A. French, A. A. Sokol, C. R. A. Catlow and P. Sherwood, J. Phys. Chem. B, 2003, 107, 7045–7057 CrossRef CAS.
- L. Yang, A. Karim and J. T. Muckerman, J. Phys. Chem. C, 2013, 117, 3414–3425 CrossRef CAS.
- J. K. Christie and N. H. de Leeuw, J. Mater. Sci., 2017, 52, 9014–9022 CrossRef CAS PubMed.
- P. Smok, J. Phys.: Conf. Ser., 2011, 289, 012030 CrossRef.
- W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136–141 CrossRef CAS PubMed.
- A. Fluegel, J. Am. Ceram. Soc., 2007, 90, 2622–2625 CrossRef CAS.
- A. Tilocca, A. N. Cormack and N. H. de Leeuw, Chem. Mater., 2006, 19, 95–103 CrossRef.
- K. Vollmayr, W. Kob and K. Binder, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 15808–15827 CrossRef CAS PubMed.
- A. Tilocca, Proc. R. Soc. A, 2009, 465, 1003–1027 CrossRef CAS.
- K. Vollmayr-Lee, W. Kob, K. Binder and A. Zippelius, Int. J. Mod. Phys. C, 1999, 10, 1443–1451 CrossRef.
- R. Hill, J. Mater. Sci. Lett., 1996, 15, 1122–1125 CrossRef CAS.
- S. N. Rath, A. Brandl, D. Hiller, A. Hoppe, U. Gbureck, R. E. Horch, A. R. Boccaccini and U. Kneser, PLoS One, 2014, 9, e113319 CrossRef PubMed.
- M. Tayar Galante, A. Živković, J. C. Alvim, C. C. Calchi Kleiner, M. Sangali, S. F. R. Taylor, A. J. Greer, C. Hardacre, K. Rajeshwar, R. Caram, R. Bertazzoli, R. T. Macaluso, N. H. de Leeuw and C. Longo, ACS Appl. Mater. Interfaces, 2021, 13, 32865–32875 CrossRef CAS PubMed.
- L. Wang, H. Wu, S. R. Desai and L. Lou, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(12), 8028–8031 CrossRef CAS PubMed.
- M. Jansen and J. C. Schon, Structure Prediction in Solid-State Chemistry as an Approach to Rational Synthesis Planning, Elsevier Ltd, 2013 Search PubMed.
- C. Gattinoni and A. Michaelides, Surf. Sci. Rep., 2015, 70, 424–447 CrossRef CAS.
- A. Silvestri, S. Tonietto, F. DAcapito and G. Molin, J. Cult. Herit., 2012, 13, 137–144 CrossRef.
- L. Grund Bäck, S. Ali, S. Karlsson, L. Wondraczek and B. Jonson, J. Non-Cryst. Solids: X, 2019, 3, 100029 Search PubMed.
- F. DAcapito, S. Colonna, S. Mobilio, F. Gonella, E. Cattaruzza and P. Mazzoldi, Appl. Phys. Lett., 1997, 71, 2611–2613 CrossRef CAS.
- F. DAcapito, S. Mobilio, J. R. Regnard, E. Cattaruzza, F. Gonella and P. Mazzoldi, J. Non-Cryst. Solids, 1998, 232–234, 364–369 CrossRef CAS.
- K. Fukumi, A. Chayahara, K. Kadono, H. Kageyama, T. Akai, N. Kitamura, M. Makihara, K. Fujii and J. Hayakawa, J. Non-Cryst. Solids, 1998, 238, 143–151 CrossRef CAS.
- J. Lee, T. Yano, S. Shibata, A. Nukui and M. Yamane, J. Non-Cryst. Solids, 2000, 277, 155–161 CrossRef CAS.
- C. Maurizio, F. dAcapito, M. Benfatto, S. Mobilio, E. Cattaruzza and F. Gonella, Eur. Phys. J. B, 2000, 14, 211–216 CrossRef CAS.
- L. Tröger, T. Yokoyama, D. Arvanitis, T. Lederer, M. Tischer and K. Baberschke, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 888–903 CrossRef PubMed.
- B. Murphy, Coord. Chem. Rev., 2003, 243, 237–262 CrossRef CAS.
- F. dAcapito, S. Mobilio, G. Battaglin, E. Cattaruzza, F. Gonella, F. Caccavale, P. Mazzoldi and J. R. Regnard, J. Appl. Phys., 2000, 87, 1819–1824 CrossRef CAS.
- I. A. Demichev, A. I. Sidorov, N. V. Nikonorov and T. A. Shahverdov, Sci. Tech. J. Inf. Technol., Mech. Opt., 2015, 54–59 Search PubMed.
- I. Demichev, N. Nikonrov and A. Sidorov, Ion Exch.: Theory Appl., 2017, 251–312 Search PubMed.
- M. Suszynska, M. Maczka, M. Ptak and L. Krajczyk, J. Non-Cryst. Solids, 2014, 401, 92–95 CrossRef CAS.
- Y. Xiang and J. Du, Chem. Mater., 2011, 23, 2703–2717 CrossRef CAS.
- J. Bejarano, P. Caviedes and H. Palza, Biomed. Mater., 2015, 10, 025001 CrossRef PubMed.
- S. Watts, PhD thesis, Imperial College London, 2010.
| This journal is © The Royal Society of Chemistry 2023 |