Open Access Article
Open Access ArticleFlexible percolation fibrous thermal insulating composite membranes for thermal management†
Lu
An
 a,
Massimigliano
Di Luigi
a,
Jingye
Tan
a,
Danial
Faghihi
a and
Shenqiang
Ren
a,
Massimigliano
Di Luigi
a,
Jingye
Tan
a,
Danial
Faghihi
a and
Shenqiang
Ren
 *abc
*abc
aDepartment of Mechanical and Aerospace Engineering, University at Buffalo, The State University of New York, Buffalo, New York 14260, USA. E-mail: shenren@buffalo.edu
bDepartment of Chemistry, University at Buffalo, The State University of New York, Buffalo, NY 14260, USA
cResearch and Education in Energy, Environment & Water (RENEW), University at Buffalo, The State University of New York, Buffalo, NY 14260, USA
First published on 23rd November 2022
Abstract
Flexible thermal insulating membranes are ubiquitous in thermal management. Nevertheless, difficulties arise for composite membranes to combine a resilient, robust structural framework with uniform percolation networks purposefully conceived for thermal insulation. Herein, by controlling the microstructure homogeneity, we report flexible, hydrophobic thermal insulating membranes consisting of ceramic fiber and porous silica materials. The resulting nanofibrous membrane composites exhibit a low thermal insulation of 11.4 mW m−1 K−1, a low density of 0.245 g cm−3, mechanical flexibility with a bending rigidity of 1.25 cN mm−1, and hydrophobicity with a water contact angle of 144°. These nanofibrous-reinforced, silica-aerogel-based nanocomposite membranes are potential candidates for advanced thermal management applications.
1 Introduction
Thermal insulating materials are essential for thermal management in buildings, electronics, and wearable systems.1–4 The thermal insulating performance of these materials originates from the percolation porous networks, i.e. silica aerogels, with narrow pore size distribution, efficiently limiting the gaseous thermal conduction.5–8 However, silica aerogels show inherent weak interparticle connections causing poor mechanical performance. The incorporation of fibers could improve porous materials’ mechanical performance, while the thermal insulating performance could be degraded by the non-uniform microstructures.9–15 The occurrence of an accelerated heat transfer through fibers and large void spaces, as part of solid phase thermal conduction, dramatically limits the thermal insulating performance of fibrous composite materials and their subsequent structural instability under applied mechanical stress.16,17In this work, we report flexible, hydrophobic thermal insulating membrane nanocomposites consisting of ceramic fibers and silica aerogels. Through a meticulous control of the microstructure of silica aerogels and fiber networks, these thermally insulating membrane nanocomposites achieve mechanical robustness and flexibility. Highly thermal insulating silica aerogels interfacing with fibers effectively restrain the heat transfer from fiber to fiber, which provide a path to preserve the high thermal insulating properties of the composite material.4,18–20 Hydrophobic surface modification is carried out by using 1H, 1H, 2H, 2H-perfluorodecyltrichlorosilane (PFDTS). The resulting nanofibrous membrane composites exhibit a low thermal insulation of 11.4 mW m−1 K−1, a low density of 0.245 g cm−3, mechanical flexibility with a bending rigidity of 1.25 cN mm−1, and hydrophobicity with a water contact angle of 144°. These nanofibrous-reinforced, silica-aerogel-based nanocomposite membranes are promising alternatives in applications related to advanced thermal management.
2 Materials and methods
2.1 Fibrous nanocomposite membranes
The whole process includes (1) mesoporous silica powder preparation, (2) ceramic fiber treatment, and (3) fibrous nanocomposite membrane fabrication.The synthesis of tetraethyl orthosilicate (TEOS) based mesoporous silica powders used in this study follows a previous work.10 The following materials have been used during the synthesis of silica powders: tetraethyl orthosilicate (TEOS-[Si(OC2H5)4; ≥99.0% (GC) |Sigma Aldrich]); cetrimonium bromide (CTAB – [C19H42BrN; high purity| VWR]); 3,3′,5,5′-tetramethylbenzidine (TMB-[–C6H2(CH3)2-4-NH2]2; ≥99%| Sigma Aldrich). The chemical molar ratio of TEOS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CTAB
CTAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Urea
Urea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TMB
TMB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O is 1
H2O is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.122
0.122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.21
2.21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.063
0.063![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49.25, respectively. The sol–gel process with an initial pH of 8 is carried out below 60 °C. Urea could decompose into ammonia for promoting the pH during the gelation process, and carbon dioxide resists the pore collapse. The ambient pressure dried samples would be sintered at 600 °C for 1 h to remove the chemical residue. The powders would be blended in water for 15 seconds and then treated with high frequency ultrasound for less than 30 min. The original ceramic fibers are dispersed in water using a homogenizer and blended using a commercial blender for 15 seconds to make the fibers short. These fibers would be washed with diluted HCl solution (1% v/v).
49.25, respectively. The sol–gel process with an initial pH of 8 is carried out below 60 °C. Urea could decompose into ammonia for promoting the pH during the gelation process, and carbon dioxide resists the pore collapse. The ambient pressure dried samples would be sintered at 600 °C for 1 h to remove the chemical residue. The powders would be blended in water for 15 seconds and then treated with high frequency ultrasound for less than 30 min. The original ceramic fibers are dispersed in water using a homogenizer and blended using a commercial blender for 15 seconds to make the fibers short. These fibers would be washed with diluted HCl solution (1% v/v).
The solutions of the above powders and fibers are mixed using a homogenizer and under high frequency ultrasound. This ultrasound process would help in the deposition of porous silica onto the acid treated fiber surface. The composite membrane is fabricated through vacuum filtration, and the wet membrane covered by the PET film is loaded onto a hot press stage at 60 °C and 0.3 MPa pressure for 3 hours, which is performed to densify and flatten the membrane. Afterwards the composite membrane covered by two rigid paper and a metal plate is transferred to the oven for drying to resist the buckling. The porous silica mass concentration is adjusted by the mass weight of the used porous silica powders and fibers mentioned above. The thickness is adjusted by the amount of total mixture solution through the control of the porous silica concentration ratio. The hydrophobic surface modification is carried out by depositing 1H,1H,2H,2H-perfluorodecyltrichlorosilane (PFDTS) onto the membrane composites. The sintering treatments at different temperatures (i.e., 150 °C, 200 °C, and 400 °C) are compared with the dried membrane samples.
2.2 Microstructural characterization
A Carl Zeiss AURIGA scanning electron microscope (SEM) and a JEOL 2010 high-resolution transmission electron microscope (HRTEM) are used to characterize the microstructures of the porous silica and composite membranes. The X-ray diffraction patterns of samples were obtained using a Rigaku Ultima IV with an operational X-ray tube power of 1.76 kW (40 kV, 44 mA) with Cu Ka radiation (l = 1.54184 Å). BET analysis is performed on a Tristar II 3020 (Micromeritics Corp. Atlanta, GA). The specific surface area (SSA) and the pore size distributions are evaluated with the low-temperature nitrogen adsorption–desorption isotherm measurement method. The pure aerogels are degassed at 200 °C for 2 hours before analysis. The surface areas are calculated with the Brunauer–Emmett–Teller (BET) theory using the isotherm adsorption data at P/P0 from 0.05 to 0.30. The pore size is calculated from the adsorption branch based on the Barrett, Joyner, and Halenda (BJH) method with the average pore diameter calculated using equation d = 4 V A−1.2.3 Thermal performance measurement
The thermal conductivity of the composite membranes is determined using a Thermtest HFM-100 following the ASTM C518 standard. Pertinent calibration is performed on commercial extruded polystyrene boards of an appropriate thickness and with a known value of thermal conductivity. The membrane thickness is automatically determined using the HFM-100. The measurement begins by fixing the upper and lower plates at 30 °C and 40 °C, respectively, and the thermal conductivity is determined when the heat flux becomes a constant value. Infrared images are recorded using a Fotric 225 Pro Thermal Camera.2.4 Mechanical performance measurement
The flexibility of membranes with different thicknesses is evaluated using the vertical ring bend method and specimens with dimensions of 50 mm × 50 mm are evaluated with an ultra-sensitive load cell on a universal test frame (Model DSTM-50KN from United Testing Systems).3 Results and discussion
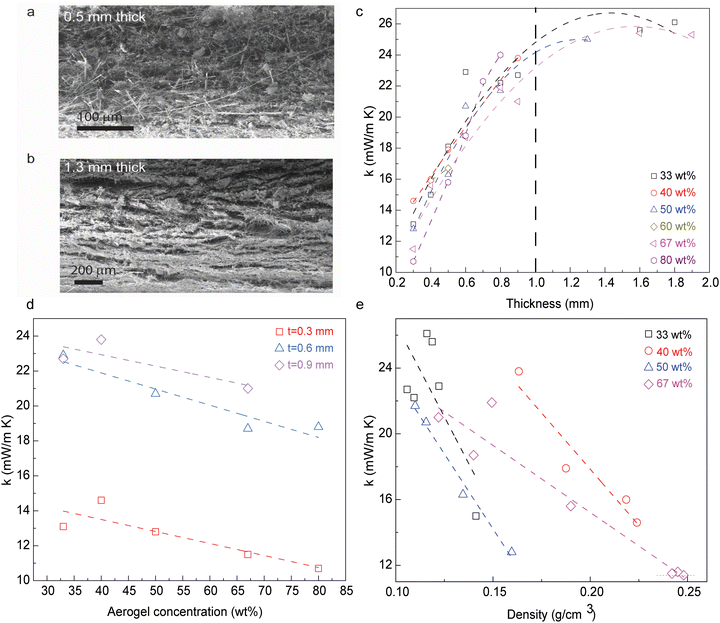
The hierarchical fibrous structure combined with silica aerogels ensures superlative thermal insulating performance, while at the same time achieving structural integrity and mechanical flexibility (Fig. 1a). The TEM images show the hierarchical mesoporous silica aerogel and the aerogel/fiber interface, respectively. The silica aerogel materials are shown in Fig. S1 (ESI†), which exhibit the existence of a homogeneous mesoporous silica network that effectively percolates through the voids between the structural fiber network originating from the ceramic fibers, thus giving rise to a uniform fiber/silica aerogel framework. This homogeneous microstructure circumvents the heat transfer from the layered structure21,22 while the uniformly distributed silica aerogel provides an effective thermal barrier to potential heat transfer among fibers.19,22 The aforementioned fiber network mostly comprises short fibers with an average length of around 100 μm as highlighted in Fig. 1f (cross-section of a membrane specimen), which promotes a much larger uniformity of the fiber/aerogel structural network than the one that could be achieved with long threads of fiber due to a greater intricacy between short fibers and mesoporous silica aerogel particles. Moreover, a noticeable flexibility is achieved in the composite membrane by virtue of the resulting entanglement between fibers and porous silica, as highlighted in Fig. 1b.On the other hand, inducing resistance to moisture on the fibrous membrane could improve its thermal insulating performance under humid conditions, which is achieved by means of hydrophobic surface modification through PFDTS treatment that results in a water contact angle of 144° (inset of Fig. 1b). The in-plane and cross-sectional SEM images (Fig. 1e and f, respectively) show the membrane microstructure featuring an extremely uniform distribution of the non-layered silica aerogel and fiber network structure. Furthermore, the presence of porous fibrous networks significantly reduces the solid phase thermal conductivity within the membrane, hence enhancing its thermal insulating performance.
Thermal insulation of nanocomposite membrane is derived from the restrained solid thermal conduction through fibers, as well as through effective restriction of the gaseous heat transfer among the matrix. The fibrous percolation networks provide a platform to reduce the solid heat transfer, while silica aerogel coating could block the heat transfer from fiber to fiber. Such a hierarchical architecture obtained in this type of composite materials becomes critical during the improvement of their thermal insulating performance. The sought-after homogeneous network can then be achieved in membranes with the thickness between 500 μm and 1.3 mm (Fig. 2a and b), with a thickness dependence developing for materials beyond this range. The microstructure of the thickness-dependent composite materials is easily affected by the filtration process, where the layer-by-layer deposition occurs along the fluid flow and gravity direction. Larger gaps and voids between layers could increase the gaseous heat transfer that translates into a reduced thermal insulating performance. The thermal conductivity of membrane nanocomposites with thickness in the region of 300 μm falls within 10–15 mW m−1 K−1, showing a roughly linear increment as the thickness increases up to 1.0 mm. Subsequently, the thermal conductivity increases to 23–27 mW m−1 K−1 as the thickness increases above 1.0 mm (Fig. 2c).
The incorporation of silica aerogels serves as the thermal barrier within the fibrous percolation networks. Therefore, the thermal conductivity of nanocomposite membranes with similar thicknesses would decrease as the concentration of silica aerogel increases (Fig. 2c and d). The membranes show ∼33% lower thermal conductivity when the concentration of silica aerogels increases from 40 wt% to 80 wt%. Even though a higher loading of silica aerogels benefits thermal insulating performance, the structural integrity of membranes needs to be considered, especially for the membrane with 80 wt% silica aerogels. The mass density of the nanocomposite membranes is strictly related to the unit volume of silica aerogels and fibrous networks, with a clear trend showing a decrease in thermal conductivity as the density increases (Fig. 2e). This is probably induced by the gaseous phase component through the fiber/silica aerogel structural network, where a membrane with lower density may feature a higher gaseous phase component of thermal conductivity.
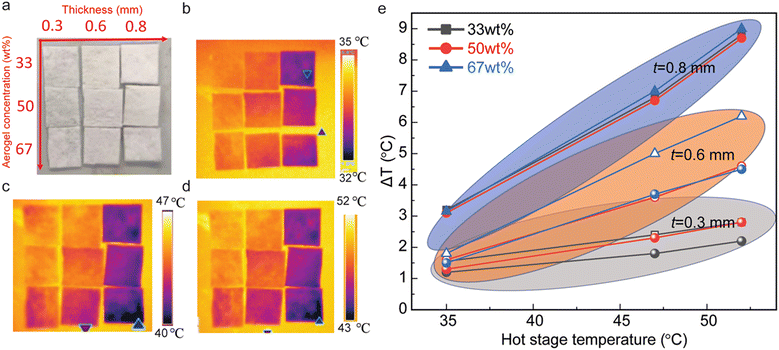
The fibrous nanocomposite membranes with different concentrations of silica aerogels (33 wt%, 50 wt% and 67 wt%) and thicknesses (300 μm, 600 μm, and 800 μm) show great potential for heat resistance (Fig. 3a). Infrared images in Fig. 3b–d are recorded with the surface hot plate kept at different temperatures (i.e.: 35 °C, 47 °C, and 52 °C). As the thickness of the nanocomposites increases, the temperature of their top surface decreases, while increasing the concentration of silica aerogels induces a further reduction of the top surface temperature (Fig. 3b–d). Fig. 3e summarizes the temperature difference (ΔT) between the top surface of the fibrous nanocomposite membrane and that of the surface hot plate. Under dissimilar heating temperatures, membranes with different thicknesses have a noticeable temperature difference ΔT, such as 1.5 °C for 33 wt% with 300 μm thickness compared with 8.5 °C for 33 wt% with 800 μm thickness. On the other hand, for membranes with similar thicknesses, the temperature difference ΔT is larger at higher temperatures, while higher concentrations of silica aerogels show a larger ΔT, especially for the thickness of 300 μm and 600 μm.
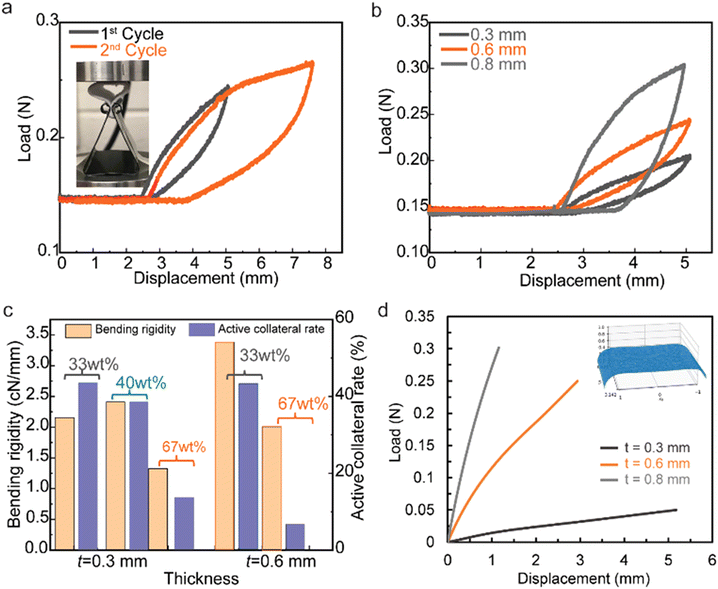
The mechanical flexibility of thermal-insulating composite membranes can be affected under different external load conditions. The fiber entanglement is a key aspect for preserving the integrity of the structure network bearing loads/stresses, while the type of microstructure of the membrane would also affect its mechanical performance. Here, the mechanical flexibility of the nanocomposite membranes is evaluated using a multi-cycle bend method, which is shown in Fig. 4. After the top plate comes into contact with the membrane's surface, it compresses the shell-like membrane ring (vertical height of 15 mm) from ‘point contact’ to ‘flat-surface contact’ with the increase of both displacement and load force simultaneously (Fig. 4a). During the unloading process, the bent membrane would recover back within the elastic region. For a 600 μm thick membrane with 33 wt% silica, the 1st cycle with a displacement of 2.5 mm is recoverable with a maximum load of 0.11 N (after subtracting the base initial load of 0.14 N), while the 2nd cycle with a total displacement of 5 mm is beyond elastic response with a residual displacement of 1.4 mm after complete unloading (Fig. 4a). The concept of mechanical recoverability derives from the microstructural resilience in the fibrous composite membrane, which is affected by silica aerogel concentrations and hierarchical architectures. The load–displacement cycles for the nanocomposite membranes with 33 wt% silica aerogels (0.3 mm, 0.6 mm, and 0.8 mm thickness) are compared in Fig. 4b, revealing that a thicker sample bears higher load forces during the loading–unloading cycle.
Membranes with thickness below 0.8 mm maintain their recoverability, while membranes with thickness in the region of 0.8 mm have a residual displacement of 1.3 mm. The loss of recoverability for thicker samples could be the result of stress concentration among the non-homogeneous microstructures. The flexibility performance could be quantified by the parameters of bending rigidity and active collateral rate calculated from the load–displacement cycle of the membranes.4 For membranes with thickness in the region of 0.3 mm and different concentrations of silica aerogel materials (33 wt%, 40 wt%, and 67 wt%), the bending rigidity of the membrane with 40 wt% silica aerogels shows a higher value of 2.5 cN mm−1 compared with 2.1 cN mm−1 for the membrane with 33% aerogel, and 1.3 cN mm−1 for the membrane with 67 wt% aerogel (Fig. 4c). It should be noted that nanocomposites with superior bending rigidity properties require a synergistic contribution from fiber networks with uniformly distributed silica aerogels. When the thickness increases to 0.6 mm, the bending rigidity increases to 3.4 cN mm−1 for the membrane with 33 wt% silica aerogel. The active collateral rate decreases from 43% to 18% when the concentration of silica aerogels increases from 33 wt% to 67 wt%. A smaller active collateral rate indicates larger energy dissipation.
The membrane bending of the material in the vertical ring experiments is modeled using finite element methods. Simulations were conducted with a nonlinear thin-shell assumption and via an enriched mixed-element formulation implemented in the finite element library FEniCS.23–25 Following this,26 cubic bubble shape functions and reduced integration are employed to resolve the numerical locking issue in this simulation. The top surface of the simulated membrane is subjected to a uniformly distributed compression load. The bottom edges are modeled as a roller support with zero displacement boundary conditions in the vertical direction and allowing it to slide horizontally. To model the increase in the contact area between the plate and the membrane's surface during the vertical ring experiment, the applied load is increased linearly with time. Fig. 4d shows the load-displacement computed from the finite element simulations for three different sample thicknesses. The deformed configuration of the midplane of the top half of the membrane in this figure agrees with the deformed samples in the experiment shown in Fig. 4a. Both the experimental and numerical results demonstrate a nonlinear increase in membrane stiffness with sample thickness.
4 Conclusions
In conclusion, flexible, hydrophobic, and thermal-insulating composite membranes consisting of ceramic-based fibers and silica aerogels featuring a three-dimensional-type network structure are reported.Moreover, through effective control of the homogeneous microstructure across the membrane nanocomposite, as a result of the combination of short fibers and aerogel precursors under meticulously optimized processing parameters, a low thermal conductivity of 11.4 mW m−1 K−1, hydrophobicity with a water contact angle of 144°, and mechanical flexibility with a bending rigidity of 1.25 cN mm−1 are successfully accomplished.
Fabricated through a scalable, vacuum-filtration-assisted procedure, the nanofibrous-reinforced silica aerogel composite membranes are potential candidates for advanced thermal management applications.
Author contributions
All authors discussed the results and commented on the manuscript. L. A. and S. R. designed all experiments. L. A. and M. D. prepared the materials and conducted experiments for investigating their mechanical and thermal properties, as well as structural and physicochemical characterization. J. T. and D. F. conducted and supervised the modelling of the mechanical property study, respectively. S. R. conceived the project and directed the research. All authors contributed to the writing and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work at the University at Buffalo was supported by the U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy (EERE) under the Building Technology Office (BTO) Award Number DE-EE0008675 and the U.S. National Science Foundation (NSF) under the CAREER Award Number CMMI-2143662.Notes and references
- E. Cuce, P. M. Cuce, C. J. Wood and S. B. Riffat, Toward aerogel based thermal superinsulation in buildings: a comprehensive review, Renewable Sustainable Energy Rev., 2014, 34, 273–299 CrossRef CAS.
- S. Zhao, G. Siqueira, S. Drdova, D. Norris, C. Ubert, A. Bonnin, S. Galmarini, M. Ganobjak, Z. Pan and S. Brunner, Additive manufacturing of silica aerogels, Nature, 2020, 584(7821), 387–392 CrossRef CAS PubMed.
- Z. Liu, J. Lyu, D. Fang and X. Zhang, Nanofibrous kevlar aerogel threads for thermal insulation in harsh environments, ACS Nano, 2019, 13(5), 5703–5711 CrossRef CAS PubMed.
- X. Mao, J. Hong, Y.-X. Wu, Q. Zhang, J. Liu, L. Zhao, H.-H. Li, Y.-Y. Wang and K. Zhang, An Efficient Strategy for Reinforcing Flexible Ceramic Membranes, Nano Lett., 2021, 21(22), 9419–9425 CrossRef CAS PubMed.
- D. W. Schaefer and K. D. Keefer, Structure of random porous materials: silica aerogel, Phys. Rev. Lett., 1986, 56(20), 2199 CrossRef CAS PubMed.
- F. Hu, S. Wu and Y. Sun, Hollow-structured materials for thermal insulation, Adv. Mater., 2019, 31(38), 1801001 CrossRef PubMed.
- D. M. Butts, P. E. McNeil, M. Marszewski, E. Lan, T. Galy, M. Li, J. S. Kang, D. Ashby, S. King and S. H. Tolbert, Engineering mesoporous silica for superior optical and thermal properties. MRS Energy &, Sustainability, 2020, 7 Search PubMed.
- X. Xu, Q. Zhang, M. Hao, Y. Hu, Z. Lin, L. Peng, T. Wang, X. Ren, C. Wang and Z. Zhao, Double-negative-index ceramic aerogels for thermal superinsulation, Science, 2019, 363(6428), 723–727 CrossRef CAS PubMed.
- M. Marszewski, A. Dashti, P. E. McNeil, M. Fox, V. Wall, D. M. Butts, S. C. King, G. N. Kashanchi, S. H. Tolbert and B. Dunn, Elastic and plastic mechanical properties of nanoparticle-based silica aerogels and xerogels, Microporous Mesoporous Mater., 2022, 330, 111569 CrossRef CAS.
- L. An, M. Di Luigi, D. Petit, Y. Hu, Y. Chen, J. N. Armstrong, Y. C. Li and S. Ren, Nanoengineering Porous Silica for Thermal Management, ACS Appl. Nano Mater., 2022, 5(2), 2655–2663 CrossRef CAS.
- G. Hasegawa, T. Shimizu, K. Kanamori, A. Maeno, H. Kaji and K. Nakanishi, Highly flexible hybrid polymer aerogels and xerogels based on resorcinol-formaldehyde with enhanced elastic stiffness and recoverability: insights into the origin of their mechanical properties, Chem. Mater., 2017, 29(5), 2122–2134 CrossRef CAS.
- T. Linhares, M. T. P. de Amorim and L. Durães, Silica aerogel composites with embedded fibres: a review on their preparation, properties and applications, J. Mater. Chem. A, 2019, 7(40), 22768–22802 RSC.
- S. Iswar, S. Galmarini, L. Bonanomi, J. Wernery, E. Roumeli, S. Nimalshantha, A. M. B. Ishai, M. Lattuada, M. M. Koebel and W. J. Malfait, Dense and strong, but superinsulating silica aerogel, Acta Mater., 2021, 213, 116959 CrossRef CAS.
- S. C. King, M. Li, T. Galy, Y. Yan, J. S. Kang, V. M. Basile, Y. L. Li, M. Marszewski, L. Pilon and Y. Hu, Examining the Role of Atomic Scale Heterogeneity on the Thermal Conductivity of Transparent, Thermally Insulating, Mesoporous Silica–Titania Thin Films. The, J. Phys. Chem. C, 2020, 124(50), 27442–27452 CrossRef CAS.
- L. Dou, X. Cheng, X. Zhang, Y. Si, J. Yu and B. Ding, Temperature-invariant superelastic, fatigue resistant, and binary-network structured silica nanofibrous aerogels for thermal superinsulation, J. Mater. Chem. A, 2020, 8(16), 7775–7783 RSC.
- K. W. Oh, D. K. Kim and S. H. Kim, Ultra-porous flexible PET/Aerogel blanket for sound absorption and thermal insulation, Fibers Polym., 2009, 10(5), 731–737 CrossRef CAS.
- T. Xie, Y.-L. He and Z.-J. Hu, Theoretical study on thermal conductivities of silica aerogel composite insulating material, Int. J. Heat Mass Transfer, 2013, 58(1–2), 540–552 CrossRef CAS.
- X. Xu, S. Fu, J. Guo, H. Li, Y. Huang and X. Duan, Elastic ceramic aerogels for thermal superinsulation under extreme conditions, Mater. Today, 2021, 42, 162–177 CrossRef CAS.
- D. Tao, X. Li, Y. Dong, Y. Zhu, Y. Yuan, Q. Ni, Y. Fu and S. Fu, Super-low thermal conductivity fibrous nanocomposite membrane of hollow silica/polyacrylonitrile, Compos. Sci. Technol., 2020, 188, 107992 CrossRef CAS.
- J. Sheng, Y. Xu, J. Yu and B. Ding, Robust fluorine-free superhydrophobic amino-silicone oil/SiO2 modification of electrospun polyacrylonitrile membranes for waterproof-breathable application, ACS Appl. Mater. Interfaces, 2017, 9(17), 15139–15147 CrossRef CAS PubMed.
- Z. An, X. Hou, P. Zhou, R. Zhang and D. Fang, A novel flexible, layered, recoverable SiO2 fiber skeleton and aerogel composites material prepared by papermaking process, Ceram. Int., 2021, 47(9), 12963–12969 CrossRef CAS.
- L. An, J. N. Armstrong, Y. Hu, Y. Huang, Z. Li, D. Zhao, J. Sokolow, Z. Guo, C. Zhou and S. Ren, High temperature ceramic thermal insulation material, Nano Res., 2022, 1–8 CAS.
- M. Alnæs, J. Blechta, J. Hake, A. Johansson, B. Kehlet, A. Logg, C. Richardson, J. Ring, M. E. Rognes and G. N. Wells, The FEniCS project version 1.5, Archive of Numerical Software, 2015, 3, 100 Search PubMed.
- J. S. Hale; M. Brunetti; S. Bordas and C. Maurini, FENICS-SHELLS: an open-source library for simulating thin structures. 2018.
- J. S. Hale, M. Brunetti, S. P. Bordas and C. Maurini, Simple and extensible plate and shell finite element models through automatic code generation tools, Comput. Struct., 2018, 209, 163–181 CrossRef.
- D. Arnold and F. Brezzi, Locking-free finite element methods for shells, Math. Comput., 1997, 66(217), 1–14 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the microstructure (including TEM images), surface area, pore width, average particle size, structural characterization (XRD spectra), and the thermogravimetric study of aerogel and composite specimens, respectively; in addition to assessment of hydrophobic performance, SEM images, thermal conductivity, and mechanical properties of the composite membrane. See DOI: https://doi.org/10.1039/d2ma00915c |
| This journal is © The Royal Society of Chemistry 2023 |