Single-bonded nitrogen chain and porous nitrogen layer via Ce–N compounds

Abstract

Cerium ions can exist in the trivalent or tetravalent forms such as in Ce₂O₃ and CeO₂, respectively. Therefore, they can provide different chemical environments for stabilizing novel polymeric nitrogen species. This article explored the phase diagram of binary Ce–N compounds under pressures of up to 150 GPa using the crystal structure prediction method MAGUS. In this work, we find that nitrogen atoms can exist in the form of N₂, N₄, N₅, N₆, and N₈ units. In addition, we identified an infinite helical N₄ chain in I4₁/a CeN₄ at about 100 GPa. Differing from the well-known zigzag or armchair nitrogen chains which are mixed with single and double bonds, the helical N₄ chain is purely single-bonded. Moreover, it can be quenched to ambient pressure and exhibit excellent denotation properties. We also identified a layered porous nitrogen network in CeN₈. After the removal of cerium atoms, the nitrogen network is also dynamically stable in the R3̄ phase, which has a lower energy than the previously identified P1̄ phase. For the pentazolate salts, the I4/m CeN₁₀ exhibits ferromagnetism, while the C2 and P2₁2₁2 CeN₁₅ exhibit anti-ferromagnetism. Overall, the newly discovered Ce–N compounds with polymeric nitrogen exhibit fascinating structural and electronic characteristics, which may lead to potential application in areas such as explosives or catalysis.

---

Introduction

The element nitrogen plays an important role on earth. It takes the valence configuration of s²p³ which needs three extra electrons to fill the 2p shell. The easiest way is to share six electrons with another nitrogen atom forming the N≡N triple bond. Alternatively, it can form N–N single bonds with other nitrogen atoms to constitute three-coordinated nitrogen frameworks. Most strikingly, there exists a large energy difference between a single bond (∼160 kJ mol⁻¹) and a triple bond (∼954 kJ mol⁻¹).¹ Therefore, a great amount of chemical energy will be released when single-bonded nitrogen compounds are broken down into nitrogen gases, and polymeric nitrogen has potential application values in the energy-storage field or as explosives or propellants.^2,3

Researchers have predicted a series of stable nitrogen allotropes under high pressure, from the molecular crystals to the single-bonded cubic-gauge nitrogen in 1992 (cg-N),⁴ and then to the layered Pba2 phase in 2009,⁵ a cage-like diamondoid structure in 2012,⁶ and metallic salts in 2013.⁷ In addition, some metastable all-nitrogen polymeric structures are also predicted, such as the N₆ unit in 2016, N₈ in 2014, N₁₀ in 2020,^8–10 the chain-like Cmcm phase in 2003 and 2004,^11,12 and the layered black phosphorous structure in 2005.¹³ Because the N≡N triple bond is one of the strongest chemical bonds on earth, we need a large amount of energy to break it before forming polymerized structures. Extreme conditions such as high pressure and high temperature are inevitable for the experimental synthesis of pure polynitrogen. Although cubic gauge nitrogen (cg-N)⁴ has been proposed for a long time, the first experimental breakthrough was made by Eremets et al. in 2004.¹⁴ They synthesized cg-N under a high pressure of 110 GPa and a high temperature of over 2000 K. After that, people managed to acquire more polymeric nitrogen allotropes under higher pressure, including LP-N in 2014, HLP-N in 2019, and BP-N (black phosphorous phase) in 2020.^15–18 However, none of these polymeric phases have been recovered under ambient pressure, which limits their applications.

As an alternative way, people began to explore nitrogen-rich compounds that might be stabilized at much lower pressure. Among them, a variety of novel polynitrogen species were identified in alkali and alkaline-earth metal nitrides, for example, the azide N₃⁻ unit in XN₃ (X = Li, Na, and K),^19–21 the pentazolate N₅⁻ ring in LiN₅ in 2020,²² the cis-N₄ unit in Mg₂N₄ in 2019,²³ and the infinite one-dimensional (1D) armchair poly-N₄ chain in XN₄ (X = Be predicted in 2021, Mg in 2019, etc.).^23,24 These poly-nitrogen units are likely to capture extra electrons to fill the nitrogen 2p orbitals, thus serving as anions, while alkali or alkali-earth metals provide extra electrons, thus serving as cations. The alkali-earth metals can also form salts with pentazolates.^25–27 The transition metal elements with larger chemical valences and ionic radius can help attract more nitrogen species to reach larger energy densities.^2,28–32 For example, trivalent metal pentazolate salts (AlN₁₅, GaN₁₅, YN₁₅, etc.)³¹ predicted in the year 2020 have a much larger energy density (>4.5 kJ g⁻¹) than monovalent pentazolate salts LiN₅ (∼0.5 kJ g⁻¹).²² So are many other transition metal pentazolate salts that possess large energy densities.²⁹ On the other hand, the chain-like polymeric units in these compounds are just one or two-coordinated, and most of the bonds are mixed with single and double bonds. The first purely single-bonded polymeric nitrogen chain was experimentally realized in h-WN₆ in the form of an armchair-like N₆ ring in 2021.³³ It not only possesses very high energy density but also exhibits superhard properties.³⁴ With these concerns, we believe that nitrides with transition metal elements with large chemical valences might capture more nitrogen species or help form novel nitrogen configurations with striking properties.

Cerium is a typical rare-earth element and has the highest abundance among them on earth. It can exist in the trivalent and tetravalent forms just as in Ce₂O₃ and CeO₂, respectively.³⁵ Therefore, cerium might provide different chemical environments for stabilizing novel nitrogen species. However, only cerium pnictides have been widely studied to date,^36–39 and other stoichiometries have been paid little attention. In this work, we made full use of crystal structure search methods to explore the phase binary diagram of Ce–N compounds under high pressures of up to 150 GPa. We discovered the common N₂, N₄, N₅, N₆, and N₈ nitrogen units in these phases. In addition, we identified a novel purely single-bonded nitrogen chain in tetragonal CeN₄ that can be quenched to ambient pressure. It possesses a large energy density with detonation pressures close to 100 GPa. In addition, we identified a layered nitrogen configuration in CeN₈. After the removal of these cerium atoms, the pure nitrogen framework with the R3̄ space group can be recovered under ambient pressure, and it has a lower energy than the previously predicted P1̄ phase which has a different stacking way.

Results and discussion

1. Convex hull and phase diagrams

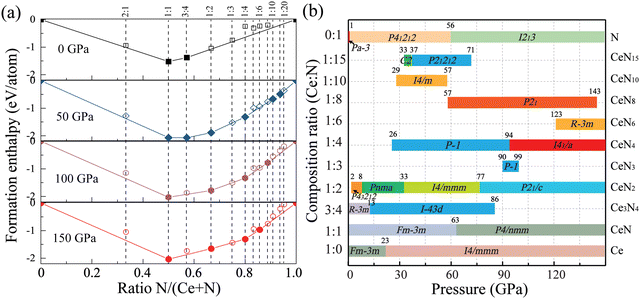
First-principles structure predictions were performed to explore the most stable Ce–N compounds at specific pressures of 0, 50, 100, and 150 GPa. To systematically investigate the potential Ce–N compounds and find novel nitrogen species, we performed fixed-composition crystal structure predictions for nitrogen-rich integer stoichiometries (CeN_n and CeN_2m with n, m = 1–5). Molecular crystal structure predictions with pentazolates (N₅) were then performed for Ce(N₅)_n with n = 1–4. Moreover, to explore tetravalent cerium nitrides and cerium-rich compounds, we also take into account the stoichiometries of 3 : 4 and 2 : 1. Most of the identified structures are discussed below, and some crystal structures are present in Fig. S1 (ESI†). As a result, Fig. 1(a) displays the final obtained convex hull curves at specific pressures. The curves are plotted according to the formation enthalpies, which are defined as ΔH = [H(Ce_xN_y) − xH(Ce) − yH(N)]/(x + y). The enthalpies for pure nitrogen or cerium are calculated with the most stable phases at corresponding pressures. For nitrogen, it is α-N (Pa3̄), P2₁/c, P4₁2₁2, and cg-N (I2₁3) at pressure sequences.⁴⁰ For cerium, it has been found that cerium transforms from the α phase (space group Fm3̄m) to monoclinic α′′ phase (space group C2/m) at about 5 GPa and then to the body-centered-tetragonal (bct) phase (spacegroup I4/mmm) at about 12 GPa with pressure increasing at zero temperature,^41,42 and the bct-Ce maintains the most stable phase up to at least 208 GPa.^41,43 We then calculated the pressure-dependent enthalpy curves of the α, α′′, and bct phases at the PBE level, as plotted in Fig. S1 (ESI†). The α′′ phase has a similar enthalpy curve as the bct phase. The α phase will transform into the bct phase at about 10 GPa at the PBE level. In addition, the PBE functional underestimates the lattice constants of the α phase (Table S1, ESI†). For the CeN compounds, it has been found that the B1 phase will transform into the B10 phase at about 65 GPa. But the calculated phase transition pressure at the PBE level is only about 45 GPa (see Table S2, ESI†). Due to the f electrons of cerium being very localized, it is necessary to employ the DFT+U method. We further employed the PBE+U method with a series of U values, while keeping the exchange parameters J at 0 eV, by which the phase transition pressure can be raised to a more reasonable value. The PBE+U with U = 3.5 gives a phase transition pressure of 63 GPa, which is close to the experimental value of 65 GPa. In the following, we employed both the PBE and PBE+U method for enthalpy calculations.

Fig. 1 (a) Convex hull curves of the Ce–N system at pressures of 0, 50, 100, and 150 GPa at the PBE+U level. The solid symbols represent the thermodynamically stable phases. (b) The pressure- and composition-dependent phase diagram of Ce–N compounds in the pressure range of 0–150 GPa at the PBE+U level, the numbers above the phase boundary represent the thermodynamically stable pressure range in the unit GPa.

We then calculated the detailed enthalpies of these stable phases and some metastable structures in the pressure range of 0–150 GPa with an interval of 5 GPa. The detailed phase transition pressure and thermodynamical stability ranges are determined with an accuracy of 1 GPa through the interpolated enthalpy curves as plotted in Fig. S2 (ESI†). Specifically, the cerium mononitride CeN stays thermodynamically stable throughout the pressure range studied. At ambient pressure, it exists in the typical NaCl-type B1 structure with the space-group Fm3̄m. The phases on the convex hull are thermodynamically stable, while those close to the convex hulls which are dynamically stable might also be synthesized in the experiments. We also explored some of these metastable phases with an energy window not larger than those of the convex hulls by 200 meV.⁴⁴ The calculated lattice parameters and enthalpy results are presented in Tables S3 and S4 (ESI†), respectively. We also present the results for pure nitrogen, cerium, and CeN phases in Table S5 (ESI†). The calculated phonon spectra of these structures are displayed in Fig. S3 and S4 (ESI†), and the phonon spectra of some of the structures quenched to ambient pressure are displayed in Fig. S5 and S6 (ESI†).

2. The Ce₂N compound

Firstly, we looked into the Ce₂N compounds. The P3̄m1 phase is thermodynamically stable at around 45 GPa at the PBE level, but it is not thermodynamically stable when taking into account the Hubbard U as shown in Fig. S2 (ESI†). However, its enthalpy is higher than that of the convex hull with a value of 80 meV per atom at about 60 GPa at the PBE+U level. The calculated phonon spectrum exhibits no imaginary frequency indicating its dynamical stability. The P3̄m1 phase is composed of the sandwiched Ce₂N layers as shown in Fig. S1 (ESI†). The calculated electronic density of states predicts the P3̄m1 phase to be metallic (see the density of states in Fig. S7, ESI†). It has been found that the Ba₂N compound also crystalizes in the P3̄m1 structure, which is predicted to be an electride with interstitial electrons.²⁵ However, no interstitial electrons are found in the electron localization function (ELF) of the P3̄m1 Ce₂N phase, and thus it should not be an electride.

3. The Ce₃N₄ compound

Except for the CeN compounds, we discovered another thermodynamically stable compound at ambient pressure with a stoichiometry of 3 : 4 as shown in Fig. 2. It takes the space group of R3̄m, and there are two types of layers in the unit cell, the sandwiched CeN₂ layer, which is isostructural to the trigonal transition metal dichalcogenide such as 1T-WS₂; and the double-layered Ce₂N₂ structure. The calculated electronic band structure predicts the R3̄m Ce₃N₄ to be an insulator with a band gap of about 1 eV at 0 GPa. This phase is thermodynamically stable from 0 GPa to 13 GPa, above which it will transform into the I4̄3d Ce₃N₄ which is thermodynamically stable in the pressure range of 13–86 GPa. The I4̄3d Ce₃N₄ is isostructural to I4̄3d Sn₃N₄.⁴⁵ However, the band gaps of I4̄3d Ce₃N₄ decrease with increasing pressure as displayed in Fig. S8 (ESI†), which is different from Sn₃N₄.

Fig. 2 The structural and electronic properties of the R3̄m Ce₃N₄ compounds at 0 GPa. (a) The side view of the structure. There are two different layers in this phase, we present the top views of (b) the double-layered Ce₂N₂ and (c) the sandwiched CeN₂. (d) The calculated band structure at the PBE+U level.

4. The CeN₂ compound

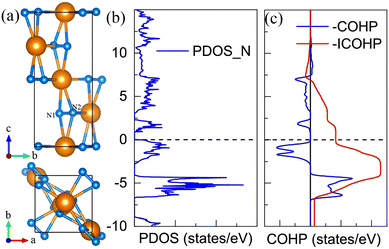
For the CeN₂ compound, there are only two stable phases at the PBE level, that is the P4₃2₁2 phase and the Pnma phase. However, when taking into account the Hubbard U, the I4/mmm and P2₁/c phases also turn out to be thermodynamically stable. At the PBE+U level, the P4₃2₁2 phase is thermodynamically stable from 2 GPa to 8 GPa, after that, it will transform into the Pnma phase at about 8 GPa, and then to the I4/mmm phase at about 33 GPa, and finally to the P2₁/c phase at about 77 GPa, which remains thermodynamically stable up to at least 150 GPa. Nitrogen atoms exist in the form of diatomic configurations in these phases. It has been found that such diatomic configurations can possess a formal charge of −4 with tetravalent cations M⁴⁺(N₂)⁴⁻, which are called pernitrides and has a typical N–N bond length of 1.42 Å;⁴⁶ or they exhibit a formal charge of −2 with divalent cations M²⁺(N₂)²⁻, which are called dinitrides and has a typical double bond length of about 1.22 Å.^47,48 However, for these CeN₂ phases, the nitrogen bond length is around 1.35 Å, and the calculated bond orders run from 1.43 to 1.87 as listed in Table S6 (ESI†). Both the bond length and bond orders indicate that these bonds are between single and double bonds, which are different from those of the pernitrides or dinitrides. The nitrogen bond lengths in CeN₂ are closer to those in LaN₂ and YN₂ systems, which are 1.30 Å and 1.33 Å, respectively.⁴⁹ The La and Y atoms exist in the form of trivalent cations, and the N₂ configuration has a formal charge of −3. For the LaN₂ or YN₂ phases, 3/4 of the two degenerate anti-bonding π* orbitals of the diatomic N₂ unit are occupied by 3 electrons, and therefore they exhibit metallic properties. For the P4₃2₁2 CeN₂, we presented the –COHP results of two p_z orbitals from the N1–N2 unit, more than half of the anti-bonding state is occupied as shown in Fig. 3(b). The total two anti-bonding orbitals should also be occupied by three electrons, but contrary to the LaN₂ structure, the CeN₂ phase exhibits semiconducting properties as shown in Fig. 3(c). Such separated anti-bonding orbitals might be attributed to the local environment of the N₂ units, which are not located in the middle of the cavities surrounded by cerium atoms. The Pnma and I4/mmm phases exhibit metallic properties, while the P2₁/c phase is a semiconductor as shown in Fig. S7 (ESI†).

Fig. 3 The structural and electronic properties of the P4₃2₁2 CeN₂ compounds at 5 GPa. (a) The side and top view of the structure. (b) The projected density of states for the nitrogen atoms. (c) The minus Crystal Orbital Hamilton Population (–COHP) and the Integrated COHP (–ICOHP) for the p_z orbitals of the N1 and N2 nitrogen diatomic configuration. The cartesian axis of z is along the lattice direction of c.

5. The P1̄ CeN₃

For the CeN₃ compound, it is thermodynamically stable in the pressure range of 90–99 GPa (PBE+U) with the space group of P1̄. There are two nitrogen configurations in it: the diatomic N₂ and trans-N₄. The bond length in diatomic N₂ is 1.30 Å and the bond order is 1.59, both of which are similar to that in the CeN₂ phase. The diatomic N₂ in CeN₃ should also acquire three electrons. For the trans-N₄, the bond lengths are all 1.31 Å. The bond order between the terminal N2 atom and the two-coordinated internal N3 atom (Table S6, ESI†) is 1.46, and the bond order between the internal N3 and N3′ is 1.25, both of which are between those of the single and double bonds. There are totally four p_z orbitals for the N₄ unit, forming two bonding π orbitals and two anti-bonding π* orbitals. The neutral N₄ unit has 2 electrons occupying these p_z orbitals. If the N₄ unit acquires 4 electrons, the total 6 electrons will occupy two bonding π orbitals and one anti-bonding π* orbital, the total bond order for these π orbitals should be one. Taking three single σ bonds into account, the perfect [N₄]⁴⁻ unit should possess one double bond and two single bonds. Such a situation has been identified in many alkaline-earth metal nitrides.^50,51 Take the CaN₂ compound as an example,⁵⁰ the bond between the terminal and internal atoms has an order of 1.67, which is considered as a double bond. But the bond between two internal atoms has an order of 1.01, which is assigned as a single bond. The former bond order is larger than the latter, and the total bond order is 3.69, less than 4 of the perfect [N₄]⁴⁻ unit. For the N₄ unit in the CeN₃, the bond order between two internal atoms is 1.25, but the bond order between the terminal atom and the internal atom is 1.46, and the former bond order is smaller than the latter; such situation is different from that in CaN₂. Moreover, the total bond order of the N₄ unit in CeN₃ is 4.17, larger than 4 of the perfect [N₄]⁴⁻ unit. As a rational explanation, the N₄ unit in CeN₃ is more likely to acquire 3 electrons, and the total 5 p_z electrons occupy two bonding orbitals and 1/4 of two anti-bonding orbitals, which should give a bond order larger than 4, consistent with the calculated bond order of 4.17. The calculated density of states predicts the P1̄ CeN₃ to be metallic as shown in Fig. S7 (ESI†).

6. The P1̄ CeN₄

The P1̄ CeN₄ with molecular N₈ units becomes thermodynamically stable above 26 GPa at the PBE+U level. The calculated phonon spectrums of this phase at both high pressure and ambient pressure exhibit no imaginary frequency, indicating its dynamical stability. The N₈ unit is centrosymmetric with the nitrogen atoms from the terminal to the internal denoted as N1, N2, N3, and N4, respectively. Such N₈ configuration has been found in Sn–N phases.⁴⁵ It has a formal charge of −8 in the P1̄ SnN₄ with two double bonds in the Lewis structure, while it has a formal charge of −6 in the P1̄ SnN₅ with only one double bond in the middle of the N₈ unit for the Lewis structure. For the P1̄ CeN₄, six internal nitrogen atoms take the normal armchair-like structure with little rotation, while the two terminal atoms N1 have a large deviation from the armchair configuration. Bader charges analysis⁵² reveals that the N1 atom acquires 0.85e, N2 acquires 0.46e, and the remaining nitrogen atoms each acquire approximately 0.36e. To reveal the bonding properties, we calculated the electron localized function⁵³ (ELF) (Fig. 4(b)), the high localization around each nitrogen atom represents electron lone pairs, which take the crescentic shape for the six internal nitrogen atoms, and the disk shape pointing to the terminal N1 atom. There are four different bonds in the N₈ unit differentiated by their lengths, which are 1.35 Å, 1.40 Å, 1.32 Å, and 1.38 Å at 50 GPa from the terminal to the internal. The corresponding bond orders are 1.42, 1.12, 1.34, and 1.16, respectively. As a result, the N2–N3 and N4–N4′ bonds are close to the single bond, while the N1–N2 or N3–N4 bonds are between the single and double bonds. The calculated total bond order for the N₈ unit with 7 bonds is about 8.9, and thus it is more likely for the Lewis structure of the N₈ unit to possess two double bonds instead of one. As the bonds between N3 and N4 possess the shortest length, a reasonable Lewis structure might be constructed as shown in Fig. 4(d), in which the double bond only appears between the N3 and N4 atoms. As a result, the two coordinated N2, N3, and N4 nitrogen atoms belong to the AX₂E₂, AX₂E₁, and AX₂E₁, respectively. Therefore, this nitrogen configuration presents a bent geometry according to the VSEPR. According to the bond orders, another possible Lewis structure might be constructed as shown in Fig. S9 (ESI†), in which the N1–N2 bond is assigned as a double bond. The electronic band structure calculation shows that the P1̄ CeN₄ is a semimetal as shown in Fig. 4(e).

Fig. 4 The structural and electronic properties of the P1̄ CeN₄ compounds at 50 GPa. (a) The side view of the P1̄ phase at 50 GPa, (b) the corresponding electron localization function (ELF) with an isosurface value of 0.85, (c) the top view of the P1̄ phase at 50 GPa, (d) a possible Lewis structure for the N₈ molecular unit, and (e) the band structure and projected density of states (PDOS) of P1̄ CeN₄.

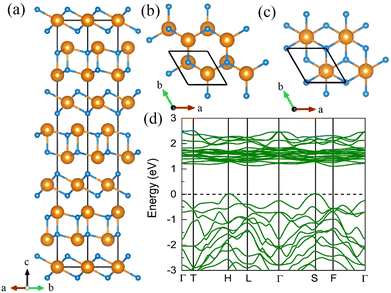
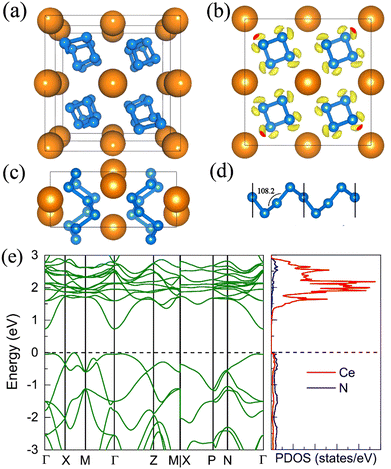
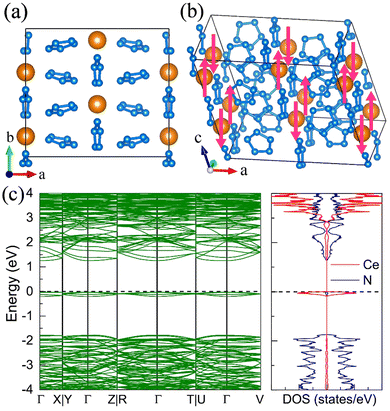
7. The I4₁/a CeN₄

With increasing pressure to 94 GPa, the P1̄ CeN₄ will be energetically substituted by a tetragonal I4₁/a phase which is composed of cerium ions and infinite nitrogen chains (Fig. 5). This kind of chain possesses a helical structure with four nitrogen atoms in one period along the c direction. To the best of our knowledge, armchair and zigzag-like polymeric nitrogen chains have been widely studied in many systems,^54,55 but the helical chains have not been studied up to now. The infinite spiral chain has been predicted for the oxygen and realized in sulfur and selenium element phases.^56,57 All the nitrogen atoms in this chain have equivalent Wyckoff positions, and there is only one type of bond, which is calculated to be 1.36 Å at 120 GPa. The bond length is similar to that in cg-N, and the helical-N₄ chain should be purely single-bonded. In addition, the distance between cerium and nitrogen is 2.45 Å, and the angle between two adjacent bonds is 108° at 120 GPa. Bader charge analysis shows that each nitrogen atom captures 0.48e from cerium atoms, revealing their ionic interactions. Furthermore, ELF calculations show that two electron lone pairs exist around each nitrogen atom (Fig. 5(b)). The nitrogen atoms in the helical-N₄ chain should be sp³-hybridized such that two of these orbitals are single-bonded with two adjacent nitrogen atoms and the remaining two orbitals are occupied by two electron lone pairs. Each nitrogen atom in the helical-N₄ chain should acquire one extra electron, and the cerium atoms exhibit tetravalent properties. The bent configuration of the helical chain can also be explained by the VSEPR that every nitrogen atom belongs to the AX₂E₂.

Fig. 5 The structural and electronic properties of the I4₁/a CeN₄ compound at 120 GPa. (a) The top view of I4₁/a CeN₄, (b) the ELF result with an isosurface value of 0.89, (c) the side view of I4₁/a CeN₄, (d) the helical structure of the infinite nitrogen chain. (e) The band structure and PDOS at the PBE+U level.

We further calculated the electronic band structure of this novel phase at 120 GPa. It turns out to be a semiconductor with an indirect bandgap of approximately 1 eV. The nitrogen orbitals and cerium orbitals contribute most to the valence bands, while the conduction bands are only contributed by cerium orbitals. There are no imaginary frequencies found in the phonon spectrum at both 0 GPa and 120 GPa, indicating that this phase might be quenched to ambient pressure. We also employed the AIMD simulations for it at 0 GPa, which remains stable at 300 K, but some N₂ units split from the helical chains at 400 K (see Fig. S10, ESI†). The bond length between nitrogen atoms in the helical-N₄ chain is calculated to be 1.42 Å at 0 GPa, close to that of the single bond. Thus, the I4₁/a CeN₄ might be a good candidate for high-energy-density materials. Although the cerium atoms are rather heavy and the abundance of nitrogen is not high in I4₁/a CeN₄, it still possesses a large gravimetric energy density of 1.81 kJ g⁻¹ with the decomposition products of Ce₃N₄ and N₂. By using the Kamlet–Jacobs empirical equations, its detonation pressure is calculated to be approximately 100 GPa (see Table 1), which is about 5 times TNT (∼19.0 GPa) and 2.5 times HMX (∼39.3 GPa).⁵⁸ However, it is worth noting that the cerium dioxide which should be the product of the Ce–N compounds in the atmospheric environment is toxic, and that the Ce–N compounds cannot be used as safe HEDMs. The energy density properties with other decomposition products are also presented in Table S7 (ESI†). The single-bonded nitrogen configuration has been realized in WN₆ with armchair like N₆ rings, and in TaN₅ with infinite chains. We believe that the CeN₄ with all single-bonded nitrogen chains is likely to be synthesized in the near future.

Table 1 The calculated energy density and denotation properties of I4₁/a CeN₄ at the PBE+U level at 0 GPa, the energy difference between the crystal α-N₂ and gaseous nitrogen molecule is taken as 0.25 eV per atom.² The experimental values from the well-known explosives TNT and HMX are also presented

Materials	ρ (g cm^−3)	E g (kJ g^−1)	E v (kJ cm^−3)	V d (km s^−1)	P d (GPa)
I41/a CeN4	6.43	1.81	11.62	11.69	98.6
TNT	1.64	4.30	7.05	6.90	19.0
HMX	1.90	5.70	10.83	9.10	39.3

---

8. The R3̄m CeN₆

The R3̄m CeN₆ becomes thermodynamically stable above 123 GPa. It is isostructural to h-WN₆ or MoN₆ with a 6-membered ring in a chair conformation as shown in Fig. S1 (ESI†).^32,34 However, unlike h-WN₆, the R3̄m CeN₆ is calculated to be metallic. We calculated the bond properties of this phase at 140 GPa. The obtained bond lengths are 1.34 Å, which is close to the bond length of cg-N (1.33 Å) at the same pressure. The calculated bond order in the N₆ unit is 1.13 at 140 GPa, which is also close to that of the single bond. For the N₆ ring, six p_z orbitals form three bonding π orbitals and three anti-bonding π* orbitals. The neutral N₆ ring has 6 electrons occupying these orbitals. Thus, the cerium atoms are likely to lose four electrons to the N₆ ring and the total 10 π electrons can satisfy the 4n + 2 (n = 2) Hückel rule. Six of the 10 π electrons will occupy 3 bonding states, and four of the 10 π electrons will occupy 2 anti-bonding states. As a result, the total bond order for the N₆ ring should be about 7 (take six σ bonds into account), and the average bond order should be 1.17 which is close to the calculated values of 1.13. There should be an energy gap between the occupied two degenerate π* levels and the unoccupied π* levels according to the molecular orbital analysis.⁵⁹ We then calculated the band structure of the CeN₆ phase at 140 GPa. It is metallic at the PBE+U level but becomes a semimetal at the HSE06 level (Fig. S11, ESI†). However, this phase should be a semiconductor at a much lower pressure. (Fig. S12, ESI†), consistent with the molecular orbital analysis. The very high pressure induces the gap closing in this phase.

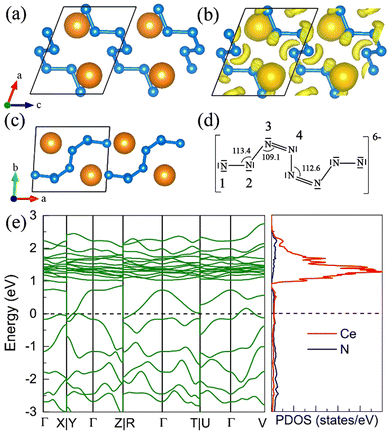
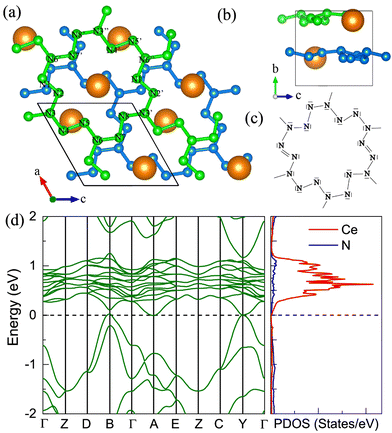
9. P2₁ CeN₈

The P2₁ CeN₈ turns out to be thermodynamically stable above 58 GPa. It is composed of two atomically thick CeN₈ layers in the unit cell. There are two types of nitrogen atoms by the coordination numbers. Six 3-coordinated atoms and twelve 2-coordinated nitrogen atoms are combined to form the extended covalent two-dimensional networks with 18-membered hexagonal rings, and the cerium atoms are rightly located in the center of the hexagonal hole. It is worth noting that such kind of poly-nitrogen network has been first predicted in K₂N₁₆ by Steele and Oleynick in 2017,⁶⁰ and then in high-pressure XeN₈ and Xe(N₈)₂(N₂) solid-state compounds,⁶¹ and then in YN₈ in 2022.⁶² For the P2₁ CeN₈, the average distance between two adjacent layers is about 2.38 Å at 60 GPa. The top layer has a shift of about half the lattice along the [101] direction as compared to the bottom layer. This kind of shift results in the non-equivalence of the 2-coordinated nitrogen atoms. We have presented the ELF results in Fig. S13 (ESI†); there are electrons localized outside the two-coordinated nitrogen atoms, indicating the electron lone pairs. Bader charge analysis reveals that the two-coordinated N1 (N2), N4 (N5), and N7 (N8) atoms each capture about 0.29e, 0.46e, and 0.23e, respectively; the three-coordinated nitrogen atoms each acquire electrons less than 0.1e. The calculated bond orders for the bonds between two two-coordinated nitrogen atoms of N1–N2, N4–N5, and N7–N8 are 1.32, 1.21, and 1.27, respectively, which are between the single and double bonds indicating a strong π delocalization. The bond orders for the bonds between the two-coordinated and three-coordinated atoms run from 1.0 to 1.1, which indicates the single bonds. Given these bonding properties, we propose a possible Lewis structure as shown in Fig. 6(c), in which the N4–N5 and N7–N8 are assigned as a single bond and N1–N2 as the double bond. Given the similarities between the N1–N2 and N7–N8 bonds, other Lewis structures might be drawn. With this configuration, each ring possesses 14 π electrons. The eight two-coordinated N4 (N5, N4′, and N5′) and N7 (N8, N7′, and N8′) atoms each denote one π lone pair shared by two rings (8 × 1/2 π pairs), the two bonds N1–N2 (N1′–N2′) each denote one π pair also shared by two rings (2 × 1/2 π pairs), and the six three-coordinated atoms each denote one π lone pair shared by three rings (6 × 1/3 π pairs). Wang et al. have identified a similar 2D polynitrogen with the 18-membered ring in Xe–N systems, and they proposed that each ring has formally 10 π electrons, which follow the Hückel rule with 4n + 2 π electrons and can be classified as an aromatic. As to the CeN₈, each nitrogen ring has 14 π electrons, which also follow the Hückel rule with n = 3. Such a configuration possesses the formal charge −4. In addition, the two coordinated N1 (N2) and N4 (N5, N7, and N8) atoms belongs to the AX₂E₁ and AX₂E₂, respectively. Therefore, this nitrogen configuration presents a bent geometry according to the VSEPR. The strong π electron delocalization makes the trigonal geometry planar, the same as in the Xe–N systems. The calculated band structure at the PBE+U level predicted the P2₁ CeN₈ to be a semimetal with a Dirac point at the Y point, The HSE06 calculation does not change the semimetal properties of this phase as shown in Fig. S14 (ESI†). The PBE+U+SOC calculation opens the Dirac point at the Y point.

Fig. 6 The structural and electronic properties of the P2₁ CeN₈ compounds at 60 GPa. (a) The top and (b) side view of the structure. There are two nitrogen layers in the primitive cell as shown by the green and blue colors, different nitrogen atoms in the top layer are denoted with numbers. (c) The Lewis structure for the 18-membered ring with two double bonds. (d) The calculated electronic band structure and projected density of states at the PBE+U level.

10. The metastable R3̄ CeN₈

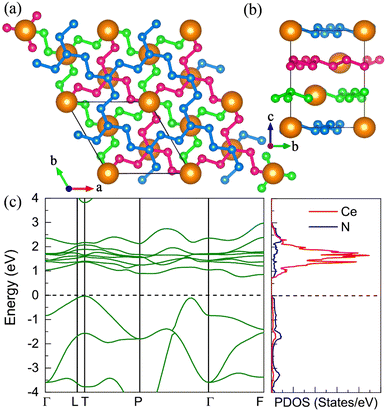
On the other hand, we found the R3̄ CeN₈ has higher energy than the P2₁ CeN₈ below 150 GPa. The R3̄ phase is also composed of the above-mentioned porous polynitrogen but in a different stacking way. There are three layers in the unit cell, as painted with three colors in Fig. 7. Within this configuration, the two-coordinated atoms are all equivalent. The bond length between N1 and N2 (see Table S6, ESI†) is approximately 1.32 Å at 120 GPa, and the distance between the two-coordinated N2 and N2′ atoms is 1.35 Å. The nitrogen bond lengths in the R3̄ phase are also between those of the single and double bonds, indicating strong delocalization. The electronic band structure and density of states show that the R3̄ phase is a semiconductor with an indirect bandgap of approximately 0.8 eV. We further calculated the band structure of the R3̄ phase at 60 GPa at the HSE06 level (Fig. S15, ESI†) for comparison with the P2₁ phase. The HSE06 functional also predicts the R3̄ phase to be a band insulator. The band gap increases from the P2₁ phase to the R3̄ phase. We looked into the band structure of the P2₁ phase, the conduction and valence bands get close to each other at the B(0, 0, 0.5) and Y(0.5, 0, 0) points, which means that the metallic properties are almost along the a and c directions, that is within the CeN₈ layers. We then compared the geometric structures of these two structures at 60 GPa. The average distance between the cerium atoms and the adjacent nitrogen atoms within the same layer in the P2₁ phase is about 2.368 Å, but the result is 2.441 Å in the R3̄ phase. The closer distance between the cerium and nitrogen atoms makes the cerium orbitals overlap more with electron lone pairs outside the two-coordinated nitrogen atoms. As a result, the contribution of cerium orbitals into the valence band increases it and decreases the band gaps.

Fig. 7 The structural and electronic properties of the R3̄ CeN₈ compounds at 120 GPa. (a) The top and (b) side view of the structure. There are three nitrogen layers in the unit cell as shown with the blue, green, and magenta colors. (c) The calculated electronic band structure and projected density of states at the PBE+U level.

After the removal of the cerium atoms, the nitrogen networks in the R3̄ phase remain in the same symmetry, and its phonon spectrum exhibits no imaginary frequency at ambient pressure indicating its dynamical stability. We also presented the AIMD results for its bulk and monolayer forms in Fig. S16 and S17 (ESI†), respectively. We found that the R3̄ nitrogen phase has lower energy than the previously identified P1̄ phase by about 9 meV per atom at the SCAN + rvv10 level.⁶¹ The energy results from other pure nitrogen phases are also listed in Table S8 (ESI†).

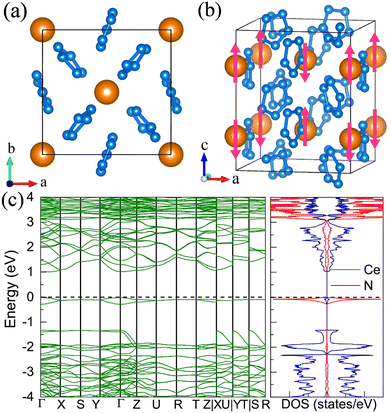
11. Pentazolate salts

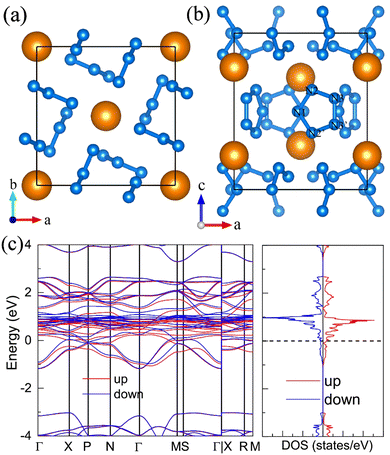
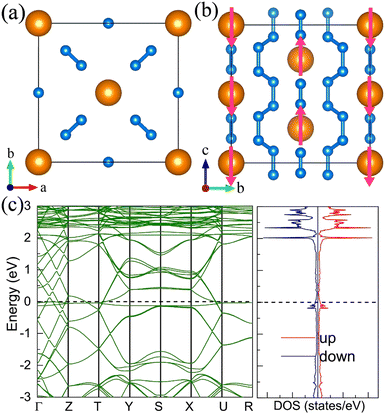
For the molecular crystals with nitrogen pentazolates, the I4/m CeN₁₀ is thermodynamically stable from 29 GPa to 57 GPa. The DOS calculation predicts it to be metallic as shown in Fig. S7 (ESI†). These pentazolates are parallel to the lattice axis c. Most interestingly, the spin-polarized calculations predict the I4/m CeN₁₀ to be iterant ferromagnetic (see Fig. 8) with the magnetic moment being 0.2μ_B per formula unit at about 50 GPa at the PBE+U level. For the CeN₁₅ phases, the C2 phase is not thermodynamically stable at the PBE level, but it turns out to be thermodynamically stable from 33 GPa to 37 GPa at the PBE+U level (see Fig. S2, ESI†). The pentazolates are almost parallel along the c-axis and the cerium atoms take hexagonal arrays in the ab plane. The spin-nonpolarized calculations predict this phase to be metallic. However, the antiferromagnetic (AFM) configuration is found to possess the lowest energy as displayed in Fig. 9 by magenta arrows, which exhibits a zigzag-type anti-ferromagnetism within the ab plane and anti-ferromagnetism along the c-axis. The AFM phase is insulating with a band gap of about 1.23 eV. The highest occupied valence bands are mostly projected to the cerium orbitals as shown in Fig. 9, and the calculated magnetic moment is about 1μ_B per cerium atom at about 35 GPa at the PBE+U level. As a result, one of the f-orbitals of the cerium atom is half-filled, and that cerium atom exhibits trivalent properties. When pressure is increased above 37 GPa, the C2 phase will transform into the P2₁2₁2 phase, which also exhibits antiferromagnetic properties (see Fig. 10).

Fig. 8 The structural and electronic properties of the I4/m CeN₁₀ compounds at 50 GPa. (a) The top and (b) side view of the structure. Nitrogen atoms in one pentazolate are denoted with numbers. (c) the spin-polarized electronic band structure and density of states at the PBE+U level.

Fig. 9 The structural and electronic properties of the C2 CeN₁₅ compounds at 35 GPa. (a) The top and (b) side view of the 1 × 2 × 2 superstructure. The antiferromagnetism arrays of the cerium atoms are denoted by magenta arrows. (c) The spin-polarized electronic band structure and density of states at the PBE+U level.

Fig. 10 The structural and electronic properties of the P2₁2₁2 CeN₁₅ compounds at 50 GPa. (a) The top and (b) side view of the 1 × 1 × 2 superstructure. The antiferromagnetism arrays of the cerium atoms are denoted by magenta arrows. (c) The spin-polarized electronic band structure and density of states at the PBE+U level.

12. The metastable Immm CeN₁₀

The I4/m CeN₁₀ is thermodynamically stable above 29 GPa, but the Immm CeN₁₀ phase has a lower enthalpy than the I4/m phase below 25 GPa at which the enthalpy of the Immm phase is about 19 meV per atom higher than the convex hull. Moreover, the Immm phase is dynamically stable (Fig. S4, ESI†). Therefore, it is metastable and likely to be synthesized. As shown in Fig. 11, this phase should be isostructural to the Immm HfN₁₀ with isolated nitrogen diatomic molecules and infinite armchair chains parallel to the c-axis.² The calculated bond length of the diatomic N₂ is 1.11 Å, and the bond order is 2.45 at 20 GPa, which predicts a bond length between double and triple bond. The calculated bond lengths for the N2–N3 and N3–N4 (see Table S7, ESI†) within the armchair chains are 1.31 Å and 1.33 Å, respectively. The corresponding bond orders are 1.45 and 1.35, respectively. These bonds should be between the single and double bonds with strongly delocalized π electrons. In addition, the Immm CeN₁₀ is calculated to the spin-polarized, and the enthalpy lowest magnetic configuration is displayed in Fig. 11(b), in which the cerium atom is ferromagnetic along the c-axis, while the nearest cerium atoms in the ab plane are anti-ferromagnetic. The spin-polarized band structure also predicts the Immm CeN₁₀ to be metallic.

Fig. 11 The structural and electronic properties of the Immm CeN₁₀ compounds at 20 GPa. (a) The top and (b) side view of the 1 × 1 × 2 superstructure. The antiferromagnetism arrays of the cerium atoms are denoted by magenta arrows. (c) The spin-polarized electronic band structure and density of states at the PBE+U level.

Conclusions

In summary, we performed a systematic crystal structure prediction for Ce–N compounds under high pressures of up to 150 GPa. A variety of nitrogen-rich phases are predicted to be thermodynamically stable at specific pressures. Among them, the infinite helical nitrogen chain is discovered for the first time within the I4₁/a CeN₄, in which the cerium atom exhibits tetravalent properties and the nitrogen chains are purely single-bonded. This phase can be recovered under ambient conditions. Although the cerium atoms are rather heavy in I4₁/a CeN₄, it still possesses a large gravimetric energy density of 1.81 kJ g⁻¹ when broken down into Ce₃N₄ and N₂. Moreover, its detonation pressure is close to 100 GPa, which is about 5 times TNT (∼19.0 GPa) and 2.5 times HMX (∼39.3 GPa).⁵⁸ In addition, we identified two CeN₈ phases with the space group of P2₁ and R3̄, in which the cerium atoms are embedded in the porous nitrogen frameworks. After the removal of these cerium atoms, the pure nitrogen framework with R3̄ symmetry is still stable and has a lower energy than the previously identified P1̄ phase at ambient pressure. Moreover, we found that the I4/m CeN₁₀ with pentazolates exhibits iterant ferromagnetism while the C2 and P2₁2₁2 CeN₁₅ exhibit antiferromagnetic properties with one of the cerium f-orbitals half-filled, in which the cerium atoms exhibit trivalent properties.

Computational details

First-principles structure predictions were performed at pressure points of 0, 50, 100, and 150 GPa using our recently developed machine learning and graph theory accelerated crystal structure prediction software MAGUS.^34,63 This method has been successfully applied in many systems.^64–67 Variable composition searches are carried out with the unit cell containing up to 40 atoms. Fixed composition non-molecular crystal structural searches were employed for given compositions, in which the unit cells contain up to four corresponding Ce_xN_y formula units. For the molecular crystal structure predictions, we adopted up to 5 formula units for CeN₅, 3 formula units for CeN₁₀ and CeN₁₅, and 2 formula units for CeN₂₀. 40 random structures were generated in the first generation and subsequent generations contain 30 structures. Structural optimizations and electronic structure analysis were performed according to density functional theory (DFT) within the generalized gradient approximation (GGA) using Perdew–Burke–Ernzerhof (PBE) functionals⁶⁸ as implemented in the VASP package.⁶⁹ Due to the f-electrons of cerium atoms being very localized, we employed the PBE+U method with U = 3.5 to have a better description of the electronic properties of Ce–N compounds. The projector augmented wave (PAW)⁷⁰ potentials were used with core electrons for cerium and nitrogen being [Kr]4d¹⁰ and [He], respectively. We used the Monkhorst–Pack⁷¹ scheme to sample the Brillouin Zone with a grid spacing of 2π × 0.03 Å⁻¹ and a kinetic energy cutoff of 1050 eV for plane-wave expansion. The DFT-D3 scheme was used to describe the van der Waals (vdW) interactions within the layered configuration.⁷² We optimized these novel structures with convergence criteria 2 × 10⁻⁴ eV Å⁻¹ and 1 × 10⁻⁵ eV for force and total energy per atom, respectively. The bond orders are calculated from Manz's bond order equation with DDEC6 partitioning as employed in the Chargemol program.^73–77 All the phonon frequencies were calculated using the finite displacements method as implemented in the PHONOPY package.⁷⁸ The energy reduction from the solid nitrogen phase to the gaseous state is taken as 0.25 eV per atom. We check the thermal stability of these phases at finite temperatures by ab initio molecular dynamics (AIMD) simulations. The simulations were performed for 10 ps with an interval of 1 fs using the NVT ensemble with a Nosè–Hoover thermostat.^79,80 Crystal structure visualization was performed through VESTA software.⁸¹

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

J. S. gratefully acknowledges the financial support from the National Natural Science Foundation of China (grant no. 12125404, 11974162, and 11834006) and the Fundamental Research Funds for the Central Universities. The calculations were carried out using supercomputers at the High-Performance Computing Center of Collaborative Innovation Center of Advanced Microstructures, the high-performance supercomputing center of Nanjing University.

References

1. M. I. Eremets, M. Y. Popov, I. A. Trojan, V. N. Denisov, R. Boehler and R. J. Hemley, Polymerization of nitrogen in sodium azide, J. Chem. Phys., 2004, 120, 10618–10623.
2. J. Zhang, A. R. Oganov, X. Li and H. Niu, Pressure-stabilized hafnium nitrides and their properties, Phys. Rev. B, 2017, 95, 020103.
3. K. O. Christe, Recent advances in the chemistry of N₅⁺N₅⁻ and high-oxygen compounds, Propellants, Explos., Pyrotech., 2007, 32, 194–204.
4. C. Mailhiot, L. H. Yang and A. K. McMahan, Polymeric nitrogen, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 14419–14435.
5. Y. Ma, A. R. Oganov, Z. Li, Y. Xie and J. Kotakoski, Novel High Pressure Structures of Polymeric Nitrogen, Phys. Rev. Lett., 2009, 102, 065501.
6. X. Wang, Y. Wang, M. Miao, X. Zhong, J. Lv, T. Cui, J. Li, L. Chen, C. J. Pickard and Y. Ma, Cagelike Diamondoid Nitrogen at High Pressures, Phys. Rev. Lett., 2012, 109, 175502.
7. J. Sun, M. Martinez-Canales, D. D. Klug, C. J. Pickard and R. J. Needs, Stable All-Nitrogen Metallic Salt at Terapascal Pressures, Phys. Rev. Lett., 2013, 111, 175502.
8. M. J. Greschner, M. Zhang, A. Majumdar, H. Liu, F. Peng, J. S. Tse, Y. Yao and A. New, Allotrope of Nitrogen as High-Energy Density Material, J. Phys. Chem. A, 2016, 120, 2920–2925.
9. B. Hirshberg, R. B. Gerber and A. I. Krylov, Calculations predict a stable molecular crystal of N₈, Nat. Chem., 2014, 6, 52–56.
10. S. Liu, L. Zhao, M. Yao, M. Miao and B. Liu, Novel All-Nitrogen Molecular Crystals of Aromatic N₁₀, Adv. Sci., 2020, 7, 1902320.
11. M. M. G. Alemany and J. L. Martins, Density-functional study of nonmolecular phases of nitrogen: Metastable phase at low pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 024110.
12. W. D. Mattson, D. Sanchez-Portal, S. Chiesa and R. M. Martin, Prediction of New Phases of Nitrogen at High Pressure from First-Principles Simulations, Phys. Rev. Lett., 2004, 93, 125501.
13. F. Zahariev, A. Hu, J. Hooper, F. Zhang and T. Woo, Layered single-bonded nonmolecular phase of nitrogen from first-principles simulation, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214108.
14. M. I. Eremets, A. G. Gavriliuk, I. A. Trojan, D. A. Dzivenko and R. Boehler, Single-bonded cubic form of nitrogen, Nat. Mater., 2004, 3, 558–563.
15. C. Ji, A. A. Adeleke, L. X. Yang, B. Wan, H. Y. Gou, Y. S. Yao, B. Li, Y. Meng, J. S. Smith, V. B. Prakapenka, W. J. Liu, G. Y. Shen, W. L. Mao and H. K. Mao, Nitrogen in black phosphorus structure, Sci. Adv., 2020, 6, eaba9206.
16. D. Laniel, B. Winkler, T. Fedotenko, A. Pakhomova, S. Chariton, V. Milman, V. Prakapenka, L. Dubrovinsky and N. Dubrovinskaia, High-Pressure Polymeric Nitrogen Allotrope with the Black Phosphorus Structure, Phys. Rev. Lett., 2020, 124, 216001.
17. D. Tomasino, M. Kim, J. Smith and C. S. Yoo, Pressure-Induced Symmetry-Lowering Transition in Dense Nitrogen to Layered Polymeric Nitrogen (LP-N) with Colossal Raman Intensity, Phys. Rev. Lett., 2014, 113, 205502.
18. D. Laniel, G. Geneste, G. Weck, M. Mezouar and P. Loubeyre, Hexagonal Layered Polymeric Nitrogen Phase Synthesized near 250 GPa, Phys. Rev. Lett., 2019, 122, 066001.
19. K. Ramesh Babu and G. Vaitheeswaran, Ab initio study of structural and vibrational properties of KN₃ under pressure, Chem. Phys. Lett., 2012, 533, 35–39.
20. X. Wang, J. Li, J. Botana, M. Zhang, H. Zhu, L. Chen, H. Liu, T. Cui and M. Miao, Polymerization of nitrogen in lithium azide, J. Chem. Phys., 2013, 139, 164710.
21. X. Wang, J. Li, H. Zhu, L. Chen and H. Lin, Polymerization of nitrogen in cesium azide under modest pressure, J. Chem. Phys., 2014, 141, 044717.
22. W. Yi, X. Jiang, T. Yang, B. Yang, Z. Liu and X. Liu, Crystalline Structures and Energetic Properties of Lithium Pentazolate under Ambient Conditions, ACS Omega, 2020, 5, 24946–24953.
23. D. Laniel, B. Winkler, E. Koemets, T. Fedotenko, M. Bykov, E. Bykova, L. Dubrovinsky and N. Dubrovinskaia, Synthesis of magnesium-nitrogen salts of polynitrogen anions, Nat. Commun., 2019, 10, 4515.
24. M. Bykov, T. Fedotenko, S. Chariton, D. Laniel, K. Glazyrin, M. Hanfland, J. S. Smith, V. B. Prakapenka, M. F. Mahmood, A. F. Goncharov, A. V. Ponomareva, F. Tasnádi, A. I. Abrikosov, T. Bin Masood, I. Hotz, A. N. Rudenko, M. I. Katsnelson, N. Dubrovinskaia, L. Dubrovinsky and I. A. Abrikosov, High-Pressure Synthesis of Dirac Materials: Layered van der Waals Bonded BeN₄ Polymorph, Phys. Rev. Lett., 2021, 126, 175501.
25. B. Huang and G. Frapper, Barium–Nitrogen Phases Under Pressure: Emergence of Structural Diversity and Nitrogen-Rich Compounds, Chem. Mater., 2018, 30, 7623–7636.
26. K. Xia, X. Zheng, J. Yuan, C. Liu, H. Gao, Q. Wu and J. Sun, Pressure-Stabilized High-Energy-Density Alkaline-Earth-Metal Pentazolate Salts, J. Phys. Chem. C, 2019, 123, 10205–10211.
27. J. Yuan, K. Xia, J. Wu and J. Sun, High-energy-density pentazolate salts: CaN₁₀ and BaN₁₀, Sci. China: Phys., Mech. Astron., 2020, 64, 218211.
28. M. Bykov, E. Bykova, A. V. Ponomareva, I. A. Abrikosov, S. Chariton, V. B. Prakapenka, M. F. Mahmood, L. Dubrovinsky and A. F. Goncharov, Stabilization of Polynitrogen Anions in Tantalum–Nitrogen Compounds at High Pressure, Angew. Chem., Int. Ed., 2021, 60, 9003–9008.
29. B. Huang, B. Wang, S. Wu, F. Guégan, W. Hu and G. Frapper, Predicted Polymeric and Layered Covalent Networks in Transition Metal Pentazolate M(cyclo-N₅)_x Phases at Ambient and High Pressure: Up to 20 Nitrogen Atoms per Metal, Chem. Mater., 2021, 33, 5298–5307.
30. X. Du, Y. Yao, J. Wang, Q. Yang and G. Yang, IrN₄ and IrN₇ as potential high-energy-density materials, J. Chem. Phys., 2021, 154, 054706.
31. K. Xia, J. Yuan, X. Zheng, C. Liu, H. Gao, Q. Wu and J. Sun, Predictions on High-Power Trivalent Metal Pentazolate Salts, J. Phys. Chem. Lett., 2019, 10, 6166–6173.
32. Q. Wei, C. Zhao, M. Zhang, H. Yan and B. Wei, High-pressure phases and pressure-induced phase transition of MoN₆ and ReN₆, Phys. Lett. A, 2019, 383, 2429–2435.
33. N. P. Salke, K. Xia, S. Fu, Y. Zhang, E. Greenberg, V. B. Prakapenka, J. Liu, J. Sun and J.-F. Lin, Tungsten Hexanitride with Single-Bonded Armchairlike Hexazine Structure at High Pressure, Phys. Rev. Lett., 2021, 126, 065702.
34. K. Xia, H. Gao, C. Liu, J. N. Yuan, J. Sun, H. T. Wang and D. Y. Xing, A novel superhard tungsten nitride predicted by machine-learning accelerated crystal structure search, Sci. Bull., 2018, 63, 817–824.
35. N. V. Skorodumova, R. Ahuja, S. I. Simak, I. A. Abrikosov, B. Johansson and B. I. Lundqvist, Electronic, bonding, and optical properties of CeO₂ and Ce₂O₃ from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 115108.
36. V. Kanchana, G. Vaitheeswaran, X. Zhang, Y. Ma, A. Svane and O. Eriksson, Lattice dynamics and elastic properties of the 4f electron system: CeN, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205135.
37. T. Y. Lee, D. Gall, C. S. Shin, N. Hellgren, I. Petrov and J. E. Greene, Growth and physical properties of epitaxial CeN layers on MgO(001), J. Appl. Phys., 2003, 94, 921–927.
38. M. B. Nielsen, D. Ceresoli, J.-E. Jørgensen, C. Prescher, V. B. Prakapenka and M. Bremholm, Experimental evidence for pressure-induced first order transition in cerium nitride from B1 to B10 structure type, J. Appl. Phys., 2017, 121, 025903.
39. J. S. Olsen, J. E. Jørgensen, L. Gerward, G. Vaitheeswaran, V. Kanchana and A. Svane, Compressibility and structural stability of CeN from experiment and theory. The B1–B2 transition, J. Alloys Compd., 2012, 533, 29–32.
40. C. J. Pickard and R. J. Needs, High-Pressure Phases of Nitrogen, Phys. Rev. Lett., 2009, 102, 125702.
41. J. S. Olsen, L. Gerward, U. Benedict and J. P. Itié, The crystal structure and the equation of state of cerium metal in the pressure range 0–46 Gpa, Physica B+C, 1985, 133, 129–137.
42. M. I. McMahon and R. J. Nelmes, Different Results for the Equilibrium Phases of Cerium above 5 GPa, Phys. Rev. Lett., 1997, 78, 3884–3887.
43. Y. K. Vohra, S. L. Beaver, J. Akella, C. A. Ruddle and S. T. Weir, Ultrapressure equation of state of cerium metal to 208 GPa, J. Appl. Phys., 1999, 85, 2451–2453.
44. W. Sun, C. J. Bartel, E. Arca, S. R. Bauers, B. Matthews, B. Orvañanos, B.-R. Chen, M. F. Toney, L. T. Schelhas, W. Tumas, J. Tate, A. Zakutayev, S. Lany, A. M. Holder and G. Ceder, A map of the inorganic ternary metal nitrides, Nat. Mater., 2019, 18, 732–739.
45. B. Wang, R. Larhlimi, H. Valencia, F. Guégan and G. Frapper, Prediction of Novel Tin Nitride Sn_xN_y Phases Under Pressure, J. Phys. Chem. C, 2020, 124, 8080–8093.
46. J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Synthesis and Characterization of the Nitrides of Platinum and Iridium, Science, 2006, 311, 1275–1278.
47. G. V. Vajenine, G. Auffermann, Y. Prots, W. Schnelle, R. K. Kremer, A. Simon and R. Kniep, Preparation, Crystal Structure, and Properties of Barium Pernitride, BaN₂, Inorg. Chem., 2001, 40, 4866–4870.
48. G. Auffermann, Y. Prots and R. Kniep, SrN and SrN₂: Diazenides by Synthesis under High N₂-Pressure, Angew. Chem., Int. Ed., 2001, 40, 547–549.
49. M. Wessel and R. Dronskowski, Nature of N–N Bonding within High-Pressure Noble-Metal Pernitrides and the Prediction of Lanthanum Pernitride, J. Am. Chem. Soc., 2010, 132, 2421–2429.
50. S. Zhu, F. Peng, H. Liu, A. Majumdar, T. Gao and Y. Yao, Stable Calcium Nitrides at Ambient and High Pressures, Inorg. Chem., 2016, 55, 7550–7555.
51. S. Wei, L. Lian, Y. Liu, D. Li, Z. Liu and T. Cui, Pressure-stabilized polymerization of nitrogen in alkaline-earth-metal strontium nitrides, Phys. Chem. Chem. Phys., 2020, 22, 5242–5248.
52. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
53. A. Savin, R. Nesper, S. Wengert and T. F. Fässler, ELF: The Electron Localization Function, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832.
54. C. Ding, J. Wang, Y. Han, J. Yuan, H. Gao and J. Sun, High Energy Density Polymeric Nitrogen Nanotubes inside Carbon Nanotubes, Chin. Phys. Lett., 2022, 39, 036101.
55. J. Yuan, K. Xia, C. Ding, X. Wang, Q. Lu and J. Sun, High-energy-density metal nitrides with armchair chains, Matter Radiat. Extremes, 2022, 7, 038402.
56. L. Zhu, Z. Wang, Y. Wang, G. Zou, H.-K. Mao and Y. Ma, Spiral chain O₄ form of dense oxygen, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 751–753.
57. H. Fujihisa, Y. Akahama, H. Kawamura, H. Yamawaki, M. Sakashita, T. Yamada, K. Honda and T. Le Bihan, Spiral chain structure of high pressure selenium-II′ and sulfur-II from powder X-ray diffraction, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 134106.
58. M. J. Kamlet and C. Dickinson, Chemistry of Detonations. III. Evaluation of the Simplified Calculational Method for Chapman-Jouguet Detonation Pressures on the Basis of Available Experimental Information, J. Chem. Phys., 1968, 48, 43–50.
59. S. Yu, B. Huang, Q. Zeng, A. R. Oganov, L. Zhang and G. Frapper, Emergence of Novel Polynitrogen Molecule-like Species, Covalent Chains, and Layers in Magnesium–Nitrogen Mg_xN_y Phases under High Pressure, J. Phys. Chem. C, 2017, 121, 11037–11046.
60. B. A. Steele and I. I. Oleynik, Novel Potassium Polynitrides at High Pressures, J. Phys. Chem. A, 2017, 121, 8955–8961.
61. B. Wang, F. Guégan and G. Frapper, Putting xenon and nitrogen under pressure: towards new layered and two-dimensional nitrogen allotropes with crown ether-like nanopores, J. Mater. Chem. C, 2022, 10, 10374–10381.
62. F. Wang, Q. Rui, Q. Jiang, J. Li, H. Zhu, Q. Wang and X. Wang, Stable nitrogen-rich yttrium nitrides under high pressure, Solid State Commun., 2022, 358, 115001.
63. H. Gao, J. Wang, Y. Han and J. Sun, Enhancing crystal structure prediction by decomposition and evolution schemes based on graph theory, Fundam. Res., 2021, 1, 466–471.
64. H. Gao, C. Liu, A. Hermann, R. J. Needs, C. J. Pickard, H.-T. Wang, D. Xing and J. Sun, Coexistence of plastic and partially diffusive phases in a helium-methane compound, Natl. Sci. Rev., 2020, 7, 1540–1547.
65. H. Gao, C. Liu, J. Shi, S. Pan, T. Huang, X. Lu, H.-T. Wang, D. Xing and J. Sun, Superionic Silica-Water and Silica-Hydrogen Compounds in the Deep Interiors of Uranus and Neptune, Phys. Rev. Lett., 2022, 128, 035702.
66. C. Liu, H. Gao, Y. Wang, R. J. Needs, C. J. Pickard, J. Sun, H.-T. Wang and D. Xing, Multiple superionic states in helium–water compounds, Nat. Phys., 2019, 15, 1065–1070.
67. C. Liu, J. Shi, H. Gao, J. Wang, Y. Han, X. Lu, H.-T. Wang, D. Xing and J. Sun, Mixed Coordination Silica at Megabar Pressure, Phys. Rev. Lett., 2021, 126, 035701.
68. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
69. G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
70. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
71. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
72. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
73. T. A. Manz and D. S. Sholl, Methods for Computing Accurate Atomic Spin Moments for Collinear and Noncollinear Magnetism in Periodic and Nonperiodic Materials, J. Chem. Theory Comput., 2011, 7, 4146–4164.
74. T. A. Manz and N. G. Limas, Introducing DDEC6 atomic population analysis: part 1. Charge partitioning theory and methodology, RSC Adv., 2016, 6, 47771–47801.
75. T. A. Manz, Introducing DDEC6 atomic population analysis: part 3. Comprehensive method to compute bond orders, RSC Adv., 2017, 7, 45552–45581.
76. N. G. Limas and T. A. Manz, Introducing DDEC6 atomic population analysis: part 4. Efficient parallel computation of net atomic charges, atomic spin moments, bond orders, and more, RSC Adv., 2018, 8, 2678–2707.
77. T. Chen and T. A. Manz, Bond orders of the diatomic molecules, RSC Adv., 2019, 9, 17072–17092.
78. A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl₂-type SiO₂ at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
79. W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
80. S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519.
81. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma01012g

---