Open Access Article
Open Access ArticleCore–shell nanoheterodimers: laser-assisted deposition of single bimetallic Au@M (M = Au, Ag, Pd, Pt) nanodots on TiO2 nanoparticles†
Fenghuan
Zhao‡
ab,
Qingguo
Bai‡§
ab,
Chenghui
Xia
c,
Junjie
Hao¶
 ab,
Marion
Gayot
d,
Jean-Pierre
Delville
ab,
Marion
Gayot
d,
Jean-Pierre
Delville
 *b and
Marie-Helene
Delville
*b and
Marie-Helene
Delville
 *a
*a
aUniv. Bordeaux, CNRS, Bordeaux INP, ICMCB, UMR 5026, Pessac F-33608, France. E-mail: marie-helene.delville@icmcb.cnrs.fr
bUniv. Bordeaux, CNRS, LOMA, UMR 5798, Talence F-33405, France. E-mail: jean-pierre.delville@u-bordeaux.fr
cCollege of Materials Science and Engineering, Ocean University of China, QingDao 266100, China
dUniv. Bordeaux, UMS 3626, Pessac F-33608, France
First published on 14th December 2022
Abstract
We propose to synthesize well-controlled core–shell nanoheterodimers (NHDs) based on single bimetallic Au@M (M = Au, Ag, Pd, Pt) nanodots (BNDs) grown on bare TiO2 nanoparticles (NPs) by a two-step laser-assisted deposition. The high photon flux emitted by a focused UV laser triggers nucleation and growth of a single core nanodot (ND) and its size is quantitatively controlled by varying the time exposure and the concentration of gold ions in the solution in the first step. A second laser deposition is performed after adding a new metal precursor to the Au–TiO2 NHDs thus prepared. Due to the vectorial nature of the first Au–TiO2 NHDs when photo-excited, and thus the subsequent efficient carrier separation, the second photodeposition strictly takes place on the first gold NDs. Growth is epitaxial for both Au@Au–TiO2 and Au@Ag–TiO2, while Au@Pt–TiO2 shows a discontinuous shell with the formation of separate domains, which further rearrange. Au@Pd–TiO2 exhibits an intermediate situation where the shell surface becomes progressively irregular, in agreement with surface energies and lattice mismatch between the two metals. Still, unlike conventional wet chemistry, where the metal atoms in the shell come from the bulk solution (external production), photodeposition produces carriers through the TiO2 substrate and the gold ND (internal process). Such a process highlights the role of the work function (WF) mismatch between the two metals in electron transport at their interface for shell growth. It provides a unique opportunity to accurately control a thin shell with a thickness of typically two layers of metal atoms. This control is of significant interest to couple the synergy between catalysis and plasmonics. We, hence, propose a general methodology for synthesizing single BNDs with a core–shell structure loaded on semiconductor NPs, providing advanced asymmetric nano-texturing for Au–TiO2-based photocatalysis and plasmonic photocatalysis applications.
Introduction
It is well known that the presence of noble-metal nanoclusters on semiconductor nanoparticles (NPs) can dramatically enhance visible-light absorption through the surface plasmon resonance (SPR),1–3 and it has rapidly been devised that nanostructures with more than one noble metal would offer even accentuated versatility and maximization of visible light efficiency. The first type of investigated bimetallic nanostructures, consisting of two different metals deposited separately on the same NP, already showed unique optical, catalytic, and electronic properties due to the synergistic effects of these two kinds of metal nanodots (NDs).4–7 To improve the photocatalytic efficiency, Au–Ag,8,9 Au–Cu,10 Au–Pd,4,11,12 Au–Cu,13 Ag–Ni,14 and other bimetallic nanodots (BNDs) with core–shell structures have been loaded onto semiconductor materials as cocatalysts.15 As the core–shell morphology offers better control than random deposition of two types of NDs, a step forward over the regulation of light absorption, charge recombination dynamics, and photoredox catalytic active sites has been reached with this second type of nanostructure.Two-step photodeposition appears to be the best strategy for the preparation of core–shell structured BNDs on semiconductor oxide NPs to prevent the formation of alloyed metallic NDs as illustrated a long time ago by Hermann,16 Sclafani,17 and more recently by Chen et al.18 In this way, the first deposited metal ND acts as a sink for photo-induced electrons and favours the site-specific reduction and deposition of the second metal at the surface of the first metal ND during the second deposition process. In 1990, Fernandez et al.19 studied the photocatalytic reduction of rhodium on a photosensitive support (titania) already loaded with another metal (Pt). They found that the size and location of the Rh NDs depended on the reaction medium, and rhodium NDs of 1–1.5 nm diameter (respectively 2–3 nm diameter) were well distributed on TiO2 in water (respectively in 2-propanol-water (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v)), while in a basic medium, the deposition of rhodium selectively occurred on the pre-existing platinum NDs. In one case, the effect of 2-propanol was mainly attributed to its hole-scavenging properties, which reduced the recombination of photo-produced carriers and then promoted the reduction of Rh3+ and the growth of rhodium NDs. In the other one (ammonia), even if the adsorption of Rh3+ ions on TiO2 is hindered by a large amount of NH4+ ions, the easier hole-trapping at the negatively charged surface of the semiconductor allows a better separation of electron–hole pairs. These two phenomena explain the selective deposition of rhodium on the platinum NDs, which are enriched in electrons by transfer from TiO2 P25 during irradiation. This study also indicates that in the presence of efficient hole scavenging, the second metal prefers to locate on a metal ND that already exists on semiconductors and finally forms core/shell bimetallic heteronanostructures, which could be of great interest in catalysis and photoelectronic devices, as demonstrated later on.
1, v/v)), while in a basic medium, the deposition of rhodium selectively occurred on the pre-existing platinum NDs. In one case, the effect of 2-propanol was mainly attributed to its hole-scavenging properties, which reduced the recombination of photo-produced carriers and then promoted the reduction of Rh3+ and the growth of rhodium NDs. In the other one (ammonia), even if the adsorption of Rh3+ ions on TiO2 is hindered by a large amount of NH4+ ions, the easier hole-trapping at the negatively charged surface of the semiconductor allows a better separation of electron–hole pairs. These two phenomena explain the selective deposition of rhodium on the platinum NDs, which are enriched in electrons by transfer from TiO2 P25 during irradiation. This study also indicates that in the presence of efficient hole scavenging, the second metal prefers to locate on a metal ND that already exists on semiconductors and finally forms core/shell bimetallic heteronanostructures, which could be of great interest in catalysis and photoelectronic devices, as demonstrated later on.
Zheng et al.7 reported more recently that Au, Ag, and Au–Ag BNDs were site-selectively photo-deposited on the reduction sites of TiO2. Au–Ag BND loading provided not only good activity performance for oxidizing 2-propanol but also high stability under visible light. They, however, focused on the catalytic aspect of their work and did not analyse the structure of their Au–Ag BNDs. Tanaka and co-authors11 successfully synthesized multi-core–shell Au@Pd BNDs supported on TiO2 (Au@Pd–TiO2), by using a two-step photodeposition method. Au3+ was reduced first via photoirradiation at wavelengths λ > 300 nm with a 400 W high-pressure mercury lamp and many NDs were deposited on TiO2; in a second step, Au–Pd core–shell structures were prepared by photoirradiation of the mixture of palladium chloride and Au–TiO2 solution with the same light source. They found that Au–TiO2 and Au-free Pd–TiO2 were inactive, whereas the core–shell Au@Pd–TiO2 samples were active in the photocatalytic conversion of chlorobenzene and 2-propanol to benzene and acetone under visible light irradiation. Moreover, they indicated that the thickness control of the Pd shell (1 nm corresponding to ∼3 layers) was important for both a satisfactory cocatalyst effect and the absorption of the SPR of the Au ND core. A year later, Su et al.20 investigated the metal structural composition of the Au/Pd–TiO2 systems showing the importance of the nature of the external layer for catalysis. In a recent report, Sun et al.21 applied a two-step deposition method to prepare bimetallic Au@Pd–TiO2 catalysts with varied Pd deposition amounts using Hg lamp irradiation, and their results indicated that the Pd atoms were preferentially deposited on exposed Au surfaces in the form of a monolayer. They also mentioned the catalytic oxidation of benzyl alcohol with prepared bimetallic Au@Pd–TiO2 catalysts and showed that the benzyl alcohol conversion increased with Pd deposition amount at Pd loading below 0.049 wt%, whereas the activity of the catalysts with a higher Pd deposition amount remained nearly identical. Consequently, the deposition of core–shell BNDs, even small, numerous, and randomly distributed on the surface of the TiO2 NPs, already represents a well-established added value in terms of photocatalytic yields as compared to the multi-deposition of separated NDs of two types of metals.
Furthermore, although not yet commonly accepted, Nakibli et al.22 elegantly showed, using II–VI semiconductor nanorods, that they could increase the quantum efficiency for hydrogen reduction on the surface of NHDs composed of a single Pt ND deposited at one tip of CdSe@CdS nanorods by ∼30 compared to the deposition of multiple randomly distributed NDs of the same mass amount. This is because single ND deposition produces a morphological asymmetry that triggers efficient vectorial charge separation. Moreover, using nickel instead of platinum, the same group demonstrated that the photocatalytic efficiency could be increased by varying the size of the deposited metal ND to achieve a better balance between the Coulomb blockade and size-dependent Schottky barrier that optimizes charge transfer.23
Here we propose to combine these two crucial aspects, the photodeposition of a single ND with controlled size on a semiconductor (SC) on the one hand, and the possibility to make this ND a bimetallic core–shell structure, on the other hand. We used bare TiO2 anatase NPs usually considered a benchmark material for photocatalysis in the near-UV wavelength range.24 Since photon exposure from UV spectral lamps or LEDs is known to lead to the multideposition of randomly distributed tiny NDs, which prevents the targeted asymmetry, we recently proposed to overcome this difficulty using a focused continuous UV laser (363.8 nm), to photosynthesize NHDs25 and we extend here this method to produce single core–shell NHDs by a two-step laser-deposition process. Indeed, continuous lasers offer the possibility to reach very high light intensities so that electrons and holes for surface reaction and deposition are produced in quantities large enough to become almost insensitive to the bulk and surface defect trapping sites of TiO2. Moreover, the nucleation of a first deposit builds a high electric field gradient inside the NPs, which strongly favours charge separation and then the growth of the already existing ND against the nucleation of a new deposit. This “high field” mechanism is at the heart of the deposition and growth of a single metal ND, and the laser-driven growth of a metallic shell on top of it during a second deposition step should thus offer the possibility to produce NHDs with a single core–shell BND. Even if some M1@M2–TiO2 were synthesized and used in photocatalysis, there are virtually no studies dedicated to the growth mechanism of the second metal on the first one when directly initiated by the carrier production inside the host NP. Since we control Au–TiO2 NHDs synthesis, we propose here such a platform, which will allow us to observe how the shell atoms self-organize on the surface of the metal core when they are reduced by electrons photoproduced in the band gap of TiO2 NPs. Nonetheless, layered heterostructures also have their specificities, and from the epitaxial point of view,26–30 it appears that two main mechanisms for the growth of a crystal layer (the shell) on a pre-existing crystal made of a different material (the core) may be at work depending on (i) the Gibbs excess free surface energy ΔGS = γshell/solution − γcore/solution + γcore/shell, where γi/j is the surface energy related to the interface between media i and j, and (ii) the lattice mismatch between the core and the shell (which also has a significant contribution to γcore/shell). If ΔGS ≤ 0 and the lattice mismatch is “small”, ideally Au@Au and typically Au@Ag, then epitaxial growth should be favoured (so-called Frank–van der Merwe (FM) growth mode), and a core–shell structure is expected. Conversely, if ΔGS ≥ 0 and the lattice mismatch is “large”, likely for Au@Pt, the growth of the shell becomes discontinuous and occurs via the formation of separated domains (so-called Volmer–Weber (VW) growth mode). An intermediate growth mechanism also exists, the Stranski–Krastanov (SK) mode, which combines temporally the two previous ones: growth starts to be layered and after reaching some critical interfacial strain due to lattice mismatch, the relief of the layer becomes more and more irregular to minimize the surface energy, likely corresponding to Au@Pd; this is well illustrated with metal (Ag, Pd, and Pt) overgrown by wet chemical reduction on gold nanorods within mesoporous silica shells.31 Investigating direct epitaxial growth of Au@M (M = Ag, Pd, Pt) by wet chemistry, Tian et al.27 already suggested that other metal properties, such as metal electronegativity, may play a role as the Au@Pd interface presents a large lattice mismatch (suggesting a Vomer-Weber growth of Pd) and nonetheless showed the formation of a layered structure (suggesting a Frank–van der Merwe (FM) growth). Finally, while not yet totally clarified, the possible effect of a mismatch in electric properties, such as work function, has recently been raised32 and suggests that the electron transfer at the core@shell interface may be hindered, thus contributing to an increase of γcore/shell and the involved growth mode.
Here, after synthesizing well-controlled Au–TiO2 NHDs by laser deposition, we performed a second deposition to form single BNDs of core–shell structure Au@M–TiO2 with M = Au, Ag, Pd, and Pt for the shell. A comparison of these photo-produced metallic shells is then established, based on the same starting material and comparable experimental conditions. Their growth, conceptually different from that observed in a wet chemistry approach in the sense that growth is now internally triggered from electron–hole pairs photoproduced inside the semiconductor NPs, shows the robustness of the laser-deposition technique, and the morphology of the Au@M–TiO2 NHDs illustrates the entanglement with epitaxial growth modes depending on surface energies, lattice mismatch and possibly on electrical properties.
Experimental
Chemicals
Titanium(IV) isopropoxide (TIPO, 97%), triethanolamine (TEOA, ≥99%), sodium hydroxide (NaOH, 99.99%), potassium gold(III) chloride (KAuCl4, 99.995%), hexachloroplatinic acid (H2PtCl6 99.9%) silver nitrate (AgNO3, 99%), and methanol (anhydrous, 99.8%), were purchased from Sigma-Aldrich and used as received without further purification. Deionized water (18.2 MΩ·cm) was obtained with a Milli-Q filtration station.Characterization
XPS surface analysis was performed on a ThermoFisher Scientific K-ALPHA spectrometer with a monochromatized Al Kα source (hν = 1486.6 eV). The powdered samples were pressed onto small indium foils or directly examined on the Transmission Electron Microscopy (TEM) grids with a 200 μm X-ray spot size. The overall spectra (0–1100 eV) were obtained with a constant pass energy of 200 eV and high-resolution spectra at 40 eV. Charge neutralization was applied during analysis and sputtering was achieved with 3 keV Ar+ ions at an angle of incidence, θ, of 45° to the normal of the sample. High-resolution spectra were quantified and/or fitted with the software AVANTAGE provided by ThermoFisher Scientific (Scofield sensitivity factors were used for quantification). The binding energy (BE) of the spectra was corrected with that of adventitious carbon C1s (C–C, C–H) at 284.8 (0.2) eV. The phase identification of the samples was performed with X-ray diffraction (XRD) using a powder diffractometer (PANalytical X’Pert Pro) equipped with Cu Kα1 radiation, λ = 1.540598 Å. The TEM grid preparation is performed according to the following procedures: The solution is sonicated for 10 min to disperse the nanoparticles, and then one drop is cast on a TEM copper grid covered with a carbon film (previously activated by UV light, carbon film, face up). A paper tissue can help absorb the liquid from the carbon film side to the backside of the grid, which only allows the liquid to pass through and leaves the nanoparticles on the top side. Two or more nitric acid drops (at pH 3) are also cast to clean the sample particles. The grid was finally air-dried for at least 30 min. TEM and high-resolution transmission electron microscopy (HRTEM) observations were performed using a JEOL 2200 FS equipped with a field emission gun, operating at 200 kV and with a point resolution of 0.23 nm. HRTEM micrographs were acquired with a GatanUltrascan CCD 2k–2k and digital diffractograms were calculated using the Gatan Digital Micrograph program. Moreover, to be representative and statistically meaningful, many images from several regions of various samples were recorded and the most characteristic results are presented here, and at least 250 NPs were treated. The UV-vis absorption spectra were recorded with a 3600 Shimadzu UV-Vis-NIR spectrophotometer using 1 cm path-length quartz cuvettes.Synthesis of TiO2
TiO2 anatase polyhedrons used as the substrate for the single ND photodeposition were prepared with the method developed by Sugimoto.33,34 First, 0.1 mol of TIPO and 0.2 mol of TEOA were mixed under an Ar flow and stirred at room temperature for 24 h. Then, 144 mL of deionized water were added giving a stock solution with [Ti4+] = 0.5 mol L−1. Then, for the TiO2 NP preparation, 10 mL of this stock solution were diluted with deionized water up to 20 mL (pH = 9.4; [Ti4+] = 0.25 mol L−1) in a 35 mL glass bottle and aged at 100 °C for 24 h. The solution was then directly transferred into a Teflon-lined autoclave and aged at 140 °C for 72 h. Finally, the autoclave was cooled down to room temperature and the product was collected by centrifugation at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 45 min. The precipitated product was washed several times with NaOH solutions (pH = 12), 2 M HNO3, and water (to pH 7) by sonication/centrifugation. The synthesized NPs, of size 11 × 11 × 18 nm3, were kept in an aqueous solution to avoid aggregation (see Fig. S1, ESI† for TEM and XRD characterisations of the anatase phase (JCPDS card no. 21-1272)). Mass concentrations were measured by drying a known volume of solution and weighing the extracted powder.
000 rpm for 45 min. The precipitated product was washed several times with NaOH solutions (pH = 12), 2 M HNO3, and water (to pH 7) by sonication/centrifugation. The synthesized NPs, of size 11 × 11 × 18 nm3, were kept in an aqueous solution to avoid aggregation (see Fig. S1, ESI† for TEM and XRD characterisations of the anatase phase (JCPDS card no. 21-1272)). Mass concentrations were measured by drying a known volume of solution and weighing the extracted powder.
Synthesis of the nanoheterodimers
The photodeposition of core–shell BNDs on TiO2 was performed in a square cuvette using a two-step laser-deposition method to prevent the already demonstrated alloying. The experimental setup is conceptually similar to that previously used for single metal ND deposition on CdSe@CdS nanorods.35 We used a continuous Ar+ laser (Innova 305C, Coherent) working in UV at λ0 = 363.8 nm, within the bandgap of TiO2 anatase (Eg ∼ 3.2 eV). The PMMA cuvette (1 × 1 × 4 cm3 filled with 1 cm3 solution), transparent at the used optical wavelength, is placed on a magnetic stirrer; a stirring speed of 300 rpm is enough to keep the solution homogeneous. Experiments are performed at room temperature. The beam is first set at the same height as the reaction cuvette using a home built periscope and then expended to eventually get an incident laser spot of diameter 1cm to shine on the 1cm wide square cuvette, using a UV microscope objective Newport U-13X and a fused silica lens (f = 75 mm). The beam power range at the exit of the laser head can be varied from PL = 0 to 160 mW in light control mode. The beam power Papp applied to the solution after crossing the incident PMMA wall is calculated in the following way: the transmission of the optical setup up to incidence to the cuvette is Pi/PL = 0.785 and the transmission of the cuvette when filled with water is Pt/Pi = 0.945, so that finally Papp/PL = 0.76; for the sake of simplicity Papp will be denoted P in the following.The first reaction solution was performed by mixing under Ar the as-prepared TiO2 aqueous solution (19 mM, 0.289 mL), and a freshly prepared KAuCl4 aqueous solution (10 mM, 50 μL). Then the oxygen-free hole scavenger, methanol (50 vol%), was added to the aqueous solution with a pH adjusted to 3.3 using nitric acid (0.1N). The solutions were purged with Ar gas for 10 min to remove the oxygen and then mixed just before laser exposure. The volume of the solution was always kept to 1 cm3 to ensure that it was fully exposed to laser light and the cuvette was sealed by a rubber septum.
After the deposition step of the first single gold ND onto TiO2 NPs, a given amount of the second metal precursor (KAuCl4, AgNO3, Na2PdCl4, H2PdCl4, and H2PtCl6) solution was added to the as-prepared Au–TiO2 solution to perform the second-round laser-deposition. When mentioned, the first synthesized Au–TiO2 particles were also separated via centrifugation (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g, 20 min) and washed with deionized water to remove the existing chloride ions and methanol in the solution and prevent flocculation/aggregation or reactivity due to this anion as in the case of AgNO3. After purification by centrifugation, these Au–TiO2 particles were re-dispersed into a pH 3.3 nitric acid solution and methanol; the metal precursor was then added to perform the second step deposition.
000 g, 20 min) and washed with deionized water to remove the existing chloride ions and methanol in the solution and prevent flocculation/aggregation or reactivity due to this anion as in the case of AgNO3. After purification by centrifugation, these Au–TiO2 particles were re-dispersed into a pH 3.3 nitric acid solution and methanol; the metal precursor was then added to perform the second step deposition.
Results
First stage: synthesis of single nanodot Au–TiO2 nanoheterodimers
The synthesis of the initial Au–TiO2 NHDs in a cuvette is analogous to that performed previously in a microchannel25 except that now the exposure time can be made much longer and growth can be investigated up to the completion of the photodeposition. Even if the beam intensity becomes significantly smaller than in a microchannel experiment due to a smaller beam focusing, we checked that it remains within the so-called “high-intensity” excitation regime far beyond a classical UV lamp or LED exposure. With this synthesis, we can reach yields in Au–TiO2 NHDs as high as 80% (see Fig. S2, ESI†). However, we purposely chose experimental conditions leading to a yield of only 50% for the first photochemical step to be able to easily observe a secondary nucleation of the metal in case it occurred in the second step. An example of single gold ND growth law when varying the time exposure is presented in Fig. 1a (for [TiO2] = 5.5 mM, [Au3+]0 = 0.5 mM and P = 56.1 mW) and shows that the completion of the photodeposition is reached after ∼4 min of exposure.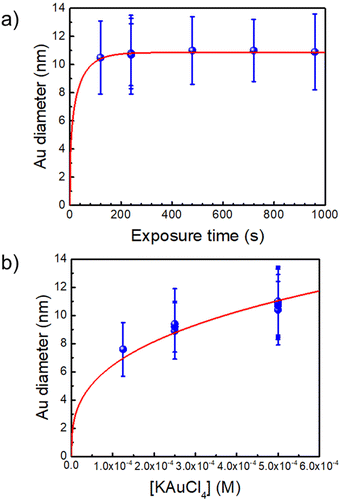 | ||
| Fig. 1 (a) Au NDs growth versus exposure time for [Au3+]0 = 0.5 mM (the red line is a fit according to dynamic modelling presented in Ref. 35. (b) Variation of the Au NDs size at completion vs. [Au3+]0 (the fit corresponds to mass conservation at completion, see text). [TiO2] = 5.5 mM and P = 56.1 mW for all experiments. | ||
A second experiment, performed under the same conditions with an exposure time of t = 4 min and now varying [Au3+]0 (Fig. 1b), shows that working up to completion provides a safe way to produce the initial Au–TiO2 NHDs with controllable gold ND sizes; the corresponding TEM images are presented in Fig. 2a1, b1 and c1 as illustrations of the starting Au–TiO2 materials for the second step laser-deposition to synthesize Au@M–TiO2 core–shell NHDs.
The mass conservation at completion leads to Ȳ[NP]πκ(θ)D∞Au3/8 = νAu[Au3+]max0, where D∞Au is the gold ND diameter at t → ∞, Ȳ ≈ 50% is the mean yield in NHDs for the chosen experimental conditions, [NP] is the concentration in TiO2 NPs ([NP] = 3.7310−6·[TiO2] for the size of the chosen NPs). [Au3+]max0 = β[Au3+]0 is the maximum concentration involved in the ND growth (β ≤ 1 and β = 1 if the initial concentration is completely consumed by the photodeposition), 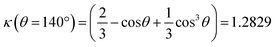 is a dimensionless factor related to the contact angle θ of the gold ND on the TiO2 (θ = 140° angle was measured) and νAu is the volume of a gold atom (νAu = MAu/(NAρAu) where MAu = 196.97 g in the molar mass and ρAu = 19.3 g cm−3 the density).
is a dimensionless factor related to the contact angle θ of the gold ND on the TiO2 (θ = 140° angle was measured) and νAu is the volume of a gold atom (νAu = MAu/(NAρAu) where MAu = 196.97 g in the molar mass and ρAu = 19.3 g cm−3 the density).
We experimentally obtain D∞Au = (139 ± 3)[Au3+]01/3 nm from the fit presented in Fig. 1b. We deduce β ≈ 0.81 ± 0.06 from the comparison with the expected behaviour 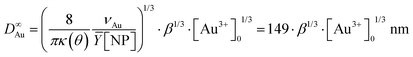 so that we can assume that almost 100% of the Au3+ ions present in the solution are reduced to Au0 and participate in the growth up to completion.
so that we can assume that almost 100% of the Au3+ ions present in the solution are reduced to Au0 and participate in the growth up to completion.
Considering these reproducible Au–TiO2 NHDs as starting materials, a second laser-deposition step is applied to investigate the synthesis of single core–shell BND structures of the type Au@M–TiO2. As nicely illustrated in the epitaxial growth of metal onto metallic nanocrystals from wet chemistry,27,31 this secondary growth process is also driven by the surface energies γcore/solution and γshell/solution, the lattice constant mismatch between the two metals influencing the mutual surface energy γcore/shell, and the electronic junction between the two metals. Even if the growth mechanism of metal over another metallic ND by photodeposition is intrinsically different from wet chemistry methods (internally triggered by carriers vs. reduction from the external bulk phase), the morphology of the final deposit should eventually satisfy these metal–metal interactions so that we will follow the lines traced by Fan et al.27 and Van der Hoeven et al.31 to set the laser-deposition of a second metal (Au, Ag, Pd, and Pt) on Au–TiO2, characterize the morphology of the resulting shell and eventually see whether or not laser deposition offers the opportunity to consolidate the vectorial nature of the initial Au–TiO2 NHDs with increasing functionalities raised by the deposition of a shell. To distinguish them from the initial Au–TiO2 NHDs material, the catalysts made by the second deposition are named Au@M–TiO2.
Photodeposition synthesis of single dot Au@Au–TiO2 NHDs
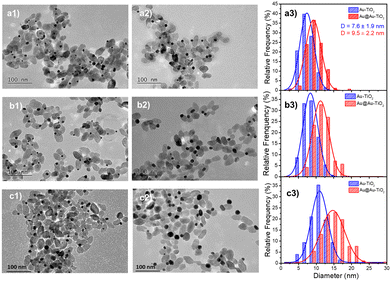
As a proof-of-concept for seeded growth of single ND by laser deposition in both the lattice-matching and electric equilibration cases, we first undertook photodeposition of a gold shell coating on the surface of the pre-existing gold ND. In this “ideal” case, the Gibbs free surface energy ΔGS = 0, as γcore = γshell and γcore/shell = 0, so that the second deposition is driven by a pure Franck–van der Merwe mechanism,26 with the growth forming an ideally uniform shell.As the Au NDs on TiO2 act as electron sinks for further deposition, their size, and the corresponding exposed facets, may have some effect on the second-step laser deposition. Then, we considered three initial sizes of Au NDs obtained at completion by adjusting the concentration of the precursor KAuCl4 (examples are shown in Fig. 2a1, b1, and c1 for three concentrations: 0.125, 0.250, and 0.500 mM), and chose the same three concentrations: 0.125, 0.250, and 0.500 mM, for the second step laser-deposition (Fig. 2a2, b2 and c2).
We kept the same applied power P = 56.1 mW and fixed the exposure time to 4 min to ensure growth close to completion. The histograms presented in Fig. 2a3, b3, and c3 show that the metal ND size distributions and the metal size increase after the second laser exposure. The Au@Au–TiO2 NHD yields remained virtually unchanged between the first and second step depositions (Table 1), confirming that growth indeed occurred only on already nucleated gold NDs; secondary nucleation is energetically much less favourable than growth on a pre-existing Au ND. Moreover, this second-step deposition induced an increase in the diameter size distribution, an increase of the coating thickness with the precursor concentration, and the results are in good agreement with literature reports.4,19 A fit of the final Au@Au ND size as a function of the total concentration of KAuCl4 after steps 1 and 2 shown in Table 1, gives D∞Au = (149 ± 2)[Au3+]01/3 nm, which perfectly compares with the expected amplitude D∞Au = 149[Au3+]01/3 when 100% of gold ions are consumed.
| KAuCl4 (μmol) | Metal particle size (nm) | NHDs yield (%) | Au shell (nm) | |
|---|---|---|---|---|
| First step | 0.125 | 7.6 ± 1.9 | 46 | 0.95 |
| Second step | 0.125 | 9.5 ± 2.2 | 48 | |
| First step | 0.250 | 8.6 ± 2.0 | 57 | 1.20 |
| Second step | 0.250 | 11.5 ± 2.3 | 54 | |
| First step | 0.500 | 10.8 ± 2.5 | 55 | 2.15 |
| Second step | 0.500 | 15.1 ± 3.3 | 53 |
Thus, we successfully obtained Au@Au–TiO2 with 0.95, 1.20, and 2.15 nm Au shells in close agreement with expectations, respectively corresponding to 2, 3, and 5 gold atom layers of mean lattice constant: αAu = 4.08 Å.36 These results also show that the chosen sizes of the first Au ND seeds have no influence on the Au shell thickness after the second-step deposition completion when an ideal Franck–van der Merwe mechanism is at work.
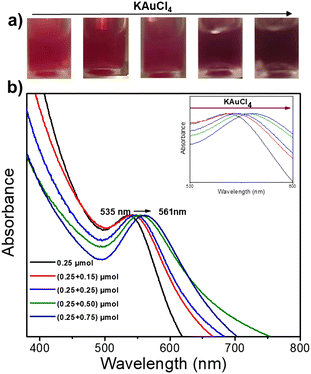
We then fixed the size of the Au NDs obtained in the first-step deposition and played with the concentration of the gold precursor during the second-step deposition to study its impact on the final Au size. The colour of the Au@Au–TiO2 solution changed with increasing amounts of KAuCl4 (Fig. 3a). The initial pink solution acquired during the first step of deposition gradually deepened and turned dark purple indicating that the Au NDs were getting bigger. This speculation is further confirmed by the UV-vis spectra displayed in Fig. 3b, which show a continuous red-shift of the SPR band of Au from 535 to 561 nm due to the increase of the Au size.
The TEM characterization shows the variation of the Au shell size on the Au–TiO2 NHDs (Fig. S2, ESI† and Table 2, see also Fig. 4). Starting with an 8.7 nm mean diameter obtained after the first deposition step, the Au ND size continuously increases with the added concentration of KAuCl4, from 0.15 mM to 0.75 mM, as illustrated by the histograms of Au ND size distributions in Fig. S2 (ESI†).
KAuCl4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) added (μmol) added (μmol) |
Au NDs size (nm) | NHDs yield (%) | Au shell (nm) | |
|---|---|---|---|---|
| First step | 0.25 | 8.7 ± 2.0 | 44 | — |
| Second step | 0.15 | 10.3 ± 2.7 | 53 | 0.80 |
| 0.25 | 11.4 ± 2.6 | 45 | 1.35 | |
| 0.35 | 13.2 ± 2.3 | 44 | 2.25 | |
| 0.50 | 14.3 ± 3.4 | 51 | 2.8 | |
| 0.75 | 14.5 ± 2.9 | 51 | 2.9 | |
The NHDs yields (Table 2), in the narrow range of 44–53%, are almost the same as those measured in the first deposition step confirming again that the laser deposition strongly favours the growth of seeds against secondary nucleation.
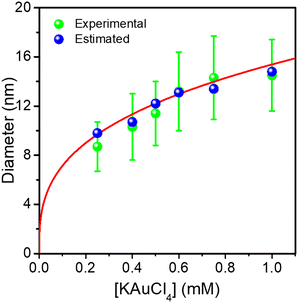
The Au NDs can be enlarged up to 14.5 nm from the initial 8.7 nm, indicating that a 2.9 nm thick Au shell, corresponding to 7 gold atom layers, was produced for the highest KAuCl4 ratio used (0.25 μmol + 0.75 μmol). Furthermore, the sizes of Au NDs are all very close to the estimated values, showing again that the amount of gold precursor was completely consumed to grow the shell on the preformed Au NDs. This is illustrated in Fig. 4 by the plot of the experimental and calculated Au@Au ND sizes as a function of the total concentration of KAuCl4 corresponding to variations in steps 1 and 2.
The global fit gives D∞Au = (154 ± 4)[Au3+]01/3 nm, which again compares very well with the expected amplitude D∞Au = 149[Au3+]01/3 when 100% of gold ions are consumed. So, this “ideal” situation for the growth of a gold ‘shell’, shows that (i) the second-step growth occurs on pre-existing seeds, (ii) the epitaxial Frank–van der Merwe growth mode is indeed at work, (iii) the size of the Au shell can be varied over large proportions likely because electric properties are also the same, and (iv) the final size can even be predicted from mass conservation.
Finally, as illustrated with the growth of seeded gold nanoparticles in bulk solution,37,38 this multi-step approach represents an efficient way to heterogeneously grow large single NDs without side effects, such as secondary nucleation, which may occur during the single-step reaction at very high gold ion concentrations.
Photodeposition synthesis of single dot Au@Ag–TiO2 NHDs
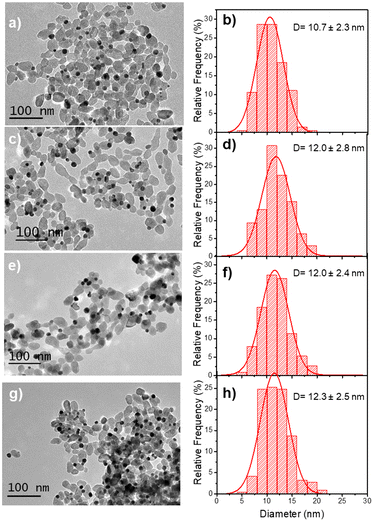
Based on these results on pure epitaxial Frank–van der Merwe growth, we aimed to synthesize authentic BNDs Au@Ag of core–shell type on TiO2 by sequential deposition of Au and Ag. This first choice was motivated by (i) a very small lattice constant mismatch between the two metals of 0.145% (respectively αAu = 4.08 Å, αAg = 4.09 Å), reducing the surface energy γAu/Ag, and (ii) γAg/solution < γAu/solution, respectively γAg/solution = 1.25 J m−2 and γAu/solution = 1.5 J m−2,39 so that ΔGS ≤ 0 and the epitaxial Frank–van der Merwe mode should be favoured. A mismatch between Ag and Au nonetheless appears in their electric work function,40 respectively 4.26 eV for Ag and 5.10 eV for Au, which may influence the electron transfer at the Au/Ag interface,32 required for silver ion reduction.The Au@Ag–TiO2 HNDs were synthesized using the procedure described above using AgNO3 as the Ag precursor in the second-round photodeposition. Exposure time, laser power, and precursor concentration were again varied to achieve this goal. As an example, TEM images of the heterostructures and the corresponding size distribution histograms of the Au@Ag NDs are presented in Fig. 5. Two types of Au–TiO2 NHDs with 9.1 ± 2.1 nm Au NDs (Fig. 5a), and 10.7 ± 2.3 nm (Fig. 5d), were made in the first photodeposition step. AgNO3 aqueous solution (0.5 μmol of AgNO3) was then added to the as-prepared Au–TiO2 NDs solutions. The mixtures were photo-irradiated a second time (P = 56.1 mW, t = 4 min) to get the Au@Ag–TiO2 HNDs, which developed BNDs with diameters of 10.6 ± 2.3 nm (Fig. 5b and c) and 11.7 ± 3.2 nm (Fig. 5e and f) respectively, with yields of Au@Ag–TiO2 BND NHDs remaining in the 45–53% range obtained after the first-step gold deposition. Similar NHDs yields and an increased metallic BND size confirm that Ag grew on the Au NDs with negligible secondary nucleation on bare TiO2.
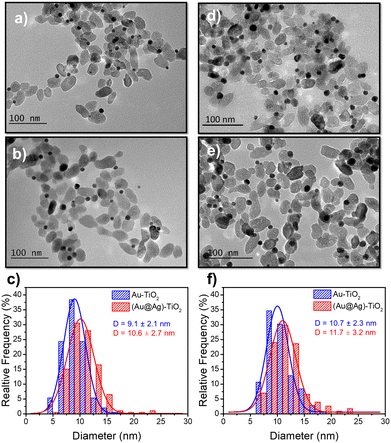 | ||
| Fig. 5 TEM images of (a and d) Au–TiO2 and (b and e) Au@Ag–TiO2 BND NHDs, and (c and f) their corresponding size distributions. Experimental conditions: first step deposition, [TiO2] = 5.5 mM, (a–c) [KAuCl4] = 0.25 mM (0.25 μmol of KAuCl4) and d), (e and f) [KAuCl4] = 0.50 mM (0.50 μmol of KAuCl4) (row 7 in Table 3), 50 vol% methanol as a hole scavenger, P = 56.1 mW, exposure time t = 4 min. Second step deposition: addition of 0.5 μmol of AgNO3 at the end of the first step, identical operational conditions. | ||
Moreover, considering again the mass conservation, we expect that 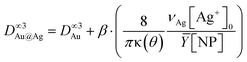 , where the mean yield is Ȳ ≈ 50%, the contact angle θ of a silver ND on TiO2 is almost the same as for gold (θ = 140° so that κ(θ = 140°) = 1.2829) and νAg is the volume of a silver atom (νAg = MAg/(NAρAg) where MAg = 107.87 g is the molar mass and ρAg = 10.49 g cm−3 is the density).
, where the mean yield is Ȳ ≈ 50%, the contact angle θ of a silver ND on TiO2 is almost the same as for gold (θ = 140° so that κ(θ = 140°) = 1.2829) and νAg is the volume of a silver atom (νAg = MAg/(NAρAg) where MAg = 107.87 g is the molar mass and ρAg = 10.49 g cm−3 is the density).
Using [Ag+]0 = 0.5 mM, we find respectively β = 26% and 23% when starting with 9.1 nm and 10.7 nm Au NDs. This means that only 25% of [Ag+]0 is consumed during the second step up to completion. Moreover, the Ag shell thickness remains limited in the range of 0.5–1.0 nm, which corresponds to the deposition of a silver shell lying between 1 and 2 atom layers (mean silver lattice constant: αAg = 4.09 Å). This result is confirmed by photodeposition experiments performed at larger laser powers and exposures.
Influence of the time and the laser power on the Ag deposition on Au–TiO2
As for Au@Au–TiO2, we undertook a systematic study of the variation of the BNDs sizes and the Au@Ag–TiO2 yields with the laser power and the photoreaction time; the results are gathered in Table 3 and Fig. 6 for the effect of the laser power variation.| Power (mW) | Exposure time (min) | BNPs NHDs yield (%) | Diam. of BNPs NDs (nm) | Ag thickness (nm) |
|---|---|---|---|---|
| 10 | 4 | 50 | 11.8 ± 2.8 | 0.55 |
| 10 | 8 | 52 | 12.4 ± 2.6 | 0.85 |
| 10 | 16 | 53 | 12.0 ± 2.8 | 0.65 |
| 20 | 4 | 50 | 11.7 ± 2.8 | 0.5 |
| 20 | 8 | 53 | 12.0 ± 2.8 | 0.65 |
| 20 | 16 | 48 | 12.0 ± 2.4 | 0.65 |
| 56.1 | 4 | 47 | 11.7 ± 3.2 | 0.5 |
| 56.1 | 8 | 48 | 11.8 ± 2.4 | 0.6 |
| 56.1 | 16 | 52 | 12.3 ± 2.5 | 0.8 |
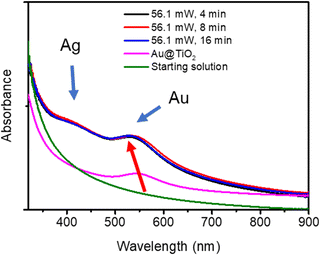
The Ag shell thickness obtained under different laser powers and time exposures is once again in the range of 0.5 to 0.9 nm, far smaller than expected from 100% silver ion consumption. The Ag shell has almost reached its final size after t = 4 min exposure and, as expected, there is no noticeable variation of the stationary thickness value whatever the beam power. This is well illustrated by the UV-vis spectra in Fig. 7, which shows, besides that of the starting solution before any irradiation (green curve), the characteristic SPR band of the Au NDs at 541 nm corresponding to the Au–TiO2 NHDs of the first stage deposition (pink curve).25 The other spectra show the two expected absorption bands corresponding to the presence of the BND core–shell structures. As already observed,41–43 the SPR band corresponding to the Au core blue shifts as the Ag shell emerges (red arrow); this new band due to the Ag shell is observed around 415 nm.44–46 The presence of these two bands and their respective positions exclude the presence of metal alloying.41,42,47,48
In addition to the TEM data, scanning TEM (STEM) combined with elemental mapping was also performed to gain a better insight into the bimetallic structure. The elemental mapping of Au and Ag confirmed the presence of a core@shell structure of the metallic part with Au as the core, and Ag as the shell (Fig. 8). Since the Ag shell is thin, the signal intensity is not as bright as we would expect with 100% consumption of the silver ions but much more explicit than many results from the literature.7 Comparing the difference in the size of the gold and silver mappings, it is easy to see that silver ones are bigger than gold ones, forming a shell and confirming the results already obtained by UV-vis spectroscopy. The core–shell structure does not seem as clear as for classical spherical nanoobjects with thicker shells because the Au NPs are crystalline, as well illustrated in Fig. S3 (ESI†). Finally, there is no distinguishable growth of silver NDs on bare TiO2.
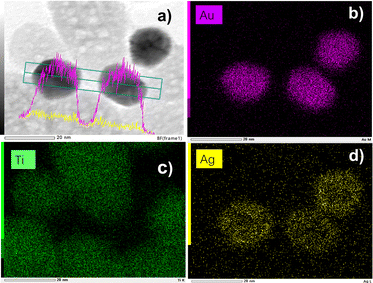 | ||
| Fig. 8 (a) STEM-EDS images of Au@Ag–TiO2 BND NHDs and their compositional mapping of the distributions of (b) Au (pink), (c) Ti (green), and (d) Ag (yellow) of the sample synthesized with and (detailed sample information is shown in Table 3). | ||
Influence of the concentration of AgNO3 on the Ag deposition on Au–TiO2
Since the first deposition was performed using KAuCl4 as the Au3+ ion precursor, and the silver ion precursor AgNO3 was directly added to the solution for the second deposition, both at the same concentration of 0.5 mM, we speculated that a fraction of the AgNO3 would readily react with these four equivalents of chloride to form the low solubility AgCl, reduce the concentration of silver ions available for deposition, and explain why only 25% of [Ag+]0 were consumed during the second step; some large micrometer scale Ag-based structures were sometimes observed on TEM imaging and by EDS analysis (not shown). We then used different amounts of AgNO3 to see whether the Ag shell thickness would increase with higher contents of the precursor.TEM images (Fig. S4, ESI†) and data gathered in Table 4 show once again that the addition of extra silver precursor leads to an increase in the growth of the silver layer on the gold NDs. The Ag shell doubles in between 0.25 and 0.5 μmol but rapidly reaches the same saturation value of about 0.8 nm after which some additional tiny Ag NDs start to nucleate on TiO2 for AgNO3 contents higher than 2 μmol, i.e. when we start to be close to or beyond the concentration of four equivalent chlorides.
| Amount of AgNO3 (μmol) | NHDs yield (%) | Ag thickness (nm) |
|---|---|---|
| 0.25 | 50 | 0.4 |
| 0.5 | 51 | 0.8 |
| 1.0 | 50 | 0.7 |
| 2.0 | 48 | 0.7 |
| 4.0 | 50 | 0.8 |
To confirm these observations, we perform the experiments in the absence of chloride ions, by extensively washing the Au–TiO2 NHDs obtained in the first-step photodeposition. The purified Au–TiO2 HNDs were dispersed again in a pH 3.3 water solution with 0.1N HNO3, 0.5 mM AgNO3, and 50% volume of methanol as a hole scavenger.
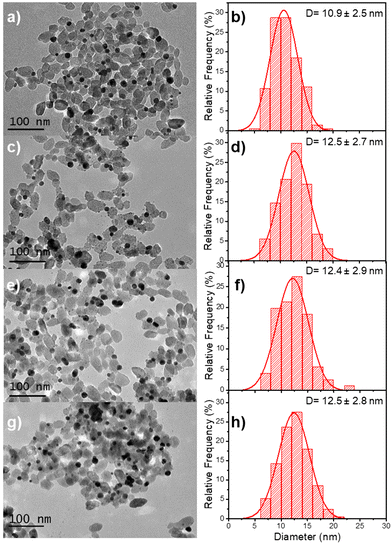
The beam power was varied with an exposure time of 16 min to ensure the completion of the photoreduction of silver ions. The TEM results illustrate the influence of the different applied laser powers (Fig. 9 and Table 5). The final thickness of the Ag shell remains the same (∼0.8 nm) whatever the laser power (Table 5), but as in the case where the silver ion concentration becomes higher than the chloride one, we can observe in Fig. 9 the nucleation of additional tiny silver NDs, which grow when increasing the laser power at fixed irradiation exposure.
| Sample | Power (mW) (second step) | NHDs yield (%) | NDs Diam. (nm) | Ag thickness (nm) |
|---|---|---|---|---|
| Au–TiO2 | — | 51 | 10.9 ± 2.5 | 0 |
| Au@Ag–TiO2 | 10 | 50 | 12.5 ± 2.7 | 0.8 |
| Au@Ag–TiO2 | 20 | 49 | 12.4 ± 2.9 | 0.75 |
| Au@Ag–TiO2 | 56.1 | 51 | 12.5 ± 2.8 | 0.8 |
Based on these results, we can conclude that the close matching between the lattice constants of gold and silver indeed leads to the expected epitaxial growth of a silver shell by laser deposition according to the Frank–van der Merwe mode.49,50 Nonetheless, unlike wet chemistry deposition, the photodeposited layer is limited to two layers of silver atoms. As in photodeposition, the electrons are provided internally by the excitation of TiO2 NPs, suggesting a weak transfer at the Au/Ag interface, which could be explained by a work function mismatch,32 with respectively φAu = 5.10 eV and φAg = 4.26 eV;40 as φTiO2 ≈ 5.10 eV for TiO2 anatase,51 the electron transfer should not be disturbed at the TiO2/Au interface. Indeed, when two dissimilar metals are brought into contact, their Fermi levels tend to equilibrate so that free electrons redistribute locally from the metal with the lowest work function (Ag) to the other one (Au). As a result, a dipole layer emerges at their interface, acting as a sort of barrier to electron migration; the greater the mismatch in work functions, the higher and wider the barrier.
The width of the dipole layer should behave as 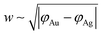 so that the electron work gradient at the Au/Ag interface behaves as
so that the electron work gradient at the Au/Ag interface behaves as 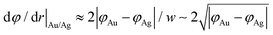 ;32 electrons should thus be mainly retained in the gold core, and the larger the silver shell the lower the electron density reaching its interface for the reduction of silver ions. An electrical barrier is thus established since the beginning of the shell growth. At the early stage, its energy and width remain sufficiently weak so that electrons can cross the interface and reach the shell surface; the shell growth is favoured against the secondary nucleation at the surface of TiO2. The height and width of the dipole layer go on increasing with the shell growth so that the electron density at the silver shell surface continuously decreases down to almost zero for a shell thickness close to two layers of silver atoms. In these conditions, one can say that the silver shell is “electronically starved internally” so that secondary nucleation on the TiO2 surface starts to be favoured by continuous light production of carriers if silver ions are still available in the solution. Experimentally this starvation limit seems to be reached for 1 to 2 silver atom layers, so that the width of the dipole barrier, twice as large, should be in the range of 0.8–1.6 nm as already suggested by atomic force microscopy measurements of adhesive forces between Si3N4 and several metals.52
;32 electrons should thus be mainly retained in the gold core, and the larger the silver shell the lower the electron density reaching its interface for the reduction of silver ions. An electrical barrier is thus established since the beginning of the shell growth. At the early stage, its energy and width remain sufficiently weak so that electrons can cross the interface and reach the shell surface; the shell growth is favoured against the secondary nucleation at the surface of TiO2. The height and width of the dipole layer go on increasing with the shell growth so that the electron density at the silver shell surface continuously decreases down to almost zero for a shell thickness close to two layers of silver atoms. In these conditions, one can say that the silver shell is “electronically starved internally” so that secondary nucleation on the TiO2 surface starts to be favoured by continuous light production of carriers if silver ions are still available in the solution. Experimentally this starvation limit seems to be reached for 1 to 2 silver atom layers, so that the width of the dipole barrier, twice as large, should be in the range of 0.8–1.6 nm as already suggested by atomic force microscopy measurements of adhesive forces between Si3N4 and several metals.52
Photodeposition synthesis of single dot Au@Pd–TiO2 NHDs
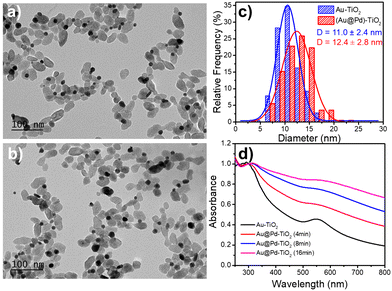
After investigating epitaxial Frank–van der Merwe growth triggered by laser deposition, we aimed to synthesize authentic BNDs Au@Pd of core–shell type on TiO2 by sequential deposition of Au and Pd. This second choice is motivated by (i) a large lattice constant mismatch between the two metals of 4.64% (respectively αAu = 4.08 Å, αPd = 3.89 Å), increasing the surface energy γAu/Pd, and (ii), respectively γPd/solution = 2.0 J m−2 and γAu/solution = 1.5 J m−2,39 so that ΔGS = γshell/solution − γcore/solution + γcore/shell ≥ 0 and the intermediate Stranski–Krastanov or the Volmer–Weber growth mode should be favoured. Moreover, as Pd and Au present almost the same values of work function,40 respectively φAu = 5.10 eV and φPd = 5.12 eV, the electron transfer at the Au/Pd interface required for the palladium ion reduction should not be disturbed and the formation of the shell should just be dependent on the lattice constant mismatch.In the same way, we directly added a 0.5 μmol solution of the palladium precursor (PdCl2 or Na2PdCl4) to the as-prepared Au–TiO2 NHDs (average diameter of Au NDs of 11.0 ± 2.4 nm, mean yield Ȳ = 51%), and irradiated for 8 min with the laser beam (P = 56.1 mW). TEM images show that the size of the BNDs increased to 12.4 ± 1.4 nm when using PdCl2 (Fig. 10), (Fig. S5, ESI† for Na2PdCl4, Au: 10.4 ± 2.7 nm, Au@Pd: 11.7 ± 2.8 nm) with a shell thickness of about 0.65–0.7 nm (Fig. 10c), corresponding to 1.7–1.8 atomic layers, more in agreement with the intermediate Stranski–Krastanov growth mode than the Volmer–Weber one. Once again, similar trends (NHDs yields and increased metallic BND size) confirm that Pd grew on Au NDs and not on TiO2. Moreover, using [Pd2+]0 = 0.5 mM, a mean yield of Ȳ ≈ 50%, a contact angle of a palladium ND on TiO2 of θ ≈ 140°, and the volume of a palladium atom νPd = MPd/(NAρPd) with MPd = 106.42 g the molar mass and is ρPd = 12.02 g cm−3 the density, we find from mass conservation that 40% and 33.5% of the palladium precursor were deposited starting respectively with 11.0 nm Au NDs and PdCl2, and 10.4 nm Au NDs and Na2PdCl4.
The variation of the UV-Vis spectra of Au–TiO2 and Au@Pd–TiO2 solutions with time shows that the characteristic peak of Au NDs at 550 nm of Au–TiO2 NHDs, exhibits a slight red shift and gets broader after Pd deposition due to the resulting increase of the refractive index of the medium surrounding the Au NDs (Fig. 10d).21,53–55 The Pd shell also has a strong damping effect on the dipole plasma oscillation of the Au core; adding even a thin Pd shell is indeed known to nearly suppress the SPR peak of the Au core in the Au@Pd core–shell BNDs.56,57
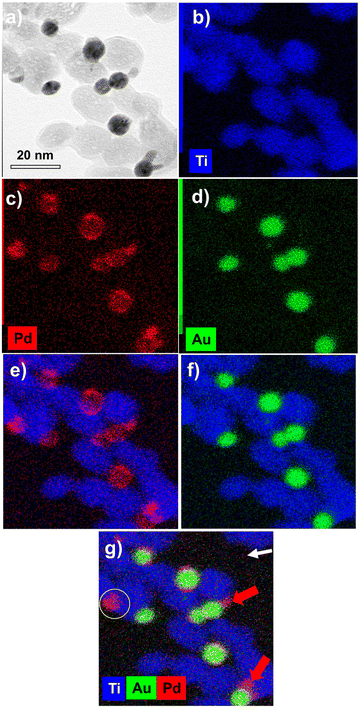
The EDS elemental mapping analysis on Au@Pd–TiO2 NHDs (Fig. 11) shows that the Au and Pd signals are spatially correlated even though very few pure Pd NDs photodeposited on TiO2 are present (compare Fig. 11c and d, see the yellow circle in Fig. 11g). Moreover, if most NHDs show a nearly uniform Pd shell on the Au core, some others present protrusions on the shell (red arrows). They are linked to the non-negligible lattice constant mismatch (4.64%) between Au and Pd, which first allows selective epitaxial growth of palladium on the Au NDs but then generates interfacial strains which prevent the continuous formation of a uniform shell (Fig. 11e and g (red arrows)).30,58 This observed growth is coherent with the intermediate Stranski–Krastanov mode, which describes the growth of a thin layer becoming more and more irregular due to interfacial strain and explains why we deduced non-integer mean shell thicknesses at completion and why they are so thin when grown from electrons internally provided by the excitation of TiO2 NPs; the high value of the surface energy γAu/Pd strongly influences the electron transfer at the Au/Pd interface. Finally, XPS analysis (not shown) confirmed the presence of the metallic Au 4f peaks at 83.7 (0.2) and 87.4 (0.2) eV Au and the Pd 3d peaks at 335.1 (0.2) and 340.1 (0.2) eV binding energies as well as the convoluted Au 4d peaks in the Pd 3d binding energy region, Au peaks that increase in intensity with Ar+ etching.59
Doubling the amount of PdCl2 to 1.0 μmol provided the same Pd shell thickness (∼0.7 nm) as expected from the first stage of the Stranski–Krastanov growth mode, as well as an increase in the amplitude of the Pd protrusions/dendrites,60 in agreement with the late stage Stranski–Krastanov growth mode (Fig. S6, ESI†). This result will certainly be beneficial for the photocatalytic generation of H259 or CO2 conversion18 thanks to the highly active surface area developed.
We also used large-size Au NDs (16.2 ± 4.1 nm) for Pd deposition; to obtain such a large size, a five times lower TiO2 concentration was used so that not only was the Au NDs diameter bigger but also the yield of heterodimers was higher (75%). After the second-step deposition, the average diameter of BNDs increased by 2.6 nm (Fig. S7, ESI†), the average Pd shell thickness (1.3 nm) is larger than that obtained from smaller Au NDs (0.6–0.7 nm) and the protrusions are still present (Fig. S8a and b, ESI†). Such large photodeposited Au NDs on TiO2 are highly polycrystalline so we suspect interfacial stresses to be decreased compared to those at the surface of monocrystals, thus lowering the mean surface energy γAu/Pd and allowing the first stage of the Stranski–Krastanov growth mode to develop for a longer time. This approach then offers an alternative to the Pd dendrites formed on 15 nm size Au NDs with an external reduction process.60 The control of a thin Pd shell thickness is indeed very important to get both a satisfactory catalytic effect and the absorption of the Au ND SPR. Tanaka et al.11 already mentioned that the optical and physical properties of the Au NDs were completely shielded for a Pd thickness of 2.5 nm but that the synthesis of a thinner Pd shell on gold was very difficult to achieve via classical chemical methods. Then, a Pd shell with a 0.6–1.6 nm thickness like the one obtained in a controlled way by photodeposition represents an efficient route to fulfil both conditions.
Photodeposition synthesis of single dot Au@Pt–TiO2 NHDs
We finally aimed to synthesize BNDs Au@Pt of core–shell type on TiO2 NPs by sequential deposition of Au and Pt to investigate laser deposition-triggered Volmer–Weber growth. This third choice is motivated by (i) a reasonably large lattice constant mismatch between the two metals of 3.82% (respectively αAu = 4.08 Å, αPt = 3.92 Å), increasing the surface energy γAu/Pt, and (ii) γPt/solution > γAu/solution, respectively γPt/solution = 2.5 J m−2 and γAu/solution = 1.5 J m−2,39 so that ΔGS = γshell/solution − γcore/solution + γcore/shell ≥ 0, and even larger than for Au@Pd, to favour a Volmer–Weber growth mode. Moreover, Pt and Au exhibit a mismatch in their electric work functions,40 respectively φAu = 5.10 eV and φPt = 5.65 eV, which is smaller than that between Ag and Au, but may nonetheless influence the electron transfer at the Au/Pt interface required for platinum ion reduction.After the deposition of the Pt precursor (0.2 μmol K2PtCl6), the pink colour due to the gold SPR turned grey; TEM images of the resulting Pt@Au–TiO2 BNDs NHDs are shown at respectively t = 1day in Fig. 12(a, d and g), t = 15 days in Fig. 12(b, e and h), and three months in the solution after laser exposure in Fig. 12(c, f and i). Instead of a core–shell-like structure, many tiny platinum nanoclusters with star-like shapes were deposited on gold. The magnified TEM images (Fig. 12(g, h and i) clearly show these Pt NDs forming clusters around the Au NDs and the absence of shell, whatever the elapsed time and even if some rearrangement (Ostwald ripening), seemed to take place and remain stable after some time (15 days).
This observed morphology of Pt on Au is coherent with the Volmer–Weber growth mode, with growth taking place via the formation of separated domains, and is expected when the lattice mismatch and the surface energy γAu/Pt are both high; the work function mismatch even reinforces this statement by reducing the electron transfer at the Au/Pt interface. These hybrid NHDs with such a cluster-like morphology would probably give rise to a high catalytic activity thanks to their relatively high specific surface area, even higher than that of Au@Pd–TiO2 HNDs.
The EDS mapping performed on these samples (Fig. 13) illustrates the selective distribution of the elements on the TEM grid (titanium and oxygen occupying the same surface, and gold surrounded by platinum). Fig. S9 (ESI†) confirms these results with the line-scan distribution profile of both gold and platinum and their representative EDS mapping images and overlay.
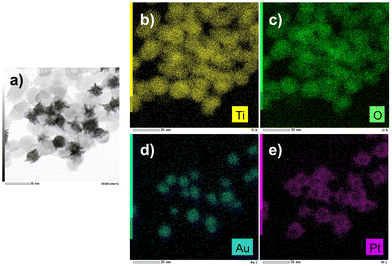 | ||
| Fig. 13 (a) STEM-EDS images of Au@Pt–TiO2 and (b and e) their compositional mapping of the distribution of Ti (yellow), Oxygen (green), Au (blue), and Pt (pink) of the sample synthesized as in Fig. 12. | ||
The high-resolution X-ray photoelectron spectroscopy (XPS) analysis performed to probe the surface state of the BNDs is illustrated in Fig. S10 (ESI†) within the binding-energy regions of O1s, Ti2p, Au4f, and Pt4f elements with a comparison between two Ar+ etching times: 0 s (Fig. S10a, c and e, ESI†) and 6 s (Fig. S10b, e and f, ESI†). The high-resolution spectra show that the O 1s oxygen peaks located at the binding energies around 530.3 (0.2) eV (Fig. S10a and b, ESI†) correspond to the lattice oxygen in TiO2.61
These peaks are polluted with high asymmetric contributions at higher binding energies, ascribed to oxygen from surface hydroxyl groups as effectively confirmed after etching; the latter strongly decreases the contribution due to pollution. The fit of Au 4f identifies the two binding energy peaks attributed to respectively the Au0 4f7/2 (83.5 (0.2) eV) and Au0 4f5/2 (87.2 (0.2) eV) electronic states.62 The fit of Pt 4f revealed two dominant peaks at 70.7 and 74.0 eV, which are due to metallic Pt0 4f7/2 and Pt0 4f5/2, respectively.63 These two peaks are slightly asymmetric due to a small contribution by PtII 4f7/2 and PtII 4f5/2 at 72.0 (0.2) eV and 75.3 (0.2) eV, respectively, which corresponds to a thin layer of PtO on the platinum NDs surface, which effectively decreases again with etching (Fig. S10e and f, ESI†). Additionally, the etching process (from 0 to 16 s) shows no change in the peak positions of Pt and Au (Fig. S11, ESI†) and an increase in the intensity ratio of the Au and Pt peaks from 0.32 to 0.53 with etching time, indicating that more Au is exposed, and Pt indeed grows on gold NDs. However, this etching process is detrimental to the TiO2 template since a partial reduction of titanium dioxide is detected with a broad shoulder, which appears on the low binding energy (BE) side of the Ti 2p1/2 and Ti 2p3/2 lines.64,65 A peak fit analysis of the Ti 2p3/2 signal (Fig. S11d, ESI†) reveals two underlying components at binding energies of 456.1 (0.2) eV and 457.5 (0.2) eV characteristic of titanium in various Ti3+ oxidation states or less, respectively.
Discussion
Photodeposition of these four types of metal shells on a gold core illustrates the three epitaxial growth modes expected when varying surface energies and lattice constant mismatch: the Frank–van der Merwe layered growth for Au and Ag, the island Volmer–Weber growth for Pt, and the intermediate Stranski–Krastanov growth for Pd.28,30Thus, regardless of the method used, wet chemistry,27,31 electrons beams60 for externally driven deposition, or photodeposition with internally produced carriers, the morphology of the shell is robustly monitored by the interaction between the two metals. However, the growth of Au@Pd raised some questions as the Pd shell should grow according to the Volmer–Weber mode when considering surface energies and lattice constants and nonetheless shows a Stranski–Krastanov-like behaviour. Consequently, it was suggested that electronic properties might play a role, some authors suggesting electronegativity as a key factor27 and others referring to the metal bond energy.31 To facilitate the formation of a layered shell, the electronegativity of the metal shell should be lower than that of the metal core. This is always the case when comparing the different metals involved: Au (2.54 eV), Ag (1.93 eV), Pd (2.20 eV), and Pt (2.28 eV)66 meaning that electronegativity does not seem so crucial in the shell growth mode. By looking at the bond dissociation energies,31 epitaxial growth is expected when the interaction between the shell and core atoms is higher than that between atoms within the shell; this is the case for a silver shell on a gold core. Likewise, the comparison between dissociation energies is in agreement with the discontinuous growth of Au@Pt. These two comparisons essentially confirm what was already predicted from the lattice mismatch and surface energies. But the case of Au@Pd remains puzzling because (i) the interaction between Pd and Au atoms is stronger than that between Pd atoms in the shell, favouring epitaxial growth, and (ii) γPd/solution > γAu/solution suggests the growth of separate domains; with the observation of protrusions, the experiments indicate that the intermediate Stranski–Krastanov growth mode31 is eventually at work.
Moreover, when carriers are produced internally, as in photodeposition, their transport within the structure becomes crucial, particularly at the interface between the two metals, to provide electrons to the growing shell surface. Thus, electronic properties do play a role, entangle with growth processes and finally shed light on their crucial role. The photo-induced epitaxial growth of Au@Au–TiO2, where the core and shell have the same properties, shows no difference from other growth methods. This demonstrates that when electron transfer at the TiO2/Au interface is significant, consistent with the fact that the work functions of TiO2 anatase and Au are close, the reduction of gold ions is not specifically affected by the method used, either internal or external. This is not the case for the photo-induced epitaxial growth of Au@Ag–TiO2. While it seems that there is no limitation on the shell thickness growth when silver ions are reduced externally, either by a wet chemistry approach or by an external electron source, photodeposition shows conversely that the shell cannot exceed a few atom layers. Then, as the surface and lattice properties of Au and Ag are close, electron transport should be affected by the Au@Ag interface. Li et al.32 raised the importance of the work function mismatch between different materials to analyse their adhesion. While TiO2 anatase and Au have close work function values, the greatest mismatch appears between Au and Ag, which creates a nanometer-scale dipolar barrier during shell growth, progressively deprives the shell interface of electrons, and stops its growth; this is probably the reason why photodeposition allows the control of a very thin shell. Moreover, since Au and Pd have almost equivalent work functions, the morphology of the Au@Pd–TiO2 HNDs, and then the Pd shell growth, are mainly driven by epitaxial considerations. Finally, the same applies to Au@Pt, which exhibits so different material properties; the growth of Au@Pt–TiO2 NHDs is entirely dominated by the surface energy and lattice mismatch, making difficult any observation of electronic specificities.
Conclusion
Single bimetallic core–shell structured Au@M–TiO2 (M = Au, Ag, Pd) were synthesized by a two-step photodeposition method using a focused UV laser as a continuous light source to control the growth and the size of a primary single gold ND on a TiO2 NP surface and then to grow a second metal on top of it. Characterization, including TEM, UV-vis spectroscopy, and EDS mapping, confirmed the synthesis of the core–shell structures. The morphology of the single BNDs Au@M is mainly controlled by the surface energies and lattice constants. However, the added value of the laser photodeposition, for which carriers are produced internally as opposed to other methods where the reduction of the metallic ion is external to the nanostructure, concerns the transport of electrons within the produced HNDs, particularly at the heterogeneous interfaces, which leads to the formation of very thin layers. The epitaxial growth of Au@Au was precisely controlled, with a maximum “shell” thickness of 2.9 nm in the present investigation, by varying the gold precursor concentration in agreement with the mass conservation; thus, the laser deposition provides a way to grow a single gold ND of significant size, preserving the NHD structure. Au@Ag also shows the epitaxial growth of an Ag shell, but the work function mismatch strongly limits the shell to two atomic layers regardless of the experimental conditions. Since Au and Pd have similar work functions, the Stranski–Krastanov growth mode of Pd on Au is at the origin of a thin shell formation followed by non-isotropic growth. Finally, due to the huge differences in surface energy and lattice mismatch between Au and Pt, the growth of Au@Pt occurs via the nucleation of numerous Pt NDs, which then ripen into a quasi-dendritic shell. Laser-deposition is easy to set up and can reliably provide stable high-yield nano-heterostructures with controlled morphologies for the versatile design of single core@shell ND plasmonic photocatalysts. Additionally, these NHDs are produced on a ligand-free surface, as for NPs synthesized by pulsed laser ablation,67 further facilitating any potential (photo-)catalytic reaction and opening the route toward NHDs with coupled bimetallic SPR31 synergy for so-called plasmonic photocatalysis applications.10,68Author contributions
The manuscript was written with the contributions of all authors. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the China Scholarship Council for a PhD Grant to FZ and QB. This project has received financial support from the CNRS through the MITI interdisciplinary programs (Action MITI: Nouveaux Matériaux 2020–2021). All the TEM observations were performed on the microscopes of the Plateforme Aquitaine de Caractérisation des Matériaux (PLACAMAT, UMS 3626, CNRS–Univ.de Bordeaux, Pessac, France) and the Bordeaux Imaging Centre. MHD and QB want to acknowledge Jerome Majimel for preliminary TEM, and Christine Labrugère from UMS 3626 for XPS data.References
- B. Gupta, A. A. Melvin, T. Matthews, S. Dash and A. K. Tyagi, Renewable Sustainable Energy Rev., 2016, 58, 1366–1375 CrossRef CAS.
- L. Gomathi Devi and R. Kavitha, Appl. Surf. Sci., 2016, 360, 601–622 CrossRef CAS.
- G. T. Forcherio, D. R. Baker, J. Boltersdorf, A. C. Leff, J. P. McClure, K. N. Grew and C. A. Lundgren, J. Phys. Chem. C, 2018, 122, 28901–28909 CrossRef CAS.
- J. F. S. Fernando, M. P. Shortell, K. L. Firestein, C. Zhang, K. V. Larionov, Z. I. Popov, P. B. Sorokin, L. Bourgeois, E. R. Waclawik and D. V. Golberg, Langmuir, 2018, 34, 7334–7345 CrossRef CAS PubMed.
- S.-F. Hung, Y.-C. Yu, N.-T. Suen, G.-Q. Tzeng, C.-W. Tung, Y.-Y. Hsu, C.-S. Hsu, C.-K. Chang, T.-S. Chan and H.-S. Sheu, Chem. Commun., 2016, 52, 1567–1570 RSC.
- P. Kalisman, L. Houben, E. Aronovitch, Y. Kauffmann, M. Bar-Sadan and L. Amirav, J. Mater. Chem. A, 2015, 3, 19679–19682 RSC.
- Z. Zheng, N. Murakami, J. Liu, Z. Teng, Q. Zhang, Y. Cao, H. Cheng and T. Ohno, ChemCatChem, 2020, 12, 3783–3792 CrossRef CAS.
- J. Liu, Z. Wu, Q. He, Q. Tian, W. Wu, X. Xiao and C. Jiang, Nanoscale Res. Lett., 2019, 14, 35 CrossRef PubMed.
- H. L. Jiang, T. Akita, T. Ishida, M. Haruta and Q. Xu, J. Am. Chem. Soc., 2011, 133, 1304–1306 CrossRef CAS PubMed.
- Y. Sato, S.-i Naya and H. Tada, APL Mater., 2015, 3, 104502 CrossRef.
- A. Tanaka, K. Fuku, T. Nishi, K. Hashimoto and H. Kominami, J. Phys. Chem. C, 2013, 117, 16983–16989 CrossRef CAS.
- F. Wang, C. Li, H. Chen, R. Jiang, L.-D. Sun, Q. Li, J. Wang, J. C. Yu and C.-H. Yan, J. Am. Chem. Soc., 2013, 135, 5588–5601 CrossRef CAS.
- S. Bhardwaj and B. Pal, Adv. Powder Technol., 2018, 29, 2119–2128 CrossRef CAS.
- D. Gao, W. Liu, Y. Xu, P. Wang, J. Fan and H. Yu, Appl. Catal., B, 2020, 260, 118190 CrossRef CAS.
- Y.-H. Li, J.-Y. Li and Y.-J. Xu, EnergyChem, 2021, 3, 100047 CrossRef CAS.
- J.-M. Herrmann, J. Disdier, P. Pichat, A. Fernández, A. González-Elipe, G. Munuera and C. Leclercq, J. Catal., 1991, 132, 490–497 CrossRef CAS.
- A. Sclafani and J. M. Herrmann, J. Photochem. Photobiol., A, 1998, 113, 181–188 CrossRef CAS.
- Q. Chen, X. Chen, M. Fang, J. Chen, Y. Li, Z. Xie, Q. Kuang and L. Zheng, J. Mater. Chem. A, 2019, 7, 1334–1340 RSC.
- A. Fernandez, G. Munuera, A. Gonzalez-Elipe, J. Espinos, J.-M. Herrmann, P. Pichat and C. Leclercq, Appl. Catal., 1990, 57, 191–202 CrossRef CAS.
- R. Su, R. Tiruvalam, A. J. Logsdail, Q. He, C. A. Downing, M. T. Jensen, N. Dimitratos, L. Kesavan, P. P. Wells, R. Bechstein, H. H. Jensen, S. Wendt, C. R. A. Catlow, C. J. Kiely, G. J. Hutchings and F. Besenbacher, ACS Nano, 2014, 8, 3490–3497 CrossRef CAS PubMed.
- J. Sun, Y. Han, H. Fu, X. Qu, Z. Xu and S. Zheng, Chem. Eng. J., 2017, 313, 1–9 CrossRef CAS.
- Y. Nakibli, P. Kalisman and L. Amirav, J. Phys. Chem. Lett., 2015, 6, 2265–2268 CrossRef CAS PubMed.
- Y. Nakibli, Y. Mazal, Y. Dubi, M. Wachtler and L. Amirav, Nano Lett., 2018, 18, 357–364 CrossRef CAS PubMed.
- F. E. Osterloh, Chem. Mater., 2008, 20, 35–54 CrossRef CAS.
- Q. Bai, I. Shupyk, L. Vauriot, J. Majimel, C. Labrugere, M.-H. Delville and J.-P. Delville, ACS Nano, 2021, 15, 2947–2961 CrossRef CAS PubMed.
- E. Bauer and J. H. van der Merwe, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 3657–3671 CrossRef CAS.
- F.-R. Fan, D.-Y. Liu, Y.-F. Wu, S. Duan, Z.-X. Xie, Z.-Y. Jiang and Z.-Q. Tian, J. Am. Chem. Soc., 2008, 130, 6949–6951 CrossRef CAS.
- L. Carbone and P. D. Cozzoli, Nano Today, 2010, 5, 449–493 CrossRef CAS.
- B. Xu, G. Zhou and X. Wang, NPG Asia Mater., 2015, 7, e164 CrossRef.
- J. Liu and J. Zhang, Chem. Rev., 2020, 120, 2123–2170 CrossRef CAS.
- J. E. S. van der Hoeven, T.-S. Deng, W. Albrecht, L. A. Olthof, M. A. van Huis, P. E. de Jongh and A. van Blaaderen, ACS Omega, 2021, 6, 7034–7046 CrossRef CAS.
- D. Y. Li, L. Guo, L. Li and H. Lu, Sci. Rep., 2017, 7, 9673 CrossRef CAS.
- K. Kanie and T. Sugimoto, Chem. Commun., 2004, 1584–1585, 10.1039/b404220d.
- T. Sugimoto, X. Zhou and A. Muramatsu, J. Colloid Interface Sci., 2003, 259, 53–61 CrossRef CAS PubMed.
- J. Hao, H. Liu, K. Wang, X. W. Sun, J.-P. Delville and M.-H. Delville, ACS Nano, 2021, 15, 15328–15341 CrossRef CAS PubMed.
- S. M. Foiles, M. I. Baskes and M. S. Daw, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7983–7991 CrossRef CAS PubMed.
- C. Ziegler and A. Eychmüller, J. Phys. Chem. C, 2011, 115, 4502–4506 CrossRef CAS.
- N. G. Bastús, J. Comenge and V. Puntes, Langmuir, 2011, 27, 11098–11105 CrossRef.
- L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, Surf. Sci., 1998, 411, 186–202 CrossRef CAS.
- H. B. Michaelson, J. Appl. Phys., 1977, 48, 4729–4733 CrossRef CAS.
- P. Peljo, J. A. Manzanares and H. H. Girault, Langmuir, 2016, 32, 5765–5775 CrossRef CAS PubMed.
- M. B. Cortie and A. M. McDonagh, Chem. Rev., 2011, 111, 3713–3735 CrossRef CAS.
- C. M. Gonzalez, Y. Liu and J. C. Scaiano, J. Phys. Chem. C, 2009, 113, 11861–11867 CrossRef CAS.
- K. K. Patra and C. S. Gopinath, ChemCatChem, 2016, 8, 3294–3311 CrossRef CAS.
- K. Mao, Z. Zhou, S. Han, X. Zhou, J. Hu, X. Li and Z. Yang, Talanta, 2018, 190, 263–268 CrossRef CAS PubMed.
- V. Prabhawathi, P. M. Sivakumar, T. Boobalan, C. M. Manohar and M. Doble, Mater. Sci. Eng., C, 2019, 94, 656–665 CrossRef CAS.
- A. C. Templeton, J. J. Pietron, R. W. Murray and P. Mulvaney, J. Phys. Chem. B, 2000, 104, 564–570 CrossRef CAS.
- P. Mulvaney, J. Pérez-Juste, M. Giersig, L. M. Liz-Marzán and C. Pecharromán, Plasmonics, 2006, 1, 61–66 CrossRef CAS.
- R. J. Culbertson, L. C. Feldman, P. J. Silverman and H. Boehm, Phys. Rev. Lett., 1981, 47, 657–660 CrossRef CAS.
- A. Hutzler, T. Schmutzler, M. P. M. Jank, R. Branscheid, T. Unruh, E. Spiecker and L. Frey, Nano Lett., 2018, 18, 7222–7229 CrossRef CAS PubMed.
- D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798–801 CrossRef CAS PubMed.
- R. C. Setiawan, M. Wu and D. Y. Li, Langmuir, 2022, 38, 1672–1679 CrossRef CAS PubMed.
- H. Wang, Z. Sun, Q. Lu, F. Zeng and D. Su, Small, 2012, 8, 1167–1172 CrossRef CAS PubMed.
- H. Wang, Z. Sun, Y. Yang and D. Su, Nanoscale, 2013, 5, 139–142 RSC.
- S. W. Kang, Y. W. Lee, Y. Park, B.-S. Choi, J. W. Hong, K.-H. Park and S. W. Han, ACS Nano, 2013, 7, 7945–7955 CrossRef CAS PubMed.
- Y. W. Lee, M. Kim, Z. H. Kim and S. W. Han, J. Am. Chem. Soc., 2009, 131, 17036–17037 CrossRef CAS PubMed.
- C. Fernández-Lodeiro, J. Fernández-Lodeiro, E. Carbó-Argibay, C. Lodeiro, J. Pérez-Juste and I. Pastoriza-Santos, Nano Res., 2020, 13, 2351–2355 CrossRef.
- A. A. Teixeira-Neto, R. V. Gonçalves, C. B. Rodella, L. M. Rossi and E. Teixeira-Neto, Catal. Sci. Technol., 2017, 7, 1679–1689 RSC.
- J. Boltersdorf, A. C. Leff, G. T. Forcherio and D. R. Baker, Crystals, 2021, 11, 226 CrossRef CAS.
- K. L. Jungjohann, S. Bliznakov, P. W. Sutter, E. A. Stach and E. A. Sutter, Nano Lett., 2013, 13, 2964–2970 CrossRef CAS PubMed.
- U. Diebold and T. E. Madey, Surf. Sci. Spectra, 1996, 4, 227–231 CrossRef CAS.
- D. Wang, Q. Bi, G. Yin, P. Wang, F. Huang, X. Xie and M. Jiang, Catal. Lett., 2018, 148, 11–22 CrossRef CAS.
- W. Fang, Z. Qin, J. Liu, Z. Wei, Z. Jiang and W. Shangguan, Appl. Catal., B, 2018, 236, 140–146 CrossRef CAS.
- R. Beranek and H. Kisch, Photochem. Photobiol. Sci., 2008, 7, 40–48 CrossRef CAS.
- J. A. Rengifo-Herrera, K. Pierzchała, A. Sienkiewicz, L. Forró, J. Kiwi, J. E. Moser and C. Pulgarin, J. Phys. Chem. C, 2010, 114, 2717–2723 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, Internet Version, ed. D. R. Lide, Taylor and Francis, Boca Raton, FL., 2007 Search PubMed.
- J. Theerthagiri, K. Karuppasamy, S. J. Lee, R. Shwetharani, H.-S. Kim, S. K. K. Pasha, M. Ashokkumar and M. Y. Choi, Light: Sci. Appl., 2022, 11, 250 CrossRef CAS PubMed.
- C. Zhang, T. Kong, Z. Fu, Z. Zhang and H. Zheng, Nanoscale, 2020, 12, 8768–8774 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1. (a) TEM image; (b) length distribution and (c) width distribution of the TiO2 NPs used for photodeposition experiments; (d) XRD pattern of anatase TiO2 NPs. Fig. S2. TEM images of Au-TiO2 NHDs synthesized by one-step and two-step deposition with different KAuCl4 contents. Fig. S3. (a) STEM image of (Au@Ag)–TiO2, (b–f) the representative EDS mapping images and their respective overlapping. Fig. S4. TEM images of Au@Ag–TiO2 synthesized using different amounts of AgNO3. Fig. S5. TEM images of Au–TiO2 (a) and Au@Pd–TiO2 (c) NPs and their corresponding size distributions (b and d). Fig. S4. TEM images of Au@Pd–TiO2 (a and b) NPs and size distributions (c). Fig. S6. TEM images of Au–TiO2 (a) and Au@Pd–TiO2 (c) NPs and the corresponding size distributions (b and d). Fig. S7. High-resolution XPS spectra of O1s, Ti2p, Au4f, and Pt4f in the Au@Pt–TiO2 NHDs (a, c and e) before and (b, d and f) after 6 s of Ar+ etching. Fig. S8a. STEM image of (Au@Pd)–TiO2, and 3 line-scan distribution profiles showing that the shell layer is not that homogeneous, and the presence of the protrusions. Fig. S8b. STEM image of (Au@Pd)–TiO2, and the representative EDS mapping images and their overlapping. Fig. S9. (a) STEM image of (Au@Pt)–TiO2, (b) line-scan distribution profile showing both gold and platinum and (c–e) the representative EDS mapping images and overlay of the two metals. Fig. S10. High-resolution XPS spectra of O1s, Ti2p, Au4f, and Pt4f in the Au@Pt–TiO2 NHDs (a, c and e) before and (b, d and f) after 6 s of Ar+ etching. Fig. S11. Variation of the XPS spectra of Au4f and Pt4f of the Au@Pt–TiO2 NHDs with Ar+ etching times. See DOI: https://doi.org/10.1039/d2ma01018f |
| ‡ These authors (FZ and QB) contributed equally to the experimental work. |
| § Present address: Ira A. Fulton School of Engineering, Arizona State University, Tempe, Arizona 85281, USA. |
| ¶ Present address: Key Laboratory of Energy Conversion and Storage Technologies (Southern University of Science and Technology), Ministry of Education, Shenzhen 518055, China. |
| This journal is © The Royal Society of Chemistry 2023 |