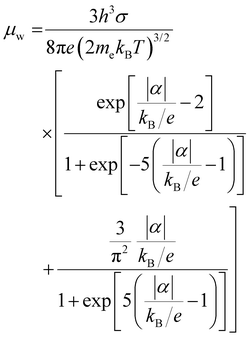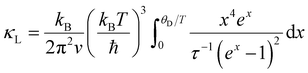Open Access Article
Open Access ArticleApproaching the minimum lattice thermal conductivity in TiCoSb half-Heusler alloys by intensified point-defect phonon scattering†
Ajay Kumar
Verma
abcd,
Shamma
Jain
ab,
Kishor Kumar
Johari
ab,
Christophe
Candolfi
 e,
Bertrand
Lenoir
e,
Bertrand
Lenoir
 *e,
Sumeet
Walia
cd,
S. R.
Dhakate
*e,
Sumeet
Walia
cd,
S. R.
Dhakate
 ab and
Bhasker
Gahtori
*ab
ab and
Bhasker
Gahtori
*ab
aCSIR-National Physical Laboratory, Dr. K. S. Krishnan Marg, New Delhi 110012, India. E-mail: bhasker@nplindia.org; Fax: +91-11-45609310; Tel: +91-11-45608556
bAcademy of Scientific & Innovative Research (AcSIR), Ghaziabad, 201002, India
cFunctional Materials and Microsystems Research Group and the Micro Nano Research Facility, RMIT University, Melbourne, VIC 3001, Australia
dSchool of Engineering, RMIT University, GPO Box 2476, Melbourne, Victoria 3001, Australia
eInstitut Jean Lamour UMR 7198 CNRS – Université de Lorraine Campus ARTEM, 2 allée André Guinier, BP 50840, Nancy 54011, France. E-mail: bertrand.lenoir@univ-lorraine.fr
First published on 27th November 2023
Abstract
Half-Heusler (HH) alloys based on TiCoSb are becoming popular semiconducting materials for mid-temperature thermoelectric (TE) applications, due to their superior Seebeck coefficient, moderate electrical conductivity, and excellent mechanical properties. However, their practical applicability is mainly limited by their high lattice thermal conductivity. Here, we show how a multi-alloying approach that involves co-substitution of Zr and Hf on the Ti site and Bi on the Sb site can significantly lower the heat transport of the TiCo0.85Fe0.15Sb alloy due to enhanced mass and strain-field fluctuations in the lattice. The substantial rise in point-defect phonon scattering leads to a sharp reduction in the lattice thermal conductivity from 8 to 2 W m−1 K−1 at ∼300 K and from 5 to 1.74 W m−1 K−1 at ∼843 K in Ti0.5Zr0.2Hf0.3Co0.85Fe0.15Sb0.96Bi0.4. The achieved thermal conductivity is the lowest value reported so far among TiCoSb-based alloys. Importantly, the reduction in thermal conductivity outweighs the concomitant decrease in the power factor, ultimately leading to an improved thermoelectric figure of merit ZT. Our findings show that creating large point defects through heavy isovalent substitution is an effective approach to significantly reduce the phonon transport in HH alloys.
Introduction
The investigation of thermoelectric (TE) materials has accelerated during the past two decades, and optimized compounds have been incorporated into thermoelectric devices that can be utilized for both cooling and green power production.1 Performance of a TE device mainly depends on a dimensionless parameter, the thermoelectric figure of merit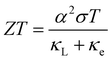 , where α is the Seebeck coefficient, σ is the electrical conductivity, α2σ is the power factor (PF), T is absolute temperature, κL is the lattice thermal conductivity and κe is the electronic contribution to the thermal conductivity. However, due to the fact that α, σ, and κe are highly reliant upon one another via the carrier concentration, the electronic band structure, and the scattering processes, the design of highly efficient thermoelectric materials has been a persistently difficult task.2,3 The general strategy to enhance the power factor includes optimization of carrier concentration by doping,4,5 and electronic band engineering.6,7 Due to the independency of κL on electronic transport, limiting the propagation of heat-carrying acoustic phonons can be realized by various approaches8 that notably include point-defect (atomic scale alloying) scattering,9,10 bonding effect,11,12 edge dislocations,13,14 grain boundaries,15,16 nano-sized grains, and the formation of in situ inclusion of nano precipitates in the host material.17,18
, where α is the Seebeck coefficient, σ is the electrical conductivity, α2σ is the power factor (PF), T is absolute temperature, κL is the lattice thermal conductivity and κe is the electronic contribution to the thermal conductivity. However, due to the fact that α, σ, and κe are highly reliant upon one another via the carrier concentration, the electronic band structure, and the scattering processes, the design of highly efficient thermoelectric materials has been a persistently difficult task.2,3 The general strategy to enhance the power factor includes optimization of carrier concentration by doping,4,5 and electronic band engineering.6,7 Due to the independency of κL on electronic transport, limiting the propagation of heat-carrying acoustic phonons can be realized by various approaches8 that notably include point-defect (atomic scale alloying) scattering,9,10 bonding effect,11,12 edge dislocations,13,14 grain boundaries,15,16 nano-sized grains, and the formation of in situ inclusion of nano precipitates in the host material.17,18
In addition to chalcogenides,19,20 skutterudites,21,22 silicides23,24 and clathrates25,26 extensively studied over the last decade for power generation applications, half-Heuslers (HH) alloys are promising candidates owing to their decent thermoelectric performance, low cost, composed via environmentally-friendly elements, good thermal stability and high mechanical robustness.27–30 The cubic crystal structure of HH compounds with the XYZ stoichiometry is built up by four interpenetrated face-centered cubic (fcc) lattices with one vacant position. Semiconducting properties generally emerge when the chemical composition is valence-balanced. Both n-(XNiSn; X = Ti, Zr or Hf) and p-type (XCoSb and X′FeSb; X = Ti, Zr or Hf and X′ = Nb or Ta) compositions can be designed to achieve high thermoelectric performance via proper optimization. More complex compositions such as vacancy-containing  , double, triple and high-entropy HHs have been recently studied, providing interesting avenues to engineer novel compositions with improved thermoelectric performance.31–33
, double, triple and high-entropy HHs have been recently studied, providing interesting avenues to engineer novel compositions with improved thermoelectric performance.31–33
Among these compositions, TiCoSb-based alloys have received significant attention because of the tuning ability to develop both n- and p-type compatible counterparts with similar thermal expansion coefficients which are prerequisite for TE devices. TiCoSb has complex electronic band structure that can be engineered to increase valley degeneracy, which contributes to the high power factors achieved in p-type alloys.7 However, high κL is one of the key factors that restricts the TE performance of TiCoSb based compounds. Significant efforts were devoted to lowering κL using various approaches such as doping,34 nanostructuring35 or nano-composite.36 The possibility to parallel enhance point-defect scattering through atomic substitutions and induce electronic band convergence in p-type TiCoSb alloys have been demonstrated in recent studies, yielding decreased κL values of 2.5 W m−1 K−1 at 823 K in Ti0.8Zr0.2Co0.85Fe0.15Sb0.96Sn0.04.37 The resulting improved maximum ZT value of 0.54 at 823 K places this alloy among the best reported p-type TiCoSb-based compositions without phase separation.
In this work, we explore alternative routes to further reduce κL by creating additional point defects in p-type TiCo0.85Fe0.15Sb via heavy substitution on the Ti and Sb sites with Zr/Hf and Bi, respectively. These substitutions enhance mass and strain field fluctuations in the lattice which drive a significant decrease in κL of ∼65%, eventually reaching ∼1.74 W m−1 K−1 at 843 K for Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb0.96Bi0.04. This reduced heat transport improves the ZT values by ∼60% compared to TiCo0.85Fe0.15Sb, leading to a peak ZT value of ∼0.3 at 843 K. Not only do these findings further demonstrate the benefit from heavy alloying to reduce the phonon heat transport in HH alloys but they also indicate the importance of carefully choosing the substituting elements to maintain the convergence of the valence band edges in TiCoSb alloys.
Experimental details
All the samples with chemical compositions Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb1−xBix (x = 0–0.04) were synthesized by weighing stoichiometric quantities of high-purity Ti granules (99.9%), Co pieces (99.9%), Sb shots (99.9999%), Zr foil (99.8%), Hf powders (99.6%), Fe powders (99+%) and Bi powders (99.999%), all purchased from Alfa Aesar. As a first step, a solid pellet composed of mixed powders of Hf, Fe, and Bi was cold-pressed. This pellet and the remaining elements were combinedly arc melted and alloyed using an arc-melter (Edmund Bühler GmbH, MAM-1) under argon atmosphere. To achieve homogeneous stoichiometry, melting done be several times with flipping the ingots. The melted ingots were first crushed into fine powders, then placed into a graphite die, and then processed to a spark plasma sintering (Dr Sinter, 725) system at a temperature of 1373 K with a constant pressure of 50 MPa, that route was optimized in our previous study.38 The density d of each polished sample was measured based on the Archimedes’ principle using a Mettler Toledo apparatus (model ML204/A01).Patterns of powder X-ray diffraction (PXRD) were acquired at room temperature for each of the samples by using an X-ray diffractometer (Rigaku Miniflex II). The PXRD data have been performed for Rietveld refinements using the FullProf software.39 The field-emission scanning electron microscope (FESEM, TESCAN MAGNA GMH) and the energy-dispersive X-ray spectroscopy (EDS, EDAX OCTANE ELECT SUPER) were used to investigate the surface morphology and chemical homogeneity, respectively. In order to further investigate microstructural features at the atomic scale, high-resolution transmission electron microscopy (HRTEM; JEM 2100F-JOEL 200 kV) was performed.
Electrical resistivity and Seebeck coefficient were simultaneously measured with a ZEM-3 system (ULVAC-RIKO) in the temperature range of 300 to 823 K. The Hall carrier density pH and mobility μH were measured at room temperature using a Hall effect instrument (HEMS, Nanomagnetics). Using sapphire as a standard and a differential scanning calorimeter system (DSC-NETZSCH, 404 F3), the isobaric specific heat (cp) of each sample was determined between 300 and 773 K. The thermal diffusivity (D) of disk-shaped samples was measured by employing a laser flash method (Netzsch LFA 427). The total thermal conductivity κ (= κL + κe) was calculated using the relation κ = cpDd.
Result and discussion
The PXRD patterns of the synthesized samples Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb1−xBix (0 ≤ x ≤ 0.04) are exhibited in Fig. 1(a). The diffraction peaks reflect the cubic crystal structure of HH phase for each sample. Rietveld refinements against the PXRD data, performed for each sample with an illustrative example for x = 0.04 shown in Fig. 1(b), confirm the absence of obvious impurity within the detection limit of this technique. The Rietveld refined parameters of each sample are listed in Table S1 in ESI.†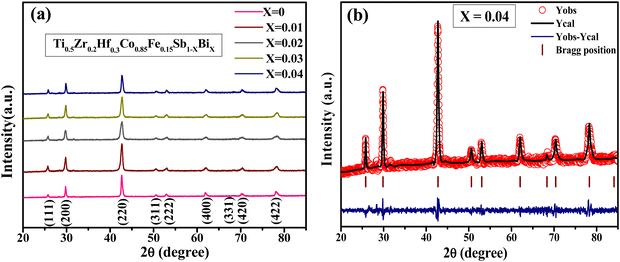 | ||
| Fig. 1 (a) Room-temperature PXRD patterns and (b) Rietveld refinement performed on the illustrative sample Ti0.8Zr0.2Hf0.3Co0.85Fe0.15Sb0.96Bi0.04. | ||
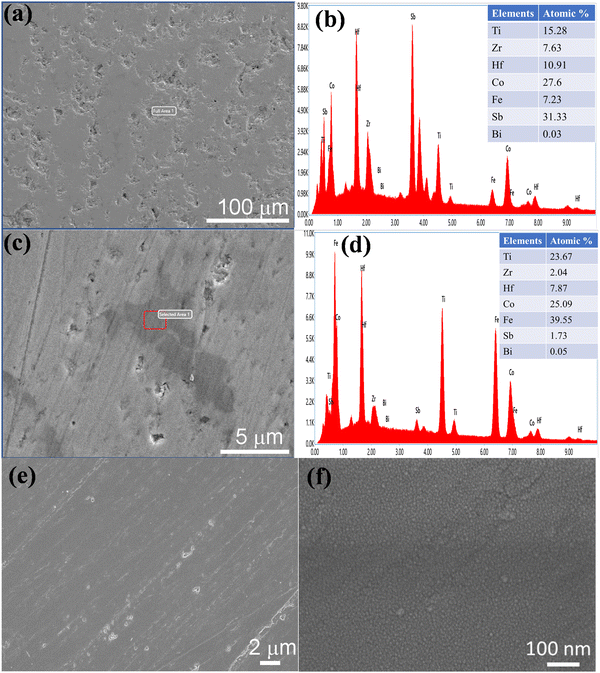
The surface morphology and elemental chemical configuration of the illustrative sample Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb0.96Bi0.04 were investigated by FESEM and EDXS as depicted in Fig. 2. The FESEM images show that the sample is densely packed with the presence of few minor secondary phases in the HH matrix. The chemical compositions (Fig. 2(b)), corresponding to the broad area shown in Fig. 2(a), is very close to the nominal stoichiometry. The minor secondary phase observed in Fig. 2(c) corresponds to a Fe-rich phase (Fig. 2(d), dark contrast region). Fig. 2(d) and (e) show the FESEM images of alumina-polished samples at low and high resolution, which confirm their high density. The elemental mapping of the representative sample x = 0.04 (Fig. S1 in ESI†) confirms the uniform distribution of the elements with only the Fe-rich phase as a minor secondary phase.
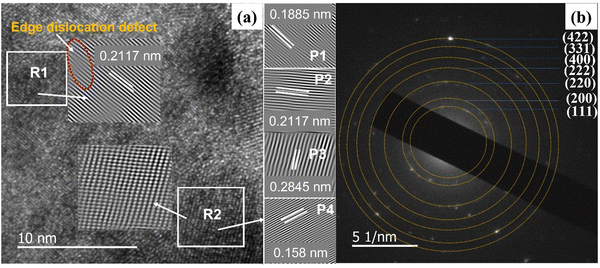
To further investigate the microstructure at the atomic scale, HRTEM analysis of the representative sample Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb0.96Bi0.04 was carried out (Fig. 3). The extracted interplanar spacing of the lattice planes are in good agreement with that of the TiCoSb HH phase. Two regions, R1, and R2 were analyzed at the atomic scale. The region R1 consists of a plane of calculated d-spacings 0.2117 nm nearly corresponding to the (220) family of planes, which is more dominating in TiCoSb HH phase as found in XRD data. Moreover, the edge dislocation defects are observed in region R1, while the region R2 consists of four overlapping planes of d-spacing 0.2845 nm, 0.2117 nm, 0.1885 nm, and 0.158 nm, which are nearly corresponding to (200), (220), (311), and (400) family of planes of TiCoSb HH phase, and also show the edge dislocations. The analyses demonstrate the presence of a large distribution of edge dislocation defects, which are expected to impact the transport properties. Fig. 3(b) shows the selected area electron diffraction (SAED) pattern of the same sample, where the superimposition of bright spots with Debye rings, are clearly visible, confirming the polycrystalline nature of the material.40 The diffraction pattern reflects the material's crystal structure in the reciprocal space where Debye rings are found corresponding to the family of planes (111), (200), (220), (222), (400), (311), (422) of TiCoSb HH phase.
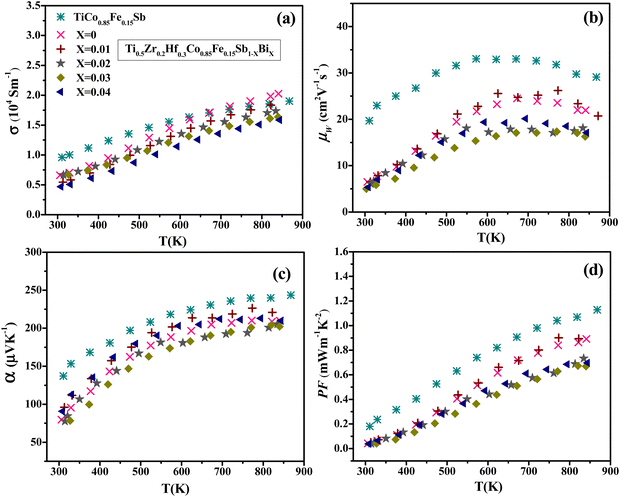
Fig. 4 illustrates the temperature dependence of the electronic transport parameters of all the samples Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb1−xBix (0 ≤ x ≤ 0.04). In order to facilitate a valuable comparison, the transport parameters of TiCo0.85Fe0.15Sb, which were determined in a previous experiment, have been included.7 At 300 K, σ tends to decrease in samples alloyed with Zr and Hf with respect to TiCo0.85Fe0.15Sb. Further alloying with Bi (0 ≤ x ≤ 0.04) weakly affects σ due to the small concentration of Bi introduced on the Sb site. The increasing trend of σ with increasing temperature indicates semiconducting behavior of all samples. Hall effect measurements carried out at 300 K (Table 1) reveal that the hole concentration pH drops from 5.4 to 1.2 × 1020 cm−3 as the Bi content increases. A similar behavior of decreased carrier density upon isoelectronic Bi doping on Sb has also been observed in other p-type compounds.41,42 The corresponding hole mobilities μH remain very low, varying in the range 0.68–1.57 cm2 V−1 s−1 at 300 K. These values are similar to those achieved in other heavily-alloyed HH compounds43 and can be mainly ascribed to alloy scattering that strongly limits hole mobility.
| Parameters | X = 0 | X = 0.01 | X = 0.02 | X = 0.03 | X = 0.04 |
|---|---|---|---|---|---|
| Hole density pH (×1020 cm−3) | 5.40 | 4.68 | 1.54 | 2.59 | 1.21 |
| Mobility μH (cm2 V−1 s−1) | 0.68 | 0.67 | 1.36 | 1.38 | 1.57 |
The temperature dependence of the weighted mobility (μw) was calculated using the measured σ and α:44
 , see below), in comparison to other reported p-type TiCoSb compositions with improved electronic properties (Fig. S2, ESI†).
, see below), in comparison to other reported p-type TiCoSb compositions with improved electronic properties (Fig. S2, ESI†).
Fig. 4(c) displays the temperature-dependent Seebeck coefficient α for each sample. The positive value of α over the entire temperature range indicates an electrical conduction dominated by holes. The room-temperature α values significantly decrease upon Zr and Hf alloying from 137 to 80 μV K−1 in spite of the concomitant decrease in the Hall carrier density. This counterintuitive trend might be rationalized through modifications of the electronic band structure and, in particular, to an increase in the energy offset between the valence band maxima located at the Γ and L points of the Brillouin zone. The energy offset of 51 meV in TiCoSb can be manipulated by alloying on the Co and Sb sites, which modifies the energy of the band edges at the L and Γ point, respectively. In contrast to Fe and Sn doping in TiCo0.85Fe0.15Sb that promotes band convergence,7 Zr and Hf might tend to induce the opposite effect. This trend suggests that the Ti orbitals mainly control the energy of the valence band edge at the Γ point, as evidenced in the ZrNiSn, NbCoSn and NbFeSb HH alloys by electronic band structure calculations.6 The isovalent substitution of Bi for Sb only weakly affects the α values at 300 K with values ranging between 78 and 96 μV K−1, indicating that Bi is either ineffective in inducing band convergence or that the highest concentration considered herein remains too low to observe any beneficial influence. At high temperatures, α tends to saturate, a behavior that can be ascribed to minority carrier excitation across the electronic band gap due to thermal energy.
These lowered α values are responsible for the decrease in the power factor PF = α2σ over the entire temperature range with respect to the values achieved in TiCo0.85Fe0.15Sb and in TiCo0.85Fe0.15Sb1−xSnx7 (Fig. 4(d)). Alloying with Bi has virtually no effect on PF at 300 K, while a marginal decrease is observed at higher temperatures.
The temperature dependence of the total thermal conductivity κ of each sample Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb1−xBix (0 ≤ x ≤ 0.04) is shown in Fig. 5(a). A sharp decrease in κ ∼ 62% at 300 K and ∼47% at ∼850 K is achieved upon Zr and Hf alloying with respect to TiCo0.85Fe0.15Sb. The addition of Bi further lowers κ by ∼29% to reach ∼2 W m−1 K−1 at ∼850 K in Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb0.96Bi0.04. This substantial reduction in thermal conductivity is due to the enhanced disorder induced by these substitutions. As shown in Fig. 5(b), which presents a comparison with the current literature on both n- and p-type TiCoSb-based alloys, this value is among the lowest ever obtained in TiCoSb-based alloys.
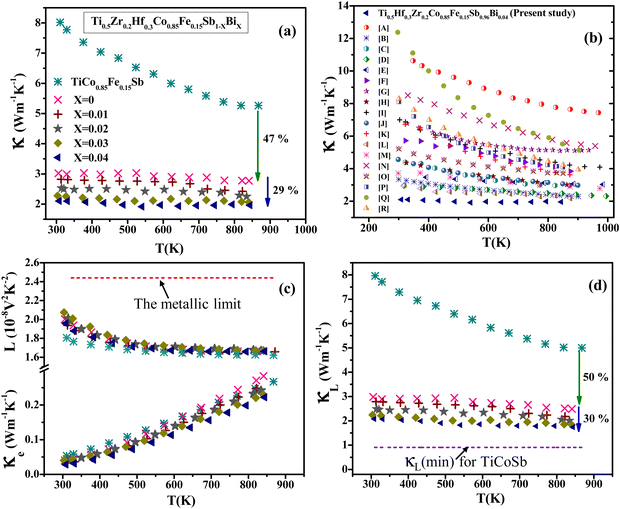 | ||
| Fig. 5 Temperature dependence of the (a) total thermal conductivity κ. (b) Comparison of κ of various TiCoSb-based HH alloys, with [A]-TiCoSb,45 [B]-Ti0.5Zr0.25Hf0.25Co0.95Ni0.05Sb,46 [C]-TiCo1.05Sb0.8Sn0.2,35 [D]-Ti0.6Hf0.4CoSb0.8Sn0.2,47 [E]-Ti0.5Hf0.5CoSb0.8Sn0.2,48 [F]-Ti0.9Nb0.1CoSb,49 [G]-Ti0.8Nb0.1Ta0.1CoSb0.8Sn0.2,50 [H]-Ti0.341Zr0.343Hf0.316Co0.957Pd0.043Sb,51 [I]-TiCoNi0.2Sb,52 [J]-Ti0.6Hf0.4Co0.87Ni0.13Sb,53 [K]-TiCoSb0.8Sn0.2,54 [L]-Ti0.6Zr0.4CoSb0.8Sn0.2,54 [M]-Ti0.5Hf0.4Ta0.1CoSb,34 [N]-TiCoSb0.9Sn0.1,55 [O]-TiFe0.3Co0.7Sb,56 [P]-TiCoGe0.2Sb0.8,57 [Q]-TiCo0.9Ni0.1Sb,58 [R]-Ti0.92Ta0.08CoSb,59 (c) Lorenz number L, electronic thermal conductivity κe and (d) lattice thermal conductivity κL. In panels (c) and (d), the horizontal dashed lines stand for the degenerate limit of L and the minimum lattice thermal conductivity κL,min, respectively. | ||
To further shed light on the influence of this heavy alloying on the heat transport, κ was decoupled into the electronic thermal conductivity κe and lattice thermal conductivity κL (Fig. 5(c) and (d)). κe was estimated according to the Wiedemann–Franz law κe = LσT, where L is the Lorenz number. L was calculated by the relation L = 1.5 + exp(−|α|/116) where L and α are expressed in 10−8 V2 K−2 and μV K−1, respectively.60 The L values are significantly lower than the degenerate limit L0 of 2.44 × 10−8 V2 K−2 and monotonically decrease with increasing temperature for each sample, as is frequently seen in heavily-doped semiconductors. Fig. 5(c) demonstrates that κe increases with temperature and does not vary significantly with the substitution of Bi for Sb. The lattice thermal conductivity κL = κ − κe decreases by ∼50% to reach ∼2.49 W m−1 K−1 at 843 K upon alloying on the Ti site. The κL is further reduced by Bi substitution, leading to the lowest κL value of ∼1.74 W m−1 K−1 achieved at 843 K in the sample Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb0.96Bi0.04 (Fig. 5(d)). This lowest value is approaching the minimum limit κL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min = 0.907 W m−1 K−1, which was calculated for TiCoSb using the model developed by Cahill and Pohl61 (see equations in ESI†). The drop in κL over the whole temperature range primarily stems from the large enhancement in point-defect scattering caused by the substitutions of Zr, Hf, and Bi for Ti and Sb, respectively, which yield a pronounced increase in the mass and strain field fluctuations.
min = 0.907 W m−1 K−1, which was calculated for TiCoSb using the model developed by Cahill and Pohl61 (see equations in ESI†). The drop in κL over the whole temperature range primarily stems from the large enhancement in point-defect scattering caused by the substitutions of Zr, Hf, and Bi for Ti and Sb, respectively, which yield a pronounced increase in the mass and strain field fluctuations.
To further investigate the role played by these substitutions on κL, the Debye–Callaway model that depends on the relaxation time approximation and assuming the absence of dispersion in the vibrational spectrum with no variations between the longitudinal and transverse polarizations, was considered.62,63 The correction factor for phonon–phonon interactions is not taken into account in the simplified form of this model, which yields the following equation:63,64
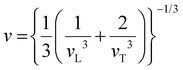 and atom density n were used to calculate θD according to the equation θD = v(6π2N)1/3/kB.64 Taking the values for the sound velocities used to calculate κL
and atom density n were used to calculate θD according to the equation θD = v(6π2N)1/3/kB.64 Taking the values for the sound velocities used to calculate κL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min yield v = 3597 m s−1 and θD = 417 K.65 By following Matthiessen's rule, τ can be determined by summing the inverses of the various scattering relaxation times
min yield v = 3597 m s−1 and θD = 417 K.65 By following Matthiessen's rule, τ can be determined by summing the inverses of the various scattering relaxation times 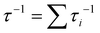 , where τi denotes the relaxation time of the ith scattering process. Here, point-defect (PD) scattering, Umklapp (U) scattering, and boundary (B) scattering were taken into account for the calculation of κL. The details of these calculations can be found in the ESI.†
, where τi denotes the relaxation time of the ith scattering process. Here, point-defect (PD) scattering, Umklapp (U) scattering, and boundary (B) scattering were taken into account for the calculation of κL. The details of these calculations can be found in the ESI.†
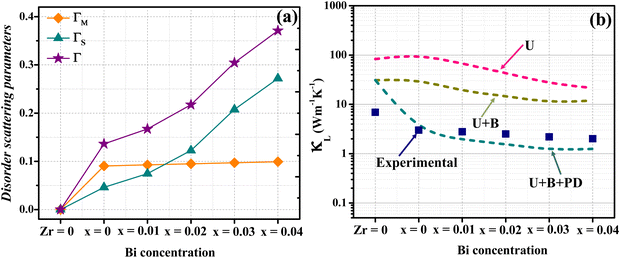
Fig. 6(a) shows the disorder scattering parameters ΓM, ΓS, and Γ for all samples. All these parameters abruptly rise in the samples alloyed with Zr and Hf, indicating enhanced mass and strain field fluctuations in the crystal lattice due to the pronounced differences in atomic mass and size between Zr, Hf, and Ti. Moreover, a monotonic increase in ΓM, ΓS, and Γ is observed in the Bi-substituted samples, which favors further lowering in κL. The calculated value of Grüneisen parameter γ of each sample (Fig. S3 in the ESI†) shows a peak value of 3.4 for the alloy Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb0.96Bi0.04, which is higher than that determined for TiCo0.85Fe0.15Sb. These high γ values are indicative of effective phonon–phonon scattering, which is a contributing factor to reduce κL.66
The relaxation time of various scattering mechanisms as a function of phonon frequency is depicted in Fig. S4 of the ESI.† The relaxation time curves for different scattering have been calculated for the representative sample Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb0.96Bi0.04 at 450 K (higher than Debye temperature of TiCoSb), assuming that all the vibrational modes have been populated at this temperature and contribute to phonon scattering. High-frequency phonons are scattered primarily by point defects and Umklapp processes, while low-frequency phonons are scattered mostly by grain boundaries.62,64 These predictions have been proven in the current set of alloys, where it was shown that grain boundary scattering is important at low frequency but point defect and Umklapp phonon scattering dominate at high frequency. The point-defect scattering mechanism shows the minimal relaxation time of τPD ∼ 1 × 10−14 s when it is excited at the Debye frequency, indicating that this mechanism outweighs the other processes and is predominantly responsible for the suppression in κL observed experimentally. Fig. 6(b) shows the calculated κL for different combinations of scattering mechanisms, that is, (U), (U + PD) and (U + PD + B). The κL values measured at 450 K for all samples have also been added in Fig. 6(b). The combination of the three scattering mechanisms (U + PD + B) yields a good agreement, indicating that all these scattering mechanisms are influencing the heat transport in these alloys.
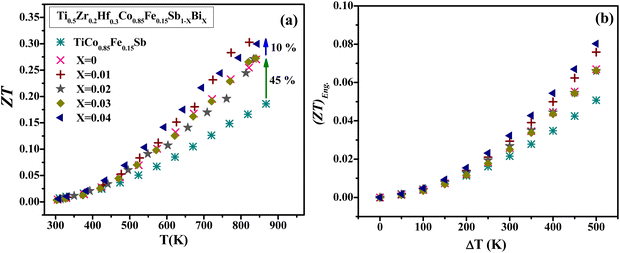
Fig. 7(a) shows the temperature dependence of the dimensionless thermoelectric figure of merit ZT. The co-substitution of Zr and Hf for Ti leads to a significant rise in the ZT values with a peak ZT of 0.27 at 843 K, which is ∼47% higher than that of parent alloy TiCo0.85Fe0.15Sb. The significant lowering in κL is the key factor behind this ZT improvement, which counterbalances the reduction in the power factor. The small concentration of Bi does not significantly impact the ZT values that reaches the moderate value of 0.3 at 843 K in the Ti0.5Hf0.3Zr0.2Fe0.15Co0.85Sb0.96Bi0.04 alloy. Finally, the engineering figure of merit (ZT)Eng was calculated as a function of the temperature difference ΔT within the cumulative temperature dependency (CTD) model (see ESI† for detailed information). (ZT)Eng increases with Zr, Hf and Bi doping, confirming that the reduction in thermal conductivity outweighs the decrease in the electronic properties. The peak (ZT)Eng value of ∼0.08 for ΔT = 500 K is realized for the x = 0.04 sample, which is ∼60% greater than that determined for TiCo0.85Fe0.15Sb as shown in Fig. 7(b).
Conclusion
In the present study, a pronounced drop in the lattice thermal conductivity of the HH alloy TiCoSb has been successfully achieved through a heavy isovalent atomic substitution strategy using Zr, Hf and Bi. The strong mass and strain field fluctuations induced by these substitutions led to a large decrease in κ, ultimately reaching ∼2 W m−1 K−1 for the composition Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb0.96Bi0.04, which is among the lowest values reported so far in n- and p-type TiCoSb-based HH compounds. While this approach is particularly effective in lowering the phonon-mediated heat transport, the accompanying increased atomic disorder has a detrimental influence on the power factor due to the effectively reduced hole mobility and the possible increase in the energy difference between the valence band maxima. Nevertheless, the overall beneficial impact of heavy alloying on the phonon transport outweighs this decrease, yielding a peak ZT value of ∼0.3 at 843 K in Ti0.5Hf0.3Zr0.2Co0.85Fe0.15Sb0.96Bi0.04. Further optimization of the electronic properties may be achieved by varying the Co-to-Fe ratio or substituting Sn for Sb, thereby helping to maintain the low lattice thermal conductivity while optimizing the power factor by bringing the valence band manifold closer to band convergence.Author contributions
Ajay Kumar Verma: synthesis, characterization, methodology, data analysis and original drafting of the manuscript. Shamma Jain: methodology, and formal analysis. Kishor Kumar Johari: review and editing. Christophe Candolfi: investigation, review, and editing. Bertrand Lenoir: investigation, review, and editing. Sumeet Walia: review, editing and supervision. Sanjay R. Dhakate: review, editing and supervision. Bhasker Gahtori: conceptualization, visualization, review, editing and supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to express their gratitude to Director, CSIR-NPL, New Delhi, India for his encouragement and support. AKV and SJ would like to express gratitude for the financial support provided by UGC-India. KKJ wishes to express gratitude for the financial support offered by CSIR-India. The authors appreciate the technical assistance provided by Mr Radhey Shyam and Dr Naval Kishor Upadhyay. We also acknowledge Dr J. S. Tawale for the FESEM and EDS measurements. The authors are thankful to Mr Abhishek for plagiarism check utilizing the software iThenticate available in the library of CSIR-NPL, New Delhi, India.References
- N. Jaziri, et al., A comprehensive review of Thermoelectric Generators: Technologies and common applications, Energy Rep., 2020, 6, 264–287 CrossRef.
- J. Mao, et al., Advances in thermoelectrics, Adv. Phys., 2018, 67(2), 69–147 CrossRef.
- L. You, et al., Realization of higher thermoelectric performance by dynamic doping of copper in n-type PbTe, Energy Environ. Sci., 2019, 12(10), 3089–3098 RSC.
- E. Rausch, et al., Charge carrier concentration optimization of thermoelectric p-type half-Heusler compounds, APL Mater., 2015, 3(4), 041516 CrossRef.
- C. Bhandari and D. M. Rowe, Optimization of carrier concentration, in CRC handbook of thermoelectrics, CRC Press, 2018, pp. 43–54 Search PubMed.
- S. Guo, et al., Conduction band engineering of half-Heusler thermoelectrics using orbital chemistry, J. Mater. Chem. A, 2022, 10(6), 3051–3057 RSC.
- A. K. Verma, et al., Realization of Band Convergence in p-Type TiCoSb Half-Heusler Alloys Significantly Enhances the Thermoelectric Performance, ACS Appl. Mater. Interfaces, 2023, 15(1), 942–952 CrossRef CAS PubMed.
- C. Chang and L.-D. Zhao, Anharmoncity and low thermal conductivity in thermoelectrics, Mater. Today Phys., 2018, 4, 50–57 CrossRef.
- R. He, et al., Improved thermoelectric performance of n-type half-Heusler MCo1−xNixSb (M = Hf, Zr), Mater. Today Phys., 2017, 1, 24–30 CrossRef.
- W. Li, et al., Promoting SnTe as an eco-friendly solution for p-PbTe thermoelectric via band convergence and interstitial defects, Adv. Mater., 2017, 29(17), 1605887 CrossRef PubMed.
- J. He, et al., Accelerated discovery and design of ultralow lattice thermal conductivity materials using chemical bonding principles, Adv. Funct. Mater., 2022, 32(14), 2108532 CrossRef CAS.
- J. Ji, et al., Functional-Unit-Based Material Design: Ultralow Thermal Conductivity in Thermoelectrics with Linear Triatomic Resonant Bonds, J. Am. Chem. Soc., 2022, 144(40), 18552–18561 CrossRef CAS PubMed.
- Z. Chen, et al., Vacancy-induced dislocations within grains for high-performance PbSe thermoelectrics, Nat. Commun., 2017, 8(1), 1–8 CrossRef PubMed.
- Z. Chen, et al., Lattice dislocations enhancing thermoelectric PbTe in addition to band convergence, Adv. Mater., 2017, 29(23), 1606768 CrossRef PubMed.
- J. Mao, et al., Phonon scattering by nanoscale twin boundaries, Nano Energy, 2017, 32, 174–179 CrossRef CAS.
- C. Fu, et al., Enhancing the figure of merit of heavy-band thermoelectric materials through hierarchical phonon scattering, Adv. Sci., 2016, 3(8), 1600035 CrossRef PubMed.
- W. Kim, Strategies for engineering phonon transport in thermoelectrics, J. Mater. Chem. C, 2015, 3(40), 10336–10348 RSC.
- H. Kim, et al., Strategies for manipulating phonon transport in solids, ACS Nano, 2021, 15(2), 2182–2196 CrossRef CAS PubMed.
- H. Meng, et al., Thermoelectric applications of chalcogenides, in Chalcogenide, Elsevier, 2020, pp. 31–56 Search PubMed.
- S. Gautam, et al., Structural, Electronic and Thermoelectric Properties of Bi2Se3 Thin Films Deposited by RF Magnetron Sputtering, J. Electron. Mater., 2022, 51(5), 2500–2509 CrossRef CAS.
- Z.-Y. Liu, et al., A review of CoSb3-based skutterudite thermoelectric materials, J. Adv. Ceram., 2020, 9(6), 647–673 CrossRef CAS.
- R. Bhardwaj, et al., CoSb3 based thermoelectric elements pre-requisite for device fabrication, Solid State Sci., 2022, 129, 106900 CrossRef CAS.
- S. Fiameni, et al., Synthesis and characterization of Bi-doped Mg2Si thermoelectric materials, J. Solid State Chem., 2012, 193, 142–146 CrossRef CAS.
- Y.-C. Tseng, et al., Advancing the reliability of thermoelectric materials: A case study of silicides through statistics, Appl. Phys. Lett., 2021, 119(19), 193903 CrossRef CAS.
- G. S. Nolas, G. A. Slack and S. B. Schujman, Semiconductor clathrates: A phonon glass electron crystal material with potential for thermoelectric applications, in Semiconductors and semimetals, Elsevier, 2001, pp. 255–300 Search PubMed.
- T. Takabatake, et al., Phonon-glass electron-crystal thermoelectric clathrates: Experiments and theory, Rev. Mod. Phys., 2014, 86(2), 669 CrossRef CAS.
- N. S. Chauhan, et al., Enhanced thermoelectric performance in p-type ZrCoSb based half-Heusler alloys employing nanostructuring and compositional modulation, J. Materiomics, 2019, 5(1), 94–102 CrossRef.
- K. K. Johari, et al., In Situ Evolution of Secondary Metallic Phases in Off-Stoichiometric ZrNiSn for Enhanced Thermoelectric Performance, ACS Appl. Mater. Interfaces, 2022, 14(17), 19579–19593 CrossRef CAS PubMed.
- K. K. Johari, et al., The charge carrier density modulation in off-stoichiometric ZrNiSn leads to enhanced thermoelectric performance, Ceram. Int., 2023, 49(16), 26558–26567 CrossRef CAS.
- T. Zhu, et al., High efficiency half-Heusler thermoelectric materials for energy harvesting. Advanced Energy, Materials, 2015, 5(19), 1500588 Search PubMed.
- K. Berarma, et al., Opto-electronic, thermodynamic and charge carriers transport properties of Ta2FeNiSn2 and Nb2FeNiSn2 double half-Heusler alloys, Semicond. Sci. Technol., 2022, 37(5), 055013 CrossRef.
- P.-F. Luo, et al., Alloyed triple half-Heuslers: a route toward high-performance thermoelectrics with intrinsically low lattice thermal conductivity, J. Mater. Chem. A, 2023, 11(16), 9125–9135 RSC.
- K. Chen, et al., Synthesis and thermoelectric properties of high-entropy half-Heusler MFe1−xCoxSb (M = equimolar Ti, Zr, Hf, V, Nb, Ta), J. Alloys Compd., 2022, 892, 162045 CrossRef CAS.
- R.-F. Wang, et al., Enhanced thermoelectric performance of n-type TiCoSb half-Heusler by Ta doping and Hf alloying, Rare Met., 2021, 40(1), 40–47 CrossRef CAS.
- N. S. Chauhan, et al., Spinodal decomposition in (Ti, Zr) CoSb half-Heusler: A nanostructuring route toward high efficiency thermoelectric materials, J. Appl. Phys., 2019, 126(12), 125110 CrossRef.
- C.-C. Hsu, Y.-N. Liu and H.-K. Ma, Effect of the Zr0.5Hf0.5CoSb1−xSnx/HfO2 half-Heusler nanocomposites on the ZT value, J. Alloys Compd., 2014, 597, 217–222 CrossRef CAS.
- A. K. Verma, et al., Coupling of electronic transport and defect engineering substantially enhances the thermoelectric performance of p-type TiCoSb HH alloy, J. Alloys Compd., 2023, 947, 169416 CrossRef CAS.
- A. K. Verma, et al., Role of sintering temperature on electronic and mechanical properties of thermoelectric material: A theoretical and experimental study of TiCoSb half-Heusler alloy, Mater. Chem. Phys., 2022, 281, 125854 CrossRef CAS.
- J. Rodríguez-Carvajal, Recent developments of the program FULLPROF. Commission on powder diffraction (IUCr), Newsletter, 2001, 26, 12–19 Search PubMed.
- A. V. Humbe, et al., Rietveld refinement, morphology and superparamagnetism of nanocrystalline Ni0.70−xCuxZn0.30Fe2O4 spinel ferrite, Ceram. Int., 2018, 44(5), 5466–5472 CrossRef CAS.
- L. Zhou, et al., Effect of Bi doping on the thermoelectric properties of Zn4Sb3, J. Alloys Compd., 2010, 503(2), 464–467 CrossRef CAS.
- R. Bhardwaj, et al., Optimization of electrical and thermal transport properties of Fe0.25Co0.75Sb3 Skutterudite employing the isoelectronic Bi-doping, Intermetallics, 2020, 123, 106796 CrossRef CAS.
- Q. Wang, et al., Enhanced thermoelectric performance in Ti(Fe, Co, Ni)Sb pseudo-ternary half-Heusler alloys, J. Materiomics, 2021, 7(4), 756–765 CrossRef.
- G. J. Snyder, et al., Weighted mobility, Adv. Mater., 2020, 32(25), 2001537 CrossRef CAS PubMed.
- T. Sekimoto, et al., Annealing effect on thermoelectric properties of TiCoSb half-Heusler compound, J. Alloys Compd., 2005, 394(1–2), 122–125 CrossRef CAS.
- W. Xie, Q. Jin and X. Tang, The preparation and thermoelectric properties of Ti0.5Zr0.25Hf0.25Co1−xNixSb half-Heusler compounds, J. Appl. Phys., 2008, 103(4), 043711 CrossRef.
- I. Ioannou, et al., High thermoelectric performance of p-type half-Heusler (Hf, Ti)Co(Sb, Sn) solid solutions fabricated by mechanical alloying, J. Alloys Compd., 2021, 858, 158330 CrossRef CAS.
- E. Rausch, et al., Enhanced thermoelectric performance in the p-type half-Heusler (Ti/Zr/Hf) CoSb0.8Sn0.2 system via phase separation, Phys. Chem. Chem. Phys., 2014, 16(46), 25258–25262 RSC.
- A. Vishwakarma, et al., Compositional modulation is driven by aliovalent doping in n-type TiCoSb based half-Heuslers for tuning thermoelectric transport, Intermetallics, 2020, 125, 106914 CrossRef CAS.
- Y. Kawaharada, et al., High temperature thermoelectric properties of CoTiSb half-Heusler compounds, J. Alloys Compd., 2004, 384(1–2), 308–311 CrossRef CAS.
- W. Xie, et al., Synthesis and thermoelectric properties of (Ti, Zr, Hf)(Co, Pd) Sb half-Heusler compounds, J. Phys. D: Appl. Phys., 2009, 42(23), 235407 CrossRef.
- L. Liu, et al., Interfacial Decoration Tailoring the Thermoelectric Performance of TiCoNixSb Half-Heusler Compounds, ACS Appl. Energy Mater., 2021, 4(7), 7148–7156 CrossRef CAS.
- P. Qiu, et al., Enhanced thermoelectric performance by the combination of alloying and doping in TiCoSb-based half-Heusler compounds, J. Appl. Phys., 2009, 106(10), 103703 CrossRef.
- N. S. Chauhan, et al., Enhanced thermoelectric performance in Hf-Free p-type (Ti, Zr) CoSb half-heusler alloys, J. Electron. Mater., 2019, 48(10), 6700–6709 CrossRef CAS.
- T. Sekimoto, et al., Thermoelectric properties of Sn-doped TiCoSb half-Heusler compounds, J. Alloys Compd., 2006, 407(1–2), 326–329 CrossRef CAS.
- T. Wu, et al., Thermoelectric properties of p-type Fe-doped TiCoSb half-Heusler compounds, J. Appl. Phys., 2007, 102(10), 103705 CrossRef.
- T. Wu, et al., Effects of Ge doping on the thermoelectric properties of TiCoSb-based p-type half-Heusler compounds, J. Alloys Compd., 2009, 467(1–2), 590–594 CrossRef CAS.
- M. Zhou, et al., Effects of partial substitution of Co by Ni on the high-temperature thermoelectric properties of TiCoSb-based half-Heusler compounds, J. Alloys Compd., 2005, 391(1–2), 194–197 CrossRef CAS.
- M. Zhou, et al., Moderate-temperature thermoelectric properties of TiCoSb-based half-Heusler compounds Ti1−xTaxCoSb, J. Appl. Phys., 2007, 101(11), 113714 CrossRef.
- H.-S. Kim, et al., Characterization of Lorenz number with Seebeck coefficient measurement, APL Mater., 2015, 3(4), 041506 CrossRef.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Lower limit to the thermal conductivity of disordered crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(10), 6131 CrossRef CAS PubMed.
- C. M. Bhandari and D. M. Rowe, Thermal conduction in semiconductors, Wiley, 1988 Search PubMed.
- J. Callaway, Model for lattice thermal conductivity at low temperatures, Phys. Rev., 1959, 113(4), 1046 CrossRef CAS.
- H. Xie, et al., Beneficial contribution of alloy disorder to electron and phonon transport in half-Heusler thermoelectric materials, Adv. Funct. Mater., 2013, 23(41), 5123–5130 CrossRef CAS.
- T. Sekimoto, et al., Thermoelectric and thermophysical properties of TiCoSb, ZrCoSb, HfCoSb prepared by SPS, in ICT 2005. 24th International Conference on Thermoelectrics, IEEE, 2005.
- Y.-L. Pei, et al., High thermoelectric performance of oxyselenides: intrinsically low thermal conductivity of Ca-doped BiCuSeO, NPG Asia Mater., 2013, 5(5), e47 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00923h |
| This journal is © The Royal Society of Chemistry 2023 |