An experimental and computational study of a low-temperature electrolyte design utilizing iodide-based ionic liquid and butyronitrile
Wendy J.
Lin
 ,
Yifei
Xu
,
Yifei
Xu
 ,
Marisa E.
Gliege
,
Christopher
Whitney
,
Mu-Tao
Chen
,
Marisa E.
Gliege
,
Christopher
Whitney
,
Mu-Tao
Chen
 ,
Ryan
Gunckel
,
Ryan
Gunckel
 and
Lenore L.
Dai
*
and
Lenore L.
Dai
*
School for Engineering of Matter, Transport and Energy, Arizona State University, Tempe, Arizona 85287, USA. E-mail: Lenore.Dai@asu.edu; Tel: +1 480 965 4112
First published on 14th October 2022
Abstract
Wide liquidus range electrolytes are in popular demand to extend the operating temperature windows of electrochemical devices. Different from conventional electrolytes, which dissolve salt in molecular liquids, highly tunable ionic liquids (ILs) offer attractive properties as competitive candidates in recent electrolyte developments. While IL-based electrolytes showcase satisfying performances at high and room temperatures, their functionality at low temperatures remains a challenge with the most reported progress around −40 to −70 °C. Herein, we present experimental and computational studies on low-temperature liquid electrolyte systems consisting of iodide containing IL, 1-butyl-3-methylimidazolium iodide ([BMIM][I]), nitrile solvents, acetonitrile (ACN) and butyronitrile (BuCN), and lithium iodide (LiI). While the [BMIM][I]/ACN/LiI system exhibits first-order phase transitions with increasing ACN concentration, [BMIM][I]/BuCN/LiI systems remain as glass-forming liquids over a wide composition range. More impressively, [BMIM][I]/BuCN/LiI-5/90/5 possesses an extremely low glass transition temperature of −152 °C, which marks the lowest liquidus range limit of reported IL-based mixtures to the best of our knowledge. Correspondingly, enhancements in transport properties are observed, especially at temperatures below −40 °C in comparison to our previous work. Moreover, iodide/triiodide electrochemistry in BuCN is validated as active and stable within the identified potential window. We attribute the bulk property evolution of the designed electrolytes to microscopic intermolecular interaction optimization, specifically, solvation of BuCN around the imidazolium cation via hydrogen bonding, as characterized using Fourier transform infrared (FTIR) and Raman spectroscopies. Furthermore, the effects of BuCN on the ion and molecular ordering are investigated through molecular dynamics simulation, which elucidates a different mechanism from IL/water mixtures. This work presents IL/BuCN systems with an exceptionally wide liquidus range and improvements in transport, which not only benefits iodide/triiodide-based technologies but also serves as a foundation for further task-specific optimization to support electrochemical devices at ultralow temperatures.
Design, System, ApplicationThe presented work demonstrates a design strategy for low-temperature iodide ionic liquid-based electrolytes through optimization of intermolecular interactions, specially between the nitrile solvent and the imidazolium iodide ionic liquid. Via optimization, the formulated electrolyte systems exhibit wide liquidus range with an ultralow glass transition temperature of −152 °C, enhanced transport properties at low temperatures, and adequate iodide/triiodide redox reactions for iodide-based technologies. In addition to experimental studies, results from computational simulations further reveal the complex intermolecular interaction between nitrile solvent molecules and ionic liquid cations and anions. Unique microscopic molecular dynamics are discovered for developed electrolytes, different from the previously studied ionic liquid/water mixtures, and support transport evolutions of respective electrolyte systems over a wide temperature range. The presented electrolytes are designed with tailored thermal, transport, and electrochemical properties for molecular electronic transducer sensors in space applications, targeting planetary objects where low surface temperatures impose challenges on molecular liquid electrolytes. Moreover, the facile design strategy is expected to guide future low-temperature electrolyte developments for other task-specific applications. |
Introduction
Ionic liquids (ILs) are a unique class of materials that consist entirely of ions and remain liquid at room temperature.1,2 Due to the weak coordination of their bulky and asymmetric constituent ions, ILs inherit the characteristics from both inorganic salts and molecular solvents.3,4 This unique combination allows ILs to possess remarkable properties,5,6 including wide liquidus range, intrinsic ionic conductivity, electrochemical stability, non-volatility, non-flammability, and tunability, which have expanded their applications to a variety of fields, for instance, chemical synthesis and processing,7 catalysis,8 separation,9 lubricants,10 biology,11 and nuclear waste treatment.12 Among the diverse applications, ILs have also become appealing electrolyte materials to electrochemical devices, such as batteries,13 supercapacitors,14 and sensors,15 because of their versatility to support a variety of electrochemistry for the improved performance,16 enhanced safety,17 and extended operation temperature window.18 Despite the novel attributes of ILs, the highly viscous nature originating from long-range coulombic forces between ions imposes one of the main challenges when employing them as electrolytes. The high viscosity hinders the transport of charge carriers between charged electrodes, causing insufficient ionic conductivity, thus greatly constraining the performance of the electrochemical devices. Attempts have been made to increase the electrode surface area with mesoporous hierarchical structures, but the electrolyte accessibility remains an issue for using carbon-based nanomaterials with ILs due to the relatively large size of ions and poor wetting ability.19,20 Modifying operation parameters toward higher temperature and voltage can offset the negative impact from low fluidity to some extent but significantly limits the applicability of the devices. On the other hand, as temperature decreases, ILs not only suffer from poor transport but also undergo early phase transitions from liquid to crystalline solid or amorphous glass, rendering the failure of operations with liquid electrolytes. The significance of such an issue continues to be highlighted with increasing demands in low-temperature electrochemical devices. Besides the pure IL design, the physicochemical properties of electrolyte systems can also be tailored by forming mixtures of ILs with other liquids.Adding a second IL component in the mixture can disrupt coulombic attractions and inhibit lattice formation to prevent crystallization by additional intermolecular interactions and a size mismatch of ions between the primary and the secondary ILs.21 For example, Lin et al. reported a eutectic mixture of ILs prepared by selecting a combination of different cations to increase the asymmetry of the system, which significantly broadened the temperature range of operation for capacitive energy storage.22 Incorporating water into an IL system, as another strategy to reduce the viscosity, has also been extensively studied for employing IL-based binary electrolytes in electrochemical applications. Dye-sensitized solar cells (DSSC), which utilize iodide-containing ILs, were reported to allow a diffusivity increase of 1-ethyl-3-methylimidazolium ([EMIM]+) cations and bis(trifluoromethylsulfonyl)imide (TFSI−) anions upon the addition of water, improving the work efficiency of DSSC at an optimal composition.23 Besides water, organic solvents are a strong complement when developing advanced liquid electrolytes and hence have been incorporated with ILs for mixtures, accompanied by intensive investigations on the electrochemical energy storage device electrolyte development. Specifically, IL/organic solvent electrolytes have also shown encouraging results on improving electrochemical stability for safety without significantly compromising ionic conductivity, which is known to be the weakness for electrolytes with water as solvents.24,25 More interestingly, since organic solvents offer large selections of varying functional groups and chemical structures, new-appealing functionalities of electrolytes can be tailored when introducing specific organic solvents for targeted systems. For example, carbonate solvents, such as vinylene carbonate (VC) and ethylene carbonate (EC), can dilute ILs that often lack reductive stability to not only boost the ion diffusion of the electrolyte but also form a protective interface layer on the carbon-based anode materials, shielding ILs away from the electrode surface to prevent side reactions and decompositions during the reduction process.26
Although the aforementioned IL/organic solvent electrolytes present appealing characteristics, a critical challenge remains for them to operate as functional liquids at extremely low temperatures. Low-temperature electrolyte developments have shown considerable progress over the past two decades. Recent reviews continue to highlight promising strategies for IL eutectic systems,27–29 salts dissolved in molecular solvents,30–32 and design of IL/molecular liquid mixtures for a variety of electrochemical applications down to −40 to −70 °C.33,34 For IL/ML electrolyte systems, popular solvent candidates such as carbonates,35,36 carboxylates,37 gamma-butyrolactone (GBL),36,38–40 and acetonitrile (ACN) serve as an attractive option to obtain tailored physicochemical properties over a broad temperature range. Typical electrolytes for commercialized electrochemical capacitors consist of quaternary ammonium salt dissolved in ACN or PC for adequate ionic conductivity and electrochemical stability. Brandon et al. presented mixtures of ACN with formats, esters, or cyclic ethers, as cosolvents to further extend the liquidus range from −45 to around −70 °C, allowing for operations at −55 °C.41 More recently, Lang et al. reported a 1-ethyl-3-methylimidazolium tetrafluoroborate/ACN/methyl acetate system to support the functionality of supercapacitors down to −50 °C, informing progression and emerging opportunities of low-temperature IL/molecular liquid electrolyte developments.42 Yet, the intrinsic freezing point of ACN at −45 °C calls for the incorporation of other cosolvents to form eutectic mixtures and thus limits the versatility of the electrolyte composition design. For instance, Cheng et al. formulated ternary systems of spiro-(1,1′)-bipyrolidinium tetrafluoroborate (SBP-BF4), ACN and dibutyl carbonate (DBC) as novel electrolytes for low-temperature supercapacitors.43 Dibutyl carbonate was selected to achieve a synergetic effect with ACN primarily due to its low melting point of −96 °C and relatively low viscosity. Nonetheless, the SBP-BF4/ACN/DBC mixture exhibited a slightly lower capacitance than the SBP-BF4/AN mixture from 20 to −50 °C and only showcased exceeding performance at −60 °C, demonstrating an inevitable compromise in transport with the reduced ACN concentration. On the other hand, another liquid of the nitrile family, butyronitrile (BuCN), is a unique solvent that possesses an extremely wide liquidus range suitable for developing electrolytes aiming for operations at extreme temperatures. Due to superior physicochemical and transport properties, BuCN has been explored as a favorable solvent to form binary electrolytes with ILs for energy storage applications.44,45 Despite its attractive potential in combining with ILs, to the best of our knowledge, BuCN has not been systematically studied with iodide-containing ILs, which are the primary ion sources in the key electrochemical redox reactions for applications including DSSC and molecular electronic transducer (MET) sensing technology.46–49
In this work, we investigated mixtures of iodide-containing ionic liquid 1-butyl-3-methylimidazolium iodide ([BMIM][I]) with nitrile-based solvents, ACN and BuCN, to further explore the liquidus range limits of IL-based liquid-state electrolytes. Specifically, these systems were designed to support MET motion sensors, a promising instrumentation for seismic investigation under challenging environmental conditions including extreme operating temperatures.50,51 The thermal and transport properties of the developed mixtures were studied experimentally over a broad range of concentrations and temperatures. Electrochemical stability and I−/I3− redox were validated at room temperature with an understanding of kinetic/transport dynamics that serves as a critical factor for MET technology. Additionally, the underlying intermolecular interactions between BuCN and [BMIM][I] at the molecular level were examined through molecular dynamics (MD) simulations and spectroscopic characterizations. More importantly, the identified inter-ionic and ionic-molecular interactions elucidated the role of BuCN on the property enhancement through a different mechanism than the one previously developed for the IL/water systems and thus reflected in low-temperature ionic conductivity.47,48 The findings in this research demonstrate the high tunability of [BMIM][I]/BuCN/LiI systems as low-temperature electrolytes and will guide future directions to further tailor electrolyte properties toward task-specific applications.
Materials and methodology
Materials
The organic solvents acetonitrile (99.9%) and butyronitrile (≥99%) were purchased from Honeywell and Sigma-Aldrich, respectively. Ionic liquid 1-butyl-3-methylimidazolium iodide ([BMIM][I]) (>98%) was purchased from IoLiTec, and anhydrous lithium iodide (≥98%) was purchased from VWR International. All the chemicals were used as received without any further purification.Electrolyte formulation preparation
Designed electrolytes consisting of organic solvent, IL, and lithium iodide were manually weighed, mixed, and ultrasonically agitated in a water bath for at least 15 min by a VWR Symphony ultrasonic cleaner. Lithium iodide salt was fixed at 5 mol% for all electrolytes to increase the iodide concentration for the targeted iodide-dependent applications. After sonication, all electrolyte solutions were determined as homogeneous and fully miscible upon visual inspection. In the following sections, each electrolyte is notated by its composition in mol%; for instance, an electrolyte composition of 20 mol% [BMIM][I], 75 mol% ACN, and 5 mol% LiI is denoted as [BMIM][I]/ACN/LiI-20/75/5. The solution consisting of only one chemical species is noted as “neat”.Differential scanning calorimetry
A TA Instruments Q-20 differential scanning calorimeter (DSC) was employed to characterize the low-temperature thermal behaviors of the prepared electrolyte formulations. Each electrolyte solution was quench-cooled with liquid nitrogen from 40 to −160/−175 °C, equilibrated, and then heated at a controlled rate of 5 °C min−1 back to 40 °C.Rheology
The rheological information of the sample solutions was obtained using an AR-G2 rheometer from TA Instruments, and the measurements were performed at a shear rate of 1 rad s−1 under a cone-plate geometrical setup. The temperature was controlled by a water-cooled/heated Peltier plate.Electrochemical impedance spectroscopy
All electrochemical results presented in this work were collected with a Bio-Logic VMP3 multichannel potentiostat and a Bio-Logic SP-150 potentiostat. The ionic conductivities were characterized by electrochemical impedance spectroscopy (EIS). A customized conductivity cell consisting of two fixed platinum electrodes was used for measurements, and its cell constant was calibrated with 0.1 and 0.01 m potassium chloride before the experiments. Measurements were performed at respective equilibrated temperatures, monitored by an Omega OMEGATTE HH 303A thermometer/data logger after the open circuit voltage was stabilized for at least 1 min. The impedances of electrolytes were characterized via a sinusoidal voltage with an amplitude of 10 mV over the frequency range of 900 kHz to 1 Hz. The ionic conductivity was calculated based on the real impedance obtained at high frequency, which represents the resistance of the electrolyte.Fourier transform infrared spectroscopy (FTIR)
The FTIR spectra of samples, including both neat and mixture solutions, were obtained in a vacuum environment using a Bruker IFS 66V/S FTIR with deuterated lanthanum α-alanine doped triglycine sulphate (DLATGS) detector, a KBr mid-IR beam-splitter, and a Pike diamond-ATR module.Ramen spectroscopy
The measurements were taken using a 70 mW wavelength stabilized diode laser with a wavelength of 633 nm as the excitation source, and the spectra were obtained using 1800 g mm−1 grafting and 45 sec acquisition time.Electrochemical window
Cyclic voltammetry (CV) was applied to determine the electrochemical windows of the respective electrolytes. Electrolytes were contained in Dr. Bob's electrochemical cell purchased from Gamry, with a platinum disk (3 mm diameter) as the working electrode, a platinum wire as the counter electrode, and a silver wire as the reference electrode. A glass frit and a bridge tube were used to separate the counter electrode and the reference electrode, respectively, from the electrolyte to minimize contamination during experiments. At room temperature, electrochemical windows (EW) were determined at a scan rate of 100 mV s−1 with reproducible profiles for at least 10 cycles. Afterwards, CV scans were performed at varying scan rates from 10–400 mV s−1 within the previously identified EW.Molecular dynamic (MD) simulation
The molecular dynamics simulations were carried out using the GROMACS 5.1.4 package.52–54 Each simulation was designed to emulate the electrolyte formulations as studied in the experimental sections, and therefore, concentrations were reflected through the number of solvent or solute molecules within the simulation boxes divided by the total number of molecules. Table 1 summarizes the number of each ion pair and butyronitrile molecules that constitute the four simulation boxes for the respective composition. To remain consistent between each simulation, the molecules or ion pairs were inserted into 5 × 5 × 5 nm3 boxes randomly, where [BMIM][I] and [Li][I] molecules were inserted pairwise. The ionic liquid and butyronitrile were described by an OPLS-AA force field. Parameters for the [BMIM]+ cation were implemented from the works of Canongia Lopes and later revisited by Bhargava and Balasubramanian, while parameters for butyronitrile were taken from the GROMACS built-in OPLS-AA force field.55–57 Respective Lennard-Jones parameters were applied to the iodide and lithium ions to maintain consistency with the forcefield.58,59 The initial configurations underwent an energy minimization step using the steepest descent method to create an appropriate-starting geometry for the simulations. An equilibration was then performed for 0.5 ns to aid further in finding low-energy starting structure and to minimize close contacts. Next, a 20 ns constant pressure, constant temperature (NPT) simulation was performed. The results presented in this study were from the NPT simulations between 5 ns and 10 ns, where the simulation was fully equilibrated. Each simulation used the leapfrog algorithm to integrate Newton's equations of motion with a time step of 0.002 ps, and hydrogen bonds were constrained with the LINCS algorithm.60,61 Long-range electrostatic interactions were treated using the particle-mesh Ewald (PME). The Lennard-Jones forces were treated with a cut-off of 1.2 nm, which is consistent with the OPLS-AA forcefields referenced above. The velocity-rescale thermostat was used in the constant volume, constant temperature (NVT) equilibration.62 For the NPT simulations, the Berendsen thermostat, and Parinello-Rahman barostat were used with a reference temperature and pressure of 295 K and 1 bar, respectively.63,64 Simulation results including densities and radial distribution functions were computed using the GROMACS package between 5 and 10 ns. The visual molecular dynamics package (VMD) aided in the visualization of the simulation boxes,65 and the molecular structure of the [BMIM]+ cation and BuCN are shown in Fig. 1 with the labeling on atoms of interest for later discussions.| Formulation [BMIM][I]/BuCN/LiI | [BMIM][I] pairs | BuCN | [Li][I] pairs | ρ sim | ρ exp | % error |
|---|---|---|---|---|---|---|
| 5-90-5 | 40 | 720 | 40 | 0.932 | 0.910 | 2.354 |
| 10-85-5 | 80 | 680 | 40 | 0.990 | 0.969 | 2.055 |
| 20-75-5 | 160 | 600 | 40 | 1.096 | 1.072 | 2.154 |
| 40-55-5 | 320 | 440 | 40 | 1.255 | 1.232 | 1.855 |
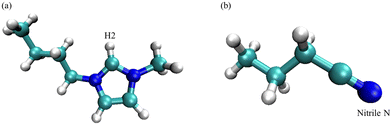 | ||
| Fig. 1 The molecular structure of (a) 1-butyl-3-methylimidazolium cation and (b) butyronitrile with chosen atoms for MD simulations labeled, respectively. | ||
Results and discussions
Effects of incorporating nitrile organic solvents on the thermal properties of iodide IL-based electrolytes
Designed mixtures of [BMIM][I]/nitrile solvent (ACN or BuCN)/LiI were examined by DSC to understand the thermal properties, which revealed the respective working temperature window for each of the liquid-state electrolytes. DSC results exhibited good reproducibility, where all the determined thermal transition temperatures were within ±1.5 °C between measurements. Fig. 2(a) presents the thermograms of [BMIM][I]/ACN/LiI formulations. It is observed that the incorporation of ACN effectively suppressed the glass transition temperature (Tg) compared to the neat [BMIM][I], and the effect became greater with the increasing ACN concentration. However, while the incorporation of 75 mol% ACN further reduced the Tg to −107.8 °C, prominent recrystallization and melting heat flows were also measured at around −72.4 °C and −7.9 °C, respectively, indicating that partial regimes in the system underwent phase transitions before the glass transition occurred. On the other hand, as shown in Fig. 2(b), electrolytes with BuCN as the solvent exhibited satisfying thermal characteristics over a broad range of compositions for electrolyte design, where a glass transition was determined without other detectable heat flow corresponding to first-order phase transitions. Specifically, with 75 mol% solvents, [BMIM][I]/BuCN/LiI extended the Tg to −131.4 °C, an additional 23.6 °C in comparison to that of [BMIM][I]/ACN/LiI. Furthermore, when BuCN was increased to 90 mol%, the electrolyte still appeared to sustain fluidity until the glass transition at −152.3 °C. To the best of our knowledge, such a temperature marks the lowest liquidus limit of IL-based electrolytes that have been reported thus far.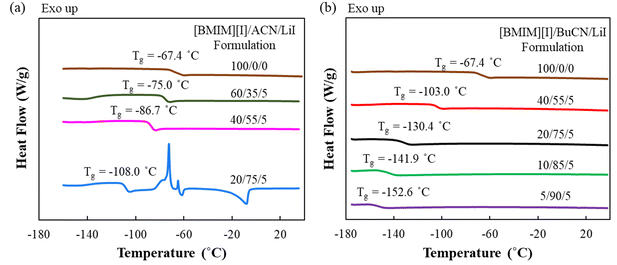 | ||
| Fig. 2 DSC thermograms (exothermic up) of neat [BMIM][I] and electrolyte formulations of (a) [BMIM][I]/ACN/LiI and (b) [BMIM][I]/BuCN/LiI. | ||
Compared to the neat [BMIM][I] with a Tg of −67.4 °C, both nitrile solvents demonstrated remarkable effects on the extension of the liquidus range. We hypothesize that such an improvement was attributed to intermolecular interactions between nitrile solvents and ionic liquids. Studies have demonstrated that hydrogen bonds could be formed between imidazolium cations and molecules of organic solvents in their mixture solutions.66–68 Such an observation also stands true in iodide-based IL/organic solvent mixtures, where the imidazolium head of [BMIM]+ was discovered to interact with the carbonyl groups of gamma-butyrolactone and propylene carbonate molecules via hydrogen bonding and contributed to shifting the glass transition towards a lower temperature.49 A similar intermolecular interaction is also anticipated between the lone-pair electrons of the nitrile functional group from ACN and BuCN and [BMIM]+ cations, which have been observed experimentally and validated through computational simulations.69,70 Consequently, the overall cohesive energies of the mixture solutions were modified, resulting in decreasing Tg as a function of increasing nitrile solvent concentration, where a lower Tg corresponds to reduced cohesive energy of a material system.71 However, it is quite apparent that even at the same concentration of 75 mol%, ACN and BuCN resulted in different microscopic regimes in the mixtures, which determined the occurrence of the additional phase transitions. Nanostructures of IL/molecular liquid mixtures are highly dependent on constituent species and compositions. At high-solvent concentrations, aggregates, chains, or network-like distinct regimes were reported and attributed to free solvent molecules that did not participate in the ion solvation shell, which may lead to crystallization at a relatively high temperature.72,73 We hypothesize that although both ACN and BuCN possess nitrile groups to interact with the imidazolium ring, the different alkyl chain lengths (1C vs. 4C) can also result in van der Waals interactions among themselves and with the alkyl chain in the imidazolium ring, leading to different solvation and molecule ordering within the mixture. Moreover, in addition to the intrinsic differences in the tendency to undergo crystallization as suggested by their respective freezing point, BuCN is also known as a supercooled liquid with a Tg of −179 °C.74–76 Such a characteristic may also contribute to the absence of first-order phase transitions even at a high concentration of 90 mol%. Low-temperature electrolyte systems previously reported by our group required cosolvent pairs, e.g. ethylammonium nitrate ([EA][N])/water and PC/GBL, to mitigate excessive solvent molecules while retaining a low Tg.48,49 The promising result of [BMIM][I]/BuCN/LiI without the incorporation of another cosolvent is intriguing and provides a wider composition window for electrolyte design to further tailor specific properties. In the following sections, studies of transport properties, intermolecular interactions, and electrochemical behaviors are focused on [BMIM][I]/BuCN/LiI systems.
Effects of composition and temperature on transport properties
Fig. 3 shows a comparison of the viscosity and ionic conductivity of [BMIM][I]/BuCN/LiI electrolytes at room temperature. Effects of molecular solvents on the transport properties of molecular solvents/ILs mixtures have been well studied, where the incorporation of molecular solvents in IL results in a rearrangement of the original closely packed ions and leads to a significant decrease in the viscosities of the mixtures.77,78 As expected, viscosities of the developed electrolytes decreased exponentially with increasing BuCN concentration. Particularly, the difference in viscosities between [BMIM][I]/BuCN/LiI-40/55/5 and 5/90/5 was more than one order of magnitude. Again, we hypothesize that interactions between BuCN and [BMIM]+ cation have altered the arrangement of existing species on a microscopic level that significantly reduces the bulk viscosity. Similar observations were also reported in various mixtures of acetonitrile and imidazolium ILs.79–81 In correspondence with the trend of viscosity, an increasing BuCN concentration led to a higher ionic conductivity. Since ion mobility for the conduction mechanism depends on the fluidity of the solution, such an inverse relationship between these two transport properties agrees with each other to some extent. However, unlike viscosity, which decreased exponentially with increasing BuCN, the increase in ionic conductivity occurred in more of a linear fashion, suggesting that other factors are in play. In addition to fluidity, Galiński et al. further disclosed the contribution of ionicity, the extent of ion disassociation, on the bulk ionic conductivity in IL-based mixtures.82 In pure ILs, strong attraction between cations and anions often results in neutral ion pairs and ion aggregates that do not serve functionalities of charge carriers. By introducing cosolvents into ILs, a higher ionicity is achieved via the solvation effect of solvent molecules around ions and thus an improved ionic conductivity.83,84 While such an enhancement on transport properties was also studied experimentally and computationally in acetonitrile/IL systems,85–87 research on the effects of other nitrile-based solvents such as propionitrile (PCN) and BuCN in ILs are limited. Ruiz et al. observed viscosity reduction and ionic conductivity improvement in mixtures of N-butyl-n-methylpyrrolidinium bis(trifluoromethane sulfonyl)imide ([PYR14][TFSI])/ACN and [PYR14][TSFI]/BuCN, respectively.44 However, correlations were made more on the intrinsic properties of molecular liquids with resulting mixture properties, leaving effects of the complex interplay between IL and molecular solvents unrevealed. Moreover, although the addition of ACN in ionic liquids was reported to disrupt ion clusters, both computational and spectroscopy results indicated that hydrogen bonding between the nitrile group and imidazolium cation was not effective enough to break ion pairs, leading to a poorer solvation effect.88,89 Such a phenomenon can potentially explain the linear relationship between the conductivity and composition in [BMIM][I]/BuCN/LiI systems, different from the exponential profile reported for [BMIM][I]/water mixtures.47 Lastly, as previously hypothesized, the longer alkyl chain of BuCN can lead to van der Waal forces, which might also considerably affect the transport properties.90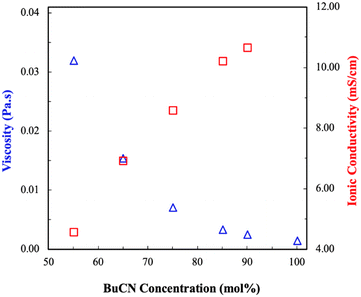 | ||
| Fig. 3 Transport properties, viscosity (blue), and ionic conductivity (red), of [BMIM][I]/BuCN/LiI electrolytes at room temperature. | ||
To compare the low-temperature performance of the optimized [BMIM][I]/BuCN/LiI-5/90/5 formulation with the previously developed systems, conductivity measurements were extended to −70 °C and showed good fitting (R2 > 99) when using the Vogel–Fulcher–Tammann (VFT) model to validate its property as glass-forming liquids for low-temperature predictions.91,92Fig. 4 shows conductivity evolutions of [BMIM][I]/BuCN/LiI-5/90/5 along with optimized electrolytes of [BMIM][I]/[EA][N]/water/LiI,48 [BMIM][I]/GBL/LiI,49 and [BMIM][I]/PC/GBL/LiI.49 At room temperature, the optimized electrolyte with [EA][N] and water showed the highest ionic conductivity among all systems. As temperature decreased, the ionic conductivity of optimized organic solvent-based electrolytes started to catch up and eventually exceeded that of [EA][N]/water-based system. Peculiarly, ionic conductivity curves of [BMIM][I]/BuCN/LiI-5/90/5 and the optimized [BMIM][I]/[EA][N]/water/LiI intersected at −40 °C, presenting even more promising results than those of GBL and PC/GBL systems by 30 °C. As previously discussed, the ionic conductivity of ionic liquid-based electrolytes is governed by both the actual ion concentration and viscosity of the system, and the two factors may show dominance in different temperature ranges. We hypothesize that at higher temperatures the effective solvation of water for efficient ion disassociation prevails along with the boosted ion concentration due to the involvement of [EA][N] in preventing crystallization. At lower temperatures, sufficient diffusion of ions is achieved by the incorporation of organic solvents in comparison to strong hydrogen bonding between water molecules during freezing, compensating for the poorer ionicity and the lower ion concentration. Consequently, the changing dynamics of the governing factors were reflected in low-temperature conductivity, where [BMIM][I]/BuCN/LiI-5/90/5 exhibited the highest ionic conductivity among all the reported systems by an order of magnitude at the lowest measurement temperature around −75 °C. Although the effects of the composition and solvent have been studied very thoroughly across various IL-based mixtures, limited results were reported to understand their effects towards extremely low temperatures.93 The observation from the optimized [BMIM][I]/BuCN/LiI system further strengthens the discussions from our previous studies, suggesting the fluidity of the electrolytes to be a more significant factor, especially for low-temperature electrolytes.
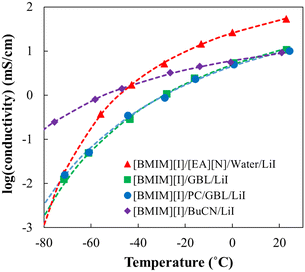 | ||
| Fig. 4 The ionic conductivity of developed low-temperature electrolyte systems from −75 to 25 °C, including [BMIM][I]/BuCN/LiI-5/90/5 selected from this work and optimized [BMIM][I]/[EA][N]/water/LiI,48 [BMIM][I]/GBL/LiI,49 and [BMIM][I]/PC/GBL/LiI.49 Data points were experimental data and dotted lines were plotted based on the VFT model fitting results. | ||
Understanding the intermolecular interactions in [BMIM][I]/BuCN/LiI systems through computational and experimental approaches
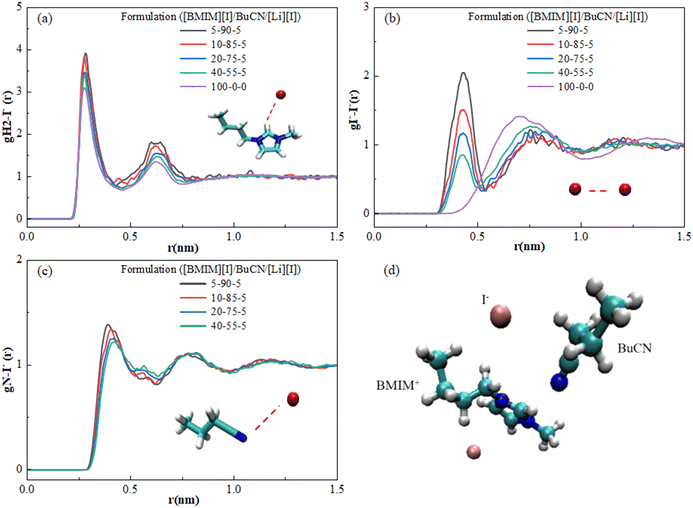
In order to further understand the underlying physics in the mixture system, MD simulation was employed to reveal and identify key molecular interactions between the [BMIM]+ cation, [I]− anion, and BuCN solvent molecule. Presented radial distribution functions (RDF) were calculated about the center mass of the chosen atom(s) and normalized against the bin volume and density. Interactions between IL and BuCN solvent molecules have been highlighted and hypothesized to play a key role in intermolecular interaction optimization, which resulted in improved thermal and transport properties. Fig. 5(a) shows RDFs between the imidazolium protic hydrogen H2 and BuCN nitrogen of varying electrolyte compositions. This site on the imidazolium cation is known to be highly reactive due to its acidity, serving as a probable hydrogen bond donor.94 For each formulation, two distinctive peaks were identified, indicating probable interactions of BuCN molecules around the [BMIM]+ ring at 0.27 and 0.6 nm, respectively. The first peak could possibly be a hydrogen bonding between the nitrile group and imidazolium H2, given the distance and probability in agreement with the other reported imidazolium IL/ACN systems;95 however, further investigations would need to be performed to confirm the type of bonding. The second peak indicates another BuCN located at a further position, which can be an interaction with another imidazolium cation and will be elaborated on later. These two clusters were fairly consistent in terms of relative position with slight variations in the probability of the first peak with respect to compositions, validating the existence of the hypothesized nitrile–imidazolium interaction in all formulations as a key contributor to the bulk property evolutions. While a consistent interaction can be drawn in all presented formulations qualitatively, a quantitative correlation is yet be established, specifically for the lower probability of the peak at 0.27 nm for [BMIM][I]/BuCN/LiI-10/85/5. Such a feature implies that the interaction of imidazolium H2 and BuCN nitrile group can be highly sensitive to compositions and requires additional simulations with smaller incremental formulation changes for the elucidation of subtle evolutions. Consequently, RDFs were calculated between the imidazolium head at H2 and the alkyl chain to elucidate how the involvement of BuCN and their interactions with [BMIM]+ affect the cation ordering. In Fig. 5(b), probability changes corresponding to different formulations were observed in contrast to BuCN nitrile N–imidazolium H2 (Fig. 5(a)). The neat ionic liquid function exhibits one small peak at 0.27 nm and other weaker peaks ranging from 0.27–0.6 nm, depicting the intrinsic ordering of imidazolium cation head and tail without the interference of solvents. Upon the addition of BuCN, the changes in the ratio of these two peaks clusters are summarized in Table 2. Specifically, the probability of peak at 0.27 nm increases with higher BuCN concentrations. Moreover, in neat [BMIM][I], the normalized probability of the peak at 0.476 nm was higher than the peak at 0.378 nm; however, once BuCN is incorporated to form mixtures, peak 0.378 nm becomes more prominent with increasing BuCN concentration, suggesting an alternation of ionic liquid ordering that may be a result from solvent networks or clustering. Nitrile solvents are known to form various interactions with imidazolium cations, including hydrogen bonding at the imidazolium ring and alkyl chain (less active) via the nitrile group and orientation within the non-polar domain.96 Judging from the peak placements of the RDFs in Fig. 5, we hypothesize that they reflect a competition of several probable interactions between BuCN and imidazolium cation. This competition may become more enhanced with increasing BuCN concentration and thus resulting in more complex interaction mechanisms within the ternary system.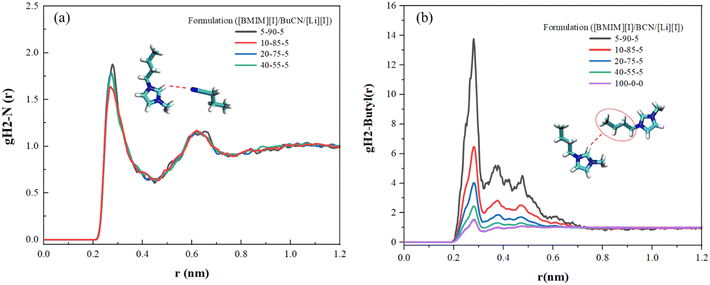 | ||
| Fig. 5 RDFs for various [BMIM][I]/BuCN/LiI electrolytes of (a) interaction of the imidazolium ring H2 and BuCN nitrile N and (b) interaction of the imidazolium head group and alkyl chain. | ||
| Peak | [BMIM][I]/BuCN/LiI | ||||
|---|---|---|---|---|---|
| 5/90/5 | 10/85/5 | 20/75/5 | 40/55/5 | 100/0/0 | |
| 1 (0.27 nm) | 11.36 | 5.62 | 3.52 | 2.15 | 1.33 |
| 2 (0.378 nm) | 5.20 | 2.82 | 1.86 | 1.31 | 1.00 |
| 3 (0.476 nm) | 4.51 | 2.49 | 1.69 | 1.30 | 1.09 |
| Normalized probability (peak 2/peak 1) | 0.46 | 0.50 | 0.53 | 0.61 | 0.75 |
| Normalized probability (peak 3/peak 1) | 0.40 | 0.44 | 0.48 | 0.60 | 0.82 |
The low-temperature electrolytes were developed aiming for iodide-based applications, and hence nanoscale interactions around the iodide anions remain as our highest interest. Fig. 6 displays RDFs calculated with iodide anions as the reference and reveals their interactions with BuCN nitrile N, imidazolium H2, and other iodides. Fig. 6(a) depicts iodide–imidazolium H2 interaction, where two peaks are observed for neat [BMIM][I] and are in good agreement with other simulation results with slight differences in relative positions due to the employed force field.97,98 The first well-defined peak at 0.25 nm is correlated with the preferred cation–anion pair due to the electrostatic interaction, while the second weaker peak at 0.63 nm implies the existence of another cluster at a further distance. The high resemblance between neat [BMIM][I] and mixtures suggests that the incorporation of BuCN does not affect the pre-existing ionic liquid structure by much. However, we note the slight peak changes in the 5-90-5 and 10-85-5 formulations. The first peaks and the second peak shift slightly closer to each other. Interestingly, the probability of both clusters increases with increasing BuCN, exhibiting a consistent trend as [BMIM]+–[BMIM]+ interactions (Fig. 5(b)). Chaban and Prezhdo reported similar effects of the nitrile solvent from MD simulation results of the [BMIM][BF4]/ACN binary mixtures, in which they attributed the increased probability of cation–anion to the relatively weak interactions between ions and ACN molecules that enforced interactions between the ion pair.99Fig. 6(b) displays the function of iodide–iodide, where an observant difference is identified between the neat IL and IL-based mixtures. Neat [BMIM][I] exhibits a broad distribution of iodide–iodide, which is attributed to the less electrostatic and more polarizable nature of anions.98 In the [BMIM][I]/BuCN/LiI mixtures, distributions of iodides have been altered, where partial iodides appear to be more clustered, as evident by the emergence of a sharper peak at ∼0.4 nm, while the rest form a second group shifting to a further relative distance. The two peaks display an interesting dynamic in the probability with respect to BuCN concentration, where the closer cluster only becomes more probable at BuCN > 85%. Interactions between BuCN nitrile N and iodide in mixtures are disclosed in Fig. 6(c), with two peaks at 0.43 nm and 0.75 nm, respectively. This established the probable existence of the interaction for all formulations. We hypothesize that RDFs for data from Fig. 6(b) and (c) depict clustering of BuCN and iodide about the imidazole ring but not directly to one other, as shown in Fig. 6(d), suggesting that iodide ordering is still mostly governed by the imidazolium cations.
In the [BMIM][I]/water binary systems, Nickerson et al. observed prominent hydrogen bonding of two water molecules around one iodide, causing effective ion disassociation between the [BMIM]+–[I]− and consequent transport property enhancements.47 However, RDFs of [BMIM][I]/BuCN/LiI indicated that the BuCN–imidazolium cation interactions were at a comparable distance as that of [BMIM]+–[I]−, and the [BMIM]+–[I]− interaction was not significantly interrupted. Despite the inefficiency of disrupting ion pairs, Chaban et al. still observed potential conductivity boosts in [BMIM][BF4]/ACN mixtures up to 50 times.88 They identified that increasing ACN concentrations can ruin greater ion aggregates in the mixtures, leading to the evolution of cluster size and distribution. Therefore, we speculate that although BuCN cannot solvate and dissociate ion pairs as effectively as water, it can still trigger ionic liquid rearrangement to facilitate overall fluidity. Moreover, we hypothesize that the potentially weak interactions between BuCN and cations increase the overall mobility of the clusters and hence result in a lower Tg and higher ionic conductivity, as both phenomena are governed by mixture fluidity. Different mechanisms of the altered ionic liquid ordering with water and BuCN strengthen the previous discussion on low-temperature ionic conductivity evolution, where their efficacy varies with the dominance of ionicity and fluidity at respective temperatures. Future work will focus on extending simulation endeavors on a wider range of formulations to further disclose the subtle evolutions of the imidazolium ionic liquid/nitrile solvent mixture structure, clustering, and caging mechanisms with approaches such as the calculation of coordination numbers, angle, and a lifetime of hydrogen bonds.
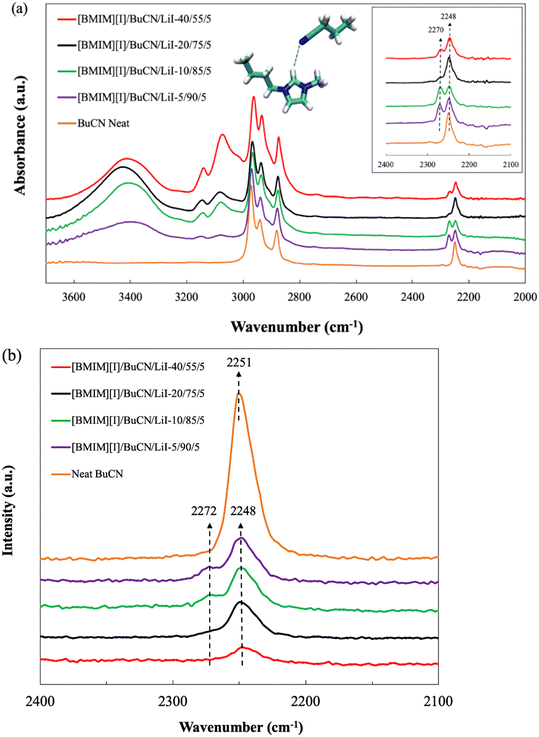
Spectroscopic studies were performed to characterize and validate the hypothesized intermolecular forces between BuCN and [BMIM][I], particularly, the nitrile group and the imidazolium cation. The C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching vibrations are known to be sensitive to the microenvironment of solutions and therefore have been utilized as a probe to further disclose complex interactions in ionic liquids.100,101 The FTIR spectra of neat BuCN and electrolyte mixtures with varying BuCN concentrations are shown in Fig. 7(a). Characteristic peaks corresponding to the respective functional groups in neat BuCN were confirmed from the FTIR spectrum, where peaks from 2800–3000 cm−1 were assigned to C–H stretching of the butyl group on BuCN while the C
N stretching vibrations are known to be sensitive to the microenvironment of solutions and therefore have been utilized as a probe to further disclose complex interactions in ionic liquids.100,101 The FTIR spectra of neat BuCN and electrolyte mixtures with varying BuCN concentrations are shown in Fig. 7(a). Characteristic peaks corresponding to the respective functional groups in neat BuCN were confirmed from the FTIR spectrum, where peaks from 2800–3000 cm−1 were assigned to C–H stretching of the butyl group on BuCN while the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching of the nitrile group was identified as a single peak at 2249 cm−1, consistent with other report.102 Upon the introduction of [BMIM][I] and LiI, in addition to the original C
N stretching of the nitrile group was identified as a single peak at 2249 cm−1, consistent with other report.102 Upon the introduction of [BMIM][I] and LiI, in addition to the original C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N absorbance wavenumber, a second peak emerged at 2270 cm−1, implying an altered vibration mode due to the additional interactions between the nitrile group and other species. Observations from Raman spectra of neat BuCN and various electrolyte formulations were also in good agreement with the FTIR results. As shown in Fig. 7(b), vibrational peaks of the nitrile group were observed across all the formulations in the range of 2100–2400 cm−1. Neat BuCN showed a strong single peak at 2251 cm−1, whereas formulated mixtures exhibited an alternation of the C
N absorbance wavenumber, a second peak emerged at 2270 cm−1, implying an altered vibration mode due to the additional interactions between the nitrile group and other species. Observations from Raman spectra of neat BuCN and various electrolyte formulations were also in good agreement with the FTIR results. As shown in Fig. 7(b), vibrational peaks of the nitrile group were observed across all the formulations in the range of 2100–2400 cm−1. Neat BuCN showed a strong single peak at 2251 cm−1, whereas formulated mixtures exhibited an alternation of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching mode. In these mixtures, the primary nitrile peak was identified at 2248 cm−1 with a minor shift in wavenumber, and secondary nitrile peaks were found to appear as subtle shoulder-like features at approximately 2272 cm−1. Those features were more distinguishable from the formulations [BMIM][I]/BCN/LiI-5/90/5 and 10/85/5, but much weaker to the extent of almost disappearing in [BMIM][I]/BCN/LiI-20/75/5 and 40/55/5. Zhou et al. discussed the complex C
N stretching mode. In these mixtures, the primary nitrile peak was identified at 2248 cm−1 with a minor shift in wavenumber, and secondary nitrile peaks were found to appear as subtle shoulder-like features at approximately 2272 cm−1. Those features were more distinguishable from the formulations [BMIM][I]/BCN/LiI-5/90/5 and 10/85/5, but much weaker to the extent of almost disappearing in [BMIM][I]/BCN/LiI-20/75/5 and 40/55/5. Zhou et al. discussed the complex C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N vibration in mixtures of 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([EMIM][Tf2N]) and acetonitrile utilizing FTIR and excess IR spectroscopy techniques.103 A blue shift of the C
N vibration in mixtures of 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([EMIM][Tf2N]) and acetonitrile utilizing FTIR and excess IR spectroscopy techniques.103 A blue shift of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N peak was observed with increasing [EMIM][Tf2N] concentrations due to the interactions between C
N peak was observed with increasing [EMIM][Tf2N] concentrations due to the interactions between C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and hydrogens on the imidazolium ring. In Yang's and Kou's work, the emergence of a new band from the original C
N and hydrogens on the imidazolium ring. In Yang's and Kou's work, the emergence of a new band from the original C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N absorption frequencies at a higher wavenumber was identified in mixtures of ethanenitrile and [BMIM][Cl]/metal chloride.104 They attributed the new absorption band to the Lewis acidity of the selected ionic liquid and metal halides, resulting in interactions to different extents with Lewis base solvents. Findings from both works shared certain resemblance with our characterization results. We hypothesize that the newly-emerging peak can be attributed to intermolecular interactions between the organic solvents and [BMIM][I], while the primary peak represents vibrations of the free solvent molecules that were not engaged in the solvation. In this case, as the nitrile group can also act as a hydrogen bond acceptor, with the presence of an acidic imidazolium H2, the resulting hydrogen bonding is highly probable of causing the subtle secondary peak of C
N absorption frequencies at a higher wavenumber was identified in mixtures of ethanenitrile and [BMIM][Cl]/metal chloride.104 They attributed the new absorption band to the Lewis acidity of the selected ionic liquid and metal halides, resulting in interactions to different extents with Lewis base solvents. Findings from both works shared certain resemblance with our characterization results. We hypothesize that the newly-emerging peak can be attributed to intermolecular interactions between the organic solvents and [BMIM][I], while the primary peak represents vibrations of the free solvent molecules that were not engaged in the solvation. In this case, as the nitrile group can also act as a hydrogen bond acceptor, with the presence of an acidic imidazolium H2, the resulting hydrogen bonding is highly probable of causing the subtle secondary peak of C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching.
N stretching.
Electrochemical behaviors of iodide/triiodide redox couple in BuCN
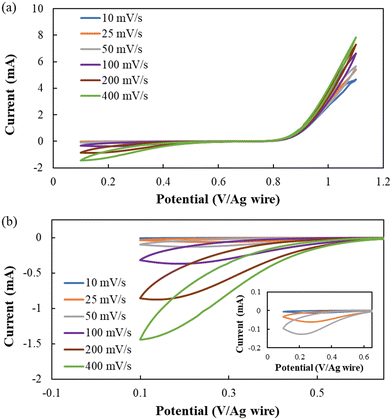
Lastly, electrochemical studies were conducted on the optimized formulation [BMIM][I]/BuCN/LiI-5/90/5 to evaluate its electrochemical stability and more importantly the iodide/triiodide redox reactions that determine electrochemical device performance. For MET technology, the transducer converts detected motions to electrical currents via I3− reduction and I− oxidation, which occur at cathodes and anodes, respectively.34 While I−/I3− electrochemical behaviors have been investigated in different ILs and molecular solvents, specifically those commonly used for DSSC electrolytes,105–108 understanding of iodide electrochemistry in BuCN is still limited.The electrochemical window (EW) for developed electrolytes refers to a potential range where I−/I3− redox reactions can be steadily activated without additional faradic processes originating from other species with the MET working mechanism as the premise. Cyclic voltammetry (CV) measurements were conducted at varying scanning rates from 10–400 mV s−1 to further disclose the dynamics between redox kinetics and ion transport. Fig. 8 shows the cyclic voltammograms of [BMIM][I]/BuCN/LiI-5/90/5 at various scan rates, where iodide oxidation and triiodide reduction were activated successfully during positive and negative polarizations, respectively. The identified potential range for [BMIM][I]/BuCN/LiI with satisfying reproducibility over 10 cycles was around 1.0 V. Furthermore, the open circuit potential between consecutive measurements from 10–400 mV s−1 was in the range of 0.643–0.646 V, validating a steady equilibrium potential of the electrolyte as long as it was scanned within the identified EW. Similar to previous observations from the developed systems with organic solvents, gradual reductions of generated current were observed if scanning was performed beyond the EW limits.49 To be specific, anodic overpotential resulted in the accumulation of an oxidation product, which appeared as observable brown traces diffusing from the electrode surface. It is known that iodide electrochemistry often undergoes two oxidation steps, first iodide to triiodide and then followed by triiodide to iodine, in organic solvents due to the stabilization effect from the solvation between the solvent molecule and triiodide.109 We speculate that at the defined anodic limit of 1.1 V, the oxidation of I3− is activated and starts to generate iodine. The potential is about +0.31 V from the identified I− oxidation potential of 0.8 V, agreeing with results from iodide electrochemistry in acetonitrile.109,110 Generation of iodine can potentially hinder ion transfer towards the electrode surface, alter ion diffusion behavior, and slowly change the electrolyte composition.111,112 On the other hand, cathodic polarization beyond 0.1 V did not result in additional reduction currents but would affect the consecutive oxidation process with a gradual decrease in the anodic current. Such a phenomenon has also been observed from I3− reduction in other organic solvents due to the high sensitivity of I3− reduction to the electrode surface conditions.113 Hence, we hypothesize that complex non-faradaic mechanisms may occur at the electrode surface, such as the formation of a double layer structure from the adsorption of other species, which requires follow-up experimentation to form a better understanding of its effect on iodide electrochemistry stability.
As the MET sensor extracts cathodic currents as a record of detected seismic activities, Fig. 8(b) focuses on cathodic currents from I3− reduction with the inset-magnifying features of 10, 25, and 50 mV s−1 scans. The electrochemical quasi-reversibility of I3− reduction in BuCN was observed, as the cathodic peak potential shifted towards a more negative potential with increasing scan rate due to the relatively slow kinetics. Although the solvation effect of molecular liquid benefits the enhancement of the thermal and transport property of IL-based electrolytes, the intermolecular interaction may also affect the electrochemical activity of species to varying extents. Bently et al. attributed shifts in activation potential for I−/I3− and I3−/I2 redox to the stabilization of I3− in the respective molecular liquids.114 From their study, both PC and ACN exhibited higher stability constants of log10(7.8) and log10(7.1) than that of water and ethanol, resulting in two distinct peaks during anodic and cathodic polarizations. With BuCN, the triiodide reduction exhibited even slower kinetics with a shift of 0.13 V in the cathodic peak potential when increasing the scan rate from 25 to 200 mV s−1, which is 0.3 V more than that of the previously reported [BMIM][I]/PC/LiI-5/90/5.49 Despite a lower electroactivity of triiodide for reduction, the appearance of cathodic current peaks from 10–200 mV s−1 informed a transition in the governing mechanism of output current from kinetics to transport, which fulfills the fundamental working principle of MET sensors. Moreover, Van Duyne and Reilley have employed BuCN as the media for low-temperature electrochemical investigation due to desirable low-temperature properties, demonstrating its promise to host electroactive species for ultralow temperature operations.115,116 Future endeavors will be focused on identifying a proper working potential window to address the highly sensitive iodide/triiodide redox couple in BuCN at varying temperatures to ensure optimal performance for the targeted applications.
Conclusions
In this work, we designed low-temperature electrolytes consisting of [BMIM][I]/nitrile solvent/LiI aiming to support iodide/triiodide applications. While systems with ACN failed to extend the liquidus range further due to higher Tg along with additional phase transitions onset at higher temperatures, [BMIM][I]/BuCN/LiI systems all exhibited a sole Tg as a result of the supercooled nature of BuCN. Remarkably, the formulation [BMIM][I]/BuCN/LiI-5/90/5 reported a record low-liquidus range limit of −152 °C for IL-based electrolytes. The evolution of the microscopic configuration corresponded to the intermolecular interaction between BuCN and the imidazolium cation and has been revealed via MD simulation, FTIR, and Raman spectroscopy. Furthermore, different from IL/water binary systems where enhancement in the transport was achieved via effective ion disassociation from water solvation, RDFs suggested that BuCN–imidazolium interaction was not prominent enough to break the electrostatic attraction within an ion pair but could breakdown larger ion clusters and thus change the size distribution of ion pairs and aggregates. Such an effect of BuCN may be less significant compared to water at room temperature but eventually prevailed at decreasing temperatures, as evident by the better ionic conductivity of [BMIM][I]/BuCN/LiI at temperatures below −40 °C. The targeted I−/I3− redox reactions were confirmed to be active and steady at room temperature despite the quasi-irreversibility of the couple and relatively slow kinetics. Within the identified EW, the output current of I3− reduction was governed by the transport to adequately support the MET-sensing technology. We anticipate that discoveries from this work can redirect the focus of low-temperature electrolyte design strategy to fluidity enhancement over higher ionicity, and the presented [BMIM][I]/BuCN/LiI systems may be further tailored upon its extraordinary wide liquidus range down to −152 °C for a variety of task-specific applications at ultralow temperatures.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We gratefully acknowledge the financial support from NASA 80NSSC20K0826, NNX17AF70G and the Fulton Undergraduate Research Initiative at Arizona State University. We also acknowledge Professor Candace Chan and LeRoy Eyring Center for Solid State Science at Arizona State University for the equipment access and Research Computing at Arizona State University for providing high performance computing and storage resources that have contributed to the computational research results.References
- I. Krossing, J. M. Slattery, C. Daguenet, P. J. Dyson, A. Oleinikova and H. Weingartner, J. Am. Chem. Soc., 2006, 128, 13427–13434 CrossRef CAS PubMed.
- R. Shi and Y. Wang, Sci. Rep., 2016, 6, 19644 CrossRef.
- K. Ueno, H. Tokuda and M. Watanabe, Phys. Chem. Chem. Phys., 2010, 12, 1649–1658 RSC.
- D. S. Frost, E. M. Nofen and L. L. Dai, Adv. Colloid Interface Sci., 2014, 206, 92–105 CrossRef CAS PubMed.
- A. C. Angell, Y. Ansari and Z. Zhao, Faraday Discuss., 2012, 154, 9–27 RSC.
- T. Welton, Biophys. Rev., 2018, 10, 691–706 CrossRef CAS.
- J. F. Brennecke and E. J. Maginn, AIChE J., 2001, 47, 2384–2389 CrossRef CAS.
- H. Olivier-Bourbigou, L. Magna and D. Morvan, Appl. Catal., A, 2010, 373, 1–56 CrossRef CAS.
- J. E. Bara, D. E. Camper, D. L. Gin and R. D. Nobel, Acc. Chem. Res., 2010, 43, 152–159 CrossRef CAS.
- F. Zhou, Y. Liang and W. Liu, Chem. Soc. Rev., 2009, 38, 2590–2599 RSC.
- F. Van Rantwijk, R. M. Lau and R. A. Sheldon, Trends Biotechnol., 2003, 21, 131–138 CrossRef CAS.
- C. Yan and T. Mu, Phys. Chem. Chem. Phys., 2014, 16, 5071–5075 RSC.
- N. Madria, T. A. Arunkumar, N. G. Nair, A. Vadapalli, Y.-W. Huang, S. C. Jones and V. P. Reddy, J. Power Sources, 2013, 234, 277–284 CrossRef CAS.
- M. P. S. Mousavi, B. E. Wilson, S. Kashefolgheta, E. L. Anderson, S. He, P. Buhlmann and A. Stein, ACS Appl. Mater. Interfaces, 2016, 8, 3396–3406 CrossRef CAS PubMed.
- D. S. Silvester, Analyst, 2011, 136, 4871–4882 RSC.
- G. A. Giffin, J. Mater. Chem. A, 2016, 4, 13378 RSC.
- R. Thangavel, A. G. Kannan, R. Ponraj, V. Thangavel, D.-W. Kim and Y.-S. Lee, J. Power Sources, 2018, 383, 102–109 CrossRef CAS.
- W.-Y. Tsai, R. Lin, S. Murali, L. L. Zhang, J. K. McDonough, R. S. Ruoff, P.-L. Taberna, Y. Gogotsi and P. Simon, Nano Energy, 2013, 2, 403–411 CrossRef CAS.
- P. Tamailarasan and S. Ramaprabhu, J. Phys. Chem. C, 2012, 116, 14179–14187 CrossRef CAS.
- N. Xu, J. M. Klein, P. Huang, H. A. Alwusaydi, E. K. Mann and B. E. Gurkan, J. Appl. Electrochem., 2019, 49, 151–162 CrossRef CAS.
- M. Kunze, S. Jeong, G. B. Appetecchi, M. Schonhoff, M. Winter and S. Passerini, Electrochim. Acta, 2012, 82, 69–74 CrossRef CAS.
- R. Lin, P.-L. Taberna, S. Fantini, V. Presser, C. R. Perez, F. Malbosc, N. L. Rupesinghe, K. B. K. Teo, Y. Gogotsi and P. Simon, J. Phys. Chem. Lett., 2011, 2, 2396–2401 CrossRef CAS.
- J. Jeon, H. Kim, W. A. Goddard III, T. A. Pascal, G.-I. Lee and J. K. Kang, J. Phys. Chem. Lett., 2012, 3, 556–559 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- S. Pan, M. Yao, J. Zhang, B. Li, C. Xing, X. Song, P. Su and H. Zhang, Front. Chem., 2020, 8, 261 CrossRef CAS.
- G. H. Lane, A. S. Best, D. R. MacFarlane, M. Forsyth, P. M. Bayley and A. F. Hollenkamp, Electrochim. Acta, 2010, 55, 8947–8952 CrossRef CAS.
- R. Newell, J. Faure-Vincent, B. Iliev, T. Schubert and D. Aradilla, Electrochim. Acta, 2018, 267, 15–19 CrossRef CAS.
- E. P. Yambou, B. Gorska, V. Pavlenko and F. Beguin, Electrochim. Acta, 2020, 350, 136416 CrossRef.
- E. P. Yambou, B. Gorska and F. Beguin, ChemSusChem, 2021, 14, 1196–1208 CrossRef CAS PubMed.
- X. Bu, Y. Zhang, Y. Sun, L. Su, J. Meng, X. Lu and X. Yan, J. Energy Chem., 2020, 49, 198–204 CrossRef.
- R. R. Galimzyanov, S. V. Stakhanova, I. S. Krechetov, A. T. Kalashnik, M. V. Astakov, A. V. Lisitsin, A. Y. Rychagov, T. R. Galimzyanov and F. S. Tabarov, J. Power Sources, 2021, 495, 229442 CrossRef CAS.
- J. Holoubek, H. Liu, Z. Wu, Y. Yin, X. Xing, G. Cai, S. Yu, H. Zhou, T. A. Pascal, Z. Chen and P. Liu, Nat. Energy, 2021, 6, 303–313 CrossRef CAS PubMed.
- P.-Y. Hung, H. Zhang, H. Lin, Q. Guo, K.-T. Lau and B. Jia, J. Energy Chem., 2022, 68, 580–602 CrossRef CAS.
- N. Zhang, T. Deng, S. Zhang, C. Wang, L. Chen, C. Wang and X. Fan, Adv. Mater., 2022, 34, 2107899 CrossRef CAS PubMed.
- L. Aguilera, J. Scheers and A. Matic, Phys. Chem. Chem. Phys., 2016, 18, 25458–25464 RSC.
- J. Tian, C. Cui, Q. Xie, W. Qian, C. Xue, Y. Miao, Y. Jin, G. Zhang and G. Baohua, J. Mater. Chem. A, 2018, 6, 3593–3601 RSC.
- S. Oh, M. J. Keating and E. J. Biddinger, Ind. Eng. Chem. Res., 2022, 61, 12118–12131 CrossRef CAS.
- M. Anouti and L. Timperman, Phys. Chem. Chem. Phys., 2013, 15, 6539–6548 RSC.
- L. Dagousset, G. Pognon, G. T. M. Nguyen, F. Vidal, S. Jus and P.-H. Aubert, J. Power Sources, 2017, 359, 242–249 CrossRef CAS.
- J. Li, Y. Zhou, J. Tian, L. Peng, J. Deng, N. Wang, W. Qian and W. Chu, J. Mater. Chem. A, 2020, 8, 10386 RSC.
- E. J. Brandon, W. C. West, M. C. Smart, L. D. Whitcanack and G. A. Plett, J. Power Sources, 2007, 170, 225–232 CrossRef CAS.
- J. Lang, X. Zhang, L. Liu, B. Yang, J. Yang and X. Yan, J. Power Sources, 2019, 423, 271–279 CrossRef CAS.
- F. Cheng, X. Yu, J. Wang, Z. Shi and C. Wu, Electrochim. Acta, 2016, 200, 106–114 CrossRef CAS.
- V. Ruiz, T. Huynh, S. R. Sivakkumar and A. G. Pandolfo, RSC Adv., 2012, 2, 5591–5598 RSC.
- A. R. Neale, C. Schutter, P. Wilde, P. Goodrich, C. Hardcare, S. Passerini, A. Balducci and J. Jacquemin, J. Chem. Eng. Data, 2017, 62, 376–390 CrossRef CAS.
- F. Sauvage, S. Chhor, A. Marchioro, J.-E. Moster and M. Graetzel, J. Am. Chem. Soc., 2011, 133, 13103–13109 CrossRef CAS PubMed.
- S. D. Nickerson, E. M. Nofen, H. Chen, M. Ngan, B. Shindel, H. Yu and L. L. Dai, J. Phys. Chem. B, 2015, 119, 8764–8772 CrossRef CAS.
- Y. Xu, W. J. Lin, M. Gliege, R. Gunckel, Z. Zhao, H. Yu and L. L. Dai, J. Phys. Chem. B, 2018, 122, 12077–12086 CrossRef CAS PubMed.
- W. J. Lin, Y. Xu, S. MacDonald, R. Gunckel, Z. Zhao and L. L. Dai, RSC Adv., 2019, 9, 36796–36807 RSC.
- H. Huang, V. Agafonov and H. Yu, Sensors, 2013, 13, 4581–4597 CrossRef.
- Y. Hou, R. Jiao and H. Yu, Sens. Actuators, A, 2021, 318, 112498 CrossRef CAS.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- H. J. C. Berendsen, D. van der Spoel and R. van Duran, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Pall, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- J. N. Canongia Lopes, J. Deschampls and A. A. H. Padua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
- B. L. Bhargava and S. Balasubramanian, J. Chem. Phys., 2007, 127, 114510 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and T.-R. Julian, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- J. N. Glosli and M. R. Philpott, J. Chem. Phys., 1993, 98, 9995–10008 CrossRef CAS.
- W. L. Jorgensen, J. D. Madura and C. J. Swenson, J. Am. Chem. Soc., 1984, 106, 6638–6646 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- B. R. Mellein, S. N. V. K. Aki, R. L. RLadewski and J. F. Brennecke, J. Phys. Chem. B, 2007, 111, 131–138 CrossRef CAS PubMed.
- A. Ali, M. Ali, N. A. Malik, S. Uzair and A. B. Khan, J. Chem. Eng. Data, 2014, 59, 1755–1765 CrossRef CAS.
- N. Zec, A. Idrissi, M. Bester-Rogac, M. Vranes and S. Gadzuric, J. Mol. Liq., 2018, 268, 481–489 CrossRef CAS.
- D. Lengvinaite, V. Klimavicius, V. Belevicius and K. Aidas, J. Phys. Chem. B, 2020, 124, 10776–10786 CrossRef CAS PubMed.
- F. Bardak, D. Xiao, L. G. Hines Jr., P. Son, R. A. Bartsch, E. L. Quitevis, P. Yang and G. A. Voth, ChemPhysChem, 2012, 13, 1687–1700 CrossRef CAS PubMed.
- T. L. Greaves, A. Weerawardena, C. Fong, I. Krodkiewska and C. J. Drummond, J. Phys. Chem. B, 2006, 110, 22479–22487 CrossRef CAS PubMed.
- C. E. S. Bernardes, M. E. Minas da Piedade and J. N. Canongia Lopes, J. Phys. Chem. B, 2011, 115, 2067–2074 CrossRef CAS PubMed.
- A. Chagnes, H. Allouchi, B. Carre and D. Lemordant, Solid State Ionics, 2005, 176, 1419–1427 CrossRef CAS.
- M. Oguni, H. Hikawa and H. Suga, Thermochim. Acta, 1990, 158, 143–156 CrossRef CAS.
- N. Ito, K. Duvvuri, D. V. Matyushov and R. Richert, J. Chem. Phys., 2006, 125, 024504 CrossRef PubMed.
- R. F. Tournier, Phys. B, 2014, 454, 253–271 CrossRef CAS.
- H. Rodriguez and J. F. Brennecke, J. Chem. Eng. Data, 2006, 51, 2145–2155 CrossRef CAS.
- M. T. Zafarani-Moattar and R. Majdan-Cegincara, J. Chem. Eng. Data, 2007, 52, 2359–2364 CrossRef CAS.
- J. Wang, Y. Tian, Y. Zhao and K. Zhuo, Green Chem., 2003, 5, 618–622 RSC.
- J.-Y. Wu, Y.-P. Chen and C.-S. Su, J. Solution Chem., 2015, 44, 395–412 CrossRef CAS.
- O. Ciocirlan, O. Croitoru and O. Iulian, J. Chem. Thermodyn., 2016, 101, 285–292 CrossRef CAS.
- M. Galiński, Z. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567–5580 CrossRef.
- K. R. Seddon, A. Stark and M.-J. Torres, in Clean Solvents: Alternative Media for Chemical Reactions and Processing, ed. M. A. Abraham and L. Moens, American Chemical Society, 2002, vol. 819, pp. 33–49 Search PubMed.
- X.-X. Zhang, M. Liang, N. P. Ernsting and M. Maroncelli, J. Phys. Chem. Lett., 2013, 4, 1205–1210 CrossRef CAS PubMed.
- A. Stoppa, J. Hunger and R. Buchner, J. Chem. Eng. Data, 2009, 54, 472–479 CrossRef CAS.
- M. Liang, X.-X. Zhang, A. Kaintz, N. P. Ernsting and M. Maroncelli, J. Phys. Chem. B, 2014, 118, 1340–1352 CrossRef CAS PubMed.
- B. Conway, C. Uitvlugt and M. Maroncelli, J. Phys. Chem. B, 2018, 122, 7385–7393 CrossRef CAS PubMed.
- V. V. Chaban, I. V. Voroshylova, O. N. Kalugin and O. V. Prezhdo, J. Phys. Chem. B, 2012, 116, 7719–7727 CrossRef CAS PubMed.
- Y.-Z. Zheng, Y. Zhou, G. Deng, R. Guo and D.-F. Chen, Spectrochim. Acta, Part A, 2020, 226, 117641 CrossRef PubMed.
- S. Zhang, J. Wang, X. Lu and Q. Zhuou, Structures and interactions of ionic liquids, Springer, Berlin, Heidelberg, 2014 Search PubMed.
- J. C. Mauro, Y. Yue, A. J. Ellison, P. K. Gupta and D. C. Allan, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19780–19784 CrossRef CAS PubMed.
- X. Wang, Y. Chi and T. Mu, J. Mol. Liq., 2014, 193, 262–266 CrossRef CAS.
- A. Jarosik, S. R. Krajewski, A. Lewandowski and P. Radzimski, J. Mol. Liq., 2006, 123, 43–50 CrossRef CAS.
- G. Gonfa, M. A. Bustam, Z. Man and M. I. Abdul Multalib, Asian Trans. Eng., 2011, 1, 24–34 Search PubMed.
- X. Wu, Z. Liu, S. Huang and W. Wang, Phys. Chem. Chem. Phys., 2005, 7, 2771–2779 RSC.
- A. A. H. Padua, M. F. Costa Gomes and J. N. Canongia Lopes, Acc. Chem. Res., 2007, 40, 1087–1096 CrossRef CAS PubMed.
- M. H. Ghatee, A. R. Zolghadr, F. Moosavi and Y. Ansari, J. Chem. Phys., 2012, 136, 124706 CrossRef PubMed.
- Y. Umebayashi, H. Hamano, S. Tsuzuki, J. N. Canongia Lopes, A. A. H. Padua, Y. Kameda, S. Kohara, T. Yamaguchi, K. Fujii and S.-I. Ishiguro, J. Phys. Chem. B, 2010, 114, 11715–11724 CrossRef CAS PubMed.
- V. V. Chaban and O. V. Prezhdo, Phys. Chem. Chem. Phys., 2011, 13, 19345–19354 RSC.
- Y. Umebayashi, J.-C. Jiang, K.-H. Lin, Y.-L. Shan, K. Fujii, S. Seki, S.-I. Ishiguro, S. H. Lin and H.-C. Chang, J. Chem. Phys., 2009, 131, 234505 CrossRef PubMed.
- Y.-Z. Zheng, Y. Zhou, H.-Y. He, R. Guo and D.-F. Chen, J. Mol. Liq., 2021, 322, 114548 CrossRef CAS.
- N. K. Karthick, G. Arivazhagan, A. C. Kumbharkhane, Y. S. Joshi and P. P. Kannan, J. Mol. Struct., 2016, 1108, 203–208 CrossRef CAS.
- Y. Zhou, Y.-Z. Zheng, G. Deng and Z.-W. Yu, ChemPhysChem, 2017, 18, 1370–1375 CrossRef CAS PubMed.
- Y.-L. Yang and Y. Kou, Chem. Commun., 2004, 226–227 RSC.
- P. Cheng, W. Wang, T. Lan, R. Chen, J. Wang, J. Yu, H. We, H. Yang, C. Deng and S. Guo, J. Photochem. Photobiol., A, 2010, 212, 147–152 CrossRef CAS.
- A. Ejigu, K. R. J. Lovelock, P. Licence and D. A. Walsh, Electrochim. Acta, 2011, 56, 10313–10320 CrossRef CAS.
- L. Bay, K. West, B. Winther-Jensen and T. Jacobsen, Sol. Energy Mater. Sol. Cells, 2006, 90, 341–351 CrossRef CAS.
- F. Bella, S. Galliano, M. Falco, G. Viscardi, C. Barolo, M. Gratzel and C. Gerbaldi, Chem. Sci., 2016, 7, 4880–4890 RSC.
- R. T. Iwamoto, Anal. Chem., 1959, 31, 955 CrossRef CAS.
- I. V. Nelson and R. T. Iwamoto, J. Electroanal. Chem., 1964, 7, 218–221 CAS.
- S. Swathirajan and S. Bruckenstein, J. Electroanal. Chem., 1983, 143, 167–178 CrossRef CAS.
- S. Swathirajan and S. Bruckenstein, J. Electroanal. Chem., 1981, 125, 63–71 CrossRef CAS.
- K. J. Hanson and C. W. Tobias, J. Electrochem. Soc., 1987, 134, 2204–2210 CrossRef CAS.
- C. L. Bentley, A. M. Bond, A. F. Hollenkamp, P. J. Mahon and J. Zhang, J. Phys. Chem. C, 2015, 119, 22392–22403 CrossRef CAS.
- R. P. Van Duyne and C. N. Reilley, Anal. Chem., 1972, 44, 142–152 CrossRef.
- R. P. Van Duyne and C. N. Reilley, Anal. Chem., 1972, 44, 156–169 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |