Superhydrophobic microstructures for better anti-icing performances: open-cell or closed-cell?†
Lizhong
Wang
 ,
Guochen
Jiang
,
Ze
Tian
,
Guochen
Jiang
,
Ze
Tian
 ,
Changhao
Chen
,
Xinyu
Hu
,
Rui
Peng
,
Hongjun
Zhang
,
Peixun
Fan
and
Minlin
Zhong
*
,
Changhao
Chen
,
Xinyu
Hu
,
Rui
Peng
,
Hongjun
Zhang
,
Peixun
Fan
and
Minlin
Zhong
*
Laser Materials Processing Research Center, Key Laboratory for Advanced Materials Processing Technology (Ministry of Education), Joint Research Center for Advanced Materials & Anti-icing of Tsinghua University (SMSE)-AVIC ARI, School of Materials Science and Engineering, Tsinghua University, Beijing 100084, P. R. China. E-mail: zhml@mail.tsinghua.edu.cn
First published on 2nd November 2022
Abstract
Based on geometrical characteristics, all surface microstructures are categorized into two types: closed-cell and open-cell structures. Closed-cell structures are well-known to have more stable and durable superhydrophobicity at room temperatures. However, in low-temperature environments where massive environmentally induced physical changes emerge, whether closed-cell surfaces can maintain good anti-icing performances has not yet been confirmed, and thus how to design optimal superhydrophobic anti-icing microstructures is rarely reported. Here, we apply an ultrafast laser to fabricate superhydrophobic surfaces with tunable patterned micro-nanostructures from a complete closed-cell to different ratios and to a complete open-cell. We discover that droplets on closed-cell structures completely degrade to the high-adhesion Wenzel state after icing and melting cycles while those on the open-cell structures well recover to the original Cassie-Baxter state. We propose an improved ideal gas model to clarify the mechanisms that the decreased air pocket pressure and the air dissolution on closed-cell structures induce easy impalement during icing and the difficult recovery during melting, paving the way for optimizing the anti-icing structure design. The optimized open-cell surfaces exhibit over 33 times lower ice adhesion strengths (1.4 kPa) and long-term icephobic durability (<20 kPa after 33 deicing cycles) owing to the increased air pocket pressure at low temperatures. Significant dewetting processes during condensation endow the open-cell structures with more remarkable high-humidity resistance and anti-frosting properties. Our study reveals the general design principle of superhydrophobic anti-icing structures, which might guide the design of superhydrophobic anti-icing surfaces in practical harsh environments.
New conceptsWe demonstrate for the first time that superhydrophobic surfaces with open-cell structures perform better in anti-icing applications than those with closed-cell structures, and reveal the general design principle of superhydrophobic anti-icing surfaces that preferentially adopts open structures. We report unprecedented discoveries that droplets on surfaces with similar superhydrophobicity but different open-structural area ratios can be tuned to any state from the complete Wenzel state to the complete Cassie-Baxter state after icing & melting cycles. We establish the improved ideal gas model to confirm the underlying mechanisms that the decreased air pocket pressure and the air dissolution on the closed-cell structures lead to easily-impaled and difficultly-recovered air pockets during icing & melting cycles. Based on the new design concept, we develop an ultrafast laser fabrication strategy to obtain optimized open-cell structures, realizing over 33 times lower ice adhesion strengths (1.4 kPa) and long-term icephobic durability (<20 kPa after 33 deicing cycles). Even if in high-humidity environments, significant dewetting processes still ensure extraordinary anti-frosting properties. Our discoveries improve the understanding of icing and melting phenomena, and provide the design guideline for superhydrophobic anti-icing surfaces, which will accelerate their practical applications. |
Introduction
Icing phenomena have brought dramatic troubles in the fields of energy, transportation, telecommunication, etc.1–3 Traditional deicing technologies such as electrothermal or aerodynamic deicing tend to result in a colossal waste of energy and low-efficiency deicing.4–6 Inspired by the water-repellency of lotus in nature, superhydrophobic surfaces have been recently regarded as one of the most promising candidates for realizing low-energy passive anti-icing.7–9 However, superhydrophobicity is not equal to icephobicity.10,11 Only when air pockets exist between droplets and micro-nanostructures to retain the Cassie-Baxter (CB) state do the delayed icing and icephobicity work.12,13 Once air pockets are impaled, droplets will be stuck in a large number of micro-nanostructures and thus show the high-adhesion Wenzel state,14,15 accelerating the occurrence of icing. Numerous reports confirm that air pockets are extremely fragile so that impalement phenomena and CB-to-Wenzel transitions inevitably occur under external disturbances (especially during icing processes).16–18 Our recent work reported that Marangoni effects during melting processes could induce the bubble impact to contribute to a spontaneous Wenzel-to-CB transition,16 but has not considered the effects of structural styles on the transitions, and the Wenzel-to-CB transitions cannot yet be regulated artificially. Besides, although massive reports successfully fabricated various micro-nanostructured surfaces with similar superhydrophobicity by different methods (including chemical etching,19 spraying,20,21etc.), their icephobic performances are significantly different, which triggers the doubt whether superhydrophobic surfaces could truly be applied in the practical anti-icing fields.14 The underlying mechanisms and effects of different micro-nanostructures on anti-icing still need to be adequately elucidated.In terms of classical wetting models, surface hydrophobicity directly depends on micro-nanostructures, where more hierarchical micro-nanostructures lead to more excellent water-repellency.22–24 A flurry of state-of-the-art micro-nanostructured surfaces have been elaborately designed based on the principle to endow surfaces with extraordinary superhydrophobicity.25–29 In light of geometrical characteristics, all micro-nanostructures can be divided into two fundamental structures:30,31 the open-cell and the closed-cell. On the open-cell micro-nanostructured surfaces, the valleys among micro-nanostructures are not enclosed, through which the ambient atmosphere can freely flow inside and outside. Many reports have successfully fabricated open-cell structures for anti-icing applications. Pan et al. combined ultrafast laser ablation and chemical oxidation to obtain triple-scale open-cell surfaces with ultralow ice adhesion strengths (∼1.7 kPa).32,33 Vercillo et al. fabricated open-cell micropillars on Ti6Al4V surfaces by direct laser interference patterning techniques and adopted surfaces in icing wind tunnel tests to achieve good anti-icing effects.27 However, owing to the disability of storing and accumulating gas pressure, the air pockets in the open-cell micro-nanostructures are usually less stable at room temperature (RT) compared with those in the closed-cell. Wu et al. compared the air pocket pressures of the closed-cell and open-cell micro-nanostructures by theoretical calculation, and found that closed-cell micro-nanostructures had higher critical collapse pressure at RT.34 Similar results were also confirmed by Zhang et al. by droplet impacting experiments.31 Besides, closed-cell structures, as a robust mechanical skeleton, can further protect inner fragile nanostructures from damage at RT.35,36 Most famously, Wang et al. constructed a combined micro-nanostructure with amour-like microstructures and deposited nanostructures, realizing ultrahigh superhydrophobic durability.37 However, these excellent properties are only shown in RT environments. Mishchenko et al. demonstrated the droplet bounce properties on closed-cell structures were better than on open-cell structures at −25 °C to −30 °C,38 but the referred closed-cell microstructures did not yet constitute complete closed systems during droplet impacting processes, where air pockets were still open before droplet touching surfaces. And the test results only applied to droplet impact processes under low humidity conditions (∼5%), which are different from practical anti-icing environments. It is well-known that massive new physical changes (such as phase changes,39 gas contraction,40etc.) occur in practical anti-icing environments, which will greatly affect the superhydrophobicity and anti-icing properties.41 Whether the durability and air pocket stability of the closed-cell micro-nanostructures can still be retained in low-temperature anti-icing environments and how to design surface micro-nanostructures for better anti-icing applications are seldom investigated but of vital significance for the theoretical research and practical applications of superhydrophobic anti-icing surfaces.
Here, we adopted ultrafast laser direct writing technologies, facilely fabricating tunable patterned micro-nanostructures to simulate the common microstructures from the complete closed-cell to different ratios and then to the complete open-cell. Regular microstructures attached with abundant nanoparticles endowed different surfaces with similarly extraordinary superhydrophobicity at RT. While during icing & melting cycles, it was demonstrated that as the ratio of the open-structural area to the total area of one cell (ROT) increased, the CB-to-Wenzel transitions during icing processes were effectively slowed down, and the recovery of the CB state during melting processes was greatly improved. The melted droplets on open-cell surfaces almost completely recovered to the CB state while those on the closed-cell maintained the Wenzel state with the 180° sliding angle. Based on the improved ideal gas law, the mechanisms were elucidated that the decreased air pocket pressures and the dissolution of air pocket gas into supercooled droplets on closed-cell structures as temperatures decreased, together resulted in easy impalement of air pockets during icing and difficult recovery during melting. While on the open-cell structures, the increased air pocket pressures during icing processes decelerated the impalement proceeding, and the enhanced Marangoni-induced bubble impact accelerated the recovery of air pockets. The ice adhesion strengths on the optimized open-cell surfaces were even over 33 times lower than on the closed-cell, and less structural and chemical loss well ensured long-term icephobic durability. Furthermore, we demonstrated open-cell micro-nanostructures exhibited more significant dewetting properties during condensation, effectively inhibiting the condensation frosting and the loss of icephobicity. Our work confirms the effects of microstructures on the icephobicity experimentally and theoretically, and reveals that open-cell structures perform better for anti-icing applications. The summarized design principle and discoveries will be a powerful impact on guiding the design and development of superhydrophobic anti-icing surfaces in many related fields.
Results and discussion
Tunable micro-nanostructures and characterization
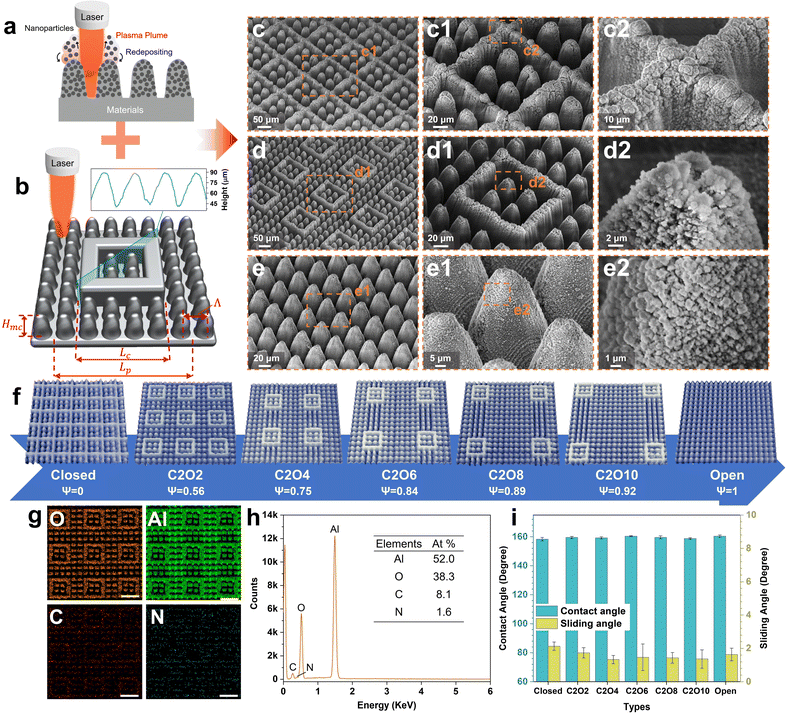
Ultrafast laser direct writing, as a top-down processing strategy, can facilely fabricate tunable micro-nanostructures on nearly any material42,43 and own ultrahigh structural repeatability. Taking these advantages, micro-nanostructures with tunable patterns were prepared on aviation aluminum alloy surfaces. Fig. 1a and b show the fabrication processes. In high-energy-fluence pulse duration, mechanical ablation, plasma formation and particle deposition occur together.44 The laser-focused zones are ablated to construct regular microstructures (microcones/frames) in specific scanning paths (Fig. S1 ESI†). The plasma plume during ablation contains a large number of nanoparticles, which rapidly deposit on microstructures as the surface temperatures cool down, forming stable nanostructures. Combining the laser ablation and programmable characteristics, the micro-nanostructured surfaces with tunable patterns from the complete closed-cell to the complete open-cell are constructed well. As shown in Fig. 1c–e, all laser-fabricated surfaces consist of double-scale micro-nanostructures with abundant nanoparticles (diameter 100–400 nm) densely distributed on the regular microcones/frames. Affected by the Gaussian distribution of laser energy intensity, the sidewalls of microframes are not straight but conical, whose cross-sectional shapes and sizes are the same as those of microcones (Fig. 1b). The height of microcones and microframes is 45 μm. The width of the closed microframe is denoted as Lc and fixed at 140 μm, four times the interval of microcones (denoted as Λ, Λ = 35 μm). The periodical distance of one cell is denoted as Lp. The ROT can be calculated by ψ = 1 − Lc2/Lp2. To conveniently investigate the effects of different structural styles on the icing & melting behaviors and icephobicity, the number of microcones in the closed microframes was set as 2 × 2. In terms of the number of microcones outside the microframes in the diagonal of one cell, different patterned surfaces are named, respectively. For example, C2O2 denotes the surfaces where exist two closed microcones and two open microcones in the diagonal of one cell. Different patterned surfaces and their corresponding ROTs are displayed in Fig. 1f. By observing the elemental distributions on patterned surfaces (Fig. 1g and h), it is found that there exists no difference in elements on the closed microcones and the open microcones. After fluoroalkyl silane modification, all surfaces show excellent superhydrophobicity with contact angles of more than 158° and sliding angles of less than 3° (Fig. 1i and Table S2, ESI†). Although surfaces with different ROTs have different solid fractions, all the solid fractions are similarly small so the differences in superhydrophobicity are not significant (Fig. S2, ESI†). However, the superhydrophobic durability of these surfaces is different, where surfaces with smaller ROTs are more durable at RT (15 °C). Even after 30 linear abrasion cycles, the closed-cell surfaces can still maintain the good superhydrophobicity while the open-cell surfaces cannot (Fig. S3, ESI†). The results are mainly attributed to the robust amour structures of closed-cell surfaces, which corresponds to the former reports.37Icing & melting behaviors and mechanism discussion
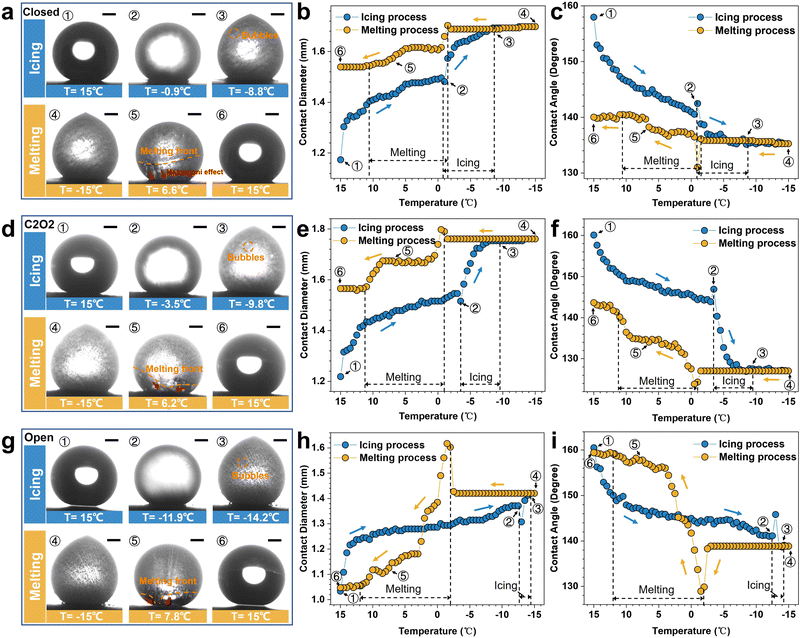
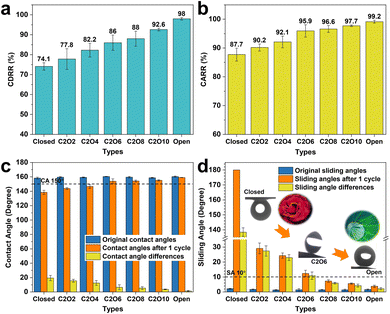
To investigate the icing & melting behaviors of droplets on different patterned surfaces, the icing & melting cycle experiments were conducted by gradually cooling surfaces from 15 °C to −15 °C to freeze water droplets, followed by natural warming to 15 °C to melt the ice droplets. During the cycles, the liquid–gas interfaces and the solid–gas interfaces between droplets and surfaces together form a whole system, as shown in Fig. S4 (ESI†). 5 μL droplets were adopted, whose contact diameters (>1 mm) on the surfaces are larger than the width of closed microframes (Lc = 0.14 mm), ensuring the formation of closed systems. Fig. 2 and Movie S1 (ESI†) show the experimental results of icing & melting cycles on the closed-cell (ψ = 0), C2O2 (ψ = 0.56) and open-cell (ψ = 1) surfaces. It can be observed that as the surface temperatures decrease, droplets on the three surfaces have the same transition from the CB state to the Wenzel state (Fig. 2a, d and g), which is consistent with our former work.16 But differently, the increased rate of contact diameters and the decreased rate of contact angles on the open-cell surfaces are slower than on the other two surfaces. In particular below 0 °C, the changes in contact diameters and contact angles are not significant. During melting processes, droplets on the three surfaces show the trend of contact diameter decreasing and contact angle increasing. Noteworthily, compared with closed-cell and C2O2 surfaces, ice droplets on the open-cell surfaces nearly completely recover to the original state (Fig. 2h and i). The recovered contact diameter and contact angle on the open-cell surfaces reach 1.0 mm and 159.29° while those on the closed-cell surfaces and C2O2 surfaces are more than 1.5 mm (Fig. 2b and e) and less than 144° (Fig. 2c and f). Besides, by investigating the icing and melting processes on the three surfaces (Fig. S5, ESI†), it is found that the shorter delayed icing time on the closed-cell and C2O2 surfaces leads to fewer bubbles dissolved out in the ice droplets than on the open-cell surfaces, further causing fewer bubbles to impact downwards under Marangoni effects to prompt the recovery of the CB state. After complete melting, the CB states of droplets on the closed-cell and C2O2 surfaces are greatly lost.In terms of the changes in contact diameters and contact angles before and after the icing & melting cycles, the contact diameter recovery rate (CDRR) and the contact angle recovery rate (CARR) were adopted to characterize the recovery extents of the CB state during icing & melting cycles. It can be explicitly observed that as the ROTs of surfaces increase, the CDRR and CARR significantly increase (Fig. 3a and b). The CDRR and CARR on open-cell surfaces even reach up to 98% and 99.2% after melting, respectively, much higher than those on closed-cell surfaces. By further investigating the differences in contact angles and sliding angles after icing & melting cycles, we find in Fig. 3c and d that the melted droplets on the C2O8 (ψ = 0.89), C2O10 (ψ = 0.92) and the open-cell (ψ = 1) surfaces can recover to the superhydrophobic CB state with the contact angles of more than 150° and the sliding angles of less than 10°, well ensuring easy-removal after melting. Moreover, it is confirmed that the phenomena are greatly dependent on the microstructured patterns since solid fractions of surfaces are similarly small (Fig. S6, ESI†). The Wenzel-to-CB transitions during melting processes can be easily tuned by changing the ROTs of micro-nanostructured surfaces (Fig. 3d). Droplets on the surfaces with the same room-temperature superhydrophobicity can be transited to any state ranging from the complete Wenzel state like rose petals to the complete CB state like lotuses after melting, which might be promising to be applied in the fields of microfluid chips,45 droplet transportation46,47 as well as the anti-icing applications.
Based on the experimental phenomena, the schematic of the liquid-gas-solid interfacial states during icing processes is depicted in Fig. 4a. For the closed-cell zones on C2O2 surfaces, the gas in the air pockets contracts gradually as the temperature decreases. Owing to the absent replenishment of air from the ambient atmosphere in the closed systems, the air pocket pressure will greatly decrease, accelerating the impalement of air pockets. While for the open-cell zones, the gas in the air pockets circulates with the ambient atmosphere freely, forming the open systems thermodynamically. As the temperature decreases, the atmospheric pressure gradually increases owing to the contraction and supply of ambient air, directly leading to the increase of air pocket pressure in the open-cell zones. By improving the ideal gas model, the air pocket pressure in the open-cell zones can be expressed as:
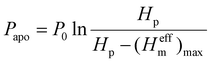 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1 + sin3α1)]/(−3cos3α1); rgeff denotes the equivalent geometric radius for hierarchically structured surfaces with pillars; α1 denotes the sag angle of the liquid-vapor interface; (Heffm)max denotes the maximum of Heffm. Noteworthily, the air pocket gas is prone to dissolving in the supercooled droplets during icing processes since the dissolvability of air in water gradually increases with the decrease of temperatures. For the open-cell zones, due to the supply of the external atmosphere, the replenished gas amount can rapidly reach the balance with the dissolved amount of air pocket gas in supercooled droplets during icing processes, thus sustaining a constant amount of air pocket gas. Whereas for the closed-cell zones, without the ambient replenishment, the trapped air pocket gas greatly dissolves in the supercooled droplets during icing processes, resulting in the decrease of gas amount. Taking into account the mass loss of gas, the air pocket pressure in the closed-cell zones can be expressed by:
α1 + sin3α1)]/(−3cos3α1); rgeff denotes the equivalent geometric radius for hierarchically structured surfaces with pillars; α1 denotes the sag angle of the liquid-vapor interface; (Heffm)max denotes the maximum of Heffm. Noteworthily, the air pocket gas is prone to dissolving in the supercooled droplets during icing processes since the dissolvability of air in water gradually increases with the decrease of temperatures. For the open-cell zones, due to the supply of the external atmosphere, the replenished gas amount can rapidly reach the balance with the dissolved amount of air pocket gas in supercooled droplets during icing processes, thus sustaining a constant amount of air pocket gas. Whereas for the closed-cell zones, without the ambient replenishment, the trapped air pocket gas greatly dissolves in the supercooled droplets during icing processes, resulting in the decrease of gas amount. Taking into account the mass loss of gas, the air pocket pressure in the closed-cell zones can be expressed by: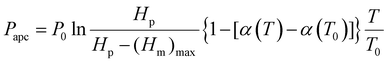 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1 + sin3α1)]/(−3cos3α1); rc is the effective radius in the closed-cell; α(T) is the air solubility in water, … In terms of eqn (1) and (2), the phase diagram of air pocket pressure in the surfaces with different ROTs at different temperatures is obtained in Fig. 4b and Fig. S7 (ESI†). It can be explicitly found that the air pocket pressure of closed-cell surfaces gradually decreases as the temperature decreases while that of open-cell surfaces shows an increasing trend. The results correspond to the former analyses. During cooling processes, as the surface ROT increases, the variation trend of air pocket pressure steadily changes from the decrease to the increase, showing the saddle-shaped trend (Fig. S7b, ESI†). At −0.6 °C, the air pockets of surfaces with different ROTs have the same air pocket pressure (34.7 kPa). When below −0.6 °C, the air pocket pressures on the surfaces with higher ROTs are higher, decelerating the impalement proceedings to some extent. In this case the retardatory impalement further slows down the increase of the solid–liquid contact area and the decrease of interfacial thermal resistances, eventually elongating the delayed icing time (Fig. S8, ESI†). As displayed in Fig. 4c, the delayed icing time increases significantly as the ROT increases. On the open-cell surfaces, the delayed icing time (82.0 ± 12.3 s) is even over twice longer than that on the closed-cell surfaces (37.3 ± 3.6 s). But differently, the icing duration time slightly decreases with the increase of ROT. This is mainly attributed to the fact that the lower icing temperatures on surfaces with higher ROTs accelerate droplet freezing more easily. Fig. 4d shows the amounts of the bubbles dissolved out in ice droplets on different surfaces, which are calculated using eqn (S14) (ESI†). The bubble amounts in the ice droplets are closely related to the delayed icing time and the contact angles of ice droplets. According to the above results (Fig. 3c and 4c), it can be found that droplets on the surfaces with higher ROTs tend to have a longer delayed icing time and a slower deterioration rate of contact angles, which together prompt more bubbles dissolved out in ice droplets. Meanwhile, more bubbles contained in ice droplets means more bubbles impact downwards to promote the recovery of the CB state during melting processes. Hence droplets on the surfaces with higher ROTs (especially on open-cell surfaces) can not only more effectively slow down the CB-to-Wenzel transitions owing to higher air pocket pressure but also better accelerate the recovery of the CB state under more bubble impact. In contrast, on closed-cell surfaces, the low air pocket pressure at low temperatures induces the air pockets can be easily impaled. Most gas in the air pockets dissolves in the supercooled droplets to form frozen bubbles after icing. Since there is no external gas supply and few bubbles are frozen in the ice droplets, the melted droplets on the closed-cell surfaces cannot well recover to the original CB state but maintain the high-adhesion Wenzel state, resulting in the difficult-removal of droplets after melting. Besides, we also conducted the icing & melting tests on different substrate materials to confirm the phenomena are highly dependent on the microstructure patterns but less dependent on the substrate materials (Fig. S9 and S10, ESI†).
α1 + sin3α1)]/(−3cos3α1); rc is the effective radius in the closed-cell; α(T) is the air solubility in water, … In terms of eqn (1) and (2), the phase diagram of air pocket pressure in the surfaces with different ROTs at different temperatures is obtained in Fig. 4b and Fig. S7 (ESI†). It can be explicitly found that the air pocket pressure of closed-cell surfaces gradually decreases as the temperature decreases while that of open-cell surfaces shows an increasing trend. The results correspond to the former analyses. During cooling processes, as the surface ROT increases, the variation trend of air pocket pressure steadily changes from the decrease to the increase, showing the saddle-shaped trend (Fig. S7b, ESI†). At −0.6 °C, the air pockets of surfaces with different ROTs have the same air pocket pressure (34.7 kPa). When below −0.6 °C, the air pocket pressures on the surfaces with higher ROTs are higher, decelerating the impalement proceedings to some extent. In this case the retardatory impalement further slows down the increase of the solid–liquid contact area and the decrease of interfacial thermal resistances, eventually elongating the delayed icing time (Fig. S8, ESI†). As displayed in Fig. 4c, the delayed icing time increases significantly as the ROT increases. On the open-cell surfaces, the delayed icing time (82.0 ± 12.3 s) is even over twice longer than that on the closed-cell surfaces (37.3 ± 3.6 s). But differently, the icing duration time slightly decreases with the increase of ROT. This is mainly attributed to the fact that the lower icing temperatures on surfaces with higher ROTs accelerate droplet freezing more easily. Fig. 4d shows the amounts of the bubbles dissolved out in ice droplets on different surfaces, which are calculated using eqn (S14) (ESI†). The bubble amounts in the ice droplets are closely related to the delayed icing time and the contact angles of ice droplets. According to the above results (Fig. 3c and 4c), it can be found that droplets on the surfaces with higher ROTs tend to have a longer delayed icing time and a slower deterioration rate of contact angles, which together prompt more bubbles dissolved out in ice droplets. Meanwhile, more bubbles contained in ice droplets means more bubbles impact downwards to promote the recovery of the CB state during melting processes. Hence droplets on the surfaces with higher ROTs (especially on open-cell surfaces) can not only more effectively slow down the CB-to-Wenzel transitions owing to higher air pocket pressure but also better accelerate the recovery of the CB state under more bubble impact. In contrast, on closed-cell surfaces, the low air pocket pressure at low temperatures induces the air pockets can be easily impaled. Most gas in the air pockets dissolves in the supercooled droplets to form frozen bubbles after icing. Since there is no external gas supply and few bubbles are frozen in the ice droplets, the melted droplets on the closed-cell surfaces cannot well recover to the original CB state but maintain the high-adhesion Wenzel state, resulting in the difficult-removal of droplets after melting. Besides, we also conducted the icing & melting tests on different substrate materials to confirm the phenomena are highly dependent on the microstructure patterns but less dependent on the substrate materials (Fig. S9 and S10, ESI†).
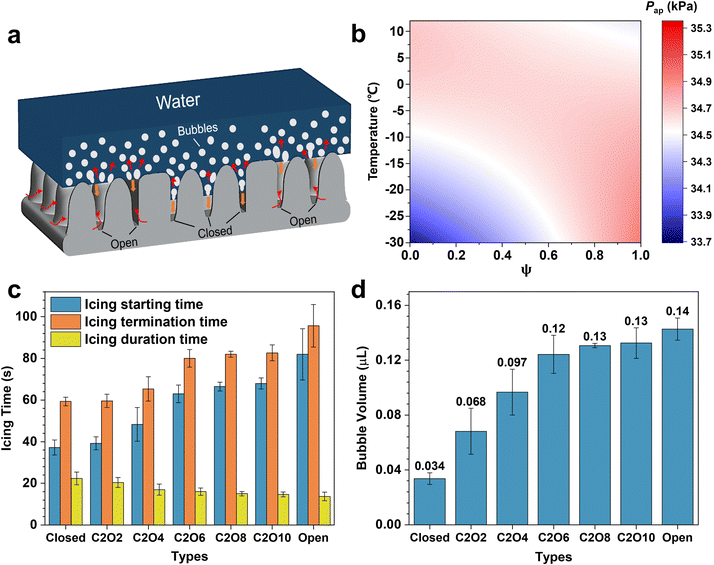 | ||
| Fig. 4 Mechanism analyses for the icing and melting phenomena on surfaces with different ROTs. (a) Schematic describing the liquid-gas-solid interfacial state changes on closed structures and open structures during icing processes. Closed and open structures are marked by black lines. The dissolved bubbles in droplets are emphasized by a white line. Red straight arrows and curved arrows denote the moving directions of bubbles and the airflow directions, respectively. Orange arrows represent the moving directions of the three-phase contact line during icing processes. (b) Phase diagram of air pocket pressure at different temperatures and on the surfaces with different ROTs. (c) Icing times of droplets on the surfaces with different ROTs. The icing starting times are recorded from the beginning of the icing process (15 °C) to the occurrence of recalescence, and the icing termination times are recorded from the beginning of the icing process to the complete freezing. Icing duration times are the differences between the termination times and the starting times. (d) Amounts of frozen bubbles in ice droplets on different surfaces. The calculation methods can be found in S8 (ESI†). Data are mean ± s.d. from at least three independent measurements. | ||
Ice adhesion strengths and icephobic durability
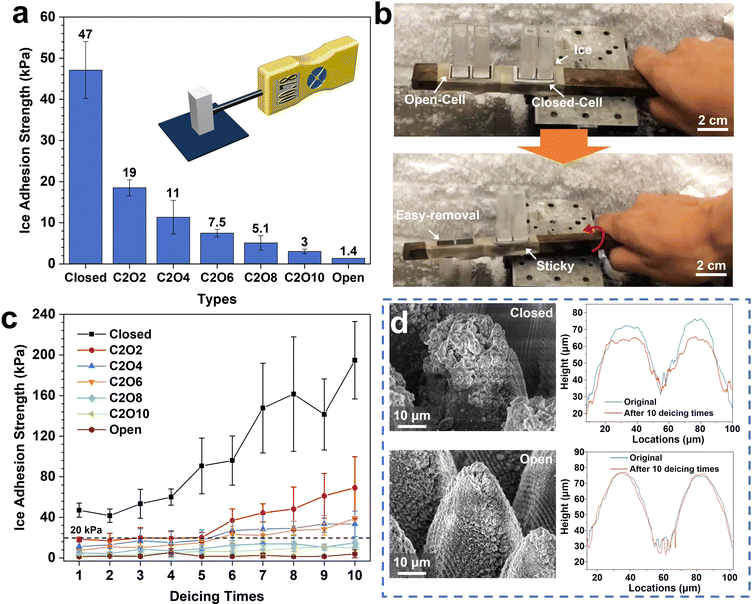
In light of the above analyses, ice adhesion strength tests were conducted on the surfaces with different ROTs to examine the easy-removal properties after icing. The results are shown in Fig. 5. It can be explicitly observed that the ice adhesion strengths significantly decrease as the ROT increases (Fig. 5a). The ice adhesion strengths on the optimized open-cell surfaces (1.4 kPa) are even more than 33 times lower than those on the closed-cell surfaces (47 kPa). After a slight vibration,48 the ice on the open-cell surfaces can be easily removed while that on the closed-cell surfaces firmly adheres to surfaces (Fig. 5b and Movie S2, ESI†). The phenomena can be attributed to the lower air pocket pressure at low temperatures on the closed-cell surfaces than on the open-cell surfaces. As the temperature decreases, the air pocket pressure on the closed-cell surfaces gradually decreases. More air pockets are prone to be impaled, resulting in rapid penetration of supercooled liquids into the micro-nanostructures. In this case, the formed ice on the surfaces is greatly stuck in micro-nanostructures and is difficult to remove. While on the open-cell surfaces, the air pocket pressure steadily increases with the decrease of temperature, leading to shallower impaled depths and fewer impaled fractions. Hence the ice adhesion strengths on the open-cell surfaces are lower. Meanwhile, after multiple deicing cycles, it is found that the surfaces with higher ROTs have more robust deicing durability. After 10 deicing cycles, the ice adhesion strengths on the open-cell surfaces are only 4.1 ± 3.9 kPa (Fig. 5c). However, on the closed-cell surfaces, the ice adhesion strengths dramatically increase to 194.8 ± 38.2 kPa after 10 deicing cycles, close to the values on the untreated surfaces.33Fig. 5d and Fig, S11, S13 (ESI†) show the SEM images and elemental distributions of the open-cell and closed-cell surfaces after 10 deicing times. The significantly deteriorated icephobicity on the closed-cell surfaces is mainly due to the structural and chemical damage caused by the impalement phenomena. Compared with the original microcones, the microcones after 10 deicing cycles were greatly abrased, leading to about 10 μm height reduction. And the loss of F and C elements on the closed-cell structures also further destroys the superhydrophobicity and icephobicity. In contrast, under the support of gradually increasing air pocket pressure as the temperature decreases, the micro-nanostructures and chemical elements on the open-cell surfaces are protected well during continuous deicing cycles. Even after 33 deicing cycles, the ice adhesion strengths on the optimized open-cell surfaces still maintain below 20 kPa, ensuring long-term icephobic durability (Fig. S14, ESI†). By analyzing and comparing the icephobicity of reported surfaces, it is found that most open-cell structured surfaces have lower ice adhesion strengths while those of irregular and closed-cell structured surfaces are significantly higher (Fig. S15, ESI†). The phenomena are consistent with our above results. Meanwhile, our laser-fabricated open-cell structures own more extraordinary icephobic durability (Fig. S16, ESI†) since the highly tunable laser direct writing method can well avoid the introduction of closed-cell structures compared with other fabricating methods (e.g., chemical etching, spraying, etc.). These discoveries could provide guidelines for fabricating and designing durable superhydrophobic anti-icing surfaces.High-humidity resistance and anti-frosting
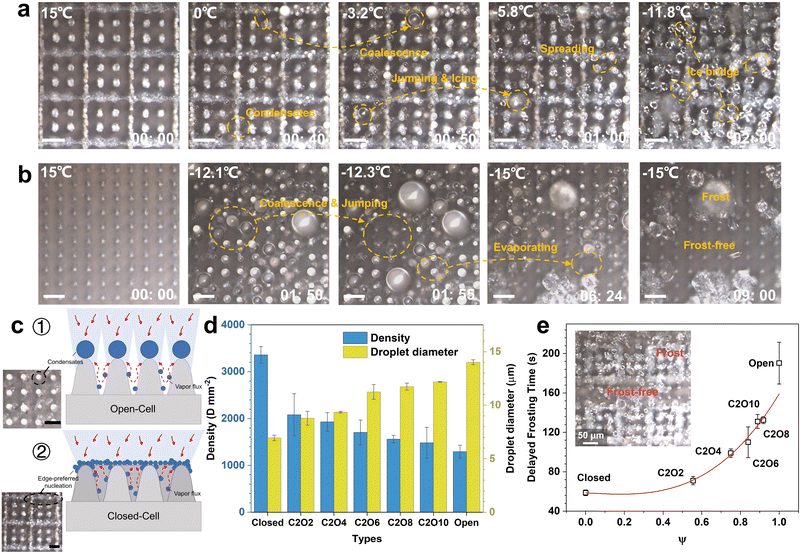
In addition to the icing issues discussed above, condensation frosting also exists ubiquitously in practical anti-icing applications.49–51 When the surface temperature falls below the dew point, water vapor in the air tends to condense into liquid droplets, which eventually freeze after the surface temperature decreases to subzero.52 The frozen droplets connect by ice bridges, forming condensation frosts. Once the condensation frosts on superhydrophobic surfaces are not effectively inhibited, the superhydrophobicity and anti-icing properties of surfaces will be greatly degraded owing to the high affinity of frost to water.15 Deposited droplets will rapidly spread and freeze on the frost layer. Former reports about the design of superhydrophobic anti-icing surfaces adopted the low-humidity test environments, where condensation frosting could not occur.38 Hence the results do not apply to practical anti-icing environments. Considering the effects of condensation frosting on the anti-icing properties of superhydrophobic surfaces in practical applications, we conducted the condensation frosting tests on the surfaces with different ROTs, as shown in Fig. 6.Fig. 6a, b and Movie S3 (ESI†) show the condensation frosting processes on the close-cell and open-cell surfaces. On the closed-cell surfaces, condensates preferentially nucleate on the microframe and microcone tops as the surface temperature decreases (Fig. 6c ②). This is mainly attributed to the enhanced diffusion at the sharp corners.53 Although the coalescence and jumping of condensates occur at low temperatures, the dewetting processes cannot yet be well realized under the constraints of microframes, and there exist abundant tiny droplets stuck in micro-nanostructures to form the Wenzel ice. Tiny frozen droplets gradually spread and connect, forming dense frosting layers just after 2 minutes (Fig. 6a). In this case, the superhydrophobic micro-nanostructures fail, and the anti-icing properties are greatly lost. While on the open-cell surfaces, condensates preferentially nucleate on the microcone tops (Fig. 6c ①). Unconstrained by microstructures, condensation droplets intensely coalesce and jump off surfaces to realize significant dewetting processes. The released latent heat during the top condensation is conducted along microstructures to prompt the evaporation of bottom tiny condensates to some extent, which together with the droplet coalescence and jumping phenomena further contributes to the formation of large CB droplets (Fig. S17, ESI†). Under the high interfacial thermal resistance of the CB state,54 the icing time of condensation droplets is significantly elongated. After completely freezing, most zones on the open-cell surfaces are still frost-free (Fig. 6b), where abundant micro-nanostructures are exposed, maintaining superhydrophobicity and anti-icing properties well. Through investigating the density and diameters of condensation droplets, it is demonstrated that as the surface ROT increases, larger and sparser condensation CB droplets will form to promote the surface dewetting processes and the formation of the frost-free zone (Fig. 6d). Moreover, the delayed frosting time on surfaces with high ROTs is also greatly elongated. The delayed frosting time on the open-cell surfaces even reaches up to 190.3 ± 21.2 s, more than three times longer than that on the closed-cell surfaces. By adjusting the distributions of open-cell structures and closed-cell structures, the patterns of the frosting and the frost-free can be tuned well (Fig. 6e).
These results confirm that the open-cell surfaces have better high-humidity resistance and anti-frosting properties. Even after completely frosting, the released latent heat during condensing and freezing can also greatly contribute to the evaporation of tiny droplets to form a frost-free zone, guaranteeing the good anti-icing properties of surfaces.
Conclusions
In summary, we combine laser ablation and programmable characteristics to fabricate tunable patterned micro-nanostructures from the complete closed-cell to different ratios and then to the complete open-cell. All the constructed surfaces consist of regular microcones (or microframes) and abundant nanoparticles, and have similarly extraordinary superhydrophobicity in room-temperature environments. However, in the low-temperature icing environments, it is found that droplets on the closed-cell surfaces rapidly degrade to the Wenzel state during icing and cannot recover to the CB state after melting. In contrast, droplets on the open-cell surfaces have a slower CB-to-Wenzel transition rate, and well realize the spontaneous recovery of the CB state after melting. By changing the ratio of the open-structural area in one cell, droplets on the surfaces with similar RT superhydrophobicity can be facilely tuned to any state from the complete Wenzel state like rose petals to the complete CB state like lotuses after melting. We adopt the improved ideal gas law to clarify the mechanisms that the decreased air pocket pressure on the closed-cell structures at low temperatures accelerates the impalement of air pockets and the freezing processes. Fewer bubbles dissolve out in ice droplets during icing and impact downwards under Marangoni forces during melting, eventually resulting in the difficult recovery of air pockets. While on the open-cell structures, the increased air pocket pressure well avoids the easy impalement and difficult recovery of air pockets during icing & melting cycles. Furthermore, it is further demonstrated that the high air pocket pressure on the optimized open-cell surfaces ensures over 33 times lower ice adhesion strengths (1.4 kPa) and more excellent icephobic durability (<20 kPa after 33 deicing cycles). Even during condensation, fewer condensate nucleation sites, more intense droplet coalescence and jumping endow the open-cell surfaces with more extraordinary high-humidity resistance and anti-frosting properties. After completely freezing, most zones on the open-cell surfaces are still frost-free. Our study confirms that open-cell structures are more favorable for anti-icing applications, and reveals the general design principle of superhydrophobic anti-icing surfaces that preferentially adopts the open structures. We believe our findings and design strategy will improve the understanding of anti-icing and push superhydrophobic anti-icing surfaces to practical applications.Experimental
Micro-nanostructure fabrication
A Trumpf TruMicro 5000 ultrafast laser system with 800 fs pulses at a central wavelength of 1030 nm and a repetition rate of 200 kHz was used to fabricate micro-nanostructrues on the aviation aluminum alloy surface AA6061. An x–y galvo was adopted to focus and scan the laser beam on the surfaces in the designed patterns in an atmospheric environment. The tunable patterns were realized by adjusting the scanning paths. After laser processing, all samples were washed with ethanol and deionized water, respectively, to remove some unstable micro-nanostructure. Pure nitrogen was used to slowly dry the samples. Finally, the low-surface-energy treatments were conducted, where all the micro-nanostructured surfaces were immersed in 1H,1H,2H,2H-perfluorodecyltrimethoxysilane alcohol solution with a concentration of 1% for 2 h and dried in an oven at 90 °C for 60 min. After finishing the above steps, all the samples are endowed with excellent superhydrophobicity. Laser fabrication parameters are shown in Table S1 (ESI†).Characterization and measurement
The SEM images and elemental distributions of the samples were obtained using a field-emission scanning electron microscope (SEM, TESCAN MIRA 3 LMH) equipped with an energy-dispersive spectrometer (EDS, Oxford). The 3D topography measurement was characterized using a 3D digital optical microscope (OLYMPUS LEXT 4100). Contact angles and sliding angles were measured using a video-based optical contact angle measuring device (OCA 15 Plus from Data Physics Instruments). The adopted droplets are deionized water with a volume of 5 μL. The contact and sliding angles of every sample were examined at randomly different locations at least three times.Icing & melting cycle experiments
A Peltier cooling plate (TEC2-19006) with a dual-probe temperature recorder (measuring accuracy: 0.1 °C) was adopted to perform the icing & melting experiments. Samples were attached to the cooling plate horizontally using thermally conductive silicone (RG-ICFN-200G-B1). The ambient temperature and humidity were maintained at 15 ± 1 °C and 20 ± 5%. The tests were conducted under a normal laboratory atmosphere. After running the cooling system, the temperature of the samples gradually decreased from 15 °C to −15 °C. When reaching −15 °C, the cooling system was powered off to naturally warm samples to 15 °C. The CCD camera with 10 frames per second and a resolution of 0.2 μm was used to record the side view of droplets in real-time. For icing & melting cycle experiments including contact angle and sliding angle characterizations, the volume of all droplets is fixed at 5 μL. The standard deviation of the measured contact angles is less than 3° for CA ≥ 150° and around 5° for CA ≤ 140°. The uncertainty of the contact diameter evaluation is 0.002–0.03 mm (the average standard deviation is 0.02 mm).Ice adhesion strength measurement
The ice adhesion strengths were obtained using a force transducer (Imada ZP-100N), which was connected to a computer. The test temperatures and humidity of ice adhesion strengths were set at −20 °C and 20 ± 5%, respectively. The test environment was maintained in a normal laboratory atmosphere. Firstly, cuvettes were gently placed on the samples and filled with 2 mL of water. Then, the filled cuvettes on the samples were placed in a refrigerator to freeze for 2 h, guaranteeing complete freezing. Finally, a force transducer probe was driven to push the ice columns at a speed of 0.5 mm s−1. The curves of forces versus displacement applied to detach ice columns were recorded in the software. The ice adhesion strengths were acquired by calculating the ratio of the peak force and the ice column cross-sectional area. The force accuracy is up to 0.01 N. The cross-sectional size of the ice column is 10 × 10 mm. Each ice adhesion strength of different samples is measured at least three times.Condensation phenomena observation
The condensation experiments of different samples were conducted on the above-mentioned Peltier cooling plate. A top-view microscopy setup (Olympus LEXT OLS4100) consisting of an upright optical microscope was used to observe in real-time. The tested samples were placed horizontally on the cooling stage whose cooling conditions and temperature changes are the same as the icing processes in the icing & melting cycle experiments. The environmental temperature and humidity were maintained at 15 ± 1 °C and 20 ± 5%. The test environment was also in the normal laboratory atmosphere. The air humidity in the test chamber was automatically adjusted using a humidity sensor via an air humidifier. The microscopy lens was set at 50× magnification, and the capture rate was 10 fps.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the funding support from the National Key Research and Development Program of China (Grant No. 2017YFB1104300, M. Z.), the Tsinghua University Initiative Scientific Research Program (Grant No. 2018Z05JZY009, M. Z.), and the National Natural Science Foundation of China (Grant No. 51575309 and 51210009, M. Z.).References
- T.-S. Wong, S. H. Kang, S. K. Y. Tang, E. J. Smythe, B. D. Hatton, A. Grinthal and J. Aizenberg, Nature, 2011, 477, 443–447 CrossRef CAS.
- M. J. Kreder, J. Alvarenga, P. Kim and J. Aizenberg, Nat. Rev. Mater., 2016, 1, 15003 CrossRef CAS.
- Y. Shen, X. Wu, J. Tao, C. Zhu, Y. Lai and Z. Chen, Prog. Mater. Sci., 2019, 103 Search PubMed.
- I. Bayer, Mechanisms of surface icing and deicing technologies, in Ice Adhesion: Mechanism, Measurement and Mitigation, ed. K. L. Mittal and C.-H. Choi, Wiley, 1st edn, 2020, Part 3, pp. 325–359.
- F. Chu, Condensed and Melting Droplet Behavior on Superhydrophobic Surfaces, Springer-Verlag, 2020 Search PubMed.
- K. Golovin, A. Dhyani, M. D. Thouless and A. Tuteja, Science, 2019, 364, 371–375 CrossRef CAS.
- T. M. Schutzius, S. Jung, T. Maitra, G. Graeber, M. Köhme and D. Poulikakos, Nature, 2015, 527, 82–85 CrossRef CAS.
- X. Tian, T. Verho and R. H. A. Ras, Science, 2016, 352, 142–143 CrossRef CAS PubMed.
- Y. Li, W. Ma, Y. S. Kwon, W. Li, S. Yao and B. Huang, Adv. Funct. Mater., 2022, 2113297 CrossRef CAS.
- M. Nosonovsky and V. Hejazi, ACS Nano, 2012, 6, 8488–8491 CrossRef CAS.
- A. J. Meuler, G. H. McKinley and R. E. Cohen, ACS Nano, 2010, 4, 7048–7052 CrossRef CAS.
- L. B. Boinovich, A. M. Emelyanenko, K. A. Emelyanenko and E. B. Modin, ACS Nano, 2019, 13, 4335–4346 CrossRef CAS.
- R. Pan, H. Zhang and M. Zhong, ACS Appl. Mater. Interfaces, 2020, 13 Search PubMed.
- J. Chen, J. Liu, M. He, K. Li, D. Cui, Q. Zhang, X. Zeng, Y. Zhang, J. Wang and Y. Song, Appl. Phys. Lett., 2012, 101, 111603 CrossRef.
- K. K. Varanasi, T. Deng, J. D. Smith, M. Hsu and N. Bhate, Appl. Phys. Lett., 2010, 97, 234102 CrossRef.
- L. Wang, Z. Tian, G. Jiang, X. Luo, C. Chen, X. Hu, H. Zhang and M. Zhong, Nat. Commun., 2022, 13, 378 CrossRef CAS PubMed.
- Y. Li, D. Quéré, C. Lv and Q. Zheng, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3387–3392 CrossRef CAS.
- P. Guo, Y. Zheng, M. Wen, C. Song, Y. Lin and L. Jiang, Adv. Mater., 2012, 24, 2642–2648 CrossRef CAS PubMed.
- M. Jin, Y. Shen, X. Luo, J. Tao, Y. Xie, H. Chen and Y. Wu, Appl. Surf. Sci., 2018, 455, 883–890 CrossRef CAS.
- T. Cheng, R. He, Q. Zhang, X. Zhan and F. Chen, J. Mater. Chem. A, 2015, 3, 21637–21646 RSC.
- Y. Hou and K. L. Choy, Prog. Org. Coat., 2022, 163 Search PubMed.
- R. N. Wenzel, Trans. Faraday Soc., 1936, 28, 988–994 CAS.
- A. Lafuma and D. Quéré, Nat. Mater., 2003, 2, 457–460 CrossRef CAS.
- R. Pan, M. Cai, W. Liu, X. Luo, C. Chen, H. Zhang and M. Zhong, J. Mater. Chem. A, 2019, 7, 18050–18062 RSC.
- L. Wang, Q. Gong, S. Zhan, L. Jiang and Y. Zheng, Adv. Mater., 2016, 28, 7729–7735 CrossRef CAS.
- J. Ma, Z. Zheng, M. J. Hoque, L. Li, K. F. Rabbi, J. Y. Ho, P. V. Braun, P. Wang and N. Miljkovic, ACS Nano, 2022, 16, 4251–4262 CrossRef CAS.
- V. Vercillo, S. Tonnicchia, J.-M. Romano, A. Garcia-Giron, A. Aguilar, S. Alamri, S. Dimov, T. Kunze, A. Lasagni and E. Bonaccurso, Adv. Funct. Mater., 2020, 30, 1910268 CrossRef CAS.
- Z. Dong, M. Vuckovac, W. Cui, Q. Zhou, R. H. A. Ras and P. A. Levkin, Adv. Mater., 2021, 33, 2106068 CrossRef CAS.
- S. Wu, Y. Du, Y. Alsaid, D. Wu, M. Hua, Y. Yan, B. Yao, Y. Ma, X. Zhu and X. He, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11240–11246 CrossRef CAS.
- D. G. K. Aboud and A.-M. Kietzig, Langmuir, 2021, 37, 4678–4689 CrossRef CAS.
- R. Zhang, P. Hao, X. Zhang and F. He, Soft Matter, 2016, 12, 5808–5817 RSC.
- R. Pan, H. Zhang and M. Zhong, ACS Appl. Mater. Interfaces, 2021, 13, 1743–1753 CrossRef CAS.
- R. Pan, H. Zhang and M. Zhong, Chin. J. Lasers-Zhongguo Jiguang, 2021, 48 Search PubMed.
- H. Wu, Z. Yang, B. Cao, Z. Zhang, K. Zhu, B. Wu, S. Jiang and G. Chai, Langmuir, 2017, 33, 407–416 CrossRef CAS.
- W. Zhang, D. Wang, Z. Sun, J. Song and X. Deng, Chem. Soc. Rev., 2021, 50, 4031–4061 RSC.
- Y. Fanfei, D. Wang, J. Yang, W. Zhang and X. Deng, Acc. Mater. Res., 2021, 920–932 Search PubMed.
- D. Wang, Q. Sun, M. J. Hokkanen, C. Zhang, F.-Y. Lin, Q. Liu, S.-P. Zhu, T. Zhou, Q. Chang, B. He, Q. Zhou, L. Chen, Z. Wang, R. H. A. Ras and X. Deng, Nature, 2020, 582, 55–59 CrossRef CAS.
- L. Mishchenko, B. Hatton, V. Bahadur, J. A. Taylor, T. Krupenkin and J. Aizenberg, ACS Nano, 2010, 4, 7699–7707 CrossRef CAS PubMed.
- F. Tavakoli and H. Pirouz Kavehpour, Langmuir, 2015, 2120–2126 CrossRef CAS.
- Y. Shen, X. Xie, J. Tao, H. Chen, Z. Cai, S. Liu and J. Jiang, Coatings, 2021, 11, 522 CrossRef CAS.
- O. F. Devereux and OwenFrancis, Topics in metallurgical thermodynamics, Topics in metallurgical thermodynamics, 1983.
- G. Jiang, Z. Tian, L. Wang, X. Luo, C. Chen, X. Hu, R. Peng, H. Zhang and M. Zhong, Langmuir, 2022, 38, 6665–6675 CrossRef CAS.
- G. Jiang, Z. Tian, X. Luo, C. Chen, X. Hu, L. Wang, R. Peng, H. Zhang and M. Zhong, Int. J. Heat Mass Transfer, 2022, 190, 122762 CrossRef CAS.
- P. Fan, B. Bai, M. Zhong, H. Zhang, J. Long, J. Han, W. Wang and G. Jin, ACS Nano, 2017, 11, 7401–7408 CrossRef CAS.
- W. Liu, X. Luo, C. Chen, G. Jiang, X. Hu, H. Zhang and M. Zhong, Lab Chip, 2021, 21, 1373–1384 RSC.
- W. Liu, R. Pan, M. Cai, X. Luo, C. Chen, G. Jiang, X. Hu, H. Zhang and M. Zhong, J. Mater. Chem. A, 2020, 8, 6647–6660 RSC.
- J. Long, P. Fan, D. Gong, D. Jiang, H. Zhang, L. Li and M. Zhong, ACS Appl. Mater. Interfaces, 2015, 7, 9858–9865 CrossRef CAS.
- L. Wang, Z. Tian, X. Luo, C. Chen, G. Jiang, X. Hu, R. Peng, H. Zhang and M. Zhong, Nano Res., 2022 DOI:10.1007/s12774-022-4887-2.
- P. Kim, T.-S. Wong, J. Alvarenga, M. J. Kreder, W. E. Adorno-Martinez and J. Aizenberg, ACS Nano, 2012, 6, 6569–6577 CrossRef CAS.
- X. Sun and K. Rykaczewski, ACS Nano, 2017, 11, 906–917 CrossRef CAS.
- R. Chatterjee, H. Bararnia and S. Anand, Adv. Mater., 2022, 2109930 CrossRef CAS.
- C. S. Sharma, A. Milionis, A. Naga, E. Lam, G. Rodriguez, M. Ponte, V. Negri, R. Hopf, M. D'Acunzi, H. J. Butt, D. Vollmer and D. Poulikakos, Adv. Funct. Mater., 2022, 32, 2109633 CrossRef CAS.
- H. Park, F. Ahmadi and J. Boreyko, Phys. Rev. Lett., 2021, 127, 044501 CrossRef CAS.
- C. Chen, Z. Tian, X. Luo, G. Jiang, X. Hu, L. Wang, R. Peng, H. Zhang and M. Zhong, Chem. Eng. J., 2022, 450, 137936 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh01083f |
| This journal is © The Royal Society of Chemistry 2023 |