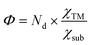A simple descriptor for the nitrogen reduction reaction over single atom catalysts†
Zhanzhao
Fu
,
Mingliang
Wu
,
Qiang
Li
 ,
Chongyi
Ling
,
Chongyi
Ling
 * and
Jinlan
Wang
* and
Jinlan
Wang
 *
*
School of Physics, Southeast University, Nanjing, 211189, China. E-mail: lingchy@seu.edu.cn; jlwang@seu.edu.cn
First published on 15th December 2022
Abstract
The performance of supported catalysts is largely decided by metal–support interactions, which is of great significance for the rational design of catalysts. However, how to quantify the structure–activity relationship of supported catalysts remains a great challenge. In this work, taking MoS2 and WS2 supported single atom catalysts (SACs) as prototypes, a simple descriptor, namely, effective d electron number (labeled as Φ), is constructed to quantitatively describe the effect of metal–support interaction on the nitrogen reduction reaction (NRR) activity. This descriptor merely consists of intrinsic properties of the catalyst (including the number of d electrons, electronegativity of the metal atoms and generalized electronegativity of the substrate atoms) and can accurately predict the limiting potential (UL) for the NRR, with no need for any density functional theory calculations. Moreover, this descriptor possesses superb expansibility that can be applied to other materials, including other metal dichalcogenide (MoSe2, MoTe2, WSe2, WTe2 and NbS2) and even MXene (V2CO2, Ti2CO2 and Nb2CO2)-supported SACs. On this basis, a fast screening of excellent NRR catalysts among these systems is performed and three promising NRR catalysts (i.e. Mo@WTe2, Mo@V2CO2 and Re@NbS2) are successfully selected with UL as low as −0.32, −0.24 and −0.31 V, respectively. This work offers new opportunities for advancing the rapid discovery of high-efficiency NRR catalysts, and the design principle is expected to be widely applicable to other catalytic systems and beyond.
New conceptsThe electrocatalytic nitrogen reduction reaction (NRR) is a promising approach to realize green and sustainable production of NH3, a very important chemical in various fields. One of the key bottlenecks to the practical application of the technology is the lack of efficient electrocatalysts. Thus, exploring highly efficient electrocatalysts is of significance and necessary. When faced with thousands of materials, the traditional trial and error method is inefficient and requires huge manpower, resources and time. In this work, we developed a simple descriptor Φ, which merely consists of intrinsic properties of the catalysts. This descriptor enables qualitative prediction of the NRR activity of single atom catalysts, by just using simple computations (addition, subtraction, multiplication and division). This work provides a novel approach for the rapid screening of highly efficient NRR catalysts. |
Introduction
SACs have exhibited superior performance to other catalysts in the electrochemical NRR.1–3 Even so, the activity and selectivity of reported SACs are still far below the requirements for commercial applications.4,5 Thus, it is highly desirable to explore more excellent SACs. In fact, as a typical supported catalyst, the performance of SACs is largely determined by the metal–support interactions.6 However, how to quantitatively characterize the effect of metal–support interactions on catalytic performance to achieve rational design or rapid screening of catalysts remains a critical challenge.7,8 Descriptors that directly associate the intrinsic features with the complex catalytic performance (e.g. UL, reaction energy, activation barriers or exchange-current densities) of the catalyst provide an effective strategy to tackle this challenge.9–12Previous works have reported various descriptors for different systems, such as the d-band center of transition metals or alloys, the eg filling of perovskites, the valence band of non-metallic carbon materials, the generalized coordination number of metallic catalysts and the charge density of the unsaturated metal centers of transition-metal oxides.13–17 These descriptors have been successfully applied to these specific systems but lack expansibility, due to the differences in the intrinsic properties of distinct systems. Moreover, most descriptors (e.g. d-band center, valence band and charge density) rely on density functional theory (DFT) calculations, making the large-scale screening and rational design of catalysts based on these descriptors actually very inefficient. Recently, Zeng et al. proposed a descriptor that consists of atomic properties (such as electron number and electronegativity), which can evaluate the activity of the oxygen reduction reaction (ORR), oxygen evolution reaction (OER) and hydrogen evolution reaction (HER) over graphene-based SACs.18 Our group also constructed a descriptor to quantify the interfacial effect on electrochemical reduction reactions over supported dual-atom catalysts.19 Such kinds of descriptors offer direct principles for catalyst design and enable fast screening of promising catalysts with no need for DFT computation. Therefore, descriptors based on intrinsic atomic properties are of vital importance, but the studies to date are very limited.
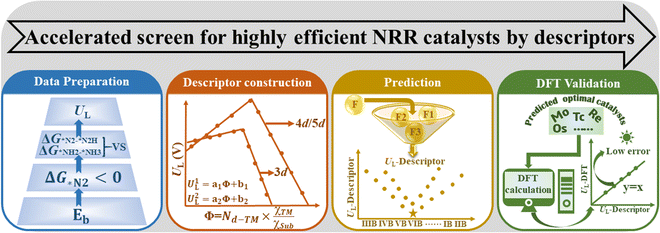
In this work, we propose a simple descriptor to describe the effect of metal–support interactions on NRR activity and enable efficient screening of promising SACs, via a four-step flow procedure (Fig. 1). Reaction free energies for the first and last electrochemical steps (labeled as ΔG*N2–*N2H and ΔG*NH2–*NH3, respectively) over 46 kinds of MoS2/WS2 supported SACs are calculated first to determine UL.20 Based on these data, the descriptor Φ (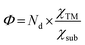 , Nd, χTM and χsub are the number of d electrons of the metal atoms, and electronegativity of the metal atoms and substrate, respectively) is constructed by analyzing the activation and reduction mechanisms of N2 molecules, which can be understood as the effective d electron number and exhibits strong correlation with the calculated UL. Using Φ as the descriptor, we perform a fast high-throughput screen for excellent catalysts among 8 different 2D material-supported SACs and 16 catalysts with low UL are selected from 184 candidates. The activity of these selected candidates is further verified by DFT calculations, where the mean absolute error (MAE) between the prediction and computational results is only 0.07 V. In addition, Mo@WTe2, Mo@V2CO2 and Re@NbS2 are predicted to be excellent catalysts for the NRR with UL as low as −0.32, −0.24 and −0.31 V, respectively.
, Nd, χTM and χsub are the number of d electrons of the metal atoms, and electronegativity of the metal atoms and substrate, respectively) is constructed by analyzing the activation and reduction mechanisms of N2 molecules, which can be understood as the effective d electron number and exhibits strong correlation with the calculated UL. Using Φ as the descriptor, we perform a fast high-throughput screen for excellent catalysts among 8 different 2D material-supported SACs and 16 catalysts with low UL are selected from 184 candidates. The activity of these selected candidates is further verified by DFT calculations, where the mean absolute error (MAE) between the prediction and computational results is only 0.07 V. In addition, Mo@WTe2, Mo@V2CO2 and Re@NbS2 are predicted to be excellent catalysts for the NRR with UL as low as −0.32, −0.24 and −0.31 V, respectively.
Computational methods
All the spin-polarized DFT calculations were implemented in the Vienna ab initio simulation package (VASP).21,22 The projector augmented wave (PAW) method was adopted to describe the interaction of ions and electrons.23 The Perdew, Burke, and Ernzerhof (PBE) function in the generalized gradient approximation (GGA) was used to describe electron exchange and correction.24,25 The cutoff energy of the plane wave basis was set to 500 eV, and the criteria of energy and force were 10−5 eV and 0.02 eV Å−1, respectively. To avoid the interaction of two periodic units, the thickness of the vacuum layer was set to 18 Å. A 4 × 4 × 1 supercell was applied and the Brillouin zones were sampled with 3 × 3 × 1 Monkhorst–Pack meshes.26 The DFT-D3 method was employed to describe long-range van der Waals interactions.27,28 The computational hydrogen electrode (CHE) model developed by Nørskov and coworkers was adopted to obtain the Gibbs free energy change (ΔG) of the NRR elementary steps.29 Meanwhile, ΔG was evaluated based on the pristine SACs, as the oxidized metal atoms can be reduced during the N2 reduction process (Fig. S1, ESI†). The N2 capture ability of the catalysts was evaluated by:| ΔG*N2 = G*N2 − G* − GN2 | (1) |
Results and discussion
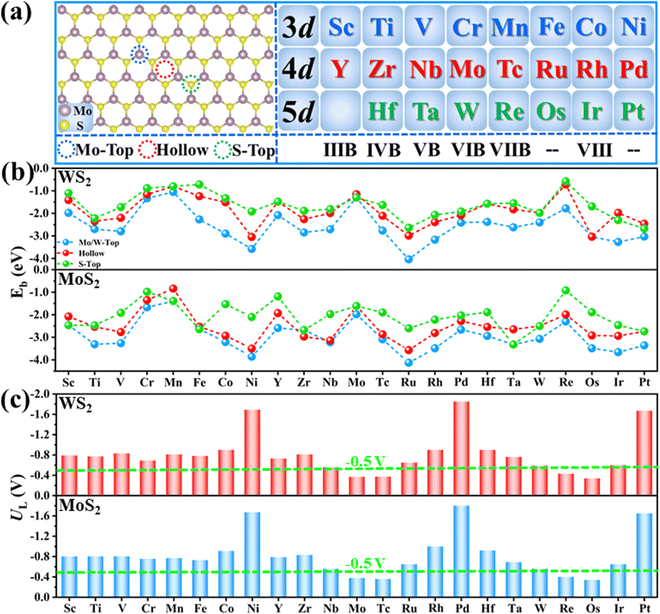
The chemisorption of N2 is believed to be a prerequisite for an efficient NRR process, where the existence of empty orbitals of active sites to accept the lone-pair electrons of N2 is the key. Therefore, 23 different metal atoms (Fig. 2(a)) supported on two different substrates (MoS2 and WS2) are selected as the models for data preparation. For each atom, three possible binding sites are considered (Fig. 2(a)), including the M-top site, hollow site and S-top site. Therefore, the binding energies (Eb) of all metal atoms on these three sites are calculated firstly and the most stable structures are used as models for further computations. As shown in Fig. 2(b), the M-top site is energetically most favorable for all the systems; thus, single metal atoms supported on the M-top site are selected.The NRR activity of these SACs is evaluated by calculating the UL. Generally, there are three possible associative mechanisms for the NRR, namely, alternating, distal and enzymatic mechanisms (Fig. S2a, ESI†), depending on the adsorption pattern of N2 (end on or side on, as shown in Fig. S3, ESI†).30,31 Therefore, the adsorption free energies of N2 (ΔG*N2) via different patterns are firstly calculated and the pattern with lower energy is selected for further computation (Fig. S4, ESI†). To reduce the computational cost, a two-step strategy (Fig. S2b, ESI†) was adopted for the activity evaluation, as proposed in our previous work.20,32 Specifically, reaction free energies for the first (*N2 + H+ + e− = *N2H, ΔG*N2–*N2H) and last hydrogenation steps (*NH2 + H+ +e− = *NH3, ΔG*NH2–*NH3) are calculated and the more positive one (ΔGPDS) is adopted to obtain UL (UL = −ΔGPDS/e). This is because one of these two elementary steps is usually the potential determining step (PDS) of the whole NRR process, as the breaking of the inert N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond unavoidably requires high energy injection and meanwhile, sp3 hybridization of the N atom in *NH2 intermediates usually leads to stronger binding strength of *NH2 as compared to *NH3.20,32 The calculated ΔG*N2–*N2H and ΔG*NH2–*NH3 are presented in Fig. S5 (ESI†) and the corresponding UL values of the different TM@MoS2 and TM@WS2 are displayed in Fig. 2(c), and are used as the data for descriptor construction.
N triple bond unavoidably requires high energy injection and meanwhile, sp3 hybridization of the N atom in *NH2 intermediates usually leads to stronger binding strength of *NH2 as compared to *NH3.20,32 The calculated ΔG*N2–*N2H and ΔG*NH2–*NH3 are presented in Fig. S5 (ESI†) and the corresponding UL values of the different TM@MoS2 and TM@WS2 are displayed in Fig. 2(c), and are used as the data for descriptor construction.
Understanding the origin of intrinsic activity of different catalysts to uncover the structure–activity relationships is crucial to the construction of descriptors. According to the previous reports, the features like bonding network, local charges, N-adsorption energy, etc.33–35 usually possess a close relationship with the NRR activity. Nevertheless, the values of these features rely on DFT calculations, making the large-scale screening and rational design of catalysts based on these features actually very inefficient. Thus, in our work, these features were not considered. Instead, only the features that can be directly obtained from the Physical Chemistry Database were used to construct the descriptor. As mentioned above, one prerequisite for an efficient NRR process is the relatively strong binding strength of N2 to sufficiently activate the inert N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond. Specifically, too weak N2 binding strength corresponds to insufficient N2 activation, leading to a high reaction free energy for the first elementary step. On the contrary, too strong N2 binding strength usually indicates very stable adsorption of reaction intermediates, making the high energy injection of the last elementary step. Undoubtedly, N2 activation degree is the key to NRR activity. As depicted in Fig. S6 (ESI†), the electron “acceptance and back-donation” mechanism has been widely accepted as the route for the efficient activation of N2 molecules.31 According to this mechanism, the lone-electron pair of N2 can be accepted by the unoccupied d orbitals of a TM atom, and simultaneously, the electrons in the filled d orbitals of the TM atom can be donated into the anti-bonding orbitals of N2 to weaken the inert N
N triple bond. Specifically, too weak N2 binding strength corresponds to insufficient N2 activation, leading to a high reaction free energy for the first elementary step. On the contrary, too strong N2 binding strength usually indicates very stable adsorption of reaction intermediates, making the high energy injection of the last elementary step. Undoubtedly, N2 activation degree is the key to NRR activity. As depicted in Fig. S6 (ESI†), the electron “acceptance and back-donation” mechanism has been widely accepted as the route for the efficient activation of N2 molecules.31 According to this mechanism, the lone-electron pair of N2 can be accepted by the unoccupied d orbitals of a TM atom, and simultaneously, the electrons in the filled d orbitals of the TM atom can be donated into the anti-bonding orbitals of N2 to weaken the inert N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond. Thus, the distribution of d electrons of the TM atom should be the decisive factor to the N2 adsorption and activation. In fact, our computational results validate the above analysis. As shown in Fig. 2(c), the calculated UL of different SACs correlates closely to the corresponding d electron number of the supported metal atoms. Specifically, for metal atoms in the same period, the UL generally decreases first and then increases with the increase of the atomic number or Nd. As a result, MoS2 and WS2-supported middle transition metal atoms, such as Mo, Tc, Re and Os, usually exhibit lower UL for the NRR than other systems. Based on the above analysis, the number of d electrons of the TM atom (Nd) should be a major feature for descriptor construction.
N triple bond. Thus, the distribution of d electrons of the TM atom should be the decisive factor to the N2 adsorption and activation. In fact, our computational results validate the above analysis. As shown in Fig. 2(c), the calculated UL of different SACs correlates closely to the corresponding d electron number of the supported metal atoms. Specifically, for metal atoms in the same period, the UL generally decreases first and then increases with the increase of the atomic number or Nd. As a result, MoS2 and WS2-supported middle transition metal atoms, such as Mo, Tc, Re and Os, usually exhibit lower UL for the NRR than other systems. Based on the above analysis, the number of d electrons of the TM atom (Nd) should be a major feature for descriptor construction.
Moreover, as seen from Fig. 2(c), the same metal atom deposits on different supports exhibit different activity. This can be ascribed to the aforementioned metal–support interaction, which leads to the redistribution of d electrons of the supported metal atom. To address this issue, the electronegativity of the metal atom (χTM) and substrate (χsub, which is defined as 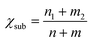 , details can be found in the ESI†), which describes the atom's ability to attract electrons, is introduced to quantify the effect of metal–support interaction on the electron redistribution. Accordingly, a descriptor Φ is constructed, defined as:
, details can be found in the ESI†), which describes the atom's ability to attract electrons, is introduced to quantify the effect of metal–support interaction on the electron redistribution. Accordingly, a descriptor Φ is constructed, defined as:
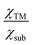 quantifies the metal–support interaction. Therefore, Φ can be understood as the effective d electron number of the supported TM atoms. Thus, we believe that the descriptor Φ should correlate closely to the N2 activation ability and NRR activity.
quantifies the metal–support interaction. Therefore, Φ can be understood as the effective d electron number of the supported TM atoms. Thus, we believe that the descriptor Φ should correlate closely to the N2 activation ability and NRR activity.
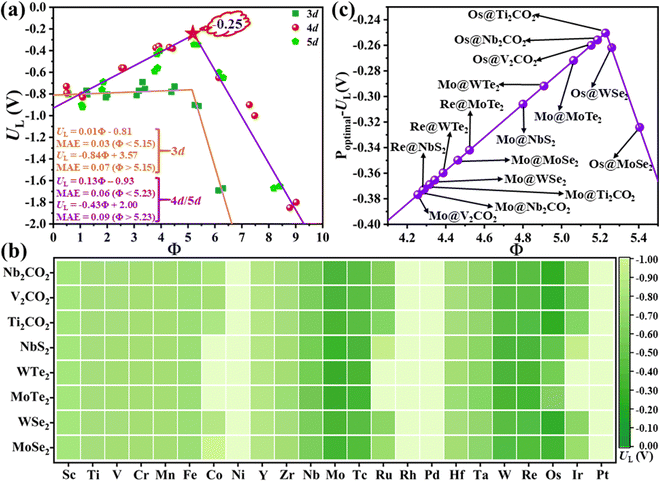
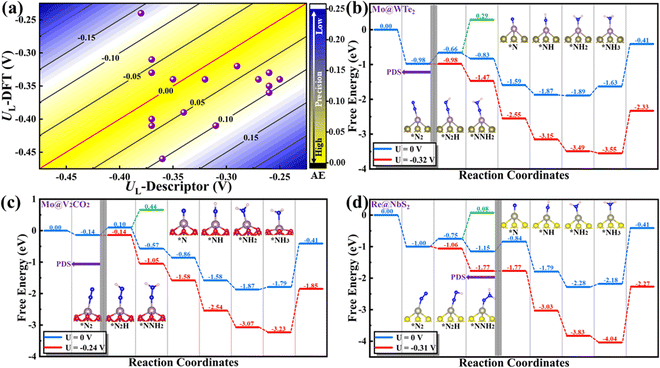
To prove this hypothesis, the relationship between the UL and the descriptor Φ is constructed, as shown in Fig. 3(a), where the volcano-type plot is obtained. In general, the corresponding MAE of different lines are all lower than 0.10 V, demonstrating that the proposed descriptor Φ can well describe the effect of metal–support interaction on the catalytic activity for the NRR over MoS2 and WS2 supported SACs. The UL for the NRR over 3d and 4d/5d TM atoms shows different relationships with Φ, where 4d/5d TM atoms possess a lower UL value than that of 3d TM atoms. This might be ascribed to the following two aspects: (i) qualitatively, the filling degree of d electrons at the Fermi level between 3d and 4d/5d TM atoms is clearly different, where 4d/5d atoms generally have higher filling degree at the Fermi level than that of 3d atoms;36 (ii) quantitatively, the number of d electrons and the electronegativity of the 3d TM atoms are quite distinct from that of the 4d/5d TM atoms in the same group (e.g. d electron number: 8 for Ni vs. 10/9 for Pd/Pt, electronegativity: 1.92 for Ni vs. 2.20/2.28 for Pd/Pt etc., as shown in Table S1 and Fig. S7a and b, ESI†). Moreover, the early and late TM atoms locate at the left and right branch of the volcano plot, respectively. Accordingly, the middle TM atoms, such as Nb, Mo, Re, etc., usually locate near the top of the volcano plot, indicating that these metals hold lower UL and more advantageous activity for the NRR. In addition, optimal activity can be achieved when Φ = 5.23 for supported 4d/5d SACs, where the corresponding UL is as low as −0.25 V (as denoted by the red star in Fig. 3(a)). Overall, the proposed Φ can serve as a simple descriptor to quantify the interfacial effect on the charge distribution and NRR activity of supported SACs, and provide a direct principle for optimizing the NRR activity by modifying the substrate and supported metal atoms.
Above, we have constructed a simple descriptor (Φ) based on intrinsic atomic properties (electronegativity and d electron number), for qualitative evaluation of NRR activity over MoS2 and WS2-supported SACs. To evaluate the expansibility of Φ to other systems, a fast high-throughput screening of excellent SACs for the NRR is further performed. 184 kinds of SACs, including 23 kinds of single metal atoms supported on 8 different 2D materials (five metal dichalcogenides, MoSe2, MoTe2, WSe2, WTe2 and NbS2 as well as three MXenes, V2CO2, Ti2CO2 and Nb2CO2) are considered and the calculated χsub values of different substrates are shown in Table S2 (ESI†). Similar to MoS2 and WS2-supported SACs, the middle TM atoms, such as Mo, Tc, W, Re and Os, usually exhibit lower UL than other metal atoms, regardless of the substrates (Fig. 3(b)). This can be ascribed to the fact that Nd is the determining factor of the NRR activity of these catalysts, according to the proposed descriptor Φ. The effect of the substrate on the activity can also be well understood from this aspect. As mentioned above, Φ is the effective d electron number of the supported single atom. Due to the electronegativity difference of different substrates, the same supported metal atoms can donate different numbers of electrons to the substrate, leading to different UL for the NRR. According to the expression of Φ, the electron transferred from a certain metal atom to different substrates increases with the increase of χsub. To prove this point, the electrons transferred from the single metal atom to different substrates were calculated by taking Mo SAC as an example. As shown in Table S2 (ESI†), the number of electrons transferred to different substrates increases broadly with the increase of the electronegativity of the substrate, in line with the assumption based on our descriptor. Moreover, 16 SACs with predicted UL lower than −0.40 V are further selected, as presented in Fig. 3(c). To evaluate the accuracy of the predicted UL, reaction free energies of the first and last elementary steps over these 16 SACs are calculated to determine the UL. As illustrated in Fig. 4(a) and Table S3 (ESI†), the predicted UL is well consistent with the calculated UL, where the absolute errors for most systems (15 of 16) are lower than 0.10 V and the MAE is as low as 0.07 V. These results indicate not only the superb accuracy of the predicted UL, but also the expansibility of the proposed simple descriptor. In addition to the metal dichalcogenide and MXene substrates, the applicability of the descriptor to N-doped graphene supported SACs (M–Nx) has also been evaluated. For these systems, a difficult problem to solve is the computation of χsub. On the one hand, the metal atom deposited on the defect sites of the substrate, making our definition of χsub (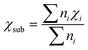 ) no longer applicable. On the other hand, it's hard to simply describe the χsub of M–Nx as it is determined by many factors, such as defect type, N doping concentration, N doping type, etc. To avoid this issue, M–Nx with the same coordination environment was considered, making the χsub a constant value that has no effect on the obtained tendency, as the substrate is fixed. Therefore, χsub can be set to 1 to simplify the expression of the descriptor (labeled as Φ′ = Nd × χTM). Thus, we plotted the UL of M-N4 SACs for the NRR as a function of Φ′. As displayed in Fig. S8 (ESI†), volcano-type relationships can be observed, indicating that our proposed descriptor can be used for M–Nx SACs.
) no longer applicable. On the other hand, it's hard to simply describe the χsub of M–Nx as it is determined by many factors, such as defect type, N doping concentration, N doping type, etc. To avoid this issue, M–Nx with the same coordination environment was considered, making the χsub a constant value that has no effect on the obtained tendency, as the substrate is fixed. Therefore, χsub can be set to 1 to simplify the expression of the descriptor (labeled as Φ′ = Nd × χTM). Thus, we plotted the UL of M-N4 SACs for the NRR as a function of Φ′. As displayed in Fig. S8 (ESI†), volcano-type relationships can be observed, indicating that our proposed descriptor can be used for M–Nx SACs.
Now, there is still one issue that needs to be clarified. That is, to reduce the computational cost, a “two-step strategy” is adopted to preliminarily evaluate the NRR activity, making the reaction mechanism and reaction free energies for other elementary steps unclear. Therefore, the most promising SACs (with smallest UL) for different substrates (i.e. Mo@MoS2, Mo@WS2, Mo@MoSe2, Mo@WSe2, Mo@MoTe2, Mo@WTe2, Re@NbS2, Os@Ti2CO2, Mo@V2CO2 and Os@Nb2CO2) are selected to calculate the complete free energy diagram for the NRR. And the calculated zero point energies and entropy of different intermediates are illustrated in Table S4 (ESI†). Herein, for the MXene-supported SACs, two binding sites for the TM single atom were taken into consideration, namely, the hollow C site and hollow Ti site,25 as displayed in Fig. S9 (ESI†). For the studied systems (Os@Ti2CO2, Mo@V2CO2 and Os@Nb2CO2), the hollow C site is more favorable for the deposition of single metal atoms (Table S5, ESI†), which were used as the models for subsequent calculations. As the end-on adsorption pattern is always favorable for all of these ten systems, only the distal and alternating pathways are considered and the calculated reaction free energies for all the elementary steps are presented in Tables S6–S10 (ESI†). Correspondingly, the free energy diagrams are shown in Fig. 4(b)–(d) and Fig. S10 (ESI†), where the green and blue lines represent the alternating and distal pathways, respectively. It can be clearly observed that the distal pathway (*N2 → *NNH → *NNH2 → *N + NH3 → *NH → *NH2 → *NH3) is preferred for all of the selected catalysts. Moreover, the PDS is either the first or the last elementary step for most systems, except for Re@NbS2 (the PDS is the third hydrogenation step with reaction free energy that close to the first step, 0.31 eV vs. 0.25 eV), which proves that the “two-step strategy” is highly effective and efficient once again. Moreover, the UL values for the NRR over Mo@WTe2, Mo@V2CO2 and Re@NbS2 are as low as −0.32, −0.24 V and −0.31 V, respectively, indicative of the ultra-high NRR activity of these catalysts. All in all, these results prove that the proposed simple descriptor can quantify the metal–support interfacial effect on the NRR activity over 2D material supported SACs and enable the fast screening or rapid design of excellent NRR catalysts with no need for DFT computations.
Conclusion
In summary, by means of DFT calculations, we have constructed a simple descriptor Φ by carefully analyzing the activation and reduction mechanism of N2. The success of this descriptor can quantitatively characterize the metal–support interfacial effect on the NRR catalytic activity over supported SACs. Meanwhile, this descriptor only consists of intrinsic atomic properties of the catalyst (Nd, χTM and χsub) and thus, enables fast estimation of the NRR activity with no need for DFT computations. More importantly, the proposed descriptor possesses excellent generalization that can be used to evaluate UL for the NRR over other MX2 and MXene supported SACs, with a MAE as low as 0.07 V. Using this descriptor, a fast high-throughput screening has been performed, where three excellent potential NRR catalysts, Mo@WTe2, Mo@V2CO2 and Re@NbS2 are selected with UL as low as −0.32, −0.24 and −0.31 V, respectively. Overall, the high accuracy and expansibility of this simple descriptor provides feasible principles for rational design and rapid screening of optimal NRR catalysts. We hope that our work can inspire the development of more simple descriptors that can be used for different reactions and complicated systems.Author contributions
J. L. Wang and C. Y. Ling supervised the project. Z. Z. Fu conceived the study and did calculations. Z. Z. Fu., C. Y. Ling and J. L. Wang co-wrote the paper with all authors contributing to the discussion and preparation of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work is supported by the National Key Research and Development Program of China (2021YFA1500700), the National Natural Science Foundation of China (22033002, 92261112), the Basic Research Program of Jiangsu Province (BK20220800) and the Fundamental Research Funds for the Central Universities (3207022214A1, 4060692201/003). The authors thank the computational resources from the Big Data Center of Southeast University and the National Supercomputing Center of Tianjin.References
- W. Guo, K. Zhang, Z. Liang, R. Zou and Q. Xu, Chem. Soc. Rev., 2019, 48, 5658–5716 RSC
.
- Y. Pang, C. Su, G. Jia, L. Xu and Z. Shao, Chem. Soc. Rev., 2021, 50, 12744–12787 RSC
.
- G. Qing, R. Ghazfar, S. T. Jackowski, F. Habibzadeh, M. M. Ashtiani, C.-P. Chen, M. R. Smith III and T. W. Hamann, Chem. Rev., 2020, 120, 5437–5516 CrossRef CAS PubMed
.
- C. Ling, Y. Cui, S. Lu, X. Bai and J. Wang, Chem, 2022, 8, 1575–1610 CAS
.
- L. Hui, Y. Xue, H. Yu, Y. Liu, Y. Fang, C. Xing, B. Huang and Y. Li, J. Am. Chem. Soc., 2019, 141, 10677–10683 CrossRef CAS PubMed
.
- Y. Wang, D. Wang and Y. Li, J. Energy Chem., 2022, 65, 103–115 CrossRef CAS
.
- J. Yang, W. Li, D. Wang and Y. Li, Adv. Mater., 2020, 32, 2003300 CrossRef CAS PubMed
.
- Y. Wang, D. Wang and Y. Li, Adv. Mater., 2021, 33, 2008151 CrossRef CAS PubMed
.
- Z. Xue, X. Zhang, J. Qin and R. Liu, Nano Energy, 2021, 80, 105527 CrossRef CAS
.
- L. Ge, W. Xu, C. Chen, C. Tang, L. Xu and Z. Chen, J. Phys. Chem. Lett., 2020, 11, 5241–5247 CrossRef CAS PubMed
.
- Z.-K. Han, D. Sarker, R. Ouyang, A. Mazheika, Y. Gao and S. V. Levchenko, Nat. Commun., 2021, 12, 1–9 CrossRef PubMed
.
- H. Zhuang, A. J. Tkalych and E. A. Carter, J. Phys. Chem. C, 2016, 120, 23698–23706 CrossRef CAS
.
-
B. Hammer and J. K. Nørskov, Adv. Catal., Elsevier, 2000, vol. 45, pp.71–129 Search PubMed
.
- J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3, 546–550 CrossRef CAS PubMed
.
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, J. Am. Chem. Soc., 2014, 136, 4394–4403 CrossRef CAS PubMed
.
- F. Calle-Vallejo, D. Loffreda, M. T. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS PubMed
.
- H. B. Tao, L. Fang, J. Chen, H. B. Yang, J. Gao, J. Miao, S. Chen and B. Liu, J. Am. Chem. Soc., 2016, 138, 9978–9985 CrossRef CAS PubMed
.
- H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348 CrossRef CAS
.
- C. Ren, S. Lu, Y. Wu, Y. Ouyang, Y. Zhang, Q. Li, C. Ling and J. Wang, J. Am. Chem. Soc., 2022, 144, 12874–12883 CrossRef CAS PubMed
.
- C. Ling, Y. Ouyang, Q. Li, X. Bai, X. Mao, A. Du and J. Wang, Small Methods, 2018, 3, 1800376 CrossRef
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- B. Wang, X. Zhang, Y. Zhang, S. Yuan, Y. Guo, S. Dong and J. Wang, Mater. Horiz., 2020, 7, 1623–1630 RSC
.
- Y. Wu, W. Sun, S. Liu, B. Wang, C. Liu, H. Yin and Z. Cheng, Nanoscale, 2021, 13, 16564–16570 RSC
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- Z. Fu, C. Ling and J. Wang, J. Mater. Chem. A, 2020, 8, 7801–7807 RSC
.
- D. Chadi, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 16, 1746 CrossRef
.
- T. Yang, T. T. Song, J. Zhou, S. Wang, D. Chi, L. Shen, M. Yang and Y. P. Feng, Nano Energy, 2020, 68, 104304 CrossRef CAS
.
- Z. Fu, Q. Li, X. Bai, Y. Huang, L. Shi and J. Wang, Nanoscale, 2021, 13, 12233–12241 RSC
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef
.
- L. Shi, Q. Li, C. Ling, Y. Zhang, Y. Ouyang, X. Bai and J. Wang, J. Mater. Chem. A, 2019, 7, 4865–4871 RSC
.
- C. Ling, X. Niu, Q. Li, A. Du and J. Wang, J. Am. Chem. Soc., 2018, 140, 14161–14168 CrossRef CAS PubMed
.
- Y. Chen, X. Zhang, J. Qin and R. Liu, Nanoscale, 2021, 13, 13437–13450 RSC
.
- C. Ling, Y. Ouyang, Q. Li, X. Bai, X. Mao, A. Du and J. Wang, Small Methods, 2019, 3, 1800376 CrossRef
.
- H. Li, Y. Liu, K. Chen, J. T. Margraf and K. Reuter, ACS Catal., 2021, 11, 7906–7914 CrossRef CAS
.
- Y. Xiao, C. Shen and T. Long, Chem. Mater., 2021, 33, 4023–4034 CrossRef CAS
.
- I. Chapnik, J. Struct. Chem., 1964, 5, 146–161 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh01197b |
| This journal is © The Royal Society of Chemistry 2023 |