Lattice disorder influences the photocarrier dynamics in lead halide perovskites†
Haijuan
Zhang
 a,
Taiyang
Zhang
b,
Yong
Wang
b,
Yuetian
Chen
a,
Taiyang
Zhang
b,
Yong
Wang
b,
Yuetian
Chen
 b,
Yixin
Zhao
b,
Yixin
Zhao
 *b and
Jie
Chen
*a
*b and
Jie
Chen
*a
aCenter for Ultrafast Science and Technology, Key Laboratory for Laser Plasmas (Ministry of Education), School of Physics and Astronomy, Collaborative Innovation Center of IFSA (CICIFSA), Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai 200240, P. R. China. E-mail: jiec@sjtu.edu.cn
bSchool of Environmental Science and Engineering, Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai 200240, P. R. China. E-mail: yixin.zhao@sjtu.edu.cn
First published on 6th January 2023
Abstract
Revealing the structural impact of lead halide perovskites on photocarrier dynamics is essential for the associated solar cells but deficient in experimental visualization. In this study, with femtosecond spectroscopy, we for the first time explored the contribution of the disorder of the distorted PbX6 octahedrons and A-site cations on the carrier behaviours. It was found that photoinduced carriers recombine almost twice slower and diffuse 20% faster in the disordered, β-phased samples than in the ordered, γ-phased ones. Yet within the same phase, with a similar PbX6 orientation but various A-site mobility, the carrier diffusion and recombination have no apparent difference. Thus we firmly conclude that lattice disorder effectively influences the carrier dynamics and therein the Pb–X sublattice is worth more than A-site cations, which should inspire future lead halide perovskite design and applications.
New conceptsUsing femtosecond spectroscopy, we monitored photocarrier dynamics in β-phase CsPbI3, MAPbI3, FA0.9Cs0.1PbI3 and γ-phase MAPbI3 and CsPbI3 perovskites. We found that photoinduced carriers recombine almost two times slower and diffuse 20% faster in the disordered, β-phase samples than in the ordered, γ-phase ones. Yet within the same phase, with a similar PbX6 orientation but various A-site mobility, the carrier diffusion and recombination have no apparent difference. These results indicate that lattice disorder is the main factor that influences the carrier dynamics and therein the Pb–X sublattice is worth more than A-site cations. |
Introduction
Lead halide perovskites (LHPs) with a general chemical formula APbX3 [A = CH3NH3+ (MA+), CH(NH2)2+ (FA+), Cs+; X = I−, Br−, Cl−] have been demonstrated as one of the most attractive candidates for various optoelectronic applications, especially for the next-generation solar cells.1,2 Owing to the combination of low-cost fabrication and outstanding photoelectric properties including high carrier mobility and high defect tolerance, the power conversion efficiency of perovskite solar cells has soared from the initial unstable 3.8%3 to the certified 25.7%.4 Some latest device studies have suggested that the record high efficiency is contributed by the lattice strain management of LHPs through suppressing defects and reducing carrier recombination.5–7 The lattice structure (phase)1,8 of LHPs is determined by the distortion and orientation ordering of PbX6 octahedrons and A-site cations (Table 1).9–17 To further improve the efficiency, it is extremely important to reveal the relationship between the structure and the underlying physical mechanisms, such as carrier dynamics in the perovskite absorber layer. Although the important influence of both the PbX6 octahedron and A-site cation has been predicted theoretically,9–16 their contribution to carrier recombination and diffusion is still unclear limited by the lack of direct experimental evidence.| Structure/phase | PbX6 distortion | PbX6 orientation | A-site orientation organic/inorganic |
|---|---|---|---|
| Cubic/α | Undistorted | Disorder | Disorder/order |
| Tetragonal/β | Randomly distorted | Disorder | Disorder/order |
| Orthorhombic/γ | Harmonically distorted | Order | Order/order |
In this work, using the ultrafast transient reflectance (TR) technique we explored the influence of the distorted PbX6 octahedrons by tracing the photocarrier dynamics in β- and γ-phased perovskites with disorderly and orderly Pb–I sublattices, respectively. The effect of the A-site cations is revealed as well by the photocarrier dynamics in the same phase, i.e. either β-phased (MAPbI3, FA0.9Cs0.1PbI3 and CsPbI3),18–21 or γ-phased (MAPbI3 and CsPbI3) perovskites, which have a similar distorted Pb–I sublattice, but a different A-site component. We found that the photoinduced carriers recombined almost 2 times slower and diffused 20% faster in the β-phased samples than in the γ-phased ones, while within the β- or γ-phased siblings, the carrier diffusion and recombination rates have no obvious difference. Since the crystal phase is majorly determined by the distortion property of the PbX6 octahedrons and then modified by the mobility of the A-site cations, we firmly conclude that the Pb–X sublattice is worth more than A-site cations in the carrier dynamics of LHPs. Considering that both are kinds of strain relaxation,17 our results provide a new perspective on the effect of strain management, i.e. assisting carrier diffusion and retarding electron–hole recombination, besides suppressing defects.5,6
Experiments and data analysis
The recently established preparation methods for the room-temperature thermodynamically stable β-22 and γ-23 phased CsPbI3 films form the prerequisites of this work. Following them and the standard fabrication procedures for the β-phased MAPbI324,25 and FA0.9Cs0.1PbI3,26 we obtained all room-temperature stable films using a single-step spin-coating method with a thickness of about 200 nm. It should be noted that normally at room temperature FAPbI3 is in the cubic α phase and in order to realize a β-phased perovskite with FA+ dominated A-site cations, a partial substitution of FA+ with Cs+ was induced as FA0.9Cs0.1PbI3.26–28 The crystalline quality of all samples was well-recognized at room temperature with full characterizations (for more details, see S1, ESI†). As has been proved by many experimental studies, the crystal structure of MAPbI3 can be controlled by temperature.1,29,30 At room temperature, the MAPbI3 film is in the β phase, and the γ-phased MAPbI3 applied in the TR measurement was realized by cooling the sample to 100 K using a temperature-controlled cryostat.The bandgaps of the β-CsPbI3, γ-CsPbI3, β-MAPbI3 and β-FA0.9Cs0.1PbI3 films were determined by the absorption spectra shown in Fig. S1(b) (ESI†) to be 1.68, 1.73, 1.58 and 1.55 eV, respectively. Thus, in TR measurements, 395 nm (3.14 eV) and 790 nm (1.57 eV) were selected as the pump and probe light, respectively. The former would excite electrons from the valence band to the conduction band and modulate the reflectance of the perovskites, R. The latter is very sensitive to such change since its photon energy is close to the bandgaps and its real time relative reflectance change −ΔRt/R was recorded as a reflection of excited carrier density nt at any delay time t (the TR experimental setup is detailed in S2, ESI†).
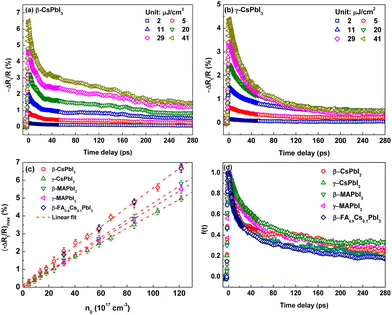
The carrier dynamics are presented by −ΔRt/R in Fig. 1(a) and (b) and Fig. S2(a)–(c) (ESI†) for β-CsPbI3, γ-CsPbI3, β-MAPbI3, γ-MAPbI3 and β-FA0.9Cs0.1PbI3 films, respectively. All TR traces exhibit a sharp increase initially (<1 ps) to the maximum reflectivity change (−ΔRt/R)max and then a slow recovery (tens to hundreds of picoseconds). The former is typically assigned to the photoinduced electron/hole assemblage in the conduction/valence bands right after the 3.14 eV photoexcitation.31,32 The initial assembled photocarrier density n0 can be calculated as n0 = α(F/3.14 eV),31 where F is the pump fluence and α is the sample absorption coefficient at the 395 nm pump wavelength (α ∼ 1.5 × 105 cm−1 for all samples33–36). As shown in Fig. 1(c), (−ΔRt/R)max linearly depends on n0 for all samples, which leads to the connection as (−ΔRt/R)max = bn0 with a positive linear coefficient b. In the following we assume that −ΔRt/R and nt share the same recovery function f(t) as −ΔRt/R = (−ΔRt/R)max·f(t) = bn0·f(t) = bnt. Therefore, the slow recovery is actually the depopulation process of the excited carrier in the probed volume, as discussed below through diffusion and electron–hole recombination. The normalized TR traces, essentially f(t), shown in Fig. 1(d) hint that from the perspective of carrier dynamics, these five samples could be roughly divided into two clusters, which is in agreement with the structure phase, i.e. samples with the same phase have similar carrier behaviour, especially in the first 40 ps.
In LHPs, the photocarrier depopulation is usually described by the rate equation31 −dnt/dt = k1nt + k2nt2 + k3nt3, in which the three terms on the right hand side are successively ascribed to: (1) a first-order Shockley–Reed (trap state-mediated) recombination or carrier diffusion out of the probing region; (2) a second-order non-geminate/free carrier recombination; and (3) a three-body Auger recombination,32 with k1, k2 and k3 being the corresponding depopulation rate constants, respectively. Owing to the low pump fluence (2–42 μJ cm−2) used in this work, Auger recombination could be neglected. Further analysis confirms that the carrier dynamics are mainly dominated by the first and second order mechanisms (detailed in S3, ESI†) and as a result the rate equation is simplified as −dnt/dt = k1nt + k2nt2 with its analytic solution nt = k1n0/[(k2n0 + k1)ek1t − k2n0]. Thus, the TR traces could be analyzed and fitted by −ΔRt/R = bk1n0/[(k2n0 + k1)ek1t − k2n0] to extract the rate constants k1 and k2. For each sample, the fluctuation of the fitted constants at different pump fluences is slight and therefore the average values from all fluences (2–42 μJ cm−2) are used for discussion and summarized in Fig. 2.
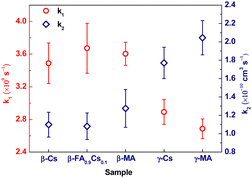 | ||
| Fig. 2 Diffusion rate constant k1 and electron–hole recombination rate constant k2 for various APbI3 films with their phase and A-site cation listed at the horizontal axis. | ||
In LHPs, the first-order decay process observed by transient reflectance/transmittance is usually assigned to Shockley-Reed recombination13 or carrier diffusion.32 The former usually occurs on tens to hundreds of nanoseconds,13 while all the first-order processes observed in this study are on a tens-of-picosecond time scale; therefore, we tentatively assign the first-order decay process to carrier diffusion. And for the second-order depopulation process, electron–hole recombination is suggested to be the main mechanism as proposed in many previous studies.1,13,31,37,38 Thus, k1 and k2 obtained here are the photocarrier diffusion and electron–hole recombination rate constants, respectively. As shown in Fig. 2, both have a strong dependence on the crystal structure phase. Specifically, k1 for three β-phased samples is ∼3.6 × 109 s−1, which decreases to ∼2.8 × 109 s−1 for two γ-phased ones, with an amplitude reduction of ∼20%; while k2 for the β-phased samples is ∼1.1 × 10−10 cm3 s−1, which increases to ∼1.9 × 10−10 cm3 s−1 for the γ-phased ones, with an amplitude growth of almost 2 times.
It should be noted that the observed different carrier behaviours in these five samples originate from their distinctive intrinsic characters, and the impact from extrinsic factors such as grain size is negligible. Firstly, in TR experiments (detailed in S2, ESI†), the diameters of both the pump and probe light are in the millimetre range, while the film thickness is ∼200 nm. As a result, only the longitudinal diffusion along the thickness needs to be considered within 1 ns. Since the majority grain size of all samples, 200–800 nm (Fig. S1(c), ESI†), is larger than the thickness, the monitored diffusion process should not be limited by the grain size. Secondly, the observed recombination is a second-order electron–hole recombination, which occurs mainly within the grains and therefore should not be affected by the grain size.
Discussion
In a lead iodide perovskite, the corner-shared PbI6 octahedrons build up a skeleton or framework with the A-site cations embedding as the limbs. In the low symmetry tetragonal (β) and orthorhombic (γ) crystalline structures, the PbI6 octahedrons show different tilted and distorted levels, as sketched in Fig. 3 and summarized in Table 1. Both experimental studies18,28,39,40 and theoretical predictions19,27,41,42 have suggested that at room temperature the organic–inorganic hybrid MAPbI3 and FA0.9Cs0.1PbI3 are in the β phase. The distorted PbI6 octahedrons are dynamically disordered owing to their anharmonic vibration, and the A-site cations are randomly oriented. Both the distorted PbI6 octahedrons and A-site cations become ordered in the γ phase as the PbI6 octahedrons vibrate harmonically and the organic cations orient regularly. In β-CsPbI3, Cs+ cations are ordered and only the dynamic disorder of the PbI6 octahedrons is still present, which will disappear when the β to γ phase change occurs.8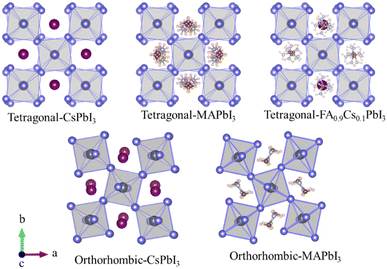 | ||
| Fig. 3 Sketched dynamic crystal structures for β-phased tetragonal CsPbI3, MAPbI3 and FA0.9Cs0.1PbI318,23,27,28 and γ-phased orthorhombic CsPbI3 and MAPbI317,25 perovskites. | ||
In the following, we focus firstly on the carrier recombination process. In the past decade, the key factors dominating the carrier dynamics were extensively explored in LHPs, yet majorly in the organic–inorganic hybrid ones.1,9,13,39,43–49 For example, the bimolecular recombination rate of MAPbI3 was observed to be much smaller in the β-phase than in the γ-phase,1,43 which was proposed to be assisted by the disordered orientation of the organic cations with the apparent fact that the orientation of the MA+ cation is dynamically disordered in β-MAPbI3 but ordered in γ-MAPbI3 (Fig. 3).39,44 Following this supposition, the charge separation model,9,45 polaron model13,46 and others were put forward to explain the underlying physical mechanism. The charge separation model suggested that electrons and holes were separated by the different nanoscale localizations of the conduction and valence band-edges, while the separation efficiency was improved in β-MAPbI3 by the long-range potential fluctuation created by the randomly oriented dipole moment of the A-site organic cation, MA+.9,45 The polaron model proposed that the self-trapped electron (or hole) and the associated atomic displacement formed a polaron,13,46 and the random rotation of MA+ in the β phase would assist the formation of the polaron.47–49 The direct observation of a faster polaron formation process in the disordered cubic and tetragonal phases than in the ordered orthorhombic phase by the time-resolved optical Kerr effect technique50 further strengthened the belief that the disordered A-site orientation was the major factor retarding the bimolecular recombination in LHPs. In summary, those models only took account of the phase dependent orientation of the A-site cations, and completely ignored the order degree of the Pb–I inorganic sublattice in different phases.
The experimental results provided in this study as k2 in Fig. 2 do not agree on the above negligence. Instead, the influence induced by the disorder degree of the A-site cation is found to be much weaker than that by the Pb–I sublattice. In this study, the all-inorganic LHP β-CsPbI3 does not have any organic cation, while the organic–inorganic hybrid LHP β-MAPbI3 carries the disordered organic cations. The experimental results show that they exhibit a similar bimolecular recombination rate, which hints that the orientation of the A-site cations contributes little to the recombination. However, all recombination rates in the β-phase are significantly diverse from those in the γ-phase (Fig. 2). In the γ-phased perovskites, the Pb–I sublattice becomes regularly ordered, and the bimolecular recombination rate is almost 2 times higher than their twin siblings in the β-phase. Therefore, we propose that the disordered Pb–I sublattice is the essential structural factor dominating the recombination process, which also agrees with some previous theoretical studies based on DFT calculations.12,14 Though the charge localization can be induced by both the potential fluctuation created by the randomly oriented dipole moment of the organic cation and the disordered field generated by the anharmonically vibrated Pb–I sublattice, those calculations show that its stabilization is mainly contributed by the latter.12,14 We attribute the greatly different recombination rates in the β- and γ-phased LHPs to their diverse orientation of the distorted PbI6. Since the electron–hole recombination occurs only after the release of charge localization, the stabilized charge localization in the β-phase by mainly the disorderly distorted Pb–I sublattice is unfavorable and therefore retards the recombination process, twice slower than in the γ-phase. As a result, the β-phase may precede the γ-phase in photoconversion by slower recombination.
The dominant influence of the Pb–I sublattice is also presented in the carrier diffusion dynamics as k1 in Fig. 2. We observed experimentally that within the same phase, either β or γ, the carrier diffusion is neck and neck; yet it is prominently, 20%, faster in the β-phased samples than γ-phased ones. This indicates that the carrier diffusion is mainly assisted by the disorderly orientation of the distorted Pb–I sublattice. This influence could be explained by a modified polaron model below. Its original version13,46 was applied to explain the retarded carrier recombination in the disordered β phase as discussed above and here we modified and extended it to carrier mobility described as polaron transport. We propose that the polaron formation and transport benefits from the disordering of distorted PbI6 instead of A-site organic cations in the original model. A recent experimental study51 found that hot carriers diffuse on the hundreds of femtosecond to tens of picoseconds timescale and then slow down consecutively as they cool down. Polarons usually form at a sub-picosecond timescale,46 in competition with the hot carrier cooling process.50 If polarons establish before the carriers cool down, they will inherit partial excess energy, namely hot polarons. Some experimental investigations50,52,53 have already shown that polarons form faster in the disordered phases than in the ordered phases. We suggest that the softness of the Pb–I sublattice in the β-phase is essential to help the formation of the hot polarons and increase their portion in the polaron family. Owing to the higher kinetic energy, the hot polarons will transport faster than the normal polarons.46 Hence, a faster carrier diffusion is observed in the β-phased samples than in the γ-phased ones here. In return, a β-phased sample with organic A-site components may advance in photoconversion by such faster diffusion.
Interestingly, strain relaxation was also suggested to assist the improvement of the power conversion efficiency by suppressing defects and reducing nonradiative recombination in some latest studies.5,6 The dynamically disordered Pb–X sublattice/A-site in the β-phased LHPs, which is softer than the ordered Pb–X sublattice/A-site in the γ-phased ones, is actually a kind of strain relaxation.17 Our study also provides a new perspective for the strain effect as the strain relaxation will both assist photocarrier diffusion and retard electron–hole recombination.
Conclusions
Using the ultrafast TR technique, we found that photoinduced carriers recombined almost 2 times slower and diffused 20% faster in the disordered β-phase than in the ordered γ-phase, both promoting the photoconversion, yet with subtle difference within the same phase. These results demonstrate that the carrier dynamics have a significant dependence on the sample phase but trivial on the A-site component. Such phase dependence is contributed majorly by the distortion property of the Pb–X skeleton and insignificantly by the mobility of the A-site cation limbs. We hope that this study may stimulate further theoretical and structural dynamic experimental studies to understand the contribution of the Pb–X sublattice. For example, the influence of PbX6 distortion on carrier dynamics is worth further investigation, which is pending on the maturation of the fabrication methods for samples in the α phase.Author contributions
H. Z., J. C. and Y. Z. designed the research; Y. W., T. Z. and Y. C. prepared the samples; H. Z. performed the TR research; H. Z. and J. C. analysed the data and wrote the paper; Y. Z. and J. C. supervised the whole work.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors thank Mr Conglong Chen for the discussion of data analysis. This work was supported by the National Natural Science Foundation of China under Grant No. 11704246, 21927809, 51861145101, 21777096 and the Foundation of National Key Laboratory of Shock Wave and Detonation Physics under Grant No. 6142A03182007.Notes and references
- R. L. Milot, G. E. Eperon, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Funct. Mater., 2015, 25, 6218–6227 CrossRef CAS.
- W. Rehman, R. L. Milot, G. E. Eperon, C. Wehrenfennig, J. L. Boland, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Mater., 2015, 27, 7938–7944 CrossRef CAS PubMed.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS.
- Best Research-Cell Efficiency Chart-NREL, https://www.nrel.gov/pv/assets/pdfs/best-research-cell-efficiencies-rev220126.pdf, (accessed 11.10.2022).
- T. W. Jones, A. Osherov, M. Alsari, M. Sponseller, B. C. Duck, Y.-K. Jung, C. Settens, F. Niroui, R. Brenes, C. V. Stan, Y. Li, M. Abdi-Jalebi, N. Tamura, J. E. Macdonald, M. Burghammer, R. H. Friend, V. Bulović, A. Walsh, G. J. Wilson, S. Lilliu and S. D. Stranks, Energy Environ. Sci., 2019, 12, 596–606 RSC.
- G. Kim, H. Min, K. S. Lee, D. Y. Lee, S. M. Yoon and S. I. Seok, Science, 2020, 370, 108–112 CrossRef CAS PubMed.
- A. Maiti and A. J. Pal, Rep. Prog. Phys., 2022, 85, 024501 CrossRef CAS PubMed.
- A. Marronnier, G. Roma, S. Boyer-Richard, L. Pedesseau, J.-M. Jancu, Y. Bonnassieux, C. Katan, C. C. Stoumpos, M. G. Kanatzidis and J. Even, ACS Nano, 2018, 12, 3477–3486 CrossRef CAS PubMed.
- C. Quarti, E. Mosconi and F. De Angelis, Phys. Chem. Chem. Phys., 2015, 17, 9394–9409 RSC.
- Y. Chen, H. T. Yi, X. Wu, R. Haroldson, Y. N. Gartstein, Y. I. Rodionov, K. S. Tikhonov, A. Zakhidov, X. Y. Zhu and V. Podzorov, Nat. Commun., 2016, 7, 12253 CrossRef CAS PubMed.
- S. Dastidar, S. Li, S. Y. Smolin, J. B. Baxter and A. T. Fafarman, ACS Energy Lett., 2017, 2, 2239–2244 CrossRef CAS.
- F. Ambrosio, J. Wiktor, F. De Angelis and A. Pasquarello, Energy Environ. Sci., 2018, 11, 101–105 RSC.
- D. W. deQuilettes, K. Frohna, D. Emin, T. Kirchartz, V. Bulovic, D. S. Ginger and S. D. Stranks, Chem. Rev., 2019, 119, 11007–11019 CrossRef CAS PubMed.
- F. Ambrosio, D. Meggiolaro, E. Mosconi and F. De Angelis, ACS Energy Lett., 2019, 4, 2013–2020 CrossRef CAS.
- Y. W. Woo, Y.-K. Jung, G. Y. Kim, S. Kim and A. Walsh, Discovery Mater., 2022, 2, 8 CrossRef.
- A. Singh, W. Kaiser and A. Gagliardi, Sol. Energy Mater. Sol. Cells, 2021, 221, 110912 CrossRef CAS.
- J. Xu, H. Dong, J. Xi, Y. Yang, Y. Yu, L. Ma, J. Chen, B. Jiao, X. Hou, J. Li and Z. Wu, Nano Energy, 2020, 75, 104940 CrossRef CAS.
- Y. Kawamura, H. Mashiyama and K. Hasebe, J. Phys. Soc. Jpn., 2002, 71, 1694–1697 CrossRef CAS.
- M. A. Carignano, S. A. Aravindh, I. S. Roqan, J. Even and C. Katan, J. Phys. Chem. C, 2017, 121, 20729–20738 CrossRef CAS.
- M. Z. Mayers, L. Z. Tan, D. A. Egger, A. M. Rappe and D. R. Reichman, Nano Lett., 2018, 18, 8041–8046 CrossRef CAS PubMed.
- T. Zhu and E. Ertekin, Energy Environ. Sci., 2019, 12, 216–229 RSC.
- Y. Wang, M. I. Dar, L. K. Ono, T. Zhang, M. Kan, Y. Li, L. Zhang, X. Wang, Y. Yang, X. Gao, Y. Qi, M. Grätzel and Y. Zhao, Science, 2019, 365, 591–595 CrossRef CAS PubMed.
- B. Zhao, S. F. Jin, S. Huang, N. Liu, J. Y. Ma, D. J. Xue, Q. Han, J. Ding, Q. Q. Ge, Y. Feng and J. S. Hu, J. Am. Chem. Soc., 2018, 140, 11716–11725 CrossRef CAS PubMed.
- W. Shi, Y. Wang, T. Zhang, H. Zhang, Y. Zhao and J. Chen, J. Phys. Chem. A, 2019, 123, 2674–2678 CrossRef CAS PubMed.
- Y. Wang, H. Zhang, T. Zhang, W. Shi, M. Kan, J. Chen and Y. Zhao, Sol. RRL, 2019, 3, 1900197 CrossRef.
- R. Prasanna, A. Gold-Parker, T. Leijtens, B. Conings, A. Babayigit, H. G. Boyen, M. F. Toney and M. D. McGehee, J. Am. Chem. Soc., 2017, 139, 11117–11124 CrossRef CAS PubMed.
- D. Ghosh, A. R. Smith, A. B. Walker and M. S. Islam, Chem. Mater., 2018, 30, 5194–5204 CrossRef CAS.
- S. Kawachi, M. Atsumi, N. Saito, N. Ohashi, Y. Murakami and J. I. Yamaura, J. Phys. Chem. Lett., 2019, 10, 6967–6972 CrossRef CAS PubMed.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- C. Quarti, E. Mosconi, J. M. Ball, V. D’Innocenzo, C. Tao, S. Pathak, H. J. Snaith, A. Petrozza and F. De Angelis, Energy Environ. Sci., 2016, 9, 155–163 RSC.
- J. S. Manser and P. V. Kamat, Nat. Photonics, 2014, 8, 737–743 CrossRef CAS.
- Y. Yang, Y. Yan, M. Yang, S. Choi, K. Zhu, J. M. Luther and M. C. Beard, Nat. Commun., 2015, 6, 7961 CrossRef CAS PubMed.
- K. M. Sim, A. Swarnkar, A. Nag and D. S. Chung, Laser Photonics Rev., 2018, 12, 1700209 CrossRef.
- H. W. Chen, D. P. Gulo, Y. C. Chao and H. L. Liu, Sci. Rep., 2019, 9, 18253 CrossRef CAS PubMed.
- H. Fujiwara, M. Kato, M. Tamakoshi, T. Miyadera and M. Chikamatsu, Phys. Status Solidi A, 2018, 215, 1700730 CrossRef.
- B. Subedi, L. Guan, Y. Yu, K. Ghimire, P. Uprety, Y. Yan and N. J. Podraza, Sol. Energy Mater. Sol. Cells, 2018, 188, 228–233 CrossRef CAS.
- C. La-O-Vorakiat, T. Salim, J. Kadro, M. T. Khuc, R. Haselsberger, L. Cheng, H. Xia, G. G. Gurzadyan, H. Su, Y. M. Lam, R. A. Marcus, M. E. Michel-Beyerle and E. E. Chia, Nat. Commun., 2015, 6, 7903 CrossRef CAS PubMed.
- N. Mondal and A. Samanta, Nanoscale, 2017, 9, 1878–1885 RSC.
- M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183 RSC.
- G. Schuck, D. M. Többens, M. Koch-Müller, I. Efthimiopoulos and S. Schorr, J. Phys. Chem. C, 2018, 122, 5227–5237 CrossRef CAS.
- W. Geng, L. Zhang, Y.-N. Zhang, W.-M. Lau and L.-M. Liu, J. Phys. Chem. C, 2014, 118, 19565–19571 CrossRef CAS.
- M. A. Pérez-Osorio, Q. Lin, R. T. Phillips, R. L. Milot, L. M. Herz, M. B. Johnston and F. Giustino, J. Phys. Chem. C, 2018, 122, 21703–21717 CrossRef.
- E. M. Hutter, M. C. Gelvez-Rueda, A. Osherov, V. Bulovic, F. C. Grozema, S. D. Stranks and T. J. Savenije, Nat. Mater., 2017, 16, 115–120 CrossRef CAS PubMed.
- T. Baikie, N. S. Barrow, Y. Fang, P. J. Keenan, P. R. Slater, R. O. Piltz, M. Gutmann, S. G. Mhaisalkar and T. J. White, J. Mater. Chem. A, 2015, 3, 9298–9307 RSC.
- J. Ma and L. W. Wang, Nano Lett., 2015, 15, 248–253 CrossRef CAS PubMed.
- P. P. Joshi, S. F. Maehrlein and X. Zhu, Adv. Mater., 2019, 31, 1803054 CrossRef CAS PubMed.
- T. Etienne, E. Mosconi and F. De Angelis, J. Phys. Chem. Lett., 2016, 7, 1638–1645 CrossRef CAS PubMed.
- F. Zheng, L. Z. Tan, S. Liu and A. M. Rappe, Nano Lett., 2015, 15, 7794–7800 CrossRef CAS PubMed.
- X. Y. Zhu and V. Podzorov, J. Phys. Chem. Lett., 2015, 6, 4758–4761 CrossRef CAS PubMed.
- H. Zhu, K. Miyata, Y. Fu, J. Wang, P. P. Joshi, D. Niesner, K. W. Williams, S. Jin and X.-Y. Zhu, Science, 2016, 353, 1409–1413 CrossRef CAS PubMed.
- Z. Guo, Y. Wan, M. Yang, J. Snaider, K. Zhu and L. Huang, Science, 2017, 356, 59–62 CrossRef CAS PubMed.
- S. A. Bretschneider, I. Ivanov, H. I. Wang, K. Miyata, X. Zhu and M. Bonn, Adv. Mater., 2018, 30, 1707312 CrossRef PubMed.
- T. J. S. Evans, K. Miyata, P. P. Joshi, S. Maehrlein, F. Liu and X. Y. Zhu, J. Phys. Chem. C, 2018, 122, 13724–13730 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh01212j |
| This journal is © The Royal Society of Chemistry 2023 |