Eco-friendly inorganic molecular novel antiperovskites for light-emitting application

Abstract

The development of perovskite light-emitting diodes (PeLEDs) has progressed rapidly over the past several years, with high external quantum efficiencies exceeding 20%. However, the deployment of PeLEDs in commercial devices still faces severe challenges, such as environmental pollution, instability and low photoluminescence quantum yields (PLQYs). In this work, we perform high-throughput calculations to exhaustively search the unexplored and eco-friendly novel antiperovskite space (formula: X₃B[MN₄], with octahedron [BX₆] and tetrahedron [MN₄]). The novel antiperovskites have a unique structure whereby a tetrahedron can be embedded into an octahedral skeleton as a light-emitting center causing a space confinement effect, leading to the characteristics of a low-dimensional electronic structure, which then makes these materials potential light-emitting material candidates with a high PLQY and light-emitting stability. Under the guidance of newly derived tolerance, octahedral, and tetrahedral factors, 266 stable candidates are successfully screened out from 6320 compounds. Moreover, the antiperovskite materials Ba₃I_0.5F_0.5(SbS₄), Ca₃O(SnO₄), Ba₃F_0.5I_0.5(InSe₄), Ba₃O_0.5S_0.5(ZrS₄), Ca₃O(TiO₄), and Rb₃Cl_0.5I_0.5(ZnI₄) possess an appropriate bandgap, thermodynamic and kinetic stability, and excellent electronic and optical properties, making them promising light-emitting materials.

---

New concepts

Metal halide perovskites (MHPs) have proved to be promising candidates for light-emitting application, while the development of perovskite light-emitting diodes (PeLEDs) has progressed rapidly over the past several years, reaching high external quantum efficiencies of over 20%. However, the large-scale commercial applications of perovskites are impeded by low stability and toxicity. Novel antiperovskites (X₃B[MN₄]) are actually electronically inverted perovskite derivatives, inheriting the flexible structural features of perovskites while being rich in cations at the X and [MN₄] sites, and exhibiting a diverse array of subtle physical and chemical properties. This work proposes a series of lead-free antiperovskites (LFAPs) with versatile inorganic molecules in the cuboctahedral spaces, producing a unique structure whereby a tetrahedron can be embedded into an octahedral skeleton as a light-emitting center causing a space confinement effect, leading to the characteristics of a low-dimensional electronic structure, which then makes these materials potential light-emitting material candidates. Furthermore, the dominating colour gamut of the LFAPs can be tuned over the visible light range with respect to the composition change caused by engineering of the octahedra and tetrahedra. On the basis of these advantages, LFAPs may serve as a highly efficient and stable light-emitting material, while overcoming some known challenging issues inherent in PeLEDs.

1. Introduction

Metal halide perovskites (MHPs) have gained extensive attention because of their rapid progress in the photovoltaic field.^1,2 In a short period, perovskite solar cells have exceeded a power conversion efficiency of 25%.^3,4 In addition to their superior photovoltaic properties, halide perovskites also exhibit excellent optoelectronic properties suitable for light-emitting diodes (LEDs),⁵ such as high PLQYs, a tunable bandgap, a narrow emission width, and high carrier mobility. Notably, the perovskite light-emitting diodes (PeLEDs) reported in recent years have undergone vigorous development, especially in the green and near-infrared regions.^6–13 To gain these desired red and blue colors, the halogens of the perovskites are mixed to well-adjust the bandgaps of perovskite emissive layers, causing the instability problem of phase segregation. Additionally, the large-scale commercialization of PeLEDs is still impeded by toxicity originating from the heavy metal lead.^14,15 Recent reports have indicated that the toxicity of lead has significant negative effects on the population growth of worldwide wild animals, being a developmental neurotoxicant, and the average lead-linked loss in cognitive ability was 2.6 IQ points per person exposed to high-lead levels in early childhood.^16,17 To address these concerns of toxicity, post-conduction metal ions with similar valence electron configurations (ns²np²) to those of lead have attracted extensive attention in the perovskite community, leading to the discovery of several candidates as light-emitting materials, such as ASnI₃ (A = methylammonium (MA), formamidinium (FA), Cs) and Cs₂BB′X₆ (B = In, Tl, Ag, Sn; B′ = Sb, Bi, Ge; X = Cl, Br, I).^5,18 Chao et al. reported CsSnI₃-based efficient low-temperature solution-processed lead-free PeLEDs.¹⁰ Tang et al. described the efficient and stable emission of warm-white light from the lead-free perovskites Cs₂(Ag_0.60Na_0.40)InCl₆.¹³ Despite rapid development in lead-free PeLEDs, there are still various crucial challenges, such as oxidation, device degradation, large indirect bandgaps, poor visible absorption, and low PLQYs.

To overcome the current limitations, their counterpart, antiperovskites,¹⁹ with the chemical formula X₃BA as actually electronically inverted perovskite derivatives, provide another interesting material design strategy.^19,20 Analogous to the prototype perovskite, the advantage of antiperovskites is their flexible structural features. The compositions can vary with the X-site cations, and B- and A-site anions, using different simple ions or complex molecular ions. The structure can also be deformed, through displacements and rotations of the atomic building blocks, which leads to an extended family of lower-symmetry polymorphs. Han et al. reported an excellent design of antiperovskites, leading to a series of potential antiperovskite photovoltaic materials.²¹ In addition, some interesting designs of antiperovskites have also undergone rapid development in related fields.^19,22,23

The A cation in ABX₃ perovskites occupying the cuboctahedral spaces is conventionally believed to hardly affect their optoelectronic properties. However, recent developments have uncovered that the versatility of the A cation enables regulation of the physicochemical and optoelectronic properties of perovskites.²⁴ The critical role of the A cation in perovskites has been rethought in the perovskite community. These works also inspired reconsideration of the role of the A anion in X₃BA antiperovskites. Furthermore, the A site can be filled by complex inorganic molecular anions such as [MN₄], which could significantly expand the compositional space and improve tunability. Interestingly, Wang et al. recently reported LEDs based on antiperovskites with [MnX₄] (X = Cl, Br, I) anions, demonstrating the promising potential of this class of materials for light-emitting application.²⁵ How does the versatility of the A anion influence the optoelectronic properties of antiperovskites? Another very interesting question is whether antiperovskites, as a derivative of electron reverse perovskites, also have potential applications as PeLEDs. Due to their local carriers and soft lattices, low dimensional perovskites generally exhibit broadband and white light emissions usually originating from self-trapped excitons (STEs).^5,13,26,27 Compared with the typical perovskite, despite the three-dimensional crystal structure of the novel antiperovskites X₃B[MN₄], [MN₄] anions are separated by a three-dimensional octahedral skeleton [BX₆], leading to low electronic dimensionality.^19,28,29 The octahedron of one dimensional perovskites is often separated by a large organic spacer,^30,31 leading to strong dielectronic and quantum confinement effects.³² The electronic structure of antiperovskites X₃B[MN₄] exhibits a similar dispersion profile around the band edges with respect to that of a one dimensional perovskite, demonstrating that the space separated luminescence center [MN₄] contributes to the flat bands around the band edges and that novel antiperovskites X₃B[MN₄] possess low electronic dimensionality due to a similar confinement effect. Owing to the space confinement effect, these unique structures can show significantly improved exciton binding energies and the localized formation of electron–hole pair, endowing these materials with higher PLQYs and light-emitting color stability.

In this study, we exhaustively search the unexplored and eco-friendly novel antiperovskite space and identify 49 stable novel lead-free antiperovskites (LFAPs) that have potential application in PeLEDs. We focus on two new classes of inorganic molecular antiperovskites with the formulas of X₃B[MN₄] and 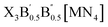. On the basis of the perovskite network and A-site inorganic molecule of antiperovskites, the tetrahedral factor, octahedral factor and Goldschmidt tolerance factor are deduced to estimate the formability of the inorganic molecular antiperovskites so that 266 LFAP compounds are screened out from 6320 compounds. Then, through a series of high-throughput first-principles calculations, the bandgaps of the corresponding compounds are gained, leading to 49 inorganic molecular antiperovskites with criteria targeting specific photoelectric properties. Moreover, based on the thermodynamic and kinetic stability and properties of excited states, we have predicted that Ba₃I_0.5F_0.5(SbS₄), Ca₃O(SnO₄), Ba₃F_0.5I_0.5(InSe₄), Ba₃O_0.5S_0.5(ZrS₄), Ca₃O(TiO₄), and Rb₃Cl_0.5I_0.5(ZnI₄) LFAPs are promising light-emitting materials.

2. Results and discussion

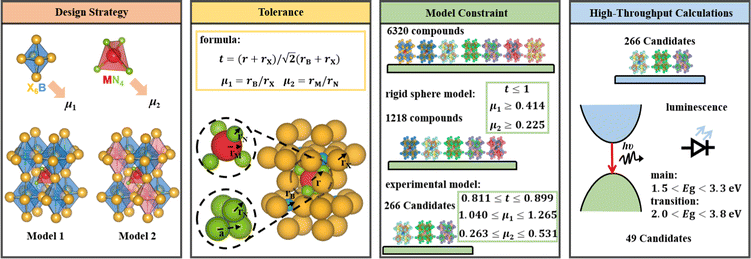
2.1. Design strategy of LFAPs with formulas of X₃B[MN₄] and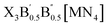

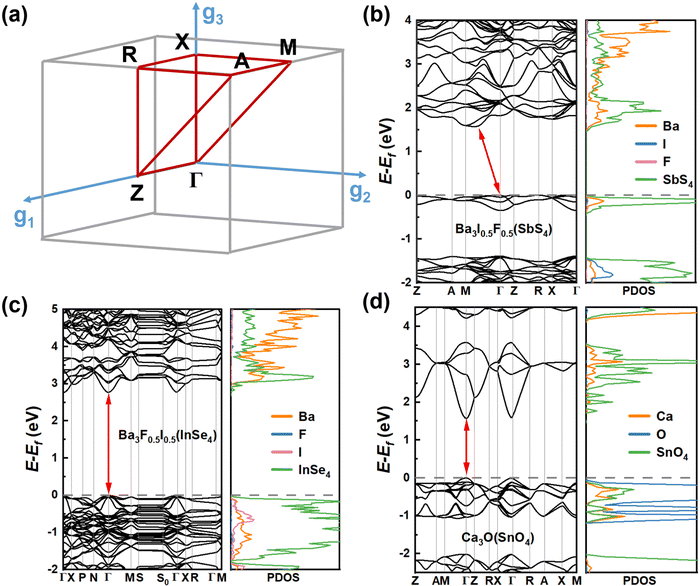
The crystal structures of the LFAPs with a chemical formula of X₃B[MN₄] were considered, where X₃B is the octahedral part (X is the octahedral vertex cation, B is the octahedral central anion) and MN₄ is the tetrahedral part (M is the tetrahedral central cation, N is the tetrahedral vertex anion) (Fig. 1(a)). These crystal structures are capable of forming a tetragonal phase with space group I4/mcm symmetry. The corner-sharing octahedral cells comprise a B-site central anion surrounded by six X-site cations twisted along the (001) direction to form a 3D twisted network structure at the molecular level. Meanwhile, analogous to the mixed perovskites, mixed LFAPs with a chemical formula of 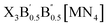were also considered in this study, where B → B′ + B′′. Since the cuboctahedral spaces of LFAPs are occupied by a tetrahedron instead of the single anion in the traditional antiperovskites, the versatility of the tetrahedron can improve the tunability of the related antiperovskite material.

Fig. 1 (a) Structural diagrams of the new antiperovskites. (b) Element selection in structural design strategy.

As well as the significant transfer of knowledge from conventional perovskites, LFAPs are capable of their own peculiarities and complexities. In this study, there are four classes of combinations of formal oxidation states of the constituent ions, as shown in Table S1 (ESI†). For instance, when a metal cation with a +1 oxidation state occupies the M-site, there are anions with −1 and −3 oxidation states, and a metal cation with a +2 oxidation state respectively occupying the corners of the tetrahedron (N-site), the corners of the octahedron (X-site) and the center of the octahedron (B-site), to maintain the electronic neutrality of the compound. Considering the environmental eco-friendliness of the compounds, the corresponding elements in the periodic table are displayed in Fig. 1(b).

An empirical method to assess the formability of perovskite ABX₃ was proposed by Goldschmidt about a century ago.³³ In this approach, the perovskite structure is described as a collection of rigid spheres whose size is determined by the constituent ionic radii. These radii can be combined into two dimensionless descriptors, the Goldschmidt tolerance factor t₀ and octahedral factor μ₀. Based on Pauling's rules, perovskites should be arranged in such a way that “the number of anions around the cation tends to be as large as possible under the condition that all anions are in contact with the cation”. This statement constitutes the “no microperturbation” principle and limits the range of values for t₀ and μ₀ that can be used to empirically assess the formability of perovskites.^34–36 Analogously, antiperovskites possess the same crystal structure as perovskites,^19,37 therefore owing to the principle of maximum contact and no small disturbance principle, the tolerance factor t, octahedral factor μ₁ and tetrahedral factor μ₂ are also suitable to assess the formability of antiperovskites.¹⁹ According to the rigid sphere model, the constraint ranges of the related factors are t ≤ 1, 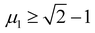, 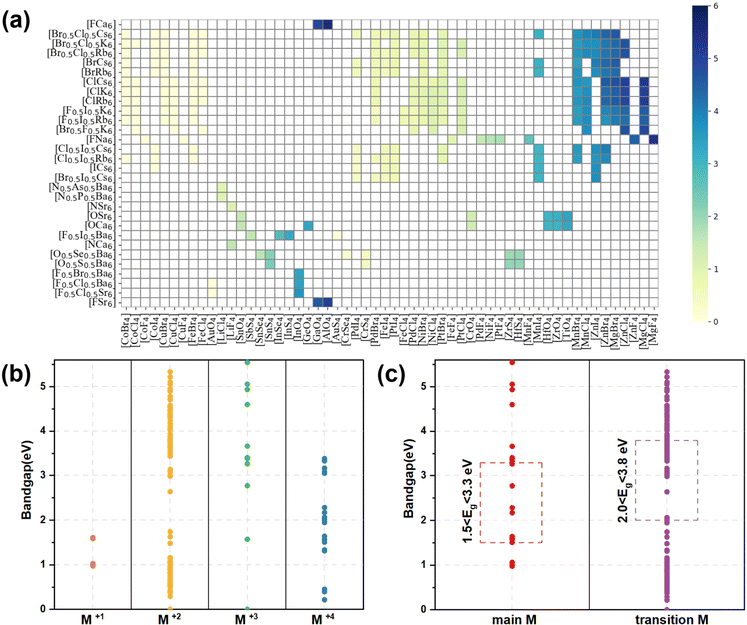and 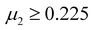, and 1218 compounds were extracted from a candidate space of 6320 compounds complying with the electronic neutrality of LFAPs. To further improve the reliability of the rigid sphere model, the constraint ranges were strengthened by the experimental parameters (0.811 ≤ t ≤ 0.899, 1.040 ≤ μ₁ ≤ 1.265 and 0.263 ≤ μ₂ ≤ 0.5321 (see ESI† for details). Therefore, 266 compounds were predicted as potential stable compounds based on the more accurate constraints originating from experimental data (Fig. 2).

Fig. 2 The screening framework of the LFAP materials with the rigid sphere model and bandgaps of these compounds.

2.2. High throughput calculations and screening with bandgaps

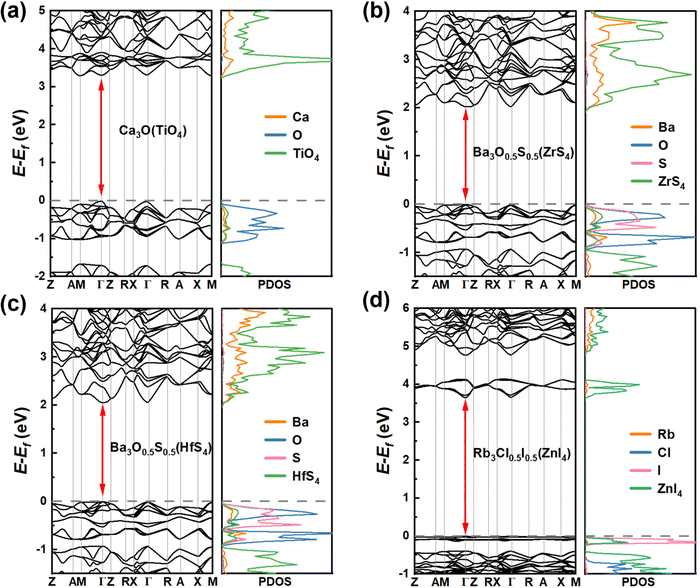
The bandgap distribution of all 266 candidates (see ESI† for details, data1) is displayed according to their combination of tetrahedron and octahedron in Fig. 3(a). It can be seen that most of the squares are white in color, implying that these compounds consisting of the corresponding octahedrons and tetrahedrons are unstable due to the aforementioned empirical factors. The rest of the squares stem from the stable compounds according to the constraint ranges, exhibiting gradual color changes from pale yellow to dark blue and indicating the flexible tunability of bandgaps of these compounds in the range of 0–6 eV. Especially, the octahedron centers are occupied by elements in the main groups VA, VIA and VIIA, while the corners of the octahedron are occupied by alkali metal and alkaline earth elements. In contrast, the elements of the tetrahedral center are widely distributed, including main group elements and transition metal elements and the corners of tetrahedron are mostly occupied with halogens and chalcogens. Owing to the diversity of constituent elements of the tetrahedron, the bandgaps of these compounds gradually increase, whereas the bandgaps are only slightly affected by changes in the octahedra, implying that the band-edge states of the compounds are mostly contributed by the tetrahedrons, rather than the octahedrons (see Fig. 3(a)).

Fig. 3 (a) The bandgap (obtained using the SCAN functional) distribution of all 266 candidates composed of a tetrahedron and octahedron. (b) Band gap distributions of the 266 candidates classified according to the valence states of the tetrahedral center M ions. M(I), M(II), M(III), and M(IV) represent the +1, +2, +3, and +4 valence states of the M cations, respectively. (c) The band gap distribution of the 266 candidates; red and purple represent the tetrahedral center M of main group metals and transition metal elements, respectively.

According to the formal oxidation state of the M-site cation at the tetrahedral centers, we can divide these compounds into four categories, and the corresponding distributions of bandgaps are shown in Fig. 3(b). There are only 4 compounds with M(I) at the tetrahedral centers and their bandgaps are in the range of 1–2 eV. Interestingly, owing to the stable +2 valence states of most of the metal ions, there are 227 compounds with the M(II) cation at the tetrahedral centers, resulting in a wide distribution of bandgaps between 0 and 5.5 eV. When the M cation has +3 and +4 valence states, there are 14 and 21 compounds with the respective M(III) and M(IV) cation at the tetrahedral centers. The bandgap distribution of the compounds with M(III) is discrete and most of the compounds with wide bandgaps exhibit electronic properties of insulators, whereas the bandgap distribution of compounds with M(IV) is mostly below 3.5 eV, leading to electronic properties of semiconductors. Notably, most compounds contain transition metal elements (245) and only 21 compounds contain main group elements. It can be seen that the compounds containing main group elements only exhibit properties of semiconductors and insulators, whereas compounds containing transition metal elements, exhibit electronic properties of metals, semiconductors, and insulators. The transition metal compounds with bandgaps in the range of 2.0–3.8 eV were further assessed as potential light-emitting materials. Due to the underestimation (about 20%, see Table S3, ESI†) of bandgaps between the strongly constrained and appropriately normed (SCAN) and Perdew–Burke–Ernzerhof (PBE) functionals, compounds comprising only main group elements with bandgaps in the range of 1.5–3.3 eV were selected as potential light-emitting materials (see Fig. 3(c)). Preliminarily, based on the empirical formability and bandgaps, 49 LFAPs were screened as candidates for light-emitting application (see Table S4, ESI†). It can be seen that there are only 9 different metal ions at the tetrahedral centers in the 49 candidates, including 4 main group elements, Sn, Sb, Li, and In, and 5 transition elements, Ti, Zr, Hf, Zn, and Mn. Among the candidates, the compounds with Mn exhibit similar crystal structures with a reported light-emitting material from previous experimental work,²⁸ and they are not further discussed in this study. In the novel antiperovskites, due to the spatial restriction effect caused by the octahedral skeleton, the tetrahedrons are separated to form benign luminous centers. Note that the metal elements at the tetrahedral center mostly contribute the band edge states, thereby dominating the optoelectronic properties of the antiperovskites. 8 candidates, (Ca₃N(LiF₄), Ba₃F_0.5I_0.5(SbS₄), Ca₃O(SnO₄), Ba₃F_0.5I_0.5(InSe₄), Ba₃O_0.5S_0.5(ZrS₄), Ba₃O_0.5S_0.5(HfS₄), Ca₃O(TiO₄), and Rb₃Cl_0.5I_0.5(ZnI₄)), which contain all the different metal ions at the tetrahedral centers, were selected to further estimate their stability and optoelectronic properties.

2.3. Stability and electronic properties of LFAPs with suitable bandgaps

To accurately estimate the thermodynamic and kinetic stabilities, we performed ab initio molecular dynamics (AIMD) simulations and calculations of phonon dispersion along the high-symmetry lines in the first Brillouin zone of these 8 candidates. From Fig. S2 (ESI†), it can be seen that the eight candidates exhibit different kinetic stabilities. There is no appreciable imaginary frequency in the phonon spectra of Ba₃F_0.5I_0.5(InSe₄), Ba₃O_0.5S_0.5(ZrS₄), and Ba₃O_0.5S_0.5(HfS₄), suggesting excellent kinetic stabilities of the three materials. In addition, note that some small virtual modes are a common feature of the perovskite structure,^38,39 and this has been confirmed by both experiments⁴⁰ and theoretical calculations.⁴¹ Although Ca₃O(TiO₄), Ba₃F_0.5I_0.5(SbS₄), and Ca₃O(TiO₄) have very small imaginary modes (<0.3 THz), these candidates are considered as kinetically stable materials. The temperature-dependent phonon spectra of Ba₃F_0.5I_0.5(InSe₄) were computed and the imaginary frequency was effectively eliminated with increasing temperature (see Fig. S3a and b, ESI†). However, for the candidates Ca₃O(SnO₄) and Ca₃O(TiO₄), though the imaginary frequency was not effectively eliminated with temperature, stable phases of Ca₃O(SnO₄) and Ca₃O(TiO₄) are still expected to exist due to the stable region of related compounds in their phase diagrams (see Fig. S3c and d, ESI†). Unfortunately, due to a very large number of imaginary frequencies, Ca₃N(LiF₄) was excluded. The AIMD simulations revealed that the seven candidates with kinetic stabilities reached thermodynamically stable states after 0.5 ps (see Fig. S2, ESI†). Along with the evolution of temperature and total energy, the inorganic frameworks of these candidates were well sustained in the final configuration with the network of corner-sharing octahedrons, suggesting that these candidates have robust thermodynamic stability.

To get insight into the optoelectronic properties, we further computed the band structures and projected density of states (PDOS) of the seven candidates (Fig. 4, 5 and Fig. S6, ESI†). Note that there are four transition metal compounds, while three candidates are only composed of main group elements. Ba₃I_0.5F_0.5(SbS₄), Ba₃F_0.5I_0.5(InSe₄), and Ca₃O(SnO₄) were first considered in this study. It can be seen that, analogous to double perovskites,⁴² both Ba₃F_0.5I_0.5(SbS₄) and Ba₃F_0.5I_0.5(InSe₄) possess similar double perovskite crystal structures and constituting ions, except for the different metal ions at the tetrahedral centers, implying a certain similarity of their electronic properties. Ba₃F_0.5I_0.5(SbS₄) has an indirect bandgap of 1.96 eV according to the Heyd–Scuseria–Ernzerhof 06 (HSE06) functional (see Fig. S4, ESI†), in which the valence band maximum (VBM) is located at the Γ point and the conduction band minimum (CBM) is located between the Γ point and M point (see Fig. 4(b)). From the PDOS and spatial distribution of charge density of the VBM and CBM, it is clear that the VBM of Ba₃F_0.5I_0.5(SbS₄) is contributed by S p and Sb s orbitals of the SbS₄ tetrahedron, while the CBM is contributed by S p and Sb p orbitals of the SbS₄ tetrahedron (see Fig. S5, ESI†). Ba₃F_0.5I_0.5(InSe₄) has a direct bandgap of 3.31 eV according to the HSE06 functional (see Fig. S4, ESI†), in which the VBM and the CBM are located at the Γ point (Fig. 4(c)). Analogous to Ba₃F_0.5I_0.5(SbS₄), both the VBM and CBM are mostly contributed by tetrahedrons, respectively contributed by the Se p orbitals and hybrid orbital of In s and Se p orbitals of the InSe4 tetrahedron (see Fig. S5, ESI†). For Ba₃F_0.5I_0.5(SbS₄) and Ba₃F_0.5I_0.5(InSe₄), the band edge states mostly originate from separated tetrahedrons embedded in the corner-sharing octahedral network, leading to a flat band dispersion and exhibiting a low-dimensional electronic property, which is beneficial for exciton binding and luminescence. Interestingly, Ca₃O(SnO₄) has a direct bandgap of 2.55 eV according to the HSE06 functional (see Fig. S4, ESI†), in which the VBM and the CBM are located at the Γ point, as shown in Fig. 4(d). The VBM is mostly contributed by the O p orbitals of the octahedral center, while the CBM is contributed by the O p and Sn s orbitals of the tetrahedron (see Fig. S5, ESI†). The band edge states of Ca₃O(SnO₄) are contributed by different components, implying that the LFAPs have more flexible tunability than the traditional perovskite compounds, in which the band edge states are only contributed by the octahedron. This shows that a synergy of the tetrahedron and octahedron can have a certain effect on the optoelectronic properties of LFAP materials.

Fig. 4 (a) The gray area is the Brillouin zone and the band structure of the majority of candidates was computed along the red path. Band structures and PDOS obtained by using the SCAN functional for the 3 candidates of (b) Ba₃I_0.5F_0.5(SbS₄), (c) Ba₃F_0.5I_0.5(InSe₄), and (d) Ca₃O(SnO₄).

Fig. 5 Band structures and PDOS obtained using the SCAN functional of the 4 candidates of (a) Ca₃O(TiO₄), (b) Ba₃O_0.5S_0.5(ZrS₄), (c) Ba₃O_0.5S_0.5(HfS₄), and (d) Rb₃Cl_0.5I_0.5(ZnI₄).

Note that the metal elements at the tetrahedral centers in the transition metal compounds, Ca₃O(TiO₄), Ba₃O_0.5S_0.5(ZrS₄) and Ba₃O_0.5S_0.5(HfS₄), are localized in the IVB group. Among them, it is obvious that Ca₃O(TiO₄) exhibits different electronic properties from Ba₃O_0.5S_0.5(ZrS₄) and Ba₃O_0.5S_0.5(HfS₄), which possess similar double perovskite crystal structures and constituting ions. Ca₃O(TiO₄) has a direct bandgap of 3.306 eV according to the SCAN functional, in which the VBM and the CBM are located at the Γ point (see Fig. 5(a)) and the VBM is contributed by the O p orbitals of the octahedral center, whereas the CBM is contributed by O p orbitals of the TiO₄ tetrahedron. Interestingly, both Ba₃O_0.5S_0.5(ZrS₄) and Ba₃O_0.5S_0.5(HfS₄) exhibit direct bandgaps of about 2 eV, according to the SCAN functional, and their VBM and CBM are located at the Γ point (see Fig. 5(b) and (c)). The VBMs are contributed by the O p and S p orbitals of the octahedral center, while the CBM is contributed by S p orbitals of the MS₄ (M = Zr or Hf) tetrahedron (see Fig. S5, ESI†). It can be seen that Ba₃O_0.5S_0.5(ZrS₄) and Ba₃O_0.5S_0.5(HfS₄) exhibit similar electronic structures, due to Zr and Hf having a similar valence electron configuration. Rb₃Cl_0.5I_0.5(ZnI₄) has a direct bandgap of 3.653 eV according to the SCAN functional and the VBM and the CBM are located at the Γ point (see Fig. 5(d)). The VBM is contributed by the I p orbitals of the octahedral center and the CBM is contributed by the Zn s and I p orbitals of the ZnI₄ tetrahedron (see Fig. S5, ESI†). Though the candidates have three dimensional crystal structures, their electronic structures with flat valence bands inevitably exhibit certain low-dimensional properties, leading to a strong space confinement effect and strong binding of excitons, implying that they are ideal candidates for light-emitting application.

For metal halide perovskites, radiative recombination can be bimolecular or excitonic. Owing to the small exciton binding energies close to the room-temperature thermal energy, excitons in three-dimensional perovskites readily dissociate into free charge carriers, therefore bimolecular recombination dominates in radiative recombination. In this study, the exciton binding energies were calculated to assess the mechanisms of radiative recombination for these candidates (Table 1). The binding strength of excitons in semiconductors is evaluated using the binding energy of excitons, and the binding energy of excitons for the 7 candidate materials was calculated according to the Wannier model.⁴³ Exciton binding energy is defined as E_b = μe⁴/2ℏ²ε_∞², where ε_∞ and μ are the high frequency dielectric constant and reduced effective mass, respectively. 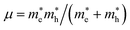.⁴⁴ The average effective mass and the three tensors related to the three orientations are shown in Table 1 and Table S5 (ESI†), respectively. It is obvious that the exciton binding energies of these candidates are significantly larger than the room-temperature thermal energy, implying that excitonic recombination may be dominant in the radiative recombination processes of the LFAPs, in which excitons can undergo radiative decay to emit relatively broadband and white light emission. Furthermore, our simulations of the excited states show a strong spatial localization of electron–hole pairs. The distributions of the electron–hole pairs are localized in the same polyhedron in Fig. S7a and b (ESI†) or concentrated on the adjacent tetrahedrons and octahedrons in Fig. S7c–e, g (ESI†). Candidates with localized excitons and low electronic dimensionality are expected to have similar luminescence properties with respect to low-dimensional perovskites, instead of directly forming STE. Unfortunately, due to the delocalized excitons, which suppress luminescence for Ba₃O_0.5S_0.5(HfS₄), we excluded this candidate (Fig. S7f, ESI†).

Table 1 Computed bandgap (E_g) values of Ba₃F_0.5I_0.5(SbS₄), Ba₃F_0.5I_0.5(InSe₄), and Ca₃O(SnO₄) with the HSE06 functional and Ca₃O(TiO₄), Ba₃O_0.5S_0.5(ZrS₄), Ba₃O_0.5S_0.5(HfS₄), and Rb₃Cl_0.5I_0.5(ZnI₄) with the SCAN functional. Computed electron (m_e) and hole (m_h) effective masses (averaged quantity) with the SCAN function. m₀ stands for electron rest mass. Computed exciton binding energy (E_b), optical bandgap (E_opt), and emission energy (E_PL). Wavelength corresponds to the emission energy (E_PL)

System	E g (eV)	m e (m0)	m h (m0)	E b (meV)	E opt (eV)	E PL (eV)	Wavelength (nm)
Ba3F0.5I0.5(SbS4)	1.96	0.78	2.18	144.63	1.82	1.77	690.3 (red)
Ba3F0.5I0.5(InSe4)	3.31	0.56	0.47	80.65	3.23	3.16	392.5 (blue-violet)
Ca3O(SnO4)	2.55	0.41	1.97	226.00	2.32	2.16	572.9 (yellow)
Ca3O(TiO4)	3.31	1.73	1.32	487.71	2.82	2.67	464.7 (blue)
Ba3O0.5S0.5(ZrS4)	2.02	1.70	1.56	259.52	1.76	1.67	744.6 (red)
Ba3O0.5S0.5(HfS4)	2.02	1.33	1.50	244.20	1.78	—	—
Rb3Cl0.5I0.5(ZnI4)	3.65	0.47	5.77	402.95	3.25	3.12	397.3 (blue-violet)

---

2.4. Excited state properties of LFAPs as light-emitting materials

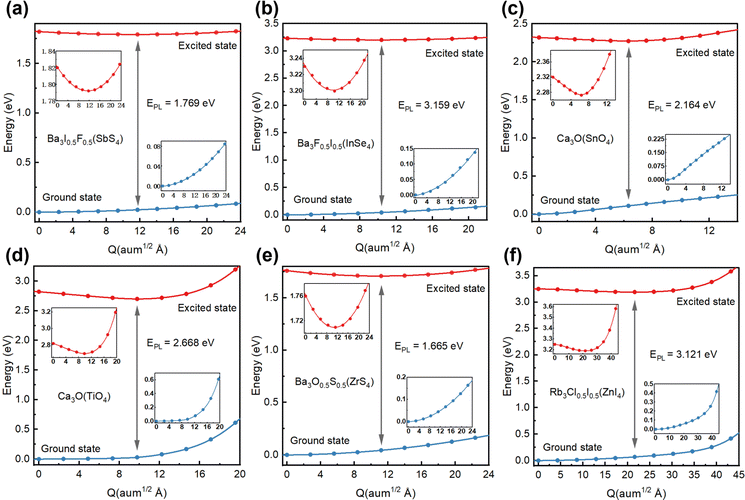
Considering the excitonic radiative recombination, we estimated the dominant color of emission light based on the emission energies of these candidates. By linear interpolation between the equilibrium structures of the ground state and the excited state, and calculating the two state energies of each obtained structure, we constructed a configuration coordinate diagram (CCD), as shown in Fig. 6. The initial energy of the excited state of each structure is the optical band gap.²⁷ We estimated the emission energy E_PL (Table 1) for each candidate. It can be seen that Ba₃I_0.5F_0.5(SbS₄) with an E_PL of 1.769 eV and wavelength of 690.3 nm emits red light (Fig. 6(a)). The excited state electrons and holes are both localized on the SbS₄ tetrahedron (Fig. S7a, ESI†). The tetrahedron is isolated by the larger octahedron, which significantly enhances the electron–hole interaction. Therefore, Ba₃I_0.5F_0.5(SbS₄) with a three-dimensional crystal structure possesses zero-dimensional electronic properties, similar to a zero-dimensional perovskite with Sb as the light-emitting center, which has been reported to emit red light with a wavelength of about 710 nm,³⁰ demonstrating their intrinsic similarity in electronic structures. Analogously, Ba₃F_0.5I_0.5(InSe₄) with an E_PL of 3.159 eV and wavelength of 392.5 nm emits blue-violet light (Fig. 6(b)), exhibiting similar optoelectronic properties and origin of the emission center (Fig. S7b, ESI†), because of the similar valence configuration of Sb and In. Ca₃O(SnO₄) with an E_PL of 2.164 eV and wavelength of 572.9 nm emits yellow light (Fig. 6(c)). Its distributions of excited state electrons and holes are respectively localized on an adjacent [Ca₆O] octahedron and [SnO₄] tetrahedron, resulting in strong coupling of electrons and holes (Fig. S7c, ESI†). The electron–phonon coupling caused by structural distortion will promote the formation of an effective recombination center. Interestingly, Ca₃O(TiO₄), with an E_PL of 2.668 eV and wavelength of 464.7 nm, emits blue light (Fig. 6(d)), with excited state electrons and holes localized on an adjacent [Ca₆O] octahedron and [TiO₄] tetrahedron (Fig. S7d, ESI†), leading to similar excited state characteristics to those of Ca₃O(SnO₄). Ba₃O_0.5S_0.5(ZrS₄), with an E_PL of 1.665 eV and wavelength of 744.6 nm, emits red light (Fig. 6(e)), with excited state electrons localized on the [ZrS₄] tetrahedron and excited state holes localized on [Ba₆O] octahedrons (Fig. S7e, ESI†). Rb₃Cl_0.5I_0.5(ZnI₄), with an E_PL of 3.121 eV and wavelength of 397.3 nm, emits blue-violet light (Fig. 6(f)), exhibiting zero-dimensional electronic properties because its excited state electrons and holes are both localized on the [ZnI₄] tetrahedron (Fig. S7g, ESI†). It should be noted that some zero-dimensional perovskites with Zn as the blue luminescence center have been reported.^45,46 The candidate materials with a low self-trapping energy are not involved in the direct formation of STEs, which are generally observed in low dimensional perovskites. However, owing to the low electronic dimensionality and strongly localized excitons in these novel antiperovskites, the candidate materials exhibit benign light-emitting properties. The transition from the excited state to the ground state could emit light of the corresponding wavelength.

Fig. 6 Configuration coordinate diagram (CCD) for the excited states of (a) Ba₃I_0.5F_0.5(SbS₄), (b) Ba₃F_0.5I_0.5(InSe₄), (c) Ca₃O(SnO₄), (d) Ca₃O(TiO₄), (e) Ba₃O_0.5S_0.5(ZrS₄), and (f) Rb₃Cl_0.5I_0.5(ZnI₄). E_PL is the energy of emission. The insets display an enlarged view of the potential energy surface (PES) obtained by linear interpolation. In the insets, the blue line represents the PES of the ground state, while the red line represents the PES of the excited state.

In addition, through high-throughput calculations, we also obtained some candidates whose tetrahedral center is a Mn ion. For example, the optoelectronic properties of Rb₃Cl_0.5I_0.5(MnBr₄) were investigated for comparison (see Fig. S8, ESI†). These results showed that the highest valence band and lowest conduction band are particularly flat, related to the characteristics of a low-dimensional electronic structure. The distributions of electrons and holes in the excited state are also both localized on the MnBr₄ tetrahedron. Rb₃Cl_0.5I_0.5(MnBr₄) with an E_PL of 2.385 eV and wavelength of 519.8 nm emits green light, consistent with the emission of green light in most tetrahedral light-emitting compounds with Mn.^45,47 Therefore, these candidates have strong local excitons and suitable light-emitting band gaps, making them potential light-emitting friendly materials.

3. Conclusions

In summary, we have predicted a series of LFAP materials for light-emitting application. By combining the empirical formation descriptors of perovskite structures, i.e. the tolerance factor t, octahedral factor μ₁, and tetrahedral factor μ₂, 266 LFAPs have been screened out from 6320 compounds. Considering environmental friendliness and suitable bandgaps, 49 LFAPs have been preliminarily identified to possess promising potential for light-emitting applications. Among them, eight materials with different tetrahedral central elements were selected for further comprehensive exploration. Based on the thermodynamic and kinetic stabilities, electronic structures, exciton binding energies and excited states of these compounds, Ba₃I_0.5F_0.5(SbS₄), Ba₃F_0.5I_0.5(InSe₄), Ca₃O(SnO₄), Ca₃O(TiO₄), Ba₃O_0.5S_0.5(ZrS₄), and Rb₃Cl_0.5I_0.5(ZnI₄) were identified as promising light-emitting materials. Moreover, though six candidates have three-dimensional crystal structures, their electronic structures with characteristics of a flat band around the band edge inevitably exhibit certain low-dimensional properties, leading to a strong space confinement effect and strong binding of excitons, which is beneficial for excitonic radiative recombination. Most importantly, through the study of excited states, the emission wavelengths of six candidates have been predicted, namely, Ba₃I_0.5F_0.5(SbS₄): 690.3 nm (red), Ca₃O(SnO₄): 572.9 nm (yellow), Ba₃F_0.5I_0.5(InSe₄): 392.5 nm (blue-violet), Ba₃O_0.5S_0.5(ZrS₄): 744.6 nm (red), Ca₃O(TiO₄): 464.7 nm (blue), and Rb₃Cl_0.5I_0.5(ZnI₄): 397.3 nm (blue-violet). The dominant colors of light emission can be tuned over a wide range (about 390–745 nm) with respect to the composition change involved in the engineering of octahedra and tetrahedra. If confirmed by experiments, these LFAPs may serve as highly efficient and stable light-emitting materials, while addressing some known challenging issues inherent in PeLEDs.

4. Computational methods

All first-principles computations were performed based on density functional theory (DFT) methods as implemented in the Vienna Ab initio Simulation Package.⁴⁸ The projector-augmented wave method⁴⁹ with the generalized gradient approximation (GGA) of the PBEsol exchange–correlation functional⁵⁰ and Meta-GGA of the SCAN exchange–correlation functional^51,52 were used for structure optimization and electronic structure calculations, respectively. The cut-off energy of the plane wave was set as 520 eV. The threshold for energy convergence and force was 10⁻⁵ eV and 0.01 eV Å⁻¹, respectively. Monkhorst–Pack k-point meshes of 3 × 3 × 3 and 5 × 5 × 5 were adopted for Brillouin zone integration for structure optimization and electronic structure calculations, respectively. For the three candidates composed of main group elements, the HSE06 functional⁵³ was adopted to compute the electronic structure. The compounds with transition metals, such as Chromium, Manganese, iron, cobalt, nickel, Palladium, and Platinum, were computed by using SCAN functionals with spin. The primitive cells of antiperovskites are about 8 Å × 8 Å × 15 Å and contain 36 atoms. A 2 × 2 × 1 supercell containing 144 atoms was adopted in the simulations of AIMD. The AIMD simulations adopted the NVT ensemble at constant temperature. A Nosé–Hoover thermostat was used to set the temperature to 300 K, and simulation of each structure based on the Γ point lasted 5 ps with a time step of 1.0 fs. The phonon dispersions were calculated by the finite-difference method with the 2 × 2 × 1 supercell approach at 0 K. The temperature-dependent phonon with anharmonic effects was computed using the DynaPhoPy⁵⁴ package.

To study the excited state properties, we adopted the restricted open–shell Kohn–Sham (ROKS) theory,^55–57 as implemented in the cp2k code by Wang X et al.^13,58 Supercells (of about 15 × 15 × 16 ų) were used in the calculation with a single Γ point, the double-zeta valence polarization molecularly optimized basis sets,⁵⁹ PBE exchange–correlation functional, Goedecker–Teter–Hutter pseudopotentials⁶⁰ and an energy cutoff of 600 Ry (1 Rydberg, 1 Ry = 13.605 eV). The delocalization error of the PBE functional was removed using the scaled Perdew–Zunger self-interaction correction^61,62 (PZ-SIC) only on the unpaired electrons.⁶² The cc diagrams were constructed by linear interpolation of coordinates between free exciton and excited state configurations, then the ground state and excited state energies were calculated at each coordinate. The coordinate difference between the free exciton and excited state configuration is 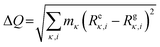,⁶³ where κ is the atom label, i = (x, y, z), m is the atomic mass, and R is the atomic coordinates with e and g representing the excited and ground state, respectively.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (grant 2021YFA1500703 and 2021YFA1200700), the Natural Science Foundation of China (grant 22173019, 22033002, and 92056112), and the Fundamental Research Funds for the Central Universities (grant 2242022R40072). We thank the National Supercomputing Center of Tianjin and the Big Data Computing Center of Southeast University for providing the facility support for the calculations.

References

1. K. X. Steirer, P. Schulz, G. Teeter, V. Stevanovic, M. Yang, K. Zhu and J. J. Berry, ACS Energy Lett., 2016, 1, 360–366.
2. M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647.
3. L. Xu, D. Wu, W. Lv, Y. Xiang, Y. Liu, Y. Tao, J. Yin, M. Qian, P. Li, L. Zhang, S. Chen, O. F. Mohammed, O. M. Bakr, Z. Duan, R. Chen and W. Huang, Adv. Mater., 2021, 2107111.
4. L. Xu, X. Feng, W. Jia, W. Lv, A. Mei, Y. Zhou, Q. Zhang, R. Chen and W. Huang, Energy Environ. Sci., 2021, 14, 4292–4317.
5. L. N. Quan, B. P. Rand, R. H. Friend, S. G. Mhaisalkar, T.-W. Lee and E. H. Sargent, Chem. Rev., 2019, 119, 7444–7477.
6. T.-H. Han, K. Y. Jang, Y. Dong, R. H. Friend, E. H. Sargent and T.-W. Lee, Nat. Rev. Mater., 2022, 7, 757–777.
7. X.-K. Liu, W. Xu, S. Bai, Y. Jin, J. Wang, R. H. Friend and F. Gao, Nat. Mater., 2021, 20, 10–21.
8. Z.-K. Tan, R. S. Moghaddam, M. L. Lai, P. Docampo, R. Higler, F. Deschler, M. Price, A. Sadhanala, L. M. Pazos, D. Credgington, F. Hanusch, T. Bein, H. J. Snaith and R. H. Friend, Nat. Nanotechnol., 2014, 9, 687–692.
9. X. Zhang, C. Wang, Y. Zhang, X. Zhang, S. Wang, M. Lu, H. Cui, S. V. Kershaw, W. W. Yu and A. L. Rogach, ACS Energy Lett., 2019, 4, 242–248.
10. W.-L. Hong, Y.-C. Huang, C.-Y. Chang, Z.-C. Zhang, H.-R. Tsai, N.-Y. Chang and Y.-C. Chao, Adv. Mater., 2016, 28, 8029–8036.
11. T. Chiba, Y. Hayashi, H. Ebe, K. Hoshi, J. Sato, S. Sato, Y.-J. Pu, S. Ohisa and J. Kido, Nat. Photonics, 2018, 12, 681–687.
12. Y. Shen, L. Cheng, Y. Li, W. Li, J. Chen, S. Lee and J. Tang, Adv. Mater., 2019, 1901517.
13. J. Luo, X. Wang, S. Li, J. Liu, Y. Guo, G. Niu, L. Yao, Y. Fu, L. Gao, Q. Dong, C. Zhao, M. Leng, F. Ma, W. Liang, L. Wang, S. Jin, J. Han, L. Zhang, J. Etheridge, J. Wang, Y. Yan, E. H. Sargent and J. Tang, Nature, 2018, 563, 541–545.
14. Z. Shi, J. Guo, Y. Chen, Q. Li, Y. Pan, H. Zhang, Y. Xia and W. Huang, Adv. Mater., 2017, 29, 1605005.
15. B. Li, B. Chang, L. Pan, Z. Li, L. Fu, Z. He and L. Yin, ACS Energy Lett., 2020, 5, 3752–3772.
16. V. A. Slabe, J. T. Anderson, B. A. Millsap, J. L. Cooper, A. R. Harmata, M. Restani, R. H. Crandall, B. Bodenstein, P. H. Bloom, T. Booms, J. Buchweitz, R. Culver, K. Dickerson, R. Domenech, E. Dominguez-Villegas, D. Driscoll, B. W. Smith, M. J. Lockhart, D. McRuer, T. A. Miller, P. A. Ortiz, K. Rogers, M. Schwarz, N. Turley, B. Woodbridge, M. E. Finkelstein, C. A. Triana, C. R. DeSorbo and T. E. Katzner, Science, 2022, 375, 779–782.
17. M. J. McFarland, M. E. Hauer and A. Reuben, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2118631119.
18. J. Y. Kim, J.-W. Lee, H. S. Jung, H. Shin and N.-G. Park, Chem. Rev., 2020, 120, 7867–7918.
19. Y. Wang, H. Zhang, J. Zhu, X. Lü, S. Li, R. Zou and Y. Zhao, Adv. Mater., 2020, 32, 1905007.
20. W. Xia, Y. Zhao, F. Zhao, K. Adair, R. Zhao, S. Li, R. Zou, Y. Zhao and X. Sun, Chem. Rev., 2022, 122, 3763–3819.
21. D. Han, C. Feng, M.-H. Du, T. Zhang, S. Wang, G. Tang, T. Bein and H. Ebert, J. Am. Chem. Soc., 2021, 143, 12369–12379.
22. L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696.
23. Y. Mochizuki, H.-J. Sung, A. Takahashi, Y. Kumagai and F. Oba, Phys. Rev. Mater., 2020, 4, 044601.
24. J.-W. Lee, S. Tan, S. I. Seok, Y. Yang and N.-G. Park, Science, 2022, 375, eabj1186.
25. K. Tang, Y. Lin, Y. Ren, W. Tian, H. Chen, T. Lin, L. Qiu, X. Pan and W. Wang, ACS Energy Lett., 2021, 6, 1901–1911.
26. Y. Zhang, X. Liu, H. Sun, J. Zhang, X. Gao, C. Yang, Q. Li, H. Jiang, J. Wang and D. Xu, Angew. Chem., Int. Ed., 2021, 60, 7587–7592.
27. X. Wang, W. Meng, W. Liao, J. Wang, R.-G. Xiong and Y. Yan, J. Phys. Chem. Lett., 2019, 10, 501–506.
28. S. Yan, K. Tang, Y. Lin, Y. Ren, W. Tian, H. Chen, T. Lin, L. Qiu, X. Pan and W. Wang, ACS Energy Lett., 2021, 6, 1901–1911.
29. C. Katan, N. Mercier and J. Even, Chem. Rev., 2019, 119, 3140–3192.
30. A. Ben-Akacha, C. Zhou, M. Chaaban, D. Beery, S. Lee, M. Worku, X. Lin, R. Westphal and B. Ma, ChemPhotoChem, 2021, 5, 326–329.
31. C. Zhou, Y. Tian, M. Wang, A. Rose, T. Besara, N. K. Doyle, Z. Yuan, J. C. Wang, R. Clark, Y. Hu, T. Siegrist, S. Lin and B. Ma, Angew. Chem., Int. Ed., 2017, 56, 9018–9022.
32. C. Katan, N. Mercier and J. Even, Chem. Rev., 2019, 119, 3140–3192.
33. V. M. Goldschmidt and S. N. Videnskaps-Akad, Oslo I Math.-Naturv. Klasse, No. 1, 1926, vol. 8.
34. C. Li, K. C. K. Soh and P. Wu, J. Alloys Compd., 2004, 372, 40–48.
35. C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693.
36. M. R. Filip and F. Giustino, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5397–5402.
37. B. Saparov and D. B. Mitzi, Chem. Rev., 2016, 116, 4558–4596.
38. G. Long, Y. Zhou, M. Zhang, R. Sabatini, A. Rasmita, L. Huang, G. Lakhwani and W. Gao, Adv. Mater., 2019, 31, 1807628.
39. N. A. Benedek and C. J. Fennie, J. Phys. Chem. C, 2013, 117, 13339–13349.
40. I. P. Swainson, C. Stock, S. F. Parker, L. Van Eijck, M. Russina and J. W. Taylor, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 100303.
41. F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goñi, A. M. A. Leguy, P. R. F. Barnes and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144308.
42. X.-G. Zhao, J.-H. Yang, Y. Fu, D. Yang, Q. Xu, L. Yu, S.-H. Wei and L. Zhang, J. Am. Chem. Soc., 2017, 139, 2630–2638.
43. M.-G. Ju, J. Dai, L. Ma and X. C. Zeng, J. Am. Chem. Soc., 2017, 139, 8038–8043.
44. Y. Shen, L. Liang, S. Zhang, D. Huang, J. Zhang, S. Xu, C. Liang and W. Xu, Nanoscale, 2018, 10, 1622–1630.
45. G. Zhou, Z. Liu, J. Huang, M. S. Molokeev, Z. Xiao, C. Ma and Z. Xia, J. Phys. Chem. Lett., 2020, 11, 5956–5962.
46. A. Yangui, R. Roccanova, T. M. McWhorter, Y. Wu, M.-H. Du and B. Saparov, Chem. Mater., 2019, 31, 2983–2991.
47. V. Morad, I. Cherniukh, L. Pöttschacher, Y. Shynkarenko, S. Yakunin and M. V. Kovalenko, Chem. Mater., 2019, 31, 10161–10169.
48. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
49. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
50. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
51. J. Sun, R. C. Remsing, Y. Zhang, Z. Sun, A. Ruzsinszky, H. Peng, Z. Yang, A. Paul, U. Waghmare, X. Wu, M. L. Klein and J. P. Perdew, Nat. Chem., 2016, 8, 831–836.
52. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
53. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
54. A. Carreras, A. Togo and I. Tanaka, Comput. Phys. Commun., 2017, 221, 221–234.
55. M. Filatov and S. Shaik, Chem. Phys. Lett., 1999, 304, 429–437.
56. T. Kowalczyk, T. Tsuchimochi, P.-T. Chen, L. Top and T. Van Voorhis, J. Chem. Phys., 2013, 138, 164101.
57. I. Frank, J. Hutter, D. Marx and M. Parrinello, J. Chem. Phys., 1998, 108, 4060–4069.
58. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
59. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
60. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
61. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
62. M. d’Avezac, M. Calandra and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205210.
63. A. Alkauskas, J. L. Lyons, D. Steiauf and C. G. Van de Walle, Phys. Rev. Lett., 2012, 109, 267401.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh01216b

‡ These authors have contributed equally.

---