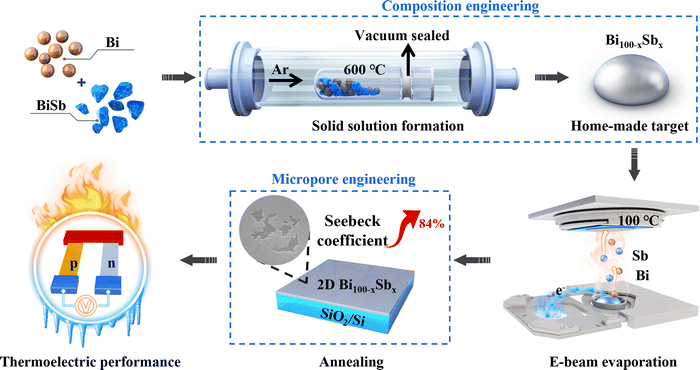
Large-area 2D bismuth antimonide with enhanced thermoelectric properties via multiscale electron–phonon decoupling†
Hanliu
Zhao‡
a,
Yuxin
Xue‡
a,
Yu
Zhao‡
 b,
Jiayi
Chen
a,
Bo
Chang
a,
Hao
Huang
b,
Jiayi
Chen
a,
Bo
Chang
a,
Hao
Huang
 a,
Tao
Xu
a,
Tao
Xu
 c,
Litao
Sun
c,
Litao
Sun
 c,
Yunfei
Chen
c,
Yunfei
Chen
 b,
Jingjie
Sha
*b,
Beibei
Zhu
*a and
Li
Tao
b,
Jingjie
Sha
*b,
Beibei
Zhu
*a and
Li
Tao
 *a
*a
aSchool of Materials Science and Engineering, Jiangsu Key Laboratory of Advanced Metallic Materials, Southeast University, Nanjing 211189, People's Republic of China. E-mail: tao@seu.edu.cn; 101012333@seu.edu.cn
bSchool of Mechanical Engineering, Jiangsu Key Laboratory for Design and Manufacture of Micro-Nano Biomedical Instruments, Southeast University, Nanjing 211189, People's Republic of China. E-mail: major212@seu.edu.cn
cSEU-FEI Nano-Pico Center, Key Laboratory of MEMS of Ministry of Education, Collaborative Innovation Center for Micro/Nano Fabrication, Device and System, Southeast University, Nanjing 211189, People's Republic of China
First published on 8th March 2023
Abstract
It is a challenge to obtain high thermoelectric efficiency owing to the conflicting parameters of the materials that are required. In this work, the composition-adjustable 2D bismuth antimonide (Bi100−xSbx) is synthesized using an e-beam evaporation system with homemade targets. Engineering multiscale defects is done to optimize the thermoelectric performance in the compound. Sb alloying introduces atomic defects, lattice distortion and increased grain boundary. They drastically decrease the thermal conductivity, with an ultralow value of ∼0.23 W m−1 K−1 obtained for the composition with x = 18. It is noticed that the atomic and nanoscale defects do not deteriorate the electrical conductivity (105 S m−1), and the value is even comparable to the bulk counterpart over a wide composition range (0 ≤ x ≤ 35). Annealing induces pore structure with microscale defects, which increase the Seebeck coefficient by 84% due to the energy barrier. The resultant ZT of 0.13 is enhanced by 420% in the annealed Bi82Sb18 when compared with the as-grown Bi. This work demonstrates a cost-effective and controllable way to decouple electrons and phonons in the thermoelectric field.
Conceptual insightsIt has long been a challenge for thermoelectric performance development to overcome the coupling between phonons and electrons. Effective scattering sources in different dimensions can scatter phonons in a wide range of frequencies. However, this usually deteriorates electron transportation, since the mean free paths (MFPs) of phonons and electrons are close in most thermoelectric materials. In the 2D scenario, the dominant topological surface states have linear dispersion-induced larger relaxation times, indicating high electrical conductivity outweighing the bulk states. In this work, multiscale defects involving atomic, nano and microscales selectively target phonons and low-energy electrons, respectively, for improved thermoelectric performance. Therefore, one can obtain decreased thermal and maintained electrical conductivity with improved Seebeck coefficient simultaneously. This work presents a multiscale electron–phonon decoupling strategy to tune the coupled thermoelectric properties independently in 2D topological materials. |
1. Introduction
Bismuth antimonide is a topological material that has attracted considerable research attention due to its striking band structure and electrical properties.1 Located adjacently, antimony (Sb) shares the same rhombohedral crystal structure (A7, space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) as Bi.2,3 The atomic diameters of Bi (1.63 Å) and Sb (1.53 Å) differ a little, and the mismatch in lattice parameters is Δa/a = 5.4% and Δc/c = 5.1%.4 Thus, they can constitute a continuous solid solution (Bi100−xSbx) over the entire composition range.2 When 7 < x < 22, the transformation from semimetal to semiconductor occurs in Bi100−xSbx. When it goes to low dimensional form, this semiconductor composition range could be widened to 0 ≤ x < 35 as a result of quantum confinement.5 The maximum bandgap is ∼30 meV at x = 15.6–8 The narrow bandgap is attributed to the weaker SOC effect after the addition of Sb to the Bi crystal removes the band overlap in Bi.9 Bi100−xSbx has been reported to be an n-type thermoelectric material, and exhibits high thermoelectric performance with x from 8 to 15 owing to the narrow bandgap,4,10–12 holding potential for application in waste heat utilization and thermoelectric refrigeration.
m) as Bi.2,3 The atomic diameters of Bi (1.63 Å) and Sb (1.53 Å) differ a little, and the mismatch in lattice parameters is Δa/a = 5.4% and Δc/c = 5.1%.4 Thus, they can constitute a continuous solid solution (Bi100−xSbx) over the entire composition range.2 When 7 < x < 22, the transformation from semimetal to semiconductor occurs in Bi100−xSbx. When it goes to low dimensional form, this semiconductor composition range could be widened to 0 ≤ x < 35 as a result of quantum confinement.5 The maximum bandgap is ∼30 meV at x = 15.6–8 The narrow bandgap is attributed to the weaker SOC effect after the addition of Sb to the Bi crystal removes the band overlap in Bi.9 Bi100−xSbx has been reported to be an n-type thermoelectric material, and exhibits high thermoelectric performance with x from 8 to 15 owing to the narrow bandgap,4,10–12 holding potential for application in waste heat utilization and thermoelectric refrigeration.
The thermoelectric properties of single crystal bismuth antimonide with various compositions were investigated in 1972 by Yim et al.11 Thermal conductivity of ∼2 W m−1 K−1 and ZT ∼0.55 along the trigonal axis at 80 K were obtained.11 Recently, Gao et al. demonstrated that spark plasma sintering could produce fine-grained Bi85Sb15, which has a low thermal conductivity of 1.5 W m−1 K−1 and a ZT ∼0.6 at ∼125 K.12 Besides decreasing grain size, another nanostructure engineering method to reduce thermal conductivity is decreasing the dimensions. For instance, 2D materials tend to exhibit lower thermal conductivity than their bulk counterparts because of the size effect. However, it inevitably deteriorates the electron transportation, but doping or alloying might resolve the problem. When the electrical conductivity is drastically increased owing to extra carrier injection or Fermi level tuning, the thermal conductivity can be decreased simultaneously or increased negligibly, as has been widely investigated in several thermoelectric materials, such as Bi2Te3,13,14 Bi2Se315 and Bi0.5Sb1.5Te3.16 For instance, when doping Cu in Bi2Se3,15 the electrical conductivity increased by around twofold while the thermal conductivity only changed by 10%. In Bi100−xSbx, alloying Sb has been found to change the electrical conductivity by 300%.11 Therefore, combining dimension reduction and Sb tuning might be an effective way to decouple the electron and phonon transportation in this material.
Low dimensional systems are expected to produce a sharp increase of density of states and increase the Seebeck coefficient.17 However, the Seebeck coefficient has been observed to be lower in bismuth antimonide and other thinner Bi-based topological materials owing to the surface states.10,18,19 When the thickness modification is widely used to change the Seebeck coefficient in bismuth antimonide,10,20 Walker et al.21 recently found that the Sb composition determines the crystal orientation and suppresses the surface states, which may also have an effect on Seebeck coefficient of 2D bismuth antimonide. In addition, post-annealing is a facial approach for tuning the morphology and thermoelectric properties. Annealing-induced porous structures were successfully utilized to increase the Seebeck coefficient and reduce the thermal conductivity due to the energy filtering effect and enhanced scattering intensity.22,23
To investigate the thermoelectric properties, an accessible facial method is in great demand to realize large-area 2D Bi100−xSbx on a preferred substrate. Up to now, various physical vapor deposition methods have already been reported, including molecular beam epitaxy (MBE),5,21 magnetron sputtering24 and thermal evaporation.10 Here, highly oriented Bi100−xSbx on a SiO2/Si substrate was obtained by employing a cost-effective electron beam (e-beam) evaporation method using homemade bismuth antimonide as targets, with x ranging from 0 to 35. Various structures, morphologies and thermoelectric parameters were investigated. It was found that low thermal conductivity and a high Seebeck coefficient could be acquired while maintaining high electrical conductivity in 2D Bi82Sb18 by tuning the composition and annealing. Our work provides insights into independently tailoring the thermoelectric transport coefficients of 2D materials, which are compatible for use in small-scale devices such as portable refrigerators, cooling laser diodes, terahertz detectors and integrated circuits.25,26
2. Results and discussion
Large-area bismuth antimonide with precisely controlled composition is deposited using homemade targets in an e-beam evaporation system, as shown in Fig. 1. The atomic ratio could be easily and cost-effectively adjusted during the target preparation, providing a convenient way to investigate the properties of bismuth antimonide over the entire semiconductor composition range. The typical thickness of our investigated samples is 17 nm.2.1 Structure and morphology characterization
Fig. 2a shows the XRD patterns of Bi100−xSbx (0 ≤ x ≤ 35) and no oxides were detected in any of the samples. All the diffraction peaks can be indexed to Bi with rhombohedral crystal structure (PDF#44-1246). A slight degradation of crystallinity is observed when x = 35 due to the lower average atomic migration capability in the growth process.27 The e-beam-evaporated bismuth antimonide shows a stronger preferred (00l) (parallel to the trigonal axis) texture than other PVD methods.10,24 As x increases, the (00l) diffraction peaks gradually shift to higher angles because Sb has a smaller atomic radius than Bi.28 Therefore, the calculated lattice parameter c decreases almost linearly as x increases (Fig. 2b), agreeing with Vegard's law (dashed line).29,30 Moreover, it is noted that as x increases, the intensity of the (012) peak increases, which has been reported in MBE-synthesized bismuth antimonide.21 The characteristic peaks in the Raman spectra are consistent with those of bulk bismuth antimonide31–33 (Fig. 2c). A monotonic blue shift is observed in the mode frequency of Eg (Bi) as x increases (Fig. 2d). Moreover, the full width at half maximum (FWHM) increases, implying the decreased crystallinity and consistent with the XRD results.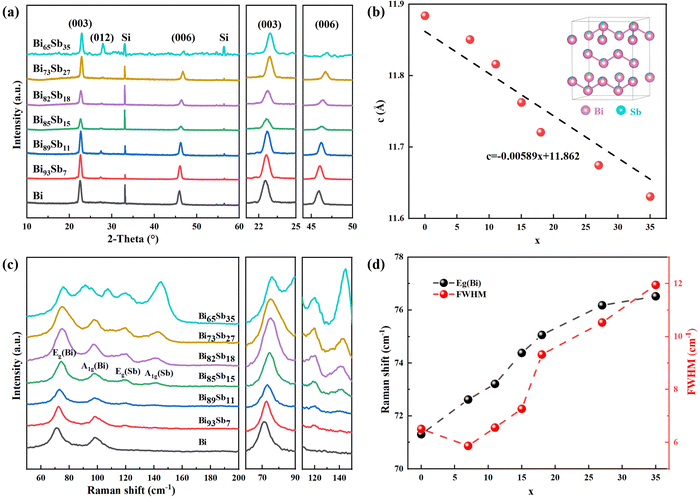 | ||
| Fig. 2 (a) XRD patterns of e-beam-evaporated 2D bismuth antimonide. The diffraction peaks can be indexed to the standard PDF#44-1246 (Bi). Note that (003) planes used here in the hexagonal coordinates are equal to (111) in the rhombohedral coordinates.34 (b) Lattice parameter c of 2D bismuth antimonide. The dashed line indicates Vegard's law and the inset is the crystal structure of bismuth antimonide. (c) Raman spectra of 2D bismuth antimonide. (d) Mode frequencies and FWHM of Eg (Bi) peak. | ||
The diffraction rings (Fig. 3a) and morphology image (Fig. 3b) indicate the polycrystalline nature of 2D bismuth antimonide with nanograins (∼30 nm) in our work. High-resolution TEM images (Fig. 3c and d) of Bi82Sb18 reveal that the lattice fringes are 0.227 nm and 0.329 nm, corresponding to the (110) and (012) planes, respectively. Moreover, the disordered atomic arrangement within the grain boundary region can be observed in Fig. S1a and b (ESI†). The respective morphologies of the as-grown 2D Bi100−xSbx (x = 0, 7, 18, and 35) are displayed in Fig. 3e–h. Protruded grains of several tens of nanometers are embedded randomly on the surface, as reported before.35,36 The formation of the protruded grains could be attributed to the Stranski–Krastanov growth mechanism during the deposition process.37 The resultant surface roughness is ∼5 nm (Fig. S1c, ESI†). There is almost no difference in the composition of the flat area and the protruded grains (Fig. S1d and e, ESI†), eliminating the element segregation. EDS and Raman mapping (Fig. S1f–h) also confirm the homogeneity of the film. As x increases, the number and size of the protruded grains decrease (Fig. 3e–h), possibly due to the decreased atomic migration capability. In addition, it can be seen in the AFM images (Fig. 3i–l) that the grain size gradually decreases as x increases from 0 to 35, which will cause the increase of grain boundaries, leading to the phonon or electron scattering.
2.2 Thermoelectric properties of as-grown bismuth antimonide
The thermoelectric conversion efficiency can be quantified by a dimensionless figure of merit ZT = S2σT/κ, in which S, σ, T, and κ refer to Seebeck coefficient, electrical conductivity, absolute temperature, and thermal conductivity, respectively. Almost all the thermal conductivity values in this work are smaller than the reported counterparts as compared in Fig. 4a. For instance, the thermal conductivity for Bi85Sb15 bulk11 was reported to be 3 W m−1 K−1, but in this work, the same composition only obtains κ = 0.35 W m−1 K−1. This indicates the size effect can enhance the phonon scattering in bismuth antimonide. The trend of the change of thermal conductivity with composition in this work is similar to bulk bismuth antimonide.38,39 When x < 18, thermal conductivity decreases as x increases. The lowest thermal conductivity in this work is 0.23 W m−1 K−1 in Bi82Sb18, which is 60% lower compared with x = 0 (0.58 W m−1 K−1) in Fig. 4b. The decreased thermal conductivity can be attributed to two factors: i) the lattice distortion scattering in Fig. 2b, from the different sizes between Sb and Bi, which affects the high-frequency phonons; and ii) the grain boundary scattering (Fig. 3i–l and Fig. S1a and S1b, ESI†), from grain size dwindling and atomic disorder in the boundary regime, which results in suppressed low- to mid-frequency phonon relaxation time.40 When x > 18, the upward trend of thermal conductivity is due to the larger thermal conductivity of Sb (20 W m−1 K−1) than Bi (6 W m−1 K−1)11 and increasing electrical conductivity, as shown in Fig. 4c.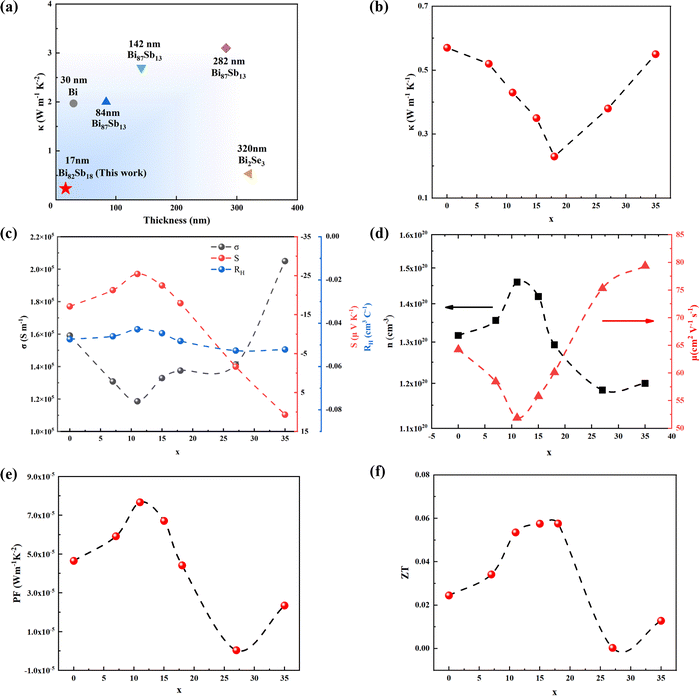 | ||
| Fig. 4 Electric and thermoelectric properties of as-grown 2D bismuth antimonide with 17 nm thickness. (a) Comparison of thermal conductivity of our Bi82Sb18 with other Bi-based materials.10,12,50–54 (b) Thermal conductivity (the thermal conductivity is measured by TDTR method, fitting curves are shown in Fig. S2, ESI†). (c) Electrical conductivity, Seebeck coefficient and Hall coefficient. (d) Carrier concentration and Hall mobility. (e) Power factor. (f) ZT value. | ||
The electrical conductivity of the as-grown 2D bismuth antimonide exceeds 105 S m−1, comparable to the values reported for bismuth antimonide bulks or films, and higher than that of Bi–X (X = Te, Se) by one order of magnitude.5 This is because the charge carrier concentration in Fig. 4d is higher than those for the bulk or thick film counterparts.38,41–43 Decreased thickness inducing increased charge carrier density has been reported in our previous work on 2D bismuth44 and other Bi-based topological insulators, such as Bi2Te3 and Bi2Se3.45,46 This can be attributed to the Fermi level increasing inspired by metallic surface states.46–48 It has to be noted that, when Sb is added, the mobility varies in the opposite way to the carrier concentration (Fig. 4d), but there are no patterns in lattice distortion (Fig. 2a and c) or grain size (Fig. 3i–l). Therefore, in this work, the electron scattering could be dominated by charge carriers rather than the above defects. Moreover, the addition of Sb only results in a 19% decrease in the carrier mobility (Fig. 4d), but drastically suppresses the thermal conductivity by 60% (Fig. 4b), providing a platform to study “phonon-glass electron-crystal”.49
The Seebeck coefficient in Fig. 4c shows a negative value before x = 25, indicating n-type nature with the electrons as the major carriers.10 When x increases from 0 to 11, the absolute value of the Seebeck coefficient increases by 42%, which could be a result of the increased Eg.5 The Seebeck coefficient gains a peak value of −25.4 μV K−1 when x = 11. Similarly, the turning point of bulk Bi100−xSbx reported by Yim et al. is around x = 12.11 When x > 11, since the p-type Sb may bring in more holes in bismuth antimonide, the total Seebeck coefficient can be influenced by both electrons and holes:55
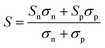 | (1) |
ZT finally reaches a maximum value of 0.058 (Fig. 4f) in Bi82Sb18, which has the lowest thermal conductivity and achieves a significant improvement of 142% compared to 2D Bi. The results prove that the Sb composition can tune the thermoelectric performance of e-beam-evaporated 2D bismuth antimonide owing to the suppressed thermal conductivity via lattice distortion and grain boundaries.
2.3 Thermoelectric properties of annealed bismuth antimonide
In order to further improve the thermoelectric performance of bismuth antimonide, annealing is conducted. It has been reported to simultaneously improve the electrical conductivity and Seebeck coefficient in thick Bi100−xSbx (4 < x < 23) thin films before,57 which may be ascribed to the increased crystallinity after heat treatment. Moreover, the annealing has also succeeded in increasing the thermoelectric performance in other Bi-based materials.22,23 Since the highest ZT was obtained in Bi82Sb18 after Sb optimization (Fig. 4f), in this section, this sample is selected for the detailed discussion. The information of the other samples is in Fig. S3 and S4 (ESI†).After annealing, according to the XRD patterns and Raman Spectra in Fig. S3 (ESI†), the crystallinity is increased in Bi82Sb18. Moreover, pores or the purple SiO2 substrate are exposed after annealing, as seen in Fig. 5b. The sublimation of bismuth antimonide may happen since the melting point (271–630 °C) is higher than the annealing temperature. A similar phenomenon has occurred in copper thin film.58 AFM and SEM images (Fig. S5, (ESI†)) indicate that the pore depth is the same as the film thickness, and the lateral size of the exposed area is <3 μm.
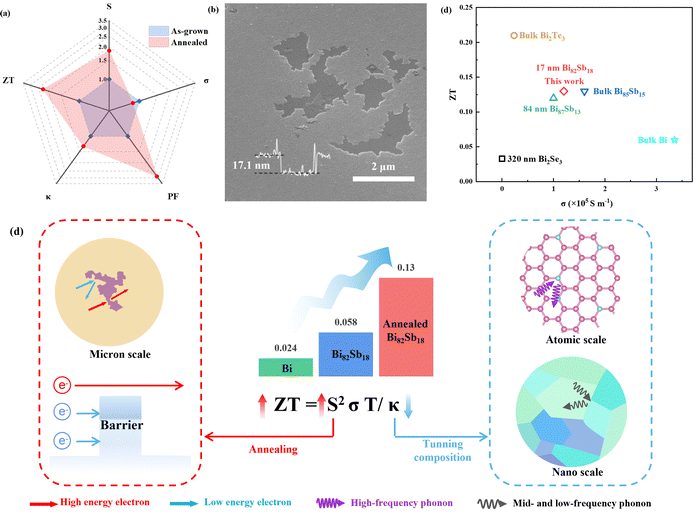 | ||
| Fig. 5 (a) Normalized thermoelectric parameters of as-grown and annealed 2D Bi82Sb18. (b) SEM images of annealed 2D Bi82Sb18. (c) Schematic diagram of improving thermoelectric performance through tuning composition and annealing in bismuth antimonide: Sb composition optimized the thermal conductivity through lattice distortion and nanograin boundaries; annealing further enhanced the Seebeck coefficient via sublimated micropores. (d) Comparison of ZT and σ of bismuth53 and Bi–X (X = Te,51 Se,52 Sb,10,43,53). | ||
As shown in Fig. 5a, annealing leads to a larger change in the Seebeck coefficient than in electrical conductivity and thermal conductivity. There is an 84% increase in the Seebeck coefficient from the as-grown sample (−17.9 μV K−1) to the annealed one (−33.0 μV K−1). This might be due to the energy barrier formation-induced energy filtering from the grain boundary, pore structure, or exposed SiO2.59–61 According to the Scherrer equation, the grain size of Bi82Sb18 is decreased by 14.67% after annealing. The energy filtering effect can be partially attributed to the grain boundaries.
The pores or exposed SiO2 areas produced by annealing could also act as potential barriers to scatter low-energy charge carriers by changing their momentum62 (Fig. 5c). When the exposed area increases, higher Seebeck coefficient can be obtained (Fig. S6, ESI†). Moreover, SiO2 can be seen clearly in the annealed Bi85Sb15, Bi73Sb27, and Bi65Sb35 in Fig. S7 (ESI†), in which the increased Seebeck coefficient is achieved (Fig. S4a, ESI†). The pore structure or secondary phase oxides have been reported to improve the Seebeck coefficient in bulk or thin films such as Bi and Bi2Te3.22,63,64 However, it has to be noted that the size of the pores or oxides in their work (nm) is much smaller than ours (μm). Although the electrical conductivity in Fig. 5a is reduced a bit, it is still higher than that of other Bi–X films by one order of magnitude (Fig. 5d). An improved PF ∼ 1.3 × 10−4 W m−1 K−2 is obtained, which is ∼189% higher than that of the as-grown one (Table 1). It is noticed that the thermal conductivity of Bi82Sb18 slightly increases from 0.23 to 0.3 W m−1 K−1 after annealing. This can be attributed to the exposed SiO2 substrate having higher thermal conductivity (κ = 1.3 W m−1 K−165), and it can be detected during the TDTR measurement. The resultant ZT value of annealed Bi82Sb18 improves by 124% and reaches 0.13 (Table 1), which is mainly attributed to the enhanced |S|. Such a ZT value is comparable to thicker Bi–X (X = Sb, Se, Te) films and even bulk counterparts at room temperature, as compared in Fig. 5d and Table 1.
| σ (105 S m−1) | S (μV K−1) | PF (W m−1 K−2) | κ (W m−1 K−1) | ZT | Ref. | |
|---|---|---|---|---|---|---|
| Bulk Bi | 3.35 | −58 | 1.1 × 10−5 | 5.4 | 0.06 | 53 |
| Bulk Bi2Te3 | 0.235 | −156.2 | 5.7 × 10−4 | 0.78 | 0.21 | 51 |
| Bi2Se3 thin film | 0.0019 | 556 | 5.8 × 10−5 | 0.534 | 0.033 | 52 |
| Bulk Bi85Sb15 | 1.6 | −87 | 1.2 × 10−3 | 2.8 | 0.12 | 53 |
| Bi87Sb13 thin film | 1 | −85 | 7 × 10−4 | 2 | 0.12 | 10 |
| Bi82Sb18 (as-grown) | 1.4 | −17.9 | 4.4 × 10−5 | 0.23 | 0.058 | This work |
| Bi82Sb18 (annealed) | 1.2 | −33.0 | 1.3 × 10−4 | 0.30 | 0.13 |
Briefly, when the Sb composition decreases the thermal conductivity by 60% through lattice distortion and nanograin boundaries, the annealing-induced microporous structure increases the Seebeck coefficient by 84%. They both contribute to the improvement of ZT in 2D Bi82Sb18, as shown in Fig. 5c. Moreover, our bismuth antimonide also possesses high electrical conductivity, providing a platform for the study of topological and transistor devices.
3. Conclusion
In summary, we investigated the thermoelectric properties of 2D Bi100−xSbx (0 ≤ x ≤ 35) prepared on a SiO2/Si substrate using an e-beam evaporation system. The XRD patterns for the samples show the preferred (00l) (parallel to the trigonal axis) texture. When x increases, (00l) the diffraction peaks gradually shift to higher angles and the grain size decreases (∼30 nm). All the thermal conductivity values are smaller than the previous report due to the size effect in 2D bismuth antimonide. The lowest thermal conductivity is 0.23 W m−1 K−1 in Bi82Sb18, which is 91% lower than that reported for the bulk materials, and 60% lower than 2D Bi in this work, which can be attributed to the lattice distortion and increased grain boundaries after Sb alloying. Those defects do not deteriorate the electrical conductivity, which maintains around 105 S m−1. The following annealing process results in a further 84% increase in the Seebeck coefficient in Bi82Sb18, which can be attributed to the produced pores or exposed SiO2 areas acting as potential barriers to scatter low-energy charge carriers. Finally, a ZT value of 0.13 is achieved, an increase of 124% compared to the as-grown one and 420% to the as-grown Bi at RT. The study demonstrates a convenient and controllable strategy to independently tune the transport of carriers and phonons for better thermoelectric performance.4. Experimental methods
4.1 Preparation
2D bismuth antimonide was synthesized via e-beam evaporation using a VZS 600 Pro system. The target was alloyed beforehand by weighing high-purity Bi (99.999%) and BiSb (99.99%) accurately according to the stoichiometric ratio. The mixed shots were then vacuum-sealed and placed horizontally in the tube furnace. They were heated to 600 °C, held for 4 h and then naturally cooled down to room temperature (RT). 2D bismuth antimonide was deposited on 100 °C-heated SiO2/Si substrate (p ∼ 5 × 10−4 Pa) with a growth rate of ∼0.1 Å s−1. A crystal oscillator acted as an in-situ thickness monitor and a Dimension ICON atomic force microscope (AFM) was used to confirm the thickness. The thickness in our work is around 17 nm. The as-grown 2D bismuth antimonide samples were annealed at 250 °C for 1 h under a 100 sccm Ar atmosphere in a quartz tube furnace (∼100 Pa).4.2 Characterization
The crystal structure of deposited 2D bismuth antimonide was identified using an Ultima IV X-ray diffractometer (XRD) with 1.54 Å Cu Kα radiation. The Raman spectra were obtained using a LabRAM HR UV-Visible Raman spectrometer with a 532 nm green laser. The surface morphology and energy dispersive spectrometry (EDS) analyses were done using an FEI Sirion scanning electron microscope (SEM) and AFM. High-resolution images and selected area electron diffraction (SAED) images were acquired via transmission electron microscopy (TEM). Electrical conductivity and Seebeck coefficient were measured by the four-probe method and using a portable Joule Yacht PTM-3 apparatus at room temperature, respectively. Hall effect measurement was performed on an HET-RT system. The thermal conductivity of 2D bismuth antimonide was determined by employing the time-domain thermoreflectance (TDTR) method.50 Before measurement, 70 nm-thick aluminum was deposited on the films by e-beam evaporation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key R&D Program of China (2022YFB4400100 & 2022YFB4400101), National Natural Science Foundation of China (92164102, 52075099), and Jiangsu Province Six-Category Talent Program (DZXX-011).References
- S. Guo, Y. Zhang, Y. Ge, S. Zhang, H. Zeng and H. Zhang, Adv. Mater., 2019, 31, 1902352 CrossRef PubMed.
- S. Singh, W. Ibarra-Hernandez, I. Valencia-Jaime, G. Avendano-Franco and A. H. Romero, Phys. Chem. Chem. Phys., 2016, 18, 29771–29785 RSC.
- S. Zhang, S. Guo, Z. Chen, Y. Wang, H. Gao, J. Gomez-Herrero, P. Ares, F. Zamora, Z. Zhu and H. Zeng, Chem. Soc. Rev., 2018, 47, 982–1021 RSC.
- V. S. Zemskov, A. D. Belaya, U. S. Beluy and G. N. Kozhemyakin, J. Cryst. Grow., 2000, 212, 161–166 CrossRef CAS.
- Y. Ueda, N. H. Duy Khang, K. Yao and P. N. Hai, Appl. Phys. Lett., 2017, 110, 062401 CrossRef.
- B. Lenoir, H. Scherrer and T. Caillat, Semicond. Semimetals, 2001, 69, 101–137 CAS.
- S. Barth, P. Birrer, F. N. Gygax, B. Hitti, E. Lippelt and A. Schenck, Hyperfine Interact., 1989, 51, 881–890 CrossRef.
- B. Lenoir, M. Cassart, J.-P. Michenaud, H. Scherrer and S. Scherrer, J. Phys. Chem. Solids, 1996, 57, 89–99 CrossRef CAS.
- D. Hsieh, D. Qian, L. Wray, Y. Xia, Y. S. Hor, R. J. Cava and M. Z. Hasan, Nature, 2008, 452, 970–974 CrossRef CAS PubMed.
- V. Linseis, F. Völklein, H. Reith, R. Hühne, L. Schnatmann, K. Nielsch and P. Woias, Semicond. Sci. Technol., 2018, 33, 085014 CrossRef.
- W. M. Yim and A. Amith, Solid-State Electron., 1972, 15, 1141–1165 CrossRef CAS.
- S. Gao, J. Gaskins, X. Hu, K. Tomko, P. Hopkins and S. J. Poon, Sci. Rep., 2019, 9, 14892 CrossRef PubMed.
- C. Kim, J. Cho, T. Kim and D. H. Lopez, J. Mater. Chem. A, 2022, 10, 13780–13792 RSC.
- Y. Zhao, Y. Li, J. Qiao, S. Jiang, P. Mao, J. Qiu, S. Kang, J. Tan, K. Tai and C. Liu, Carbon, 2020, 170, 191–198 CrossRef CAS.
- C. Dun, C. A. Hewitt, H. Huang, J. Xu, C. Zhou, W. Huang, Y. Cui, W. Zhou, Q. Jiang and D. L. Carroll, Nano Energy, 2015, 18, 306–314 CrossRef CAS.
- S. Li, W. Zhao, Y. Cheng, L. Chen, M. Xu, K. Guo and F. Pan, ACS Appl. Mater. Interfaces, 2023, 15, 1167–1174 CrossRef CAS PubMed.
- L. D. Hicks and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 12727–12731 CrossRef CAS PubMed.
- M. Zhang, W. Liu, C. Zhang, J. Qiu, S. Xie, F. Hua, Y. Cao, Z. Li, H. Xie, C. Uher and X. Tang, Appl. Phys. Lett., 2020, 117, 153902 CrossRef CAS.
- M. Guo, Z. Wang, Y. Xu, H. Huang, Y. Zang, C. Liu, W. Duan, Z. Gan, S.-C. Zhang, K. He, X. Ma, Q. Xue and Y. Wang, New J. Phys., 2016, 18, 015008 CrossRef.
- F. Völklein and E. Kessler, Thin Solid Films, 1987, 155, 197–208 CrossRef.
- E. S. Walker, S. Muschinske, C. J. Brennan, S. R. Na, T. Trivedi, S. D. March, Y. Sun, T. Yang, A. Yau, D. Jung, A. F. Briggs, E. M. Krivoy, M. L. Lee, K. M. Liechti, E. T. Yu, D. Akinwande and S. R. Bank, Phys. Rev. Mater., 2019, 3, 064201 CrossRef CAS.
- Z. Wu, E. Mu, Z. Che, Y. Liu, F. Sun, X. Wang and Z. Hu, J. Alloys Compd., 2020, 828, 154239 CrossRef CAS.
- J. Qiao, Y. Zhao, Q. Jin, J. Tan, S. Kang, J. Qiu and K. Tai, ACS Appl. Mater. Interfaces, 2019, 11, 38075–38083 CrossRef CAS PubMed.
- C. Rochford, D. L. Medlin, K. J. Erickson and M. P. Siegal, APL Mater., 2015, 3, 126106 CrossRef.
- N. F. Güler and R. Ahiska, Appl. Therm. Eng., 2002, 22, 1271–1276 CrossRef.
- A. K. Huhn, G. Spickermann, A. Ihring, U. Schinkel, H.-G. Meyer and P. Haring Bolívar, Appl. Phys. Lett., 2013, 102, 121102 CrossRef.
- J. A. Van Hulst, H. M. Jaeger and S. Radelaar, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 5953–5961 CrossRef CAS PubMed.
- W. Martienssen and H. Warlimont, Springer Handbook of Condensed Matter and Materials Data, Springer, Berlin Heidelberg, Germany, 2005 Search PubMed.
- P. Cucka and C. S. Barrett, Acta Crystallogr., 1962, 15, 865 CrossRef CAS.
- S. Cho, A. DiVenere, G. K. Wong, J. B. Ketterson and J. R. Meyer, J. Vac. Sci. Technol., A, 1999, 17, 9–13 CrossRef CAS.
- R. Sultana, G. Gurjar, B. Gahtori, S. Patnaik and V. P. S. Awana, Mater. Res. Express, 2019, 6, 106102 CrossRef CAS.
- J. S. Lannin, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 2390–2393 CrossRef CAS.
- R. N. Zitter and P. C. Watson, Phys. Rev. B: Solid State, 1974, 10, 607–611 CrossRef CAS.
- P. Hofmann, Prog. Surf. Sci., 2006, 81, 191–245 CrossRef CAS.
- X. F. Qin, C. Y. Sui and L. X. Di, Vacuum, 2019, 166, 316–322 CrossRef CAS.
- L. Kumari, S. J. Lin, J. H. Lin, Y. R. Ma, P. C. Lee and Y. Liou, Appl. Surf. Sci., 2007, 253, 5931–5938 CrossRef CAS.
- A. Pilidi, A. Tzanis, T. Helm, M. Arfanis, P. Falaras and T. Speliotis, ACS Appl. Nano Mater., 2020, 3, 9669–9678 CrossRef CAS.
- E. Güneş, B. Landschreiber, G. Homm, C. Wiegand, P. Tomeš, C. Will, M. T. Elm, S. Paschen, P. J. Klar, S. Schlecht and M. S. Wickleder, J. Electron. Mater., 2018, 47, 6007–6015 CrossRef.
- K. Ciesielski, J. Qu, L. C. Gomes, K. Synoradzki, J. M. Adamczyk, S. Rogers, R. Orenstein, E. Ertekin and E. S. Toberer, Virtual Conf. Thermoelectr., 2022, 17 Search PubMed.
- Z. Chen, X. Zhang and Y. Pei, Adv. Mater., 2018, 30, 1705617 CrossRef PubMed.
- F. Wei, W. Y. Zhao, Y. F. Chen, H. W. Zhang, C. F. Shen and Y. Deng, Thin Solid Films, 2021, 737, 138948 CrossRef CAS.
- K. Ueda, Y. Hadate, K. Suzuki and H. Asano, Thin Solid Films, 2020, 713, 138361 CrossRef CAS.
- E. Gunes, F. Gundlach, M. T. Elm, P. J. Klar, S. Schlecht, M. S. Wickleder and E. Muller, ACS Appl. Mater. Interfaces, 2017, 9, 44756–44765 CrossRef PubMed.
- X. H. Sun, H. L. Zhao, J. Y. Chen, W. Zhong, B. B. Zhu and L. Tao, Nanoscale, 2021, 13, 2648–2657 RSC.
- M. Guo, Z. Wang, Y. Xu, H. Huang, Y. Zang, C. Liu, W. Duan, Z. Gan, S.-C. Zhang, K. He, X. Ma, Q. Xue and Y. Wang, New J. Phys., 2016, 18, 015008 CrossRef.
- M. Zhang, W. Liu, C. Zhang, J. Qiu, S. Xie, F. Hua, Y. Cao, Z. Li, H. Xie, C. Uher and X. Tang, Appl. Phys. Lett., 2020, 117, 153902 CrossRef CAS.
- C. A. Hoffman, J. R. Meyer, F. J. Bartoli, A. Di Venere, X. J. Yi and C. L. Hou, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 11431–11434 CrossRef CAS PubMed.
- C. R. Ast and H. Hochst, Phys. Rev. Lett., 2001, 87, 177602 CrossRef CAS PubMed.
- J. Liu, B. van der Zee and R. Alessandri, Nat. Commun., 2020, 11, 5694 CrossRef CAS PubMed.
- W. Zhong, Y. Zhao, B. Zhu, J. Sha, E. S. Walker, S. Bank, Y. Chen, D. Akinwande and L. Tao, Nanotechnology, 2020, 31, 475202 CrossRef CAS PubMed.
- Q. Zhang, X. Ai, L. Wang, Y. Chang, W. Luo, W. Jiang and L. Chen, Adv. Funct. Mater., 2015, 25, 966–976 CrossRef CAS.
- N. S. Patil, A. M. Sargar, S. R. Mane and P. N. Bhosale, Mater. Chem. Phys., 2009, 115, 47–51 CrossRef CAS.
- E. Güneş, B. Landschreiber, D. Hartung, M. T. Elm, C. Rohner, P. J. Klar and S. Schlecht, J. Electron. Mater., 2014, 43, 2127–2133 CrossRef.
- E. Combe, R. Funahashi, T. Takeuchi, T. Barbier and K. Yubuta, J. Alloys Compd., 2017, 692, 563–568 CrossRef CAS.
- T. M. Tritt, Annu. Rev. Mater. Res., 2011, 41, 433–448 CrossRef CAS.
- J. Schmitt, Z. M. Gibbs, G. J. Snyder and C. Felserd, Mater. Horiz., 2015, 2, 68–75 RSC.
- P. Lorenz, G. Zieger, J. Dellith, and H. Schmidt, Thin Solid Films, 2022, 745, 139082 Search PubMed.
- A. L. Lee, L. Tao and D. Akinwande, ACS Appl. Mater. Interfaces, 2015, 7, 1527–1532 CrossRef CAS PubMed.
- C. Gayner and Y. Amouyal, Adv. Funct. Mater., 2020, 30, 1901789 CrossRef CAS.
- A. Pakdel, Q. Guo, V. Nicolosi and T. Mori, J. Mater. Chem. A, 2018, 6, 21341–21349 RSC.
- H. Cho, S. Y. Back, J. H. Yun, S. Byeon, H. Jin and J. S. Rhyee, ACS Appl. Mater. Interfaces, 2020, 12, 38076–38084 CrossRef CAS PubMed.
- C. Gayner and Y. Amouyal, Adv. Funct. Mater., 2019, 30, 1901789 CrossRef.
- F. Brochin, B. Lenoir, X. Devaux, R. Martin-Lopez and H. Scherrer, J. Appl. Phys., 2000, 88, 3269–3275 CrossRef CAS.
- Q. Hu, W. Qiu, L. Chen, J. Chen, L. Yang and J. Tang, ACS Appl. Mater. Interfaces, 2021, 13, 38526–38533 CrossRef CAS PubMed.
- J. H. Kim, A. Feldman and D. Novotny, J. Appl. Phys., 1999, 86, 3959–3963 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh01226j |
| ‡ Equal contribution to this work. |
| This journal is © The Royal Society of Chemistry 2023 |