Hexagonal boron nitride nanophotonics: a record-breaking material for the ultraviolet and visible spectral ranges

Abstract

A global trend towards miniaturization and multiwavelength performance of nanophotonic devices drives research on novel phenomena, such as bound states in the continuum and Mietronics, as well as surveys for high-refractive index and strongly anisotropic materials and metasurfaces. Hexagonal boron nitride (hBN) is one of the promising materials for future nanophotonics owing to its inherent anisotropy and prospects of high-quality monocrystal growth with an atomically flat surface. Here, we present highly accurate optical constants of hBN in the broad wavelength range of 250–1700 nm combining imaging ellipsometry measurements, scanning near-field optical microscopy and first-principles quantum mechanical computations. hBN's high refractive index, up to 2.75 in the ultraviolet (UV) and visible range, broadband birefringence of ∼0.7, and negligible optical losses make it an outstanding material for UV and visible range photonics. Based on our measurement results, we propose and design novel optical elements: handedness-preserving mirrors and subwavelength waveguides with dimensions of 40 nm operating in the visible and UV ranges, respectively. Remarkably, our results offer a unique opportunity to bridge the size gap between photonics and electronics.

---

New concepts

High refractive index, optical anisotropy, and transparency are the main figures of merit for the materials that define modern nanophotonics. Novel natural materials combining all three properties are in high demand. In this work, we present hBN as a promising material for the visible and ultraviolet ranges. We determined the exact values of anisotropic dielectric permittivity tensor of hBN in a broad spectral range (250–1700 nm) using cross-validation of far- and near-field techniques, accompanied by first-principles calculations. Our results show high refractive index, transparency over the whole studied spectral range and giant optical anisotropy of Δn ∼ 0.7. Based on our measurement results, we propose and design novel optical elements: handedness-preserving mirrors and subwavelength waveguides with dimensions of 40 nm operating in the visible and UV ranges, respectively. Remarkably, our results offer a unique opportunity to bridge the size-gap between photonics and electronics.

Introduction

The rise of all-dielectric nanostructures,¹ consisting of Mie-resonant nanoparticles,² makes clear the importance of lossless high refractive index materials.³ For a given wavelength of light λ, it is the refractive index n that controls the minimum size (∼λ/n) of nanostructure features, and boosts the field enhancement factor and resonance figure of merit.⁴ In turn, the absence of loss guarantees the presence of high-quality resonance and/or secures long-distance light propagation.⁵ For this purpose, researchers usually leverage silicon (Si),⁶ gallium phosphide (GaP),⁷ or titanium dioxide (TiO₂).⁸

At the same time, recent works^9–12 have revealed that layered materials such as transition metal dichalcogenides (TMDs)¹³ could also serve as high refractive index materials. Furthermore, the layered structure, unlike in the case of traditional semiconductors (Si, GaP, and TiO₂), essentially produces a giant optical anisotropy,¹⁴ which is now recognized as an indispensable degree of freedom. As a result, TMDs enable numerous photonic phenomena: extreme skin-depth engineering,¹⁵ exciton–polariton transport,¹⁶ Zenneck surface waves,¹⁷ and sophisticated anapole states.¹¹ Nevertheless, TMDs strongly absorb light in the visible and ultraviolet spectral intervals, which severely limits their operation range.

By contrast, hexagonal boron nitride (hBN) is a promising wide-band gap material,¹⁸ as it consolidates all three advantages: broadband zero optical losses, high-index, and giant optical anisotropy. Besides, hBN is an essential building block for two-dimensional electronic and optoelectronic devices,¹⁹ being widely used as a high-quality dielectric and encapsulation material.²⁰ Despite the wide use of hBN in nanophotonics and optoelectronics, only a few studies^21–23 have determined its anisotropic optical response and in the relatively narrow wavelength ranges of 245–310 nm,²¹ 220–780 nm,²² and 1530 nm.²³ Furthermore, the optical properties were studied via transmittance spectroscopy and micro-reflectance, which have a limited accuracy, and the near-field microscopy, which yields a result at a single wavelength. Therefore, highly accurate broadband optical properties of hBN measured by ellipsometry are in strong demand. However, the typical flake size of hBN is much smaller than required for most ellipsometers, which makes its ellipsometry challenging.

In this work, we performed the first broadband (250–1700 nm) ellipsometric measurement of the anisotropic dielectric function of hBN using an imaging ellipsometer that can collect the signal from a single flake.¹⁴ We refined and validated the measured optical properties via a combined experimental and theoretical study, which included micro-transmittance,²⁴ scattering near-field optical microscopy,^14,23 and first-principles quantum mechanical computations.^14,25 We discovered that hBN has no losses and giant birefringence (Δn ∼ 0.7) throughout the whole spectral range. As a result, hBN complements titanium dioxide in the deep-, mid-, and near-ultraviolet intervals as a high-index material. The acquired optical properties allow hBN to take its place among other high refractive index anisotropic materials, including MoS₂,¹⁴ InGaS₃,²⁶ BaTiS₃,²⁷ and α-MoO₃.²⁸ hBN enables the next-generation high-performance photonic elements, operating at visible and ultraviolet frequencies,²⁹ which we demonstrate by designing a handedness-preserving mirror and a 50 nm-wide subwavelength waveguide with an unprecedented integration density.

Results

Far- and near-field studies of hBN's dielectric tensor

Fig. 1a shows the crystal structure of hBN. Similar to many other layered materials (MoS₂, WS₂, etc.), hBN has a honeycomb lattice within the layers bound by weak van der Waals forces. Therefore, hBN has a diagonal dielectric tensor in the form of diag(n_ab², n_ab², n_c²), where n_ab and n_c are the complex refractive indices along the crystallographic ab-plane and c-axis, respectively (see Fig. 1a).¹⁴

Fig. 1 Optical properties of hBN. (a) Crystal structure of hBN. (b) Optical and (c) AFM images of a hBN flake. (d) Refractive index (n) and extinction coefficient (k) along the crystallographic ab-plane and c-axis. DFT (density functional theory) in labels refers to the first-principles computations. (e) Measured (black line) and calculated (blue line) transmittance spectra. The inset shows Raman spectra taken from the flake presented in (b).

The measurement of the hBN anisotropic dielectric tensor is a challenging task owing to numerous experimental difficulties. First of all, etalon data can be acquired only with exfoliated flakes. Indeed, exfoliation produces monocrystals with a minimum number of defects,³⁰ whereas chemically⁹ or physically³¹ synthesized thin films have a polycrystalline structure and numerous defects. As a result, we expect that chemically or physically synthesized hBN will result in slightly lower optical constants and, therefore, slightly lower device performance, compared to exfoliated ones, by analogy with MoS₂.³¹ Nonetheless, the rapid development in van der Waals crystals’ synthesis gives us hope that soon chemically or physically synthesized hBN will achieve the optical response of its exfoliated counterpart,³² since they are more promising for industry owing to their large scale. However, exfoliation, at best, could provide a sample size of only a hundred micrometers (Fig. 1b), which severely limits the choice of spectroscopy techniques. Secondly, standard transmittance and reflectance measurements probe only the in-plane dielectric response and are not sensitive to the out-of-plane component.^33,34 Fortunately, the imaging spectroscopic ellipsometer¹⁴ can solve both problems. It is a hybrid of an optical microscope and an ellipsometer, which allows us to record the local optical signal (microscope advantage), and at oblique angles, thereby probing the full dielectric tensor (ellipsometry advantage).

Note S1 (ESI†) shows experimental spectra of ellipsometric parameters Ψ (amplitude) and Δ (phase). Note that we chose a thick sample of 310 nm to identify the transparency region (see Fig. 1c). Remarkably, one can notice pronounced Fabri–Perot oscillations in Ψ and Δ (Note S1, ESI†) in the whole measured spectral interval (250–1700 nm). This implies zero optical losses of hBN in this range. Therefore, the Cauchy model¹⁴ describes both parts (n_ab and n_c) of the dielectric tensor (see Methods). Fig. 1d shows the resulting dielectric function in comparison with the first-principles calculations (see Methods). Experimental optical constants have a perfect match with the theoretical values (see Fig. 1d). As an additional verification, we also recorded transmittance spectra, which yield a good agreement (see Fig. 1e) with the transfer matrix calculations³⁵ based on the dielectric function from Fig. 1d, whereas the Raman measurements (see the inset of Fig. 1e) confirm the hexagonal structure of hBN.³⁶ However, far-field measurements can only confirm the in-plane component of the dielectric tensor.

For this reason, we also analysed the near-field distribution of the signal scattered by the hBN flake, which forms a planar waveguide, using a scattering-type near-field optical microscope (s-SNOM). The effective mode index in such a configuration strongly depends on both the in-plane and the out-of-plane dielectric functions allowing us to conduct an unambiguous validation. We used incident wavelengths in the range of 700–1000 nm to excite the mode inside the structure by focusing the light on the tip of a s-SNOM. The excited cylindrical waves propagate inside the hBN flake and scatter at the edge of the flake. That scattered field interferes with the background signal thus giving the oscillating pattern of the near-field amplitude signal (see Fig. 2a and b). To retrieve the effective mode index from the measurements we analyzed the near-field phase and amplitude simultaneously by studying the complex Fourier transform (FT) (see Fig. 2c). FT has two pronounced peaks: the one around q = 0 corresponds to the strong tip-sample interaction; meanwhile, the one at finite q corresponds to the waveguide mode. Note that the observed effective mode index is different from the real effective index of the mode, which is a consequence of the specific geometry of the experiment.^14,16,23 The shift from the actual mode is described by the following relation:

n_eff = n_SNOM − cos(α) sin(β),

where n_eff is the effective index of the mode, propagating inside the planar waveguide n_SNOM is the effective index obtained from the near-field measurements, α = 45° is the angle between the illumination wavevector and its projection on the sample's surface plane and β = 30° is the angle between the projection of the wavevector and the flake edge. Additionally, we did not observe standing waves (reflection from the edge) during the near-field measurements. Otherwise, the observable effective mode index would be doubled compared to the effective index of the propagating mode and would be around 3,³⁷ which is clearly not the case, as seen from the Fourier spectra in Fig. 2c.

Fig. 2 Near-field analysis of hBN. (a) Near-field images, real part Re(E) and phase Arg(E), of the electric field E taken at 1000 nm (top) and 720 nm (bottom). (b) x-Line scans taken from panel (a) and averaged over 1.1 μm along the y-axis (other wavelength images are collected in Note S2, ESI†). (c) Fourier transform (FT) amplitude of the complex near-field signal in (b). Green arrows mark the peak associated with the waveguide mode. (d and e) Transfer matrix calculations for the hBN/SiO₂ system for anisotropic and isotropic (with the assumption of optical constants for the c-axis being equal to those for the ab-plane) hBN optical models. The experimental (q = 1/λ, E = hc/λ) data points (blue circles) show good agreement with the calculated dispersion based on the anisotropic dielectric function presented in Fig. 1d.

Given the extracted refractive index components n_ab and n_c, we calculated the energy (E = hc/λ)−momentum (q = 1/λ) dispersion relation of the waveguide mode using the transfer matrix method.³⁵ The experimental data points (blue circles) can be observed on the top of the dispersion color map (see Fig. 2d and e). Apparently, experimental points agree perfectly with the anisotropic model (see Fig. 2d) and sharply disagree with an isotropic model (see Fig. 2e) where n_c is set to be equal to n_ab. Consequently, the excellent agreement between the experimental and theoretical dispersion unambiguously validates our dielectric permittivity of hBN, presented in Fig. 1d.

Comparison of hBN's optical response with those of other materials

It is worth comparing hBN's optical properties with those of other materials (see Fig. 3). Firstly, hBN's transparency region is the widest among those of traditionally used and novel materials. As a result, it fills the spectral gap for short wavelengths (gray areas in Fig. 3) and favors hBN in broadband all-dielectric nanophotonics. Secondly, its refractive index is higher than 2 in the visible and infrared spectral intervals and approaches 2.75 at the ultraviolet wavelengths. Thus, hBN enriches the list of high-index materials. Finally, hBN's birefringence outperforms most anisotropic materials and thereby complements the library of materials with giant optical anisotropy. Altogether, these properties create a firm foothold for advanced photonic engineering, as demonstrated in the next section, especially for ultraviolet and visible frequencies.

Fig. 3 hBN in the core of high-refractive-index birefringent materials. (a) Refractive index and (b) birefringence of conventional materials compared in their respective transparency windows. Gray areas show the panel's spectral ranges, where hBN outperforms other materials in refractive index and birefringence, making it the best candidate for photonic applications.

Handedness-preserving mirrors and subwavelength waveguides

Reasonably high refractive index (∼2.2) and negligible absorption loss in the visible range make hBN an interesting material for a variety of optical applications. As an example of a potential application, we demonstrate the performance of a handedness-preserving mirror. By this term we refer to a planar structure that, at a particular wavelength, can reflect a circularly polarized plane wave of a given handedness without flipping its handedness but is transparent for the wave of opposite handedness at the same wavelength.^38,39

To that end, we utilize the design proposed by Semnani and coworkers.⁴⁰ The structure is presented by a dielectric photonic crystal slab with a square lattice and its unit cell containing a circular hole in the middle and two satellite elliptical holes, shown in Fig. 4a. As a result of this arrangement, the structure possesses only mirror symmetry with respect to the horizontal plane, M_xy, and two-fold rotational symmetry around the z-axis C_z². These symmetries are crucial for the desired polarization response of the structure.⁴¹

Fig. 4 Prospective applications of high refractive index birefringent hBN. Handedness-preserving mirror (a–c) and subwavelength waveguide (d and e). (a) Geometry of the unit cell of the dielectric handedness-preserving mirror. (b) Spectra of intensity reflection and transmission coefficients of the optimal handedness-preserving mirror made of an hBN film on the circular polarization basis for a right-handed incident plane wave. (c) The same as (b) for a left-handed incident plane wave. (d) Schematic comparison of the dimensions of waveguides made from high-refractive index materials: 48 × 48 nm² for hBN, 81 × 81 nm² for MoS₂, 88 × 88 nm² for TiO₂, and 250 × 250 nm² for Si. (e) Waveguide width for different materials with constant . The inset shows the adjacent waveguides. (f) Relation of crosstalk length and distance between cores of the waveguides for high-refractive index materials. The width is optimized for each point.

We illustrate the applicability of hBN for this purpose by designing such a handedness-preserving mirror at a target wavelength of 550 nm. Numerical optimization was performed with the use of the particle swarm algorithm in a finite-difference time domain (FDTD) commercial solver (Lumerical). By enforcing sub-diffraction periodicity of the mirror, we obtain the set of unit cell dimensions yielding near-perfect polarization conversion for normally incident light at the target wavelength: L = 490 nm, H = 235 nm, r_c = 55 nm, r_x = 155 nm, r_y = 66 nm, C_x = 48 nm, C_y = 100 nm, and θ = 0°. With this set of dimensions, the mirror reflects a normally incident right-handed (RH) plane wave back into an RH wave with near-unity efficiency, |r_RR|² ≈ 0.93 (see Fig. 4b). At the same time, a left-handed (LH) incident wave is nearly perfectly transmitted into an RH wave, |t_RL|² ≈ 0.96, as seen from Fig. 4c.

Aside from chiral optics, we envision the usage of hBN in integrated nanophotonics,⁴² a promising technology for efficient parallel data processing required for artificial intelligence systems.⁴³ However, integrated photonic elements are still much larger compared to electronic counterparts, due to the diffraction limit imposed by the wave nature of light. Hence, to make photonic elements compact, one should operate close to the minimum wavelength of the material transparency window, which is the smallest for hBN (see Fig. 2).

To assess hBN as a photonic material, we studied the performance of the photonic waveguides based on hBN and compared them with the waveguides based on other high-index materials, such as MoS₂, TiO₂, and Si (see Fig. 4d). We considered waveguides operating at the lowest possible wavelength λ (250, 370, 700, and 1000 nm for hBN, TiO₂, MoS₂, and Si, respectively), where the core material optical losses are negligible. For material comparison, we limited our analysis to square-shape waveguides with a given exponential decay 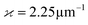(see inset in Fig. 4e) of mode field in the cladding (SiO₂), defined as:

where n_eff is the effective index of the mode, and n_s is the refractive index of the waveguide cladding. Such a strong decay ensures relatively low crosstalk noise. Under these constraints, we concluded that the hBN waveguide width can be as small as 47 nm, bringing the size scale of photonic elements down to that of electronic components (see Fig. 4e). This surprising result originates from the low operation wavelength (λ ∼ 250 nm), high refractive index (n ∼ 2.8), and giant anisotropy (Δn ∼ 0.9). Notably, MoS₂ outperformed TiO₂ (see Fig. 4e) despite its twice as high operating wavelength thanks to its much higher refractive index and stronger optical anisotropy.

The integration density of photonic elements is not limited by their physical dimensions but rather by the evanescent field coupling between adjacent waveguides. When the lateral distance between waveguides d decreases, the crosstalk distance L_ct characterizing the coupling strength decreases exponentially (Fig. 4f). During calculations, the width of the square-shaped waveguide was optimized to maximize L_ct. Again, hBN and MoS₂ demonstrate the best results, owing to their high refractive index and giant anisotropy. For instance, hBN waveguides with a 10 mm crosstalk length can only be separated by 270 nm. Hence, a 1 mm chip can accommodate up to 3700 separate waveguides, operating at a high frequency (ν = c/λ = 1.2 × 10¹⁵ Hz). However, the current realization of hBN integrated circuits and ultraviolet nanophotonics is in its infancy nowadays.²⁹ Although, major challenges here are technical: related to assembling of the measurements setup consisting of an ultraviolet laser with λ ∼ 250 nm with corresponding optical elements. As a result, photonic integrated circuits based on such waveguides can potentially revolutionize integrated photonics and the semiconductor industry.

Conclusions

High refractive index, optical anisotropy, and transparency are the main figures of merit for the materials that define modern nanophotonics. Novel natural materials combining all three properties are in high demand. In this work, we present hBN as a promising material for the visible and ultraviolet range. We determined the exact values of the anisotropic dielectric permittivity tensor of hBN in the broad spectral range (250–1700 nm) using cross-validation of far- and near-field techniques, accompanied by first-principles calculations. Our results show high refractive index, transparency over the whole studied spectral range and giant optical anisotropy of Δn ∼ 0.7. Furthermore, we suggest applications of hBN for chiral optics and integrated photonics. We propose designs of handedness-preserving mirrors and subwavelength waveguides based on hBN. In the case of waveguides, hBN shows outstanding performance: the waveguide width can be as small as 40 nm with the integration density exceeding 3000 elements per mm. These conclusions are also applicable to few-layer hBN samples. Indeed, the optical response of few-layer van der Waals crystals is slightly lower than those for bulk samples,⁴⁴ because increased electron–electron interaction results in an enlarged quasiparticle band gap and, therefore, enlarged optical band gap. In general, according to the Kramers–Kronig relation, it leads to a small reduction of optical constants for few-layered samples. Overall, our results demonstrate that hBN can become a key material for future ultraviolet nanophotonics.

Methods

Sample preparation

Bulk hBN crystals were purchased from 2D Semiconductors (Scottsdale, USA) and exfoliated on top of required substrates: Si/SiO₂ and CaF₂. Prior to exfoliation, the corresponding substrates were sequentially cleaned in acetone, iso-propanol, and deionized water. Then, these were subjected to oxygen plasma (O₂) to remove the ambient adsorbates. Following the plasma cleaning, substrates were put on a hot plate at temperatures of 120–140 °C for 2 minutes. After the heating, scotch-tape from Nitto Denko Corporation (Osaka, Japan) with loaded crystal hBN was brought in contact with the substrates. Afterwards, the tape was removed completing the exfoliation procedure.

Imaging ellipsometry

For determination of the hBN anisotropic dielectric tensor, we used a Accurion nanofilm_ep4 ellipsometer. Measurements were performed in a broad spectral range of 250–1700 nm in steps of 1 nm at several incident angles 45°, 50°, and 55° with a 7× objective. Our imaging spectroscopic ellipsometer Accurion nanofilm_ep4 device is equipped with a monochromator. Here, each wavelength is measured separately to survey the spectra. The manufacturer proposes 1 μm² threshold for the size of the measured samples. Meanwhile, from our experience, to achieve reliable data in the case of hBN, the smallest sample should have a surface area of 10 μm². For optical constant dispersion analysis, we implemented Cauchy model n(λ) = A + B/λ² + C/λ⁴, where A, B, and C are Cauchy fitting parameters, for both the in-plane and the out-of-plane components.

First-principles calculations

First-principles calculations of optical constants of hBN were performed within the Vienna ab initio simulation package (VASP).^45,46 First, the atomic positions of the crystal were relaxed using a standard density functional theory (DFT) approach until the interatomic forces were less than 10⁻³ eV Å⁻¹. Second, the initial Kohn–Sham orbitals were calculated with electronic self-consistent cycle convergence criteria of 10⁻⁸ eV. Finally, the real and imaginary parts of the frequency-dependent dielectric function were obtained using single-shot GW calculation.⁴⁷ The cutoff energy of the plane wave basis set was set to 500 eV, and the Γ-centered 15 × 15 × 5 k-points mesh was used to sample the first Brillouin zone. The GW-type projector-augmented wave pseudopotentials⁴⁸ were used to describe the behaviour of the wavefunctions in the core region and the exchange–correlation effects of electrons.

Raman spectroscopy

The Raman spectra were measured with a confocal scanning Raman microscope Horiba LabRAM HR Evolution (HORIBA Ltd, Kyoto, Japan) equipped with a 632.8 nm linearly polarized laser, 600 lines per mm diffraction grating, and ×100 objective (N.A. = 0.90) in a spectral range of 1200–2400 cm⁻¹. The spectra were recorded with 0.7 mW incident laser power, a spot size of ∼0.86 μm and an integration time of 10 s with 10 spectra accumulation. Unpolarised detection was used to provide a higher signal-to-noise ratio.

Microtransmittance spectra

An Accurion nanofilm_ep4 ellipsometer was used for microtransmittance measurements at normal incidence for 250–1700 nm in steps of 1 nm. Input and output ellipsometer branches were set vertically with polarizer, compensator, and analyser positions at 0°. During the measurements at each wavelength, we recorded the intensity image and used only a part of the sample. For reference, we also measured air transmittance intensity.

Near-field optical nano-spectroscopy

Near-field imaging was performed with the use of a commercially available scattering scanning near-field optical microscope (s-SNOM, neaSNOM www.neaspec.com). For sample illumination, we used a monochromatic tunable Ti:sapphire laser (https://www.avesta.ru) of wavelength from 700 to 1000 nm spectral interval. The microscope was used in reflection mode, which means that to focus the light on and collect the signal from the probe-sample interface the same parabolic mirror was used (Note S2, ESI†). The near-field signal was filtered from the raw detector data using a pseudo-heterodyne interferometer at high harmonics (the third one). For the measurement a platinum/iridium5 (PtIr₅) coated AFM tip (ARROW-NCPt-50, https://www.nanoworld.com) with a resonant frequency of around 275 kHz and tapping amplitude 47 nm was used.

Numerical calculations for handedness-preserving mirrors

Numerical simulations of the handedness-preserving mirrors were performed using commercial finite-difference time-domain solver (Lumerical). The structure was excited with two normally-incident plane wave sources emulating either a right-handed, or a left-handed circularly polarized plane wave. Elements of the scattering matrix on the basis of circular polarizations were obtained by calculating the overlap of the scattered (reflected and transmitted) field with the fields of right-handed and left-handed waves.

Numerical calculations for waveguides

Numerical calculations for waveguide width with constant and waveguide crosstalk length were performed using a combination of COMSOL Multiphysics and MATLAB via a live link. COMSOL was used as a solver, and for every task a simple 2D geometry model was used. MATLAB was used to optimize the geometry for the solver, finding the exact width of the waveguide for a given and optimizing the width of the waveguides to achieve maximum crosstalk length with a given distance between the centers of the cores. For the first task, a simple binary search algorithm was used. For the second task we used modification of a gradient descent algorithm.

Author contributions

V. V. S., N. K. S., A. A. V., G. D. A., B. D. G., and E. G. A. suggested and directed the project. T. A. N. and G. D. A. prepared the samples. G. D. V., S. A.S., T. A. N., and E. G. A. performed the measurements. G. D. V., E. G. A., B. D. G., V. A. A., M. A. B., K. I. A., and V. K. V. provided theoretical support. G. D. V., E. G. A., and B.D.G., wrote the original manuscript. G. D. V., E. G. A., B. D. G., V. A. A., G. D. A., A. A. V., N. K. S., and V. V. S. reviewed and edited the paper. All the authors contributed to the discussions and commented on the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the MIPT's Shared Research Facilities Center for the use of their equipment. The authors gratefully acknowledge financial support from the Ministry of Science and Higher Education of the Russian Federation (Agreement no. 075-15-2021-606). A. A. V. acknowledges support from Russian Science Foundation (RSF) under grant number 22-19-00558 (ellipsometry), S. A. S. acknowledges support from RSF under grant number 21-72-10163 (s-SNOM), V. A. A. acknowledges support from RSF under grant number 22-79-10312 (theoretical investigations). N. K. S. is grateful to the Ministry of Education, Singapore (Research Center of Excellence award to the Institute for Functional Intelligent Materials I-FIM, project no. EDUNC-33-18-279-V12) and to the Royal Society (UK, grant number RSRP\R\190000) for support.

References

1. Y. Kivshar, Nano Lett., 2022, 22, 3513–3515.
2. A. B. Evlyukhin, S. M. Novikov, U. Zywietz, R. L. Eriksen, C. Reinhardt, S. I. Bozhevolnyi and B. N. Chichkov, Nano Lett., 2012, 12, 3749–3755.
3. J. B. Khurgin, ACS Photonics, 2022, 9, 743–751.
4. D. G. Baranov, D. A. Zuev, S. I. Lepeshov, O. V. Kotov, A. E. Krasnok, A. B. Evlyukhin and B. N. Chichkov, Optica, 2017, 4, 814.
5. A. H. Atabaki, S. Moazeni, F. Pavanello, H. Gevorgyan, J. Notaros, L. Alloatti, M. T. Wade, C. Sun, S. A. Kruger, H. Meng, K. Al Qubaisi, I. Wang, B. Zhang, A. Khilo, C. V. Baiocco, M. A. Popović, V. M. Stojanović and R. J. Ram, Nature, 2018, 556, 349–354.
6. A. B. Evlyukhin, M. Matiushechkina, V. A. Zenin, M. Heurs and B. N. Chichkov, Opt. Mater. Express, 2020, 10, 2706.
7. D. Khmelevskaia, D. I. Markina, V. V. Fedorov, G. A. Ermolaev, A. V. Arsenin, V. S. Volkov, A. S. Goltaev, Y. M. Zadiranov, I. A. Tzibizov, A. P. Pushkarev, A. K. Samusev, A. A. Shcherbakov, P. A. Belov, I. S. Mukhin and S. V. Makarov, Appl. Phys. Lett., 2021, 118, 201101.
8. G. A. Ermolaev, S. E. Kushnir, N. A. Sapoletova and K. S. Napolskii, Nanomaterials, 2019, 9, 651.
9. G. A. Ermolaev, Y. V. Stebunov, A. A. Vyshnevyy, D. E. Tatarkin, D. I. Yakubovsky, S. M. Novikov, D. G. Baranov, T. Shegai, A. Y. Nikitin, A. V. Arsenin and V. S. Volkov, npj 2D Mater. Appl., 2020, 4, 21.
10. T. D. Green, D. G. Baranov, B. Munkhbat, R. Verre, T. Shegai and M. Käll, Optica, 2020, 7, 680.
11. R. Verre, D. G. Baranov, B. Munkhbat, J. Cuadra, M. Käll and T. Shegai, Nat. Nanotechnol., 2019, 14, 679–684.
12. A. A. Popkova, I. M. Antropov, G. I. Tselikov, G. A. Ermolaev, I. Ozerov, R. V. Kirtaev, S. M. Novikov, A. B. Evlyukhin, A. V. Arsenin, V. O. Bessonov, V. S. Volkov and A. A. Fedyanin, Laser Photon. Rev., 2022, 16, 2100604.
13. G. Ermolaev, K. Voronin, D. G. Baranov, V. Kravets, G. Tselikov, Y. Stebunov, D. Yakubovsky, S. Novikov, A. Vyshnevyy, A. Mazitov, I. Kruglov, S. Zhukov, R. Romanov, A. M. Markeev, A. Arsenin, K. S. Novoselov, A. N. Grigorenko and V. Volkov, Nat. Commun., 2022, 13, 2049.
14. G. A. Ermolaev, D. V. Grudinin, Y. V. Stebunov, K. V. Voronin, V. G. Kravets, J. Duan, A. B. Mazitov, G. I. Tselikov, A. Bylinkin, D. I. Yakubovsky, S. M. Novikov, D. G. Baranov, A. Y. Nikitin, I. A. Kruglov, T. Shegai, P. Alonso-González, A. N. Grigorenko, A. V. Arsenin, K. S. Novoselov and V. S. Volkov, Nat. Commun., 2021, 12, 854.
15. G. Ermolaev, D. Grudinin, K. Voronin, A. Vyshnevyy, A. Arsenin and V. Volkov, Photonics, 2022, 9, 744.
16. F. Hu, Y. Luan, M. E. Scott, J. Yan, D. G. Mandrus, X. Xu and Z. Fei, Nat. Photonics, 2017, 11, 356–360.
17. V. E. Babicheva, S. Gamage, L. Zhen, S. B. Cronin, V. S. Yakovlev and Y. Abate, ACS Photonics, 2018, 5, 2106–2112.
18. J. D. Caldwell, I. Aharonovich, G. Cassabois, J. H. Edgar, B. Gil and D. N. Basov, Nat. Rev. Mater., 2019, 4, 552–567.
19. C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Nat. Nanotechnol., 2010, 5, 722–726.
20. D. A. Bandurin, E. Mönch, K. Kapralov, I. Y. Phinney, K. Lindner, S. Liu, J. H. Edgar, I. A. Dmitriev, P. Jarillo-Herrero, D. Svintsov and S. D. Ganichev, Nat. Phys., 2022, 18, 462–467.
21. M. A. McKay, J. Li, J. Y. Lin and H. X. Jiang, J. Appl. Phys., 2020, 127, 053103.
22. A. Segura, L. Artús, R. Cuscó, T. Taniguchi, G. Cassabois and B. Gil, Phys. Rev. Mater., 2018, 2, 1–6.
23. D. Hu, X. Yang, C. Li, R. Liu, Z. Yao, H. Hu, S. N. G. Corder, J. Chen, Z. Sun, M. Liu and Q. Dai, Nat. Commun., 2017, 8, 1471.
24. R. Frisenda, Y. Niu, P. Gant, A. J. Molina-Mendoza, R. Schmidt, R. Bratschitsch, J. Liu, L. Fu, D. Dumcenco, A. Kis, D. P. De Lara and A. Castellanos-Gomez, J. Phys. D: Appl. Phys., 2017, 50, 074002.
25. G. Álvarez-Pérez, T. G. Folland, I. Errea, J. Taboada-Gutiérrez, J. Duan, J. Martín-Sánchez, A. I. F. Tresguerres-Mata, J. R. Matson, A. Bylinkin, M. He, W. Ma, Q. Bao, J. I. Martín, J. D. Caldwell, A. Y. Nikitin and P. Alonso-González, Adv. Mater., 2020, 32, 1908176.
26. A. N. Toksumakov, G. A. Ermolaev, A. S. Slavich, N. V. Doroshina, E. V. Sukhanova, D. I. Yakubovsky, A. V. Syuy, S. M. Novikov, R. I. Romanov, A. M. Markeev, A. S. Oreshonkov, D. M. Tsymbarenko, Z. I. Popov, D. G. Kvashnin, A. A. Vyshnevyy, A. V. Arsenin, D. A. Ghazaryan and V. S. Volkov, npj 2D Mater. Appl., 2022, 6, 85.
27. S. Niu, G. Joe, H. Zhao, Y. Zhou, T. Orvis, H. Huyan, J. Salman, K. Mahalingam, B. Urwin, J. Wu, Y. Liu, T. E. Tiwald, S. B. Cronin, B. M. Howe, M. Mecklenburg, R. Haiges, D. J. Singh, H. Wang, M. A. Kats and J. Ravichandran, Nat. Photonics, 2018, 12, 392–396.
28. W. Ma, P. Alonso-González, S. Li, A. Y. Nikitin, J. Yuan, J. Martín-Sánchez, J. Taboada-Gutiérrez, I. Amenabar, P. Li, S. Vélez, C. Tollan, Z. Dai, Y. Zhang, S. Sriram, K. Kalantar-Zadeh, S. T. Lee, R. Hillenbrand and Q. Bao, Nature, 2018, 562, 557–562.
29. D. Zhao, Z. Lin, W. Zhu, H. J. Lezec, T. Xu, A. Agrawal, C. Zhang and K. Huang, Nanophotonics, 2021, 10, 2283–2308.
30. K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, Science, 2016, 353, 6298.
31. G. A. Ermolaev, M. A. El-Sayed, D. I. Yakubovsky, K. V. Voronin, R. I. Romanov, M. K. Tatmyshevskiy, N. V. Doroshina, A. B. Nemtsov, A. A. Voronov, S. M. Novikov, A. M. Markeev, G. I. Tselikov, A. A. Vyshnevyy, A. V. Arsenin and V. S. Volkov, Nanomaterials, 2021, 11, 1411.
32. L. Zhang, J. Dong and F. Ding, Chem. Rev., 2021, 121, 6321–6372.
33. S. Yoo and Q.-H. Park, Nanophotonics, 2022, 11, 2811–2825.
34. S. Lee, T. Jeong, S. Jung and K. Yee, Phys. Status Solidi, 2019, 256, 1800417.
35. N. C. Passler and A. Paarmann, J. Opt. Soc. Am. B, 2017, 34, 2128.
36. I. Stenger, L. Schué, M. Boukhicha, B. Berini, B. Plaçais, A. Loiseau and J. Barjon, 2D Mater., 2017, 4, 031003.
37. S. Dai, Z. Fei, Q. Ma, A. S. Rodin, M. Wagner, A. S. McLeod, M. K. Liu, W. Gannett, W. Regan, K. Watanabe, T. Taniguchi, M. Thiemens, G. Dominguez, A. H. C. Neto, A. Zettl, F. Keilmann, P. Jarillo-Herrero, M. M. Fogler and D. N. Basov, Science, 2014, 343, 1125–1129.
38. K. Voronin, A. S. Taradin, M. V. Gorkunov and D. G. Baranov, ACS Photonics, 2022, 9, 2652–2659.
39. A. Taradin and D. G. Baranov, J. Phys. Conf. Ser., 2021, 2015, 012012.
40. B. Semnani, J. Flannery, R. Al Maruf and M. Bajcsy, Light: Sci. Appl., 2020, 9, 23.
41. C. Menzel, C. Rockstuhl and F. Lederer, Phys. Rev. A, 2010, 82, 053811.
42. C. Sun, M. T. Wade, Y. Lee, J. S. Orcutt, L. Alloatti, M. S. Georgas, A. S. Waterman, J. M. Shainline, R. R. Avizienis, S. Lin, B. R. Moss, R. Kumar, F. Pavanello, A. H. Atabaki, H. M. Cook, A. J. Ou, J. C. Leu, Y.-H. Chen, K. Asanović, R. J. Ram, M. A. Popović and V. M. Stojanović, Nature, 2015, 528, 534–538.
43. B. J. Shastri, A. N. Tait, T. Ferreira de Lima, W. H. P. Pernice, H. Bhaskaran, C. D. Wright and P. R. Prucnal, Nat. Photonics, 2021, 15, 102–114.
44. G. A. Ermolaev, Y. V. Stebunov, A. A. Vyshnevyy, D. E. Tatarkin, D. I. Yakubovsky, S. M. Novikov, D. G. Baranov, T. Shegai, A. Y. Nikitin, A. V. Arsenin and V. S. Volkov, npj 2D Mater. Appl., 2020, 4, 1–6.
45. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
46. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
47. M. Shishkin and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 1–13.
48. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00215b

‡ G. D. V. and E. G. A. contributed equally.

---