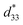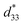Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhanced thermal stability by short-range ordered ferroelectricity in K0.5Na0.5NbO3-based piezoelectric oxides†
Soo-Yoon
Hwang‡
 a,
Gyoung-Ja
Lee‡
b,
Yuzhao
Qi
c,
Michael Abraham
Listyawan
d,
Kyung
Song
e,
Youngho
Kang
f,
Jungho
Ryu
a,
Gyoung-Ja
Lee‡
b,
Yuzhao
Qi
c,
Michael Abraham
Listyawan
d,
Kyung
Song
e,
Youngho
Kang
f,
Jungho
Ryu
 d,
Xiaoyan
Lu
d,
Xiaoyan
Lu
 c,
Min-Ku
Lee
*b and
Si-Young
Choi
c,
Min-Ku
Lee
*b and
Si-Young
Choi
 *agh
*agh
aDepartment of Materials Science and Engineering, Pohang University of Science and Technology, Pohang 37673, Republic of Korea. E-mail: youngchoi@postech.ac.kr
bNuclear System Integrity Sensing & Diagnosis Division, Korea Atomic Energy Research Institute, Daejeon 34057, Republic of Korea. E-mail: leeminku@kaeri.re.kr
cSchool of Civil Engineering, Harbin Institute of Technology, Harbin 150001, China
dSchool of Materials Science and Engineering, Yeungnam University, Gyeongsan 38541, Republic of Korea
eDepartment of Materials Analysis and Evaluation, Korea Institute of Materials Science, Changwon 51508, Republic of Korea
fDepartment of Materials Science and Engineering, Incheon National University, Incheon 22012, Republic of Korea
gCenter for Van der Waals Quantum Solids, Institute for Basic Science, Pohang 37673, Republic of Korea
hDepartment of Semiconductor Engineering, Pohang University of Science and Technology, Pohang, 37673, Republic of Korea
First published on 28th April 2023
Abstract
Industrial application of lead-free piezoelectric ceramics is prevented by intrinsic thermal instability. Herein, we propose a method to achieve outstanding thermal stability of converse piezoelectric constant (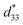 ) in lead-free potassium sodium niobate (KNN)-based ceramics by inducing a synergistic interaction between the grain size and polar configuration. Based on computational methods using phase-field simulations and first-principles calculations, the relationship between the grain size and polar configuration is demonstrated, and the possibility of achieving improved thermal stability in fine grains is suggested. A set of KNN systems is presented with meticulous dopant control near the chemical composition at which the grain size changes abnormally. Comparing the two representative samples with coarse and fine grains, significant enhancement in the thermal stability of
) in lead-free potassium sodium niobate (KNN)-based ceramics by inducing a synergistic interaction between the grain size and polar configuration. Based on computational methods using phase-field simulations and first-principles calculations, the relationship between the grain size and polar configuration is demonstrated, and the possibility of achieving improved thermal stability in fine grains is suggested. A set of KNN systems is presented with meticulous dopant control near the chemical composition at which the grain size changes abnormally. Comparing the two representative samples with coarse and fine grains, significant enhancement in the thermal stability of 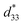 is exhibited up to 300 °C in the fine grains. The origin of the thermal superiority in fine-grained ceramics is identified through an extensive study from a microstructural perspective. The thermal stability is realized in a device by successfully demonstrating the temperature dependence of piezoelectricity. It is notable that this is the first time that lead-free piezoelectric ceramics are able to achieve exceptionally stable piezoelectricity up to 300 °C, which actualizes their applicability as piezoelectric devices with high thermal stability.
is exhibited up to 300 °C in the fine grains. The origin of the thermal superiority in fine-grained ceramics is identified through an extensive study from a microstructural perspective. The thermal stability is realized in a device by successfully demonstrating the temperature dependence of piezoelectricity. It is notable that this is the first time that lead-free piezoelectric ceramics are able to achieve exceptionally stable piezoelectricity up to 300 °C, which actualizes their applicability as piezoelectric devices with high thermal stability.
New conceptsDue to environmental concerns, lead-free piezoelectric oxides have been widely investigated for replacing conventional Pb-based oxides. Unfortunately, their application has been limited by the intrinsic thermal degradation of piezoelectric properties. We provide a new approach to enhance the thermal stability of piezoelectricity in lead-free K0.5Na0.5NbO3(KNN)-based oxides. Through computational prediction, we obtained a clue as to improving temperature stability by microstructural control of polycrystalline KNN; the short-range ordered ferroelectricity is sustainable up to high temperatures in fine grains, thereby increasing thermal stability with the synergistic effect of polar pinning by more grain boundaries together. Compared to coarse-grained KNN with typical long-range ordered ferroelectricity, ferroelectric ordering is largely prohibited in fine-grained KNN, and we finally realize thermally-stable KNN oxides with exceptional sustainability at high temperatures up to 300 °C. This is the first time that lead-free piezoelectric ceramics achieve the extraordinary thermal stability of piezoelectricity at high temperatures, up to 300 °C, with negligible loss and fluctuation. This highly-enhanced thermal stability is especially prominent in harsh environments, and we actually applied our fine-grained KNN ceramics to sense the safety of nuclear reactors. We believe our study will contribute significantly to designing high temperature lead-free piezoelectric materials. |
Introduction
Piezoelectric ceramics, such as sensors, actuators, and transducers, are widely utilized in industry to convert mechanical energy to electrical energy and vice versa.1 While lead zirconate titanate (PZT), a representative piezoelectric material, has sufficiently fulfilled its role, its use will be restricted in the near future due to the toxicity, impact on human health, and environmental issues associated with lead. Therefore, lead-free piezoelectric substitutes have been suggested, including potassium sodium niobate (KNN), bismuth sodium titanate (BNT), barium titanate (BT), and barium calcium zirconium titanate (BCZT).2–10 KNN is known for its relatively higher piezoelectric constant (dij) and Curie temperature (Tc) compared to other lead-free ceramics; however, it still cannot completely replace lead-based ceramics with better performance. A polymorphic/morphotropic phase boundary (PPB/MPB) was introduced to improve the piezoelectric performance of KNN.11–13 The phase boundaries can stabilize multiphase coexistence, enabling easy polarization rotation and low domain wall energy, thereby improving piezoelectricity. However, this boundary engineering has limitations in terms of thermal stability. This is because the structural changes in the boundary region are sensitive to slight temperature deviations. This rapid phase transition with temperature-dependent fluctuations in piezoelectric characteristics can lead to undesirable temperature sensitivity.14 The thermal instability prevents industrial applications, which prioritize constant performance without loss or fluctuation at high temperatures. To solve this thermal weakness, a broad and successive phase boundary, that is, diffused with merged dielectric peaks with respect to temperature, was constructed over a wide temperature range via composition optimization.15 The designed KNN systems were reported with improved thermal stability of converse piezoelectric constant,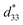 (Smax/Emax), for example, varying ∼5% to 100 °C,16 ∼5% to 150 °C,17 and ∼19% to 170 °C.18 The excellent piezoelectric performance and improved thermal stability were enabled by the suppression of abrupt structural transitions and the reduction of temperature sensitivity with a broad phase boundary.
(Smax/Emax), for example, varying ∼5% to 100 °C,16 ∼5% to 150 °C,17 and ∼19% to 170 °C.18 The excellent piezoelectric performance and improved thermal stability were enabled by the suppression of abrupt structural transitions and the reduction of temperature sensitivity with a broad phase boundary.
Another prevalent method for maintaining large piezoelectric properties in a wide temperature range is inducing relaxor ferroelectric behavior with diffused dielectric permittivity, which is favorable for high-temperature applications.11,19,20 However, the effect of relaxor behavior on the thermal stability of the piezoelectric property, 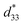 , still needs to be further investigated. Previous studies have shown that relaxor behavior is generally accomplished via multi-element doping with various ionic radii and valence states, resulting in (i) the mixing of polar and nonpolar phases or (ii) random electric fields with nanosized polar domains (polar nanoregions, PNRs).21–25 In polycrystalline ceramics, the relaxor ferroelectric behavior is also closely correlated with the grain size.26 Many studies have reported that relaxor ferroelectric behavior is preferred with decreasing grain size, which is analogous with the fact that domain size is proportional to the (grain size)1/2 in ferroelectric ceramics. The origin of this trend is complex. Some researchers have suggested that this tendency is caused by the weakening of long-range polar interactions due to the unreleased internal stresses in fine grains.27 Others have assumed that dopants acting as grain growth inhibitors simultaneously hinder the long-range domain configuration in fine grains.28 Yet others have reported that a large ratio of grain boundaries with low permittivity can be attributed to relaxor behavior in fine grains.29
, still needs to be further investigated. Previous studies have shown that relaxor behavior is generally accomplished via multi-element doping with various ionic radii and valence states, resulting in (i) the mixing of polar and nonpolar phases or (ii) random electric fields with nanosized polar domains (polar nanoregions, PNRs).21–25 In polycrystalline ceramics, the relaxor ferroelectric behavior is also closely correlated with the grain size.26 Many studies have reported that relaxor ferroelectric behavior is preferred with decreasing grain size, which is analogous with the fact that domain size is proportional to the (grain size)1/2 in ferroelectric ceramics. The origin of this trend is complex. Some researchers have suggested that this tendency is caused by the weakening of long-range polar interactions due to the unreleased internal stresses in fine grains.27 Others have assumed that dopants acting as grain growth inhibitors simultaneously hinder the long-range domain configuration in fine grains.28 Yet others have reported that a large ratio of grain boundaries with low permittivity can be attributed to relaxor behavior in fine grains.29
In this work, we studied the effect of grain size on polar configuration and thermal stability at the nanoscale through phase-field simulations and first-principles calculations. Based on computational prediction, we synthesized a set of KNN-based ceramics via meticulous segmentation of the BiScO3 (BS) doping concentration near the chemical composition where abnormal grain growth exists.30 Through a comprehensive evaluation of the microstructure, phase distribution, electrical properties, and thermal stability of piezoelectricity, two representative samples with coarse and fine grains were selected. The origin of the thermal stability of piezoelectricity was elucidated by atomic-scale analysis using (scanning) transmission electron microscopy ((S)TEM). Then, cantilever-type bending actuators were fabricated using coarse-/fine-grained KNN-based ceramics and tested at temperatures up to 150 °C. This is the first study to achieve lead-free piezoelectric ceramics with an outstanding thermal stability of 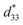 up to 300 °C and to realize its applicability as an actual piezoelectric device with high thermal stability.
up to 300 °C and to realize its applicability as an actual piezoelectric device with high thermal stability.
Results and discussion
Computational approaches to design thermally stable lead-free KNN ceramics
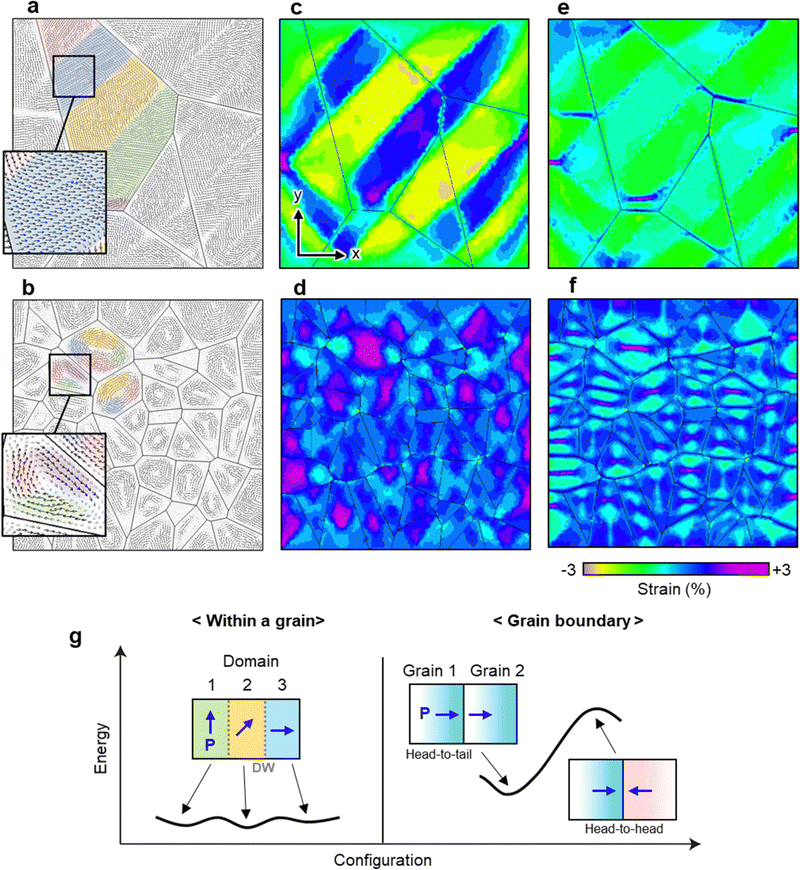
We first performed phase-field simulations to model the relationship between the grain size and polar domain configurations in a macroscopic view, as shown in Fig. 1a and b. The size of the simulation was taken as 100 nm × 100 nm for reference. The area was segmented into 6 and 50 grains for coarse and fine grains, respectively. In the case of the coarse grains (Fig. 1a), stripe-shaped domains exist with a typical width of approximately 20 nm. As the grain size decreases, the grain boundary effect increases, which enhances the perturbation of the polarization inside the limited grain range and smaller domains are formed in the fine grains (Fig. 1b). We note that most polarization orders are segmented into short ones, forming swirling multidirectional nanodomains in the fine grains. As a result of different domain configurations, the strain distribution also varies. Fig. 1c and d show total strain maps along x for the coarse and fine grains, respectively. The total strain in coarse-KNN represents good matching with the polar domain structures showing stripe-shaped separation. In contrast, distinctive strain separation is suppressed in fine-KNN, forming multidirectional nanodomain structures. Referring to Fig. 1e and f, the elastic strain maps along x indicate the coarse and fine grains, respectively. The final elastic strains in coarse-KNN are small due to the favorable domain configuration. However, the elastic strains in fine-KNN, both for the normal and shear strains, are relatively large due to the swirling-like domain structures with non-uniform low symmetry phases. Internal strain is hardly released in fine grains because the strain in the polycrystalline form can be relaxed during grain growth; and thus the long-range ordering can be hindered in the fine grains, resulting in short-range ordered ferroelectricity.27,31 This short range ordering is closely related to the lattice vibration; and thus the inhomogeneous structure and/or composition can exhibit a higher temperature stability with strong phonon scattering and phonon broadening.32–34 Therefore, the short range ordering by a residual strain in fine grains can lead to higher thermal stability.Using first-principles calculations, we also investigated the effect of grain size on the domain configurations and thermal stability at an atomic-scale. For simplicity, we considered the polar tetragonal phase of pure KNN without dopants. We evaluated the domain wall (DW) energy (γDW) for the 180° domain wall within a single grain. It turns out that γDW is only moderate (9.77 mJ m−2) and the value is an order of magnitude smaller than that of PbTiO3.35 This implies that the energy cost to form domain walls in KNN is insignificant, facilitating multidomain formation within a grain (Fig. 1g). In contrast, in the case of the grain boundary of KNN, certain polar configurations such as head-to-tail polarization configurations is strongly preferred. The neutral head-to-tail polarization configurations are energetically favorable, whereas other polarization configurations such as head-to-head polarizations are found to be unstable (Fig. 1g). This preference indicates the capability of grain boundaries to pin the polarization directions after a poling process, compensating for the thermal effects that tend to randomize the polarization direction in a system. Because the grain boundary effects become important as the grain size decreases, it can be expected that the fine grains guarantee a higher thermal stability of piezoelectricity compared to the large grains.
Ferroelectric-relaxor ferroelectric transition accompanying abnormal grain growth
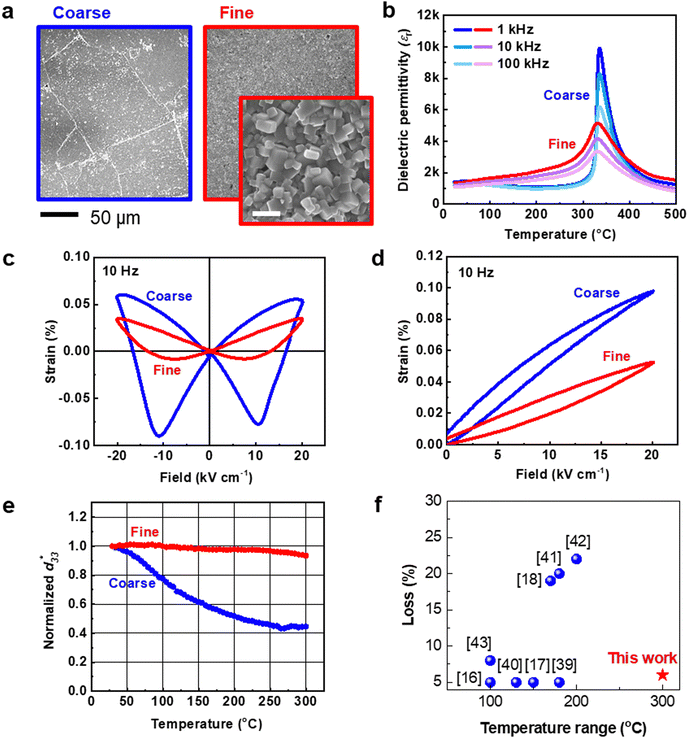
Based on the above calculation results, we decided to make a set of KNN ceramics by meticulously subdividing the doping concentration near the chemical composition inducing an abrupt change in grain size. We synthesized KNN compounds doped with bismuth-based perovskites Bi0.5(Li0.7Na0.2K0.1)0.5ZrO3 (BNKLZ) and BiScO3 (BS), that is, (0.97 − x)KNN-0.03BNKLZ-xBS (x = 0.0075–0.015) (for more details see the “Experimental” section and Fig. S11, ESI†). This KNN system has been proven to involve abnormal grain growth near x = 0.01 with a morphotropic phase boundary (MPB) where rhombohedral and tetragonal phases coexist.30 As an infinitesimal BS was added, the grain size abnormally decreased at a certain point (Fig. S2, ESI†). Within the deliberately controlled BS doped KNN set, we selected two representative samples with an average grain size of ∼52 μm (at x = 0.01, referred as “coarse”) and ∼0.3 μm (x = 0.01375, referred as “fine”) shown in Fig. 2a. It should be noted that the grain size unprecedentedly decreased with a relatively small change in chemical composition.Measurement of the electrical properties revealed evident differences between the coarse- and fine-grained KNN ceramics. For long-range ordered ferroelectric (conventional ferroelectric) materials, the sharp dielectric peak maximum appears at Tc regardless of the frequency as shown in Fig. 2b. In contrast, the short-range ordered ferroelectric (relaxor ferroelectric) materials show a broad dielectric peak maximum with frequency dependence because the local domains with the short-range ordering have different domain motions during the phase transition, as shown in the fine grained KNN in Fig. 2b.36 In a coarse grained KNN, the ferroelectric domains with long-range ordering aligns along with the external electric field; and the domains are rotated through the negative electro–strain and then realigned in the opposite direction of the external electric field. This phenomenon is accompanied with a clear butterfly-shaped bipolar strain–electric field (S–E) curve in Fig. 2c; but the large electro–strain can appear in a unipolar mode as shown in Fig. 2d.37 In a fine grained KNN, the short-range ordered polar phases are aligned along the external field without the significant negative electro–strain, which gives rise to the flat butterfly shape in the bipolar S–E curve in Fig. 2c and accordingly the weaker electro–strain is measured in the unipolar S–E curve in Fig. 2d.38 Likewise, these two ceramics can show distinct physical characteristics by the different grain growth behavior despite the negligible chemical difference.
The most intriguing phenomenon occurred at high temperatures. Fig. 2e shows the normalized 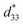 values for coarse and fine grains as a function of temperature. From the unipolar S–E curve (Fig. 2d), the
values for coarse and fine grains as a function of temperature. From the unipolar S–E curve (Fig. 2d), the 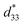 value at room temperature was estimated as
value at room temperature was estimated as 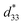 ∼ 516 pm V−1 and ∼263 pm V−1 for the coarse- and fine-sized grains, respectively (Fig. S4d, ESI†). For the coarse grains, the normalized
∼ 516 pm V−1 and ∼263 pm V−1 for the coarse- and fine-sized grains, respectively (Fig. S4d, ESI†). For the coarse grains, the normalized 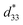 starts to lose its value immediately above room temperature and steadily deteriorates to ∼55% loss until 300 °C. Interestingly, for the fine grains, the normalized
starts to lose its value immediately above room temperature and steadily deteriorates to ∼55% loss until 300 °C. Interestingly, for the fine grains, the normalized 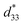 remains stable, with ∼6% loss up to 300 °C. This shows an incomparably enhanced thermal stability in terms of the temperature range or loss compared to the recently studied KNN piezoelectric ceramics (Fig. 2f).16–18,39–43 In Fig. 2e a well-retained polar state against thermal energy indicates that the polarization is pinned harder in the fine grains than in coarse grains. More precisely, in Fig. S2 and S4e (ESI†), the average grain size rapidly decreased to less than 1 μm at x = 0.0125, even with a few abnormally large grains, but the thermal stability did not improve accordingly. In fact, where the thermal stability greatly enhanced, x = 0.01375, exactly corresponds to where all grains became homogeneously fine without any large grains. Thus, it also corresponds to where the perimeter significantly increases. These results strongly suggest that a significant increase in proportion of grain boundaries, rather than a decrease in grain size itself, is a major contributor to the enhancement of the thermal stability of piezoelectricity. These results also concur with our prediction based on phase-field theory and first-principles calculations, as shown in Fig. 1. Therefore, we experimentally confirmed that the fine grains can sustain pinned polarization to high temperatures due to the grain boundary effect.
remains stable, with ∼6% loss up to 300 °C. This shows an incomparably enhanced thermal stability in terms of the temperature range or loss compared to the recently studied KNN piezoelectric ceramics (Fig. 2f).16–18,39–43 In Fig. 2e a well-retained polar state against thermal energy indicates that the polarization is pinned harder in the fine grains than in coarse grains. More precisely, in Fig. S2 and S4e (ESI†), the average grain size rapidly decreased to less than 1 μm at x = 0.0125, even with a few abnormally large grains, but the thermal stability did not improve accordingly. In fact, where the thermal stability greatly enhanced, x = 0.01375, exactly corresponds to where all grains became homogeneously fine without any large grains. Thus, it also corresponds to where the perimeter significantly increases. These results strongly suggest that a significant increase in proportion of grain boundaries, rather than a decrease in grain size itself, is a major contributor to the enhancement of the thermal stability of piezoelectricity. These results also concur with our prediction based on phase-field theory and first-principles calculations, as shown in Fig. 1. Therefore, we experimentally confirmed that the fine grains can sustain pinned polarization to high temperatures due to the grain boundary effect.
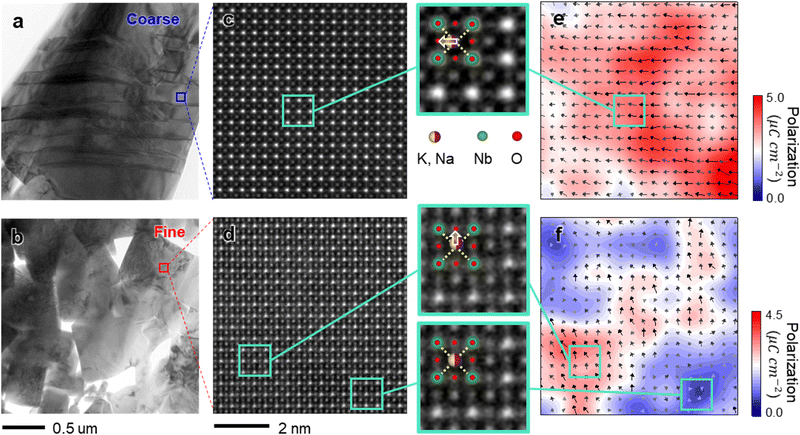
Phase analysis and atomic scale imaging unveiling the origin of thermal stability
To further elucidate the origin of the high thermal stability of piezoelectricity in fine grains, we investigated several possible factors. As stated in the introduction, relaxor-like behavior can arise from (i) the mixing of polar and nonpolar phases or (ii) the presence of PNRs. To determine whether the improved thermal stability of the fine grains is due to (i) a mixture of polar/nonpolar phases, we carried out selected area electron diffraction (SAED) analysis using TEM. Fig. S5–S7 (ESI†) verify that there was no polar/nonpolar phase difference between the coarse- and fine-sized grains. In addition, we analyzed the phase distribution changes from room temperature to 400 °C using in situ heating X-ray diffraction (XRD) (Fig. S9 and Table S1, ESI†). Both samples showed similar tendencies, in which the rhombohedral phase decreased and the tetragonal phase relatively increased as the temperature increased to Tc (over 300 °C), so it was inferred that the phase distribution according to temperature is not a factor that significantly affects the difference in thermal stability of the coarse- and fine-grained KNN samples.Therefore, it should be clarified that the thermal stability of fine grains originates from the (ii) existence of PNRs. However, directly demonstrating the existence of PNRs is a complex task because PNRs are only a few nanometers in size and consist of ionic displacements only on the order of picometers. Hence, we adopted an advanced electron microscopy, spherical aberration-corrected STEM, which is a powerful characterization tool providing localized atomic scale information with high temporal/spatial resolution to visualize PNRs.44 In the low-magnification images (Fig. 3a and b), coarse grains clearly depict stripe-shaped ferroelectric domain structures, while fine grains do not show such domain structures, as expected from Fig. 1a and b. Fig. 3c and d show inversed annular bright-field (ABF)-STEM atomic images along the 〈100〉 projection for the coarse and fine grains, respectively. Fig. 3e and f show the polarization maps of the same region as depicted in Fig. 3c and d, respectively. In Fig. 3e, the polarizations in the coarse grains are aligned along one direction in the long-range with relatively high polarization, which is consistent with conventional ferroelectric models. The inset shows the shift of A-site ions (K, Na) to the left, resulting in ionic polarization to the left in the unit cells. In contrast, atoms in fine grains are polarized in a short-range, forming polar clusters (colored red) within the relatively neutral matrix (colored blue), thereby generating PNRs (Fig. 3f). The size of the PNR is found to be approximately 2–3 nm. The upper inset of Fig. 3f shows the upward displacement of A-site ions in the PNR, whereas the lower inset shows no apparent displacement of A-site ions in the nonpolar matrix. This atomic-scale analysis directly reveals that the fine grains are composed of nanosized polar domains (short-range ordering), unlike the coarse grains with long-range ordering.
In relation to the presence of PNRs, studies analyzing the thermal stability of piezoelectricity in the KNN system have recently been reported. In a Na, Sb doped KNN-based system, a strong dependence between the content of nanosized domains and 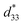 was observed. The in situ heating PFM measurements revealed that
was observed. The in situ heating PFM measurements revealed that 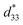 decreased rapidly owing to the sudden disappearance of nanodomains over ∼80 °C, while
decreased rapidly owing to the sudden disappearance of nanodomains over ∼80 °C, while 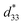 was well maintained at ∼80 °C, where nanodomains were rather well sustained.45 In the (Bi, Na)0.5ZrO3 doped KNN system, the enhanced piezoelectric strain retention with ∼20% loss at 180 °C was attained by forming PNRs. This suggests that the tradeoff from long-range ordered domains into PNRs relieved the thermal sensitivity.46 In the CaZrO3 doped KNN system, the temperature range of
was well maintained at ∼80 °C, where nanodomains were rather well sustained.45 In the (Bi, Na)0.5ZrO3 doped KNN system, the enhanced piezoelectric strain retention with ∼20% loss at 180 °C was attained by forming PNRs. This suggests that the tradeoff from long-range ordered domains into PNRs relieved the thermal sensitivity.46 In the CaZrO3 doped KNN system, the temperature range of 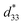 with fluctuation ±10% advanced from 110 °C to 200 °C by converting sub-micron long-range ordered domains to PNRs.47 The above studies confirmed that the existence of PNRs is crucial for ensuring the thermal stability of piezoelectricity. Referring to related studies, it can be extrapolated that the excellent thermal stability of fine-grained KNN originates from the presence of PNRs. Furthermore, from our calculations and experimental results, the grain boundaries, as well as the presence of PNRs, contributed to preserving the polar state at high temperatures (∼300 °C) with little loss (∼6%) by pinning polarization in PNRs. Thus, we can conclude that the PNRs and grain boundaries interact in a synergistic manner owing to the abrupt decrease in grain size, achieving superior thermal stability.
with fluctuation ±10% advanced from 110 °C to 200 °C by converting sub-micron long-range ordered domains to PNRs.47 The above studies confirmed that the existence of PNRs is crucial for ensuring the thermal stability of piezoelectricity. Referring to related studies, it can be extrapolated that the excellent thermal stability of fine-grained KNN originates from the presence of PNRs. Furthermore, from our calculations and experimental results, the grain boundaries, as well as the presence of PNRs, contributed to preserving the polar state at high temperatures (∼300 °C) with little loss (∼6%) by pinning polarization in PNRs. Thus, we can conclude that the PNRs and grain boundaries interact in a synergistic manner owing to the abrupt decrease in grain size, achieving superior thermal stability.
Device application reproducing thermal stability
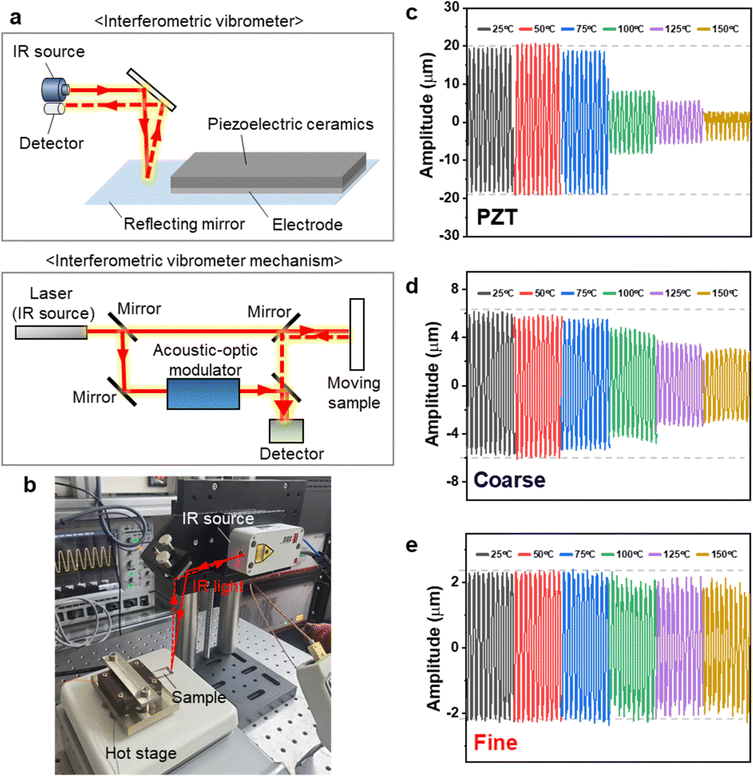
Next, the applicability of fine-grained KNN ceramics as cantilever-type bending actuators was investigated at high temperatures. Because the operational performance of the actuator (deflection of the cantilever (pm) per applied voltage (V)) is closely related to the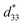 (pm V−1) of the piezoelectric ceramics, analysis of the temperature-dependent performance of actuators is an effective way to demonstrate that the thermal stability of
(pm V−1) of the piezoelectric ceramics, analysis of the temperature-dependent performance of actuators is an effective way to demonstrate that the thermal stability of 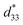 has been imparted into devices. A schematic diagram of the manufactured cantilever-type actuators and the experimental setup are shown in Fig. 4a and Fig. S10a (ESI†). The actuators are composed of piezoelectric ceramics and a titanium elastic shim. The rectangle-shaped and electrode containing KNN ceramics were bonded with a high-temperature resistance adhesive. One end of the cantilever–structured bender was clamped with an electrically insulating rig. Three types of piezoelectric ceramics were used: coarse-grained KNN, fine-grained KNN, and commercial PZT, as a reference to compare their actuating performance over a wide temperature range. Upon applying a voltage, the piezoelectric ceramic layer in the actuator gets strained and the cantilever bends. The amplitude and direction of this deflection were detected using a laser interferometer illuminated toward the mirror at the edge of the cantilever. The setup was installed in a heating chamber for in situ heating evaluation. The actual fabrication and experimental setup are shown in Fig. 4b and Fig. S10b (ESI†).
has been imparted into devices. A schematic diagram of the manufactured cantilever-type actuators and the experimental setup are shown in Fig. 4a and Fig. S10a (ESI†). The actuators are composed of piezoelectric ceramics and a titanium elastic shim. The rectangle-shaped and electrode containing KNN ceramics were bonded with a high-temperature resistance adhesive. One end of the cantilever–structured bender was clamped with an electrically insulating rig. Three types of piezoelectric ceramics were used: coarse-grained KNN, fine-grained KNN, and commercial PZT, as a reference to compare their actuating performance over a wide temperature range. Upon applying a voltage, the piezoelectric ceramic layer in the actuator gets strained and the cantilever bends. The amplitude and direction of this deflection were detected using a laser interferometer illuminated toward the mirror at the edge of the cantilever. The setup was installed in a heating chamber for in situ heating evaluation. The actual fabrication and experimental setup are shown in Fig. 4b and Fig. S10b (ESI†).
We applied an external voltage of 70 Vp–p with a frequency of 100 Hz heating from room temperature to 150 °C and evaluated the amplitude of the deflecting motion. Fig. 4c–e describe the amplitude of the deflecting displacement. The PZT-based device was most sensitive to thermal degradation and rapidly degraded above 75 °C (Fig. 4c). The actuator comprising coarse-grained KNN held out a higher temperature than the PZT, but its performance also gradually declined (Fig. 4d). In contrast, the device composed of fine-grained KNN revealed superior thermal stability of the operational performance (Fig. 4e), which is directly related to the thermally stable piezoelectricity shown in Fig. 2e. The application results faithfully reflect the thermal stability of 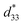 up to 150 °C, the highest temperature up to which reliable evaluation was possible without any thermal damage on the adhesive layer, electrode, and wire. Since the actuating performance is consistent with the thermal stability of
up to 150 °C, the highest temperature up to which reliable evaluation was possible without any thermal damage on the adhesive layer, electrode, and wire. Since the actuating performance is consistent with the thermal stability of 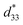 up to 150 °C, it is believed that the stability will be well-reproduced up to 300 °C without any significant deviation, if only the problem of deterioration of the device at high temperatures is solved. Due to the extraordinary thermal stability and its reproducibility, fine-KNN is a promising candidate for applications in thermally-harsh environments. We are currently utilizing our fine-grained KNN ceramics to sense the safety of a nuclear reactor, which confirms the industrial applicability. Also, there are further potential applications in dynamic electronic devices including ferroelectric memristors or solid-state synapses requiring continuous resistors.48–50
up to 150 °C, it is believed that the stability will be well-reproduced up to 300 °C without any significant deviation, if only the problem of deterioration of the device at high temperatures is solved. Due to the extraordinary thermal stability and its reproducibility, fine-KNN is a promising candidate for applications in thermally-harsh environments. We are currently utilizing our fine-grained KNN ceramics to sense the safety of a nuclear reactor, which confirms the industrial applicability. Also, there are further potential applications in dynamic electronic devices including ferroelectric memristors or solid-state synapses requiring continuous resistors.48–50
Experimental
Phase-field calculations
The areas of the simulation were taken as 100 nm × 100 nm and segmented into 6 and 50 grains and for coarse and fine grains, respectively. The polarization vector P was selected as the order parameter, and the domain structure was predicted by solving the time-dependent Ginzburg–Landau equations as follows: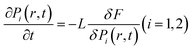 | (1) |
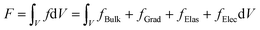 | (2) |
Bulk energy density fBulk can be expanded as:
| fBulk = α1(P12 + P22) + α11(P14 + P24) + α12P12P22 + α111(P16 + P26) + α112(P12P24 + P14P22) | (3) |
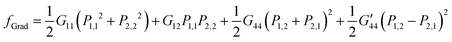 | (4) |
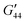 are the gradient energy coefficients, and Pi,j = ∂Pi/∂xj.
are the gradient energy coefficients, and Pi,j = ∂Pi/∂xj.
The elastic energy density fElas can be written as
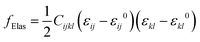 | (5) |
The electrostatic energy density fElec contains the energy of the static electric field and the potential energy of spontaneous polarization in this static electric field; it can be written as
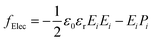 | (6) |
To calculate the elastic energy and electric energy, two other equations, the mechanical equilibrium equation and electrostatic equilibrium equation, should be solved as follows:
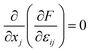 | (7) |
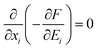 | (8) |
In the numerical calculation, the mesh grid size Δx was approximately equal to 1 nm. The displacement and electric potential were only fixed at the area boundaries, and the polarization was set as zero on the grain boundaries.
For simplicity, we used the material parameters of PbTiO3 found in the literature:51α1 = 3.8(T − 479) × 105 C−2 m2 N, α11 = −7.3 × 107 C−4 m6 N, α12 = 7.5 × 108 C−4 m6 N, α111 = 2.6 × 108 C−6 m10 N, α112 = 6.1 × 108 C−6 m10 N, Q11 = 0.089 C−2 m4, Q12 = −0.026 C−2 m4, Q44 = 0.03375 C−2 m4, C11 = 1.746 × 1011 Nm−2, C12 = 7.937 × 1010 Nm−2, C44 = 1.111 × 1011 Nm−2 and εr = 66.
To solve these equations, the backward Euler method was used for the discrete time domain, and the nonlinear finite element method was used for the discrete spatial domains. A detailed description of the finite element method can be found in the literature.52 The nonlinear finite element method was performed using FreeFEM++.53 Detail information regarding FreeFEM++ is available at https://freefem.org/. A polycrystalline geometric model was generated using Neper.54
Density functional theory calculations (first-principles calculations)
DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP) code with projector-augmented wave (PAW) pseudopotentials.55 Perdew–Burke–Ernzerhof (PBE) functional was used for the exchange–correlation energy, and the plane-wave cutoff was set to 500 eV.56 We generated a periodic unit cell of tetragonal K0.5Na0.5NbO3 with eight formula units. To consider the effects of the random distribution of K and Na positions in real materials, we generated a special quasirandom structure using the mcsqs code.57 This periodic unit cell was then used to generate the 180° DW (32 formula units) and Σ3(112) GB (96 formula units) structures. We used the algorithm suggested by Cheng et al. to build a grain boundary structure within a periodic boundary condition.58 For Brillouin zone sampling, we used 1 × 2 × 2 for the DW structure and Γ-only k-point grids for the GB structure. All atomic coordinates were relaxed until the forces acting on each atom were less than 0.05 eV Å−1. The grain boundary energy (γGB) of KNN was calculated to be 905.04 mJ m−2, which is comparable to the grain boundary energies found in PbTiO3 from previous calculations.59Synthesis
Piezoceramic samples with (1 − x − y)KNN-xBNKLZ-yBS compositions (x = 0.03, y = 0.0075–0.015) were prepared using the conventional solid-state powder method. The starting powders were K2CO3 (≥99.0%, 150 μm, Sigma-Aldrich), Na2CO3 (≥99.5%, 10 μm, Sigma-Aldrich), Li2CO3 (99.997%, 20 μm, Sigma-Aldrich), Nb2O5 (99.9%, 2 μm, Sigma-Aldrich), Bi2O3 (99.9%, 10 μm, Sigma-Aldrich), ZrO2 (99.0%, 5 μm, Sigma-Aldrich), and Sc2O3 (≥99.9%, 10 μm, Sigma-Aldrich). The hygroscopic powders Na2CO3 and K2CO3 were fully dried at 120 °C for more than 24 h to remove the absorbed moisture before weighing. The weighed powders were ball-milled in ethanol for 24 h, calcined at 850 °C for 6 h, and pressed into disks of 10 mm diameter using polyvinyl alcohol (PVA) as a binder. All the samples were sintered at 1120 °C for 6 h after burning off the PVA at 650 °C in a conventional furnace at a heating rate of 4 °C min−1. Finally, the sintered ceramics were ground to a thickness of 1 mm.Characterization
The crystal structures of the sintered ceramics were examined using XRD (D/Max-2500; Rigaku, Tokyo, Japan) with Cu Kα radiation at 40 kV and 30 mA. Rietveld refinement of the XRD patterns was performed using Rigaku's PDXL software using the Whole Pattern Powder Fitting (WPPF) method, connected to the Inorganic Crystal Structure Database (ICSD; FIZ Karlsruhe, Germany). The initial models used for refinement were two KNbO3 crystal structures, that is, rhombohedral (R3m; JCPDS 01-071-0947; ICSD code 9534) and tetragonal (P4mm; JCPDS 01-071-0948; ICSD code 9535); their crystal structure parameters were acquired from the ICSD. The grain structure was investigated via SEM (JSM 6300; JEOL, Tokyo, Japan). Grain size measurements using automatic image analysis software (Matrox imaging library 10) were conducted for ∼1100 grains taken from each sample.For electrical measurements, silver paste was coated onto the two main surfaces of the ceramics, after which they were fired at 650 °C for 10 min. The prepared samples were then poled in silicon oil at room temperature. The piezoelectric coefficient (d33) was measured using a piezo-d33 meter (ZJ-6B, IACAS, Beijing, China). The dielectric properties were measured over a temperature range of 25–400 °C using an impedance analyzer (SI 1260; Solartron; Farnborough, England) with an HTSH-110 sample holder system and an HTF-1100 furnace (temperature accuracy: ±0.3 °C; Bio-Logic, France). Polarization versus electric field (P–E) hysteresis loops, field-dependent piezoelectric coefficient d33(E) loops, and electric-field-induced unipolar strain curves were measured using a commercial aixPES setup with a Piezo-Sample Holder HT (aixACCT Systems GmbH, Germany) and optical interferometry (a commercial single-beam laser interferometer, aixACCT Systems). Using the unipolar strain curves, 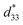 was determined from the ratio of the maximum strain to the peak electric field.
was determined from the ratio of the maximum strain to the peak electric field.
(Scanning) transmission electron microscopy
TEM samples were prepared by mechanical flat polishing to a thickness of <10 μm and Ar+ ion beam milling (PIPS II, Gatan). Ion beam milling started at 3.5 keV and 8°, and subsequently lowered to 0.1 keV and 1°. Diffraction patterns in the TEM experimental flows were simulated using Java Electron Microscopy Software (JEMS, Stadelmann, EPFL). Bright-field and dark-field imaging, including diffraction patterns, were conducted using an acceleration voltage of 200 keV with a field-emission TEM (JEM-2100F, JEOL) at the Materials Imaging & Analysis Center of POSTECH, Republic of Korea.ABF-STEM images were acquired using a STEM (JEM-ARM200F, JEOL) at 200 keV equipped with 5th order probe corrector (ASCOR, CEOS GmbH) at the Materials Imaging & Analysis Center of POSTECH, Republic of Korea. The probe size was ∼0.8 Å for atomic-scale images. The convergence semi-angle was fixed at 28 mrad for ABF-STEM imaging. The inner and outer angles of the detectors were 10 mrad and 20 mrad for ABF, respectively, with a camera length of 10 cm. A-site ions (K, Na) have light atomic numbers; therefore, the incident electron beam scatters at low scattering angles. To image the light ions, we collected scattered electrons at relatively small angles. The raw ABF images were processed by stacking 10 slices using SmartAlign and band-pass diffraction filtering to cancel the background noise (SmartAlign and Filters Pro, HREM Research Inc., Japan).
The polarization was calculated in unit cells by the displacement length of off-centered A-site atoms (K, Na) with respect to the centrosymmetric positions of the B-site atoms (Nb). The centrosymmetric positions of each unit cell were calculated using the four neighboring B-site atomic columns in the ABF-STEM image. From the obtained centrosymmetric position, the positive-charge position in a unit cell was defined by the A-site atomic columns. The atomic polarization was calculated using the following equation:
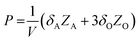 | (9) |
Application
The Ag-electrode PZT and KNN samples were initially machined with dimensions of 10 × 20 × 0.5 mm3 before poling and assembling the elastic Ti plate (dimensions of 35 × 15 × 0.3 mm3) for the bending actuator. The samples were then poled. The piezoelectric properties (d33) of the poled samples (PZT, 0.01BS, and 0.01375BS) were as follows: 734, 270, and 140 pC N−1 respectively. Subsequently, PZT and KNN were attached to the elastic Ti plate using high-temperature epoxy (Steel Reinforced Epoxy, J-B Weld, USA). Before clamping the laminated beam of piezoelectric ceramics and Ti plate for bending actuation, we connected the upper part (PZT or KNN) and the bottom part (Ti plate) with silver wires as a connection for applying AC electricity, which triggered the inverse piezoelectric effect. The laminated bending actuator was clamped with a Bakelite clamp and a metallic fixture. The clamped bending actuator was placed in a thermally insulated temperature-controllable chamber. A laser interferometric vibrometer (SP-S, SIOS Meßtechnik GmbH, Germany) was used for accurate piezoelectric bending actuation measurements under an AC electric field, with an accuracy of up to 5 pm. A thermometer probe was attached to the actuator clamping rig to measure the actuator temperature during testing. Under a constant driving AC voltage of 70 Vrms at 100 Hz applied by a function generator (WF1946, NF Corporation, Japan) and a high-speed bipolar amplifier (HSA4025, NF Corporation, Japan), the bending deflection of the actuator was measured by increasing the temperature from room temperature to 150 °C. The full measurement setup is shown in Fig. S10a and b (ESI†).Conclusions
We unveiled a method to achieve outstanding thermal stability of piezoelectricity in lead-free materials by inducing a synergistic interaction between the grain size effect and polar configuration. Based on computational methods using phase-field simulations and first-principles calculations, improved thermal stability of polarization is possible because of the large effect of grain boundaries in fine grains. A set of KNN systems were presented with meticulous dopant control near the chemical composition at which abnormal grain growth occurs. Consistent with the computational prediction, we verified two representative samples with coarse and fine grains, exhibiting significant enhancement in the thermal stability of piezoelectricity up to 300 °C in the fine grains. The origin of the thermal superiority in fine-grained ceramics was identified through an extensive study from a microstructural perspective. The thermal stability was realized in the form of a cantilever-type actuator successfully demonstrating temperature-independent piezoelectricity in fine-grained KNN. It is notable that this is the first time that lead-free piezoelectric ceramics have been able to achieve exceptionally stable piezoelectricity up to 300 °C, which actualizes their applicability as piezoelectric devices with high thermal stability.Author contributions
Soo-Yoon Hwang: conceptualization, visualization, writing – original draft preparation, and writing – review & editing. Gyoung-Ja Lee: conceptualization, validation, and writing – review & editing. Yuzhao Qi, Xiaoyan Lu: methodology, software, and visualization. Michael Abraham Listyawan, and Jungho Ryu: validation. Kyung Song: visualization. Youngho Kang: methodology, software, and visualization. Min-Ku Lee and Si-Young Choi: project administration, supervision, writing – original draft preparation, and writing – review & editing. All authors contributed to the investigation and data curation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S.-Y. H. and S.-Y. C. acknowledge the Korea Basic Science Institute (National research Facilities and Equipment Center) grant funded by the Ministry of Education (2020R1A6C101A202). G.-J. L. and M.-K. L. acknowledge the support from the National Research Foundation of Korea (NRF) grant funded by the Korea government (Ministry of Science and ICT) (RS-2022-00144147) and in part by the Korea Atomic Energy Research Institute (KAERI) R&D program. L. X. acknowledges the support from the National Key Research and Development Program of China (No. 2021YFF0501001), the Heilongjiang Provincial Natural Science Foundation of China (No. LH2020A006), the National Science Foundation of China (No. 11872019), and Open Fund of Key Laboratory for Intelligent Nano Materials and Devices of the Ministry of Education NJ2022002 (INMD-2022M08). Y. K. acknowledges that the first-principles calculations were carried out at the KISTI supercomputing center (Grant no. KSC-2022-CRE-0006).References
- S. Zhang and F. Yu, J. Am. Ceram. Soc., 2011, 94, 3153–3170 CrossRef CAS.
- T. Takenaka, K.-I. Maruyama and K. Sakata, Jpn. J. Appl. Phys., 1991, 30, 2236–2239 CrossRef CAS.
- Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya and M. Nakamura, Nature, 2004, 432, 84–87 CrossRef CAS PubMed.
- T. R. Shrout and S. J. Zhang, J. Electroceram., 2007, 19, 113–126 CrossRef.
- X. Liu and X. Tan, Adv. Mater., 2016, 28, 574–578 CrossRef CAS PubMed.
- M. H. Lee, D. J. Kim, J. S. Park, S. W. Kim, T. K. Song, M.-H. Kim, W.-J. Kim, D. Do and I.-K. Jeong, Adv. Mater., 2015, 27, 6976–6982 CrossRef CAS PubMed.
- J. Rödel, K. G. Webber, R. Dittmer, W. Jo, M. Kimura and D. Damjanovic, J. Eur. Ceram. Soc., 2015, 35, 1659–1681 CrossRef.
- W. Liu and X. Ren, Phys. Rev. Lett., 2009, 103, 257602 CrossRef PubMed.
- T. Takenaka and H. Nagata, J. Eur. Ceram. Soc., 2005, 25, 2693–2700 CrossRef CAS.
- M.-H. Zhang, K. Wang, Y.-J. Du, G. Dai, W. Sun, G. Li, D. Hu, H. C. Thong, C. Zhao, X.-Q. Xi, Z.-X. Yue and J.-F. Li, J. Am. Chem. Soc., 2017, 139, 3889–3895 CrossRef CAS PubMed.
- K. Chen, J. Ma, C. Shi, W. Wu and B. Wu, J. Alloys Compd., 2021, 852, 156865 CrossRef CAS.
- R. Mahdi, N. J. Al-Bahnam, M. A. Ajeel, A. Al-Keisy, T. A. Hussein and W. Abd Majid, Ceram. Int., 2020, 46, 21762–21770 CrossRef CAS.
- C. Zhou, J. Zhang, W. Yao, D. Liu and W. Su, Scr. Mater., 2019, 162, 86–89 CrossRef CAS.
- B. Wu, J. Ma, Q. Gou, W. Wu and M. Chen, J. Am. Ceram. Soc., 2020, 103, 1698–1708 CrossRef CAS.
- Q. Liu, J.-F. Li, L. Zhao, Y. Zhang, J. Gao, W. Sun, K. Wang and L. Li, J. Mater. Chem. C, 2018, 6, 1116–1125 RSC.
- Y. Huang, C. Zhao, B. Wu and J. Wu, J. Am. Ceram. Soc., 2019, 102, 2648–2657 CAS.
- N. Zhang, C. Zhao and J. Wu, Ceram. Int., 2019, 45, 24827–24834 CrossRef CAS.
- C. Zhao, B. Wu, K. Wang, J.-F. Li, D. Xiao, J. Zhu and J. Wu, J. Mater. Chem. A, 2018, 6, 23736–23745 RSC.
- H. Du, W. Zhou, F. Luo, D. Zhu, S. Qu and Z. Pei, J. Appl. Phys., 2009, 105, 124104 CrossRef.
- J. Sun, X. Chen, X. Li, X. Yan, X. Li, H. Zhou, X. Liu and H. Ruan, J. Mater. Sci.: Mater. Electron., 2019, 30, 695–700 CrossRef CAS.
- G.-Y. Kim, K.-D. Sung, Y. Rhyim, S.-Y. Yoon, M.-S. Kim, S.-J. Jeong, K.-H. Kim, J. Ryu, S.-D. Kim and S.-Y. Choi, Nanoscale, 2016, 8, 7443–7448 RSC.
- S.-Y. Choi, S.-J. Jeong, D.-S. Lee, M.-S. Kim, J.-S. Lee, J. H. Cho, B. I. Kim and Y. Ikuhara, Chem. Mater., 2012, 24, 3363–3369 CrossRef CAS.
- K.-C. Meyer, M. Gröting and K. Albe, J. Solid State Chem., 2015, 227, 117–122 CrossRef CAS.
- A. Kumar, J. N. Baker, P. C. Bowes, M. J. Cabral, S. Zhang, E. C. Dickey, D. L. Irving and J. M. Lebeau, Nat. Mater., 2021, 20, 62–67 CrossRef CAS PubMed.
- W. Zheng, J. Lin, X. Liu, W. Yang and Y. Li, RSC Adv., 2021, 11, 2616–2623 RSC.
- X. Liu, S. Xue, F. Wang, J. Zhai and B. Shen, Acta Mater., 2019, 164, 12–24 CrossRef CAS.
- M. Hagiwara and S. Fujihara, Appl. Phys. Lett., 2015, 107, 012903 CrossRef.
- X. Zhu, Y. Gao, R. Kang, P. Shi, Z. Wang, Y. Yuan, W. Qiao, J. Zhao, Z. Ren and X. Lou, J. Alloys Compd., 2022, 897, 163212 CrossRef CAS.
- N. Salazar, D. Pérez-Mezcua, M. L. Calzada, A. Gil and J. Ricote, J. Am. Ceram. Soc., 2019, 102, 5941–5951 CrossRef CAS.
- M.-K. Lee, S.-A. Yang, J.-J. Park and G.-J. Lee, Sci. Rep., 2019, 9, 1–7 CrossRef PubMed.
- J. Ryu, G. Han, T. K. Song, A. Welsh, S. Trolier-McKinstry, H. Choi, J.-P. Lee, J.-W. Kim, W.-H. Yoon, J.-J. Choi, D.-S. Park, C.-W. Ahn, S. Priya, S.-Y. Choi and D.-Y. Jeong, ACS Appl. Mater. Interfaces, 2014, 6, 11980–11987 CrossRef CAS PubMed.
- F. Körmann, Y. Ikeda, B. Grabowski and M. H. F. Sluiter, npj Comput. Mater., 2017, 3, 36 CrossRef.
- S. Mu, R. J. Olsen, B. Dutta, L. Lindsay, G. D. Samolyuk, T. Berlijn, E. D. Specht, K. Jin, H. Bei, T. Hickel, B. C. Larson and G. M. Stocks, npj Comput. Mater., 2020, 6, 4 CrossRef CAS.
- Y. Dong, X. Lu, J. Fan, S.-Y. Choi and H. Li, Coatings, 2022, 12, 542 CrossRef CAS.
- B. Meyer and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104111 CrossRef.
- Z. Raddaoui, S. El Kossi, J. Dhahri, N. Abdelmoula and K. Taibi, RSC Adv., 2019, 9, 2412–2425 RSC.
- H. Sahota, Continuum Mech. Thermodyn., 2004, 16, 163–175 CrossRef CAS.
- A. Ullah, H. B. Gul, A. Ullah, M. Sheeraz, J. S. Bae, W. Jo, C. W. Ahn, I. W. Kim and T. H. Kim, APL Mater., 2018, 6, 016104 CrossRef.
- X. Lv and J. Wu, J. Mater. Chem. C, 2019, 7, 2037–2048 RSC.
- Y. Zhai, J. Du, C. Chen, J. Hao, P. Fu, W. Li and Z. Xu, J. Mater. Sci.: Mater. Electron., 2019, 30, 4716–4725 CrossRef CAS.
- H. Tao, C. Zhao, R. Zhang and J. Wu, J. Alloys Compd., 2019, 795, 401–407 CrossRef CAS.
- B. Yin, Y. Huan, Z. Wang, X. Lin, S. Huang and T. Wei, J. Mater. Sci.: Mater. Electron., 2019, 30, 18659–18665 CrossRef CAS.
- T. Wang, C. Wu, J. Xing, J. Wu, B. Li-Chen, X. Xu, K. Wang and J. Zhu, J. Am. Ceram. Soc., 2019, 102, 6126–6136 CrossRef CAS.
- C. Li, B. Liu, N. Jiang and Y. Ding, Nano Res. Energy, 2022, 1, e9120031 CrossRef.
- T. Zheng, H. Wu, Y. Yuan, X. Lv, Q. Li, T. Men, C. Zhao, D. Xiao, J. Wu and K. Wang, Energy Environ. Sci., 2017, 10, 528–537 RSC.
- X. Lv, J. Wu and X.-X. Zhang, Chem. Eng. J., 2020, 402, 126215 CrossRef CAS.
- Z. Cen, Y. Huan, W. Feng, Y. Yu, P. Zhao, L. Chen, C. Zhu, L. Li and X. Wang, J. Mater. Chem. A, 2018, 6, 19967–19973 RSC.
- S. Boyn, J. Grollier, G. Lecerf, B. Xu, N. Locatelli, S. Fusil, S. Girod, C. Carrétéro, K. Garcia, S. Xavier, J. Tomas, L. Bellaiche, M. Bibes, A. Barthélémy, S. Saïghi and V. Garcia, Nat. Commun., 2017, 8, 14736 CrossRef CAS PubMed.
- X. Liang, Y. Luo, Y. Pei, M. Wang and C. Liu, Nat. Electron., 2022, 5, 859–869 CrossRef.
- Y. Kaneko, Y. Nishitani and M. Ueda, IEEE Trans. Electron Devices, 2014, 61, 2827–2833 CAS.
- L.-Q. Chen, Physics of Ferroelectrics, Springer, 2007, pp. 363–372 Search PubMed.
- J. Wang and M. Kamlah, Smart Mater. Struct., 2009, 18, 104008 CrossRef.
- F. Hecht, J. Numer. Math., 2012, 20, 251–266 Search PubMed.
- R. Quey, P. Dawson and F. Barbe, Comput. Meth. Appl. Mech. Eng., 2011, 200, 1729–1745 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. van de Walle, P. Tiwary, M. de Jong, D. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L.-Q. Chen and Z.-K. Liu, Calphad, 2013, 42, 13–18 CrossRef CAS.
- J. Cheng, J. Luo and K. Yang, Comput. Mater. Sci., 2018, 155, 92–103 CrossRef CAS.
- P. Marton, T. Shimada, T. Kitamura and C. Elsässer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 064110 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00285c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |