(LaCrO₃)_m/SrCrO₃ superlattices as transparent p-type semiconductors with finite magnetization

Abstract

The electronic and magnetic properties of (LaCrO₃)_m/SrCrO₃ superlattices are investigated using first principles calculations. We show that the magnetic moments in the two CrO₂ layers sandwiching the SrO layer compensate each other for even m but give rise to a finite magnetization for odd m, which is explained by charge ordering with Cr³⁺ and Cr⁴⁺ ions arranged in a checkerboard pattern. The Cr⁴⁺ ions induce in-gap hole states at the interface, implying that the transparent superlattices are p-type semiconductors. The availability of transparent p-type semiconductors with finite magnetization enables the fabrication of transparent magnetic diodes and transistors, for example, with a multitude of potential technological applications.

---

Introduction

The correlated nature of d-electrons and the occurence of different valence states are responsible for many unusual properties of transition metal oxides related to, for example, electrical transport, magnetism, or superconductivity.^1–4 In particular, superlattices of transition metal oxides (which experimentally can be prepared atomically sharp^5–8) attract increasing interest due to the possibility of tailoring new functionalities not available in their component materials.^9–21 Indeed, at the interfaces of superlattices the transition metal atoms experience different chemical environments, giving possibly rise to charge, spin, and orbital ordering. For example, the perovskites LaAlO₃ and SrTiO₃ form a highly conductive interface (in fact, a two-dimensional electron gas) despite the fact that both are wide bandgap insulators.¹⁰ The calculated charge distribution in (LaMnO₃)_n/(SrMnO₃)_2n superlattices points to a mixed valency of the Mn atoms located close to an interface;²² and it is known that in vanadate superlattices distortions of the VO₆ octahedra can lead to complex effects in the orbital occupations, giving rise to rich physics.²³ Experimentally, both V³⁺ and V⁴⁺ ions are present at the interfaces of the (LaVO₃)₆/(SrVO₃)₃ (ref. 24) and (LaVO₃)_m/SrVO₃ (m ≥ 2) (ref. 25) superlattices. The analysis of the magnetic coupling between these ions points to strong electronic correlations and reveals an even-odd m-dependence of the magnetization,²⁵ in agreement with theoretical results for m = 5 and 6.²⁶

The closely related (LaCrO₃)_m/SrCrO₃ superlattices, on the other hand, were not studied so far. In particular, it will be interesting to evaluate whether the magnetic coupling and/or even-odd m-dependence of the magnetization is modified due to the extra valence electron of Cr as compared to V. LaCrO₃ has an orthorhombic structure (Pbnm) with G-type antiferromagnetic (AFM) ordering at room temperature^27,28 and a bandgap of 2.8 eV.^27,29,30 While SrCrO₃ initially was reported to have a cubic structure without magnetic ordering,³¹ recent studies point to a tetragonal structure and metallicity with C-type AFM ordering.^32,33 Therefore, it can be expected that the (LaCrO₃)_m/SrCrO₃ superlattices are subject to a complex interplay between the different crystal structures and magnetic orderings. We study this interplay in the present work for m = 2 to 6.

As the substitution of La³⁺ by Sr²⁺ introduces holes in the valence band, the La_1−xSr_xBO₃ (B = T, V, Cr, Mn, and Co) solid solutions exhibit insulator-to-metal transitions with increasing Sr content x,^34–38 which may affect the charge ordering in superlattices composed of LaCrO₃ (Cr³⁺, 3d³) and SrCrO₃ (Cr⁴⁺, 3d²). The La_1−xSr_xCrO₃ solid solutions are transparent p-type semiconductors in the La-rich region of the phase diagram.³⁹ Transparent semiconducting oxides are used in various technologies including photovoltaics,⁴⁰ infrared plasmonics,⁴¹ and transparent transistors.^42,43 However, many potential applications in electronics and optoelectronics are limited by the lack of p-type materials.^44–46 This shortage originates from the facts that for most oxides the valence band edge is formed by the O 2p orbitals and that the high electronegativity of O makes it difficult to introduce shallow acceptors.⁴⁷ Magnetic semiconductors^48,49 are applied, for example, in spin diodes and bipolar magnetic junction transistors,^50,51 and they allow the current in field-effect transistors to be controlled by a magnetic field.⁵² Additional transparency would vastly expand the range of applications, including sensors, displays, and coatings.^46,53–55 In this context, we demonstrate that (LaCrO₃)_m/SrCrO₃ superlattices with odd m combine the properties of transparency, p-type semiconductivity, and finite magnetization, opening up a new class of functional materials.

Computational details

Spin-polarized first-principles calculations within the framework of density functional theory are conducted using the Quantum-ESPRESSO package.⁵⁶ The generalized gradient approximation (Perdew–Burke–Ernzerhof flavor) is used for the exchange–correlation functional. Correlation effects of the Cr 3d electrons are taken into account by means of an on-site Coulomb interaction U.⁵⁷ We set U = 3 eV, because this value provides the best agreement between theory and experiment for LaCrO₃ and SrCrO₃.^38,58 After careful testing of the required fineness of the mesh for Brillouin zone sampling in the case m = 2, Monkhorst–Pack 8 × 8 × 4 (m = 2, 3, and 4) and 8 × 8 × 2 (m = 5 and 6) meshes are employed. Calculations of the density of states (DOS) are based on the tetrahedron method with 12 × 12 × 6 (m = 2, 3, and 4) and 12 × 12 × 4 (m = 5 and 6) meshes. The experimental pseudo-cubic lattice parameter a_pseudo = 3.88 Å of LaCrO₃ (ref. 59 and 60) is used to build tetragonal supercells with 30, 40, 50, 60, and 70 atoms, respectively. The mismatch between a_pseudo and the cubic lattice parameter of SrCrO₃ (3.82 Å (ref. 33)) is less than 1.6%. All structures are relaxed (atomic positions and lattice parameters) until the Hellmann–Feynman force remains below 0.26 meV Å⁻¹ for each atom.

Results and discussion

Fig. 1(a) and (b) show the total and partial densities of states obtained for bulk LaCrO₃ and bulk SrCrO₃, respectively. The G-AFM ordering of bulk LaCrO₃ (Cr³⁺ ions with a magnetic moment of 2.8 μ_B) and C-AFM ordering of bulk SrCrO₃ (Cr⁴⁺ ions with a magnetic moment of 2.1 μ_B) result in zero magnetization. While bulk LaCrO₃ turns out to be a semiconductor with a bandgap of 2.7 eV, metallicity is found for bulk SrCrO₃. Our choice of U = 3 eV thus provides excellent agreement of the bandgap with the experimental observations (Fig. S4;† see Fig. S5† for the effect of U on the magnetic ordering). For comparison to our following results for the (LaCrO₃)_m/SrCrO₃ superlattices, we start our considerations with an analysis of the La_0.5Sr_0.5CrO₃ solid solution, see the optimized structure (assuming alternating La and Sr atoms) with experimental lattice parameters³⁹ in Fig. 1(e). C-type AFM ordering is found to be energetically favorable over G-type AFM ordering by 35 meV, over ferromagnetic ordering by 83 meV, and over A-type AFM ordering by 110 meV. The appearance of Cr–O bond lengths of 1.90 Å and 1.98 Å demonstrates the simultaneous presence of Cr³⁺ and Cr⁴⁺ ions, respectively, while the Cr–O–Cr bond angle of 162° deviates only slightly from the 160° of bulk LaCrO₃.²⁷ Due to the C-type AFM ordering, we obtain zero magnetization. Fig. 1(c and d) shows in-gap hole states consistent with the experimental observation of a transparent p-type semiconductor.³⁹

Fig. 1 Total and partial densities of states (sum over all atoms, divided by the number of Cr atoms) of (a) LaCrO₃, (b) SrCrO₃, and (c) the La_0.5Sr_0.5CrO₃ solid solution. Positive/negative values represent here and in the following the spin up/down channel. (d) Band structure and (e) optimized structure of the La_0.5Sr_0.5CrO₃ solid solution. The O, Cr, Sr, and La atoms are shown in red, blue, green, and dark green colors, respectively. (f) Brillouin zone.

Turning to the (LaCrO₃)_m/SrCrO₃ superlattices, we consider ferromagnetic ordering and the AFM orderings illustrated in Fig. 2 for the representative cases m = 5 and 6. The optimized structures of all the superlattices are shown in Fig. 3(a). In each case the CrO₂ layers are labelled starting at the interface (L1 to L4). The obtained out-of-plane Cr–O bond lengths and Cr–O–Cr bond angles of the superlattices are summarized in Table 1. We find at the interface long and short Cr–O bonds (SrO-L1) arranged in a checkerboard pattern, corresponding to Cr³⁺ and Cr⁴⁺ ions, see Fig. 3(b), which is confirmed by the occupation matrices.⁶¹ All Cr³⁺ ions show a 3d^2.8 charge state with a magnetic moment of 2.8 μ_B and all Cr⁴⁺ ions show a 3d^2.0 charge state with a magnetic moment of 2.0 μ_B. As one moves away from the interface the Cr–O bond lengths and Cr–O–Cr bond angles approach the bulk values of LaCrO₃ (2.02 ± 0.02 Å,²⁸ 160° (ref. 27)); and also the (significant) distortions of the CrO₆ octahedra resemble those of bulk LaCrO₃. It is remarkable that the results in Table 1 are comparable to previous reports on the appearance of short (1.84 Å for m = 5 and 1.83 Å for m = 6) and long (2.04 Å for m = 5 and 2.03 Å for m = 6) out-of-plane V–O bonds at the interface of the (LaVO₃)_m/SrVO₃ superlattice (combined with V–O–V bond angles of 163° for m = 5 and 172° for m = 6, decreasing to the bulk value of LaVO₃, 157°, as one moves away from the interface).²⁶

Fig. 2 Considered AFM orderings, viewed along a + b. Red color indicates the atomic layers forming the interface. The CrO₂ layers are labelled (L1 to L4) starting at the interface.

Fig. 3 (a) Optimized structures of the (LaCrO₃)_m/SrCrO₃ superlattices with the CrO₂ layers labelled starting at the interface (L1 to L4), viewed along a + b. (b) Checkerboard pattern of Cr³⁺ and Cr⁴⁺ ions. (c) Atomic labels in layers L1 and L2 around the interface. The O, Cr, Sr, and La atoms are shown in red, blue, green, and dark green color, respectively.

Table 1 Out-of-plane Cr–O bond lengths and Cr–O–Cr bond angles across the atomic layers of the superlattices, see Fig. 3(a)

Cr–O bond length	m = 2	m = 3	m = 4	m = 5	m = 6
SrO → L1 (Å)	1.87, 1.99	1.86, 2.03	1.86, 2.00	1.86, 2.03	1.86, 2.00
L1 → LaO (Å)	1.99	2.02	2.00	2.02	2.00
LaO → L2 (Å)	1.99	2.02	2.01	2.02	2.01
L2 → LaO (Å)	2.01	2.02	2.02	2.02	2.02
LaO → L3 (Å)			2.01	2.02	2.02
L3 → LaO (Å)					2.02
LaO → L4 (Å)					2.02

---

Cr–O–Cr bond angle	m = 2	m = 3	m = 4	m = 5	m = 6
L1 → SrO → L1 (°)	174	163	172	163	172
L1 → LaO → L2 (°)	167	160	163	160	163
L2 → LaO → L3 (°)			158	157	158
L3 → LaO → L4 (°)					157

---

According to Fig. 4, for all the superlattices, G-type AFM ordering is energetically favorable, i.e., they retain the magnetic ordering of bulk LaCrO₃. (LaVO₃)_m/SrVO₃ superlattices, on the contrary, favor A-type AFM ordering over the C-type AFM ordering of bulk LaVO₃ (by 142 and 126 meV for m = 5 and 6, respectively),²⁶ which can be explained by the development of tetragonal distortions.²⁵ We do not observe such distortions for the superlattices under investigation. Note that LaCrO₃ and LaVO₃ show different magnetic orderings in the bulk, because the 3d t_2g states (high spin) are half-filled for Cr³⁺ ions, i.e., the magnetic exchange is isotropic, but not for V³⁺ ions. The fact that the energy differences between the magnetic orderings are less pronounced for smaller m in Fig. 4 (both for even and odd m) implies that the stability of the G-type AFM ordering against thermal fluctuations is reduced. For odd m we obtain a magnetization of 2.0 μ_B, because the magnetic moments in the two L1 layers do not compensate each other due to the checkerboard pattern of Cr³⁺ and Cr⁴⁺ ions, compare Fig. 2 and 3(b). For even m the orientations of the magnetic moments are identical in the two L1 layers, implying that the checkerboard pattern of Cr³⁺ and Cr⁴⁺ ions does not prohibit compensation, i.e., we obtain zero magnetization. We note that (LaVO₃)_m/SrVO₃ superlattices have zero magnetization for odd m and a magnetization of 2.0 μ_B for even m, i.e., they show the opposite even–odd behavior than the superlattices under investigation, because for A-type AFM ordering the compensation of magnetic moments at the interface is exactly inverted.

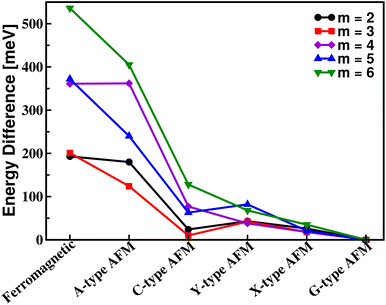Fig. 4 Total energy differences per supercell of different magnetic orderings with respect to the G-type AFM ordering.

In order to clarify whether a deviation from G-type AFM ordering at the interface is energetically favorable, we consider the X- and Y-type AFM orderings shown in Fig. 2, with the result that the total energy increases by 21 and 82 meV for the m = 5 superlattice and by 35 and 68 meV for the m = 6 superlattice, respectively. While the Cr³⁺ ions away from the interface are subject to superexchange (G-type AFM ordering) as in bulk LaCrO₃, both Cr³⁺ and Cr⁴⁺ ions are found at the interface, joined by O²⁻ anions, which facilitates ferromagnetic double-exchange. The competition between superexchange and double-exchange (governed by the Goodenough–Kanamori rules^62–64), for example, plays a decisive role in La_1−xSr_xMnO₃ (ref. 65) and rare-earth nickelates.⁶⁶ Double-exchange is found between Cr²⁺ and Cr³⁺ ions in LaCrO₃ ceramics⁶⁷ and between Cr³⁺ and Cr⁴⁺ ions in rutile CrO₂.⁶⁸ However, our total energy considerations show that a parallel alignment of the magnetic moments of the Cr³⁺ and Cr⁴⁺ ions at the interface, see Fig. 2 and 3(b), is not favorable in the in-plane directions and is favorable in the out-of-plane direction only in the case of even m. The reason is that for even m the superlattice comprises an odd number of CrO₂ layers such that in two of these layers the magnetic moments must have the same orientation. Realizing the out-of-plane parallel alignment at the interface is favorable due to the ferromagnetic double-exchange. However, the magnetic ordering cannot explain the appearance of a checkerboard pattern of Cr³⁺ and Cr⁴⁺ ions, since the arrangement of all Cr³⁺ ions in a single layer would lead to additional favorable in-plane superexchange. The formation of a checkerboard pattern, therefore, is not related to the magnetic ordering but rather to the reduction of electrostatic repulsion by the delocalization of the additional charge around the Sr atoms (due to the presence of Cr³⁺ ions instead of only Cr⁴⁺ ions).

The total and partial Cr 3d and O 2p densities of states obtained for the m = 5 (m = 3) superlattice are shown in Fig. 5 (S2†) together with the corresponding band structure. As the bandgaps are comparable to that of the La_0.5Sr_0.5CrO₃ solid solution, the superlattices are transparent. We find that the valence band edge is formed by strongly hybridized Cr 3d and O 2p states, whereas the conduction band edge is formed by almost pure Cr 3d states. Localized shallow in-gap states (dominated by Cr 3d states with notable contributions of O 2p states) appear about 0.3 eV above the valence band edge. Fig. 5 (S2†) shows the orbitally projected Cr 3d densities of states for the CrO₂ layers L1 and L2 of the m = 5 (m = 3) superlattice. The in-gap states turn out to be mainly due to the d_xz and d_yz orbitals of the Cr 1b and Cr 1c atoms, which agrees with the fact that these atoms adopt 4+ oxidation states and carry magnetic moments of 2.0 μ_B. The Cr⁴⁺ ions at the interface thus are responsible for the fact that the superlattices are p-type semiconductors. Notably, in the case of the (LaVO₃)₅/SrVO₃ superlattice the same orbitals give rise to localized in-gap states, however, located about 0.8 eV above the valence band edge.²⁶

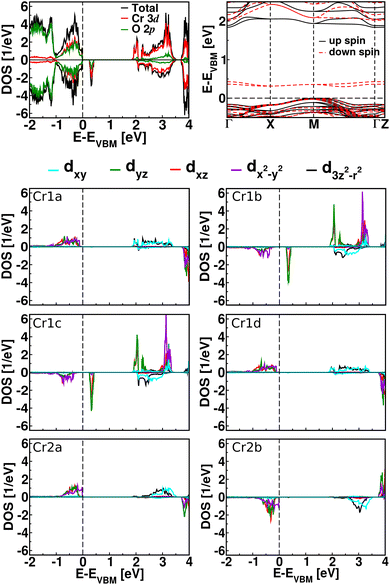Fig. 5 Total and partial densities of states (sum over all atoms, divided by the number of Cr atoms) as well as band structure of the m = 5 superlattice, along with orbitally projected densities of states of the Cr atoms in layers L1 and L2. The labels of the atoms are indicated in Fig. 3.

We find that the valence band edge is due to the d_xy orbitals of the Cr 2a and Cr 2b atoms and that the conduction band edge is due to the d_xz and d_yz orbitals of the Cr 1b and Cr 1c atoms (localized states that correspond to the in-gap states in the other spin channel). The orbital occupations and magnetic moments (2.8 μ_B) of the Cr 1a and Cr 1d atoms agree with results for bulk LaCrO₃,³⁸ which shows that these atoms realize 3+ oxidation states. The spin up/down channel of the Cr 2a atom resembles the spin down/up channel of the Cr 2b atom due to the in-plane AFM ordering. While there is charge ordering in layer L1 with Cr³⁺ and Cr⁴⁺ ions arranged in a checkerboard pattern, the Cr atoms in layer L2 already maintain the 3+ oxidation state of bulk LaCrO₃.

The total and partial Cr 3d and O 2p densities of states obtained for the m = 6 (m = 2, m = 4) superlattice are shown in Fig. 6 (S1, S3†) together with the corresponding band structure. Again the bandgaps are comparable to the bandgap of the La_0.5Sr_0.5CrO₃ solid solution, implying transparency. Similar to the superlattices with odd m, the valence band edge is due to hybridized Cr 3d and O 2p states and the conduction band edge is due to almost pure Cr 3d states. In all cases, the bandgap is reduced because of the creation of shallow in-gap states located about 0.2 eV above the valence band edge. Fig. 6 (S1, S3†) shows the orbitally projected Cr 3d densities of states for the CrO₂ layers L1 and L2 of the m = 6 (m = 2, m = 4) superlattice. We find that the in-gap states, because of which the superlattices again are p-type semiconductors, are due to the d_xz and d_yz orbitals of the Cr 1a and Cr 1d atoms (4+ oxidation states, magnetic moments of 2.0 μ_B). In contrast to the case of odd m, the in-gap states appear in both spin channels, as the orientations of the magnetic moments here are identical in the two L1 layers (Fig. 2) while the charge ordering follows a checkerboard pattern. In the case of the (LaVO₃)₆/SrVO₃ superlattice localized in-gap states, due to the same orbitals, appear about 0.7 eV above the valence band edge.²⁶

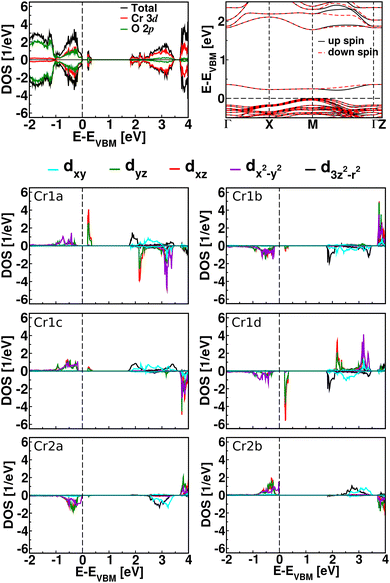Fig. 6 Total and partial densities of states (sum over all atoms, divided by the number of Cr atoms) as well as band structure of the m = 6 superlattice, along with orbitally projected densities of states of the Cr atoms in layers L1 and L2. The labels of the atoms are indicated in Fig. 3.

We find that the valence band edge is due to the d_xy orbitals of the Cr 2a and Cr 2b atoms and that the conduction band edge is due to the d_3z²−r² orbitals of the Cr 1a, Cr 1b, Cr 1c, and Cr 1d atoms. The orbital occupations and magnetic moments (2.8 μ_B) of the Cr 2a and Cr 2b atoms confirm their Cr³⁺ oxidation states. The spin up/down channel of the Cr 2a atom resembles the spin down/up channel of the Cr 2b atom due to in-plane AFM ordering. Similar to the superlattices with odd m, the checkerboard pattern of Cr³⁺ and Cr⁴⁺ ions is limited to the immediate vicinity of the interface, while the Cr atoms in layer L2 already maintain the 3+ oxidation state of bulk LaCrO₃.

Conclusion

Our theoretical study of (LaCrO₃)_m/SrCrO₃ superlattices demonstrates that both Cr³⁺ and Cr⁴⁺ ions appear at the interface (next to the SrO layer) and form a checkerboard pattern. The Cr⁴⁺ ions resemble the properties of bulk SrCrO₃. Their d_xz and d_yz orbitals introduce shallow in-gap hole states because of which the superlattices are p-type semiconductors. The magnetic moments in the two CrO₂ layers surrounding the SrO layer compensate each other for even m but give rise to a finite magnetization for odd m. This even–odd m-dependence of the magnetization is opposite to previous results for the closely related (LaVO₃)_m/SrVO₃ superlattices, which is a consequence of the fact that the G-type AFM ordering of bulk LaCrO₃ is retained in the Cr case while there is A-type AFM ordering in the V case. For even m, for example, the Cr magnetic moments at the interface thus do not share the parallel alignment of the V magnetic moments in all directions but only in the out-of-plane direction. It also turns out that the created in-gap states are significantly shallower for the Cr than for the V superlattices, which enables effective hole doping. Our results demonstrate that the (LaCrO₃)_m/SrCrO₃ superlattices with odd m combine transparency with p-type semiconductivity and finite magnetization. This unique set of functionalities is of considerable interest for a multitude of applications.

Data availability

The authors declare that the data supporting the findings of this study are available within the paper.

Author contributions

S. T. and P. C. R. conducted the calculations. All authors contributed to the writing of the manuscript.

Conflicts of interest

The authors declare that there are no conflicts of interest.

Acknowledgements

The research reported in this publication was supported by funding from King Abdullah University of Science and Technology (KAUST). Funding was also received from the Deutsche Forschungsgemeinschaft (project number 107745057, TRR 80). The authors gratefully acknowledge the KAUST supercomputing laboratory for providing computational resources.

References

1. Z.-X. Shen and D. S. Dessau, Electronic structure and photoemission studies of late transition-metal oxides – Mott insulators and high-temperature superconductors, Phys. Rep., 1995, 253, 1.
2. H. Yakabe, K. Kikuchi, I. Terasaki, Y. Sasago, and K. Uchinokura, Thermoelectric properties of transition-metal oxide NaCo₂O₄ system, in 16th International Conference on Thermoelectrics, 1997, pp. 523–527.
3. Z. Fang and K. Terakura, Structural distortion and magnetism in transition metal oxides: crucial roles of orbital degrees of freedom, J. Phys.: Condens. Matter, 2002, 14, 3001.
4. F. J. Wong and S. Ramanathan, Electrical transport in transition metal oxides, in Resistive Switching: from Fundamentals of Nanoionic Redox Processes to Memristive Device Applications, 2016, pp. 165–196.
5. A. Perucchi, L. Baldassarre, A. Nucara, P. Calvani, C. Adamo, D. G. Schlom, P. Orgiani, L. Maritato and S. Lupi, Optical properties of (SrMnO₃)_n/(LaMnO₃)_2n superlattices: an insulator-to-metal transition observed in the absence of disorder, Nano Lett., 2010, 10, 4819.
6. S. Middey, D. Meyers, M. Kareev, E. J. Moon, B. A. Gray, X. Liu, J. W. Freeland and J. Chakhalian, Epitaxial growth of (111)-oriented LaAlO₃/LaNiO₃ ultra-thin superlattices, Appl. Phys. Lett., 2012, 101, 261602.
7. W. Dai, S. Adhikari, A. C. Garcia-Castro, A. H. Romero, H. Lee, J.-W. Lee, S. Ryu, C.-B. Eom and C. Cen, Tailoring LaAlO₃/SrTiO₃ interface metallicity by oxygen surface adsorbates, Nano Lett., 2016, 16, 2739.
8. M. Briggeman, H. Lee, J.-W. Lee, K. Eom, F. Damanet, E. Mansfield, J. Li, M. Huang, A. J. Daley, C.-B. Eom, P. Irvin and J. Levy, One-dimensional Kronig-Penney superlattices at the LaAlO₃/SrTiO₃ interface, Nat. Phys., 2021, 17, 782.
9. A. Ohtomo, D. A. Muller, J. L. Grazul and H. Y. Hwang, Artificial charge-modulation in atomic-scale perovskite titanate superlattices, Nature, 2002, 419, 378.
10. A. Ohtomo and H. Y. Hwang, A high-mobility electron gas at the LaAlO₃/SrTiO₃ heterointerface, Nature, 2004, 427, 423.
11. A. Brinkman, M. Huijben, M. Van Zalk, J. Huijben, U. Zeitler, J. C. Maan, W. G. van der Wiel, G. J. H. M. Rijnders, D. H. A. Blank and H. Hilgenkamp, Magnetic effects at the interface between non-magnetic oxides, Nat. Mater., 2007, 6, 493.
12. S. A. Chambers, L. Qiao, T. C. Droubay, T. C. Kaspar, B. W. Arey and P. V. Sushko, Band alignment, built-in potential, and the absence of conductivity at the LaCrO₃/SrTiO₃(001) heterojunction, Phys. Rev. Lett., 2011, 107, 206802.
13. A. David, R. Frésard, P. Boullay, W. Prellier, U. Lüders and P.-E. Janolin, Structural transition in LaVO₃/SrVO₃ superlattices and its influence on transport properties, Appl. Phys. Lett., 2011, 98, 212106.
14. H. Y. Hwang, Y. Iwasa, M. Kawasaki, B. Keimer, N. Nagaosa and Y. Tokura, Emergent phenomena at oxide interfaces, Nat. Mater., 2012, 11, 103.
15. F. Hou, T.-Y. Cai, S. Ju and M.-R. Shen, Half-metallic ferromagnetism via the interface electronic reconstruction in LaAlO₃/SrMnO₃ nanosheet superlattices, ACS Nano, 2012, 6, 8552.
16. E. Assmann, P. Blaha, R. Laskowski, K. Held, S. Okamoto and G. Sangiovanni, Oxide heterostructures for efficient solar cells, Phys. Rev. Lett., 2013, 110, 078701.
17. Y. Zhou and K. M. Rabe, Coupled nonpolar–polar metal–insulator transition in 1 : 1 SrCrO₃/SrTiO₃ superlattices: a first-principles study, Phys. Rev. Lett., 2015, 115, 106401.
18. S. Y. Park, A. Kumar and K. M. Rabe, Charge-order-induced ferroelectricity in LaVO₃/SrVO₃ superlattices, Phys. Rev. Lett., 2017, 118, 087602.
19. S. Zhang, H. Y. Xiao, S. M. Peng, G. X. Yang, Z. J. Liu, X. T. Zu, S. Li, D. J. Singh, L. W. Martin and L. Qiao, Band-gap reduction in (BiCrO₃)_m/(BiFeO₃)_n superlattices: designing low-band-gap ferroelectrics, Phys. Rev. Appl., 2018, 10, 044004.
20. J. A. Santana, J. T. Krogel, S. Okamoto and F. A. Reboredo, Electron confinement and magnetism of (LaTiO₃)₁/(SrTiO₃)₅ heterostructure: a diffusion quantum Monte Carlo study, J. Chem. Theory Comput., 2019, 16, 643.
21. A. T. Lee, H. Park and S. Ismail-Beigi, Origin of the orbital polarization of Co²⁺ in La₂CoTiO₆ and (LaCoO₃)₁ + (LaTiO₃)₁: a DFT + U and DFMT study, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103, 125105.
22. C. Adamo, C. A. Perroni, V. Cataudella, G. De Filippis, P. Orgiani and L. Maritato, Tuning the metal–insulator transitions of (SrMnO₃)_n/(LaMnO₃)_2n superlattices: role of interfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 045125.
23. J. Varignon, N. C. Bristowe, E. Bousquet and P. Ghosez, Coupling and electrical control of structural, orbital and magnetic orders in perovskites, Sci. Rep., 2015, 5, 15364.
24. H. Tan, R. Egoavil, A. Béché, G. T. Martinez, S. Van Aert, J. Verbeeck, G. Van Tendeloo, H. Rotella, P. Boullay, A. Pautrat and W. Prellier, Mapping electronic reconstruction at the metal–insulator interface in LaVO₃/SrVO₃ heterostructures, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 155123.
25. U. Lüders, W. C. Sheets, A. David, W. Prellier and R. Frésard, Room-temperature magnetism in LaVO₃/SrVO₃ superlattices by geometrically confined doping, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 241102.
26. Q. Dai, U. Lüders, R. Frésard, U. Eckern and U. Schwingenschlögl, Electronic reconstruction in (LaVO₃)_m/SrVO₃ (m = 5 and 6) superlattices, Adv. Mater. Interfaces, 2018, 80, 1701169.
27. K. Maiti and D. D. Sarma, Electronic structure of La_1−xSr_xCrO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 7816.
28. L. Qiao, H. Y. Xiao, S. M. Heald, M. E. Bowden, T. Varga, G. J. Exarhos, M. D. Biegalski, I. N. Ivanov, W. J. Weber and T. C. Droubay, The impact of crystal symmetry on the electronic structure and functional properties of complex lanthanum chromium oxides, J. Mater. Chem. C, 2013, 1, 4527.
29. K. P. Ong, P. Blaha and P. Wu, Origin of the light green color and electronic ground state of LaCrO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 073102.
30. P. V. Sushko, L. Qiao, M. Bowden, T. Varga, G. J. Exarhos, F. K. Urban III, D. Barton and S. A. Chambers, Multiband optical absorption controlled by lattice strain in thin-film LaCrO₃, Phys. Rev. Lett., 2013, 110, 077401.
31. B. L. Chamberland, Preparation and properties of SrCrO₃, Solid State Commun., 1967, 5, 663.
32. K.-W. Lee and W. E. Pickett, Orbital-ordering driven structural distortion in metallic SrCrO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125133.
33. A. C. Komarek, T. Möller, M. Isobe, Y. Drees, H. Ulbrich, M. Azuma, M. T. Fernandez-Diaz, A. Senyshyn, M. Hoelzel and G. André, Magnetic order, transport and infrared optical properties in the ACrO₃ system (A = Ca, Sr, and Pb), Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125114.
34. A. Chainani, M. Mathew and D. D. Sarma, Electron-spectroscopy study of the semiconductor–metal transition in La_1−xSr_xCoO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 9976.
35. Y. Tokura, Y. Taguchi, Y. Okada, Y. Fujishima, T. Arima, K. Kumagai and Y. Iye, Filling dependence of electronic properties on the verge of metal–Mott-insulator transition in Sr_1−xLa_xTiO₃, Phys. Rev. Lett., 1993, 70, 2126.
36. T. Saitoh, A. E. Bocquet, T. Mizokawa, H. Namatame, A. Fujimori, M. Abbate, Y. Takeda and M. Takano, Electronic structure of La_1−xSr_xMnO₃ studied by photoemission and X-ray-absorption spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 13942.
37. I. Chaitanya Lekshmi, A. Gayen and M. S. Hegde, The suppression of structural phase transformation in LaVO₃ and La_1−xSr_xVO₃ thin films fabricated by pulsed laser deposition, J. Phys. Chem. Solids, 2005, 66, 1647.
38. K. H. L. Zhang, Y. Du, P. V. Sushko, M. E. Bowden, V. Shutthanandan, S. Sallis, L. F. J. Piper and S. A. Chambers, Hole-induced insulator-to-metal transition in La_1−xSr_xCrO₃ epitaxial films, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155129.
39. K. H. L. Zhang, Y. Du, A. Papadogianni, O. Bierwagen, S. Sallis, L. F. J. Piper, M. E. Bowden, V. Shutthanandan, P. V. Sushko and S. A. Chambers, Perovskite Sr-doped LaCrO₃ as a new p-type transparent conducting oxide, Adv. Mater., 2015, 27, 5191.
40. A. Klein, C. Körber, A. Wachau, F. Säuberlich, Y. Gassenbauer, S. P. Harvey, D. E. Proffit and T. O. Mason, Transparent conducting oxides for photovoltaics: manipulation of Fermi level, work function and energy band alignment, Materials, 2010, 3, 4892.
41. Z. Wang, C. Chen, K. Wu, H. Chong and H. Ye, Transparent conductive oxides and their applications in near infrared plasmonics, Phys. Status Solidi A, 2019, 216, 1700794.
42. K. Nomura, H. Ohta, A. Takagi, T. Kamiya, M. Hirano and H. Hosono, Room-temperature fabrication of transparent flexible thin-film transistors using amorphous oxide semiconductors, Nature, 2004, 432, 488.
43. O. Lahr, M. S. Bar, H. V. Wenckstern and M. Grundmann, All-oxide transparent thin-film transistors based on amorphous zinc tin oxide fabricated at room temperature: approaching the thermodynamic limit of the subthreshold swing, Adv. Electron. Mater., 2020, 6, 2000423.
44. H. Kawazoe, H. Yanagi, K. Ueda and H. Hosono, Transparent p-type conducting oxides: design and fabrication of p–n heterojunctions, MRS Bull., 2000, 25, 28.
45. A. N. Banerjee and K. K. Chattopadhyay, Recent developments in the emerging field of crystalline p-type transparent conducting oxide thin films, Prog. Cryst. Growth Charact. Mater., 2005, 50, 52.
46. Z. Wang, P. K. Nayak, J. A. Caraveo-Frescas and H. N. Alshareef, Recent developments in p-type oxide semiconductor materials and devices, Adv. Mater., 2016, 28, 3831.
47. G. Hautier, A. Miglio, G. Ceder, G.-M. Rignanese and X. Gonze, Identification and design principles of low hole effective mass p-type transparent conducting oxides, Nat. Commun., 2013, 4, 2292.
48. W. Liu, H. Zhang, J. Shi, Z. Wang, C. Song, X. Wang, S. Lu, X. Zhou, L. Gu, D. V. Louzguine-Luzgin, M. Chen, K. Yao and N. Chen, A room-temperature magnetic semiconductor from a ferromagnetic metallic glass, Nat. Commun., 2016, 7, 13497.
49. T. Dietl, A. Bonanni and H. Ohno, Families of magnetic semiconductors – an overview, J. Semiconduct., 2019, 40, 080301.
50. B. W. Wessels, Bipolar magnetic junction transistors for logic applications, in Rare Earth and Transition Metal Doping of Semiconductor Materials, Woodhead Publishing, 2016, pp. 435–445.
51. M. A. Masud, M. S. Islam, and Q. D. M. Khosru, Modified Ebers-Moll model of magnetic bipolar transistor, in 2015 IEEE International Conference on Electron Devices and Solid-State Circuits, 2015, pp. 812–815.
52. R. N. Gurzhi, A. N. Kalinenko, A. I. Kopeliovich, A. V. Yanovsky, E. N. Bogachek and U. Landman, A magnetic-field-effect transistor and spin transport, Appl. Phys. Lett., 2003, 83, 4577.
53. S. Jin, T. N. Tiefel and R. Wolfe, Directionally-conductive, optically-transparent composites by magnetic alignment, IEEE Trans. Magn., 1992, 28, 2211.
54. R. Polícia, A. C. Lima, N. Pereira, E. Calle, M. Vázquez, S. Lanceros-Mendez and P. Martins, Transparent magnetoelectric materials for advanced invisible electronic applications, Adv. Electron. Mater., 2019, 5, 1900280.
55. H. He, Z. Yang, Y. Xu, A. T. Smith, G. Yang and L. Sun, Perovskite oxides as transparent semiconductors: a review, Nano Converg., 2020, 7, 32.
56. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. Fabris, G. Fratesi, S. de Gironcoli, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, Quantum espresso: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502.
57. M. Cococcioni and S. De Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the LDA + U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
58. K. H. L. Zhang, Y. Du, P. V. Sushko, M. E. Bowden, V. Shutthanandan, L. Qiao, G. X. Cao, Z. Gai, S. Sallis and L. F. J. Piper, Electronic and magnetic properties of epitaxial perovskite SrCrO₃(001), J. Phys.: Condens. Matter, 2015, 27, 245605.
59. J. Yang, Structural analysis of perovskite LaCr_1−xNi_xO₃ by Rietveld refinement of X-ray powder diffraction data, Acta Crystallogr. Sect. B Struct. Sci., 2008, 64, 281.
60. L. Qiao, T. C. Droubay, M. E. Bowden, V. Shutthanandan, T. C. Kaspar and S. A. Chambers, LaCrO₃ heteroepitaxy on SrTiO₃(001) by molecular beam epitaxy, Appl. Phys. Lett., 2011, 99, 061904.
61. P. H. L. Sit, R. Car, M. H. Cohen and A. Selloni, Simple, unambiguous theoretical approach to oxidation state determination via first-principles calculations, Inorg. Chem., 2011, 50, 10259.
62. J. B. Goodenough, Theory of the role of covalence in the perovskite-type manganites [La, M(II)] MnO₃, Phys. Rev., 1955, 100, 564.
63. J. Kanamori, Superexchange interaction and symmetry properties of electron orbitals, J. Phys. Chem. Solids, 1959, 10, 87.
64. E. O. Wollan, Magnetic coupling in crystalline compounds. A phenomenological theory of magnetism in 3d metals, Phys. Rev., 1960, 117, 387.
65. A. T. Apostolov, I. N. Apostolova and J. M. Wesselinowa, La_1−xSr_xMnO₃ nanoparticles for magnetic hyperthermia, Phys. Status Solidi B, 2018, 255, 1700587.
66. Y. Lu, D. Betto, K. Fürsich, H. Suzuki, H.-H. Kim, G. Cristiani, G. Logvenov, N. B. Brookes, E. Benckiser, M. W. Haverkort, G. Khaliullin, M. Le Tacon, M. Minola and B. Keimer, Site-selective probe of magnetic excitations in rare-earth nickelates using resonant inelastic X-ray scattering, Phys. Rev. X, 2018, 8, 031014.
67. H.-S. Xu, Y.-W. Yang, R.-L. Wang, H.-B. Xiao, L.-F. Xu, S.-H. Liang and C.-P. Yang, High-pressure synthesis, structure and magnetic properties of LaCrO₃ ceramics, Phys. Lett. A, 2019, 383, 125837.
68. S. Seong, E. Lee, H. W. Kim, B. I. Min, S. Lee, J. Dho, Y. Kim, J.-Y. Kim and J.-S. Kang, Experimental evidence for mixed-valent Cr ions in half-metallic CrO₂: temperature-dependent XMCD study, J. Magn. Magn. Mater., 2018, 452, 447.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2na00656a

---