Real-time thermal decomposition kinetics of GaAs nanowires and their crystal polytypes on the atomic scale

Abstract

Nanowires (NWs) offer unique opportunities for tuning the properties of III–V semiconductors by simultaneously controlling their nanoscale dimensions and switching their crystal phase between zinc-blende (ZB) and wurtzite (WZ). While much of this control has been enabled by direct, forward growth, the reverse reaction, i.e., crystal decomposition, provides very powerful means to further tailor properties towards the ultra-scaled dimensional level. Here, we use in situ transmission electron microscopy (TEM) to investigate the thermal decomposition kinetics of clean, ultrathin GaAs NWs and the role of distinctly different crystal polytypes in real-time and on the atomic scale. The whole process, from the NW growth to the decomposition, is conducted in situ without breaking vacuum to maintain pristine crystal surfaces. Radial decomposition occurs much faster for ZB- compared to WZ-phase NWs, due to the development of nano-faceted sidewall morphology and sublimation along the entire NW length. In contrast, WZ NWs form single-faceted, vertical sidewalls with decomposition proceeding only via step-flow mechanism from the NW tip. Concurrent axial decomposition is generally faster than the radial process, but is significantly faster (∼4-fold) in WZ phase, due to the absence of well-defined facets at the tip of WZ NWs. The results further show quantitatively the influence of the NW diameter on the sublimation and step-flow decomposition velocities elucidating several effects that can be exploited to fine-tune the NW dimensions.

---

The versatile growth and crystal structure control of III–V semiconductor nanowires (NW) has opened up various new avenues in fundamental and applied physics research of one-dimensional (1D) nanostructures in recent years. Most remarkably, the inherent 1D-structure of NWs represents not only a unique architecture allowing both electronic and optical confinement along the axis and radial directions,^1,2 but also facilitates ample opportunities for heterogeneous integration and development of novel heterostructure design not possible in the bulk or thin-film form. For example, III–V NWs are readily grown on dissimilar, highly lattice-mismatched substrates, such as silicon (Si) thanks to strain relaxation at the sidewall free surfaces.^3,4 As a result, in the limit of very thin NWs, coherent, dislocation-free axial and radial heterostructures can be realized with interesting functional properties.^5,6 Likewise, the 1D-NW geometry offers access to crystal structure design different from the bulk phase. For classical III–Vs, like GaAs, InAs, or InP, the metastable wurtzite (WZ) crystal phase can coexist with the stable zincblende (ZB) phase, enabling the formation of controlled polytype heterostructures along the NW axis.^7–9 Such polytype heterostacks provide unprecedented scope for engineering electronic and phononic properties.^10,11 They can also generate distinct sidewall facets along the NW axis which can inhibit non-radiative surface recombination, as demonstrated in photonic NW-devices.¹² Moreover, WZ/ZB interfaces or even single twin defects enable formation of crystal phase quantum dots (CPQD) in regimes of strong radial quantum confinement.^13–16

Access to such properties is commonly facilitated by direct bottom-up growth, where regimes of axial and radial confinement are accurately designed by growth parameters in conventional epitaxial methods employed for III–V NWs. Hereby, epitaxial growth is, however, by itself a metastable process (especially for typical low-pressure growth methods) that proceeds via non-equilibrium kinetically limited reactions – namely, the forward (growth) reaction and the competing reverse (decomposition) reaction.^17,18 As such, growth of III–V NWs can only take place if the forward driving reaction, mostly limited by the supply rate of active species, exceeds the reverse reaction that mainly depends on substrate temperature through a kinetic barrier for decomposition and desorption. Interestingly, whilst much effort has been directed to controlling and understanding the forward/growth dynamics of III–V NWs, relatively little attention has been paid to the reverse/thermal decomposition dynamics. Understanding of thermal decomposition dynamics – ideally in the native epitaxial environment – is crucial for two reasons: first, most III–V NW systems are grown at highest possible temperature (close to the thermal limit) to achieve highest crystal quality and aspect ratio;^19–21 secondly, thermal decomposition can be intentionally exploited to create confined 1D-quantum wires (QWR) in situ from pre-grown NWs.^15,22,23 Such ultrathin NWs are useful not only for NW-based QDs in quantum technologies mentioned above, but for many other applications in quantum electronics,²³ nano-thermoelectrics,²⁴ as well as strain-engineering of functional core–shell heterostructures.^25–27 In fact, ultra-thin cores can mitigate strain relaxation and enable exceptionally large shell thicknesses in core–shell NWs far beyond the classical critical layer thickness limit.²⁶

So far, in situ thermal decomposition dynamics of NWs have been investigated by several studies in recent years. Hereby, two main approaches can be distinguished, each coming with certain compromises: first, decomposition experiments within the epitaxial growth environment inside the growth reactor, combined with ex situ analysis, usually by scanning electron microscopy (SEM) and transmission electron microscopy (TEM).^{22,23,28–31} And, secondly, conventional growth of NWs combined with subsequent transfer for ex situ decomposition and analysis, mostly by heating NWs inside a TEM.^32–35 The first approach enables best quality of the NWs because contamination and oxidation of the surfaces is prevented. It also enables studies of the influence of growth parameters, not only of temperature but also of pressure, e.g., group-V atmosphere in the decomposition of III–V materials, which allows tuning of the congruent evaporation temperature.³⁶ However, the true microscopic behavior and structural changes during the dynamic decomposition process cannot be fully elucidated using these methods, because they offer only static information from post-decomposition analysis but not during the actual experiment. This would require surface-structure sensitive in situ methods, such as e.g., real-time X-ray scattering³⁷ or reflection high-energy electron diffraction (RHEED)³⁸ previously established for thin-film processes, but which are impractical for mapping the decomposition from single NWs due to their non-planar, and relatively complex three-dimensional facet structure. Nevertheless, basic studies of in situ decomposition and ex situ analysis were applied to e.g., GaN,^28,29 GaAs^22,31 and InAs²³ NWs and it was shown that their diameters could be reduced to sub-20 nm dimensions, enabling the observation of 1D quantum confinement effects.

In contrast, combining decomposition and analysis from ex situ, transferred NWs allows the second approach to investigate the dynamic microscopic behavior, but it is challenging to accurately mimic the conditions of the native growth environment. Especially the removal of NWs from the growth substrate (e.g., silicon or III–V substrate) and transfer to a TEM holder (usually with a carbon or SiN support film) can introduce unwanted and spurious effects that strongly influence experimental results. Specifically, an amorphous shell of native oxide can form on the NWs during transfer, which is more stable against thermal decomposition than the studied material itself and can locally even prevent decomposition.^33,35,39,40 In addition, in such experiments, the NW is lying on the support film and has a different heat contact to the substrate, which can lead to non-uniform decomposition,^33–35,41 unlike decomposition inside conventional growth environments.^22,23 Moreover, several thermal decomposition studies performed on NWs using in situ TEM were influenced by other extrinsic features, such as the inherent Au-catalyst droplet often used for the growth. This catalyst strongly accelerates the axial decomposition process due to interaction of the liquid Au alloy with the NW.^32,39

To reconcile these various drawbacks, the ultimate solution is to perform the epitaxial growth, the entire decomposition process and the real-time TEM analysis of these steps in a single instrument, as has been demonstrated for the growth and decomposition of CuO NWs.⁴² However, for the technologically relevant III–V NW materials, such uncompromising approaches aiming for complete microscopic dynamics within the true native environment and on intrinsically clean NWs have not been explored at all so far. In this work, we close this gap by performing real-time thermal decomposition analysis of entirely catalyst-free GaAs NWs grown and studied directly by in situ TEM. Our investigations not only provide access to the native growth surface, due to the absence of foreign catalyst droplets, but further enable the real-time decomposition studies of different crystal phase polytypes (ZB vs. WZ) and their related mixtures. In addition, we also highlight the relevance of the distinct facet structure in ZB vs. WZ NWs on the atomistic modes governing the decomposition process.

The NWs were grown in the self-catalyzed vapor–liquid–solid growth mode immediately before the decomposition inside the same TEM, using conventional effusion and valved cracker sources for group-III and -V elements (similar to molecular-beam epitaxy (MBE)) attached to the microscope^43,44 and a specifically designed silicon heating cantilever.^45,46 As the cantilever acts as an epitaxial growth substrate and defines the NW's crystal orientation, this experimental design enables direct and real-time studies of NWs in their intrinsic growth environment. Hereby, the cantilever simultaneously serves as a resistive heater, such that heating is performed on as-grown NWs in their free-standing geometry with a sole contact to the substrate at the bottom. This closely resembles the conditions of post-growth annealing of bottom-up grown NWs in conventional epitaxial growth reactors. Real-time monitoring via high-resolution TEM videos of the NWs was then performed in the 〈11̄0〉 (ZB)/〈112̄0〉 (WZ) zone axis, which allows us to distinguish between WZ and ZB polytypes. The focus of the following experiments is to quantitatively assess the impact of the two crystal phases, as well as their characteristic surface facet structure and shape on the NW decomposition dynamics. In order to achieve this, three experiments are presented in detail. First, we analyse three adjacent mixed-phase NWs. This allows direct comparison of the influence of the shape and layer stacking on the decomposition, under conditions where the temperature is the same for all NWs. In addition, we compare the decomposition dynamics of an almost phase pure ZB with a WZ NW. By placing a focus on the dynamic evolution of the crystal facets we highlight markedly different decomposition mechanisms for the two respective crystal phases.

1. Mixed-phase NWs

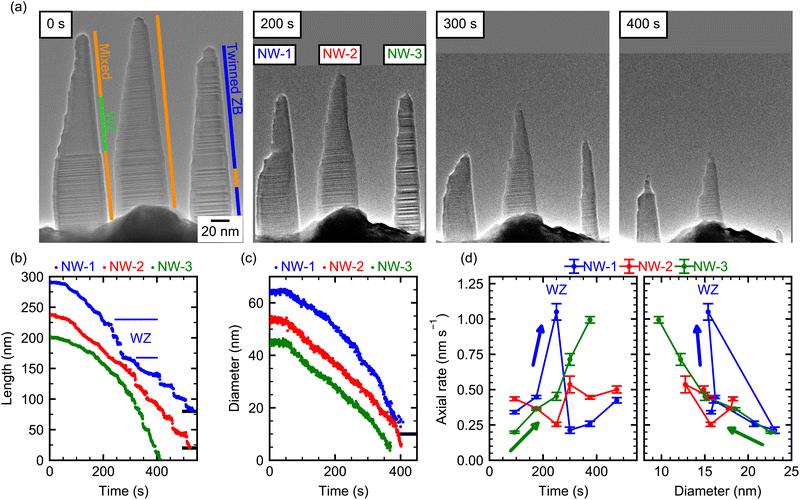
Fig. 1(a) shows an image of the GaAs NWs prior to the decomposition experiment, which were exposed to As-atmosphere to consume and crystallize the Ga catalyst droplet subsequent to the growth. The NWs have an initial length of ∼200 nm and consist mostly of a mixed ZB/WZ crystal structure. Since the cantilever on which the NWs are grown has a thickness of 4 μm in viewing direction, the distance between NWs can be larger than apparent from this projection. All NWs show a similar shape with a tapered left side and an almost vertical, untapered right side. This shape is characteristic for low-temperature growth inside this TEM, which does not support substrate rotation as in standard MBE growth chambers. Hence, the initial asymmetrically tapered shape is due to the Ga and As flux impinging onto the NW facets from the top-right and top-left corner, respectively. The NW micro-structure was determined from additional high-resolution TEM images (see ESI Section S3†). Apart from the predominant stacking disorder, the three NWs in view show additional characteristic differences: NW-1 has a large phase-pure WZ segment in the middle, whereas the top and bottom of the NW consist of a mixed ZB/WZ crystal structure with stacking faults every few monolayers. Meanwhile, NW-2 shows similar micro-structure as NW-1 but without any extended WZ segments, and NW-3 is almost pure ZB with a high density of twin defects.

Fig. 1 (a) Time evolution of three GaAs NWs during decomposition. The scalebar is valid for all images. (b) Length and (c) diameter at the bottom of the NWs as a function of time. Some curves are offset to higher values for clarity as indicated by the thick black line on the right axis which indicates this curve's zero position. This offset applies to the length of NW-1 (80 nm) and NW-2 (20 nm) and diameter of NW-1 (10 nm). (d) Corresponding axial decomposition rates as a function of time and diameter close to the NW tip. The arrows indicate the direction of time.

To initiate thermal decomposition, the supply of Ga and As is interrupted and the heating current through the cantilever is increased, until the decomposition process visibly starts taking place via changes in the surface structure and subsequent removal of atoms from the surface. The exact value of the temperature is, however, not known because of the incertitude in the pre-calibration of cantilevers. Nevertheless, we can estimate the temperature at the NW position in the range of 650 °C to 700 °C based on knowledge of the decomposition rate from previous experiments in ultra-high vacuum (UHV).²² Moreover, the substrate temperature can drift during the experiment due to the change of device resistance induced by deposition (and subsequent desorption) of GaAs on the heating elements. To minimize this effect, the entire experiment was performed under constant heating power (within 1%). As the temperature is the same for all three NWs at each time point, we further circumvent the temperature uncertainties by comparing the decomposition rates of the different NWs over the same time period (see ESI Section S1†).

In the following, we describe several features of the decomposition process as seen by the temporal evolution in Fig. 1(a). First, as expected, the length and diameter of all NWs decrease over the course of the experiment. In addition, the shape of the NWs changes in very peculiar ways. For example, after about 200 s of decomposition, NW-1 shows a region of small diameter at the top of the NW and a region with large diameter at the bottom. The abrupt change in diameter in its center was not present before annealing. Further on, after 300 s, the thin top segment disappeared, leaving behind an apparently more stable bottom part of the NW. Note, in Fig. 1(a) the lower part of the rapidly decomposing top segment consists of a large WZ segment, which is specific to NW-1. Hence, we tentatively suggest that this shape along with the quick axial decomposition is a characteristic result of the WZ phase. Indeed, these features are not observed in NW-2 which has a similar shape and crystal structure but does not contain such a long WZ segment. For this NW, the tapered shape stays roughly the same over the course of the experiment, while length and diameter decrease at any given position. NW-3, composed mainly of heavily twinned ZB structure, has initially a smaller diameter and length than the other two NWs. It remains the thinnest NW throughout the decomposition process, and after 400 s it has decomposed almost completely with only a short stem with a diameter below 10 nm remaining.

To quantitatively describe the length and diameter evolution at different positions of each NW, their shape was analyzed for each video frame during the entire decomposition process (see ESI Section S2†). The resulting data is depicted in Fig. 1(b) and (c). Some curves are offset to higher values for clarity as indicated by the black line at the right axis, which indicates this curve's zero position. Within the first ∼50 s, the length (and also the diameter) decreases slowly for all three NWs. This might be due to an inhibiting barrier at the beginning of the experiment, but we cannot rule out a somewhat lower temperature at the beginning of the experiment. After that, the length of all NWs decreases over time, but all three NWs show both qualitatively and quantitatively different behavior. NW-1 shows an initially slow length reduction, which accelerates between 200 s and 280 s and then abruptly slows down again. In contrast to this, the length of NW-2 decreases almost linearly with time and NW-3 shows a clear non-linear behavior with an accelerating reduction in length as decomposition progresses. In regions of small NW diameters and towards the end of the experiment, plateaus of constant lengths followed by abrupt length reductions are evidenced. These can be due to accumulation of amorphous material at the thinned NW tip, which inhibits evaporation (see ESI Section S4†). Fig. 1(c) shows the diameter evolution of the three NWs, evaluated at the bottom (150 nm below the initial tip position). Here, NW-1 shows a continuous acceleration of the radial decomposition with time. In contrast, the diameter of NW-2 and NW-3 decreases almost linearly. ESI Section S5† shows the same data plotted as NW volume over time, which shows an overall decreasing volumetric decomposition rate due to the smaller size of the NW towards the end of the experiment. Since the temperature is the same for all NWs, we deduce that the strong differences can only be caused by variations in crystal phase and shape of the NWs, which are analysed in more detail in the following. To account for these more quantitatively, we extract the respective decomposition rates as a function of time and shape, which allow us to better demarcate changes due to different crystal phase stackings. For the axial decomposition rate, the length variation was fitted with a linear function in suitable time-frames. The results are shown in Fig. 1(d) as a function of time and diameter (measured 20 nm below the NW tip). Since the position where the diameter is evaluated is relative to the tip position, it moves towards the bottom just like the tip as decomposition progresses. The diameter is, thus, influenced by the concurrent radial decomposition and the tapering of the NW. We first focus on NW-1 (blue): initially, the diameter below the tip is ∼15 nm (see 0 s, 200 s in (a) and (d)) and the axial decomposition is ∼0.3 nm s⁻¹. At 250 s, the axial decomposition accelerates strongly (more than two-fold), leading to the abrupt reduction in length evidenced also in Fig. 1(b). This increased rate coincides exactly with the time-frame, where the WZ segment is situated at the tip of the NW and ends when the WZ segment is fully decomposed, exposing an adjacent ZB segment beneath (see ESI Section S3†). This suggests that the WZ phase is thermally less stable than the ZB phase regarding axial decomposition. Indeed, faster decomposition of WZ GaAs compared to ZB has been observed, albeit under different experimental conditions.³⁵ The remaining bottom-part of the NW is left with a larger diameter (∼25 nm) near its top end compared to the beginning of the experiment (∼15 nm, see 0 s and 300 s frames in (a) and (d)). This increased diameter is correlated with a drop in axial decomposition rate to ∼0.2 nm s⁻¹; lower than during the beginning of the experiment. This might suggest that the radial dimension of the NW has a direct impact on the axial decomposition rate, since the crystal structure at the very top and bottom part of the NW shows the same microstructure. This is supported by the temporal evolution of the axial decomposition rate of NW-1 during the final stages of the experiment, where it increases again accompanied by a decrease in the diameter (see Fig. 1(d)). However, from a single NW such a dependence cannot be unambiguously deduced due to the possibility of a temperature drift simultaneously influencing the axial decomposition. Yet, NW-2 and NW-3 show distinctively different behavior: NW-2 shows a constant axial decomposition rate and also has an almost constant diameter near the tip, because the tapering compensates the diameter reduction due to radial decomposition. On the contrary, the axial decomposition of NW-3 accelerates with time. Concurrently, the diameter near the tip decreases with time due to radial decomposition from 25 nm to below 10 nm, because the tapering of NW-3 is lower. The temporal evolution of the axial decomposition rate of NW-2 and NW-3 could not be correlated to differences in their crystal phase, because they contain no large phase-pure segments.

To explain the different axial decomposition dynamics, we suspect that the diameter of the NW close to the tip impacts the axial evaporation rate. For smaller NW diameter, the curvature of the surface is increased, which increases the relative amount of crystal edges. Since such edges act as preferential sites for evaporation,⁴⁷ we expect that a reduced radius leads to a larger axial (and radial) decomposition rate. Likewise, if surface diffusion precedes desorption, an increased surface to volume ratio at smaller diameter increases the surface area available for desorption and, thus, might increase the decomposition rate. Both NW-3 and NW-1 (except for the WZ-segment) show this trend of increasing decomposition rate for smaller diameters quite clearly (Fig. 1(d), right panel). Remarkably, the lowest axial rates of NW-1 are at 300 s with higher rates at the beginning and the end of the experiment. In contrast, for NW-3 the lowest rates are at the beginning and the axial rate increases at all times. The fact that the correlation between decomposition rate and diameter is observed for different temporal evolution, indicates that the correlation is not due to uncontrolled changes in the sample temperature or due to an increase in surface roughness. These observations are, therefore, driven by the time-dependent evolution of the NW-shape and diameter.

In contrast, for the radial decomposition, no clear dependence on the NW diameter has been observed for these three NWs (see ESI Section S6†). This is most likely due to the relatively strong crystal phase mixing in these NWs. However, experiments on pure ZB NWs show that, in that case, their radial decomposition depends on the diameter. Hence, to fully understand the effect of the crystal phase on the decomposition dynamics, we performed experiments on almost phase-pure NWs along with higher resolution.

2. Zincblende NW

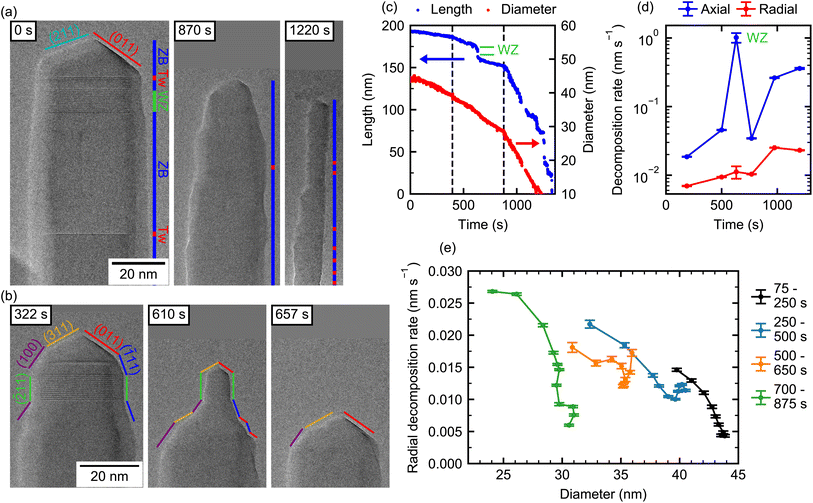
In the second experiment, we investigate a NW (NW-4) that is initially untapered and which consists mainly of ZB crystal phase, except for a single 10 nm long WZ segment close to the tip. Such a small WZ segment is caused by the droplet consumption upon growth termination due to the reduction of the contact angle of the self-catalyzed Ga droplet.^44,48 Below the WZ segment, the NW contains two long phase-pure ZB segments (45 nm and 65 nm) separated by a single twin defect. Further down, the twin density is increased with only short twin-free segment lengths of typically 3 nm to 5 nm. In order to achieve atomistic resolution, only the tip of the NW is observed during the experiment, as shown in Fig. 2. A full view of the NW during decomposition (at 500 s) is shown in the ESI Section S7.†

Fig. 2 (a) TEM image of the mainly ZB-NW (NW-4) imaged at the NW tip at different times with indicated facets and crystal phases. (b) Evolution of facets at the tip during early stages of the decomposition. (c) Length and diameter as a function of time. The dashed lines mark instances, where changes in decomposition rate were not correlated to a change in crystal phase (see text). (d) Respective decomposition rates. (e) Radial decomposition rate as a function of the NW diameter at a fixed position for different time-intervals.

The high resolution employed here allows us to also map the role of the crystal facets in the tip region of the NW, and thereby providing direct insights into the microscopic decomposition dynamics. The facets are determined here from their inclination angle as directly visible in the TEM video. Since the images are measured in the 〈11̄0〉 zone axis, the real facets can be different from the angle of the projection determined here. We assume, that the NW growth direction is [111] B ([1̄1̄1̄]), which is the preferred growth direction of III–V NWs^49–52 and we are viewing from the [011̄] direction.

Initially (0 s), the NW is terminated by a segment of ZB having a tetrahedral shape defined by three {110} facets.⁵³ In the chosen zone axis we observe one of the {110} facets parallel to the beam and the intersection of the two opposite facets forming an edge normal to the [211] direction. Once decomposition starts (322 s), new (311) and (100) facets develop in place of the [211] edge on the left, while the (011) facet is still visible on the right side of the tip, but it is now neighbored by a (1̄11) facet. In the same manner, the edges formed by the NW's {11̄0} sidewalls are not stable^54–56 and evolve into {111̄} and other nano-facets during decomposition. This leads to a complex three-dimensional structure, that cannot be resolved from a single 2D-projection. In contrast, the sidewalls of the WZ segment remain straight edges normal to the [2̄11] direction in ZB notation ([11̄00] in WZ-notation) without strong tapering, which can be explained by the overall lower energy of WZ compared to ZB sidewalls.⁵⁷

Now, to illustrate the role of these facets on the decomposition, we first focus on the section interfacing the ZB tip and the 10 nm WZ segment beneath. At 610 s, the WZ segment forms a thin “neck” on top of a thicker ZB NW, indicating that the short ZB cap on top of the WZ segment prevents an axial decomposition of the WZ phase. This reproduces nicely the observations made in the first experiments shown previously (Section 1). The short ZB segment on top of the WZ segment decomposes in the axial direction. However, its top part consists of the same family of facets (see frame 322 s and 610 s), which limits the width of the WZ segment. In the ESI (Section S8†) we show the decomposition process at the interface between ZB and WZ segments more closely. As we note, on one side of a ZB nano-facet, there is a spontaneous decomposition, which then extends over the entire facet via a step flow mechanism. If there is a neighboring well-defined facet, the layer decomposition can extend from one facet to the other. In this example, a step starts on the (1̄11) facet and continues on the WZ sidewall. This leads to a quick radial decomposition of the WZ segment whenever the ZB segment on top of it is reduced in diameter. This process is only limited by the step flow velocity and results in mostly untapered WZ sidewalls, as we observe here and further illustrate below. Therefore, the diameter of the WZ segment is governed purely by the ZB segment on top and not by its native radial decomposition. Such a step flow decomposition mechanism has been observed for monoclinic CuO⁴² and has been hypothesized for WZ GaN NWs.^28,29

Further down, the dominant pure ZB-regions of the NW exhibit sidewalls with few-nm long {111̄} facets, but for the most part no clear facets are visible (see 870 s and 1220 s). From these images it can be seen that twin defects (positions marked in red) do not lead to any change in sidewall morphology and, thus, have no strong impact on the local radial decomposition rate. Even though step flow decomposition on the short {111̄} facets is visible (see ESI Video V1†), the absence of neighboring facets limits the propagation distance for step-flow. Therefore, the decomposition is mostly dominated by direct decomposition from the undefined sidewalls and the decomposition of ZB NWs appears isotropic when analysed with lower magnification as done in the first experiment (Section 1). From this “macroscopic” point of view, decomposition appears as free sublimation with different rates from the top and side facets.

To illustrate this decomposition behavior on such overall ZB NW, we evaluate the NW length and diameter reduction over time as shown in Fig. 2(c). The evolution of length and diameter shows a section-wise linear behavior over time. Specifically, both the axial and radial decomposition rates (Fig. 2(d)) are initially slow and appear to accelerate at certain points. Note, here the NW diameter is evaluated 50 nm below the position that the tip occupies during the course of the experiment. The axial decomposition rate is initially very slow (0.02 nm s⁻¹) and increases to 0.36 nm s⁻¹ towards the end. At one point, the axial decomposition rate shoots up to ∼1 nm s⁻¹ (at around 625 s). This is directly associated with the WZ segment in the otherwise ZB crystal, as already observed previously for NW-1. As expected, the radial decomposition rate is much lower than the axial rate over the entire experiment. It is increasing with time from 0.007 nm s⁻¹ to 0.023 nm s⁻¹. It is worth noting that while the radial decomposition rate in terms of change in diameter tends to continue to increase towards the end of the experiment, the volumetric radial decomposition rate decreases for very small diameters due to an overall smaller size of the NW as demonstrated for NW-1 to NW-3 in the ESI Section S5.† Differences between rates at the beginning and the end of the experiment may include the combined effect of changes in NW shape, crystal structure, and potential changes in temperature, which makes conclusions about individual contributions challenging. However, certain differentiations can be made: for example, at two instances in the video the axial and radial decomposition simultaneously and abruptly accelerate (400 s and 900 s), which are marked by dashed lines in (c). This is likely caused by a change in temperature because no change in the crystal phase or shape is present at these particular times. Interestingly, here the radial and axial rates are affected by a different magnitude. Around 400 s the radial decomposition rate increases by ∼35%, while the axial rate increases by ∼150%. The same trend holds true around 900 s, where the radial rate abruptly increases by ∼140%, while the axial rate increases by ∼660%. Therefore, the ratio of axial to radial decomposition is larger for increased decomposition rates (i.e., higher temperature). If such in situ decomposition is used to reduce the NW diameter, the axial decomposition is not desired. Our results, thus, suggest that the axial decomposition can be reduced relative to radial decomposition by performing the process at lower temperature but for longer time.

In the latest stages of the experiment (>1000 s) the axial decomposition dynamics change from a linear to a step-like behavior (Fig. 2(c)). The average axial rate increases further, while no change in the radial decomposition rate is visible (Fig. 2(d)). A temperature effect can thus be ruled out and the increased axial rate should rather be attributed to the small diameter, as already observed in the first experiment (Section 1). The step-like behavior is partly caused by accumulations of amorphous material at the tip of the NW, which inhibits axial decomposition (see ESI Video V1 and Section S4†). However, this does not particularly affect the radial decomposition. Towards the very end of the experiment, when the diameter of the NW close to the tip becomes extremely small (∼3 nm), it abruptly decomposes leading to a sudden drop in length. Similar abrupt changes in length have been observed for decomposition in similar NW systems, where even extended (hundreds of nm long) segments of small diameter abruptly disappear because the diameter gets too small.^23,31

In order to investigate if the effect of increasing decomposition rate for smaller diameters also applies to radial decomposition, we take a close look at the radial decomposition rates throughout different stages of the decomposition experiment. However, care needs to be taken in the analysis, because decomposition rates at different times may not be directly related to geometric parameters only, due to the imperfect stability of the local temperature. In order to circumvent possible variations of the local temperature during the experiment, radial decomposition rates at different positions along the NW axis during the same time-frame are evaluated. Thereby, these also correspond to different diameters, given by the underlying tapering of the NW. It is therefore assumed that within one time-frame the temperature is equal at different positions along the NW axis. In addition, we limit our analysis to pure ZB segments, such that any remaining differences in our observations can only be caused by the NW geometry. The evaluated positions are limited to those that are visible over the entire duration of each time-frame. Therefore, for different time-frames different positions are shown. To do this, each frame of the video is mapped to an absolute coordinate system using crystal phase features of the NW (WZ segment, twin defects). This allows the evaluation of the diameter at a fixed position in the ZB region of the NW (see ESI Section S2†). The corresponding data is shown in Fig. 2(e) for decomposition times until 875 s. For each individual time interval plotted here the diameter varies by ∼5 nm along the visible NW segment.

We find the following interesting characteristics: for the first interval 75 s to 250 s, the radial decomposition rate varies from 0.004 nm s⁻¹ to 0.014 nm s⁻¹, yet, the overall rates are comparatively low. Within this time interval, the highest rates correspond to the positions along the NW, where the diameter is lowest. These positions are typically the ones located towards the tip of the NW as seen in Fig. 2(a) and (b). For the consecutive time intervals, this trend towards high radial decomposition rates at lower diameter continues. Note, the relative difference in rate between different positions along the NW axis is as high as a factor of five. However, a certain change in diameter is not always reflected by the same magnitude in the decomposition rate. For example, the time interval 500 s to 650 s shows a similar change in diameter compared to the other intervals but only a much smaller variation of the decomposition rate. As discussed earlier, the complex and dynamic composition of the tip facets strongly influences its decomposition process. Therefore, a single morphological parameter (i.e., diameter) only partly explains changes in the decomposition rate. For the late stages of the experiment, both diameter and radial decomposition rate change only weakly within one time interval (see ESI Fig. S8†). However, from the entire experiment performed on such ZB-dominated NW, we can observe that the radial decomposition increases towards small NW diameters as shown in Fig. 2(e). Such increasing radial decomposition for small diameters is expected to accentuate the tapering of the NW over time. Further, for very small diameters a fast radial decomposition leads to abrupt reduction of the NW length. Controlling the tapering and this non-linearity is, therefore, a prime challenge in achieving long ZB NWs with diameters <10 nm using the decomposition method. As we illustrate in the next section WZ NWs show remarkably different behavior.

3. Wurtzite NW

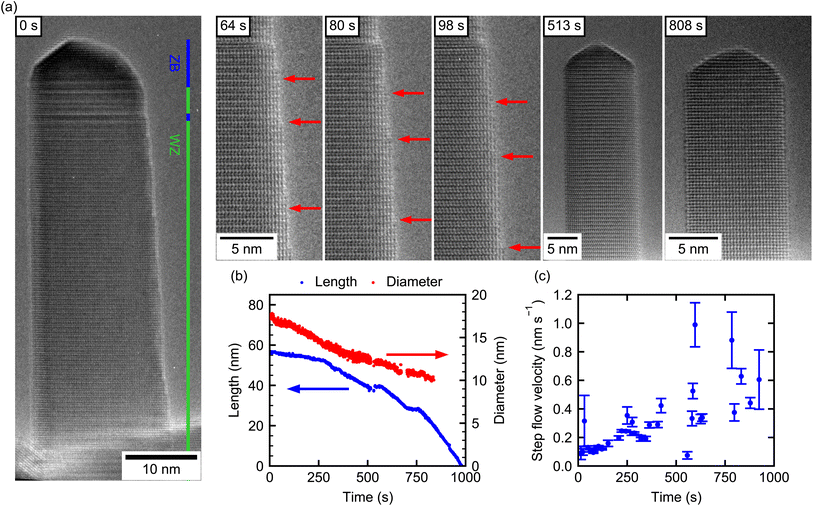
Using the same growth procedure, GaAs NWs with predominant WZ-phase were also observed. These form the basis of our final experiment, where we determine the decomposition dynamics of an almost pure WZ NW (NW-5) with no adjacent ZB segment. Only at the very top, the NW consists of 6 nm ZB, followed by ∼5 nm mixed ZB/WZ and below that a 45 nm long defect-free WZ segment. This is evidenced in Fig. 3(a), which also shows the shape evolution over time. Initially, the NW has a flat sidewall on the left, but shows tapering on the right side. From previous experiments it is known that NWs grown under such conditions have {112̄0} side facets. In this projection, the NW side is given by an edge normal to a 〈11̄00〉 direction. Quite interestingly, and in contrast to the mixed-phase NWs (NW-1–NW-3), the tapering vanishes completely over the course of the experiment, resulting in well-defined side facets at the end. Also contrary to the ZB NW-4, the tip of the WZ NW does not show well-defined facets but a rounded-off shape (see frames at 513 s, 808 s).

Fig. 3 (a) TEM images of the WZ-NW (NW-5) over the course of the experiment. Individual steps at the surface are marked by red arrows. (b) Length and diameter 10 nm below the NW tip as a function of time. (c) Velocity of individual steps on the NW sidewalls.

Fig. 3(b) shows the NW length and diameter (10 nm below the NW tip) evolution over time. The length evolution consists of several almost linear evaporation intervals, demonstrating an overall increasing decomposition rate over time as for all other NWs. The radial decomposition process, however, slows down with time (red curve). Here, two linear regions are identified, first relatively fast radial decomposition (∼0.006 nm s⁻¹) until 400 s and after that slower radial decomposition (∼0.003 nm s⁻¹). It is surprising, that the axial rate increases while the radial rate decreases as the NW gets smaller. This very different trend with respect to the axial decomposition highlights again, that a temperature effect cannot cause these interesting dynamics by itself.

Most of the features observed during the decomposition process can, hence, be understood in terms of the underlying microstructure. First, from the beginning until 280 s the axial decomposition rate is small (∼0.015 nm s⁻¹). At this time, the length decreased by ∼6 nm and thus reaches the end of the small ZB segment at the top of the NW and the decomposition dynamics switches to that for the WZ phase. Here, the slope in length reduction increases by ∼300% (see ESI Section S11† for decomposition rates). Between 515 s and 570 s the experiment was put in standby to adjust the imaging conditions, which is reflected in the plateau seen in the length and diameter data. The plateau at 750 s was likely caused by a temperature instability.

The decelerating trend of the radial decomposition can be explained by closely resolving the microscopic decomposition mechanism in relation to the underlying WZ-structure. Note, that already in NW-4, which contains a short WZ-segment, we observed a characteristic step-flow decomposition process on the side of the segment. This is also now corroborated to be the dominant mechanism responsible for the reduction in diameter via the {112̄0} side facets of this NW. The flow of individual steps moving downwards along the NW can be directly visualized from the video. In the beginning of the experiment there are many steps already present on the right NW sidewall due to the initial tapering. Exemplary images are shown in Fig. 3(a) with individual steps marked by red arrows. Here and in the video (see also ESI Video V2†) we find that the nucleation of new steps is slower than the disappearance of existing steps by them moving out of sight. This causes the number of steps to decrease with time and, as a consequence, a reduction of the tapering of the NW. Due to this effect, the radial decomposition is first limited by the movement of the initial steps, and once the steps from initial tapering disappeared (after 425 s), also by the nucleation of new steps from the NW top. For this reason, radial decomposition is fast initially and slow after the tapering disappeared. Only nucleation of new steps at the NW tip and their subsequent motion downwards was observed and never sublimation from a flat sidewall surface by nucleation of a new step on a terrace. This is in stark contrast to the NWs with ZB crystal phase, where the latter is the dominant radial decomposition mechanism (cf. Section 2). ESI Video V2† shows the nucleation of individual steps at the edge of the tip and their flow on the NW sidewall. This observation is typical for the late stages of the experiment. A similar result of decelerating radial decomposition with time has been reported by Brockway et al.²⁸ for WZ GaN NWs. Combined with a narrowing of the diameter distribution, the result was attributed to a reduced step-nucleation rate at smaller diameter. In contrast, our results suggest that the initially higher radial decomposition results directly from the initial tapering.

For the axial decomposition, no step flow is visible on the tip of the NW as seen in ESI Video V2.† Here, decomposition usually starts at the corner between tip and side facets, where material first disappears and is then followed by sublimation of the material closer to the center of the tip. This axial decomposition occurs much more frequently than the nucleation of a new step on the side facets. As mentioned, the axial rate increases with time after the initial tapering disappeared, as opposed to the radial rate. This indicates that the decomposition at the tip is not directly responsible for the formation of steps on the side facets, which might allow tuning the experimental parameters to optimize the ratio of axial to radial rate.

Tracking the motion of individual steps over time, allows us to determine a step flow velocity of the steps on the WZ-GaAs. As shown in Fig. 3(c), the velocity increases from ∼0.1 nm s⁻¹ to ∼0.5 nm s⁻¹ as decomposition progresses. This increase over time might be indicative of an increasing temperature, which could also be partly responsible for the increasing axial decomposition rate.

4. Comparison of decomposition rates in ZB and WZ

The same step-flow analysis was performed for the nano-facets at the tip of the ZB NW-4 in the time interval from 0 to 550 s. Due to the small size of the facets of NW-4, the related uncertainty is much larger, but we find that the step flow velocity on the short WZ segment is similar (∼0.5 nm s⁻¹), while it is higher on the (1̄11) and (011) ZB facets (∼1–4 nm s⁻¹). Under the assumption that the same step flow velocity on the {112̄0} WZ side facets implies a similar temperature, the temperature is then the same in the beginning of the experiment of NW-4 and the end of the experiment of NW-5.

This allows now a direct comparison of the ZB (NW-4, Fig. 2(d)) with the WZ (NW-5, ESI Section S11†) axial decomposition rates at the same temperature, which are estimated as ∼0.13 nm s⁻¹ (WZ) and ∼0.032 nm s⁻¹ (ZB). This value of ∼300% faster axial decomposition of WZ compared to ZB is similar to the value obtained for the transition from ZB to WZ at the tip of NW-5 (∼300%). It is also consistent with the 2-3 fold increase in axial rate of the WZ segment of NW-1 (Fig. 1(d)). In NW-4 the relative increase of the axial rate due to the WZ segment is much larger (∼2000%). This is possibly due to the very small diameter (“neck”) and short length of the WZ segment. Differences between the values are caused by the uncertainty in temperature and effects of faceting and NW shape. However, in all cases, we observe a reduced axial decomposition of the ZB phase, which is likely caused by the formation of stable facets on the tip.

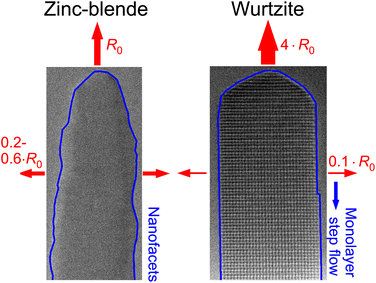
For the radial decomposition the trend is opposite. In the late stages of NW-5 (WZ) the average radial decomposition rate is ∼0.0032 nm s⁻¹, which is limited by nucleation of steps at the tip of the NW. In contrast, the absence of defined sidewall facets in the ZB crystal (NW-4) leads to simultaneous sublimation on the entire sidewall and, hence, exhibits very different rates. At the beginning of the experiment of NW-4 the radial decomposition rate is 0.005 nm s⁻¹ to 0.02 nm s⁻¹ (Fig. 2(e)), which is significantly larger than the radial decomposition rate in WZ. Fig. 4 summarizes schematically these observed differences between ZB and WZ and gives order of magnitude estimations of the relative axial and radial decomposition rates at similar temperature. Certainly, the exact relation between the rates varies depending on temperature, shape and facet formation.

Fig. 4 Summary of the observed differences between ZB and WZ decomposition with an order of magnitude estimation of the relative axial and radial decomposition rates (red arrows) at the same temperature (R₀ = 0.032 nm s⁻¹). The blue arrow indicates the step flow mechanism on the WZ sidewalls.

5. Conclusion

To conclude, we investigated the decomposition dynamics of GaAs NWs with different crystal phases by in situ TEM in real-time. We find that ZB NWs have much lower axial but larger radial decomposition rates compared to WZ. Both effects are linked to spontaneous faceting of the NW surface. On the tip of ZB NWs {110} and {311} facets can inhibit decomposition, while for WZ NWs a rounded tip without defined facets decomposes more quickly. This behavior is reversed for the side facets. ZB NWs show pronounced nano-faceting, even in phase-pure segments. This leads to a concurrent sublimation along the entire sidewall with step flow limited to the size of the nano-facets and a significant radial decomposition rate. For WZ NWs, well-defined vertical {112̄0} facets form during decomposition. The radius decreases only by step flow starting from the tip of the NW or due to initial tapering, because nucleation of new steps on the flat sidewall surface is not observed. This leads to very small radial decomposition rates. Furthermore, we have shown that for small diameters the axial decomposition rate of mixed-phase NWs and the radial decomposition rate of ZB NWs both increase.

Our results have important practical implications for growers wanting to utilize such a decomposition technique in order to tune NW properties. The increase of the radial decomposition rate with decreasing diameter in ZB leads to an increase of NW tapering with time. This makes it mandatory to start the decomposition process with untapered NWs if one wants to achieve extended thin NW segments. In order to preserve as much length of the NWs as possible, low temperature and long decomposition time should be preferred, because the axial rate increases faster than the radial rate with increasing temperature. Furthermore, we observe nano-faceting on the sides of ZB NWs, which might have a significant impact on the electronic properties of the NW or the properties of subsequent shell growth, especially for lattice-mismatched shells. A thin homoepitaxial regrowth might be able to restore {11̄0} side facets and alleviate some of these problems. Controlling the As-flux during decomposition can be used to further control decomposition rates, congruent temperature and surface energies of the various facets.^23,36,56

For the case of WZ NWs the decomposition technique can be used advantageously to reduce the tapering of NWs by inducing a step flow on the {112̄0} side facets. Recent works have shown possibilities to control the crystal phase of NWs with deliberate stacking of WZ and ZB phases.^44,58,59 For example, if a sufficiently thick ZB top segment can be added, then such a reduced tapering can be achieved even without decreasing the NW length because the ZB segment inhibits axial decomposition. This could also be used to decrease the diameter of the WZ segment without reducing its length, because the diameter is determined by the diameter of the ZB segment on top. Such scenarios could be exploited for generating size-controlled crystal phase quantum dots (CPQDs), where particularly the symmetry properties of the WZ-phase are very beneficial for ideal single and entangled photon sources.⁶⁰

Our study demonstrates the importance of individual crystal facets on the decomposition mechanism and its kinetics. Future work could be directed, on the one hand, towards exploring the effects of growth species on the formation of individual facets and, on the other hand, towards tuning the local temperature. This would allow determination of the activation barriers and respective energies of individual processes, further extending the comprehension of the microscopic dynamics, while facilitating transfer of results to classical growth reactors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported financially by the ERC project QUANtIC (ID: 771747) funded by the European Research Council. Further support was provided by the Deutsche Forschungsgemeinschaft (DFG) via Project Grants KO-4005/6-1, KO-4005/7-1, and FI-947/4-1 and via Germany's Excellence Strategy-EXC2089/1-390776260 (e-conversion). We acknowledge Agence Nationale de la Recherche, the French funding agency, in the framework of “Equipements d'excellence” Project No. 10-EQPX-0050, TEMPOS-NANOMAX.

Notes and references

1. Y. Li, F. Qian, J. Xiang and C. M. Lieber, Mater. Today, 2006, 9, 18–27.
2. S. W. Eaton, A. Fu, A. B. Wong, C.-Z. Ning and P. Yang, Nat. Rev. Mater., 2016, 1, 16028.
3. T. Mårtensson, C. P. T. Svensson, B. A. Wacaser, M. W. Larsson, W. Seifert, K. Deppert, A. Gustafsson, L. R. Wallenberg and L. Samuelson, Nano Lett., 2004, 4, 1987–1990.
4. K. Tomioka, M. Yoshimura and T. Fukui, Nature, 2012, 488, 189–192.
5. C.-Y. Wen, M. C. Reuter, J. Bruley, J. Tersoff, S. Kodambaka, E. A. Stach and F. M. Ross, Science, 2009, 326, 1247–1250.
6. L. J. Lauhon, M. S. Gudiksen, D. Wang and C. M. Lieber, Nature, 2002, 420, 57–61.
7. K. A. Dick, C. Thelander, L. Samuelson and P. Caroff, Nano Lett., 2010, 10, 3494–3499.
8. S. Lehmann, J. Wallentin, D. Jacobsson, K. Deppert and K. A. Dick, Nano Lett., 2013, 13, 4099–4105.
9. R. E. Algra, M. A. Verheijen, M. T. Borgström, L.-F. Feiner, G. Immink, W. J. P. van Enckevort, E. Vlieg and E. P. A. M. Bakkers, Nature, 2008, 456, 369–372.
10. S. Xiong, Y. A. Kosevich, K. Sääskilahti, Y. Ni and S. Volz, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195439.
11. M. D. Luca, C. Fasolato, M. A. Verheijen, Y. Ren, M. Y. Swinkels, S. Kölling, E. P. A. M. Bakkers, R. Rurali, X. Cartoixà and I. Zardo, Nano. Lett., 2019, 19, 4702–4711.
12. Z. Azimi, N. Gagrani, J. Qu, O. L. C. Lem, S. Mokkapati, J. M. Cairney, R. Zheng, H. H. Tan, C. Jagadish and J. Wong-Leung, Nanoscale. Horiz., 2021, 6, 559–567.
13. L. Zhang, J.-W. Luo, A. Zunger, N. Akopian, V. Zwiller and J.-C. Harmand, Nano. Lett., 2010, 10, 4055–4060.
14. N. Akopian, G. Patriarche, L. Liu, J.-C. Harmand and V. Zwiller, Nano. Lett., 2010, 10, 1198–1201.
15. B. Loitsch, J. Winnerl, G. Grimaldi, J. Wierzbowski, D. Rudolph, S. Morkötter, M. Döblinger, G. Abstreiter, G. Koblmüller and J. J. Finley, Nano. Lett., 2015, 15, 7544–7551.
16. I. Geijselaers, N. Vainorius, S. Lehmann, C. E. Pryor, K. A. Dick and M.-E. Pistol, Appl. Phys. Lett., 2021, 119, 263102.
17. R. Heckingbottom, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct., 1985, 3, 572.
18. N. Newman, J. Ross and M. Rubin, Appl. Phys. Lett., 1993, 62, 1242–1244.
19. P. Krogstrup, R. Popovitz-Biro, E. Johnson, M. H. Madsen, J. Nygård and H. Shtrikman, Nano. Lett., 2010, 10, 4475–4482.
20. Q. Gao, D. Saxena, F. Wang, L. Fu, S. Mokkapati, Y. Guo, L. Li, J. Wong-Leung, P. Caroff, H. H. Tan and C. Jagadish, Nano. Lett., 2014, 14, 5206–5211.
21. K. Tomioka, P. Mohan, J. Noborisaka, S. Hara, J. Motohisa and T. Fukui, J. Cryst. Growth., 2007, 298, 644–647.
22. B. Loitsch, D. Rudolph, S. Morkötter, M. Döblinger, G. Grimaldi, L. Hanschke, S. Matich, E. Parzinger, U. Wurstbauer, G. Abstreiter, J. J. Finley and G. Koblmüller, Adv. Mater., 2015, 27, 2195–2202.
23. F. del Giudice, J. Becker, C. de Rose, M. Döblinger, D. Ruhstorfer, L. Suomenniemi, J. Treu, H. Riedl, J. J. Finley and G. Koblmüller, Nanoscale, 2020, 12, 21857–21868.
24. S. Fust, A. Faustmann, D. J. Carrad, J. Bissinger, B. Loitsch, M. Döblinger, J. Becker, G. Abstreiter, J. J. Finley and G. Koblmüller, Adv. Mater., 2019, 32, 1905458.
25. R. B. Lewis, P. Corfdir, H. Küpers, T. Flissikowski, O. Brandt and L. Geelhaar, Nano. Lett., 2018, 18, 2343–2350.
26. L. Balaghi, G. Bussone, R. Grifone, R. Hübner, J. Grenzer, M. Ghorbani-Asl, A. V. Krasheninnikov, H. Schneider, M. Helm and E. Dimakis, Nat. Commun., 2019, 10, 2793.
27. P. Schmiedeke, A. Thurn, S. Matich, M. Döblinger, J. J. Finley and G. Koblmüller, Appl. Phys. Lett., 2021, 118, 221103.
28. L. Brockway, C. Pendyala, J. Jasinski, M. K. Sunkara and S. Vaddiraju, Cryst. Growth. Des., 2011, 11, 4559–4564.
29. J. K. Zettler, P. Corfdir, C. Hauswald, E. Luna, U. Jahn, T. Flissikowski, E. Schmidt, C. Ronning, A. Trampert, L. Geelhaar, H. T. Grahn, O. Brandt and S. Fernández-Garrido, Nano. Lett., 2016, 16, 973–980.
30. T. Auzelle, G. Calabrese and S. Fernández-Garrido, Phys. Rev. Mater., 2019, 3, 013402.
31. I. Ilkiv, D. Kirilenko, K. Kotlyar and A. Bouravleuv, Nanotechnology, 2019, 31, 055701.
32. M. Tornberg, D. Jacobsson, A. R. Persson, R. Wallenberg, K. A. Dick and S. Kodambaka, Nano. Lett., 2019, 19, 3498–3504.
33. H. Potts, PhD thesis, École Polytechnique Fédérale de Lausanne, 2017.
34. S. Choi, J. Lee, M. Pin, J.-H. Kwon, I. Kim, M. S. Yeom, C. S. Kim, H. S. Lee, S. J. Ahn, S.-H. Yi and Y. H. Kim, Nanoscale, 2019, 11, 6685–6692.
35. G. W. Gang, J. H. Lee, S. Y. Kim, T. Jeong, K. B. Kim, N. T. H. Men, Y. R. Kim, S. J. Ahn, C. S. Kim and Y. H. Kim, Nanotechnology, 2021, 32, 145709.
36. Z. Y. Zhou, C. X. Zheng, W. X. Tang, D. E. Jesson and J. Tersoff, Appl. Phys. Lett., 2010, 97, 121912.
37. G. B. Stephenson, J. A. Eastman, C. Thompson, O. Auciello, L. J. Thompson, A. Munkholm, P. Fini, S. P. DenBaars and J. S. Speck, Appl. Phys. Lett., 1999, 74, 3326–3328.
38. S. Fernández-Garrido, G. Koblmüller, E. Calleja and J. S. Speck, J. Appl. Phys., 2008, 104, 033541.
39. Z. Zhang, N. Liu, L. Li, J. Su, P.-P. Chen, W. Lu, Y. Gao and J. Zou, Nano. Lett., 2018, 18, 6597–6603.
40. J. W. L. Yim, B. Xiang and J. Wu, J. Am. Chem. Soc., 2009, 131, 14526–14530.
41. H. Zheng, J. Wang, J. Y. Huang, J. Wang, Z. Zhang and S. X. Mao, Nano. Lett., 2013, 13, 6023–6027.
42. S. Rackauskas, S. D. Shandakov, H. Jiang, J. B. Wagner and A. G. Nasibulin, Sci. Rep., 2017, 7, 12310.
43. J.-C. Harmand, G. Patriarche, F. Glas, F. Panciera, I. Florea, J.-L. Maurice, L. Travers and Y. Ollivier, Phys. Rev. Lett., 2018, 121, 166101.
44. F. Panciera, Z. Baraissov, G. Patriarche, V. G. Dubrovskii, F. Glas, L. Travers, U. Mirsaidov and J.-C. Harmand, Nano. Lett., 2020, 20, 1669–1675.
45. C. Kallesøe, C.-Y. Wen, K. Mølhave, P. Bøggild and F. M. Ross, Small, 2010, 6, 2058–2064.
46. F. Panciera, M. M. Norton, S. B. Alam, S. Hofmann, K. Mølhave and F. M. Ross, Nat. Commun., 2016, 7, 12271.
47. J. Hirth and G. Pound, in Condensation and Evaporation: Nucleation and Growth Kinetics, Macmillan, 1963.
48. M. H. T. Dastjerdi, J. P. Boulanger, P. Kuyanov, M. Aagesen and R. R. LaPierre, Nanotechnology, 2016, 27, 475403.
49. J. Johansson, L. S. Karlsson, C. P. T. Svensson, T. Mårtensson, B. A. Wacaser, K. Deppert, L. Samuelson and W. Seifert, Nat. Mater., 2006, 5, 574–580.
50. A. F. i Morral, C. Colombo, G. Abstreiter, J. Arbiol and J. R. Morante, Appl. Phys. Lett., 2008, 92, 063112.
51. E. Russo-Averchi, M. Heiss, L. Michelet, P. Krogstrup, J. Nygard, C. Magen, J. R. Morante, E. Uccelli, J. Arbiol and A. F. i Morral, Nanoscale, 2012, 4, 1486.
52. M. de la Mata, C. Magen, J. Gazquez, M. I. B. Utama, M. Heiss, S. Lopatin, F. Furtmayr, C. J. Fernández-Rojas, B. Peng, J. R. Morante, R. Rurali, M. Eickhoff, A. F. i Morral, Q. Xiong and J. Arbiol, Nano. Lett., 2012, 12, 2579–2586.
53. D. Ruhstorfer, M. Döblinger, H. Riedl, J. J. Finley and G. Koblmüller, J. Appl. Phys., 2022, 132, 204302.
54. J. Platen, A. Kley, C. Setzer, K. Jacobi, P. Ruggerone and M. Scheffler, J. Appl. Phys., 1999, 85, 3597–3601.
55. K. Jacobi, L. Geelhaar, J. Márquez, J. Platen and C. Setzer, Appl. Surf. Sci., 2000, 166, 173–178.
56. A. Jenichen and C. Engler, Surf. Sci., 2013, 608, 204–211.
57. A. Jenichen, C. Engler and B. Rauschenbach, Surf. Sci., 2013, 613, 74–79.
58. M. M. Jansen, P. Perla, M. Kaladzhian, N. von den Driesch, J. Janßen, M. Luysberg, M. I. Lepsa, D. Grützmacher and A. Pawlis, ACS. Appl. Nano. Mater., 2020, 3, 11037–11047.
59. T. Dursap, M. Vettori, C. Botella, P. Regreny, N. Blanchard, M. Gendry, N. Chauvin, M. Bugnet, A. Danescu and J. Penuelas, Nanotechnology, 2021, 32, 155602.
60. R. Singh and G. Bester, Phys. Rev. Lett., 2009, 103, 063601.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00135k

---