Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Identification of nanoparticles as vesicular cargo via Airy scanning fluorescence microscopy and spatial statistics†
Christian
Wimmenauer
and
Thomas
Heinzel
 *
*
Institute of Experimental Condensed Matter Physics, Heinrich-Heine-University, Universitätsstr. 1, 40225 Düsseldorf, Germany. E-mail: thomas.heinzel@uni-duesseldorf.de
First published on 14th June 2023
Abstract
Many biomedical applications of nanoparticles on the cellular level require a characterisation of their subcellular distribution. Depending on the nanoparticle and its preferred intracellular compartment, this may be a nontrivial task, and consequently, the available methodologies are constantly increasing. Here, we show that super-resolution microscopy in combination with spatial statistics (SMSS), comprising the pair correlation and the nearest neighbour function, is a powerful tool to identify spatial correlations between nanoparticles and moving vesicles. Furthermore, various types of motion like for example diffusive, active or Lévy flight transport can be distinguished within this concept via suitable statistical functions, which also contain information about the factors limiting the motion, as well as regarding characteristic length scales. The SMSS concept fills a methodological gap related to mobile intracellular nanoparticle hosts and its extension to further scenarios is straightforward. It is exemplified on MCF-7 cells after exposure to carbon nanodots, demonstrating that these particles are stored predominantly in the lysosomes.
1 Introduction
To employ nanoparticles in biomedical applications such as drug or gene delivery, it is mandatory to determine their subcellular location after uptake. A common approach relies on using fluorescent or fluorescence-marked particles in combination with staining the candidate organelles, after which the system is studied by fluorescence imaging and subsequent co-localization analysis. This powerful concept has provided many highly relevant results, like the clarification of viral uptake mechanisms1,2 or the characterisation of a variety of potential nanoparticle systems for drug delivery and photodynamic therapy.3–5 However, the technique experiences also several limitations. One of these arises in a typical scenario, where the two fluorescence channels have to be detected with the same sensor, thus requiring sequential sampling of the two images for each channel and subsequent data analysis. In this case, the measured spatial correlation can be disturbed by the motion of the nanoparticles and vesicles during the single image data acquisition time. Object based colocalization methods have been established which relate spatially the structures in both channels after a segmentation step. Prominent methods from this field include Voronoi tessellation,6 trajectory correlation7 and overlap analysis.8 More recently, methods from spatial statistics found their way into this field, with the best known example being the bivariate version of Ripley's K-function.9,10 Further numerical instruments such as the pair correlation function11 (PCF), the estimation of interaction probabilities based on point patterns10,12,13 or the nearest neighbour function (NNF)8 have also been successfully applied to co-localization problems. In some cases, however, these powerful methods also experience limitations, in particular for vesicles that move significantly on the time scale set by the microscopy scans and regarding the spatial resolution limits by conventional confocal microscopy.In the present work, we show that these problems can be reduced or avoided altogether, respectively, by a combination of super-resolution microscopy, here in the form of Airy scanning fluorescence microscopy, with a subsequent spatial statistics analysis which we denote by SMSS in the following. Airy scanning microscopy yields a higher resolution and superior signal-to-noise ratio compared to conventional confocal imaging, as required for vesicles with sizes below ≈500 nm. We apply the PCF and the NNF to the measured data and create envelopes representing 95%-confidence intervals. They are based on Monte-Carlo-simulations of complete spatial randomness (CSR) and a model for transport with heavily tailed jump distances. It is shown that these envelopes are of relevance for hypothesis testing and for proving consistency of the measured data with an underlying assumption.14,15
As a topical model system, MCF-7 cells incubated with ultra-small carbon nanodots (CNDs) are used. Even though the family of CNDs is relatively diverse,16 common features such as good solubility in water,17,18 low toxicity19,20 and accessible functionalization protocols21,22 put them in the focus for biomedical applications. Proof of principle experiments for drug delivery,23–25 photosensitizing,26,27 deep tissue imaging28,29 and intracellular sensing18,29 have been reported. Their intracellular storage in different target organelles depends on the composition, surface functional groups and periphery of the particle.30 While several groups have identified the vesicles of the endolysosomal system as primary location,31,32 they appear to be stored in the Golgi apparatus,33 mitochondria34 or in the nuclei35 in other experiments. We have designed a study of the colocalization of CNDs with lysosomes. The computed statistical functions are compared with model envelopes and are discussed in the context of a positive control (double labelled lysosomes) and a negative control (labelled lysosomes and Golgi apparatus).
The same detector is used for both fluorescence channels to be compared, which thus have to be acquired by sequential scanning. Sequential scanning is favored in some colocalization problems, since it minimizes the bleed through from a fluorophore with a broad emission spectrum into the other channel, which is detrimental to colocalization analysis. Especially for nanoparticles with intrinsic fluorescence properties it may be, therefore, hard to optimize for a simultaneous acquisition. Furthermore, limitations in the available instrumentation may pose a problem since for sophisticated methods like Airy scanning or STED simultaneous acquisition of multiple fluorophores, while possible, sets high requirements on the setup. Since the acquisition of an image takes up to 2 s, intensity correlation based colocalization analysis fails due to the vesicular motion by a distance comparable to, or even larger than, their size within the acquisition time of one frame, see Fig. 3 (zoom-in, second row). Therefore, in this typical scenario, an object based analysis method needs to be applied.
2 Materials and methods
2.1 Carbon nanodots
The absorbance spectrum shows two pronounced peaks in the UV-region, one around 230 nm commonly attributed to the π–π*-transition of the graphitic carbon domains and one around 350 nm which is attributed to the n–π*-transition of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moieties.17 The employed CNDs display their strongest emission around 460 nm, if excited at 360 nm. A quantum yield of 23% was obtained for these particles.
O moieties.17 The employed CNDs display their strongest emission around 460 nm, if excited at 360 nm. A quantum yield of 23% was obtained for these particles.
2.2 Cell experiments
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–15
000–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) cells per well in an 8 well μ-slide (no. 1.5 polymer coverslip, tissue culture treated, Ibidi™) 48 hours prior to imaging. CNDs are added to respective wells to yield a concentration of 500 μg mL−1. The cells in the respective chambers were transfected with reagents from the CellLight™ BacMam 2.0 product series (Invitrogen™) 24 hours prior to imaging. To label the lysosomes CellLight™ Lysosomes-RFP and CellLight™ Lysosomes-GFP was used yielding MCF-7 cells expressing a fusion protein of LAMP1 and the respective fluorescent protein. To label the Golgi apparatus CellLight™ Golgi-GFP was used yielding MCF-7 cells expressing a fusion protein of the human Golgi resident enzyme N-acetylgalactosaminyltransferase and GFP. One hour before imaging the samples were washed with PBS and the medium was exchanged with fresh full medium. Between the preparation steps the sample was kept in the incubator at 37 °C and 5% CO2.
000) cells per well in an 8 well μ-slide (no. 1.5 polymer coverslip, tissue culture treated, Ibidi™) 48 hours prior to imaging. CNDs are added to respective wells to yield a concentration of 500 μg mL−1. The cells in the respective chambers were transfected with reagents from the CellLight™ BacMam 2.0 product series (Invitrogen™) 24 hours prior to imaging. To label the lysosomes CellLight™ Lysosomes-RFP and CellLight™ Lysosomes-GFP was used yielding MCF-7 cells expressing a fusion protein of LAMP1 and the respective fluorescent protein. To label the Golgi apparatus CellLight™ Golgi-GFP was used yielding MCF-7 cells expressing a fusion protein of the human Golgi resident enzyme N-acetylgalactosaminyltransferase and GFP. One hour before imaging the samples were washed with PBS and the medium was exchanged with fresh full medium. Between the preparation steps the sample was kept in the incubator at 37 °C and 5% CO2.
2.3 Data analysis
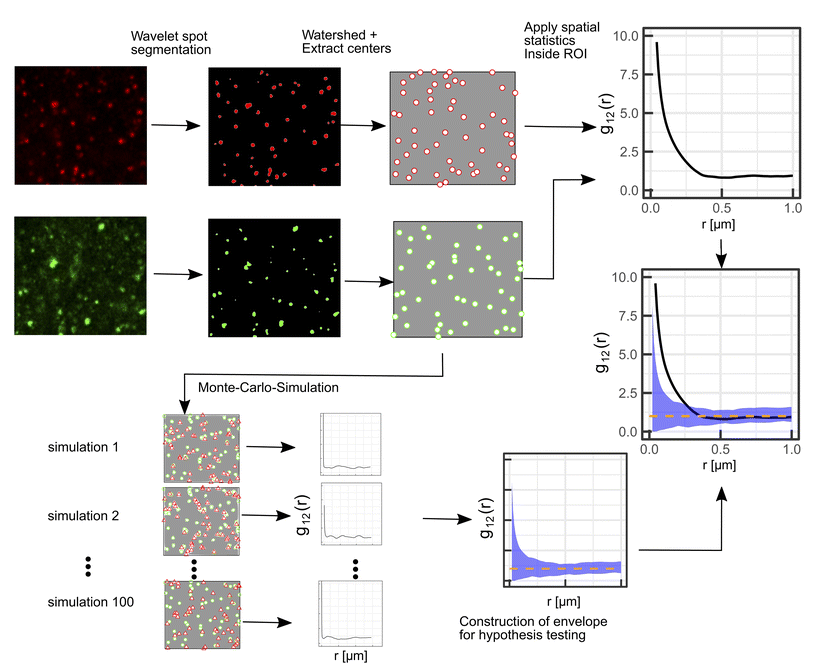
A schematic representation of the SMSS protocol is shown in Fig. 1.Wavelet segmentation is performed via the implementation of the open image analysis platform Icy.38 The watershed method is then applied to the binary image, and the point pattern is extracted with the analyze particles function implemented in Fiji.39
The bivariate G-function
 | (1) |
The bivariate pair correlation function is related to the probability of finding a spot of type 1 a given distance r from a spot of type 2. It is defined via the derivative of the bivariate K-function
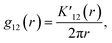 | (2) |
 | (3) |
For the interpretation, the spatial statistical functions as obtained from the measured data are compared to reference envelopes. To construct them, an ensemble of N = 100 simulated point patterns is generated under a model assumption. For these simulated point patterns an ensemble of summary functions is calculated, capturing the behaviour of the model. For a significance level α = 0.05 the 5% that deviate the most from the mean are excluded from the ensemble of simulated summary functions at each distance r. The minimum and maximum of the remaining points describe the borders of the envelope. If the respective summary function of the measured data lies outside of the envelope inside of a certain interval in r, the p-value is grater than the significance level (p > α) and the underlying model (null hypothesis) is rejected in this interval. The first tested model was a uniform random distribution inside the ROI of the type 2 spots (red channel), while the type 1 spots had the same distribution as the measured data. The underlying null hypothesis is that the positions of the type 2 spots are independent of the type 1 spots. In the second tested model the positions of the type 1 spots are again the same as for the measured data. To test the null hypothesis of transport with a lognormal distribution of jump distances the simulated type 2 spots were generated by shifting each of the type 1 spots by a vector 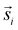 . Length
. Length 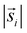 was sampled from a lognormal distribution that was fitted to the jump distance distribution of the measured data and the angle θ that describes the direction was sampled form a uniform distribution. If a simulated point of type 2 was generated outside of the ROI a new vector
was sampled from a lognormal distribution that was fitted to the jump distance distribution of the measured data and the angle θ that describes the direction was sampled form a uniform distribution. If a simulated point of type 2 was generated outside of the ROI a new vector 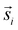 was generated. To ensure that the number of type 2 points in every simulation (ns) corresponds to the number of type 2 points in the measurement (nm), spots in random locations were added (if nm > ns) or the set of simulated points was sub-sampled to match nm (if nm < ns).
was generated. To ensure that the number of type 2 points in every simulation (ns) corresponds to the number of type 2 points in the measurement (nm), spots in random locations were added (if nm > ns) or the set of simulated points was sub-sampled to match nm (if nm < ns).
3 Results and discussion
3.1 Single particle tracking of lysosomes
Lysosomes are actively transported via kinesin and dynein along the microtubuli,46 which manifests itself in short bursts of directed motion. In between these intervals of active transport, lysosomes show (sub-) diffusive behaviour, which has been attributed to lingering at the intersections of microtubuli.47This bimodal motion resembles a Lévy walk.48–50 To construct envelopes for the assumption of transport, knowledge about the jump distance distribution is necessary. To obtain insight in the underlying transport dynamics, single particle tracking was performed on a time series measurement over 100 time points with an acquisition time of 827 ms per frame. After excluding trajectories shorter than 8.3 s, 763 trajectories remain, which form the input of the analysis. Typical trajectories are reproduced in Fig. 2(a).
 | ||
| Fig. 2 Single particle tracking of lysosomes. (a) Extracted single particle trajectories colored according to the identified cluster via cluster analysis with t-distributed stochastic neighbor embedding (tSNE)44 and density-based spatial clustering of applications with noise (DBSCAN).45 The size of the scale bar amounts to 5 μm. (b) A lognormal distribution was fitted to the frame to frame jump distance for all trajectories. (c) Three different subtypes of lysosomal motion, namely immobile, subdiffusive and diffusive, were identified for the four clusters by inspection of their MSD scaling. | ||
The distribution of frame-to-frame jump distances is heavy tailed and can be described reasonably well by a log-normal distribution with σ = 0.94 and μ = −1.87, see Fig. 2(b), in agreement with recent results.50 Following a similar workflow to the method presented by Pinholt et al.,51 the trajectories are classified prior to an analysis of their time dependent ensemble mean square displacement (MSD) as follows. Eight descriptive features, i.e., the mean, standard deviation, skewness and kurtosis of the jump distance distribution, as well as the straightness, sinuosity, average MSD and turn angle correlation52 are calculated for each trajectory, providing a space for classification via the density based clustering algorithm density-based spatial clustering of applications with noise (DBSCAN).45 A non-linear dimensionality reduction via t-distributed stochastic neighbor embedding (tSNE)44 was applied prior to the clustering. From the six emerging clusters, see the ESI† for detailed information, two consisted of very few points and where therefore excluded from the subsequent MSD analysis. Fig. 2(c) shows the resulting averaged MSD curves for the three clearly distinguishable extracted states (full curves in ESI†). Fitting the data to the standard expression MSD = 4Dtα gives the fit parameters as summarized in displayed in Table 1. Class 1 (cluster 2, red), which forms by far the largest group, is diffusive, i.e., α ≈ 1. The trajectories of class 2 (cluster 3, blue) are immobile to a good approximation, while class 3 (cluster 1, black and cluster 4, green) is subdiffusive.
| Cluster | Type | D [μm2 s−1] | α | N | R 2 |
|---|---|---|---|---|---|
| 1 | Subdiffusive | 0.048 ± 0.003 | 0.66 ± 0.03 | 147 | 0.98 |
| 2 | Diffusive | 0.036 ± 0.002 | 1.06 ± 0.019 | 466 | 0.99 |
| 3 | Immobile | 0.025 ± 0.003 | 0.14 ± 0.06 | 33 | 0.30 |
| 4 | Subdiffusive | 0.047 ± 0.004 | 0.77 ± 0.05 | 108 | 0.95 |
Typical sample trajectories of the three classes are shown in Fig. 2(a). Class 1 trajectories correspond to lysosomes travelling predominantly along filaments without changes of the direction by large angles. The lysosomes with class 2 trajectories are essentially captured at some structure, for example a filament junction. Lysosomes travelling along the filaments with frequent large-angle changes of the path form class 3. The values for the diffusion constant are within a reasonable range compared to the literature.50,53 It should be noted that this classification treats the trajectories globally, in contrast to segmentation of the trajectories into different diffusive states, in which bursts of directed motion appear on smaller time scales below 10 s.50 A finer temporal resolution in combination with a more sophisticated segmentation algorithm may provide more insight into the lysosomal movement patterns on a single particle level, but is beyond the scope of this work. These studies show that a significant fraction of the lysosomes move farther than their size within the capture time of a picture frame, which suggests them a suitable test bed for the SMSS analysis.
3.2 Control experiments
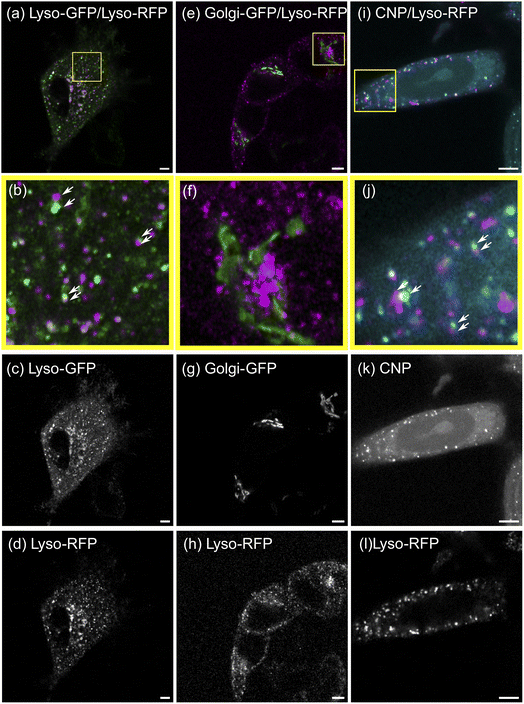
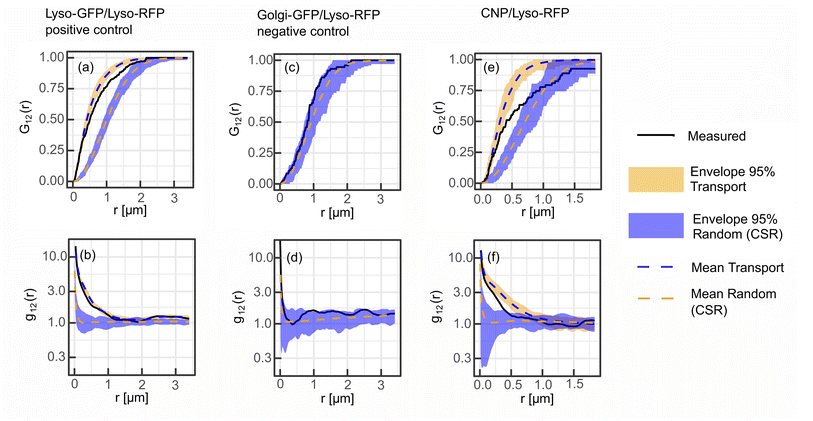
To validate the SMSS protocol, we perform two control experiments and determine their corresponding reference envelopes. In the positive control experiment, MCF-7 cells are transfected to express a fusion protein of the lysosome resident protein LAMP1 and RFP as well as a fusion protein of LAMP1 and GFP. Fig. 3(a)–(d) reproduce characteristic fluorescence microscope images. Since both channels capture the location of the same subcellular structure the employed method is expected to yield maximum colocalisation under the present experimental conditions. The two bivariate functions G12(r) and g12(r) of the experimental data should therefore reside inside the reference envelope for the transport model, i.e. spatial correlation. As can be seen in Fig. 4(a) and (b), respectively, the measured bivariate functions lie inside the confidence intervals for r ≤ 500 nm, deviate slightly from them for larger distances, but remain close up to the largest distances studied, i.e. 3.3 μm. The reference envelope for spatial independence, on the other hand, is distinctly separated from the experimental data, showing some overlap only at large distances above r = 1.8 μm for G12(r), and in the range r = 1.2 μm for g12(r). As an interpretation example, we evaluate that therefore, for distances r < 1.2 μm, the null hypothesis of the spatial randomness can be rejected with p < 0.05. From G12(r = 1.2 μm) ≈ 0.8, on the other hand, we can infer that 80% of points in the green channel have a nearest neighbor distance of less than 1.2 μm to points in the red channel. This positive control experiment shows how a close to perfect cross-correlation will look like in our experiments. We explain the deviations between the measured trace and the reference envelope for correlation at larger distances with the three-dimensional character of the cell. As soon as lysosomes move into or out of the focal plane, the correlation is blurred. This will set in at the focal length of the microscope, which in our case equals approximately 500 nm. Furthermore, the treatment of points exiting the edge of the ROI in the simulation may also introduce a bias. If a simulated point is generated outside of the ROI, a new point is generated until it lies inside of the ROI. This treatment may introduce a bias that favours small jump distances for points close to the cellar border. Nonetheless, reasonable agreement of the measured data with the transport model persists.For the negative control experiment, the cells were transfected to express a LAMP1/RFP fusion protein labeling the lysosomes, but this time co-labeled with a fusion protein for an enzyme resident in the Golgi, namely N-acetylgalactosaminyltransferase with GFP, see Fig. 3(e)–(h) for fluorescence microscopy images. The labeled organelles are spatially disjunct and correlate only in the sense that their locations mutually exclude each other. Therefore, the bivariate functions are expected to reside inside the reference envelope for spatial independence. As can be seen in Fig. 4(c) and (d), both G12(r) and g12(r) lie inside the reference envelope, i.e., the null hypothesis can not be rejected. It can therefore be inferred that the spatial spot pattern for the negative control is indistinguishable from an independent distribution for the two spot types.
3.3 Spatial correlation between CNDs and lysosomes
With the control experiments at hand, we apply the SMSS protocol to quantify the subcellular localisation of the CNDs. MCF-7 cells are transfected to express the LAMP1/RFP fusion protein and are afterwards incubated with CNDs for 48 h, leading to typical bicolor fluorescence patterns as shown in Fig. 3(i)–(l). The resulting bivariate functions are reproduced in Fig. 4(e) and (f) together with the reference envelopes. For distances r < 0.5 μm, both spatial statistical functions lie outside the reference envelope for independent motion. Thus, the hypothesis of the lysosomal distribution being independent of the CND distribution can be rejected with p < 0.05. Rather, G12(r) and g12(r) are found inside the envelope functions for correlated motion for small distances. From G12(r = 0.5 μm) > 0.5, see Fig. 4(e), we conclude that more than 50% of the nearest neighbor distances between CNDs and lysosomes are smaller than 0.5 μm. At larger distances, G12 runs outside this reference envelope but, as we have seen during the study of the correlated reference envelope, this is the case even for perfect correlation and can be explained by lysosomes CNDs entering or leaving the focal plane within the period set by the single picture acquisition time. These results show that with a significance level of 0.05, more than 50% of the fluorescent CNDs are captured in the lysosomes in our experiments, which therefore form the dominant host for the CNDs.3.4 Generalizability and critical evaluation of the method
The proposed SMSS protocol can be applied to explore the subcellular distribution of a wide variety of nanoparticles, since it requires simply that the nanoparticle possess intrinsic fluorescence and a moderate photostability, in order not to bleach out on the time scale of the acquisition. It may be furthermore useful for nanoparticles with a wide emission spectrum, which benefit from sequential scanning in colocalization experiments to minimize bleed through. The presented workflow is modular and may be adapted to a given problem. First of all, the presented segmentation pipeline may not be appropriate in all situations. Wavelet based segmentation was used since it is known that this approach is well-suited to extract small spots even for varying levels of intensity. For more specialized problems, other segmentation pipelines54,55 may be employed. Second, the transport characteristic that is used to model the envelope for transport has to be evaluated on a case-by-case basis. While a log-normal distribution of jump distances is well-suited for the presented problem, this cannot be applied to all transport process in a cellular context. In the case of normal diffusion, for example, a Gaussian distribution of the displacement in x- and y-direction would be more appropriate. We illustrate the analysis of diffusive objects on synthetic data found in the ESI.† Directed motion with a negligible diffusive component, for example, has to be treated differently again.Furthermore, application of the SMSS concept requires sufficiently dilute objects in the following sense. The mean spacing between the objects to be traced sets the length scale of the objects' motion distance in between two consecutive recording times: if objects move more than the mean spacing during this time interval, complete spatial randomness (CSR) and the underlying transport process can no longer be distinguished, leading to a significant overlap of the respective envelopes. This is illustrated by synthetic data in the ESI† showing the analysis of points subject to a radial drift. At high object densities, the directed motion of the ensemble becomes indistinguishable from CSR. Finally, optical aberrations may interfere with the spatial statistics analysis. Chromatic aberrations in particular may present a problem since they distort the location of the objects in both fluorescence channels differently. As for all fluorescence colocalization experiments it is essential to minimize this effect by centering the region of interest on the optical axis of the imaging system and using achromatic objectives. If a significant amount of chromatic aberration is present, the image would be subject to stretching that increases from the center to the periphery.
4 Conclusions
It has been demonstrated that Airy scanning fluorescence microscope in combination with spatial statistics functions and reference envelopes provides a powerful tool to quantify correlated motion of nanoparticles and/or vesicles on a subcellular level. It is particularly suited for setups where locations measured in subsequent pictures may be correlated, which may be for instance necessary to minimize bleed through when fluorophores with a broad emission spectrum must be used. The reference envelopes corresponding to the hypotheses to be tested (here: uncorrelated motion and motion with a log-normal distribution) enable the specification of significance levels according to the requirements (set to the frequently used value of 0.05 in our work). This rather broadly applicable scheme, with selectable targets for labelling as well as several established spatial statistical functions, has been exemplified by a study the spatial colocalization of carbon nanodots in lysosomes. The results do not exclude that a fraction of the CNDs reside inside the Golgi apparatus or the nucleoli, for example. This would require additional experiments along the lines discussed above. However, it can be concluded that the major fraction of the CNDs is localized inside mobile lysosomes with a significance level of 0.05. The experienced limitations of the SMSS protocol in its present form have been identified being manly due to motion of the detected fluorescent units into or out of the focal length of the microscope. Therefore, confinement of the system under study to a plane with a thickness of about 500 nm appears to be one promising future way to improve the presented protocol.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. W. gratefully acknowledges the support of the Jürgen Manchot Stiftung. The authors thank the Center of Advanced Imaging (CAi) of the HHU for providing their microscopes, laboratories and support. Cornelia Monzel is gratefully thanked for the fruitful discussion in the early stages of this work and for providing access to the laboratories of the chair for experimental medical physics at the HHU.Notes and references
- Q. Li, W. Li, W. Yin, J. Guo, Z.-P. Zhang, D. Zeng, X. Zhang, Y. Wu, X.-E. Zhang and Z. Cui, ACS Nano, 2017, 11, 3890–3903 CrossRef CAS PubMed.
- K. Gorshkov, K. Susumu, J. Chen, M. Xu, M. Pradhan, W. Zhu, X. Hu, J. C. Breger, M. Wolak and E. Oh, ACS Nano, 2020, 14, 12234–12247 CrossRef CAS PubMed.
- Y. Cheng, A. C. Samia, J. Li, M. E. Kenney, A. Resnick and C. Burda, Langmuir, 2010, 26, 2248–2255 CrossRef CAS PubMed.
- L. P. Fernando, P. K. Kandel, J. Yu, J. McNeill, P. C. Ackroyd and K. A. Christensen, Biomacromolecules, 2010, 11, 2675–2682 CrossRef CAS PubMed.
- Y. Wang, G. Wei, X. Zhang, X. Huang, J. Zhao, X. Guo and S. Zhou, Small, 2018, 14, 1702994 CrossRef PubMed.
- L. Andronov, I. Orlov, Y. Lutz, J.-L. Vonesch and B. P. Klaholz, Sci. Rep., 2016, 6, 1–9 CrossRef PubMed.
- D. Vercauteren, H. Deschout, K. Remaut, J. F. Engbersen, A. T. Jones, J. Demeester, S. C. De Smedt and K. Braeckmans, ACS Nano, 2011, 5, 7874–7884 CrossRef CAS PubMed.
- J.-F. Gilles, M. Dos Santos, T. Boudier, S. Bolte and N. Heck, Methods, 2017, 115, 55–64 CrossRef CAS PubMed.
- B. D. Ripley, J. Appl. Probab., 1976, 13, 255–266 CrossRef.
- T. Lagache, N. Sauvonnet, L. Danglot and J.-C. Olivo-Marin, Cytometry, Part A, 2015, 87, 568–579 CrossRef PubMed.
- C. Coltharp, X. Yang and J. Xiao, Curr. Opin. Struct. Biol., 2014, 28, 112–121 CrossRef CAS PubMed.
- J. A. Helmuth, G. Paul and I. F. Sbalzarini, BMC Bioinf., 2010, 11, 1–12 CrossRef PubMed.
- S. Mukherjee, C. Gonzalez-Gomez, L. Danglot, T. Lagache and J.-C. Olivo-Marin, IEEE Signal Process. Lett., 2020, 27, 1085–1089 Search PubMed.
- B. D. Ripley, J. Roy. Stat. Soc. B, 1977, 39, 172–192 Search PubMed.
- T. Wiegand, P. Grabarnik and D. Stoyan, Ecosphere, 2016, 7, e01365 CrossRef.
- S. Zhu, Y. Song, X. Zhao, J. Shao, J. Zhang and B. Yang, Nano Res., 2015, 8, 355–381 CrossRef CAS.
- D. Qu, M. Zheng, J. Li, Z. Xie and Z. Sun, Light: Sci. Appl., 2015, 4, e364 CrossRef CAS.
- Z. L. Wu, M. X. Gao, T. T. Wang, X. Y. Wan, L. L. Zheng and C. Z. Huang, Nanoscale, 2014, 6, 3868–3874 RSC.
- S. Fasbender, L. Zimmermann, R.-P. Cadeddu, M. Luysberg, B. Moll, C. Janiak, T. Heinzel and R. Haas, Sci. Rep., 2019, 9, 1–13 CrossRef CAS PubMed.
- F. Chen, W. Gao, X. Qiu, H. Zhang, L. Liu, P. Liao, W. Fu and Y. Luo, Frontiers in Laboratory Medicine, 2017, 1, 192–199 CrossRef.
- R. Buiculescu, D. Stefanakis, M. Androulidaki, D. Ghanotakis and N. A. Chaniotakis, Analyst, 2016, 141, 4170–4180 RSC.
- Z. Ji, A. Sheardy, Z. Zeng, W. Zhang, H. Chevva, K. Allado, Z. Yin and J. Wei, Molecules, 2019, 24, 152 CrossRef PubMed.
- X. Sun, Z. Liu, K. Welsher, J. T. Robinson, A. Goodwin, S. Zaric and H. Dai, Nano Res., 2008, 1, 203–212 CrossRef CAS PubMed.
- L. He, T. Wang, J. An, X. Li, L. Zhang, L. Li, G. Li, X. Wu, Z. Su and C. Wang, CrystEngComm, 2014, 16, 3259–3263 RSC.
- I. J. Gomez, B. Arnaiz, M. Cacioppo, F. Arcudi and M. Prato, J. Mater. Chem. B, 2018, 6, 5540–5548 RSC.
- A. Cadranel, J. T. Margraf, V. Strauss, T. Clark and D. M. Guldi, Acc. Chem. Res., 2019, 52, 955–963 CrossRef CAS PubMed.
- R. Knoblauch and C. D. Geddes, Materials, 2020, 13, 4004 CrossRef CAS PubMed.
- Q. Liu, B. Guo, Z. Rao, B. Zhang and J. R. Gong, Nano Lett., 2013, 13, 2436–2441 CrossRef CAS PubMed.
- P. Lesani, G. Singh, C. M. Viray, Y. Ramaswamy, D. M. Zhu, P. Kingshott, Z. Lu and H. Zreiqat, ACS Appl. Mater. Interfaces, 2020, 12, 18395–18406 CrossRef CAS PubMed.
- H. Liu, J. Guo, A. A. Aryee, L. Hua, Y. Sun, Z. Li, J. Liu and W. Tang, Front. Chem., 2021, 9, 784851 CrossRef CAS PubMed.
- D. Kersting, S. Fasbender, R. Pilch, J. Kurth, A. Franken, M. Ludescher, J. Naskou, A. Hallenberger, C. von Gall and C. J. Mohr, et al. , Nanotechnology, 2019, 30, 395101 CrossRef CAS PubMed.
- C. Nollmann, C. Wimmenauer, S. Fasbender, S. Mayer, R.-P. Caddedu, P. Jäger, T. Heinzel and R. Haas, RSC Adv., 2021, 11, 26303–26310 RSC.
- M. Yuan, Y. Guo, J. Wei, J. Li, T. Long and Z. Liu, RSC Adv., 2017, 7, 49931–49936 RSC.
- X.-W. Hua, Y.-W. Bao, Z. Chen and F.-G. Wu, Nanoscale, 2017, 9, 10948–10960 RSC.
- Z. Zhu, Q. Li, P. Li, X. Xun, L. Zheng, D. Ning and M. Su, PLoS One, 2019, 14, e0216230 CrossRef CAS PubMed.
- J. Huff, Nat. Methods, 2015, 12, i–ii CrossRef CAS.
- K. Weisshart, Zeiss Technology Note, 2014, vol. 22 Search PubMed.
- F. De Chaumont, S. Dallongeville, N. Chenouard, N. Hervé, S. Pop, T. Provoost, V. Meas-Yedid, P. Pankajakshan, T. Lecomte and Y. Le Montagner, et al. , Nat. Methods, 2012, 9, 690–696 CrossRef CAS PubMed.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld and B. Schmid, et al. , Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- A. Baddeley, E. Rubak and R. Turner, Spatial Point Patterns: Methodology and Applications with R, Chapman and Hall/CRC Press, London, 2015 Search PubMed.
- J. Ohser, Statistics, 1983, 14, 63–71 Search PubMed.
- J.-Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90 CrossRef CAS PubMed.
- K. Jaqaman, D. Loerke, M. Mettlen, H. Kuwata, S. Grinstein, S. L. Schmid and G. Danuser, Nat. Methods, 2008, 5, 695–702 CrossRef CAS PubMed.
- L. Van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- M. Ester, H.-P. Kriegel, J. Sander and X. Xu, et al. , Data Min. Knowl. Discov., 1998, 2, 169–194 CrossRef.
- B. Cabukusta and J. Neefjes, Traffic, 2018, 19, 761–769 CrossRef CAS PubMed.
- Š. Bálint, I. V. Vilanova, Á. S. Álvarez and M. Lakadamyali, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3375–3380 CrossRef PubMed.
- K. Chen, B. Wang and S. Granick, Nat. Mater., 2015, 14, 589–593 CrossRef CAS PubMed.
- V. Zaburdaev, S. Denisov and J. Klafter, Rev. Mod. Phys., 2015, 87, 483 CrossRef CAS.
- K. Polev, D. V. Kolygina, K. Kandere-Grzybowska and B. A. Grzybowski, Cells, 2022, 11, 270 CrossRef CAS PubMed.
- H. D. Pinholt, S. S.-R. Bohr, J. F. Iversen, W. Boomsma and N. S. Hatzakis, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104624118 CrossRef CAS PubMed.
- J. Signer, J. Fieberg and T. Avgar, Ecol. Evol., 2019, 9, 880–890 CrossRef PubMed.
- W. Durso, M. Martins, L. Marchetti, F. Cremisi, S. Luin and F. Cardarelli, Int. J. Mol. Sci., 2020, 21, 3397 CrossRef PubMed.
- A. Rizk, G. Paul, P. Incardona, M. Bugarski, M. Mansouri, A. Niemann, U. Ziegler, P. Berger and I. F. Sbalzarini, Nat. Protoc., 2014, 9, 586–596 CrossRef CAS PubMed.
- D. Ershov, M.-S. Phan, J. W. Pylvänäinen, S. U. Rigaud, L. Le Blanc, A. Charles-Orszag, J. R. Conway, R. F. Laine, N. H. Roy and D. Bonazzi, et al. , Nat. Methods, 2022, 19, 829–832 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00188a |
| This journal is © The Royal Society of Chemistry 2023 |