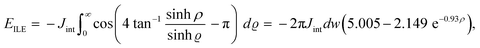Open Access Article
Open Access ArticleStabilization and adiabatic control of antiferromagnetically coupled skyrmions without the topological Hall effect†
Rawana
Yagan
 a,
Arash Mousavi
Cheghabouri
a and
Mehmet C.
Onbasli
a,
Arash Mousavi
Cheghabouri
a and
Mehmet C.
Onbasli
 *ab
*ab
aDepartment of Electrical and Electronics Engineering, Koç University, Sarıyer, Istanbul 34450, Turkey. E-mail: monbasli@ku.edu.tr
bDepartment of Physics, Koç University, Sarıyer, Istanbul 34450, Turkey
First published on 26th July 2023
Abstract
Synthetic antiferromagnetically coupled (SAF) multilayers provide different physics of stabilizing skyrmions while eliminating the topological Hall effect (THE), enabling efficient and stable control. The effects of material parameters, external current drive, and a magnetic field on the skyrmion equilibrium and propagation characteristics are largely unresolved. Here, we present a computational and theoretical demonstration of the large window of material parameters that stabilize SAF skyrmions determined by saturation magnetization, uniaxial anisotropy, and Dzyaloshinskii–Moriya interaction. Current-driven SAF skyrmion velocities reach ∼200 m s−1 without the THE. The SAF velocities are about 3–10 times greater than the typical ferromagnetic skyrmion velocities. The current densities needed for driving SAF skyrmions could be reduced to 108 A m−2, while 1011 A m−2 or above is needed for ferromagnetic skyrmions. By reducing the SAF skyrmion drive current by 3 orders, Joule heating is reduced by 6 orders of magnitude. These results pave the way for new SAF interfaces with improved equilibrium, dynamics, and power savings in THE-free skyrmionics.
Skyrmions are chiral topologically protected quasi-particles that exist in chiral magnets.1,2 These quasi-particles entail rich materials physics such as competing short- or long-range magnetic order in both non-centrosymmetric and symmetric lattices,3,4 lower order vortex or antivortex topologies such as (anti)merons,5 coupling with other quasi-particles such as non-Abelian anyons,6 and ferroelectric or thermal control in 2D van der Waals heterostructures.7,8 In addition, great interest is directed toward developing skyrmion-based memory and logic devices for next-generation applications that require fast and energy-efficient operations.9,10 Their nanoscale dimensions enable high-density and low-power nonvolatile devices. For the low and room temperature stabilization and manipulation of skyrmions for such applications, new ferromagnetic (FM) and antiferromagnetic (AFM) thin films and multilayers with unique combinations of magnetic material properties are needed.11,12
Ferromagnetic (FM) thin films can stabilize skyrmions for the optimal combinations of saturation magnetization (Msat), uniaxial anisotropy (Ku), and Dzyaloshinskii–Moriya Interaction (DMI) terms at low and room temperatures.13 Their current pulse-driven control hints14,15 that these skyrmions might be applied in racetrack memories.16,17 Nevertheless, several limitations of FM skyrmions have been observed, such as the topological Hall effect (THE), skyrmion pinning sites, and a narrow window of stability under external magnetic fields and drive currents, and strong dependence on temperature. To eliminate these shortcomings, synthetic antiferromagnetically coupled (SAF) multilayers could be used for stabilizing skyrmions while eliminating the topological Hall effect (THE), achieving faster, more efficient, and more stable current-driven propagation. To obtain these advantageous characteristics, the effects of material and external drive conditions on the SAF skyrmion equilibrium and propagation need to be understood.
Topologically non-trivial spin textures such as SAF skyrmions and domain walls have been previously proposed for magnetic tunability for applications.18–20 In SAF structures, as in Fig. 1(a), the two thin FM films couple antiferromagnetically through the non-magnetic spacer by interlayer exchange interaction (ILE), known as the Ruderman–Kittel–Kasuya–Yoshida (RKKY) interaction.21,22 This effect has been shown to enhance the stability and the velocity of SAF skyrmions.23 Previous studies suggested that the chiral SAF structures help stabilize skyrmions, eliminate the THE and might enable efficient and stable control.24,25 The theory of ferromagnetic skyrmions has been established,26,27 but the effects of material parameters, external current drive, and a magnetic field on the SAF skyrmion equilibrium and propagation characteristics have not been fully understood. A complete understanding of such characteristics should enable design of SAF skyrmion physics with low current requirements and high velocities. In addition, the effect of material imperfections such as polycrystallinity and side wall roughness as well as temperature effects on the advantages of SAF skyrmions need to be investigated. Thus, a comprehensive theory and modelling study is necessary to explain the SAF skyrmion physics. Such a study could help explain the dominant material and control parameters and regimes that could help design stable, efficient, fast, and THE-free devices.
 | ||
| Fig. 1 Stability of skyrmions in SAF. (a) Simulated structure and visualization of a SAF skyrmion. The black arrows over the nonmagnetic layer show the interlayer exchange coupling mainly through RKKY interactions. (b) The calculated total energy of the skyrmion in a single FM layer and its energy terms as functions of its radius. Material parameters are from ref. 35: Msat = 954 × 103 A m−1, A = 10 × 10−12 J m−1, Ku = 0.85 × 106 J m−3, Dind = 2.0 × 10−3 J m−2, Jint = −0.13 × 10−3 J m−2, damping α = 0.1, and the FM layer thickness d = 1 nm. | ||
In this paper, we investigate and stabilize SAF skyrmions in FM/NM (nonmagnetic)/FM layers. We developed and ran micromagnetic28 and semi-analytical models to show that the intrinsic layer magnetic properties Msat, Ku and interfacial DMI constant (Dind) play a central role in the stability, energy cost and skyrmion size control. The interlayer exchange coupling effect, which mainly depends on the interaction coefficient Jint, contributes a weaker but an essential term in eliminating the THE. Jint helps robust stabilization and prevents skyrmion decoupling under external magnetic fields and current densities perpendicular to the film plane (CPP). We investigated the effect of spin–orbit torque-driven current control in the CPP configuration, which allows for stable SAF skyrmion propagation over 3 orders of magnitude current densities (108 to 1011 A m−2). The current densities needed for driving SAF skyrmions could be reduced to 108 A m−2 (adiabatic limit), which is up to 3 orders of magnitude lower than the currents needed for ferromagnetic skyrmions (1011 A m−2 or above).29 Thus, Joule heating might be reduced by 6 orders of magnitude. The current-driven SAF skyrmion velocities reach ∼200 m s−1 without the THE, which is about an order of magnitude greater than the ferromagnetic skyrmion velocities.30 Earlier studies25 showed high SAF skyrmion velocities exceeding 1000 m s−1 at 3 × 108 A cm−2 (or 3 × 1012 A m−2), but in our case, we report current density requirements of 108 to 1011 A m−2 for ∼200 m s−1, where 1–3 orders of lower current densities in our study might benefit device applications.
Significant polycrystallinity or material parameter variations over each nanoscale grain have been found to cause SAF skyrmion pinning and change the current needed for SAF skyrmion propagation. Thus, uniform material characteristics are necessary for experiments. Side wall roughness does not significantly affect the SAF skyrmion stability or propagation. Stabilizing SAF skyrmions at higher temperatures required larger uniaxial anisotropy constants. These results and the semi-analytical model here provide insights into new SAF interfaces for improved equilibrium and dynamics of skyrmions without the THE. Thus, THE-free long-distance propagation and operation of skyrmions on chip without undergoing deflection or significant heating might become feasible.
Our modeling approach identified the effects of polycrystallinity that previous studies did not uncover.31,32 Earlier studies used hysteresis loop models for coercivity and remanence for arrays of nickel nanowires31 but did not investigate current drive, skyrmion formation or stability or antiferromagnetic coupling. In our case, we studied the SAF skyrmion pair equilibria under magnetic compensation and current drive and material imperfections.
In the next section, we first describe the stabilization of SAF skyrmions using both micromagnetic modelling and semi-analytical energy minimization. Then, we present the dependence of the SAF skyrmion stability and radius on the intrinsic magnetic layer parameters (Msat, Dind, and Ku), the interlayer exchange (Jint), and the applied external magnetic field and current density. Next, we discuss and identify the main parameters that must be used for SAF skyrmion stabilization and adiabatic drive with no or negligible THE. We compare our results with those of previous studies on the elimination of the THE and highlight that THE-free SAF skyrmions can be driven with current densities over several orders of magnitude.
Results
SAF and stabilization of AFM coupled skyrmions
An SAF skyrmion consists of two ferromagnetic skyrmions coupled antiferromagnetically through a FM/NM/FM heterostructure. The magnetization of each FM layer's skyrmion core is opposite to the film plane and has opposite topological charge with respect to their antiferromagnetically coupled skyrmion counterpart as shown in Fig. 1(a).For each layer, the skyrmion and its related analytical energy approximation expressions are adapted from the FM skyrmion system of equations.27 In each layer, the moment is represented by the normalized unit magnetization vector, m = (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, sin
φ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, cos
φ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), in spherical coordinates and described by the polar and azimuthal angles, θ and φ, respectively. The domain wall in a skyrmion, as shown in Fig. 1(a), is defined as the transition region from the oppositely polarized spins (from red to blue) within a skyrmion. m is assumed to be uniform across the layer thickness (φ is constant) and has a constant saturation magnetization Msat. φ is the angle between the domain wall magnetic moments and the radial direction (r) and θ(ϱ,ρ) is the skyrmion profile modeled by the 360° domain wall proposed by Braun:33
θ), in spherical coordinates and described by the polar and azimuthal angles, θ and φ, respectively. The domain wall in a skyrmion, as shown in Fig. 1(a), is defined as the transition region from the oppositely polarized spins (from red to blue) within a skyrmion. m is assumed to be uniform across the layer thickness (φ is constant) and has a constant saturation magnetization Msat. φ is the angle between the domain wall magnetic moments and the radial direction (r) and θ(ϱ,ρ) is the skyrmion profile modeled by the 360° domain wall proposed by Braun:33
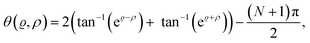 | (1) |
 and
and 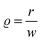 . RSk is the skyrmion radius, w is the skyrmion domain wall width and N is the skyrmion core (= 1 here since skyrmion core moments point upwards for the top FM layer).
. RSk is the skyrmion radius, w is the skyrmion domain wall width and N is the skyrmion core (= 1 here since skyrmion core moments point upwards for the top FM layer).
The total energy of a single FM layer within the SAF heterostructure consists of the energy terms that are driven by the intrinsic, interaction and external bias magnetic energy terms: demagnetizing field energy, Heisenberg exchange EA, effective anisotropy EK, DMI EDMI, interlayer exchange EILE and Zeeman energy EZ:
| Etot = EA + EK + EDMI + EILE + EZ | (2) |
Each magnetic anisotropy energy term shown below and in eqn (2) is calculated for each FM layer separately:
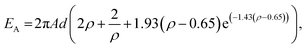 | (3) |
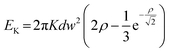 | (4) |
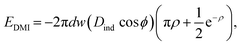 | (5) |
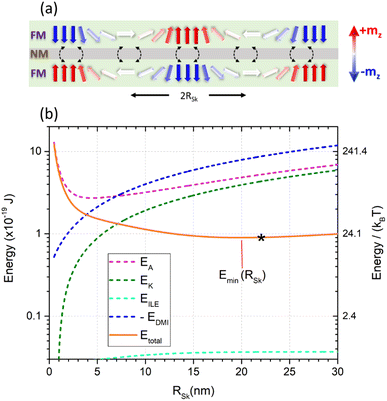
| EILE = −2πJintdw(5.005–2.149 e−0.93ρ). | (6) |
The demagnetization field energy is included in the EK term using:
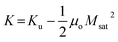 | (7) |
In these calculations, EA, Ek, and EDMI are determined by each layer's intrinsic magnetic parameters and geometry. EILE is the term that couples the FM skyrmions antiferromagnetically through the nonmagnetic layer and depends on the geometry (thickness), the interface characteristics, and ρ, whose equilibrium value is affected by all the other magnetic energy terms. EZ is the external magnetic field bias control term for stabilizing the SAF skyrmion. In the semi-analytical model, the thin film aspect ratio is assumed.
We first find the equilibrium skyrmion radii using both self-consistent solutions of the approximations given in eqn (1)–(7) and using numerical micromagnetic modelling of the Landau–Lifshitz–Gilbert equation. These two models help identify the key energy terms and the material parameters that strongly affect the SAF skyrmion stability.
The equilibrium radius of the SAF skyrmion for an experimentally relevant35 set of material parameters is found by minimizing the total magnetic anisotropy energy with respect to the coupled SAF skyrmion radius RSk. Fig. 1(b) shows the dependence of the radius of the SAF skyrmion on one of the FM/NM interfaces to the total effective magnetic energy and the different energy terms (EA, EK, EDMI, and EILE) contributing to the equilibrium, as shown in eqn (3)–(7) of our semi-analytical model. This curve is identical for the skyrmion stabilized at the opposite interface of the FM/NM/FM trilayer. The star on the total energy curve corresponds to the calculated equilibrium radius and energy using a LLG-based micromagnetic model. Both numerical micromagnetic models (Req = 22 nm) and the semi-analytical model (Req = 19.99 nm) yield almost identical equilibrium skyrmion radii for the SAF trilayer system.
Effect of material parameters on SAF skyrmion stability
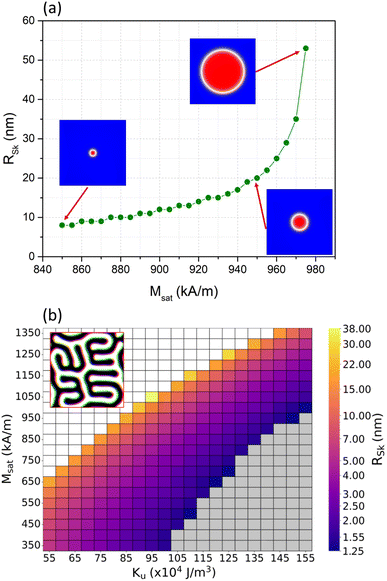
We now investigate the stability and equilibrium radii of the SAF skyrmions using LLG-based micromagnetic models as functions of different Msat, Dind (DMI) and Ku values.Fig. 2(a) shows the effect of the saturation magnetization and demagnetization field on the radius of the skyrmion along the top FM/NM surface. The energy terms for both top and bottom FM/NM interfaces include the uniaxial anisotropy, DMI, Heisenberg exchange, and interlayer exchange; therefore, the resulting plots for the skyrmions at both interfaces are identical. RSk shows a linear scaling trend with the increase in Msat until 950 kA m−1, and then the radius scales exponentially with Msat as the demagnetization energy starts dominating the total magnetic energy of the skyrmions. This effect is also mirrored in the second FM layer (not shown).
We next calculated the phase diagram of RSk as a function of Msat and the uniaxial anisotropy constant, Ku, shown in Fig. 2(b). On the top left corner of the phase diagram (low Ku and high Msat), a transition from a labyrinth domain structure (shown in the inset figure) is observed and skyrmions cannot be stabilized. As Ku is increased, the skyrmion radii decrease from 38 to 1.25 nm. With further increase in Ku and reduction in Msat, skyrmions would be expected to shrink further but since the micromagnetic model cell size cannot be smaller than the lattice constant of cobalt, smaller skyrmion size regions have been excluded from the phase diagram. The lower right-hand corner of the phase diagram (gray area; high Ku and low Msat) reaches the minimum allowed mesh size of the micromagnetic model (exchange length > minimum cell size > lattice constant of cobalt). No result is shown for this region since the LLG model cannot account for the atomic scale interactions. Higher Ku shrinks the skyrmion radius, while greater Msat enlarges the skyrmion.
Fig. 3 shows the effect of interfacial Dzyaloshinskii–Moriya interaction strength, Dind, and uniaxial anisotropy Ku on the relaxed and equilibrated skyrmion size. Increasing Ku for a fixed Dind equilibrates the skyrmions at lower radii (Req < 5 nm). For a fixed Ku, the equilibrium skyrmion radii increase to 15 to 30 nm with higher Dind values. For low Ku and high Dind values, the skyrmions are not stable and labyrinth domains form as shown in the inset of the figure. The gray region does not include any results as in Fig. 2(b), since the required cell size approaches the lattice constant.
Effect of external control fields on SAF skyrmion stability
The stability of SAF skyrmions relies on the intrinsic material parameters as well as the extrinsic control conditions including the magnetic field (Bz = μoHz) and the current density. To elucidate the effect of an external magnetic field on the SAF skyrmion stability and coupling, the approximated Zeeman energy term shown27 in eqn (8) is added to the total energy terms (eqn (2)) for both top and bottom skyrmions calculated using the micromagnetic solver.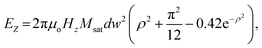 | (8) |
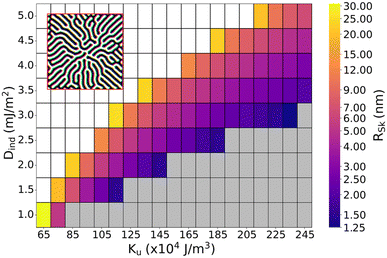
Because these skyrmions are coupled with each other through the ILE, the skyrmion scaling with the applied field and the ILE coefficient needs to be understood. For this purpose, we calculated and plotted the radii of the bottom skyrmion as functions of Jint (interlayer exchange coupling coefficient) and the applied field Bz in Fig. 4(b).
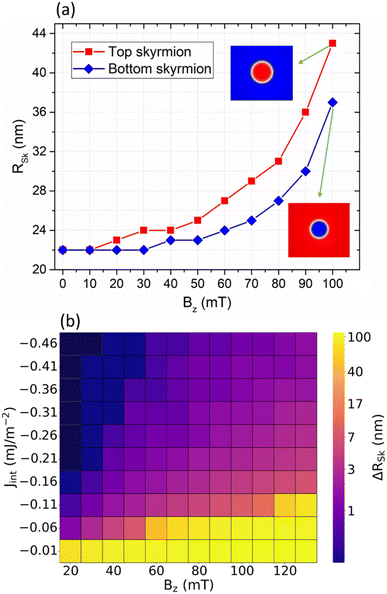
Finally, we investigated the effect of current density on the dynamical stability and velocity of the SAF skyrmions. We studied this effect by applying current-induced spin–orbit torque (SOT) perpendicular-to-plane (CPP) to the SAF structure (eqn (11) in the Methods) that allows the skyrmion pair to travel in the in-plane direction (+x). In Fig. 5(a), we apply a current density of Je = 2.5 × 1011 A m−2 from left to right to push the skyrmion pair along the structure with a spin Hall angle θHall = 0.25.35 We observe that for the lower applied field, the SAF skyrmion with the higher ILE coupling constant Jint experiences higher velocity; however at a critical Bz field of near 80 mT, all curves show the same velocity, and the order is reversed. The smallest Jint curve gives the highest skyrmion velocity at higher fields. At this critical value of Bz, the coupling between the skyrmions and the skyrmion cores is expected to be affected by the polarizing field, and this is observed in Fig. 4(b). Jint proves to play a role in the translational motion of the skyrmion as larger ILE strength could provide stronger stability against the current pushing the skyrmion. For magnitudes below the decoupling field limits shown in Fig. 4(b), higher Bz leads to greater velocity when current is applied.
To elucidate the effect of the applied current density in different driving regimes of the SAF skyrmions, we present the current density–skyrmion pair velocity-Bz field phase diagram in Fig. 5(c). The phase diagram ends at high current densities due to the decoupling of the top and bottom skyrmions (white region). The skyrmion decoupling current decreases with the increase in the field Bz. This effect is due to breakdown of the coupling under larger magnetic fields under reduced symmetry as mentioned in Fig. 4(b). The maximum velocity reached for this system is about 196 m s−1 at the lower field. On the other hand, the lower limit for Je that can still drive the SAF skyrmion adiabatically (0.04 m s−1) is observed on the order of 1 × 108 A m−2. As power dissipation scales quadratically with the applied current density, adiabatic skyrmion velocities might be identified as an ultra-low power skyrmion driving regime.
At the lowest current density limit (108 A m−1, 0.03 m s−1 SAF skyrmion velocity), the operation time to move an SAF skyrmion of 20 nm diameter across a 20 nm distance at this velocity is around 0.7 μs. The operation rate is therefore on the order of 1/(0.7 μs) = 1.43 MHz. This rate is already sufficient or an order of magnitude higher than the standard data transfer interface rates such as those at the SPI (serial peripheral interface) and those in I2C commonly used by state-of-the-art sensors (i.e., BMP581 Barometric Pressure Sensor36 and BMI323 inertial measurement unit from Bosch Sensortec37). Therefore, despite the slow rate, many practical applications can be implemented with the SAF skyrmions. Our SAF skyrmion system's much lower power consumption with respect to microelectronics and its nonvolatile data processing characteristics provide significant potential advantages. For many embedded systems or Internet of things applications, GHz rates are not needed or even preferred because of the higher power consumption. Since not all technological applications need GHz rates, these small velocities should be fine also for the relevant niche applications like sensor nodes and networks. For sensor deployment and networks, power consumption can be the main figure of merit to be optimized and the information processing rate can be traded off to obtain low power consumption.
Temperature dependence, sidewall roughness, pinning sites and polycrystallinity typically hinder experimental realization of many of the useful properties of skyrmions. Despite their significance, very few computational or theoretical studies on skyrmions quantify these detrimental effects or provide guidance on how to overcome them.38,39 Increasing temperature in the SAF multilayer from 0 K to 100 K blurs the skyrmion borders and diminishes their stability (Fig. S1 in the ESI†). For the same SAF skyrmion multilayer configuration, a slight increase of uniaxial anisotropy Ku from 85 × 104 J m−3 to 95 × 104 J m−3 at 100 K offsets the random temperature fluctuations and restores the 0 K-like stability. The applied external field, however, cannot provide the same stabilizing effect as Ku since the field contributes Zeeman terms with opposite signs at the coupled skyrmion interfaces (Fig. S2 in the ESI†). Uniaxial anisotropy variations have been found to profoundly affect SAF skyrmion pairing and current-driven motion (Fig. S5 and S6 in the ESI†), where a random change of 5% or more of the nominal uniaxial anisotropy (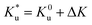 , where
, where 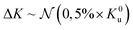 ) can hinder current-driven skyrmion propagation (Videos V1–V4 in the ESI†). In addition, 3° or more of off-axis misorientation of uniaxial anisotropy (i.e., due to substrate miscuts) has been found to be sufficient to completely hinder current-driven skyrmion motion (Fig. S6 in Videos V5–V9 in the ESI†). Unlike temperature or uniaxial anisotropy, sidewall roughness does not prevent SAF skyrmion pairing or their paired current-driven motion (Fig. S7 and Videos V10–V13 in the ESI†) when the random sidewall roughness within 3σ ≤ 60% of the channel widths of SAF multilayer slabs can sustain coupled skyrmions and their propagation. These results emphasize the significance of temperature, the uniaxial anisotropy parameter, minimal substrate miscuts, and uniform and single crystal magnetic film quality for experimental demonstrations of skyrmion devices.
) can hinder current-driven skyrmion propagation (Videos V1–V4 in the ESI†). In addition, 3° or more of off-axis misorientation of uniaxial anisotropy (i.e., due to substrate miscuts) has been found to be sufficient to completely hinder current-driven skyrmion motion (Fig. S6 in Videos V5–V9 in the ESI†). Unlike temperature or uniaxial anisotropy, sidewall roughness does not prevent SAF skyrmion pairing or their paired current-driven motion (Fig. S7 and Videos V10–V13 in the ESI†) when the random sidewall roughness within 3σ ≤ 60% of the channel widths of SAF multilayer slabs can sustain coupled skyrmions and their propagation. These results emphasize the significance of temperature, the uniaxial anisotropy parameter, minimal substrate miscuts, and uniform and single crystal magnetic film quality for experimental demonstrations of skyrmion devices.
Discussion
Dependence of SAF skyrmion stability on material constants
The two coupled skyrmions along the two interfaces of the SAF trilayer are stabilized as a balance of the competing energy terms mentioned in eqn (2). Fig. 1 shows that the main driver of the coupled skyrmions is the uniaxial anisotropy energy (EK), which also contains both magnetocrystalline (uniaxial) and demagnetizing (shape) anisotropy terms. After the uniaxial anisotropy energy, DM interaction EDMI changes by more than an order magnitude within the radius range of 30 nm and contributes to the equilibrium configuration. The Heisenberg exchange interaction EA, which is constant within each ferromagnetic layer, also helps equilibrate the SAF skyrmion at below a 30 nm radius. The interlayer exchange term, EILE, is about two orders of magnitude weaker than the other magnetic energy terms within the radius range of 5–30 nm. This term is too weak to participate substantially in the stabilization of the skyrmion radius within each layer. The main contribution of this term is in the antiferromagnetic coupling of the skyrmions on the opposite ends of the multilayer. Overall, for stabilizing the skyrmion radius, the main terms that contribute are EK, EDMI, and EA. For coupling the skyrmions antiferromagnetically, EILE is the critical and unique term which does not exist in ferromagnetic skyrmion systems.Comparison of our semi-analytical model and numerical micromagnetic LLG model
We modelled the equilibrium radii of the SAF skyrmions both using a semi-analytical model that we developed and the numerical LLG model. The details of both models are presented in the results and methods parts. The semi-analytical model is an approximation, but its closed form expressions allow for interpreting how these terms scale with the geometric or material parameters while micromagnetic LLG models do not allow for it. Thus, the competing driving forces and the prominent materials and geometric factors can be better understood. The results in Fig. 1 are based on both the semi-analytical model and the micromagnetic model, while the rest of the figures show results from the micromagnetic LLG models.In eqn (2)–(8), the equilibrium radius and the domain wall width are the key parameters that both affect these energy terms and are also affected by these terms. Below is a term-by-term analysis of the equilibrated SAF skyrmion pairs:
Overall, Msat, Ku, DMI constant Dind and their contributions affect the stability of the SAF skyrmion the most. The increase in the uniaxial anisotropy of the system will allow the skyrmion to stabilize at larger radii. On the other hand, the interlayer exchange interaction has the lowest contribution to the total energy, which also implies that it has little effect on the skyrmion size. However, this term is crucial for maintaining the SAF skyrmion structure against externally applied conditions, such as the current density that moves the skyrmion in the structure. We observe that the equilibrium state of the SAF skyrmion at minimum total energy is attained at a radius of 20 nm, and we also obtain a close value by simulating the SAF skyrmion in MuMax3 with the same parameters. The MuMax3 micromagnetic model based on the LLG equation is described further in the Methods.
Since Msat, Ku, and the DMI constant Dind affect the skyrmion stability and sizes the most, Fig. 2 and 3 show the effect of these parameters in further detail. The skyrmion sizes generally increase linearly with increasing saturation magnetization of the ferromagnetic layers, but after a critical Msat, the skyrmion sizes are dominated mainly by Msat. Fig. 2(a) shows that the equilibrium coupled SAF skyrmion sizes are below 15 nm in radius for Msat < 930 kA m−1. For Msat beyond this threshold, the equilibrium skyrmion radii increase exponentially.
The effects of the uniaxial anisotropy constant and saturation magnetization on the equilibrium coupled SAF skyrmion radii are shown in the phase diagram in Fig. 2(b). For a constant Msat, higher Ku shrinks the skyrmion radius, since the skyrmion minimizes its energy with a smaller total uniaxial anisotropy and demagnetizing energy term. Greater Msat for a constant Ku increases the equilibrium skyrmion radii since the larger demagnetizing fields with higher magnetization minimize the total energy when the skyrmion radius is larger. The skyrmion radius can be changed from 1.25 nm to 38 nm due to the total effective magnetic energy expression formed with the different uniaxial anisotropy and the saturation magnetization values, as shown in the color shaded region. The white region of the phase diagram with high Msat and low Ku (below 106 J m−3) shows the stabilization of labyrinth domain structures and here, skyrmions are no longer supported. In the gray-shaded region, no results are reported since the cell sizes of the simulations become comparable to the lattice constants. Around these cell sizes, the micromagnetic assumption of homogeneous micromagnetic cell approximation no longer applies to the discrete atomic spins. Thus, the phase diagram excludes the gray region. These results show that the balance of Msat and Ku establishes the equilibrium size of the coupled SAF skyrmions.
The FM/NM/FM layer has mirror symmetry in its geometry, but the DMI constant of both interfaces is an important parameter that can preserve or break the topology and chirality of the skyrmion. As a result, large Dind values at the interfaces break the symmetry and cause labyrinth structures to form, as shown in the upper white regions of Fig. 3. In the low Dind and higher Ku cases, as shown in the gray region of the phase diagram, the skyrmion sizes fall below the lower cell size thresholds for micromagnetic models to be valid. Below 1.25 nm, atomically small domain features can no longer be captured by micromagnetic models, and therefore, no results are reported in that region of the phase diagram. For a constant Dind constant, larger uniaxial anisotropy tends to shrink the skyrmion sizes due to the positive sign of the anisotropy constant that would minimize the total energy only if the skyrmion becomes smaller. The formation of a stable skyrmion window and the opposing effects of Dind and Ku on the skyrmion sizes indicates the competition of uniaxial anisotropy and Dzyaloshinskii–Moriya interaction.
The effect of interlayer exchange (ILE) and an external magnetic field have been investigated as shown in Fig. 4. The top and bottom skyrmions are coupled to each other through the ILE term. In Fig. 4(a), increasing the Bz enlarges the top skyrmion while it tries to shrink the bottom skyrmion. The ILE can no longer keep the top and bottom layer skyrmions perfectly aligned since the core of the top skyrmion (+z) expands and overcomes the AFM coupling. The difference is observed at Bz = 100 mT.
In Fig. 4(b), the ILE interaction constant Jint with a higher magnitude keeps the top and bottom skyrmions tightly bound with similar radii especially for low Bz fields. Increasing the external field reduces the coupling without complete detachment. For weak ILE constants, any external magnetic field Bz is going to cause a significant radius difference. Fig. S3 in the ESI† includes further details on the effect of Jint and Bz on the skyrmion radius of the bottom interface. While the external field can cause the detachment of the SAF skyrmions above a critical field threshold, the SAF skyrmion velocity is not significantly affected by the external magnetic field. The driving force for exponential increase in skyrmion velocity is the applied current density, as shown in Fig. 5(b) and (c).
Although the same parameters reported in ref. 35 are used, our study is fundamentally different from the earlier skyrmion investigations in terms of the purpose, methods, and the results. Different from ref. 35 and similar skyrmion investigations, our study has three unique aspects. First, our study presents a semi-analytical model, which helped identify the key driving forces and anisotropy fields and this model was used in the supplementary section to overcome temperature effects (ESI Fig. S1†). Second, our study shows the effects of changing the key material parameters (saturation magnetization, uniaxial anisotropy, DMI parameter, and interlayer exchange) and the external magnetic field on the skyrmion and skyrmion pair stability. Third, our study shows the effects of imperfections on the device operation for the first time for SAF skyrmions. The effects of different material parameters due to fabrication imperfections (Fig. 2–5), sidewall roughness, substrate miscuts or crystalline misorientation and finite temperature effects on device performance are analyzed and discussed (ESI†). We also proposed ways to overcome finite temperature effects using uniaxial anisotropy (ESI†). Different from earlier studies, we analyzed SAF skyrmion propagation from a power consumption standpoint and focused on skyrmions, not domain-like micron-scale bubbles as in previous studies.35 Each of these effects is too hard or impossible to test experimentally. Therefore, our computational study helped elucidate the key driving anisotropy field forces and regimes that would not otherwise be identified, and new insights are obtained through our models.
SAF skyrmions could be explored in new 2D semiconducting NbSi2N4, VSi2N4, and VSi2P4 with near or above room temperature magnetism. Since the magnetic easy axis of VSi2N4 can be tuned from in-plane to out-of-plane by applying tensile biaxial strain or electron doping,40 these new 2D magnetic semiconductors could be explored for SAF skyrmion demonstrations. Their nontrivial topological properties, 2D ferromagnetism, Ising superconductivity, and valley polarization also make these spin gapless semiconductors and bipolar magnetic semiconductors interesting candidates for topological magnetotransport studies.41,42 Interfacial DMI is increased for monolayer or very thin magnetic films and this effect can be beneficial for making nanometer scale SAF spintronic devices.43 Implementing SAF skyrmions in such 2D materials with higher Curie temperatures might be a fruitful future research direction.
To conclude, we investigated the theory of SAF skyrmions and the stability conditions that allow for their applications in logic and memory-based devices. The theory of SAF skyrmions helped elucidate new insights into which terms prominently contribute to the equilibrium and propagation of these coupled skyrmions. Further investigation into the effect of an external vertical magnetic bias field and the current density revealed that SAF skyrmions can reach ∼200 m s−1 without the THE. The SAF velocities are an order of magnitude higher than those of the typical ferromagnetic skyrmions. Skyrmion drive current densities could be reduced to as low as 108 A m−2 and a more than 3 orders of magnitude-wide window of current densities can be feasible for stable, fast, and THE-free skyrmion propagation. The reduction in current density could quadratically reduce Joule heating by as much as 6 orders of magnitude. Furthermore, the models emphasized the significance of temperature, the uniaxial anisotropy parameter, minimal substrate miscuts, and uniform and single crystal magnetic film quality for experimental demonstrations of skyrmion devices. These results complete the theory of SAF skyrmions and pave the way to experimental demonstrations of THE-free SAF interfaces with improved equilibrium, dynamics, and power savings.
Methods
Micromagnetic model of the SAF skyrmion system
The SAF structure shown in Fig. 1(a) consists of two ferromagnetic (FM) layers and a nonmagnetic (NM) layer is in between. The antiferromagnetically (AFM) coupled top and bottom layers in the synthetic antiferromagnetic (SAF) system were modelled using the MuMax3 micromagnetic solver.28 This software solves the Landau–Lifshitz–Gilbert (LLG) equation using the finite-difference method.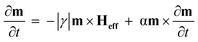 | (9) |
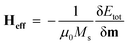 | (10) |
The geometry and parameters were set according to the (Co/CoFeB)/Ir/(Co/CoFeB) (FM/NM/FM) system.35 The following parameters are used in the calculations (unless otherwise mentioned): Msat = 954 × 103 A m−1, A = 10 × 10−12 J m−1, Ku = 0.85 × 106 J m−3, Dind = 2.0 × 10−3 J m−2, and α = 0.1. The structure in the simulation (512 × 512 × 2 nm3) consisted of two FM layers (each has a thickness of 1 nm), while the NM layer was not explicitly included and instead the interlayer exchange constant was scaled to a RKKY value of −0.13 × 10−3 J m−2 for a given thickness of the NM layer of 1 nm. The cell size was set to cx = 1 nm, cy = 1 nm, and cz = 1 nm. For the phase diagrams, the sweeps on MuMax3 were done for the cell size cx = cy = 0.25 nm to obtain the minimum skyrmion radius range in the micromagnetic limits, both cell size values chosen in-plane yield the same results (see Fig. S4 in the ESI† for cx = cy = 1 nm).
For the dynamic simulations of the SAF skyrmion we used SOT-driven current in the SAF structure. We applied the current density in the CPP configuration so that the SAF skyrmion could move in the in-plane direction (+x) and the spin hall angle θHall was set to + 0.25. The LLG equation including the SOT term then becomes:
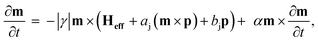 | (11) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and the surface normal of the heavy metal layer n = ẑ.
and the surface normal of the heavy metal layer n = ẑ.
Interlayer exchange energy functional
The interlayer exchange coupling (RKKY) energy in the SAF multilayer system34 is defined asEILE = −Jint(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 θ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2 + sin θ2 + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 θ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2 θ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos (φ1 − φ1)), cos (φ1 − φ1)), |
φ
2 = φ1 + π and θ2 = θ1 + π for the Néel type of skyrmion pairs shown in Fig. 1(a), and then EILE reduces to
EILE = −Jint(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (2θ1 − π)), (2θ1 − π)), |
Using the definition of θ from ref. 27 and integrating with respect to the ratio term ϱ we finally present the energy as the following approximated expression,
Data availability
Data supporting the findings of this study are available within the article and its ESI† and from the corresponding authors upon request. Source data are provided with this paper and in the link: … (link to be provided if requested by the reviewers or the journal after acceptance).Author contributions
M. C. O. conceived and coordinated the project. R. Y. performed most of the micromagnetic simulations with support from A. M. C. M. C. O. and R. Y. interpreted the results and prepared the manuscript. All authors commented on the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This study has been funded by the European Research Council (ERC) Starting Grant SKYNOLIMIT Grant No. 948063, ERC Proof of Concept Grant SuperPHOTON Grant No. 101100718 and partially from TÜBİTAK Grant No. 120F230.References
- Y. Tokura and N. Kanazawa, Chem. Rev., 2021, 121, 2857–2897 CrossRef CAS PubMed.
- A. Fert, N. Reyren and V. Cros, Nat. Rev. Mater., 2017, 2, 17031 CrossRef CAS.
- N. D. Khanh, T. Nakajima, X. Yu, S. Gao, K. Shibata, M. Hirschberger, Y. Yamasaki, H. Sagayama, H. Nakao, L. Peng, K. Nakajima, R. Takagi, T.-h. Arima, Y. Tokura and S. Seki, Nat. Nanotechnol., 2020, 15, 444–449 CrossRef CAS PubMed.
- N. Kanazawa, S. Seki and Y. Tokura, Adv. Mater., 2017, 29, 1603227 CrossRef PubMed.
- N. Gao, S. G. Je, M. Y. Im, J. W. Choi, M. Yang, Q. Li, T. Y. Wang, S. Lee, H. S. Han, K. S. Lee, W. Chao, C. Hwang, J. Li and Z. Q. Qiu, Nat. Commun., 2019, 10, 5603 CrossRef CAS PubMed.
- G. Yang, P. Stano, J. Klinovaja and D. Loss, Phys. Rev. B, 2016, 93, 224505 CrossRef.
- Y. Wu, S. Zhang, J. Zhang, W. Wang, Y. L. Zhu, J. Hu, G. Yin, K. Wong, C. Fang, C. Wan, X. Han, Q. Shao, T. Taniguchi, K. Watanabe, J. Zang, Z. Mao, X. Zhang and K. L. Wang, Nat. Commun., 2020, 11, 3860 CrossRef PubMed.
- K. Huang, D.-F. Shao and E. Y. Tsymbal, Nano Lett., 2022, 22, 3349–3355 CrossRef CAS PubMed.
- B. Dieny, I. L. Prejbeanu, K. Garello, P. Gambardella, P. Freitas, R. Lehndorff, W. Raberg, U. Ebels, S. O. Demokritov, J. Akerman, A. Deac, P. Pirro, C. Adelmann, A. Anane, A. V. Chumak, A. Hirohata, S. Mangin, S. O. Valenzuela, M. C. Onbaşlı, M. D'Aquino, G. Prenat, G. Finocchio, L. Lopez-Diaz, R. Chantrell, O. Chubykalo-Fesenko and P. Bortolotti, Nat. Electron., 2020, 3, 446–459 CrossRef.
- X. Zhang, Y. Zhou, K. Mee Song, T.-E. Park, J. Xia, M. Ezawa, X. Liu, W. Zhao, G. Zhao and S. Woo, J. Phys.: Condens. Matter, 2020, 32, 143001 CrossRef CAS PubMed.
- R. Juge, N. Sisodia, J. U. Larrañaga, Q. Zhang, V. T. Pham, K. G. Rana, B. Sarpi, N. Mille, S. Stanescu, R. Belkhou, M.-A. Mawass, N. Novakovic-Marinkovic, F. Kronast, M. Weigand, J. Gräfe, S. Wintz, S. Finizio, J. Raabe, L. Aballe, M. Foerster, M. Belmeguenai, L. D. Buda-Prejbeanu, J. Pelloux-Prayer, J. M. Shaw, H. T. Nembach, L. Ranno, G. Gaudin and O. Boulle, Nat. Commun., 2022, 13, 4807 CrossRef CAS PubMed.
- W. Legrand, D. Maccariello, F. Ajejas, S. Collin, A. Vecchiola, K. Bouzehouane, N. Reyren, V. Cros and A. Fert, Nat. Mater., 2020, 19, 34–42 CrossRef CAS PubMed.
- H. Wang, Y. Liu, P. Wu, W. Hou, Y. Jiang, X. Li, C. Pandey, D. Chen, Q. Yang, H. Wang, D. Wei, N. Lei, W. Kang, L. Wen, T. Nie, W. Zhao and K. L. Wang, ACS Nano, 2020, 14, 10045–10053 CrossRef CAS PubMed.
- G. Yu, P. Upadhyaya, X. Li, W. Li, S. K. Kim, Y. Fan, K. L. Wong, Y. Tserkovnyak, P. K. Amiri and K. L. Wang, Nano Lett., 2016, 16, 1981–1988 CrossRef CAS PubMed.
- X. Zhang, Y. Zhou and M. Ezawa, Nat. Commun., 2016, 7, 10293 CrossRef CAS PubMed.
- S. Luo and L. You, APL Mater., 2021, 9, 050901 CrossRef CAS.
- L. Gnoli, F. Riente, M. Vacca, M. Ruo Roch and M. Graziano, Electronics, 2021, 10, 155 CrossRef CAS.
- R. A. Duine, K.-J. Lee, S. S. P. Parkin and M. D. Stiles, Nat. Phys., 2018, 14, 217–219 Search PubMed.
- J. Xia, X. Zhang, K.-Y. Mak, M. Ezawa, O. A. Tretiakov, Y. Zhou, G. Zhao and X. Liu, Phys. Rev. B, 2021, 103, 174408 CrossRef CAS.
- X. Zhang, Y. Zhou and M. Ezawa, Sci. Rep., 2016, 6, 24795 CrossRef CAS PubMed.
- A. Fernández-Pacheco, E. Vedmedenko, F. Ummelen, R. Mansell, D. Petit and R. P. Cowburn, Nat. Mater., 2019, 18, 679–684 CrossRef PubMed.
- S. Krishnia, P. Sethi, W. L. Gan, F. N. Kholid, I. Purnama, M. Ramu, T. S. Herng, J. Ding and W. S. Lew, Sci. Rep., 2017, 7, 11715 CrossRef CAS PubMed.
- A. G. Kolesnikov, M. E. Stebliy, A. S. Samardak and A. V. Ognev, Sci. Rep., 2018, 8, 16966 CrossRef PubMed.
- S. Qiu, J. Liu, Y. Chen, X. Qi and L. Fang, J. Magn. Magn. Mater., 2022, 554, 169144 CrossRef CAS.
- R. Tomasello, V. Puliafito, E. Martinez, A. Manchon, M. Ricci, M. Carpentieri and G. Finocchio, J. Phys. D: Appl. Phys., 2017, 50, 325302 CrossRef.
- X. S. Wang, H. Y. Yuan and X. R. Wang, Commun. Phys., 2018, 1, 31 CrossRef.
- F. Büttner, I. Lemesh and G. S. D. Beach, Sci. Rep., 2018, 8, 4464 CrossRef PubMed.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. V. Waeyenberge, AIP Adv., 2014, 4, 107133 CrossRef.
- S. Woo, K. M. Song, X. Zhang, Y. Zhou, M. Ezawa, X. Liu, S. Finizio, J. Raabe, N. J. Lee, S.-I. Kim, S.-Y. Park, Y. Kim, J.-Y. Kim, D. Lee, O. Lee, J. W. Choi, B.-C. Min, H. C. Koo and J. Chang, Nat. Commun., 2018, 9, 959 CrossRef PubMed.
- J. Sampaio, V. Cros, S. Rohart, A. Thiaville and A. Fert, Nat. Nanotechnol., 2013, 8, 839–844 CrossRef CAS PubMed.
- G. P. Fuentes, J. Holanda, Y. Guerra, D. B. O. Silva, B. V. M. Farias and E. Padrón-Hernández, J. Magn. Magn. Mater., 2017, 423, 262–266 CrossRef CAS.
- J. Weissmüller, A. Michels, J. G. Barker, A. Wiedenmann, U. Erb and R. D. Shull, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 214414 CrossRef.
- H.-B. Braun, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 16485–16500 CrossRef CAS PubMed.
- Z. Zhang, L. Zhou, P. E. Wigen and K. Ounadjela, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6094–6112 CrossRef CAS PubMed.
- T. Dohi, S. Duttagupta, S. Fukami and H. Ohno, Nat. Commun., 2019, 10, 5153 CrossRef PubMed.
- B. Sensortec, BMP581 Barometric Pressure Sensor Datasheet, B. Sensortec Report BST-BMP581-DS004, Bosch Sensortec, 2023 Search PubMed.
- B. Sensortec, BMI323 Small, Versatile 6DoF Sensor Module Datasheet, Report BST-BMI323-DS000-09, Bosch Sensortec, 2023 Search PubMed.
- A. M. Cheghabouri and M. C. Onbasli, Sci. Rep., 2019, 9, 9496 CrossRef CAS PubMed.
- A. Mousavi Cheghabouri, F. Katmis and M. C. Onbasli, Phys. Rev. B, 2022, 105, 054411 CrossRef CAS.
- M. R. K. Akanda and R. K. Lake, Appl. Phys. Lett., 2021, 119, 052402 CrossRef CAS.
- Y. Feng, Z. Wang, X. Zuo and G. Gao, Appl. Phys. Lett., 2022, 120, 092405 CrossRef CAS.
- Q. Cui, Y. Zhu, J. Liang, P. Cui and H. Yang, Phys. Rev. B, 2021, 103, 085421 CrossRef CAS.
- M. R. K. Akanda, I. J. Park and R. K. Lake, Phys. Rev. B, 2020, 102, 224414 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The data and the part of the code used for the models. See DOI: https://doi.org/10.1039/d3na00236e |
| This journal is © The Royal Society of Chemistry 2023 |