Open Access Article
Open Access ArticleInfluence of organic ligands on the stoichiometry of magnetite nanoparticles†
Phoomipat
Jungcharoen
ab,
Rémi
Marsac
 a,
Fadi
Choueikani
c,
Delphine
Masson
a and
Mathieu
Pédrot
a,
Fadi
Choueikani
c,
Delphine
Masson
a and
Mathieu
Pédrot
 *a
*a
aUniv Rennes, CNRS, Géosciences Rennes – UMR 6118, F-35000 Rennes, France. E-mail: mathieu.pedrot@univ-rennes.fr
bDepartment of Environmental Engineering, Faculty of Engineering and Research Center for Environmental and Hazardous Substance Management, Khon Kaen University, Khon Kaen 40002, Thailand
cSynchrotron SOLEIL, L'Orme des Merisiers, Saint-Aubin BP48, 91192 Gif-sur-Yvette Cedex, France
First published on 19th July 2023
Abstract
Magnetite, a ubiquitous mineral in natural systems, is of high interest for a variety of applications including environmental remediation, medicine, and catalysis. If the transformation of magnetite to maghemite through the oxidation of Fe2+ has been well documented, mechanisms involving dissolution processes of Fe2+ in aqueous solutions have been overlooked. Here, the effect of dissolved organic ligands (EDTA (ethylenediaminetetraacetic acid), acetic, lactic and citric acids) on Fe2+ solubility and on the stoichiometry (Fe(II)/Fe(III)) of magnetite–maghemite nanoparticles (∼10 nm) was investigated. These ligands were chosen because of their environmental relevance and because they are widely used as coating agents for nanotechnology applications. Results show an insignificant effect of 2 organic ligands (acetate and lactate) on the dissolution of Fe. By contrast, citrate and EDTA enhanced Fe solubility because of the formation of dissolved Fe(II)– and Fe(III)–ligand complexes. Both ligands selectively bound Fe(II) over Fe(III), but EDTA was much more selective than citrate. The combined effects of oxidation and H+- and ligand-promoted dissolution of Fe from magnetite were predicted using a magnetite–maghemite solid solution model, accounting for the formation of dissolved Fe(II)– and Fe(III)–ligand complexes. Therefore, these results show that citrate and EDTA (i) enhance Fe solubility in the presence of magnetite nanoparticles and (ii) modify magnetite stoichiometry, which affects its environmental behavior and its properties for nanotechnology applications.
1. Introduction
Magnetite nanoparticles have been studied extensively for various scopes (medicine, high-technology, catalysis, etc.) owing to intrinsic magnetite properties (magnetic, semi-conductor, redox, etc.).1–4 and their small size leading to a large reactive surface area. Magnetite is ubiquitous in the Earth's crust, soils, and sediments,5–7 and plays an important role as an electron source or sink for microorganisms in the environment.8 Magnetite nanoparticles are also used in various environmental remediation and water treatment processes because of their capacity to degrade or adsorb organic and inorganic contaminants.9–12Variations in the physico-chemical conditions, such as pH and redox potential (Eh) variations, can lead to magnetite (Fe3O4) transformation to maghemite (γ-Fe2O3 or [Fe5/33+□1/3]Fe3+O42−), containing vacant octahedral (Oh) sites (□) instead of Fe2+ according to eqn (1) and (2), respectively:
| Fe3O4 + 2H+ ⇌ Fe2O3 + H2O + Fe2+ | (1) |
| 2Fe3O4 + ½O2 ⇌ 3Fe2O3 | (2) |
| R = [Fe(II)]/[Fe(III)] | (3) |
In soil and groundwater, magnetite nanoparticles might not only be sensitive to pH and Eh but also to the presence of naturally occurring organic acids. For instance, in the rhizosphere, low-molecular-weight organic acids (LMWOAs) play an important role in metal tolerance and plant–microbe interactions operating at the root and soil interface.22 Some of the LMWOAs are microbial metabolites and crucial plant exudates. It is often considered that acetic and lactic acids are more emanating from rhizosphere bacteria.23 The LMWOAs are present in every natural soil but their concentrations may differ considerably. Furthermore, ligands can be used to modify the surface of magnetite nanoparticles for various applications. In particular, citric acid is used in a variety of syntheses24–26 and applications27 including wastewater purification,28 NMR imaging,29–31 and biomolecule extraction.32 Ethylenediaminetetraacetic acid (EDTA) is one of the most used chelating agents for environmental treatment33–35 and medical therapy,36,37 and is usually used to determine the bioavailability of elements for plant due to its chelating properties.
Until now, very little has been known about the effects of organic ligands on Fe release by magnetite and on the magnetite stoichiometry. A recent study demonstrated that H+-promoted dissolution of magnetite is very efficient in modifying magnetite stoichiometry even under moderately acidic conditions.16 It also suggested that ligands like citrate do not protect magnetite, as they are supposed to,38,39 but slightly enhanced Fe2+ release, hence favoring magnetite transformation to maghemite. Such a process could drastically affect magnetite nanoparticle redox reactivity as well as magnetic properties, which could have a detrimental effect on various applications and on the understanding of the magnetite role in biogeochemical reactions in natural systems.
The objective of this study was to determine the effect of selected organic ligands (acetate, lactate, citrate and EDTA) on magnetite stoichiometry. For this purpose, Fe solubility was investigated at various pH and initial magnetite stoichiometry. Spectrophotometric analysis allowed the investigation of both Fe(II) and Fe(III) aqueous behavior in the presence of the ligands. Solid phases were analyzed by soft X-ray absorption spectroscopy (XAS) and X-ray magnetic circular dichroism (XMCD), unique tools to separately probe the electronic properties of Fe as a 3d transition element, thanks to their chemical selectivity and valence state sensitivity.15,16,40–44 The results were used to test and validate a predictive model of magnetite stoichiometry in aqueous solutions, by accounting for the effect of Fe(II) and Fe(III) complexation by dissolved organic ligands. Therefore, the finding of the present study could have implications in various fields (medicine, biology, chemistry, environment, etc.), and the model could be a powerful quantitative tool for many applications.
2. Materials and methods
2.1 Chemical reagents and materials
All chemicals were of analytical grade or better. Iron(III) chloride hexahydrate (FeCl3·6H2O) and iron(II) chloride tetrahydrate (FeCl2·4H2O) were purchased from AnalaR NORMAPUR. Hydrogen peroxide (H2O2), acetate, citrate, lactate, and EDTA were obtained from Sigma-Aldrich. The sample solutions were prepared with ultrapure “Milli-Q” water (specific resistivity is 18.2 MΩ cm−1). All experiments were carried out in an anaerobic chamber (N2-glovebox, JACOMEX, O2(g) < 1 ppm), and all solutions were purged with N2(g) for at least 12 h inside the glovebox before use.2.2 Synthesis and characterization of magnetites with various stoichiometries
Magnetite nanoparticle (average size 10 nm) preparation and characterization were described previously.16 The samples used in the present study come from the same batch. The synthesis procedure is repeated for clarity. A stoichiometric magnetite (R0.5) has been firstly synthesized in a N2-glove box following a well-known protocol, which produces 10 nm sized particles.15,45 Stoichiometric magnetite (R0.5) was prepared by using a room temperature aqueous precipitation method in an anaerobic chamber (JACOMEX). A 0.5 M HCl solution (40 mL) containing 0.5 M FeCl2 and 1 M FeCl3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio) was added dropwise into a 0.5 M NaOH solution (250 mL), while continuously stirring, leading to instantaneous precipitation of magnetite particles. After the synthesis, the samples were washed at pH 8.5 (using NaOH) to avoid the release of Fe2+, as observed in previous work,18,46 and thus, to guarantee the stoichiometry R0.5.
2 molar ratio) was added dropwise into a 0.5 M NaOH solution (250 mL), while continuously stirring, leading to instantaneous precipitation of magnetite particles. After the synthesis, the samples were washed at pH 8.5 (using NaOH) to avoid the release of Fe2+, as observed in previous work,18,46 and thus, to guarantee the stoichiometry R0.5.
Specific amounts of H2O2 were added to R0.5 to produce two sets of partly oxidized non-stoichiometric magnetites (R0.1 and R0.3) as described in our previous work.15 Initial Fe(II)/Fe(III) ratios (Rini) were checked by acid digestion, followed by spectrophotometric determination of dissolved [Fe(II)] and total [Fe] (=[Fe(III)] + [Fe(II)]) using the 1–10 phenanthroline colorimetric method.47 The results were in excellent agreement with values expected from the amount of added H2O2, as in previous studies,14,15,18 with an error of ±0.01 in the determination of Rini.16
2.3 Batch studies
Equilibrium studies were conducted for a total of 6.5 mM Fe (∼0.5 g L−1 of magnetite) and in 15 mL tubes containing 10 mL of solution following the same procedure as our previous studies.15,16 All magnetite suspensions (R0.1, R0.3 and R0.5) were prepared in 10 mM NaCl. Magnetite solubility was investigated in the presence of 1 mM organic ligand (acetic, lactic, citric acids, and EDTA), a relevant environmental concentration, within soil solution at close proximity to plant roots.48 The Fe solubility was studied under different pH conditions (pH 5–11) by using HCl and NaOH for pH adjustment (no buffer was used). Results in the absence of dissolved ligands, denoted as “bare magnetite”, were taken from our previous study.15 The samples of all studies were stirred for 20 days in order to confirm the equilibrium for pH above around 5.15,49 In the absence of organic ligands (bare magnetite nanoparticles), an almost complete release of Fe(II) from the magnetite nanoparticles is expected at pH < 5. In addition, equilibrium is hard to achieve due to strong kinetic inhibition.16 Consequently, the investigated ligands might hardly show an effect on Fe solubility at pH < 5 in the present study. For these reasons, experiments were limited to pH ≥ 5.After 20 days, pH and redox potential were measured using a Pt electrode prior to the sampling of an aliquot for further analysis. Redox potential reading was converted to Eh by correcting for the electrode potential of the reference Ag/AgCl electrode. A commercial redox-buffer (220 mV, Hach) was used for calibration. An equilibrium time of 15 minutes was applied for all Eh measurements.50 The suspension was stirred prior to the Eh measurements. The electrode surface was periodically cleaned by exposing it to 0.1 M HCl for 1 h.51 After recording pH and Eh, an aliquot was filtered using 0.2 μm cellulose acetate filters (Sartorius Minisart). The absence of magnetite nanoparticles in the filtrates was checked by dynamic light scattering (DLS; VASCO Flex) in order to confirm that there is no interference during the measurement of Fe by spectrophotometry. However, DLS analysis showed that citric acid increased the colloidal stability of Fe nanoparticles. Hence, ultrafiltration at 5 kDa (Vivaspin 15RH12, Sartorius) was performed to eliminate Fe nanoparticles in the presence of citric acid. After (ultra)filtration, [Fe(II)]aq and total dissolved [Fe]aq were measured by spectrophotometry using the 1–10 phenanthroline colorimetric method. The error in [Fe]aq determination was assumed to be equal to 5%. It was possible to calculate the effective Fe(II)/Fe(III) ratio (Reff) knowing the total [Fe(II)] and [Fe(III)] in the suspension (i.e. solid + solution) and dissolved [Fe(II)]aq and [Fe(III)]aq after filtration, according to the following eqn (4).
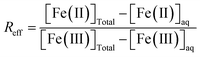 | (4) |
By assuming 5% uncertainty in [Fe(II)]aq and [Fe(III)]aq determination by spectrophotometry, and accounting for the uncertainty in Rini, we determine that the absolute error in Reff was between 0.02 and 0.04.
The concentrations of organic ligands were determined by dissolved organic carbon analysis (Shimadzu TOC-L) after (ultra)filtration in order to quantify ligand adsorption to magnetite.
2.4 XMCD characterization
Soft X-ray absorption spectra (XAS) and X-ray magnetic circular dichroism (XMCD) provide key insights into magnetite stoichiometry.40–44 The XAS and XMCD signals were recorded at the Fe L2,3 edges (700–730 eV) on the DEIMOS beamline at the French synchrotron light source SOLEIL.52 The measurement protocol was detailed in our previous studies15,16,53,54 and is repeated briefly here for clarity. All samples were transported and manipulated strictly under anoxic conditions. Colloidal suspensions of nanoparticles were drop-cast on silicon substrates. The silicon substrates were transferred into a superconducting magnet at the end station, under ultra-high vacuum (UHV-10-10 mbar). All spectra were recorded in Total Electron Yield (TEY) mode at 4.2 K and under an applied magnetic field H (H+ = +6 Tesla and H− = −6 Tesla) parallel to the beam. The beam size was 800 × 800 μm2 and the resolution was 100 meV. Fe L2,3 edge XAS and XMCD with TEY detection probe approximately a 5 nm thick layer at the surface of the particle, and hence both the bulk and surface of 10 nm-sized nanomagnetite. XAS and XMCD spectra were plotted by considering the absorption cross-section measured with left (σL) and right (σR) circularly polarized X-rays. XAS spectra were plotted as the average of σ+ and σ−, while XMCD spectra were plotted as σXMCD= (σ+ − σ−), where σ+ = [σL(H+) + σR(H−)]/2 and σ− = [σL(H−) + σR(H+)]/2. The circularly polarized X-rays are provided by an Apple-II HU-52 helical undulator for XMCD measurements and by sweeping the magnetic field from +6 T to −6 T. XMCD signals were normalized by dividing the raw signal by the XAS edge jump.2.5 Characterization by TEM
Transmission Electron Microscopy (TEM; Jeol JEM 1230 microscope) was used for characterization of magnetite nanoparticles after interaction with the organic molecules, specifically with citrate and EDTA. The aim is to characterize their size and shape and to determine a potential effect of these organic molecules on the morphology of magnetite nanoparticles before a pH change, for Rini 0.5 and 0.1 at pH 8. Briefly, a small aliquot of magnetite suspension was diluted with ultrapure water and sonicated for 20 min. A droplet of the diluted suspension was deposited on a carbon-coated 200-mesh copper grid and dried inside the anaerobic chamber. The samples were transported to the microscope in an N2 atmosphere using a hermetic holder and the samples were analyzed at an acceleration voltage of 200 kV. At pH 8 after 20 days, the particle size (about 10 nm) and shape (spherical) did not evolve much in the presence of citric acid and EDTA (Fig. S1 and Table S1†).2.6 Geochemical modeling
Calculations were made using the geochemical speciation code PHREEQC (version 2)55 and the database “Minteq.v4.dat”. PHREEQC is a computer code designed to perform speciation and saturation-index calculations in water. The Davies equation was used for activity coefficient calculation, being valid up to an ionic strength of 0.1 M. Previous work demonstrated that non-stoichiometric magnetite can be considered as a binary solid-solution between maghemite and magnetite. To use the Guggenheim equation, the Fe9O12–Fe8O12 system is considered. The Gibbs free energies of formation of the solid-solution (ΔGss,nano) of magnetite (mt)–maghemite (mm) nanoparticles is expressed as:| ΔGss,nano = XΔGmt,nano + (1 − X)ΔGmm,nano + ΔGmix | (5) |
| ΔGmix = a0X(1 − X)RT | (6) |
Fe(II) and Fe(III) complexation reactions and constants with all ligands are included in the database “Minteq.v4.dat”. However, a preliminary test with available citrate reactions gave unsatisfactory results. Therefore, citrate protonation constants as well as Fe reactions and constants with citrate were taken from more recent studies (Table S2†).58,59
3. Results and discussion
3.1 Effect of organics on the dissolution of stoichiometric magnetite
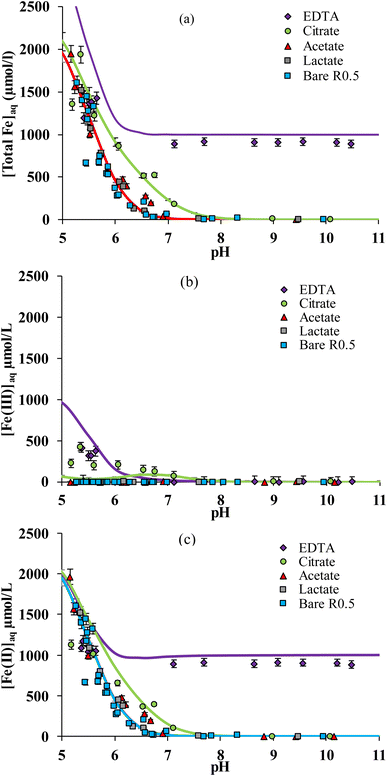
The solubility of iron strongly depends on pH both in the absence and the presence of organic ligands.15,33,37,60Fig. 1a compares total dissolved Fe concentration ([Fe]aq = [Fe(II)]aq + [Fe(III)]aq) versus pH measured in solution in the presence of stoichiometric magnetite (R0.5) and each of the 4 organic ligands. In the absence of organic ligands (bare R0.5), [Fe]aq increases with decreasing pH due to the proton-promoted Fe(II) release. The presence of acetic or lactic acid did not increase [Fe]aq at any pH value (Fig. 1a) with respect to the corresponding experiments in their absence. This is due to the weak binding of Fe to these ligands.61,62 By contrast, [Fe]aq increased in the presence of citric acid at circum-neutral pH (6–8), and in the presence of EDTA, at any pH investigated (5–11). For instance, at pH ≈ 7, [Fe]aq is below the detection limit for magnetite in the absence of organic ligands or in the presence of acetic acid and lactic acid, but it is equal to ca. 200 μM for citric acid and 900 μM for EDTA. Fe release was larger with EDTA than with citrate because the former is a stronger Fe chelating agent.63–66 This can be related to the number of binding groups in the molecule: EDTA may form hexadentate complexes with metal ions as it contains four carboxylic groups and two amines,37,67,68 while citrate includes three carboxylic groups and one –OH group that might also be involved in the complex formation.59,69,70The adsorption of ligands on nanomagnetite was determined and is plotted in Fig. S2.† No significant adsorption of acetate and lactate was determined, in line with their weak binding to iron oxides in general (see e.g. ref. 71) and the very large surface loadings investigated in the present work) (i.e. 50 m2 g−1 reactive surface with 10−3 mol L−1 of ligand). EDTA adsorption was also negligible, although it is known to form strong complexes at mineral surfaces,33,37,60 because of the large [EDTA] investigated and the formation of aqueous Fe–EDTA complexes that limit EDTA adsorption. Indeed, according to the adsorption isotherm data of Blesa et al.67 we estimated that less than 5% adsorption can be expected under the presently investigated conditions. By contrast with other ligands, citrate adsorption was significant and equal to about 10% over the whole pH range investigated. This phenomenon must be taken into account because it is expected to affect Fe solubility in our study.
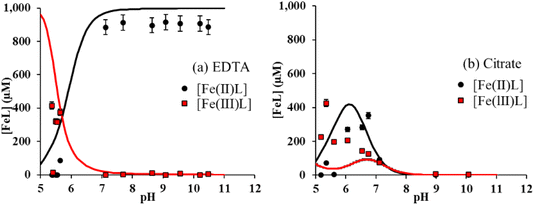
Using spectrophotometric methods, it is possible to differentiate dissolved Fe3+ and Fe2+, and hence, to study their intrinsic solubility versus pH (Fig. 1b and c). In the absence of ligands, [Fe(III)]aq is below the detection limit as shown in Fig. 1b, that is, total Fe solubility is due to the preferential dissolution of Fe(II) over Fe(III) (Fig. 1c).13,16,49 No significant effect of both acetic and lactic acids on dissolved Fe(II) and Fe(III) concentrations is observed (Fig. 1b and c). By contrast, the solubility of both Fe(II) and Fe(III) was enhanced by their complexation to citrate and EDTA. While [Fe(III)]aq was comparable in the presence of both ligands (Fig. 1b), binding of Fe(II) to EDTA was much stronger than to citrate (Fig. 1c). Because Fe(II) solubility is large at pH < 7 in the absence of ligands,16 Fe(II)–ligand complexation was plotted by subtracting [Fe(II)]aq released from the bare magnetite modality. The concentration of Fe(II) bound to EDTA ([Fe(II)–EDTA]) is compared to [Fe(III)–EDTA] in Fig. 2a. Large values of [Fe(III)–EDTA] are measured at pH ∼ 5.5, by contrast with [Fe(II)–EDTA] values that are close to 0. When pH increases, [Fe(III)–EDTA] drops to 0 for pH values above 7, whereas [Fe(II)–EDTA] increases up to ∼900 μM and remains nearly constant up to pH = 11. Hence, EDTA more selectively binds (i) Fe(III) than Fe(II) at pH ∼ 5.5 and (ii) Fe(II) than Fe(III) at pH > 7. The concentration of Fe(II) bound to citrate ([Fe(II)–citrate]) is compared to [Fe(III)–citrate] in Fig. 2b. Like EDTA, citrate more selectively binds Fe(III) than Fe(II) at pH values around 5.5 because [Fe(II)–citrate] ≈ 0, while the [Fe(III)–citrate] value is maximal. [Fe(II)–citrate] increases with pH and reaches a maximum at pH values between 6 and 7, and decreases above. At pH 6–7, citrate binds slightly more selectively Fe(II) than Fe(III) and become non-selective between pH 7 and 8.
3.2 Solid phase analysis of stoichiometric magnetite
The selective binding of Fe(II) and Fe(III) may influence magnetite stoichiometry. The effective stoichiometry (Reff, eqn (4)) of R0.5 is shown in Fig. 3aversus pH in the absence and presence of organic ligands. Eqn (4) depends on the solubilization of Fe(II) and Fe(III), which may be ligand-induced and implicitly depend on pH and ligand concentration. For instance, the values of Reff of bare magnetite decrease with decreasing pH because of the solubilization of Fe(II) while that of Fe(III) is negligible (Fig. 2a).16 Acetic acid and lactic acid had little effect on the solubility of Fe and, hence, on Reff in agreement with results shown in Fig. 2a. For pH < 5.5, where selective binding of Fe(III) occurs, no clear impact of either EDTA or citrate on Reff can be noticed because of the very high [Fe(II)]aq found due to the H+-promoted dissolution process. For 5.5 ≤ pH ≤ 7, citrate only slightly affects Reff due to selective binding of Fe(II) over Fe(III) as discussed above. By contrast, the presence of EDTA dramatically decreases Reff from 0.5 to 0.3, which remains then stable at this value at pH above 5.5.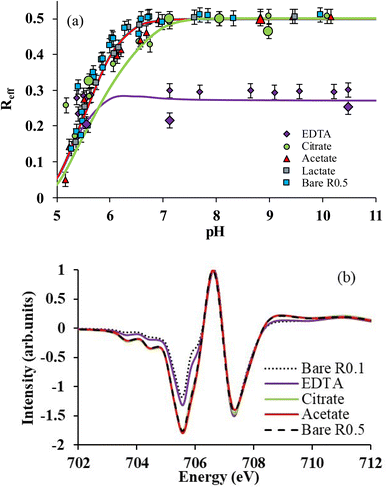 | ||
| Fig. 3 (a) Reff as a function of pH for R0.5 in the presence of 1 mM of each ligand in 10 mM NaCl. Lines correspond to magnetite–maghemite solid solution modelling results. Large symbols correspond to Reff determined by X-ray magnetic circular dichroism (XMCD). (b) Normalized XMCD spectra at the Fe L3-edge of R0.5 in the absence (pH 7) and presence of ligands (citrate and EDTA at pH 7; acetate at pH = 9). Spectrum of bare R0.1 was taken from previous work.15 | ||
To confirm these observations, solid phases of some samples were analyzed by XMCD at the Fe L3-edge. XMCD spectra (Fig. 3b) exhibit three main peaks at the Fe L3-edge. The peak S1 (at 705.5 eV) corresponds to both Fe(II) and Fe(III) on Oh sites; from a quasi-maghemite (R0.1), the evolution of this peak is exclusively due to the Fe(II) on the Oh site.15 The peak S2 (at 706.6 eV) corresponds to the contribution of Fe(III) in tetrahedral sites while the peak S3 (at 707.3 eV) is attributed to Fe(III) in Oh sites. S1 and S3 are coupled antiparallel to S2 due to the ferrimagnetic behavior of the inverse spinel structure of Fe3−δO4 nanoparticles. Because the XMCD spectrum of stoichiometric magnetite with acetate (pH 9) and citrate (ca. pH 7) is similar to that of the bare R0.5 at pH = 7, it can be concluded that acetate and citrate do not significantly affect magnetite stoichiometry, in agreement with wet chemistry results (Fig. 3a). By contrast, the presence of EDTA (pH 7) strongly decreased S1 intensity because of the large binding of Fe(II) in solution. XMCD spectra were recorded at different pH values for citrate (5.5, 7, 8 and 9) and EDTA (5.5, 7 and 10.5). By using a linear combination fit (LCF) procedure involving magnetite and maghemite references from a previous study,15Reff could be determined and plotted in Fig. 3a.15,16 LCF results are in relatively good agreement with wet chemistry data, although slightly smaller for EDTA. The discrepancy between spectrophotometric determination of dissolved Fe(II) and XMCD might suggest the presence of a small number of adsorbed Fe(II) ions that are not detected by XMCD because they are magnetically silent. This might be due to the presence of ternary magnetite–Fe(II)–EDTA (or magnetite–EDTA–Fe(II)) complexes.67
3.3 Effect of organics on magnetite with different stoichiometries
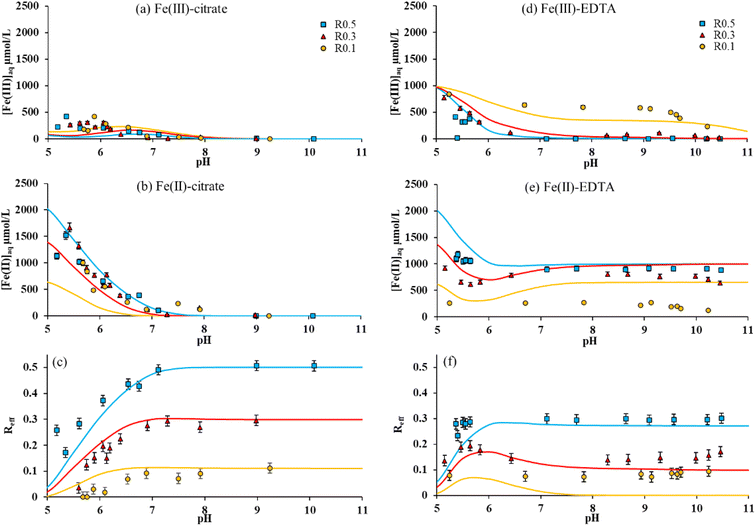
Magnetites with different initial stoichiometries (R0.1 and R0.3) were synthesized by oxidizing R0.5 with H2O2. Then, the impact of initial stoichiometry on dissolved [Fe(III)]aq and dissolved [Fe(II)]aq, and the effective stoichiometry of magnetite in the presence of acetate, citrate and EDTA was studied. The adsorption of the ligands to the magnetite surface was also monitored but the results were found almost independent of the initial stoichiometry (Fig. S2†). Acetate had no significant impact of Fe solubility in any case in the presence of R0.1 and R0.3, as previously observed for R0.5 (Fig. S2†). Fig. 4a and b show respectively dissolved [Fe(III)]aq and [Fe(II)]aq in the presence of citrate. Both concentrations decrease with increasing pH for all stoichiometries. Interestingly, [Fe(III)]aq and [Fe(II)]aq are found weakly dependent to the initial magnetite stoichiometry in the presence of citrate, which affected Reff values similarly to the experiments with R0.5 (Fig. 4c). By contrast, in the presence of EDTA, [Fe(III)]aq is found to increase when magnetite initial stoichiometry decreases (Fig. 4d), while [Fe(II)]aq decreases (Fig. 4e). This can be explained by the competitive effects between Fe(II) and Fe(III) for EDTA binding. Fe(II)–EDTA complexes are favored in the presence of Fe(II)-rich nanoparticles (i.e. R0.5), whereas, in the presence of a limited amount of Fe(II) (i.e. R0.1), Fe(III)–EDTA complexation becomes important. Because variations of both [Fe(III)]aq and [Fe(II)]aq with pH remain relatively small at pH > 6, the corresponding Reff values remain constant with pH for each magnetite (Fig. 4f) according to eqn (4). Indeed, EDTA is a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 chelating molecule, so the amount of solubilized Fe(II) is stable as soon as all EDTA molecules are bound in EDTA–Fe complexes. Therefore, Reff values remain constant for Rini = 0.5 and 0.3 at pH > 7. This observation also applies to R0.1, but for pH ≥ 5, due to the limited amount of Fe(II) leading to the formation of Fe(III)–EDTA complexes. Therefore, the presence of EDTA strongly decreases the effective stoichiometry of magnetites. This decrease depends on the amount of Fe(II) initially present within the magnetite.
1 chelating molecule, so the amount of solubilized Fe(II) is stable as soon as all EDTA molecules are bound in EDTA–Fe complexes. Therefore, Reff values remain constant for Rini = 0.5 and 0.3 at pH > 7. This observation also applies to R0.1, but for pH ≥ 5, due to the limited amount of Fe(II) leading to the formation of Fe(III)–EDTA complexes. Therefore, the presence of EDTA strongly decreases the effective stoichiometry of magnetites. This decrease depends on the amount of Fe(II) initially present within the magnetite.
3.4 Modeling
Chemical thermodynamic modeling of the magnetite–maghemite solid solution series16 allowed the total solubility of Fe, dissolved [Fe(III)]aq, [Fe(II)]aq, and Reff in the presence of the four presently investigated ligands. Modeling results are depicted in each figure of this manuscript, when relevant (Fig. 1–4). As expected, the model predicts no significant effect of acetate and lactate on Fe behavior (Fig. 1, 2a and S3†).As an attempt to account for citrate adsorption to magnetite, we used a surface complexation model, previously developed for the adsorption of another organic molecule (nalidixic acid, NA).18,72 We applied the same formalism and equations by assuming that citrate binds to two surface hydroxyl groups by involving two of its carboxylates, while the third carboxylic groups and the alcohol groups are, respectively, deprotonated and protonated:
| 2 ≡FeOH + 2H+ + CitrateH3− ⇌ (≡Fe)2CitrateH− + 2H2O | (7) |
Note that a single reaction is only considered for the sake of simplicity: the formation of other surface species cannot be excluded. Because of the very high surface loading, the available site density was raised from 1.5 to 3 nm−2, which might reflect the involvement of sites that are not necessary at lower loadings investigated for NA. The present work did not provide enough data to model an effect of magnetite stoichiometry on citrate adsorption (Fig. S2b†). Therefore, a single log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K value for eqn (7) was used. The value (27.6) was similar to that of NA on stoichiometric magnetite (25.5). Although (i) [Fe(III)]aq is underestimated at pH < 6.5 for all Rini (Fig. 1b, 2b and 4a) and (ii) [Fe(II)]aq is underestimated for Rini = 0.1 (Fig. 4b), the effect of citrate on Fe(II) and Fe(III) solubility and magnetite stoichiometry (Fig. 3a and 4c) is relatively well captured.
K value for eqn (7) was used. The value (27.6) was similar to that of NA on stoichiometric magnetite (25.5). Although (i) [Fe(III)]aq is underestimated at pH < 6.5 for all Rini (Fig. 1b, 2b and 4a) and (ii) [Fe(II)]aq is underestimated for Rini = 0.1 (Fig. 4b), the effect of citrate on Fe(II) and Fe(III) solubility and magnetite stoichiometry (Fig. 3a and 4c) is relatively well captured.
The effect of EDTA is also relatively well predicted. Fe(II)–EDTA complexation is slightly overestimated (Fig. 1a, c, 2a and 4e). However, if the resulting Reff is underestimated, the model Reff values fall between the wet chemistry and XMCD data (Fig. 3a). The largest discrepancies are observed for Rini = 0.1, where the model predicts a complete release of Fe(II). This has two consequences: (i) the Fe(II) competitive effect on Fe(III)–EDTA is too strong so Fe(III) solubility is underestimated and (ii) Reff drops to 0 for pH > 7.5. As previously shown,16 the complete release of Fe(II) might be kinetically limited and could take several years to reach a steady-state, especially for Reff < 0.1, which would explain the discrepancies with the model.
The prediction of the redox potential of the magnetite suspensions was also made in the presence of ligands and compared to the measured data. As previously suggested for bare magnetite,16 at pH < 7, experimental determination of the Eh values with a Pt electrode might be achieved thanks to the large amount of dissolved Fe2+ and the small size of the nanoparticles that could react with the electrode.73 At pH > 7, Fe2+ is retained in the solid phase, making experimental Eh determination less reliable and a large scatter is observed (Fig. S4†).16,74 Accordingly, in the presence of all ligands, experimental and model Eh values agree because magnetite stoichiometry and Fe(II) dissolution are primarily controlled by the pH. For pH > 7, experimental data for citrate and acetate might not be reliable. Under these conditions, the model predicts no significant difference between Eh values in the presence or absence of these ligands. By contrast, in the presence of EDTA, [Fe(II)]aq is large. However, both experimental and calculated Eh values were found larger for bare magnetite, because EDTA stabilizes Fe(II)aq, notably at pH > 7 (Fig. 2a), and thus, creates less reducing solution conditions.
3.5 Conclusions
Nanomagnetite particles with different stoichiometries may be present in environmental systems and their compositions are dependent on pH and redox conditions, and the presence of organic ligands in soils. In addition, magnetite coating by organic molecules is widely used to modify the surface properties and the stability of magnetite suspensions in various applied fields in chemistry or medicine. This study investigated the effects of several small organic ligands, which can be found in soils and soil solutions such as acetate, lactate, and citrate, and the effect of EDTA which belongs to a group of anthropogenic aminocarboxylate chelating agents widely used in environmental remediation processes or in agriculture. The results showed an insignificant effect of 2 organic ligands (acetic and lactic acid) on the solubility of magnetite. By contrast, citrate and EDTA can significantly modify magnetite solubility compared to experiments without organic molecules. Furthermore, citrate and EDTA affect magnetite effective stoichiometry. By accounting for the complexation of Fe(II) and Fe(III) by citric acid and EDTA, Fe solubility as well as magnetite stoichiometry can be well predicted. The results show that Fe release from magnetite is not only dependent on the pH conditions but ligand-controlled dissolution processes need to be taken into account when evaluating the chemical stability of magnetite (e.g. in natural systems such as redox transition zones). Finally, these results show that the use of organic ligands for some nanotechnological applications of magnetite (e.g. citrate in order to ameliorate the colloidal stability of stoichiometric magnetite) should be performed with attention because processes like Fe release could significantly modify the expected properties of the magnetite nanoparticles. Hence, these results call for the reconsideration of how to assess the properties of magnetite nanoparticles before nanotechnological applications in solution under the influence of a variety of conditions.Author contributions
Phoomipat Jungcharoen: writing – original draft, data curation, investigation, and visualization. Rémi Marsac: data curation, investigation, writing – review & editing, resources, supervision, project administration, and funding acquisition. Fadi Choueikani: investigation, data curation, and writing – review & editing. Delphine Masson: data curation, investigation, and writing – review & editing. Mathieu Pédrot: data curation, investigation, writing – review & editing, resources, supervision, project administration, and funding acquisition.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This work was supported by Campus France, Khon Kaen University (Thailand), the C-FACTOR project funded by ANR (project number ANR-18-CE01-0008), the SURFNANO project funded by the CNRS-INSU EC2CO program and the SynFeSol project funded by the Brittany Region (AAP TRANSFERT 2019). Through the support of the GeOHeLiS analytical platform of Rennes University, this publication is also supported by the European Union through the European Regional Development Fund (FEDER), the French Ministry of Higher Education and Research, and the French Region of Brittany and Rennes Metropole. The authors acknowledge the SOLEIL synchrotron for beamtime allocation at the DEIMOS beamline (proposal 20200250). The authors are grateful to V. Dorcet and L. Rault for the assistance in TEM experiments performed on the THEMIS platform (ScanMAT, UMS 2011 University of Rennes 1-CNRS; CPER-FEDER 2007–2014).References
- M. Usman, J. M. Byrne, A. Chaudhary, S. Orsetti, K. Hanna, C. Ruby, A. Kappler and S. B. Haderlein, Magnetite and Green Rust: Synthesis, Properties, and Environmental Applications of Mixed-Valent Iron Minerals, Chem. Rev., 2018, 118(7), 3251–3304, DOI:10.1021/acs.chemrev.7b00224.
- C. J. Goss, Saturation Magnetisation, Coercivity and Lattice Parameter Changes in the System Fe3O4-ΓFe2O3, and Their Relationship to Structure, Phys. Chem. Miner., 1988, 16, 164–171, DOI:10.1007/BF00203200.
- D. M. Sherman, Molecular Orbital (SCF-Xα-SW) Theory of Metal–Metal Charge Transfer Processes in Minerals, Phys. Chem. Miner., 1987, 14(4), 355–363, DOI:10.1007/BF00309810.
- F. Walz, TOPICAL REVIEW: The Verwey Transition – a Topical Review, J. Phys.: Condens. Matter, 2002, 14, R285–R340, DOI:10.1088/0953-8984/14/12/203.
- R. M. Cornell and U. Schwertmann, The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses, 2nd, Completely Revised and Extended Edition, Wiley, 2003 Search PubMed.
- I. A. M. Ahmed and B. A. Maher, Identification and Paleoclimatic Significance of Magnetite Nanoparticles in Soils, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(8), 1736–1741, DOI:10.1073/pnas.1719186115.
- P. C. Lippert, Big Discovery for Biogenic Magnetite, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(46), 17595–17596, DOI:10.1073/pnas.0809839105.
- J. M. Byrne, N. Klueglein, C. Pearce, K. M. Rosso, E. Appel and A. Kappler, Redox Cycling of Fe(II) and Fe(III) in Magnetite by Fe-Metabolizing Bacteria, Science, 2015, 347(6229), 1473–1476, DOI:10.1126/science.aaa4834.
- D. L. Huber, Synthesis, Properties, and Applications of Iron Nanoparticles, Small, 2005, 1(5), 482–501, DOI:10.1002/smll.200500006.
- C. A. Gorski and M. M. Scherer, Influence of Magnetite Stoichiometry on Fe II Uptake and Nitrobenzene Reduction, Environ. Sci. Technol., 2009, 43(10), 3675–3680, DOI:10.1021/es803613a.
- D. M. Singer, S. M. Chatman, E. S. Ilton, K. M. Rosso, J. F. Banfield and G. A. Waychunas, U(VI) Sorption and Reduction Kinetics on the Magnetite (111) Surface, Environ. Sci. Technol., 2012, 46(7), 3821–3830, DOI:10.1021/es203878c.
- J. Klausen, S. P. Troeber, S. B. Haderlein and R. P. Schwarzenbach, Reduction of Substituted Nitrobenzenes by Fe(II) in Aqueous Mineral Suspensions, Environ. Sci. Technol., 1995, 29(9), 2396–2404, DOI:10.1021/es00009a036.
- J.-P. Jolivet and E. Tronc, Interfacial Electron Transfer in Colloidal Spinel Iron Oxide. Conversion of Fe3O4-ΓFe2O3 in Aqueous Medium, J. Colloid Interface Sci., 1988, 125(2), 688–701, DOI:10.1016/0021-9797(88)90036-7.
- C. A. Gorski and M. M. Scherer, Determination of Nanoparticulate Magnetite Stoichiometry by Mossbauer Spectroscopy, Acidic Dissolution, and Powder X-Ray Diffraction: A Critical Review, Am. Mineral., 2010, 95(7), 1017–1026, DOI:10.2138/am.2010.3435.
- P. Jungcharoen, M. Pédrot, F. Choueikani, M. Pasturel, K. Hanna, F. Heberling, M. Tesfa and R. Marsac, Probing the Effects of Redox Conditions and Dissolved Fe2+ on Nanomagnetite Stoichiometry by Wet Chemistry, XRD, XAS and XMCD, Environ. Sci.: Nano, 2021, 8(7), 2098–2107, 10.1039/D1EN00219H.
- P. Jungcharoen, M. Pédrot, F. Heberling, K. Hanna, F. Choueikani, C. Catrouillet, A. Dia and R. Marsac, Prediction of Nanomagnetite Stoichiometry (Fe(II)/Fe(III)) under Contrasting PH and Redox Conditions, Environ. Sci.: Nano, 2022, 9(7), 2363–2371, 10.1039/D2EN00112H.
- C. A. Gorski, J. T. Nurmi, P. G. Tratnyek, T. B. Hofstetter and M. M. Scherer, Redox Behavior of Magnetite: Implications for Contaminant Reduction, Environ. Sci. Technol., 2010, 44(1), 55–60, DOI:10.1021/es9016848.
- W. Cheng, R. Marsac and K. Hanna, Influence of Magnetite Stoichiometry on the Binding of Emerging Organic Contaminants, Environ. Sci. Technol., 2018, 52(2), 467–473, DOI:10.1021/acs.est.7b04849.
- E. Tombácz, I. Y. Tóth, D. Nesztor, E. Illés, A. Hajdú, M. Szekeres and L. Vékás, Adsorption of Organic Acids on Magnetite Nanoparticles, PH-Dependent Colloidal Stability and Salt Tolerance, Colloids Surf., A, 2013, 435, 91–96, DOI:10.1016/j.colsurfa.2013.01.023.
- H. Catalette, J. Dumonceau and P. Ollar, Sorption of Cesium, Barium and Europium on Magnetite, J. Contam. Hydrol., 1998, 35(1–3), 151–159, DOI:10.1016/S0169-7722(98)00123-5.
- L. Giraldo, A. Erto and J. C. Moreno-Piraján, Magnetite Nanoparticles for Removal of Heavy Metals from Aqueous Solutions: Synthesis and Characterization, Adsorption, 2013, 19(2–4), 465–474, DOI:10.1007/s10450-012-9468-1.
- J. López-Bucio, M. F. Nieto-Jacobo, V. Ramírez-Rodríguez and L. Herrera-Estrella, Organic Acid Metabolism in Plants: From Adaptive Physiology to Transgenic Varieties for Cultivation in Extreme Soils, Plant Sci., 2000, 160(1), 1–13, DOI:10.1016/S0168-9452(00)00347-2.
- D. L. Jones, Organic Acids in the Rhizosphere – a Critical Review, Plant Soil, 1998, 205(1), 25–44 CrossRef CAS.
- C. Hui, C. Shen, T. Yang, L. Bao, J. Tian, H. Ding, C. Li and H.-J. Gao, Large-Scale Fe 3 O 4 Nanoparticles Soluble in Water Synthesized by a Facile Method, J. Phys. Chem. C, 2008, 112(30), 11336–11339, DOI:10.1021/jp801632p.
- K. M. Ø. Jensen, H. L. Andersen, C. Tyrsted, E. D. Bøjesen, A.-C. Dippel, N. Lock, S. J. L. Billinge, B. B. Iversen and M. Christensen, Mechanisms for Iron Oxide Formation under Hydrothermal Conditions: An in Situ Total Scattering Study, ACS Nano, 2014, 8(10), 10704–10714, DOI:10.1021/nn5044096.
- J. Liu, Z. Sun, Y. Deng, Y. Zou, C. Li, X. Guo, L. Xiong, Y. Gao, F. Li and D. Zhao, Highly Water-Dispersible Biocompatible Magnetite Particles with Low Cytotoxicity Stabilized by Citrate Groups, Angew. Chem., Int. Ed., 2009, 48(32), 5875–5879, DOI:10.1002/anie.200901566.
- S. Laurent, D. Forge, M. Port, A. Roch, C. Robic, L. Vander Elst and R. N. Muller, Magnetic Iron Oxide Nanoparticles: Synthesis, Stabilization, Vectorization, Physicochemical Characterizations, and Biological Applications, Chem. Rev., 2008, 108(6), 2064–2110, DOI:10.1021/cr068445e.
- H. Baseri and S. Tizro, Treatment of Nickel Ions from Contaminated Water by Magnetite Based Nanocomposite Adsorbents: Effects of Thermodynamic and Kinetic Parameters and Modeling with Langmuir and Freundlich Isotherms, Process Saf. Environ. Prot., 2017, 109, 465–477, DOI:10.1016/j.psep.2017.04.022.
- H.-M. Fan, M. Olivo, B. Shuter, J.-B. Yi, R. Bhuvaneswari, H.-R. Tan, G.-C. Xing, C.-T. Ng, L. Liu, S. S. Lucky, B.-H. Bay and J. Ding, Quantum Dot Capped Magnetite Nanorings as High Performance Nanoprobe for Multiphoton Fluorescence and Magnetic Resonance Imaging, J. Am. Chem. Soc., 2010, 132(42), 14803–14811, DOI:10.1021/ja103738t.
- N. Lee, D. Yoo, D. Ling, M. H. Cho, T. Hyeon and J. Cheon, Iron Oxide Based Nanoparticles for Multimodal Imaging and Magnetoresponsive Therapy, Chem. Rev., 2015, 115(19), 10637–10689, DOI:10.1021/acs.chemrev.5b00112.
- E. Mazarío, J. Sánchez-Marcos, N. Menéndez, M. Cañete, A. Mayoral, S. Rivera-Fernández, J. M. de la Fuente and P. Herrasti, High Specific Absorption Rate and Transverse Relaxivity Effects in Manganese Ferrite Nanoparticles Obtained by an Electrochemical Route, J. Phys. Chem. C, 2015, 119(12), 6828–6834, DOI:10.1021/jp510937r.
- S. Nigam, K. C. Barick and D. Bahadur, Development of Citrate-Stabilized Fe3O4 Nanoparticles: Conjugation and Release of Doxorubicin for Therapeutic Applications, J. Magn. Magn. Mater., 2011, 323(2), 237–243, DOI:10.1016/j.jmmm.2010.09.009.
- S. J. Keny, A. G. Kumbhar, G. Venkateswaran and K. Kishore, Radiation Effects on the Dissolution Kinetics of Magnetite and Hematite in EDTA- and NTA-Based Dilute Chemical Decontamination Formulations, Radiat. Phys. Chem., 2005, 72(4), 475–482, DOI:10.1016/j.radphyschem.2003.12.055.
- M. Wang, N. Wang, H. Tang, M. Cao, Y. She and L. Zhu, Surface Modification of Nano-Fe 3 O 4 with EDTA and Its Use in H 2 O 2 Activation for Removing Organic Pollutants, Catal. Sci. Technol., 2012, 2(1), 187–194, 10.1039/C1CY00260K.
- M. Xu, Y. Zhang, Z. Zhang, Y. Shen, M. Zhao and G. Pan, Study on the Adsorption of Ca2+, Cd2+ and Pb2+ by Magnetic Fe3O4 Yeast Treated with EDTA Dianhydride, Chem. Eng. J., 2011, 168(2), 737–745, DOI:10.1016/j.cej.2011.01.069.
- W. M. Daoush, Co-Precipitation and Magnetic Properties of Magnetite Nanoparticles for Potential Biomedical Applications, J. Nanomed. Res., 2017, 5(3), 00118, DOI:10.15406/jnmr.2017.05.00118.
- Y. Yi, Y. Zhang, Y. Wang, L. Shen, M. Jia, Y. Huang, Z. Hou and G. Zhuang, Ethylenediaminetetraacetic Acid as Capping Ligands for Highly Water-Dispersible Iron Oxide Particles, Nanoscale Res. Lett., 2014, 9(1), 27, DOI:10.1186/1556-276X-9-27.
- Z. R. Stephen, F. M. Kievit and M. Zhang, Magnetite Nanoparticles for Medical MR Imaging, Mater. Today, 2011, 14(7), 330–338, DOI:10.1016/S1369-7021(11)70163-8.
- J. Liu, Z. Sun, Y. Deng, Y. Zou, C. Li, X. Guo, L. Xiong, Y. Gao, F. Li and D. Zhao, Highly Water-Dispersible Biocompatible Magnetite Particles with Low Cytotoxicity Stabilized by Citrate Groups, Angew. Chem., Int. Ed., 2009, 48(32), 5875–5879, DOI:10.1002/anie.200901566.
- E. Pellegrin, M. Hagelstein, S. Doyle, H. O. Moser, J. Fuchs, D. Vollath, S. Schuppler, M. A. James, S. S. Saxena, L. Niesen, O. Rogojanu, G. A. Sawatzky, C. Ferrero, M. Borowski, O. Tjernberg and N. B. Brookes, Characterization of Nanocrystalline G-Fe2O3 with Synchrotron, Radiat. Tech., 1999, 215, 797–801 CAS.
- C. Carvallo, P. Sainctavit, M.-A. Arrio, N. Menguy, Y. Wang, G. Ona-Nguema and S. Brice-Profeta, Biogenic vs. Abiogenic Magnetite Nanoparticles: A XMCD Study, Am. Mineral., 2008, 93(5–6), 880–885, DOI:10.2138/am.2008.2713.
- V. S. Coker, C. I. Pearce, R. A. D. Pattrick, G. van der Laan, N. D. Telling, J. M. Charnock, E. Arenholz and J. R. Lloyd, Probing the Site Occupancies of Co-, Ni-, and Mn-Substituted Biogenic Magnetite Using XAS and XMCD, Am. Mineral., 2008, 93(7), 1119–1132, DOI:10.2138/am.2008.2681.
- F. Jiménez-Villacorta, C. Prieto, Y. Huttel, N. D. Telling and G. van der Laan, X-Ray Magnetic Circular Dichroism Study of the Blocking Process in Nanostructured Iron-Iron Oxide Core-Shell Systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(17), 172404, DOI:10.1103/PhysRevB.84.172404.
- H. Peng, C. I. Pearce, W. Huang, Z. Zhu, A. T. N'Diaye, K. M. Rosso and J. Liu, Reversible Fe(II) Uptake/Release by Magnetite Nanoparticles, Environ. Sci.: Nano, 2018, 5(7), 1545–1555, 10.1039/C8EN00328A.
- E. Demangeat, M. Pédrot, A. Dia, M. Bouhnik-le-Coz, F. Grasset, K. Hanna, M. Kamagate and F. Cabello-Hurtado, Colloidal and Chemical Stabilities of Iron Oxide Nanoparticles in Aqueous Solutions: The Interplay of Structural, Chemical and Environmental Drivers, Environ. Sci.: Nano, 2018, 5(4), 992–1001, 10.1039/C7EN01159H.
- R. Marsac, M. Pasturel and K. Hanna, Reduction Kinetics of Nitroaromatic Compounds by Titanium-Substituted Magnetite, J. Phys. Chem. C, 2017, 121(21), 11399–11406, DOI:10.1021/acs.jpcc.7b01920.
- W. B. Fortune and M. G. Mellon, Determination of Iron with O-Phenanthroline: A Spectrophotometric Study, Ind. Eng. Chem., Anal. Ed., 1938, 10(2), 60–64, DOI:10.1021/ac50118a004.
- M.-H. Feng, X.-Q. Shan, S.-Z. Zhang and B. Wen, Comparison of a Rhizosphere-Based Method with Other One-Step Extraction Methods for Assessing the Bioavailability of Soil Metals to Wheat, Chemosphere, 2005, 59(7), 939–949, DOI:10.1016/j.chemosphere.2004.11.056.
- Z.-X. Sun, F.-W. Su, W. Forsling and P.-O. Samskog, Surface Characteristics of Magnetite in Aqueous Suspension, J. Colloid Interface Sci., 1998, 197(1), 151–159, DOI:10.1006/jcis.1997.5239.
- R. Marsac, N. L. Banik, J. Lützenkirchen, C. M. Marquardt, K. Dardenne, D. Schild, J. Rothe, A. Diascorn, T. Kupcik, T. Schäfer and H. Geckeis, Neptunium Redox Speciation at the Illite Surface, Geochim. Cosmochim. Acta, 2015, 152, 39–51, DOI:10.1016/j.gca.2014.12.021.
- P. R. Teasdale, A. I. Minnett, K. Dixon, T. W. Lewis and G. E. Batley, Practical Improvements for Redox Potential (Eh) Measurements and the Application of a Multiple-Electrode Redox Probe (MERP) for Characterising Sediment in situ, Anal. Chim. Acta, 1998, 367, 201–213, DOI:10.1016/S0003-2670(98)00171-8.
- P. Ohresser, E. Otero, F. Choueikani, K. Chen, S. Stanescu, F. Deschamps, T. Moreno, F. Polack, B. Lagarde, J.-P. Daguerre, F. Marteau, F. Scheurer, L. Joly, J.-P. Kappler, B. Muller, O. Bunau and Ph. Sainctavit, DEIMOS: A Beamline Dedicated to Dichroism Measurements in the 350–2500 EV Energy Range, Rev. Sci. Instrum., 2014, 85(1), 013106, DOI:10.1063/1.4861191.
- N. Daffé, F. Choueikani, S. Neveu, M.-A. Arrio, A. Juhin, P. Ohresser, V. Dupuis and P. Sainctavit, Magnetic Anisotropies and Cationic Distribution in CoFe2O4 Nanoparticles Prepared by Co-Precipitation Route: Influence of Particle Size and Stoichiometry, J. Magn. Magn. Mater., 2018, 460, 243–252, DOI:10.1016/j.jmmm.2018.03.041.
- K. Sartori, G. Cotin, C. Bouillet, V. Halté, S. Bégin-Colin, F. Choueikani and B. P. Pichon, Strong Interfacial Coupling through Exchange Interactions in Soft/Hard Core–Shell Nanoparticles as a Function of Cationic Distribution, Nanoscale, 2019, 11(27), 12946–12958, 10.1039/C9NR02323B.
- D. L. Parkhurst and C. A. J. Appelo, User's Guide to PHREEQC (Version 2): A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; Water-Resources Investigations Report; USGS Numbered Series 99–4259; Water-Resources Investigation Report 99–4259, USGS, Denver, Colorado, 1999, p. 312 Search PubMed.
- E. A. Guggenheim, The Theoretical Basis of Raoult's Law, Trans. Faraday Soc., 1937, 33, 151, 10.1039/tf9373300151.
- P. Glynn, Solid-Solution Solubilities and Thermodynamics: Sulfates, Carbonates and Halides, Rev. Mineral. Geochem., 2000, 40(1), 481–511, DOI:10.2138/rmg.2000.40.10.
- A. M. N. Silva, X. Kong and R. C. Hider, Determination of the PKa Value of the Hydroxyl Group in the α-Hydroxycarboxylates Citrate, Malate and Lactate by 13C NMR: Implications for Metal Coordination in Biological Systems, BioMetals, 2009, 22(5), 771–778, DOI:10.1007/s10534-009-9224-5.
- P. Vukosav, M. Mlakar and V. Tomišić, Revision of Iron(III)–Citrate Speciation in Aqueous Solution. Voltammetric and Spectrophotometric Studies, Anal. Chim. Acta, 2012, 745, 85–91, DOI:10.1016/j.aca.2012.07.036.
- E. B. Borghi, A. E. Regazzoni, A. J. G. Maroto and M. A. Blesa, Reductive Dissolution of Magnetite by Solutions Containing EDTA and FeII, J. Colloid Interface Sci., 1989, 130(2), 299–310, DOI:10.1016/0021-9797(89)90109-4.
- M. Gotić and S. Musić, Synthesis of Nanocrystalline Iron Oxide Particles in the Iron(III) Acetate/Alcohol/Acetic Acid System, Eur. J. Inorg. Chem., 2008, 2008(6), 966–973, DOI:10.1002/ejic.200700986.
- H. Zhao, K. Saatchi and U. O. Häfeli, Preparation of Biodegradable Magnetic Microspheres with Poly(Lactic Acid)-Coated Magnetite, J. Magn. Magn. Mater., 2009, 321(10), 1356–1363, DOI:10.1016/j.jmmm.2009.02.038.
- B. A. Holmén and W. H. Casey, Hydroxamate Ligands, Surface Chemistry, and the Mechanism of Ligand-Promoted Dissolution of Goethite [α-FeOOH(s)], Geochim. Cosmochim. Acta, 1996, 60(22), 4403–4416, DOI:10.1016/S0016-7037(96)00278-5.
- B. E. Kalinowski, L. J. Liermann, S. Givens and S. L. Brantley, Rates of Bacteria-Promoted Solubilization of Fe from Minerals: A Review of Problems and Approaches, Chem. Geol., 2000, 169(3), 357–370, DOI:10.1016/S0009-2541(00)00214-X.
- K. A. Mies, J. I. Wirgau and A. L. Crumbliss, Ternary Complex Formation Facilitates a Redox Mechanism for Iron Release from a Siderophore, BioMetals, 2006, 19(2), 115–126, DOI:10.1007/s10534-005-4342-1.
- B. W. Alderman, A. E. Ratliff and J. I. Wirgau, A Mechanistic Study of Ferrioxamine B Reduction by the Biological Reducing Agent Ascorbate in the Presence of an Iron(II) Chelator, Inorg. Chim. Acta, 2009, 362(6), 1787–1792, DOI:10.1016/j.ica.2008.08.024.
- M. A. Blesa, E. B. Borghi, A. J. G. Maroto and A. E. Regazzoni, Adsorption of EDTA and Iron-EDTA Complexes on Magnetite and the Mechanism of Dissolution of Magnetite by EDTA, J. Colloid Interface Sci., 1984, 98(2), 11 CrossRef.
- M. Shailaja and S. V. Narasimhan, Dissolution Kinetics of Nickel Ferrite in Chelating and Reducing Agents, J. Nucl. Sci. Technol., 1991, 28(8), 748–756, DOI:10.1080/18811248.1991.9731423.
- R. E. Hamm, C. M. Shull and D. M. Grant, Citrate Complexes with Iron(II) and Iron(III) 1, J. Am. Chem. Soc., 1954, 76(8), 2111–2114, DOI:10.1021/ja01637a021.
- M. Răcuciu, D. E. Creangă and A. Airinei, Citric-Acid-Coated Magnetite Nanoparticles for Biological Applications, Eur. Phys. J. E, 2006, 21(2), 117–121, DOI:10.1140/epje/i2006-10051-y.
- K. Norén and P. Persson, Adsorption of Monocarboxylates at the Water/Goethite Interface: The Importance of Hydrogen Bonding, Geochim. Cosmochim. Acta, 2007, 71(23), 5717–5730, DOI:10.1016/j.gca.2007.04.037.
- J. Deng, S. Bae, S. Yoon, M. Pasturel, R. Marsac and K. Hanna, Adsorption Capacity of the Corrosion Products of Nanoscale Zerovalent Iron for Emerging Contaminants, Environ. Sci.: Nano, 2020, 7(12), 3773–3782, 10.1039/D0EN00886A.
- E. Silvester, L. Charlet, C. Tournassat, A. Géhin, J.-M. Grenèche and E. Liger, Redox Potential Measurements and Mössbauer Spectrometry of FeII Adsorbed onto FeIII (Oxyhydr)Oxides, Geochim. Cosmochim. Acta, 2005, 69(20), 4801–4815, DOI:10.1016/j.gca.2005.06.013.
- D. K. Nordstrom and K. M. Campbell, 7.2 – Modeling Low-Temperature Geochemical Processes, in Treatise on Geochemistry, ed. H. D. Holland and K. K. Turekian, Elsevier, Oxford, 2nd edn, 2014, pp. 27–68, DOI:10.1016/B978-0-08-095975-7.00502-7.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00240c |
| This journal is © The Royal Society of Chemistry 2023 |