Open Access Article
Open Access ArticleSecond-order Jahn–Teller effect induced high-temperature ferroelectricity in two-dimensional NbO2X (X = I, Br)†
Huasheng
Sun
,
Kaiming
Deng
,
Erjun
Kan
 * and
Yongping
Du
* and
Yongping
Du
 *
*
MIIT Key Laboratory of Semiconductor Microstructure and Quantum Sensing, and Department of Applied Physics, Nanjing University of Science and Technology, Nanjing 210094, People's Republic of China. E-mail: njustdyp@njust.edu.cn; ekan@njust.edu.cn
First published on 28th April 2023
Abstract
Based on the first-principles calculations, we investigated the ferroelectric properties of two-dimensional (2D) materials NbO2X (X = I, Br). Our cleavage energy analysis shows that exfoliating one NbO2I monolayer from its existing bulk counterpart is feasible. The phonon spectrum and molecular dynamics simulations confirm the dynamic and thermal stability of the monolayer structures for both NbO2I and NbO2Br. Total energy calculations show that the ferroelectric phase is the ground state for both materials, with the calculated in-plane ferroelectric polarizations being 384.5 pC m−1 and 375.2 pC m−1 for monolayers NbO2I and NbO2Br, respectively. Moreover, the intrinsic Curie temperature TC of monolayer NbO2I (NbO2Br) is as high as 1700 K (1500 K) from Monte Carlo simulation. Furthermore, with the orbital selective external potential method, the origin of ferroelectricity in NbO2X is revealed as the second-order Jahn–Teller effect. Our findings suggest that monolayers NbO2I and NbO2Br are promising candidate materials for practical ferroelectric applications.
Introduction
Ferroelectric (FE) materials, which exhibit spontaneous polarization that can be switched by an external electric field, have attracted tremendous research interest over the past decades due to their wide applications in capacitors, sensors, and non-volatile memories.1–4 In the literature, many efforts have been made to develop perovskite-type oxides, such as BaTiO3, PbTiO3, PbZr1-xTixO3, and La1/3NbO3 in which the cations have an electron configuration of d0 (Ti4+, Zr4+, Nb5+).5–8 Moreover, the spontaneous polarization of these compounds is usually induced by off-centering of cations which originates from the second-order Jahn–Teller (SOJT) effect.9,10 SOJT-active cations have been shown to induce structural distortion, which would break the inversion symmetry, by anisotropic covalent bonding with ligands. Interestingly, the Curie temperature Tc of these compounds is far above room temperature (i.e., the Tc of BaTiO3, PbTiO3, PbZr1−xTixO3, and La1/3NbO3 is 393, 763, 659, and 473 K respectively).11–14 This inspires us to search for high-temperature ferroelectric materials with SOJT-activated cations.On the other hand, the urgent requirement for the miniaturization of electronic devices stimulates researchers to devote significant effort to reducing the thickness of thin-film ferroelectrics.15,16 However, the depolarization field will destroy ferroelectricity at critical thicknesses for conventional ferroelectric compounds.17 Recently, the discovery of ferroelectricity in monolayer or few-layer van der Waals (vdW) materials provides new opportunities for reducing the size of ferroelectric devices to atomic thickness.18–22 In addition, the weak interlayer interaction and the dangling bond-free surface of two-dimensional (2D) vdW materials make it easy to integrate them with other materials in applications.
Thanks to the development of high-throughput calculations and machine learning methods, plenty of calculations have been proposed to predict promising 2D ferroelectric materials. However, only a few dozens of them have been confirmed by experiments.13,14 The most intuitive strategy for designing new 2D ferroelectric materials is to use the structure of existing 2D ferroelectric materials in the databases as a prototype and then test different combinations of chemical elements. To date, only tens of prototypes, like CuInP2S6 type,15,16 SnTe type,17,18 α-In2Se3 type,19,20 1T′-MoTe2 type,21,22 sliding ferroelectrics and so on, are proposed theoretically and experimentally. Another strategy is to design new prototypes of 2D ferroelectric structures. Investigating the cation off-centring induced by the SOJT effect may provide insight into the design of new 2D ferroelectric structure prototypes.
In this work, we propose a new 2D ferroelectric structure prototype whose structural distortion is induced by the SOJT effect. Using first-principles calculations, we comprehensively investigate the ferroelectric properties of monolayer NbO2I cleaved from its existing bulk counterpart. Total energy calculations show that the ferroelectric phase is the ground state with an in-plane ferroelectric polarization of 384.5 pC m−1, and the intrinsic Curie temperature Tc as high as 1700 K. Moreover, with the orbital selective external potential (OSEP) method,23 we reveal that the SOJT effect originates ferroelectricity in NbO2I. The finite indirect band gap is about 0.95 eV, which indicates that monolayer NbO2I is a semiconductor. The carrier mobilities of electrons and holes along the two directions are different due to the crystal anisotropy. We also systematically studied the electronic and ferroelectric properties of monolayer NbO2Br, which has the same structure as NbO2I with the replacement of I atoms by Br atoms. Our numerical results show that the properties of NbO2Br are very similar to the ones of NbO2I.
Calculation methods
All calculations in this work were based on density functional theory (DFT) implemented in the Vienna Ab initio simulation package (VASP).24 The generalized gradient approximation (GGA) with the form proposed by Perdew, Burke, and Ernzerhof (PBE)25 was chosen as the exchange–correlation functional. The Projector Augmented Wave (PAW) method26 was used to describe electron–ion interactions. The vacuum distance was set larger than 30 Å in order to avoid spurious periodic interactions. The kinetic energy cutoff was set to 550 eV, and the first Brillouin zone was sampled with a grid of 17 × 15 × 1 k points according to the Monkhorst–Pack scheme.27 The convergence criteria for electronic and ionic relaxations are 10−6 eV per atom and 10−3 eV Å−1, respectively. van der Waals (vdW) correction was included using the D2 method.28 The electronic contribution to polarization was calculated using the Berry phase method.29,30. The nudged elastic band (NEB) approach31,32 was used to simulate the minimum energy path (MEP) and associated energy barriers.Results and discussion
The bulk NbO2I material was successfully synthesized experimentally in 2007.33 The crystal structure of NbO2I possesses a centrosymmetric space group Pnma with a 7-coordinated Nb5+ cation and is shown as an example in Fig. 1. Interestingly, 7 ligands of Nb5+ form a pentagonal bipyramid that is connected via the apical O1 atoms to chains and via three O2 atoms to the double-layer structure (Fig. 1(b)). Between these double layers there are only weak van der Waals interactions of I atoms. Two I atoms and three O2 atoms are on the pentagonal base plane. At the same time, the axial sites are occupied by the O1 atom with very different Nb–O1 distances of 1.78 and 2.20 Å, which indicate the shift of Nb5+ and form the structural distortion which could cause the polarization denoted in Fig. 1(c). However, the other Nb5+ ion in the double layer shifts to the opposite direction (Fig. 1(a)), and thus the bulk NbO2I does not exhibit macroscopic polarization. As a comparison, the compound UO2Br has a crystal structure very similar to NbO2I except for equal U–O1 distances and no displacement of the U atom (for details see Fig. S1†).34 Thus, the space group of UO2Br is Cmcm with inversion symmetry and has only the paraelectric (PE) phase without spontaneous polarization.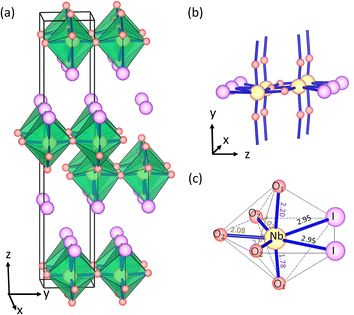 | ||
| Fig. 1 (a) The layered bulk crystal structure of NbO2I. (b) The connectivity of the polyhedral in NbO2I. (c) Coordination polyhedron and bond length of Nb5+ in NbO2I. | ||
Because the bulk NbO2I has a layered structure, it is of much interest to investigate the NbO2I monolayer for promising ferroelectricity and other valuable properties. We first calculate the cleavage energy to check the accessibility of exfoliation and show the results in Fig. 2(a). The cleavage energy for NbO2I and NbO2Br is 0.28 and 0.21 J m−2, respectively. They are smaller than the one of graphite.35 The smaller cleavage energy means that the exfoliation of NbO2I and NbO2Br is feasible. Thus, one layer NbO2I and NbO2Br can be exfoliated from their bulk counterparts, as shown in the inset of Fig. 2.
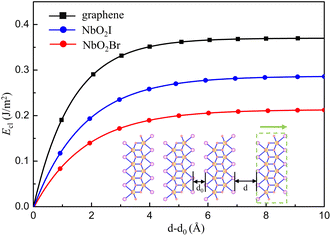 | ||
| Fig. 2 Cleavage energy Eclversus the separation distance d–d0 in the process of exfoliating one NbO2X (X = I, Br) layer from their bulk counterparts illustrated by the inset. | ||
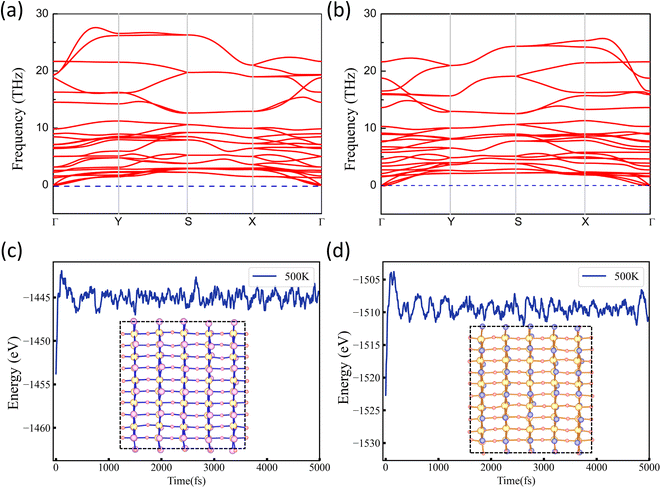
The crystal structure dynamics and thermal stability can be explored by calculating the phonon spectra and molecular dynamics (MD) simulations. The phonon spectra of NbO2I and NbO2Br along the high-symmetry lines are plotted in Fig. 4(a) and (b). It is observed that there is no imaginary phonon frequency in the entire Brillouin zone, confirming that NbO2I and NbO2Br are dynamically stable. Considering the probability of successful experimental fabrication, the MD simulation of a 5 × 5 supercell at 500 K with 5 ps time is carried out. The results are presented in Fig. 4(c) and (d) for NbO2I and NbO2Br, respectively. The MD simulation suggests the thermal stability of the two monolayers. For monolayer NbO2Br, we systematically search all possible 2D structures with the Nb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O
O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Br composition equal to 1
Br composition equal to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 using the particle swarm optimization (PSO)36 structure search algorithm and first-principles calculations. After comprehensive calculation, we found that there are six most energetically stable structures, as listed in Fig. S2.† However, the most stable structure is still our NbO2I prototype structure, which again confirms that our NbO2I monolayer prototype is stable.
1 using the particle swarm optimization (PSO)36 structure search algorithm and first-principles calculations. After comprehensive calculation, we found that there are six most energetically stable structures, as listed in Fig. S2.† However, the most stable structure is still our NbO2I prototype structure, which again confirms that our NbO2I monolayer prototype is stable.
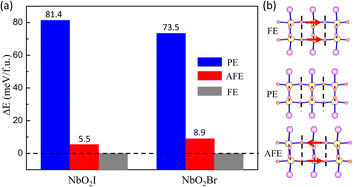
Now we start to explore the ferroelectric properties of monolayers NbO2I and NbO2Br. As we analyzed before, Nb5+ has a displacement from the centre of pentagonal bipyramids, causing the spontaneous polarization. To find the ground state, we set three configurations of Nb5+ in the monolayer, namely ferroelectric (FE), paraelectric (PE), and antiferroelectric (AFE), as shown by the schematics in Fig. 3(b). The total energies of the three configurations are illustrated in Fig. 3(a), in which we use the energy of FE as a reference energy and set it to zero. We can easily see that the FE state is the ground state, which is totally different from bulk NbO2I with two Nb5+ ions in one layer shifting in opposite directions.
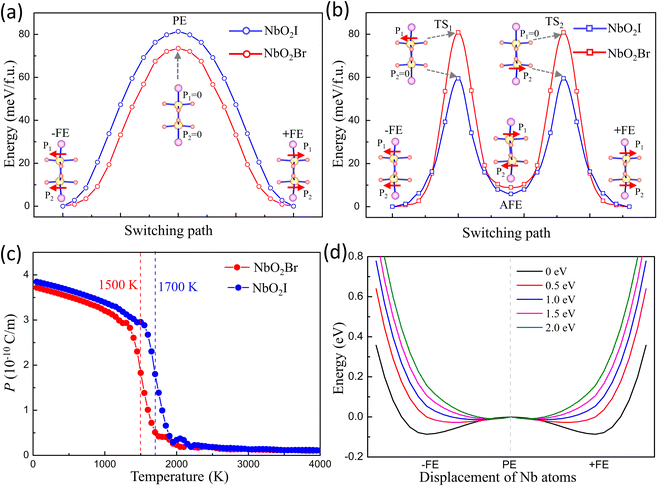
The fully relaxed monolayer structure reveals that the Nb5+ ion shifts from the centre of pentagonal bipyramids with an unequal bond length with two apical O1 atoms. The polarization is therefore in the in-plane direction. By using the Berry phase method, the polarization Ps was estimated, with values equal to 384.5 and 375.2 pC m−1 for NbO2I and NbO2Br, respectively. The reversal of polarization is realized through a phase transition between two symmetry-equivalent ferroelectric states with opposite Ps. We constructed two potential switching paths and computed the energy evolution using the NEB approach as shown in Fig. 5(a) and (b) in order to explore the polarization switching and the pertinent energy barrier of 2D NbO2I and NbO2Br. The PE phase is the intermediate state of the first path, and the AFE phase is the intermediate state of the second path. We discovered that the first path's energy barrier, which uses the PE phase as an intermediate state, is around 80 meV, whereas the second path's energy barrier is 60 meV. As a result, we came to the conclusion that the FE-AFE-FE transformation is possible during the NbO2I monolayer's ferroelectric switching. However, in the case of the NbO2Br monolayer, there is a slight difference (7 meV) of the energy barrier between the first and second paths. This indicates a potential transformation path of FE-PE-FE for the NbO2Br monolayer that differs from the behaviour of the NbO2I monolayer.
Ferroelectricity is further emphasized by the Curie temperature above which the macroscopic spontaneous polarization disappears. The effective Hamiltonian of NbO2I and NbO2Br supercells is carried out by applying the Landau–Ginzburg phase transition theory (for more details see ESI†). After fitting the parameters of effective Hamiltonian we perform the Monte Carlo simulation to investigate the Tc of 2D NbO2I and NbO2Br. The numerical results are shown in Fig. 5(c), and the Tc of the NbO2I (NbO2Br) monolayer is as high as 1500 K (1700 K) that again proves that NbO2X is a stable and robust 2D ferroelectric material.
It is well known that in the local coordinate of a pentagonal bipyramid, the d orbitals will be split into three groups by the crystal field. The dxz and dyz orbitals possess the lowest energy. When we transfer to the global coordinate of NbO2I, the local dxz and dyz of Nb5+ in the pentagonal bipyramid will transfer to dxy and dxz. In the following parts, we will discuss the results in the global coordinate. The critical mechanism and feature of the SOJT effect are the hybridization between the empty cation's d orbitals (i.e., Ti4+, Nb5+) and occupied anion's p orbitals (i.e., O2−, I1−).37 Moreover, Wheeler and Hoffman et al.38 and Kunz and Brown39 pointed out that the magnitude of the distortion of the cation surrounded by its ligands (i.e., TiO62−, NbO5I2 pentagonal bipyramid in this work) attributable to the SOJT effect depends on the strength of hybridization between the empty cation's d orbitals and occupied anion's 2p orbitals.
The density of states of NbO2I is plotted in Fig. 6(c). The partial density of states (PDOS) clearly shows that both apical O1-2p and planar O2-2p orbitals are mainly located between −8 and −1 eV, indicating that the 2p orbitals of apical O1 and planar O2 are fully occupied. The I-5p orbitals are mainly distributed from −5 eV to Fermi energy with a narrower bandwidth. The Nb-4d orbitals are located above the Fermi energy with the 4d0 configuration. However, there are finite states of 2py and 2pz of apical O1 distributing between 0.5 and 3 eV, where there are also major contributions from Nb 4dxy and 4dxz, which means that there are strong hybridizations between unoccupied Nb 4dxy and 4dxz orbitals and occupied apical O1 2py and 2pz, indicating the SOJT effect in NbO2I. The electronic structure of NbO2Br shown in Fig. 6(d) is very similar to that of NbO2I. As a result, we will not give a detailed discussion about NbO2Br.
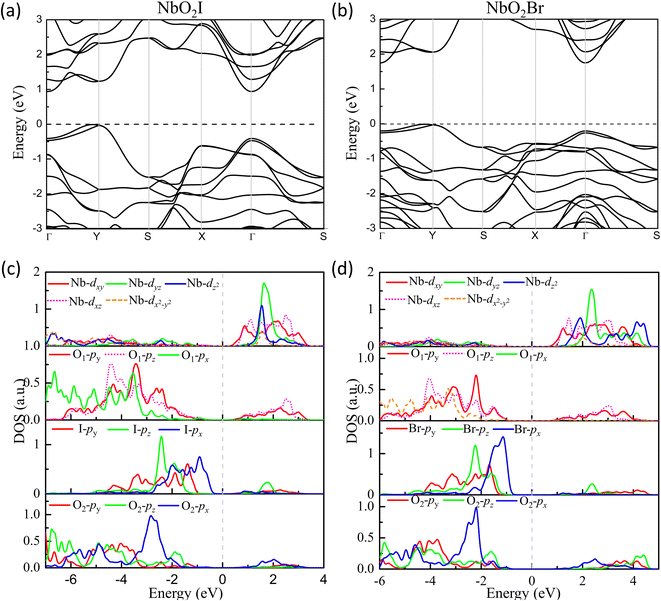 | ||
| Fig. 6 Energy band structures (a) and (b) for FE NbO2X monolayers. Projected density of states (PDOS) for monolayers (c) NbO2I and (d) NbO2Br. | ||
According to our discussion above, if we tune the strength of the hybridization, we can adjust the SOJT effect and further investigate the FE phase transition. Here, we apply the OSEP method by adding an external potential to raise the energy of Nb-4dxy and 4dxz orbitals by different values to increase the energy difference between them and O1 2py and 2pz. The OSEP approach can introduce an exceptional external potential that only can be felled by certain appointed orbitals.23 We take the 2 eV potential on Nb-4dxy and 4dxz as an example shown in Fig. S7.† The DOS of Nb-4dxy and 4dxz is indeed shifted-up by almost 2 eV, which indicates that the OSEP approach can effectively shift the energy of certain selective orbitals. More interestingly, due to a larger energy difference between Nb 4dxy/4dxz and O1 2py/2pz, the strength of hybridization between them is decreased. One can expect that the SOJT effect induced distortion will disappear and result in a PE ground state instead of FE when hybridization between them vanishes.
Thus, we apply different external potentials on Nb-4dxy and 4dxz to study the FE phase transition in NbO2I. Fig. 5(d) illustrates the results. When the external potential on Nb-4dxy and 4dxz rises, the characteristic double well of monolayer NbO2I becomes shallower and eventually disappears, suggesting that the ground state becomes the PE phase. The same calculation is also carried out for NbO2Br, and the same behaviour of double well evolution is obtained (shown in Fig. S6†). These results demonstrate that the SOJT effect is the reason for the ferroelectric phase transition.
Regarding the ferroelectricity, the band structure of NbO2X monolayers is also calculated. Our numerical results demonstrate that both monolayers NbO2I and NbO2Br are Indirect bandgap semiconductors with Eg = 0.95 eV and 1.75 eV, respectively. As illustrated in Fig. 4, their valence band maximum (VBM) is near the Y point, while their conduction band minimum (CBM) is at the Γ point. The effective mass at the VBM for NbO2I is 0.48 m0 along the x axis and 1.37 m0 along the y axis, and the effective mass at the CBM is 0.44 m0 along the x axis and 1.18 m0 along the y axis, where m0 is the electron mass (for more details see ESI†). Different effective mass values along the two axes show band structure anisotropy, which is caused by crystal structure anisotropy. Interestingly, the carrier mobility of holes is an order of magnitude greater than that of electrons, implying that NbO2I is an excellent P-type semiconductor.
Conclusions
In summary, we explored the crystal structure, ferroelectric, and electronic properties of monolayers NbO2I and NbO2Br using first-principles calculation. We clarified that the FE phase is the energetically stable phase. The origin of polarization comes from the displacement of Nb5+ cations driven by the SOJT effect. The monolayers NbO2I and NbO2Br are indirect semiconductors with the calculated band gap of 0.95 eV and 1.75 eV respectively. In addition, the carrier mobility shows anisotropy along two directions. Our findings add a new member to the family of 2D ferroelectric prototypes, providing a microscopic mechanism of the FE phase transition that will help the discovery and design of new FE materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Ministry of Science and Technology of the People's Republic of China (no. 2022YFA1402901), the National Science Fund for Distinguished Young Scholars (T2125004), the Nature Science Foundation of China (no. 12274228), and the Fundamental Research Funds for the Central Universities (no. 30922010805 and 30920041115).References
- C. Wang, Y. Lu, D. Cobden and J. Wang, Nat. Mater., 2023, 22, 542–552 CrossRef CAS PubMed.
- L. Qi, S. Ruan and Y.-J. Zeng, Adv. Mater., 2021, 33, 2005098 CrossRef CAS PubMed.
- X.-K. Wei, N. Domingo, Y. Sun, N. Balke, R. E. Dunin-Borkowski and J. Mayer, Adv. Energy Mater., 2022, 12, 2201199 CrossRef CAS.
- Z. Guan, H. Hu, X. Shen, P. Xiang, N. Zhong, J. Chu and C. Duan, Adv. Electron. Mater., 2020, 6, 1900818 CrossRef CAS.
- D. Kepaptsoglou, J. D. Baran, F. Azough, D. Ekren, D. Srivastava, M. Molinari, S. C. Parker, Q. M. Ramasse and R. Freer, Inorg. Chem., 2018, 57, 45–55 CrossRef CAS PubMed.
- V. F. Michel, T. Esswein and N. A. Spaldin, J. Mater. Chem. C, 2021, 9, 8640–8649 RSC.
- J. Zhao, J. Gao, W. Li, Y. Qian, X. Shen, X. Wang, X. Shen, Z. Hu, C. Dong, Q. Huang, L. Cao, Z. Li, J. Zhang, C. Ren, L. Duan, Q. Liu, R. Yu, Y. Ren, S.-C. Weng, H.-J. Lin, C.-T. Chen, L.-H. Tjeng, Y. Long, Z. Deng, J. Zhu, X. Wang, H. Weng, R. Yu, M. Greenblatt and C. Jin, Nat. Commun., 2021, 12, 747 CrossRef CAS PubMed.
- R. Cervasio, Y. Peperstraete, T. Maroutian, R. Haumont, M. Verseils, J.-B. Brubach, R. Tétot, J. Creuze, P. Roy and E. Amzallag, J. Phys. Chem. C, 2022, 126, 12860–12869 CrossRef CAS.
- A. S. Ivanov, K. V. Bozhenko and A. I. Boldyrev, Inorg. Chem., 2012, 51, 8868–8872 CrossRef CAS PubMed.
- I. B. Bersuker, Chem. Rev., 2021, 121, 1463–1512 CrossRef CAS PubMed.
- L. Gigli, M. Veit, M. Kotiuga, G. Pizzi, N. Marzari and M. Ceriotti, npj Comput. Mater., 2022, 8, 209 CrossRef CAS.
- G. Sághi-Szabó, R. E. Cohen and H. Krakauer, Phys. Rev. Lett., 1998, 80, 4321–4324 CrossRef.
- H. Brunckova, L. Medvecky, A. Kovalcikova, M. Fides, E. Mudra, J. Durisin, M. Sebek, M. Kanuchova and J. Skvarla, J. Rare Earths, 2017, 35, 1115–1125 CrossRef CAS.
- N. Zhang, H. Yokota, A. M. Glazer, Z. Ren, D. A. Keen, D. S. Keeble, P. A. Thomas and Z. G. Ye, Nat. Commun., 2014, 5, 5231 CrossRef CAS PubMed.
- G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano, V. R. Cooper, L. Liang, S. G. Louie, E. Ringe, W. Zhou, S. S. Kim, R. R. Naik, B. G. Sumpter, H. Terrones, F. Xia, Y. Wang, J. Zhu, D. Akinwande, N. Alem, J. A. Schuller, R. E. Schaak, M. Terrones and J. A. Robinson, ACS Nano, 2015, 9, 11509–11539 CrossRef CAS PubMed.
- L. W. Martin and A. M. Rappe, Nat. Rev. Mater., 2016, 2, 16087 CrossRef.
- J. Junquera and P. Ghosez, Nature, 2003, 422, 506–509 CrossRef CAS PubMed.
- R. Fei, W. Kang and L. Yang, Phys. Rev. Lett., 2016, 117, 097601 CrossRef PubMed.
- C. Liu, R. Gao, X. Cheng, X. Yang, G. Qin, H. Gao, S. Picozzi and W. Ren, Phys. Rev. B, 2023, 107, L121402 CrossRef CAS.
- H. Ai, X. Song, S. Qi, W. Li and M. Zhao, Nanoscale, 2019, 11, 1103–1110 RSC.
- C. Cui, F. Xue, W.-J. Hu and L.-J. Li, npj 2D Mater. Appl., 2018, 2, 18 CrossRef.
- L. H. Jin, H. D. Wang, R. Cao, K. Khan, A. K. Tareen, S. Wageh, A. A. Al-Ghamdi, S. J. Li, D. B. Li, Y. Zhang and H. Zhang, APL Mater., 2022, 10, 060903 CrossRef CAS.
- (a) X. Wan, J. Zhou and J. Dong, Europhys. Lett., 2010, 92, 57007 CrossRef; (b) Y. Du, H.-C Ding, H.-C Sheng, S.Y. Savrasov, X. Wan, C.-G. Duan and J. Phys, Condens. Matter, 2013, 26, 025503 CrossRef PubMed.
- (a) Y. Du, H.-C. Ding, L. Sheng, S. Y. Savrasov, X. Wan and C.-G. Duan, J. Phys.: Condens. Matter, 2013, 26, 025503 CrossRef PubMed; (b) G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651–1654 CrossRef CAS PubMed.
- R. Resta, Rev. Mod. Phys., 1994, 66, 899–915 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- N. A. Zarkevich and D. D. Johnson, J. Chem. Phys., 2015, 142, 024106 CrossRef PubMed.
- S. Hartwig and H. Hillebrecht, Z Naturforsch B, 2007, 62, 1543–1548 CrossRef CAS.
- M.-J. Crawford, A. Ellern, K. Karaghiosoff, P. Mayer, H. Nöth and M. Suter, Inorg. Chem., 2004, 43, 7120–7126 CrossRef CAS PubMed.
- R. Zacharia, H. Ulbricht and T. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406 CrossRef.
- H. Wang, Y. Wang, J. Lv, Q. Li, L. Zhang and Y. Ma, Comput. Mater. Sci., 2016, 112, 406–415 CrossRef CAS.
- Y. Inaguma, A. Aimi, Y. Shirako, D. Sakurai, D. Mori, H. Kojitani, M. Akaogi and M. Nakayama, J. Am. Chem. Soc., 2014, 136, 2748–2756 CrossRef CAS PubMed.
- R. A. Wheeler, M. H. Whangbo, T. Hughbanks, R. Hoffmann, J. K. Burdett and T. A. Albright, J. Am. Chem. Soc., 1986, 108, 2222 CrossRef CAS PubMed.
- M. Kunz and I. D. Brown, J. Solid State Chem., 1995, 115, 395 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00245d |
| This journal is © The Royal Society of Chemistry 2023 |