Open Access Article
Open Access ArticleThe luminescence mechanism of ligand-induced interface states in silicon quantum dots†
Jian
Zhou
a,
Fengyang
Ma
a,
Kai
Chen
a,
Wuyan
Zhao
a,
Riyi
Yang
a,
Chong
Qiao
 b,
Hong
Shen
a,
Wan-Sheng
Su
b,
Hong
Shen
a,
Wan-Sheng
Su
 *cde,
Ming
Lu
a,
Yuxiang
Zheng
af,
Rongjun
Zhang
*cde,
Ming
Lu
a,
Yuxiang
Zheng
af,
Rongjun
Zhang
 af,
Liangyao
Chen
a and
Songyou
Wang
af,
Liangyao
Chen
a and
Songyou
Wang
 *afg
*afg
aShanghai Ultra-Precision Optical Manufacturing Engineering Center, Department of Optical Science and Engineering, Fudan University, Shanghai 200433, China. E-mail: songyouwang@fudan.edu.cn
bSchool of Mathematics and Physics, Nanyang Institute of Technology, Nanyang 473004, China
cNational Taiwan Science Education Center, Taipei 111081, Taiwan. E-mail: wssu@mail.ntsec.gov.tw
dDepartment of Electro-Optical Engineering, National Taipei University of Technology, Taipei 106344, Taiwan
eDepartment of Physics, National Sun Yat-sen University, Kaohsiung 804201, Taiwan
fYiwu Research Institute of Fudan University, Chengbei Road, Yiwu City, 322000 Zhejiang, China
gKey Laboratory for Information Science of Electromagnetic Waves (MoE), Shanghai 200433, China
First published on 20th June 2023
Abstract
Over decades of research on photoluminescence (PL) of silicon quantum dots (Si-QDs), extensive exploratory experiments have been conducted to find ways to improve the photoluminescence quantum yield. However, the complete physical picture of Si-QD luminescence is not yet clear and needs to be studied in depth. In this work, which considers the quantum size effect and surface effect, the optical properties of Si-QDs with different sizes and surface terminated ligands were calculated based on first principles calculations. The results show that there are significant differences in the emission wavelength and emission intensity of Si-QD interface states connected by different ligands, among which the emission of silicon–oxygen double bonds is the strongest. When the size of the Si-QD increases, the influence of the surface effect weakens, and only the silicon–oxygen double bonds still localize the charge near the ligand, maintaining a high-intensity luminescence. In addition, the presence of surface dangling bonds also affects luminescence. This study deepens the understanding of the photoluminescence mechanism of Si-QDs, and provides a direction for both future improvement of the photoluminescence quantum efficiency of silicon nanocrystals and for fabricating silicon-based photonic devices.
I. Introduction
Silicon, with its remarkable semiconductor properties, non-toxicity, and abundance in the earth's crust, has found widespread application in the microelectronics industry.1–7 However, as semiconductor technology has progressed, Moore's Law appears to have reached a bottleneck. As a result, researchers have turned their attention towards silicon optoelectronic integration technology as a new direction. Compared to materials which are based on group III–V elements, silicon-based semiconductors offer the advantage of being compatible with CMOS processes. The development of silicon-based light-emitting materials is crucial for the advancement of silicon optoelectronic integration technology, enabling the combination of silicon photonic devices with microelectronic devices.8,9 Furthermore, silicon-based photonic devices play a central role in the field of integrated silicon optoelectronics and are essential for realizing monolithic integrated silicon optoelectronics. However, silicon is typically an indirect bandgap material, necessitating the involvement of phonons during electronic transitions. This characteristic poses challenges for efficient light emission and hinders the progress of silicon photonic devices.10,11Since the discovery by Canham et al. in 1991 that porous nano-silicon exhibits light emission,12 silicon nanocrystals (SiNCs) have attracted global attention, and SiNCs capable of emitting light in different colors have been fabricated.2,13 According to Heisenberg's uncertainty principle, the smaller the size of SiNCs, the greater the uncertainty in its momentum. This increases the probability of electron transitions from the valence band to the conduction band, enhancing the possibility of light emission from SiNCs.14,15 Research has demonstrated that the size of quantum dots is a crucial factor influencing luminescence.16,17 Quantum confinement leads to the distortion of the spatial distribution of excited-state electrons by localizing Bloch waves within the SiNC core. This results in increased overlap between holes and electrons, facilitating rapid optical processes.18 Furthermore, the choice of different ligands for surface termination also impacts the luminescence intensity and wavelength of SiNCs.19–24 Other external factors, such as pressure, temperature, and ambient humidity, can also influence luminescence.25–28 Reports have emerged of silicon nanocrystals emitting red light, blue-violet light2 and even white light,4 which has spurred rapid developments in silicon-based photonic devices. However, the luminescence intensity achievable with lasers remains insufficient. Numerous exploratory experiments have been undertaken to identify strategies for improving the photoluminescence quantum yield of silicon nanocrystals.
In 2000, Pavesi et al. published the first observation of the optical gain phenomenon in silicon nanocrystals embedded in silicon dioxide films, indicating the potential application of nano-scale silicon materials in laser gain.29 This sparked a surge of interest in silicon-based light-emitting devices. However, compared to other photonic components, silicon-based light sources have lagged behind in terms of development, posing a challenge to achieving photonic integration and optical interconnection.30–32 There is an urgent need to develop monolithically-integrated silicon-based lasers. The primary obstacle in creating such silicon-based light-emitting devices lies in the fabrication of SiNCs with high PLQY. Consequently, a significant number of exploratory experiments have been conducted, and various theoretical and experimental approaches are being continuously explored.33–38 While lasers with a certain level of luminescence intensity have been manufactured,39–41 their luminous efficiency and intensity still require improvement.
Due to limitations in experimental techniques and computing power, a comprehensive theoretical framework to explain the effect of photoluminescence intensity is still lacking, and the underlying physical mechanisms behind the emission of silicon quantum dots remain unclear. To address these challenges, this study employs density functional theory (DFT) and time-dependent density functional theory (TDDFT) calculations to investigate the ground and excited states of Si-QDs, taking into account the influence of size and surface ligands. The findings reveal two distinct luminescence mechanisms: luminescence originating from the quantum confinement effects within the silicon quantum dot core, and luminescence dominated by surface-induced defect states. The latter mechanism exhibits stronger luminescence and has the potential to display size-independent emission.
II. Calculation method
The PL spectrum calculations were performed using the quantum chemical chemistry package ORCA based on the DFT and TD-DFT theories.42 Hybrid exchange–correlation functionals (PBE0)43 and Gaussian basis (def-SVP) are used to calculate the luminescence spectrum and charge density distribution. The combination of the B3LYP functional and def-SVP basis set is used to calculate the Fourier transform infrared (FTIR) spectrum.44 The calculation of band anti-folding is obtained by the calculation method of DFT software FIREBALL.45,46 Nanoclusters of different sizes were cut from the diamond-structured silicon material and the dangling bonds on the surface were saturated with hydrogen atoms. Si-QDs with diameters of 1.1 nm, 1.5 nm and 1.9 nm were constructed respectively. The surface of the quantum dots prepared experimentally is mainly terminated by hydrogen, and there may be a small number of other ligands at the same time. This study focuses on the structure of silicon quantum dots (Si-QDs) that are capped with different ligands at a specific site. The luminescence of Si-QDs was also computed while taking into account the possibility of unsaturated dangling bonds on their surface, which may not be completely passivated during the experiment.When calculating the emission spectrum, the structure of the S1 state is optimized to locate the minimum point of its potential energy surface.47 The energy difference of the vertical transition from the S1 state to the ground state is used as the position of the emission peak in the photoluminescence (PL) spectrum.
To calculate Fourier transform infrared spectra, the structure is relaxed to its most stable form, and the molecular vibrational frequencies and modes are determined. Each vibrational mode is approximated as a harmonic oscillator, characterized by Gaussian functions representing its frequency and amplitude. By superimposing these Gaussian functions, the entire FTIR spectrum of the molecule is obtained. Symmetry and coupling effects between the vibrational modes are considered during the calculation to improve accuracy. Fourier transformation converts the FTIR spectrum from the time domain to the frequency domain, providing the relationship between frequency and absorbance.
To analyze the distribution of electron–hole density, the DFT method is utilized to calculate the electronic structure and energy of the molecule. The electronic wave function is expanded using a basis set, and the optimization of electron distribution minimizes the total energy. By calculating the molecular orbitals, both occupied and unoccupied orbitals (electron–holes) can be determined. Analyzing the energy and distribution of the unoccupied orbitals allows for the calculation of the density distribution of electrons–holes.
An analysis using the program Multiwfn is performed to obtain information about the distribution and properties of electrons–holes within the molecule based on the electron–hole density distribution.48–50
The study considered non-radiative recombination using Fermi's golden rule and the energy gap law, and calculated the internal conversion (IC) rate and intersystem crossing (ISC) rate to estimate the quantum yield of silicon quantum dots. The ESI† contains specific details on the calculations.51,52
III. Results and discussion
A. Structure
Fig. 1 shows the structures of Si-QDs terminated by hydrogens and one oxygen double bond of 1.1 nm, 1.5 nm, and 1.9 nm, containing 35, 87, and 172 silicon atoms, respectively. Blue spheres represent silicon atoms, light yellow spheres represent hydrogen atoms, and the red spheres represent oxygen atoms. To compare the effects of different ligands on the quantum luminescence properties, all the ligands used for termination were attached at the same position, as shown in Fig. 1. The structure of quantum dots was represented using symbols for simplicity. The notation used was d–x, where d refers to the diameter of the quantum dot and x represents the substituted ligand. Specifically, Si-QDs with hydrogen-terminated surfaces were denoted as 1.1-H, 1.5-H, and 1.9-H, depending on their respective diameters. Si-QDs with dangling bonds were denoted as d–x–n, where n indicates the number of dangling bonds present. In the case of Si-QDs with diameters of 1.1 nm and two or four dangling bonds on their surfaces, their structures are depicted in Fig. S1(a) and (b), respectively, in the ESI.†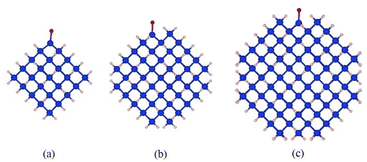 | ||
| Fig. 1 Schematic diagram of the structure of Si-QDs terminated by hydrogens and one oxygen double bond of different sizes: (a) 1.1 nm diameter, (b) 1.5 nm diameter, and (c) 1.9 nm diameter. | ||
B. Optical properties
Si-QDs prepared by different experimental methods will have different sizes and surface ligands. The type and quantity of ligands on the surface of Si-QDs can be characterized by methods such as Fourier infrared absorption spectroscopy and Raman spectroscopy. The surface of Si-QDs prepared by Taisei Ono5 is mainly terminated by hydrogen and decyl, with a small number of silicon–oxygen bonds. In order to verify the correctness of the calculation method, the structural model shown in Fig. 2(a) was constructed (a silicon–oxygen double bond and a silicon–oxygen–silicon bridge bond are connected on the surface of the silicon cluster with a diameter of 1.1 nm, and there are five decyl groups, with the remaining positions all saturated by hydrogen atoms). The Fourier transform infrared (FTIR) spectrum and photoluminescence (PL) spectrum were calculated. The theoretical calculation (Fig. 2(b)) is consistent with the experimentally measured Fourier transform infrared spectrum (Fig. 2(c)). When the number of decyl groups on the surface of Si-QDs changes, it can be seen that the peak height of CH2 (about 3000 cm−1) and the peak height of Si–Hx (about 2200 cm−1), where subscript x represents the number of hydrogen atoms attached to a silicon atom, also clearly change. The structure and FTIR spectrum of Si-QDs with different numbers of decyl group ligands on the surface are given in the ESI as Fig. S2(a)–(f).† As the number of decyl groups increases, the peak height of CH2 (about 3000 cm−1) increases and the peak height of Si–Hx (about 2200 cm−1) decreases. For the calculation of the PL spectrum, Kasha's rule53 states that polyatomic molecules react with appreciable yield only from the lowest excited state (S1 state) for a given multiplicity. Moreover, the emission wavelength is not related to the wavelength of excitation light. In this work, the transition from the S1 state to the ground state was calculated. The theoretically calculated luminescence peak position (Fig. 2(d)) exhibits a red shift when compared to the case measured experimentally due to the vertical excitation approximation based on the Franck–Condon principle when calculating the luminescence spectrum.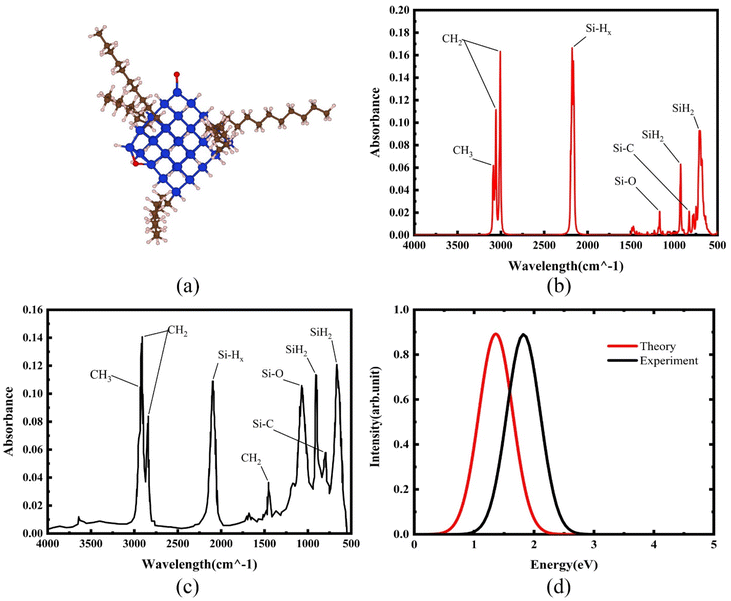 | ||
| Fig. 2 (a) Structural model and (b) FTIR spectrum of Si-QDs by theoretical calculations and (c) FTIR spectrum of Si-QDs measured by experiment. Reproduced with permission from ref. 5, copyright American Chemical Society, 2022. (d) PL spectra of Si-QDs obtained theoretically and experimentally, where the black line is the experimental result in ref. 5, and the red line is the result of theoretical calculations (peak height is normalized). | ||
Experiments demonstrated that for the hydrogen-terminated Si-QDs, the measured photoluminescence observed with the naked eye immediately after etching is green, and it only becomes red after oxidation, with the red light mainly coming from the silicon–oxygen double bonds on the surface of the quantum dots.24,54 In 2021, Shen et al. explained the luminescence principle and confirmed that the red emission of Si-QDs is indeed dominated by silicon–oxygen double bonds.24 The luminescence mechanism of Si-QDs is mainly divided into two types: silicon bulk luminescence based on the quantum size effect and interface state luminescence based on the surface effect.21,55 Hydrogen, oxygen, hydroxyl, methyl, vinyl, amino, and tolyl groups are commonly used as ligands for surface passivation of Si-QDs.6,56 Their effects on the luminescent properties of Si-QDs have been previously discussed.
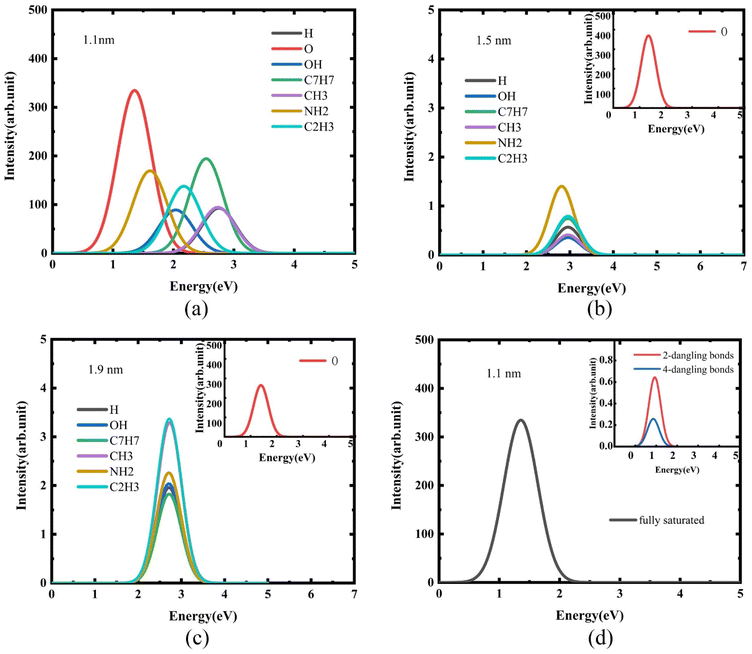
For quantum dots with a diameter of 1.1 nm, luminescence curves with Si-QDs terminated by different ligands were calculated. As shown in Fig. 3(a), the luminescence intensity and luminescence wavelength of these Si-QDs were significantly different for different terminal ligands. Among them, Si-QDs terminated by silicon–oxygen double bonds had the highest luminescence intensity, followed by those with terminal tolyl or amino groups. In contrast, those with terminal methyl groups or completely terminated by hydrogen were relatively weak. This suggests that the emission energy of Si-QDs terminated with Si–O double bonds is in the red band, while Si-QDs terminated with toluene groups emit light in the blue-violet band. The emission bands of quantum dots terminated by different ligands cover almost the entire visible light range. By mixing single quantum dots terminated with different ligands in a certain proportion, white light emission can be achieved.
It is clear that the surface ligand is an important, and even decisive, factor affecting the luminescence of quantum dots. In order to study the effect of the size of Si-QDs on their luminescence, the luminescence was calculated for the surfaces of Si-QDs with diameters of 1.5 nm (Fig. 3(b)) and 1.9 nm (Fig. 3(c)) with different terminal ligands. With the increase in size, the luminescence intensity of other ligand-terminated Si-QDs decreased by nearly two orders of magnitude, except for the Si-QDs terminated by silicon–oxygen double bonds.
Furthermore, it can be seen from Fig. 3(b) and (c) that for the luminescence of Si-QDs with diameters of 1.5 nm and 1.9 nm, the effect of surface ligands becomes less obvious. Except for the quantum dots terminated by the silicon–oxygen double bonds, the luminescence properties of the quantum dots terminated by other ligands, including luminescence intensity and luminescence wavelength, are close to those of quantum dots that are completely terminated by hydrogen.
Surface effects are a property of nanomaterials. During the experimental preparation of quantum dots, it is difficult to ensure that the dangling bonds on the surface of the quantum dots are completely passivated. When there are unsaturated dangling bonds on the surface of quantum dots, the chemical activity of nanomaterials will change. To this end, the effect of the presence of dangling bonds on the luminescence of Si-QDs was studied.
Fig. 3(d) shows the luminescence when there are different numbers of dangling bonds on the surface of Si-QDs with terminal silicon–oxygen double bonds. Clearly, when there are dangling bonds in the Si-QDs, the luminescence intensity is significantly reduced. In other words, reducing the number of dangling bonds can enhance the luminescence. This explains why the luminescence of silicon nanocrystals is significantly enhanced after high-pressure hydrogenation.57
In addition to the luminescence energy and luminescence intensity, the luminescence lifetime is also an important indicator for evaluating fluorescent luminescence. The luminescence lifetime τ is the reciprocal of Einstein's spontaneous emission coefficient Aa→k, which is determined by the transition matrix element |rka2| = |〈Ψk|r|Ψa〉|.
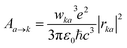 | (1) |
The oscillator strength is defined as:
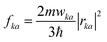 | (2) |
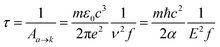 | (3) |
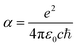 and E = hν = ℏw are in atomic units. When the unit of τ is s and the unit of E is cm−1, the formula can be written as:
and E = hν = ℏw are in atomic units. When the unit of τ is s and the unit of E is cm−1, the formula can be written as: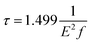 | (4) |
The luminescence lifetime of different quantum dots was calculated according to eqn (1), and the results are shown in Table 1. The lifetime of ordinary direct bandgap materials is generally on the order of 0.1 μs.26 The luminescence lifetime of Si-QDs terminated with Si–O double bonds is only minimally affected by size, and is in the order of 1 μs, which can be considered as a quasi-direct bandgap. The lifetime of Si-QDs terminated by other groups such as hydroxyl, amino, methyl and toluene groups is closely related to size. As the size increases, the luminescence lifetime of Si-QDs increases from 1 microsecond to tens or even hundreds of microseconds. When the diameter of Si-QDs is 1.1 nm, the luminescence lifetime of all ligand-capped Si-QDs is in the order of 1 μs, which is close to that of the direct bandgap. When the size increases to 1.5 nm and 1.9 nm, the luminescence lifetime increases significantly, and begins to show the characteristics of an indirect bandgap. Long lifetime implies a low fluorescence emission rate, resulting in reduced quantum yield and weaker luminescence.
| Diameter (nm) | Surface ligand | Oscillator strength | Excitation energy (cm−1) | Lifetime (μs) | PLQY (%) |
|---|---|---|---|---|---|
| 1.1 | –H | 2.56 × 10−3 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201.6 201.6 |
1.18 | 97.66 |
| –O | 5.94 × 10−3 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 943.8 943.8 |
2.11 | 94.43 | |
| –OH | 1.24 × 10−3 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 443.7 443.7 |
4.46 | 99.75 | |
| –CH3 | 2.61 × 10−3 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 077.6 077.6 |
1.18 | 99.94 | |
| –C2H3 | 3.56 × 10−3 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521.4 521.4 |
1.37 | 99.90 | |
| –C7H7 | 4.05 × 10−3 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502.8 502.8 |
0.88 | 99.90 | |
| –NH2 | 5.44 × 10−3 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 008.0 008.0 |
1.63 | 99.85 | |
| 1.5 | –H | 5.41 × 10−6 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 826.0 826.0 |
487.64 | 53.13 |
| –O | 8.16 × 10−3 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796.1 796.1 |
1.58 | 99.20 | |
| –OH | 3.91 × 10−6 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 841.3 841.3 |
674.30 | 44.88 | |
| –CH3 | 4.79 × 10−6 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842.4 842.4 |
550.97 | 49.76 | |
| –C2H3 | 1.29 × 10−5 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837.2 837.2 |
204.58 | 85.24 | |
| –C7H7 | 9.24 × 10−6 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815.5 815.5 |
285.97 | 65.61 | |
| –NH2 | 6.04 × 10−5 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650.0 650.0 |
48.34 | 90.69 | |
| 1.9 | –H | 4.73 × 10−5 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 879.8 879.8 |
66.09 | 85.83 |
| –O | 6.80 × 10−3 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238.2 238.2 |
1.75 | 99.10 | |
| –OH | 6.27 × 10−5 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866.3 866.3 |
50.03 | 89.01 | |
| –CH3 | 7.54 × 10−5 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970.9 970.9 |
41.19 | 90.76 | |
| –C2H3 | 7.65 × 10−5 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 943.9 943.9 |
40.70 | 90.84 | |
| –C7H7 | 4.62 × 10−5 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 913.9 913.9 |
67.63 | 85.51 | |
| –NH2 | 4.31 × 10−5 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 847.5 847.5 |
72.94 | 84.79 |
C. Luminescence mechanism
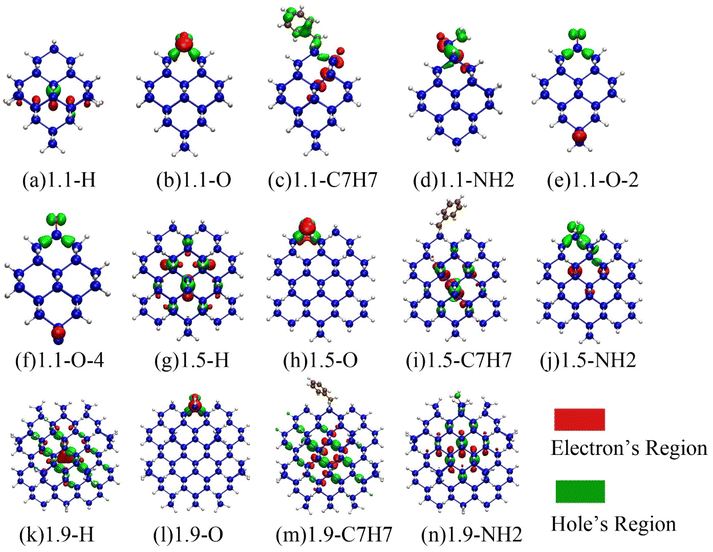
To investigate the mechanism of Si-QDs emitting light, the electron and hole density distributions were analyzed.49,58Fig. 4 shows the electron and hole density distributions of various Si-QDs, where red represents the electron density distribution and green represents the hole density distribution.It has been discovered that electrons and holes are dispersed within a 1.1 nm diameter quantum dot when it is fully terminated by hydrogen. However, when other ligands are attached to the surface, the symmetry of the quantum dot is disrupted, causing electrons and holes to be confined near the ligands. In particular, when silicon–oxygen double bonds are present, the distribution of electrons and holes becomes more concentrated. The model given by Wolkin suggests that when terminated by hydrogen, the radiative recombination of Si-QDs of different sizes is the recombination of free excitons, and the PL energy is equal to the band gap of free excitons, following the quantum constraint model. However, when Si-QDs are terminated by the silicon–oxygen double bond, the radiative recombination may result from the localized stable electron state (or even the trapped exciton) in the vicinity of the silicon–oxygen double bond.54 The calculation results of electron–hole distribution in Fig. 4 confirm this model. In combination with the previous analysis of the luminescence curve, it can be concluded that when the diameter is as small as 1.1 nm, the surface-terminated ligand is an important factor affecting the luminescence of the quantum dot. At this time, the luminescence mainly comes from the interface state luminescence affected by the ligand on the surface of the quantum dot. When the size increases, except for the silicon–oxygen double bonds, the distribution of electrons and holes of the quantum dots terminated by other ligands is no longer localized, and the influence of surface ligands on the luminescence of the quantum dots becomes smaller. The luminescence of quantum dots gradually changes from interface luminescence to bulk luminescence of silicon quantum dots. The indirect bandgap feature of silicon will obviously affect the luminescence at this time, significantly reducing the luminescence intensity.59
When there are dangling bonds in the quantum dots connected by silicon–oxygen double bonds, electrons are distributed far away from the silicon–oxygen double bond, and holes are concentrated near the silicon–oxygen double bonds as shown in Fig. 4(e) and (f), which clearly makes luminescence difficult and thus reduces luminous efficiency.
The electron–hole density distributions of the Si-QDs terminated by other ligands are shown in ESI Fig. S3.† The localization for electron and holes of Si-QDs terminated by other ligands except the silicon–oxygen double bond is not so strong, and when the size increases, and the luminescence transforms into the bulk luminescence of silicon quantum dots, the luminescence intensity drops drastically.
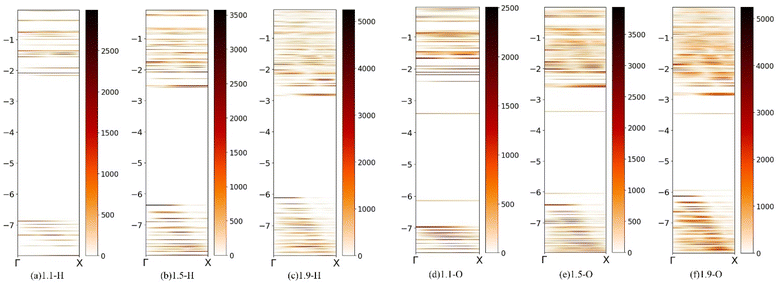
To further study the luminescence mechanism of Si-QDs, the band expansion method was used to reproject the wavefunction in real space back to the inverted space, and analyze the molecular orbitals of Si-QDs with different sizes.60
In the quantum dot system, the finite quantum dot can be regarded as a supercell, and its electronic state can be reverse folded into the Brillouin zone of silicon so as to analyze the bandgap characteristics of quantum dots.
Fig. 5 shows molecular orbitals of silicon quantum dots (fuzzy band) with diameters of 1.1 nm, 1.5 nm, and 1.9 nm. Quantum dots completely terminated by hydrogen and those terminated by silicon–oxygen double bonds are discussed separately. The fuzzy bands of other ligand-terminated quantum dots are given in ESI Fig. S3.† The scale on the left represents the energy with the unit eV, and the color represents the density of states, which gradually increases from light to dark. As shown in Fig. 5, Si-QDs exhibit direct bandgap features at small sizes. As the size increases, this slowly transitions to an indirect bandgap similar to that of bulk silicon. This can explain the phenomenon where the luminous efficiency decreases with increasing size, so it is necessary to control the quantum dots to remain smaller when preparing silicon-based light-emitting materials. It is clear in the fuzzy band diagrams of the three sizes of Si-QDs terminated by silicon–oxygen double bonds, that there is an obvious bright line near −3.4 eV, which is a defect state energy level related to the silicon–oxygen double bonds. The luminescence belonging to Si–O double bonds is caused by the direct transition of the interface state. Unlike the quantum dots that are completely terminated by hydrogen, the luminescence belongs to the luminescence of the silicon quantum dots themselves, caused by indirect transition, such that the luminescence becomes weaker as the size increases. The quantum dots with a diameter of 1.1 nm terminated by toluene groups also showed obvious interface state luminescence (Fig. S4(a)†), but with the increase in size, this gradually transformed into the luminescence of silicon quantum dots themselves, resulting in a decrease in luminescence intensity.
IV. Conclusions
This study employs density functional theory and time-dependent density functional theory to investigate the luminescence mechanism of silicon quantum dots. Si-QDs with varying sizes and surface termination ligands (including hydrogen, silicon–oxygen double bond, and hydroxyl, methyl, amino, and vinyl and toluene groups) were considered, along with the presence or absence of dangling bonds. The luminescence intensity, luminescence wavelength and luminescence lifetime of Si-QDs were calculated, and their electron–hole density distribution and molecular orbital were analyzed. In the spectral calculation, it was found that the surface ligands have a great influence on the luminescence of small-sized quantum dots, emitting light covering almost all visible light bands. Mixing quantum dots terminated by different ligands in a certain proportion can produce white light emission. The quantum dots containing silicon–oxygen double bonds have the strongest luminescence, and with the increase in size, they can still maintain a high luminescence intensity. However, quantum dots whose surface is terminated by other ligands can obtain a large luminescence intensity at a diameter of 1.1 nm, and when the diameter increases, the luminescence intensity clearly declines. Therefore, when fabricating silicon-based light-emitting devices, it is necessary to maintain the size of the quantum dots on a smaller scale. In addition, the existence of dangling bonds will weaken the luminescence intensity, and it is necessary to passivate the surface dangling bonds as much as possible. Through the analysis of the distribution of electron holes related to the radiative transition, the luminescence induced by the silicon–oxygen double bonds originates from the luminescence of the interface state caused by the defect state, and its luminescence lifetime is between the indirect bandgap transition and the direct bandgap transition, which can be considered a quasi-direct transition. Through fuzzy band analysis, it is found that the silicon–oxygen double bonds cause an obvious defect state energy level, which may be the main reason for their high luminescence intensity. Our results help to explain the luminescence mechanism of Si-QDs and provide possible directions for how to experimentally improve the luminescence intensity of silicon nanocrystals.Author contributions
Zhou, J. and Wang, S.-Y. designed the research; Zhou, J. and Wang, S.-Y. carried out all the simulation and data analyses; Ma, F.-Y., Yang, R.-Y., Chen, K., Zhao, W.-Y., Shen, H., Qiao, C. and Su, W.-S. discussed and interpreted the results; and Zhou, J., Ma, F.-Y., Su, W.-S. and Wang, S.-Y. wrote the paper. All authors read and commented on the manuscript description.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Work at the Fudan University was supported by the key projects of basic research of the Shanghai Municipal Science and Technology Commission (No. 22JC400300 and 18JC1411500), the National Natural Science Foundation of China (Grant No. 11374055 and 61427815) and the Zhangjiang Fudan International Innovation Center.; W.-S. Su would like to thank the Ministry of Science and Technology for financially supporting this research under Contract No. MOST-111-2112-M-979-001. Support from the National Centers for Theoretical Sciences and High-Performance Computing of Taiwan in providing significant computing resources to facilitate this research is also gratefully acknowledged.Notes and references
- A. R. Hawkins, T. E. Reynolds, D. R. England, D. I. Babic, M. J. Mondry, K. Streubel and J. E. Bowers, Appl. Phys. Lett., 1996, 68, 3692–3694 CrossRef CAS.
- Y. Xin, K. Nishio and K.-I. Saitow, Appl. Phys. Lett., 2015, 106, 201102 CrossRef.
- D. Wang, C. Zhang, P. Zeng, W. Zhou, L. Ma, H. Wang, Z.-q. Zhou, F. Hu, S. Zhang, M. Lu and X. J. C. S. B. Wu, Sci. Bull., 2018, 63, 75–77 CrossRef CAS PubMed.
- C. Zhang, B. Yang, J. Chen, D. Wang, Y. Zhang, S. Li, X. Dai, S. Zhang and M. Lu, Opt. Express, 2020, 28, 194–204 CrossRef CAS PubMed.
- T. Ono, Y. Xu, T. Sakata and K.-I. Saitow, ACS Appl. Mater. Interfaces, 2021, 14, 1373–1388 CrossRef PubMed.
- Y.-C. Zhang, Z.-Y. Yu, X.-Y. Xue, F.-L. Wang, S. Li, X.-Y. Dai, L. Wu, S.-Y. Zhang, S.-Y. Wang and M. Lu, Opt. Express, 2021, 29, 34126–34134 CrossRef CAS PubMed.
- R. Kuladeep, L. Jyothi, C. Sahoo, D. Narayana Rao and V. Saikiran, J. Mater. Sci., 2022, 57, 1863–1880 CrossRef CAS.
- B. Jalali and S. Fathpour, J. Lightwave Technol., 2006, 24, 4600–4615 CAS.
- J. Wang, I. Glesk and L. R. Chen, Sci. Bull., 2016, 61, 879–888 CrossRef CAS.
- R. Gherabli, M. Grajower, J. Shappir, N. Mazurski, M. Wofsy, N. Inbar, J. B. Khurgin and U. Levy, Opt. Lett., 2020, 45, 2128–2131 CrossRef PubMed.
- S. Li, J.-P. Chou, H. Zhang, Y. Lu and A. Hu, J. Appl. Phys., 2018, 125, 082520 CrossRef.
- A. G. Cullis and L. T. Canham, Nature, 1991, 353, 335–338 CrossRef CAS.
- M. Dasog, K. Bader and J. G. C. Veinot, Chem. Mater., 2015, 27, 1153–1156 CrossRef CAS.
- R. J. Walters, J. Kalkman, A. Polman, H. A. Atwater and M. J. A. de Dood, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 132302 CrossRef.
- T. Takagahara and K. Takeda, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 15578–15581 CrossRef CAS PubMed.
- D. Beri, D. Busko, A. Mazilkin, I. A. Howard, B. S. Richards and A. Turshatov, RSC Adv., 2018, 8, 9979–9984 RSC.
- L. A. Gómez-González, A. Dutt, B. M. Monroy, J. D. Escobar-Carrasquilla, G. Santana, C. Álvarez-Macías and A. Ponce, Funct. Mater. Lett., 2017, 10, 1750014 CrossRef.
- F. Wang, Q. Ou and S. Zhang, Phys. Rev. B, 2022, 105, 155425 CrossRef.
- M. Bürkle, M. Lozac'h, C. McDonald, D. Mariotti, K. Matsubara and V. Švrček, Adv. Funct. Mater., 2017, 27, 1701898 CrossRef.
- M. Dasog, K. Bader and J. G. C. Veinot, Chem. Mater., 2015, 27, 1153–1156 CrossRef CAS.
- M. Dasog, G. de los reyes, L. Titova, F. Hegmann and J. Veinot, ACS Nano, 2014, 8, 9636–9648 CrossRef CAS PubMed.
- E. Draeger, J. Grossman, A. Williamson and G. Galli, J. Chem. Phys., 2004, 120, 10807–10814 CrossRef CAS PubMed.
- M. B. Javan, Phys. B, 2015, 456, 321–329 CrossRef CAS.
- H. Shen, Z. Yu, J. Wang, M. Lu, C. Qiao, W.-S. Su, Y. Zheng, R. Zhang, Y. Jia, L. Chen, C. Wang, K. Ho and S. Wang, Nanoscale Adv., 2021, 3, 2245–2251 RSC.
- X.-Y. Dai, Y.-C. Zhang, L.-X. Wang, F. Hu, Z.-Y. Yu, S. Li, S.-J. Li, X.-J. Yang and M. Lu, Chin. Phys. B, 2020, 29, 118801 CrossRef CAS.
- O. Labeau, P. Tamarat and B. Lounis, Phys. Rev. Lett., 2003, 90, 257404 CrossRef PubMed.
- S. Mitra, V. Švrček, M. Macias-Montero, T. Velusamy and D. Mariotti, Sci. Rep., 2016, 6, 27727 CrossRef CAS PubMed.
- J. Yang, H. Fang and Y. Gao, Nano Energy, 2016, 30, 614–620 CrossRef CAS.
- L. Dal Negro, L. Pavesi, G. Pucker, G. Franzò and F. Priolo, Opt. Mater., 2001, 17, 41–44 CrossRef CAS.
- D. Dai, J. Bauters and J. E. Bowers, Light: Sci. Appl., 2012, 1, e1 CrossRef.
- S. Koeber, R. Palmer, M. Lauermann, W. Heni, D. L. Elder, D. Korn, M. Woessner, L. Alloatti, S. Koenig, P. C. Schindler, H. Yu, W. Bogaerts, L. R. Dalton, W. Freude, J. Leuthold and C. Koos, Light: Sci. Appl., 2015, 4, e255 CrossRef CAS.
- L. Vivien, A. Polzer, D. Marris-Morini, J. Osmond, J. M. Hartmann, P. Crozat, E. Cassan, C. Kopp, H. Zimmermann and J.-M. J. O. e. Fédéli, Opt. Express, 2012, 20, 1096–1101 CrossRef CAS PubMed.
- N.-V. Hoang, A. N. Baranov, Z. Loghmari, L. Cerutti, J.-B. Rodriguez, J. Tournet, G. Narcy, G. Boissier, G. Patriarche, M. Bahriz, E. Tournie and R. Teissier, Sci. Rep., 2018, 8, 7206 CrossRef PubMed.
- Y. Wan, D. Inoue, D. Jung, J. C. Norman, C. Shang, A. C. Gossard and J. E. Bowers, Photonics Res., 2018, 6, 776–781 CrossRef CAS.
- D.-C. Wang, C. Zhang, P. Zeng, W.-J. Zhou, L. Maa, H.-T. Wang, Z.-Q. Zhou, F. Hu, S.-Y. Zhang, M. Lu and X. Wu, Sci. Bull., 2018, 63, 75–77 CrossRef CAS PubMed.
- Y. Wang, S. Chen, Y. Yu, L. Zhou, L. Liu, C. Yang, M. Liao, M. Tang, Z. Liu, J. Wu, W. Li, I. Ross, A. J. Seeds, H. Liu and S. Yu, Optica, 2018, 5, 528–533 CrossRef CAS.
- J. Klamkin, S. Zhu, B. Shi, L. Wang and B. Song, presented in part at the Conference on Novel In-Plane Semiconductor Lasers XXI, San Francisco, CA, 2022 Search PubMed.
- Z.-Y. Yu, Y.-C. Zhang, S. Li, X.-Y. Dai, X.-Y. Xue, H. Shen, S. Y. Wang and M. Lu, Vacuum, 2022, 197, 110822 CrossRef CAS.
- C. Zhang, B. Yang, J. Chen, D. Wang, Y. Zhang, S. Li, X. Dai, S. Zhang and M. Lu, Opt. Express, 2020, 28, 194–204 CrossRef CAS PubMed.
- C. Zhang, P. Zeng, W.-J. Zhou, Y.-C. Zhang, X.-P. He, Q.-Y. Jin, D.-C. Wang, H.-T. Wang, S.-Y. Zhang, M. Lu and X. Wu, IEEE J. Sel. Top. Quantum Electron., 2020, 26, 1 Search PubMed.
- Y.-C. Zhang, Z.-Y. Yu, X.-Y. Xue, F.-L. Wang, S. Li, X.-Y. Dai, L. Wu, S.-Y. Zhang, S.-Y. Wang and M. Lu, Opt. Express, 2021, 29, 34126–34134 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- P. Hapala, K. Krusov’a, I. Pelant and P. J. P. R. B. Jelínek, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195420 CrossRef.
- H. Vázquez, P. Jelínek, M. Brandbyge, A. P. Jauho and F. Flores, Appl. Phys. A: Mater. Sci. Process., 2009, 95, 257–263 CrossRef.
- J. Yang, H. Fang and Y. Gao, J. Phys. Chem. Lett., 2016, 7, 1788–1793 CrossRef CAS PubMed.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed.
- Z. Liu, T. Lu and Q. Chen, Carbon, 2020, 165, 461–467 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- P. A. M. Dirac, The Quantum Theory of the Emission and Absorption of Radiation, 1927 Search PubMed.
- K. Petr and W. Jakob, A Crash Course in Photophysics and a Classification of Primary Photoreactions, 2009 Search PubMed.
- M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19 RSC.
- M. Wolkin, J. Jorne, P. Fauchet, G. Allan and C. Delerue, Phys. Rev. Lett., 1999, 82, 197–200 CrossRef CAS.
- D. De Boer, D. Timmerman and K. Dohnalová, et al. , Nat. Nanotechnol., 2010, 84, 878 CrossRef PubMed.
- X. Liu, S. Zhao, W. Gu, Y. Zhang, X. Qiao, Z. Ni, X. Pi and D. Yang, ACS Appl. Mater. Interfaces, 2018, 10, 5959–5966 CrossRef CAS PubMed.
- Y. Zhang, C. Zhang, S. Li, X.-Y. Dai, X. Ma, R. Gao, W. Zhou and M. Lu, Opt. Express, 2020, 28, 23320–23328 CrossRef CAS PubMed.
- T. Lu and F. Chen, Carbon, 2012, 33, 580–592 CAS.
- V. Kocevski, O. Eriksson and J. Rusz, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245401 CrossRef.
- P. Medeiros, S. Stafström and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 041407(R) CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00251a |
| This journal is © The Royal Society of Chemistry 2023 |