Open Access Article
Open Access ArticleVacancy-plane-mediated exfoliation of sub-monolayer 2D pyrrhotite†
Jian-Jhang
Lee
 ab,
Yi-Hung
Chu
bc,
Zhi-Long
Yen
ab,
Jeyavelan
Muthu
a,
Chu-Chi
Ting
c,
Ssu-Yen
Huang
a,
Mario
Hofmann
ab,
Yi-Hung
Chu
bc,
Zhi-Long
Yen
ab,
Jeyavelan
Muthu
a,
Chu-Chi
Ting
c,
Ssu-Yen
Huang
a,
Mario
Hofmann
 a and
Ya-Ping
Hsieh
a and
Ya-Ping
Hsieh
 *bc
*bc
aDepartment of Physics, National Taiwan University, Taipei, Taiwan
bInstitute of Atomic and Molecular Sciences, Academia Sinica, Taipei, Taiwan. E-mail: yphsieh@gate.sinica.edu.tw
cGraduate Institute of Opto-Mechatronics, National Chung Cheng University, Chiayi, Taiwan
First published on 14th June 2023
Abstract
Conventional exfoliation exploits the anisotropy in bonding or compositional character to delaminate 2D materials with large lateral size and atomic thickness. This approach, however, limits the choice to layered host crystals with a specific composition. Here, we demonstrate the exfoliation of a crystal along planes of ordered vacancies as a novel route toward previously unattainable 2D crystal structures. Pyrrhotite, a non-stoichiometric iron sulfide, was utilized as a prototype system due to its complex vacancy superstructure. Bulk pyrrhotite crystals were synthesized by gas-assisted bulk conversion, and their diffraction pattern revealed a 4C superstructure with 3 vacancy interfaces within the unit cell. Electrochemical intercalation and subsequent delamination yield ultrathin 2D flakes with a large lateral extent. Atomic force microscopy confirms that exfoliation occurs at all three supercell interfaces, resulting in the isolation of 2D structures with sub-unit cell thicknesses of 1/2 and 1/4 monolayers. The impact of controlling the morphology of 2D materials below the monolayer limit on 2D magnetic properties was investigated. Bulk pyrrhotite was shown to exhibit ferrimagnetic ordering that agrees with theoretical predictions and that is retained after exfoliation. A complex magnetic domain structure and an enhanced impact of vacancy planes on magnetization emphasize the potential of our synthesis approach as a powerful platform for modulating magnetic properties in future electronics and spintronics.
Introduction
In recent years, two-dimensional (2D) materials have emerged as a new class of materials with unique physical, chemical, and electronic properties. These materials, which are only a few atoms thick, have attracted significant attention due to their potential applications in electronics, optoelectronics, energy, and biomedical fields.To produce atomically-thin 2D materials, the structural anisotropy of 2D materials is exploited. Bottom-up growth processes and mechanical exfoliation rely on the difference in bonding character between in-plane and out-of-plane bonds.1 Chemical exfoliation processes, on the other hand, utilize the difference in composition within a layered crystal.2 While those approaches have yielded 2D materials with high quality and scale, they are limited to producing crystal compositions and phases that intrinsically exhibit a layered structure.
Here, we demonstrate the atomically precise exfoliation along ordered vacancy interfaces within a compositionally uniform crystal. In many systems, the vacancy-induced strain relaxation in crystals results in the distribution of vacancies into complex and periodic superstructures. Vacancy interfaces are a universal characteristic of a wide variety of materials and crystal structures.3 Moreover, the spacing of vacancy interfaces can be finely controlled by adjusting vacancy concentration and thermodynamic conditions, which could provide unprecedented freedom in designing the morphology of 2D materials.
We utilize pyrrhotite as a platform to demonstrate the exfoliation of 2D materials along vacancy planes for the first time. Pyrrhotite represents a range of materials with a composition Fe1−xS (0 ≤ x ≤ 0.15). Depending on the concentration of vacancies in the metal cation site, four different commensurate and a multitude of incommensurate superstructures have been identified. These structures differ in the repeat number along the crystallographic c-axis, which can take on the integer values 3, 4, 5, and 6 as well as non-rational numbers.4,5
Bulk pyrrhotite was synthesized by the sulfurization of iron foil. The resulting pyrrhotite structure was confirmed by X-ray diffraction and Raman spectroscopy. Electrochemical intercalation with chlorine ions and subsequent delamination was found to retain the pyrrhotite structure. The diffraction characterization revealed that the crystal structure of the exfoliated pyrrhotite was of the 4C type. We found that the thickness of the thus-exfoliated pyrrhotite could be below the predictions of a complete unit cell, achieving fractional monolayer thickness, which is consistent with the predictions for exfoliation along the vacancy planes. Our results provide a novel route for controlling the properties of 2D materials, and we demonstrate its application in tailoring magnetic 2D materials. Similar to bulk pyrrhotite, vacancy-delaminated 2D pyrrhotite retains ferrimagnetic ordering. Sub-unit 2D pyrrhotites were found to have enhanced magnetic ordering and complex magnetic domain structures, making them promising for future applications in spintronics and memory.
Experimental
Bulk pyrrhotite was synthesized by directly sulfurizing iron using iron foil (Alfa Aesar, 99.5% (metals basis), 0.025 mm thick) as a precursor. The iron foil was annealed under hydrogen at 400 °C for 2 hours and then heated to 850 °C in 30 minutes to remove the natural surface oxide. The iron foil and sulfur powder were placed in a ceramic boat (Fig. 1(a)), and the sample was annealed at 350 °C for 6 hours to sulfurize iron at a pressure of 10−3 Torr. The ESI† provides details on the types and measurement parameters of all instruments used for material analysis.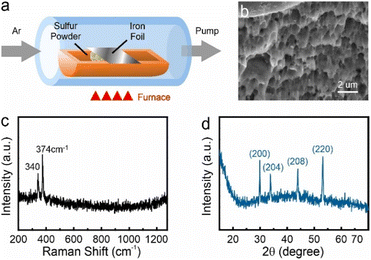 | ||
| Fig. 1 (a) CVD setup diagram, (b) the layer structure at pyrrhotite cross-section SEM image, (c) Raman characterization for pyrrhotite sample, (d) XRPD characterization for pyrrhotite sample. | ||
Results and discussions
After the bulk conversion process, the produced material is characterized by electron microscopy and spectroscopy. Scanning Electron Microscope (SEM) images demonstrate a layered structure (Fig. 1(b)), which agrees with previous reports on pyrrhotite.6 Elemental analysis reveals a Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio of 0.96
S ratio of 0.96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as expected for pyrrhotite (see ESI†). This assessment is supported by spectroscopy and diffraction. Raman spectroscopy demonstrates the presence of two peaks at 340 cm−1 and 374 cm−1 (Fig. 1(c)), which exclude several other substoichiometric iron sulfides (see ESI†).
1, as expected for pyrrhotite (see ESI†). This assessment is supported by spectroscopy and diffraction. Raman spectroscopy demonstrates the presence of two peaks at 340 cm−1 and 374 cm−1 (Fig. 1(c)), which exclude several other substoichiometric iron sulfides (see ESI†).
The X-ray powder diffractogram (XRPD) for the sample is presented in Fig. 1(d). The interatomic spacings, d, can be calculated by using Bragg's equation from the angles which give diffraction peaks. XRPD data shows that the sample is hexagonal Fe1−xS. Consider a set of values of h1, k1, l1, and d1, where d1 is the interatomic spacing of atoms in the planes with Miller indices (h1k1l1), and h2, k2, l2, and d2, where d2 is the interatomic spacing of atoms in the planes with Miller indices (h2k2l2). The matrix equation for a hexagonal system (a = b ≠ c) obtained is as follows:
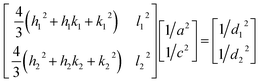 | (1) |
The lattice constants (a and c) for a hexagonal crystal from eqn (1) are obtained as:
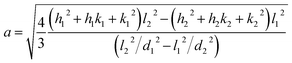 | (2) |
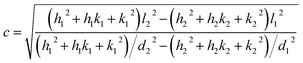 | (3) |
If either h1 = k1 = 0 or h2 = k2 = 0, we obtain
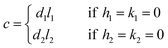 | (4) |
If l1 = l2 = 0 or h1 = k2 = h2 = k2 = 0, eqn (2) and (3) cannot be used.
By using eqn (2) and (3) and the values from the XRPD data, we obtain Table 1 and the lattice constants for pyrrhotite, which are a = 6.895(6) Å and c = 22.788(0) Å. The calculated results agree with those reported by Nkoma and Ekosse.7
| (h1k1l1) | d 1 (Å) | (h2k2l2) | d 2 (Å) | a (Å) | c (Å) |
|---|---|---|---|---|---|
| (200) | 2.9869(0) | (204) | 2.6459(8) | 6.8979 | 22.8127 |
| (204) | 2.6459(8) | (208) | 2.0585(1) | 6.9074 | 22.6991 |
| (208) | 2.0585(1) | (220) | 1.7518(4) | 6.8873 | 22.7591 |
| (200) | 2.9869(0) | (208) | 2.0585(1) | 6.8979 | 22.7273 |
| (204) | 2.6459(8) | (220) | 1.7218(4) | 6.8873 | 22.9418 |
| Mean | 6.895(6) | 22.788(0) |
Two-dimensional pyrrhotite has been produced by several methods, such as a hydrothermal method,8–10 systematic reduction of pyrite FeS2 films by vacuum annealing,11 and a molecular sieve-assisted CVD method.12 In 2017, Chen et al. obtained pyrrhotite nanosheets in a top-down approach from a pyrrhotite–hexylamine intermediate (inorganic–organic hybrid intermediate) synthesized by the hydrothermal method through ultrasonic treatment in an organic solvent.13 However, these bottom-up methods produce stable stoichiometries without ordered vacancy planes and only yield 2D layers with thicknesses that are limited by the unit cell dimension.
Instead of utilizing mechanical exfoliation14,15 to exfoliate bulk crystals into 2D layers, which has little control over the delamination process, we conduct top-down patterning of the bulk crystal to take advantage of pyrrhotite's vacancy superstructure. We employ electrochemical exfoliation instead, due to its demonstrated ability to exert minimal delamination force and produce large, defect-free 2D layers.16
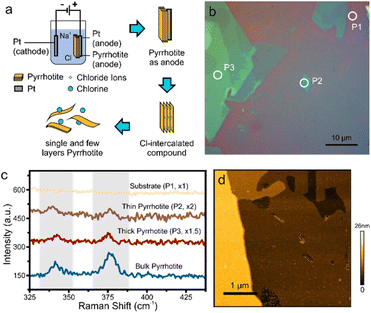
For this purpose, bulk pyrrhotite was used as the working electrode, and a platinum rod served as the counter-electrode. A 1 M sodium chloride aqueous solution was employed as the electrolyte. A static bias of +1 V was first applied to the pyrrhotite electrode for 5 minutes, followed by ramping the bias to +10 V for 1 minute. Under these conditions, the electrochemical intercalation of Cl− anions occurs when the initial low potential is applied. Upon the formation of Cl2 at a higher overpotential (see ESI†), the interlayer distance of pyrrhotite is increased, and exfoliation occurs (Fig. 2(a)).17
The resulting material suspension was drop-casted onto substrates and characterized by Optical Microscopy (OM). As with other 2D materials, a distinct color contrast is observed compared to the substrate, which originates from interference at the interfaces of the 2D material (Fig. 2(b)).18 From the extent of uniform contrast regions, layer dimensions of tens-of micrometers can be extracted. Raman spectroscopy of the exfoliated flakes demonstrates the presence of the same features as bulk pyrrhotite (Fig. 2(c)). However, changes in peak position and peak intensity are observed, which can be attributed to the change of the inter-atomic distances upon isolation of 2D layers.19,20
Finally, we demonstrate the presence of large and uniform sheets by atomic force microscopy (Fig. 2(d)).
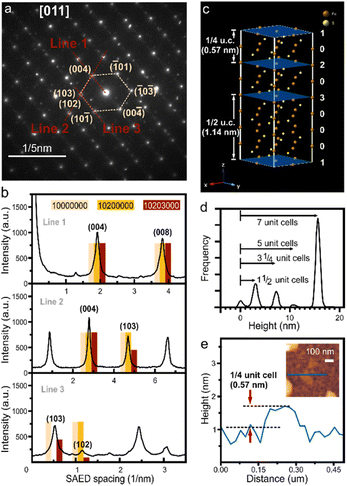
We characterize the exfoliated pyrrhotite by selected area electron diffraction (SAED) (Fig. 3(a)). Diffraction is a powerful tool to establish the complex structure of pyrrhotite. In addition to revealing the hexagonal structure of the material, SAED shows varying intensity for several characteristic diffraction peaks (Fig. 3(b)). Through the correlation of this intensity distribution with simulation, the structure of a unit cell can be established.21 We observe a low-intensity (102) feature that rules out a defect-free octuple unit (Fig. 3(b)). Moreover, a high-intensity (103) peak indicates that the structure is not symmetrically divided into two sub-units. The analysis of diffraction intensity suggests that the exfoliated pyrrhotite consists of three vacancy planes in the form (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 203
203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), where 1, 2, 3 are the indices of the vacancy planes, and 0 denotes vacancy-free pyrrhotite planes (Fig. 3(c)).
000), where 1, 2, 3 are the indices of the vacancy planes, and 0 denotes vacancy-free pyrrhotite planes (Fig. 3(c)).
The unique pyrrhotite superstructure suggests that cleavage can occur at three equivalent sites: if cleaved at the 1 vacancy plane, a complete octuple unit cell emerges, whereas cleavage at the 2 or 3 planes leads to subdivisions of the unit cell into 1/4 or 1/2, respectively.
Statistical analysis of atomic force micrographs demonstrates that the exfoliation into sub-units indeed occurs along these vacancy planes. Fig. 3(d) shows a height histogram taken across a large-scale AFM image, and each distinct peak corresponds to the number of layers with similar thicknesses. We observe that the separation of these peaks is not in full increments of the unit-cell (u.c.) dimension but 1/2 and 1/4 fractions occur. From these observations that the exfoliation of pyrrhotite occurs in vacancy layers. We observe sheets with a minimum thickness of 0.57 nm representing the thinnest possible vacancy-terminated layer in the pyrrhotite unit cell, e.g. 1/4 of a monolayer (Fig. 3(e)).
Our results open up a new route toward tailoring the morphology of 2D materials with unprecedented precision and control. To date, 2D materials exfoliation could only be conducted from layered host crystals,22 which limits the achievable compositional variability. The universal nature of vacancy interfaces could extend the range of compositions and symmetries beyond layered structures.
We investigate the impact of this powerful method on the emerging field of 2D magnetism. Previous work has demonstrated the strong connection between structural and magnetic properties in 2D materials with complex morphology. Wu et al. demonstrated the formation of Néel skyrmions at the interface between WTe2 and Fe3GeTe2 2D layers.23 Moreover, the magnetic transition temperature and coercive field of 2D magnetic materials were enhanced by interfacial coupling with suitable nonmagnetic 2D materials.24 Finally, the stacking thickness and twisting angle were shown to drastically affect the magnetic behavior of 2D materials.25
The control over pyrrhotite morphology offers a promising route to manipulating its magnetic response. The magnetic behavior of pyrrhotite is intimately linked to its crystal and vacancy structure. The crystallographic c-direction features antiferromagnetic (AFM) interactions between adjacent Fe atoms, while the ab-plane is characterized by ferromagnetic (FM) interactions between iron atoms occupying every other corner of a hexagon. The exchange coupling constants J1 and J2, which are negative and positive, respectively, dominate these interactions (see ESI†). The magnetic behavior in pyrrhotite can be understood following the Goodenough–Kanamori–Anderson (GKA) rules.26–28 The Fe–Fe distance of atoms stacked along the crystallographic c-direction is less than 3 Å, which enables effective d orbital overlap without ligand participation. This arrangement explains the origin of the AFM interaction between adjacent spin-alternating Fe layers. On the other hand, the FM interacting iron atoms occupy every other corner of the hexagon formed in the ab-plane, and the distances allow for orbital overlap, minimizing the intra-site Coulomb energy and favoring FM coupling.
This competition between AFM and FM coupling is perturbed by the presence of vacancies. The periodic arrangement of Fe vacancies in the c-direction will weaken the AFM coupling and result in a small average moment29 leading to weak ferrimagnetism.
We confirm this mechanism in bulk pyrrhotite. The hysteresis of pyrrhotite 4C bulk observed from SQUID shows that the magnetic moment at saturation for Fe is 2.67μB (Fig. 4(a)), which is close to the value predicted by density functional theory (DFT) and Monte Carlo simulations (lit.,30 2.62μB).
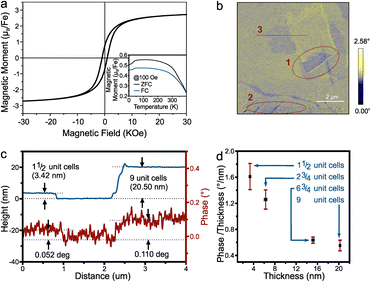 | ||
| Fig. 4 (a) The room temperature hysteresis and (insert) temperature dependent magnetization of pyrrhotite 4C bulk, (b) the MFM phase image at P2 in Fig. 2(b). Red dotted circles mark opposite contrast regions, (c) the height profile and the corresponding phase contrast of line 3 in (b) and (d) the relation between the magnetic phase contrast/thickness and the thickness. | ||
Fig. 4(a) insert shows the magnetization temperature dependence from 400 K to 4 K. It shows a Besnus transition of ferrimagnetic characteristics at 34 K, as observed by Rochette et al.,31 which was attributed to a change in the magnetization easy axis direction within the basal plane. The Curie temperature obtained by the graphical method is about 473 K (see ESI†), which is quite close to the 450 K reported by Kuhn et al.32
We investigated the magnetic response of 2D pyrrhotite using magnetic force microscopy (MFM). The MFM phase image (Fig. 4(b)) shows the retention of ferrimagnetism for the exfoliated pyrrhotite, with distinct domains observed within layers of the same thickness. Opposite magnetization directions can be found in the same flakes (regions 1 and 2 in Fig. 4(b)), demonstrating the magnetization's stability even at room temperature.33 At the same time, as observed in ferrimagnetic nanosheets by Cheng et al., uniform domains with anti-parallel magnetization shrink with decreasing thickness (the thickness of region 1 is 9-unit-cell, and the thickness of region 2 is 1½-unit-cell), indicating a tendency toward single-domain behavior.34
Finally, a relationship between thickness and magnetic phase contrast shows an increase in contrast with thickness as expected for the bulk material (Fig. 4(c)). Closer analysis, however, reveals that the magnetic response from each iron atom decreases with thickness (Fig. 4(d)). This result is not only consistent with the trend of ferrimagnetic materials reported,33,35 but also confirms the importance of vacancy planes to the magnetic response of pyrrhotite and indicates that layer-by-layer assembly of 2D pyrrhotite could lead to enhanced ferrimagnetism.
Conclusions
In a top-down approach, we first demonstrate the exfoliation of 2D materials along vacancy planes in pyrrhotite. This not only confirms the importance of vacancy planes to the magnetic response of pyrrhotite but also opens up the possibility of tailoring non-vdW magnetic 2D materials. The experimental results display that the vacancy-delaminated 2D pyrrhotite maintains ferrimagnetic ordering, which is similar to that of bulk pyrrhotite, and indicates that layer-by-layer assembly of 2D pyrrhotite can enhance ferrimagnetism. These results advance our understanding of the complex structure–property relation in 2D magnets and enable promising applications in future electronics and spintronics.Author contributions
Conceptualization, Y.-P. H.; methodology, J.-J. L.; software, J.-J. L.; validation, J.-J. L.; formal analysis, J.-J. L. and M. H.; investigation, J.-J. L., Y.-H. C., Z.-L. Y. and J. M.; resources, J.-J. L., Y.-H. C. and J. M.; data curation, J.-J. L.; writing—original draft preparation, J.-J. L.; writing—review and editing, Y.-P. H., S.-Y. H. and M. H.; visualization, J.-J. L., Y.-H. C. and Z.-L. Y.; supervision, Y.-P. H.; project administration, Y.-P. H.; funding acquisition, Y.-P. H. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors would like to thank Mr Yung-Sheng Chen and the Instrumentation Center at National Tsing Hua University for their assistance in the magnetic measurements. The authors acknowledge the Instruments Center at National Chung Cheng University for the FE-SEM measurement. Finally, the authors also thank the Ministry of Science and Technology grant number 108-2112-M-001-040-MY3 and Academia Sinica grant number AS-GCS-112-M04 for funding this work.References
- A. Puthirath Balan, S. Radhakrishnan, C. F. Woellner, S. K. Sinha, L. Deng, C. L. Reyes, B. M. Rao, M. Paulose, R. Neupane, A. Apte, V. Kochat, R. Vajtai, A. R. Harutyunyan, C. W. Chu, G. Costin, D. S. Galvao, A. A. Marti, P. A. van Aken, O. K. Varghese, C. S. Tiwary, A. Malie Madom Ramaswamy Iyer and P. M. Ajayan, Nat. Nanotechnol., 2018, 13, 602–609 CrossRef CAS PubMed.
- Y. Gogotsi and B. Anasori, ACS Nano, 2019, 13, 8491–8494 CrossRef CAS PubMed.
- N. B. Zhang, Z. Fang, Y. L. Zhu, Y. J. Wang, Y. L. Tang, M. J. Zou and X. L. Ma, J. Phys. Chem. C, 2022, 126, 20627–20635 CrossRef CAS.
- C.-h. Zhao, B.-z. Wu and J.-h. Chen, J. Cent. South Univ., 2015, 22, 466–471 CrossRef CAS.
- Z. Zhao, J. Zhou, L. Liu, N. Liu, J. Huang, B. Zhang, W. Li, Y. Zeng, T. Zhang, W. Ji, T. Yang, Z. Zhang, S. Li and Y. Hou, Nano Lett., 2022, 22, 1242–1250 CrossRef CAS PubMed.
- A. M. Paca and P. A. Ajibade, Nanomaterials, 2018, 8, 187 CrossRef PubMed.
- J. S. Nkoma and G. Ekosse, J. Phys.: Condens. Matter, 1999, 11, 121–128 CrossRef CAS.
- L. Argueta-Figueroa, N. Torres-Gómez, R. García-Contreras, A. R. Vilchis-Nestor, O. Martínez-Alvarez, L. S. Acosta-Torres and M. C. Arenas-Arrocena, Prog. Nat. Sci.: Mater. Int., 2018, 28, 447–455 CrossRef CAS.
- J. G. Lozano, F. Dillon, A. J. Naylor, L. Y. Lee, C. Lippard, D. Johnstone, P. G. Bruce and N. Grobert, Chem. Phys. Lett., 2020, 739, 136993 CrossRef CAS.
- I. S. Lyubutin, C.-R. Lin, S.-Z. Lu, Y.-J. Siao, Y. V. Korzhetskiy, T. V. Dmitrieva, Y. L. Dubinskaya, V. S. Pokatilov and A. O. Konovalova, J. Nanopart. Res., 2011, 13, 5507–5517 CrossRef CAS.
- X. Zhang, T. Scott, T. Socha, D. Nielsen, M. Manno, M. Johnson, Y. Yan, Y. Losovyj, P. Dowben, E. S. Aydil and C. Leighton, ACS Appl. Mater. Interfaces, 2015, 7, 14130–14139 CrossRef CAS.
- B. Wang, Y. Yao, W. Hong, Z. Hong, X. He, T. Wang, C. Jian, Q. Ju, Q. Cai, Z. Sun and W. Liu, Small, 2023, e2207325, DOI:10.1002/smll.202207325.
- S. Chen, Z. Kang, X. Zhang, J. Xie, H. Wang, W. Shao, X. Zheng, W. Yan, B. Pan and Y. Xie, ACS Cent. Sci., 2017, 3, 1221–1227 CrossRef CAS PubMed.
- M. Yusuf, M. Kumar, M. A. Khan, M. Sillanpaa and H. Arafat, Adv. Colloid Interface Sci., 2019, 273, 102036 CrossRef CAS PubMed.
- D. D. L. Chung, J. Mater. Sci., 2015, 51, 554–568 CrossRef.
- M. Hofmann, W. Y. Chiang, T. D. Nguyen and Y. P. Hsieh, Nanotechnology, 2015, 26, 335607 CrossRef PubMed.
- A. R. Kamali, J. Ind. Eng. Chem., 2017, 52, 18–27 CrossRef CAS.
- Y. C. Lee, S. W. Chang, S. H. Chen, S. L. Chen and H. L. Chen, Adv. Sci., 2022, 9, e2102128 CrossRef PubMed.
- A. Puthirath Balan, E. F. Oliveira, G. Costin, T. Gray, N. Chakingal, A. Biswas and A. B. Puthirath, Oxford Open Materials Science, 2023, 3, itac020 CrossRef.
- S. h. Urashima, K. Narahara and H. Yui, J. Raman Spectrosc., 2022, 53, 2129–2136 CrossRef CAS.
- I. Dodony and M. Posfai, Eur. J. Mineral., 1990, 2, 529–535 CrossRef CAS.
- W. Zheng and L. Y. S. Lee, Matter, 2022, 5, 515–545 CrossRef CAS.
- Y. Wu, S. Zhang, J. Zhang, W. Wang, Y. L. Zhu, J. Hu, G. Yin, K. Wong, C. Fang, C. Wan, X. Han, Q. Shao, T. Taniguchi, K. Watanabe, J. Zang, Z. Mao, X. Zhang and K. L. Wang, Nat. Commun., 2020, 11, 3860 CrossRef PubMed.
- Q. Hao, H. Dai, M. Cai, X. Chen, Y. Xing, H. Chen, T. Zhai, X. Wang and J. B. Han, Adv. Electron. Mater., 2022, 8, 2200164 CrossRef CAS.
- W. Chen, Z. Sun, Z. Wang, L. Gu, X. Xu, S. Wu and C. Gao, Science, 2019, 366, 983–987 CrossRef CAS PubMed.
- J. B. Goodenough, J. Appl. Phys., 1962, 33, 1197–1199 CrossRef CAS.
- J. Kanamori, Prog. Theor. Phys., 1957, 17, 177–196 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1950, 79, 350–356 CrossRef.
- D. S. Parker, Sci. Rep., 2017, 7, 3388 CrossRef PubMed.
- R. Bouachraoui, A. G. El Hachimi, Y. Ziat, L. Bahmad and N. Tahiri, Solid State Commun., 2018, 274, 46–50 CrossRef CAS.
- P. Rochette, G. Fillion, J.-L. Mattéi and M. J. Dekkers, Earth Planet. Sci. Lett., 1990, 98, 319–328 CrossRef CAS.
- S. J. Kuhn, M. K. Kidder, D. S. Parker, C. dela Cruz, M. A. McGuire, W. M. Chance, L. Li, L. Debeer-Schmitt, J. Ermentrout, K. C. Littrell, M. R. Eskildsen and A. S. Sefat, Phys. C, 2017, 534, 29–36 CrossRef CAS.
- H. Basumatary, J. A. Chelvane, D. V. S. Rao, A. Talapatra, J. Mohanty, D. Kumar, V. Singh, S. V. Kamat and R. Ranjan, J. Alloys Compd., 2021, 869, 159571 CrossRef CAS.
- R. Cheng, L. Yin, Y. Wen, B. Zhai, Y. Guo, Z. Zhang, W. Liao, W. Xiong, H. Wang, S. Yuan, J. Jiang, C. Liu and J. He, Nat. Commun., 2022, 13, 5241 CrossRef CAS PubMed.
- A. V. Svalov, O. A. Adanakova, V. O. Vas'kovskiy, K. G. Balymov, A. Larrañaga, G. V. Kurlyandskaya, R. Domingues Della Pace and C. C. Plá Cid, J. Magn. Magn. Mater., 2018, 459, 57–60 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00263b |
| This journal is © The Royal Society of Chemistry 2023 |