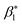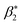DOI:
10.1039/D3NA00338H
(Paper)
Nanoscale Adv., 2023,
5, 4863-4872
Entropy generation in bioconvection hydromagnetic flow with gyrotactic motile microorganisms
Received
18th May 2023
, Accepted 7th August 2023
First published on 8th August 2023
Abstract
Here, the magnetohydrodynamic bioconvective flow of a non-Newtonian nanomaterial over a stretched sheet is scrutinized. The characteristics of convective conditions are analyzed. Irreversibility analysis in the presence of gyrotactic micro-organisms is discussed. Energy expression is assisted with thermal radiation, heat generation and ohmic heating. Buongiorno's model is employed to discuss the characteristics of the nanoliquid through thermophoresis and random diffusions. Nonlinear expressions of the given model are transformed through adequate transformations. The obtained expressions have been computed by the Newton built in-shooting technique. Results of influential variables for velocity, concentration, microorganism field, temperature and entropy rate are graphically studied. Clearly, velocity reduction is witnessed for the bioconvection Rayleigh number and magnetic variable. A higher heat generation variable leads to augmentation of temperature. An increase in the magnetic variable results in entropy and temperature enhancement. A higher Peclet number results in microorganism field reduction. Temperature distribution rises for radiation and the thermal Biot number. A higher solutal Biot number intensifies the concentration. The entropy rate for radiation and diffusion variables is enhanced.
1 Introduction
Recently, nanotechnology has gained much consideration amongst researchers and investigators. It is due to its involvement in chemical processes, microelectronics, engineering, hybrid powered engines and biological processes. Nanomaterials are basically homogeneous colloidal suspensions of nano-size (1–10 nm) particles in an ordinary liquid which enhances the thermal conductivity of conventional liquids.1,2 Nanofluids have specific characteristics that make them more applicable materials. Nanomaterials have innovative characteristics about heat transfer enhancement. Buongiorno3 gave a theoretical model for heat transport rate enhancement of conventional liquids. He highlighted that only random and thermophoresis diffusions are main mechanisms for thermal transportation enhancement. Nanomaterials are very significant in improving the thermal productivity of hybrid power engines, electronic devices, nuclear system chillers, domestic refrigerators and many others. Shahzad et al.4 analyzed the bioconvection convectively heated micropolar nanomaterial flow between two rotating disks. The mixed convective magnetohydrodynamic flow of a viscoelastic nanomaterial with heat generation was discussed by Waqas et al.5 Anjum et al.6 explored activation energy in the bioconvective MHD flow of a modified Eyring–Powell nanomaterial. Mabood et al.7 reported chemically reactive micropolar nanoliquid flow considering thermal radiation. Numerical analysis of hydromagnetic unsteady nanomaterial flow towards an irregular stretched sheet was reported by Kalpana et al.8 Thermal analysis for the hydromagnetic flow of a nanomaterial subject to entropy was addressed in Riaz et al.9 Further investigations about nanomaterial flow are highlighted through ref. 10–17.
In recent years the bioconvection phenomenon in nanomaterials along motile microorganisms has attracted much attention from researchers. It is because of its significance in tremendous engineering, pharmaceutical and biological processes in fields such as biofuel, biomedicine, fertilizer, biotechnology, bio-microsystem and enzyme biosensor. Bioconvection occurs due to up swimming of microorganisms. Commonly the density of microorganisms is heavier than the base fluid and therefore it raises unsteady upper surface density stratification.18,19 Bio convection is extensively used in environmental science, conversion in engineering, bio-microsystems, biological processes with microbial-upgraded oil recovery systems, enzyme biosensors, mass transport and bioengineering in biotechnology and the ecosystem. Prime utilization of this mechanism is to enhance the capacity of appropriate fraternization and mass transfer. Bio convection refers to macroscopic movement of liquid induced by a density gradient organized by an alternating floating system based on motile microbes. Thermal radiation impact in a bioconvective ferromagnetic Williamson material subject to dissipation was studied by Kada et al.20 Majeed et al.21 highlighted the features of gyrotactic microorganisms in magnetized time-dependent nanoliquid flow. Waqas et al.22 scrutinized thermo and solutal stratification impacts in Casson nanomaterial flow with convective boundary conditions. Azam et al.23 examined activation in the bioconvection flow of a cross nanoliquid subject to gyrotactic microorganisms. Some interesting explorations of bioconvective flow can be seen in Ref. 24–32.
Motivation of current analysis is to address the bioconvective flow of the Reiner–Rivlin nanoliquid. Gyrotactic microorganisms in the presence of convective conditions are discussed. The characteristics of thermophoresis and random diffusions are analyzed. Energy expression consists of radiation, heat generation and ohmic heating. Irreversibility analysis along with chemical reaction is analyzed. The Newton built in-shooting technique (ND-solve) is employed to develop numerical solutions of the considered model. Graphical analysis illustrating the influence of liquid flow, concentration, microorganism field, temperature and entropy rate is organized. Main results are listed in conclusion.
2 Formulation
Here the flow of the bioconvection Reiner–Rivlin nanomaterial past a stretched boundary is examined. Convective conditions along with chemical reaction are analyzed. Thermophoresis, random diffusion and involvement of motile microorganisms are considered. Influences of radiation, magnetic field and heat generation are considered. Physical impact for the entropy rate is explored. A uniform magnetic field of strength (B0) is applied. The surface is stretched with velocity (uw = ax) subject to rate constant (a > 0). Fig. 1 consists of flow configuration.33
 |
| | Fig. 1 Flow configuration. | |
Under the above assumptions, the related equations are:34–38
| | 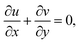 | (1) |
| | 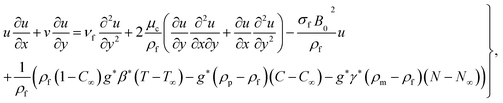 | (2) |
| | 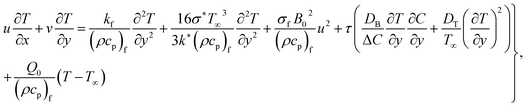 | (3) |
| | 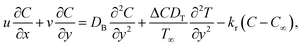 | (4) |
| | 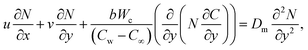 | (5) |
with the boundary condition:
36–38| | 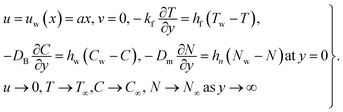 | (6) |
In the above expressions (
u,
v) denote the velocity components,
νf the kinematic viscosity,
μc the cross viscosity,
g* the gravity, (
x,
y) characterize Cartesian coordinates,
β* the thermal expansion coefficient,
ρp the particle density,
ρm the microorganism density,
γ* the average volume of microorganisms,
hf the heat transfer rate,
B0 the magnetic field strength,
μf the dynamic viscosity,
ρf the liquid density,
b the chemotaxis constant,
σf the electrical conductivity,
hw the mass transfer rate,
T the temperature,
DB the Brownian diffusion coefficient,
Wc the cell swimming speed,
Q0 > 0 the heat generation coefficient,
Tw the wall temperature,
τ the ratio of heat capacitance,
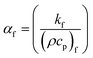
the thermal diffusivity, (
cp)
f the specific heat,
T∞ the ambient temperature,
σ* the Stefan–Boltzmann constant,
DT the thermophoresis coefficient,
kf the thermal conductivity,
hn the microorganism transfer rate,
k* the mean absorption coefficient,
C the concentration, Δ
C the concentration difference,
Cw the wall concentration,
kr the reaction rate,
C∞ the ambient concentration,
N the motile microorganisms,
Nw the wall motile microorganisms,
Dm the microorganism diffusion coefficient and
N∞ the wall motile microorganisms.
Letting l as the reference length and transformations:38
| | 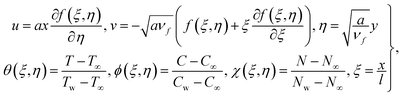 | (7) |
one has
| | 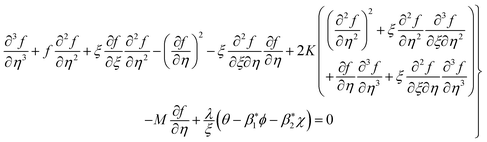 | (8) |
| | 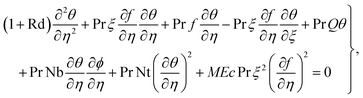 | (9) |
| | 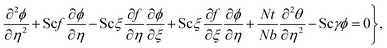 | (10) |
| | 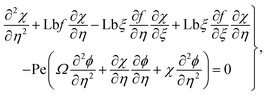 | (11) |
| | 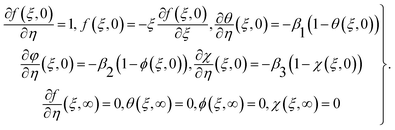 | (12) |
In the above equations
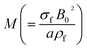
represents the magnetic variable,
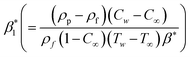
the buoyancy ratio variable,
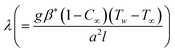
the mixed convection variable,

the material variable,
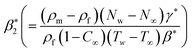
the bioconvection Rayleigh number,
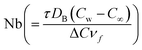
the Brownian motion variable,

the thermal Biot number,
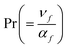
the Prandtl number,
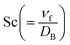
the Schmidt number,

the radiation variable,
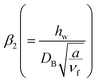
the solutal Biot number,
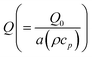
the heat generation parameter,
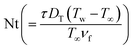
the thermophoresis variable,

the microorganism Biot number,
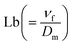
the bioconvective Lewis number,
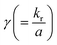
the reaction variable,
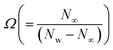
the microorganisms concentration difference factor and
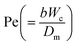
the Peclet number.
3 Entropy generation
In mathematical form one can express that:39–45| | 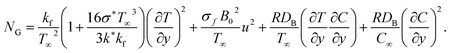 | (13) |
Non-dimensional form is
| | 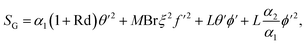 | (14) |
in which
R indicates the real gas constant,
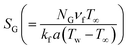
the entropy rate,
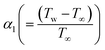
the temperature difference variable,
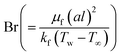
the Brinkman number,
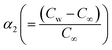
the concentration difference variable and
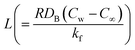
the diffusion variable.
4 Solution methodology
We consider 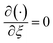 and denoting
and denoting 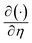 by prime in eqn (8)–(12). We can express that
by prime in eqn (8)–(12). We can express that| | 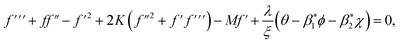 | (15) |
| | 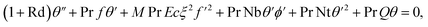 | (16) |
| | 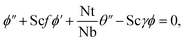 | (17) |
| | 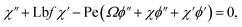 | (18) |
| | 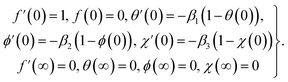 | (19) |
4.1 Numerical scheme
The ND-solve technique computes the analysis. The Mathematica software is employed to get the numerical solution. For this we set| | 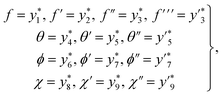 | (20) |
| |  | (21) |
| | 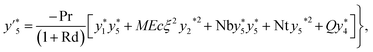 | (22) |
| | 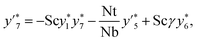 | (23) |
| | 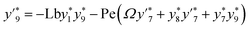 | (24) |
with| | 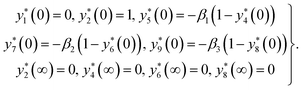 | (25) |
5 Results validation
A comparative study of the present investigation with Kaswan et al.46 is constructed in Table 1 in a limiting sense. From Table 1 it is clearly detected that results here are in excellent agreement.
Table 1 Thermal transport rate comparison with Kaswan et al.46
| Pr |
Kaswan et al.46 |
Present results |
| 0.07 |
0.065539 |
0.065536 |
| 0.7 |
0.164035 |
0.164039 |
| 1.0 |
0.418237 |
0.418235 |
| 2.0 |
0.826737 |
0.826738 |
| 7.0 |
1.804291 |
1.804295 |
| 20.0 |
3.256791 |
3.256797 |
| 70.0 |
6.346675 |
6.346679 |
6 Graphical analysis
In this section, the physical description of emerging variables is organized.
6.1 Velocity
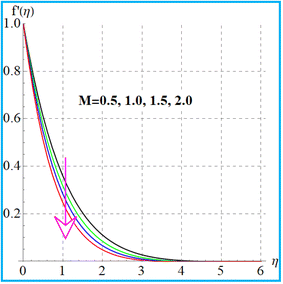
Fig. 2 displays the behavior of the magnetic variable for velocity. Physically the magnetic field enhances the Lorentz force which induces a resistance in the liquid flow region and the velocity declines. Fig. 3 shows the impact of the material variable on (f′(η)). Increasing values of the material variable lead to viscous force reduction which intensifies the velocity. Fig. 4 displays the outcomes of the buoyancy ratio variable for velocity. Here reduction in velocity occurs for the buoyancy ratio variable. Fig. 5 elucidates the impact of the bioconvection Rayleigh number. A larger approximation of the bioconvection Rayleigh number (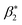 ) corresponds to a decline in liquid flow (f′(η)).
) corresponds to a decline in liquid flow (f′(η)).
 |
| | Fig. 2
f′(η) variation versus M. | |
 |
| | Fig. 3
f′(η) variation versus K. | |
 |
| | Fig. 4
f′(η) variation versus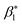 . . | |
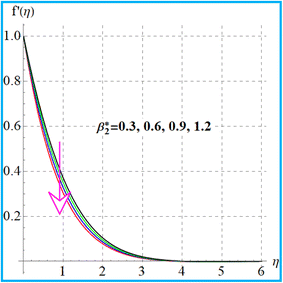 |
| | Fig. 5
f′(η) variation versus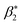 . . | |
6.2 Temperature
The feature of temperature distribution for the magnetic field is illustrated in Fig. 6. A higher magnetic field increases the Lorentz force which produces disturbance in the flow region and consequently the kinetic energy of the system is increased. Therefore thermal distribution is intensified. Fig. 7 shows the outcomes of (β1) on temperature. An enhancement in thermal distribution occurs for a higher thermal Biot number. Results of radiation for temperature are portrayed in Fig. 8. As anticipated, higher radiation impact intensified the thermal field. Fig. 9 and 10 display (Nt) and (Nb) variations for temperature. A larger approximation of (Nt) corresponds to augmentation of the temperature. Additionally, it is seen through Fig. 10 that temperature improves with a higher random motion (Nb) variable.
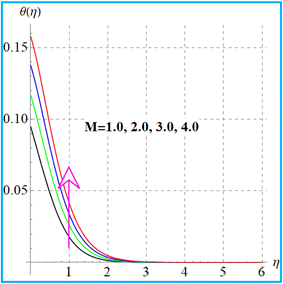 |
| | Fig. 6
θ(η) variation versus M. | |
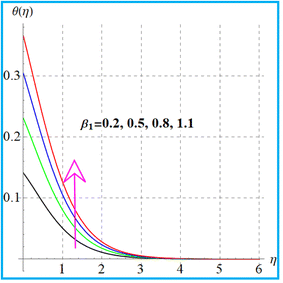 |
| | Fig. 7
θ(η) versus β1. | |
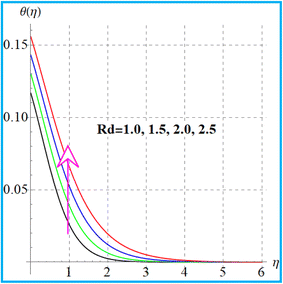 |
| | Fig. 8
θ(η) versus Rd. | |
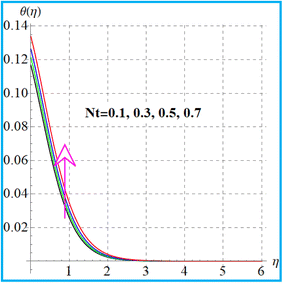 |
| | Fig. 9
θ(η) versus Nt. | |
 |
| | Fig. 10
θ(η) versus Nb. | |
6.3 Concentration
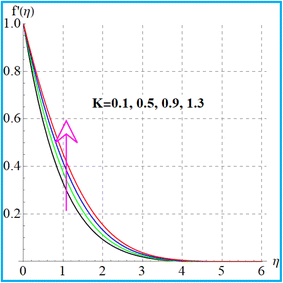
Fig. 11 illustrates the impact of (Nt) on concentration. An increment in concentration occurs through a higher thermophoresis variable. The feature of concentration (ϕ(η)) for (Sc) is depicted in Fig. 12. Here due to an increase in (Sc), the concentration decays due to reduction in mass diffusivity. Fig. 13 displays the variation of (β2) for concentration. Clearly, the concentration boosts up for a higher solutal Biot number. Additionally, it is evident through Fig. 14 that concentration decays with a random motion variable.
 |
| | Fig. 11
ϕ(η) versus Nt. | |
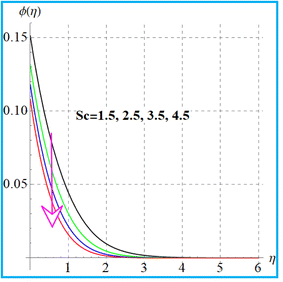 |
| | Fig. 12
ϕ(η) versus Sc. | |
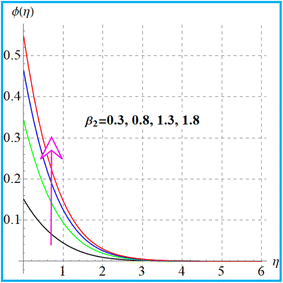 |
| | Fig. 13
ϕ(η) versus β2. | |
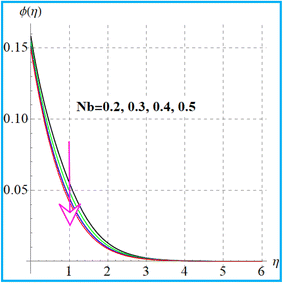 |
| | Fig. 14
ϕ(η) versus Nb. | |
6.4 Microorganism field
Fig. 15 exhibits the result of the bioconvection Lewis number on (χ(η)). Clearly, microorganism field degradation is detected against a higher bioconvection Lewis number (Lb). The influence of (β3) on the microorganism field (χ(η)) is shown in Fig. 16. A higher estimation of (β3) leads to augmentation of the microorganism (χ(η)) field. The graphical feature of (χ(η)) versus the Peclet number is portrayed in Fig. 17. A clearly decreasing trend of microorganisms (χ(η)) is witnessed for a higher Peclet (Pe) number.
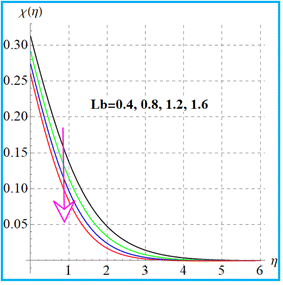 |
| | Fig. 15
χ(η) versus Lb. | |
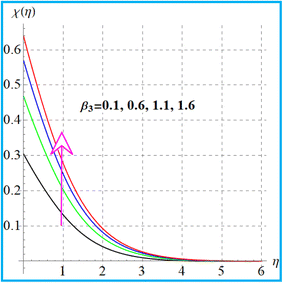 |
| | Fig. 16
χ(η) versus β3. | |
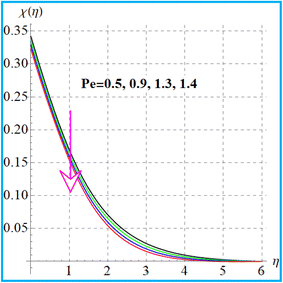 |
| | Fig. 17
χ(η) versus Pe. | |
6.5 Entropy production
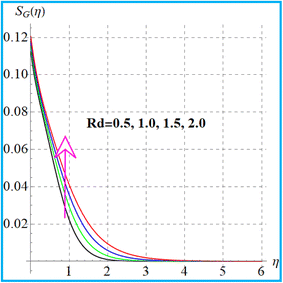
Fig. 18 shows the entropy variation against the magnetic variable. With an increase in the magnetic field the Lorentz force causes more resistance in the flow region. As a result, the internal energy of the system increases and consequently the entropy rate is augmented. Fig. 19 displays the impact of the diffusion parameter (L) on (SG(η)). Here entropy rises against the diffusion variable. Effects of (Br) on the entropy rate are given in Fig. 20. An increment in entropy generation is found for a larger Brinkman number due to a larger kinetic energy. Fig. 21 elucidates the outcomes of the radiation parameter (Rd) for (SG(η)). The entropy rate against radiation is enhanced.
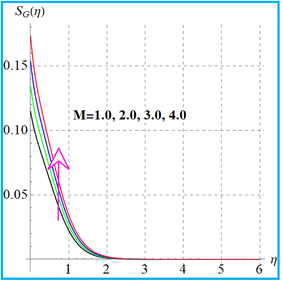 |
| | Fig. 18
S
G(η) versus M. | |
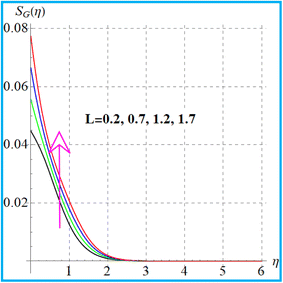 |
| | Fig. 19
S
G(η) versus L. | |
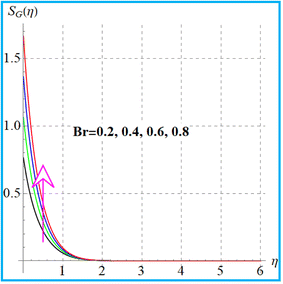 |
| | Fig. 20
S
G(η) versus Br. | |
 |
| | Fig. 21
S
G(η) versus Rd. | |
7 Closing remarks
Here the magnetized bioconvective flow of the Reiner–Rivlin nanomaterial by convective conditions is examined. Entropy analysis in the presence of chemical reaction is addressed. Gyrotactic micro-organisms are taken into account. Key points of recent analysis are given below.
• Reduction occurs in liquid flow for the magnetic field and bioconvection Rayleigh number.
• Velocity improves for higher values of the material variable while the reverse impact holds for the buoyancy ratio variable.
• Temperature enhancement is noted for thermophoresis and radiation variables.
• An increase in temperature distribution and entropy rate is witnessed for the magnetic field.
• Higher random motion leads to temperature enhancement.
• A larger approximation of the thermal Biot number intensifies the temperature distribution.
• The reverse trend holds for concentration against random motion and thermophoresis variables.
• A decline in concentration occurs for a higher Schmidt number.
• Concentration increases for a higher solutal Biot number.
• Reduction in microorganisms occurs versus the Peclet number.
• Microorganism field decays against a higher bioconvection Lewis number.
• Entropy rate has similar behavior against radiation and diffusion variables.
• Entropy rate increases versus a larger Brinkman number.
Conflicts of interest
There are no conflicts to declare.
References
- S. U. S. Choi, Enhancing thermal conductivity of fluids with nanoparticles, J. Fluids Eng., 1995, 231, 99–106 CAS.
- J. A. Eastman, S. U. S. Choi, S. Li, W. Yu and L. J. Thompson, Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles, Appl. Phys. Lett., 2001, 78, 718–720 CrossRef CAS.
- J. Buongiorno, Convective transport in nanofluids, J. Heat Transf., 2006, 128, 240–250 CrossRef.
- A. Shahzad, M. Imran, M. Tahir, S. A. Khan, A. Akgül, S. Abdullaev, C. Park, H. Y. Zahran and I. S. Yahia, Brownian motion and thermophoretic diffusion impact on Darcy-Forchheimer flow of bioconvective micropolar nanofluid between double disks with Cattaneo-Christov heat flux, Alexandria Eng. J., 2023, 62, 1–15 CrossRef.
- M. Waqas, M. I. Khan, T. Hayat, M. M. Gulzar and A. Alsaedi, Transportation of radiative energy in viscoelastic nanofluid considering buoyancy forces and convective conditions, Chaos, Solitons Fractals, 2020, 130 DOI:10.1016/j.chaos.2019.109415.
- N. Anjum, W. A. Khan, A. Hobiny, M. Azam, M. Waqas and M. Irfan, Numerical analysis for thermal performance of modified Eyring Powell nanofluid flow subject to activation energy and bioconvection dynamic, Chaos, Solitons Fractals, 2022, 39 DOI:10.1016/j.csite.2022.102427.
- F. Mabood, M. D. Shamshuddin and S. R. Mishra, Characteristics of thermophoresis and Brownian motion on radiative reactive micropolar fluid flow towards continuously moving flat plate: HAM solution, Math. Comput. Simul., 2022, 191, 187–202 CrossRef.
- G. Kalpana, K. R. Madhura and R. B. Kudenatti, Numerical study on the combined effects of Brownian motion and thermophoresis on an unsteady magnetohydrodynamics nanofluid boundary layer flow, Math. Comput. Simul., 2022, 200, 78–96 CrossRef.
- A. Riaz, T. Abbas, A. Zeeshan and M. H. Doranehgard, Entropy generation and MHD analysis of a nanofluid with peristaltic three dimensional cylindrical enclosures, Int. J. Numer. Methods Heat Fluid Flow, 2021, 31, 2698–2714 CrossRef.
- M. Hussain and M. Sheremet, Convection analysis of the radiative nanofluid flow through porous media over a stretching surface with inclined magnetic field, Int. Commun. Heat Mass Transfer, 2023, 140 DOI:10.1016/j.icheatmasstransfer.2022.106559.
- W. A. Khan, M. Waqas, S. Kadry, Z. Asghar, S. Z. Abbas and M. Irfan, On the evaluation of stratification based entropy optimized hydromagnetic flow featuring dissipation aspect and Robin conditions, Comput. Methods Programs Biomed., 2020, 190 DOI:10.1016/j.cmpb.2020.105347.
- M. Jawad, M. K. Hameed, K. S. Nisar and A. H. Majeed, Darcy-Forchheimer flow of Maxwell nanofluid flow over a porous stretching sheet with Arrhenius activation energy and nield boundary conditions, Chaos, Solitons Fractals, 2023, 44 DOI:10.1016/j.csite.2023.102830.
- F. Shah, T. Hayat and S. Momani, Non-similar analysis of the Cattaneo-Christov model in MHD second-grade nanofluid flow with Soret and Dufour effects, Alexandria Eng. J., 2023, 70, 25–35 CrossRef.
- N. Vijay and K. Sharma, Dynamics of stagnation point flow of Maxwell nanofluid with combined heat and mass transfer effects: A numerical investigation, Int. Commun. Heat Mass Transfer, 2023, 141 DOI:10.1016/j.icheatmasstransfer.2022.106545.
- C. Sulochana, G. P. Ashwinkumar and N. Sandeep, Transpiration effect on stagnation point flow of a Carreau nanofluid in the presence of thermophoresis and Brownian motion, Alexandria Eng. J., 2016, 55, 1151–1157 CrossRef.
- I. Waini, K. B. Hamzah, N. S. Khashi'ie, N. A. Zainal, A. R. M. Kasim, A. Ishak and I. Pop, Brownian and thermophoresis diffusion effects on magnetohydrodynamic Reiner-Philippoff nanofluid flow past a shrinking sheet, Alexandria Eng. J., 2023, 67, 183–192 CrossRef.
- A. Alsaedi, A. Razaq, T. Hayat and S. A. Khan, Modeling and simulation of Cattaneo-Christov fluxes in entropy induced flow through Reiner–Rivlin fluid conveying tiny particles, Alexandria Eng. J., 2023, 74, 1–19 CrossRef.
- T. J. Pedley, N. A. Hill and J. O. Kessler, The growth of bioconvection patterns in a uniform suspension of gyrotactic micro-organisms, J. Fluid Mech., 1988, 195, 223–237 CrossRef CAS PubMed.
- T. J. Pedley and J. O. Kessler, A new continuum model for suspensions of gyrotactic micro-organisms, J. Fluid Mech., 1990, 212, 155–182 CrossRef CAS PubMed.
- B. Kada, I. Hussain, A. A. Pasha, W. A. Khan, M. Tabrez, K. A. Juhany, M. Bourchak and R. Othman, Significance of gyrotactic microorganism and bioconvection analysis for radiative Williamson fluid flow with ferromagnetic nanoparticles Therm, Sci. Eng. Prog., 2023, 39 DOI:10.1016/j.tsep.2023.101732.
- A. Majeed, A. Zeeshan, N. Amin, N. Ijaz and T. Saeed, Thermal analysis of radiative bioconvection magnetohydrodynamic flow comprising gyrotactic microorganism with activation energy, J. Therm. Anal. Calorim., 2021, 143, 2545–2556 CrossRef CAS.
- M. Waqas, W. A. Khan, A. A. Pasha, N. Islam and M. M. Rahman, Dynamics of bioconvective Casson nanoliquid from a moving surface capturing gyrotactic microorganisms, magnetohydrodynamics and stratifications, Therm. Sci. Eng. Prog., 2022, 36 DOI:10.1016/j.tsep.2022.101492.
- M. Azam, T. Xu, F. Mabood and M. Khan, Non-linear radiative bioconvection flow of cross nano-material with gyrotactic microorganisms and activation energy, Int. Commun. Heat Mass Transfer, 2021, 127 DOI:10.1016/j.icheatmasstransfer.2021.105530.
- N. Fatima, W. Belhadj, K. S. Nisar, Usman, M. K. Alaoui, M. B. Arain and N. Ijaz, Heat and mass transmission in a boundary layer flow due to swimming of motile gyrotactic microorganisms with variable wall temperature over a flat plate, Chaos, Solitons Fractals, 2023, 45 DOI:10.1016/j.csite.2023.102953.
- A. K. Kushwaha and Y. D. Sharma, Significance of vertical vibration on the stability of thermo-bioconvection in a suspension of oxytactic microorganisms, Int. Commun. Heat Mass Transfer, 2022, 133 DOI:10.1016/j.icheatmasstransfer.2022.105943.
- A. A. Avramenko, Y. Y. Kovetska and I. V. Shevchuk, Lorentz approach for analysis of bioconvection instability of gyrotactic motile microorganisms, Chaos, Solitons Fractals, 2023, 166 DOI:10.1016/j.chaos.2022.112957.
- N. Biswas, D. K. Mandal, N. K. Manna and A. C. Benim, Enhanced energy and mass transport dynamics in a thermo-magneto-bioconvective porous system containing oxytactic bacteria and nanoparticles: Cleaner energy application, Energy, 2023, 263 DOI:10.1016/j.energy.2022.125775.
- A. Majeed, N. Golsanami, B. Gong, Q. A. Ahmad, S. Rifaqat, A. Zeeshan and F. M. Noori, Analysis of thermal radiation in magneto-hydrodynamic motile gyrotactic micro-organisms flow comprising tiny nanoparticle towards a nonlinear surface with velocity slip, Alexandria Eng. J., 2023, 66, 543–553 CrossRef.
- A. S. M. Aljaloud, L. Manai and I. Tlili, Bioconvection flow of Cross nanofluid due to cylinder with activation energy and second order slip features, Chaos, Solitons Fractals, 2023, 42 DOI:10.1016/j.csite.2023.102767.
- R. R. Kairi, S. Roy and S. Raut, Stratified thermosolutal Marangoni bioconvective flow of gyrotactic microorganisms in Williamson nanofluid, Eur. J. Mech. B/Fluids, 2023, 97, 40–52 CrossRef.
- S. Hussain, A. M. Aly and N. Alsedias, Bioconvection of oxytactic microorganisms with nano-encapsulated phase change materials in an omega-shaped porous enclosure, J. Energy Storage, 2022, 56 DOI:10.1016/j.est.2022.105872.
- M. Irfan, W. A. Khan, A. A. Pasha, M. I. Alam, N. Islam and M. Zubair, Significance of non-Fourier heat flux on ferromagnetic Powell-Eyring fluid subject to cubic autocatalysis kind of chemical reaction, Int. Commun. Heat Mass Transfer, 2022, 138 DOI:10.1016/j.icheatmasstransfer.2022.106374.
- S. A. Khan, T. Hayat and A. Alsaedi, Entropy generation in chemically reactive flow of Reiner–Rivlin liquid conveying tiny particles considering thermal radiation, Alexandria Eng. J., 2023, 66, 257–268 CrossRef.
- M. Reiner, A mathematical theory of dilatancy, Am. J. Math., 1945, 67, 350–362 CrossRef.
- R. S. Rivlin, The hydrodynamics of non-Newtonian fluids, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1948, 193, 260–281 Search PubMed.
- M. Tabassum and M. Mustafa, A numerical treatment for partial slip flow and heat transfer of non-Newtonian Reiner–Rivlin fluid due to rotating disk, Int. J. Heat Mass Transfer, 2018, 123, 979–987 CrossRef.
- B. Sahoo, R. A. V. Gorder and H. I. Andersson, Steady revolving flow and heat transfer of a non-Newtonian Reiner–Rivlin fluid, Int. Commun. Heat Mass Transfer, 2012, 39, 336–342 CrossRef.
- S. A. Khan, T. Hayat and A. Alsaedi, Simultaneous features of Soret and Dufour in entropy optimized flow of Reiner–Rivlin fluid considering thermal radiation, Int. Commun. Heat Mass Transfer, 2022, 137 DOI:10.1016/j.icheatmasstransfer.2022.106297.
- M. A. Sadiq and T. Hayat, Entropy optimized flow of Reiner–Rivlin nanofluid with chemical reaction subject to stretchable rotating disk, Alexandria Eng. J., 2022, 61, 3501–3510 CrossRef.
- Z. Abbas, M. Naveed, M. Hussain and N. Salamat, Analysis of entropy generation for MHD flow of viscous fluid embedded in a vertical porous channel with thermal radiation, Alexandria Eng. J., 2020, 59, 3395–3405 CrossRef.
- Y. Liu, J. Xing and Y. Jian, Heat transfer and entropy generation analysis of electroosmotic flows in curved rectangular nanochannels considering the influence of steric effects, Int. Commun. Heat Mass Transfer, 2022, 139 DOI:10.1016/j.icheatmasstransfer.2022.106501.
- R. Sarma, A. K. Shukla, H. S. Gaikwad, P. K. Mondal and S. Wongwises, Effect of conjugate heat transfer on the thermo-electro-hydrodynamics of nanofluids: entropy optimization analysis, J. Therm. Anal. Calorim., 2022, 147, 599–614 CrossRef CAS.
- B. Iftikhar, T. Javed and M. A. Siddiqu, Entropy generation analysis during MHD mixed convection flow of non-Newtonian fluid saturated inside the square cavity, J. Comput. Sci., 2023, 66 DOI:10.1016/j.jocs.2022.101907.
- W. Ibrahim and D. Gamachu, Entropy generation in radiative magnetohydrodynamic mixed convective flow of viscoelastic hybrid nanofluid over a spinning disk, Heliyon, 2022, 8 DOI:10.1016/j.heliyon.2022.e1185.
- A. Alsaedi, A. Razaq, T. Hayat and S. A. Khan, On bioconvective chemically reactive flow involving applications of magnetohydrodynamic and radiation, Alexandria Eng. J., 2023, 75, 549–563 CrossRef.
- P. Kaswan, M. Kumar and M. Kumari, Analysis of a bioconvection flow of magnetocross nanofluid containing gyrotactic microorganisms with activation energy using an artificial neural network scheme, Results Eng., 2023, 17 DOI:10.1016/j.rineng.2023.101015.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
T.
Hayat
a and
A.
Alsaedi
*a,
T.
Hayat
a and
A.
Alsaedi
 b
b
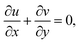
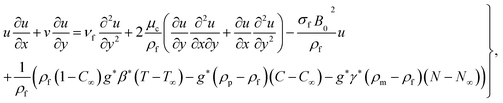
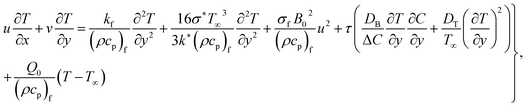
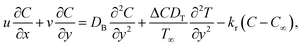
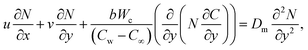
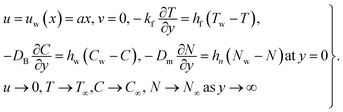
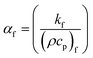 the thermal diffusivity, (cp)f the specific heat, T∞ the ambient temperature, σ* the Stefan–Boltzmann constant, DT the thermophoresis coefficient, kf the thermal conductivity, hn the microorganism transfer rate, k* the mean absorption coefficient, C the concentration, ΔC the concentration difference, Cw the wall concentration, kr the reaction rate, C∞ the ambient concentration, N the motile microorganisms, Nw the wall motile microorganisms, Dm the microorganism diffusion coefficient and N∞ the wall motile microorganisms.
the thermal diffusivity, (cp)f the specific heat, T∞ the ambient temperature, σ* the Stefan–Boltzmann constant, DT the thermophoresis coefficient, kf the thermal conductivity, hn the microorganism transfer rate, k* the mean absorption coefficient, C the concentration, ΔC the concentration difference, Cw the wall concentration, kr the reaction rate, C∞ the ambient concentration, N the motile microorganisms, Nw the wall motile microorganisms, Dm the microorganism diffusion coefficient and N∞ the wall motile microorganisms.
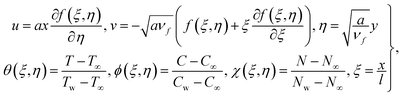
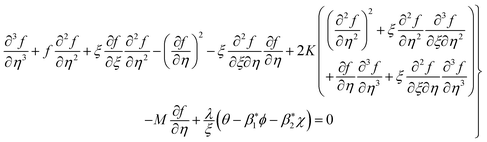
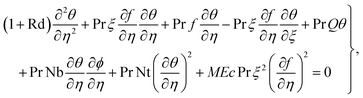
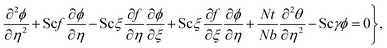
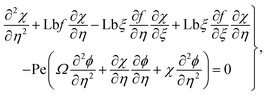
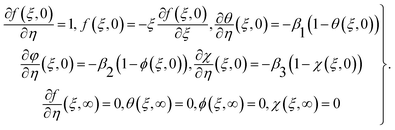
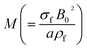 represents the magnetic variable,
represents the magnetic variable, 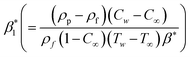 the buoyancy ratio variable,
the buoyancy ratio variable, 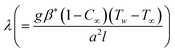 the mixed convection variable,
the mixed convection variable,  the material variable,
the material variable, 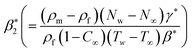 the bioconvection Rayleigh number,
the bioconvection Rayleigh number, 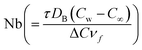 the Brownian motion variable,
the Brownian motion variable,  the thermal Biot number,
the thermal Biot number, 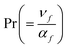 the Prandtl number,
the Prandtl number, 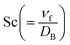 the Schmidt number,
the Schmidt number,  the radiation variable,
the radiation variable, 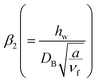 the solutal Biot number,
the solutal Biot number, 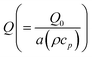 the heat generation parameter,
the heat generation parameter, 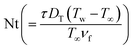 the thermophoresis variable,
the thermophoresis variable,  the microorganism Biot number,
the microorganism Biot number, 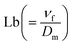 the bioconvective Lewis number,
the bioconvective Lewis number, 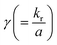 the reaction variable,
the reaction variable, 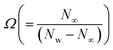 the microorganisms concentration difference factor and
the microorganisms concentration difference factor and 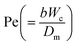 the Peclet number.
the Peclet number.
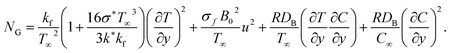
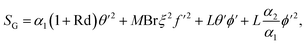
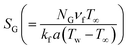 the entropy rate,
the entropy rate, 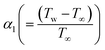 the temperature difference variable,
the temperature difference variable, 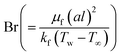 the Brinkman number,
the Brinkman number, 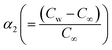 the concentration difference variable and
the concentration difference variable and 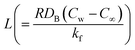 the diffusion variable.
the diffusion variable.
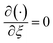 and denoting
and denoting 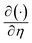 by prime in eqn (8)–(12). We can express that
by prime in eqn (8)–(12). We can express that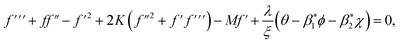
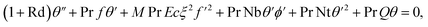
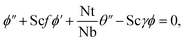
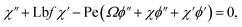
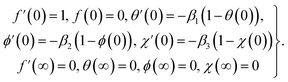
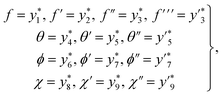

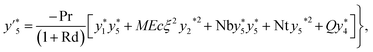
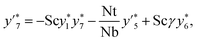
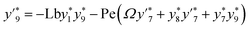
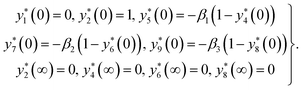
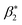 ) corresponds to a decline in liquid flow (f′(η)).
) corresponds to a decline in liquid flow (f′(η)).