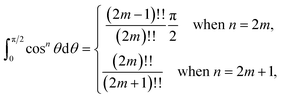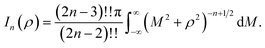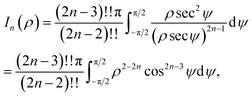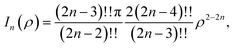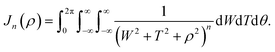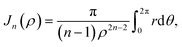Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Catalytic effect of graphene on the inversion of corannulene using a continuum approach with the Lennard-Jones potential
Panyada
Sripaturad
 a,
Amir
Karton
a,
Amir
Karton
 *b,
Kyle
Stevens
*b,
Kyle
Stevens
 c,
Ngamta
Thamwattana
c,
Ngamta
Thamwattana
 *c,
Duangkamon
Baowan
*c,
Duangkamon
Baowan
 a and
Barry J.
Cox
d
a and
Barry J.
Cox
d
aDepartment of Mathematics, Faculty of Science, Mahidol University, Rama VI Rd, Bangkok 10400, Thailand
bSchool of Science and Technology, University of New England, Armidale, NSW 2351, Australia. E-mail: amir.karton@une.edu.au
cSchool of Information and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia. E-mail: natalie.thamwattana@newcastle.edu.au
dSchool of Mathematical Sciences, University of Adelaide, Adelaide, SA 5005, Australia
First published on 3rd August 2023
Abstract
The catalytic effect of graphene on the corannulene bowl-to-bowl inversion is confirmed in this paper using a pair-wise dispersion interaction model. In particular, a continuum approach together with the Lennard-Jones potential are adopted to determine the interaction energy between corannulene and graphene. These results are consistent with previous quantum chemical studies, which showed that a graphene sheet reduces the barrier height for the bowl-to-bowl inversion in corannulene. However, the results presented here demonstrate, for the first time, that the catalytic activity of graphene can be reproduced using pair-wise dispersion interactions alone. This demonstrates the major role that pair-wise dispersion interactions play in the catalytic activity of graphene.
1 Introduction
Geodesic polyarenes are polycyclic aromatic hydrocarbons in which structural constraints result in a curved π-system.1–4 Geodesic hydrocarbons exhibit unique chemical properties, such as large dipole moments and dynamic bowl-inversion behavior.2–9 Corannulene (C20H10) is a prototypical geodesic molecule in which a pentagon surrounded by five hexagons results in a bowl-shaped structure.10 Corannulene undergoes a rapid bowl-to-bowl inversion via a planar transition structure as illustrated in Fig. 1.11 Catalysis of this bowl-to-bowl inversion has attracted considerable attention after it was demonstrated that a cyclophane receptor catalyzes this process via induced-fit catalysis.12–14 It was later found that graphene (a planar two-dimensional (2D) material composed of sp2-hybridized carbons) can also catalyze the bowl-to-bowl inversion in corannulene15–17 as well as rotation and inversion reactions in related molecules.18–20 It has also been demonstrated via extensive density functional theory (DFT) and ab initio calculations that these catalytic processes are driven by strong noncovalent interactions that typically exceed a hundred kJ mol−1.15–24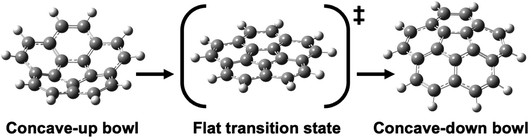 | ||
| Fig. 1 Optimized DFT structures of the equilibrium and transition structures involved in the bowl-to-bowl inversion in corannulene. | ||
In the system where graphene is used as a catalyst for corannulene bowl-to-bowl inversion, we envisage that the favourable conformation of corannulene (either concave-up or concave-down bowl) can be determined from the structure that gives rise to the minimum interaction energy with the graphene. Since van der Waals forces dominate the interaction between corannulene and graphene, this paper adopts the Lennard-Jones potential to determine the interaction energy between the two molecules. Here, we assume that carbon atoms on graphene are evenly distributed on its surface so we can use continuum surface approximation to model graphene. For corannulene, its three possible conformations are considered, which are concave-up bowl, concave-down bowl and flat circular structure. Two approaches to model corannulene–graphene interaction are used. The first approach considers corannulene as a collection of 30 discrete atoms (20 carbon and 10 hydrogen atoms), and so the total energy is obtained by summing 30 pairwise interaction energies between each atom on corannulene and a graphene sheet. In the second approach, due to its geometry, we model corannulene as a collection of four circular rings (three carbon rings and one hydrogen ring) centred on the same axis (Fig. 2), and on each ring, atoms are assumed uniformly distributed. As a result, the total interaction energy can be obtained from summing four pairwise interaction energies between each ring and a graphene sheet. For each of corannulene conformations, we find that both approaches give the same energy profile, which is also in agreement with molecular dynamics studies. These results confirm the catalytic effect of graphene on the ability to control the orientation of corannulene that minimises the interaction energy of the system.
In the following section, we give mathematical background for the two approaches to model corannulene–graphene interactions. Detailed calculation of the integrals involved are provided in Appendices A and B. Numerical results for the interaction energies are shown in Section 3 for the three conformations of corannulene. These results are also confirmed by molecular dynamics (MD) and density functional theory (DFT) simulations which their detailed set-ups are given in Appendices C and D, respectively. Finally, concluding remarks is provided at the end of Section 3.
2 Interaction energy between corannulene and graphene
Due to its simple form, the Lennard-Jones potential is commonly employed to determine the interaction energy between two non-bonded atoms, which is given by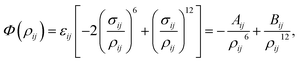 | (1) |
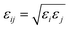 is the energy well depth and σij = (σi + σj)/2 is the van der Waals diameter. In this paper, the van der Waals parameters for carbon (C) and hydrogen (H) are taken from Rappe et al.25 where εC = 0.4393 kJ mol−1, σC = 3.8510 Å, εH = 0.1841 kJ mol−1 and σH = 2.8860 Å. Thus, the Lennard-Jones constants Aij and Bij can be evaluated as given in Table 1.
is the energy well depth and σij = (σi + σj)/2 is the van der Waals diameter. In this paper, the van der Waals parameters for carbon (C) and hydrogen (H) are taken from Rappe et al.25 where εC = 0.4393 kJ mol−1, σC = 3.8510 Å, εH = 0.1841 kJ mol−1 and σH = 2.8860 Å. Thus, the Lennard-Jones constants Aij and Bij can be evaluated as given in Table 1.
| Interaction | A ij (kJ mol−1 Å6) | B ij (kJ mol−1 Å12) |
|---|---|---|
| C–C | 2865.84 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673 673![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 725.47 725.47 |
| C–H | 830.93 | 606![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947.72 947.72 |
In a fully discrete approach, the total interaction energy between two non-bonded molecules can be obtained by summing the pairwise potential energy (1) between atom i on the first molecule and atom j on the second molecule, which is given by
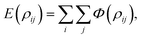 | (2) |
Another method to model the interaction between two non-bonded molecules is known as a continuum approach. This approach assumes that atoms on each interacting molecule are uniformly distributed over its entire surface of the molecule. Thus, the double summation in (2) can be replaced by two surface integrals, namely
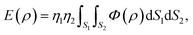 | (3) |
The advantage of using (3) over (2) is the reduction in computational time, especially for large molecules. However, for the integrals in (3) to be traceable to yield analytical expressions, regular shape structures are generally assumed for the interacting molecules. Accordingly, this approach has been commonly adopted to determine the interaction energy involving carbon nanostructures, such as nanotubes, fullerenes, graphene, graphite and nanocones.26
In the interest of modelling an irregularly shaped molecule interacting with a regular shaped structure, an alternative hybrid discrete-continuum approach is introduced, which is given by
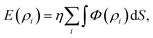 | (4) |
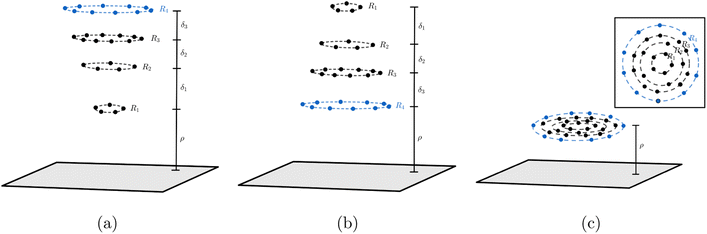
In this paper, we use (4) to determine the non-bonded interaction energy between a graphene sheet and a corannulene. Three conformations of corannulene are considered which are depicted in Fig. 2. We model graphene sheet as a continuum flat surface lying on the xy-plane. For corannulene, we first assume a fully discrete structure with 30 atoms (10 hydrogen atoms (blue) and 20 carbon atoms (black)) as shown in Fig. 2 (Section 2.1). In Section 2.2, we consider corannulene as a structure comprising four continuous rings, where each ring is arranged as shown in Fig. 2.
2.1 Discrete model of corannulene
Here, we model a corannulene as a collection of 30 discrete atoms. The coordinates of a corannulene in all three conformations can be found from Karton.15 Mathematically, we represent an atom on a corannulene as a typical point with coordinates (x, y, ρ) as shown Fig. 3. Each atom then interacts with a flat graphene surface on which a typical point has coordinates (p, q, 0). Since there are 20 carbon and 10 hydrogen atoms on the corannulene, using (4) the total energy becomes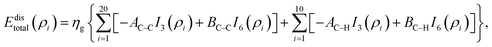 | (5) |
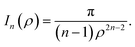 | (6) |
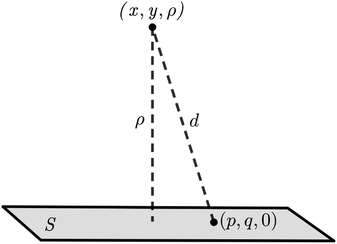 | ||
| Fig. 3 An atom of corannulene located at (x, y, ρ) interacting with an infinite plane of graphene sheet situated on the plane z = 0. | ||
We note that the derivation of In(ρ) is given in Appendix A.
2.2 Ring model of corannulene
Since the positions of atoms on a corannulene are as shown in Fig. 2, we assume that these atoms are located on rings R1 to R4 (see Fig. 2). We note that rings R1 and R2 each consists of five carbon atoms, ring R3 consists of ten carbon atoms and ring R4 consists of ten hydrogen atoms. We also note that of these rings, R1 involves chemically bonded carbons (i.e., the central pentagon ring of corannulene), whereas R2, R3, and R4 involve non-bonded atoms. These rings are chosen since they are co-planar in the equilibrium (bowl-shaped) and transition state (flat) structures of corannulene. Fig. 2 shows the mathematical representations of the equilibrium and transition state structures of corannulene along with the quantum chemically optimized structures. Further, physical parameters of each ring are given in Table 2.| r i (Å) | c i (Å) | η i (Å−1) | |
|---|---|---|---|
| Carbon ring 1 (R1) | 1.2108 | 7.6074 | 0.6573 |
| Carbon ring 2 (R2) | 2.4958 | 15.6818 | 0.3188 |
| Carbon ring 3 (R3) | 3.2688 | 20.5384 | 0.4870 |
| Hydrogen ring (R4) | 4.2572 | 26.7488 | 0.3738 |
Mathematically, the problem reduces to finding the interaction energy between a ring and a graphene sheet as shown in Fig. 4 and by using (4) we can obtain the total interaction energy as
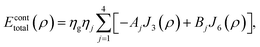 | (7) |
 | (8) |
In the next section, we plot the interaction energies for the three conformations of corannulene interacting with a graphene sheet. The results are also benchmarked with molecular dynamics simulations.
3 Results and concluding remarks
Here, the interaction energy is determined as a function of ρ which is the closest distance between corannulene and graphene sheet. We obtain identical results for both discrete and continuous ring approaches, which are plotted as solid lines in Fig. 5 for the three conformations. The results from our model also agree with those of molecular dynamic simulations, which are plotted as square boxes in Fig. 5. From the figure, we can see that there is a preferred distance (ρmin) for each conformation of corannulene that minimises the interaction energy of the system. The values of ρmin and the corresponding minimum energy are given in Table 3. The interaction energy between the planar corannulene transition structure and the graphene sheet amounts to 178.6 kJ mol−1, whereas the interaction energy between the concave-up bowl and concave-down bowl and the graphene sheet amount to 129.7 kJ mol−1 and 167.3 kJ mol−1, respectively. Thus the pair-wise dispersion interactions between the planar graphene sheet and the planar transition structure are stronger by 48.9 and 11.3 kJ mol−1, respectively, than the concave-up and concave-down structures. This result is due to the closer proximity of the carbon atoms of corannulene and graphene in the planar transition structure than in the concave-up and concave-down structures.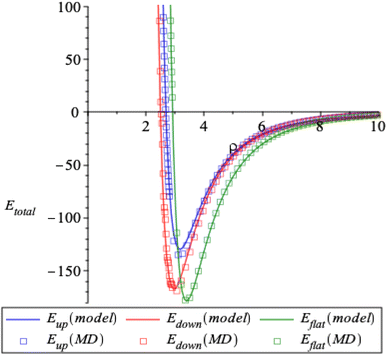 | ||
| Fig. 5 Plot of interaction energy Etot(ρ) (kJ mol−1) using our model (solid lines) and molecular dynamics simulations (square boxes) for three conformations of corannulene. | ||
| Conformation | E total (kJ mol−1) | ρ min (Å) | ||
|---|---|---|---|---|
| Our model | MD simulations | Our model | MD simulations | |
| Concave-up bowl | −129.663 | −135.618 | 3.163 | 3.153 |
| Flat circular | −178.597 | −178.851 | 3.390 | 3.390 |
| Concave-down bowl | −167.288 | −170.404 | 2.959 | 2.947 |
The above results are significant since they demonstrate that even in the absence of any explicit quantum chemical interactions, pair-wise dispersion interactions alone would result in a graphene sheet catalyzing the bowl-to-bowl inversion in corannulene. This result is consistent with previous dispersion-corrected, double-hybrid DFT calculations, which were obtained on the Gibbs free potential energy surface.15,17 In order to compare on an even keel between the interaction energies obtained using our pair-wise dispersion model we need to calculate the DFT interaction energies on the electronic potential energy surface. For this purpose, we performed DFT calculations on the electronic potential energy surface using the PW6B95-D4 functional (see Appendix D for further details). At the PW6B95-D4/def2-TZVPP level of theory with basis set superposition error (BSSE) corrections, we obtain the following interaction energies between corannulene and graphene 82.6 (concave-up bowl), 111.3 (planar TS), and 87.1 (concave-down bowl) kJ mol−1. Using a larger quadruple-ζ basis set without BSSE corrections, namely at the PW6B95-D4/def2-QZVPP level of theory, we obtain similar interaction energies of 87.1 (concave-up bowl), 117.1 (planar TS), and 91.6 (concave-down bowl) kJ mol−1. There is little to choose between the two levels of theory since both have different advantages and disadvantages in terms of basis-set completeness. However, the differences of 4.4–5.8 kJ mol−1 between both sets of results indicate that we are only a few kJ mol−1 away from the complete basis set limit. Here, we will focus on the results obtained with the larger def2-QZVPP basis set. The pair-wise dispersion model predicts much larger interaction energies of 129.7 (concave-up bowl), 178.6 (planar TS), and 167.3 (concave-down bowl) kJ mol−1 (Table 3). However, due to the systematic overestimation of the interaction energies for the concave-up, planar, and concave-down complexes, the catalytic enhancements predicted by the pair-wise dispersion model are in reasonable agreement with the PW6B95-D4/def2-QZVPP results. In particular, the pair-wise dispersion model predicts catalytic enhancements of 48.9 and 11.3 kJ mol−1 for the forward and reverse directions, whereas the PW6B95-D4/def2-QZVPP level of theory results in catalytic enhancements of 30.0 and 25.5 kJ mol−1 for the forward and reverse directions. We note that the smaller interaction energies obtained in the DFT simulations are partly attributed to the use of a C96H24 graphene nanoflake model. We expect that using larger graphene nanoflake models would result in larger interaction energies (for further details, see ref. 23). We also note that the pair-wise dispersion model and DFT interaction energies both suggest that the concave-down complex is energetically more stable on the electronic potential energy surface, albeit the DFT results suggest a smaller energy difference between the concave-up and concave-down complexes. Overall, these results demonstrate that pair-wise dispersion interactions play a major role in the catalytic activity of graphene.
Appendix A evaluation of integral In in section 2.1
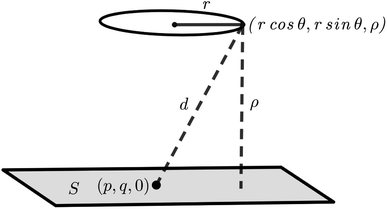
Here, we consider a typical point (x, y, ρ) as a location of an atom on corannulene interacting with a graphene sheet lying on the xy-plane on which its typical point has coordinates (p, q, 0). To determine the interaction energy between a single atom and a graphene sheet using the Lennard-Jones potential, we introduce the integral In(ρ) which is given as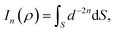 | (9) |
| d2 = (x − p)2 + (y − q)2 + ρ2. |
Since we assume that the size of graphene is much larger than the dimension of a corannulene, we can model graphene as an infinite plane. Thus, (9) can be written as
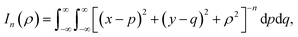 | (10) |
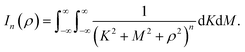 | (11) |
Next, we substitute 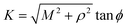 , where ϕ ∈ (−π/2, π/2) so that (11) becomes
, where ϕ ∈ (−π/2, π/2) so that (11) becomes
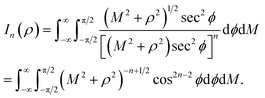 | (12) |
Since
By further substituting M = ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ where ψ ∈ (−π/2, π/2), we obtain
ψ where ψ ∈ (−π/2, π/2), we obtain
and upon simplifying gives (6).
Appendix B evaluation of integral Jn in section 2.2
Here, we consider a ring of radius r with typical point (r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, r
θ, r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, ρ) interacting with a graphene sheet lying on the xy-plane on which its typical point has coordinates (p, q, 0). To determine the interaction energy between a ring and a graphene sheet using the Lennard-Jones potential, we introduce the integral Jn(ρ) which is defined by
θ, ρ) interacting with a graphene sheet lying on the xy-plane on which its typical point has coordinates (p, q, 0). To determine the interaction energy between a ring and a graphene sheet using the Lennard-Jones potential, we introduce the integral Jn(ρ) which is defined by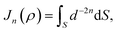 | (13) |
d2 = (r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − p)2 + (r θ − p)2 + (r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − q)2 + ρ2. θ − q)2 + ρ2. |
Thus we may write (13) as
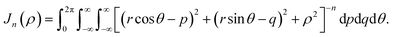 | (14) |
Now let W = p − r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and T = q − r
θ and T = q − r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, hence (14) becomes
θ, hence (14) becomes
By noting that 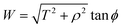 and T = ρ
and T = ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ and following the same procedure as in Appendix A, we find
ψ and following the same procedure as in Appendix A, we find
Appendix C molecular dynamics simulations
The large-scale atomic/molecular massively parallel simulator (LAMMPS) software package27 was used to perform the simulations for the corannulene–graphene interaction. Results of these simulations are reported in Section 3. The system is simulated in a domain of size 100 Å × 100 Å × 100 Å. The Lennard-Jones pair potential is used with a cut-off distance of 14 Å and only atomic coordinates are considered, no bonds, angles nor dihedrals. To compare simulation results with the models mentioned in Section 2, the corannulene is forced to move along the z-axis as opposed to allowing the program to determine the movement from a set of initial conditions. The corannulene molecule is also rotated about its own axis during the run time in order to minimise effects from configuration bias, since the ring model it is being compared to does not account for this. This method of simulation is equivalent to numerical solution where corannulene is modelled as a collection of discrete atoms.Appendix D density functional theory simulations
Density functional theory (DFT) calculations were performed using the hybrid meta-GGA (generalized gradient approximation) DFT method PW6B95-D4 in conjunction with the triple- and quadruple-ζ def2-nZVPP basis sets (n = T, Q).28,29 Where the recently developed, atomic-charge dependent D4 dispersion correction is employed.30,31 The PW6B95 exchange-correlation functional has been extensively benchmarked and found to be robust for both reaction energies and barrier heights involving related systems.18,20,32–38 We were able to perform basis set superposition error (BSSE) calculations in conjunction with the def2-TZVPP basis set.39–41 However, the BSSE calculations in conjunction with the def2-QZVPP basis set proved beyond our computational resources. All optimized geometries were taken from ref. 17. All calculations were carried out using the Gaussian 16 program suite.42Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
P. S. is grateful for the financial support from the Development and Promotion of Science and Technology Talents Project (DPST), Thailand. The authors also acknowledge the School of Information and Physical Sciences at the University of Newcastle for hosting the research visits by P. S. and D. B.References
- L. T. Scott and M. Petrukhina, Fragments of fullerenes and carbon nanotubes: designed synthesis, unusual reactions, and coordination chemistry, John Wiley & Sons, 2011 Search PubMed.
- V. M. Tsefrikas and L. T. Scott, Geodesic polyarenes by flash vacuum pyrolysis, Chem. Rev., 2006, 106, 4868–4884 CrossRef CAS PubMed.
- Y.-T. Wu and J. S. Siegel, Aromatic molecular-bowl hydrocarbons: Synthetic derivatives, their structures, and physical properties, Chem. Rev., 2006, 106, 4843–4867 CrossRef CAS PubMed.
- P. W. Rabideau and A. Sygula, Buckybowls: Polynuclear aromatic hydrocarbons related to the buckminsterfullerene surface, Acc. Chem. Res., 1996, 29, 235–242 CrossRef CAS.
- M. Saito, H. Shinokubo and H. Sakurai, Figuration of bowl-shaped p-conjugated molecules: properties and functions, Mater. Chem. Front., 2018, 2, 635–661 RSC.
- Y.-T. Wu and J. S. Siegel, Synthesis, structures, and physical properties of aromatic molecular-bowl hydrocarbons, Top. Curr. Chem., 2014, 349, 63–120 CrossRef CAS PubMed.
- A. Sygula, Chemistry on a half-shell: Synthesis and derivatization of buckybowls, Eur. J. Org. Chem., 2011, 2011, 1611–1625 CrossRef.
- S. Higashibayashi and H. Sakurai, Synthesis of sumanene and related buckybowls, Chem. Lett., 2011, 40, 122–128 CrossRef CAS.
- M. A. Petrukhina and L. T. Scott, Coordination chemistry of buckybowls: from corannulene to a hemifullerene, Dalton Trans., 2005, 18, 2969–2975 RSC.
- J. C. Hanson and C. E. Nordman, The crystal and molecular structure of corannulene, C20H10, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, B32, 1147–1153 CrossRef CAS.
- L. T. Scott, M. M. Hashemi and M. S. Bratcher, Corannulene bowl-to-bowl inversion is rapid at room temperature, J. Am. Chem. Soc., 1992, 114, 1920–1921 CrossRef CAS.
- M. Jurícek, N. L. Strutt, J. C. Barnes, A. M. Butterfield, E. J. Dale, K. K. Baldridge, J. F. Stoddart and J. S. Siegel, Induced-fit catalysis of corannulene bowl-to-bowl inversion, Nat. Chem., 2014, 6, 222–228 CrossRef PubMed.
- A. A. Kroeger and A. Karton, Perylene bisimide cyclophanes as receptors for planar transition structures – catalysis of stereoinversions by shape-complementarity and noncovalent π − π interactions, Org. Chem. Front., 2021, 8, 4408–4418 RSC.
- S. Ibáñez and E. Peris, Dimensional matching versus induced-fit distortions: Binding affinities of planar and curved polyaromatic hydrocarbons with a tetragold metallorectangle, Angew. Chem., 2020, 59, 6860–6865 CrossRef PubMed.
- A. Karton, Inversion and rotation processes involving non-planar aromatic compounds catalyzed by extended polycyclic aromatic hydrocarbons, Chem. Phys. Lett., 2014, 614, 156–161 CrossRef CAS.
- P. A. Denis, Pristine graphene-based catalysis: Significant reduction of the inversion barriers of adsorbed and confined corannulene, sumanene, and dibenzo[a,g]corannulene, J. Phys. Chem. A, 2015, 119, 5770–5777 CrossRef CAS PubMed.
- A. Karton, Catalysis on pristine 2D materials via dispersion and electrostatic interactions, J. Phys. Chem. A, 2020, 124(35), 6977–6985 CrossRef CAS PubMed.
- A. A. Kroeger and A. Karton, Catalysis by pure graphene - From supporting actor to protagonist through shape complementarity, J. Org. Chem., 2019, 84, 11343–11347 CrossRef CAS PubMed.
- A. A. Kroeger, J. F. Hooper and A. Karton, Pristine graphene as a racemization catalyst for axially chiral binol, ChemPhysChem, 2020, 21, 1675–1681 CrossRef CAS PubMed.
- A. A. Kroeger and A. Karton, π − π catalysis in carbon flatland—flipping [8]annulene on graphene, Chem.–Eur. J., 2021, 27, 3420–3426 CrossRef CAS PubMed.
- T. Janowski, A. R. Ford and P. Pulay, Accurate correlated calculation of the intermolecular potential surface in the coronene dimer, Mol. Phys., 2010, 108, 249–257 CrossRef CAS.
- T. Janowski and P. Pulay, A benchmark quantum chemical study of the stacking interaction between larger polycondensed aromatic hydrocarbons, Theor. Chem. Acc., 2011, 130, 419–427 Search PubMed.
- A. Karton, π − π interactions between benzene and graphene by means of large-scale DFT-D4 calculations, Chem. Phys., 2022, 561, 111606 CrossRef CAS.
- P. A. Denis, Helicene adsorption on graphene, hexagonal boron nitride, graphane, and fluorographene, Chem. Phys. Lett., 2022, 806, 139998 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- D. Baowan, B. J. Cox, T. A. Hilder, J. M. Hill, and N. Thamwattana, Modelling and Mechanics of Carbon-based Nanostructured Materials, Micro and Nano Technologies, Elsevier Science, 2017, ISBN 9780128124642 Search PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS – a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Design of density functionals that are broadly accurate for thermochemistry, thermochemical kinetics, and nonbonded interactions, J. Phys. Chem. A, 2005, 109, 5656 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 dispersion coefficient model, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, A generally applicable atomic-charge dependent london dispersion correction, J. Chem. Phys., 2019, 150, 154112 CrossRef PubMed.
- L. Goerigk and S. Grimme, A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions, Phys. Chem. Chem. Phys., 2011, 13, 6670 RSC.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184 RSC.
- A. Karton, How reliable is DFT in predicting relative energies of polycyclic aromatic hydrocarbon isomers? comparison of functionals from different rungs of Jacob's ladder, J. Comput. Chem., 2017, 38, 370 CrossRef CAS PubMed.
- L. Goerigk and R. Sharma, The INV24 test set: how well do quantum-chemical methods describe inversion and racemization barriers?, Can. J. Chem., 2016, 94, 1133 CrossRef CAS.
- A. Karton, D. Gruzman and J. M. L. Martin, Benchmark thermochemistry of the CnH2n+2 alkane isomers (n = 2–8) and performance of DFT and composite ab initio methods for dispersion-driven isomeric equilibria, J. Phys. Chem. A, 2009, 113, 8434 CrossRef CAS PubMed.
- J. Zheng, Y. Zhao and D. G. Truhlar, The DBH24/08 database and its use to assess electronic structure model chemistries for chemical reaction barrier heights, J. Chem. Theory Comput., 2009, 5, 808 CrossRef CAS PubMed.
- A. Karton, A. Tarnopolsky, J.-F. Lamère, G. C. Schatz and J. M. L. Martin, Highly accurate first-principles benchmark datasets for the parametrization and validation of density functional and other approximate methods. derivation of a robust, generally applicable, double-hybrid functional for thermochemistry and thermochemical kinetics, J. Phys. Chem. A, 2008, 112, 12868 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Calculation of small molecular interactions by differences of separate total energies – some procedures with reduced errors, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- H. B. Jansen and P. Ros, Non-empirical molecular orbital calculations on the protonation of carbon monoxide, Chem. Phys. Lett., 1969, 3, 140 CrossRef CAS.
- B. Liu and A. D. Mclean, Accurate calculation of the attractive interaction of two ground state helium atoms, J. Chem. Phys., 1973, 59, 4557 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc, Wallingford CT, 2016 Search PubMed.
| This journal is © The Royal Society of Chemistry 2023 |