Open Access Article
Open Access ArticleModelling the quenching effect of chloroaluminum phthalocyanine and graphene oxide interactions: implications for phototherapeutic applications†
Fernando Teixeira
Bueno
a,
Leonardo Evaristo
de Sousa
 b,
Leonardo Giordano
Paterno
c,
Alan Rocha
Baggio
c,
Demétrio Antônio
da Silva Filho
b,
Leonardo Giordano
Paterno
c,
Alan Rocha
Baggio
c,
Demétrio Antônio
da Silva Filho
 a and
Pedro Henrique de Oliveira
Neto
a and
Pedro Henrique de Oliveira
Neto
 *a
*a
aInstitute of Physics, University of Brasília, Brasília, DF 70910-900, Brazil. E-mail: pedrohenrique@unb.br
bDepartment of Energy Conversion and Storage, Technical University of Denmark, Anker Engelunds Vej 301, 2800 Kongens Lyngby, Denmark
cLaboratory of Research on Polymers and Nanomaterials, Institute of Chemistry, University of Brasília, Brasília, DF 70910-900, Brazil
First published on 15th September 2023
Abstract
Photodynamic therapy (PDT) and photothermal therapy (PTT) are promising candidates for cancer treatment and their efficiency can be further enhanced by using a combination of both. While chloroaluminum phthalocyanine (AlClPc) has been studied extensively as a photosensitizer in PDT, nanographene oxide (nGO) has shown promise in PTT due to its high absorption of near-infrared radiation. In this work, we investigate the energy transport between AlClPc and nGO for their combined use in phototherapies. We use density functional theory (DFT) and time-dependent DFT to analyze the electronic structure of AlClPc and its interaction with nGO. Based on experimental parameters, we model the system's morphology and implement it in Kinetic Monte Carlo (KMC) simulations to investigate the energy transfer mechanism between the compounds. Our KMC calculations show that the experimentally observed fluorescence quenching requires modeling both the energy transfer from dyes to nGO and a molecular aggregation model. Our results provide insights into the underlying mechanisms responsible for the fluorescence quenching observed in AlClPc/nGO aggregates, which could impact the efficacy of photodynamic therapy.
I. Introduction
Cancer is a leading cause of death worldwide, with thousands of deaths happening each year.1 The most effective treatments currently include chemotherapy, radiotherapy, and surgical removal. On a quest for complementary treatments, researchers have been exploring phototherapies such as photodynamic therapy (PDT) and photothermal therapy (PTT). Depending on how advanced the disease is or how deep inside the tissue the affected cells are, the isolated use of PDT may not be enough. Different studies have shown that both types of therapies have also been found to be effective when used in combination with other treatments.2–5 PDT involves using photosensitizing agents, often biocompatible dyes, to generate oxidative stress in cancerous cells and produce reactive oxygen species.6–9 Over the last decade, significant progress was made in applying PDT with different photosensitizers or a combination of compounds. Two photosensitizers that have been studied extensively and were shown to be effective are methylene blue (MB)10–12 and chloroaluminum phthalocyanine.13–16 Concurrently to advancements in PDT, photothermal therapy has also gained ground in the medical field when it comes to cancer treatments. PTT uses photosensitive agents to generate local heat and destroy cancer cells through thermal ablation. PTT employs various compounds, such as gold nanoparticles, dye-based nanoparticles, carbon nanotubes, and graphene oxide nanoparticles.17 Graphene-based systems have been found to be particularly promising due to their high absorption of near-infrared radiation, which makes them an effective choice for PTT.6,18,19In a previous study, mice with human cervical cancer tumors were treated with a formulation of nanographene oxide (nGO) and methylene blue, and were divided into groups that received only PDT, only PTT, or a combination of both therapies. Results showed that the combination of both treatments when they were administered simultaneously was most effective in causing cell death in comparison to both treatments being given separately.20–22 Another study found that similar concentrations of MB and nGO were effective in reducing breast cancer tumors when both PDT and PTT were administered concurrently, also indicating the previously mentioned synergistic effect, but for a different type of cancer.23 Overall, the combination of these two agents presents itself as a promising candidate for combined PDT and PTT treatments.
In pure PDT applications, both plain and metalated phthalocyanines have demonstrated superior efficiency compared to methylene blue. This is attributed to their elevated fluorescence quantum yields (QY) and their ability to generate long-lived singlet and triplet oxygen states.24,25 In light of these considerations, the photophysical attributes of the combination involving AlClPc—substituting methylene blue—and various species of graphene oxide were explored in the work by Baggio et al.26 The authors found that the presence of nanographene oxide caused significant quenching of the samples' fluorescence spectra, which would likely hinder the effects of PDT due to its dependence on high emission rates from the photodynamic agent. The energy carrier in these compounds is a quasiparticle known as the exciton and it can only be transferred from one donor molecule to a corresponding acceptor if their respective fluorescence and absorption spectra overlap. In that sense, said result was unexpected due to an apparent lack of spectral overlap. In addition, the hypothesis of an inner-filter effect, characterized as the attenuation of the excitation beam due to high solution concentration, was tested, but deemed insufficient to explain the fluorescence suppression. Therefore, it was suggested that an undesired energy transfer between the dye and nanographene oxide was the cause of the observed quenching.
In this work, we investigate exciton dynamics between AlClPc and nGO in the context of such combination being a candidate for applications related to phototherapies. With density functional theory (DFT) and its time dependent extension (TD-DFT) we analyze AlClPc's electronic structure and its interaction with nGO. We model the system's morphology based on experimental parameters and implement them on Kinetic Monte Carlo (KMC) simulations to investigate the energy transfer mechanism between the compounds. We show that the experimentally observed fluorescence quenching requires not only the modeling of energy transfer from dyes to nGO, but also the consideration of a molecular aggregation model (data shown in Section II of the ESI†), which allows for experimental fluorescence spectra to be reproduced by our KMC calculations across a range of nGO concentrations. This study makes significant contributions to our comprehension of energy transfer mechanisms among compounds employed in integrated phototherapeutic applications. These findings offer insights that could facilitate a reevaluation of the foundational science behind the synergy among diverse medical agents.
II. Methods
Using DFT and TD-DFT at the ωB97XD/6-31G(d,p) level of theory, geometry optimizations and normal mode analyses were run for AlClPc's ground (S0) and first excited (S1) states. Such calculations were performed in gas phase and in solution via the polarization continuum model27,28 (PCM), considering ethanol as the solvent. PCM was employed in its state specific approach, using the corrected linear response correction.29 All electronic structure calculations were performed using Gaussian 16.30The nuclear ensemble method31,32 was used to simulate absorption and fluorescence spectra. Ensembles of 500 conformations were produced by sampling geometries from the Wigner distribution at T = 300 K. The contribution of each conformation to the spectrum was broadened by a normalized Gaussian function with standard deviation of kBT = 0.026 eV, kB being the Boltzmann constant. The simulated spectra were used to calculate Förster radii between dye molecules as well as radiative lifetimes.33,34
Kinetic Monte Carlo simulations were performed on three distinct lattices, each constructed to mirror the experimental concentrations of AlClPc and nGO as documented in ref. 26. These experimental concentrations acted as the guiding framework for the creation of lattice compositions. Detailed explanations about the KMC algorithm utilized in our simulations can be found in Section IC of the ESI.† Within these lattices, the perimeter sites represent the graphene oxide sheets, while the residual sites signify the presence of AlClPc molecules. The dimensions of these lattices were computed based on the correlation between nGO sheets and AlClPc molecules. Table 1 offers an overview of the site count (Nsites) and the lattice width (Lbox) corresponding to each distinctive experimental concentration.
| ρ dye (g L−1) | ρ nGO (g L−1) | N sites | L box (nm) |
|---|---|---|---|
| 0.31 | 2.96 | 33 × 33 × 33 | 476.0 |
| 6.30 | 26 × 26 × 26 | 370.4 | |
| 12.65 | 20 × 20 × 20 | 293.1 |
The average intermolecular distance was estimated from AlClPc concentrations to be approximately ravg = 145 Å. In this sense, two distinct schemes for site distribution within the lattice were employed (Fig. 1). The first approach (Fig. 1a) consists in the homogeneous distribution of AlClPc molecules, resulting in a cubic lattice with intermolecular distances given by ravg, such that exciton diffusion is not favored in any direction. The second scheme represents an aggregation model (Fig. 1b) in which AlClPc molecules are positioned following two rules: first, distances to the nearest lattice border decrease geometrically with a ratio q; second, the average intermolecular distance remains equal to ravg. Further details about the modeling of system morphology are presented in Section I of the ESI.†
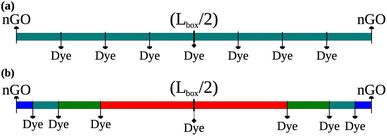 | ||
| Fig. 1 Equally distanced dye molecules, representing equally spaced sites in all directions (a). Different distances between dye molecules according to the present geometric progression (b). | ||
In organic compounds, energy transfer for singlet excitons occurs via Förster Resonance Energy Transfer (FRET),33,35 which is a non-radiative process where excitation energy is transferred from one molecule to the other given the existence of overlap between the fluorescence and absorption spectra of the donor and acceptor molecules, respectively. Its rate, kF, is calculated as
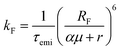 | (1) |
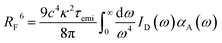 | (2) |
To each site in the lattice is assigned an energy value sampled from a Gaussian distribution centered in the dye's peak emission energy. Said energy and the spectral width were retrieved from experimentally obtained data. As such, fluorescence spectra can be generated by looking into the distribution of energies of excitons that decay radiatively during the simulation.
III. Results
The analysis starts with a comparison between simulated and experimental spectroscopic results for AlClPc. Fig. 2 shows normalized absorption (in blue) and fluorescence (in red) for simulated (a) and experimental spectra (b) obtained in ethanol solution. The experimental absorption spectrum has its peak at 1.85 eV, matching the peak of the simulated spectrum. The experimental fluorescence spectrum has its maximum value at 1.82 eV in a narrow peak. Maximum simulated fluorescence is seen at 1.80 eV, presenting a similar shape over a wider energy range. Although simulated spectra are wider, they are in good agreement with experimental results.39,40 In both cases, a large spectral overlap between absorption and fluorescence spectra and small Stokes' Shift can be seen. Such features are associated with the dye's rigid structure, which results in its ground and first excited states having similar optimized geometries as well as a low reorganization energy. Furthermore, exciton radiative lifetime could be estimated as 5.1 ns, which is also in good agreement with experimental data of 7.4 ns.24,26 Additional information concerning the synthesis and spectroscopic characterization of the compounds under investigation can be found in ref. 26.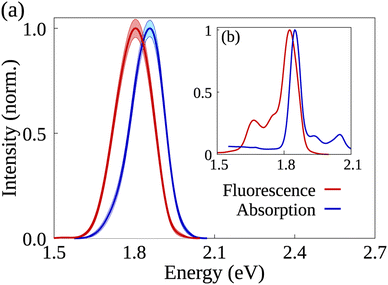 | ||
| Fig. 2 AlClPc's simulated (a) and experimentally obtained (b) absorption and emission spectra in blue and red, respectively. Shaded areas represent the error bars in the simulated spectra. | ||
The Förster radius, which governs exciton transfers between AlClPc molecules, was calculated to be 87.8 ± 3.6 Å, using the orientation factor κ2 = 2/3 that corresponds to an isotropic distribution of molecules.41 While such radius is considered high for conventional organic semiconductors,34 it is essential to note that a high Förster radius does not inherently guarantee efficient energy transfer. This is due to the distance-dependent nature of exciton hopping rates (see eqn (1)). In our specific case, the situation is influenced by the system's concentration in solution, with an average intermolecular distance of 145 Å, as elaborated in the ESI.† This intermolecular distance exceeds the Förster radius by 65%, significantly diminishing the likelihood of successful exciton transfer. To illustrate this argument, the dye's emission rate was calculated as kemi = 1.9 × 108 s−1. Meanwhile, the Förster transfer rate for the aforementioned radius and intermolecular distance is kF = 8.5 × 105 s−1, corresponding to an exciton being 200 times more likely to fluoresce than to be transferred.
We examined the experimental spectra of AlClPc and nGO, and although there was minimal overlap observed surrounding the peak energy for either compound,26,42,43 it is important to note that nGO has a non-negligible absorption cross-section that extends beyond its maximum intensity point. This means that some overlap may occur with the fluorescence spectrum of the phthalocyanine. Due to nGO's extended nature and uncertain detailed chemical composition, simulating its fluorescence spectrum was not possible. Notwithstanding, the relevant physical quantities usually derived from said spectrum were treated as parameters in our simulations.
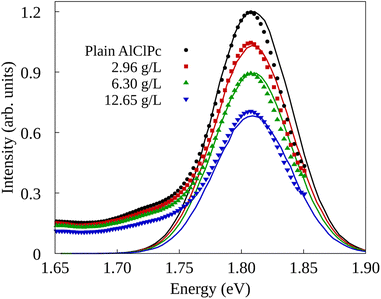
The experimental setup in ref. 26 investigated two types of quenching of the emission spectrum of AlClPc as a function of nGO concentration. In the first one, fluorescence spectrum measurements were taken with AlClPc and nGO samples placed in separate cuvettes, preventing any form of energy transfer between AlClPc and nGO. As a result, the observed quenching, also called inner-filter effect,44–46 is attributed to nGO absorbing light before it can reach the dyes. The results for this experiment are presented in Fig. 3 in the form of solid data points displayed in black, red, green and blue, for each nGO concentration. The relative fluorescence quantum yield can be estimated by fitting a Gaussian function to the experimental spectra and using the ratio between the area of the fitted curve for different nGO concentrations and that of the spectrum obtained from a plain dye sample. Table 2 shows the calculated values corresponding to the different experimental settings. As shown in Section II of the ESI,† fluorescence quenching happens, but in a much less expressive manner than what was observed experimentally when samples are placed in the same cuvette.
| ρ dye | ρ nGO | Relative quantum yield (%) | |
|---|---|---|---|
| Separate cuvette | Same cuvette | ||
| 0.31 | 2.96 | 84.7 | 41.3 |
| 6.30 | 68.6 | 29.5 | |
| 12.65 | 53.7 | 26.9 | |
Given these experimental results, we turn to KMC simulations results aimed at elucidating the mechanism behind the quenching phenomena. We estimated the proportion of photons that are absorbed by AlClPc molecules from the relative quantum yields calculated with the experimental data in the case of separate cuvettes. This allows us to select the appropriate number of excitons employed in the KMC simulations for each concentration of nGO. Plain dye samples were simulated using one exciton per round in a total of 106 excitons. This number is multiplied by the corresponding relative quantum yield in the case of simulations that include nGO. As such, the relative intensities of the fluorescence spectra can be captured.
In the experimental setup, the second type of quenching was measured with both materials placed in the same cuvette as a combined mixture. In this case, the observed quenching is a result of the combination of the inner-filter effect and the energy transfer from dye to graphene oxide. Notably, for the lowest graphene oxide concentration, the mixture's relative QY was reduced by over 50% when materials were in the same cuvette. In addition, a non-linear progression is seen between nGO concentration and the observed QY, i.e. an approximate four-fold increase in nGO concentration only led the QY going from 84.7% to 53.7% when samples are on different cuvettes while it went from 41.3% to 26.9% when materials are on the same cuvette. It is worth mentioning that the dye concentration remained the same during all measurements, such that an increase in nGO presence translates into more graphene oxide being added to interact with the same number of dye molecules.
Summarizing, within the context of the experimental framework, the separate cuvette setup is characterized by the absence of any direct interaction between the nGO solution and the AlClPc solution. Correspondingly, in our simulations, this setup is emulated by setting a null Förster radius from the dye to nGO. On the other hand, the same cuvette experimental setup involves a mixed solution of both compounds being analyzed while performing spectroscopic measurements. To accurately simulate this setup, we account for the molecular aggregation arising from the presence of nGO and consider a high Förster radius from AlClPc to nGO.
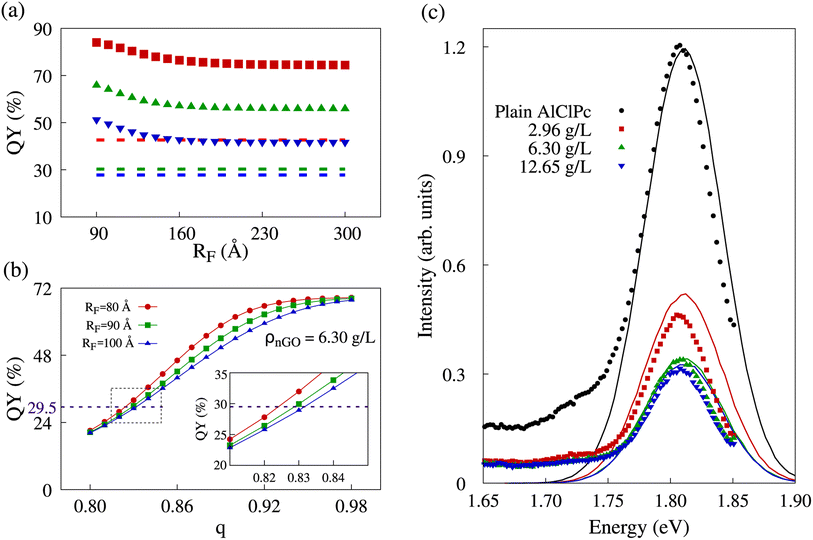
As previously stated, the initial morphology we simulated was a cubic lattice of equally spaced dye molecules between which excitons can hop, in which there is the possibility of excitons being transferred to graphene oxide, only present at the edges of said lattice. In our model, quenching results from the collection of excitons by nGO. It was observed that the amount of collected excitons showed little variation with incremental increases of RF value. Naturally, with no significant variation in exciton collection, QY also remained nearly unchanged. In Fig. 4a, we show quantum yields for different RF values in all three nGO concentrations. The dashed lines represent the experimentally observed QY in the concentration corresponding to the data color. One can see that in the range of RF ∈ [90; 180] Å, the QY in all three concentrations decreases as more excitons are collected. However, regardless of the increase in RF ≥ 180 Å, QY remains constant. In comparison with experimental data (dashed lines), there is no value of RF that would be able to produce the same QY for any concentration. The presented behavior shows that excitons that reach a AlClPc + nGO interface are highly likely to be collected. Nevertheless, not enough excitons are being transferred between dye molecules to reach said interface and produce the observed quenching. Low transfer rates between dye molecules were already expected due to the ratio of Förster radius between dye molecules (87.8 Å) and the average intermolecular distance between them (145 Å). Notably, Förster radii higher than 100 Å are considered non physical, further supporting that the observed exciton collection is not exclusively dependent on a high transfer rate from dye to nGO, but also on there being enough transfer between the dye molecules so that excitons can reach an interface.
Since the intermolecular distance is the only physical quantity that can change in the calculation of transfer rates, we made use of the previously described aggregation model to the phthalocyanine molecules. The only adjustable parameter in the geometric progression is the ratio q, while the sum of the terms in the progression is fixed by the lattice size. A scan over this parameter from 0.80 to 0.98 in 0.01 increments was performed for different RF values and the fluorescence and quenching intensities were analyzed in all three nGO concentrations. In Fig. 4b, we show how the behavior of QY is altered by changes in aggregation, represented by q. It is worth noting that a smaller q corresponds to more intense aggregation—distance between dye molecules decreasing faster as molecules approach the lattice's edges and nGO—therefore favoring FRET between AlClPc molecules. The curves shown in red, green and blue in the referred plot represent different RF values for the case of ρnGO = 6.30 g L−1. All three of them present non-linear fluorescence decrease with the reduction of q (increased aggregation). A higher RF translates into higher transfer rates for exciton collection, which leads to sharper changes on the plot. That can be seen by comparing the different profiles for the curves in red and blue in Fig. 4b. Nevertheless, for q values on the extremities of the scan range, fluorescence is virtually the same. This goes to show that having dye molecules closer together has a more vital role in allowing for excitons to be collected than knowing the precise transfer rate from AlClPc to nGO does. In addition, for the represented concentration, experimental QY of 29.5% (shown in the purple dashed line) could be achieved in our simulation with all three radii, but with aggregation varying approximately from 17% (q 0.83) to 18% (q ≈ 0.82). The same analysis was performed for all experimental nGO concentrations where Förster radius was scanned from 80 Å to 100 Å in increments of 1 Å.
In order to obtain fluorescence spectra from KMC simulations that are consistent with experimental observations across various concentrations of nGO, as presented in ref. 26, it is necessary to identify a value for the Förster radius for AlClPc to nGO transfers as well as the proper aggregation factor q for each concentration. By minimizing the root mean squared deviation between KMC-generated and experimental spectra, we were able to find optimum values for these features: RF = 96 Å and q values of 0.87, 0.83 and 0.81 for ρnGO = 2.96 g L−1, ρnGO = 6.30 g L−1 and ρnGO = 12.65 g L−1, respectively. The simulated spectra obtained from KMC simulations using these parameters are shown in Fig. 4c in the form of continuous lines in black, red, green and blue, according to nGO concentration. The intensity of the spectrum was put in the same scale as the experimental spectra for comparison. One can observe the quenching behavior in very good agreement with what was obtained experimentally. Experimental data is shown in the same plot in the form of solid data points following the same labels. Although the overlap between experimental and simulated spectra for ρnGO = 2.96 g L−1 does not seem precise, the ratio between such spectrum and plain dye data (shown in black) is the same seen experimentally, in accordance to the numbers displayed in Table 2. Additionally, the presence of nGO in its lowest concentration is enough to cause intense aggregation, which, in combination with the inner-filter effect, reduced dye's fluorescence by over 50%. By comparing the observed quenching between the lowest and highest nGO concentrations we see a difference of less than 15% in fluorescence for a six-fold increase in nGO concentration. It is worth noting that the previously mentioned inner-filter effect was also taken into account for same cuvette simulations, where the number of initial excitons per simulation varied according to data from separate cuvette experiments, shown in Table 2.
From these results, we were able to establish how the morphology may drastically affect exciton diffusion in AlClPc + nGO system. Specifically, it was determined that molecular aggregation was necessary for sufficient energy transfer from the dye to nGO to occur and for experimental results to be accurately simulated. Furthermore, we determined the intensity of said aggregation as a function of nGO concentration.
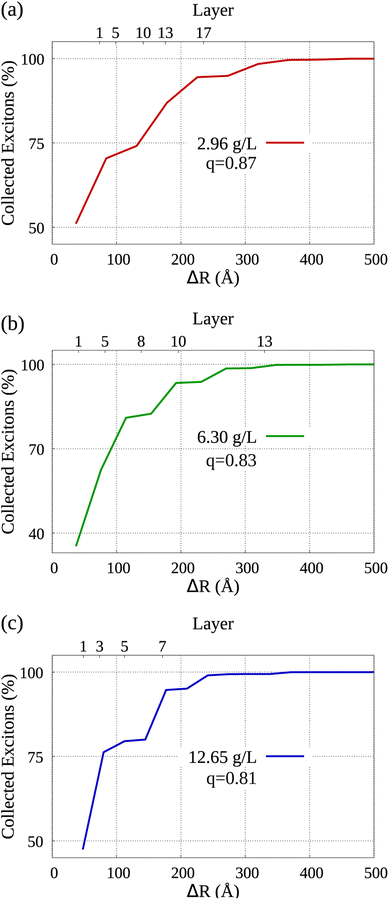
By analyzing the diffusion of collected excitons, we are able to learn which sections of the dye molecules within the system's aggregated morphology contributed more to the occurrence of exciton collection. Bearing that in mind, Fig. 5 displays the distribution of collected excitons' mean displacement in the lower horizontal axis, while in the vertical axis we see the cumulative percentage of collected excitons. It's important to note that the parameter q represents the ratio employed in the modeled molecular aggregation for each simulation, as elaborated in Section IB of the ESI† accompanying our work. In the upper horizontal axis we label some of the layers starting from the nGO (see Fig. 1, each dye marker represents one of the AlClPc layers in relation to the central molecule towards the nGO), i.e., the fifth layer of dye from nGO in (a) is at approximately 100 Å from the nGO. We can observe that in all cases, over 70% of collected excitons are generated, on average, in the first half of dye layers. From the morphologies detailed in Sections IA and IB of the ESI,† to simulate the lowest nGO concentration, there are 17 layers of dye between the central molecule and nGO wall, which means 34 layers in total between parallel nGO walls. Notably, for the same concentration approximately 80% of all excitons were generated no farther than the 10th layer starting from nGO. This goes to show that quenching at such intensity can only be seen due to molecular aggregation and that dye molecules that come to be separated by larger distances, i.e. dye layers farther from nGO, do not significantly contribute to fluorescence reduction. This analysis provides further evidence that for equally spaced dye molecules, such quenching results could not have been obtained with the Förster transfer mechanism being solely responsible for the observed effect.
IV. Conclusions
To summarize, we have investigated exciton dynamics in AlClPc and nGO. By combining electronic structure calculations for the dye molecule of interest and the nuclear ensemble method, we were able to estimate its pertinent photophysical quantities via absorption and fluorescence spectra. The Förster radius for transfers between AlClPc molecules was calculated and fluorescence and transfer rates were determined.Inner-filter effects and a quenching due to AlClPc interactions with nGO were studied via KMC simulations. To emulate experimental conditions, the system morphology was modeled following experimental concentrations. Results indicated that a homogeneous cubic lattice was not an appropriate description of the observed phenomena due to high intermolecular distance. From that, we created an aggregation model for positioning AlClPc molecules in a lattice according to how close they are to a nanographene oxide sheet. Through thorough analysis of KMC results taking molecular aggregation into account, experimental results were accurately reproduced and the relevant physical parameters were determined.
Our results point to the formation of molecular aggregates being responsible for an intense unwanted fluorescence quenching. With that in mind, the choice of photodynamic agent has to account for the possible formation of molecular complexes as well as the possibility of unexpected energy transfer between the used compounds. Furthermore, we showed that any transfer that may occur between non-aggregate molecules hardly contributes to the observed quenching.
Conflicts of interest
There are no conflicts of interest to declare.References
- E. Ward, R. L. Sherman, S. J. Henley, A. Jemal, D. A. Siegel, E. J. Feuer, A. U. Firth, B. A. Kohler, S. Scott, J. Ma, R. N. Anderson, V. Benard and K. Cronin, JNCI, J. Natl. Cancer Inst., 2019, 111(12), 1279–1297, DOI:10.1093/jnci/djz106 , http://oup.prod.sis.lan/jnci/advance-article-pdf/doi/10.1093/jnci/djz106/28704872/djz106.pdf.
- J. Shi, B. Wang, Z. Chen, W. Liu, J. Pan, L. Hou and Z. Zhang, Pharm. Res., 2016, 33, 1472 CrossRef CAS.
- X. Yan, H. Hu, J. Lin, A. J. Jin, G. Niu, S. Zhang, P. Huang, B. Shen and X. Chen, Nanoscale, 2015, 7, 2520 RSC.
- J. Zhang, N. Wang, Q. Li, Y. Zhou and Y. Luan, Chem. Commun., 2021, 57, 2305 RSC.
- X. Sun, K. Chen, Y. Liu, G. Zhang, M. Shi, P. Shi and S. Zhang, Nanoscale Adv., 2021, 3, 6669 RSC.
- Z. Huang, Technol. Cancer Res. Treat., 2005, 4, 283 CrossRef CAS PubMed.
- M. H. Schmidt, G. A. Meyer, K. W. Reichert, J. Cheng, H. G. Krouwer, K. Ozker and H. T. Whelan, J. Neuro-Oncol., 2004, 67, 201 CrossRef PubMed.
- T. Okunaka, H. Kato, H. Tsutsui, T. Ishizumi, S. Ichinose and Y. Kuroiwa, Lung Cancer, 2004, 43, 77 CrossRef PubMed.
- H. Kato, Gan to Kagaku Ryoho, 1996, 23, 8 CAS.
- D. B. Tada, L. L. Vono, E. L. Duarte, R. Itri, P. K. Kiyohara, M. S. Baptista and L. M. Rossi, Langmuir, 2007, 23, 8194 CrossRef CAS PubMed.
- J. P. Tardivo, A. Del Giglio, C. S. De Oliveira, D. S. Gabrielli, H. C. Junqueira, D. B. Tada, D. Severino, R. de Fátima Turchiello and M. S. Baptista, Photodiagn. Photodyn. Ther., 2005, 2, 175 CrossRef CAS PubMed.
- K. Orth, G. Beck, F. Genze and A. Rück, J. Photochem. Photobiol., B, 2000, 57, 186 CrossRef CAS PubMed.
- L. A. Muehlmann, B. C. Ma, J. P. F. Longo, M. d. F. M. A. Santos and R. B. Azevedo, Int. J. Nanomed., 2014, 9, 1199 CrossRef PubMed.
- S. Dutta, D. Ray, B. K. Kolli and K.-P. Chang, Antimicrob. Agents Chemother., 2005, 49, 4474 CrossRef CAS PubMed.
- R. M. Amin, C. Hauser, I. Kinzler, A. Rueck and C. Scalfi-Happ, Photochem. Photobiol. Sci., 2012, 11, 1156 CrossRef CAS PubMed.
- L. A. Muehlmann, M. C. Rodrigues, J. P. F. Longo, M. P. Garcia, K. R. Py-Daniel, A. B. Veloso, P. E. N. de Souza, S. W. da Silva and R. B. Azevedo, J. Nanobiotechnol., 2015, 13, 1 CrossRef CAS PubMed.
- E. A. Hussein, M. M. Zagho, G. K. Nasrallah and A. A. Elzatahry, Int. J. Nanomed., 2018, 13, 2897 CrossRef CAS PubMed.
- J. Liu, L. Cui and D. Losic, Graphene and graphene oxide as new nanocarriers for drug delivery applications, Acta Biomater., 2013, 9(12), 9243–9257 CrossRef CAS PubMed.
- J. H. Lim, D. E. Kim, E.-J. Kim, C. D. Ahrberg and B. G. Chung, Macromol. Res., 2018, 26, 557 CrossRef CAS.
- A. Sahu, W. I. Choi, J. H. Lee and G. Tae, Biomaterials, 2013, 34, 6239 CrossRef CAS PubMed.
- W. Zhang, Z. Guo, D. Huang, Z. Liu, X. Guo and H. Zhong, Biomaterials, 2011, 32, 8555 CrossRef CAS PubMed.
- W. Miao, G. Shim, S. Lee, S. Lee, Y. S. Choe and Y.-K. Oh, Biomaterials, 2013, 34, 3402 CrossRef CAS PubMed.
- M. S. C. dos Santos, A. L. Gouvêa, L. D. de Moura, L. G. Paterno, P. E. N. de Souza, A. P. Bastos, E. A. M. Damasceno, F. H. Veiga-Souza, R. B. de Azevedo and S. N. Báo, J. Nanobiotechnol., 2018, 16, 9 CrossRef PubMed.
- C. S. de Paula, A. C. Tedesco, F. L. Primo, J. M. C. Vilela, M. S. Andrade and V. C. F. Mosqueira, Eur. J. Pharm. Sci., 2013, 49, 371 CrossRef PubMed.
- Z. Jiang, J. Shao, T. Yang, J. Wang and L. Jia, J. Pharm. Biomed. Anal., 2014, 87, 98 CrossRef CAS PubMed.
- A. R. Baggio, M. S. Santos, F. H. Souza, R. B. Nunes, P. E. N. Souza, S. N. Báo, A. O. T. Patrocinio, D. W. Bahnemann, L. P. Silva and M. J. A. Sales, et al. , J. Phys. Chem. A, 2018, 122, 6842 CrossRef CAS PubMed.
- S. Bhandari, M. S. Cheung, E. Geva, L. Kronik and B. D. Dunietz, J. Chem. Theory Comput., 2018, 14, 6287 CrossRef CAS PubMed.
- S. Bhandari and B. D. Dunietz, J. Chem. Theory Comput., 2019, 15, 4305 CrossRef CAS PubMed.
- C. Guido and S. Caprasecca, Corrected linear response state-specific correction to solvent polarization response, 2016 Search PubMed.
- M. J. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, et al., Gaussian 16, 2016 Search PubMed.
- L. E. de Sousa and P. de Silva, J. Chem. Theory Comput., 2021, 17, 5816 CrossRef CAS PubMed.
- R. Crespo-Otero and M. Barbatti, in Marco Antonio Chaer Nascimento, Springer, 2014, pp. 89–102 Search PubMed.
- T. Forster, Zwischenmolekulare energiewanderung und fluoreszenz, Ann. Phys., 1948, 437, 55–75 CrossRef.
- L. E. de Sousa, F. T. Bueno, G. M. e Silva, D. A. da Silva Filho and P. H. de Oliveira Neto, J. Mater. Chem. C, 2019, 7, 4066 RSC.
- T. Förster, Faraday Soc., 1959, 27, 7–17 RSC.
- T. Förster, Ann. Phys., 1948, 437, 55 CrossRef.
- V. May and O. Kühn, Charge and energy transfer dynamics in molecular systems, John Wiley & Sons, 2023 Search PubMed.
- S. R. Yost, E. Hontz, S. Yeganeh and T. Van Voorhis, J. Phys. Chem. C, 2012, 116, 17369 CrossRef CAS.
- R. Khairutdinov and N. Serpone, J. Phys. Chem. B, 1999, 103, 761 CrossRef CAS.
- B. H. Vilsinski, A. P. Gerola, É. O. Lemos, P. M. Barbosa, K. S. Campanholi, G. B. César, N. Hioka and W. Caetano, Quim. Nova, 2015, 38, 631 CAS.
- A. Köhler and H. Bässler, Electronic processes in organic semiconductors: An introduction, John Wiley & Sons, 2015 Search PubMed.
- I. R. Calori and A. C. Tedesco, J. Photochem. Photobiol., B, 2016, 160, 240 CrossRef CAS PubMed.
- J.-L. Li, B. Tang, B. Yuan, L. Sun and X.-G. Wang, Biomaterials, 2013, 34, 9519 CrossRef CAS PubMed.
- S. K. Panigrahi and A. K. Mishra, J. Photochem. Photobiol., C, 2019, 41, 100318 CrossRef.
- K. J. Goswami, N. Sultana and N. S. Sarma, Sens. Actuators, B, 2023, 374, 132778 CrossRef CAS.
- L. Han, S. G. Liu, J. Y. Liang, Y. J. Ju, N. B. Li and H. Q. Luo, J. Hazard. Mater., 2019, 362, 45 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00432e |
| This journal is © The Royal Society of Chemistry 2023 |