Open Access Article
Open Access ArticleModeling size and edge functionalization of MXene-based quantum dots and their effect on electronic and magnetic properties†
Barbora
Vénosová
 and
František
Karlický
and
František
Karlický
 *
*
Department of Physics, Faculty of Science, University of Ostrava, 30. dubna 22, 7013 Ostrava, Czech Republic. E-mail: frantisek.karlicky@osu.cz; Tel: +420 553 46 2155
First published on 9th November 2023
Abstract
In the last six years, the synthesis of MXene-based quantum dots (MXQDs) has gained widespread attention. Due to the quantum confinement effect, it is possible to significantly improve their properties compared to 2D counterparts, such as higher chemical stability and better electronic and optical properties. However, despite the growing interest in their properties, much remains unexplored. One of the biggest challenges is to study in more detail the structure of quantum dots, in particular, their edge functionalization and its effect on their properties. In this paper, the structural stability and electronic and magnetic properties of Ti2CO2 QDs based on different lateral dimensions and edge functionalization (–O, –F, and –OH) are investigated using density functional theory. The study shows that the energy gap of Ti2CO2–O QDs decreases with increasing lateral size for both nonmagnetic (spin-unpolarized, close shell) and magnetic (spin-polarized, open shell) cases. Furthermore, the magnetic behavior of quantum dots was revealed by shrinking from 2D Ti2CO2 to 0D Ti2CO2 QDs with lateral dimensions below 1.4 nm. The binding energy confirms the stability of all three types of edge functionalization, while the most stable structure was observed under fully saturated edge oxygenation. Moreover, it was also found that the spin density distribution and the energy gap of Ti2CO2–X QDs (X = O, F, and OH) are both dependent on the type of atom saturation. Size and edge confinement modeling has been demonstrated to be an effective tool for tuning the electronic and magnetic properties of MXQDs. Moreover, the observed enhanced spin polarization together with tunable magnetic properties makes the ultrafine Ti2CO2–X QDs promising candidates for spintronic applications.
1 Introduction
In 2011, a new class of 2D materials named MXenes was discovered with the general chemical formula Mn+1XnTx, where M is a transition metal atom (e.g., Ti, V, Sc, Mo, Ta, or Nb), X can be carbon or nitrogen atoms and T represents surface terminating groups like –O, –OH, –F and/or –Cl and n = 1–4.1 They have a typical planar morphology with excellent structural stability, good electrical conductivity, a tunable surface, and other unique chemical properties, thus having a wide range of applications in various fields (e.g., biosensors, batteries, adsorption, catalysis, energy storage, and environmental research).2–4 Despite the appearance of some interesting phases (semiconductors,5 excitonic insulators,6 or antiferromagnets7), unfortunately, most of the MXenes have exhibited metallic conductivity without an intrinsic band gap, which limits their applications in several fields (e.g., applications in laser diodes, light emitting diodes, and field-effect transistors).8 Furthermore, MXenes exhibit a low photoluminescence (PL) response in aqueous solution and their use in biological and optical applications is significantly limited.9 Recently, theoretical and experimental studies have shown that shrinking 2D materials to a 0D structure (a quantum dot, QD, which is less than 10 nanometers in size) can bring about additional unexpected and fascinating properties due to a combination of edge effects, surface area, and quantum confinement. At the same time, the inherent advantages of 2D counterparts are preserved.10 There are several types of QDs, such as graphene,11 black phosphorus12 and/or boron nitride,13 that have benefited from the quantum confinement and edge effect. For instance, when a 2D graphene sheet is reduced to 0D, it begins to fluoresce.14 In addition, hBN-derived QDs have shown improvements in photoluminescence, band gap tunability, and functionality compared to their 2D counterparts.13Motivated by these unique characteristics of QDs, interest in MXene-derived QDs (MXQDs) has also begun to grow in the last six years. Several studies suggest that MXQDs can be synthesized and exhibit quite different photoluminescence and absorption properties than 2D MXenes. The first described MXQDs were Ti3C2 monolayers synthesized by the hydrothermal method.9 Xue et al. found that the average size, shape, and properties of MXQDs can be tailored by choosing the reaction temperature, pressure, and pH of the solution. The authors prepared water-soluble Ti3C2 MXQDs at 100 °C, 120 °C, and 150 °C with average lateral particle sizes of 2.9, 3.7, and 6.2 nm, respectively.9 Later, MXQDs with one or two heteroatoms (S, N, P, etc.) were also synthesized by mixing the corresponding elemental precursors. For example, Xu et al.15 prepared S, N co-doped Ti3C2Tx QDs ranging in size from 2.6 to 4.7 nm, which exhibited multi-color blue, yellow, and orange luminescence. In addition, Guan et al.16 reported N, P co-doped Ti3C2Tx QDs with an average lateral size of 2.7 nm. Similarly, this type of QD realized green fluorescence for the first time at a wavelength of approximately 560 nm. The second widely used method is the solvothermal method, in which the precursor solution is usually a non-aqueous organic solvent instead of water. This method is more efficient than the hydrothermal method, because it allows precise control of the size or shape of the products. For example, Xu and co-workers17 synthesized three different Ti3C2Tx MXQDs by a solvothermal method using ethanol (e-Ti3C2Tx), DMF (f-Ti3C2Tx), and DMSO (s-Ti3C2Tx QDs). The average particle size depends on the solvent, i.e., 2.5, 3.3, and 1.8 nm for e-Ti3C2Tx, f-Ti3C2Tx and s-Ti3C2Tx QDs, respectively. Furthermore, the optical properties can also be tailored by using different solvents with white PL emission achieved in DMSO and blue in DMF and ethanol.
Although many successful syntheses have been achieved and many studies indicate interesting optical and electronic properties of MXQDs, much is to be explored. The least information is known about the structure of MXQDs, in particular on the functionalization of the edges/surfaces and their influence on the properties. Although several studies on the influence of functional groups on the electronic, optical, or magnetic properties of other types of QDs have been reported,18–21 information on the functionalization of MXQDs is lacking, except for the study by Ding and co-authors,8 in which they revealed that with increasing lateral size, the energy gaps of Ti3C2 QDs with H passivation range from 2.76 to 1.14 eV. To the best of our knowledge, no studies have been published on the different sizes and types of edge functionalization of Ti2CO2 QDs. In this work, we constructed four Ti2CO2 QDs with different lateral sizes and we model the edge termination using three functional atoms/groups such as –O, –F, and –OH. Moreover, we investigated the effect of these models on their electronic and magnetic properties too. In the case of the size effect, the energy gap of fully oxygenated Ti2CO2 QDs decreases gradually with increasing lateral size for both the nonmagnetic (spin-unpolarized, closed-shell) and magnetic (spin-polarized, open-shell) quintet states from 4.89 to 3.34 eV and from 7.29α to 5.84α eV, respectively (the α index means major α spin). Furthermore, our study reveals that Ti2CO2 QDs with a high edge-to-area ratio (lateral size less than 1.4 nm) have spin-polarized edge states, which theoretically can generate magnetic properties. In all three edge-functionalization cases (–O, –F, and –OH), the stability was confirmed by the edge binding and Gibbs energies with the most stable structure observed for fully saturated edge oxygenation. The lowest ground state energy for all edge functionalizations of Ti2CO2–X QDs was found to be a spin-polarized state (open shell). Moreover, the study demonstrates the possibility of tuning the energy gap and spin density distribution by using different kinds of edge functionalization (O, F, and OH) of Ti2CO2–X QDs. In this study, we also focused on the appropriate computational method and basis set to describe both electronic and magnetic properties, where hybrid functionals were found to be the most suitable.
2 Computational methods
A 2D Ti2CO2 nanosheet5 was used as a model system to prepare different lateral sizes of Ti2CO2 quantum dots (QDs) composed of 67 to 145 atoms. All calculations were performed using the Gaussian16 program package22 and GaussView23 was used to visualize the optimized structures and spin density. In vacuo geometry optimization of all studied Ti2CO2 QDs was performed in various spin states at the ωB97XD24 level of theory employing the 6-31G**25 basis set and in the case of open-shell systems, unrestricted DFT formalism was used. For comparison, additional geometry optimization of the QD1 (Ti24C7O36) model was performed at several levels of theory (CAM-B3LYP,26 B3LYP,27–29 HSE06,30 PBE,31 BLYP,28,32 RevTPSS33 and M06L34) using different basis sets: 6-311G**,35,36 cc-pVTZ37 and Def2TZVP.38 The RMS strength criterion was set to 3.0 × 10−4 in atomic units in the geometry optimization case. Due to the problematic convergence of the studied molecules, the quadratically convergent (XQC) SCF39 procedure was used. We carefully inspected the magnetic behavior of our system, i.e., we performed calculations for various values of the spin S. The values of spin S are represented by the multiplicity M = 2S + 1 as well as the magnetic moment m = 2S. Subsequently, the stability of the unrestricted wave function for systems with higher spin contamination was tested (by using the Stable = Opt calculation). Spin contamination occurs when higher spin states are mixed with the desired spin state in a wave function, potentially causing a slight decrease/increase in the calculated total energy due to increased variations freedom. However, this variation is an artifact of an incorrect wave function. If there is no spin contamination, the expected value of the total spin, 〈S2〉, should be equal to S(S + 1), where S can take the values 0 (singlet), 1/2 (doublet), 1 (triplet), 3/2 (quartet), and so forth.40 Common consensus is that if [〈S2〉 − S(S + 1)]/[S(S + 1)] < 10%, sufficiently accurate energies are obtained.41 The frequency calculations have also been carried out using the same level of theory as that of geometry optimization to ensure that they correspond to true minima in the potential energy surface. To verify the correctness of the ground state, a more detailed analysis of the ferromagnetic/antiferromagnetic spin density distribution was performed using the definition region (by using Guess = fragment).The relative energy ΔE [eV] is defined as the difference between the total energy of the lower and higher spin states and the energy gap Δg [eV] is defined as:
| Δg = εLUMO − εHOMO, | (1) |
| Eeb/0 = ((EMXQD) − (EB + nEE))/n | (2) |
| Geb = ((GMXQD) − (GB + nGE))/n | (3) |
3 Results and discussion
3.1 Basis sets and density functional effects
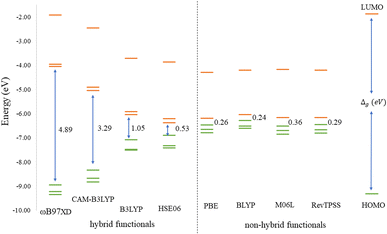
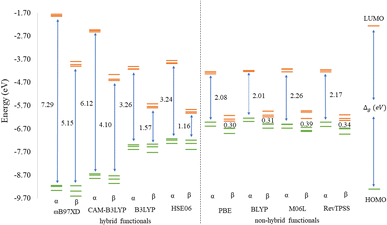
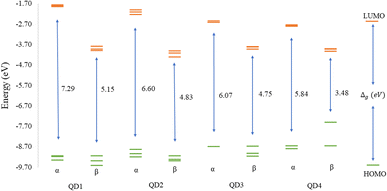
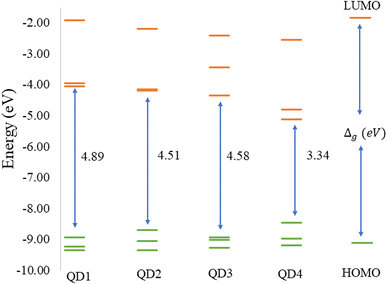
Before discussing the modeling of QDs (size and edge functionalization) and their electronic and magnetic properties, the first results on the influence of basis sets and the level of theory are presented. For this comparison, a fully edge-saturated Ti24C7O36 QD (denoted as QD1) was chosen as the most stable model (for more information on the choice, see ESI, Fig. S1 and Table S1†). In the subsequent step, we have chosen closed-shell (denoted as CS) singlet and open-shell (denoted as OPS) quintet states (S = 2 and M = 5) with magnetic moment m = 4 μB as the reference states (inspired by the ground state in the case of the PBE and the ωB97XD functional, respectively, see Table S2†). We fully optimized all considered structures and evaluated singlet-quintet energy differences ΔE. In addition, the HOMO and LUMO energies are essential parameters that determine the electronic and optical behavior of molecules. Therefore, ΔE and Δg were chosen as the comparison parameters.Method differences were also found in the case of the energy gaps which are depicted in Fig. 1 and 2. It is found that the highest value of the energy gap is observed for the ωB97XD hybrid functional, i.e., 4.89 eV for the singlet and 7.29α/5.15β eV for the quintet state (m = 4 μB). The most significant energy gap reduction can be observed for non-hybrid functionals, i.e., for all four used functionals, the energy gap value for the singlet is approximately 0.30 eV and about 2.00α/0.30β eV for the quintet (with magnetic moment 4 μB). In addition, Fig. 1 shows that in the case of non-hybrid functionals in the singlet state, LUMO/LUMO−1 energies are degenerate, while no degeneracy is observed in the case of hybrid functionals. Similarly, in the quintet state case (Fig. 2), degeneracy for both HOMO/HOMO+1 and LUMO/LUMO−1 pairs is found in the case of non-hybrid functionals, while in the case of hybrid functionals, degeneracy is observed in the case of LUMO/LUMO−1. Our results, in line with the conclusion we made for Ti2CO2 MXene,7 suggest that the GGA and meta-GGA density functionals underestimate the energy gap and incorrectly describe the magnetism in MXQD.
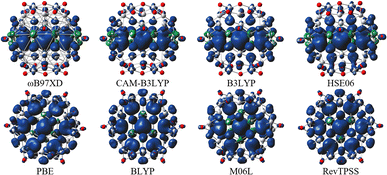
For all hybrid functionals, the spin density distribution (Fig. 4) is localized on three carbon atoms, and the ferromagnetic configuration is located in the center of the molecule. Meanwhile for non-hybrid functions the largest spin density is observed localized on the central carbon and the rest of the spin density is symmetrically distributed on all other carbon atoms (for the values of the magnetic moment see Table S5 in Fig. S3†).
In general, it is essential to note that hybrid functionals prefer higher spin states, whereas pure GGA functionals prefer lower spin states. Thus, to reliably determine the ground state, further study is required, especially at the experimental level. Nevertheless, hybrid functionals provide typically more accurate results compared to GGA functionals.43 Moreover, Radoń44 in his study observed that in some of the transition metal complexes investigated, the effect of the exact exchange admixture on the spin-state energetics (i.e., strong stabilization of the high-spin state versus the low-spin state) was often not observed. He has found that metal-centered exchange interactions are not particularly sensitive to the admixture of exact exchange and the sensitivity to the exchange functional comes from the metal–ligand bond.
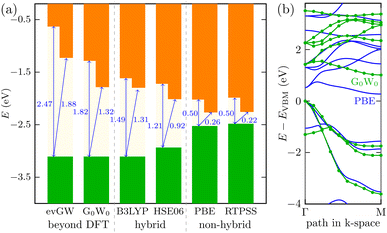
It is most likely that the hybrid functional will be the best choice for the QD description; however, the Ti24C7O36 cluster is quite an unknown system. We, therefore, decided to perform additional calculations on the Ti2CO2 monolayer (using the periodic plane-wave VASP program). We reoptimized the geometrical structure from our previous studies5,7 and tested the energy spectrum of the monolayer system. Besides GGA (PBE), meta-GGA (RevTPSS), and hybrid density functionals (HSE06 and B3LYP), we also used the many-body perturbation GW method. This method is far beyond DFT and is regarded as quite an established reference method in condensed matter physics. We also recently proved good accuracy of the GW approach in the Sc-based monolayer MXene case.45 We can see in Fig. 3 that the trend of opening the gap when moving from GGA to hybrid density functionals is preserved as in the QD case. In periodic calculations, we could not use long-range hybrid functionals and, instead, focused on the GW method providing a quasiparticle band structure. Direct comparison of the quasiparticle band structure from the so-called single-shot (PBE orbital-based) variant G0W0 and GGA PBE structure is depicted in Fig. 3b for the most important Γ − M path of the 2D Ti2CO2 hexagonal Brillouin zone. As shown in Fig. 3a, the G0W0 quasiparticle gap is slightly larger than the hybrid B3LYP gap. On the other hand, when one iterates GW eigenvalues (evGW variant of the GW method), both direct and indirect gaps are significantly opened (cf.Fig. 3a for final values, and Fig. S4† for the gap evolution with GW iterations): Δdirg = 1.82 eV → 2.47 eV and Δindirg = 1.32 eV → 1.82 eV, respectively. We note that our GW calculations with a “standard” setting46 were renormalized to the well-converged precise values of G0W0 of Ding et al.47 In summary, to recover the behavior of the accurate GW method, density functionals providing larger gaps than standard hybrid density functionals HSE06 or B3LYP (as long-range hybrid ones) should be used for modeling Ti-based quantum dot systems, where GW cannot be used.
For all the aforementioned reasons and following many-body GW results on 2D Ti2CO2, we decided to use the long-range corrected ωB97XD hybrid functional to further study the MXene quantum dots (MXDQs). Moreover, with respect to possible later calculations of MXQD absorption spectra by the TD-DFT method, long-range hybrid density functionals (as ωB97XD) seem prospective. We note that such density functionals with the Pople-style double-zeta 6-31G** basis set were useful also in studies of the structural and optical properties of carbon dots.48
3.2 Modeling of size
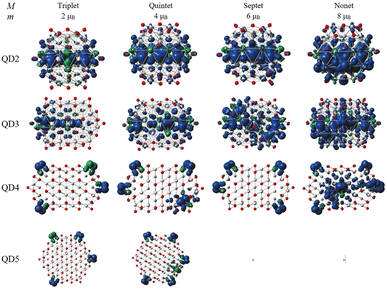
The second part of the study examined the effect of lateral size on the electronic and magnetic properties of oxygen-edged Ti2CO2 QDs, referred to as Ti2CO2–O. We constructed four Ti2CO2–O QDs denoted as QDn (n = 1–4): Ti24C7O36 (QD1), Ti32C10O46 (QD2), Ti40C13O56 (QD3), and Ti54C19O72 (QD4); see Fig. 5. The corresponding lateral sizes were between 1.1 and 1.75 nm. In general, the 2D Ti2CO2 monolayers form hexagonal cells,5,7 and only a slight elongation of the Ti–O bond on the lateral side occurs after shrinkage to QDs (see the ESI† for details). A crucial aspect to consider is the spin multiplicity M and/or magnetic moment μB of the studied QDs. For the larger models (QD3 and QD4 with lateral sizes greater than 1.5 nm), the nonmagnetic spin-nonpolarized, singlet state is energetically preferred as shown in Table 1. In contrast, in the case of QD1 and QD2 (with lateral sizes smaller than 1.4 nm), the magnetic spin-polarized state with higher multiplicity (quintet state, m = 4 μB) is energetically preferred. For the QD1 model, the singlet open shell (antiferromagnetic) state is energetically very close with an absolute energy difference of 0.03 eV, as shown in Table 1. However, the expected values of the total spin, 〈S2〉 = 1.97, is highly biased for the antiferromagnetic case (the open shell singlet theoretical value should be S(S − 1) = 0 with zero unpaired electrons), which leads to an increase in the total energy due to the admixture of the higher-energy state. In contrast, the expected values of the total spin 〈S2〉 = 6.05 for the quintet state corresponds to the theoretical value of S(S − 1) = 6 for three unpaired electrons, i.e., no spin contamination occurs. Therefore, it can be assumed that the true ground state is the quintet state with a magnetic moment of 4 μB.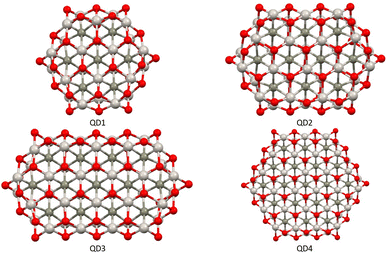 | ||
| Fig. 5 Top views of optimized Ti2CO2–O QDs with different sizes. Titanium, carbon, and oxygen atoms are shown in light grey, dark grey, and red, respectively. | ||
| S | M | m | QD1 | QD2 | QD3 | QD4 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔE | 〈S2〉 | ΔE | 〈S2〉 | ΔE | 〈S2〉 | ΔE | 〈S2〉 | |||
| a The open shell singlet was converted to the closed shell. b Spin states were not calculated. | ||||||||||
| 0 | Singlet CS | 0 | 0.65 | 0.00 | 0.59 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0 | Singlet OPS | 0 | 0.03 | 1.97 | 0.40 | 1.03 | 2.93 | 2.04 | —a | — |
| 1 | Triplet | 2 | 0.21 | 2.95 | 0.37 | 2.04 | 2.92 | 3.04 | 3.17 | 3.03 |
| 2 | Quintet | 4 | 0.00 | 6.05 | 0.00 | 6.06 | 2.17 | 6.04 | 6.29 | 6.06 |
| 3 | Septet | 6 | 2.10 | 12.05 | 2.54 | 12.08 | 4.34 | 12.08 | –b | — |
| 4 | Nonet | 8 | 4.77 | 20.07 | 4.95 | 20.08 | 6.92 | 20.09 | –b | — |
The values of the gap Δg are shown in Fig. 6 and 7 for quintet (m = 4 μB) and singlet (m = 0 μB) states, respectively. It is evident that Δg is strongly affected by the size of the Ti2CO2–O QD, because the gap energy decreases due to the quantum confinement effect: the Δg decreases from 7.29α/5.15β eV in QD1 to 5.84α/3.48β eV in QD4 (see Fig. 6) in the case of the quintet state (with magnetic moment 4 μB). This trend is also confirmed for the nonmagnetic (singlet) state, which is preferred for QD3 and QD4, where the value of Δg decreases from 4.89 eV in QD1 to 3.34 eV in QD4 (see Fig. 7). Thus, the value of the gap can be expected to be close to the value of 2D materials if the QD size is large enough, consistent with the theoretical study of Ding.8 In addition, Δg is an important stability index that may be used to characterize the chemical reactivity and stability of molecules via the principle of maximum hardness.49 In this sense, a molecule with a larger energy gap is termed a hard molecule, meaning higher chemical stability. Thus, from the reduction of Δg with the increase of the system, it is evident that the largest chemical hardness coincides with the smallest size, which is the most stable structure. This characteristic behavior gives rise to the possibility of tuning the properties (mainly electronic, magnetic and/or optical) of quantum dots depending on their size.
The spin density distribution of Ti2CO2–O QDs with different sizes obtained at the ωB97XD/6-31G** level of theory is shown in Fig. 8. At the small quantum dot sizes (QD1–QD2, lateral size up to 1.4 nm), positive spin densities (blue color) are found to be more localized in the center of the molecule on carbon atoms with ferromagnetic configuration. However, the aforementioned high spin contamination can have significant effects on the geometry and population analysis and can significantly affect the spin density. Therefore, alternative spin distribution possibilities were explored in particular antiferromagnetic ordering and/or spin distribution on titanium and oxygen atoms (edge functionalization). Nevertheless, ferromagnetic spin ordering as well as localization on carbon atoms proved to be more advantageous. Conversely, in the case of quantum dots with lateral sizes larger than 1.5 nm (QD3 and QD4), the spin density localizes to oxygen atoms at the edge of the molecule due to edge functionalization. This spin distribution implies that the magnetism is the result of edge functionalization groups and an edge-to-area ratio that vanishes with increasing size. The edge-to-area ratio of a quantum dot is defined as the ratio of the number of atoms located on the surface (edge) to the total number of atoms (area) and is crucial in determining the electronic and magnetic properties of quantum dots. In smaller QDs with a high edge-to-area ratio, the edge may contain a larger number of unpaired electrons, which can interact to create a magnetic field, leading to magnetism involving inner atoms. While in larger QDs with a smaller edge-to-area, the edge effect is negligible and the 2D material properties dominate. This effect is evident in Fig. 8, where for QDs with lateral sizes above 1.5 nm (QD3 and QD4), only a weak polarization at the edge of the QD is observed, which is induced by the oxygen atoms at the edge. The edge effect of the oxygen atoms is not spread inside the quantum dot, and the non-magnetic behavior rather mimics the 2D material (2D Ti2CO2 is non-magnetic5,7). In contrast, for QDs with lower lateral dimensions up to 1.4 nm (QD1 and QD2), the edge-to-area ratio is higher and the edge-atom effect dominates, producing more spin-polarized segments that interact and can generate magnetic behavior inside the quantum dot. Based on the obtained results, it can be assumed that, when the quantum dot size is sufficiently shrunk (lateral size smaller than 1.4 nm), the edge functionalization can affect its magnetic properties, and the finite size model converges to a magnetic solution. Similar behavior has been observed in the case of graphene quantum dots (GQDs) with zigzag edges where the magnetic properties of GQDs have been theoretically predicted and subsequently experimentally demonstrated.50–52 In addition, hydroxyl passivation of the zigzag edge has been investigated as a promising method to obtain magnetic properties.53 For this reason, we also decided to investigate the possibility of tuning the properties of QDs by modeling their edges (see the next section).
3.3 Edge termination
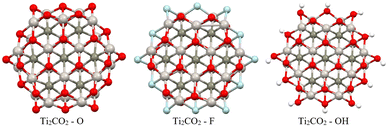
Firstly, full optimization of Ti2CO2–X structures was done including subsequent frequency analysis (to ensure that all eigenvalues of the Hessian are positive). In order to evaluate the thermodynamic stability of the investigated Ti2CO2–X, the edge binding energy Eeb, zero point energy-corrected edge binding energy E0, and Gibbs free energy G were defined according to eqn (2) and (3) presented in Section 2. Based on these definitions, negative values of Eeb and G represent a spontaneous reaction that leads to higher stability of the product as a reactant. And a more negative value indicates a more energetically favorable (spontaneous) reaction. From the negative values of Eeb and G (see Table 2), we conclude that all structures/edges of Ti2CO2–X QDs under investigation are thermodynamically stable. The negative value of Gibbs energy also indicates that the formation of Ti2CO2–X QDs is an exothermic (spontaneous) reaction. From the relevant values of Eeb and G, it is clear that oxygen saturation is the preferred edge-termination since the order decreases with the terminal group and the sequence is in the order Ti2CO2–O < Ti2CO2–F < Ti2CO2–OH (see Table 2). The lowest values of Eeb and G for the Ti2CO2–O QDs may be due to the stronger interaction between the O and Ti atoms resulting from the shorter bond length of Ti–O, which ranges from 1.77 to 2.05 Å, than those of Ti–F from 1.98 to 2.22 Å and Ti–OH from 2.03 to 2.44 Å. It can also be clearly seen from Fig. 9 that the overall QD structure is not affected by the change of atoms at the edge, where we observe only a slight shortening of the bonds between Ti–C in the case of –F and –OH saturation (see also Table S8†).
| S | M | m | O | F | OH | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔE | 〈S2〉 | Δ g | ΔE | 〈S2〉 | Δ g | ΔE | 〈S2〉 | Δ g | |||
| a Values of zero point corrected relative energy E0 in eV. | |||||||||||
| 0 | Singlet CS | 0 | 0.65 | 0.00 | 4.89 | 0.94 | 0.00 | 4.36 | 0.65 | 0.00 | 4.29 |
| 0 | Singlet OPS | 0 | 0.03 | 1.97 | 5.14α/5.11β | 0.36 | 3.94 | 5.11α/4.82β | 0.01 | 3.64 | 5.03α/5.22β |
| 1 | Triplet | 2 | 0.21 | 2.95 | 4.73α/5.03β | 0.35 | 4.78 | 4.94α/5.39β | 0.00 | 4.70 | 5.31α/5.11β |
| 2 | Quintet | 4 | 0.00 | 6.05 | 7.29α/5.15β | 0.00 | 7.42 | 5.38α/5.02β | 0.05 | 7.60 | 5.31α/5.14β |
| 3 | Septet | 6 | 2.10 | 12.05 | 5.92α/5.42β | 0.32 | 12.77 | 5.29α/5.11β | 0.46 | 13.04 | 5.22α/5.12β |
| 4 | Nonet | 8 | 4.77 | 20.07 | 6.00α/5.22β | 0.69 | 20.05 | 5.29α/6.89β | 0.48 | 20.08 | 5.23α/6.85β |
| E eb | −7.04, −6.94a (−6.52) | −6.62, −6.23a (−6.23) | −5.78, −5.56a (−5.10) | ||||||||
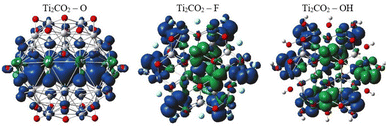
In order to provide an additional study on the effect of edge functionalization on the magnetic properties, we plot spin density distribution for the studied Ti2CO2–X QDs in Fig. 10 (see also Fig. S2†). The spin densities are observed at the center of the molecule, around the carbon atoms in the Ti2CO2–O QD, which indicates that the origin of the ferromagnetism in these flakes is the active unpaired electrons from C atoms and the neighboring transition Ti metals. And the spin-up density is dominant, as shown by the blue cubes in Fig. 10.
In contrast, for bare Ti2CO2, Ti2CO2–F and Ti2CO2–OH QDs, the spin densities are localized around the transition Ti atoms predominantly at the edge of the molecule, where both the spin-up and spin-down densities are comparable (see Fig. 10 and S2†). Thus, the observed ferrimagnetism in these flakes is activated by unpaired electrons from transition metals. These differences arise from the charge transfer between Ti and edge atoms, where the two unpaired electrons in the oxygen atoms affect the magnetic ordering at the edge more strongly and significantly weaken the ferrimagnetic ordering (which is observed in the bare structure) compared to the –F/OH groups. The comparable spin up/down densities will decrease the spin polarization in these QDs with respect to Ti2CO2–O QDs. Thus, the enhancement of spin polarization and the tunable magnetic properties make ultra-small Ti2CO2–O QDs interesting for spintronic devices. Previous studies have demonstrated that quantum confinement and finite-size effects cause a sensitive electronic structure to chemical edge modifications.18–21 Our results are consistent with these studies, where an increase in Δg is observed for QDs with saturated edges compared to the bare structure. The energy gap of bare QDs is increased by approximately 50% upon edge oxidation (see Table S1†). In the case of the quintet state (m = 4 μB), changing the edge termination leads to a decrease in Δgα from 7.3 eV for edge oxygenation to about 5 eV for edge fluorination and hydroxylation, as shown in Table 2. This result demonstrates that the energy gap can be tuned significantly by chemical modification of the Ti2CO2–X QD edge with different atomic and molecular groups. Moreover, in the context of the maximum hardness principle, where the molecule with the highest value of Δg can be considered the most stable, these results confirm previous findings, i.e., edge-oxygenation can be considered the most likely edge termination.
4 Conclusions
The structural stability and electronic, and magnetic properties of hexagonal Ti2CO2 QDs with edge termination have been investigated under the effect of different lateral sizes and edge functionalization. The calculated negative binding and Gibbs free energies indicate that all selected Ti2CO2–X QDs (X = O, F, OH) are stable and the edge termination reaction is exothermic, with the highest stability observed for fully saturated Ti2CO2–O QDs. The electronic and magnetic properties are highly dependent on the size of the Ti2CO2–O QDs, and in parallel, the study demonstrated that the energy gaps, as well as the spin density, can be tuned by changing the functionalization of the edges. We subsequently revealed that the reduction of 2D Ti2CO2 MXenes to sufficiently small Ti2CO2–X QDs (less than 1.4 nm in size) can produce magnetic behavior due to an edge-to-area ratio that vanishes with increasing size. Meanwhile the change of the edge group does not affect the overall magnetic behavior observed for all types of terminations. However, the change in the type of confinement has a significant influence on the type of magnetization and distribution of spin density.In the case of Ti2CO2–O QDs, we found that the distribution of spin density is strongly localized in the carbon atoms in the center of the MXQD as a ferromagnetic one. In Ti2CO2–F and Ti2CO2–OH QDs, the up and down spin densities are distributed as more ferrimagnetic ones located mainly near the edge with a total spin of 4 originated from the unpaired electrons of the titanium metal and neighbor C atoms. The spin polarization is then higher in the Ti2CO2–O QD due to the higher spin-up density. Furthermore, the study showed that the size and functionalization of the edges affect the energy gaps. In the case of Ti2CO2–O QDs, the energy gap decreases significantly with increasing lateral size for both the magnetic (the open shell) case (from 7.29α/5.15β to 5.84α/3.48β eV) and the nonmagnetic (closed shell) case (from 4.89 to 3.34 eV). In the case of edge-functionalization change, we observe an increased energy gap compared to bare Ti2CO2 QDs, with the highest value of the energy gap observed for Ti2CO2–O QDs (the energy gap of the ground state (quintet, m = 4 μB) for the bare Ti2CO2 and Ti2CO2–X QDs with –O, –F and –OH is 4.21/4.31, 7.29/5.15, 5.38/5.02, and 5.31/5.11 eV, respectively).
Finally, we proved that standard GGA density functional theory fails in the right description of the ground magnetic properties of MXene-based QDs by comparison to hybrid DFT calculations and showed that our approach is necessary for correct predictions and design. It is expected that this study will provide valuable information to understand the design of new lateral sizes as well as edge modeling of MXQDs to further study the tuning of electronic, magnetic, and optical behavior for desired applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This article has been produced with the financial support of the Czech Science Foundation (number 21-28709S) and the European Union under the LERCO project (number CZ.10.03.01/00/22_003/0000003) via the Operational Programme Just Transition. The computations were performed at the IT4Innovations National Supercomputing Center through e-INFRA CZ (ID:90140).Notes and references
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed.
- J. Zhu, E. Ha, G. Zhao, Y. Zhou, D. Huang, G. Yue, L. Hu, N. Sun, Y. Wang, L. Y. S. Lee, C. Xu, K.-Y. Wong, D. Astruc and P. Zhao, Coord. Chem. Rev., 2017, 352, 306–327 CrossRef CAS.
- D. Xiong, X. Li, Z. Bai and S. Lu, Small, 2018, 14, 1703419 CrossRef PubMed.
- T. Ketolainen and F. Karlický, J. Mater. Chem. C, 2022, 10, 3919–3928 RSC.
- N. Kumar and F. Karlický, Appl. Phys. Lett., 2023, 122, 183102 CrossRef CAS.
- T. Sakhraoui and F. Karlický, ACS Omega, 2022, 7, 42221–42232 CrossRef CAS PubMed.
- Y. Ding, X. Nie, H. Dong, N. Rujisamphan and Y. Li, Phys. E, 2020, 124, 114328 CrossRef CAS.
- Q. Xue, H. Zhang, M. Zhu, Z. Pei, H. Li, Z. Wang, Y. Huang, Y. Huang, Q. Deng, J. Zhou, S. Du, Q. Huang and C. Zhi, Adv. Mater., 2017, 29, 1604847 CrossRef PubMed.
- X. Wang, G. Sun, N. Li and P. Chen, Chem. Soc. Rev., 2016, 45, 2239–2262 RSC.
- D. Pan, J. Zhang, Z. Li and M. Wu, Adv. Mater., 2010, 22, 734–738 CrossRef CAS PubMed.
- P. Chen, N. Li, X. Chen, W.-J. Ong and X. Zhao, 2D Materials, 2017, 5, 014002 CrossRef.
- B. Huo, B. Liu, T. Chen, L. Cui, G. Xu, M. Liu and J. Liu, Langmuir, 2017, 33, 10673–10678 CrossRef CAS PubMed.
- Z. Zhang, J. Zhang, N. Chen and L. Qu, Energy Environ. Sci., 2012, 5, 8869–8890 RSC.
- X. Quan, Y. Wenjing, W. Yangyang, L. Shengkun, L. Zheng, O. Wee-Jun and L. Neng, Appl. Mater. Today, 2019, 16, 90–101 CrossRef.
- Q. Guan, J. Ma, W. Yang, R. Zhang, X. Zhang, X. Dong, Y. Fan, L. Cai, Y. Cao, Y. Zhang, N. Li and Q. Xu, Nanoscale, 2019, 11, 14123–14133 RSC.
- G. Xu, Y. Niu, X. Yang, Z. Jin, Y. Wang, Y. Xu and H. Niu, Adv. Opt. Mater., 2018, 6, 1800951 CrossRef.
- J. Feng, Q. Guo, H. Liu, D. Chen, Z. Tian, F. Xia, S. Ma, L. Yu and L. Dong, Carbon, 2019, 155, 491–498 CrossRef CAS.
- H. Abdelsalam, H. Elhaes and M. A. Ibrahim, Chem. Phys. Lett., 2018, 695, 138–148 CrossRef CAS.
- Y. Li, H. Shu, X. Niu and J. Wang, J. Phys. Chem. C, 2015, 119, 24950–24957 CrossRef CAS.
- H. Abdelsalam, V. A. Saroka, M. Ali, N. H. Teleb, H. Elhaes and M. A. Ibrahim, Phys. E, 2019, 108, 339–346 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci and D. J. Hratch, Gaussian 16, Revision B.01, 2016 Search PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView Version 6, Semichem Inc., Shawnee Mission, KS, 2019 Search PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Phys. Rev. Lett., 2011, 106, 179902 CrossRef.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062–1065 CrossRef.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- G. B. Bacskay, Chem. Phys., 1981, 61, 385–404 CrossRef CAS.
- A. Szabo and N. S. Ostlund, Modern Quantum Chemistry, Dover Publications, Mineola, New York, 1996 Search PubMed.
- F. Karlický and M. Otyepka, Int. J. Quantum Chem., 2014, 114, 987–992 CrossRef.
- F. Karlický and M. Otyepka, J. Chem. Theory Comput., 2011, 7, 2876–2885 CrossRef PubMed.
- M. Reiher, O. Salomon and B. Artur Hess, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- M. Radoń, Phys. Chem. Chem. Phys., 2014, 16, 14479–14488 RSC.
- M. Dubecký, S. Minárik and F. Karlický, J. Chem. Phys., 2023, 158, 054703 CrossRef PubMed.
- GW calculations by the VASP code using NB = 384 bands (24 of them updated in GW), plane-wave energy cut-off Ecut = 500 eV, GW cut-off EGWcut = 200 eV, Δz = 20 Å distance to perpendicular image, and 18 × 18 × 1 k-point grid.
- Y. Ding, X. Nie, H. Dong, N. Rujisamphan and Y. Li, Nanoscale Adv., 2020, 2, 2471–2477 RSC.
- M. Sudolská, M. Dubecký, S. Sarkar, C. J. Reckmeier, R. Zbořil, A. L. Rogach and M. Otyepka, J. Phys. Chem. C, 2015, 119, 13369–13373 CrossRef.
- R. G. Pearson, Acc. Chem. Res., 1993, 26, 250–255 CrossRef CAS.
- W. L. Wang, S. Meng and E. Kaxiras, Nano Lett., 2008, 8, 241–245 CrossRef CAS PubMed.
- J. Fernández-Rossier and J. J. Palacios, Phys. Rev. Lett., 2007, 99, 177204 CrossRef PubMed.
- G. Z. Magda, X. Jin, I. Hagymási, P. Vancsó, Z. Osváth, P. Nemes-Incze, C. Hwang, L. P. Biró and L. Tapasztó, Nature, 2014, 514, 608–611 CrossRef CAS PubMed.
- Y. Sun, Y. Zheng, H. Pan, J. Chen, W. Zhang, L. Fu, K. Zhang, N. Tang and Y. Du, npj Quantum Mater., 2017, 5, 2397–4648 Search PubMed.
- R. Ibragimova, M. J. Puska and H.-P. Komsa, ACS Nano, 2019, 13, 9171–9181 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00474k |
| This journal is © The Royal Society of Chemistry 2023 |