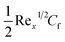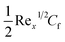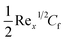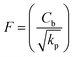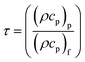Open Access Article
Open Access ArticleA dissipative and entropy-optimized MHD nanomaterial mixed convective flow for engineering applications
Faqir
Shah
a,
Tasawar
Hayat
b,
Asad
Ullah
 a,
Sohail A.
Khan
a,
Sohail A.
Khan
 *b and
Shaher
Momani
c
*b and
Shaher
Momani
c
aDepartment of Mathematical Sciences, Karakoram International University Gilgit, Gilgit 15100, Pakistan
bDepartment of Mathematics, Quaid-I-Azam University, Islamabad 44000, Pakistan. E-mail: sohailahmadkhan93@gmail.com
cNonlinear Dynamics Research (NDRC), Ajman University, Ajman, United Arab Emirates
First published on 15th November 2023
Abstract
Background and objective: Nanomaterials play significant roles in numerous industrial and engineering applications, like nuclear plants, paper production, thermal power plants, glass fibres, manufacturing of medicines, medical instruments, micro-electronics and polymer sheet extrusion. In view of such important applications, in this study, we discuss the magnetohydrodynamic flow of a nanofluid over an inclined surface by employing the Darcy–Forchheimer model. The Buongiorno model is applied to understand the various important aspects of the nanofluid. Radiation, magnetic field, dissipation and entropy generation in a chemically reactive flow are also discussed. Methodology: The governing nonlinear expressions were transformed into a dimensionless system through adequate transformations. The obtained non-dimensional systems were computed by the NDSolve approach. Results: Physical illustrations for the flow, temperature, concentration and entropy rate via emerging variables were examined. Here an enhancement in velocity was seen for the mixed convection variable, while opposite impacts on flow and temperature were noticed through the Hartman number. A higher Eckert number was obtained with a rise in temperature, while a decrease in concentration was noticed for the thermophoresis variable. An augmentation in the entropy rate was detected for radiation, while the thermal transport rate was boosted by thermophoresis.
1 Introduction
Nanofluids are a mixture of nano-sized (1–100 nm) solid particles (metals, carbides, oxides and carbon nanotubes) and conventional fluids (water, lubricant oil, ethylene and propylene glycol). Nanofluids play a vital role in the heat-transfer processes of conventional liquids. Nanomaterials play significant roles in numerous industrial and engineering applications, like nuclear plants, paper production, thermal power plants, glass fibre, manufacturing of medicines, medical instruments, micro-electronics and polymer sheet extrusion. The thermal conduction processes of conventional materials can be improved by the addition of nano-sized particles. Various industrial processes face a low-heat transportation problem caused by the utilization of conventional fluids. This issue is often tackled by using nanofluids and hybrid nanomaterials. The enhancement of the thermal conductivity of conventional materials through the addition of nano-sized metallic particles was first reported by Choi.1 Buongiorno2 later gave a mathematical model and discussed seven slip mechanisms for the enhancement of the thermal characteristics of fluids, with Brownian motion and thermophoresis as the most important factors. Waini et al.3 reported on the magnetohydrodynamic radiative flow of a Reiner–Philippoff nanoliquid subjected to a random motion and thermophoresis. Heat transfer in the electrically conductive flow of a nanoliquid with thermophoresis and random motion was discussed by Kalpana et al.4 The hydromagnetic convective flow of an Eyring–Powell nanomaterial considering multiple diffusions was analysed by Patil and Kulkarni.5 Random and thermophoresis diffusions for a Casson nanoliquid flow considering a gyrotactic microorganism was studied by Upreti et al.6 Ohmic heating in the magnetized convective flow of a Reiner–Rivlin nanoliquid considering the entropy rate was explored by Khan et al.7 Cattaneo–Christov fluxes for the bioconvective flow of a Maxwell nanomaterial subjected to the Arrhenius activation energy were examined by Bagh et al.8 Some further related studies on nanomaterials are listed in ref. 9–20.Measurement of the wastage energy in any thermodynamical system refers to the entropy. Entropy generation is an important thermodynamical approach that is used to analyse the thermal performance of systems in industrial and engineering fields. Entropy is produced due to heat transfer, molecule collision, thermal radiation, Joule heating, diffusion, fluid friction, and spinning motion, etc. In any thermodynamical system, a significant part of the thermal energy is wasted, meaning it is not fully utilized for useful work. Therefore, several researchers have paid attention to this important issue. Bejan21,22 was the first to introduce entropy minimization in convective flow. Entropy in the squeezing flow of a CNT nanoliquid was examined by Dawar et al.23 Hayat et al.24 investigated an unsteady nanoliquid flow considering Sort and Dufour characteristics. A few important studies concerning the entropy rate are mentioned in ref. 25–32.
Our prime objective here was to analyse the magnetohydrodynamic convective flow of a nanoliquid by an inclined surface. The Darcy–Forchheimer relation was considered and is discussed in this context. Radiation, magnetic field, and dissipation were considered in relation to energy. Brownian motion and thermophoresis diffusion were accounted for. The entropy rate for a chemically reactive flow was studied. Nonlinear partial differential equations were reduced to non-dimensional systems through suitable transformation. The ND-solve technique was implemented for the computations. Graphical discussions were used to consider the flow, Nusselt number, entropy rate, drag force, concentration, and temperature via sundry variables.
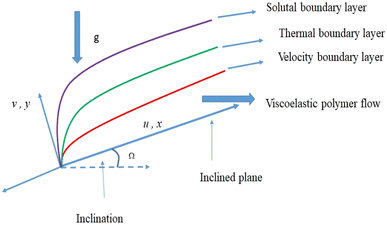
2 Statement
The hydromagnetic mixed convective flow of a nanoliquid over an inclined surface is studied. The Darcy–Forchheimer relation was considered here. Random and thermophoresis diffusions were accounted. Dissipation, magnetic field Joule heating, first-order reaction, and radiation were also taken into account. Entropy optimization for the chemically reactive flow was elaborated. Flow tests in the presence of a constant magnetic field were conducted. A sketch of the problem is presented in Fig. 1.33Here, the governing expressions satisfy:24–28
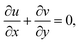 | (1) |
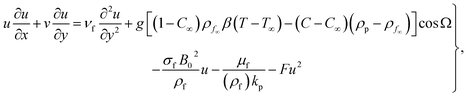 | (2) |
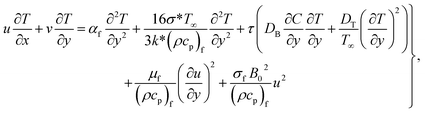 | (3) |
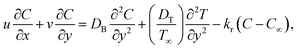 | (4) |
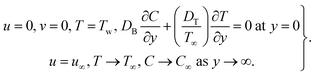 | (5) |
Letting:34,35
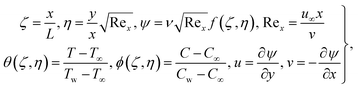 | (6) |
we get
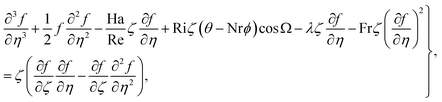 | (7) |
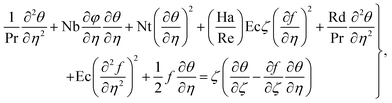 | (8) |
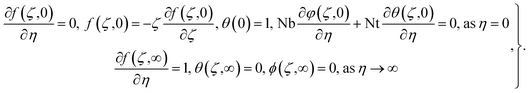 | (9) |
subject to conditions
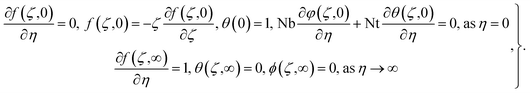 | (10) |
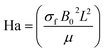 ,
, 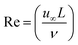 ,
, 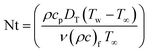 ,
, 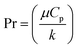 ,
, 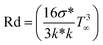 ,
, 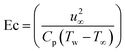 ,
, 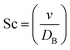 ,
, 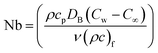 ,
, 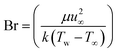 ,
, 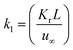 ,
, 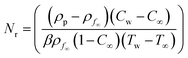 ,
, 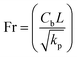 ,
, 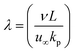 ,
, 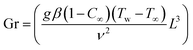 and
and 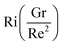 .
.
2.1 Solution
First-order truncation:In 1st order truncation we assume the derivatives w.r.t. ζ are zero. i.e.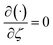 then eqn (7)–(10) become,
then eqn (7)–(10) become,
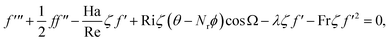 | (11) |
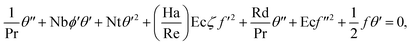 | (12) |
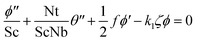 | (13) |
subject to the conditions
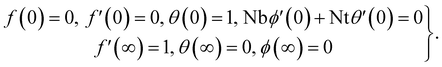 | (14) |
Second-order truncation:
Here we consider 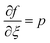 ,
, 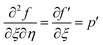 ,
, 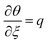 ,
, 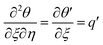 ,
, 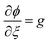 ,
, 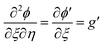 and denote
and denote 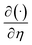 by primes. Expressions (7)–(10) become
by primes. Expressions (7)–(10) become
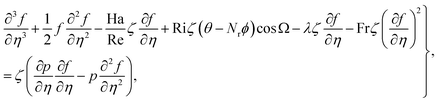 | (15) |
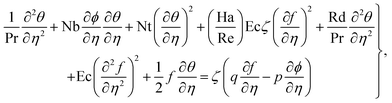 | (16) |
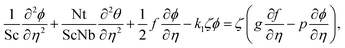 | (17) |
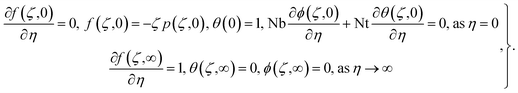 | (18) |
Differentiating eqn (15)–(18) w.r.t. ζ and neglecting the terms 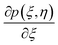 ,
, 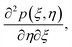
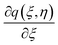 ,
, 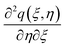 ,
, 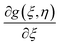 , and
, and 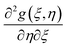 we get
we get
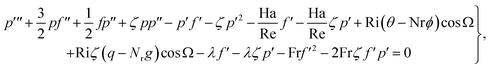 | (19) |
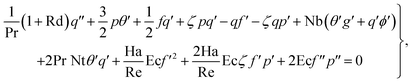 | (20) |
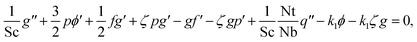 | (21) |
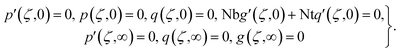 | (22) |
3 Physical quantities
3.1 Coefficient of skin fraction
One may write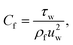 | (23) |
with shear stress τw given by
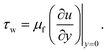 | (24) |
We now have
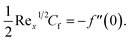 | (25) |
3.2 Nusselt number
One may define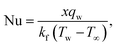 | (26) |
in which heat flux qw obeys
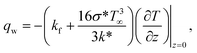 | (27) |
Finally, we may have
| Rex−1/2Nu = −(1 + Rd)θ′(0). | (28) |
3.3 Sherwood number
Mathematically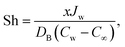 | (29) |
in which mass flux Jw obeys
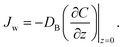 | (30) |
From eqn (21) and (22) we have (31)
| Rex−1/2Sh = −ϕ′(0). | (31) |
In which 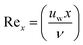 depicts the local Reynolds number.
depicts the local Reynolds number.
4 Entropy rate
Mathematically one can write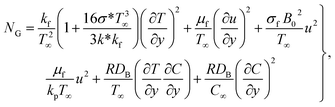 | (32) |
In the dimensionless version, we have
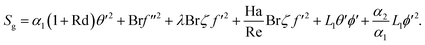 | (33) |
In the above expression, the dimensionless variables are 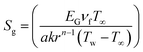 ,
, 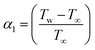 ,
, 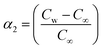 , and
, and 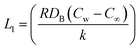 .
.
5 Analysis
The ND-solve technique was implemented for the solution. The velocity, surface drag force, concentration, Nusselt number, temperature, Bejan number, and entropy rate against the emerging variables were explored. A comparative analysis of the recent outcomes with those by Wang36 is highlighted in Table 1. Here an outstanding consensus could be noticed.| Pr | Wang36 | Recent outcomes |
|---|---|---|
| 0.07 | 0.0656 | 0.065621 |
| 0.20 | 0.1691 | 0.169109 |
| 0.70 | 0.4539 | 0.453901 |
| 2.00 | 0.9114 | 0.911409 |
| 7.00 | 1.8954 | 1.895412 |
| 20.00 | 3.3539 | 3.353925 |
5.1 Velocity
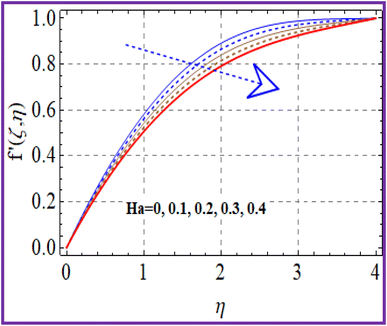
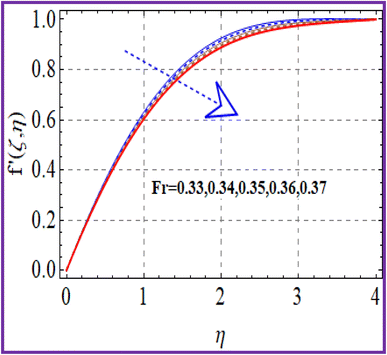
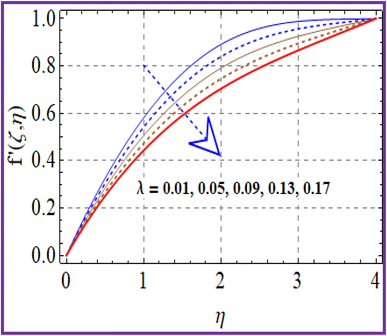
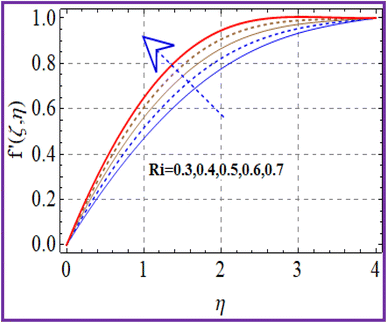
A plot of the velocity against Hartman number (Ha) is depicted in Fig. 2. A decreasing behavior was noticed for higher Hartman numbers due to the increment in resistive force. The effect of (Fr) on (f′(ζ,η)) is portrayed in Fig. 3. A reduction in velocity was noticed for higher Forchheimer (Fr) numbers due to the stronger resistance produced in the fluid flow. The influence of velocity (f′(ζ,η)) via the porosity parameter (λ) is illustrated in Fig. 4. An increase in the porosity variable corresponded to a more intensive viscous force Therefore the velocity (f′(ζ,η)) decayed. A plot of the velocity against the mixed convection variable is illustrated in Fig. 5. An increasing impact on the velocity was noted through utilizing the mixed convection variable.5.2 Temperature
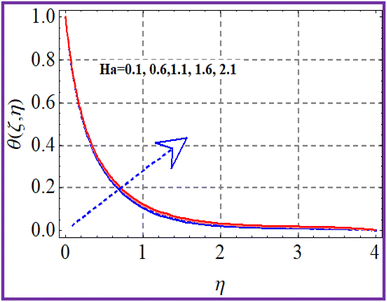
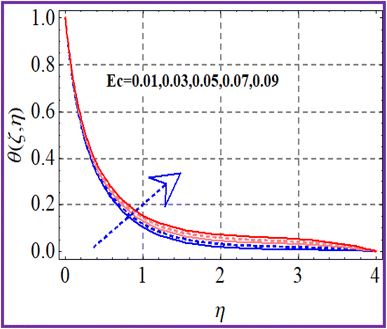
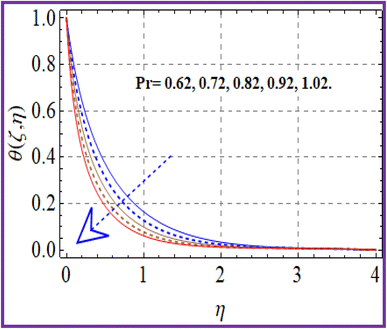
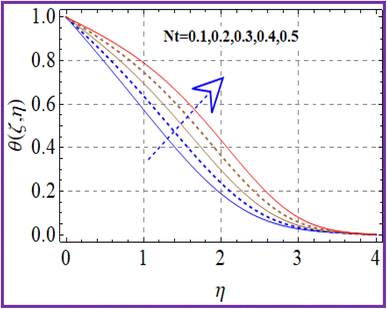
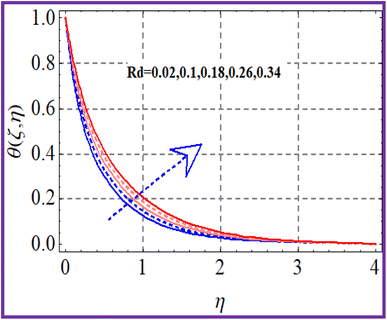
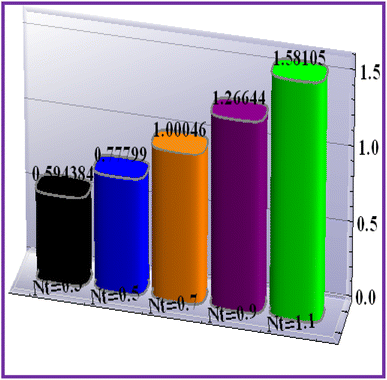
A plot of temperature versus the Hartman number (Ha) in shown in Fig. 6. A larger approximation of the Hartman number increases the Lorentz force, which creates extra heat in the system. Thus the temperature increased. Fig. 7 exhibits the temperature (θ(ζ,η)) performance versus the (Ec) Eckert number. The Eckert number increases the kinematic energy of the thermal system, which increases the temperature. A reduction in thermal diffusivity was observed against the Prandtl number, which decreased the temperature (see Fig. 8). The temperature (θ(ζ,η)) behavior with the thermophoresis parameter (Nt) is displayed in Fig. 9. The thermophoresis variable increased the temperature distribution. Fig. 10 shows the impact of radiation (Rd) on the temperature. An enhancement in the thermal field was observed with the radiation variable due to the production of additional energy in the system.5.3 Concentration
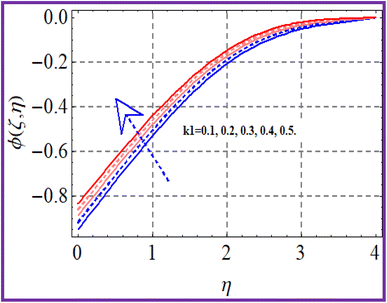
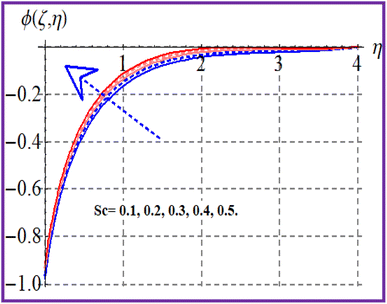
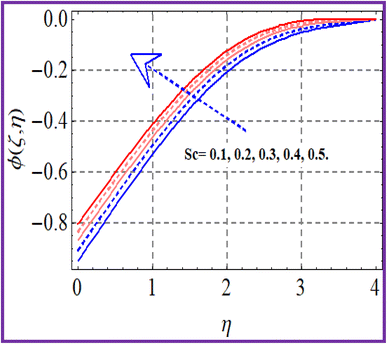
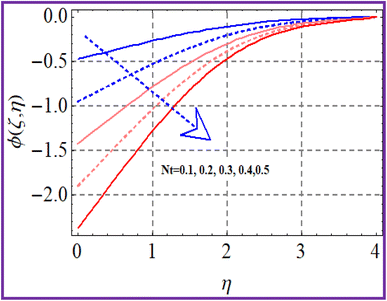
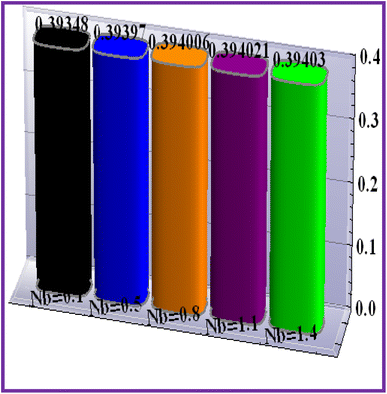
The influence of concentration (ϕ(ζ,η)) with the reaction parameter (k1) is shown in Fig. 11. An enhancement in concentration was observed with the reaction parameter. The random motion (Nb) impact on the concentration is explored in Fig. 12. Here, the concentration of the nanoliquid had an enhancing effect through the random motion variable. Fig. 13 depicts the concentration performance for the Schmidt number. An augmentation in concentration was seen through the Schmidt number. Fig. 14 depicts (ϕ(ζ,η)) against (Nt). A decreasing trend for concentration was seen through the thermophoresis variable variation.6 Entropy rate
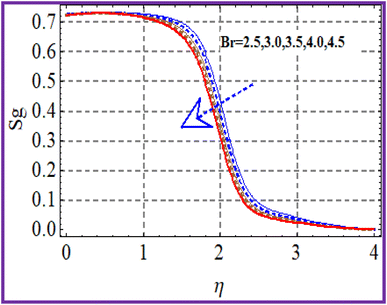
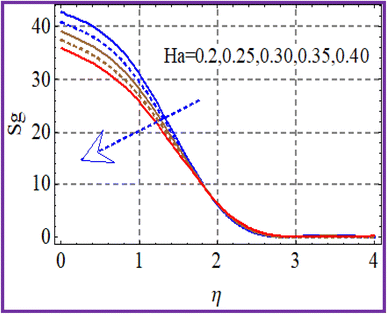
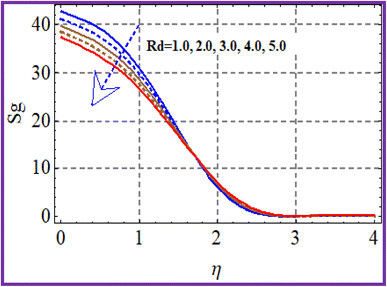
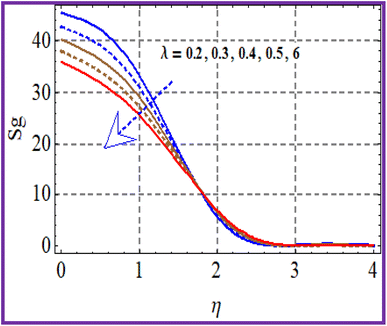
Fig. 15 illustrates the entropy performance considering the Brinkman (Br) number. Clearly, the entropy rate increased with the Brinkman number. The effect of the variation of the Hartman (Ha) number on (Sg) is portrayed in Fig. 16. A higher estimation of Hartman number decreased the entropy rate. Fig. 17 shows the impact of (Sg) via radiation. A decrease in entropy was detected against the radiation variable. From Fig. 18, it could be noticed that the entropy reduced with higher porosity.7 Quantities under interest
Graphical illustrations for the skin friction coefficient and Nusselt number are addressed.7.1 Skin friction coefficient
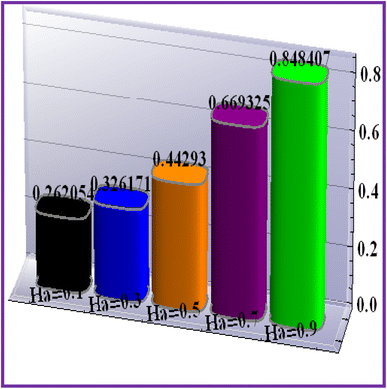
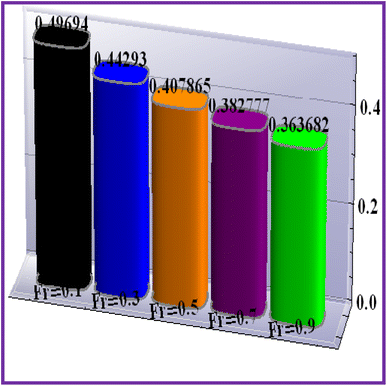
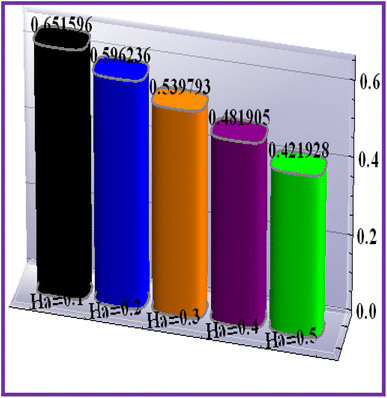
Fig. 19–21 display the impacts of the velocity gradient with the Hartman number, mixed convection variable, and Forchheimer number. An increasing behavior was observed against rising values of (Ha) and (Ri), but the opposite scenario held for (Fr).7.2 Heat transfer rate
The impact of emerging variables ((Nt), (Nb) and (Ec)) on (Re1/2Nu) are displayed in Fig. 22–24. Clearly, the thermal transport rate increased versus higher random motion (Nb) and thermophoresis (Nb) variables. From Fig. 7b, it could be detected that the heat transport rate declined for higher Eckert numbers.8 Conclusions
Key observation are listed below.➢ Mixed convection and porosity had opposite impacts on the flow.
➢ Hartman number yielded an opposite outcome for the flow and entropy rate.
➢ Flow was decreased by Forchheimer number.
➢ An enhancement in Hartman number led to enhanced drag force and higher temperature.
➢ Higher Eckert numbers led to an enhancement in temperature.
➢ Prandtl number led to a reduction in temperature.
➢ An opposite trend for entropy and thermal field was witnessed through considering radiation.
➢ An enhancement in temperature and the heat transport rate were noticed for the thermophoresis variable.
➢ Concentration was reduced versus a higher thermophoresis variable.
➢ Increasing trend for concentration was noted through the Schmidt number.
➢ Brinkman number corresponded an enhancement in entropy.
➢ Thermal transport rate surged upwards against the random motion variable.
➢ Decrease in entropy rate was witnessed versus the Brinkman number.
➢ Higher Eckert numbers decreased the temperature gradient.
Further investigations in the future should consider bioconvection and motile microorganisms, of which almost nothing is known yet. Such attempts for mixed, bioconvection and Marangoni convection, activation energy and slip and melting conditions should be examined.
Abbreviations
Conflicts of interest
There are no conflicts to declare.References
- S. U. S. Choi, Enhancing thermal conductivity of fluids with nanoparticle, ASME J. Fluids Eng. Publication Fed., 1995, 231, 99–105 CAS.
- J. Buongiorno, Convective transport in nanofluids, ASME J. Heat Mass Transfer, 2006, 128, 240–250 CrossRef.
- I. Waini, K. B. Hamzah, N. S. Khashiie, N. A. Zainal, A. R. M. Kasim, A. Ishak and I. Pop, Brownian and thermophoresis diffusion effects on magnetohydrodynamic Reiner–Philippoff nanofluid flow past a shrinking sheet, Alexandria Eng. J., 2023, 67, 183–192 CrossRef.
- G. Kalpana, K. R. Madhura and R. B. Kudenatti, Numerical study on the combined effects of Brownian motion and thermophoresis on an unsteady magnetohydrodynamics nanofluid boundary layer flow, Math. Comput. Simul., 2022, 200, 78–96 CrossRef.
- P. M. Patil and M. Kulkarni, MHD quadratic mixed convective Eyring-Powell nanofluid flow with multiple diffusions, Chin. J. Phys., 2022, 77, 393–410 CrossRef CAS.
- H. Upreti, A. K. Pandey, Z. Uddin and M. Kumar, Thermophoresis and Brownian motion effects on 3D flow of Casson nanofluid consisting microorganisms over a Riga plate using PSO: a numerical study, Chin. J. Phy., 2022, 78, 234–270 CrossRef.
- S. A. Khan, T. Hayat and A. Alsaedi, Entropy generation in chemically reactive flow of Reiner-Rivlin liquid conveying tiny particles considering thermal radiation, Alexandria Eng. J., 2023, 66, 257–268 CrossRef.
- B. Ali, P. K. Pattnaik, R. A. Naqvi, H. Waqas and S. Hussain, Brownian motion and thermophoresis effects on bioconvection of rotating Maxwell nanofluid over a Riga plate with Arrhenius activation energy and Cattaneo-Christov heat flux theory, Therm. Sci. Eng. Prog., 2021, 23, 100863 CrossRef CAS.
- M. Mustaq, S. Asghar and M. A. Hossian, Mixed convection flow of second grade fluid along vertical stretching flat surface with variable surface temperature, Heat Mass Transfer, 2007, 43, 1049–1061 CrossRef.
- T. Hayat, T. Muhammad, S. A. Shehzad, G. Q. Chen and I. A. Abbas, Interaction of magnetic field in flow of Maxwell nanofluid with convective effect, J. Magn. Magn. Mater., 2015, 389, 48–55 CrossRef CAS.
- F. Mabood, M. D. Shamshuddin and S. R. Mishra, Characteristics of thermophoresis and Brownian motion on radiative reactive micropolar fluid flow towards continuously moving flat plate: HAM solution, Math. Comput. Simul., 2022, 191, 187–202 CrossRef.
- S. Ahmed, H. Xu, Y. Zhou and Q. Yu, modelling convective transport of hybrid nanofluid in a lid driven square cavity with consideration of Brownian diffusion and thermophoresis, Int. Commun. Heat Mass Transfer, 2022, 137, 106226 CrossRef CAS.
- S. Patil, C. Kataria, A. Kumar and A. Kumar, Effect of segregation and advection governed heterogeneous distribution of nanoparticles on NEPCM discharging behavior, Journal of Energy Storage, 2023, 57, 106230 CrossRef.
- G. Rasool, N. A. Ahammad, M. R. Ali, N. A. Shah, X. Wang, A. Shafiq and A. Wakif, Hydrothermal and mass aspects of MHD non-Darcian convective flows of radiating thixotropic nanofluids nearby a horizontal stretchable surface: passive control strategy, Case Stud. Therm. Eng., 2023, 42, 102654 CrossRef.
- M. Turkyilmazoglu, Nanofluid flow and heat transfer due to a rotating disk, Comput. Fluids, 2014, 94, 139–146 CrossRef CAS.
- A. Majeed, N. Golsanami, B. Gong, Q. A. Ahmad, S. Rifaqat, A. Zeeshan and F. M. Noori, Analysis of thermal radiation in magnetohydrodynamic motile gyrotactic micro-organisms flow comprising tiny nanoparticle towards a nonlinear surface with velocity slip, Alexandria Eng. J., 2023, 66, 543–553 CrossRef.
- M. Yasir, A. Ahmed, M. Khan, A. K. Alzahrani, Z. U. Malik and A. M. Alshehri, Mathematical modelling of unsteady Oldroyd-B fluid flow due to stretchable cylindrical surface with energy transport, Ain Shams Eng. J., 2023, 14 DOI:10.1016/j.asej.2022.101825.
- M. Basavarajappa and D. Bhatta, Unsteady nonlinear convective flow of a nanofluid over a vertical plate due to impulsive motion: optimization and sensitivity analysis, Int. Comm. Heat Mass Transf., 2022, 134, 106036 CrossRef CAS.
- M. Hussain and M. Sheremet, Convection analysis of the radiative nanofluid flow through porous media over a stretching surface with inclined magnetic field, Int. Commun. Heat Mass Transfer, 2023, 140, 106559 CrossRef CAS.
- H. Khoshtarash, M. Siavashi, M. Ramezanpour and M. J. Blunt, Pore-scale analysis of two-phase nanofluid flow and heat transfer in open-cell metal foams considering Brownian motion, Appl. Therm. Eng., 2023, 221, 119847 CrossRef CAS.
- A. Bejan, A study of entropy generation in fundamental convective heat transfer, J. Heat Transfer, 1979, 101, 718–725 CrossRef.
- A. Bejan, Second law analysis in heat transfer, Energy, 1980, 5, 721–732 CrossRef.
- A. Dawar, Z. Shah, W. Khan, M. Idrees and S. Islam, Unsteady squeezing flow of magnetohydrodynamic carbon nanotube nanofluid in rotating channels with entropy generation and viscous dissipation, Adv. Mech. Eng., 2019, 11, 1–18 Search PubMed.
- T. Hayat, L. Sajjad, M. I. Khan, M. I. Khan and A. Alsaedi, Salient aspects of thermodiffusion and diffusion thermo on unsteady dissipative flow with entropy generation, J. Mol. Liq., 2019, 282, 557–565 CrossRef CAS.
- K. B. Sharma, R. Gandhi and M. M. Bhatti, Entropy analysis of thermally radiating MHD slip flow of hybrid nanoparticles (Au-Al2O3/Blood) through a tapered multi-stenosed artery, Chem. Phys. Lett., 2022, 790, 139348 CrossRef.
- S. A. Khan, T. Hayat and A. Alsaedi, Entropy optimization for nanofluid flow with radiation subject to a porous medium, J. Pet. Sci. Eng., 2022, 217, 110864 CrossRef CAS.
- B. Iftikhar, T. Javed and M. A. Siddiqu, Entropy generation analysis during MHD mixed convection flow of non-Newtonian fluid saturated inside the square cavity, J. Comput. Sci., 2023, 66, 101907 CrossRef.
- T. Hayat, A. Razaq, S. A. Khan and S. Momani, Soret and Dufour impacts in entropy optimized mixed convective flow, Int. Commun. Heat Mass Transfer, 2023, 141, 106575 CrossRef CAS.
- H. Maiti, A. Y. Khan, S. Mondal and S. K. Nandy, Scrutinization of unsteady MHD fluid flow and entropy generation: Hybrid nanofluid model, J. Comput. Appl., 2023, 6, 100074 Search PubMed.
- M. Sankar, H. A. K. Swamy, Q. A. Mdallal and A. Wakif, Non-Darcy nanoliquid buoyant flow and entropy generation analysis in an inclined porous annulus: effect of source-sink arrangement, Alexandria Eng. J., 2023, 68, 239–261 CrossRef.
- M. M. Bhatti and S. I. Abdelsalam, Scientific breakdown of a ferromagnetic nanofluid in hemodynamics: enhanced therapeutic approach, Math. Modell. Nat. Phenom., 2022, 17 DOI:10.1051/mmnp/2022045.
- M. M. Bhatti and R. Ellahi, Numerical investigation of non-Darcian nanofluid flow across a stretchy elastic medium with velocity and thermal slips, Numer. Heat Transfer, Part B, 2023, 83, 323–343 CrossRef.
- N. Vedavathi, G. Dharmaiah, S. A. Gaffar and K. Venkatadri, Entropy analysis of nanofluid magnetohydrodynamic convection flow past an inclined surface: a numerical review, Heat Transfer, 2021, 50(6), 5996–6021 CrossRef.
- E. M. Sparrow and H. S. Yu, Local non-similarity thermal boundary-layer solutions, J. Heat Transfer, 1971, 93, 328–334 CrossRef.
- R. Razzaq, U. Farooq, J. Cui and T. Muhammad, Non-similar solution for magnetized flow of Maxwell nanofluid over an exponentially stretching surface, Math. Probl. Eng., 2021, 2021 DOI:10.1155/2021/5539542.
- C. Y. Wang, Free convection on a vertical stretching surface, J. Appl. Math. Mech., 1989, 69, 418–420 Search PubMed.
| This journal is © The Royal Society of Chemistry 2023 |