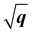Open Access Article
Open Access ArticleMomentum and thickness dependent excitonic and plasmonic properties of 2D h-BN and MoS2 restored from supercell calculations†
Guang
Yang
a,
Jiachen
Fan
a and
Shang-Peng
Gao
 *ab
*ab
aDepartment of Materials Science, Fudan University, Shanghai 200433, P. R. China. E-mail: gaosp@fudan.edu.cn
bYiwu Research Institute of Fudan University, Yiwu, Zhejiang 322000, P. R. China
First published on 1st November 2023
Abstract
The comprehension and manipulation of the propagation characteristics of elementary excitations, such as excitons and plasmons, play a crucial role in tailoring the optical properties of low-dimensional materials. To this end, investigations into the momentum (q) dispersions of excitons and plasmons in confined geometry are required fundamentally. Due to advancements in momentum-resolved spectroscopy techniques, research on the q-dependent excitons or plasmons in low-dimensional materials is beginning to emerge. However, previous simulations of low-dimensional systems are adversely affected by the artificial vacuum spacing employed in the supercell approximation. Furthermore, the significance of layer thickness in determining the excitonic and plasmonic characteristics of two-dimensional (2D) materials remains largely unexplored in the context of finite q. Therefore, an extensive investigation into the momentum and thickness dependent behaviours of both excitons and plasmons in 2D materials, which are free of the influence of vacuum spacing, is lacking at present. In this article, we develop a restoration procedure to eliminate the influence of vacuum spacing, and obtain a comprehensive picture of momentum and layer thickness dependent excitonic and plasmonic properties of 2D hexagonal boron nitride (h-BN) and molybdenum disulphide (MoS2). Our restored simulations are not only found to be in excellent agreement with available experiments, but also elucidate the roles of momentum and layer thickness in the excitonic and plasmonic properties of 2D h-BN and MoS2. We further unveil the dimensionality effect on the dispersion characteristics of excitons and plasmons in h-BN and MoS2. Our contribution will hopefully promote the understanding of the elementary excitations propagating in low-dimensional materials and pave the way for next-generation nanophotonic and optoelectronic devices.
1. Introduction
Two-dimensional (2D) materials have attracted significant attention due to their versatile applications in a wide variety of fields,1–9 including optoelectronics, photovoltaic cells, phototransistors, and other related areas. For the design of next-generation nanophotonic devices, it is imperative to comprehend and manipulate the propagation of the elementary electronic excitations such as excitons and plasmons in low-dimensional materials, considering that the excitons and plasmons can carry convertible and exploitable excitation energies when propagating in materials. A fundamental stride in this realm is to determine the excitonic and plasmonic properties at different momentum transfers q and obtain the energy–momentum dispersion relations. Previously published studies have tended to focus on the excitonic or plasmonic properties in the optical limit (q = 0) by optical spectroscopy. Thanks to the growth of momentum-resolved spectroscopy techniques such as q-resolved electron energy-loss spectroscopy (q-EELS) and resonant inelastic X-ray spectroscopy, research on dispersions of excitons or plasmons with finite q has flourished over the past few years. To date, notwithstanding, relevant experimental and theoretical focuses have been mainly on three-dimensional (3D) systems,10–19 while the study of q-dependent excitons and plasmons of low-dimensional materials is just beginning to emerge.20–29 For example, Cudazzo et al.23 calculated the behaviours of the lowest-energy excitons of graphene, monolayer hexagonal boron nitride (h-BN) and phosphorene at different momenta and predicted them to have positive dispersions. Torbatian et al.25 predicted the dispersions of intraband plasmons in electron-doped 2D materials such as graphene and phosphorene. In terms of experimental research, Liou et al.27 discovered positive dispersions for both π and π + σ plasmons of graphene through q-EELS, while Mohn et al.28 measured the EELS of monolayer molybdenum disulphide (MoS2) with the increase of q and detected positive dispersions for the π + σ plasmons. It was also concluded by Thygesen29 that the collective excitations of a 2D material are of excitonic nature for small q while plasmons become increasingly important for larger q. To sum up, extensive research on the excitonic and plasmonic dispersions with q in low-dimensional systems requires further refinement.In the context of periodic calculations for low-dimensional materials, the construction of supercells is necessary for the inclusion of adequate vacuum spacing between atom layers. However, the adverse effects caused by vacuum spacing on the q-dependent excitonic or plasmonic properties of low-dimensional systems have been long neglected. The elimination of the influence of vacuum spacing has been reported to be essential to obtaining the polarizability for calculating the Raman spectra,30 while eliminating the vacuum's influence on the excitonic or plasmonic properties of low-dimensional systems at finite q has rarely been performed. Furthermore, the role of layer thickness in the excitonic or plasmonic properties of 2D materials is also of paramount importance. For instance, the plasmonic peaks of h-BN and MoS2 were found to blueshift with the increasing thickness at q = 0,31 whereas the lowest-energy excitons of MoS2 did not show apparent layer thickness dependence on the optical limit.32 Beyond the optical limit, the plasmonic peaks B and C of PtSe2 were observed to blueshift with sample thickness at finite q in both experimental results and calculations.33 In conclusion, comprehensive investigations into the intrinsic momentum and thickness dependent behaviours of both excitons and plasmons in 2D materials, which are free of the influence of vacuum spacing, are in high demand at the moment.
As a consequence, we develop an effective restoration procedure based on our prior work34 to eliminate the influence of artificial vacuum spacing in the periodic supercell calculations and further obtain the intrinsic excitonic and plasmonic properties of 2D h-BN and MoS2 at finite q for the first time. We not only analyse the dependences of excitons and plasmons on the momentum transfer and layer thickness, but also disclose distinct dispersion modes of 2D excitons and plasmons compared with their 3D counterparts in h-BN and MoS2. Corroborated by the latest experimental measurements, our calculations and analysis provide a deeper insight into the elementary electronic excitations propagating in low-dimensional materials, which guides the design of next-generation nanodevices involving light harvesting and transport of excitation energy.
2. Methods
2.1 Computational details
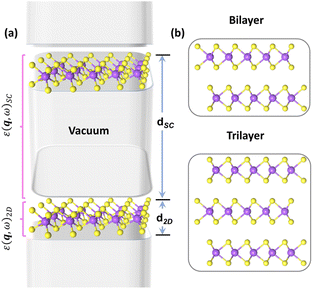
The Vienna ab initio simulation package (VASP) code35 is used to perform ground state calculations, where projector-augmented-wave (PAW) potentials36 are chosen and the generalized gradient approximation (GGA) in Perdew–Burke–Ernzerhof (PBE) is employed for the exchange and correlation functional.37 The plane-wave cut-off energy is set as 400 eV for h-BN and 520 eV for MoS2, and Monkhorst–Pack grids of 12 × 12 × 3 and 12 × 12 × 1 are chosen for bulk and 2D systems, respectively. The atomic positions of the h-BN and MoS2 are relaxed with the maximum Hellmann–Feynman forces on each atom being less than 0.001 eV Å−1 to obtain in-plane lattice constants of h-BN and MoS2 as 2.51 Å and 3.20 Å, respectively. The DFT-D3 method with Becke–Johnson damping38 is adopted for van der Waals dispersion correction. To avoid spurious interactions between periodically repeated slabs, all calculations are performed in a supercell geometry where the 2D slabs have been separated by vacuum layers larger than 20 Å as depicted in Fig. 1(a). Moreover, stable configurations for few-layer h-BN and MoS2 are further considered to adopt 2H (bilayer) and ABA (trilayer) stacking orders just as their bulk counterparts (see Fig. 1(b)). Note that the thicknesses of n-layer 2D materials d2D are estimated from the distance between the centres of the outermost layers of (n + 1)-layer 2D materials as we estimated in previous work,34 which also has been adopted in the work of Laturia et al.39 Other estimation methods entail considering the thickness of monolayer systems as the interlayer spacing of the respective bulk materials40 or as the vertical distance between the outermost atoms plus extensions of the orbitals into the vacuum region. All three estimation methods are effective in restoring the excitonic or plasmonic properties of 2D materials and the difference arising from these methods is negligible.As for the q-dependent excitonic properties of 2D materials, the electron–hole interaction is essential for accounting for the excitonic effects. Hence, we employ the GW method and solve the Bethe–Salpeter equation (BSE)41,42 within the VASP code. To generate quasiparticle energies, single-shot G0W0 calculations are conducted using the screened Coulomb potential and polarizability computed from the PBE-GGA wavefunctions and eigenvalues. The number of empty bands is no less than 200. Based on the G0W0 quasiparticle energies, the BSE calculations at finite q can be performed. Since this approach is computationally demanding, the numbers of occupied and unoccupied bands are carefully selected as the same and equal 4, 8, 12, and 8 for monolayer, bilayer, trilayer, and bulk h-BN, respectively. For more demanding systems of MoS2, as many as 13 occupied and 13 unoccupied bands are chosen.
The plasmons of 2D materials are usually recognized in the energy-loss functions at energies higher than the excitons, which means more unoccupied bands need to be included in the computations. However, including more unoccupied bands will substantially increase the computational cost in the GW-BSE formalism. Therefore, a feasible alternative—the linear response time-dependent density functional theory (LR-TDDFT)43 method with the random phase approximation (RPA)—is employed to calculate the q-dependent plasmonic properties within the GPAW code,44 where the same k-points and plane-wave cut-off energies are used as above for the ground-state DFT calculation. With lower cost in computation, the empty bands can be more than 50 for h-BN and MoS2. All momentum transfers are set along the ΓM direction in the first Brillouin zone of the corresponding hexagonal lattices.
2.2 The restoration procedure for extracting intrinsic q-dependent excitonic and plasmonic properties from supercell calculations
In periodic calculations, supercells need to be constructed for low-dimensional materials. As for the supercells for 2D materials, sufficient vacuum spacing is added between periodic 2D slabs to avert unphysical interlayer interaction. Even though the ground-state properties, quasiparticle band structures, and exciton binding energies of supercells can well converge with respect to the vacuum thickness, the drawback of the supercell approximation is that the dielectric functions could only converge to the properties of the vacuum instead of the original 2D systems. We have already tackled this problem and devised a restoration method for the dielectric functions and optical properties of low-dimensional materials. Following our previous procedures,34 we will reveal how to obtain intrinsic q-dependent excitonic and plasmonic properties explicitly.To begin with, the macroscopic dielectric function εM at finite q calculated within the many-body BSE formalism41,45,46 can be written out as follows:
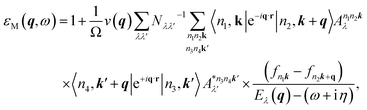 | (1) |
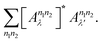 Ω is the volume of the calculated system's unit cell in real space, which will be altered with the choice of vacuum thickness d in the supercell approximation. In practice, the vacuum spacing employed is large enough for the electronic structures to converge, but εM is still affected by Ω.
Ω is the volume of the calculated system's unit cell in real space, which will be altered with the choice of vacuum thickness d in the supercell approximation. In practice, the vacuum spacing employed is large enough for the electronic structures to converge, but εM is still affected by Ω.
The imaginary and real parts of the macroscopic dielectric functions at finite q can further be obtained from eqn (1) to analyse this influence of vacuum spacing as follows:
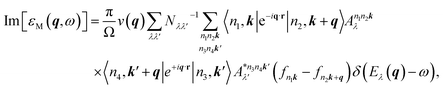 | (2) |
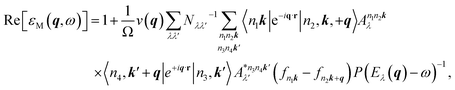 | (3) |
Meanwhile, a similar derivation process within the random phase approximation can be performed based on the following expression:47
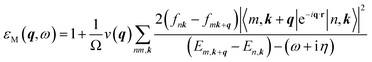 | (4) |
Therefore, the q-dependent imaginary and real parts of the dielectric function in the RPA can also be obtained as:
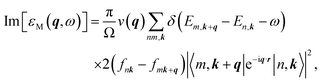 | (5) |
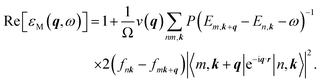 | (6) |
From eqn (2) and (3) or eqn (5) and (6), we can conclude that when the vacuum spacing is large enough for the electronic structures to converge, the values of Im[εM(q, ω)] and Re[εM(q, ω)] − 1 should both be proportional to the inverse of unit cell volume Ω, regardless of the level of theory. Hence, the intrinsic q-dependent imaginary and real dielectric functions of 2D materials independent of vacuum spacing can be restored from the results of supercells as follows:
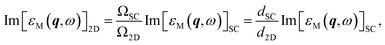 | (7) |
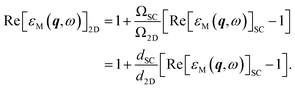 | (8) |
From the intrinsic imaginary dielectric functions at different momenta, the intrinsic q-dependent excitonic properties of 2D materials can be obtained. It is worth noting that the restoration procedure could not alter the peak positions of the imaginary dielectric functions but their intensities, which can reflect the oscillator strength of the excitons. As for the intrinsic plasmonic properties of 2D materials, we should pay attention to the energy-loss functions at finite q, which involve both the imaginary and real parts of the dielectric functions as follows:
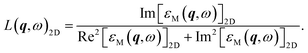 | (9) |
Therefore, the intrinsic q-dependent excitonic and plasmonic properties of 2D materials can finally be obtained from periodic supercell calculations viaeqn (7)–(9). It is noted that previous works48–51 primarily focused on truncating the long-range Coulomb interaction when it comes to considering the influence of vacuum spacing in supercell calculations. However, the dielectric functions calculated with the truncated Coulomb interaction still vary significantly with the increasing vacuum thickness and are not consistent with the experimental measurements, as depicted in Fig. S1 and S2.† Hence, the dependences on the vacuum thickness predicted by eqn (7) and (8) are independent of the employment of the Coulomb truncation. Our restoration approach is actually distinct from the effect of cancelling the spurious Coulomb interaction.
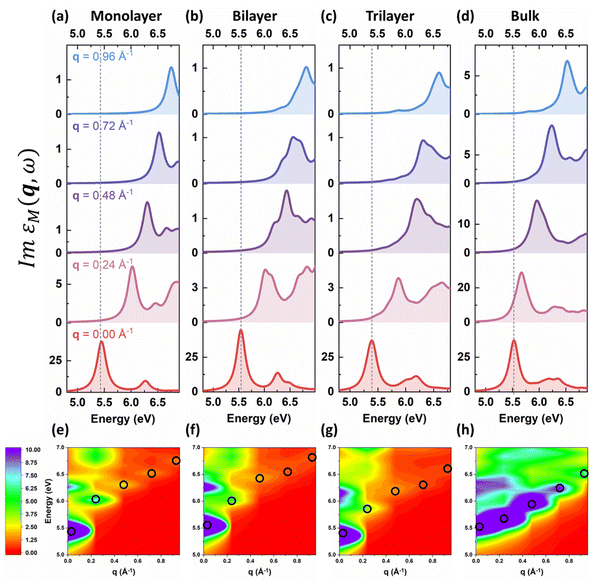
Furthermore, our simulation results after restoration show great consistency with experimental measurements. As shown in Fig. 2, the q-dependent restored (solid lines) and unrestored (dashed lines) energy-loss functions L(q,ω) of monolayer MoS2 are compared with available experimental measurements28,31 illustrated as green dots. As a result, the restored energy-loss functions agree well with experimental results from vanishing q to finite q, while the unrestored L(q,ω) directly obtained from supercell calculations demonstrate red-shifts from measurements, suggesting the necessity to extract the intrinsic dielectric functions and energy-loss functions of low-dimensional materials from periodic supercell calculations. Note that the q-dependent energy-loss functions of monolayer MoS2 restored with different vacuum thicknesses, i.e. different scaling factors, are also consistent with experimental results as illustrated in Fig. S3.†
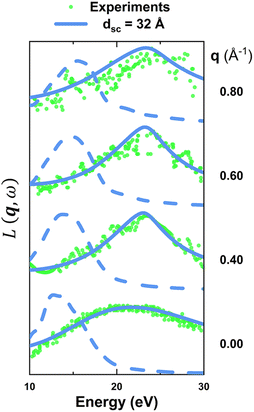 | ||
| Fig. 2 The restored energy-loss functions of monolayer MoS2 compared with experimental measurements27,30 (green dots) from vanishing q to finite q along ΓM. The restorations are based on the supercell thickness of 32 Å, and unrestored results are also illustrated as dashed lines for comparison. | ||
3. Results and discussion
3.1 Intrinsic q-dependent excitonic properties of 2D h-BN and MoS2
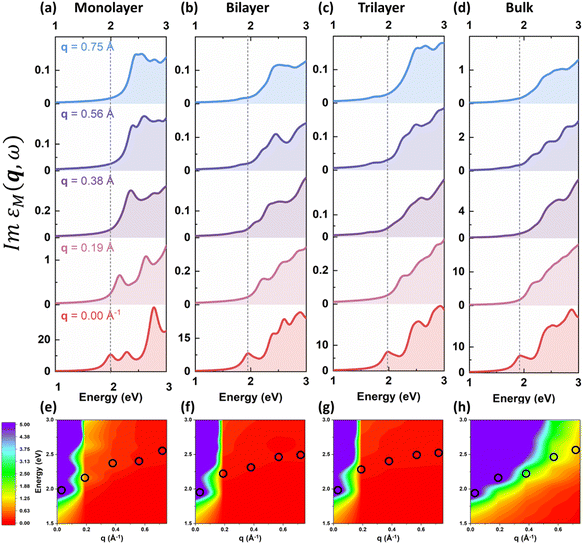
As shown in Fig. 3 and 4, the intrinsic excitonic properties of 2D h-BN and MoS2 beyond the optical limit can be characterized by the q-dependent imaginary dielectric functions and the q–E dispersion diagrams. We chose the lowest-energy excitations (also called A excitons in this article) as exemplary excitons for the following analysis. For 2D h-BN, the A excitons are mainly situated at around 5.5 eV in the optical limit and show positive dispersions with the increase of q as shown in Fig. 3(a)–(c) and (e)–(g). A similar dispersion has been found for the 3D counterpart in Fig. 3(d) and (h), which agrees well with previous experiments on bulk h-BN.52 Note that according to eqn (7), our restoration method only rescales the imaginary part of the dielectric function with no change in the peak positions. Therefore, the intrinsic exciton dispersion of monolayer h-BN in Fig. 3(e) agrees well with unrestored predictions by Cudazzo et al.23 As for 2D MoS2, the lowest-energy excitonic features appear at around 2.0 eV at vanishing q, and also demonstrate positive dispersions as q increases (see Fig. 4(a)–(c) and (e)–(g)). Likewise, bulk MoS2 exhibits a positively dispersive A exciton as shown in Fig. 4(d) and (h), which is consistent with the results measured by Habenicht et al.16 Moreover, we can observe declines in the exciton peak intensities as q increases for both h-BN and MoS2 regardless of 2D or 3D form, which is universally observed in previous experiments.3.2 Intrinsic q-dependent plasmonic properties of 2D h-BN and MoS2
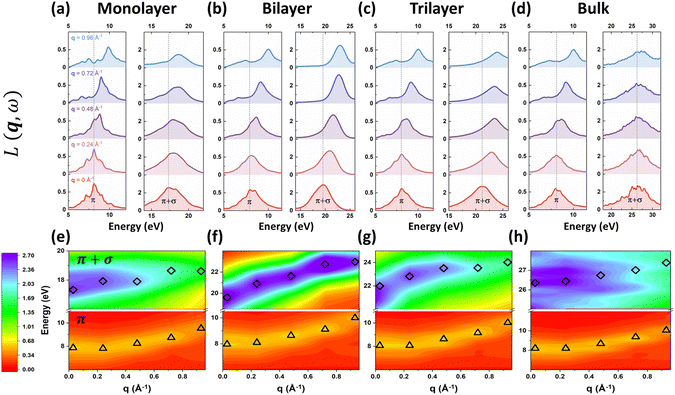
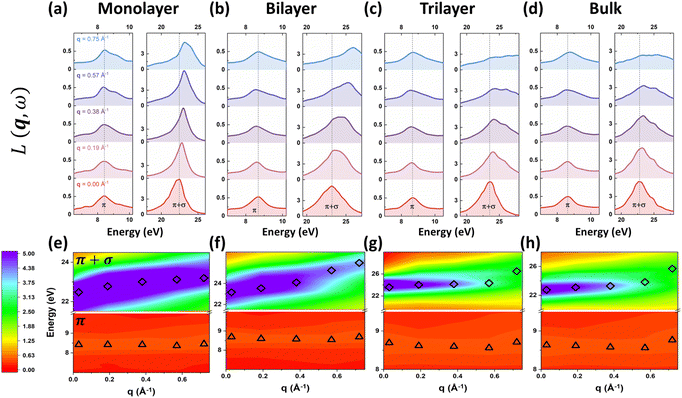
As for the intrinsic plasmonic properties of 2D h-BN and MoS2 shown in Fig. 5 and 6, we mainly focus on the two prominent plasmons in the energy-loss functions. To keep in line with analogous peaks in graphite and graphene, we label the two peaks as the π peak (low-energy feature) and the π + σ peak (high-energy feature) throughout this paper. For 2D h-BN, we discover positive dispersions for both π and π + σ plasmons as shown in Fig. 5(a)–(c) and (e)–(g). Meanwhile, the plasmonic dispersion in 3D h-BN is predicted to resemble its 2D counterpart as depicted in Fig. 5(d) and (h), and is also in good agreement with previous measurements on bulk h-BN.15,52 Furthermore, the peak intensities of both 2D and 3D π and π + σ plasmons of h-BN are predicted to decrease with the increase of q, as shown in Fig. 5(a)–(d). Note that the decreases in the π plasmon peaks are subtler compared to those in the π + σ plasmons. In 2D MoS2 the plasmonic dispersions are more complicated: the π plasmons show no obvious dispersion as q increases, while the π + σ plasmons demonstrate positive dispersions as depicted in Fig. 6(a)–(c) and (e)–(g). It is worth noting that the dispersions of the π and π + σ plasmons in monolayer MoS2 agree well with the latest experimental results.28 Likewise, 3D π and π + σ plasmons are predicted to have similar dispersions as 2D plasmons for MoS2 as shown in Fig. 6(d) and (h), which are also consistent with the experimental results of bulk MoS2.18 As for the peak intensities in the energy-loss spectra of 2D and 3D MoS2, the π plasmon peaks barely change with the increase of q, while the π + σ plasmon peaks show apparent declines, as shown in Fig. 6(a)–(d).3.3 Dimensionality effects in the dispersion modes of excitons and plasmons of h-BN and MoS2
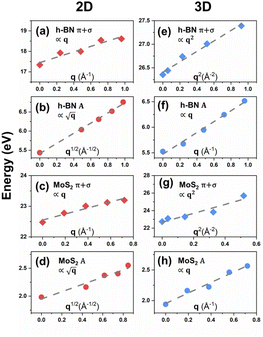
We have observed similar positive dispersions of excitons and plasmons in both 2D and 3D forms of h-BN and MoS2. This raises the question of whether the dimensionality has any impact on the excitonic and plasmonic properties beyond the optical limit. Upon closer examination of the dispersion curvatures depicted in Fig. 3–6, distinctions in these dispersions emerge as the dimensionality changes from 2D to 3D. We can classify the dispersions of excitons and plasmons into three modes. Mode I is the quasilinear dispersion (proportional to q), which has been measured in the plasmon excitations of carbon nanotubes26 and graphene.53 Mode II is the parabolic dispersion (proportional to q2) and is predicted as the characteristics of 2D Wannier–Mott excitons (such as the lowest-energy bright exciton in graphene23) and experimentally measured in the plasmons of 3D bulks.18,52,54 Mode III is called the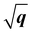 dispersion (proportional to
dispersion (proportional to 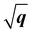 ) and has been considered as the characteristics of 2D Frenkel excitons (such as the lowest-energy bright exciton in h-BN23) and plasmons of 2D electron gas.55 We first look at the dispersion behaviours of the lowest-energy excitons in h-BN and MoS2. It is obvious that A excitons in both monolayer h-BN and MoS2 have characteristic
) and has been considered as the characteristics of 2D Frenkel excitons (such as the lowest-energy bright exciton in h-BN23) and plasmons of 2D electron gas.55 We first look at the dispersion behaviours of the lowest-energy excitons in h-BN and MoS2. It is obvious that A excitons in both monolayer h-BN and MoS2 have characteristic 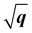 dispersions, which are consistent with the dispersion mode of Frenkel excitons according to Cudazzo et al.,23 whereas their bulk counterparts show linear-like dispersions which also influence the dispersions of bilayer and trilayer systems. As for the dispersion behaviours of plasmons, the situation becomes different between π and π + σ plasmons. The π plasmon dispersions are predicted to have the same modes in 2D and 3D forms for h-BN (parabolic mode) and MoS2 (non-dispersive mode). Nevertheless, the π + σ plasmons show distinct features in dispersion modes between 2D and 3D forms. In both h-BN and MoS2, the dispersions of π + σ plasmons demonstrate linear-like modes in monolayer systems. Meanwhile, their bulk counterparts show 3D-characteristic parabolic dispersion modes, which are often detected in bulk h-BN and MoS218,52 and affect the bilayer and trilayer dispersions as well. We can further rescale the 2D and 3D excitonic and plasmonic dispersions of h-BN and MoS2 with different dependences on q, q2 or
dispersions, which are consistent with the dispersion mode of Frenkel excitons according to Cudazzo et al.,23 whereas their bulk counterparts show linear-like dispersions which also influence the dispersions of bilayer and trilayer systems. As for the dispersion behaviours of plasmons, the situation becomes different between π and π + σ plasmons. The π plasmon dispersions are predicted to have the same modes in 2D and 3D forms for h-BN (parabolic mode) and MoS2 (non-dispersive mode). Nevertheless, the π + σ plasmons show distinct features in dispersion modes between 2D and 3D forms. In both h-BN and MoS2, the dispersions of π + σ plasmons demonstrate linear-like modes in monolayer systems. Meanwhile, their bulk counterparts show 3D-characteristic parabolic dispersion modes, which are often detected in bulk h-BN and MoS218,52 and affect the bilayer and trilayer dispersions as well. We can further rescale the 2D and 3D excitonic and plasmonic dispersions of h-BN and MoS2 with different dependences on q, q2 or 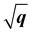 as depicted in Fig. 7. As a consequence, we observe that the dimensionality effect indeed plays an important role in the dispersion characteristics of excitons and plasmons of h-BN and MoS2.
as depicted in Fig. 7. As a consequence, we observe that the dimensionality effect indeed plays an important role in the dispersion characteristics of excitons and plasmons of h-BN and MoS2.
3.4 Thickness dependences of excitons and plasmons of h-BN and MoS2 at finite q
Apart from dispersion modes, we can study the significant interplay between the layer thickness and the positions of excitonic and plasmonic peaks at fixed q. As illustrated in Fig. 8, the energies of A excitons in h-BN and MoS2 barely change with the increase of layer thickness at finite q, which is consistent with the experimental data of MoS2 at zero momentum.32 As for plasmons, the π + σ peaks are predicted to blueshift from monolayer to bulk in both h-BN and MoS2 at finite q. However, the thickness dependences of the π plasmons beyond the optical limit are found to differ between h-BN and MoS2: in h-BN, the energies of the π plasmons show nearly no evolution as layer thickness increases, whereas the π plasmons blueshift with the increasing layer thickness in the case of MoS2. Note that the thickness dependences of the π and π + σ plasmons in MoS2 at finite q are similar to the experimental measurements at q = 0.31,56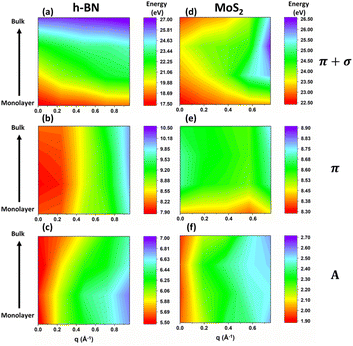 | ||
| Fig. 8 The peak positions of the A excitons, π and π + σ plasmons at different momenta along ΓM from monolayer to bulk for (a–c) h-BN and (d–f) MoS2. | ||
4. Conclusions
In conclusion, we have developed an effective restoration procedure to eliminate the influence of artificial vacuum spacing in the periodic supercell calculations based on the relationships between the vacuum volume and the dielectric functions at finite q and have successfully extracted the intrinsic excitonic and plasmonic properties of 2D h-BN and MoS2 beyond the optical limit. We have further elucidated the role of momentum transfer in the intrinsic excitonic and plasmonic properties of 2D h-BN and MoS2. Specifically, we have discovered positive dispersions for the A excitons and π + σ plasmons of 2D h-BN and MoS2. As for the π plasmons, momentum transfer is predicted to have different effects, resulting in positive dispersions for 2D h-BN and no dispersion for 2D MoS2. Moreover, we have disclosed distinct dispersion modes in 2D excitons and plasmons of h-BN and MoS2 compared with their 3D counterparts, manifesting the important role of the dimensionality effect in the excitonic and plasmonic dispersions. We have also discovered the thickness dependences of the intrinsic excitonic and plasmonic peaks in 2D h-BN and MoS2 at finite q. The calculations are in good consistency with the latest experimental measurements. Looking ahead, our restoration approach is promising to be extended to a broader range of materials, such as the in-plane anisotropic semiconductor phosphorene and the thin layers of transition metal carbides and nitrides (MXenes), alongside the varied realm of van der Waals heterostructures (vdWHs). In general, our simulations provide a comprehensive description of the intrinsic momentum and thickness dependent behaviours of excitons and plasmons in low-dimensional systems, which advances the understanding of the propagation mechanism of excitons and plasmons in confined geometry and paves the way for novel nano-electronic and optoelectronic devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Science Foundation of Shanghai (Grant No. 23ZR1403300).References
- Y. Li, Z. Li, C. Chi, H. Shan, L. Zheng and Z. Fang, Adv. Sci., 2017, 4, 1600430 CrossRef PubMed.
- H. Y. Hoh and Q. Bao, 2D Materials for Photonic and Optoelectronic Applications, Woodhead Publishing, 2020 Search PubMed.
- J. Jiang, X. Zou, Y. Lv, Y. Liu, W. Xu, Q. Tao, Y. Chai and L. Liao, Nat. Commun., 2020, 11, 4266 CrossRef CAS PubMed.
- P. Chen, T. L. Atallah, Z. Lin, P. Wang, S. J. Lee, J. Xu, Z. Huang, X. Duan, Y. Ping, Y. Huang, J. R. Caram and X. Duan, Nature, 2021, 599, 404–410 CrossRef CAS PubMed.
- S. Feng, C. Liu, Q. Zhu, X. Su, W. Qian, Y. Sun, C. Wang, B. Li, M. Chen, L. Chen, W. Chen, L. Zhang, C. Zhen, F. Wang, W. Ren, L. Yin, X. Wang, H. M. Cheng and D. M. Sun, Nat. Commun., 2021, 12, 4094 CrossRef CAS PubMed.
- B. Mortazavi, B. Javvaji, F. Shojaei, T. Rabczuk, A. V. Shapeev and X. Zhuang, Nano Energy, 2021, 82, 105716 CrossRef CAS.
- T. Kambe, S. Imaoka, M. Shimizu, R. Hosono, D. Yan, H. Taya, M. Katakura, H. Nakamura, S. Kubo, A. Shishido and K. Yamamoto, Nat. Commun., 2022, 13, 1037 CrossRef CAS PubMed.
- J. Liu, F. Yang, J. Lu, S. Ye, H. Guo, H. Nie, J. Zhang, J. He, B. Zhang and Z. Ni, Nat. Commun., 2022, 13, 3855 CrossRef CAS PubMed.
- J. H. Tong, Q. Jiang, A. J. Ferguson, A. F. Palmstrom, X. M. Wang, J. Hao, S. P. Dunfield, A. E. Louks, S. P. Harvey, C. W. Li, H. P. Lu, R. M. France, S. A. Johnson, F. Zhang, M. J. Yang, J. F. Geisz, M. D. McGehee, M. C. Beard, Y. F. Yan, D. Kuciauskas, J. J. Berry and K. Zhu, Nat. Energy, 2022, 7, 642–651 CrossRef CAS.
- M. N. Faraggi, A. Arnau and V. M. Silkin, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035115 CrossRef.
- P. Cudazzo, M. Gatti and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075121 CrossRef.
- J. van Wezel, R. Schuster, A. Konig, M. Knupfer, J. van den Brink, H. Berger and B. Buchner, Phys. Rev. Lett., 2011, 107, 176404 CrossRef PubMed.
- P. Wachsmuth, R. Hambach, G. Benner and U. Kaiser, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 235434 CrossRef.
- J. H. Hong, K. Li, C. H. Jin, X. X. Zhang, Z. Zhang and J. Yuan, Phys. Rev. B, 2016, 93, 075440 CrossRef.
- S. Galambosi, L. Wirtz, J. A. Soininen, J. Serrano, A. Marini, K. Watanabe, T. Taniguchi, S. Huotari, A. Rubio and K. Hamalainen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 081413 CrossRef.
- C. Habenicht, M. Knupfer and B. Buchner, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 245203 CrossRef.
- C. Habenicht, R. Schuster, M. Knupfer and B. Buchner, J. Phys.: Condens. Matter, 2018, 30, 205502 CrossRef PubMed.
- B. B. Yue, F. Hong, K. D. Tsuei, N. Hiraoka, Y. H. Wu, V. M. Silkin, B. Chen and H. K. Mao, Phys. Rev. B, 2017, 96, 125118 CrossRef.
- F. Fossard, L. Sponza, L. Schue, C. Attaccalite, F. Ducastelle, J. Barjon and A. Loiseau, Phys. Rev. B, 2017, 96, 115304 CrossRef.
- Z. Torbatian and R. Asgari, J. Phys.: Condens. Matter, 2017, 29, 465701 CrossRef CAS PubMed.
- E. Moynihan, S. Rost, E. O'Connell, Q. Ramasse, C. Friedrich and U. Bangert, J. Microsc., 2020, 279, 256–264 CrossRef CAS PubMed.
- J. Koskelo, G. Fugallo, M. Hakala, M. Gatti, F. Sottile and P. Cudazzo, Phys. Rev. B, 2017, 95, 035125 CrossRef.
- P. Cudazzo, L. Sponza, C. Giorgetti, L. Reining, F. Sottile and M. Gatti, Phys. Rev. Lett., 2016, 116, 066803 CrossRef PubMed.
- D. Y. Qiu, T. Cao and S. G. Louie, Phys. Rev. Lett., 2015, 115, 176801 CrossRef PubMed.
- Z. Torbatian and R. Asgari, Appl. Sci., 2018, 8, 238 CrossRef.
- C. Kramberger, R. Hambach, C. Giorgetti, M. H. Rummeli, M. Knupfer, J. Fink, B. Buchner, L. Reining, E. Einarsson, S. Maruyama, F. Sottile, K. Hannewald, V. Olevano, A. G. Marinopoulos and T. Pichler, Phys. Rev. Lett., 2008, 100, 196803 CrossRef CAS PubMed.
- S. C. Liou, C. S. Shie, C. H. Chen, R. Breitwieser, W. W. Pai, G. Y. Guo and M. W. Chu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045418 CrossRef.
- M. J. Mohn, R. Hambach, P. Wachsmuth, C. Giorgetti and U. Kaiser, Phys. Rev. B, 2018, 97, 235410 CrossRef CAS.
- K. S. Thygesen, 2D Mater., 2017, 4, 022004 CrossRef.
- L. Wirtz, M. Lazzeri, F. Mauri and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 241402 CrossRef.
- J. N. Coleman, M. Lotya, A. O'Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H. Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568–571 CrossRef CAS PubMed.
- Y. Yu, Y. Yu, Y. Cai, W. Li, A. Gurarslan, H. Peelaers, D. E. Aspnes, C. G. Van de Walle, N. V. Nguyen, Y. W. Zhang and L. Cao, Sci. Rep., 2015, 5, 16996 CrossRef CAS PubMed.
- J. Hong, M. K. Svendsen, M. Koshino, T. Pichler, H. Xu, K. Suenaga and K. S. Thygesen, ACS Nano, 2022, 16, 12328–12337 CrossRef CAS PubMed.
- G. Yang and S. P. Gao, Nanoscale, 2021, 13, 17057–17067 RSC.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. Laturia, M. L. Van de Put and W. G. Vandenberghe, npj 2D Mater. Appl., 2018, 2, 6 CrossRef.
- Y. Li, A. Chernikov, X. Zhang, A. Rigosi, H. M. Hill, A. M. van der Zande, D. A. Chenet, E.-M. Shih, J. Hone and T. F. Heinz, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 205422 CrossRef.
- S. Albrecht, L. Reining, R. Del Sole and G. Onida, Phys. Rev. Lett., 1998, 80, 4510–4513 CrossRef CAS.
- M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 81, 2312–2315 CrossRef CAS.
- J. Yan, J. J. Mortensen, K. W. Jacobsen and K. S. Thygesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245122 CrossRef.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dulak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Moller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Hakkinen, G. K. Madsen, R. M. Nieminen, J. K. Norskov, M. Puska, T. T. Rantala, J. Schiotz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- Detailed theoretical derivation can be found on the GPAW page, https://wiki.fysik.dtu.dk/gpaw/documentation/bse/bse.html#id2.
- M. Gajdos, K. Hummer, G. Kresse, J. Furthmuller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- S. Ismail-Beigi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 233103 CrossRef.
- C. A. Rozzi, D. Varsano, A. Marini, E. K. U. Gross and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205119 CrossRef.
- F. Hüser, T. Olsen and K. S. Thygesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 245309 CrossRef.
- V. U. Nazarov, New J. Phys., 2015, 17, 073018 CrossRef.
- C. Tarrio and S. E. Schnatterly, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 7852–7859 CrossRef CAS PubMed.
- M. K. Kinyanjui, C. Kramberger, T. Pichler, J. C. Meyer, P. Wachsmuth, G. Benner and U. Kaiser, Europhys. Lett., 2012, 97, 57005 CrossRef.
- H. Venghaus, Phys. Status Solidi B, 1974, 66, 145–150 CrossRef CAS.
- F. Stern, Phys. Rev. Lett., 1967, 18, 546–548 CrossRef CAS.
- P. Johari and V. B. Shenoy, ACS Nano, 2011, 5, 5903–5908 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00670k |
| This journal is © The Royal Society of Chemistry 2023 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)