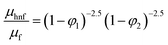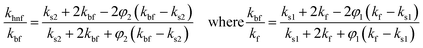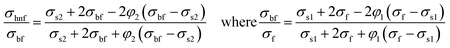DOI:
10.1039/D3NA00675A
(Paper)
Nanoscale Adv., 2023,
5, 5627-5640
Stability analysis for heat transfer flow in micropolar hybrid nanofluids
Received
22nd August 2023
, Accepted 8th September 2023
First published on 2nd October 2023
Abstract
Objective: hybrid nanofluids have superior thermal efficiency and physical durability in contrast to regular nanofluids. The stagnation point flow of MHD micropolar hybrid nanofluids over a deformable sheet with viscous dissipation is investigated. Methodology: the controlling partial differential equations are converted to nonlinear ordinary differential equations using the transmuted similarity, and are subsequently solved using the bvp4c solver in MATLAB. The hybrid nanofluids consist of aluminum and copper nanoparticles, dispersed in a base fluid of water. Results: multiple solutions are obtained in the given problem for the case of shrinking as well as for the stretching sheet due to the variation in several influential parameters. Non-unique solutions, generally, exist for the case of shrinking sheets. In addition, the first branch solution is physically stable and acceptable according to the stability analysis. The friction factor is higher for the branch of the first solution and lower in the second branch due to the higher magnetic parameters, while the opposite behavior is seen in the case of the local heat transfer rate. Originality: the novelty of this model is that it finds multiple solutions in the presence of Cu and Al2O3 nanoparticles and also performs the stability analysis. In general, non-unique solutions exist for the phenomenon of shrinking sheets.
1. Introduction
Stagnation point flow represents the attributes of fluid flow as it meets and interacts with a solid surface. At the location where the fluid comes to a halt upon meeting the surface, it separates into several streams, giving rise to the stagnation point flow effect. Hiemenz1 is the pioneer who explored the stagnation point flow due to a semi-infinite static wall. In addition, research on micropolar fluid flow has captivated many scientists because of its numerous applications including the extrusion of polymer fluids and liquid crystal solidification. The micropolar fluid theory was initiated by Eringen.2 The micro-rotational effect and the micro-rotational inertia are demonstrated by these fluids. Eventually, many researchers implement Eringen's idea in various problems such as Soid et al.3 who studied micropolar fluid magnetohydrodynamics (MHD) stagnation point flow with slip. Next, a micropolar fluid with a mixed convection flow was scrutinized by Khashi'ie et al.4 Furthermore, there are more studies on micropolar fluids.5–7
The demand for nanofluids in industrial applications has led to extensive research on their properties. One of the primary reasons for this interest is their ability to significantly enhance heat transfer in various fields, including electronics, transportation, and biomedicine. The nanofluid concept was first proposed by Choi.8 Since then, nanofluids have found extensive use in solar thermal applications, industrial cooling applications, and many other fields. Numerous researchers have examined the nanofluid, including Rahman et al.,9 Norzawary et al.10 and Wahid et al.11 Less research has been done on micropolar nanofluids, though. Hussain et al.12 examined the micropolar nanofluid via stretching sheets numerically. Following them, Patel et al.,13 Lund et al.,14 Atif et al.15 and numerous others have investigated various surfaces and angles of the micropolar nanofluid flow problem.
The term “hybrid nanofluid” involves a new sort of nanofluid that contains a base fluid mixed with two types of nanoparticles, leading to an effective enhancement in heat transfer. Extensive research has shown a significant improvement in the heat conductivity of this novel fluid, as seen in studies by Madhesh and Kalaiselvam16 and Devi and Devi.17 Therefore, many researchers have focused on investigating the mathematical aspects of the boundary layer flow in hybrid nanofluids, particularly on stretching/shrinking sheets.18–24 For instance, Subhani and Nadeem25 explored the micropolar flow for hybrid (Cu/TiO2/water) nanofluids and claimed that the heat flow capability of a micropolar hybrid nanofluid is much better in comparison to that of a micropolar nanofluid. It appears that there has been little research on micropolar hybrid nanofluids. Hence, the primary aim of this work is to examine how stretching and contraction of the surface affect the behaviour of a micropolar hybrid nanofluid.
The magnetohydrodynamic (MHD) effect is also important. MHD has great impacts on engineering due to its vital principles. These principles are also applied in numerous industrial applications such as MHD pumps, generators, nuclear reactor cooling, flow meters, heat exchangers, nuclear waste disposal, geothermal energy extractors, and space vehicle impulsion. The presence of a magnetic effect produces a Lorentz force generated by the magnetic field which usually repels the hydrodynamic field in the presence or absence of a permeable matrix. The MHD flow of micropolar nanofluid via a stretch surface was researched by Kamal et al.26 and Yasmin et al.27 However viscous dissipation is the process in which shear forces influence a fluid on the adjacent layers and transform into heat, and represented by the Eckert number, which is also considered in this work. Some authors who considered this effect are Hsiao28 and Lund et al.29 both of whom studied the micropolar nanofluid flow via stretching sheets.
As a result of the abovementioned research, we are driven to explore the MHD and viscous dissipation effects and to expand Anuar et al.30 work by implementing the stagnation point. We aim to provide a mathematical model for the problem and observe the impact of the considered parameters on the physical quantities of interest to simulate the fluid flow dynamics via the numerical perspective. These numerical findings (simulation of the fluid behaviour) could serve as guidance to those working with the fluid in experimental and practical activities. In addition, this analysis also comprises a novel era for scientists to discover the shrinking features of micropolar hybrid nanofluids. Furthermore, the novelty of this study can also be seen in the discovery of non-unique solutions and the execution of stability analysis.
2. Mathematical modeling of the problem
2.1. The description of governing equations with boundary conditions (BCs)
Consider a 2D steady incompressible stagnation point flow of magnetohydrodynamic (MHD) micropolar Cu–Al2O3/H2O nanofluid past a deformable sheet as pictured in Fig. 1. Both the velocity of stretching/shrinking and that of a fluid in the far-field, denoted as Uw(x) = ax and U∞(x) = bx, exhibit a linear variation from the stagnation point which a and b(>0) are constants. The model is formulated as (Soid et al.3 and Anuar et al.30):| | 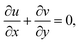 | (1) |
| | 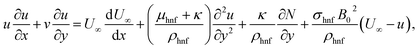 | (2) |
| | 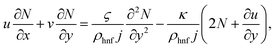 | (3) |
| | 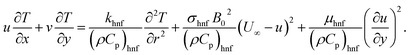 | (4) |
with conditions of:| | 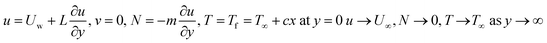 | (5) |
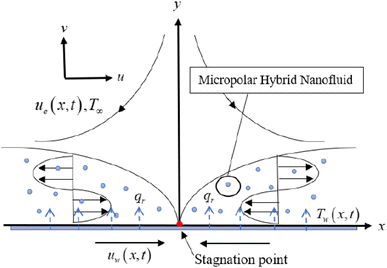 |
| | Fig. 1 Physical model of shrinking flow (Anuar et al.28). | |
The velocities in directions of x and y are u and v, independently, T is the nanofluid temperature, and L is the slip length. In addition, N refers to the angular velocity in the xy-plane, k refers to vortex viscosity, 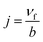 is the density of micro inertial and
is the density of micro inertial and 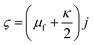 is the spin gradient viscosity.31 Additionally, m is a constant between [0,1]. When m = 0, that also signifies that N = 0; the microelements close to the surface cannot spin, which represents concentrated particle flows32 or cited in Smith and Guram,33 due to the concentrated microelements.
is the spin gradient viscosity.31 Additionally, m is a constant between [0,1]. When m = 0, that also signifies that N = 0; the microelements close to the surface cannot spin, which represents concentrated particle flows32 or cited in Smith and Guram,33 due to the concentrated microelements.
However, the stress tensor anti-symmetric portion dissipates when n = 0.5 (low microelement concentration).31 Additionally, the situation n = 1 is used to describe a flow with turbulence.34
2.2. Thermophysical features of hybrid nanofluids
Table 1 displays the physical characteristics of hybrid nanofluids, with subscripts hnf, otherwise nf, f and s, indicating nanofluid, fluid, and nanoparticle, respectively. The first and second nanoparticles are denoted as s1 and s2, respectively, where φ1 is the volume fraction of alumina (Al2O3), and φ2 that of copper (Cu), while water is the base fluid.
Table 1 Physical characteristics of the water-based Cu–Al2O3 (ref. 17)
| Properties |
Hybrid nanofluid |
| Dynamic viscosity |
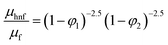
|
| Heat capacity |
(ρCp)hnf = φ2(ρCp)s2 + (1 − φ2)[(1 − φ1)(ρCp)f + φ1(ρCp)s1] |
| Thermal conductivity |
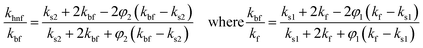
|
| Electrical conductivity |
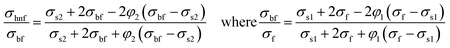
|
| Density |
ρ
Hbnf/ρf = ϕCu(ρCu/ρf) + ϕAl2O3(ρAl2O3/ρf) + (1 − ϕCu − ϕAl2O3) |
Further, the thermophysical experimental data of the base fluid (water) and the hybrid nanoparticles (copper and silver) are given in Table 2.
Table 2 Thermophysical properties of the nanoparticles and base fluid40
|
|
c
p (J kg−1 K−1) |
P (kg m−3) |
K (W mK−1) |
σ (S m−1) |
| Water |
4179 |
997.1 |
0.613 |
0.05 |
| Cu |
385 |
8933 |
400 |
5.96 × 107 |
| Al2O3 |
765 |
3970 |
40 |
3.69 × 107 |
2.3. Similarity transformation
To facilitate the analysis of the problem at hand, we hereby introduce the following set of similarity variables, which can be employed:| | 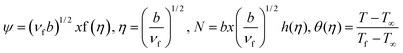 | (6) |
By introducing the stream function 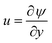 and
and 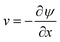 which satisfy eqn (1), then eqn (1)–(4) and conditions (5) are written as follows:
which satisfy eqn (1), then eqn (1)–(4) and conditions (5) are written as follows:
| | 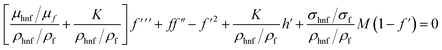 | (7) |
| | 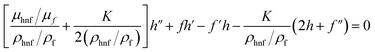 | (8) |
| | 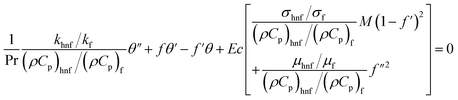 | (9) |
| | | f(0) = 0, f′(0) = ε + λf′′(0), h(0) = −mf′′(0), θ(0) = 1, f′(η) → 1, h(η) → 0, θ(η) → 0 | (10) |
where
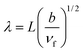
is the slip parameter and
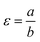
is the velocity ratio parameter such that
ε < 0 is for shrinking conditions and
ε > 0 for stretching conditions.
2.4. Skin friction coefficient and local Nusselt number
The skin friction coefficient Cf and the local Nusselt number Nux are written as| | 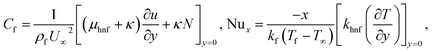 | (11) |
After performing the transformations,
| | 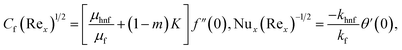 | (12) |
where
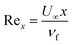
is the local Reynolds number.
2.5. Stability analysis
To further check the obtained solutions, an analysis of stability is performed. The results of this analysis support the interpretation that solely the first solution is stable whilst not the other one, which has been validated by several researchers.35–37 In order to perturb eqn (2)–(4), the unsteady case is introduced, and hence we write as| | 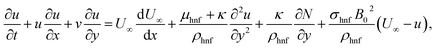 | (13) |
| | 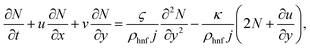 | (14) |
| | 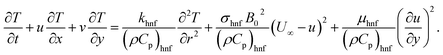 | (15) |
The following new similarity transformation is proposed:
| | 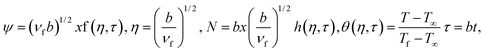 | (16) |
By applying
eqn (16) to
eqn (13)–(15), the subsequent expressions are obtained:
| | 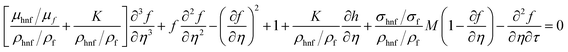 | (17) |
| | 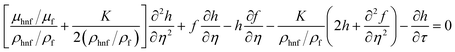 | (18) |
| | 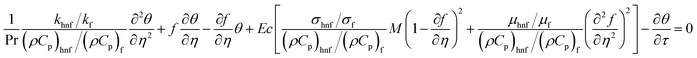 | (19) |
with conditions of:
| | 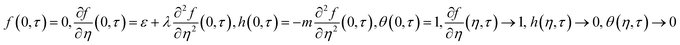 | (20) |
Subsequently, to assess the stability, the subsequent equations are employed:38
| | | f(η,τ) = f0(η) + e−γτF(η,τ), h(η,τ) = h0(η) + e−γτH(η,τ), θ(η,τ) = θ0(η) + e−γτG(η,τ) | (21) |
where
F(
η),
H(
η) and
G(
η) are low relative to
f0(
η),
h0(
η) and
θ0(
η), correspondingly, and
γ is the eigenvalue. Applying
eqn (21) to
(17)–(19), letting
τ → 0,
F(
η) =
F0(
η),
H(
η) =
H0(
η) and
G(
η) =
G0(
η), one should get:
| | 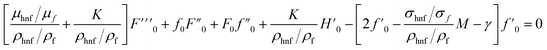 | (22) |
| | 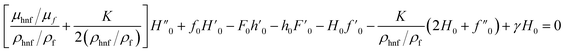 | (23) |
| | 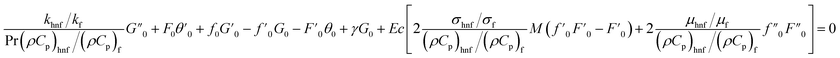 | (24) |
| | 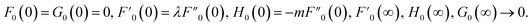 | (25) |
It was necessary to relax a boundary condition with reference to Harris et al.39 Therefore, we made modifications by setting  , and introducing a new condition of
, and introducing a new condition of  .
.
3. Results and discussion
Eqn (7)–(9) with eqn (10) are solved with the facilitation of bvp4c (Matlab). It is crucial to remember that in regards to the synthesis of the intended hybrid nanofluid, which is Cu–Al2O3/water, Al2O3 is first disseminated in water, and then Cu is added to it. The volume fraction of Al2O3 is constantly set up at 1 percent, while the fraction of Cu varies from 0 to 2 percent.
The outcomes of the comparison and variation of f′′(0) with earlier research are exemplified in Table 3. The strong agreement between the results provides assurance that the numerical outcomes obtained are valid. In addition, Table 4 signifies the values of Cf(Rex)1/2 and Nux(Rex)−1/2 for various values of the ε and nanoparticle volume fraction for the branch of first solution. It shows that for each fixed value of the nanoparticle as ε increases, as a result, the Cf(Rex)1/2 increases, but Nux(Rex)−1/2 acts in an opposite manner.
Table 3 Comparison value of f′′(0) for different ε when φ1 = φ2 = K = M = n = 0a
|
ε
|
Zainal et al.41 |
Anuar et al.30 |
Present |
|
[ ] Second solution.
|
| −0.25 |
1.40221 |
1.40221 |
1.40221 |
| −0.5 |
1.495670 |
1.495670 |
1.495670 |
| −0.75 |
1.489298 |
1.489298 |
1.489298 |
| −1 |
1.328817 |
1.328817 |
1.328817 |
| [0] |
[0] |
[0] |
| −1.1 |
1.186680 |
1.186680 |
1.186680 |
| [0.049229] |
[0.049229] |
[0.049229] |
| −1.15 |
1.082231 |
1.082231 |
1.082231 |
| [0.116702] |
[0.116702] |
[0.116702] |
| −1.2 |
0.932473 |
0.932473 |
0.932473 |
| [0.233650] |
[0.233650] |
[0.233650] |
| −1.246 |
0.609826 |
0.609826 |
0.609826 |
| [0.529035] |
[0.529035] |
[0.529035] |
| −1.2465 |
- |
0.584282 |
0.584282 |
| - |
[0.554296] |
[0.554296] |
Table 4 Values of Cf(Rex)1/2 and Nux(Rex)−1/2 for various ε for the first solution
|
φ
2
|
ε
|
C
f(Rex)1/2 |
Nux(Rex)−1/2 |
| 0 |
2 |
−1.77728 |
3.28277 |
| 1 |
0 |
3.16126 |
| 0 |
1.37770 |
1.14263 |
| −0.5 |
1.82975 |
−0.79907 |
| −1 |
1.99028 |
−4.06281 |
| 0.01 |
2 |
−1.84526 |
3.28115 |
| 1 |
0 |
3.20568 |
| 0 |
1.54532 |
1.14809 |
| −0.5 |
1.97168 |
−0.82816 |
| −1 |
2.04811 |
−4.07996 |
| 0.02 |
2 |
−1.91148 |
3.28011 |
| 1 |
0 |
3.24999 |
| 0 |
1.60478 |
1.15215 |
| −0.5 |
2.04992 |
−0.86128 |
| −1 |
2.13381 |
−4.11297 |
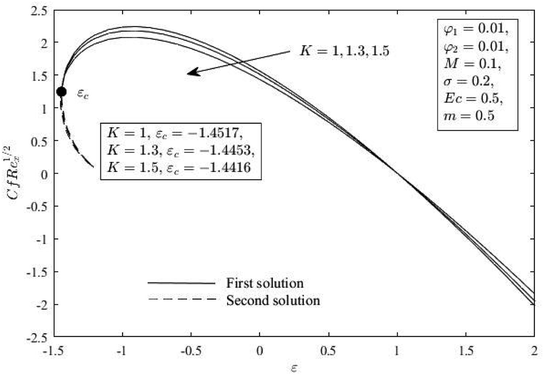
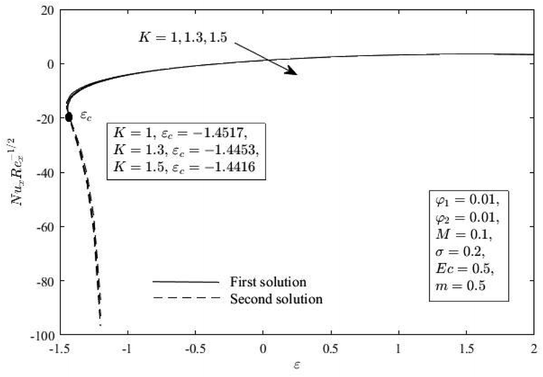
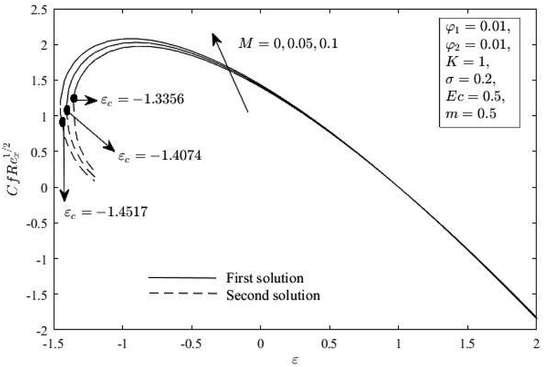
Fig. 2 and 3 reveal how the Cu nanoparticle volume fraction φ2 affects the distribution of Cf(Rex)1/2 and Nux(Rex)−1/2 as indicated in eqn (12) when compared to stretch or shrink parameter ε. When εc < ε ≤ −1, dual solutions are present, while one solution is present when ε > −1, and there is no solution when ε < εc < 0, such that εc denotes the critical value of ε. It is obvious that the issue becomes micropolar nanofluid for φ2 = 0. These figures show that an increase in φ2 improves the Cf(Rex)1/2 and Nux(Rex)−1/2 for all ranges of ε in the first solution, but only slightly so in the second. This result demonstrates that increasing φ2 can increase the effectiveness of heat transmission. This suggests that hybrid nanofluid has superior thermal performance compared to nanofluid. Additionally, the skin friction coefficient and heat transfer rate accelerate the flow separation with higher impacts of the solid nanoparticle volume fraction (φ2).
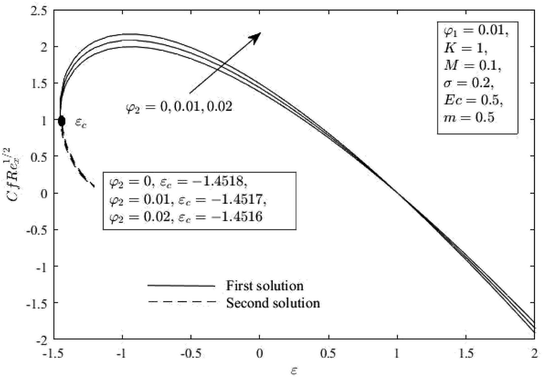 |
| | Fig. 2
C
f(Rex)1/2 for φ2 and ε. | |
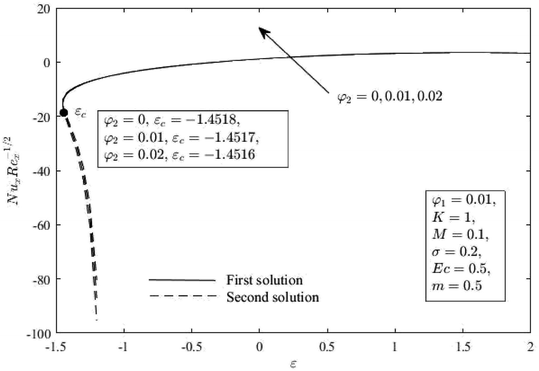 |
| | Fig. 3 Nux(Rex)−1/2 for φ2 and ε. | |
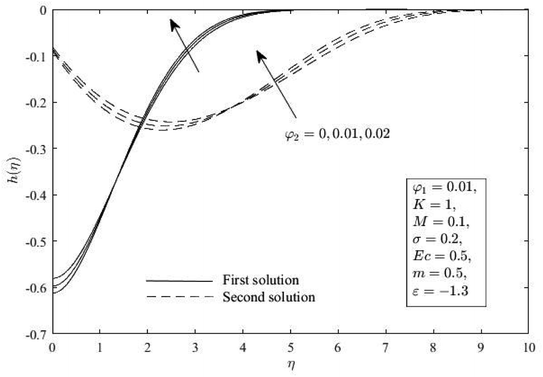
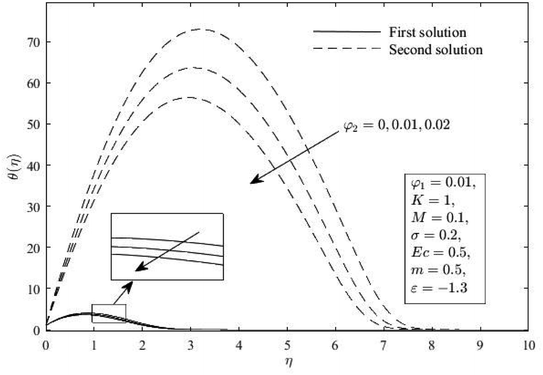
The impacts of φ2 on the distribution of f′(η), h(η) and θ(η) for shrinking sheets (ε = −1.3) are demonstrated in Fig. 4–6. The outcomes show that both solutions, increasing φ2 deflates the boundary layer thickness of momentum, microrotation, and thermal. Physically, the thermal conductivity of the fluid (TCN) boosted up with higher φ2, and as a response, the heat transfer rate increases for the stable outcomes. Additionally, all published profiles asymptotically satisfied the conditions (10) which ultimately confirmed the results shown in Fig. 2 and 3.
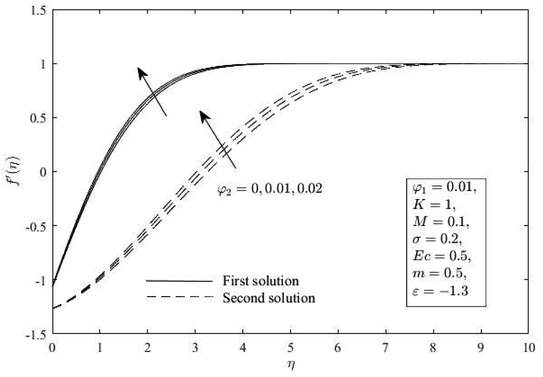 |
| | Fig. 4
f′(η) for various φ2. | |
 |
| | Fig. 5
h(η) for various φ2. | |
 |
| | Fig. 6
θ(η) for various φ2. | |
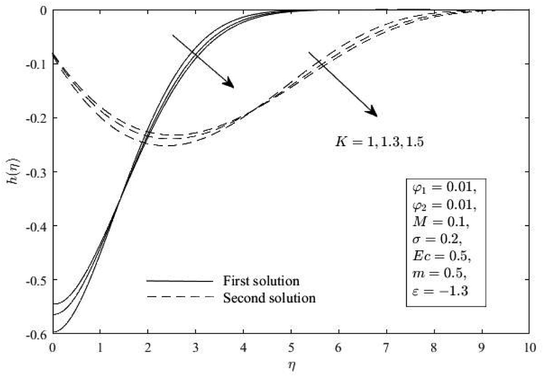
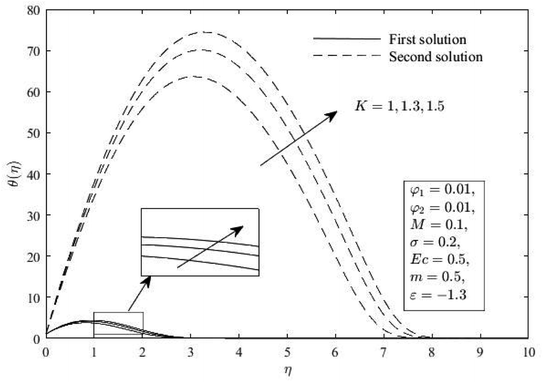
Fig. 7–11 show how the K affects Cf(Rex)1/2 and Nux(Rex)−1/2, f′(η), h(η) and θ(η). Comparing the presence of K (K = 1,2) to the exclusion of K (K = 0), or the lack of vortex viscosity, it is clear that the presence of K generates the Cf(Rex)1/2. Different outcomes, however, are shown for Nux(Rex)−1/2. The absence of the micropolar fluid (K = 0) results in an improvement over the presence of K (K = 1,2). This phenomenon shows that the increment of K causes a fluid flow to become more viscous in a vortex, which increases Cf(Rex)1/2 near the wall and slows Nux(Rex)−1/2. Additionally, both solutions' momentum and microrotation boundary layers became thicker because of the increment of K. For the thermal boundary layer thickness, the results are the opposite.
 |
| | Fig. 7
C
f(Rex)1/2 for K and ε. | |
 |
| | Fig. 8 Nux(Rex)−1/2 for K and ε. | |
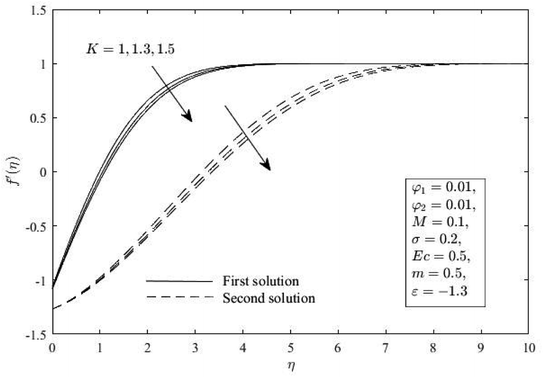 |
| | Fig. 9
f′(η) for various K. | |
 |
| | Fig. 10
h(η) for various K. | |
 |
| | Fig. 11
θ(η) for various K. | |
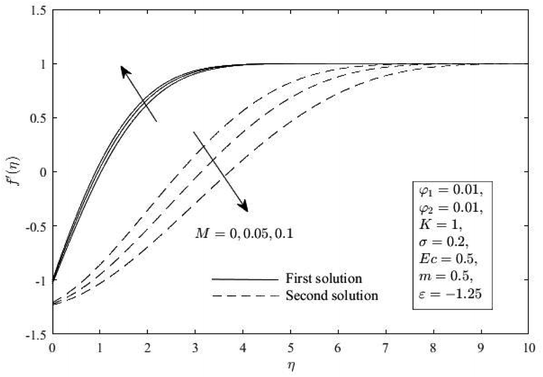
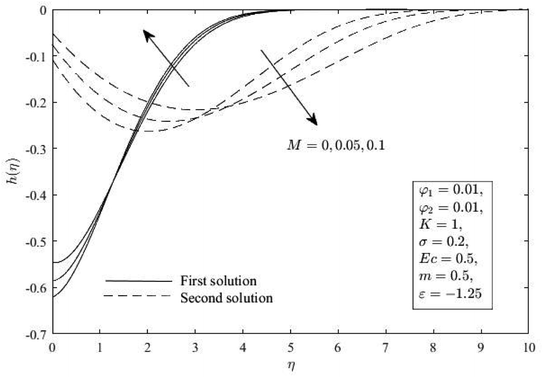
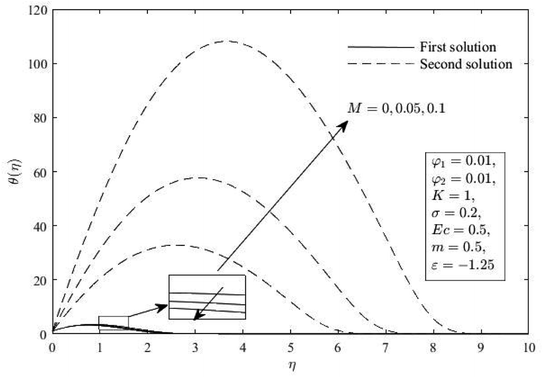
Next, Fig. 12 and 13 show the effect of M on Cf(Rex)1/2 and Nux(Rex)−1/2. These figures show that as M increases, Cf(Rex)1/2 increases, but Nux(Rex)−1/2 is reduced. This is because the magnetic field induces a resistance force on the flow, consequently retarding the momentum of the fluid and improving Cf(Rex)1/2. On the other side, f′(η), h(η) and θ(η) for various M are portrayed in Fig. 14–16. When M increases, the first solution's diminished momentum, microrotation, and thermal boundary layer thickness are noted, whereas the second solution's opposite observation is noted. This is because the Lorentzian magneto-hydrodynamic component in the momentum equation is a drag force which acts in the negative axial direction transverse to the line of application which is in the positive transverse direction. With greater M, the magnetic field strength also increases, which enhances the momentum and thermal boundary layer thickness.
 |
| | Fig. 12
C
f(Rex)1/2 for M and ε. | |
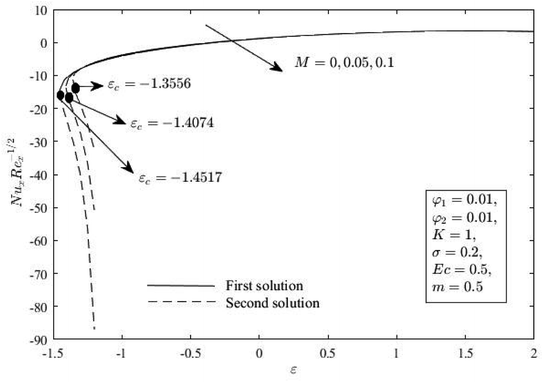 |
| | Fig. 13 Nux(Rex)−1/2 for M and ε. | |
 |
| | Fig. 14
f′(η) for various M. | |
 |
| | Fig. 15
h(η) for various M. | |
 |
| | Fig. 16
θ(η) for various M. | |
Fig. 17 illustrates the minimum eigenvalues γ plotted against different values of ε. The graph unravels that the first solution displays γ > 0, whilst the second solution displays γ < 0. As ε → εc, Fig. 8 shows that γ approaches zero for both similarity solutions, which confirms that γ equals zero when ε equals εc. Hence, out of the available solutions, only the first one remains stable.
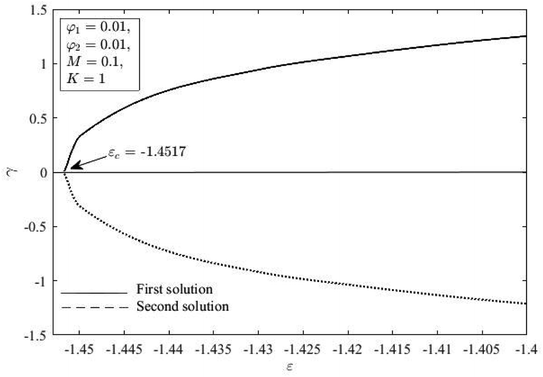 |
| | Fig. 17 Smallest eigenvalue γ against ε for K = 1, φ1 = φ2 = 0.1 and M = 0.1. | |
4. Conclusion
The MHD stagnation point flow of micropolar hybrid nanofluid with viscous dissipation via stretching/shrinking sheets was theoretically analyzed in this research. The problem at hand was successfully resolved with the aid of the Matlab bvp4c solver. The main takeaways are:
•Dual solutions are only available when ε < 0; however, only the first solution is stable.
•The increasing volume fraction φ2 in the micropolar nanofluid results in an enhancement in both Cf(Rex)1/2 and Nux(Rex)−1/2.
•The enlargement of material parameter K and MHD parameter M causes Cf(Rex)1/2 to be improved and the opposite for the Nux(Rex)−1/2.
•The domains of the similarity solutions decrease with an increase in φ2 and K, which therefore fastens the boundary layer separation. However, an increase in the value of M delays the boundary layer separation.
The findings of this study, limited to the chosen setup parameters, underscore the importance of considering that further improvements are needed to validate these conclusions in broader contexts. It is crucial to acknowledge that the current study should be extended to encompass various types of nanoparticles and base fluids, with a particular emphasis on enhancing the model for ternary hybrid nanofluids.
Data availability
The data will be available on request to the corresponding author.
Conflicts of interest
It is declared that we have no conflict of interest.
Acknowledgements
The authors extend their appreciation to the Deputyship for Research and Innovation, “Ministry of Education” in Saudi Arabia, for funding this research (IFKSUOR3-284-3).
References
- K. Hiemenz, Die Grenzchicht an einem in den gleichformingen Flussigkeitsstrom eingetauchten geraden Kreiszylinder, Dinglers Polytech. J., 1911, 326, 391–393 Search PubMed.
- A. C. Eringen, Theory of micropolar fluids, J. Math. Mech., 1966, 1–18 Search PubMed.
- S. K. Soid, A. Ishak and I. Pop, MHD stagnation-point flow over a stretching/shrinking sheet in a micropolar fluid with a slip boundary, Sains Malays., 2018, 47(11), 2907–2916 CrossRef CAS.
- N. S. Khashi’ie, N. Safwa, N. Md Arifin, R. Nazar, E. H. Hafidzuddin, N. Wahi and I. Pop, Mixed convective flow and heat transfer of a dual stratified micropolar fluid induced by a permeable stretching/shrinking sheet, Entropy, 2019, 21(12), 1162 CrossRef.
- S. R. Mishra, I. Khan, Q. M. Al-Mdallal and T. Asifa, Free convective micropolar fluid flow and heat transfer over a shrinking sheet with heat source, Case Stud. Therm. Eng., 2018, 11, 113–119 CrossRef.
- L. A. Lund, Z. Omar, I. Khan, B. Dumitru and K. S. Nisar, Triple solutions and stability analysis of micropolar fluid flow on an exponentially shrinking surface, Crystals, 2020, 10(4), 283 CrossRef CAS.
- R. I. Yahaya, N. Md Arifin, S. S. P. Mohamed Isa and M. M. Rashidi, Magnetohydrodynamics boundary layer flow of micropolar fluid over an exponentially shrinking sheet with thermal radiation: Triple solutions and stability analysis, Math. Methods Appl. Sci., 2021, 44(13), 10578–10608 CrossRef.
-
S. U. S. Choi, and J. A. Eastman, Enhancing Thermal Conductivity of Fluids with Nanoparticles, No. ANL/MSD/CP-84938; CONF-951135-29, Argonne National Lab.ANL, Argonne, IL United States, 1995 Search PubMed.
- N. H. Abd Rahman, N. Hathirah, N. Bachok and H. Rosali, MHD Stagnation-point Flow over a Stretching/Shrinking Sheet in Nanofluids, J. Adv. Res. Fluid Mech. Therm. Sci., 2019 Search PubMed.
- N. H. A. Norzawary, N. Bachok and F. M. Ali, Stagnation Point Flow over a Stretching/shrinking Sheet in a Carbon Nanotubes with Suction/Injection Effects, CFD Lett., 2020, 12(2), 106–114 Search PubMed.
- N. S. Wahid, N. Md Arifin, I. Pop, N. Bachok and M. E. H. Hafidzuddin, MHD stagnation-point flow of nanofluid due to a shrinking sheet with melting, viscous dissipation and Joule heating effects, Alexandria Eng. J., 2022, 61(12), 12661–12672 CrossRef.
- S. T. Hussain, S. Nadeem and R. Ul Haq., Model-based analysis of micropolar nanofluid flow over a stretching surface, Eur. Phys. J. Plus, 2014, 129, 1–10 CrossRef CAS.
- H. R. Patel, A. S. Mittal and R. R. Darji, MHD flow of micropolar nanofluid over a stretching/shrinking sheet considering radiation, Int. Commun. Heat Mass Transfer, 2019, 108, 104322 CrossRef CAS.
- L. A. Lund, Z. Omar, U. Khan, I. Khan, B. Dumitru and K. S. Nisar, Stability analysis and dual solutions of micropolar nanofluid over the inclined stretching/shrinking surface with convective boundary condition, Symmetry, 2020, 12(1), 74 CrossRef CAS.
- M. Atif Shahzada, M. Abbas, U. Rashid and H. Emadifar, Stagnation point flow of EMHD micropolar nanofluid with mixed convection and slip boundary, Complexity, 2021, 2021, 1–13 Search PubMed.
- D. Madhesh and S. Kalaiselvam, Experimental analysis of hybrid nanofluid as a coolant, Procedia Eng., 2014, 97, 1667–1675 CrossRef CAS.
- S. U. Devi and S. P. A. Devi, Heat transfer enhancement of cu−al2o3/water hybrid nanofluid flow over a stretching sheet, J. Niger. Soc. Math., 2017, 36(2), 419–433 Search PubMed.
- R. I. Yahaya, N. M. Arifin, R. Nazar and I. Pop, Flow and heat transfer past a permeable stretching/shrinking sheet in Cu− Al2O3/water hybrid nanofluid, Int. J. Numer. Methods Heat Fluid Flow, 2020, 30(3), 1197–1222 CrossRef.
- N. S. Anuar, N. Bachok and I. Pop, Influence of buoyancy force on Ag-MgO/water hybrid nanofluid flow in an inclined permeable stretching/shrinking sheet, Int. Commun. Heat Mass Transfer, 2021, 123, 105236 CrossRef CAS.
- N. S. Wahid, N. Md Arifin, N. S. Khashi’ie and I. Pop, Mixed convection MHD hybrid nanofluid over a shrinking permeable inclined plate with thermal radiation effect, Alexandria Eng. J., 2023, 66, 769–783 CrossRef.
- M. Sarfraz, M. Khan and Y. Muhammad, Dynamic of water conveying iron oxide and graphene nanoparticles subject to stretching/spiraling surface: An asymptotic approach, Ain Shams Eng. J., 2023, 14, 102021 CrossRef.
- M. Yasir, M. Sarfraz, M. Khan, A. K. Alzahrani and M. Z. Ullah, Estimation of dual branch solutions for Homann flow of hybrid nanofluid towards biaxial shrinking surface, J. Pet. Sci. Eng., 2022, 218, 110990 CrossRef CAS.
- M. Sarfraz and M. Khan, Thermodynamic irreversibility analysis of water conveying argentum and titania nanoparticles subject to inclined stretching surface, Phys. Scr., 2023, 98, 025205 CrossRef.
- M. Sarfraz, Y. Muhammad and M. Khan, Multiple solutions for non-linear radiative mixed convective hybrid nanofluid flow over an exponentially shrinking surface, Nature, 2023, 13, 3443 CAS.
- M. Subhani and S. Nadeem, Numerical analysis of micropolar hybrid nanofluid, Appl. Nanosci., 2019, 9(4), 447–459 CrossRef CAS.
- F. Kamal, K. Zaimi, A. Ishak and I. Pop, Stability analysis of MHD stagnation-point flow towards a permeable stretching/shrinking sheet in a nanofluid with chemical reactions effect, Sains Malays., 2019, 48(1), 243–250 CrossRef CAS.
- A. Yasmin, K. Ali and M. Ashraf, Study of heat and mass transfer in MHD flow of micropolar fluid over a curved stretching sheet, Sci. Rep., 2020, 10(1), 4581 CrossRef CAS PubMed.
- A. Ishak, Y. Y. Lok and I. Pop, Stagnation-point flow over a shrinking sheet in a micropolar fluid, Chem. Eng. Commun., 2010, 197(11), 1417–1427 CrossRef CAS.
- L. A. Lund, Z. Omar, I. Khan, J. Raza, M. El-Sayed Sherif and H. S. Asiful, "Magnetohydrodynamic (MHD) flow of micropolar fluid with effects of viscous dissipation and joule heating over an exponential shrinking sheet: triple solutions and stability analysis, Symmetry, 2020, 12(1), 142 CrossRef CAS.
- N. S. Anuar and N. Bachok, Double solutions and stability analysis of micropolar hybrid nanofluid with thermal radiation impact on unsteady stagnation point flow, Mathematics, 2021, 9(3), 276 CrossRef.
- G. Ahmadi, Self-similar solution of imcompressible micropolar boundary layer flow over a semi-infinite plate, Int. J. Eng. Sci., 1976, 14(7), 639–646 CrossRef.
- S. Ko Jena and M. N. Mathur, Similarity solutions for laminar free convection flow of a thermomicropolar fluid past a non-isothermal vertical flat plate, Int. J. Eng. Sci., 1981, 19(11), 1431–1439 CrossRef CAS.
- G. S. Guram and A. C. Smith, Stagnation flows of micropolar fluids with strong and weak interactions, Comput. Math. Appl., 1980, 6(2), 213–233 CrossRef.
- J. Peddieson Jr, An application of the micropolar fluid model to the calculation of a turbulent shear flow, Int. J. Eng. Sci., 1972, 10(1), 23–32 CrossRef.
- N. S. Anuar, N. Bachok, N. M. Arifin and H. Rosali, MHD flow past a nonlinear stretching/shrinking sheet in carbon nanotubes: Stability analysis, Chin. J. Phys., 2020, 65, 436–446 CrossRef CAS.
- N. S. Anuar, N. Bachok, M. Turkyilmazoglu, N. M. Arifin and H. Rosali, Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes, Alexandria Eng. J., 2020, 59(1), 497–507 CrossRef.
- A. Banerjee, K. Bhattacharyya, S. K. Mahato and A. J. Chamkha, Influence of various shapes of nanoparticles on unsteady stagnation-point flow of Cu-H2O nanofluid on a flat surface in a porous medium: A stability analysis, Chin. Phys. B, 2022, 31(4), 044701 CrossRef.
- P. D. Weidman, D. G. Kubitschek and A. M. J. Davis, The effect of transpiration on self-similar boundary layer flow over moving surfaces, Int. J. Eng. Sci., 2006, 44(11–12), 730–737 CrossRef CAS.
- S. D. Harris, D. B. Ingham and I. Pop, Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip, Transp. Porous Media, 2009, 77, 267–285 CrossRef.
- H. F. Oztop and E. Abu-Nada, Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids, Int. J. Heat Fluid Flow, 2008, 29(5), 1326–1336 CrossRef.
- N. A. Zainal, R. Nazar, K. Naganthran and I. Pop, Unsteady stagnation point flow of hybrid nanofluid past a convectively heated stretching/shrinking sheet with velocity slip, Mathematics, 2020, 8(10), 1649 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article c,
Muhammad Khairul
Anuar Mohamed
d,
Umair
Khan
c,
Muhammad Khairul
Anuar Mohamed
d,
Umair
Khan
 *cef,
El-Sayed M.
Sherif
*cef,
El-Sayed M.
Sherif
 g and
Ioan
Pop
h
g and
Ioan
Pop
h
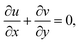
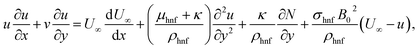
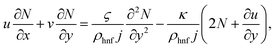
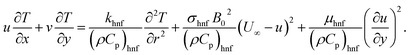
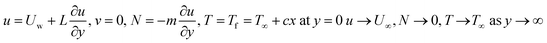

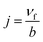 is the density of micro inertial and
is the density of micro inertial and 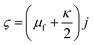 is the spin gradient viscosity.31 Additionally, m is a constant between [0,1]. When m = 0, that also signifies that N = 0; the microelements close to the surface cannot spin, which represents concentrated particle flows32 or cited in Smith and Guram,33 due to the concentrated microelements.
is the spin gradient viscosity.31 Additionally, m is a constant between [0,1]. When m = 0, that also signifies that N = 0; the microelements close to the surface cannot spin, which represents concentrated particle flows32 or cited in Smith and Guram,33 due to the concentrated microelements.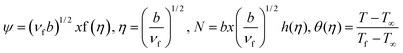
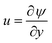 and
and 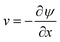 which satisfy eqn (1), then eqn (1)–(4) and conditions (5) are written as follows:
which satisfy eqn (1), then eqn (1)–(4) and conditions (5) are written as follows: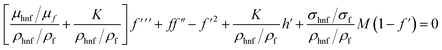
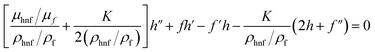
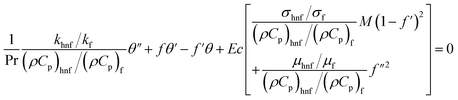
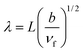 is the slip parameter and
is the slip parameter and 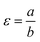 is the velocity ratio parameter such that ε < 0 is for shrinking conditions and ε > 0 for stretching conditions.
is the velocity ratio parameter such that ε < 0 is for shrinking conditions and ε > 0 for stretching conditions.
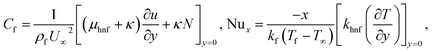
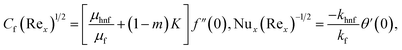
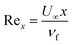 is the local Reynolds number.
is the local Reynolds number.
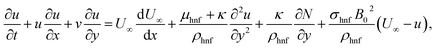
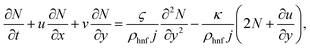
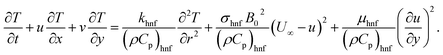
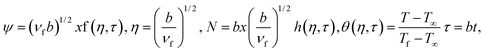
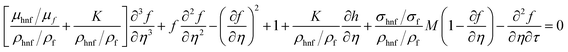
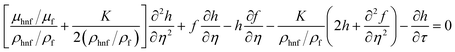
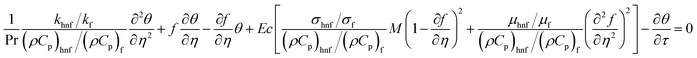
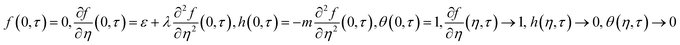
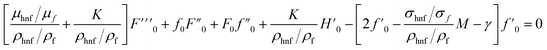
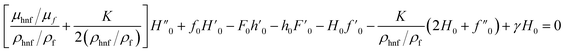
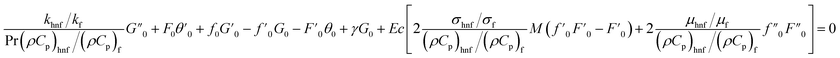
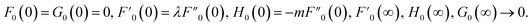
 , and introducing a new condition of
, and introducing a new condition of  .
.