Nonvolatile electro-mechanical coupling in two-dimensional lattices

Abstract

Electro-mechanical coupling is of great interest for applications in sensors, actuators and energy harvesters. While the control of electrical charge by mechanical force has been studied extensively, reverse coupling is rarely explored, especially in two-dimensional (2D) lattices. Herein, we propose a novel mechanism for electro-mechanical coupling that realizes the electric field switching of the dimensions of a 2D lattice in a reversible and nonvolatile fashion, through the mediated strength of interlayer interactions in ferroelectric bilayer systems. Based on first-principles calculations, the validity of this mechanism is demonstrated in a series of real bilayer materials, i.e., MoS₂/ReIrGe₂S₆, Sb/In₂Se₃ and bilayer In₂Se₃. The interface differences due to polarization play a crucial role in realizing such nonvolatile electro-mechanical coupling, and the underlying physical origin is discussed. These explored phenomena and insights offer a novel avenue for the highly desired nonvolatile electric field control of mechanical strain.

---

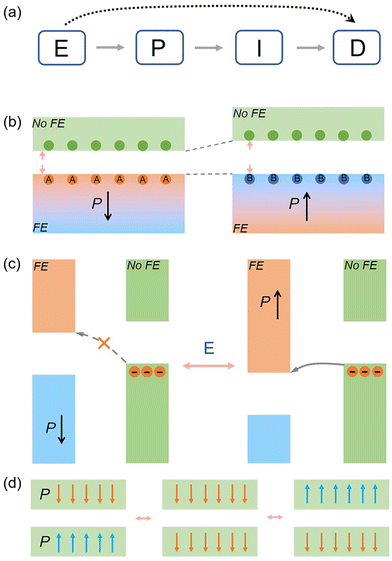
New concepts

We propose a novel mechanism for electro-mechanical coupling that realizes the electric field switching of the dimensions of a 2D lattice in a reversible and nonvolatile fashion. This mechanism is based on the paradigm of mediating the strength of interlayer interactions in 2D FE bilayers. We call this design principle EPID: the direction of electric polarization (P) can be converted by an external electric field (E), which can potentially be employed to determine the strength of interlayer interactions (I). Moreover, based on first-principles calculations, we further demonstrate the validity of this mechanism in a series of real 2D bilayer materials. We unveil that the differences in the interface from polarization play an essential role in forming such nonvolatile electro-mechanical coupling. The underlying physics is also discussed. Our work enriches the research on electro-mechanical coupling in a 2D lattice and provides a novel method for future devices based on electro-mechanical coupling.

Introduction

Electro-mechanical coupling, a fundamental phenomenon in condensed matter physics and material science, has been intensively studied owing to its novel physics and potential applications in sensors, actuators and energy harvesters.^1–6 To date, two kinds of electro-mechanical coupling have been discovered. In type-I coupling, an electrical charge is produced when mechanical force is applied to a material. The most well-known example of this coupling is piezoelectricity, which was discovered as early as 1880 by Curie brothers.^7–9 In type-II coupling, a mechanical strain is developed upon the application of electrical bias. In this case, the electrostriction effect is a typical example.^10–13 Currently, the research in this field has been mainly focused on type-I coupling,^14–19 while type-II coupling is rather scarce, although it is promising for novel device applications.²⁰

The emergence of two-dimensional (2D) materials provides an unprecedented opportunity for exploring electro-mechanical coupling by considering their rich structural and electronic properties.^21,22 For example, the piezoelectric effects with diverse mechanisms have been identified in several 2D materials, such as MoS₂, MoSSe and In₂Se₃.^23–26 Nonetheless, to date, 2D systems with robust type-II electro-mechanical coupling have not yet been reported. Recently, ferroelectricity was discovered in 2D materials. For example, In₂Se₃,²⁷ bilayer BN,²⁸ AgBiP₂Se₆²⁹ and SnS/SnSe³⁰ were theoretically predicted to be 2D ferroelectric (FE) materials.^31,32 Moreover, CuInP₂S₆,^33,34 SnTe³⁵ and In₂Se₃^36,37 have been shown to have FE properties in experiments. Notably, most type-II electro-mechanical coupling cases in conventional three-dimensional systems are based on the persistent external electric field and are volatile and energy-consuming.^38,39 These exciting discoveries have motivated us to explore the possibility of the existence of nonvolatile type-II electro-mechanical coupling in 2D FE systems.

In this work, we report the discovery of a novel mechanism of type-II electro-mechanical coupling that realizes the electric field switching of the dimensions of a 2D lattice in a reversible and nonvolatile fashion. This mechanism is based on the paradigm of the mediated strength of interlayer interactions in 2D FE bilayer systems. Based on first-principles calculations, we demonstrate the validity of this mechanism in a series of real 2D bilayer materials, e.g., MoS₂/ReIrGe₂S₆, Sb/In₂Se₃ and bilayer In₂Se₃. We unveil that the differences in the interface from polarization play an essential role in forming such nonvolatile electro-mechanical coupling. The underlying physics is also discussed. Our results greatly enrich the research on electro-mechanical coupling in the 2D lattice.

Results and discussion

EPID mechanism

The proposed mechanism is based on 2D bilayer systems containing FE materials with out-of-plane electric polarization. In such systems, the direction of electric polarization (P) can be converted by an external electric field (E), which can potentially be employed to determine the strength of the interlayer interaction (I). The change in I would affect the distance (D) of the system, thus resulting in the intriguing electro-mechanical coupling in the 2D lattice. We call this design principle EPID (electric field – electric polarization – interlayer interaction – distance) mechanism. It is worth emphasizing that different from the previous works on type-II electro-mechanical coupling wherein the persistent external E is required,^38,39 the resultant electric field switching of distances is ferroelectrically controllable and thus occurs in a nonvolatile fashion. For realizing the EPID mechanism, the 2D bilayers should be composed of one FE layer and one ordinary layer, or two FE layers. Depending on the constituent layers, the EPID mechanism can be classified into three types:

(1) In the EPID-I case, as shown in Fig. 1b, the bilayer contains one FE layer and one ordinary layer. For the FE layer, the two terminated surfaces are significantly different. When the P is upward, the A atomic surface is in contact with the ordinary layer, and under the FE switching, the B atomic surface is in contact. This quite naturally results in the nonvolatile electric field switching of its distance.

Fig. 1 (a) The EPID mechanism. (b)–(d) Three mechanisms for realizing the electric field switching of the distances of the 2D lattice in a reversible and nonvolatile fashion. “FE” and “No FE” represent the ferroelectric layer and ordinary layer, respectively.

(2) In the EPID-II case, as shown in Fig. 1c, the bilayer also contains one FE layer and one ordinary layer. However, unlike the EPID-I case, the two terminated surfaces of the FE layer are identical. Assuming that there are two different band offsets when the two surfaces of the FE layer are in contact with the ordinary layer (i.e., one is a type-II band alignment, and the other is a type-III band alignment), a significant difference in the charge transfer between the two layers can be expected under FE switching. This would change the interlayer interaction and the overall material thickness, giving rise to the nonvolatile electric field switching of its distance.

(3) In the EPID-III case, as shown in Fig. 1d, the structure contains two FE layers. In this case, unlike the EPID-I and EPID-II, there is no difference in the interface and band alignment for the two different polarization configurations. However, due to the different dipole–dipole interactions manipulated by FE switching, different interlayer interactions can occur, thus leading to the nonvolatile electric field switching of its distance.

EPID-I: differences in terminated surfaces

After establishing the three types of EPID mechanisms, we will next discuss their realization in real materials. For the EPID-I case, we selected the single-layered (SL) ReIrGe₂S₆ as the constituent FE layer. Fig. S1 (ESI†) shows the crystal structure of SL ReIrGe₂S₆. The terminated surfaces are formed by S and Ge atoms, respectively. Although there will be some Re and Ir atoms in the terminal surface in experiments, Ge and S atoms that cause interface differences are dominant. Such a structure gives rise to an out-of-plane electric polarization of 4.16 × 10⁻³ C m⁻². Because the two Ge atomic layers can be displaced up and down, the electric polarization can be reversed, giving rise to the FE behavior of SL ReIrGe₂S₆. Intriguingly, along with the FE switching, the terminated surface of SL ReIrGe₂S₆ would also be reversed, which provides the possibility for realizing the EPID-I mechanism upon contact with another ordinary layer. Here, we selected SL MoS₂ as the ordinary layer and used a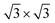 supercell MoS₂ to match a 1 × 1 unit cell ReIrGe₂S₆. The lattice mismatch between them is only about 3%, indicating the high experimental feasibility.

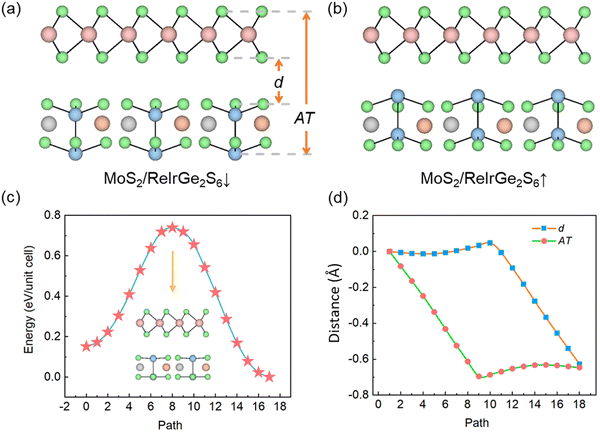
Given the structure of ReIrGe₂S₆, we constructed two types of MoS₂/ReIrGe₂S₆ bilayers: one with electric polarization pointing away from the interface (P↓), and the other with electric polarization pointing to the interface (P↑). The most stable crystal structures of P↓ and P↑ are displayed in Fig. 2a and b, which can be considered as two FE states of the MoS₂/ReIrGe₂S₆ bilayer. In the P↓ configuration, the terminated surfaces from MoS₂ and ReIrGe₂S₆ at the interface are both formed by S atoms. Due to the repulsion of these two S atomic layers, there is a large interlayer distance (d) of 3.208 Å and a large atomic thickness (AT) of 9.738 Å. Unlike the P↓ configuration, in the P↑ configuration, the terminated surfaces from MoS₂ and ReIrGe₂S₆ at the interface are formed by S and Ge atoms, respectively. Considering their different electronegativities, the repulsion between S and Ge atomic layers would be much smaller than that between S and S atomic layers, yielding significantly smaller d = 2.581 Å and AT = 9.104 Å for the P↑ configuration. The differences in d and AT for these two configurations are 0.627 Å and 0.634 Å respectively. Assuming that these two configurations can be reversed under FE switching, the nonvolatile electric field switching of dimensions was realized in MoS₂/ReIrGe₂S₆. We wish to point out that the ratio of electro-mechanical coupling is about 19.5%/24.3% (the ratio of electro-mechanical coupling is defined as (d_state-I/d_state-II−1) × 100%, where d_state-I and d_state-II are the interlayer distances for state-I and state-II, respectively), which is compared with conventional three-dimensional materials of ceramic lead lanthanum zirconate titanate.⁴⁰ Such a large electro-mechanical coupling ratio is rarely reported in 2D systems.⁴¹

Fig. 2 Crystal structures of the MoS₂/ReIrGe₂S₆ bilayer in the P↓ (a) and P↑ (b) configurations. Green, blue, gray, orange, and red spheres represent S, Ge, Re, Ir, and Mo atoms, respectively. (c) Minimum energy pathway of FE switching as a function of step number within the Climbing Image Nudged Elastic Band (CI-NEB) for the MoS₂/ReIrGe₂S₆ bilayer. (d) Variation of d and AT as a function of step number within CI-NEB for the MoS₂/ReIrGe₂S₆ bilayer.

To estimate the feasibility of ferroelectricity in the MoS₂/ReIrGe₂S₆ bilayer, we investigated its FE transformation process. Fig. 2c presents the minimum energy pathway of FE switching as a function of step number within CI-NEB for the MoS₂/ReIrGe₂S₆ bilayer. The FE switching barrier from P↑ (P↓) to P↓ (P↑) was calculated to be 0.74 (0.59) eV per unit cell. These values are comparable with those of GaTeCl (0.754 eV per unit cell), vacancy-doped CrI₃ (0.65 eV per unit cell) and SbN (0.604 eV per unit cell).^42–44 This indicates the feasibility of the ferroelectricity, as well as the nonvolatile electric field switching of dimensions, in MoS₂/ReIrGe₂S₆. Fig. 2d summarizes the variation of d and AT as a function of step number within CI-NEB. AT shows a trend of decreasing first and then increasing, indicating a nonlinear relation with the step number. The band structures of the P↑ and P↓ configurations are shown in Fig. S5 (ESI†). Both are semiconductors, indicating that ferroelectric switching does not essentially change the semiconducting properties of MoS₂/ReIrGe₂S₆. This is different from the case of EPID-II, as we will discuss in the following. This mechanism can be extended to all ferroelectric materials, wherein the polarization switching can alter the type of interfacial atoms, such as NbN, SiN, and so on.

EPID-II: differences in band offsets

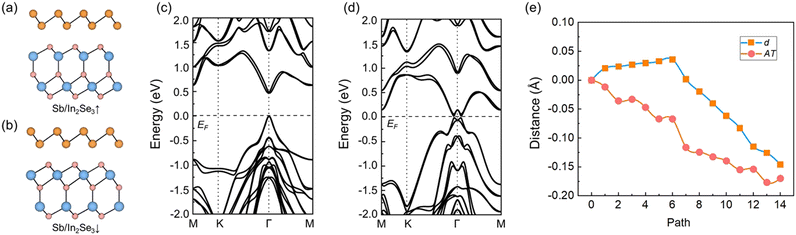
For the EPID-II case, we selected SL In₂Se₃ as the constituent FE layer. As shown in Fig. 3(a) and (b), different from SL ReIrGe₂S₆, the two terminated surfaces of SL In₂Se₃ are both formed by Se atoms. However, the asymmetric positions of Se atoms in the middle layer result in different coordination environments of In atoms and thus break the centrosymmetry, leading to an out-of-plane electric polarization of 2.31 × 10⁻³ C m⁻². Due to the existence of the large electric polarization, the work functions of the two surfaces of SL In₂Se₃ are significantly different, which were calculated to be 4.2 and 6.5 eV, respectively. Such a large difference in work function is beneficial for realizing the two different types of band alignments on the two surfaces. In this regard, the ordinary layer should harbor a work function close to one surface of SL In₂Se₃. Here, we selected SL Sb, exhibiting a work function of 4.6 eV, as the ordinary layer. The Sb monolayer was realized in recent experiments.⁴⁵ Because of the sp³ hybridization, it shows the buckled honeycomb lattice. The Sb/In₂Se₃ bilayer was constructed by using use a unit cell Sb to match a unit cell In₂Se₃. The lattice mismatch between them is within 2%, which suggests its experimental feasibility.⁴⁶

Fig. 3 (a) and (b) Crystal structures of the Sb/In₂Se₃ bilayer under P↑ and P↓ configurations. Orange, blue, and red spheres represent Sb, In, and Se atoms, respectively. (c) and (d) Band structures of the Sb/In₂Se₃ bilayer under P↑ and P↓ configurations. (e) The variation of d and AT as a function of step number within the CI-NEB for the Sb/In₂Se₃ bilayer.

Similar to MoS₂/ReIrGe₂S₆, we also constructed two types of Sb/In₂Se₃ bilayer: one with electric polarization pointing away from the interface (P↓), and the other with electric polarization pointing to the interface (P↑). Fig. 3a and b display the most stable crystal structures of P↑ and P↓ configurations, which are the two FE states of the Sb/In₂S₃ bilayer. The corresponding band structures of these two configurations are shown in Fig. 3c and d. For the P↑ configuration, the CBM from the In₂Se₃ layer is located above the Fermi level, while the VBM from the Sb layer lies below the Fermi level, giving rise to a direct band gap of 1.41 eV at the Γ point. A type-II band alignment forms between the band edges of SL In₂Se₃ and Sb in the P↑ configuration. For the P↓ configuration, as illustrated in Fig. 3d, the CBM from the In₂Se₃ layer shifts below the Fermi level, while the VBM from the Sb layer shifts above the Fermi level, indicating a type-III band alignment for the band edges of In₂Se₃ and Sb layers.

Due to the different band alignments in the P↑ and P↓ configurations of the Sb/In₂Se₃ bilayer, the charge transfers at the interfaces would also be different for the two configurations. Fig. S6 (ESI†) shows the charge density differences between the two layers for the Sb/In₂Se₃ bilayer. For the P↑ configuration, the charge densities are mainly localized in the space between the two layers, in good agreement with the type-II band alignment. For the P↓ configuration, significant electron transfer occurs between Sb and In₂S₃ layers, as shown in Fig. S3 (ESI†). Therefore, with respect to the P↑ configuration, a stronger interlayer interaction is achieved in the P↓ configuration. According to the EPID mechanism, this would result in different d and AT for these two configurations. Our calculations show that the d and AT are 2.935 (2.789) Å and 11.485 (11.315) Å, respectively, for P↑ (P↓) configurations. The differences in d and AT for these two configurations are 0.146 Å and 0.17 Å respectively. The ratio of electro-mechanical coupling is about 5.2%/5.0%. To estimate the feasibility of ferroelectricity in Sb/In₂Se₃, we investigate its FE transformation process. As shown Fig. S7 and S8 (ESI†), the transitions between P↓ and P↑ occur through the concerted motion of the lower three Se–In–Se layers, as illustrated in Fig. S7 (ESI†). In detail, the transition between P↓ and the paraelectric state is realized by the left shifting of the lower In–Se layer and the upper-inclined shifting of the inner Se layer, and the transition between the paraelectric state and P↑ phases is caused by the right shifting of the lower In–Se layer and the upper-inclined shifting of the inner Se layer. The lattice parameters hardly change during the transformation process. The FE switching barrier from P↑ (P↓) to P↓ (P↑) is calculated to be 0.295 (0.355) eV per unit cell, which is comparable with that of CrB₂ (0.363 eV per unit cell), and smaller than that of Sc₂CO₂ (0.52 eV per unit cell), vacancy-doped CrI₃ (0.65 eV per unit cell) and GaTeCl (0.754 eV per unit cell).^42,43,47,48 This indicates the feasibility of the ferroelectricity, as well as the nonvolatile electric field switching of dimensions, in Sb/In₂Se₃. The variations of d and AT as a function of step number within CI-NEB for the Sb/In₂Se₃ bilayer are displayed in Fig. 3e. Different from the case of MoS₂/ReIrGe₂S₆, AT showed a roughly linear relation with the step number. We select another candidate, monolayer PdTe₂, to further verify this mechanism. As shown in Fig. S9 (ESI†), the two polarization configurations of PdTe₂/In₂Se₃ exhibit different band alignments according to our mechanism. By reversing the ferroelectric polarization direction of In₂Se₃, we could still achieve the switching of the interlayer distance. We can extend this mechanism to similar systems, such as Bi/In₂Se₃, MnSe/In₂S₃, PtTe₂/In₂Se₃, and so on.

EPID-III: differences in dipole–dipole interactions

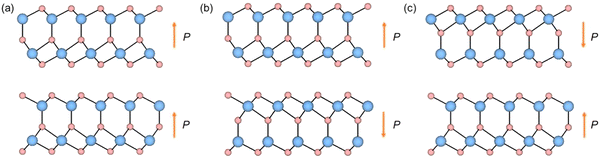
We have used the bilayer In₂Se₃ as an example to discuss the realization of the EPID-III mechanism. Considering the alignment of electric polarizations in the constituent layers, we constructed three types of bilayer In₂Se₃: one with two electric polarizations pointing along the +z direction (P↑↑), one with electric polarization pointing away from the interface (P↑↓) and another with electric polarization pointing to the interface (P↓↑), as shown in Fig. 4. As expected, due to the different dipole–dipole interactions, the AT are different for these three configurations. The AT were calculated to be 17.426 Å, 17.389 Å and 17.475 Å, respectively, for P↑↑, P↑↓ and P↓↑ configurations. The ratio of electro-mechanical coupling is about 1.3% or 3.2%. As these three configurations can be reversed under FE switching, quite naturally, the nonvolatile electric field switching of dimensions is realized in bilayer In₂Se₃. The ferroelectric transition between P↓ and P↑ in In₂Se₃ is the same as EPID-II, as shown in Fig. S10 (ESI†). The lattice parameters also hardly change during the transformation process. The results produced by this mechanism are general in two-dimensional ferroelectric materials exhibiting z-direction polarization, such as AgBiP₂S₆, CuCrP₂Se₆, and so on.

Fig. 4 Crystal structures of bilayer In₂Se₃ under different polarization configurations. (a) Two electric polarizations point along the +z direction (P↑↑). (b) Two electric polarizations point away from the interface (P↑↓). (c) Two electric polarizations point to the interface (P↓↑). Blue and red spheres represent In and Se atoms, respectively.

Discussion

For the experimental realizations of these heterobilayer systems, the most used fabrication is by a stepwise mechanical transfer of specific 2D layers onto a substrate, i.e., by the top-down manipulation of individual nanosheets one by one.⁴⁹ It should be noted that in the In₂Se₃ system, the ferroelectric inversion was experimentally realized under the external electric field (7 V/30 nm). For the corresponding heterobilayers, the switching of the ferroelectricity might be achieved under a comparable external electric field.

Conclusions

We have identified a novel mechanism for realizing the electric field switching of the dimensions of a 2D lattice in a reversible and nonvolatile fashion. This mechanism is through the mediation of the strength of interlayer interactions in 2D FE bilayer systems. Using first-principles calculations, we validated this mechanism in a series of real 2D bilayer materials, e.g., MoS₂/ReIrGe₂S₆, Sb/In₂Se₃, and bilayer In₂Se₃. The underlying physics is discussed in detail. Our work provides a new direction and method for electro-mechanical coupling in the 2D lattice.

Methods

The first-principles calculations

All calculations based on density functional theory (DFT) were performed using the Vienna ab initio Simulation Package (VASP).⁵⁰ The exchange–correlation interaction was treated by the generalized gradient approximation (GGA) parametrized by Perdew, Burke, and Ernzerhof (PBE). The ion-electron interaction was treated by the projector-augmented wave method (PAW).^51,52 The Monkhorst–Pack k-mesh was set to 9 × 9 × 1. The kinetic cutoff energy was set to 550 eV. All structures were fully relaxed until the force on each atom was less than 0.01 eV Å⁻¹. The electronic iteration convergence criterion was set to 1 × 10⁻⁵ eV. To avoid spurious interactions between periodic images, a vacuum space of at least 15 Å was introduced. The DFT-D3 method was employed for treating van der Waals (vdW) interactions in all calculations.⁵³ The DFT-D2 and PBEsol methods were also used to calculate the band structures, which gave roughly similar band offsets. The ferroelectric transition pathway and energy barrier were calculated based on the CI-NEB method.⁵⁴ Dipole moment correction was employed in all the calculations.⁵⁵

Author contributions

X.X. conceived the idea of the project and run all simulations with inputs from Y.M and Y.D. X.X., T.Z., Y.M., B.H., and Y.D. analyzed the data. All authors discussed the results and contributed to the writing of the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 12274261 and 12074217), Shandong Provincial Science Foundation for Excellent Young Scholars (No. ZR2020YQ04), Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) (No. 2019JZZY010302), Shandong Provincial QingChuang Technology Support Plan (No. 2021KJ002), and Taishan Young Scholar Program of Shandong Province.

References

1. Y. E. Pak, Circular Inclusion Problem in Antiplane Piezoelectricity, Int. J. Fract., 1992, 54, 79.
2. K. Uchino, Piezoelectric Actuators and Ultrasonic Motors, Kluwer Academic, Boston, 1996.
3. M. Kamlah and C. Tsakmakis, Phenomenological Modeling of the Non-Linear Electro-Mechanical Coupling in Ferroelectrics, Int. J. Solids Struct., 1999, 36, 669.
4. Z. L. Wang and J. Song, Piezoelectric Nanogenerators Based on Zinc Oxide Nanowire Arrays, Science, 2006, 312, 242.
5. X. Wang, J. Song, J. Liu and Z. L. Wang, Direct-Current Nanogenerator Driven by Ultrasonic Waves, Science, 2007, 316, 102.
6. A. Pramanick, D. Damjanovic, J. E. Daniels, J. C. Nino and J. L. Jones, Origins of Electro-Mechanical Coupling in Polycrystalline Ferroelectrics during Subcoercive Electrical Loading, J. Am. Ceram. Soc., 2011, 94, 293.
7. J. F. Nye, Physical Properties of Crystals, Oxford U. P., Oxford, England, 1957, Chap. 10.
8. R. M. Martin, Piezoelectricity, Phys. Rev. B, 1972, 5, 1607.
9. A. K. Tagantsev, Piezoelectricity and Flexoelectricity in Crystalline Dielectrics, Phys. Rev. B, 1986, 34, 5883.
10. H. F. Kay, Electrostriction, Rep. Prog. Phys., 1955, 18, 230.
11. J. Grindlay, Electrostriction, Phys. Rev., 1967, 160, 698.
12. P. Prior and B. J. Roth, Electrostriction of Anisotropic Tissue, Phys. Rev. E, 2007, 75, 021903.
13. V. Sundar and R. E. Newnham, Electrostriction and Polarization, Ferroelectrics, 1992, 135, 431.
14. Z. Liu, L. Wang, X. Yu, J. Zhang, R. Yang, X. Zhang, Y. Ji, M. Wu, L. Deng, L. Li and Z. Wang, Piezoelectric-Effect-Enhanced Full-Spectrum Photoelectrocatalysis in p–n Heterojunction, Adv. Funct. Mater., 2019, 29, 1807279.
15. S. Zhang, Z. Liu, M. Ruan, Z. Guo, E. Lei, W. Zhao, D. Zhao, X. Wu and D. Chen, Enhanced Piezoelectric-Effect-Assisted Photoelectrochemical Performance in ZnO Modified with Dual Cocatalysts, Appl. Catal., B, 2020, 262, 118279.
16. Y. Jiang, M. Li, Y. Mi, L. Guo, W. Fang, X. Zeng, T. Zhou and Y. Liu, The Influence of Piezoelectric Effect on The Heterogeneous Photocatalytic Hydrogen Production of Strontium Titanate Nanoparticles, Nano Energy, 2021, 85, 105949.
17. M. Fattouhi, F. García-Sánchez, R. Yanes, V. Raposo, E. Martínez and L. Lopez-Diaz, Electric Field Control of the Skyrmion Hall Effect in Piezoelectric-Magnetic Devices, Phys. Rev. Appl, 2021, 16, 044035.
18. M. Chazono, H. Watanabe and Y. Yanase, Superconducting Piezoelectric Effect, Phys. Rev. B, 2022, 105, 024509.
19. R. Peng and J. Liu, Topological Piezoelectric Response in Moiré Graphene Systems, Phys. Rev. Res., 2022, 4, L032006.
20. J. Yu and P.-E. Janolin, Defining “Giant” Electrostriction, J. Appl. Phys., 2022, 131, 170701.
21. M.-B. Rubén, G.-N. Cristina, G.-H. Julio and Z. Félix, 2D Materials: to Graphene and Beyond, Nanoscale, 2011, 3, 20.
22. A. Gupta, T. Sakthivel and S. Seal, Recent Development in 2D Materials beyond Graphene, Prog. Mater. Sci., 2015, 73, 44.
23. R. Hinchet, U. Khan, C. Falconi and S.-W. Kim, Piezoelectric Properties in Two-Dimensional Materials: Simulations and Experiments, Mater. Today, 2018, 21, 611.
24. M. Dai, Z. Wang, F. Wang, Y. Qiu, J. Zhang, C.-Y. Xu, T. Zhai, W. Cao, Y. Fu, D. Jia, Y. Zhou and P.-A. Hu, Two-Dimensional van der Waals Materials with Aligned In-Plane Polarization and Large Piezoelectric Effect for Self-Powered Piezoelectric Sensors, Nano Lett., 2019, 19, 5410.
25. M. Dai, W. Zheng, X. Zhang, S. Wang, J. Lin, K. Li, Y. Hu, E. Sun, J. Zhang, Y. Qiu, Y. Fu, W. Cao and P.-A. Hu, Enhanced Piezoelectric Effect Derived from Grain Boundary in MoS₂ Monolayers, Nano Lett., 2020, 20, 201.
26. P. C. Sherrell, M. Fronzi, N. A. Shepelin, A. Corletto, D. A. Winkler, M. Ford, J. G. Shapter and A. V. Ellis, A Bright Future for Engineering Piezoelectric 2D Crystals, Chem. Soc. Rev., 2022, 51, 650.
27. W. Ding, J. Zhu, Z. Wang, Y. Gao, D. Xiao, Y. Gu, Z. Zhang and W. Zhu, Prediction of Intrinsic Two-Dimensional Ferroelectrics in In₂Se₃ and Other III₂-VI₃ van der Waals Materials, Nat. Commun., 2017, 8, 14956.
28. L. Li and M. Wu, Binary Compound Bilayer and Multilayer with Vertical Polarizations: Two-Dimensional Ferroelectrics, Multiferroics, and Nanogenerators, ACS Nano, 2017, 11, 6382.
29. B. Xu, H. Xiang, Y. Xia, K. Jiang, X. Wan, J. He, J. Yin and Z. Liu, Monolayer AgBiP₂Se₆: An Atomically Thin Ferroelectric Semiconductor with Out-Plane Polarization, Nanoscale, 2017, 9, 8427.
30. M. Wu and X. C. Zeng, Intrinsic Ferroelasticity and/or Multiferroicity in Two-Dimensional Phosphorene and Phosphorene Analogues, Nano Lett., 2016, 16, 3236.
31. Z. Guan, H. Hu, X. Shen, P. Xiang, N. Zhong, J. Chu and C. Duan, Recent Progress in Two-Dimensional Ferroelectric Materials, Adv. Electron. Mater., 2020, 6, 1900818.
32. B. Behera, B. C. Sutar and N. R. Pradhan, Recent Progress on 2D Ferroelectric and Multiferroic Materials, Challenges, and Opportunity, Emergent Mater., 2021, 4, 847.
33. A. Belianinov, Q. He, A. Dziaugys, P. Maksymovych, E. Eliseev, A. Borisevich, A. Morozovska, J. Banys, Y. Vysochanskii and S. V. Kalinin, CuInP₂S₆ Room Temperature Layered Ferroelectric, Nano Lett., 2015, 15, 3808.
34. F. Liu, L. You, K. L. Seyler, X. Li, P. Yu, J. Lin, X. Wang, J. Zhou, H. Wang, H. He, S. T. Pantelides, W. Zhou, P. Sharma, X. Xu, P. M. Ajayan, J. Wang and Z. Liu, Room-Temperature Ferroelectricity in CuInP₂S₆ Ultrathin Flakes, Nat. Commun., 2016, 7, 12357.
35. K. Chang, J. Liu, H. Lin, N. Wang, K. Zhao, A. Zhang, F. Jin, Y. Zhong, X. Hu, W. Duan, Q. Zhang, L. Fu, Q.-K. Xue, X. Chen and S.-H. Ji, Discovery of Robust In-Plane Ferroelectricity in Atomic-Thick SnTe, Science, 2016, 353, 274.
36. Y. Zhou, D. Wu, Y. Zhu, Y. Cho, Q. He, X. Yang, K. Herrera, Z. Chu, Y. Han, M. C. Downer, H. Peng and K. Lai, Out-of-Plane Piezoelectricity and Ferroelectricity in Layered α-In₂Se₃ Nanoflakes, Nano Lett., 2017, 17, 5508.
37. C. Cui, W.-J. Hu, X. Yan, C. Addiego, W. Gao, Y. Wang, Z. Wang, L. Li, Y. Cheng, P. Li, X. Zhang, H. N. Alshareef, T. Wu, W. Zhu, X. Pan and L.-J. Li, Intercorrelated In-Plane and Out-of-Plane Ferroelectricity in Ultrathin Two-Dimensional Layered Semiconductor In₂Se₃, Nano Lett., 2018, 18, 1253.
38. D.-Y. Guo, C.-W. Chen, C.-C. Li, H.-C. Jau, K.-H. Lin, T.-M. Feng, C.-T. Wang, T. J. Bunning, I. Choon Khoo and T.-H. Lin, Reconfiguration of Three-Dimensional Liquid-Crystalline Photonic Crystals by Electrostriction, Nat. Mater., 2020, 19, 94.
39. N. Yavo, A. D. Smith, O. Yeheskel, S. Cohen, R. Korobko, E. Wachtel, P. R. Slater and I. Lubomirsky, Large Nonclassical Electrostriction in (Y, Nb)-Stabilized δ-Bi₂O₃, Adv. Funct. Mater., 2016, 26, 1138.
40. S. C. Hwang, C. S. Lynch and R. M. Mcmeeking, Ferroelectric/Ferroelastic Interactions and A Polarization Switching Model, Acta Metal. Mater., 1995, 43, 2073.
41. Y. Gao, M. Gao and Y. Lu, Two-Dimensional Multiferroics, Nanoscale, 2021, 13, 19324.
42. S.-H. Zhang and B.-G. Liu, A Controllable Robust Multiferroic GaTeCl Monolayer with Colossal 2D Ferroelectricity and Desirable Multifunctionality, Nanoscale, 2018, 10, 5990.
43. C. Liu, W. Wan, J. Ma, W. Guo and Y. Yao, Robust Ferroelectricity in Two-Dimensional SbN and BiP, Nanoscale, 2018, 10, 7984.
44. Y. Zhao, L. Lin, Q. Zhou, Y. Li, S. Yuan, Q. Chen, S. Dong and J. Wang, Surface Vacancy-Induced Switchable Electric Polarization and Enhanced Ferromagnetism in Monolayer Metal Trihalides, Nano Lett., 2018, 18, 2943.
45. P. Ares, F. Aguilar-Galindo, D. Rodríguez-San-Miguel, D. A. Aldave, S. Díaz-Tendero, M. Alcamí, F. Martín, J. Gómez-Herrero and F. Zamora, Mechanical isolation of highly stable antimonene under ambient conditions, Adv. Mater., 2016, 28, 6332.
46. J.-J. Zhang, D. Zhu and B. I. Yakobson, Heterobilayer with Ferroelectric Switching of Topological State, Nano Lett., 2021, 21, 785.
47. W. Luo, K. Xu and H. Xiang, Two-Dimensional Hyperferroelectric Metals: A Different Route to Ferromagnetic-Ferroelectric Multiferroics, Phys. Rev. B, 2017, 96, 235415.
48. A. Chandrasekaran, A. Mishra and A. K. Singh, Ferroelectricity, Antiferroelectricity, and Ultrathin 2D Electron/Hole Gas in Multifunctional Monolayer MXene, Nano Lett., 2017, 17, 3290.
49. B. V. Lotsch, Vertical 2D Heterostructures, Annu. Rev. Mater. Res., 2015, 45, 85.
50. G. Kresse and J. Furthmuller, Efficient Iterative Schemes for ab initio Total-Energy Calculations using a Plane-Wave Basis Set, Phys. Rev. B, 1996, 54, 11169.
51. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865.
52. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to The Projector Augmented-Wave Method, Phys. Rev. B, 1999, 59, 1758.
53. S. Grimme, S. Ehrlich and L. Goerigk, Effect of The Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456.
54. S. Guan, C. Liu, Y. Lu, Y. Yao and S. Yang, Tunable Ferroelectricity and Anisotropic Electric Transport in Monolayer β-GeSe, Phys. Rev. B, 2018, 97, 144104.
55. J. Neugebauer and M. Scheffler, Adsorbate-Substrate and Adsorbate-Adsorbate Interactions of Na and K Adlayers on Al (111), Phys. Rev. B, 1992, 46, 16067.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00509c

---