Open Access Article
Open Access ArticleSize-dependent diffusion of supported metal nanoclusters: mean-field-type treatments and beyond for faceted clusters†
King C.
Lai‡
 ab,
Charles T.
Campbell
ab,
Charles T.
Campbell
 c and
James W.
Evans
c and
James W.
Evans
 *ab
*ab
aDivision of Chemical & Biological Sciences, Ames National Laboratory – USDOE, Ames, Iowa 50011, USA. E-mail: evans@ameslab.gov
bDepartment of Physics & Astronomy, Iowa State University, Ames, Iowa 50011, USA
cChemistry Department, University of Washington, Seattle, Washington 98195, USA
First published on 1st August 2023
Abstract
Nanostructured systems are intrinsically metastable and subject to coarsening. For supported 3D metal nanoclusters (NCs), coarsening can involve NC diffusion across the support and subsequent coalescence (as an alternative to Ostwald ripening). When used as catalysts, this leads to deactivation. The dependence of diffusivity, DN, on NC size, N (in atoms), controls coarsening kinetics. Traditional mean-field (MF) theory for DNversus N assumes that NC diffusion is mediated by independent random hopping of surface adatoms with low coordination, and predicts that DN ∼ hN−4/3neq. Here, h = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp[−Ed/(kBT)] denotes the hop rate, and neq = exp[−Eform/(kBT)] the density of those adatoms. The adatom formation energy, Eform, approaches a finite large-N limit, as does the effective barrier, Eeff = Ed + Eform, for NC diffusion. This MF theory is critically assessed for a realistic stochastic atomistic model for diffusion of faceted fcc metal NCs with a {100} facet epitaxially attached to a (100) support surface. First, the MF formulation is refined to account for distinct densities and hop rates for surface adatoms on different facets and along the base contact line, and to incorporate the exact values of Eform and neqversus N for our model. MF theory then captures the occurrence of local minima in DNversus N at closed-shell sizes, as shown by KMC simulation. However, the MF treatment also displays fundamental shortcomings due to the feature that diffusion of faceted NCs is actually dominated by a cooperative multi-step process involving disassembling and reforming of outer layers on side facets. This mechanism leads to an Eeff which is well above MF values, and which increases with N, features captured by a beyond-MF treatment.
exp[−Ed/(kBT)] denotes the hop rate, and neq = exp[−Eform/(kBT)] the density of those adatoms. The adatom formation energy, Eform, approaches a finite large-N limit, as does the effective barrier, Eeff = Ed + Eform, for NC diffusion. This MF theory is critically assessed for a realistic stochastic atomistic model for diffusion of faceted fcc metal NCs with a {100} facet epitaxially attached to a (100) support surface. First, the MF formulation is refined to account for distinct densities and hop rates for surface adatoms on different facets and along the base contact line, and to incorporate the exact values of Eform and neqversus N for our model. MF theory then captures the occurrence of local minima in DNversus N at closed-shell sizes, as shown by KMC simulation. However, the MF treatment also displays fundamental shortcomings due to the feature that diffusion of faceted NCs is actually dominated by a cooperative multi-step process involving disassembling and reforming of outer layers on side facets. This mechanism leads to an Eeff which is well above MF values, and which increases with N, features captured by a beyond-MF treatment.
New conceptsDiverse nanostructured materials are increasingly utilized for energy and environmental technologies including catalysis. However, these systems are generally intrinsically metastable and are subject to coarsening. A key challenge is to elucidate coarsening pathways and to characterize kinetics. A prominent example is supported 3D metal nanoclusters (NCs) which can coarsen either via Ostwald ripening (OR) or via particle migration and coalescence (PMC). For PMC, coarsening kinetics is determined entirely by the size-dependence of NC diffusivity. However, only mean-field (MF) treatments of this dependence have been generally available and utilized, where NC motion is assumed to derive from independent random hopping of surface adatoms. Our analysis shows that this assumption is incorrect for faceted epitaxially-supported NCs, and that an alternative conceptual framework is needed to describe NC diffusion. We show that accounting for the appropriate cooperative multi-step mechanism underlying NC diffusion does capture the size-dependence of NC diffusion coefficients and of the associated activation energies. |
Introduction
Coarsening in nanostructured bulk and surface systems has long been of interest1,2 since such structure evolution generally impacts system properties. A common mechanism is Ostwald ripening (OR) discovered in the late 19th century,3 for which appropriate LSW theory was developed in the mid-20th century.4,5 For systems of supported 3D metal nanoclusters (NCs), rather than OR wherein metal monomers diffuse from smaller to larger NCs, coarsening can instead be mediated by particle (i.e., NC) migration and coalescence (PMC).6–14 PMC is sometimes also described as Smoluchowski ripening (SR), as opposed to OR. Coarsening via SR (as well as OR) is of particular importance with regard to deactivation for catalysts involving supported nanoparticles.6–14 The kinetics of coarsening via PMC is determined entirely by the size-dependence of the diffusion coefficient for supported NCs.6,15 Consequently, reliable treatment of PMC kinetics requires a predictive theoretical description of NC diffusivity.The standard treatment of the diffusivity of supported 3D NCs is based on a mean-field (MF) picture wherein lateral motion of the center of mass of an NC of N atoms is associated with essentially random independent hopping of mobile surface adatoms across the NC surface.6,16–19 In this treatment, such adatom diffusion is described by a single characteristic hop rate h = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βEd]. Here, Ed denotes the diffusion barrier, ν is the attempt frequency, and β = (kBT)−1 denotes the inverse temperature (where kB is the Boltzmann constant, T is the surface temperature). In this scenario, each hop of a surface atom shifts the NC center of mass (CM) laterally by δRCM ∼ a/N, where ‘a’ is the surface lattice constant. The NC surface area, A (in units of adsorption sites) scales like A ∼ N2/3, and the total rate of surface atom hopping scales like H ∼ hAneq, where neq = exp[−βEform(N)] is the density (the number per adsorption site) of mobile surface adatoms. Here, Eform is the adatom formation energy which together with neq depends on NC size as typically determined by continuum Gibbs–Thompson (GT) type relations.11,20 As an aside, natural extensions of GT relations can be developed for small faceted NCs (see the ESI†). The MF treatment predicts that the NC diffusion coefficient satisfies
exp[−βEd]. Here, Ed denotes the diffusion barrier, ν is the attempt frequency, and β = (kBT)−1 denotes the inverse temperature (where kB is the Boltzmann constant, T is the surface temperature). In this scenario, each hop of a surface atom shifts the NC center of mass (CM) laterally by δRCM ∼ a/N, where ‘a’ is the surface lattice constant. The NC surface area, A (in units of adsorption sites) scales like A ∼ N2/3, and the total rate of surface atom hopping scales like H ∼ hAneq, where neq = exp[−βEform(N)] is the density (the number per adsorption site) of mobile surface adatoms. Here, Eform is the adatom formation energy which together with neq depends on NC size as typically determined by continuum Gibbs–Thompson (GT) type relations.11,20 As an aside, natural extensions of GT relations can be developed for small faceted NCs (see the ESI†). The MF treatment predicts that the NC diffusion coefficient satisfies
DN ∼ H(δRCM)2 ∼ νa2N−4/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βEeff(N)], where Eeff(N) = Ed + Eform(N). exp[−βEeff(N)], where Eeff(N) = Ed + Eform(N). | (1) |
In the following, we first describe the atomistic-level stochastic model on which we base our analysis of the diffusion of {100} epitaxially-supported faceted fcc metal NCs. Next, a refinement of the conventional MF-treatment of NC diffusion is provided which is appropriate for faceted NCs considered here. Then, we present results from our refined MF analysis for NC diffusivity versus NC size, N, and compare these with accurate benchmark results previously obtained for the stochastic model from Kinetic Monte Carlo (KMC) simulation. Finally, we describe and present results from an appropriate beyond-MF formulation accounting for the feature that diffusion of faceted NCs is actually mediated by a cooperative multi-step process, rather than MF-type independent random hopping of NC surface atoms. Specifically, the multi-step process involves disassembly and reformation of outer layers on the side facets of the NC. Finally, conclusions are provided.
Stochastic atomistic model for {100}-epitaxial fcc metal nanoclusters
We utilize a stochastic lattice-gas model for {100} epitaxially-supported fcc metal NCs where the (potential) energy of the system is modeled by an effective nearest-neighbor (NN) pairwise attraction of strength ϕ > 0 between metal atoms.22 The effectiveness of this prescription of energetics is validated by DFT analysis,23 and by extensive previous modeling of homoepitaxial growth and relaxation of thin metal films.24,25 Note that ϕ is chosen to recover surface thermodynamics, and is well below one sixth of the bulk cohesive energy, Ec, which would recover bulk thermodynamics. The model applies for any fcc metal. However, we will perform simulations here with parameters corresponding to Ag, choosing ϕ = 0.225 eV versus Ec/6 = 0.49 eV.12 For {100}-epitaxially supported clusters, we regard each atom in the lowest {100} layer of the metal NC as interacting with each of four atoms in a top {100} layer of the support with an attraction of strength fϕ. Thus, f > 0 measures the strength of adhesion with f = 1 corresponding to fcc{100} homoepitaxy. The modeling in this paper will neglect possible vibrational entropy differences between various NC structures (but in some cases consider configurational entropy differences).For this fcc lattice-gas model with NN interactions, the large-size continuum equilibrium Wulff shape for unsupported NCs is a truncated octahedron with all edges between {100} and (111} facets of equal length.26 The large-size continuum equilibrium Winterbottom shape for supported NCs truncates a portion of the Wulff NC dependent on the value of f. See Fig. 1.
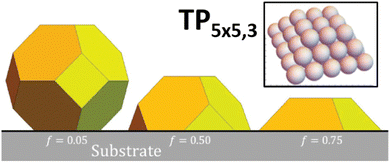 | ||
| Fig. 1 Winterbottom shapes of supported clusters for a fcc metal. We consider the case with substantial adhesion f = 0.75. | ||
To facilitate detailed atomistic-level analysis, we consider the case of strong adhesion, f = 0.75, where the continuum Winterbottom shape is a simple truncated pyramid (TP) with all edges having equal length.22 In the atomistic model, for general discrete NC sizes, N (in atoms), the most stable ground state shape will not be a perfect truncated pyramid. However, one might anticipate the existence of a sequence of closed-shell sizes, Ncs, corresponding to perfect TPs which constitute non-degenerate ground states configurations. This is the case. Such clusters with an n × m atom base (where m = n or n ± 1) which are k layers tall will be denoted by TPn×m,k.
A comprehensive analysis of ground state NC configurations and energetics (as well as their configurational degeneracy) for the lattice-gas model with f = 0.75 was performed for NC sizes N = 13–126. Extensive results are provided in the ESI.† However, an illustrative portion of these results is presented in Fig. 2 showing schematics of non-perfect TP ground state configurations between two particularly stable magic closed-shell sizes Ncs = 50 (TP5×5,3) and Ncs = 62 (TP5×6,3) with perfect TP configurations, and in Table 1 which tabulates for ground state energies and configurational degeneracies for N = 50–65. These magic sizes, which correspond to deep local minima in DN, are highlighted in bold italic font in Table 1. For non-closed shell sizes, we note that ground state degeneracy occurs in a significant fraction of cases as indicated by listing the various possible NC heights, k, as well as by listing the different possible numbers of atoms, Nbase, in the base layer of the ground state NCs configurations. We also list the total energy for the ground state of the supported NCs, EN (relative to that for gaseous metal atoms and a metal-free support surface), in units of ϕ. Note that total interaction of each base layer atom with the support surface is −4fϕ = −3ϕ, so conveniently values of EN/ϕ are all negative integers. Table 1 also lists the quantity ΔEN = EN − EN−1, where ΔEN = −6ϕ, −5ϕ, or −4ϕ takes just three values. ΔEN is a key component in the determination of the adatom formation energy, Eform(N) (which is also listed in Table 1), and thus in determination of the density, neq, of mobile surface adatoms in our refined-MF treatment.
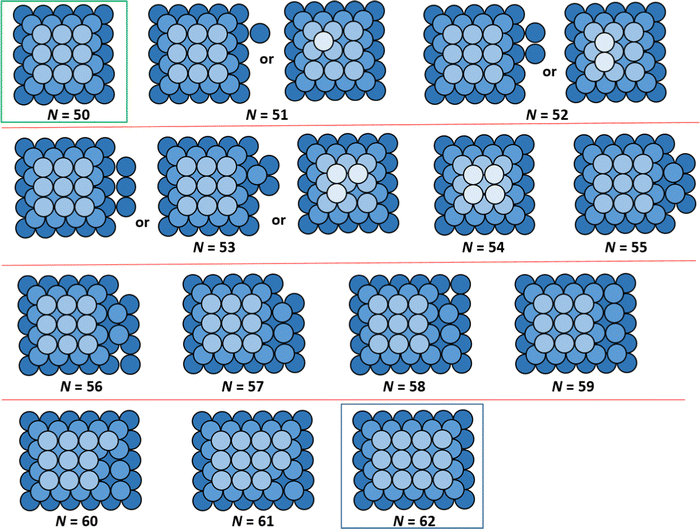 | ||
| Fig. 2 Examples of ground state configurations (top down view) of supported NCs between closed-shell TP sizes N = 50 and N = 62. Degenerate ground state configurations are also shown. | ||
| N | N base | k | −EN/ϕ | −ΔEN/ϕ | E form(100)/ϕ = Eform(base)/ϕ | E form(111)/ϕ | D 700K |
|---|---|---|---|---|---|---|---|
| 50 | 5 × 5 = 25 | 3 | 251 | 6 | 2 | 3 | min |
| 51 | 25, 26 | 3, 4 | 255 | 4 | 0 | 1 | |
| 52 | 25, 27 | 3, 4 | 260 | 5 | 1 | 2 | |
| 53 | 25, 27, 28 | 3, 4 | 265 | 5 | 1 | 2 | max |
| 54 | 5 × 5 = 25 | 4 | 271 | 6 | 2 | 3 | |
| 55 | 28 | 3 | 276 | 5 | 1 | 2 | |
| 56 | 29 | 3 | 281 | 5 | 1 | 2 | |
| 57 | 29 | 3 | 287 | 6 | 2 | 3 | |
| 58 | 30 | 3 | 292 | 5 | 1 | 2 | |
| 59 | 30 | 3 | 298 | 6 | 2 | 3 | |
| 60 | 30 | 3 | 303 | 5 | 1 | 2 | |
| 61 | 30 | 3 | 309 | 6 | 2 | 3 | ∼min |
| 62 | 5 × 6 = 30 | 3 | 315 | 6 | 2 | 3 | min |
| 63 | 30, 31 | 3, 4 | 319 | 4 | 0 | 1 | |
| 64 | 30, 32 | 3, 4 | 324 | 5 | 1 | 2 | |
| 65 | 30, 32, 33 | 3, 4 | 329 | 5 | 1 | 2 | max |
NC diffusivity also depends on the specification of hopping dynamics of surface adatoms. Our stochastic model allows hops of under-coordinated surface adatoms to unoccupied NN fcc crystalline sites, which are still connected to the NC. Hop rates, h = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βEact], have an Arrhenius form where ν ≈ 1012.5 s−1 is a prefactor or attempt frequency chosen to be identical for all hops. Most modeling of 3D crystalline NC evolution has used a standard bond-breaking or so-called Initial Value Approximation (IVA) prescription of the local environment-dependent activation barrier, Eact.11 However, this and other generic prescriptions fail qualitatively to capture realistic barriers for fcc metals.11,21 In contrast, we used a refined Brønsted–Evans–Polanyi (BEP) formalism which allows sufficient flexibility in the specification of Eact to recover DFT values for various key diffusion processes. See ref. 12, 27 and 28 for details. In the model with parameters for Ag, we recover Ed(100) = 0.425 eV and Ed(111) = 0.10 eV for terrace diffusion on {100} and {111} facets, respectively, and Ee(100) = 0.275 eV and Ee(111) = 0.30 eV for edge diffusion along {100} and {111} micro-faceted steps, respectively.
exp[−βEact], have an Arrhenius form where ν ≈ 1012.5 s−1 is a prefactor or attempt frequency chosen to be identical for all hops. Most modeling of 3D crystalline NC evolution has used a standard bond-breaking or so-called Initial Value Approximation (IVA) prescription of the local environment-dependent activation barrier, Eact.11 However, this and other generic prescriptions fail qualitatively to capture realistic barriers for fcc metals.11,21 In contrast, we used a refined Brønsted–Evans–Polanyi (BEP) formalism which allows sufficient flexibility in the specification of Eact to recover DFT values for various key diffusion processes. See ref. 12, 27 and 28 for details. In the model with parameters for Ag, we recover Ed(100) = 0.425 eV and Ed(111) = 0.10 eV for terrace diffusion on {100} and {111} facets, respectively, and Ee(100) = 0.275 eV and Ee(111) = 0.30 eV for edge diffusion along {100} and {111} micro-faceted steps, respectively.
It is appropriate to comment further on our prescription of mass transport. Hopping of under-coordinated surface atoms to neighboring crystalline sites has been the default prescription for effective modeling of homoepitaxial film growth and relaxation,24,25 as well as for surface-diffusion mediated evolution of unsupported metal NCs.29–31 Diffusion across monolayer steps and facets boundaries (particularly from one {111} side facet to an adjacent one) can impact diffusion of supported NCs. Such process occur via a sequence of hops to NN fcc crystalline sites. See the ESI.† An additional Ehrlich–Schwoebel (ES) barrier for interlayer transport above that for terrace diffusion across {111} facets of 0.1 eV is also incorporated (for Ag NCs). As an aside, interlayer diffusion sometimes involves atom exchange rather than hopping. However, for the modeling to accurately capture NC structure evolution, it is only necessary to correctly incorporate the rate of this process rather than the mechanism, and our selection of ES barriers is made to achieve this goal. For diffusion around the NC base, we relax the constraint that atoms hopping to available NN fcc sites must remain connected to the NC. Specifically, atoms can hop to second NN sites at the corner of the rectangular base of an NC, thereby allowing rounding of the corner from one side to another of the faceted NC. See the ESI.† (This atom rounding the corner still has 4 NN substrate atoms, thus avoiding a high energy configuration associated with an atom hopping to a site with no NN higher in the NC.) For corner rounding at the base, there is an additional ES barrier relative to edge diffusion along the base of 0.1 eV.
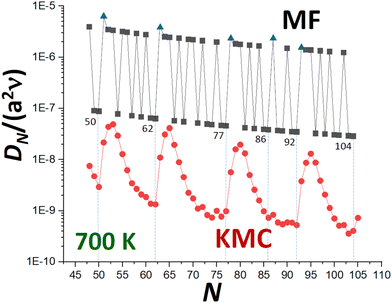
KMC simulation of Ag NC diffusion is then performed where surface hopping processes are implemented with probabilities proportional to the physical rates using a rejection-free algorithm. The diffusion coefficient, DN, is obtained by tracking the lateral mean-square displacement of the center of mass of the NC as a function of time. Fig. 3 presents illustrative results from previously performed KMC simulations22 for DNversus N for Ag NCs at 700 K. We note that similar behavior has been observed in simulations for diffusion of supported Pt NCs.32 The strong oscillatory decay with local minima at or near certain closed-shell TP sizes will motivate subsequent discussion and analysis. In this contribution, we will compare results from our refined MF theory (also shown in Fig. 3), and from a beyond-MF treatment, with those from KMC analysis.
Refined-MF treatment for diffusion of faceted NCs
Overview
The MF formulation described above requires adaption to provide a reasonable treatment of the diffusion of the faceted epitaxial NCs in our model. It is important to recognize that the density of mobile adatoms per adsorption site on the {100} top facet, n100, the {111} side facets, n111, and also at sites along the base contact line, nbase, differ primarily due to different adatom formation energies. Below we use α or α′ = 100, 111, or “base” to label these three cases. The adatom densities will be denoted by nα and the formation energies by Eform(α), where nα ∝ exp[−βEform(α)], and where both quantities depend on α and on NC size. The formation energy, Eform(α) corresponds to the minimum energy cost to extract an atom from a highly-coordinated site (generally a kink site) in a ground state configuration of the NC, and move it onto the desired facet or to the perimeter of the NC base. Note that the coordination of this atom to be extracted is given by the quantity |ΔEN|/ϕ listed in Table 1, and this coordination depends on NC size, N. Since |ΔEN| also corresponds to the energy cost to entirely remove an atom to the vapor phase from such a site in a NC of size N, it follows that| Eform(α) = |ΔEN| − |Eads(α)|, with Eads(α) = −mαϕ, for NC size N, | (2) |
Diffusion barriers, Ed(α), for mobile surface adatoms also depend on α. For Ag NCs, one has that Ed(100) = 0.425 eV and Ed(111) = 0.10 eV on {100} and {111} facets, respectively; Ed(base) = Ee(100) = 0.275 eV for edge diffusion along {100} micro-faceted steps at the NC base. Thus, the corresponding hop rates hα = ν exp[−βEd(α)] for these mobile surface adatoms also depend on α.
In our refined MF treatment, we will separately account for the contribution of these three different classes of mobile surface adatoms to NC diffusion. Below, we let A100, A111, and Abase denote the number of adsorption sites on the top {100) facet, on all four side {111} facets, and around the base, respectively. For adatoms on the top {100} facet and at the base, one has a lateral change in the NC center of mass of δRCM = a/N for each hop. Thus, the corresponding contributions to DN are
| DN(100) = a2h100n100A100/N2 and DN(base) = a2hbasenbaseAbase/N2. | (3) |
| DN(111) = (2/3)a2h111n111A111/N2. | (4) |
From (3) and (4), it is clear that for each α, we can associate an effective barrier, Eeff(α) = Ed(α) + Eform(α), for transport across the relevant facet or around the base. Values for these effective barriers are reported in Table 2 for Ag NCs revealing that Eeff(111) and Eeff(base) are significantly lower that Eeff(100). This indicates that that contributions to DN from transport across {111} side facets and around the base of the NC dominate those from transport across the {100} top facet.
| E eff(α) in eV | α = top {100} | α = side {111} | α = base |
|---|---|---|---|
| a As noted in the text, the barriers listed for N = Ncs + 1 do not correlate with NC diffusion. | |||
| N = Ncs & some other N | 0.875 | 0.775 | 0.725 |
| N = Ncs + 1 (mostly) | 0.425 | 0.325 | 0.275 |
| N = Ncs + 2,3 (mostly) | 0.650 | 0.550 | 0.500 |
To more clearly show the NC size scaling of DN, it is convenient to consider a subset of perfect closed-shell TPs of k layers with a top k × k atom {100} facet, and thus a (2k − 1) × (2k × 1) bottom {100} layer, i.e. TP(2k−1)×(2k−1),k. For these TP, which most closely mimic the continuum Winterbottom shape, one has that
| N = k(2k − 1)(7k − 1)/6, A100 = (k − 1)2, A111 = 2k(3k − 1), and Abase = 4(2k − 1). | (5) |
| A100 ∼ (3N/7)2/3, A111 ∼ 6A100, and Abase ∼ 8(3N/7)1/3. | (6) |
| DN ≈ (3/7)2/3a2N−4/3[h100n100 + 4h111n111 + 8(3N/7)−1/3hbasenbase]. | (7) |
Finally, we identify one self-evident limitation regarding the utility of the MF formulation. Consider NCs whose size exceeds that for structures with closed-shell ground states by one, i.e., N = Ncs + 1. Then, the ground state structure already has one isolated adatom either on the {100} top facet or at the base. The formation energies, Eform(100) = Eform(base) = 0 vanish, and the adatom densities n100 ≈ nbase ≈ 1/(A100 + Abase) on {100} facets and at the base are correspondingly “anomalously” high. However, these high densities do not correlate with correspondingly high NC diffusivity. In these cases, NC dynamics primarily involves this isolated atom moving around a static closed-shell “core” of the NC, which in itself does not result in NC diffusion.
Analysis of adatom densities nα including entropic effects
A detailed analysis of the mobile adatom densities, nα = n100, n111, or nbase, is possible utilizing a standard statistical mechanical formalism to determine the probability that the system is in an energetically excited state with such an adatom at the desired location. The analysis below does not apply for the cases N = Ncs + 1 (where as noted above, there is already a surface adatom in the ground state), or for N = Ncs + 2 where slight refinement of the following analysis is needed. See the ESI.† Let ΩN denote the degeneracy of the ground state of the NC with N atoms and energy EN. Then, the degeneracy of the “excited state” configuration where an atom is shifted from this ground state to a lower-coordinated adsorption site of type α is ΩN−1Aα, and the energy of this excited state is EN−1 + Eads(α). Thus, the canonical partition function for the NC of N atoms becomesQN = ΩN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βEN] + ΩN−1∑α′Aα′ exp[−βEN] + ΩN−1∑α′Aα′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−β{EN−1 + Eads(α′)}] +… exp[−β{EN−1 + Eads(α′)}] +… | (8) |
Pα = ΩN−1Aα![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−β{EN−1 + Eads(α)}]/QN. exp[−β{EN−1 + Eads(α)}]/QN. | (9) |
We consider the regime of temperatures and relatively small NC sizes where the system is most likely in the ground state (so the first term in QN dominates), and where it is unlikely that there is more than one mobile adatom on a side or top facet or at the base. Then, it follows that the density of such atoms on adsorption site type α satisfies
| nα ≈ Pα/Aα ≈ (ΩN−1/ΩN)exp[β{EN − EN−1 − Eads(α)}] = (ΩN−1/ΩN)exp[−βEform(α)]. | (10) |
Refined-MF predictions for DNversus KMC results
Refined-MF analysis for N = Ncs (low DN) and N = Ncs + j with j = 1–3 (high DN)
Motivated by the results for NC diffusivity shown in Fig. 3, we initially focus on special NC sizes, N = Ncs (for closed-shell TP ground states) where DN generally exhibits local minima, and sizes N = Ncs + j with j = 1, 2, or 3, noting that KMC values for DN exhibit local maxima for N = Ncs + 3 (and values for N = Ncs + 2 are only slightly lower). These cases are analyzed in detail separately below. We present refined-MF results for DN for Ncs = 50, 62, 77, and 92, and directly compare these with accurate results from KMC simulation.(i) For N = Ncs, the NCs have non-degenerate ground states, so that ΩN = 1. One also has that ΩN−1 = 4 corresponding to removing an atom from one of the 4 corners of the top {100} facet on the perfect TP. Since Eform(100) = Eform(base) = 2ϕ and Eform(111) = 3ϕ (see Table 1), one has from (10) that
n100 = nbase = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−2βϕ] and n111 = 4 exp[−2βϕ] and n111 = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−3βϕ]. exp[−3βϕ]. | (11) |
(ii) For N = Ncs + 1, we have already noted above that this is an anomalous case as the ground state structure already has one isolated adatom adsorbed on the {100} top facet or at the base of a closed-shell “core”. Thus, one has that Eform(100 or base) = 0, and n100 = nbase = 1/(A100 + Abase) are correspondingly high. Additional analysis reveals that n111 = nbase![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βϕ]. See the ESI.† This allows determination of the refined-MF predictions for diffusivity which are artificially high, corresponding to local maxima with respect to N, in contrast to KMC results.
exp[−βϕ]. See the ESI.† This allows determination of the refined-MF predictions for diffusivity which are artificially high, corresponding to local maxima with respect to N, in contrast to KMC results.
(iii) For N = Ncs + 2, the ground state consists of a dimer adsorbed on the {100} top facet (for Ncs ≥ 18), or at the base of a closed-shell “core”. A feature specific to this case is that when the dimer dissociates, it creates two mobile adatoms. As a result, some refinement of the formulation leading to the prefactor in (10) is required. See the ESI.† Since typically Eform(100) = Eform(base) = ϕ and Eform(111) = 2ϕ from Table 1, ignoring the prefactors it follows that
| n100 = nbase ∼ exp[−βϕ] and n111 ∼ exp[−2βϕ], | (12) |
(iv) For N = Ncs + 3, the ground state usually consists of a trimer adsorbed on the {100} top facet (for Ncs ≥ 18) or at the base of a closed-shell “core”. Then, ΩN corresponds to the number of locations on the core of a linear or bent trimer on the top {100} facet plus the number of locations of a linear or triangular trimer at the base. ΩN−1 corresponds to the number of locations on the core of a dimer. See the ESI,† for more details. These degeneracies can be readily determined in specific cases. Since typically Eform(100) = Eform(base) = ϕ and Eform(111) = 2ϕ from Table 1, it then follows that
| n100 = nbase ≈ (ΩN−1/ΩN)exp[−βϕ] and n111 ≈ (ΩN−1/ΩN)exp[−2βϕ], | (13) |
It is clear that the refined-MF treatment will capture aspects of the oscillatory trend in DNversus N shown in KMC simulation with local minimum values at N = Ncs substantially below similar high values at N = Ncs + 2 and N = Ncs + 3. As noted above, refined-MF values for N = Ncs + 1 are artificially high corresponding to local maxima (in contrast to KMC). Table 3 compares refined-MF DN values at 700 K from (3) and (4) incorporating detailed evaluation of Aα and nα with accurate KMC values. This is done for various closed-shell NC sizes, Ncs = 50, 62, 77, and 92. As already indicated above, contributions to DN from transport across {111} side facets and around the base of the NC dominate those from transport across the {100} top facet. This dominance primarily reflects the lower effective barriers, Eeff(α) for α = 111 and α = base versus α = 100 (see Table 2), but also partly reflects entropic factors.
| Refined-MF DN/(a2ν) (×10−7) | KMC DN/(a2ν) (×10−9) | |||||||
|---|---|---|---|---|---|---|---|---|
| N cs | N cs + 1 | N cs + 2 | N cs + 3 | N cs | N cs + 1 | N cs + 2 | N cs + 3 | |
| N cs = 50 | 3.31 | 57.54 | 37.29 | 23.07 | 2.91 | 21.61 | 43.53 | 48.75 |
| N cs = 62 | 2.40 | 36.01 | 24.92 | 17.12 | 1.33 | 10.95 | 30.92 | 41.12 |
| N cs = 77 | 2.03 | 22.01 | 17.21 | 12.50 | 0.98 | 5.66 | 15.84 | 19.60 |
| N cs = 92 | 1.59 | 14.67 | 12.60 | 9.71 | 0.53 | 3.79 | 8.63 | 13.01 |
It is clear that the refined-MF treatment is reasonably effective in predicting the relative values of DN at local minima at N = Ncs and the much higher values for N = Ncs + 2 and N = Ncs + 3 (the latter being a local maximum for KMC). The refined-MF treatment does not capture the more subtle feature that accurate KMC values for N = Ncs + 2 are slightly lower (not higher) than those for N = Ncs + 3. It should be emphasized, however, that all refined-MF values are roughly two orders of magnitude above those from KMC. As noted above, this discrepancy could be partly ameliorated by incorporating an additional universal factor, exp[−βδ] in the refined-MF DN which reflects an additional ES type barrier, δ > 0, for transport between different sides of the NC. However, we argue that the discrepancy primarily reflects the fundamental shortcoming that the refined-MF treatment greatly under-estimates the effective barrier for NC diffusion, as will be discussed in detail within the framework of beyond-MF treatments.
Approximate refined-MF analysis for all NC sizes versus KMC results
Here, we explore an approximate version of the refined-MF treatment which has the advantage of providing a convenient general formula for DN. To this end, we utilize a simplified form (7) which already incorporates approximations for Aα, but now we also include additional reasonable approximations for adatom densities which neglect some entropic factors as described below. We thereby obtainDN/(a2ν) ≈ (3/7)2/3N−4/3{exp[−βEd(100)] + 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−β(Ed(111) + ϕ)] + 8(3N/7)−1/3 exp[−β(Ed(111) + ϕ)] + 8(3N/7)−1/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βEd(base)]}nbase, exp[−βEd(base)]}nbase, | (14) |
In Fig. 3, we have compared the predictions of (14) with accurate KMC values for DN. As expected, the simplified MF form (14) effectively captures the local minima of DN for N = Ncs, and much higher values for N = Ncs + 2 and N = Ncs + 3. However, (14) produces “excessive” oscillatory behavior of DN reflecting the rapid oscillatory variation in Eform(N), although (14) does captures the slow overall decrease in the oscillatory DN with increasing N. Again, MF values of DN are substantially above KMC values, a shortcoming elucidated by a beyond-MF analysis.
Beyond-MF analysis for DNversus MF and KMC results
Overview
The above results reveal that refined-MF theory fails to reliably describe detailed trends in NC diffusivity with size, and also thus fails to elucidate the relationship between NC structure and diffusivity. However, this structure-diffusivity relationship can be elucidated and captured by a beyond-MF analysis tailored to the diffusion of epitaxially-supported faceted NCs. In this section, we outline such a beyond-MF analysis which recognizes that the diffusion of such NCs is controlled by a cooperative multi-step mechanism wherein the outer layer of a facet on one side of the NC is disassembled and those adatoms transferred to form (i.e., to nucleate and grow to completion) a new outer layer on a target facet another side of the NC.19 See Fig. 4. This picture of a cooperative multi-step mechanism contrasts the MF assumption that NC diffusion results from (non-cooperative) independent random hopping of surface atoms. It should also be noted that such cooperative nucleation and growth type processes have also been identified as underlying the shape equilibration of faceted fcc metal NCs with initial non-equilibrium shapes.12,27–31,33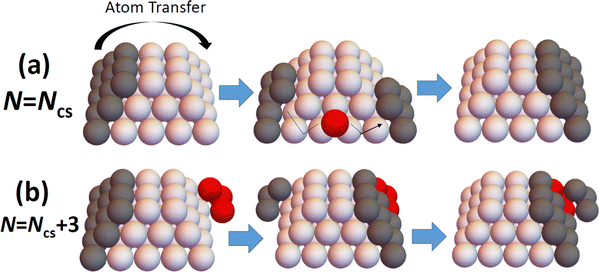 | ||
| Fig. 4 Schematic of disassembly and reformation of outer layers of facets on: (a) perfect; and (b) imperfect TPs. Ncs = 50 for the cases shown. | ||
Our beyond-MF analysis will naturally consider the change in system energy, δE(q), as a function of the number, q, of atoms transferred from the facet which is being disassembled to the target facet on another side of the NC. δE(q) will generally quickly increase from zero as q increases above zero and will then return to zero once a new outer layer of the target facet is completed on another side of the NC, or when the NC returns to a configuration identical to the initial configuration but shifted by a surface lattice constant.
Some aspects of the definition and determination of δE(q) should be mentioned. First, values of δE(q) for integer q will correspond to the change in energy after completion of transfer of the qth atom, i.e., after its incorporation at an adsorption site at the base of the target facet if q = 1, or after its incorporation into a 2D cluster of atoms forming on the target facet for q > 1. We will also define δE(q) for half-integer values of q. The value for say q = n + 0.5 for integer n, corresponds to the change in system energy when the (n + 1)st atom has been detached from the facet being disassembled, but is not yet incorporated into a 2D cluster of n + 1 atoms on the target facet. The strength of the adsorption energy of this isolated mobile atom which is in transit is taken to be 3ϕ corresponding to adsorption on a {111} facet, or at a corner site at the base of the NC. Second, for the above mass transfer process, one considers the specific scenario where atoms are removed from the disassembling outer layer of one side facet in a way which minimizes the number of broken bonds, and added to the growing 2D cluster forming the new outer layer on another side facet in order to maximize the number of bonds formed. Such a process will minimize δE(q) for each q, and thereby generate the minimum energy path (MEP) for facet disassembly and formation. Third, it should be emphasized that δE(q) is associated with energetic changes at T = 0 K rather than free energy changes, δF(q), for T > 0. The latter would also account for the influence of changes in configurational entropy to more accurately capture the effective barrier.
The effective barrier, Eeff = Eeff(N) for disassembling and forming outer layers of facets, and thus for NC diffusion, will be controlled by δEmax = δEmax(N) = maxqδE(q) for this MEP. If one neglects entropic effects, one can then identify Eeff(N) = Ediff + δEmax(N), where Ediff is an appropriate diffusion barrier for mobile surface atoms. Adatom diffusion across the top {100} facet should not contribute significantly to NC diffusion given the high terrace diffusion barrier Ed(100) = 0.425 eV. Thus, we choose a lower value of Ediff ≈ 0.15 eV reflecting a combination of transport across {111} facets and around the NC base with possible ES effects. In summary, the effective barrier, Eeff(N), for NC diffusion is actually controlled by the entire MEP for the cooperative multi-step process of disassembly and formation of outer layers on the faceted NC. This contrasts the barrier(s) in the MF treatment which are associated with the “single-step” process of forming a mobile surface adatom on various facets or at the NC base.
Detailed analysis of δE(q) vs. q and of δEmax(N) for N = Ncs + j with j = 0–3
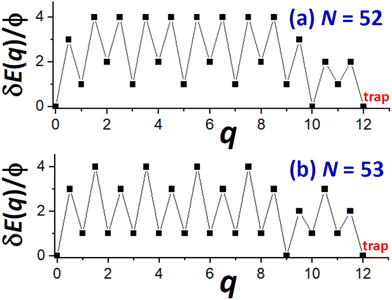
Next, we provide a detailed analysis of δE(q) versus q, extracting the associated δEmax, and focusing on comparison of cases N = Ncs (closed-shell sizes often with local minima in DN) and N = Ncs + j for j = 1–3 (with higher DN). For specificity, in Fig. 5, we show δE(q) versus q for N = Ncs + j with j = 0, 1, 3, where Ncs = 50. This closed-shell NC size corresponds to a truncated pyramid TP5×5,3.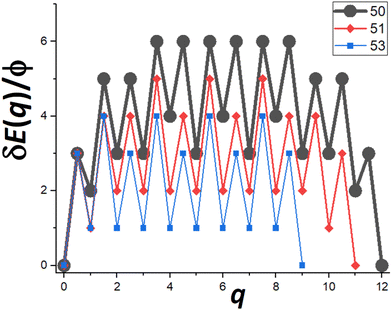 | ||
| Fig. 5 δE(q) versus q for N = 50, 51, 53 (i.e., for N = Ncs + j with j = 0, 1, and 3 with Ncs = 50 corresponding to TP5×5,3). δEmax = 6ϕ, 5ϕ, and 4ϕ for N = 50, 51, and 53 (& 52), respectively. | ||
For N = Ncs = 50, the outer layer of a complete side facet is composed of qmax = 12 atoms, and consequently Fig. 5 shows the MEP δE(q) for 0 ≤ q ≤ qmax = 12. This δE(q) initially increases quickly (as mentioned above), and is symmetric about q = qmax/2, and shows that δEmax(N = 50) = 6ϕ. Details of NC configurations versus the number q of atoms transferred are shown in the ESI.†
For N = Ncs + j with j > 0, a cluster of j atoms already exists on one facet, which reduces the energy cost δE(q) relative to j = 0 for transferring atoms from another perfect facet to grow a 2D cluster and complete a new layer on that target facet. Furthermore, to complete that layer, one now needs to transfer only qmax − j atoms. These features are shown in Fig. 5 which also presents δE(q) versus q for j = 1 (N = 51) where δEmax(N = 51) = 5ϕ, and for j = 3 (N = 53) where δEmax(N = 53) = 4ϕ. The case j = 2 (N = 52) is not shown to avoid overcrowding the plot, but in this case one has that δEmax(N = 52) = 4ϕ as for N = 53. As a final remark for cases with j > 0, a small cluster of j atoms is left behind on the disassembled facet (see Fig. 4b). However, there is a relatively low cost to transfer this cluster to another side facet recovering a shifted version of the initial NC configuration. This portion of the MEP is not shown in Fig. 5. Consequently, this feature does not impact the effective barrier, Eeff(N) = Ediff + δEmax(N), for NC diffusion.
To summarize the above analysis, a local maximum occurs in δEmax for N = Ncs, with δEmax lower for N = Ncs + 1, and lowest for N = Ncs + 2 or N = Ncs + 3. This corresponds to local minima of DN at N = Ncs and local maxima at N = Ncs + 3 (with just slightly lower values for N = Ncs + 2). While these trends are only illustrated above for Ncs = 50, they actually apply for general Ncs. This analysis effectively elucidates a NC structure – diffusivity relationship. Perhaps not surprisingly, NCs with N = Ncs and ground-state closed-shell TP structures have low diffusivity, reflecting the higher energy cost to disassemble and reassemble outer layers of side facets. Next, consider NCs where the ground state structure includes a closed shell TP core, but also additional atoms which form a 2D cluster on a side facet. Here, the presence of the additional 2D cluster lowers the energy cost of disassembling and reassembling outer layers of side facets, and thus enhances diffusivity relative to the case with N = Ncs.
As an aside, we note that in general, NC structure-diffusivity relationships can be subtle. Note from Fig. 3 that NCs for sizes just below closed-shell sizes generally have DN comparable to “local minima” for N = Ncs (and actually sometimes even slightly lower DN as is the case, e.g., for Ncs = 77). Below, we show examples where for such sizes, δEmax has the same local maximum value as for the closed-shell size, which does straightforwardly explain the low value of DN. Another observation regarding subtle NC structure – diffusivity relationships is that for single-atomic-layer 2D epitaxially-supported NCs, closed-shell structures do not correspond to local minima in diffusivity.34,35 This feature reflects the stronger influence of entropic over energetic factors in these 2D systems in determining DNversus N.
Note that the MEP for TP5×5,3 with Ncs = 50, and TP5×6,3 with Ncs = 62, should be identical. For TP5×6,3, the outer layer on a {111} side facet with base length 5 and height 3 (just as for TP5×5,3) can disassemble, forming a new outer layer on an adjacent {111} side facet with initial base length 6 which upon completion of this process will have a base length 5. Repeating this process for TP5×6,3 induces NC diffusion. Likewise, MEPs are identical for TP6×6,3 with Ncs = 77, and TP6×7,3 with Ncs = 92, etc.
Trend in δEmax(N) for increasing N
Next, we show that apart from oscillations in DN and δEmax(N) as N varies between consecutive closed-shell sizes, there is an overall increase without bound in δEmax(N) as N increases (in marked contrast to MF behavior). Specifically, we focus on a special subset of “ideal” closed-shell sizes mentioned previously. These correspond to truncated pyramids, TP(2k−1)×(2k−1),k, where the length of the edge of the top {100} facet and the edge between adjacent {111} side facets are equal (to k atoms). As a result, these structures best mimic the continuum Winterbottom shape shown on Fig. 1 for f = 0.75. Fig. 6 shows the behavior of the “upper envelope” of δE(q) versus q for cases with k = 2, 3, 4, 5, 6, 7,… where N = 13, 50, 126, 255, 451, 728,… and the number of atoms in the outer layer of a single {111} side facet of qmax = 5, 12, 22, 35, 51, 70,…, respectively. The “upper envelope” just corresponds to values of δE(q) for half-integer q associated with states where an atom is in transition between the side facet being disassembled and the target facet on which a new layer is being formed. These δE(q) exceed those for adjacent integer values of q (cf.Fig. 5), and thus suffice to determine δEmax. From Fig. 6, we find that δEmax = 4ϕ, 6ϕ, 8ϕ, 9ϕ, 11ϕ, and 13ϕ, for k = 1–7, respectively. These results reflect the feature that δEmax increases roughly linearly with increasing NC height, k (or with NC width or edge length) for ideal closed-shell TPs. Thus, MEP analysis predicts that the effective barrier, Eeff(N) = Ediff + δEmax(N), increases without bound for increasing NC size.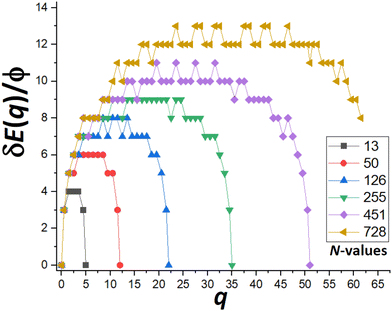 | ||
| Fig. 6 δE(q) versus q for N = 13, 50,… indicated in the legend which correspond to TP(2k−1)×(2k−1),k for k = 2, 3,…. δEmax = 4ϕ, 6ϕ,… for N = 13, 50, …, respectively. | ||
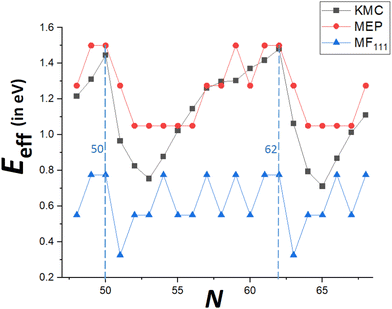
Comparison of beyond-MF MEP with KMC and refined-MF predictions
To demonstrate that our MEP analysis effectively captures the trend in accurate KMC values for Eeff(N) versus N (particularly for N = Ncs + j with j = 0–3), both MEP and KMC results are compared in Fig. 7 for N = 48–68. Values from the refined-MF treatment are also shown. The MEP analysis reasonably captures the feature that Eeff is highest for N = Ncs, lower for N = Ncs + 1, but lowest for N = Ncs + 3 (and gives an equally low value for N = Ncs + 2). In contrast the refined-MF treatment fails fundamentally as it predicts that Eeff for N = Ncs + 1 is lowest. More generally, MEP results capture the overall oscillatory variation of Eeff between closed-shell sizes N = Ncs. MEP results also include the feature that δEmax, and thus Eeff, are equal for Ncs = 62 and Ncs − 1 = 61, compatible with very similar values of DN for these sizes. However, KMC values are significantly lower than those from MEP analysis for, say, N = Ncs + j with j = 2–4. Recall that MEP values come from a T = 0 K analysis of energetics rather than a free energy analysis for T > 0, and it has been noted that entropic effects can lower the effective barrier for the somewhat similar process of reshaping faceted metal NCs.33Another limitation of the T = 0 K MEP analysis of Eeff is an inability to distinguish between behavior for N = Ncs + 2 and N = Ncs + 3. However, the MEP analysis presented above considered only δEmax(N) = maxqδE(q). For a more complete analysis to at least elucidate the feature that DN is higher for N = Ncs + 3 than for N = Ncs + 2, one could perform a first-passage time analysis based on the entire MEP profile, δE(q) versus q. See Fig. 8 for examples of the MEP with N = 52 and N = 53 corresponding to Ncs = 50. In the first-passage time analysis, the system starts in state q = 0 at time t = 0. Let P(q, t) denote the probability for the NC to be in state q with q transferred atoms at time t, so that P(q, 0) = 1 for q = 0, and P(q, 0) = 0 for q > 0. Then, one considers the evolution in time of P(q, t) based upon the set of master equations
| d/dt P(q, t) = k+(q − ½)P(q − ½, t) + k−(q + ½)P(q + ½, t) − [k+(q) + k−(q)]P(q, t). | (15) |
The relative values of τ(52) and τ(53) are not self-evident just from inspection of the different forms the MEPs in Fig. 8 for N = 52 and N = 53, which we emphasize have the same δEmax = maxqδE(q) = 4ϕ. However, numerical integration of the master eqn (15) using MathematicaTM reveals that τ(52)/τ(53) exceeds unity for all T corresponding to D53/D52 > 1 consistent with KMC results. See the ESI.† This analysis is not quantitative predicting D53/D52 ≈ 1.8 at 700 K versus 1.1 from KMC simulation. However, we note that our master equation treatment has still not incorporated the influence of “excited state” configurations above the MEP and associated configurational entropy which can significantly change predictions.33
Finally, recall that in Fig. 6, results were presented for δE(q) versus q for a broad range of “ideal” closed-shell TP sizes, N, showing that the MEP analysis predicts an increase in Eeff roughly linearly with NC height (or width). It is not viable to perform accurate KMC simulation analysis of DN for such a broad the range of N. However, Fig. 9 compares KMC, MEP and refined-MF predictions for Eeff for closed-shell TP sizes where KMC results are available providing evidence that the MEP analysis captures the key features of the variation of the effective barrier, Eeff(N), with N. The increase in Eeff(N) with N is evident from KMC analysis for smaller N similar to the MEP predictions, and in contrast to the refined-MF predictions. The feature that the variation of KMC values for Eeff(N) with N is somewhat irregular for these closed-shell TP reflects the feature that not all closed-shell TPs are equally stable (relative to other similar sized NCs). For example, the “ideal” closed-shell TP sizes N = 13, 50, 126,… (as analyzed in Fig. 6) which match the continuum Winterbottom shape are particularly stable, and the corresponding Eeff are relatively high compared to other non-ideal TP with comparable sizes. Again, accurate KMC values for Eeff tend to be somewhat below MEP predictions, presumably due to the neglect of the effects of configurational entropy, the contribution of which could increase for larger NC sizes.33
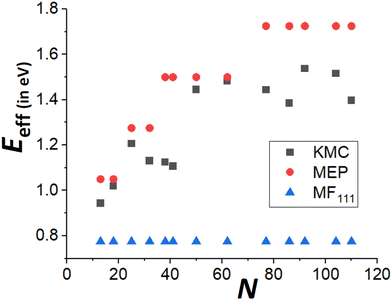 | ||
| Fig. 9 Comparison of Eeff for closed-shell Ag TP from KMC simulation, beyond-MF MEP analysis, and refined-MF analysis for a ranges of sizes, N. | ||
Conclusions
This study provided a critical assessment of mean-field (MF) treatments and their refinements for the size-dependent diffusivity, DN, for the case of {100} epitaxially supported 3D fcc metal NCs of N atoms. Essentially exact behavior for DNversus N for a realistic stochastic model for the above class of systems is obtained from KMC simulation for strong adhesion to the substrate where the large-size equilibrium Winterbottom shape of the supported NC is a truncated pyramid. MF treatments regard NC diffusion as being mediated by independent random hopping of surface atoms. As our specific focus was on faceted NCs, the traditional MF treatment was refined to account for the feature that the density of mobile surface atoms (which is primarily determined by their formation energy), as well as their hop rates, differ on distinct facets and at the base of the NC. For our specific stochastic model, we performed an exact calculation of the formation energy and associated adatom density for a range of sizes N. This analysis accounted for the atomistic details of NC structure and energetics, e.g., the existence of particularly stable close-shell sizes, N = Ncs. This refined MF treatment was able to capture the feature that DN determined accurately from KMC simulation exhibited local minima for N = Ncs, but substantially higher and similar values for N = Ncs + 2 or N = Ncs + 3 (although the former are slightly higher in the MF treatment versus the latter for KMC). However, this refined-MF treatment did fail in that it predicted local maxima in DN for N = Ncs + 1.More significantly, our analysis also revealed more fundamental shortcomings of even refined MF-type treatments. These shortcomings derive from the feature that diffusion of faceted NCs is actually not mediated by independent random hopping of surface atoms, as assumed in MF formulations. Instead, NC diffusion is mediated by a cooperative multi-step process involving disassembling outer layers of atoms on side facets, transferring those atoms to another side facet on which a new outer layer is formed. The effective barrier for this multi-step nucleation type process is typically far higher than the barrier associated with the MF formulation which just corresponds to that for the single-atom hopping process of forming a single mobile surface adatom. The actual effective barrier increases strongly with NC size in marked contrast to the effective barrier in MF type treatments which converges to a finite value in the limit of large NC size. The feature that the effective MF barrier is well below the actual barrier also accounts for the feature that MF predictions for DN are well above the actual values (a feature which is only partly ameliorated by including the effect of an additional Ehrlich-Schwoebel barrier in the MF treatment).
Finally, we note that our beyond-MF picture for diffusion of supported NCs should apply more generally for faceted NCs. Diffusion of all such NCs requires disassembly of one of more facets on one side of the NC and reassembly on another side. Of course, the process and its analysis is significantly more complicated for weak adhesion where the Winterbottom shape of the supported NC has overhanging facets (see Fig. 1), and it is clear that multiple facets must be disassembled and reassembled to shift the NC across the substrate and recover its initial structure. On a separate topic, we should note that for any faceted NC, one anticipates that as temperature increases, MF-type behavior will be recovered (implying a strong reduction in the oscillatory variation of DN with N between consecutive close-shell sizes observed for lower T).22 In this context, it should be noted that the roughening transition for small faceted metal NCs generally occurs well below the bulk roughening temperature promoting the recover of MF-type behavior.
Author contributions
K. C. L. and J. W. E. developed the stochastic model and performed related analysis of energetics and beyond-mean-field analysis of NC diffusion. K. C. L. performed KMC simulations for the stochastic model. J. W. E. developed and performed the refined mean-field analysis. K. C. L., C. T. C., and J. W. E. were involved in discussions of this work. J. W. E. wrote an initial draft of the manuscript, and C. T. C. and J. W. E. revised that draft.Conflicts of interest
The authors have no conflict of interest.Acknowledgements
J. W. E thanks Dr Da-Jiang Liu for discussions on this work. K. C. L. and J. W. E. were supported for this work by the US Department of Energy, Office of Science, Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biological Sciences through the Computational and Theoretical Chemistry project at Ames National Laboratory (AL). AL is operated by Iowa State University under contract no. DE-AC02-07CH11358. C. T. C. acknowledges the US Department of Energy, Office of Science, Basic Energy Sciences for support of this work under Grant Number DE-FG02-96ER14630.References
- L. Ratke and P. W. Voorhees, Coarsening and Growth: Ostwald Ripening in Materials Processes, Springer, Berlin, 2001 Search PubMed.
- M. Zinke-Allmang, L. C. Feldman and M. H. Grabow, Surf. Sci. Rep., 1992, 16, 377–463 CrossRef CAS.
- W. Ostwald, Lehrbuch der Allgemeinen Chemie, Leipzig, Germany, 1896, vol. 2, Part 1 Search PubMed.
- I. M. Lifshitz and V. V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- C. Z. Wagner, Electrochem, 1961, 65, 581–591 CAS.
- P. Wynblatt and N. A. Gjostein, Prog. Solid State Chem., 1975, 9, 21–58 CrossRef CAS.
- J. A. Farmer and C. T. Campbell, Science, 2010, 329, 933–936 CrossRef CAS PubMed.
- S. R. Challa, A. T. Delariva, T. W. Hansen, S. Helveg, J. Sehested, P. L. Hansen, F. Garzon and A. K. Datye, J. Am. Chem. Soc., 2011, 133, 20672–20675 CrossRef CAS PubMed.
- T. W. Hansen, A. T. DeLaRiva, S. R. Challa and A. K. Datye, Acc. Chem. Res., 2013, 46, 1720–1730 CrossRef CAS PubMed.
- F. F. Tao and P. A. Crozier, Atomic-Scale Observations of Catalyst Structures under Reaction Conditions and during Catalysis, Chem. Rev., 2016, 116, 3487–3539 CrossRef CAS PubMed.
- Y. Dai, P. Lu, Z. Cao, C. T. Campbell and Y. Xia, Chem. Soc. Rev., 2018, 47, 4314–4331 RSC.
- K. C. Lai, Y. Han, P. Spurgeon, W. Huang, P. A. Thiel, D.-J. Liu and J. W. Evans, Chem. Rev., 2019, 119, 6670–6768 CrossRef CAS PubMed.
- M. Rahmati, M. S. Safdari, T. H. Fletcher, M. D. Argyle and C. H. Bartholomew, Chem. Rev., 2020, 120, 4455–4533 CrossRef CAS PubMed.
- S. L. Hu and W. X. Li, Science, 2021, 374, 1360–1365 CrossRef CAS PubMed.
- E. Ruckenstein and B. Pulvermacher, AIChE J., 1973, 19, 356–364 CrossRef CAS.
- M. J. J. Jak, C. Konstapel, A. van Kreuningen, J. Verhoeven and J. W. M. Frenken, Surf. Sci., 2000, 457, 295–310 CrossRef CAS.
- M. J. J. Jak, C. Konstapel, A. van Kreuningen, J. Chrost, J. Verhoeven and J. W. M. Frenken, Surf. Sci., 2001, 474, 28–36 CrossRef CAS.
- S. C. Parker and C. T. Campbell, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035430 CrossRef.
- S.-L. Hu and W.-X. Li, Sci. China: Technol. Sci., 2019, 62, 762–772 CrossRef.
- P. N. Plessow and C. T. Campbell, ACS Catal., 2022, 12, 2302–2308 CrossRef CAS.
- E. E. Gruber, J. Appl. Phys., 1967, 38, 243–250 CrossRef CAS.
- K. C. Lai and J. W. Evans, Nanoscale, 2019, 11, 17506–17516 RSC.
- L. T. Roling, L. Li and F. Abild-Pedersen, J. Phys. Chem. C, 2017, 121, 23002–23010 CrossRef CAS.
- J. W. Evans, P. A. Thiel and M. C. Bartelt, Surf. Sci. Rep., 2006, 61, 1–128 CrossRef CAS.
- P. A. Thiel, M. Shen, D.-J. Liu and J. W. Evans, J. Phys. Chem. C, 2009, 113, 5047–5067 CrossRef CAS.
- C. R. Henry, Prog. Surf. Sci., 2005, 80, 92–116 CrossRef CAS.
- K. C. Lai and J. W. Evans, Phys. Rev. Mater., 2019, 3, 026001 CrossRef CAS.
- K. C. Lai, M. Chen, B. M. Williams, Y. Han, C.-K. Tsung, W. Huang and J. W. Evans, ACS Nano, 2020, 14, 8551–8561 CrossRef CAS PubMed.
- N. Combe, P. Jensen and A. Pimpinelli, Phys. Rev. Lett., 2000, 85, 110–113 CrossRef CAS PubMed.
- T. H. Lim, D. N. McCarthy, S. C. Hendy, K. J. Stevens, S. A. Brown and R. D. Tilley, ACS Nano, 2009, 3, 3809 CrossRef CAS PubMed.
- D. N. McCarthy and S. A. Brown, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 064107 CrossRef.
- L. Li, P. N. Plessow, M. Rieger, S. Sauer, R. S. Sanchez-Carrera, A. Schaefer and F. Abild-Pedersen, J. Phys. Chem. C, 2017, 121, 4261–4269 CrossRef CAS.
- K. C. Lai, D.-J. Liu and J. W. Evans, J. Chem. Phys., 2023, 158, 104102 CrossRef CAS PubMed.
- K. C. Lai, J. W. Evans and D.-J. Liu, J. Chem. Phys., 2017, 147, 201101 CrossRef PubMed.
- K. C. Lai, D.-J. Liu and J. W. Evans, Phys. Rev. B, 2017, 96, 235406 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00140g |
| ‡ Current address: Fritz Haber Institut der Max Planck Gesellschaft, 14195 Berlin, Germany. |
| This journal is © The Royal Society of Chemistry 2023 |