Synthesis, crystal structure, DFT, and photovoltaic studies of BaCeCuS₃

Abstract

We report the synthesis of single crystals of the quaternary sulfide, BaCeCuS₃, for the first time by heating a polycrystalline sample of BaCeCuS₃ with an excess of KCl flux inside a vacuum-sealed fused silica tube. The crystal structure of the compound is determined by a single-crystal X-ray diffraction study which shows that it crystallizes in the primitive orthorhombic crystal system (space group: Pnma) with cell constants of a = 10.6740(13) Å, b = 4.1200(6) Å, and c = 13.409(2) Å. The structure is best described as a pseudo-two-dimensional structure where tetrahedral CuS₄ and octahedral CeS₆ units serve as the main building blocks. The polyanionic 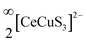layers in the structure are separated by the presence of electropositive Ba²⁺ cations. The optical absorption study on the polycrystalline sample of BaCeCuS₃ shows a semiconducting nature with a direct bandgap of 1.8(2) eV consistent with the green color of the sample. The temperature-dependent thermal conductivity (k_tot) measurements on the polycrystalline BaCeCuS₃ sample reveal an extremely low value of k_tot (0.32 W m⁻¹ K⁻¹) at 773 K. DFT calculations were carried out to obtain the electronic structure of the title compound. Our theoretical studies predict a high value of the thermoelectric figure of merit (>1) for BaCeCuS₃ by optimization of the charge carriers. To also explore a practical application of BaCeCuS₃, a liquid junction solar cell was fabricated: TiO₂/CdS/BaCeCuS₃/S_n²⁻/S²⁻/MWCNTs@Ni, and the cell delivered an efficiency enhanced by ∼45% compared to the one without the sulfide. The performance improvement is affected by the hole conducting properties of BaCeCuS₃, which allows facile hole transfer from CdS to the polysulfide, increases the charge separation, and hence increases the efficiency.

---

1. Introduction

Quaternary mixed metal chalcogenides of alkali (A)/alkaline-earth (Ak) metals, transition metals (M), and lanthanides (Ln) are well known to show a variety of physical properties, including superconductivity,¹ magnetism,^2,3 non-linear optics,⁴ photovoltaics,⁵ topological quantum science,⁶ thermoelectric properties,⁷ and applications like luminescent materials⁸ and infrared windows.⁹ Among these quaternary chalcogenides, a family of compounds with a general formula of (A/Ak)MLnQ₃ (Q = chalcogens = S, Se, and Te) is recognized for their structural diversity depending on the type of elements present in these structures. These phases are commonly referred to as 1113-phases, and more than 200 structures are reported for this family of compounds.¹⁰ These structures are quite flexible in terms of the compositions and oxidation states of metals. Thus, these 1113-phases can accommodate various types of cations. For instance, A or Ak atoms can be substituted by Pb/Th, and Ln atoms can be replaced by transition metals or early actinides (An),¹¹ which prefer octahedral coordination environments. These (A/Ak)MLnQ₃ types of structures are mainly categorized into three subtypes based on the formal oxidation state of the constituent elements: Type-I, A⁺M⁺M'⁴⁺(Q²⁻)₃ [M = Cu⁺ or Ag⁺; M' = Zr⁴⁺/Hf⁴⁺/Np⁴⁺],¹² Type-II, Ak²⁺M⁺Ln³⁺(Q²⁻)₃,^13,14 and Type-III, A²⁺M⁺M'³⁺(Q²⁻)₃ [M' = Sc³⁺/Y³⁺].¹⁵ The electropositive A⁺ and Ak²⁺ cations in these structures mainly serve as electron donors. The main frameworks of these structures are made up of metal-centered tetrahedra and octahedra of chalcogen atoms. The A⁺ and Ak²⁺ cations are packed in between the main polyanionic framework of transition metal/lanthanide/actinide atoms and chalcogen atoms.^16,17 These quaternary 1113-type chalcogenides crystallize in seven unique structural types: KZrCuS₃ (space group: Cmcm), Eu₂CuS₃ (Pnma), Ba₂MnS₃ (Pnma), BaCuLaS₃ (Pnma), NaCuTiS₃ (Pnma), TaCuTiTe₃ (P2₁/m), and BaAgErS₃ (C2/m).¹⁰

In the last twenty years, metal or main-group chalcogenides have been mainly investigated for their potential thermoelectric properties (TE). TE devices are capable of transforming heat energy directly into electricity without any moving parts. Alternatively, these devices can also create temperature gradients by using electricity and thus are used in compact refrigerators for localized cooling. TE materials mainly work on the Seebeck (for electricity generation) and the Peltier effect (for cooling). The efficiency of the thermoelectric material is expressed by the dimensionless figure of merit (zT), which is defined as zT = (S²σ/k_tot)T, where the parameters S (Seebeck coefficient), σ (electrical conductivity), and k_tot [total thermal conductivity that consists of an electrical contribution (k_el) and lattice contribution (k_lat)] are the functions of the absolute temperature (T). For a thermoelectric material, a high value of zT can be achieved by realizing a high-power factor (S²σ) value and a low thermal conductivity value¹⁸ simultaneously at the same temperature. A few examples of the current state-of-the-art TE materials are Bi₂Te₃,¹⁹ doped-AgSbTe₂,²⁰ PbTe,²¹ and SnSe.²²

Surprisingly, the TE properties of these 1113 phases were not studied in the past, and these compounds were neglected until recent theoretical studies suggested the possibility of high zT in some of the Cu-containing layered compounds such as TlCuZrSe₃, BaCuYTe₃, and KZrCuSe₃.²³ Preliminary studies of the TE properties of polycrystalline BaScCuTe₃ are indeed interesting, with low thermal conductivity values.¹⁵ The Kanatzidis group recently reported six new compounds of the 1113-family with a general formula of ACuZrQ₃ (A = Rb, Cs; Q = S, Se, and Te).¹² An ultralow thermal conductivity value of ∼0.35 W m⁻¹ K⁻¹ was observed for a polycrystalline sample of RbCuZrTe₃ at 573 K. The ultralow thermal conductivity of this compound was attributed to the rattling of Rb⁺ cations in the structure at high temperatures.

Apart from the TE properties of quaternary mixed metal chalcogenides, many of these compounds are also explored for possible photovoltaic applications. Examples include Cu(In,Ga)(S,Se)₂,²⁴ Cu₂ZnSn(S,Se)₄,²⁵AkCu₂SnS₄ (Ak = Ba,Sr), BaCu₂SnS_4−xSe_x²⁶etc. These quaternary compounds in thin film form show promising solar power conversion efficiency. Cd-free Cu(In,Ga)(S,Se)₂ chalcogenide-based thin film solar cells have been known to be good photovoltaic absorbers having a very high power conversion efficiency (PCE) of 23.35%,²⁷ but due to the toxicity and inadequacy of Cd, In, and Ga, the production of these materials is limited despite them having good PCE. Again, to the best of our knowledge, these 1113-type compounds, which offer a variety of bandgaps ranging from 0.5–2.0 eV, have not yet been subjected to photovoltaic studies.

Motivated by the promising TE and photovoltaic properties of some of the quaternary chalcogenides, we have synthesized single crystals of the quaternary mixed metal sulfide BaCeCuS₃ that belongs to the 1113-family to study its structure by single crystal X-ray diffraction methods. The synthesis of the polycrystalline sample of the BaCeCuS₃ phase has been reported earlier by Wu et al.²⁸ However, the PXRD pattern is not provided in the publication.²⁸ Thus, it is not known whether the sample was phase pure or whether it contained some secondary phase(s). Only the cell parameters were calculated from the powder X-ray diffraction study of the BaCeCuS₃ sample, and its magnetic properties were examined.²⁸ In this article, we also report the synthesis of a phase pure polycrystalline sample of BaCeCuS₃ for the first time. This work presents the synthesis, structure, and temperature-dependent thermal conductivity studies of the polycrystalline sample of BaCeCuS₃. A detailed DFT study has been carried out to understand the electronic structure, thermoelectric properties, and chemical bonding aspects of the BaCeCuS₃ structure. We have also investigated the preliminary photovoltaic (PV) properties of the polycrystalline sample for the first time, which are promising for future investigations of compounds of the 1113-family.

2. Experimental

2.1. Materials used and synthesis of BaCeCuS₃

The following starting materials were used for the synthesis of single crystals and a polycrystalline sample of BaCeCuS₃: Ba rod (Alfa Aesar, 99%), Ce ingot (Alfa Aesar, 99.8%), Cu shot (Alfa Aesar, 99.9%), S powder (Sigma Aldrich, 99.5%), and KCl powder (SRL, 99.5%). These chemicals were handled inside an Ar-filled glove box. A thin white oxidized layer on the Ba rod was first removed, then small pieces of Ba metal were cut and used in the reactions. Cerium ingots were cut into small pieces for the reactions. KCl powder was dried overnight inside an oven at 373 K before using it in the reactions as a molten flux to grow the single crystals.

2.1.1. Synthesis of a polycrystalline sample of BaCeCuS₃. A polycrystalline sample of BaCeCuS₃ was synthesized by a high-temperature reaction of stoichiometric amounts of the corresponding elements. The reactants, Ba (219.8 mg, 1.601 mmol), Ce (224.4 mg, 1.601 mmol), Cu (101.7 mg, 1.600 mmol), and S (154.1 mg, 4.806 mmol), were loaded into a carbon-coated fused silica tube inside an Ar-filled glove box. The tube was connected to a vacuum sealing line and evacuated (10⁻⁴ Torr) using a diffusion pump, and then it was flame sealed. The sealed tube was placed vertically inside a programmable muffle furnace for heat treatment. Initially, the furnace was heated to 523 K (in 4 h) from room temperature (RT) and was kept at the same temperature for 10 h. The temperature of the furnace was then raised to 1273 K (in 36 h) and the sample was annealed for 96 h at 1273 K. Finally, the reaction mixture was allowed to cool down to RT in 24 h.

The heat-treated sealed tube was cracked open under ambient conditions, and an ingot was found as the reaction product. The ingot was then homogenized into a fine powder inside the Ar-filled glove box using an agate mortar and pestle. A circular pellet (diameter = 8 mm) was then made from the powder by applying high pressure (10.3 MP) using a hydraulic press. The pellet was then transferred into a C-coated fused silica tube, evacuated (10⁻⁴ Torr), and flame sealed. The sealed tube containing the pellet was reheated inside the muffle furnace with the same heating profile as before. A small part of the pellet was then broken off and homogenized into a fine green-colored powder inside the Ar-filled glove box to collect powder X-ray diffraction data for the phase analysis.

2.1.2. Synthesis of single crystals of BaCeCuS₃. Small needle-shaped crystals of BaCeCuS₃ were recrystallized from the polycrystalline sample using a conventional high-temperature molten flux method using an excess of KCl. The melting point of KCl is 1043 K.²⁹ It expected that the powder of BaCeCuS₃ will dissolve in the liquid KCl flux at high temperatures (>1043 K) and recrystallize into crystals on slow cooling of the reaction mixture. A small amount of the polycrystalline powder of the compound was mixed well with the KCl flux in a ratio of 1 : 3 (by weight) of the polycrystalline sample to the flux. The reaction mixture was transferred into a carbon-coated fused silica tube inside an Ar-filled glove box. The tube was then evacuated (10⁻⁴ Torr) and flame sealed. The sealed tube was first heated from RT to 1223 K (in 36 h) and was equilibrated at this temperature for 48 h. The reaction mixture was then slowly cooled down to 1023 K at a rate of 4 K h⁻¹. The temperature of the furnace was then further cooled to 673 K at a rate of 5 K h⁻¹ before shutting off the furnace.

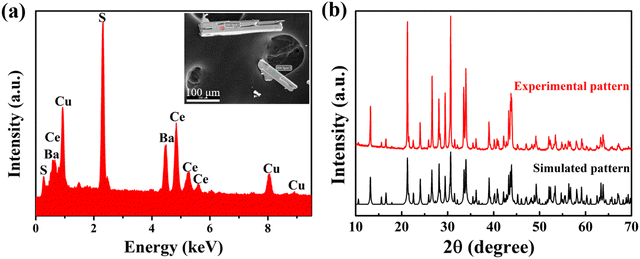
The morphology of the reaction product was first examined with the help of an optical microscope at RT. A few needle-shaped crystals were manually separated from the white colored KCl flux and placed on a carbon-taped stub. The elemental composition of these needle-shaped crystals was analyzed by energy dispersive X-ray spectroscopic (EDX) studies using an octane elite (EDAX Inc., USA) spectrometer that was attached to a field-emission scanning electron microscope (FE-SEM) (JEOL, Japan; Model: JSM 7800F). The EDX data on the crystals were collected at different spots with an accelerating voltage of 15–20 kV. The average composition of the selected crystals was found to be very close to the loaded composition, i.e., ≈1 : 1 : 1 : 3 with respect to Ba, Ce, Cu, and S, without any noticeable contamination from the KCl flux (Fig. 1a).

Fig. 1 (a) The EDX spectrum collected for a typical crystal of BaCeCuS₃. The inset of the figure shows an SEM picture of the BaCeCuS₃ crystals. (b) The experimental PXRD pattern of the polycrystalline BaCeCuS₃ sample, along with the corresponding simulated pattern obtained from the single crystal X-ray diffraction study.

2.2. Powder X-ray diffraction study (PXRD)

The PXRD data of the finely ground homogeneous powdered sample of BaCeCuS₃ was collected at RT using a PAN analytical empyrean diffractometer with a Cu-Kα radiation (λ = 1.5406 Å) source (working voltage and currents were set at 40 kV and 30 mA, respectively). The PXRD data were collected over a 2θ range of 10° to 70° using a θ–2θ geometry for about 30 minutes. The PXRD data were analyzed using Match! version 2 software.³⁰

2.3. Single crystal X-ray diffraction (SCXRD) study of BaCeCuS₃

A Bruker D8 Venture instrument equipped with a Photon III mixed mode detector with graphite monochromatized Mo-Kα radiation (λ = 0.71073 Å) was used for the SCXRD data collection of a BaCeCuS₃ crystal at RT. The crystal was coated with a thin layer of N-paratone oil and was then mounted on the tip of an X-ray transparent micro loop that was affixed to a goniometer head. The working voltage and operating current were set to 50 kV and 1.4 mA, respectively, during diffraction data collection for the crystal. The crystal-to-detector distance was held constant at 50 mm, and the exposure time of 3 sec per frame was used for the entire data collection. The intensity data set was collected as a series of 0.5° steps in ω and ϕ-scans. The cell refinements and data reduction were carried out using the APEX3 program.³¹ The absorption correction for the intensities of the measured reflections was performed using the semiempirical multiscan method of the SADABS program.³²

The SHELXL-14³³ suite of the program was used to solve and refine the crystal structure of BaCeCuS₃. The XPREP³⁴ program suggested two space groups based on the extinction conditions: non-centrosymmetric Pna2₁ (no. 33) and centrosymmetric Pnma (no. 62). The structure was straightforwardly solved and refined in the higher symmetric Pnma space group.

The asymmetric unit of the BaCeCuS₃ structure has six independent atomic positions. The full-matrix-least-squares on F² method³³ in the SHELXL³⁵ program was used to refine the crystal structure. The extinction parameter, scale factors, weight corrections, and atomic positions with anisotropic displacement parameters were refined for the structure. The ADDSYM program of PLATON³⁶ was used to validate the symmetry of the structure. Finally, the atomic positions of the structure were standardized using the STRUCTURE TIDY program.³⁷ Further crystallographic and structure refinement details are provided in Tables 1–3, and in the ESI.†

Table 1 Important crystallographic data for the BaCeCuS₃ structure^a

Chemical formula	BaCeCuS3
a λ = 0.71073 Å, T = 298(2) K. b R(F) = Σ∣∣Fo∣ − ∣Fc∣∣/Σ∣Fo∣ for Fo^2 > 2σ(Fo^2). c R w(Fo^2) = {Σ[w(Fo^2 − Fc^2)^2]/ΣwFo^4}^1/2. For Fo^2 < 0, w = 1/[σ^2(Fo^2) + (0.0173P)^2 + 3.6347P] where P = (Fo^2 + 2Fc^2)/3.
Space group	D ^162h-Pnma
a (Å)	10.6740(13)
b (Å)	4.1200(6)
c (Å)	13.409(2)
V (Å^3)	589.69(15)
Z	4
ρ (g cm^−3)	4.924
μ (mm^−1)	18.67
GOF on F^2	1.068
θ min and θmax	3.04°–30.72°
Completeness to θ = 30.722°	99.3%
R int	0.033
Largest diff. peak and hole (e Å^−3)	1.58, −1.39
Refinement method	Full-matrix least-squares on F^2
R(F)^b	0.021
R w(Fo^2)^c	0.049

---

Table 2 Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Ų)^a for the BaCeCuS₃ structure

Atoms	Wyckoff position	Site symmetry	x	y	z	U iso /U eq
a U iso/Ueq is the one-third value of the trace of the orthogonalized Uij tensor.
Ba1	4c	.m.	0.27459(3)	0.250000	0.00562(3)	0.01562(10)
Ce1	4c	.m.	0.01097(3)	0.250000	0.76097(2)	0.00934(9)
Cu1	4c	.m.	0.23815(7)	0.250000	0.28245(6)	0.01659(16)
S1	4c	.m.	0.05409(12)	0.250000	0.37875(10)	0.0107(2)
S2	4c	.m.	0.25670(12)	0.250000	0.68209(10)	0.0098(2)
S3	4c	.m.	0.41059(13)	0.250000	0.39196(10)	0.0117(2)

---

Table 3 Selected interatomic distances (Å) for the BaCeCuS₃ structure

Atomic pair	Distances (Å)	Atomic pair	Distances (Å)
Ce1–S1	2.8698(10) × 2	Ba1–S2	3.1547(12) × 2
Ce1–S2	2.8196(13)	Ba1–S3	3.2363(11) × 2
	2.8283(13)
Ce1–S3	2.8336(10) × 2	Ba1⋯Ba1	4.1200(6) × 2
Cu1–S1	2.3511(15)	Ba1⋯Cu1	3.6356(8) × 2
			3.7322(10)
Cu1–S2	2.4614(9) × 2	Ce1⋯Cu1	3.3908(7) × 2
			3.4137(7) × 2
Cu1–S3	2.3546(15)	Ce1⋯Ce1	4.1200(6) × 2
Ba1–S1	3.2376(11) × 2
	3.3622(14)

---

2.4. Solid-state ultraviolet-visible (UV-vis) spectroscopy

The optical bandgap study of the polycrystalline sample of BaCeCuS₃ was performed at RT. The polycrystalline sample was mixed with a small amount of dried BaSO₄, which acts as a standard reference for the optical absorption study. The reflectance versus wavelength data were collected over the wavelength range of 2400 nm to 400 nm using a Shimadzu UV-3600 instrument. The Kubelka–Munk equation α/S = (1 − R)²/2R (where α, S, and R are the absorption coefficient, scattering coefficient, and reflectance, respectively)³⁸ was used to calculate the bandgap of the sample by converting the reflectance data into absorption data. The value of the direct bandgap of the sample was calculated using a Tauc plot.³⁹

2.5. Thermal conductivity measurements as a function of temperature

The temperature-dependent thermal diffusivity (D) of the polycrystalline sample of BaCeCuS₃ was measured in the 323 K- 773 K range. The finely ground polycrystalline sample of BaCeCuS₃ was compacted into a circular pellet (diameter = 8 mm, thickness ∼2 mm) at RT by applying high pressure (10.3 MP) using a hydraulic press. The pellet was then sealed inside a carbon-coated fused silica tube under vacuum (10⁻⁴ Torr). To obtain a dense sample for the thermal diffusivity measurements, the circular pellet inside the sealed tube was sintered at 1123 K for 12 h. The sintered pellet was then subjected to the total thermal conductivity (k_tot) measurements.

The value of k_tot (= D × d × C_p) for the sample was calculated by multiplying the D-value with the experimental density (d) and heat capacity (C_p) values.⁴⁰ The density of the circular pellet was calculated using the Archimedes method and it was found to be 4.63 g cm⁻³. This density of the circular pellet was compared with the theoretical density and was found to be about 94% of the theoretical density as measured using the Archimedes method.⁴¹ The C_p value was determined using the Dulong-Petit law.⁴² A LINSEIS XFA 500 system that uses a xenon flash lamp to irradiate the sample was used to measure the thermal diffusivity of the circular pellet of the BaCeCuS₃ sample. Before placing the pellet into the system, the surface of the pellet was coated with a thin layer of graphite to reduce the heat loss after irradiation. During the measurements, liquid N₂ was used to cool the infrared (IR) detector. The Xe flash lamp gradually starts to heat up the pellet from the bottom, and a high-speed IR detector measures the developed temperature over the top surface of the pellet as a function of time. The measurements were performed under vacuum to avoid oxidation of the sample at higher temperatures, and the thermal diffusivity data were obtained at an interval of 50 K. Three thermal diffusivity data sets were collected at each temperature, and an average of the values was taken to calculate the total thermal diffusivity. An experimental error of 10% is associated with the calculated total thermal conductivity values. The microstructure of the pellet was also examined after the thermal diffusivity measurements using a field-emission electron microscope (FE-SEM) (JEOL, Japan; Model: JSM 7800F).

2.6. Fabrication of a photoanode and solar cell using the polycrystalline BaCeCuS₃ sample

The following reagents were used to prepare the photoanode and solar cell. A fluorine-doped tin oxide (FTO) coated glass with a sheet resistance of ∼25 Ω cm² was purchased from Pilkington. The TiO₂-P25 powder, fumed silica, and Ni-foam were purchased from Evonik, Cabosil, and Gelon, respectively. Acetyl acetone, Triton X-100, methanol, ethanol, cadmium acetate [Cd(CH₃COO)₂·2H₂O], multi-walled carbon nanotubes (MWCNTs), and sodium sulfide (Na₂S) were purchased from Merck. Ultra-pure water with a resistivity of ∼18.2 MΩ cm was obtained through a Millipore Direct-Q3 UV system.

2.6.1. Preparation of the photoanode. A TiO₂ slurry was prepared by mixing 300 mg of P25 powder with 1.5 mL of acetylacetone, 8.5 mL of deionized water, and 20 mg of Triton X-100. Then the slurry was coated on the FTO coated glass after covering it using scotch tape and exposing only 0.1 cm². The TiO₂-coated films were then dried at 333 K for 30 min and then annealed at 773 K for 30 min. Following the same method, a second layer of TiO₂ was deposited. Then the TiO₂-coated FTO electrode was immersed in a 40 mM aqueous solution of TiCl₄ and kept at 343 K for 30 min. Afterward, the electrode was washed with deionized water and annealed at 773 K for 30 min.

A layer of CdS was deposited over the TiO₂-coated FTO electrodes by a successive ionic layer adsorption reaction (SILAR) method. In two separate beakers, solutions of 0.1 M cadmium acetate and sodium sulfide in methanol were prepared. At first, the TiO₂ electrodes were dipped in a Cd²⁺ ion-containing beaker and kept there for 2 min. Then the electrodes were allowed to dry at RT. After drying, the electrodes were dipped in a S²⁻ ion-containing beaker for 2 min and then dried at RT. This completes one cycle of SILAR.

Similarly, five more cycles of SILAR were carried out to prepare the CdS/TiO₂ electrodes. Then the electrodes were dried at 333 K for 2 days in an oven. The polycrystalline BaCeCuS₃ (5 mg) sample was dispersed in 10 mL of toluene. Then 2 drops of the dispersion were drop-cast on the CdS/TiO₂ electrode, dried, and the BaCeCuS₃/CdS/TiO₂ electrode was ready for use.

2.6.2. Fabrication of the solar cell. An aqueous mixture of 1 M Na₂S and 1 M S was prepared, and then 5 wt% of fumed silica was added and dispersed by continuous stirring with the help of a glass rod for 15 min to obtain a polysulfide gel electrolyte. For the counter electrode (CE), MWCNTs (10 mg) were dispersed in 10 mL of isopropanol via ultrasonication for 30 min. Then, 3 to 4 drops of the dispersion were drop-cast over a Ni foam substrate and dried at 333 K for 30 min and the MWCNT/Ni foam CE was ready. The solar cells were fabricated by sandwiching the polysulfide gel between the photoanode and the CEs in the following configurations: FTO/TiO₂/CdS/S_n²⁻/S²⁻/MWCNTs@Ni and FTO/TiO₂/CdS/BaCeCuS₃/S_n²⁻/S²⁻/MWCNTs@Ni.

2.7. Current (I) and voltage (V) measurements of the solar cells

The I–V measurements of the solar cells were recorded on a Newport Oriel 3A solar simulator coupled with a Keithley 2420 source meter. A 450W xenon arc lamp was used as the light source with a light intensity of 100 mW cm⁻² and of air mass (AM) 1.5G illumination; the spatial uniformity of the irradiance was determined by calibration with a 2 cm × 2 cm Si reference cell and it was affirmed using a Newport power meter.

2.8. Theoretical and computational methodology

The density functional (DFT)⁴³ calculations are performed using the plane-wave expansion formalism as implemented in the VASP package.⁴⁴ The Kohn-Sham equation is solved by expanding the single-particle wavefunctions based on plane waves using the kinetic energy cutoff of 320 eV (or higher). The electrostatic potentials of the ionic cores are approximated using the projected augmented wave (PAW) pseudopotentials.⁴⁵ For Ba, Cu, S, and Ce atoms, the (5s², 5p⁶, 6s²), (3d¹⁰, 4s¹), (3s², 3p⁴), (5s², 5p⁶, 5d¹, 6s²) electrons are treated as valence electrons, respectively. In the case of Ce, the 4f electrons are treated as frozen and as the core states. Further, the formal valency of Ce is assumed to be 3. In general, the self-interaction errors in presently available density functionals lead to an incorrect description of f-electrons. However, this shortcoming may be circumvented by treating the 4f electrons as the core electrons. The exchange–correlation (XC) effects are treated using the Perdew-Burke-Ernzerhoff (PBE)⁴⁶ form of the generalized gradient approximation (GGA) and SCAN (meta-GGA)⁴⁷ schemes. The integrations in reciprocal space are performed by sampling the Brillouin zone of BaCeCuS₃ using (6 × 14 × 5) Monkhorst-Pack k-point meshes, respectively. The atomic Hellmann-Feynman forces are reduced up to ∼0.02 eV Å⁻¹ (or less) in order to obtain optimized crystal unit cells. The total energies converged to 10⁻⁶ eV cell⁻¹ to attain the self-consistent field (SCF) in the calculations. The thermoelectric parameters are calculated using the Boltzmann transport theory within the rigid band approach.⁴⁸ The ESI† file briefly summarizes the methodologies used to compute the optical⁴⁹ and thermoelectric parameters.

3. Results and discussion

3.1. Synthesis and crystal structure

The polycrystalline sample of BaCeCuS₃ was synthesized by the stoichiometric reaction of elements at 1273 K using a solid-state sealed tube method. All of the observed reflections in the experimental PXRD pattern of the polycrystalline BaCeCuS₃ sample were indexed satisfactorily with the simulated pattern obtained from the single-crystal structure data. Thus, the polycrystalline BaCeCuS₃ sample is phase pure (Fig. 1b).

The single crystals of BaCeCuS₃ were recrystallized by heating the polycrystalline sample in an excess of molten KCl flux. The slow cooling of the reaction mixture from 1223 K to RT resulted in the formation of needle-shaped crystals of the quaternary chalcogenide. The approximate yield of the crystals was about 50%.

Crystal structure description of the BaCeCuS₃ structure:. The SCXRD study at ambient temperature shows that BaCeCuS₃ crystallizes in the orthorhombic centrosymmetric Pnma (no. 62) space group. The crystal structure of BaCeCuS₃ is isotypic to the well-known Eu₂CuS₃⁵⁰ structure type. The unit cell parameters of the BaCeCuS₃ structure are provided in Table 1.

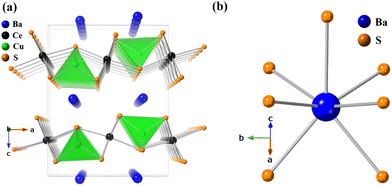
The crystal structure of BaCeCuS₃ is pseudo-two-dimensional in nature, as evident from Fig. 2a. The crystal structure is made up of six crystallographically independent atoms: Ba1, Ce1, Cu1, S1, S2, and S3, all with the same site symmetry (.m.). Each Ce atom in this structure is bonded to six S atoms having distorted octahedral geometry, whereas the Cu atom is coordinated to four S atoms to form a distorted CuS₄ tetrahedron (Fig. 3). The distortion in the geometry of the CuS₄ tetrahedra presumably results from steric factors since Cu⁺ (d¹⁰) has a closed cell electronic configuration. Thus, the role of the electronic effect in the distortion of the polyhedra could be ruled out.

Fig. 2 (a) The unit cell structure of BaCeCuS₃ and (b) the Ba coordination environment.

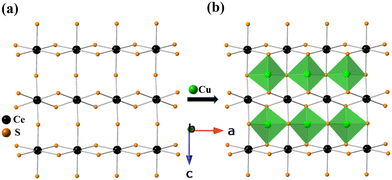Fig. 3 The views of (a) the CeS₆ octahedral units and a fragment of the (b) 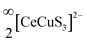layer along the [010] direction in the BaCeCuS₃ structure.

The tetrahedron of CuS₄ shares its four edges with the four octahedra of CeS₆, resulting in the formation of the polyanionic 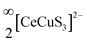layers that are extended in the [100] direction. These CuS₄ and CeS₆ polyhedra are organized in an alternate … tet oct tet oct … fashion along the [010] direction in the 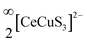layers of the BaCeCuS₃ structure, as shown in Fig. 3. The Ba²⁺ cations act as a space filler and an electron donor in the structure. The S atoms around the Ba²⁺ in the structure have a mono-capped trigonal prism geometry, as each Ba²⁺ coordinates with seven S atoms (Fig. 2b).

The Ce–S bond distances in BaCeCuS₃ (2.8196(13) – 2.8698(10) Å) are comparable to the Ce³⁺–S distances found in the quaternary sulfide BaCe₂MnS₅ (2.811(9) – 3.104(1) Å).⁵¹ The Cu–S bond distances in BaCeCuS₃ (2.3511(15) – 2.4614(9) Å) are also in good agreement with the related quaternary sulfide CsCuCeS₃ (2.319(3) – 2.413(2) Å).⁵²

The Ba–S interatomic distances in BaCeCuS₃ range from 3.1254(19) Å to 3.612(2) Å. These distances are similar to those found in BaErCuS₃ (3.106(2) – 3.407(2) Å) and BaCu₃GaS₄ (3.2156(19) – 3.2949(16) Å).⁵³

The partition of charges to individual atoms in the BaCeCuS₃ structure is straightforward as the structure does not have any homoatomic bonding. The charge-balanced formula of the compound can be written as Ba²⁺Ce³⁺Cu⁺(S²⁻)₃.

3.2. The optical absorption bandgap study of polycrystalline BaCeCuS₃

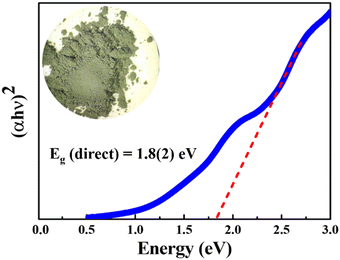
The absorption spectrum of the polycrystalline BaCeCuS₃ sample was collected at ambient temperature in the wavelength region starting from 2400 nm to 400 nm. The bandgap of the sample is deduced by extrapolating the linear region of the Tauc plot,³⁹ as shown in Fig. 4. A direct bandgap value of 1.8(2) eV is estimated for the polycrystalline BaCeCuS₃ (Fig. 4). Hence, we can conclude that the compound BaCeCuS₃ is a narrow bandgap semiconductor.

Fig. 4 The solid-state direct bandgap Tauc plot for the polycrystalline BaCeCuS₃ sample.

3.3. Thermal conductivity study of polycrystalline BaCeCuS₃

The total thermal conductivity (k_tot) of the sintered cold-pressed polycrystalline sample of BaCeCuS₃ was investigated in the temperature range of 323 K to 773 K. The k_tot value is the summation of the lattice thermal conductivity (k_lat) and electrical thermal conductivity (k_el) values of a crystalline sample. The BaCeCuS₃ sample shows a gradual decrease in the k_tot values on raising the temperature, as shown in Fig. 5. The k_tot value of the polycrystalline sample decreases from 0.62 W m⁻¹ K⁻¹ (at 323 K) to an extremely low value of 0.32 W m⁻¹ K⁻¹ at 773 K. As the BaCeCuS₃ sample has a relatively large bandgap, the contribution of k_el to the k_tot value is expected to be extremely small. Hence, it is safe to presume that the k_tot value for the sample is very close to the k_lat value. A similar ultralow thermal conductivity value of ∼0.35 W m⁻¹ K⁻¹ at 573 K is reported for the structurally related RbCuZrTe₃.¹² The rattling of relatively loosely bound Rb⁺ cations and the distortion of Zr-coordinated octahedra in RbCuZrTe₃ are responsible for the ultralow value of the lattice thermal conductivity (k_lat). On similar lines, it is expected that the rattling of Ba²⁺ cations in the BaCeCuS₃ sample at high temperatures should also lead to low values of k_lat. However, detailed studies of the thermal parameters of Ba atoms in the BaCeCuS₃ sample at high temperatures are required to confirm this conjecture.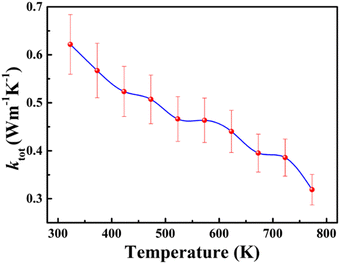

Fig. 5 The temperature-dependent total thermal conductivity (k_tot) for the polycrystalline sample of BaCeCuS₃.

The extremely small value of 0.32 W m⁻¹ K⁻¹ at 773 K for the BaCeCuS₃ sample is promising for thermoelectric applications. However, the relatively larger bandgap of this compound (1.8(2) eV) is not suitable for achieving an excellent thermoelectric figure of merit (zT). A substantial amount of electron/hole doping is required to improve the electrical conductivity of this sample in the future to achieve a reasonable zT value.

The microstructure of the fractured pellet of the BaCeCuS₃ sample was examined using FE-SEM to investigate the grain size, density, and packing of the polycrystals in the pellet. The SEM micrographs of the fractured surface of the pellet revealed that the pellet is reasonably dense with no apparent preferential orientation of the microcrystals (Fig. 6).

Fig. 6 The cross-sectional (a–c) FE-SEM images of the BaCeCuS₃ pellet used for the thermal conductivity measurements. The surface of the pellet is also visible in (b).

3.4. Solar cell study

The current density (J) versus voltage (V) plot (Fig. 7) of the FTO/TiO₂/CdS/S_n²⁻/S²⁻/MWCNTs@Ni foam cell under a 1 sun illumination condition showed an open circuit voltage (V_OC) = 460 mV, short circuit current density (J_SC) = 24.75 mA cm⁻², fill factor (FF) = 34.5%, and efficiency (η) = 3.93%. The CdS absorbs blue-green photons, and its bandgap is ∼2.3 eV.⁵⁴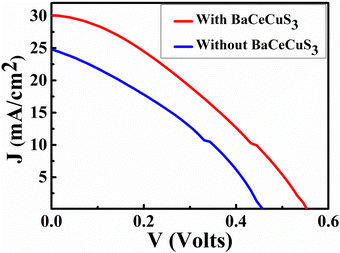

Fig. 7 The J vs. V plot of the FTO/TiO₂/CdS/S_n²⁻/S²⁻/MWCNTs@Ni, and FTO/TiO₂/CdS/BaCeCuS₃/S_n²⁻/S²⁻/MWCNTs@Ni foam cell.

Under illumination, electronic excitation takes place in CdS. Due to the favorable alignment of the conduction band (CB), the electron moves from the CB of CdS to the CB of TiO₂. Then via an external circuit, it reaches the electrocatalytic MWCNTs@Ni foam-based counter electrode (CE), where it reduces the oxidized redox species (S_n²⁻). The reduced redox species (S²⁻) reaches the photoanode, captures the holes from the valence band (VB) of CdS, and gets converted to S_n²⁻. The FTO/TiO₂/CdS/BaCeCuS₃/S_n²⁻/S²⁻/MWCNTs@Ni foam cell showed V_OC = 560 mV, J_SC = 29.74 mA cm⁻², FF = 34.35%, and η = 5.71%, respectively. The V_OC, J_SC, and η increased by 21.7%, 20.2%, and 45.3%, respectively due to the coating of the polycrystalline BaCeCuS₃. This is due to the hole-conducting ability of p-type BaCeCuS₃ and its semiconducting nature, which enhances the charge separation and reduces recombination at the photoanode/electrolyte interface.

3.5. Theoretical studies of BaCeCuS₃

3.5.1. Electronic structure of BaCeCuS₃. Next, we analyze the theoretical structural parameters and the electronic structure of BaCeCuS₃. Table 4 shows the computed lattice constants, which are found to be in good agreement with the experiment values. The computed fractional coordinates of atoms in the unit cell are also in excellent agreement with the experimental values (<0.01%). As expected, the GGA lattice parameters are slightly overestimated (∼0.1%).⁵⁵ The GGA computed bandgap for BaCeCuS₃ is found to be 1.15 eV which is underestimated as compared to the experimental values of ∼1.8 eV. The computed bandgap value is along the expected trend since, in general, the semi-local approximations such as GGA are known to systematically underestimate the bandgaps by as much as ∼50% as compared to the experiments. The bandgap of BaCeCuS₃ computed using the SCAN meta-GGA scheme is found to be 1.40 eV. As expected, the bandgap estimates obtained using the SCAN meta-GGA scheme are improved.

Table 4 Theoretical estimates of the lattice parameters and bandgap (eV) of BaCeCuS₃ obtained using the GGA and SCAN (meta-GGA) XC schemes

			a (Å)	b (Å)	c (Å)	V (Å^3)	E g (eV)
BaCeCuS3	Cal.	GGA	10.794	4.134	13.528	603.83	1.15
		SCAN	10.770	4.125	13.501	603.83	1.40
	Exp.		10.674	4.120	13.409	589.69	1.8(2)

---

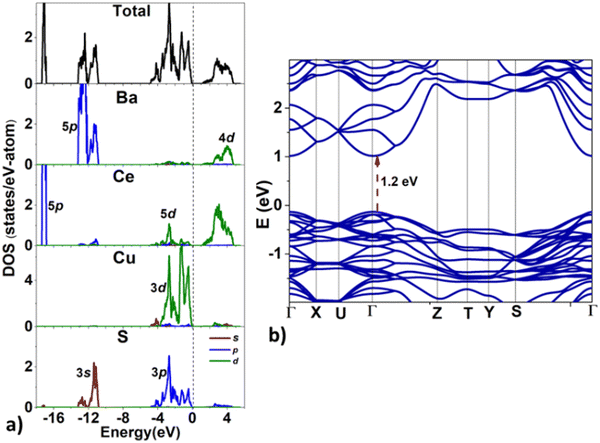
Next, we analyze the electronic structure of BaCeCuS₃. The density of states (DOS) and the band structure plots for BaCeCuS₃ are shown in Fig. 8. The valence band maximum (VBM) and the conduction band minimum (CBM) can be seen at 0 and ∼1.2 eV, respectively. The valence band (VB) in the energy window of ∼−5 eV < E < 0 eV, is formed primarily due to the overlap of Cu-3d and S-3p states along with a minor contribution of Ce-5d states. The VB in the −13.5 < E < −11 eV region comprises Ba-5p and S-3s states. The sharp peak in the VB at ∼−17 eV is formed by localized Ce-5p states. The conduction band (CB) in the ∼1.2 eV < E < 5 eV energy region is mainly formed by antibonding Ce-5d and Cu-3d states. The band structure (see Fig. 8b) suggests that the bandgap is direct since both VBM and CBM are located at the Brillouin zone center (Γ-point).

Fig. 8 (a) The total and projected density of states (DOS) and the (b) band structure for BaCeCuS₃. The dotted line in (a) indicates the valence band maximum. The high symmetry k-points in the Brillouin zone are Γ ≡ (0,0,0), , , , , , and .

3.5.2. The COHP and Bader charges for the atoms of the BaCeCuS₃ structure. Next, we estimate the relative strength and nature of the bonding between atoms from the computed projected crystal orbital Hamilton populations (COHP).⁵⁶Fig. 9a shows the negative COHP or –COHP versus energy (E) plot for Ba–S, Ce–Cu, Ce–S, and Cu–S pairs in BaCeCuS₃. In general, the positive and negative values of –COHP (E) indicate the bonding and antibonding nature of the states as a function of energy. Fig. 9b shows the integrated –COHP or –ICOHP values obtained after integrating the COHP up to the valence band maximum, indicating the energy to which all states are occupied. The –ICOHP values are indicative of the relative strength of the bonding between atoms. Incidentally, the Ce–S bond strength is higher than that of the Cu–S bond in the BaCeCuS₃ structure. The Ba–S bond strength is significantly smaller than that of the Ce–S and Cu–S pairs.

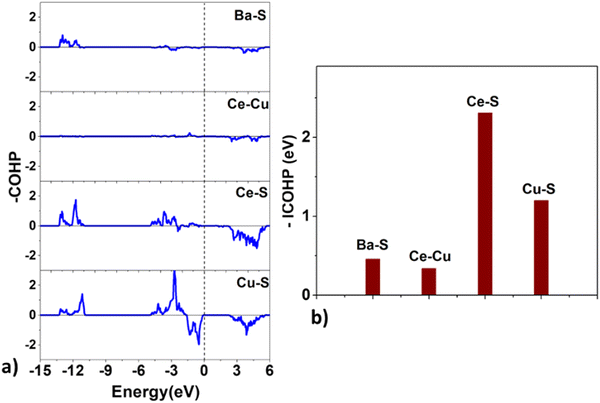Fig. 9 The (a) crystal orbital Hamilton population (COHP) and the (b) integrated COHP for the Ba–S, Ce–Cu, Ce–S, and Cu–S bonds in BaCeCuS₃.

Surprisingly, the COHP plot suggests a strong antibonding character at the Fermi level for the Cu–S bonds, and their bond strengths are smaller than those of the Ce–S pair. This deviation could be due to factors that depend on the local chemical environment and/or the overlap of atomic wavefunctions/orbitals. It is well known that the DFT-based description of f-electrons is tricky and challenging due to the presence of self-interaction errors.

Next, we estimate the relative charge transfer between bonding atoms from the computed Bader charges (Q_B).⁵⁷ The relative degree of covalent and ionic bonding between atoms as well as their oxidation states may also be estimated from the magnitudes of the ionic Bader charges. In the case of BaCeCuS₃, the Q_B for Ba, Ce, Cu, and S ions are found to be +1.46, +1.83, +0.34, and –1.23, respectively. The Q_B values indeed show the electron transfer from metals (Ba, Ce, and Cu) to more electronegative S atoms. However, these values are smaller than the formal oxidation states of the ions, i.e., Ba²⁺Ce³⁺Cu⁺(S²⁻)₃ as discussed earlier in Section 3.1. This is suggestive of the presence of some degree of covalent bonding in addition to the predominant ionic bonding in the system.

3.5.3. The optical and thermoelectric (TE) properties of BaCeCuS₃. Next, we compute the optical absorption coefficient (α) from the electronic band structure as discussed in Section S1 of the ESI† file. Fig. 10 shows α, αE, and (αE)² as a function of the photon energy (E) for BaCeCuS₃. As can be seen, α increases in the range ∼1.5 ≤ ħω ≤ 3.5 eV in the optical region. The onset of α is indicative of an electronic bandgap which may differ from the optical bandgap. The theoretical α value may vary with the experimental results due to contributions from other factors, such as sample preparation, quality, etc., in the latter.

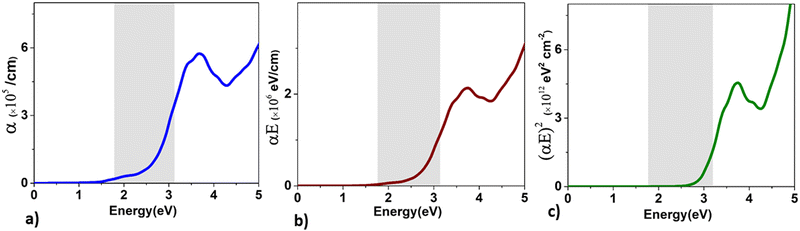Fig. 10 The variation of the values of (a) α, (b) (αE), and (c) (αE)² as a function of energy for BaCeCuS₃. The symbols α and E are the absorption and energy, respectively.

The thermoelectric parameters, such as the figure of merit (zT), Seebeck coefficient (S), power factor, etc., are also calculated from the electronic band structure and using the Boltzmann transport theory within the rigid band approach. The relevant equations to calculate these parameters are provided in Section S2 of the ESI† file.

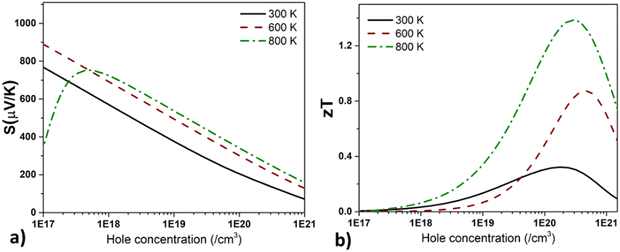
The 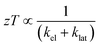where k_el and k_lat are the electronic and lattice (phonon) components of total thermal conductivity, respectively. In our calculation, k_lat is treated as an external parameter with values taken from the experimental data shown in Fig. 5 in Section 3.3. The thermoelectric parameters are computed as a function of temperature and carrier (hole and electron) concentration. The Seebeck coefficient (S) and zT for p-doped BaCeCuS₃ as a function of the carrier (holes) concentration at temperatures 300 K, 600 K, and 800 K are shown in Fig. 11. The magnitude of S is found to vary in the range ∼900 > S > μV K⁻¹ for carrier concentrations ∼10¹⁷ < p < 10²¹ cm⁻³. As expected, the Seebeck coefficient (S) decreases (increases) with increasing the carrier concentration (temperature). Using a model based on nearly free electrons, a parabolic band, and an energy-independent scattering approximation,⁵⁸ the S can be shown to depend on temperature (T), carrier concentration (p), and carrier effective mass (m*) as 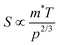. However, it may be noted that S depends on the complete band structure details and thus may deviate from this expression. Fig. 11a shows such a deviation in S at T = 800 K. zT attains a maximum value for hole concentration of ∼3 × 10²⁰ cm⁻³ as can be seen in Fig. 11b. Further, zT also increases with temperature as expected. As evident, the computed values of the TE parameters vary significantly with the value of the carrier concentration in the compound. Due to these and other reasons, the theoretical thermoelectric (TE) parameters may not be compared directly with the experimental values. Nevertheless, the ab initio results of the TE parameters may be useful in order to understand the dependence of these parameters on the electronic band structure.

Fig. 11 The variation of the (a) Seebeck coefficient (μV K⁻¹) and the (b) zT value as a function of hole concentration for BaCeCuS₃.

4. Conclusions

We have successfully synthesized single crystals and polycrystalline sample of BaCeCuS₃ using high-temperature molten flux and solid-state synthesis methods, respectively. The SCXRD study revealed that BaCeCuS₃ adopts an orthorhombic Eu₂CuS₃ structure type (space group Pnma). The main building blocks of the structure are the CeS₆ octahedron and CuS₄ tetrahedron. The BaCeCuS₃ structure is made up of two-dimensional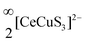 layers that are separated by Ba²⁺ cations that mainly act as space fillers. The optical absorption study of the polycrystalline sample of BaCeCuS₃ establishes its semiconducting behavior with an optical bandgap value of 1.8(2) eV. The total thermal conductivity value (k_tot) of the compound is extremely low (0.32 W m⁻¹ K⁻¹) at 773 K. The electronic structure, optical and thermoelectric properties of BaCeCuS₃ are explored theoretically using DFT methods. The computed structural parameters of the compound are found to be in good agreement with the experimental data. The nature and relative strength of the chemical bonds are explored by analyzing the computed COHP and Bader atomic charges. The optical and thermoelectric parameters are computed using the electronic band structure. The practical significance of BaCeCuS₃ was demonstrated by using it as a hole transport layer in a solar cell (TiO₂/CdS/BaCeCuS₃/S_n²⁻/S²⁻/MWCNTs@Ni), and the cell exhibited a superior efficiency of 5.7%, about 1.5 times greater than that of the cell without this layer. The enhanced performance is attributed to the efficient hole injection from CdS to the polysulfide, via BaCeCuS₃, that maximizes the charge separation and increases the efficiency.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

JP thanks DST-SERB, the Government of India (GOI), for the financial support under the core research grant (Grant number: CRG/2021/003641) and IIT Hyderabad for the research facilities. OS thanks UGC for the research fellowship. SY thanks the Ministry of Education (MOE), GOI, for the Prime Minister's Research Fellowship (PMRF). The authors also gratefully acknowledge DST-FIST (SR/FST/ETI-421/2016) for the SEM-EDX facility used in this work.

References

1. C. D. Malliakas, D. Y. Chung, H. Claus and M. G. Kanatzidis, J. Am. Chem. Soc., 2016, 138, 14694–14698.
2. M. Sturza, J. M. Allred, C. D. Malliakas, D. E. Bugaris, F. Han, D. Y. Chung and M. G. Kanatzidis, Chem. Mater., 2015, 27, 3280–3290.
3. G. Panigrahi, S. Jana, M. Ishtiyak, S. Narayanswamy, P. P. Bhattacharjee, K. V. Ramanujachary, M. K. Niranjan and J. Prakash, Dalton Trans., 2021, 50, 6688–6701.
4. D. Sahoo and R. Naik, J. Non-Cryst. Solids, 2022, 597, 121934.
5. A. Le Donne, V. Trifiletti and S. Binetti, Front. Chem., 2019, 7, 297.
6. H. Zhang, C.-X. Liu, X.-L. Qi, X. Dai, Z. Fang and S.-C. Zhang, Nat. Phys., 2009, 5, 438–442.
7. Y. Shi, A. Assoud, S. Ponou, S. Lidin and H. Kleinke, J. Am. Chem. Soc., 2018, 140, 8578–8585.
8. B. O. Dabbousi, J. Rodriguez-Viejo, F. V. Mikulec, J. R. Heine, H. Mattoussi, R. Ober, K. F. Jensen and M. G. Bawendi, J. Phys. Chem. B, 1997, 101, 9463–9475.
9. Y. Zhang, G. Hong, Y. Zhang, G. Chen, F. Li, H. Dai and Q. Wang, ACS Nano, 2012, 6, 3695–3702.
10. L. A. Koscielski and J. A. Ibers, Z. Anorg. Allg. Chem., 2012, 638, 2585–2593.
11. J. Prakash, A. Mesbah, J. C. Beard and J. A. Ibers, Z. Anorg. Allg. Chem., 2015, 641, 1253–1257.
12. C. C. Laing, B. E. Weiss, K. Pal, M. A. Quintero, H. Xie, X. Zhou, J. Shen, D. Y. Chung, C. Wolverton and M. G. Kanatzidis, Chem. Mater., 2022, 34, 8389–8402.
13. N. O. Azarapin, A. S. Aleksandrovsky, V. V. Atuchin, T. A. Gavrilova, A. S. Krylov, M. S. Molokeev, S. Mukherjee, A. S. Oreshonkov and O. V. Andreev, J. Alloys Compd., 2020, 832, 153134.
14. K. Eickmeier, R. Poschkamp, R. Dronskowski and S. Steinberg, Eur. J. Inorg. Chem., 2022, e202200360.
15. M. Ishtiyak, S. Jana, R. Karthikeyan, M. Ramesh, B. Tripathy, S. K. Malladi, M. K. Niranjan and J. Prakash, Inorg. Chem. Front., 2021, 8, 4086–4101.
16. Y. Yang and J. A. Ibers, J. Solid State Chem., 1999, 147, 366–371.
17. S. Maier, J. Prakash, D. Berthebaud, O. Perez, S. Bobev and F. Gascoin, J. Solid State Chem., 2016, 242, 14–20.
18. D. M. Rowe, CRC Handbook of Thermoelectrics, CRC Press, Boca Raton, 1995.
19. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5, 1800904.
20. S. Roychowdhury, T. Ghosh, R. Arora, M. Samanta, L. Xie, N. K. Singh, A. Soni, J. He, U. V. Waghmare and K. Biswas, Science, 2021, 371, 722–727.
21. C.-H. Su, Prog. Cryst. Growth Charact. Mater., 2019, 65, 47–94.
22. L.-D. Zhao, C. Chang, G. Tan and M. G. Kanatzidis, Energy Environ. Sci., 2016, 9, 3044–3060.
23. M. F. Mansuetto, P. M. Keane and J. A. Ibers, J. Solid State Chem., 1992, 101, 257–264.
24. L. Xu, L.-L. Deng, J. Cao, X. Wang, W.-Y. Chen and Z. Jiang, Nanoscale Res. Lett., 2017, 12, 159.
25. H. Xin, J. K. Katahara, I. L. Braly and H. W. Hillhouse, Adv. Energy Mater., 2014, 4, 1301823.
26. D. Shin, T. Zhu, X. Huang, O. Gunawan, V. Blum and D. B. Mitzi, Adv. Mater., 2017, 29, 1606945.
27. M. Nakamura, K. Yamaguchi, Y. Kimoto, Y. Yasaki, T. Kato and H. Sugimoto, IEEE J. Photovolt., 2019, 9, 1863–1867.
28. P. Wu, A. E. Christuk and J. A. Ibers, J. Solid State Chem., 1994, 110, 337–344.
29. D. Zhou, J. Dong, Y. Si, F. Zhu and J. Li, Minerals, 2020, 10, 250.
30. New Match! version 3.13 (Build 227), https://www.crystalimpact.com/news/20220314b.htm.
31. APEX3: Program for Data Collection on Area Detectors, Bruker AXS Inc., Madison, WI, USA, 2016.
32. G. M. Sheldrick, A short history of SHELX, Acta Cryst. A, 2008, 64, 112–122.
33. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct, Chem., 2015, 71, 3–8.
34. G. M. Sheldrick, XPREP Version 2008/2, Bruker AXS Inc., Madison, 2008.
35. G. M. Sheldrick, Acta Cryst. A, 2008, 64, 112–122.
36. A. L. Spek, Single-crystal structure validation with the program PLATON, J. Appl. Cryst., 2003, 36, 7–13.
37. L. M. Gelato and E. Parthé, J. Appl. Cryst., 1987, 20, 139–143.
38. G. Kortüm, Reflectance Spectroscopy, Springer, Berlin, Heidelberg, 1969.
39. A. Z. Johannes, R. K. Pingak and M. Bukit, IOP Conf. Ser. Mater. Sci. Eng., 2020, 823, 012030.
40. H. Wang, W. D. Porter, H. Böttner, J. König, L. Chen, S. Bai, T. M. Tritt, A. Mayolet, J. Senawiratne, C. Smith, F. Harris, P. Gilbert, J. Sharp, J. Lo, H. Kleinke and L. Kiss, J. Electron. Mater., 2013, 42, 1073–1084.
41. R. Piazza, S. Buzzaccaro, E. Secchi and A. Parola, Soft Matter, 2012, 8, 7112–7115.
42. E. I. Andritsos, E. Zarkadoula, A. E. Phillips, M. T. Dove, C. J. Walker, V. V. Brazhkin and K. Trachenko, J. Phys.: Condens. Matter, 2013, 25, 235401.
43. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
44. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
45. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
48. G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145.
49. Y. M. Andreev, V. V. Atuchin, G. V. Lanskii, N. V. Pervukhina, V. V. Popov and N. C. Trocenco, Solid State Sci., 2005, 7, 1188–1193.
50. P. Lemoine, D. Carré and M. Guittard, Acta Cryst. C, 1986, 42, 390–391.
51. M. Wakeshima and Y. Hinatsu, J. Solid State Chem., 2000, 153, 330–335.
52. A. C. Sutorik, J. Albritton-Thomas, T. Hogan, C. R. Kannewurf and M. G. Kanatzidis, Chem. Mater., 1996, 8, 751–761.
53. Y. Liu, X.-D. Song, R.-C. Zhang, F.-Y. Zhou, J.-W. Zhang, X.-M. Jiang, M. Ji and Y.-L. An, Inorg. Chem., 2019, 58, 15101–15109.
54. H. Chen, W. Fu, H. Yang, P. Sun, Y. Zhang, L. Wang, W. Zhao, X. Zhou, H. Zhao, Q. Jing, X. Qi and Y. Li, Electrochim. Acta, 2010, 56, 919–924.
55. M. Probert, Contemp. Phys., 2011, 52, 77.
56. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
57. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
58. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.

---

Footnote

† Electronic supplementary information (ESI) available: Additional crystallographic details of the BaCeCuS₃ structure, theoretical calculation details, and results. The CIF file of the BaCeCuS₃ structure was submitted to the joint CCDC/FIZ Karlsruhe deposition service. CCDC 2125729. For the ESI and crystallographic data in CIF or other electronic formats see DOI: https://doi.org/10.1039/d2nj06301h

---