Open Access Article
Open Access ArticleInfluence of junction resistance on spatiotemporal dynamics and reservoir computing performance arising from an SWNT/POM 3D network formed via a scaffold template technique†
Saman
Azhari‡
 *ab,
Deep
Banerjee
ab,
Takumi
Kotooka
a,
Yuki
Usami
ab and
Hirofumi
Tanaka
*ab,
Deep
Banerjee
ab,
Takumi
Kotooka
a,
Yuki
Usami
ab and
Hirofumi
Tanaka
 *ab
*ab
aResearch Center for Neuromorphic AI Hardware, Kyushu Institute of Technology (Kyutech), 2-4 Hibikino, Wakamatsu, Kitakyushu 8080196, Japan. E-mail: tanaka@brain.kyutech.ac.jp
bGraduate School of Life Science and Systems Engineering, Kyushu Institute of Technology (Kyutech), 2-4 Hibikino, Wakamatsu, Kitakyushu 8080196, Japan
First published on 24th February 2023
Abstract
For scientists in numerous fields, creating a physical device that can function like the human brain is an aspiration. It is believed that we may achieve brain-like spatiotemporal information processing by fabricating an in materio reservoir computing (RC) device because of a complex random network topology with nonlinear dynamics. One of the significant drawbacks of a two-dimensional physical reservoir system is the difficulty in controlling the network density. This work reports the use of a 3D porous template as a scaffold to fabricate a three-dimensional network of a single-walled carbon nanotube polyoxometalate nanocomposite. Although the three-dimensional system exhibits better nonlinear dynamics and spatiotemporal dynamics, and higher harmonics generation than a two-dimensional system, the results suggest a correlation between a higher number of resistive junctions and reservoir performance. We show that by increasing the spatial dimension of the device, the memory capacity improves, while the scale-free network exponent (γ) remains nearly unchanged. The three-dimensional device also displays improved performance in the well-known RC benchmark task of waveform generation. This study demonstrates the impact of an additional spatial dimension, network distribution and network density on in materio RC device performance and tries to shed some light on the reason behind such behavior.
Introduction
It is believed that artificial intelligence (AI) is shaping the future of science and technology.1–3 AI has shown great potential in prediction,4,5 recognition,6–8 and classification9 tasks, ultimately making life safer and more convenient. Currently, AI is a rapidly growing field with unimaginable possibilities. However, due to the independent processing and memory units in the von Neumann based computer architecture, the von Neumann bottleneck is instigated; therefore, attempts to achieve the full spectrum of AI abilities have faced many obstacles.10 Scientists are investigating non-von Neumann architectures such as neuromorphic computing10,11 to overcome these limitations.Neuromorphic computing was introduced as a concept in the 1980s, inspired by the human brain and the functioning of the nervous system, and it began to get much attention due to the development of artificial neural networks (ANNs). ANN is one of the critical constituents of the AI system. Among all types of available ANNs, the recurrent neural network (RNN) deals with time-dependent (temporal) information and is believed to mimic the human brain's ability to learn and understand.11 Recently, reservoir computing (RC) as a computational framework derived from a RNN has emerged,12 which is known in the fields of machine learning as an echo state network (ESN) and computational neuroscience as a liquid-state machine (LSM).13 There are several ways of RC integration. Even so generally in the RC system, the internal state consists of high dimensional recurrently connected nonlinear nodes, treated as black boxes with fixed weights and in the output layer the data are trained to fit a specific target because of the discrimination ability of the system. This is done by updating the output weights usually determined using a simple linear regression model7,12,14 (Fig. S1†). Thus, an RC system is an ideal alternative15 to overcome the complications one may face in fabricating an in materio RNN.
The rapid expansion of ANNs has helped with technological and scientific advancement, but a significant aspect was neglected: the system's ability to perform a task parallelly and energy efficiently. This issue arises due to the von Neumann bottleneck, which is why unconventional computing is getting attention.16 For instance, tens to hundreds of transistors are required to replicate a neuron-synapse circuit behaviour using complementary metal–oxide–semiconductor (CMOS) technology, which is not as energy efficient17,18 as the human brain.
The human brain is the most complex and sophisticated organic computer, capable of performing multiple tasks in parallel quickly and efficiently.19 Unlike the available computational devices, the human brain is three-dimensional (3D) with a dense network of neurons and synapses with task-dependent distribution.20 This network allows infinite possible outcomes because of its topology and its large number of neurons.21 Since fabricating a device capable of processing information like the human brain is the objective, it seems logical to fabricate a device with a similar structure and topology.
One approach for fabricating physical devices that can ideally process spatiotemporal information like the human brain and function like neurons and synapses22 is the use of in materio RC. In materio RC is attracting increasing attention due to the reports of biologically inspired systems such as the octopus robot,23,24 physical systems such as the water bucket,25 and the development of atomic switching devices using nanowires26–28 and nanoparticles29 that behave like memristors. Ultimately, as a result of utilizing the unique dynamic properties observed in such systems, which allow temporal information processing, we would perform computational tasks much more efficiently.12,30 In the studies reported thus far, 2D RC devices with the physical structure and behaviour of RNNs have been fabricated.12,31 Simultaneously 3D RC has been investigated extensively in 3D memristor arrays22,32–34 and quasi-3D nanowire networks.35,36 For instance, a 3D memristive in materio RC array has been reported following an approach similar to that of IC fabrication37,38. However, such devices’ mass production and utilization are not feasible due to the complicated fabrication process. At the same time, neither the 3D memristor array nor the quasi-3D network of nanowires has shown any improvements over their 2D counterparts.36
The other approaches for developing in materio RC devices use solution processable materials.14,29,31 For instance, a nanocomposite of single-walled carbon nanotubes (SWNTs) and polyoxometalate (POM)31 is regarded as a good candidate for such futuristic technologies because it fulfills the primary requirements for in materio RC, i.e., nonlinearity, higher dimensionality, echo state properties, and memory.13,34 To date, devices fabricated using such materials are in 2D, which begs the question of how such a random network of nanomaterials would behave in a 3D network formation. We believe that to fabricate a brain like in-materio RC; there is an easier fabrication path that facilitates the formation larger number of junctions per unit area between input and output nodes with a 3D brain-like structure which eliminates the limitations of 2D devices such as fixed pathlength and uncontrollable distribution.
The scaffold template method is an approach that enables the possibility of fabricating a 3D distribution of nanomaterials.39–44 The scaffold template method has recently been getting considerable attention mainly due to its ability to function as a network backbone, allowing the nanomaterials to embody the template's structure and topology.44 This method is underrated due to overwhelmingly rapid expansion and variation of nanomaterial-based device fabrication methods. Nonetheless, the scaffold template method is excellent for fabricating a device that requires a porous topology with multiple interconnected junctions that could overcome the limitation faced during electrode fabrication in 2D devices.
Herein we report the fabrication of a 3D network of an SWNT/POM nanocomposite capable of performing benchmark tasks of in materio RC. Comparison between the 2D and 3D devices indicates that the fabrication of a 3D reservoir device via the scaffold template method improves the reservoir dynamics and performance. Using the scaffold template approach, we have managed to fabricate a 3D in materio RC device with a higher number of junctions in a small area with limited aggregation and stacking of SWNT/POM, which increased spatiotemporal dynamics and memory capacity. Furthermore, we have tried to shed some light on the reason behind these observations.
Experimental procedure
Materials
Chemical vapor deposition (CVD) synthesized SWNTs (Sigma-Aldrich) with (6, 5) chirality and 0.7–0.9 nm diameter were purified by annealing at 200 °C for 20 h, followed by refluxing in concentrated HCl (12 M) at 110 °C for 1 h to remove the amorphous carbon and Fe catalysts.31,45 The acid treated SWNTs were filtered and washed with deionized water to achieve a pH value of 7 prior to drying at 80 °C to obtain the purified SWNTs. Phosphomolybdic acid hydrate (H3PMo12O40·12H2O, PMo12 hereafter) (Sigma-Aldrich), isopropyl alcohol (IPA) (Wako), acetone (Wako), acetonitrile (Wako), and commercially available Gekiochi melamine sponge (LEC, Inc.) were used as purchased.SWNT/POM preparation
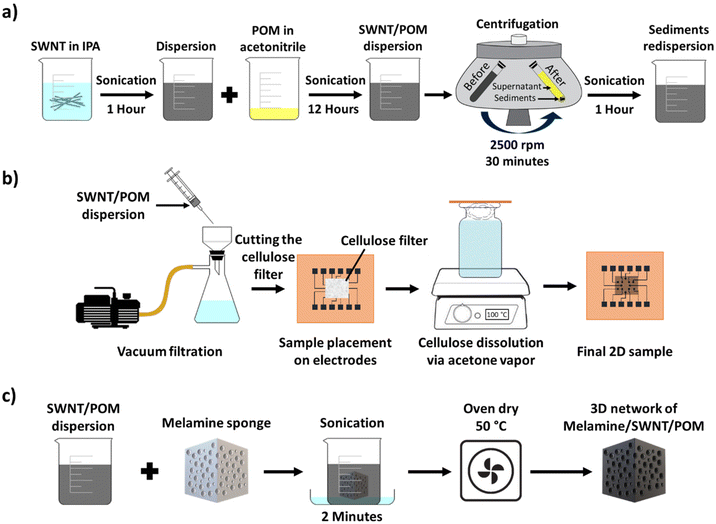
The SWNT/POM nanocomposite was prepared by dispersing 0.5 mg of SWNTs in 10 mL of IPA via sonication (40 kHz) for 1 h. PMo12 (10 mg) was dissolved in 1 mL of acetonitrile via sonication for 5 min. The PMo12 solution was added to the SWNT dispersion, followed by sonication for 4 h in a sonication bath maintained at 10 °C to prevent any damage to the SWNTs. The final dispersion was centrifuged at 2500 rpm, and after discarding the supernatant, the sediments were re-dispersed in 10 mL of IPA via sonication for 1 h.12,31Fig. 1a displays this process.2D device fabrication
To deposit the SWNT/POM thin-film toward the fabrication of 2D devices a vacuum-assisted wet transfer process was utilized.12,31 In short, the SWNT/POM dispersion (0.5 mL) was filtered through 0.1 μm-mesh nitrocellulose filter paper (MCE, Millipore) prior to cutting into a rectangle (0.6 × 0.5 cm) and placing on top of copper electrode pads fabricated using an FR-4 printed circuit board (Fig. S2†). Acetone was drop-cast on the filter paper to assist the attachment of the SWNT/POM film to the substrate. The substrate was then placed on top of a glass vial, filled with acetone and heated to 100 °C to dissolve the remaining cellulose filter paper via acetone vapour for 1 h. One electrode was denoted as the input and the remaining eleven as outputs. Fig. 1b shows the 2D sample preparation process and electrode design.123D device fabrication
The 3D in materio RC devices were fabricated by immersing the melamine sponge (scaffolding template) with the dimensions of 1.25 × 1.25 × 1.25 cm into the SWNT/POM dispersion, followed by sonication for 5 min prior to drying in an oven at 50 °C for 12 h. A 3D printed box was fabricated as a sample holder for 3D devices. The dimensions of the 3D printed box were 1.4 cm × 1.4 cm × 1.4 cm to fit the sample inside. Two holes were placed on each side of the 3D printed box to place the pin headers and adjust the lengths. The diameter of the holes on the 3D printed box was 0.85 mm ± 0.1 mm, adequate to keep the pin headers stationary. Pin headers were used as electrodes. The length of the pin headers was 1.15 cm, of which 0.2 ± 0.05 cm penetrated the 3D samples. Like 2D samples, one of the pins was denoted as the input and the remaining eleven as outputs. The 3D printed box was used to eradicate the possibility of sample deformation and control the size of the contact area between the electrodes and the sample, resembling the electrode pads in the 2D device. Fig. 1c displays the fabrication process.Characterization and measurements
Ultra-high resolution field emission scanning electron microscopy (FE-SEM) (Hitachi S-5200) was utilized to determine the network distribution, density, and topology of 2D and 3D samples. The ten fabricated samples’ (five 2D and five 3D labeled 2D-X and 3D-X with X representing the sample number) current–voltage (I–V) characteristics were recorded under a DC sweeping bias of ±3 V at a scan rate of 40 mV s−1 with a semiconductor parameter analyser (Agilent 4156B) with 50 Ω output impedance. Similarly, I–V measurements with the same parameters were performed on 3D samples with different dimensions and electrode penetration depths to evaluate the influence of an additional spatial dimension and network density on the nonlinear dynamics of the 3D in materio RC device, respectively. Python version 3.10.5 for impedance and phase angle calculation and LTspice XVII for electronic circuit simulation were used. For the samples with different dimensions, the height and length were maintained the same as those of the previously prepared samples, i.e., 1.25 cm, and the thickness was varied to 0.2, 0.7, and 1.25 cm. At the same time, the influence of network density on the nonlinear dynamics of the 3D in materio RC device was investigated by changing the electrode penetration depth to 0 (surface), 0.1, and 0.4 cm ± 0.05 cm in a 3D sample with similar dimensions to the prepared samples, i.e., 1.25 × 1.25 × 1.25 cm.All other tasks such as the I–t measurement, sinusoidal input–output relations for constructing the Lissajous plots, sinusoidal input for Higher harmonic generation and the RC benchmark task of waveform generation, and random pulse input for memory capacity were completed using National Instrument data acquisition PXIe 6363 (DAQ), terminal block SCB-68A and LabVIEW software. For I–t, a constant DC bias voltage of 1, 3, or 5 V for 60 s was supplied via the input. The voltage response was converted into current by placing an additional 2.7 MΩ resistor. The power spectral density (PSD) was obtained by fast Fourier transformation (FFT) of the respective output response of the I–t measurement. The logarithmic plots of the PSD were fitted using the power law given in eqn (1), where ‘P’ is the power, ‘A’ is the population activity, ‘f’ is the frequency, and ‘γ’ is the scale-free exponent.26,27,46,47 Both the FFT and fitting were conducted using OriginPro 2022 software.
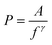 | (1) |
Memory capacity was determined by inputting random pulses of high and low voltages (1 V and 0 V) generated by LabVIEW to the device using DAQ while simultaneously collecting the reservoir states (output voltage) using DAQ for 60 seconds. Three voltages, that is, 1, 3, and 5 V were used as high voltage values. In addition, memory capacity measurement at 3 V was performed on a sample with different volumes to investigate the influence of 3D SWNT/POM network size on memory capacity. For this purpose, a 2.5 × 2.5 × 2.5 cm sample was prepared, and its height was reduced using a razor blade with steps of 0.25 cm after each measurement until the sample reached 2.5 × 2.5 × 1 cm. The memory capacity was determined using eqn (2), where ‘yk(t)’ is the linearly combined output signal trained via linear regression to reconstruct the input signal with k-step delay ‘u(t − k)’, ‘cov’ denotes covariance, and ‘σ2’ means variance. The memory capacity is determined by integrating values calculated at each k-step delay.14,48–51 The memory capacity calculation was performed using Python programming.
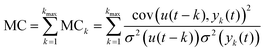 | (2) |
The nonlinear spatiotemporal dynamics between the input and output signals, higher-dimensional information mapping, which allows feature extraction from linearly inseparable input information, and the waveform generation task were examined14,34,52–54 by applying 11 Hz bipolar ±1, ±3, and ±5 V sine waves to the input, and recording the data from 11 outputs simultaneously over a total time of 60 s. The 11 outputs represented the different reservoir states ‘Oi(t)’, with ‘i’ being the number of the output electrode pad during the waveform generation task.
The output signals were transformed from the time domain to the frequency domain using the FFT algorithm to explore the higher dimensional information mapping of the in materio RC device. The devices’ nonlinear spatiotemporal dynamics were examined using the Lissajous plot (V–V), drawn using the input and output signals. The target waves of the square 11 Hz, sawtooth 11 Hz, sine 22 Hz, and sine 33 Hz were produced using the Scipy library in Python to perform the waveform generation task. A total epoch of 1 s was used for the data analysis, with 0.7 s for training and 0.3 s for testing. An offline multiple linear regression training approach was adopted, where the output weights ‘Wi’ of each reservoir state were trained to fit the supervised target waves ‘Y(t)’, using eqn (3) in the Python program.
| Wout = (OTO)−1OTY | (3) |
The bold format indicates that each parameter is in its matrix form and ‘T’ denotes the transpose of the matrix. The trained weights ‘Wout’ were used to construct the test reservoir signal ‘F(t)’ using a weighted linear combination of the reservoir states corresponding to the ‘m’ output electrodes (eqn (4)). The testing performance was evaluated by computing the normalized mean square error (NMSE) using eqn (5) between the output ‘F(t)’ and the target ‘Y(t)’, and the accuracy in eqn (6) over an epoch of 1 s.
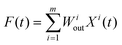 | (4) |
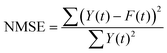 | (5) |
| Accuracy = ((1 − NMSE) × 100) | (6) |
The performances of the 2D and 3D devices were compared quantitatively by fabricating five samples of each (2D-X and 3D-X with X representing the sample number). After the measurement, two steps were taken to plot the scale-free network exponent (γ) and population activity. First, the average value of output nodes for each device was calculated, and then the average value and standard deviation amongst the five samples of each group (2D and 3D) were computed. The last step was sufficient for the memory capacity and waveform generation task accuracy as these quantities are determined by summation of all the output nodes (Fig. S3 and S4†).
Results and discussion
Network topology
Fig. 2a displays the dense distribution of the SWNT/POM network on the 2D substrate in the 2D in materio RC device. Based on the FESEM images there is clearly large SWNT/POM network connectivity in the 2D in materio RC device with a high density of SWNT junctions in the 2D plane. On the other hand, Fig. 2b reveals that in the 3D network, the SWNT/POM network forms on the melamine sponge porous structure (Fig. S5†) that behaves as the network's backbone, forming a unique 3D SWNT/POM network topology which is essentially a 2D SWNT/POM network on a 3D scaffold. The main distinctions between the two networks are the well-established porous structure of the melamine sponge with 99% porosity55 and pore sizes in the range of 100–150 μm56 in addition to the ununiform attachment of the SWT/POM network to the melamine sponge resulting in lower SWNT/POM network density. The presence of blank areas both in 2D and 3D in materio RC devices is clear, although the 3D sample exhibits larger blank surface areas indicating the lower density of conductive paths. Nonetheless the number of junctions (red dots) where a SWNT makes a junction with one or more SWNTs is significantly higher in the 3D network. The number of junctions (neglecting blank regions) in the 2D sample is approximately 2.35 μm−2 while in the 3D sample considering the volume and porosity the number of junctions increases to 174.88 μm−2. The increase in the number of junctions reveals the advantage of a porous scaffold template in fabricating a larger network in a small area.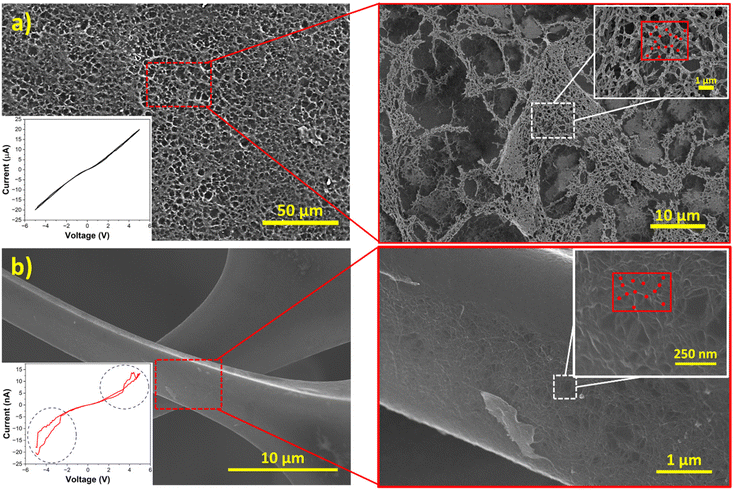 | ||
| Fig. 2 FE-SEM image and I–V characterization (inset) of the (a) 2D and (b) 3D networks of SWNT/POM (the blue dotted circle shows the region with a non-monotonic change in current). | ||
Nonlinearity
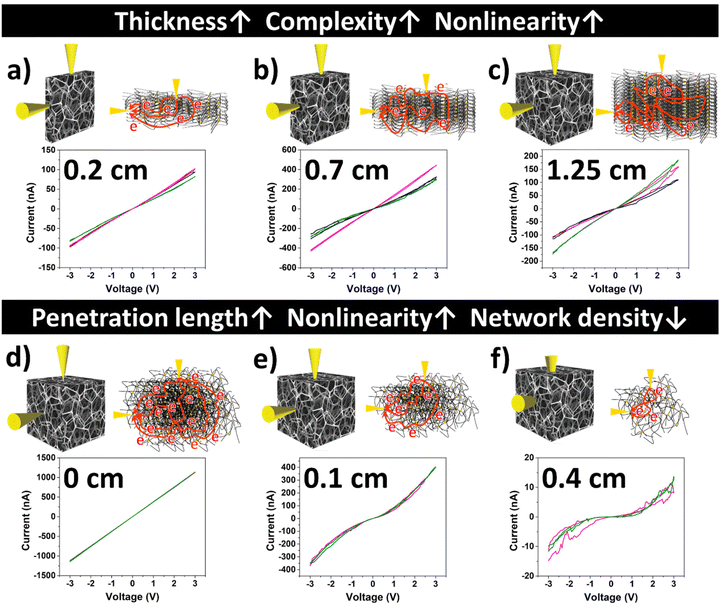
It is evident from the I–V measurements shown in Fig. 2a and b insets that in the 3D sample, the current increases non-monotonically with a simultaneous decrease with increasing bias (blue dotted circles). Such random fluctuations are attributed to the charge–discharge redox arising from POM molecules as supported by Tanaka et al.31 with the cellular automata model and are thus the source of non-linear dynamics. Since, the POM distribution is inhomogeneous, the magnitude of such charge–discharge varies within the network and thus an I–V curve with varying degrees of random fluctuations at different voltage biases is observed in Fig. 2b inset. Although random, they are not insignificant to the performance of the fabricated device. With SWNT/POM being further investigated, it has become clear that such random noise like behaviour is essential for the success of a physical reservoir system. Moreover, current in the 3D device is three orders of magnitude lower than that in the 2D device. Since the POM molecules as the redox-active species are the nonlinear components, the improved nonlinearity is correlated with the interaction of the current with POM molecules.30 On the other hand, since SWNTs are the conductive elements in the SWNT/POM network, the lower current flow in the 3D device indicates a higher junction resistance due to the presence of a higher number of SWNT junctions in the 3D device. These observations are due to the higher surface area of the porous melamine sponge, which results in a complex network topology as confirmed by the FE-SEM images, suggesting the influence of network density and connectivity on the nonlinearity of the SWNT/POM network. To understand how the network density influences the nonlinear dynamics, the thickness of the 3D sample and the electrode penetration length were varied. Although the electrode penetration lengths shown in Fig. 3a–c are closer to the penetration lengths shown in Fig. 3e, it is evident from Fig. 3a and d that the I–V performance of the 3D device on the surface and at low thickness resembles the behaviour of the 2D device (Fig. 2a, inset). In contrast, the increase in the thickness of the device or the electrode penetration length increases the nonlinearity of the 3D devices. The increased nonlinearity due to the additional spatial dimension (Fig. 3b and c) of the SWNT/POM network in the 3D device results from the increase in complexity and network density. However, due to a larger number of conductive paths (low resistance) between the input and output electrodes, the behaviour resembles the result from the sample with a similar electrode penetration length (Fig. 3e). On the other hand, the sample with a high penetration length (Fig. 3f) exhibits strong nonlinearity due to a smaller number of conductive paths (high resistance) between input and output, which increases the probability of larger current interaction with POM molecules, resulting in stronger nonlinearity. The drastic decrease in current and increase in nonlinearity are clearly observed in Fig. 3f. The SWNT/POM 3D network on the porous scaffold template could be modelled as a network of parallel resistors, note that the SWNT/POM network is typically modelled as RC circuits, but here a purely resistive model is utilized due to the DC input and for simple explanation of the mechanism; for a more detailed explanation, please refer to “Higher dimensionality and spatiotemporal dynamics” section. To elucidate the observed behaviour, let us assume a network of parallel resistors, with “RL” signifying the resistance of each conductive path without POM (low resistance), “RH” the resistance of the paths with POM (high resistance) and “RT” the total resistance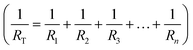 . Let us assume that there are equal numbers of RL and RH pathways (nRL = nRH) due to a homogeneous distribution, and the low and high resistance pathways, RL and RH, respectively, each have constant resistances with RH being 1000 times higher than RL (RH = 1000 × RL). From the results, it is evident that the samples with low penetration depths have low total resistance, and hence a higher number of conductive paths without POM (lowRT = high_nRL), while a sample with a high penetration depth has higher total resistance, and hence a lower number of conductive paths without POM (highRT = low_nRL) (the influence of the increase and decrease in RH is negligible in comparison with that of RL). So, since lowRT < highRT (Fig. 3d–f), based on the Kirchhoff's current law, the decrease in nRL results in a higher amount of current passing through RH resulting in stronger nonlinearity in the sample with a higher penetration depth. This is one of the advantages of an in materio 3D device which allows the change in nonlinear dynamics by repositioning the electrodes, which is not possible in 2D devices.
. Let us assume that there are equal numbers of RL and RH pathways (nRL = nRH) due to a homogeneous distribution, and the low and high resistance pathways, RL and RH, respectively, each have constant resistances with RH being 1000 times higher than RL (RH = 1000 × RL). From the results, it is evident that the samples with low penetration depths have low total resistance, and hence a higher number of conductive paths without POM (lowRT = high_nRL), while a sample with a high penetration depth has higher total resistance, and hence a lower number of conductive paths without POM (highRT = low_nRL) (the influence of the increase and decrease in RH is negligible in comparison with that of RL). So, since lowRT < highRT (Fig. 3d–f), based on the Kirchhoff's current law, the decrease in nRL results in a higher amount of current passing through RH resulting in stronger nonlinearity in the sample with a higher penetration depth. This is one of the advantages of an in materio 3D device which allows the change in nonlinear dynamics by repositioning the electrodes, which is not possible in 2D devices.
Information processing
An in materio RC device able to process spatiotemporal information follows a scale-free network topology.26,47 A scale-free network is a network in which the degree distribution (probability distribution of links at nodes in the network) follows a power-law distribution, as shown in eqn (1)26,27,46,47 (Fig. S6 and S7†). γ in eqn (1) is related to the underlying physics of the system and the mechanism of charge carrier transport. In a percolated network, the value of γ can depend on several collective properties of the system, such as the distribution of carrier mobilities, the concentration of carriers, and the dimensionality of the network. In a homogeneous system with a single carrier type and single mobility, the value of γ is related to the dimensionality of the system. In a heterogeneous system with multiple carrier types and mobilities, the value of γ can be affected by the distribution of carrier mobilities. In percolated networks, the value of γ can also depend on the concentration of carriers and the degree of percolation.57–59 In addition, the variable γ reflects the frequency dependence of the power spectral density (PSD) of a signal, and it can provide information about the dynamic properties of the system being studied.60,61 Specifically, γ can provide insight into the temporal correlations of the fluctuations in the system.62,63 For a scale-free network, ‘γ’ must be greater than 1.64 Reports suggest that the ‘γ’ value in the network of SWNT/POM is greater than 1.65 Furthermore, ‘A’ signifies the number of neurons firing simultaneously, and an increase or decrease in this value indicates an overall increase or decrease in the population activity, respectively.The charge transfer in the SWNT/POM model has been associated with the cellular automata model, in which the noise generation because of the redox reaction resulting in charge accumulation and distribution amongst neighbouring POM molecules is correlated with potential difference.31,65 In this model, the number of charges (proportional to the potential) of a POM particle at time t and the threshold number of electrons for discharge operation are defined by ai,j(t), and aTH, respectively. When ai,j < aTH, a small number of charges are transferred to one of the neighbours, whereas when ai,j > aTH, all charges should be released and transferred to their neighbours.31,65 To determine how the spatial dimension influences this property, DC voltage was applied to the device, and the output current was recorded and used to determine the PSD. The γ value was determined by fitting the PSD using eqn (1). The results indicate that the ‘γ’ value is nearly unchanged (Fig. 4a and S8†).
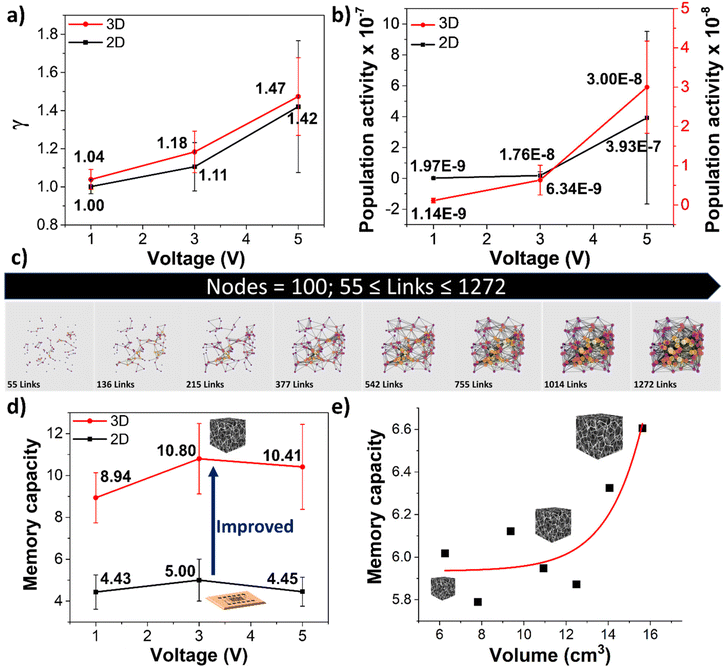 | ||
| Fig. 4 (a) The scale-free network exponent and (b) population activity of the 2D and 3D devices, obtained by applying DC voltage as the input while collecting current output and calculating the γ and A values, respectively, by fitting the PSD curve using eqn (1); (c) 3D network graph visualized using Python for a network of 100 nodes with an increasing number of links; memory capacity of (d) 2D and 3D devices and (e) 3D network of SWNT/POM with different volumes, obtained by applying random pulses and calculation using eqn (2). | ||
The value of ‘γ’ in the SWNT/POM in materio RC devices is used to characterize the noise colour; particularly it is a measure of noise type.65–67 The ‘γ’ value obtained from the samples corresponds to flicker noise or pink noise, signifying the same amount of energy at each octave, meaning that the low-frequency noises have higher intensities than the high-frequency noises, but the collective intensity of noise at lower and higher frequency ranges (octaves) remains the same, which can be modelled as a bouncing ball model.68 The scale-free network model implies numerous nodes with a low degree (few links) and very few with a high degree (many links). So, the constructive and destructive interferences due to the charge accumulation and distribution between the neighbouring POM molecules behave as if the interaction happens slowly (low frequency) at the spots where POM molecules interact with another POM molecule. In contrast, the interaction is much faster (high frequency) at the spots where POM molecules interact with thousands of other POM molecules. At the same time, the energy dissipation is not high enough for the information to disappear and not low enough to interfere with the lower frequency noises.
This similarity of the ‘γ’ value signifies a similar probability of the scale-free network distribution, suggesting that even by increasing the spatial dimension of the device, the distribution of charge in the SWNT/POM network is an intrinsic property and may be affected by the morphology of the constituent materials, i.e., the length and diameter of SWNTs and physical attachment of POM molecules to SWNTs. Nonetheless, a slight increase in the value of ‘γ’ in the 3D sample signifies the decline in the number of links between the nodes (faster energy dissipation). In addition, the population activity correlated with noise amplitude in the SWNT/POM network,65 as shown in Fig. 4b and Fig. S7,† and decreased by one order of magnitude in the 3D devices. Since the population activity corresponds to noise amplitude, its decline is due to an increased spatial dimension and the transformation of network topology (porous structure). The porous structure of the scaffold template affects the connectivity, so due to such complexities resulting in lower connectivity, the input signal travels through a lower number of nodes, which indicates the lack of connectivity in the 3D in materio RC devices due to the ununiform attachment of SWNT/POM to the scaffold template. This argument was further visualized via Python programming which exhibits the same number of nodes while the number of links increases (Fig. 4c). As it is evident from Fig. 4c, the increase in the number of links increases the connectivity and network activity depicted using coloured circles at the junctions (the bigger circles correspond to nodes with multiple numbers of links and activity). The results indicate that the 3D device may enable the powerful information processing ability of the in materio RC devices by controlling the attachment of SWNT/POM to the scaffold template and tuning the network connectivity to process information similar to biological neuronal networks, such as the human brain.69
Memory capacity
The recurrent connections present in an RC system result in the recollection of the input signal for successive time steps. The memory capacity quantifies the ability of the RC system to reconstruct its past input signal using its current state.14,48–51In the case of an in materio RC system, unlike software-based RC systems, such properties could not be tuned by changing the program algorithm or the variable. Furthermore, there would always be a physical limitation in in materio RC devices. For instance, considering Fig. 2 and 3, it is evident that the network density and connectivity can ultimately influence the network complexity. This effect is because the SWNT/POM concentration per unit area has an upper and lower limit corresponding to the saturation and lack of conductive paths, respectively, to form a stable nonlinear network.
The results suggest that by increasing the spatial dimension of the device from 2D to 3D, we could resolve such complications. As shown in Fig. 4d and Fig. S9,† the 3D devices exhibit higher memory capacity, indicating that the 3D in materio RC device could reconstruct information from a higher number of time steps in the past than the 2D device. This observation suggests the dependency of the in materio RC device performance and parameters on its physical structure, and network connectivity and topology.70–72 This observation was further examined by finding a correlation between network size (template volume) and memory capacity, as shown in Fig. 4e. The data suggest an exponential growth in memory capacity corresponding to template volume (network size) 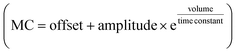 with a growth rate of 0.6. The data suggest a significant (α = 0.1) positive correlation between memory capacity and volume, r(5) = 0.701, P = 0.079. Although these values may differ depending on the distribution of SWNT/POM on the scaffold template, it does not change the fact that by manipulating the template size (network size) and network topology, we can tune the in materio RC device parameters and ultimately design a device suitable for a specific task.
with a growth rate of 0.6. The data suggest a significant (α = 0.1) positive correlation between memory capacity and volume, r(5) = 0.701, P = 0.079. Although these values may differ depending on the distribution of SWNT/POM on the scaffold template, it does not change the fact that by manipulating the template size (network size) and network topology, we can tune the in materio RC device parameters and ultimately design a device suitable for a specific task.
Higher dimensionality and spatiotemporal dynamics
As reported, the network of SWNT/POM can generate nonlinear dynamics resulting from the redox reaction occurring in POM molecules and their capacitive tendencies.31 The oscillations of charged particles due to these redox reactions generate higher-dimensional information mapping.The Lissajous plot of the 3D devices (Fig. S10c and S11†) exhibits a range of nearly linear and nonlinear dynamics between the input and output signals (<20%), depending on the position of the output electrode with respect to the input electrode. Although similar tendencies were observed in the 2D devices (Fig. S10a and S11†), the variation tended to be more linear with little to no spatiotemporal dynamics (>60%). These results indicate the dominance of the nonlinear spatiotemporal dynamics in the 3D device, making it ideal for in materio RC tasks compared to the 2D devices. The 3D devices exhibit more robust higher dimensionality (Fig. S10d and S12†) than the 2D devices (Fig. S10b and S12†). The higher harmonic generation tendencies are stronger and more prominent in the 3D devices than in the 2D devices due to the complex distribution of the SWNT/POM nanocomposite on the scaffold template, which decreases the conduction path and increases the redox probability of POM molecules (nonlinear spatiotemporal dynamics). Although electrons follow all paths during conduction, they are inclined to take the path of least resistance. At the same time, the lower resistance in the 2D device was shown to disrupt the interactions of electrons with POM molecules, resulting in a lack of charge accumulation necessary for a strong redox reaction, and hence the weaker higher harmonics generation.
This could be explained by considering that the SWNT/POM network is modelled as a parallel RC circuit,73–75 in which the resistor (R) represents the SWNT junction resistance and capacitor (C) represents the interface between SWNTs and POM molecules. To understand the observed behaviour, first we should realize that the impedance (Z) and phase angle (Φ) in the parallel RC circuit are 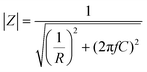 and Φ = arctan(−R2πfC), respectively, where f is the alternating current (AC) frequency (11 Hz), and R and C are the SWNT junction resistance and the SWNT–POM interface, respectively. As shown in Fig. S13a and b,† as the junction resistance increases, the impedance and phase angle increase, and based on the impedance relationship with voltage and current
and Φ = arctan(−R2πfC), respectively, where f is the alternating current (AC) frequency (11 Hz), and R and C are the SWNT junction resistance and the SWNT–POM interface, respectively. As shown in Fig. S13a and b,† as the junction resistance increases, the impedance and phase angle increase, and based on the impedance relationship with voltage and current 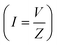 , the increase in impedance decreases the current (I). The increase in impedance results in a smaller current flow between input and output electrodes. Considering that capacitance (interface between SWNTs and POM) is the same in the samples (similar SWNT to POM ratio) and
, the increase in impedance decreases the current (I). The increase in impedance results in a smaller current flow between input and output electrodes. Considering that capacitance (interface between SWNTs and POM) is the same in the samples (similar SWNT to POM ratio) and 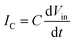 , we could conclude that
, we could conclude that 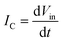 and the current drop results in a slower rate of voltage change, resulting in the presence of relatively more distinct spatiotemporal dynamics (greater phase angle) as shown in Fig. S13d and f.†
and the current drop results in a slower rate of voltage change, resulting in the presence of relatively more distinct spatiotemporal dynamics (greater phase angle) as shown in Fig. S13d and f.†
As shown in Fig. S13† the change in the junction resistance and capacitance has a significant impact on the spatiotemporal dynamics of the in materio RC device. From these results and the observation of 2D and 3D device performances, we can conclude that the presence of higher junction resistance in the 3D sample is due to scaffold template's specific surface area and topology, resulting in less conductive junctions as observed in the FESEM images (Fig. 2), I–V measurements (Fig. 2 and 3) and lower population activity (Fig. 4b).
RC waveform generation benchmark tasks
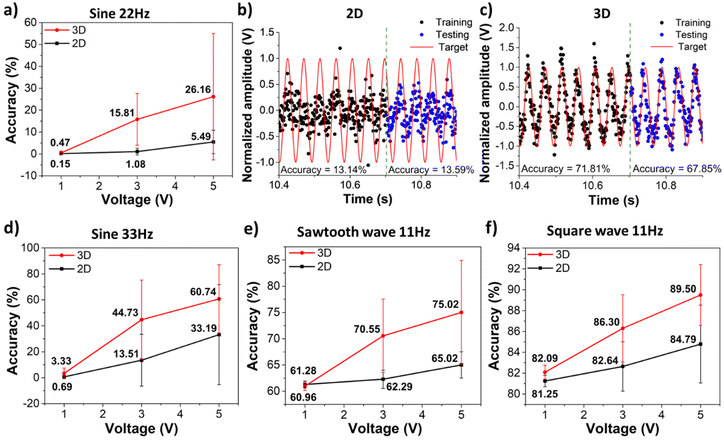
The waveform generation benchmark task is a well-established RC task, in which a sinusoidal waveform is applied to the RC system as the input, and the output signals are linearly combined via linear regression to fit a specific target waveform as shown in Fig. S4† and eqn (3) and (4). The error and accuracy of the fit are then determined viaeqn (5) and (6). The RC system's nonlinear spatiotemporal dynamics and higher dimensional information mapping allow the output signals to fit the target waveform accurately (refer to the ESI, “Waveform generation”†).As shown in Fig. 5, the 3D device increases the waveform generation task accuracy (eqn (5) and (6)), with an average of 20% for the 22 Hz sinusoidal target wave and 30% for the 33 Hz sinusoidal target wave. The additional spatial dimension of the device creates more complexity, enabling more robust spatiotemporal nonlinear dynamics and higher-dimensional mapping, which differ from sample to sample (Fig. S14–S17†) due to the variation in CNT–POM distribution, resulting in the alteration of electron interactions with POM molecules, and the SWNT/POM network as discussed in the previous sections. From Fig. 5, we see that the mean accuracy for all the target waves increases with bias through the same amount of training. This observation confirms the improved performance of the 3D network topology of the SWNT/POM network over the 2D one.
Conclusions
The 2D and 3D in materio RC devices were fabricated, and their reservoir performances were evaluated. The I–V, FFT, and Lissajous results signify a higher degree of nonlinearity, more robust higher harmonic generation, and nonlinear spatiotemporal dynamics in the 3D device. The results suggest that these tendencies may result from the scaffold template's porous structure, which influences the conductive path formation and adds complexity to the network structure. The scale-free network exponent shows similar values in the 2D and 3D devices, implying that the distribution of the SWNT/POM network is an intrinsic property. Nonetheless, the decline in the population activity of the 3D devices implies that the addition of a spatial dimension in the network topology necessitates a better control of network formation and connectivity. The memory capacity in 3D devices is more significant than that of 2D devices, and exponential growth in memory capacity correlated to network size is confirmed. Finally, the performance of the 3D in materio RC device in the waveform generation benchmark task is more significant than that of its 2D counterpart. These results signify the impact of an additional spatial dimension, network density, network distribution, and device topology on the in materio RC device performance. The complex network topology in 3D devices opens up the possibility of superior nonlinear spatiotemporal dynamics and memory.Author contributions
Saman Azhari: conceptualization, data curation, formal analysis, investigation, methodology, project administration, software, validation, visualization, writing – original draft, writing – review & editing; Deep Banerjee: methodology, validation, writing – review & editing; Takumi Kotooka: methodology, software; Yuki Usami: resources; Hirofumi Tanaka: funding acquisition, methodology, project administration, resources, supervision, validation, visualization, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the JSPS KAKENHI [grant no. 19K22114, 19H02559, 20K21819, and 22H01900], JSPS Core-to-Core program [FY2022-6], and JST CREST [grant no. JPMJCR21B5]. The work was partially conducted at the Kitakyushu Foundation for the Advancement of Industry, Science and Technology, Semiconductor Center, supported by the Nanotechnology Platform Program of the Ministry of Education, Culture, Sports, Science, and Technology (MEXT), Japan (F-19-FA-0005).Notes and references
- Z. Dlamini, F. Z. Francies, R. Hull and R. Marima, Comput. Struct. Biotechnol. J., 2020, 18, 2300–2311 CrossRef CAS PubMed.
- S. Sundin and C. Braban-Ledoux, Comput.-Aided Civ. Infrastruct. Eng, 2001, 16, 143–157 CrossRef.
- C. Koo, Z. Xiang, U. Gretzel and M. Sigala, Electron. Mark., 2021, 31, 473–476 CrossRef PubMed.
- F. E. Shamout, Y. Shen, N. Wu, A. Kaku, J. Park, T. Makino, S. Jastrzębski, J. Witowski, D. Wang, B. Zhang, S. Dogra, M. Cao, N. Razavian, D. Kudlowitz, L. Azour, W. Moore, Y. W. Lui, Y. Aphinyanaphongs, C. Fernandez-Granda and K. J. Geras, npj Digit. Med., 2021, 4, 80 CrossRef PubMed.
- H. Chung and K.-s. Shin, Neural Comput. Appl., 2020, 32, 7897–7914 CrossRef.
- N. Padoy, Minim. Invasive Ther. Allied Technol., 2019, 28, 82–90 CrossRef PubMed.
- C. Du, F. Cai, M. A. Zidan, W. Ma, S. H. Lee and W. D. Lu, Nat. Commun., 2017, 8, 2204 CrossRef PubMed.
- M. Farronato, P. Mannocci, M. Melegari, S. Ricci, C. M. Compagnoni and D. Ielmini, Adv. Mater., 2022, 2205381 CrossRef PubMed.
- Y. Xu, Z. Jia, L. B. Wang, Y. Ai, F. Zhang, M. Lai and E. I. C. Chang, BMC Bioinf., 2017, 18, 1–17 Search PubMed.
- C. Yang, X. Qiao and Y. Chen, IPSJ Trans. Syst. LSI Des. Methodol, 2019, 12, 53–64 CrossRef.
- M. M. Botvinick and D. C. Plaut, Psychol. Rev., 2006, 113, 201–233 Search PubMed.
- D. Banerjee, S. Azhari, Y. Usami and H. Tanaka, Appl. Phys. Express, 2021, 14, 105003 CrossRef CAS.
- M. Lukoševičius and H. Jaeger, Comput. Sci. Rev., 2009, 3, 127–149 CrossRef.
- Y. Usami, B. van de Ven, D. G. Mathew, T. Chen, T. Kotooka, Y. Kawashima, Y. Tanaka, Y. Otsuka, H. Ohoyama, H. Tamukoh, H. Tanaka, W. G. van der Wiel and T. Matsumoto, Adv. Mater., 2021, 33, 1–9 Search PubMed.
- M. Dale, J. F. Miller, S. Stepney and M. A. Trefzer, Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2016, vol. 9726, pp. 49–61 Search PubMed.
- V. G. Cerf, Commun. ACM, 2014, 57, 7 Search PubMed.
- S. H. Jo, T. Chang, I. Ebong, B. B. Bhadviya, P. Mazumder and W. Lu, Nano Lett., 2010, 10, 1297–1301 CrossRef CAS PubMed.
- G. Indiveri, B. Linares-Barranco, T. J. Hamilton, A. van Schaik, R. Etienne-Cummings, T. Delbruck, S. C. Liu, P. Dudek, P. Häfliger, S. Renaud, J. Schemmel, G. Cauwenberghs, J. Arthur, K. Hynna, F. Folowosele, S. Saighi, T. Serrano-Gotarredona, J. Wijekoon, Y. Wang and K. Boahen, Front. Neurosci., 2011, 5, 1–23 Search PubMed.
- X. Ji, B. D. Paulsen, G. K. K. Chik, R. Wu, Y. Yin, P. K. L. Chan and J. Rivnay, Nat. Commun., 2021, 12, 1–12 CrossRef PubMed.
- L. Pinto, K. Rajan, B. DePasquale, S. Y. Thiberge, D. W. Tank and C. D. Brody, Neuron, 2019, 104, 810–824 CrossRef CAS PubMed .e9.
- H. P. Ren, C. Bai, M. S. Baptista and C. Grebogi, Sci. Rep., 2017, 7, 1–12 CrossRef PubMed.
- J. Wang and F. Zhuge, Adv. Mater. Technol., 2019, 4, 1–20 Search PubMed.
- K. Nakajima, T. Li, H. Hauser and R. Pfeifer, J. R. Soc., Interface, 2014, 11, 20140437 CrossRef CAS PubMed.
- K. Nakajima, H. Hauser, T. Li and R. Pfeifer, Sci. Rep., 2015, 5, 1–11 CAS.
- C. Fernando and S. Sojakka, Lecture Notes in Artificial Intelligence (Subseries of Lecture Notes in Computer Science), 2003, vol. 2801, pp. 588–597 Search PubMed.
- H. O. Sillin, R. Aguilera, H.-H. Shieh, A. V. Avizienis, M. Aono, A. Z. Stieg and J. K. Gimzewski, Nanotechnology, 2013, 24, 384004 CrossRef PubMed.
- H. G. Manning, F. Niosi, C. G. da Rocha, A. T. Bellew, C. O'Callaghan, S. Biswas, P. F. Flowers, B. J. Wiley, J. D. Holmes, M. S. Ferreira and J. J. Boland, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- A. Loeffler, R. Zhu, J. Hochstetter, A. Diaz-Alvarez, T. Nakayama, J. M. Shine and Z. Kuncic, Neuromorphic Comput. Eng., 2021, 1, 014003 CrossRef.
- H. Hadiyawarman, Y. Usami, T. Kotooka, S. Azhari, M. Eguchi and H. Tanaka, Jpn. J. Appl. Phys., 2021, 60, SCCF02 CrossRef.
- D. Banerjee, T. Kotooka, S. Azhari, Y. Usami, T. Ogawa, J. K. Gimzewski, H. Tamukoh and H. Tanaka, Adv. Intell. Syst., 2022, 4, 2270014 CrossRef.
- H. Tanaka, M. Akai-Kasaya, A. Termehyousefi, L. Hong, L. Fu, H. Tamukoh, D. Tanaka, T. Asai and T. Ogawa, Nat. Commun., 2018, 9, 1–7 CrossRef CAS PubMed.
- C. Sung, H. Hwang and I. K. Yoo, J. Appl. Phys., 2018, 124, 151903 CrossRef.
- Z. Liu, J. Tang, B. Gao, P. Yao, X. Li, D. Liu, Y. Zhou, H. Qian, B. Hong and H. Wu, Nat. Commun., 2020, 11, 4234 CrossRef CAS PubMed.
- G. Tanaka, T. Yamane, J. B. Héroux, R. Nakane, N. Kanazawa, S. Takeda, H. Numata, D. Nakano and A. Hirose, Neural Networks, 2019, 115, 100–123 CrossRef PubMed.
- R. K. Daniels and S. A. Brown, Nanoscale Horiz., 2021, 6, 482–488 RSC.
- R. K. Daniels, J. B. Mallinson, Z. E. Heywood, P. J. Bones, M. D. Arnold and S. A. Brown, Neural Networks, 2022, 154, 122–130 CrossRef CAS PubMed.
- P. Lin, S. Pi and Q. Xia, Nanotechnology, 2014, 25, 405202 CrossRef PubMed.
- H. Jiang, C. Li, P. Lin, S. Pi, J. J. Yang and Q. Xia, Adv. Electron. Mater., 2019, 5, 1–8 CAS.
- J. Zhao, Q. Guo, X. Wang, H. Xie and Y. Chen, Colloids Surf., A, 2016, 488, 93–99 CrossRef CAS.
- Y. Kado, Y. Soneda, H. Hatori and M. Kodama, J. Solid State Electrochem., 2019, 23, 1061–1081 CrossRef CAS.
- M. Feng, H. Zhang, Y. Zhang, M. Zhang and H. Feng, ChemistrySelect, 2019, 4, 6148–6154 CrossRef CAS.
- J. H. Lee, I. C. Leu, M. C. Hsu, Y. W. Chung and M. H. Hon, J. Phys. Chem. B, 2005, 109, 13056–13059 CrossRef CAS PubMed.
- T. R. Michel, M. J. Capasso, M. E. Cavusoglu, J. Decker, D. Zeppilli, C. Zhu, S. Bakrania, J. A. Kadlowec and W. Xue, Microsyst. Technol., 2020, 26, 1101–1112 CrossRef CAS.
- Y. Xie, D. Kocaefe, C. Chen and Y. Kocaefe, J. Nanomater., 2016, 2016, 1–10 CrossRef.
- W. W. Aji, Y. Usami, H. Hadiyawarman, R. Oyabu and H. Tanaka, Appl. Phys. Express, 2020, 13, 101004 CrossRef CAS.
- K. J. Miller, L. B. Sorensen, J. G. Ojemann and M. den Nijs, PLoS Comput. Biol., 2009, 5, e1000609 CrossRef PubMed.
- S. Shirai, S. K. Acharya, S. K. Bose, J. B. Mallinson, E. Galli, M. D. Pike, M. D. Arnold and S. A. Brown, Netw. Neurosci., 2019, 4, 432–447 CrossRef PubMed.
- D. Verstraeten, B. Schrauwen, M. D'Haene and D. Stroobandt, Neural Networks, 2007, 20, 391–403 CrossRef CAS PubMed.
- J. B. Butcher, D. Verstraeten, B. Schrauwen, C. R. Day and P. W. Haycock, Neural Networks, 2013, 38, 76–89 CrossRef CAS PubMed.
- C. Gallicchio and A. Micheli, Cognit. Comput., 2017, 9, 337–350 CrossRef.
- T. Furuta, K. Fujii, K. Nakajima, S. Tsunegi, H. Kubota, Y. Suzuki and S. Miwa, Phys. Rev. Appl., 2018, 10, 1 Search PubMed.
- L. Sun, B. Jin, H. Yang, J. Tong, C. Liu and H. Xiong, Inf. Sci., 2019, 475, 1–17 CrossRef.
- A. Souahlia, A. Belatreche, A. Benyettou, Z. Ahmed-Foitih, E. Benkhelifa and K. Curran, Concurr. Comput., 2020, 32, 1–4 CrossRef.
- R. Nakane, G. Tanaka and A. Hirose, IEEE Access, 2018, 6, 4462–4469 Search PubMed.
- Y. Feng and J. Yao, Ind. Eng. Chem. Res., 2018, 57, 7322–7330 CrossRef CAS.
- P. Hong, Z. Liu, Y. Gao, Y. Chen, M. Zhuang, L. Chen, X. Liu and H. Xiang, Adv. Polym. Technol., 2019, 2019, 1–8 CrossRef.
- C.-K. Peng, S. V. Buldyrev, A. L. Goldberger, S. Havlin, F. Sciortino, M. Simons and H. E. Stanley, Nature, 1992, 356, 168–170 CrossRef CAS PubMed.
- J. Cottaar, L. J. A. Koster, R. Coehoorn and P. A. Bobbert, Phys. Rev. Lett., 2011, 107, 136601 CrossRef CAS PubMed.
- A. V. Nenashev, F. Jansson, J. O. Oelerich, D. Huemmer, A. V. Dvurechenskii, F. Gebhard and S. D. Baranovskii, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235204 CrossRef.
- M. Zorkot, R. Golestanian and D. J. Bonthuis, Nano Lett., 2016, 16, 2205–2212 CrossRef CAS PubMed.
- V. Joshi, P. M. Goodwin and A. Bowling, Opt. Eng., 2022, 61, 104103 Search PubMed.
- K. Linkenkaer-Hansen, V. V. Nikouline, J. M. Palva and R. J. Ilmoniemi, J. Neurosci., 2001, 21, 1370–1377 CrossRef CAS PubMed.
- Z. Eisler and J. Kertész, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 046109 CrossRef PubMed.
- A. D. Broido and A. Clauset, Nat. Commun., 2019, 10, 1–10 CrossRef CAS PubMed.
- K. L. Goh, H. Fujii, A. Setiadi, Y. Kuwahara and M. Akai-Kasaya, Jpn. J. Appl. Phys., 2019, 58, SIIB18 CrossRef CAS.
- H. Fujii, A. Setiadi, Y. Kuwahara and M. Akai-Kasaya, Appl. Phys. Lett., 2017, 111, 133501 CrossRef.
- F. Grüneis, Phys. Lett. A: Gen., 2019, 383, 1401–1409 CrossRef.
- J.-Y. Chastaing, E. Bertin and J.-C. Géminard, Am. J. Phys., 2015, 83, 518–524 CrossRef.
- B. J. He, Trends Cognit. Sci., 2014, 18, 480–487 CrossRef PubMed.
- G. Milano, G. Pedretti, K. Montano, S. Ricci, S. Hashemkhani, L. Boarino, D. Ielmini and C. Ricciardi, Nat. Mater., 2022, 21, 195–202 CrossRef CAS PubMed.
- R. Zhu, J. Hochstetter, A. Loeffler, A. Diaz-Alvarez, T. Nakayama, J. T. Lizier and Z. Kuncic, Sci. Rep., 2021, 11, 1–15 CrossRef PubMed.
- M. Dale, S. O'Keefe, A. Sebald, S. Stepney and M. A. Trefzer, Nat. Comput., 2021, 20, 205–216 CrossRef.
- J. Hu, Y. Ji, W. Chen, C. Streb and Y.-F. Song, Energy Environ. Sci., 2016, 9, 1095–1101 RSC.
- D. Banerjee, T. Kotooka, S. Azhari, Y. Usami, T. Ogawa, J. K. Gimzewski, H. Tamukoh and H. Tanaka, Adv. Intell. Syst., 2022, 4, 2100145 CrossRef.
- S. Holm, T. Holm and Ø. G. Martinsen, PLoS One, 2021, 16, e0248786 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr04619a |
| ‡ Present address: Graduate School of Information, Production and Systems (IPS), Waseda University, 2-7 Hibikino, Wakamatsu, Kitakyushu, Fukuoka 8080135, Japan. E-mail: saman@aoni.waseda.jp |
| This journal is © The Royal Society of Chemistry 2023 |