Open Access Article
Open Access ArticleSingle-molecule conductance studies on quasi- and metallaaromatic dibenzoylmethane coordination compounds and their aromatic analogs†
André
Mang
 a,
Nils
Rotthowe
a,
Nils
Rotthowe
 a,
Katawoura
Beltako
bc,
Michael
Linseis
a,
Fabian
Pauly
a,
Katawoura
Beltako
bc,
Michael
Linseis
a,
Fabian
Pauly
 *c and
Rainer F.
Winter
*c and
Rainer F.
Winter
 *a
*a
aChemistry Department, University of Konstanz, 78457 Konstanz, Germany. E-mail: rainer.winter@uni-konstanz.de
bPhysics Department, University of Lomé, 1515 Lomé, Togo
cInstitute of Physics, University of Augsburg, 86159 Augsburg, Germany. E-mail: fabian.pauly@uni-a.de
First published on 14th February 2023
Abstract
The ability to predict the conductive behaviour of molecules, connected to macroscopic electrodes, represents a crucial prerequisite for the design of nanoscale electronic devices. In this work, we investigate whether the notion of a negative relation between conductance and aromaticity (the so-called NRCA rule) also pertains to quasi-aromatic and metallaaromatic chelates derived from dibenzoylmethane (DBM) and Lewis acids (LAs) that either do or do not contribute two extra dπ electrons to the central resonance-stabilised β-ketoenolate binding pocket. We therefore synthesised a family of methylthio-functionalised DBM coordination compounds and subjected them, along with their truly aromatic terphenyl and 4,6-diphenylpyrimidine congeners, to scanning tunneling microscope break-junction (STM-BJ) experiments on gold nanoelectrodes. All molecules share the common motif of three π-conjugated, six-membered, planar rings with a meta-configuration at the central ring. According to our results, their molecular conductances fall within a factor of ca. 9 in an ordering aromatic < metallaaromatic < quasi-aromatic. The experimental trends are rationalised by quantum transport calculations based on density functional theory (DFT).
Introduction
The ability to reliably fabricate molecular junctions together with the advent of increasingly elaborate experiment designs and sophisticated instrumentation have helped to advance our present understanding of charge transport on the single-molecule level.1–6 One of the most interesting aspects of molecular electronics is that the conduction properties of molecule-based devices critically depend on the intricate electronic structure of individual molecules and the anchoring groups that tie them to electrodes.7–14 As electric transport through metal-molecule-metal junctions relies on charge tunneling through molecular states, the alignment of molecular energy levels with respect to the Fermi energy of the electrodes15–17 as well as their coupling to the metallic leads are of pivotal importance.3,5,18 A plethora of molecular architectures were hence screened in metal-molecule-metal junctions in order to identify crucial relations between the electronic structure of the molecular nexus and its conductive properties. In particular, it was established that transmission channels of π character, if available, normally dominate over channels that involve exclusively σ-frameworks.3,19,20 This renders unsaturated and π-conjugated molecular scaffolds, in particular such with a small or even reverse bond-length alternation, as present in cumulenes,19,21,22 particularly well-suited for applications in electronic devices. Polyarenes and their vinylene and ethynylene blends are synthetically well accessible in broad varieties and are hence frequently employed ingredients of molecules designed for high conductance.15,20,23–36 Other relevant factors include the positioning of the anchoring groups within the molecule,19,35,37–40 the molecular length,5,8,19,41–43 the conformation (e.g. the dihedral angle between individual repeat units along the backbone)5,8,40,44–51 or the symmetry properties of molecules.52However, there is growing evidence that aromaticity per se is not necessarily beneficial for charge transport over π-conjugated molecules – it can even attenuate it. For example, Breslow and coworkers reported that the conductance of molecules with carbocyclic or heterocyclic constituents decreases systematically with increasing resonance energy in the order cyclopentadiene > furan > thiophene.53 Such notion of a negative relationship between electrical conductance and aromaticity (the so-called NRCA rule) was later confirmed in other studies.16,54–56 It was suggested that charge transport through an aromatic ring perturbs its Clar sextet so that conduction through such a motif comes at the expense of aromatic resonance stabilisation.57 Conversely, and under the same basic considerations, antiaromatic compounds were predicted and experimentally observed to provide higher conductances than their aromatic congeners.55,57–59 Of key importance is that an improved aromatic resonance stabilisation generally lowers the energy of the highest occupied molecular orbital (HOMO),15,53 increases the energy of the lowest unoccupied molecular orbital (LUMO) and, hence, widens the electronic HOMO–LUMO gap.60–62 Both of these factors have been found to attenuate molecular conductance. Hence, a smaller energy difference between the frontier MOs, relevant for charge transport, and a better alignment of the corresponding delocalised MOs with the Fermi level of the electrodes were reported to improve electrical conductance.15,54–56
Over the years, the original concept of aromaticity63 has been supplemented by several subtypes, typically denoted by various prefixes, which fulfill only some, but not every criterion that one classically associates with this term.64 Two of these, the so-called quasi-aromaticity and metallaaromaticity, reach into the realm of coordination chemistry, where they apply to certain chelating bidentate ligands and their Lewis acid (LA) adducts.64,65 Quasi-aromatic ligands exist, at least in their predominant forms, as cyclic structures and have π-conjugated backbones. Prominent representatives of this kind of ligands are β-ketoenolates, i.e. the deprotonated forms of 1,3-diketones (1) and the β-ketoenol (2a and 2b) tautomers (Scheme 1) of 1,3-diketones, with acetylacetone and dibenzoylmethane (DBM, see Scheme 1) as the most pivotal examples. These ligands are renowned for their ability to form particularly stable coordination compounds due to resonance effects.66,67
The distinction between quasi-arenes and metallaarenes in such compounds relies on the identity of the LA that is bonded by the heteroatom donors to complement the six-membered ring. In metallaarenes the LA is commonly a transition metal ion, which contributes two dπ electrons that provide, together with the four π-electrons, a Clar-like sextet (Scheme 2, left). In quasi-arenes, however, the LA is devoid of extra π-electrons, which leaves only the heterodiene backbone (Scheme 2, right). Both types have in common that resonance effects stabilize the cyclic systems as compared to their open counterparts with localised single and double bonds, thereby decreasing bond length alternation along the backbone. This structural criterion can be regarded as one important hallmark of such systems.68,69 Other commonly employed indicators for aromaticity, such as the induction of a diamagnetic ring current on exposure to an external magnetic field or the typical values of the computed absolute magnetic shielding in the center of the ring, the so-called nucleus independent chemical shift (NICS) values,70–72 do, however, usually apply to only a limited extent.73–75
 | ||
| Scheme 2 DBM-based six-membered metallaaromatic (left) and quasi-aromatic (right) coordination compounds. | ||
In the present work, we set out to explore and compare the conductive properties of such quasi- and metallaarenes derived from DBM. To this end we have prepared and investigated DBM-based coordination compounds including two representatives of metallaaromatic (LA = Rh(COD); COD = 1,5-cyclooctadiene and Ru(CO)(H)(PiPr3)2) and three quasi-aromatic (LA = H, BF2, BPhF2 with PhF = C6F5) congeners with methylthio (SMe) anchor groups on the outer phenyl rings (Scheme 3). Our work complements earlier forays into vinylogously extended curcumin (CCM) based congeners with one additional C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond at each side of the ketoenolate chelate and either H, BF2 or CuII(tmeda) (tmeda = tetramethylethylenediamine, Me2N-C2H4-NMe2) as the LA (Scheme 4, left).76 The results of single-molecule conductance measurements, employing the STM-BJ technique, and of quantum mechanical transport calculations are discussed in the following.
C double bond at each side of the ketoenolate chelate and either H, BF2 or CuII(tmeda) (tmeda = tetramethylethylenediamine, Me2N-C2H4-NMe2) as the LA (Scheme 4, left).76 The results of single-molecule conductance measurements, employing the STM-BJ technique, and of quantum mechanical transport calculations are discussed in the following.
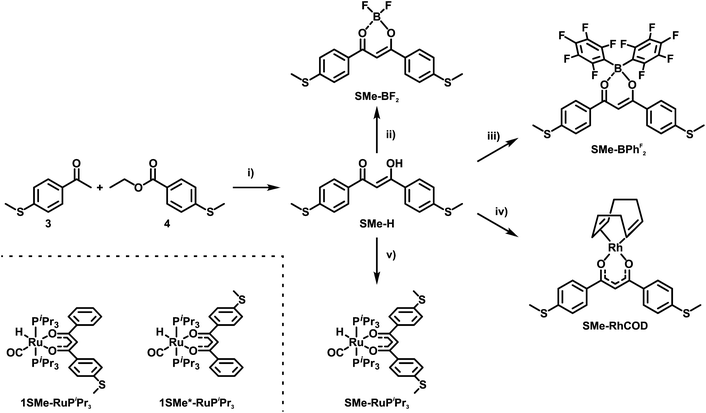 | ||
| Scheme 3 Synthesis of the free ligand SMe-H, transition metal complexes SMe-RhCOD and SMe-RuPiPr3 as well as coordination compounds SMe-BF2 and SMe-BPhF2. (i) NaH, THF, reflux, 16 h; (ii) BF3·OEt2, CH2Cl2, rt, 16 h; (iii) B(C6F5)3, toluene, rt, 16 h; (iv) {(COD)Rh(μ-Cl)}2, KOH, H2O/Et2O, rt, 16 h. (v) Ru(CO)Cl(H)Cl(PiPr3)2, K2CO3, CH2Cl2/CH3OH, rt, 16 h. The molecular structures of the two isomeric complexes 1SMe-RuPiPr3 and 1SMe*-RuPiPr3 (see the ESI†) that served as probes for possible sulfur/phospine anchoring are depicted on the bottom left. | ||
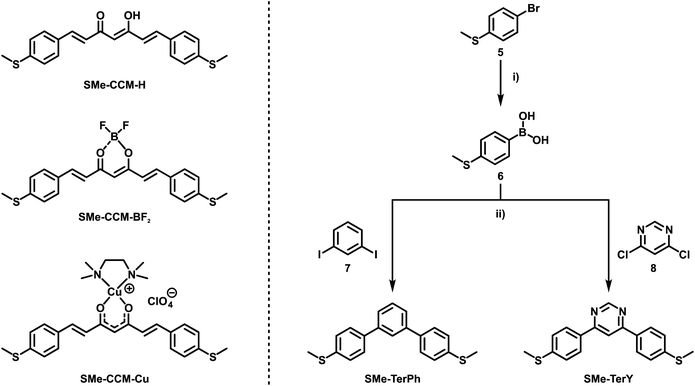 | ||
Scheme 4 Previously studied CCM-based congeners with one additional C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond at each side of the ketoenolate chelate and either H, BF2 or CuII(tmeda) as the LA (left).76 Synthetic route towards reference compounds SMe-TerPh and SMe-TerY (right). (i) (1) nBuLi (1.6 M in hexanes), THF, −78 °C, 1 h; (2) B(OiPr)3, −78 °C to rt, 16 h; (3) 1M HCl(aq), H2O, rt; (ii) K3PO4, Pd(dppf)Cl2, 1,4-dioxane, 70 °C to 80 °C, 16 h. C double bond at each side of the ketoenolate chelate and either H, BF2 or CuII(tmeda) as the LA (left).76 Synthetic route towards reference compounds SMe-TerPh and SMe-TerY (right). (i) (1) nBuLi (1.6 M in hexanes), THF, −78 °C, 1 h; (2) B(OiPr)3, −78 °C to rt, 16 h; (3) 1M HCl(aq), H2O, rt; (ii) K3PO4, Pd(dppf)Cl2, 1,4-dioxane, 70 °C to 80 °C, 16 h. | ||
Results and discussion
Synthesis
DBMs are easily accessible from acetophenones and ethylbenzoates in a simple condensation reaction. This renders the introduction of anchor groups into the DBM framework for BJ measurements straightforward. Our choice of the SMe function for that purpose rests on its known ability to form robust and well-defined contacts to single gold surface atoms.13,77,78 Furthermore, thioethers persist under the conditions of a base-mediated Claisen cross-condensation during DBM synthesis. Accordingly, ketoenol SMe-H (Scheme 3) was prepared by enolisation of 4-(methylthio)acetophenone (3) with sodium hydride and subsequent reaction with ethyl-4-(methylthio)benzoate (4), following an established procedure.79 Treatment of SMe-H with various LAs, either in the presence or absence of a base, readily produced the corresponding coordination compounds as shown in Scheme 3. Hence, the complexes SMe-RhCOD and SMe-RuPiPr3 were formed by reacting in situ generated, deprotonated SMe− with half an equivalent of the rhodium dimer {(COD)Rh(μ-Cl)}2 or equimolar amounts of the 16 valence electron ruthenium complex Ru(CO)Cl(H)(PiPr3)2. The boron(III) β-ketoenolates SMe-BF2 and SMe-BPhF2 could be prepared directly from SMe-H with boron trifluoride diethyl etherate or tris(pentafluorophenyl)borane with the concomitant release of HF or pentafluorobenzene. SMe-H was obtained as yellow needle-shaped crystals, while SMe-RhCOD and SMe-BPhF2 provided orange and SMe-RuPiPr3 red crystals. SMe-BF2 was obtained as an ochre powder. The latter compound was already reported and investigated as a reference in mechanically controllable BJ experiments by van der Zant and coworkers.76 For reasons that will become clear later we also created a ruthenium complex analogous to SMe-RuPiPr3, which lacks one of the SMe anchor groups at the DBM ligand. Owing to the presence of four different donors in the equatorial coordination plane, this complex comes as two isomers, 1SMe-RuPiPr3 and 1SMe*-RuPiPr3 (see Scheme 3 and the ESI† for details).The right side in Scheme 4 illustrates the synthesis of the organic meta-terphenyls SMe-TerPh and SMe-TerY, which were used as truly aromatic reference compounds of the same general structure and topology. A metal-halogen exchange of commercially available 4-bromothioanisole (5) with n-butyllithium followed by the addition of triisopropylborate at low temperature and subsequent aqueous workup furnished the anchor group-modified phenylboronic acid 6. Compound 6 was then reacted with either 1,3-diiodobenzene (7) or 4,6-dichloropyrimidine (8) in a Suzuki–Miyaura cross-coupling reaction to yield SMe-TerPh and SMe-TerY, respectively. The purity of all compounds was confirmed by multinuclear NMR-spectroscopy (1H-, 13C{1H}- and 19F{1H}-NMR, if applicable). Further details of the synthesis and characterisation as well as the NMR spectra of all compounds are provided in the ESI.†
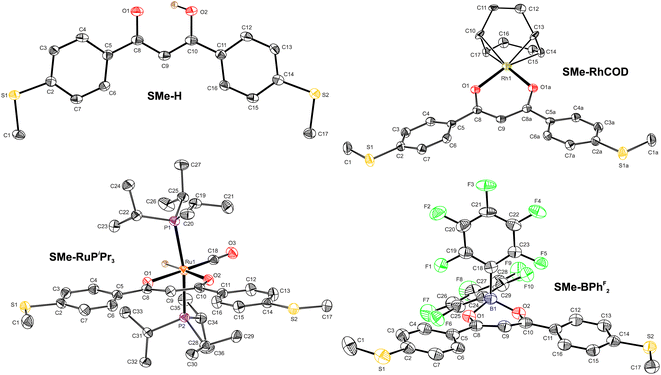
X-ray diffraction
Fig. 1 displays the molecular structures of the free ligand SMe-H, of transition metal complexes SMe-RhCOD and SMe-RuPiPr3 and of SMe-BPhF2 with a boron LA within the ketoenolate binding pocket as determined by X-ray diffraction. Pertinent metric parameters are collected in Table 1. The derived bond lengths, interatomic bond angles and torsion angles serve as structural probes of resonance stabilisation within these compounds. Aromatic ring structures are generally characterised by planarity and bond lengths that fall in between those of a typical single and a double bond. Such structural criteria also apply for the oxametallacyclic units of β-ketoenolate coordination compounds.64 Hence, even the free ligand SMe-H with a proton in the binding pocket shows only an insignificant bond length alternation for the C–C and the C–O bonds within the chelate ring. The C–C bond lengths of 1.401(6) Å and 1.388(6) Å fall accordingly in between those of 1.460 Å for C–C single and of 1.316 Å for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds of sp2-hybridised carbon atoms.80 The accuracy of the experimental data is however somewhat compromised by the fact that the proton within the binding pocket could not directly be located from the experimental electron density map and was introduced at its calculated position. Nevertheless, strong hydrogen bonding O⋯H–O with an O⋯O distance of 2.442(4) Å forces the chelate ring into a fully planar conformation with parallel C–O vectors. We note that the enolic forms of DBMs have the strongest hydrogen bonds among all β-diketones with the lowest energy barrier for intramolecular proton transfer and an almost equal distribution between asymmetrically and symmetrically H-bridged forms.81–84
C double bonds of sp2-hybridised carbon atoms.80 The accuracy of the experimental data is however somewhat compromised by the fact that the proton within the binding pocket could not directly be located from the experimental electron density map and was introduced at its calculated position. Nevertheless, strong hydrogen bonding O⋯H–O with an O⋯O distance of 2.442(4) Å forces the chelate ring into a fully planar conformation with parallel C–O vectors. We note that the enolic forms of DBMs have the strongest hydrogen bonds among all β-diketones with the lowest energy barrier for intramolecular proton transfer and an almost equal distribution between asymmetrically and symmetrically H-bridged forms.81–84
SMe-H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
SMe-RhCOD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
SMe-RuPiPr3 | SMe-BPhF2 | |
|---|---|---|---|---|
| a Torsion angles are provided as absolute values. b The proton inside the chelate binding pocket was introduced at its calculated position; related parameters are thus not specified; n. a. = not applicable. c The asymmetric unit of SMe-RhCOD comprises only half of the DBM moiety, rendering both functionalised phenylene units crystallographically equivalent. | ||||
| S⋯S | 13.4591(16) | 12.7997(13) | 12.7878(12) | 13.1113(15) |
| O⋯O | 2.442(4) | 2.910(3) | 2.903(3) | 2.419(3) |
| C8–O1 | 1.283(4) | 1.282(3) | 1.277(3) | 1.313(3) |
| C10–O2 | 1.313(4) | 1.282(3) | 1.263(3) | 1.321(4) |
| C8–C9 | 1.401(6) | 1.401(3) | 1.407(4) | 1.397(4) |
| C9–C10 | 1.388(6) | 1.401(3) | 1.409(4) | 1.391(4) |
| O1–M | n. a. | 2.0370(18) | 2.1319(19) | 1.499(4) |
| O2–M | n. a. | 2.0370(18) | 2.1865(17) | 1.502(4) |
| O1–C8–C9 | 120.3(4) | 125.5(3) | 125.9(3) | 120.0(2) |
| O2–C10–C9 | 119.6(4) | 125.5(3) | 125.3(2) | 119.8(3) |
| O1–M–O2 | n. a. | 91.16(7) | 84.48(7) | 107.5(2) |
| C6–C5–C8–C9 | 4.3(6) | 26.7(4) | 7.4(4) | 7.3(4) |
| C9–C10–C11–C16 | 1.0(6) | 26.7(4) | 0.2(4) | 11.5(4) |
| O1–C8–C9–C10 | 2.9(6) | 1.3(5) | 2.7(5) | 12.7(4) |
| O2–C10–C9–C8 | 1.3(6) | 1.3(5) | 5.3(5) | 13.0(4) |
| M–O1–C8–C9 | n. a. | 1.3(4) | 3.8(4) | 18.8(4) |
| M–O2–C10–C9 | n. a. | 1.3(4) | 1.2(4) | 17.9(4) |
In accordance with the previous assumptions, the planarity of the central chelate ring, including the metal center, also prevails in the structures of both transition metal complexes. Thus, the M–O1–C8–C9/M–O2–C10–C9 torsions measure only 1.3(4)°/1.3(4)° for SMe-RhCOD and 3.8(4)°/1.2(4)° for SMe-RuPiPr3, respectively. In addition, the C–C bond lengths C8–C9 and C9–C10 within the central chelate ring are equivalent in SMe-RhCOD, as imposed by crystallographic symmetry, and identical within the limits of accuracy in SMe-RuPiPr3, again with very similar values to SMe-H. A notable feature within the structure of SMe-RuPiPr3 are the rather different Ru–O bond lengths. The lengthening of the Ru–O2 bond to 2.1865(17) Å as compared to Ru–O1 of 2.1319(19) Å is imposed by the strong σ-trans influence of the opposite hydride ligand, which weakens the Ru–O2 bond. Equilibration of bond lengths within the central chelate is also observed for SMe-BPhF2. Structural adjustment of the chelate ligand to the bulkiness of the coordinated LA is evidenced by an opening of the chelate bite angle from 84.48(7)° in SMe-RuPiPr3 to 91.16(7)° in SMe-RhCOD and finally to 107.5(2)° in SMe-BPhF2. This large bite angle forces the boron LA out of the chelate plane, as indicated by torsion angles B1–O1–C8–C9 of 18.8(4)° and B1–O2–C10–C9 of 17.9(4)°, respectively. A common feature of all four compounds is a rather coplanar arrangement of the appended, anchor group-modified benzene rings with the central coordination plane with a maximum torsion of 26.7(4)° in SMe-RhCOD. This makes them close structural analogs to meta-terphenyls.
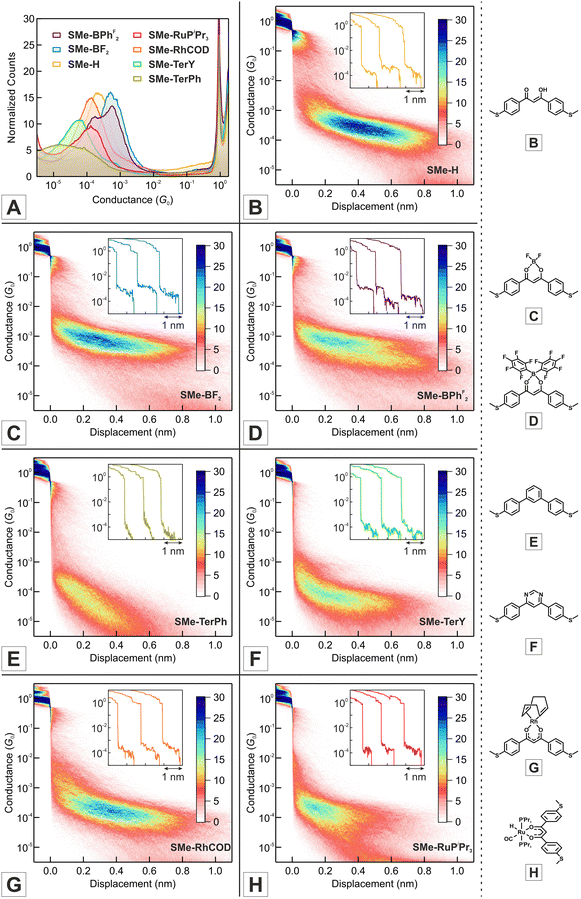
Molecular conductance measurements
All molecules in this study share the common structural motif of three interlinked, π-conjugated, six-membered rings with essentially the same end-to-end distance between their SMe anchor groups of ca. 13 Å (see Table 1). Importantly, the peripheral 4-(methylthio)phenyl-substituents connect to the central keto-enolate template in a meta-configuration (i.e. a 1,3-configuration). This template-enforced topology attenuates the conductances of our probe molecules as compared to the commonly employed para-connectivity (1,4-configuration). For the meta-configuration, the simultaneous presence of two different, competing conduction paths is known to lead to destructive quantum interference, i.e., a partial cancellation of conductance contributions of the two available paths.51,85–89In order to assess the conductive properties of the quasi-aromatic and metallaaromatic chelates at the single-molecule level, we performed STM-BJ measurements using a gold tip and a gold substrate. The results of these studies are presented in Fig. 2 with the corresponding data compiled in Table 2. We note that SMe-BF2 and the structurally related, vinylogously extended curcuminoid analogs SMe-CCM-H, SMe-CCM-BF2 and SMe-CCM-Cu (Scheme 4, left) were already the subject of previous investigations.76,90,91
| Molecular conductance (G0) | Junction length (nm) | |||
|---|---|---|---|---|
| Experimental | Calculated (top-top) | Experimental dmax | Corrected dcorra | |
| a An empirical snap-back correction of 0.50 nm is applied. For more details, see ref. 43, 92 and 93. | ||||
| SMe-BPhF2 | 5.69 × 10−4|1.75 × 10−4 | 6.04 × 10−4 | 0.70|0.90 | 1.20|1.40 |
| SMe-BF2 | 5.18 × 10−4 | 0.85 | 1.35 | |
| SMe-H | 2.21 × 10−4 | 1.39 × 10−4 | 0.90 | 1.40 |
| SMe-RuPiPr3 | 1.46 × 10−4 | 0.60 | 1.10 | |
| SMe-RhCOD | 1.36 × 10−4 | 1.40 × 10−5 | 0.90 | 1.40 |
| SMe-TerY | 5.80 × 10−5 | 0.75 | 1.25 | |
| SMe-TerPh | 1.83 × 10−5 | 0.60 | 1.10 | |
As is evident from the one-dimensional (1D) conductance histograms in panel A of Fig. 2, the parent DBM SMe-H exhibits an intense, narrow and monomodal conductance distribution with a well-defined maximum at 2.21 × 10−4G0 as the most probable conductance value (G0 = 2e2/h is the electrical conductance quantum). This signals that robust metal-molecule-metal junctions with a preferential binding geometry form with high probability. Individual conductance vs. displacement traces exhibit extended plateaus with conductance values varying from 10−3G0 to 10−4G0 with a nearly horizontal alignment and only a slight decrease of G at larger displacements. These characteristics become particularly evident in the two-dimensional (2D) conductance-displacement histogram (see panel B in Fig. 2). The most frequently encountered features extend from ca. 0.20 to 0.60 nm, but the maximum length reaches a value dmax(SMe-H) of ca. 0.90 nm. When considering the empirical snap-back correction of around 0.50 nm for gold electrodes, which accounts for the mechanical elasticity of the junction after the rupture of the last Au–Au atomic contact,43,92,93 the corrected maximum length dcorr(SMe-H) of the molecular conductance feature measures ca. 1.40 nm. This is in excellent agreement with the crystallographically determined S⋯S distance of 1.35 nm (Table 1), when the S–Au interactions at the molecule-electrode interfaces on each side of the junction are considered. The excellent match of both distances implies that, under the most favourable conditions, SMe-H molecules can be fully erected inside the junction between the metal leads before the final rupture of the contact occurs. The conductance of SMe-H exceeds that of its vinylogously expanded curcuminoid congener SMe-CCM-H with two additional C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds within the conduction pathway (Scheme 4, G = 3.90 × 10−5G0) by a factor of more than 5,76,90,91 which complies with the usual decay of tunneling currents with increasing molecular length L in the nanoscopic regime (i.e.
C double bonds within the conduction pathway (Scheme 4, G = 3.90 × 10−5G0) by a factor of more than 5,76,90,91 which complies with the usual decay of tunneling currents with increasing molecular length L in the nanoscopic regime (i.e.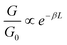 with the attenuation factor β).
with the attenuation factor β).
Under our conditions, the 1D histogram of literature-known SMe-BF2 likewise exhibits a narrow monomodal conductance distribution with a maximum value of 5.18 × 10−4G0 (see panel A of Fig. 2). This surpasses the conductance of SMe-H by a factor of more than 2 and agrees well with the reported high-conductance feature of van der Zant and coworkers of 4.70 × 10−4G0.76 However, we did not observe the electric-field induced bistability that was noted by these authors. Single-trace analysis reveals the reproducible occurrence of well-defined, horizontally aligned molecular plateaus with G values in the range of 10−3G0 to 10−4G0 (inset of panel C in Fig. 2). As observed for SMe-H, the length of the conductance feature corresponds to the fully erected molecule with a maximum electrode displacement dmax(SMe-BF2) = 0.85 nm (see 2D histogram in panel C of Fig. 2), complying with a corrected value of dcorr(SMe-BF2) = 1.35 nm. Again, low susceptibility towards conformational changes induced by mechanical stress is noted.
Replacement of the fluorine atoms by pentafluorophenyl substituents in the otherwise identical coordination compound SMe-BPhF2 leads to a bimodal conductance distribution with a global maximum at 5.69 × 10−4G0 as well as a secondary peak with a lower conductance of 1.75 × 10−4G0 (panels A and D of Fig. 2). The 2D histogram reveals the presence of two superimposed signatures. The one with the higher conductance tends to stop at a smaller corrected rupture length (ca. 1.20 nm) than the one with the lower conductance (which extends to ca. 1.40 nm). Note, however, that a significant number of the higher conductance traces still extends to the maximum rupture length of ca. 1.40 nm. We could identify a considerable number of individual traces which feature both, the high and the low G states that bimodally disperse. In these cases the molecule is initially trapped in the state with high G and transitions to the state with low G upon further stretching, while no switching back to the initial high G state could be observed. This behaviour is akin to the bistability reported by van der Zant and coworkers for SMe-BF2.76 Following their reasoning, we tentatively assign these characteristics to two different junction geometries that differ with respect to the mutual orientation of the anchor groups and the dipole moment of the SMe-BPhF2 molecule.
Complexes SMe-RhCOD and SMe-RuPiPr3 provide consistently lower values of their conductance peaks. The 1D histograms of SMe-RhCOD and SMe-RuPiPr3 display well-defined maxima at 1.36 × 10−4G0 and 1.46 × 10−4G0, respectively (panels A, G and H in Fig. 2). The conductance distribution of SMe-RhCOD is similarly narrow as that of SMe-H and SMe-BF2 and has the same maximum extension of ca. 1.40 nm. In contrast, the distribution obtained for the ruthenium complex SMe-RuPiPr3 is significantly broader and individual conductance traces show considerable variation (inset of panel H in Fig. 2). Moreover, the rupture length for the ruthenium complex tends to shorten to 1.10 nm, while there are still traces that show the expected extension. This behaviour suggests the possibility of an alternative anchoring mode, where contact might be established by only one of the SMe functions and one phosphine ligand. To test this scenario we prepared and studied the analogous complex 1SMe-RuPiPr3, which lacks one of the SMe functionalities at the DBM chelate ligand. Owing to the unsymmetrical DBM ligand and the two non-identical H and CO coligands in the equatorial coordination plane, this complex comes as a mixture of two isomers, 1SMe-RuPiPr3 and 1SMe*-RuPiPr3, which differ with respect to whether the H or the CO ligands are at the same side as the SMe anchor group (see the bottom left of Scheme 3 and the experimental section of the ESI† for further details). As shown in Fig. S1 of the ESI,† conductance traces of 1SMe-RuPiPr3 are devoid of any molecular features, thus ruling out sulfur-phospine anchoring. We therefore assume that steric hindrance, as imposed by the bulky triisopropylphosphine (PiPr3) ligands of SMe-RuPiPr3, interferes with contact formation and reduces the likeliness for full erection of the probe molecules within the junctions. This probably also accounts for the lower statistical occurrence of molecular features.
In order to gauge our probe molecules against a truly aromatic counterpart, we also prepared and investigated SMe-TerPh with the topologically identical meta-terphenyl backbone (see Scheme 4). Quite surprisingly, the simple meta-terphenyl template seems to be unexplored in molecular conductance studies, while their ethynylogous congeners were extensively studied as model compounds for exploring destructive quantum interference.51,94–96 1D histograms are shown in panel A of Fig. 2. SMe-TerPh shows a very broad conductance peak with a maximum located at 1.83 × 10−5G0. The unusual breadth of this distribution may relate to unfavourable steric interactions between the ortho protons at the central and the peripheral benzene rings. A screening of relevant entries in the Cambridge Crystallographic Data Centre (CCDC) database indicates consistent torsion angles of ca. 30° to 35° between adjacent phenyl rings in meta-terphenyls. Such unfavourable steric interactions may also explain contact rupture at lower electrode displacements (dmax(SMe-TerPh) = 0.60 nm; dcorr(SMe-TerPh) = 1.10 nm). Analysis of individual traces and of the 2D histogram reveals that the underlying molecular plateaus exhibit a rather steep conductance decay with increasing electrode displacement (see panel E in Fig. 2).
We mused that unfavourable torsions would be ameliorated in the analogous pyrimidine derivative SMe-TerY, where two C–H units in the central ring are replaced by nitrogen atoms (Scheme 4), similar to the situation encountered in the DBM complexes. In fact, the bis(dimethylaminoethyl)-substituted relative of SMe-TerY with C2H4NMe2 substituents instead of the methyl groups (Me) at the sulfur atoms exhibits significantly smaller ring torsions of 9.2° and 19.6°, which resemble those in the β-ketoenolate compounds closely.97 Indeed, the conductance distribution of pyrimidine-based SMe-TerY is significantly narrower than that of SMe-TerPh and shows a well-defined peak in its 1D histogram at 5.80 × 10−5G0 (panel A of Fig. 2). In the 2D histogram, conductance-distance traces extend to longer corrected lengths of up to 1.25 nm for SMe-TerY as compared to 1.10 nm for SMe-TerPh. We also note that conductance over the meta-terphenyl backbone of SMe-TerY and SMe-TerPh, where conductance contributions over the σ-channel become important,40 falls by a factor of ca. 5 or 15 behind those of the analogous SMe-terminated para-terphenyl.15,98
In summary, the conductances of DBM-based coordination compounds with a quasi-aromatic character of the central chelate exceed those of their metallaaromatic congeners and, even more substantially so, those of the truly aromatic 4,6-diphenylpyrimidine or meta-terphenyl with the same general molecular architecture. We note that the maximum factor of ca. 9 between the boron chelates and the SMe-TerY reference compound exceeds that of 1.75 reported for test systems with aromatic thiophene or non-aromatic cyclopentadiene linkers that have helped to coin the NRCA rule.53,54 Our experimental results thus suggest its wider applicability to include even β-ketoenolate coordination compounds.
Transport calculations
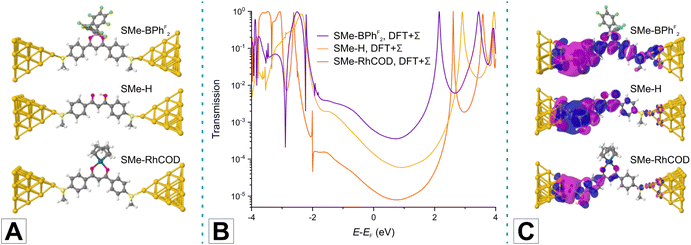
In order to rationalize the experimentally observed trends in conductance and to shed further light on their origin, we calculated charge transport properties of model junctions with three different probe molecules in three different binding geometries each. The latter were chosen to include the parent SMe-H and one member from the class of quasi-aromatic (SMe-BPhF2) and metallaaromatic (SMe-RhCOD) DBM-LA adducts, each taken as a representative of their class. We only discuss here the results for the ‘top-top’ binding geometry, where the lone pair at the sulfur atom of the SMe anchor group contacts an atomically sharp Au tip at both sides of the junction. Results for alternative ‘hollow-hollow’ or ‘top-hollow’ geometries are further discussed in the ESI (see Table S1†) and tend to provide lower conductance values.As the level of theoretical description, we use DFT, as implemented in the quantum chemistry software package TURBOMOLE, to determine junction geometries by energy minimisation.99 Transport is computed within the framework of the Landauer–Büttiker formalism of phase-coherent elastic scattering.1,100,101 Since DFT tends to underestimate the HOMO. LUMO gap of molecules we correct the electronic structure of DFT by the DFT + Σ method in the transport studies.102–105 Further technical details and the results for the other two binding configurations are presented in the ESI.†
Panels A and B in Fig. 3 display the computed junction geometries for the three selected test molecules in the top-top binding geometry and the corresponding energy-dependent transmissions. Analysis of the transmission functions (panel B of Fig. 3) reveals that charge transport through these molecules is off-resonant and HOMO-dominated. By determining the conductance as the transmission at the Fermi energy EF, the computed values of 6.04 × 10−4G0 for SMe-BPhF2, 1.39 × 10−4G0 for SMe-H, and 1.40 × 10−5G0 for SMe-RhCOD agree with the trends in our experiments with a less satisfactory consistency for the Rh complex. Our calculations thus reproduce the key finding that the DBM-LA adduct SMe-RhCOD with a metallaarene core is less conductive than its quasi-aromatic counterparts SMe-H and SMe-BPhF2. Notable differences in the transmission plots arise from contributions of in-gap states that are located 1 to 2 eV below EF. These contributions are most prominent in SMe-BPhF2, where molecular states of the C6F5 rings at the BPhF2 LA are involved, and less so in SMe-H. In contrast, the SMe-RhCOD junction shows the signature of a Fano-type resonance at ca. 2 eV below EF, which is related to the RhCOD fragment. Analysis of transmission eigenchannels,106 computed following the procedure presented in ref. 107 and shown in panel C of Fig. 3, clearly demonstrates by the weight of the wave function on the right-hand side that SMe-BPhF2 and SMe-H are electronically more transparent than SMe-RhCOD.
The HOMO–LUMO gaps of SMe-BPhF2, SMe-H and SMe-RhCOD, as computed with DFT, are 2.020 eV, 2.353 eV and 1.756 eV, respectively (see Fig. S3 of the ESI†). The theoretically determined, decreasing conductances hence do not simply correlate with an increasing HOMO–LUMO gap size. We note however that for SMe-RhCOD the HOMO is confined to the Rh ion and the donor atoms of the ligands. The MO relevant for charge transport through SMe-RhCOD is hence the delocalised HOMO - 1. The energy difference HOMO - 1–LUMO of SMe-RhCOD takes a value of 2.394 eV. Thus we find that the decreasing conductances order according to the HOMO–LUMO gap, if we consider the value of the HOMO–LUMO gap for delocalised, charge carrying MOs.
Finally, the nucleus independent chemical shift (NICS)71,72 is an established computational probe of aromaticity and was hence also considered in our evaluation. NICS(0) values of +2.07 ppm for SMe-BPhF2 and of −2.46 ppm for SMe-RhCOD agree with the notion of a larger degree of aromaticity in β-ketoenolate transition metal complexes as compared to their adducts with LAs that lack additional dπ electrons. Hence, we find a correlation between more positive NICS(0) values and higher molecular conductance, which was also demonstrated for other systems.58,59
Given the high similarity in molecular structures and the identical positioning of anchor groups, the observed differences in statistically averaged molecular conductances are unlikely to be rooted in different binding geometries. Overall our study of NICS values and of transmission characteristics for comparable junction geometries thus suggests that the NRCA rule also applies to metallaarenes and quasi-arenes.
Conclusions
β-Ketoenoles and the Lewis-acid (LA) adducts of their corresponding deprotonated forms are known to exhibit a certain degree of aromaticity. Depending on whether the LA that is coordinated within the central binding pocket donates an extra pair of dπ electrons to complete a Clar-like sextet or not, the resulting chelate is either more or less aromatic in nature. We have explored a family of dibenzoylmethane (DBM) based methylthio-terminated ketoenolate chelates with a common meta-terphenyl-like structural template, featuring identical molecular lengths and interring torsions, and measured their single-molecule charge transport properties by STM-BJ experiments. The LAs include metallaaromatic transition metal complexes SMe-RhCOD and SMe-RuPiPr3 with a Rh(COD) or a Ru(CO)(H)(PiPr3)2 fragment, as well as quasi-aromatic SMe-H, SMe-BF2 and SMe-BPhF2 with either a proton or a boron-based BF2 or B(C6F5)2 LA. Crystallographic analysis of four of the compounds provided clear structural indications of π-conjugation and resonance stabilisation. In widening the scope, we also studied truly (hetero)aromatic terphenyl or pyrimidine counterparts of the DBM-LA adducts as structurally equivalent reference systems. Measured conductances decrease in an ordering quasi-aromatic > metallaaromatic > aromatic by an overall factor of ca. 9. DFT-based transport calculations on SMe-RhCOD as a representative of metallaromatic complexes, on SMe-BPhF2 as a quasi-aromatic congener, and on the parent SMe-H, while providing a less satisfactory quantitative agreement for the Rh complex, reproduced the experimental trends. In particular, they suggest that the conductance properties relate inversely to the energy gap between the lowest unoccupied and the highest occupied energy levels, if only delocalised, charge-carrying molecular orbitals are taken into account, disregarding localised states of the LA molecular center. Overall our results show that the notion of a negative relation between aromaticity and conductance – the so-called NRCA rule – also pertains to the meta-terphenyl structural template and to ketoenolate-LA adducts.Author contributions
A. M. devised the project together with N. R., conducted all chemical syntheses, spectroscopic characterisations, and data analysis. He also performed DFT calculations of isolated molecules. A. M. and N. R. established the STM-BJ setup and performed the conductance measurements. M. L. carried out X-ray diffraction experiments and supervised the structure refinement as well as DFT calculations of isolated molecules. K. B. performed DFT-based transport calculations, supervised by F. P. R. F. W. helped in designing the experimental methodology and supervised the experimental investigations. All authors contributed to scientific discussions and the writing of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We are indebted to Latha Venkataraman for her immense help in the construction and operation of the STM-BJ setup in our laboratories and for her hospitality to Nils Rotthowe. Our charge transport experiments would not have been possible without her unconditional support. Katawoura Beltako acknowledges funding support from the European Union (grant no. DCI-PANAF/2020/420-028) through the African Research Initiative for Scientific Excellence ARISE pilot programme.References
- J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific, 2nd edn, 2017 Search PubMed.
- M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254 CrossRef CAS.
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002 CrossRef CAS.
- B. Ulgut and H. D. Abruña, Chem. Rev., 2008, 108, 2721–2736 CrossRef CAS.
- N. Xin, J. Guan, C. Zhou, X. Chen, C. Gu, Y. Li, M. A. Ratner, A. Nitzan, J. F. Stoddart and X. Guo, Nat. Rev. Phys., 2019, 1, 211–230 CrossRef.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS.
- F. Chen, X. Li, J. Hihath, Z. Huang and N. Tao, J. Am. Chem. Soc., 2006, 128, 15874–15881 CrossRef CAS.
- F. Evers, R. Korytár, S. Tewari and J. M. van Ruitenbeek, Rev. Mod. Phys., 2020, 92, 035001 CrossRef CAS.
- R. Frisenda, S. Tarkuç, E. Galan, M. L. Perrin, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Beilstein J. Nanotechnol., 2015, 6, 1558–1567 CrossRef CAS.
- Z. Huang, F. Chen, P. A. Bennett and N. Tao, J. Am. Chem. Soc., 2007, 129, 13225–13231 CrossRef CAS.
- V. Kaliginedi, A. V. Rudnev, P. Moreno-García, M. Baghernejad, C. Huang, W. Hong and T. Wandlowski, Phys. Chem. Chem. Phys., 2014, 16, 23529–23539 RSC.
- E. Leary, A. La Rosa, M. T. González, G. Rubio-Bollinger, N. Agraït and N. Martín, Chem. Soc. Rev., 2015, 44, 920–942 RSC.
- Y. S. Park, A. C. Whalley, M. Kamenetska, M. L. Steigerwald, M. S. Hybertsen, C. Nuckolls and L. Venkataraman, J. Am. Chem. Soc., 2007, 129, 15768–15769 CrossRef CAS.
- A. V. Rudnev, V. Kaliginedi, A. Droghetti, H. Ozawa, A. Kuzume, M.-A. Haga, P. Broekmann and I. Rungger, Sci. Adv., 2017, 3, e1602297 CrossRef.
- S. Li, H. Yu, J. Li, N. Angello, E. R. Jira, B. Li, M. D. Burke, J. S. Moore and C. M. Schroeder, Nano Lett., 2021, 21, 8340–8347 CrossRef CAS.
- J. R. Quinn, F. W. Foss Jr., L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2007, 129, 12376–12377 CrossRef CAS.
- L. Yuan, C. Franco, N. Crivillers, M. Mas-Torrent, L. Cao, C. S. S. Sangeeth, C. Rovira, J. Veciana and C. A. Nijhuis, Nat. Commun., 2016, 7, 12066 CrossRef CAS.
- P. Gehring, J. M. Thijssen and H. S. J. van der Zant, Nat. Rev. Phys., 2019, 1, 381–396 CrossRef.
- Y. Tsuji, R. Movassagh, S. Datta and R. Hoffmann, ACS Nano, 2015, 9, 11109–11120 CrossRef CAS.
- Z. Xie, I. Bâldea, G. Haugstad and C. D. Frisbie, J. Am. Chem. Soc., 2019, 141, 497–504 CrossRef CAS.
- M. H. Garner, W. Bro-Jørgensen, P. D. Pedersen and G. C. Solomon, J. Phys. Chem. C, 2018, 122, 26777–26789 CrossRef CAS.
- Y. Zang, T. Fu, Q. Zou, F. Ng, H. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2020, 20, 8415–8419 CrossRef CAS.
- C. Atienza, N. Martín, M. Wielopolski, N. Haworth, T. Clark and D. M. Guldi, Chem. Commun., 2006, 3202–3204 RSC.
- S. H. Choi, B. Kim and C. D. Frisbie, Science, 2008, 320, 1482–1486 CrossRef CAS.
- F. Giacalone, J. L. Segura, N. Martín and D. M. Guldi, J. Am. Chem. Soc., 2004, 126, 5340–5341 CrossRef CAS.
- W. Hong, H. Li, S.-X. Liu, Y. Fu, J. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 19425–19431 CrossRef CAS.
- M.-J. Huang, L.-Y. Hsu, M.-D. Fu, S.-T. Chuang, F.-W. Tien and C.-H. Chen, J. Am. Chem. Soc., 2014, 136, 1832–1841 CrossRef CAS.
- J. G. Kushmerick, D. B. Holt, S. K. Pollack, M. A. Ratner, J. C. Yang, T. L. Schull, J. Naciri, M. H. Moore and R. Shashidhar, J. Am. Chem. Soc., 2002, 124, 10654–10655 CrossRef CAS.
- L. Lafferentz, F. Ample, H. Yu, S. Hecht, C. Joachim and L. Grill, Science, 2009, 323, 1193–1197 CrossRef CAS.
- H. Liu, N. Wang, J. Zhao, Y. Guo, X. Yin, F. Y. C. Boey and H. Zhang, ChemPhysChem, 2008, 9, 1416–1424 CrossRef CAS.
- M. Magoga and C. Joachim, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 4722–4729 CrossRef CAS.
- F. Pauly, J. K. Viljas and J. C. Cuevas, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035315 CrossRef.
- N. Robertson and C. A. McGowan, Chem. Soc. Rev., 2003, 32, 96–103 RSC.
- E. A. Weiss, M. J. Ahrens, L. E. Sinks, A. V. Gusev, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2004, 126, 5577–5584 CrossRef CAS.
- H. Yu, S. Li, K. E. Schwieter, Y. Liu, B. Sun, J. S. Moore and C. M. Schroeder, J. Am. Chem. Soc., 2020, 142, 4852–4861 CrossRef CAS.
- X. Zhao, C. Huang, M. Gulcur, A. S. Batsanov, M. Baghernejad, W. Hong, M. R. Bryce and T. Wandlowski, Chem. Mater., 2013, 25, 4340–4347 CrossRef CAS.
- D. M. Cardamone, C. A. Stafford and S. Mazumdar, Nano Lett., 2006, 6, 2422–2426 CrossRef CAS.
- H. Liu, W. Ni, J. Zhao, N. Wang, Y. Guo, T. Taketsugu, M. Kiguchi and K. Murakoshi, J. Chem. Phys., 2009, 130, 244501 CrossRef.
- P. Sautet and C. Joachim, Chem. Phys. Lett., 1988, 153, 511–516 CrossRef CAS.
- G. C. Solomon, D. Q. Andrews, R. P. Van Duyne and M. A. Ratner, ChemPhysChem, 2009, 10, 257–264 CrossRef CAS.
- B. Capozzi, E. J. Dell, T. C. Berkelbach, D. R. Reichman, L. Venkataraman and L. M. Campos, J. Am. Chem. Soc., 2014, 136, 10486–10492 CrossRef CAS.
- V. Kaliginedi, P. Moreno-García, H. Valkenier, W. Hong, V. M. García-Suárez, P. Buiter, J. L. H. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 5262–5275 CrossRef CAS.
- P. Moreno-García, M. Gulcur, D. Z. Manrique, T. Pope, W. Hong, V. Kaliginedi, C. Huang, A. S. Batsanov, M. R. Bryce, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2013, 135, 12228–12240 CrossRef.
- L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907 CrossRef CAS.
- A. Mishchenko, L. A. Zotti, D. Vonlanthen, M. Bürkle, F. Pauly, J. C. Cuevas, M. Mayor and T. Wandlowski, J. Am. Chem. Soc., 2011, 133, 184–187 CrossRef CAS.
- A. Mishchenko, D. Vonlanthen, V. Meded, M. Bürkle, C. Li, I. V. Pobelov, A. Bagrets, J. K. Viljas, F. Pauly, F. Evers, M. Mayor and T. Wandlowski, Nano Lett., 2010, 10, 156–163 CrossRef CAS.
- V. Lloveras, J. Vidal-Gancedo, D. Ruiz-Molina, T. M. Figueira-Duarte, J.-F. Nierengarten, J. Veciana and C. Rovira, Faraday Discuss., 2006, 131, 291–305 RSC.
- M. Kamenetska, S. Y. Quek, A. C. Whalley, M. L. Steigerwald, H. J. Choi, S. G. Louie, C. Nuckolls, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, J. Am. Chem. Soc., 2010, 132, 6817–6821 CrossRef CAS.
- I.-W. P. Chen, M.-D. Fu, W.-H. Tseng, C.-H. Chen, C.-M. Chou and T.-Y. Luh, Chem. Commun., 2007, 3074–3076 RSC.
- A. C. Benniston and A. Harriman, Chem. Soc. Rev., 2006, 35, 169–179 RSC.
- C. R. Arroyo, S. Tarkuç, R. Frisenda, J. S. Seldenthuis, C. H. Woerde, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Angew. Chem., Int. Ed., 2013, 52, 3152–3155 CrossRef CAS.
- E. J. Dell, B. Capozzi, K. H. DuBay, T. C. Berkelbach, J. R. Moreno, D. R. Reichman, L. Venkataraman and L. M. Campos, J. Am. Chem. Soc., 2013, 135, 11724–11727 CrossRef CAS.
- W. Chen, H. Li, J. R. Widawsky, C. Appayee, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2014, 136, 918–920 CrossRef CAS.
- A. Mahendran, P. Gopinath and R. Breslow, Tetrahedron Lett., 2015, 56, 4833–4835 CrossRef CAS.
- S. Fujii, S. Marqués-González, J.-Y. Shin, H. Shinokubo, T. Masuda, T. Nishino, N. P. Arasu, H. Vázquez and M. Kiguchi, Nat. Commun., 2017, 8, 15984 CrossRef CAS.
- J. R. Quinn, F. W. Foss Jr., L. Venkataraman, M. S. Hybertsen and R. Breslow, J. Am. Chem. Soc., 2007, 129, 6714–6715 CrossRef CAS.
- R. Breslow and F. W. Foss Jr., J. Phys.: Condens. Matter, 2008, 20, 374104 CrossRef.
- M. Schmidt, D. Wassy, M. Hermann, M. T. González, N. Agraït, L. A. Zotti, B. Esser and E. Leary, Chem. Commun., 2021, 57, 745–748 RSC.
- X. Yin, Y. Zang, L. Zhu, J. Z. Low, Z.-F. Liu, J. Cui, J. B. Neaton, L. Venkataraman and L. M. Campos, Sci. Adv., 2017, 3, eaao2615 CrossRef.
- A. D. Allen and T. T. Tidwell, Chem. Rev., 2001, 101, 1333–1348 CrossRef CAS.
- F. De Proft and P. Geerlings, Chem. Rev., 2001, 101, 1451–1464 CrossRef CAS.
- J. Aihara, J. Phys. Chem. A, 1999, 103, 7487–7495 CrossRef CAS.
- T. M. Krygowski, M. K. Cyrañski, Z. Czarnocki, G. Häfelinger and A. R. Katritzky, Tetrahedron, 2000, 56, 1783–1796 CrossRef CAS.
- T. M. Krygowski, B. Bankiewicz, Z. Czarnocki and M. Palusiak, Tetrahedron, 2015, 71, 4895–4908 CrossRef CAS.
- H. Masui, Coord. Chem. Rev., 2001, 219, 957–992 CrossRef.
- M. Calvin and K. W. Wilson, J. Am. Chem. Soc., 1945, 67, 2003–2007 CrossRef CAS.
- J. P. Collman, Angew. Chem., Int. Ed. Engl., 1965, 4, 132–138 CrossRef.
- A. F. P. Julg, Theor. Chim. Acta, 1967, 7, 249–259 CrossRef.
- T. M. Krygowski, J. Chem. Inf. Comput. Sci., 1993, 33, 70–78 CrossRef CAS.
- P. von Ragué Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef.
- M. Kollwitz and J. Gauss, Chem. Phys. Lett., 1996, 260, 639–646 CrossRef CAS.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS.
- P. von Ragué Schleyer, K. Najafian, B. Kiran and H. Jiao, J. Org. Chem., 2000, 65, 426–431 CrossRef.
- A. Stanger, J. Org. Chem., 2006, 71, 883–893 CrossRef CAS.
- A. Ranganathan and G. U. Kulkarni, J. Phys. Chem. A, 2002, 106, 7813–7819 CrossRef CAS.
- I. J. Olavarría-Contreras, A. Etcheverry-Berríos, W. Qian, C. Gutiérrez-Cerón, A. Campos-Olguín, E. C. Sañudo, D. Dulić, E. Ruiz, N. Aliaga-Alcalde, M. Soler and H. S. J. van der Zant, Chem. Sci., 2018, 9, 6988–6996 RSC.
- E. Leary, L. A. Zotti, D. Miguel, I. R. Márquez, L. Palomino-Ruiz, J. M. Cuerva, G. Rubio-Bollinger, M. T. González and N. Agraït, J. Phys. Chem. C, 2018, 122, 3211–3218 CrossRef CAS.
- H. Vazquez, R. Skouta, S. Schneebeli, M. Kamenetska, R. Breslow, L. Venkataraman and M. S. Hybertsen, Nat. Nanotechnol., 2012, 7, 663–667 CrossRef CAS.
- P. C. Andrews, G. B. Deacon, R. Frank, B. H. Fraser, P. C. Junk, J. G. MacLellan, M. Massi, B. Moubaraki, K. S. Murray and M. Silberstein, Eur. J. Inorg. Chem., 2009, 2009, 744–751 CrossRef.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, 76th edn, 1995 Search PubMed.
- M. Etinski and B. Ensing, J. Phys. Chem. A, 2018, 122, 5945–5954 CrossRef CAS.
- V. Feyer, K. C. Prince, M. Coreno, S. Melandri, A. Maris, L. Evangelisti, W. Caminati, B. M. Giuliano, H. G. Kjaergaard and V. Carravetta, J. Phys. Chem. Lett., 2018, 9, 521–526 CrossRef CAS.
- X. Kong, A. Brinkmann, V. Terskikh, R. E. Wasylishen, G. M. Bernard, Z. Duan, Q. Wu and G. Wu, J. Phys. Chem. B, 2016, 120, 11692–11704 CrossRef CAS.
- L. H. Thomas, A. J. Florence and C. C. Wilson, New J. Chem., 2009, 33, 2486–2490 RSC.
- T. Hansen, G. C. Solomon, D. Q. Andrews and M. A. Ratner, J. Chem. Phys., 2009, 131, 194704 CrossRef.
- S.-H. Ke, W. Yang and H. U. Baranger, Nano Lett., 2008, 8, 3257–3261 CrossRef CAS.
- T. Markussen, R. Stadler and K. S. Thygesen, Nano Lett., 2010, 10, 4260–4265 CrossRef CAS.
- G. C. Solomon, D. Q. Andrews, T. Hansen, R. H. Goldsmith, M. R. Wasielewski, R. P. Van Duyne and M. A. Ratner, J. Chem. Phys., 2008, 129, 054701 CrossRef.
- X. Zhao, V. Geskin and R. Stadler, J. Chem. Phys., 2017, 146, 092308 CrossRef.
- D. Dulić, A. Rates, E. Castro, J. Labra-Muñoz, D. Aravena, A. Etcheverry-Berríos, D. Riba-López, E. Ruiz, N. Aliaga-Alcalde, M. Soler, L. Echegoyen and H. S. J. van der Zant, J. Phys. Chem. C, 2020, 124, 2698–2704 CrossRef.
- A. Etcheverry-Berríos, I. Olavarría, M. L. Perrin, R. Díaz-Torres, D. Jullian, I. Ponce, J. H. Zagal, J. Pavez, S. O. Vásquez, H. S. J. van der Zant, D. Dulić, N. Aliaga-Alcalde and M. Soler, Chem. – Eur. J., 2016, 22, 12808–12818 CrossRef.
- C. Huang, A. V. Rudnev, W. Hong and T. Wandlowski, Chem. Soc. Rev., 2015, 44, 889–901 RSC.
- S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Nat. Nanotechnol., 2009, 4, 230–234 CrossRef CAS.
- C. J. Lambert and S. X. Liu, Chem. – Eur. J., 2018, 24, 4193–4201 CrossRef CAS.
- X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z. Y. Xiao, W. Hong, C. J. Lambert and S. X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173–176 CrossRef CAS.
- C. Tang, L. Huang, S. Sangtarash, M. Noori, H. Sadeghi, H. Xia and W. Hong, J. Am. Chem. Soc., 2021, 143, 9385–9392 CrossRef CAS.
- W. D. Wilson, L. Strekowski, F. A. Tanious, R. A. Watson, J. L. Mokrosz, A. Strekowska, G. D. Webster and S. Neidle, J. Am. Chem. Soc., 1988, 110, 8292–8299 CrossRef CAS.
- P. Zhou, J. Zheng, T. Han, L. Chen, W. Cao, Y. Zhu, D. Zhou, R. Li, Y. Tian, Z. Liu, J. Liu and W. Hong, Nanoscale, 2021, 13, 7600–7605 RSC.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. M. Khah, S. K. Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS.
- M. Bürkle, J. K. Viljas, T. J. Hellmuth, E. Scheer, F. Weigend, G. Schön and F. Pauly, Phys. Status Solidi B, 2013, 250, 2468–2480 CrossRef.
- F. Pauly, J. K. Viljas, U. Huniar, M. Häfner, S. Wohlthat, M. Bürkle, J. C. Cuevas and G. Schön, New J. Phys., 2008, 10, 125019 CrossRef.
- T. Markussen, C. J. Jin and K. S. Thygesen, Phys. Status Solidi B, 2013, 250, 2394–2402 CrossRef CAS.
- D. J. Mowbray, G. Jones and K. S. Thygesen, J. Chem. Phys., 2008, 128, 111103 CrossRef CAS.
- S. Y. Quek, L. Venkataraman, H. J. Choi, S. G. Louie, M. S. Hybertsen and J. B. Neaton, Nano Lett., 2007, 7, 3477–3482 CrossRef CAS.
- L. A. Zotti, M. Bürkle, F. Pauly, W. Lee, K. Kim, W. Jeong, Y. Asai, P. Reddy and J. C. Cuevas, New J. Phys., 2014, 16, 015004 CrossRef.
- M. Paulsson and M. Brandbyge, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115117 CrossRef.
- M. Bürkle, J. K. Viljas, D. Vonlanthen, A. Mishchenko, G. Schön, M. Mayor, T. Wandlowski and F. Pauly, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 075417 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Employed materials, experimental and computational methods, synthetic protocols, NMR characterisation, crystallographic tables and additional theoretical results. CCDC 2161698 (SMe-H), 2161700 (SMe-RhCOD), 2161701 (SMe-RuPiPr3) and 2161703 (SMe-BPhF2). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2nr05670d |
| This journal is © The Royal Society of Chemistry 2023 |