Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nano-phononic metamaterials enable an anomalous enhancement in the interfacial thermal conductance of the GaN/AlN heterojunction†
Cheng-Wei
Wu
a,
Hui
Pan
b,
Yu-Jia
Zeng
b,
Wu-Xing
Zhou
*a,
Ke-Qiu
Chen
 *b and
Gang
Zhang
*b and
Gang
Zhang
 *c
*c
aSchool of Materials Science and Engineering & Hunan Provincial Key Laboratory of Advanced Materials for New Energy Storage and Conversion, Hunan University of Science and Technology, Xiangtan 411201, China. E-mail: wuxingzhou@hnu.edu.cn
bDepartment of Applied Physics, School of Physics and Electronics, Hunan University, Changsha 410082, China. E-mail: keqiuchen@hnu.edu.cn
cInstitute of High Performance Computing, A*STAR Singapore, 138632, Singapore. E-mail: zhangg@ihpc.a-star.edu.sg
First published on 13th March 2023
Abstract
Improving the interfacial thermal conductance (ITC) is very important for heat dissipation in microelectronic and optoelectronic devices. In this work, taking GaN–AlN contact as an example, we demonstrated a new mechanism to enhance the interfacial thermal conductance using nano-phononic metamaterials. First, how a superlattice affects the ITC is investigated, and it is found that with decreasing superlattice periodic length, the ITC first decreases and then increases, because of the coherent phonon interference effect. However, although constructing a superlattice is effective for tuning the ITC, it cannot enhance the ITC. We suggest that the ITC can be enhanced by 9% through constructing an interfacial nano phononic metamaterial, which is contributed by the additional phonon transport channels for high-frequency phonons with a wide incidence-angle range. These results not only establish a deep understanding of the fundamental physics of the interfacial thermal conductance, but also provide a robust and scalable mechanism, which provides a degree of freedom for efficient thermal management.
1. Introduction
The concept of interfacial thermal resistance describes the phenomenon whereby the transport of phonons is hindered when they cross the interface between two dissimilar contacts.1 In recent years, with increasing integration density, heat dissipation has become a bottleneck for developing future microelectronic and nanoelectronic devices2–4 because high power densities during operation lead to excessive temperature, which could cause system failure. Nanomaterials are used widely in microelectronic and nanoelectronic devices, so the heat dissipation in these devices depends on the thermal properties of the nanomaterials.5,6 Moreover, in nanoscale devices, with the increasing number of interfaces, the interfacial thermal conductance (ITC) is becoming increasingly important and even dominant in the heat dissipation process.7,8 There have been many experimental and theoretical studies of the ITC in different systems, including graphene–BN,9 graphene–carbon nanotubes,10 graphene–polymer interfaces,11 Si–Ge interfaces,12 silicon–nanomembrane interfaces,13 MXene–SiO2 interfaces,14 solid–superfluid interfaces,15 solid–liquid interfaces,16 metal–nonmetal interfaces,17 and van der Waals interfaces,18–21 as well as the ITC between two silica clusters.22Conventional strategies for improving the ITC are to (i) fill the gap between the two contacting surfaces with a thermal-interface material,23 (ii) improve the coupling strength of the interface, or (iii) increase the density of covalent bonds.24 A fourfold increase in the ITC between copper and silica was reported with a bonding organic nanomolecular monolayer, which provides a strong bonding interaction with both metal and dielectric materials.25 A similar increase in ITC through a molecular bridge was also reported in a gold and amorphous polyethylene system.26 However, even for two ideal smooth interfaces connected through strong covalent bonds, the interfacial thermal resistance still exists because of the large differences in lattice constants and intrinsic phonon properties between two dissimilar materials.27,28 Much effort has gone into enhancing the ITC of interfaces with strong covalent bonding. For example, Tian et al. found that the interfacial roughness induced by atomic mixing can enhance the phonon transmission coefficient and ITC.29 Also, although point defects reduce the thermal conductivity in nanomaterials, it was found that topological defects can release interfacial stress and thus induce an unexpected increase in ITC.30
In the present work, we studied the ITC of GaN–AlN interfaces and found that it first decreases and then increases with decreasing superlattice (SL) periodic length. This is because of the wave nature of phonons. However, the SL interface can only tune the ITC but cannot enhance it. To increase the ITC, we constructed a nano-phononic metamaterial that improves the ITC significantly, because it introduces additional phonon transport channels.
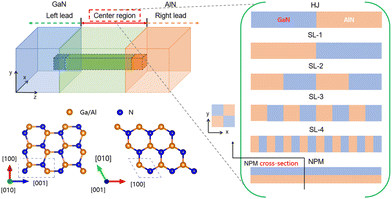
2. Computational methodology
Based on a simulation using the non-equilibrium Green's function (NEGF), the system composed of GaN–AlN has three parts, i.e., the left and right leads and the center region. The left lead is made of GaN, the right lead is made of AlN, and the center region is used to simulate their interfacial structure, as shown in Fig. 1. Here, the total length of the system is fixed, the transport direction is set along the z axis (corresponding to the [001] crystallographic direction of the conventional unit, as shown in Fig. 1), and periodic boundary conditions are applied in the xy plane. We then design different interfacial structures to adjust the ITC of the GaN–AlN interface: (i) a heterojunction (HJ) structure to simulate the conventional GaN–AlN interface; (ii) an SL of GaN–AlN with different periodic lengths (labeled as SL-1, SL-2, SL-3, and SL-4); (iii) a GaN–AlN nano-phononic metamaterial (NPM).31,32In recent years, the Stillinger–Weber (SW) potential has been proved to accurately describe the Al–Ga–N system, and it has been widely used in the study of thermal transport in the Al–Ga–N system.33–35 Therefore, the SW potential combined with the NEGF method was used to investigate the phonon transmission coefficient of the Al–Ga–N system in this work. We use the supercell method to calculate the second-order force constant with a 5 × 5 × 1 supercell, and the grid sampling of k points in the xy plane is 11 × 11. The structures are optimized by the conjugated gradient method implemented by LAMMPS with a force tolerance of 10−8 eV Å−1, and then the dynamical matrix (Hamiltonian) of the phonons is the Fourier transform of the second-order force constant, i.e.,
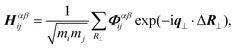 | (1) |
To assess quantitatively how the heterostructures affect the ITC, it is useful to investigate the normalized cumulative thermal conductance43
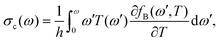 | (2) |
| T(ω) = Tr[ΓLGretΓRGadv], | (3) |
3. Results and discussion
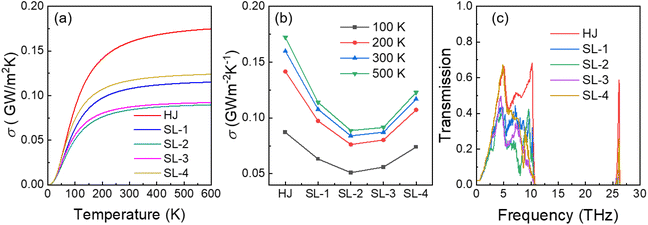
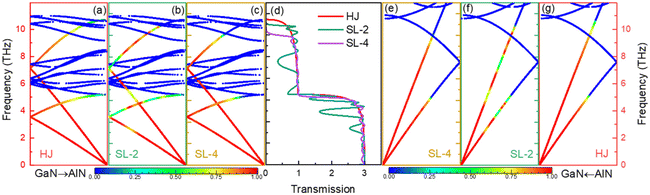
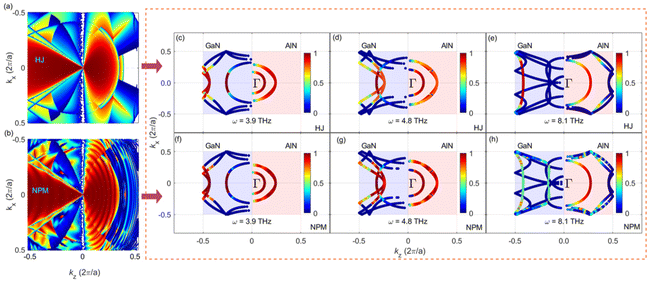
Firstly, we investigate how the ITC varies with the periodic length of the GaN–AlN SL. For the total thermal conductance, as shown in Fig. 2(a) and (b), there is a trend of first decreasing and then increasing, and the minimum ITC can be observed at different temperatures. This variation trend of ITC is consistent with the previous experimental and theoretical results for SLs revealing the wave nature of phonons. To explore this phenomenon, Fig. 2(c) shows how the total phonon transmission varies with the SL periodic length. As shown in Fig. 2, the phonon transport changes obviously with the SL periodic length, in particular in the frequency range of 2.5–11 THz. The large transmission gap at 12–25 THz results from the acoustic-optical phonon frequency gap in GaN, which leads to a giant mismatch in the phonon frequency between GaN and AlN, consequently reducing the phonon transmission. Given that phonon transmission above 11 THz contributes slightly to the ITC, we mainly discuss the phonon transport properties in the range of 0–11 THz. For the total phonon transmission, it is clear that the phonon transport is suppressed at both low and high frequencies with the introduction of interfacial layers, as shown in Fig. 2(c). In particular, there is an obvious dip in phonon transmission around 7.8 THz in SL-2, which leads to a jump in the cumulative thermal conductance at this frequency (see Fig. S1†). This effect is caused mainly by the single-path Bragg-like phonon interference.45 When the periodic length of the SL decreases, the phonon transmission of low-frequency phonons recovers to a level comparable to that of the HJ, which leads to an increased ITC.In addition, we study the transmission probability of the phonon mode to explain this phenomenon furthermore. Fig. 3 shows the mode-resolved phonon transmission probability for HJ, SL-2, and SL-4 at kx = ky = 0,46 which means that the phonons are at normal incidence at the interface. As can be seen, the phonon transport probability of normal incidence is equal to 3 in the range of 0–5 THz, which is provided by two degeneracy transverse acoustic modes and a longitudinal acoustic mode. For the low-frequency phonons, especially in the range of 0–2 THz, the three transport channels in the three different configurations are unaffected due to the phonon wavelength being significantly larger than the periodic length of the SL. When the phonon frequency exceeds 2 THz, the transmission spectrum of SL-2 contains several transport valleys, which is shown in Fig. 3(d) and is caused by phonon coherence. Moreover, Fig. 3(b) and (f) show that these transport valleys are caused specifically by these phonon modes. For the HJ and SL-4 configurations, Fig. 3(a) and (g) (for HJ) and Fig. 3(c) and (e) (for SL-4) show that the phonon transmission contributed by different phonon modes is maintained at the same level. Furthermore, we calculated the angular phonon transmission probability distribution for HJ, SL-2, and SL-4 in the first Brillouin zone which is presented in the ESI (see Fig. S2†). The angular phonon transmission at three representative frequencies (3.9 THz, 4.8 THz, and 8.1 THz) is shown in Fig. S3† as cut planes for HJ, SL-2, and SL-4. The results show that the heterostructure with a relatively large periodic length affects mainly the low-frequency phonons, whereas these phonons are mostly unaffected when the periodic length is decreased. However, in the GaN–AlN SL-4, there is an obvious selection effect for high-frequency phonons with a specific angle of incidence, which leads to an increased ITC. Therefore, the ITC of SL-4 is higher than that of SL-2 but always lower than that of HJ, as shown in Fig. 2(a) and (b).
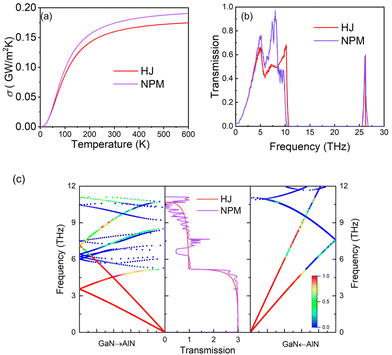
In general, the SL structure is effective for tuning the ITC but cannot enhance it. For enhancing the ITC, we constructed a new interfacial NPM, as shown in Fig. 1 (right). Fig. 4(a) shows how the total thermal conductance of HJ and NPM varies with temperature. It is obvious that compared with the ITC of HJ, that of NPM is enhanced significantly in the entire temperature range (0–600 K). The total phonon transmission shows the same trend, as shown in Fig. 4(b). The SLs actually modify the phonon transport in the whole range of frequency, as shown in Fig. 2(c). In contrast, the NPM only affects the phonon transport above 5 THz. Fig. 4(c) shows the normal-incidence phonon transmission probability for NPM: the low-frequency phonons behave the same as for HJ, but the phonon transport of NPM from the GaN lead to the AlN lead exhibits additional phonon transport channels compared with HJ. This is demonstrated clearly by the non-zero transmission probability for optical phonon modes as shown in Fig. 4(c). In NPM, in the frequency ranges of 0–5 THz, 7–8 THz, and 10–11 THz, the mode match between the GaN and AlN makes the total transmission of normal-incidence phonon modes higher than that of HJ. Moreover, the normal-incidence transmission spectrum of NPM is slightly enhanced compared with that of HJ, revealing that the contribution of non-normal-incidence phonon modes is also important.
Fig. 5(a) and (b) show the full-angle phonon transmission distribution for HJ and NPM, respectively. To understand more intuitively the transport behavior of full-angle phonons, we also show the angle-dependent phonon transmission probability of the NPM configuration in Fig. 5(f)–(h) and that of the HJ configuration in Fig. 5(c)–(e). The non-zero phonon transmission probability at 3.9 THz and 4.8 THz of the NPM configuration is completely consistent with those of the HJ configuration, and the transmission probabilities of phonons with different angles of incidence are slightly enhanced. In addition, there is a significant difference in NPM compared with HJ and SL-1–4 at 8.1 THz. Fig. 5(h) shows an additional phonon transport channel in both the GaN and AlN sides of NPM compared with HJ. This is consistent with the analysis of the transmission probability of normal-incidence phonons, revealing that the NPM provides additional transport channels for high-frequency phonons with a wide incidence-angle range. Moreover, compared with SL-4, the phonon transmission of NPM has a weak dependence on the incident angle of phonons, which results in the suppressed interface phonon scattering; consequently, the phonon transmission spectrum is enhanced. Although the transmission probability of the original phonon channel on the GaN side is suppressed to a certain extent, the total phonon transmission of NPM near 8.1 THz is enhanced significantly by the sum of the transmission probabilities of the two channels, leading to an increased ITC. Therefore, the NPM structure can enhance the ITC significantly because it provides additional phonon transport channels. And NPMs with different cross-sectional formats can all enhance ITC, as demonstrated in Fig. S4 in the ESI.†
4. Conclusions
In conclusion, we performed individual-phonon-mode-resolved NEGF calculations for phonon transmission through GaN–AlN SL structures using the force constants from the Stillinger–Weber potential. The results showed that the ITC first decreases and then increases with decreasing SL periodic length, because of the wave nature of phonons. However, the SL interface can only tune the ITC but cannot improve it. To enhance the ITC, we suggested an NPM that can enhance the ITC significantly. Through a systematic investigation on the transmission spectrum of both normal-incidence and non-normal-incidence phonons, it is found that the NPM introduces additional phonon transport channels, and thus can enhance the transmission coefficient of phonons with a frequency above 5 THz. Therefore, our work provides mode-resolved insights into phonon transport across NPMs and offers a novel strategy to enhance the interfacial thermal conductance, which benefits various ranges of applications including thermal management of micro-/nano-electronic devices.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 12074115, 11974106).References
- E. T. Swartz and R. O. Pohl, Rev. Mod. Phys., 1989, 61, 605 CrossRef.
- E. Pop, Nano Res., 2010, 3, 147 CrossRef CAS.
- A. L. Moore and L. Shi, Mater. Today, 2014, 17, 163 CrossRef CAS.
- R. Wu, R.-Z. Zhu, S.-H. Zhao, G. Zhang, H. Tian and T.-L. Ren, Sci. China Inf. Sci., 2021, 64, 140401 CrossRef.
- X. Gu, Y. Wei, X. Yin, B. Li and R. Yang, Rev. Mod. Phys., 2018, 90, 041002 CrossRef CAS.
- Z. Zhang, Y. Ouyang, Y. Cheng, J. Chen, N. Li and G. Zhang, Phys. Rep., 2020, 860, 1 CrossRef CAS.
- A. Giri and P. E. Hopkins, Adv. Funct. Mater., 2020, 30, 1903857 CrossRef CAS.
- W.-X. Zhou, Y. Cheng, K.-Q. Chen, G. Xie, T. Wang and G. Zhang, Adv. Funct. Mater., 2020, 30, 1903829 CrossRef CAS.
- J.-W. Jiang and J.-S. Wang, EPL, 2011, 96, 16003 CrossRef.
- J. Chen, J. H. Walther and P. Koumoutsakos, Adv. Funct. Mater., 2015, 25, 7539 CrossRef.
- T. Luo and J. R. Lloyd, Adv. Funct. Mater., 2012, 22, 2495 CrossRef CAS.
- B. Latour, N. Shulumba and A. J. Minnich, Phys. Rev. B, 2017, 96, 104310 CrossRef.
- D. P. Schroeder, Z. Aksamija, A. Rath, P. M. Voyles, M. G. Lagally and M. A. Eriksson, Phys. Rev. Lett., 2015, 115, 256101 CrossRef CAS PubMed.
- P. Yasaei, Z. Hemmat, C. J. Foss, S. J. Li, L. Hong, A. Behranginia, L. Majidi, R. F. Klie, M. W. Barsoum and Z. Aksamija, Adv. Mater., 2018, 30, 1801629 CrossRef PubMed.
- A. Ramiere, S. Volz and J. Amrit, Nat. Mater., 2016, 15, 512 CrossRef CAS PubMed.
- Z. Tian, A. Marconnet and G. Chen, Appl. Phys. Lett., 2015, 106, 211602 CrossRef.
- N. Yang, T. Luo, K. Esfarjani, A. Henry, Z. Tian, J. Shiomi, Y. Chalopin, B. Li and G. Chen, J. Comput. Theor. Nanosci., 2015, 12, 168 CrossRef CAS.
- D. Wu, L. Huang, P.-Z. Jia, X.-H. Cao, Z.-Q. Fan, W.-X. Zhou and K.-Q. Chen, Appl. Phys. Lett., 2021, 119, 063503 CrossRef CAS.
- Y.-J. Zeng, D. Wu, X.-H. Cao, Y.-X. Feng, L.-M. Tang and K.-Q. Chen, J. Mater. Chem. A, 2020, 8, 11884 RSC.
- P.-Z. Jia, Y.-J. Zeng, D. Wu, H. Pan, X.-H. Cao, W.-X. Zhou, Z.-X. Xie, J.-X. Zhang and K.-Q. Chen, J. Phys.: Condens. Matter, 2019, 32, 055302 CrossRef PubMed.
- D. Wu, X.-H. Cao, P.-Z. Jia, Y.-J. Zeng, Y.-X. Feng, L.-M. Tang, W.-X. Zhou and K.-Q. Chen, Sci. China: Phys., Mech. Astron., 2020, 63, 276811 Search PubMed.
- S. Xiong, K. Yang, Y. A. Kosevich, Y. Chalopin, R. D'Agosta, P. Cortona and S. Volz, Phys. Rev. Lett., 2014, 112, 114301 CrossRef PubMed.
- A. A. Balandin, ACS Nano, 2020, 14, 5170 CrossRef CAS PubMed.
- M. D. Losego, M. E. Grady, N. R. Sottos, D. G. Cahill and P. V. Braun, Nat. Mater., 2012, 11, 502 CrossRef CAS PubMed.
- P. J. O'Brien, S. Shenogin, J. Liu, P. K. Chow, D. Laurencin, P. H. Mutin, M. Yamaguchi, P. Keblinski and G. Ramanath, Nat. Mater., 2013, 12, 118 CrossRef PubMed.
- F. Sun, T. Zhang, M. M. Jobbins, Z. Guo, X. Zhang, Z. Zheng, D. Tang, S. Ptasinska and T. Luo, Adv. Mater., 2014, 26, 6093 CrossRef CAS PubMed.
- B. Li, J. Lan and L. Wang, Phys. Rev. Lett., 2005, 95, 104302 CrossRef PubMed.
- X. Li and R. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 054305 CrossRef.
- Z. Tian, K. Esfarjani and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235304 CrossRef.
- X. Liu, G. Zhang and Y.-W. Zhang, Nano Lett., 2016, 16, 4954 CrossRef CAS PubMed.
- S. Zhao, Y. Zhang, Y. Zhang, J. Yang and S. Kitipornchai, Aerosp. Sci. Technol., 2022, 130, 107906 CrossRef.
- S. Zhao, Y. Zhang, H. Wu, Y. Zhang, J. Yang and S. Kitipornchai, Compos. Struct., 2022, 301, 116222 CrossRef CAS.
- Y. Zhou, Y. Huang, J. Li and F. Zhu, Appl. Surf. Sci., 2023, 608, 155151 CrossRef CAS.
- X. W. Zhou, R. E. Jones, C. J. Kimmer, J. C. Duda and P. E. Hopkins, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 094303 CrossRef.
- Q. Wang, X. Wang, X. Liu and J. Zhang, J. Appl. Phys., 2021, 129, 235102 CrossRef CAS.
- Z.-Y. Ong and G. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174302 CrossRef.
- Z.-Y. Ong, J. Appl. Phys., 2018, 124, 151101 CrossRef.
- Z.-Y. Ong, Phys. Rev. B, 2018, 98, 195301 CrossRef CAS.
- J. Dai and Z. Tian, Phys. Rev. B, 2020, 101, 041301 CrossRef CAS.
- Y. Guo, Z. Zhang, M. Bescond, S. Xiong, M. Nomura and S. Volz, Phys. Rev. B, 2021, 103, 174306 CrossRef CAS.
- Y. Guo, M. Bescond, Z. Zhang, M. Luisier, M. Nomura and S. Volz, Phys. Rev. B, 2020, 102, 195412 CrossRef CAS.
- E. S. Landry and A. J. H. McGaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165304 CrossRef.
- J.-C. Klöckner, J. C. Cuevas and F. Pauly, Phys. Rev. B, 2017, 96, 245419 CrossRef.
- C. Caroli, R. Combescot, P. Nozieres and D. Saint-James, J. Phys. C: Solid State Phys., 1971, 4, 916–929 CrossRef.
- S. Hu, L. Feng, C. Shao, I. A. Strelnikov, Y. A. Kosevich and J. Shiomi, Phys. Rev. B, 2020, 102, 024301 CrossRef CAS.
- B. Latour, N. Shulumba and A. J. Minnich, Phys. Rev. B, 2017, 96, 104310 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information regarding the calculation details, the cumulative interfacial thermal conductance and the phonon transmission probability distribution of different configurations. See DOI: https://doi.org/10.1039/d2nr05954a |
| This journal is © The Royal Society of Chemistry 2023 |