Lanthanide metal–organic network featuring strong perpendicular magnetic anisotropy

Abstract

The coordination of lanthanides atoms in two-dimensional surface-confined metal–organic networks is a promising path to achieve an ordered array of single atom magnets. These networks are highly versatile with plenty of combinations of molecular linkers and metallic atoms. Notably, with an appropriate choice of molecules and lanthanide atoms it should be feasible to tailor the orientation and intensity of the magnetic anisotropy. However, up to now only tilted and almost in-plane easy axis of magnetizations were reported in lanthanide-based architectures. Here we introduce an Er-directed two-dimensional metallosupramolecular network on Cu(111) featuring strong out-of-plane magnetic anisotropy. Our results will contribute to pave avenues for the use of lanthanides in potential applications in nanomagnetism and spintronics.

---

Molecular magnetism is an emerging field with potential for technological applications such as high density information storage, molecular spin qubits and spintronics devices.^1,2 In the frontier of this field shines the design of low dimensional magnetic materials, in which exotic physical phenomena emerge.¹ From a fundamental point of view, lanthanides have high potential for the development of magnetic devices. Lanthanide atoms present higher magnetic moments, anisotropy and spin lifetimes than 3d elements, which can lead to an augmented magnetic stability and is essential to develop practical applications.³ Lanthanides are also ideal candidates for single atom magnets.^4–6

Some attention has already been set on lanthanide molecular magnetic systems, particularly on the double-decker phthalocyanine family (LnPc₂),^7–13 and with some insights in alternative single molecule magnets.^14–18 However, the investigation of the magnetism of lanthanides embedded in metal–organic networks remains underexplored.^19,20 This is surprising since the engineering of 2D metal–organic networks exploiting lanthanides as single atom magnets,^4–6 represents a promising path to design nanoarchitectures for information storage at the smallest scale.

We have pioneered this field with the investigation of the magnetic properties of Dy atoms coordinated with p-terphenyl-4,4′-dicarboxylic acid (TDA) and benzene-1,4-dicarboxylic acid (TPA) molecular linkers on Cu(111).¹⁹ For both TDA and TPA molecules a nearly in-plane magnetization axis was observed. More recently, we have inspected the magnetism of a different molecular linker, [1,4-bis(4-pyridyl)-biphenyl] (DPBP), coordinated with Dy and Er on Au(111).²⁰ Dy- and Er-DPBP molecular networks present the same structure with dinuclear metallic centers, but there is a significant change in the electronic and magnetic properties. While Dy-DPBP has close to in-plane anisotropy, Er-DPBP presents a tilted magnetization easy axis. This demonstrates that it is possible to tailor the orientation and intensity of the magnetic anisotropy by metal–organic coordination.

On the other side, materials featuring perpendicular magnetic anisotropy are particularly interesting for the development of spintronic applications, as high density storage devices.^21,22 These materials usually exhibit larger magnetic anisotropy, more uniform magnetization and improved thermal stability.²¹ Coordination chemistry has revealed that it is feasible for lanthanide molecular magnets on surfaces to display out-of-plane magnetic anisotropy.^9–12 However, to the best of our knowledge a lanthanide-directed metal–organic network displaying perpendicular magnetic anisotropy has remained elusive.

In this work we report an investigation of the structural, electronic and magnetic properties of a metal–organic network based on Er atoms coordinated with deprotonated TDA species. We have performed scanning tunnelling microscopy (STM) and spectroscopy (STS), X-ray absorption spectroscopy (XAS), X-ray linear dichroism (XLD) and X-ray magnetic circular dichroism (XMCD). The experimental results are complemented with density functional theory (DFT) and multiplet calculations. Our results demonstrate the feasibility of accomplishing strong out-of-plane magnetic anisotropy by on-surface synthesis of a lanthanide metal–organic network.

The metal–organic network was prepared by the deposition of TDA molecules on a clean Cu(111) surface heated at 370 K to afford full deprotonation, followed by the deposition of Er atoms with the sample still heated at 370 K and a post-annealing at 430 K. The result is a mononuclear square network, analogous to the one observed for Dy- and Gd-TDA nanoarchitectures.^19,23,24

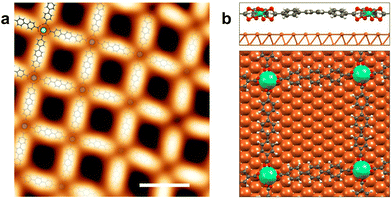
Fig. 1a presents a representative high resolution STM image of the network with a superimposed atomistic model. The network has an experimental internodal distance of (20.3 ± 0.5) Å, an Er–O distance of (2.4 ± 0.1) Å, and the average angle between the molecules is (90 ± 4)°. In order to get a commensurate lattice, the structure used in the DFT calculations diverges slightly from a square lattice and there are two different internodal distances, 20.4 Å in one direction and 20.9 Å in the other (see Fig. 1b). For the angles between molecules the theoretical values are 94° and 86°. The Er–O bond length ranges between 2.35 Å and 2.50 Å, in good agreement with the experimental values. This excellent match between the structure observed by STM and calculated by DFT for a mononuclear network confirms that the network has a single Er atom at the coordination nodes. According to the DFT calculations, the crystal field coordination is a distorted square antiprism, close to a D_4d symmetry, similar to the Dy-TDA network.¹⁹

Fig. 1 Structure of Er-TDA network on Cu(111). (a) High resolution STM image with an atomistic model superimposed. Scanning parameters: V_b = 500 mV and I_t = 500 pA, T = 4 K, scale bar: 2.0 nm. (b) Side and top views of the DFT-optimized network. C, H, O, Er and Cu atoms are represented by black, white, red, green and orange balls, respectively.

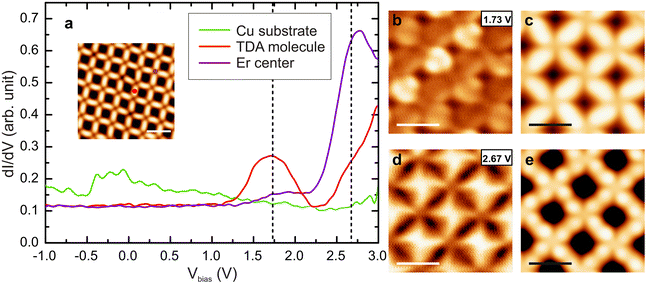
An inspection of the electronic properties by means of STS measurements reveals a resonance at 1.7 V for the Er-coordinated molecules (see Fig. 2a), that is attributed to the lowest unoccupied molecular orbital (LUMO). This resonance is at the same energy than the resonance observed for Dy-coordinated TDA molecules.¹⁹ A dI/dV map of the LUMO state (Fig. 2b) shows the presence of two lobes at the molecular backbone, being more intense in one direction of the network, which is attributed to the registry with the substrate. The main molecular resonance appears at ∼1.7 V, just like in the Dy-TDA case.¹⁹ The Er centers, on the other hand, show a resonance around 2.8 V, which is visualized in the dI/dV map as a bright protrusion (Fig. 2d). A resonance at approximately the same energy was observed in the Er-DBDP case.²⁰

Fig. 2 Electronic properties of Er-TDA metal–organic network on Cu(111). (a) STS spectra taken at Er center (purple), TDA molecule (red), and Cu substrate (green). The dashed lines indicated the energies were the dI/dV maps were taken. The inset presents a STM image showing the positions were the STS where taken. Scanning parameters: V_b = 500 mV and I_t = 500 pA, T = 4 K, scale bar: 3.0 nm. STS parameters: tip stabilization at V_b = 3 V and I_t = 700 pA; lock-in modulation of 20 mV. (b) Constant-current dI/dV map taken at 1.73 V with a tip functionalized with CO, showing the LUMO resonance. Scale bar: 2.0 nm. (c) Reference STM image for (b). Scanning parameters: V_b = 1.73 V and I_t = 200 pA, T = 4 K, scale bar: 2.0 nm. (d) Constant-current dI/dV map taken at 2.67 V with a tip functionalized with CO, showing the Er resonance. Scale bar: 2.0 nm. (e) Reference STM image for (d). Scanning parameters: V_b = 2.67 V and I_t = 200 pA, T = 4 K, scale bar: 2.0 nm.

In order to interrogate the nature of the bonds and the plausible emergence of a delocalized band (not expected) we performed angle-resolved photoemission spectroscopy (ARPES) on this sample (see ESI†). Our results only indicate the confinement of the surface state, with no fingerprint of the presence of a band that could be assigned to the network. In fact, high resolution STS close to the Fermi level reveals two distinct peaks at −0.18 V and 0.14 V in the pores (see Fig. S3†), corroborating such confinement of the surface state. Altogether, we suggest that our results could be in line with the expected dominant ionic character of the bond,^19,23,24 precluding the measurement of such a band (if at all existing).

The investigation of the magnetic properties of the Er-TDA network was performed at BOREAS beamline of ALBA synchrotron²⁵ (see ESI†). The network was prepared following the same procedures described previously and the structure was checked with STM (Fig. 3a and b). The experimental results of XAS, XMCD and XLD measurements are presented in Fig. 3d and e together with multiplet calculations performed using the MultiX code.²⁶ The peak's structure of XAS spectra indicates a Er³⁺ oxidation state,²⁷ which was confirmed by the multiplet calculations. The differences between the experimental and simulated spectra are attributed to the difficulty in reproducing the exact symmetry of the real system in the simulations, as previously observed and discussed in the related Dy-TDA network on Cu(111).¹⁹

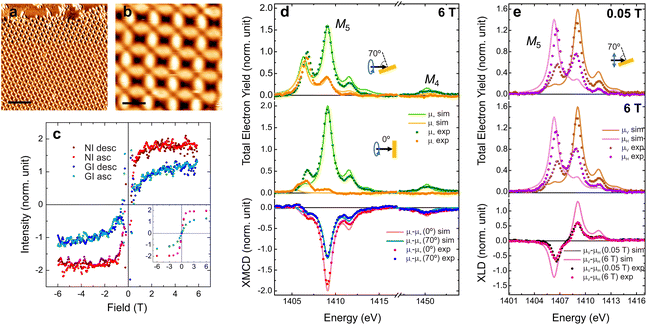Fig. 3 Characterization of the magnetic properties of the Er-TDA network on Cu(111). (a and b) STM images of the Er-TDA network on Cu(111). Scanning parameters: (a) V_b = 500 mV, I_t = 300 pA, T = 90 K, scale bar: 10 nm; (b) V_b = 500 mV, I_t = 300 pA, T = 90 K, scale bar: 2 nm. (c) Magnetization curves constructed by measuring the XMCD intensity at the most intense peak of the M₅-edge at NI (red) and GI (blue). Dark (light) dots represent the descending (ascending) branches. The inset shows field dependent measurements of the XMCD intensity for some selected fields (T = 1.7 K). See the ESI† for more details. (d) XAS spectra acquired with positive (μ₊, green dots) and negative (μ₋, orange dots) circularly polarized light and XMCD (μ₋–μ₊) taken at the Er M_4,5-edges at NI (red dots) and GI (blue dots) (B = 6 T, T = 1.7 K). (e) XAS spectra acquired with vertical (μ_V, brown dots) and horizontal (μ_H, purple dots) linearly polarized light and XLD (μ_V–μ_H) taken at the Er M₅-edge at GI at 0.05 T (black dots) and 6 T (pink dots) (T = 1.7 K). Multiplet calculations are presented in (d and e) together with the experimental data with brighter lines.

Regarding the magnetic properties, the higher intensity of the XMCD spectrum (see Fig. 3d) measured at normal incidence (NI, 0°) when compared to grazing incidence (GI, 70° respect to the surface normal) indicates an out-of-plane magnetization easy axis, in opposition to the nearly in-plane observed for Dy-TDA.¹⁹ The perpendicular anisotropy is confirmed by the magnetization curves (Fig. 3c). Besides the higher intensity, at NI the curve is squarer, saturating at a lower field than at GI. These results confirm that it is possible to tailor the magnetic anisotropy of metal–organic networks by metal exchange. Out-of-plane anisotropy was observed previously for Er trimers on Cu(111), while Er single atoms and dimers have in-plane anisotropy.²⁸ However, to our knowledge, this is the first report of a lanthanide metal–organic network with a magnetization easy axis perpendicular to the surface plane. Expectation values of spin (〈S_z〉), orbital (〈L_z〉) and total (〈J_z〉) magnetic moments (in units of ħ) are presented in Table 1, as also the total magnetic moment (m_T in units of μ_B), and the moment anisotropy (m_T = m_T(70°) − m_T(0°), as defined in the ESI†), obtained using the sum rules^29,30 for an Er³⁺ ion. The experimental value of J_z at NI indicates that the quantum number is J_z = 15/2, the maximum possible value for Er³⁺. According to the multiplet calculations the quantum numbers for this system are S_z = 3/2, L_z = 6 and J_z = 15/2, in agreement with the values obtained from the XMDC spectra measured at NI. The moment anisotropy of (−4.8 ± 1.5)μ_B is even higher (and of opposite sign) than the one measured in the Dy-TDA network.¹⁹

Table 1 Expectation values of spin (〈S_z〉), orbital (〈L_z〉) and total (〈J_z〉 = 〈S_z〉 + 〈L_z〉) moments, total magnetic moment (m_T = 2〈S_z〉 + 〈L_z〉) and moment anisotropy (Δm_T = m_T(70°) − m_T(0°) extracted by XMCD sum rules for normal (0°) and grazing (70°) incidences for Er centers on Er-TDA network on Cu(111)

Incidence angle (°)	0	70
〈Sz〉 (ħ)	1.8(2)	1.0(1)
〈Lz〉 (ħ)	6.0(6)	3.4(3)
〈Jz〉 (ħ)	7.8(8)	4.4(4)
m T (μB)	9.7(1.0)	5.4(5)
ΔmT (μB)	−4.8(1.5)

---

Fig. 3e shows that the XLD spectra feature a strong anisotropy due to the crystal field generated by the molecular network. XLD spectra measured with low and high applied magnetic fields (at 0.05 T and 6 T, respectively) are similar, both in shape and intensity. The XLD orientation is inverted when compared to Dy-TDA,¹⁹ as it can be expected for the different charge density of Er³⁺ ions with large J_z (prolate charge) when compared to Dy³⁺ (oblate charge).³ These charge densities are linked with the orientation and intensity of the magnetic moments. According to previous results for Dy-directed networks, the oblate charge of Dy³⁺ ions is associated with close to in-plane magnetic anisotropy.^19,20 In the case of Er³⁺ ions the prolate charge density can be related to an out-of-plane orientation of the magnetic anisotropy.²⁰ Accordingly, for the case of Er-TDA network the multiplet calculations indicate that the magnetic anisotropy is uniaxial and totally out-of-plane with a maximum J_z as expected for prolate Er³⁺ ions,³ which is further confirmed by the sum rule analysis.

In summary, we have investigated the structural, electronic and magnetic properties of an on-surface synthesized metal–organic network directed by Er atoms that are coordinated with TDA molecular linkers. Although the structure is analogous to the Dy-TDA nanoarchitecture, we observe a modification in the electronic and magnetic properties as a consequence of the metal exchange. The energy level alignment of the frontier states in Er-TDA is distinct from the Dy-TDA network. Moreover, the Er atoms present +3 oxidation state with strong charge anisotropy and high perpendicular magnetic anisotropy. The moment anisotropy is also significantly larger when compared to the Dy-TDA network.

Our results demonstrate that it is feasible to tune the magnetic anisotropy in isostructural supramolecular networks by metal exchange, increasing its magnitude and switching the magnetic easy axis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work received funding from the European Research Council (ERC, grant 766555), Marie Sklodowska-Curie Actions (MSCA, project 894924) under the European Union's Horizon 2020 Research and Innovation Programme, and the EMPIR Programme co-financed by the Participating States and the European and Union's Horizon 2020 Research and Innovation Programme (grant EMPIR 20FUN03 COMET). IMDEA Nanociencia acknowledges support from the “Severo Ochoa” Programme for Centres of Excellence in R&D (MINECO, Grant SEV-2016-0686). The ALBA synchrotron is acknowledged for providing beam time at BOREAS beamline (proposal number 2021025028).

References

1. E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104.
2. Z. Zhu, M. Guo, X.-L. Li and J. Tang, Coord. Chem. Rev., 2019, 378, 350–364.
3. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
4. F. Donati, S. Rusponi, S. Stepanow, C. Wäckerlin, A. Singha, L. Persichetti, R. Baltic, K. Diller, F. Patthey, E. Fernandes, J. Dreiser, Ž. Šljivančanin, K. Kummer, C. Nistor, P. Gambardella and H. Brune, Science, 2016, 352, 318–321.
5. F. D. Natterer, K. Yang, W. Paul, P. Willke, T. Choi, T. Greber, A. J. Heinrich and C. P. Lutz, Nature, 2017, 543, 226–228.
6. F. Donati and A. J. Heinrich, Appl. Phys. Lett., 2021, 119, 160503.
7. N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
8. N. Ishikawa, Polyhedron, 2007, 26, 2147–2153.
9. M. Studniarek, C. Wäckerlin, A. Singha, R. Baltic, K. Diller, F. Donati, S. Rusponi, H. Brune, Y. Lan, S. Klyatskaya, M. Ruben, A. P. Seitsonen and J. Dreiser, Adv. Sci., 2019, 6, 1901736.
10. L. Ruan, J. Tong, F. Luo, Y. Wu, G. Qin, X. Jiao and X. Zhang, Appl. Surf. Sci., 2022, 585, 152445.
11. C. Wäckerlin, F. Donati, A. Singha, R. Baltic, S. Rusponi, K. Diller, F. Patthey, M. Pivetta, Y. Lan, S. Klyatskaya, M. Ruben, H. Brune and J. Dreiser, Adv. Mater., 2016, 28, 5195.
12. V. Corradini, A. Candini, D. Klar, R. Biagi, V. De Renzi, A. Lodi Rizzini, N. Cavani, U. del Pennino, S. Klyatskaya, M. Ruben, E. Velez-Fort, K. Kummer, N. B. Brookes, P. Gargiani, H. Wende and M. Affronte, Nanoscale, 2018, 10, 277.
13. H. Wang, K. Wang, J. Tao and J. Jiang, Chem. Commun., 2012, 48, 2973–2975.
14. G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610.
15. P. Stoll, M. Bernien, D. Rolf, F. Nickel, Q. Xu, C. Hartmann, T. R. Umbach, J. Kopprasch, J. N. Ladenthin, E. Schierle, E. Weschke, C. Czekelius, W. Kuch and K. J. Franke, Phys. Rev. B, 2016, 94, 224426.
16. F. Habib, G. Brunet, V. Vieru, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 13242–13245.
17. J. J. Le Roy, L. Ungur, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2014, 136, 8003–8010.
18. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
19. S. O. Parreiras, D. Moreno, B. Cirera, M. A. Valbuena, J. I. Urgel, M. Paradinas, M. Panighel, F. Ajejas, M. A. Niño, J. M. Gallego, M. Valvidares, P. Gargiani, W. Kuch, J. I. Martínez, A. Mugarza, J. Camarero, R. Miranda, P. Perna and D. Écija, Small, 2021, 17, 2102753.
20. D. Moreno, S. O. Parreiras, J. I. Urgel, B. Muñiz-Cano, C. Martín-Fuentes, K. Lauwaet, M. Valvidares, M. A. Valbuena, J. M. Gallego, J. I. Martínez, P. Gargiani, J. Camarero, R. Miranda and D. Écija, Small, 2021, 18, 2107073.
21. R. Sbiaa, H. Meng and S. N. Piramanayagam, Phys. Status Solidi RRL, 2011, 5, 413–419.
22. S. Bhatti, R. Sbiaa, A. Hirohata, H. Ohno, S. Fukami and S. N. Piramanayagam, Mater. Today, 2017, 20, 530–548.
23. J. I. Urgel, B. Cirera, Y. Wang, W. Auwärter, R. Otero, J. M. Gallego, M. Alcamí, S. Klyatskaya, M. Ruben, F. Martín, R. Miranda, D. Ecija and J. V. Barth, Small, 2015, 11, 6358.
24. B. Cirera, L. Dordevic, R. Otero, J. M. Gallego, D. Bonifazi, R. Miranda and D. Ecija, Chem. Commun., 2016, 52, 11227.
25. A. Barla, J. Nicolas, D. Cocco, S. M. Valvidares, J. Herrero-Martın, P. Gargiani, J. Moldes, C. Ruget, E. Pellegrin and S. Ferrer, J. Synchrotron Radiat., 2016, 23, 1507.
26. A. Uldry, F. Vernay and B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125133.
27. A. Singha, R. Baltic, F. Donati, C. Wackerlin, J. Dreiser, L. Persichetti, S. Stepanow, P. Gambardella, S. Rusponi and H. Brune, Phys. Rev. B, 2017, 96, 224418.
28. A. Singha, F. Donati, C. Wäckerlin, R. Baltic, J. Dreiser, M. Pivetta, S. Rusponi and H. Brune, Nano Lett., 2016, 16, 3475–3481.
29. B. T. Thole, P. Carra, F. Sette and G. van der Laan, Phys. Rev. Lett., 1992, 68, 1943–1946.
30. P. Carra, B. T. Thole, M. Altarelli and X. Wang, Phys. Rev. Lett., 1993, 70, 694–697.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr07189d

‡ These authors contributed equally.

---